- 1State Key Laboratory of Networking and Switching Technology, Beijing University of Posts and Telecommunications, Beijing, China
- 2Henan Key Laboratory of Network Cryptography Technology, Zhengzhou, China
- 3Ruhr University Bochum, Bochum, Germany
Even-Mansour is one of the most important constructions in symmetric cryptography, both from a theoretical and practical perspective. With the rapid development of quantum computing, the security of Even-Mansour construction in quantum setting needs to be considered. For one round Even-Mansour construction, it is well settled by classical and quantum attacks. While for the iterated scheme, the situation is much more complex. In this paper, we study the next case in line in detail and depth: quantum attacks against two rounds case. We first make an asymptotic comparison with existing classical and quantum attacks. Then we give concrete resource estimation for the proposed quantum attacks on round reduced LED cipher and AES2. The resource estimation allows to deduce the most efficient attacks based on the trade-off of the number of qubits and Toffoli depth.
1 Introduction
The Even-Mansour (EM) construction [1] is a minimal block cipher that has been widely studied since its outstanding simplicity and provable classical security [1, 2]. It is made up of a n-bit public permutation P and two n-bit secret subkeys K1 and K2, i.e., E(x) = P (x ⊕ K1) ⊕ K2, where n is the block size. When P is a public random permutation, EM construction has been proven to be indistinguishable from a random permutation when D ⋅ T = Ω(2n), where D and T are the number of queries to the encryption oracle E(x) and permutation oracle P respectively. At EUROCRYPT 2012, Bogdanov et al. [3] studied EM construction into an r-round iterated EM scheme, which is defined as
where P1, … , Pr are r independent permutations and K1, … , Kr+1 are (r + 1) n-bit subkeys. This construction was proven to be secure up to 22n/3 queries against distinguishing attack for r ≥ 2 [3] and subsequently improved to 2rn/(r+1) queries [4, 5].
Recently, the security analysis of symmetric cryptography in quantum setting has also become a hot issue in cryptography research [6], in addition to quantum cryptography [7–10]. There are two different models for quantum cryptanalysis against symmetric cipher based on the notions for pseudorandom function security in quantum setting, standard security and quantum security [11]. The standard security and quantum security are also denoted as Q1 model and Q2 model respectively by Kaplan et al. [12]. In Q1 model, the adversaries could only access the encryption oracle classically but process data with quantum operations. While in Q2 model, the adversaries could query the encryption oracle with quantum superpositions and process data with quantum operations.
In 2012, Kuwakado and Morri [13] proposed a quantum key-recovery attack against EM construction in Q2 model. Compared with the classical key-recovery attack, the quantum attack can attain exponential acceleration. In other words, the EM construction has been broken in Q2 model. Very recently, at EUROCRYPT 2022, Alagic et al. [14] proved a lower bound that
At FSE 2013, Nikolić et al. [17] proposed the first nontrivial classical attack on 2EM1 construction which requires the time complexity of 2n ln n/n with 2n ln n/n known plaintexts. Later, Dinur et al. [18] improved this attack to reduce the data complexity to 2λn known plaintexts, where 0 < λ < 1. Meanwhile, they also presented an attack against 2EM3 construction with the time complexity of
Besides, there are also other quantum attacks against iterated EM construction such as the quantum slide attack on iterated EM construction with identical permutations and subkeys in Q2 model [12] and the quantum related-key attack against iterated EM cipher with identical permutations and independent subkeys in Q2 model [22]. However, these quantum attacks are in Q2 model and only consider iterated EM construction with identical permutations.
Contributions. in this paper, we study quantum key-recovery attacks against 2EM constructions. The main contributions of this paper include the following two aspects.
First, we consider the security of two-round Even-Mansour constructions with independent permutations in quantum setting. Several quantum key-recovery attacks on 2EM constructions are proposed. For 2EM1 construction, the presented quantum key-recovery attack adopts Grover algorithm [23] directly. Compared with the classical attack with optimal query complexity (including the queries to cipher and permutation), i.e., the observed by Leurent et al. [21], our attack reduces the query complexity by a factor of 2n/6. For 2EM2 and 2EM3 constructions, we consider Grover-meets-Simon algorithm [24] (GMS algorithm) and Offline Simon algorithm [25] (OS algorithm) on constructed functions. The proposed quantum attacks against 2EM2 and 2EM3 constructions require
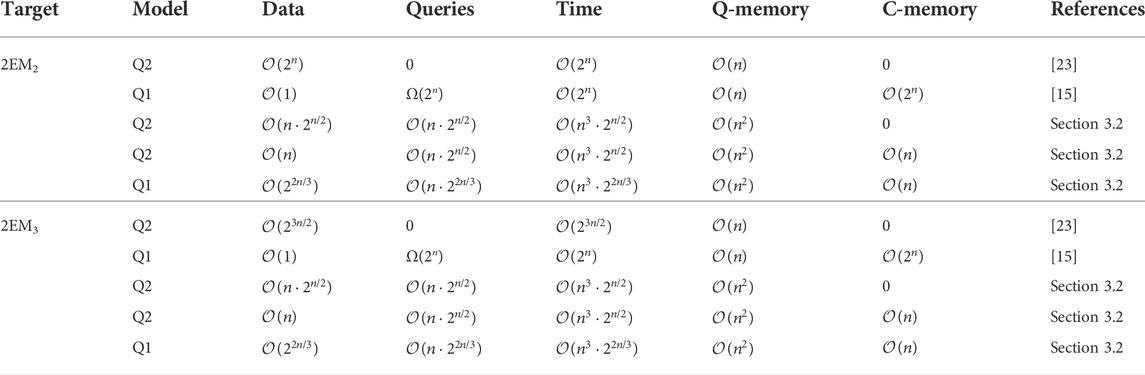
TABLE 1. Comparison of previous quantum attacks and our attacks on 2EM2 and 2EM3 constructions, where “Data” represents encryption queries, “Queries” signifies calls to Pi, “Q-memory” and “C-memory” denote quantum memory and classical memory respectively.
Second, we apply the presented quantum attacks on 2-step LED-64, 2-step LED-128 and full AES2. Then we design the quantum circuits for proposed attacks and give the corresponding resource estimation. According to the result of resource estimation, the cost imposed by the attacks based on GMS algorithm and attacks with OS algorithm in Q2 model is close. The extra overhead generated by the attacks based on GMS algorithm is mainly due to their more complex classifier oracles. Besides, the attacks based on OS algorithm in Q1 model cost more resources than corresponding attacks in Q2 model since the attacks in Q1 model require more iterations to search more bits exhaustively. Moreover, there is no doubt that the presented quantum attacks on 2-step LED-128 and AES2 cost much less than the corresponding Grover attacks, except for the number of qubits.
Organization. The rest of the paper is organized as follows. In the next section, some essential preliminaries are introduced. The quantum attacks on 2EM constructions and their application to specific ciphers are presented in Sect. 3. In Sect. 4, we give the quantum resource estimation of the proposed quantum attacks on corresponding ciphers. Finally, a short conclusion is given in Sect. 5.
2 Preliminaries
In this section, some relevant preliminaries are given.
2.1 Quantum algorithms
2.1.1 Grover algorithm
Problem 1. (Grover [23]). Assume that there exists only one marked item x′ in the N-scale unstructured datasets, the goal is to find x′, where N = 2n. In other words, let f: {0,1}n → {0, 1} be a function such that f(x) = 0 for all 0 ≤ x < 2n except x′, for which f(x′) = 1, find x′.To solve this problem, any deterministic classical algorithms need to make
Theorem 1. (Brassard et al. [26]). Let
while S0 changes the sign of zero state |0⟩ only. Finally, the measurement after the operation of

Algorithm 1. Grover algorithm [23]
2.1.2 Simon algorithm
Problem 2. (Simon [27]). Let f: {0,1}n → {0,1}n be a function. Promise that there exists s ∈ {0,1}n such that for any (x, y) ∈ {0,1}n,
2.1.3 Grover-meets-simon algorithm
Problem 3. (Leander et al. [24]). Let f: {0,1}m ×{0,1}n → {0,1}i be a function, where m is in
2.1.4 Offline Simon algorithm
Problem 4. (Bonnetain et al. [25]). Let f: {0,1}m ×{0,1}n → {0,1}l and g: {0,1}n → {0,1}l be functions, where m is in

Algorithm 2. Simon algorithm [27]
To solve this problem, we can adopt OS algorithm. The OS algorithm requires
2.2 Target ciphers
Next, we introduce three ciphers that belong to 2EM1, 2EM2 and 2EM3 constructions respectively.
2.2.1 LED
At CHES 2011, Guo et al. [29] proposed a 64-bit resource-constrained block cipher named LED. The step function Fi of LED is a 4-round AES-like permutation where the addition of the subkeys is replaced with addition of constants. There are two primary variants of LED.LED − 64 uses a 64-bit key in each step as a subkey and the number of steps is 8. It is clear that 2-step LED-64 belongs to 2EM1 construction.LED − 128 divides a 128-bit key into K1‖K2 as the subkeys alternatively and the number of steps is 12. Obviously, 2-step LED-128 belongs to 2EM2 construction.

Algorithm 3. Grover-meets-Simon algorithm [24]
2.2.2 AES2
AES2 is a 128-bit cipher designed by Bogdanov et al. [3] at EUROCRYPT 2012. It belongs to 2EM3 construction, where each of the public permutations P1 and P2 is based on an invocation of full AES-128 with a pre-fix and publicly known key. The subkeys are composed of three independently chosen 128-bit secret subkeys K1, K2 and K3.
3 Quantum attacks
In this section, several quantum key-recovery attacks on 2EM1, 2EM2 and 2EM3 constructions and the corresponding applications are given.
3.1 Quantum key-recovery Attack on 2EM1 construction
Based on 2EM1 construction, the function E1(x) = P2 (P1(x ⊕ K) ⊕ K) ⊕ K is obtained. In such a case, we adopt Grover algorithm on this function directly. Therefore, the query complexity and time complexity of this attack are both

Algorithm 4. Offline Simon algorithm [25]
3.1.1 The Application to 2-step LED-64
We can attack 2-step LED-64 by applying Grover algorithm on E(x) = F2(F1(x ⊕ K) ⊕ K) ⊕ K directly, where the block size is 64. Thus, the attack requires the query and time complexities of 232. The comparison of attacks against 2-step LED-64 is summarized in Table 2.

TABLE 2. Comparison of attacks against 2-step LED-64. Assume that one evaluation of the cipher as one complexity unit and the evaluation of one permutation costs 1/2 unit.
3.2 Quantum key-recovery Attacks on 2EM2 and 2EM3 constructions
For 2EM2 construction, we consider the function
It is easily seen that f (i, x) has the period K1 when i = K2 since
Therefore, we can employ GMS algorithm on f (i, x) to recover K1 and K2 which requires the query complexity of
Furthermore, the recovery of subkeys K1 and K2 can also be reduced to Problem 4 by defining functions f: {0,1}n ×{0,1}n → {0,1}n and g: {0,1}n → {0,1}n as
Similarly, we can obtain that
when i = K2. Then we can recover all subkeys with OS algorithm. In such a case, the quantum attack requires
On the other hand, we can also solve this problem with OS algorithm in Q1 model if the cryptographic function E2(x) can be accessed only classically. Now the functions f: {0,1}n+(n−u) ×{0,1}u → {0,1}n (0 ≤ u ≤ n) and g: {0,1}u → {0,1}n are defined as
obviously,
where the subkey
The quantum key-recovery attack against 2EM3 construction is similar to the case of 2EM2 construction, except that the functions we considered here are
Finally, we can easily obtain the value of K3 with additional encryption after recovering subkeys K1 and K2. Hence, the query and time complexities of the quantum attacks on 2EM3 construction are the same as the case of 2EM2 construction.
3.2.1 The applications to 2-step LED-128 and AES2
According to the structure of 2-step LED-128, we can obtain the cryptographic function
where |K1| = |K2| = 64. In order to attack 2-step LED-128, we consider the function
in Problem 3. Now, we can adopt GMS algorithm on f (i, x) directly. Hence, this attack requires the query complexity of 239 and time complexity of 250.
Furthermore, we can also utilize OS algorithm to recover K1 and K2 of 2-step LED-128. First, we define the functions
Then the subkeys can be recovered with OS algorithm on f (i, x) and g(x). The quantum attack requires 26 quantum queries to E(x), 238 quantum queries to f (i, x) and time complexity of 250. On the other hand, we can also consider functions
and apply OS algorithm on f (i‖j, x) and g(x) in Q1 model when E(x) can be queried only classically. In such a case, the quantum attack requires 247 classical queries to E(x), 246.5 quantum queries to f (i‖j, x) and time complexity of 258.5 when u = 47. The comparison of quantum attacks against 2-step LED-128 is summarized in Table 3.
In order to attack AES2, we need to construct functions in the case of 2EM3 construction described in Section 3.2 with block size 128. Thus, the subkeys of AES2 can be recovered by GMS algorithm with the query complexity of 272 and time complexity of 285. Furthermore, we can also attack AES2 with OS algorithm in Q1 and Q2 model respectively. In Q1 model, the attack requires 290 classical queries to E(x), 290 quantum queries to f (i‖j, x) and the time complexity of 2104 when u = 90. In Q2 model, the attack requires 27 quantum queries to E(x), 271 queries to f (i, x) and the time complexity of 285. The comparison of attacks against AES2 is summarized in Table 4.
Tables 3 and 4 show that the quantum attacks we proposed in Q1 and Q2 models are more efficient than existing classical and quantum attacks in time complexity and query complexity when we consider queries of cryptographic function and public permutations, except that more qubits are needed.
4 Resource estimation
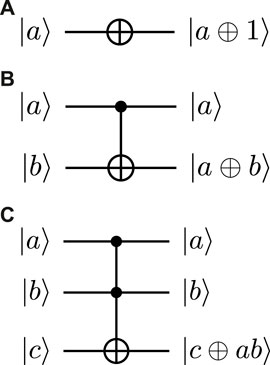
We first give some quantum gates that are used in quantum implementations of classical circuits in Figure 1. Note that the last qubit is target qubit and other qubits are control qubits in CNOT and Toffoli gates.
4.1 Resource estimation of target ciphers
Next, we give the quantum resource estimation of 2-step LED-64, 2-step LED-128 and AES2 respectively.
4.1.1 Resource estimation of 2-step LED-64 and 2-step LED-128
The internal state of LED contains 64 bits, arranged in 16 nibbles. Each nibble represents an element from GF(24) with the underlying polynomial for field multiplication given by X4 + X + 1. The step function Fi of LED cipher is a 4-round AES-like permutation. Each of these four rounds consists of operations AddConstants, SubCells, ShiftRows and MixColumnsSerial.
AddConstants. The operation consists of XOR-ing of a 32-bit round constant to the internal state of LED. Thus, it can be realized by using 32 NOT gates in quantum circuit.
SubCells. LED cipher uses a 4-bit to 4-bit S-box of PRESENT [30], which is applied in parallel 16 times to the internal state of LED. According to Algorithm 3 of Ref. [31], the quantum circuit of the S-box is redesigned in Figure 2, which requires Toffoli depth 19, 19 Toffoli gates, 5 CNOT gates, 2 NOT gates and 5 qubits. Therefore, we can obtain the resource estimation of SubCells by multiplying the resources of the S-box by 16, except for the Toffoli depth since that these 16 S-boxes are applied in parallel.

FIGURE 2. Quantum circuit of S-box used in SubCells: |a⟩|0⟩ → |S(a)⟩|0⟩, where |a3⟩ is the most significant qubit.
ShiftRows. After the operation ShiftRows, the internal state is changed into a special permutation. Hence, we do not have to perform any operation for the quantum circuit of ShiftRows since it corresponds to a permutation of qubits. In this case, we only need to adjust the position of subsequent operations to ensure that the correct input wire is used.
MixColumnsSerial. The MixColumnsSerial performs four applications of matrix A, which is equivalent to matrix M:
The first scheme of implementing MixColumnsSerial is to realize matrix A. In order to design the quantum circuit of matrix A, the quantum circuit of operations 2 and 4 in A should be considered first. It is easy to obtain that 2 ⋅ (a3, a2, a1, a0) = (a2, a1, a3 ⊕ a0, a3) and 4 ⋅ (a3, a2, a1, a0) = (a1, a3 ⊕ a0, a3 ⊕ a2, a2). Hence, the implementation of operations 2 and 4 cost 1 and 2 CNOT gates respectively. Now, we can design the quantum circuit of matrix A based on operations 2 and 4 in Figure 3.

FIGURE 3. Quantum circuit of matrix A, where U2 and U4 are quantum circuits of operations 2 and 4 respectively.
According to Figure 3, we can derive that the quantum circuit of matrix A requires (2 + 4 + 6 + 6) × 4 = 72 CNOT gates. Thus, the resource estimation for operation MixColumnsSerial is 72 × 4 = 288 CNOT gates.
The second scheme is to consider the matrix M directly. From SageMath [32], we can obtain the PLU decomposition
Similarly, we can easily obtain that 6 ⋅ (a3, a2, a1, a0) = (a2 ⊕ a1, a3 ⊕ a1 ⊕ a0, a2 ⊕ a0, a3 ⊕ a2) and 9 ⋅ (a3, a2, a1, a0) = (a0, a3, a2, a1 ⊕ a0), which can be achieved with 5 and 1 CNOT gates respectively. Then, we can know that the matrix L and U require 4×([(1 + 4 + 1) + (5 + 4 + 5) + (1 + 4 + 1)] + [(5 + 4 + 5) + (1 + 4 + 1)] + (1 + 4 + 1)) = 208 and 4 × ([2 + 4 + (1 + 4 + 1) + (1 + 4 + 1)] + [2 + 4 + (1 + 4 + 1)] + (2 + 4) + 2) = 152 CNOT gates respectively. Therefore, the resource estimation for operation MixColumnsSerial is 208 + 152 = 360 CNOT gates in second scheme. Comparing these two schemes, we adopt first one to implement the operation MixColumnsSerial since it requires fewer CNOT gates.
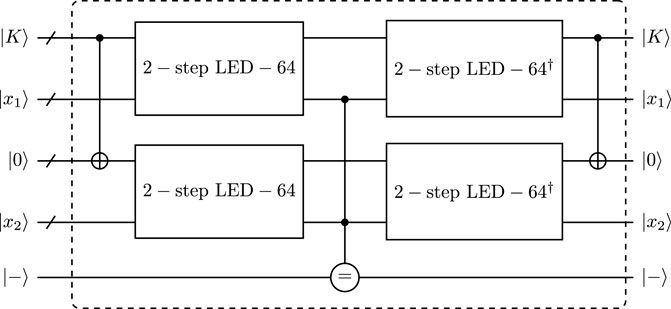
Taking all these into consideration, we can derive that the resource estimation of one round AES-like permutation costs Toffoli depth 19, 304 Toffoli gates, 368 CNOT gates, 64 NOT gates and 80 qubits. Then the quantum circuits of 2-step LED-64 and 2-step LED-128 are presented in Figure 4. In such a case, the quantum circuit of 2-step LED-64 requires Toffoli depth 152, 2432 Toffoli gates, 3136 CNOT gates, 512 NOT gates and 144 qubits. The quantum circuit of 2-step LED-128 costs Toffoli depth 152, 2432 Toffoli gates, 3136 CNOT gates, 512 NOT gates and 208 qubits.
FIGURE 4. Quantum circuit of (A) 2-step LED-64 and (B) 2-step LED-128, here ancilla qubits are not represented.
4.1.2 Resource estimation of AES2
The construction of AES2 is defined by fixing two randomly chosen 128-bit AES-128 keys, which specify the permutations P1 and P2. The subkeys are comprised of three independently chosen 128-bit secret keys K1, K2 and K3. Let AES[K] denotes the whole AES-128 encryption with the 128-bit key K. Hence, the encryption of AES2 is defined as
where two 128-bit keys π1 and π2 are defined based on the first 256 bits of the binary digit expansion of π. Recently, the implementation of AES quantum circuit received more and more attention [33–35]. Based on the fewer qubits principle, we take the quantum circuit of AES-128 from Ref. [35] for quntum circuit design of AES2. As shown in Figure 5A, this quantum circuit costs Toffoli depth 11008, 16508 Toffoli gates, 81652 CNOT gates, 1072 NOT gates and 270 qubits. In Ref. [35], the XOR of a 128-bit plaintext in first round of AES-128 is considered as XOR-ing of a 128-bit constant, which is achieved by performing 128 NOT gates on the key of AES-128 first and then canceled by 128 NOT gates again. However, the 128-bit plaintext is a quantum superposition in our proposed quantum attacks. Hence, we need to adopt 128 × 2 CNOT gates instead of 128 × 2 NOT gates here. Therefore, the quantum circuit of AES-128 used in the quantum circuit design of AES2 requires Toffoli depth 11008, 16508 Toffoli gates, 81908 CNOT gates, 816 NOT gates and 270 qubits. In such a case, we can easily design the quantum circuit of AES2 in Figure 5B and obtain the resource estimation of AES2 with Toffoli depth 22016, 33016 Toffoli gates, 164328 CNOT gates, 1632 NOT gates and 1038 qubits. Note that the ancilla qubits involved in first AES quantum circuit can be reused in second AES quantum circuit.
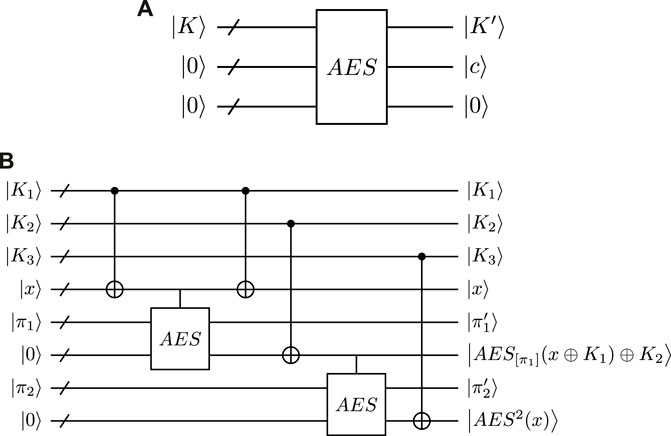
FIGURE 5. Quantum circuit of (A) AES, where the box of AES means the quantum circuit of AES-128 in Ref. [35], K′ is the subkey of the 10th round in AES and c is the ciphertext; (B) AES2, where the vertical line above the AES box indicates that 128 × 2 CNOT gates are performed instead of 128 × 2 NOT gates in the quantum circuit of AES-128. The ancilla qubits and unused outputs are not represented.
4.2 Resource estimation of Grover algorithm on 2-step LED-64
In order to adopt Grover algorithm on 2-step LED-64, we need to design the Grover oracle for 2-step LED-64 first. When designing the Grover oracle, the number of plaintext-ciphertext pairs required to recover the correct key uniquely should be considered. At EUROCRYPT 2020, Jaques et al. [34] stated that when the number of required plaintext-ciphertext pairs
Hence, the number of required plaintext-ciphertext pairs for 2-step LED-64 should be ν ≥ 1 since m = n = 64. Then the probability of finding a unique key is around 0.37 for ν = 1. For ν = 2, the probability is about 0.99. Thus, we consider the case of ν = 2 when designing the Grover oracle for 2-step LED-64. Therefore, the quantum circuit of the Grover oracle for 2-step LED-64 is illustrated in Figure 6, which requires Toffoli depth 317, 9981 Toffoli gates, 12672 CNOT gates, 2304 NOT gates and 383 qubits. In the quantum circuit of Grover oracle for 2-step LED-64, each comparison of n-bit known ciphertext and n-qubit output of 2-step LED-64 oracle requires Toffoli depth
In the process of Grover algorithm,
4.3 Resource estimation of proposed quantum attacks on 2-step LED-128 and AES2
The resource estimation of proposed quantum attacks on 2-step LED-128 and AES2 can be considered in a similar way as Grover algorithm since that Grover algorithm, GMS algorithm and OS algorithm all need to perform an iterative operator. Thus, we should consider the resource estimation of iterative oracle for target ciphers first. Here, the resource estimation of constructed functions for target ciphers in proposed quantum attacks is given in Table 5 and the corresponding quantum circuits see Supplementary A.
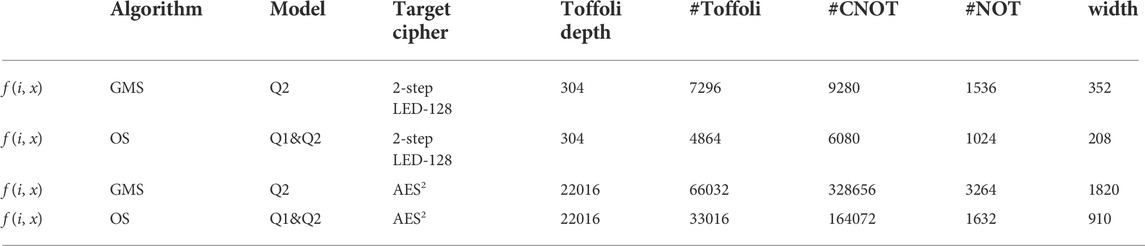
TABLE 5. Resource estimation for constructed functions of target ciphers, where #Toffoli/CNOT/NOT represents the number of Toffoli gates, CNOT gates and NOT gates respectively.
Now, the quantum circuits of iterative oracle for GMS algorithm and OS algorithm are designed in Figure 7 and Figure 8 respectively.
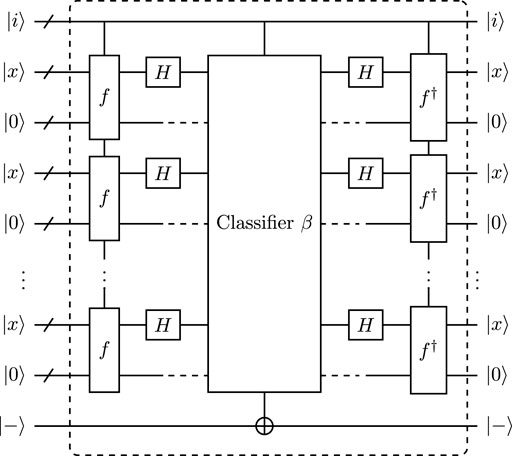
FIGURE 7. Iterative oracle for GMS algorithm, the quantum circuit for classifier β is given in Supplementary Figure S5 of Supplementary B.
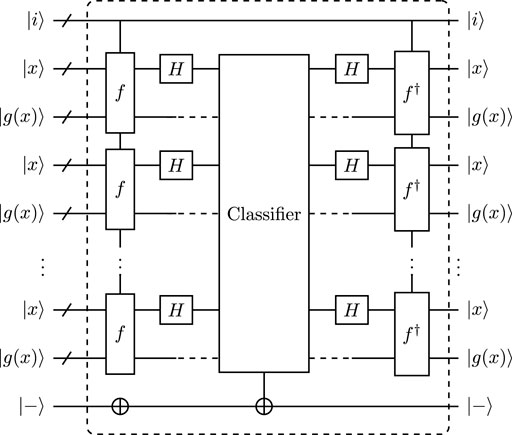
FIGURE 8. Iterative oracle for OS algorithm, the quantum circuit for classifier is provided in Supplementary Figure S6 of Supplementary B.
In Figure 7, the classifier β for GMS algorithm contains Test 1 and Test 2 (see also Supplementary Figure S5 of Supplementary B). When both two test conditions are satisfied, the phase of target qubit will be flipped. Test 1 of classifier β. The Test 1 of classifier β includes the checking of dim (⟨u1, … , uℓ⟩) and the calculation of candidate period s′. The first phase includes the computation of triangular basis and the rank checking of triangular basis. Based on Algorithm 4 of Ref. [36], we can obtain that the computation of triangular basis requires Toffoli depth
since
where t = 1, 2, … , 282 in Supplementary Figure S8. Here |i⟩ and |s′⟩ are not included in the qubits.
Hence, the classifier β for 2-step LED-128 costs
where |u1⟩, |u2⟩, ⋯ , |uℓ⟩ and |i⟩ are not included in the qubits. The classifier β for AES2 costs
Altogether, the resource estimation for iterative oracle of GMS algorithm is summarized in Table 6.

TABLE 6. Resource estimation for iterative oracle of GMS algorithm and OS algorithm, where Clifford gate denotes the CNOT gate and Hadamard gate.
In Supplementary Figure S6 of Supplementary B, the classifier oracle of OS algorithm consists of the computation of triangular basis and rank checking. Therefore, the classifier oracle costs Toffoli depth
Similarly,
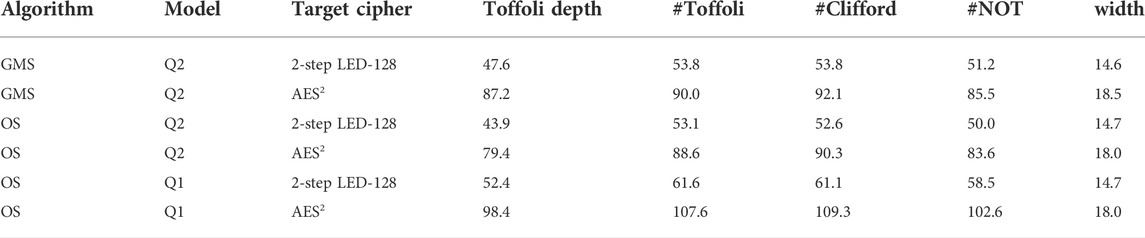
TABLE 7. Resource estimation for proposed quantum attacks on target ciphers, where all figures are in log base 2. The values of u of OS algorithm in Q1 model for 2-step LED-128 and AES2 are 47 and 90, respectively.
Besides, it is worth noting that the resource estimation for OS algorithm in Q1 model should also consider the cost of preparing the quantum state
costs Toffoli depth
5 Conclusion
In this study, we consider the security of two-round Even-Mansour constructions in quantum setting. Compared with the classical attack with optimal query complexity, the presented quantum key-recovery attack on 2EM1 construction reduces the query complexity by a factor of 2n/6. For 2EM2 and 2EM3 constructions, we design quantum key-recovery attacks in Q1 and Q2 model respectively. The comparison in Table 2 shows that our attacks are more efficient than Grover search and QMITM attack no matter in Q1 or Q2 model. Furthermore, we also give the applications of proposed quantum attacks and analyze the corresponding resource estimation.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author contributions
These authors contributed equally to this work.
Funding
This work was supported by National Natural Science Foundation of China (Grant Numbers 61972048, 61976024), Henan Key Laboratory of Network Cryptography Technology (LNCT2021-A10), BUPT Excellent Ph.D. Students Foundation (Grant Number CX2019207) and China Scholarship Council (Grant Number 202006470082).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2022.1028014/full#supplementary-material
References
1. Even S, Mansour Y. A construction of a cipher from a single pseudorandom permutation. J Cryptology (1997) 10(3):151–61. doi:10.1007/s001459900025
2. Orr D, Keller N, Shamir A. Minimalism in cryptography: The even-mansour scheme revisited. In: D Pointcheval, and T Johansson, editors. Advances in cryptology - EUROCRYPT 2012 - 31st annual international conference on the theory and applications of cryptographic techniques. Cambridge, UK: Springer (2012). p. 336–54. April 15-19, 2012. Proceedings, volume 7237 of Lecture Notes in Computer Science.
3. Bogdanov A, Knudsen LR, Leander G, Standaert F-X, Steinberger JP, Tischhauser E. Key-alternating ciphers in a provable setting: Encryption using a small number of public permutations - (extended abstract). In: D Pointcheval, and T Johansson, editors. Advances in cryptology - EUROCRYPT 2012 - 31st annual international conference on the theory and applications of cryptographic techniques. Cambridge, UK: Springer (2012). p. 45–62. April 15-19, 2012. Proceedings, volume 7237 of Lecture Notes in Computer Science.
4. Lampe R, Patarin J, Seurin Y. An asymptotically tight security analysis of the iterated even-mansour cipher. In: X Wang, and K Sako, editors. Advances in cryptology - ASIACRYPT 2012 - 18th international conference on the theory and application of cryptology and information security. Beijing, China: Springer (2012). p. 278–95. December 2-6, 2012. Proceedings, volume 7658 of Lecture Notes in Computer Science.
5. Chen S, Steinberger JP. Tight security bounds for key-alternating ciphers. In: PQ Nguyen, and E Oswald, editors. Advances in cryptology - EUROCRYPT 2014 - 33rd annual international conference on the theory and applications of cryptographic techniques. Copenhagen, Denmark: Springer (2014). p. 327–50. May 11-15, 2014. Proceedings, volume 8441 of Lecture Notes in Computer Science.
6. Jordan SP, Liu Y-K. Quantum cryptanalysis: Shor, grover, and beyond. IEEE Secur Priv (2018) 16(5):14–21. doi:10.1109/msp.2018.3761719
7. Bennett CH, Brassard G. Quantum cryptography: Public key distribution and coin tossing (2020). arXiv preprint arXiv:2003.06557.
8. Deng FG, Long GL. Bidirectional quantum key distribution protocol with practical faint laser pulses. Phys Rev A (2004) 70(1):012311. doi:10.1103/PhysRevA.70.012311
9. Ye T-Y, Li H-K, Hu J-L. Semi-quantum key distribution with single photons in both polarization and spatial-mode degrees of freedom. Int J Theor Phys (Dordr) (2020) 59(9):2807–15. doi:10.1007/s10773-020-04540-y
10. Ye T-Y, Geng M-J, Xu T-J, Chen Y. Efficient semiquantum key distribution based on single photons in both polarization and spatial-mode degrees of freedom. Quan Inf Process (2022) 21(4):123–1. doi:10.1007/s11128-022-03457-1
11. Zhandry M. How to construct quantum random functions. In: 53rd annual IEEE symposium on foundations of computer science. New Brunswick, NJ, USA: FOCSIEEE Computer Society (2012). p. 679–87. October 20-23, 2012.
12. Kaplan M, Leurent G, Anthony L, Naya-Plasencia M. Breaking symmetric cryptosystems using quantum period finding. In: M Robshaw, and J Katz, editors. Advances in cryptology - CRYPTO 2016 - 36th annual international cryptology conference. Santa Barbara, CA, USA: Springer (2016). p. 207–37. August 14-18, 2016, Proceedings, Part II, volume 9815 of Lecture Notes in Computer Science.
13. Kuwakado H, Morii M. Security on the quantum-type even-mansour cipher. In: Proceedings of the international symposium on information theory and its applications, ISITA 2012. Honolulu, HI, USA: IEEE (2012). p. 312–6. October 28-31, 2012.
14. Alagic G, Chen B, Katz J, Majenz C. Post-quantum security of the even-mansour cipher. In: Orr dunkelman and stefan DziembowskiAdvances in cryptology - EUROCRYPT 2022 - 41st annual international conference on the theory and applications of cryptographic techniques. Trondheim, Norway: Springer (2022). p. 458–87. May 30 - June 3, 2022, Proceedings, Part III, volume 13277 of Lecture Notes in Computer Science.
16. Brassard G, Høyer P, Tapp A. Quantum cryptanalysis of hash and claw-free functions. In: CL Lucchesi, and AV Moura, editors. Latin ’98: Theoretical informatics, third Latin American symposium. Campinas, Brazil: Springer (1998). p. 163–9. April, 20-24, 1998, Proceedings, volume 1380 of Lecture Notes in Computer Science.
17. Nikolic I, Wang L, Wu S. Cryptanalysis of round-reduced LED. IACR Cryptol Eprint Arch (2015) 429.
18. Dinur I, Orr D, Keller N, Shamir A. Key recovery attacks on 3-round even-mansour, 8-step led-128, and full AES2. In: K Sako, and P Sarkar, editors. Advances in cryptology - ASIACRYPT 2013 - 19th international Conference on the Theory and Application of Cryptology and information security. Bengaluru, India: Springer (2013). p. 337–56. December 1-5, 2013, Proceedings, Part I, volume 8269 of Lecture Notes in Computer Science.
19. Dinur I, Orr D, Keller N, Shamir A. Key recovery attacks on iterated even-mansour encryption schemes. J Cryptol (2016) 29(4):697–728. doi:10.1007/s00145-015-9207-3
20. Isobe T, Shibutani K. New key recovery attacks on minimal two-round even-mansour ciphers. In: T Takagi, and T Peyrin, editors. Advances in cryptology - ASIACRYPT 2017 - 23rd international Conference on the Theory and Applications of Cryptology and information security. Hong Kong, China: Springer (2017). p. 244–63. December 3-7, 2017, Proceedings, Part I, volume 10624 of Lecture Notes in Computer Science.
21. Leurent G, Sibleyras F. Low-memory attacks against two-round even-mansour using the 3-xor problem. In: S Barbara, editor. Alexandra boldyreva and daniele MicciancioAdvances in cryptology - CRYPTO 2019 - 39th annual international cryptology conference. CA, USA: Springer (2019). p. 210–35. August 18-22, 2019, Proceedings, Part II, volume 11693 of Lecture Notes in Computer Science.
22. Hosoyamada A, Aoki K. On quantum related-key attacks on iterated even-mansour ciphers. IEICE Trans Fundamentals (2019) 102(1):27–34. doi:10.1587/transfun.e102.a.27
23. Grover LK. A fast quantum mechanical algorithm for database search. In: GL Miller, editor. Proceedings of the twenty-eighth annual ACM symposium on the theory of computing. Philadelphia, Pennsylvania, USA: ACM (1996). p. 212–9. May 22-24, 1996.
24. Leander G, May A. Grover meets simon - quantumly attacking the fx-construction. In: T Takagi, and T Peyrin, editors. Advances in cryptology - ASIACRYPT 2017 - 23rd international Conference on the Theory and Applications of Cryptology and information security. Hong Kong, China: Springer (2017). p. 161–78. December 3-7, 2017, Proceedings, Part II, volume 10625 of Lecture Notes in Computer Science.
25. Bonnetain X, Hosoyamada A, Naya-Plasencia M, Sasaki Y, Schrottenloher A. Quantum attacks without superposition queries: The offline simon’s algorithm. In: SD Galbraith, and S Moriai, editors. Advances in cryptology - ASIACRYPT 2019 - 25th international Conference on the Theory and Application of Cryptology and information security. Kobe, Japan: Springer (2019). p. 552–83. December 8-12, 2019, Proceedings, Part I, volume 11921 of Lecture Notes in Computer Science.
26. Brassard G, Hoyer P, Mosca M, Tapp A. Quantum amplitude amplification and estimation. Contemp Math (2002) 305:53–74. doi:10.1090/conm/305/05215
27. Simon DR. On the power of quantum computation. SIAM J Comput (1997) 26(5):1474–83. doi:10.1137/s0097539796298637
28. Kilian J, Rogaway P. How to protect DES against exhaustive key search. In: K Neal, editor. Advances in cryptology - CRYPTO ’96, 16th annual international cryptology conference. Santa Barbara, California, USA: Springer (1996). p. 252–67. August 18-22, 1996, Proceedings, volume 1109 of Lecture Notes in Computer Science.
29. Guo J, Peyrin T, Poschmann A, Matthew JB. Robshaw. The LED block cipher. In: Bart preneel and tsuyoshi TakagiCryptographic hardware and embedded systems - CHES 2011 - 13th international workshop. Nara, Japan: Springer (2011). p. 326–41. September 28 - October 1, 2011, Proceedings, volume 6917 of Lecture Notes in Computer Science.
30. Bogdanov A, Knudsen LR, Leander G, Paar C, Poschmann A, Matthew J, et al. Present: An ultra-lightweight block cipher. In: Pascal paillier and ingrid VerbauwhedeCryptographic hardware and embedded systems - CHES 2007, 9th international workshop. Vienna, Austria: Springer (2007). p. 450–66. September 10-13, 2007, Proceedings, volume 4727 of Lecture Notes in Computer Science.
31. Rahman M, Paul G. Grover on present: Quantum resource estimation. In: IACR cryptol. ePrint arch. (2021). p. 1655.
33. Zou J, Wei Z, Sun S, Liu X, Wu W. Quantum circuit implementations of AES with fewer qubits. In: S Moriai, and H Wang, editors. Advances in cryptology - ASIACRYPT 2020 - 26th international Conference on the Theory and Application of Cryptology and information security, daejeon. South Korea: Springer (2020). p. 697–726. December 7-11, 2020, Proceedings, Part II, volume 12492 of Lecture Notes in Computer Science.
34. Jaques S, Naehrig M, Roetteler M, Virdia F. Implementing grover oracles for quantum key search on AES and lowmc. In: A Canteaut, and Y Ishai, editors. Advances in cryptology - EUROCRYPT 2020 - 39th annual international conference on the theory and applications of cryptographic techniques. Zagreb, Croatia: Springer (2020). p. 280–310. May 10-14, 2020, Proceedings, Part II, volume 12106 of Lecture Notes in Computer Science.
35. Li ZQ, Cai BB, Sun HW, Liu HL, Wan LC, Qin SJ, et al. Novel quantum circuit implementation of advanced encryption standard with low costs. Sci China Phys Mech Astron (2022) 65(9):290311–6. doi:10.1007/s11433-022-1921-y
36. Bonnetain X, Jaques S. Quantum period finding against symmetric primitives in practice. IACR Trans Cryptogr Hardw Embed Syst (2022) 2022(1):1–27. doi:10.46586/tches.v2022.i1.1-27
Keywords: even-mansour, grover algorithm, grover-meets-simon algorithm, offline simon algorithm, resource estimation
Citation: Cai B, Gao F and Leander G (2022) Quantum attacks on two-round even-mansour. Front. Phys. 10:1028014. doi: 10.3389/fphy.2022.1028014
Received: 25 August 2022; Accepted: 20 September 2022;
Published: 18 October 2022.
Edited by:
Tianyu Ye, Zhejiang Gongshang University, ChinaReviewed by:
Gang Xu, North China University of Technology, ChinaYefeng He, Xi’an University of Posts and Telecommunications, China
Jun Zhu, Guangxi Normal University, China
Copyright © 2022 Cai, Gao and Leander. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Gregor Leander, Z3JlZ29yLmxlYW5kZXJAcnViLmRl
 BinBin Cai
BinBin Cai Fei Gao
Fei Gao Gregor Leander3*
Gregor Leander3*