- State Key Laboratory for Mesoscopic Physics and Frontiers Science Center for Nano-optoelectronics, School of Physics, Peking University, Beijing, China
Based on the time-dependent density functional theory, we theoretically investigate the influence of mechanical strains on the high-order harmonic generation (HHG) in the monolayer hexagonal boron nitride (hBN) crystal. We show that mechanical strains can largely modify the band structure and facilitate the harmonic emission. Compared to uniaxial strains, we find that biaxial strains may enhance the HHG yield significantly, and the HHG spectroscopy generated by a linearly polarized laser is closely related to the symmetry of the deformed hBN. Moreover, when driven by a circularly polarized laser, we find that the appearance of the 3n-order harmonics manifests the restoration of the three-fold rotational symmetry. Our results will be useful in controlling the HHG spectroscopy and probing lattice deformations in crystals.
1 Introduction
Since the high-order harmonic generation (HHG) from the bulk ZnO was first observed in 2010 [1], much attention has been paid to the HHG from crystalline solids, which may provide a direct access to high-efficiency and high-stability light sources [2]. State-of-the-art experiments have recorded HHG in various condensed-matter systems [3–7], providing a great opportunity to all-optically image the electronic structure and ultrafast processes [5], such as valance charge imaging [4], energy band reconstruction [3, 8], Berry curvature measurement [6, 9], lattice symmetry probe [9–11] and transition moment visualization [12]. Due to the complicated interaction between solids and the intense laser field, the HHG mechanism from solids can not be sufficiently explained by the atomic three-step model [13]. At a basic level, interband and intraband transitions were demonstrated to be critical for solid HHG [14]. Up-to-now, the coupling mechanism between interband and intraband processes has not been fully understood, and more importantly, a general rule to manipulate the solid-state harmonics has not yet been proposed.
Among various solid-state materials, the ability to continuously tune the electronic structure is one of the most attractive properties of two-dimensional (2D) materials. The atomic thickness of 2D materials makes their electronic and optical properties very sensitive to external perturbations [15]. The HHG from 2D materials brings some distinctive features. For example, it has been demonstrated both experimentally [6] and theoretically [16] that the HHG from the isolated monolayer MoS2 is more efficient than that from its bulk forms. Also, it is found that the even-order HHG in the monolayer MoS2 is predominantly polarized perpendicular to the pump field, which is caused by the intraband anomalous transverse current arising from the Berry curvature of the material [6]. The HHG in the monolayer graphene shows an anomalous dependence on the laser ellipticity [7]. The monolayer hBN can generate bulk-like harmonics when it is driven by an in-plane polarized laser field, and atomic-like harmonics when driven by an out-of-plane polarized pulse [15–17]. In addition, Yu et al. [17] investigated the double-plateau structure of the HHG spectrum in the bilayer hBN crystal with the driven laser pulse at grazing incidence. They found that the photon energy of the second plateau far beyond atomic-like harmonics can be well explained by the inclusion of backscattering of ionized electrons.
In addition to modulate laser parameters, tailoring the electronic structure of solid-state materials has also been proven to be a powerful way to control the HHG. For example, this can be achieved by doping [18, 19] or growing nanostructures on the surface [20, 21], lowering the dimensionality of the material [6, 16], and changing the layer stack [16, 22, 23]. It is worth mentioning that the mechanical engineering is one of the most commonly used methods to tune the lattice deformation, band gap and the carrier effective mass, providing an effective way to change the transition temperature of the ferromagnetic-paramagnetic [24, 25], metal-insulator [26] and superconductor [27, 28]. Interestingly, the semiconductor-metal transition in the thin film MoTe2 can be realized at room temperature by applying tensile strains [29, 30].
Strain engineering, as a traditional low-cost route to manipulate the electronic structure, has been widely used in material sciences. By imposing strains, e.g., stretching or compressing the lattice structure, the device performance as well as optical properties can be effectively regulated [31, 32]. Therefore, it does stand to reason that tailoring the HHG from solid-state materials can also be achieved by applying strains. So far, to the best of our knowledge, controlling the HHG from 2D materials via strains remains seldom explored. Recently, Guan et al. demonstrated the high sensitivity of HHG by applying uniaxial strains in the monolayer MoS2 and showed strong correlations between intraband and interband contributions [33]. Generally speaking, by exerting biaxial stretching strains, the harmonic efficiency can be facilitated due to the downshifting energy level of the conduction band [34]. Besides, Qin et al. [35] showed that, under biaxial and uniaxial strains, the harmonic intensity in the zero-gap monolayer silicene can be significantly enhanced up to an order of magnitude.
As a prototype of 2D materials, the hBN attracts great interest due to its outstanding optical and structural performances, e.g., a wide band gap, excellent structrual stability [36], hardly damaged under radiations [15], and strong exciton coincidences [37]. The hBN relevant materials have been demonstrated to be a promising candidate for the HHG, such as Graphene/hBN heterostructures [22], hBN stacking forms [16] and hole-defect hBN structures [19]. More importantly, ab initio calculations showed that the exertion of strains can effectively tune the bandgap structure of the monolayer hBN, and with a certain large lateral deformation, the single-layer hBN may be turned from insulator to semiconductor [38].
In this paper, we focus on the stretching effect on the HHG. As an example, we theoretically investigate the HHG from the monolayer hBN crystal within the time-dependent density functional theory (TDDFT). Compared to the previous research, we systematically study the influence of uniaxial and biaxial strains along the zigzag direction and the armchair direction on HHG from the monolayer hBN crystal. To launch a more convincing dynamics, we compute the initial ground-state density for each stretching geometry. For the nonlinear HHG response, we consider two kinds of laser fields, i.e., the linearly polarized and the counter-rotating bicircular pulses.
This paper is organized as follows: In Section 2, we introduce the framework of the TDDFT method and numerical details. In Section 3, we discuss the strained band structure and the HHG in the monolayer hBN. Finally, in Section 4, we summarize and discuss the prospects of our results.
2 Method
The electron dynamics of the monolayer hBN is investigated by solving the following time-dependent Kohn–Sham (KS) equations (atomic units is adopted and the spin notation is omitted hereafter) [39, 40],
where ψi are KS orbitals and the subscript i corresponds to both a band and a k-point index. The KS effective potential consists of three parts: the classical Hartree potential VH, the electronic exchange-correlation (xc) potential Vxc, and the external potential Vext that contains the incident laser field and the electron-ion Coulomb potential. The total density ρ(r, t) is defined by summing up all the orbital densities,
The microscopic electric current density j(r, t) is computed from time-evolved KS orbitals:
Then, the HHG spectrum is obtained from the total time-dependent electronic current j(r, t) by the following Fourier transform,
where Ω is the volume of the computational box.
In the present work, we consider both uniaxial and biaxial stretching strains applied to the monolayer hBN crystal. For strained geometries, we optimize lattice parameters of the monolayer hBN by using the Vienna ab intio Software Package (VASP) [41, 42]. The projected augmented wave [43, 44] pseudopotentials are employed with a cutoff energy of 500 eV for the plane-wave basis, and the xc functional is treated with the generalized gradient approximation of the Perdew–Burke–Ernzerhof (PBE) functional. The ground-state structural optimizations are carried out using a cubic cell which contains four atoms, i.e., two boron atoms and two nitrogen atoms, as shown in Figure 1A. The corresponding Brillouin zone (BZ) integrations are approximated by adopting the special k-point sampling of the Monhkorst-Pack scheme with a size of 28 × 16 points. The uniaxial deformations are imposed by stretching the crystal lattice on either the x [ɛuni.(x)] or the y [ɛuni.(y)] direction, and the biaxial deformations are applied in both the x and the y directions (ɛbi.). Due to the Poisson effect [45, 46], the lattice tends to be compressed along the direction perpendicular to the uniaxial stretching direction. Therefore, during the optimization, when the uniaxial strain [ɛuni.(x) or ɛuni.(y)] is applied, the x (or y)-direction lattice parameter Lx (or Ly) in the cubic cell is fixed, and the Ly (or Lx) is obtained by the minimum process that the system relaxes to its lowest energy state. For the symmetric strain distribution (ɛbi.), we scale both the Lx and Ly by the same ratio. Here, stretching percents in the range from 0 to 6% are considered, where ɛ = 0 manifests a strain-free operation, and ɛ > 0 corresponds to a stretching operation.
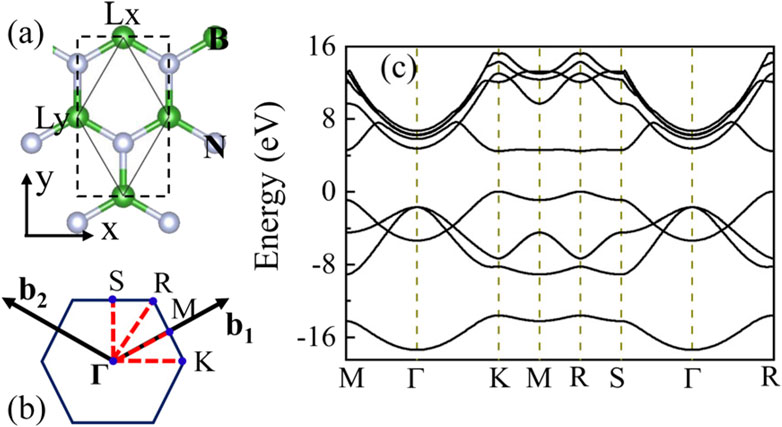
FIGURE 1. (A) Schematic diagram of the strain-free monolayer hBN. The primitive (hexagonal) cell and cubic unit cell are framed by solid and dashed lines. (B) The first Brillouin zone of the strain-free monolayer hBN and the corresponding high symmetric points Γ, K, M, R, and S in the reciprocal space. (C) The band structure of the strain-free monolayer hBN.
After the lattice parameter optimization, the corresponding simplified two-atom primitive cell framed by the thin black solid lines in Figure 1A is used for ground-state calculations and time-dependent propagations, which is performed within OCTOPUS package [47, 48]. In all the calculations, nuclei are fixed, so that the energy transfer from electrons to ions is not considered. The lattice parameter of the primitive cell for the unstrained monolayer hBN is 4.73 a0. The length of the simulation box in the out-of-plane direction is 66 a0. A complex absorbing boundary condition [49] is employed to prevent the possible electronic wave-packet reflection, and the width of the absorbing boundary is 3 a0 laying on the edges of the computational box. All the physical quantities are discretized in a three-dimensional box with a uniform grid size of 0.33 a0. We employ a local-density approximation (LDA) [50] for the electronic exchange-correlation, and Hartwigsen-Goedecker-Hutter (HGH) pseudopotentials [51] for core-electron potentials. The 2D BZ is sampled by a 44 × 44 Monkhorst–Pack k-point mesh for self-consistent converged calculations. The monolayer hBN is exposed to a linearly or a counter-rotating bichromatic circularly polarized mid-infrared laser field, polarized along the in-plane direction. The laser-matter interaction is described in the velocity gauge with the vector potential A(t) given by,
where Ai0 is the peak vector potential. ϵi and ωi are the ellipticity and the frequency of the ith pulse, respectively. The laser pulse envelope f(t) is a sin-square profile. For the linearly polarized laser, A20 and ϵi are set to be zero. For the bichromatic circularly polarized field, A10 = A20, ϵi = 1 and ω2 = 2ω1. The “±” in Eq. 5 is used to distinguish a circularly polarized field with the left-handed ( + ) or the right-handed ( − ) rotation. Both kinds of laser pulses share the same pulse length, and contain 8 cycles of the fundamental pulse. The electric field E(t) relates to the A(t) by
3 Results and discussion
The strain-free monolayer hBN is a direct-gap insulator with a hexagonal lattice. The top view of the crystal structure is shown in Figure 1A. Figures 1B,C show the first BZ and the band structure, respectively. The minimum direct band gap is located at K point with a magnitude of
By taking the lattice structure of the strain-free monolayer hBN as a reference, the symmetry of the reciprocal space will be changed under different strain strengths. In Figures 2A–C, we show electronic band structures of the monolayer hBN that under different stretching percents. We find that the band structure strongly depends on the strength and direction of the applied strains, and the band energies shift when strains are applied. For the cases of ɛuni.(x) and ɛbi., the top of the valence band (VB) and the bottom of the conduction band (CB) locate at K point, and the increase of the stretching percent always results in the decrease of the direct bandgap. For the ɛuni.(y) case, the monolayer hBN has a direct bandgap under small strains. However, its bandgap turns into indirect for larger stretching magnitude. Biaxial strains usually modify the bandgap more seriously than uniaxial strains. For instance, when ɛuni.(x) = 6% (or ɛuni.(y) = 6%), the direct bandgap at K point decreases to
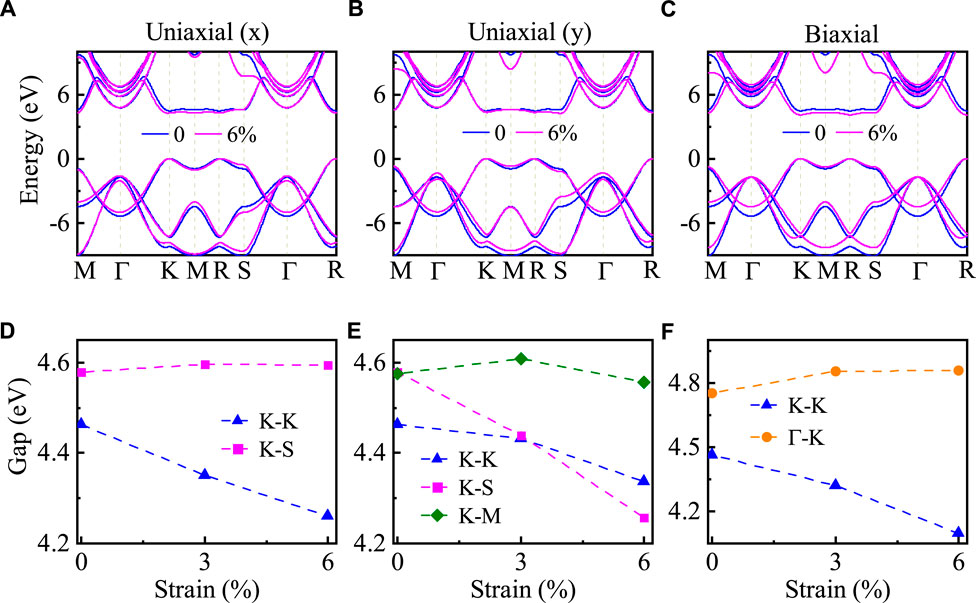
FIGURE 2. The band structures of the monolayer hBN with the uniaxial strain along (A) the x direction, (B) the y direction, and (C) the biaxial strain along both the x and y directions. The blue and magenta curves are for ɛ = 0 and ɛ = 6%, respectively. ɛ = 0 is the strain-free case. The corresponding strain-dependent direct and indirect band gap in the monolayer hBN are shown in (D) − (F).
To explain the strain effect on the HHG, we first study the HHG spectra of the monolayer hBN crystal under different strains, driven by a linearly polarized laser pulse. Our results show that the distortion of the band structure alters significantly the in-plane harmonic emission. Since the phonon effect is not considered in the present work, the electronic indirect transition may not contribute to the harmonic generation. Figure 3A shows the total HHG intensity in the monolayer hBN under stretching strain values of ɛ = 0 and ɛ = 6%. Compared with the strain-free case, both uniaxial and biaxial strains lead to the enhancement of the HHG intensity. The strain-dependent excited electron number (Nexc) of the monolayer hBN after the laser field ends is shown in Figure 3B. The Nexc is larger under the biaxial stretching, and the corresponding HHG intensity is slightly stronger than that in the uniaxial strain cases. This may be attributed to the fact that reducing the bandgap makes electrons easier transfer from the VB to the CB. This finding is in consistent with the strain-controlled HHG mechanism in silicene, in which both the intraband and the interband HHG can be enhanced due to the increase of electronic population in the CB [35].
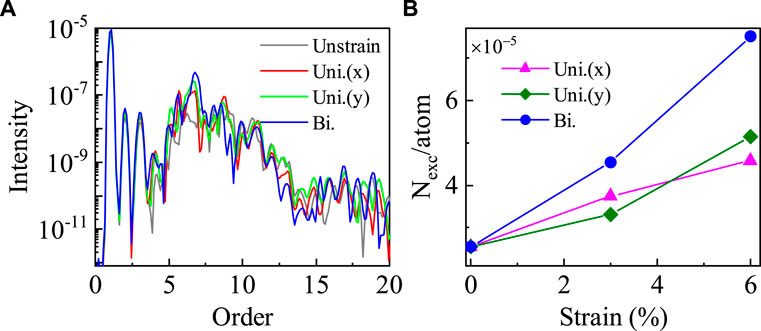
FIGURE 3. (A) The total HHG spectra in the monolayer hBN with the stretching percent of ɛ = 6% under the linear pulse polarized along the x direction. The laser wavelength is 1,600 nm with a peak intensity of 1012 W/cm2. The gray solid line is for the HHG spectra in the strain-free case. (B) The strain-dependent excited electron number after the laser ends for different strains strengths.
To explain the strained HHG mechanism, we plotted the time-frequency HHG with stretching strains in Figure 4. We find that the strained HHG mechanism is closely related to the symmetry of the monolayer hBN. For the strain-free hBN, it has the reflection symmetry with respect to the B-N bond, and the three-fold rotation symmetry with respective to the center of the hexagonal lattice [53]. However, when applied stretching strains, some symmetries are destroyed, resulting in a concert change in the HHG spectra. Specifically, under uniaxial stretching along the x or the y direction, the three-fold rotation symmetry is broken, while the reflection symmetry in the x direction is preserved. This gives rise to different HHG mechanisms that only odd harmonics are found in the x direction and only even harmonics are found in the y direction. Besides, we demonstrate that high harmonics are emitted as discrete bursts in phase concerted with the change of vector potentials, and magenta lines in Figure 4 stand for the absolute value of the vector potentials. This suggests that the electronic interband transition is the dominant mechanism for the stretching-strained harmonic emission [54].
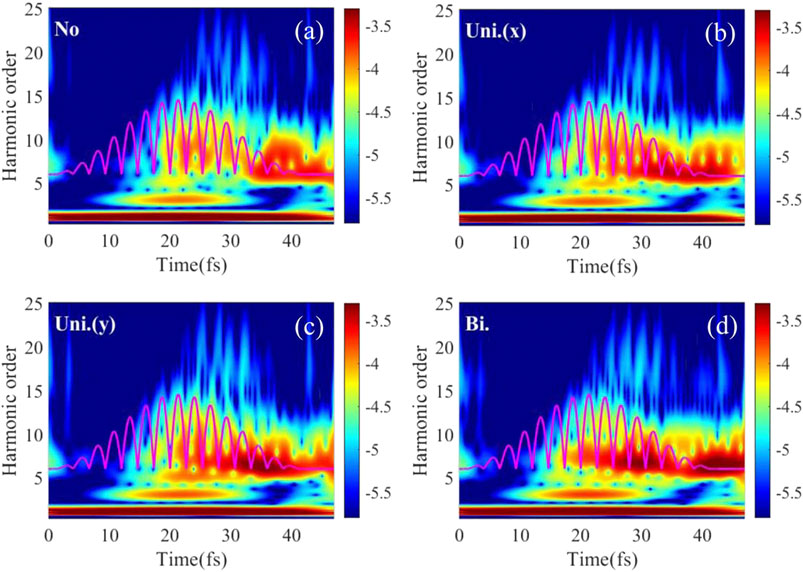
FIGURE 4. The time-frequency logarithmic intensity of x-polarized harmonics under different stretching percents, radiated by a linear polarized laser pulse along the x direction: (A) strain-free; only uniaxial stretching imposed along (B) the x direction with ɛuni.(x) = 6% and (C) the y direction with ɛuni.(y) = 6%; (D) biaxial stretching with ɛbi. = 6%.
To further investigate the energy transfer from the laser field to the strained monolayer hBN, Figure 5A shows the energy absorption per atom at different laser rotation angles that defined as the angle between the laser polarization and the x direction. The laser field is initially polarized in the x direction, and then rotates counterclockwise, as shown in the insert in Figure 5A.
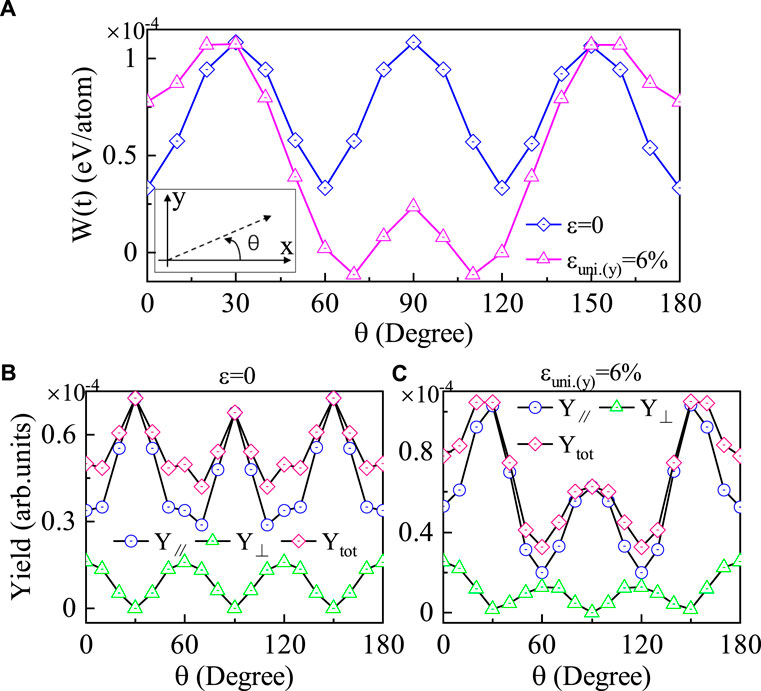
FIGURE 5. (A) The calculated energy absorption per atom of the monolayer hBN as a function of the laser rotation angle under stretching percents of ɛ = 0 and ɛuni.(y) = 6%. The inset shows the angle of the laser in-plane polarization. The laser field is first polarized in the x direction and then rotated counterclockwise. The harmonic yield as a function of the laser rotation for cases of ɛ = 0 (B) and ɛuni.(y) = 6% (C). The HHG yield component that parallel or perpendicular to the linearly polarized field is denoted by circle and triangle symbols, respectively. Cubic symbols are the total harmonic yield.
The energy absorption is an effective representation to clarify the laser-matter energy connection. The energy transfer function W in the unit cell volume of Ω can be defined as
where tend is the moment that the laser pulse ends. In Figure 5A, for the strain-free case, W vibrates with a period of
The high-energy harmonics around the cutoff region are sensitive to the interatomic distance and electronegativity [4], in other words, it can be used to reconstruct the geometric symmetry of the material. To this end, we study the (15th-22nd)-integrated HHG yield. As shown in Figures 5B,C, triangle symbols represent the composed HHG yield parallel to the polarization direction and circle symbols represent the yield component perpendicular to the polarization direction. It can be seen that the total harmonic yield is in consistent with the change of the energy absorption in Figure 5A. For both the ɛ = 0 and ɛuni.(y) = 6%, the parallel contribution to the total HHG yield is dominant. The weak perpendicular component of HHG is generally attributed to the Berry curvature. In addition, contributions of orientation-dependent HHG yield from the parallel and the perpendicular configuration are opposite to each other. A more detailed analysis of the selection rule for the strain-free monolayer hBN can be found in our previous paper [53].
Figure 6 shows the non-perturbative anisotropy map of the HHG from the monolayer hBN obtained via rotating the polarization of the linearly polarized driving field. We analyze the two polarization components of the harmonics, i.e., perpendicular and parallel to the linearly polarized laser field. For the ɛ = 0 and the ɛuni.(y) = 6% cases, the crystal symmetry is quite different. The parallel and the perpendicular HHG components reflect the symmetry of the hexagonal layered structure. Compared with the parallel component, the weak HHG perpendicular component is dominated by the even harmonics, as shown in Figure 6B. When the laser polarization is in the B-B (or N-N) direction, pure odd harmonics are embodied in the parallel component and pure even harmonics in the perpendicular component. The perpendicular harmonic component is forbidden when the laser is polarized along the B-N bond. For the ɛuni.(y) = 6% case, the breaking of the three-fold rotation symmetry is reflected by the perpendicular HHG spectrogram, e.g., the mirror symmetry with respect to the B-N bond is broken at 30° and 150°. Therefore, the HHG perpendicular component is strictly forbidden when the laser is polarized in the y direction, and the odd harmonic yield in Figure 6D is higher than that in Figure 6B. One has demonstrated that the polarization properties of the solid-state HHG are largely governed by the crystal symmetry by comparing the experimental measurements with the theoretical results [56]. The similar odd/even order contrast has been reported for many other crystals, such as the monolayer MoS2 [6], the bulk ZnO [56], α-quartz crystals [9, 57], etc. These results show that the polarization-dependent harmonics provide a powerful way to probe the crystal spatial symmetry.
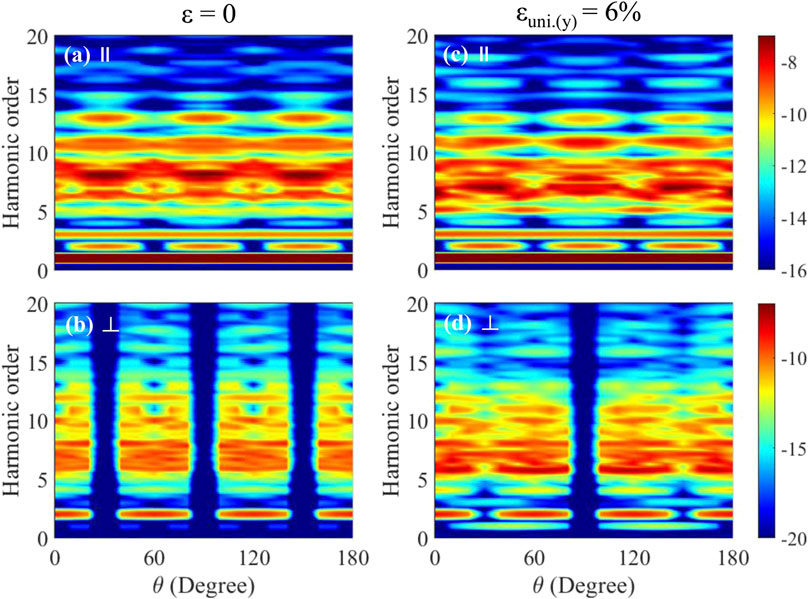
FIGURE 6. Logarithmic colormap for the polarization-dependent harmonic intensity in the monolayer hBN. Left panels: the HHG in the strain-free monolayer hBN for the (A) parallel and (B) the perpendicular components. Right panels: The HHG in the stretching monolayer hBN with ɛuni.(y) = 6% for the (C) parallel and (D) the perpendicular components.
For the HHG selection rule, it has been proven that the HHG emission must obey the same symmetry owned by the target system and the driving field [58, 59]. Therefore, if the incident laser field has the three-fold rotation symmetry as same as the monolayer hBN lattice, the 3n-order harmonics should be missing. According to this, we investigate the harmonic generation in the monolayer hBN under ɛuni.(y) stretching driven by a bichromatic counter-rotating circularly polarized laser pulse. Such a laser pulse is a combination of a circularly polarized fundamental field of frequency ω1 (1,600 nm) and its counter-rotating second harmonic ω2 (800 nm), which exhibits a three-fold rosette pattern as shown in the insert of Figure 7. The intensity of both two single circularly polarized pluses is set to be I1 = I2 = 5 × 1011 W/cm2. For the strain-free case, governed by the selection rule, it is obvious that the 3nth harmonics are forbidden. However, as the uniaxial stretching percent increases, the forbidden 3nth harmonics gradually restore. In this case, the uniaxial stretching breaks the three-fold rotation symmetry, and the selection rule is replaced by selection deviations [60]. Comparing with the results of ɛuni.(y) = 3% and ɛuni.(y) = 6%, one can find that a larger stretching percent gives rise to a stronger 3nth harmonic signal. This suggests that exerting a stronger external perturbation may result in a larger deviation, and such a signal is useful to reconstruct the lattice deformation.
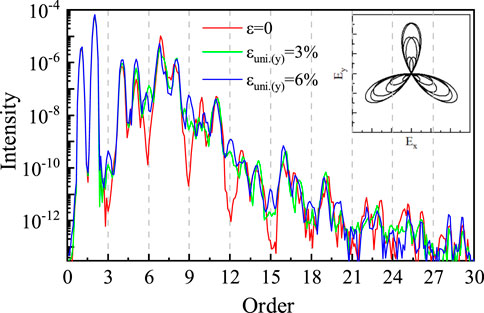
FIGURE 7. The HHG in the stretching and strain-free monolayer hBN driven by a two-color counter-rotated circularly polarized laser pulse. The insert is the Lissajous curve of the applied laser field.
4 Conclusion
In conclusion, we have studied the strain-dependent HHG in the monolayer hBN crystal within the TDDFT. The monolayer hBN is exposed to an intense linearly polarized or a counter-rotating bichromatic circularly polarized mid-infrared laser field. To ensure the structural stability of the hBN crystal, stretching percents are limited in the range of 0–6%. Using the strain-free monolayer hBN as a reference, we studied band structures and the resulting HHG under two typical kinds of strains, i.e., the uniaxial and the biaxial stretching strains. We find the band structure is sensitive to the structural deformation modulated by strains. For both the uniaxial and biaxial cases, the interband dynamics is the dominant mechanism in the strained monolayer hBN. By rotating the laser polarization direction, the HHG spectra from the strained monolayer hBN exhibit some special features compared with that from the strain-free case. The results show that the anisotropy of HHG spectra is closely related to the structural symmetry of the strained hBN. Furthermore, when exposed to a bichromatic counter-rotating circularly polarized laser pulse, the restoration of 3nth harmonics is a potential probe to reconstruct the lattice deformation. Therefore, our work provides a useful way to control the HHG by applying mechanical strains, and the results may be heuristic to enhance the optoelectronic efficiency of solid-state nano-devices.
Data availability statement
The datasets for this study can be obtained from the authors upon reasonable requests.
Author contributions
KX did all the calculations and wrote the manuscript. YW contributed to supervision and manuscript revision. GL, WX, and YW commented on the manuscript. All authors contributed to manuscript revision and approved the submitted version.
Funding
This work is supported by the National Natural Science Foundation of China (NSFC) under Grant Nos. 12104019 and 11725416 and 11961131008 and by the National Key R&D Program of China under Grant No. 2018YFA0306302.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Ghimire S, DiChiara AD, Sistrunk E, Agostini P, DiMauro LF, Reis DA. Observation of high-order harmonic generation in a bulk crystal. Nat Phys (2011) 7:138–41. doi:10.1038/nphys1847
2. Ghimire S, DiChiara AD, Sistrunk E, Ndabashimiye G, Szafruga UB, Mohammad A, et al. Generation and propagation of high-order harmonics in crystals. Phys Rev A (Coll Park) (2012) 85:043836. doi:10.1103/physreva.85.043836
3. Luu TT, Garg M, Kruchinin SY, Moulet A, Hassan MT, Goulielmakis E. Extreme ultraviolet high-harmonic spectroscopy of solids. Nature (2015) 521:498–502. doi:10.1038/nature14456
4. You YS, Reis D, Ghimire S. Anisotropic high-harmonic generation in bulk crystals. Nat Phys (2017) 13:345–9. doi:10.1038/nphys3955
5. Ndabashimiye G, Ghimire S, Wu M, Browne DA, Schafer KJ, Gaarde MB, et al. Solid-state harmonics beyond the atomic limit. Nature (2016) 534:520–3. doi:10.1038/nature17660
6. Liu H, Li Y, You YS, Ghimire S, Heinz TF, Reis DA. High-harmonic generation from an atomically thin semiconductor. Nat Phys (2017) 13:262–5. doi:10.1038/nphys3946
7. Yoshikawa N, Tamaya T, Tanaka K. High-harmonic generation in graphene enhanced by elliptically polarized light excitation. Science (2017) 356:736–8. doi:10.1126/science.aam8861
8. Vampa G, Hammond TJ, Thiré N, Schmidt BE, Légaré F, McDonald CR, et al. All-optical reconstruction of crystal band structure. Phys Rev Lett (2015) 115:193603. doi:10.1103/physrevlett.115.193603
9. Luu TT, Wörner HJ. Measurement of the berry curvature of solids using high-harmonic spectroscopy. Nat Commun (2018) 9:916. doi:10.1038/s41467-018-03397-4
10. Han S, Ortmann L, Kim H, Kim YW, Oka T, Chacon A, et al. Extraction of higher-order nonlinear electronic response in solids using high harmonic generation. Nat Commun (2019) 10:3272. doi:10.1038/s41467-019-11096-x
11. Tancogne-Dejean N, Mücke OD, Kärtner FX, Rubio A. Impact of the electronic band structure in high-harmonic generation spectra of solids. Phys Rev Lett (2017) 118:087403. doi:10.1103/physrevlett.118.087403
12. Uchida K, Pareek V, Nagai K, Dani K, Tanaka K. Visualization of two-dimensional transition dipole moment texture in momentum space using high-harmonic generation spectroscopy. Phys Rev B (2021) 103:L161406. doi:10.1103/physrevb.103.l161406
13. Corkum PB. Plasma perspective on strong field multiphoton ionization. Phys Rev Lett (1993) 71:1994–7. doi:10.1103/physrevlett.71.1994
14. Vampa G, McDonald C, Orlando G, Klug D, Corkum P, Brabec T. Theoretical analysis of high-harmonic generation in solids. Phys Rev Lett (2014) 113:073901. doi:10.1103/physrevlett.113.073901
15. Tancogne-Dejean N, Rubio A. Atomic-like high-harmonic generation from two-dimensional materials. Sci Adv (2018) 4:eaao5207. doi:10.1126/sciadv.aao5207
16. Le Breton G, Rubio A, Tancogne-Dejean N. High-harmonic generation from few-layer hexagonal boron nitride: Evolution from monolayer to bulk response. Phys Rev B (2018) 98:165308. doi:10.1103/physrevb.98.165308
17. Yu C, Jiang S, Wu T, Yuan G, Peng Y, Jin C, et al. Higher harmonic generation from bilayer nanostructures assisted by electron backscattering. Phys Rev B (2020) 102:241407. doi:10.1103/physrevb.102.241407
18. Huang T, Zhu X, Li L, Liu X, Lan P, Lu P. High-order-harmonic generation of a doped semiconductor. Phys Rev A (Coll Park) (2017) 96:043425. doi:10.1103/physreva.96.043425
19. Mrudul M, Tancogne-Dejean N, Rubio A, Dixit G. High-harmonic generation from spin-polarised defects in solids. Npj Comput Mater (2020) 6:10. doi:10.1038/s41524-020-0275-z
20. Han S, Kim H, Kim YW, Kim YJ, Kim S, Park IY, et al. High-harmonic generation by field enhanced femtosecond pulses in metal-sapphire nanostructure. Nat Commun (2016) 7:13105. doi:10.1038/ncomms13105
21. Du TY, Guan Z, Zhou XX, Bian XB. Enhanced high-order harmonic generation from periodic potentials in inhomogeneous laser fields. Phys Rev A (Coll Park) (2016) 94:023419. doi:10.1103/physreva.94.023419
22. Chen ZY, Qin R. High harmonic generation in graphene–boron nitride heterostructures. J Mater Chem C Mater (2020) 8:12085–91. doi:10.1039/d0tc02036b
23. Mrudul M, Dixit G. High-harmonic generation from monolayer and bilayer graphene. Phys Rev B (2021) 103:094308. doi:10.1103/physrevb.103.094308
24. Pertsev N, Zembilgotov A, Tagantsev A. Effect of mechanical boundary conditions on phase diagrams of epitaxial ferroelectric thin films. Phys Rev Lett (1998) 80:1988–91. doi:10.1103/physrevlett.80.1988
25. Haeni J, Irvin P, Chang W, Uecker R, Reiche P, Li Y, et al. Room-temperature ferroelectricity in strained SrTiO3. Nature (2004) 430:758–61. doi:10.1038/nature02773
26. Cao J, Ertekin E, Srinivasan V, Fan W, Huang S, Zheng H, et al. Strain engineering and one-dimensional organization of metal–insulator domains in single-crystal vanadium dioxide beams. Nat Nanotechnol (2009) 4:732–7. doi:10.1038/nnano.2009.266
27. Takahashi H, Igawa K, Arii K, Kamihara Y, Hirano M, Hosono H. Superconductivity at 43 k in an iron-based layered compound Lao1-xFxFeAs. Nature (2008) 453:376–8. doi:10.1038/nature06972
28. Gao L, Xue Y, Chen F, Xiong Q, Meng R, Ramirez D, et al. Superconductivity up to 164 k in HgBa2Cam- 1CumO2m+2+δ (m = 1, 2, and 3) under quasihydrostatic pressures. Phys Rev B (1994) 50:4260–3. doi:10.1103/physrevb.50.4260
29. Song S, Keum DH, Cho S, Perello D, Kim Y, Lee YH. Room temperature semiconductor–metal transition of MoTe2 thin films engineered by strain. Nano Lett (2016) 16:188–93. doi:10.1021/acs.nanolett.5b03481
30. Guan MX, Liu XB, Chen DQ, Li XY, Qi YP, Yang Q, et al. Optical control of multistage phase transition via phonon coupling in MoTe2. Phys Rev Lett (2022) 128:015702. doi:10.1103/physrevlett.128.015702
31. Mennel L, Furchi MM, Wachter S, Paur M, Polyushkin DK, Mueller T. Optical imaging of strain in two-dimensional crystals. Nat Commun (2018) 9:516. doi:10.1038/s41467-018-02830-y
32. Conley HJ, Wang B, Ziegler JI, Haglund RF, Pantelides ST, Bolotin KI. Bandgap engineering of strained monolayer and bilayer MoS2. Nano Lett (2013) 13:3626–30. doi:10.1021/nl4014748
33. Guan MX, Lian C, Hu SQ, Liu H, Zhang SJ, Zhang J, et al. Cooperative evolution of intraband and interband excitations for high-harmonic generation in strained MoS2. Phys Rev B (2019) 99:184306. doi:10.1103/physrevb.99.184306
34. Wang Z, Jiang S, Yuan G, Wu T, Li C, Qian C, et al. Strain effect on the orientation-dependent harmonic spectrum of monolayer aluminum nitride. Sci China Phys Mech Astron (2020) 63:257311. doi:10.1007/s11433-019-1467-2
35. Qin R, Chen ZY. Strain-controlled high harmonic generation with Dirac fermions in silicene. Nanoscale (2018) 10:22593–600. doi:10.1039/c8nr07572g
36. Pouch JJ, Alterovitz SA. Synthesis and properties of boron nitride. Aedermannsdorf: Trans Tech, Aedermannsdorf (1990).
37. Bourrellier R, Amato M, Galvão Tizei LH, Giorgetti C, Gloter A, Heggie MI, et al. Nanometric resolved luminescence in h-BN flakes: Excitons and stacking order. ACS Photon (2014) 1:857–62. doi:10.1021/ph500141j
38. Li J, Gui G, Zhong J. Tunable bandgap structures of two-dimensional boron nitride. J Appl Phys (2008) 104:094311. doi:10.1063/1.3006138
39. Runge E, Gross EK. Density-functional theory for time-dependent systems. Phys Rev Lett (1984) 52:997–1000. doi:10.1103/physrevlett.52.997
40. Leeuwen R. V. Mapping from densities to potentials in time-dependent density-functional theory. Phys Rev Lett (1999) 82:3863–6. doi:10.1103/physrevlett.82.3863
41. Kresse G, Furthmüller J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys Rev B (1996) 54:11169–86. doi:10.1103/physrevb.54.11169
42. Kresse G, Furthmüller J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput Mater Sci (1996) 6:15–50. doi:10.1016/0927-0256(96)00008-0
43. Blöchl PE. Projector augmented-wave method. Phys Rev B (1994) 50:17953–79. doi:10.1103/physrevb.50.17953
44. Kresse G, Joubert D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys Rev B (1999) 59:1758–75. doi:10.1103/physrevb.59.1758
46. Greaves GN, Greer AL, Lakes RS, Rouxel T. Poisson’s ratio and modern materials. Nat Mater (2011) 10:823–37. doi:10.1038/nmat3134
47. Andrade X, Strubbe D, De Giovannini U, Larsen AH, Oliveira MJ, Alberdi-Rodriguez J, et al. Real-space grids and the octopus code as tools for the development of new simulation approaches for electronic systems. Phys Chem Chem Phys (2015) 17:31371–96. doi:10.1039/c5cp00351b
48. Tancogne-Dejean N, Oliveira MJ, Andrade X, Appel H, Borca CH, Le Breton G, et al. Octopus, a computational framework for exploring light-driven phenomena and quantum dynamics in extended and finite systems. J Chem Phys (2020) 152:124119. doi:10.1063/1.5142502
49. De Giovannini U, Larsen AH, Rubio A. Modeling electron dynamics coupled to continuum states in finite volumes with absorbing boundaries. Eur Phys J B (2015) 88:56. doi:10.1140/epjb/e2015-50808-0
50. Onida G, Reining L, Rubio A. Electronic excitations: Density-functional versus many-body green’s-function approaches. Rev Mod Phys (2002) 74:601–59. doi:10.1103/revmodphys.74.601
51. Hartwigsen C, Goedecker S, Hutter J. Relativistic separable dual-space Gaussian pseudopotentials from H to Rn. Phys Rev B (1998) 58:3641–62. doi:10.1103/physrevb.58.3641
52. Ooi N, Rairkar A, Lindsley L, Adams J. Electronic structure and bonding in hexagonal boron nitride. J Phys : Condens Matter (2005) 18:97–115. doi:10.1088/0953-8984/18/1/007
53. Kong XS, Liang H, Wu XY, Peng LY. Symmetry analyses of high-order harmonic generation in monolayer hexagonal boron nitride. J Phys B: Mol Opt Phys (2021) 54:124004. doi:10.1088/1361-6455/ac066f
54. Wu M, Ghimire S, Reis DA, Schafer KJ, Gaarde MB. High-harmonic generation from bloch electrons in solids. Phys Rev A (Coll Park) (2015) 91:043839. doi:10.1103/physreva.91.043839
55. Neufeld O, Zhang J, Giovannini UD, Hübener H, Rubio A. Probing phonon dynamics with multidimensional high harmonic carrier-envelope-phase spectroscopy. Proc Natl Acad Sci U S A (2022) 119:e2204219119. doi:10.1073/pnas.2204219119
56. Jiang S, Gholam-Mirzaei S, Crites E, Beetar JE, Singh M, Lu R, et al. Crystal symmetry and polarization of high-order harmonics in ZnO. J Phys B: Mol Opt Phys (2019) 52:225601. doi:10.1088/1361-6455/ab470d
57. Wu XY, Liang H, Kong XS, Gong Q, Peng LY. Multiscale numerical tool for studying nonlinear dynamics in solids induced by strong laser pulses. Phys Rev E (2022) 105:055306. doi:10.1103/physreve.105.055306
58. Alon OE, Averbukh V, Moiseyev N. Selection rules for the high harmonic generation spectra. Phys Rev Lett (1998) 80:3743–6. doi:10.1103/physrevlett.80.3743
59. Neufeld O, Podolsky D, Cohen O. Floquet group theory and its application to selection rules in harmonic generation. Nat Commun (2019) 10:405. doi:10.1038/s41467-018-07935-y
Keywords: mechanical strains, high-order harmonic generation, monolayer hexagonal boron nitride crystal, time-dependent density functional theory, laser-matter interaction
Citation: Kong X-S, Wu X-Y, Geng L and Yu W-D (2022) Strain effects on high-harmonic generation in monolayer hexagonal boron nitride. Front. Phys. 10:1032671. doi: 10.3389/fphy.2022.1032671
Received: 31 August 2022; Accepted: 29 September 2022;
Published: 12 October 2022.
Edited by:
Weifeng Yang, Hainan University, ChinaReviewed by:
Ruifeng Lu, Nanjing University of Science and Technology, ChinaXiaowei Sheng, Anhui Normal University, China
Copyright © 2022 Kong, Wu , Geng and Yu. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Wan-Dong Yu, d2FuZG9uZ3l1QHBrdS5lZHUuY24=
 Xiao-Shuang Kong
Xiao-Shuang Kong Xiao-Yuan Wu
Xiao-Yuan Wu