Multi-party semi-quantum private comparison based on the maximally entangled GHZ-type states

The goal of semi-quantum privacy comparison (SQPC) is to use a small amount of quantum capabilities to compare private information for equality. In recent years, research on semi-quantum privacy comparison protocol has made some achievements. However, most of SQPC protocols can merely compare the private information of two parties, and the research of multi-party SQPC protocols are still scarce. If the number of participants is more than two, the protocol needs to be executed multiple times. Therefore, we proposed a multi-party semi-quantum private comparison protocol based on the maximally entangled GHZ-type state, which has the capability to compare the equality of n parties by executing the protocol once. What is more, the transmission of participant’s encrypted information is not through the classical channel, which improves the security of the protocol. Finally, the security analysis shows that outsider attacks, dishonest participants attacks and semi-honest TP attacks are all invalid for this protocol.

1 Introduction

Secure multi-party computing (SMC) is an momentous topic in classical cryptography. It originates from the millionaire problem proposed by Yao [1] in 1982, that is, comparing two millionaires who are richer without disclosing their real assets. With the proposal of quantum parallel algorithm, the security of SMC based on computational complexity is seriously challenged. In order to overcome the shortcomings of classical SMC in security, classical SMC has been extended to the field of quantum mechanics.

In 1984, Bennett and Brassard [2] applied quantum mechanics to classical cryptography and proposed the first quantum key distribution protocol. Since then, various quantum cryptography protocols have been proposed, such as quantum key distribution (QKD) [2–6], quantum dialogue (QD) [7, 8], quantum summation [9, 10], quantum encryption (QPQ) [11, 12], quantum signature [13–16].

The quantum privacy comparison protocol (QPC) is an essential branch of the SQPC protocol, which has attracted extensive attention of many scholars. In 2009, Yang and Wen [17] presented the first quantum privacy comparison protocol using Bell states as carrier particles. Since then, QPC protocols with different quantum states as quantum resources have been proposed one after another. For example, many QPC protocols are based on single photon [18], Bell state [19–21], GHZ state [22, 23], multi-particle entangled state [24–26], and so on.

The most of quantum privacy comparison protocols require participants to have full quantum capabilities. In other words, all participants are allowed to use various quantum devices, such as quantum memory [27], entangled state generator [28] and quantum unitary operators [29]. However, quantum resources are currently very scarce, and it is impractical for all participants to have full quantum capabilities.

In order to solve the problem of scarcity of quantum resources, in 2007, Boyer et al. [30, 31] proposed the concept of semi-quantum and designed the first semi-quantum key distribution (SQKD) protocol, where he defined two kinds of participants. One is a “full quantum user” with complete quantum capabilities, and the other is a “classical user” who is limited to the following four operations: (1) reflecting the received qubits directly.; (2) measuring the received qubits with Z basis {|0⟩, |1⟩}; (3) preparing a new qubit with Z basis {|0⟩, |1⟩}; (4) reordering the qubits via different delay lines. Since the semi-quantum protocol can reduce the use of quantum resources, the concept of semi-quantum is applied to the QPC protocol. In 2016, Chou et al. [32] introduced the semi-quantum concept into the QPC protocol and proposed the first semi-quantum privacy comparison protocol based on Bell entanglement exchange. Similar protocols have been proposed from then on. In 2018, Ye et al. [33] constructed a SQPC protocol using two-particles entangled state with measure-resend characteristics. The next year, Lin et al. [34] put forward an efficient SQPC protocol with an semi-honest third party based on single photons. Recently, Tian et al. [35] proposed a robust SQPC protocol with W-state, which can resist the loss of a single qubit. In 2021, Zhou et al. [36] proposed a semi-quantum secret comparison protocol based on Bell state, which can compare the secret relationship between two classical participants in one execution without revealing their secrets. In 2022, Tang et al. [37] presented two SQPC protocol with DF states with good robustness properties against noise in the channel.

However, most of the current SQPC protocols can only compare the equality of two parties, and it is difficult to extend to multiple parties. If one want to use these two-party SQPC protocols to complete the comparison among n participants, the protocol need to be executed n − 1 times. To solve this problem, we propose a SQPC protocol using the maximally entangled GHZ-type state, which can compare multi-party information via execute the protocol at once. What is more, the quantum states and quantum operations required in our protocol can be realized under the existing technology.

The structure of this paper is organized as follows: Section 2 describes the proposed protocol explicitly and analyze its correctness; in Section 3, the security analysis is demonstrated in terms of outsider attack and insider attack. In Section 4, we compare our protocol with some existing; finally, we give a summary about this paper in Section 5.

2 The proposed scheme

2.1 Prerequisites

Before the description of our protocol, some prerequisites of the proposed protocol should be put forward in advance as following.

1. Suppose the protocol has n participants P_i(i = 1, 2, …, n). Every participant owns the private information $X_i=x_i^1{x}_i^2\cdots x_i^m$, where $x_i^j\in \{\mathrm{0,1}\},j=\mathrm{1,2},\dots ,m$. And the aim is to compare their private information for equality with the help of the semi-honest third-party (TP). Semi-honest refers to that TP may misbehave, but cannot conspire with others.

2. All participants use SQKD to generate the same secret key $K_P=(k_P^1,k_P^2,\dots ,k_P^m)$. Here, $k_p^j\in \{\mathrm{0,1}\},(j=\mathrm{1,2},\dots ,m)$. Then, P_i encodes his secrets $x_i^j$ with the shared keys $k_p^j$:

$R_i^j=x_i^j\oplus k_P^j,$

where $R_i=\{R_i^1,R_i^2,\dots ,R_i^m\}$, $R_i^j\in \{\mathrm{0,1}\}$ is the jth bit of R_i. And “⊕” indicates the modulo 2 addition operation.

3. In this paper, the GHZ-type state is used to construct an SQPC protocol, which is described as follows:

$\begin{array}{ll}\hfill |\phi \rangle & =\frac{1}{2}\left(|000\rangle +|011\rangle +|101\rangle +|110\rangle \right)\hfill \\ \hfill & =\frac{1}{\sqrt{2}}\left(|0\rangle |{\varphi }^{+}\rangle +|1\rangle |{\psi }^{+}\rangle \right).\hfill \end{array}(1)$

Here, |ϕ⁺⟩, |ϕ⁻⟩, |ψ⁺⟩ and |ψ⁻⟩ are four Bell states, which can be expressed as:

$\begin{array}{cc}\hfill & |{\varphi }^{+}\rangle =\frac{1}{\sqrt{2}}\left(|00\rangle +|11\rangle \right),\hfill \\ \hfill & |{\varphi }^{-}\rangle =\frac{1}{\sqrt{2}}\left(|00\rangle -|11\rangle \right),\hfill \\ \hfill & |{\psi }^{+}\rangle =\frac{1}{\sqrt{2}}\left(|01\rangle +|10\rangle \right),\hfill \\ \hfill & |{\psi }^{-}\rangle =\frac{1}{\sqrt{2}}\left(|01\rangle -|10\rangle \right).\hfill \end{array}(2)$

From Eq. 2 we can also infer that:

$\begin{array}{cc}\hfill & |00\rangle =\frac{1}{\sqrt{2}}\left(|{\varphi }^{+}\rangle +|{\varphi }^{-}\rangle \right),\hfill \\ \hfill & |01\rangle =\frac{1}{\sqrt{2}}\left(|{\psi }^{+}\rangle +|{\psi }^{-}\rangle \right),\hfill \\ \hfill & |10\rangle =\frac{1}{\sqrt{2}}\left(|{\psi }^{+}\rangle -|{\psi }^{-}\rangle \right),\hfill \\ \hfill & |11\rangle =\frac{1}{\sqrt{2}}\left(|{\varphi }^{+}\rangle -|{\varphi }^{-}\rangle \right).\hfill \end{array}(3)$

2.2 Protocol steps

Now, we present our proposed protocol in detail.

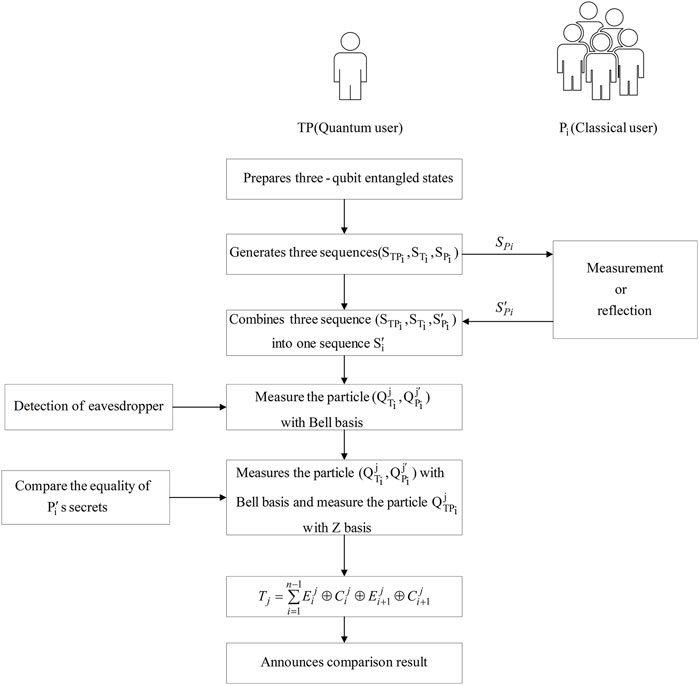
Step 1. TP prepares 2nm three-qubit entangle states |ψ⟩ described in Eq.1 to form n quantum sequence S₁, S₂, …, S_n, and each sequence S_i (i ∈ {1, 2, …, n}) includes 2m quantum states |ψ⟩, i.e.

$S_i=\left(Q_{T{P}_i}^1{Q}_{T_i}^1{Q}_{P_i}^1,Q_{T{P}_i}^2{Q}_{T_i}^2{Q}_{P_i}^2,\dots ,Q_{T{P}_i}^{2m}{Q}_{T_i}^{2m}{Q}_{P_i}^{2m}\right).$

Here, the order of GHZ-type state in S_i are indicated in superscripts 1, 2, …, 2m. Afterwards, TP divides these particles into three sequences:

$S_{T{P}_i}=\left(Q_{T{P}_i}^1,Q_{T{P}_i}^2,\dots ,Q_{T{P}_i}^{2m}\right),$

$S_{T_i}=\left(Q_{T_i}^1,Q_{T_i}^2,\dots ,Q_{T_i}^{2m}\right),$

$S_{P_i}=\left(Q_{P_i}^1,Q_{P_i}^2,\dots ,Q_{P_i}^{2m}\right).$

Finally, TP stores $S_{T{P}_i}$ and $S_{T_i}$, and transmits $S_{P_i}$ to P_i.

Step 2. For i = 1, 2, …, n:

When P_i receives the sequence $S_{P_i}$ from TP, he selects m qubits randomly to perform measurement operation, and the remaining particles are performed reflection operation. After that, the sequence $S_{P_i}$ becomes $S_{P_i}^{\prime }$, and P_i sends it back to TP.

(1) Reflection: P_i reflects the received qubits directly.

(2) Measurement: P_i measures the received qubits with Z basis {|0⟩, |1⟩} and generates a new qubit according to the value of $R_i^j$. The entangled particle will collapse to |0⟩ or |1⟩. If $R_i^j=0$, P_i generates a new particle $Q_{P_i}^{j\prime }$ is the same as the measurement result. If $R_i^j=1$, P_i generates a new quantum particle $Q_{P_i}^{j\prime }$ is contrary to the measurement result.

Step 3. For i = 1, 2, …, n:

When TP receives the sequence $S_{P_i}^{\prime }$ from P_i, TP combines the sequences $S_{T{P}_i}$, $S_{T_i}$ and $S_{P_i}^{\prime }$ to form the $S_i^{\prime }$

$S_i^{\prime }=\left(Q_{T{P}_i}^1{Q}_{T_i}^1{Q}_{P_i}^{1^{\prime }},Q_{T{P}_i}^2{Q}_{T_i}^2{Q}_{P_i}^{2^{\prime }},\dots ,Q_{T{P}_i}^{2m}{Q}_{T_i}^{2m}{Q}_{P_i}^{2m^{\prime }}\right).$

Then, P_i publishes the location of the measurement and reflection operations. If P_i performs reflection operation, then TP measures each pair of $(Q_{T_i}^j{Q}_{P_i}^{j^{\prime }})$ with Bell basis. On the basis of the entanglement properties of the GHZ-type state in Eq. 1, the measurement result should be |ϕ⁺⟩ or |ψ⁺⟩. If |ϕ⁻⟩ or |ψ⁻⟩ emerge in the measurement result, it means that there are eavesdroppers in the channel. After determines that there is no eavesdropper, the protocol will continue to the next step. Otherwise, will restart the protocol.

Step 4. TP removes the particles performing reflection operations. For the remaining particles, TP performs Bell measurement on each $(Q_{T_i}^j{Q}_{P_i}^{j^{\prime }})$. If measurement result is |ϕ^±⟩, TP sets $E_i^j=0$; and if measurement result is |ψ^±⟩, TP sets $E_i^j=1$. Then, TP performs measurement operation with Z basis on $Q_{T{P}_i}^j$ and forms the measurement results to a sequence C_i. If measured result is |0⟩, then $C_i^j=0$; if measured result is |1⟩, then $C_i^j=1$.

For j = 1, 2, …, m: TP calculates:

$T_j=\sum _{i=1}^{n-1}{E}_i^j\oplus C_i^j\oplus E_{i+1}^j\oplus C_{i+1}^j.$

If T_j = 0 for all j in the end, TP will announce that the private information X_i are equal. Otherwise, he will announce that the private information X_i are not equal.

For clarity, Figure 1 display the flow chart about the process of the above steps.

FIGURE 1

FIGURE 1. Process of the proposed SQPC protocol.

2.3 Correctness

The correctness of the proposed protocol has been demonstrated in this subsection. P_i’s private information X_i are encoded as $R_i^j=x_i^j\oplus k_P^j$. According to the rules for generating quantum states in step 2, we can deduce:

$\begin{array}{c}\hfill Q_{P_i}^{j\prime }=Q_{P_i}^j\oplus R_i^j=Q_{P_i}^j\oplus x_i^j\oplus k_P^j.\end{array}(4)$

In step 4, TP performs Bell measurement on $(Q_{T_i}^j{Q}_{P_i}^{j^{\prime }})$, and assigns value to $E_i^j$ according to the measurement result. Apparently, it can be derived that:

$\begin{array}{c}\hfill E_i^j=Q_{T_i}^j\oplus Q_{P_i}^{j^{\prime }}.\end{array}(5)$

According to Eqs. 1, 4, 5, we will obtain:

$\begin{array}{ll}\hfill T_j& =\sum _{i=1}^{n-1}{E}_i^j\oplus C_i^j\oplus E_{i+1}^j\oplus C_{i+1}^j\hfill \\ \hfill & =\sum _{i=1}^{n-1}{Q}_{T_i}^j\oplus Q_{P_i}^{j^{\prime }}\oplus Q_{T{P}_i}^j\oplus Q_{T_{i+1}}^j\oplus Q_{P_{i+1}}^{j^{\prime }}\oplus Q_{T{P}_{i+1}}^j\hfill \\ \hfill & =\sum _{i=1}^{n-1}{Q}_{T_i}^j\oplus Q_{P_i}^j\oplus R_i^j\oplus Q_{T{P}_i}^j\oplus Q_{T_{i+1}}^j\oplus Q_{P_{i+1}}^j\oplus R_{i+1}^j\oplus Q_{T{P}_{i+1}}^j\hfill \\ \hfill & =\sum _{i=1}^{n-1}{R}_i^j\oplus R_{i+1}^j\hfill \\ \hfill & =\sum _{i=1}^{n-1}{x}_i^j\oplus k_P^j\oplus x_{i+1}^j\oplus k_P^j\hfill \\ \hfill & =\sum _{i=1}^{n-1}{x}_i^j\oplus x_{i+1}^j.\hfill \end{array}(6)$

If T_j = 0 for all j in the end, TP will announce that the private information X_i are equal. Therefore, by measuring the particles in his hand, TP can easily compare the equality of all participants’ secrets.

3 Analysis

According to whether the attacker participates in the protocol, there are two kinds of attack: outsider attack and insider attack. First, we demonstrate that four common outsider attack our protocol can resist four common outsider attack. Second, the analysis of the n − 1 participant collusion attack and the TP attack proves that this protocol also has ability resistant to insider attack. Therefore, this protocol can guarantee the privacy of secrets while comparing the equality of secrets among participants.

3.1 Outsider attack

Assuming that Eve is an outsider eavesdropper, he launches some well-known attacks on the transmitted particles to obtains participant’s secret $x_i^j$.

Case 1. Intercept–resend attack

Eve intercepts $S_{P_i}$. Then, Eve generates a fake sequence $S_{Pi}^{*}$ and transmites to P_i. As described in step 2, P_i randomly chooses measurement or reflection operation, he sends $S_{Pi}^{\ast \prime }$ back to TP. At this time, Eve also intercepts $S_{Pi}^{\ast \prime }$ and sends $S_{P_i}$ back to TP. Eve measures the sequence $S_{Pi}^{\ast \prime }$ according to the positions of the measurement operation and reflection operation announced by P_i, and obtains the value of $R_i^j=x_i^j\oplus k_P^j$. However, since Eve does not know the shared key $k_P^j$, he cannot infer the participant’s private information $x_i^j$ from $R_i^j$.

Case 2. Measure-resend attack

Eve intercepts the sequence $S_{P_i}$ sent by TP to P_i. Then, Eve uses Z basis to measures them and the measured sequence is sent to P_i. Nevertheless, in this case, Eve will be detected since he does not know whether P_i will choose the measurement operation or the reflection operation in step 2. If P_i performs the measurement operation, Eve’s attack will not be found. If P_i performs the reflection operation, Eve’s attack will be found. For example, suppose that $Q_{T_i}^j{Q}_{P_i}^j$ is |ϕ⁺⟩, Eve measures the sequence $S_{P_i}$ with the Z basis. Then, |ϕ⁺⟩ will randomly collapse to |00⟩ or |11⟩. Eve sends the measured sequence to P_i. When TP uses Bell measurement to check the entanglement result of the corresponding reflected qubits in $Q_{T_i}^j{Q}_{P_i}^{j\prime }$, the measurement result will be |ϕ⁺⟩ or |ϕ⁻⟩. If the measurement is |ϕ⁻⟩, Eve will be found. In this case, the detection probability for the proposed protocol is $1-{(\frac{1}{2})}^m$. The detection probability is approximate to 1 when m is large enough.

Case 3. Entangle-measure attack

We assume that |e⟩ is an ancillary qubit generated by Eve and U_E is the unitary operation. The unitary operation U_E can be described as follows:

$\begin{array}{c}\hfill U_E|0\rangle |e\rangle =a|0\rangle |e_{00}\rangle +b|1\rangle |e_{01}\rangle ,\end{array}(7)$

$\begin{array}{c}\hfill U_E|1\rangle |e\rangle =c|0\rangle |e_{10}\rangle +d|1\rangle |e_{11}\rangle ,\end{array}(8)$

where |e₀₀⟩, |e₀₁⟩, |e₁₀⟩, |e₁₁⟩ are pure states uniquely determined by U_E; |a|² + |b|² = 1, and |c|² + |d|² = 1.

According to the entanglement properties of quantum state |φ⟩, TP can deduce the state of $(Q_{T_i}^j,Q_{P_i}^j)$ through the measurement result of $Q_{T{P}_i}^j$. If the measurement result of $Q_{T{P}_i}^j$ is |0⟩, the $(Q_{T_i}^j,Q_{P_i}^j)$ should be |ϕ⁺⟩. If the measurement result of $Q_{T{P}_i}^j$ is |1⟩, the $(Q_{T_i}^j,Q_{P_i}^j)$ should be |ψ⁺⟩. Here, we take $(Q_{T_i}^j,Q_{P_i}^j)$ is |ϕ⁺⟩ as an example to analyze the entangle-measure attack in this protocol.

Eve intercepts the sequence $S_{P_i}$ and entangles the particles in the sequence $S_{P_i}$ with |e⟩ through the integer transformation U_E. After that, the quantum system becomes

$\begin{array}{ll}\hfill U_e|{\varphi }^{+}\rangle |e\rangle & =\frac{1}{\sqrt{2}}\left[|0\rangle \left(a|0\rangle |e_{00}\rangle +b|1\rangle |e_{01}\rangle \right)+|1\rangle \left(c|0\rangle |e_{10}\rangle +d|1\rangle |e_{11}\rangle \right)\right]\hfill \\ \hfill & =\frac{1}{\sqrt{2}}\left[a|00\rangle |e_{00}\rangle +b|01\rangle |e_{01}\rangle +c|10\rangle |e_{11}\rangle +d|1\rangle |e_{11}\rangle \right]\hfill \\ \hfill & =\frac{1}{2}\left[a\left(|{\varphi }^{+}\rangle +|{\varphi }^{-}\rangle \right)|e_{00}\rangle +b\left(|{\psi }^{+}\rangle -|{\psi }^{-}\rangle \right)\right.\hfill \\ \hfill & \left.+c\left(|{\psi }^{+}\rangle +|{\psi }^{-}\rangle \right)|e_{10}\rangle +d\left(|{\varphi }^{+}\rangle -|{\varphi }^{-}\rangle \right)|e_{11}\rangle \right].\hfill \end{array}(9)$

In order to prevent Eve’s attack from being detected, the result of measuring the reflected particle $(Q_{T_i}^j,Q_{P_i}^j)$ with the Bell basis should be |ϕ⁺⟩. As a result, we can deduce that:

$b=c=0,a=d=1,$

$|e_{00}\rangle =|e_{11}\rangle .$

Then, the Eq. 9 can be rewritten as:

$\begin{array}{c}\hfill U_e|{\varphi }^{+}\rangle |e\rangle =\frac{1}{2}\left[a\left(|{\varphi }^{+}\rangle +|{\varphi }^{-}\rangle \right)|e_{00}\rangle +d\left(|{\varphi }^{+}\rangle -|{\varphi }^{-}\rangle \right)|e_{11}\rangle \right]=|{\varphi }^{+}\rangle |e_{00}\rangle .\end{array}(10)$

It is easy to find that if Eve wants to obtain X_i through ancillary qubits, some error must be introduced and his attack must be detected.

Case 4. Double CNOT attack

Subsequently, we analyze the security of the protocol under the double CNOT attack. For simplicity, we suppose that |z⟩(|z⟩ ∈ {|0⟩, |1⟩}) is an ancillary qubit produced by Eve and |φ⟩ is GHZ-type state produced by TP. Eve performs the first CNOT operation on the intercepted sequence $S_{P_i}$ and the ancillary qubit |z⟩. After that, Eve sends $S_{P_i}$ directly to P_i without any interference, and the ancillary qubit |z⟩ becomes |z′⟩. At this point, the whole quantum system is:

$\begin{array}{c}\hfill |\phi {\rangle }_1=CNOT\left(|\phi {\rangle }_{123}\otimes |z{\rangle }_E\right)=\frac{1}{2}{\left(|000z\rangle +|011\bar{z}\rangle +|101\bar{z}\rangle +|110z\rangle \right)}_{123E}\end{array}(11)$

After P_i receives $S_{P_i}$, he chooses reflection or measurement operation at random and send $S_{P_i}^{\prime }$ to TP. Eve performs the second CNOT operation on the intercepted sequence $S_{P_i}^{\prime }$ and the ancillary qubit |z′⟩. Based on the different operations chosen by P_i, we divide the attack into two situations.

• Situation 1: P_i chooses the reflection operation

In this situation, P_i performs reflection operation and do not cause any disturbance to the particles. Therefore, after the second CNOT operation, the whole quantum system becomes:

$\begin{array}{ll}\hfill |\phi {\rangle }_2& =CNOT\left(\frac{1}{2}{\left(|000z\rangle +|011\bar{z}\rangle +|101\bar{z}\rangle +|110z\rangle \right)}_{123E}\right)\hfill \\ \hfill & =\frac{1}{2}{\left(|000\rangle +|011\rangle +|101\rangle +|110\rangle \right)}_{123}\otimes |z{\rangle }_E\hfill \end{array}(12)$

Obviously, the ancillary qubit |z⟩ have not changed after two CNOT operations, thus Eve cannot get any information from the ancillary qubit |z⟩.

• Situation 2: P_i chooses the measurement operation

In this situation, P_i performs the measurement operation and produces a particle that is inverse or the same as the measurement depending on $R_i^j$. Since $R_i^j$ can be either 0 or 1, |φ⟩₁ collapses to ${(|000z\rangle +|011\bar{z}\rangle )}_{123E}$ or ${(|101\bar{z}\rangle +|110z\rangle )}_{123E}$. Then Eve performs the second CNOT operation, the whole quantum system becomes:

$\begin{array}{ll}\hfill |\phi {\rangle }_3& =CNOT\left(|0{\rangle }_F\otimes \frac{1}{2}{\left(|000z\rangle +|011\bar{z}\rangle +|101\bar{z}\rangle +|110z\rangle \right)}_{123E}\right)\hfill \\ \hfill & =\left.|0{\rangle }_F\otimes \frac{1}{2}{\left(|000z\rangle +|011\bar{z}\rangle +|101\bar{z}\rangle +|110z\rangle \right)}_{123E}\right)\hfill \end{array}(13)$

or

$\begin{array}{ll}\hfill |\phi {\rangle }_4& =CNOT\left(|1{\rangle }_F\otimes \frac{1}{2}{\left(|000z\rangle +|011\bar{z}\rangle +|101\bar{z}\rangle +|110z\rangle \right)}_{123E}\right)\hfill \\ \hfill & =\left.|1{\rangle }_F\otimes \frac{1}{2}{\left(|000\bar{z}\rangle +|011z\rangle +|101z\rangle +|110\bar{z}\rangle \right)}_{123E}\right).\hfill \end{array}(14)$

Eve can judge whether ancillary qubit have changed by measuring. Based on Eqs. 13, 14, the probability of measuring $|\bar{z}\rangle$ is 50%.

According to the above analysis, we summarize the double CNOT attack as follows:

(1) If Eve measures ancillary qubits and the result is |z⟩, then Eve does not get any private information of P_i.

(2) If Eve measures ancillary qubits and the result is $|\bar{z}\rangle$, then Eve adopts Z basis to measure the sequence $S_{P_i}^{\prime }$ to obtain $Q_{P_i}^{j\prime }=x_i^j\oplus Q_{P_i}^j\oplus k_i^j$. However, Eve does not know the shared key $k_i^j$, thus he cannot deduce the private information $x_i^j$.

According to the analysis, double CNOT attack cannot create a threat to this protocol.

Case 4. Trojan horse attack

As the proposed protocol is a two-way communication protocol, Eve may performs the Trojan horse attack [38] on the sequence $S_{P_i}$ to obtain beneficial information. However, this attack can be easily prevented by using the photon number splitter and the optical wavelength filter devices [39, 40] to detect the Trojan-Horse photons.

Therefore, we proved that the outsider attack can be detected in the proposed SQPC protocol.

3.2 Insider attack

In 2007, Gao et al. [41] proposed that we should pay more attention to attacks from participants because they participated in the implementation of the protocol. In this subsection, we show that the protocol is resistant to participants collusion attack and TP attack.

Case 1. Participants attack

We only consider the worst circumstances that n − 1 dishonest parties conspired to obtain the remaining participant’s private information, because in this situation the threat to the protocol is the greatest. We assume that the dishonest parties P₁, P₂, …, P_i−1, P_i+1, …, P_n who collude with each other in an attempt to obtain P_i’s secrets. In our protocol, the particles are only transmitted between the TP and the participants, and no particles are transmitted among the participants, so n participants are independent and do not interfere with each other. In order to obtain the secret of P_i, dishonest parties try to launch attacks during particle teleportation. For example, dishonest parties launches measure-resend attack to learn sequence $S_{P_i}$. Then, they send $S_{P_i}^{*}$ back to P_i, where $S_{P_i}^{*}$ is $S_{P_i}$ after dishonest parties’ operations. The reflection operation or measurement operation performed by P_i in step 2 is randomly selected, and the dishonest participant can only guess the correct operation with a probability of $\frac{1}{2}$. Therefore, his attack will definitely be detected during the eavesdropping detection. When there are m particles for security detection, the probability of dishonest participants being detected is $1-{(\frac{1}{2})}^m$. As the value of m increases, the probability of an attack being detected gradually approaches to 1.

Hence, the dishonest have no chance to obtain the secret of P_i.

Case 2. TP attack

In the first prerequisite of our protocol, TP is supposed to be a semi-honest who will do his best to learn participants’ secret information, but does not collude with either of them. Without loss of generality, we suppose that TP wants to learn the secret of P_i.

The only way for TP to get X_i is to measure the particles $Q_{P_i}^{j\prime }$ in sequence $S_{P_i}^{\prime }$ with Z basis. In step 2, we can deduce that $Q_{P_i}^{j\prime }=Q_{P_i}^j\oplus x_i^j\oplus k_P^j$. Even though TP can get $Q_{P_i}^{j\prime }$ and $Q_{P_i}^j$ from the measurement, he still cannot deduce the private information of P_i, since the pre-shared key K_P is used to encrypt X_i, and he has no knowledge about K_P.

Therefore, the attack of TP is invalid for this protocol.

4 Comparison

In this section, we compare some existing protocol with our protocol. Qubit efficiency is an important indicator for evaluating SQPC protocols. Here, the qubit efficiency is defined as

${\eta }_e=\frac{c}{q+b},$

where c represents the amount of classical information involved in the comparison, and q denotes the number of all particles consumed during the comparison, and b is the total number of classical bits consumed when decoding private information (classic communication for security detection is not included). In this paper, each classical participants have m classical bits respectively, and they compare nm classical bits in total. Then, to compare nm bits of private information, TP is required to generate 2nm three-qubit entangle state (6mn bit qubits). During protocol execution, each of P_i choose measurement operation with $\frac{1}{2}$ probability, and they prepare m qubits. Furthermore, our protocol use the SQKD protocol [42] to generate m bits pre-shared key which consumes 24m qubits and 16m bit to generate one key. Then we can get q = 6mn + mn + 40m = 7mn + 40m. As for the number of classical bits consumed in the protocol, P_i does not need to publish information in the classic channel, and TP demands a classical bit to publish the comparison result. Thus, b = 1. In summary, the qubit efficiency of this paper is $\frac{nm}{7mn+40m+1}$. Using the same method, we can calculate the qubit efficiency of other related protocols, and the comparison results are shown in Table 1.

TABLE 1

TABLE 1. The comparison of our protocol to the other protocols.

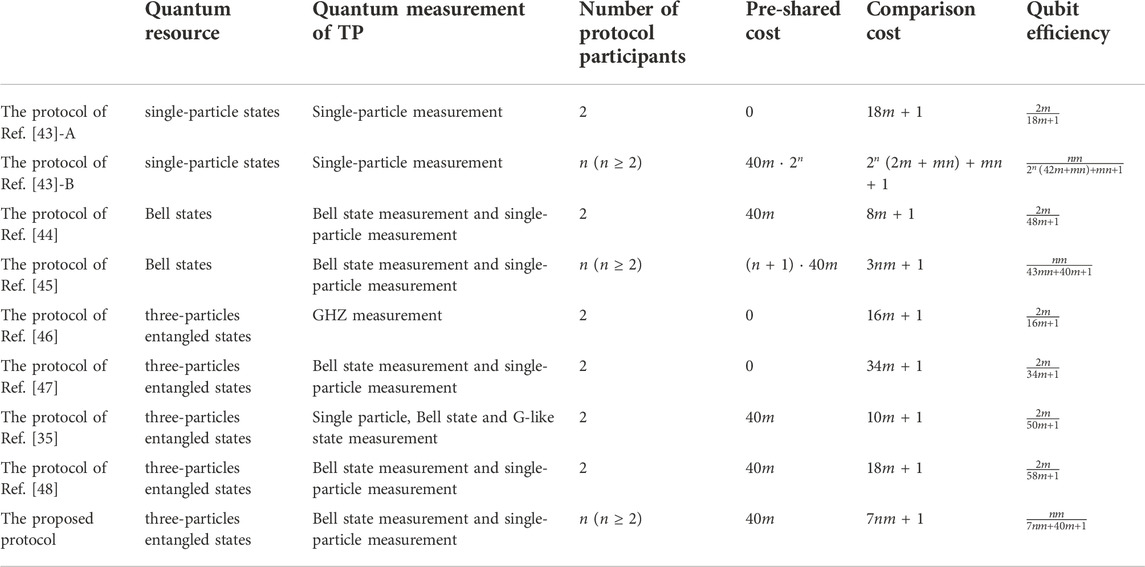
Next, the advantages of our protocol compared to existing SQPC protocols are analyzed. It should be note that there are two SQPC protocols in Ref. [43], which we denote by Ref. [43]-A and Ref. [43]-B respectively.

First, in terms of qubit efficiency, the proposed protocol has advantages over the existing SQPC protocols. It is apparent from Table 1, our protocol is more efficient than multi-party SQPC protocols Ref. [43]-B and Ref. [45]. Although the proposed protocol, Ref. [43]-B and Ref. [45] all generate the shared key using the SQKD protocol, we only need one shared key sequence while Ref. [43]-B and Ref. [45] require n + 1 shared keys sequences. As we all know, the shared key needs to consume a large number of qubits. Excessive demand for the shared key will increase the total number of qubits transmitted and reduce the efficiency of the protocol. Moreover, comparing with the current two-party protocols Ref. [43]-A, Ref. [35, 44, 46, 47, 48], our proposed protocol still has superiorities in quantum efficiency. When using two-party SQPC protocols to compare the private information of n participants, the protocol need to be executed n − 1 times. Repeating the protocol many times will increase the total number of transmitted qubits and reduce the efficiency of the protocol.

Second, our protocol does not use classical channels to transmit information except for security check steps. Most of the SQPC protocols now use quantum technology and classical computing to achieve comparison while ensuring security. As a result, there are usually quantum and classical two kinds of signals to process. The protocols in Refs. [35, 43–48] use the classical channel to transmit information, which increase the risk of classical attacks since the classical channel is the part with weak security. In order to improve the SQPC security, our protocol directly encodes the secret value of the participant to the quantum state through the measure-resend operation. And there is no classical channel to transmit information, which greatly reduces the classical attack and improves the security of the protocol.

Third, our protocol is more flexible, which is possible to compare the equality of any two participants. However, the SQPC protocols [35, 44, 46, 47, 48] can only compare the equality of two parties. When there are n (n ≥ 2) participants, the protocol needs to be executed n − 1 times, which is not only inefficient but also wastes quantum resources. The protocol proposed in this paper can compare the equality of multiple participants at one time, and can be flexibly applied to various situations.

Finally, semi-quantum protocol settles the problem that quantum communication network is restricted by expensive quantum devices. In the proposed protocol, participants in the protocol only need to have basic quantum abilities such as quantum measurement and quantum preparation, and complete the equality comparison of private information with the help of the third party quantum server. Quantum servers can be configured to the cloud and leased when users need to use them. In addition, The GHZ state we used has been proved in Ref. [49] that it can be prepared by the current quantum technology. Therefore, our protocol can be realized.

5 Conclusion

To sum up, we construct a SQPC protocol using the maximally entangled GHZ-type state. n classical participants can compare their secrets for equality via one execution of the protocol without leaking them. Comparing our protocol with some previous SQPC protocols in Section 4, it can be observed that the proposed protocol has obvious advantages in terms of flexibility and efficiency. Security analysis shows that both outsider and insider attacks are ineffective against this protocol. What is more, the participants in the SQPC protocol only need to perform a few limited operations, which reduces the cost of quantum resources to a certain extent. The SQPC protocol can be extended to more applications, because the quantum operations used in this paper can be implemented according to existing quantum technologies.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Funding

The authors are supported by the Science and technology research project of Hebei higher education Nos. ZD2021011.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Yao AC. Protocols for secure computations. In: 23rd annual symposium on foundations of computer science (sfcs 1982); 03-05 November 1982; Chicago, IL, USA. IEEE (1982). 160–4.

CrossRef Full Text | Google Scholar

2. Bennett CH, Brassard G (2020). Quantum cryptography: Public key distribution and coin tossing. arXiv preprint arXiv:2003.06557.

Google Scholar

3. Xu F, Ma X, Zhang Q, Lo HK, Pan JW. Secure quantum key distribution with realistic devices. Rev Mod Phys (2020) 92(2):025002. doi:10.1103/revmodphys.92.025002

CrossRef Full Text | Google Scholar

4. Lucamarini M, Yuan ZL, Dynes JF, Shields AJ. Overcoming the rate–distance limit of quantum key distribution without quantum repeaters. Nature (2018) 557(7705):400–3. doi:10.1038/s41586-018-0066-6

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Ye TY, Li HK, Hu JL. Semi-quantum key distribution with single photons in both polarization and spatial-mode degrees of freedom. Int J Theor Phys (Dordr) (2020) 59(9):2807–15. doi:10.1007/s10773-020-04540-y

CrossRef Full Text | Google Scholar

6. Ye TY, Geng MJ, Xu TJ, Chen Y. Efficient semiquantum key distribution based on single photons in both polarization and spatial-mode degrees of freedom. Quan Inf Process (2022) 21(4):123–1. doi:10.1007/s11128-022-03457-1

CrossRef Full Text | Google Scholar

7. Ye TY, Li HK, Hu JL. Information leakage resistant quantum dialogue with single photons in both polarization and spatial-mode degrees of freedom. Quan Inf Process (2021) 20(6):209–13. doi:10.1007/s11128-021-03120-1

CrossRef Full Text | Google Scholar

8. Qi JM, Xu G, Chen XB, Wang TY, Cai XQ, Yang YX. Two authenticated quantum dialogue protocols based on three-particle entangled states. Quan Inf Process (2018) 17(9):247–19. doi:10.1007/s11128-018-2005-8

CrossRef Full Text | Google Scholar

9. Ye TY, Hu JL. Quantum secure multiparty summation based on the phase shifting operation of d-level quantum system and its application. Int J Theor Phys (Dordr) (2021) 60(3):819–27. doi:10.1007/s10773-020-04700-0

CrossRef Full Text | Google Scholar

10. Ye TY, Xu TJ, Geng MJ, Chen Y. Two-party secure semiquantum summation against the collective-dephasing noise. Quan Inf Process (2022) 21(3):118–4. doi:10.1007/s11128-022-03459-z

CrossRef Full Text | Google Scholar

11. Shi J, Chen S, Lu Y, Feng Y, Shi R, Yang Y, et al. An approach to cryptography based on continuous-variable quantum neural network. Sci Rep (2020) 10(1):2107–13. doi:10.1038/s41598-020-58928-1

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Qi R, Sun Z, Lin Z, Niu P, Hao W, Song L, et al. Implementation and security analysis of practical quantum secure direct communication, Light. Sci Appl (2019) 8(1):1–8.

CrossRef Full Text | Google Scholar

13. Feng Y, Shi R, Shi J, Zhou J, Guo Y. Arbitrated quantum signature scheme with quantum walk-based teleportation. Quan Inf Process (2019) 18(5):154–21. doi:10.1007/s11128-019-2270-1

CrossRef Full Text | Google Scholar

14. Shi J, Chen S, Liu J, Li F, Feng Y, Shi R. Quantum dual signature with coherent states based on chained phase-controlled operations. Appl Sci (2020) 10(4):1353. doi:10.3390/app10041353

CrossRef Full Text | Google Scholar

15. Feng Y, Shi R, Shi J, Zhao W, Lu Y, Tang Y. Arbitrated quantum signature protocol with boson sampling-based random unitary encryption. J Phys A: Math Theor (2020) 53(13):135301. doi:10.1088/1751-8121/ab766d

CrossRef Full Text | Google Scholar

16. Feng Y, Zhou J, Li J, Zhao W, Shi J, Shi R, et al. Skc-ccco: An encryption algorithm for quantum group signature. Quan Inf Process (2022) 21(9):328–9. doi:10.1007/s11128-022-03664-w

CrossRef Full Text | Google Scholar

17. Yang YG, Wen QY. An efficient two-party quantum private comparison protocol with decoy photons and two-photon entanglement. J Phys A: Math Theor (2009) 42(5):055305. doi:10.1088/1751-8113/42/5/055305

CrossRef Full Text | Google Scholar

18. Wu W, Zhou G, Zhao Y, Zhang H. New quantum private comparison protocol without a third party. Int J Theor Phys (Dordr) (2020) 59(6):1866–75. doi:10.1007/s10773-020-04454-9

CrossRef Full Text | Google Scholar

19. Huang X, Zhang S-B, Chang Y, Hou M, Cheng W. Efficient quantum private comparison based on entanglement swapping of bell states. Int J Theor Phys (Dordr) (2021) 60(10):3783–96. doi:10.1007/s10773-021-04915-9

CrossRef Full Text | Google Scholar

20. Wu W, Zhang H. Cryptanalysis of zhang et al’s quantum private comparison and the improvement. Int J Theor Phys (Dordr) (2019) 58(6):1892–900. doi:10.1007/s10773-019-04084-w

CrossRef Full Text | Google Scholar

21. Wu W, Ma X. Quantum private comparison protocol without a third party. Int J Theor Phys (Dordr) (2020) 59(6):1854–65. doi:10.1007/s10773-020-04453-w

CrossRef Full Text | Google Scholar

22. Lang Y-F. Quantum private comparison without classical computation. Int J Theor Phys (Dordr) (2020) 59(9):2984–92. doi:10.1007/s10773-020-04559-1

CrossRef Full Text | Google Scholar

23. Xu Q-D, Chen H-Y, Gong L-H, Zhou N-R. Quantum private comparison protocol based on four-particle ghz states. Int J Theor Phys (Dordr) (2020) 59(6):1798–806. doi:10.1007/s10773-020-04446-9

CrossRef Full Text | Google Scholar

24. Ji Z, Zhang H, Wang H. Quantum private comparison protocols with a number of multi-particle entangled states. IEEE Access (2019) 7:44613–21. doi:10.1109/access.2019.2906687

CrossRef Full Text | Google Scholar

25. Ji ZX, Ye TY. Quantum private comparison of equal information based on highly entangled six-qubit genuine state. Commun Theor Phys (2016) 65(6):711–5. doi:10.1088/0253-6102/65/6/711

CrossRef Full Text | Google Scholar

26. Ye T-Y, Ji Z-X. Two-party quantum private comparison with five-qubit entangled states. Int J Theor Phys (Dordr) (2017) 56(5):1517–29. doi:10.1007/s10773-017-3291-0

CrossRef Full Text | Google Scholar

27. Julsgaard B, Sherson J, Cirac JI, Fiurášek J, Polzik ES. Experimental demonstration of quantum memory for light. Nature (2004) 432(7016):482–6. doi:10.1038/nature03064

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Yao XC, Wang TX, Xu P, Lu H, Pan GS, Bao XH, et al. Observation of eight-photon entanglement. Nat Photon (2012) 6(4):225–8. doi:10.1038/nphoton.2011.354

CrossRef Full Text | Google Scholar

29. Nielsen MA, Chuang I. Quantum computation and quantum information. Cambridge University Press (2002).

Google Scholar

30. Boyer M, Kenigsberg D, Mor T. Quantum key distribution with classical bob. In: 2007 First International Conference on Quantum, Nano, and Micro Technologies (ICQNM’07); 02-06 January 2007; Guadeloupe, French Caribbean. IEEE (2007). p. 10.

CrossRef Full Text | Google Scholar

31. Boyer M, Gelles R, Kenigsberg D, Mor T. Semiquantum key distribution. Phys Rev A (Coll Park) (2009) 79(3):032341. doi:10.1103/physreva.79.032341

CrossRef Full Text | Google Scholar

32. Chou WH, Hwang T, Gu J (2016). Semi-quantum private comparison protocol under an almost-dishonest third party. arXiv preprint arXiv:1607.07961.

Google Scholar

33. Ye TY, Ye CQ. Measure-resend semi-quantum private comparison without entanglement. Int J Theor Phys (Dordr) (2018) 57(12):3819–34. doi:10.1007/s10773-018-3894-0

CrossRef Full Text | Google Scholar

34. Lin PH, Hwang T, Tsai CW. Efficient semi-quantum private comparison using single photons. Quan Inf Process (2019) 18(7):207–14. doi:10.1007/s11128-019-2251-4

CrossRef Full Text | Google Scholar

35. Yan L, Zhang S, Chang Y, Wan G, Yang F. Semi-quantum private comparison protocol with three-particle g-like states. Quan Inf Process (2021) 20(1):17–6. doi:10.1007/s11128-020-02960-7

CrossRef Full Text | Google Scholar

36. Zhou NR, Xu QD, Du NS, Gong LH. Semi-quantum private comparison protocol of size relation with d-dimensional bell states. Quan Inf Process (2021) 20(3):124–15. doi:10.1007/s11128-021-03056-6

CrossRef Full Text | Google Scholar

37. Tang YH, Jia HY, Wu X, Chen HM, Zhang YM. Robust semi-quantum private comparison protocols against collective noises with decoherence-free states. Quan Inf Process (2022) 21(3):97–24. doi:10.1007/s11128-022-03444-6

CrossRef Full Text | Google Scholar

38. Cai QY. Eavesdropping on the two-way quantum communication protocols with invisible photons. Phys Lett A (2006) 351(1-2):23–5. doi:10.1016/j.physleta.2005.10.050

CrossRef Full Text | Google Scholar

39. Deng FG, Li XH, Zhou HY, Zhang Zj. Improving the security of multiparty quantum secret sharing against trojan horse attack. Phys Rev A (Coll Park) (2005) 72(4):044302. doi:10.1103/physreva.72.044302

CrossRef Full Text | Google Scholar

40. Deng FG, Zhou P, Li XH, Li CY, Zhou HY (2005). Robustness of two-way quantum communication protocols against trojan horse attack. arXiv preprint quant-ph/0508168.

Google Scholar

41. Gao F, Qin S-J, Wen Q-Y, Zhu F-C. A simple participant attack on the brádler-dušek protocol. Quan Inf Comput (2007) 7(4):329–34. doi:10.26421/qic7.4-4

CrossRef Full Text | Google Scholar

42. Krawec WO. Mediated semiquantum key distribution. Phys Rev A (Coll Park) (2015) 91:032323. doi:10.1103/physreva.91.032323

CrossRef Full Text | Google Scholar

43. Chongqiang Y, Jian L, Xiubo C, Yuan T. Efficient semi-quantum private comparison without using entanglement resource and pre-shared key. Quan Inf Process (2021) 20(8):262–19. doi:10.1007/s11128-021-03194-x

CrossRef Full Text | Google Scholar

44. Jiang LZ. Semi-quantum private comparison based on bell states. Quan Inf Process (2020) 19(6):180–21. doi:10.1007/s11128-020-02674-w

CrossRef Full Text | Google Scholar

45. Li Z, Liu T, Zhu H. Private comparison protocol for multiple semi-quantum users based on bell states. Int J Theor Phys (Dordr) (2022) 61(6):177–12. doi:10.1007/s10773-022-05167-x

CrossRef Full Text | Google Scholar

46. Yan L, Chang Y, Zhang S, Wang Q, Sheng Z, Sun Y. Measure-resend semi-quantum private comparison Scheme 燯 sing GHZ class states. Comput Mater Contin (2019) 61(2):877–87. doi:10.32604/cmc.2019.06222

CrossRef Full Text | Google Scholar

47. Tian Y, Li J, Chen XB, Ye CQ, Li CY, Hou YY. An efficient semi-quantum private comparison without pre-shared keys. Quan Inf Process (2021) 20(11):360–13. doi:10.1007/s11128-021-03294-8

CrossRef Full Text | Google Scholar

48. Tian Y, Li J, Ye C, Chen XB, Li C. W-state-based semi-quantum private comparison. Int J Theor Phys (Dordr) (2022) 61(2):18–6. doi:10.1007/s10773-022-05005-0

CrossRef Full Text | Google Scholar

49. Li Q, Chan WH, Long DY. Semiquantum secret sharing using entangled states. Phys Rev A (Coll Park) (2010) 82(2):022303. doi:10.1103/physreva.82.022303

CrossRef Full Text | Google Scholar