- 1College of Sciences, Inner Mongolia University of Technology, Hohhot, China
- 2Inner Mongolia Key Laboratory of Statistical Analysis Theory for Life Data and Neural Network Modeling, Hohhot, China
- 3Department of Mathematics and Computer Science, Hetao College, Bayannur, China
- 4College of Science, Liaoning University of Technology, Jinzhou, China
In this paper, the Mohand transform-based homotopy perturbation method is proposed to solve two-dimensional linear and non-linear shallow water wave equations. This approach has been proved suitable for a broad variety of non-linear differential equations in science and engineering. The variation trend of the water surface elevation at different time levels and depths are given by some graphs. Moreover, the obtained solutions are compared with the existing results, which show higher efficiency and fewer computations than other approaches studied in the literature.
1 Introduction
Water waves that have a horizontal scale much larger than the depth of the fluid are considered shallow water waves (SWWs). SWWs describe the evolution of incompressible flow, neglecting density change along the depth, which are widely used to simulate the propagation of tsunami waves, tidal currents, storm floods, and shock waves [1–5]. Karunakar and Chakraverty applied the homotopy perturbation method (HPM) to solve linear and non-linear one-dimensional shallow water wave equations (SWWEs) [1], while the two-dimensional equations were solved in [6]. Sahoo and Chakraverty [7] used the Sawi transform-based homotopy perturbation method to solve the one-dimensional SWWEs. The application of the variational iteration method and homotopy perturbation method (HPM) was given in [8] for solving one-dimensional shallow water equations with crisp and fuzzy uncertain initial conditions. Noeiaghdam and Sidorov [9] used the homotopy analysis method to solve the non-linear shallow water wave equation. Safari [10] gave solutions to two extended model equations for shallow water waves by He’s variational iteration method. In [11], the Adomian decomposition method was used to solve two extended model equations for SWWEs. In addition, Bekir and Aksoy [12] applied the Exp-function method to construct exact solutions to non-linear wave equations.
Mohand transform (MT) [13] is an integral transformation, which is obtained from the classical Fourier integral, and it was initiated by Mohand Mahgoub to solve some integral and differential equations (14–16). Khandelwal [17] combined the Adomian decomposition method and Mohand transform for solving a differential equation of mixing layers that arise in a viscous incompressible form. The comparison of two integral transforms between Mohand and Laplace is given in [18]; the results show that the two transforms are closely related. Aggarwal, Sharma, and Chauhan [19] gave the duality relations of Kamal transform with Laplace, Laplace−Carson, Aboodh, Sumudu, Elzaki, Mohand, and Sawi transforms [20]. They used an effective scheme based on Mohand transform and the homotopy perturbation method to find numerical solutions to non-linear fractional shock wave equations. Althobaiti, Dubey, and Prasad [21] presented the local fractional Mohand transform with the Adomian decomposition method to solve the local fractional generalized Fokker–Planck equation. Shah, Khan, and Farooq et al. [22] employed the Mohand transform to provide the analytical solution to the one-dimensional time fractional system of PDEs.
The homotopy perturbation method (HPM) [23] has been widely used for solving differential and integral equations, which was first proposed and developed by the Chinese mathematician Ji-Huan He [24–28]. Laplace transformation coupled with the homotopy perturbation method is called the He−Laplace method. Madani and Mishra [29, 30] adopted this method to solve non-linear ordinary and partial differential equations. It is proved that this method needs fewer computations and is much easier than other methods. He, Moatimid, and Zekry [31] used the two-scale transforms and He−Laplace method to get an analytic approximate solution to a fractal−differential model [32]. They presented the combination of the enhanced perturbation method and the parameter expansion technology based on Li−He’s approach, aiming to find an approximate solution to the given second-order non-linear ordinary differential equation [33]. They applied the basic idea of the perturbation method to construct a homotopy equation with a higher order; the results show a highly effective obtained solution. The approximation of the damped non-linear Klein–Gordon equation was given [34] by the coupling of the exponential decay parameter with the homotopy perturbation method, which overcomes the shortcomings of the classical method [35]. They used the reducing rank method with the homotopy perturbation method to solve the third-order Duffing equation.
The main purpose of the present work is to solve two-dimensional linear and non-linear shallow water wave equations by coupling Mohand transform with the homotopy perturbation method. The remainder of the paper is organized as follows: in Section 2, we present some preliminaries about shallow water wave equations (SWWEs), Mohand transform (MT), and the homotopy perturbation method (HPM). In Section 3, the Mohand transform (MT)-based homotopy perturbation method (HPM) is applied to solve coupled linear and non-linear SWWEs in two dimensions. In Section 4, the variations in the water surface elevation have been demonstrated at different time levels and depths. Finally, conclusions have been drawn in Section 5.
2 Preliminaries
2.1 Shallow water wave equations (SWWEs)
The linear SWWEs in two dimensions [2, 3] may be given as follows:
As such, the non-linear SWWEs [2, 3] may be written as
where
2.2 Mohand transform (MT) and some of its properties
The Mohand transform of the function
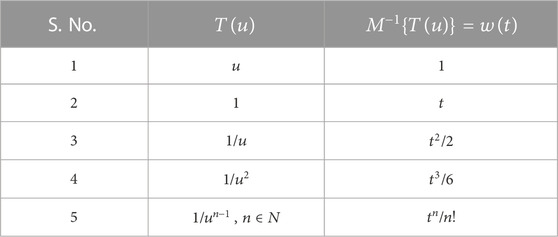
Mohand transform of some useful fundamental functions is given in Table 1.
The linearity property of MT is given as follows [15]: if
Let
The function
2.3 Homotopy perturbation method (HPM)
To illustrate the basic ideas of the HPM [19], we consider the following non-linear differential equation:
with the following boundary conditions:
Here,
The operator
Using the homotopy technique, one may construct a homotopy
or
where
The changing process of
We consider the solution to Eq. 8 as a power series in
The approximate solution to Eq. 5 will be obtained by substituting
3 Approximate solutions to shallow water wave equations using the Mohand transform-based homotopy perturbation method (MHPM)
3.1 Linear shallow water wave equations
In this section, we obtain the series solution to linear two-dimensional shallow water Eq. 1 by the MHPM.
Let us consider the Gaussian initial conditions for
Applying Mohand transform in Eq. 1, we obtain
Using the derivative characteristics of Mohand transform, Eq. 14 may be written as
Taking the inverse of Mohand transform on both sides of Eq. 17, we may obtain the following:
Similarly, on solving Eqs 15, 16 by applying the same aforementioned procedure, we may obtain
Now using the HPM technique, we may construct a homotopy for Eqs 18, 19, 20 in the following form:
By simplifying the aforementioned formulas, we may obtain
Let us consider the solution to Eq. 1 in the power series form as:
we may get the following results by applying Eq. 23 in Eq. 22 and comparing the coefficients of
Comparing the coefficients of
Similarly, comparing the coefficients of
In the same way, by correlating the coefficients of
Finally, by performing MT on the right hand side of Eq. 25 and then taking inverse MT, at a constant depth
We can also get
3.2 Non-linear shallow water wave equations
In this section, we obtain the series solution to the non-linear shallow water wave equation in two-dimensional Eq. 2 using the MHPM with the same initial conditions in Eq. 24.
Applying the MT and HPM in Eq. 2, we may obtain
Here, we again consider the power series solution to Eq. 2 as in (Eq. 23). We may get the following results by substituting Eq. 23 in Eq. 31 and comparing the coefficients of
Comparing the coefficients of
Similarly, comparing the coefficients of
By continuing to compare the coefficients of
By this way, comparing the coefficients of
where
4 Numerical results and discussion
In this section, the results obtained for both linear and non-linear SWWEs have been presented, and the graphs of solutions obtained by the MHPM for various time levels (
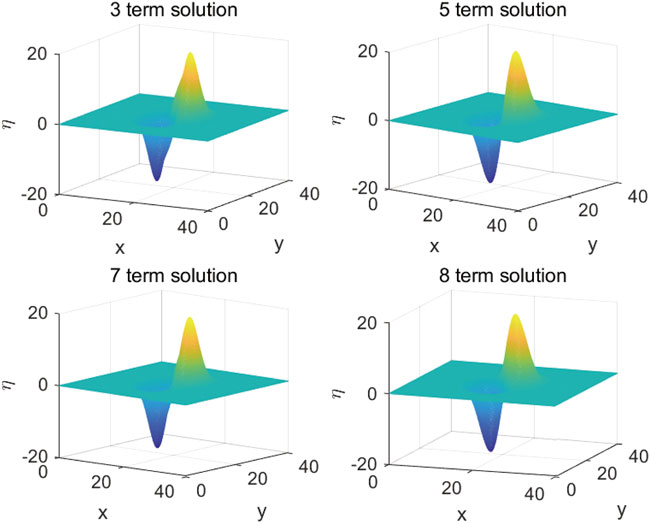
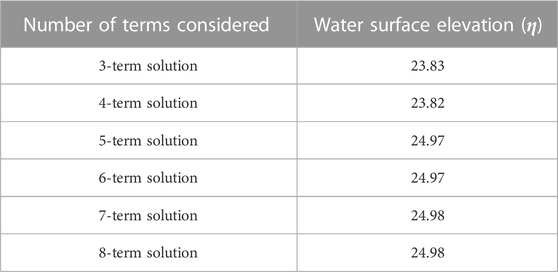
The term-wise solutions in
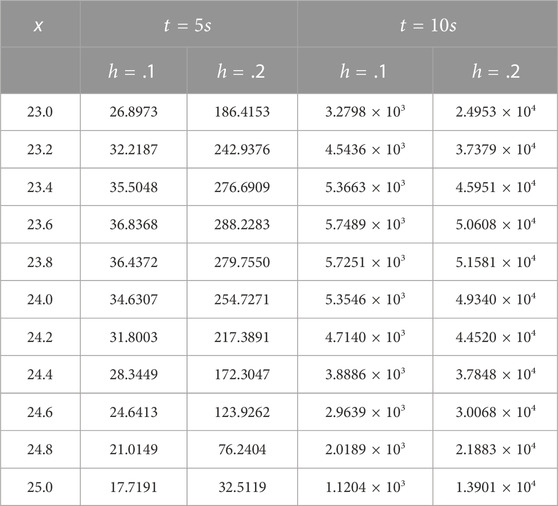
The water surface elevation (WSE) (
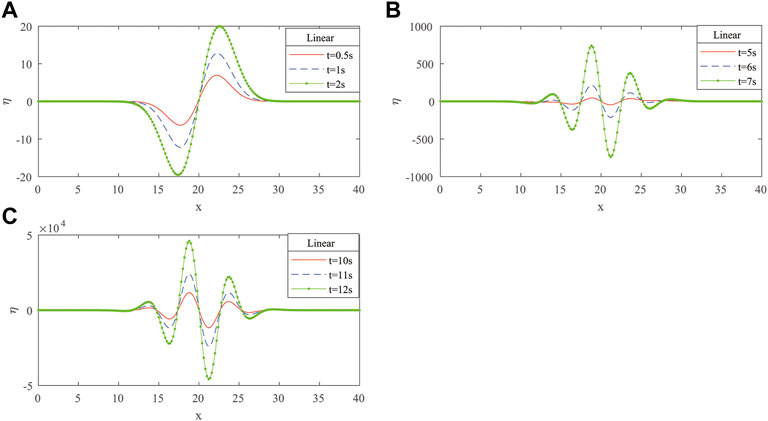
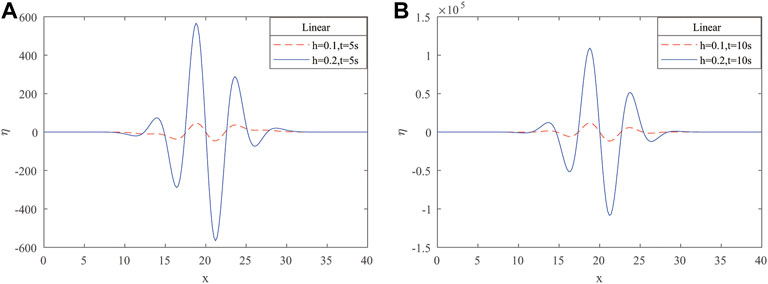
Diagrams in Figure 3 depict changes in the amplitude of linear SWWEs as the basin depth varies from
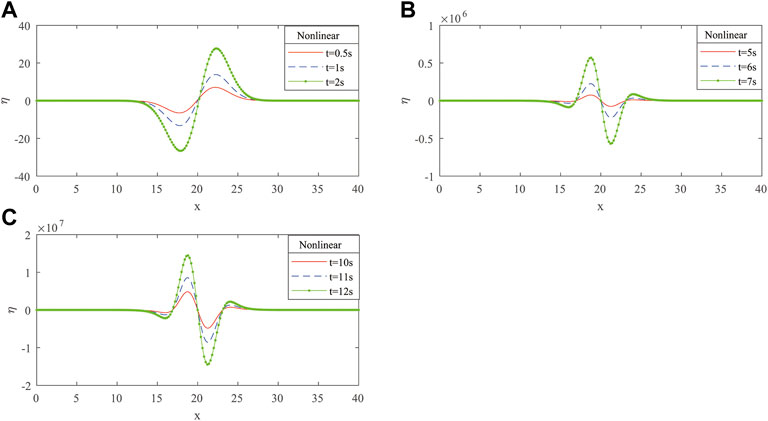
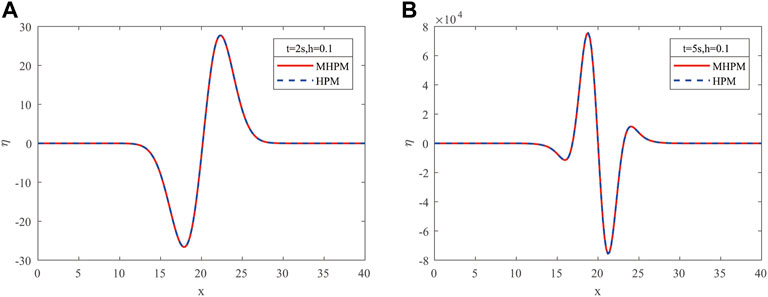
Figure 4 represents the results of WSE of non-linear SWWEs at various time levels with
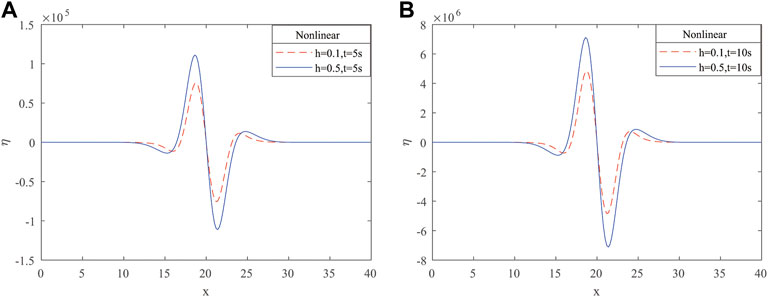
Figure 5 demonstrates changes in non-linear SWWEs as the water depth changes from
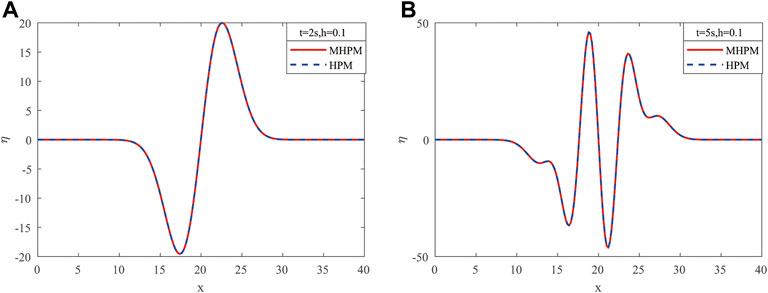
Figure 6 shows a comparison graph between the MHPM and HPM for the water surface elevation of the linear SWWEs at the fixed water depth of
From Figures 2, 4, we may conclude that as time increases, the water surface elevations also increase both in linear and non-linear cases. It can be seen in Figures 3, 5 that the amplitudes of the linear and non-linear shallow water waves increase when the water depth (
5 Conclusion
The main goal of this work is to solve shallow water wave equations using the Mohand transform-based homotopy perturbation method. The variation in the water surface height at different time levels and depths are given in this paper; the results are consistent with the characteristics of shallow water waves. It is proved that this method is a very good tool for solving SWWEs, which can easily be applied in finding out the approximate analytic solutions. The main advantage of this method over the HPM is that it is a powerful and efficient method to determine the analytical solution of the wave equation. In future research, we can also explore the effectiveness of this method in solving other problems, so as to improve the problem-solving efficiency.
Data availability statement
The original contributions presented in the study are included in the article/supplementary material; further inquiries can be directed to the corresponding authors.
Author contributions
Conceptualization, YL, YZ, and JP; methodology, YL, YZ, and JP; software, YL and YZ; validation, YL and JP; writing—original draft preparation, YL, YZ, and JP; writing—review and editing, YL, YZ, and JP; supervision, JP; funding acquisition, JP. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the National Natural Science Foundation of China (Grant No. 10561151), the Basic Science Research Fund in the universities directly under the Inner Mongolia Autonomous Region (Grant No. JY20220003), and the Scientific Research Project of Hetao College (Grant No. HYZQ202122).
Acknowledgments
The authors would like to express their gratitude to the reviewers and editors for their insightful remarks and ideas, which helped them improve the paper’s quality.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Perumandla K, Chakraverty S. Comparison of solutions of linear and non-linear shallow water wave equations using homotopy perturbation method. Int J Numer Methods Heat Fluid flow (2017) 27(9):2015–29. doi:10.1108/HFF-09-2016-0329
Liu Y, Shi Y, Yuen D A, Sevre EOD, Yuan X, Xing HL. Comparison of linear and nonlinear shallow wave water equations applied to tsunami waves over the China Sea. Acta Geotechnica (2009) 4(2):129–37. doi:10.1007/s11440-008-0073-0
3. Cho YS, Sohn DH, Lee SO. Practical modified scheme of linear shallow-water equations for distant propagation of tsunamis. Ocean Eng (2007) 34(11):1769–77. doi:10.1016/j.oceaneng.2006.08.014
4. Tandel P, Patel H, Patel T. Tsunami wave propagation model: A fractional approach. J Ocean Eng Sci (2021) 7:509–20. doi:10.1016/j.joes.2021.10.004
5. Wu NJ, Chen C, Tsay TK. Application of weighted-least-square local polynomial approximation to 2D shallow water equation problems. Eng Anal Boundary Elem (2016) 68:124–34. doi:10.1016/j.enganabound.2016.04.010
6. Karunakar P, Chakraverty S. 2-D shallow water wave equations with fuzzy parameters. Germany: Springer (2018).
7. Sahoo M, Chakraverty S. Sawi transform based homotopy perturbation method for solving shallow water wave equations in fuzzy environment. Mathematics (2022) 10:2900. doi:10.3390/math10162900
8. Perumandla K, Chakraverty S. Solving shallow water equations with crisp and uncertain initial conditions. Int J Numer Methods Heat Fluid Flow (2018) 28:2801–15. doi:10.1108/hff-09-2017-0351
9. Noeiaghdam L, Sidorov DN, Noeiaghdam S. Dynamical control on the homotopy analysis method for solving nonlinear shallow water wave equation. Dynamic Syst Comp Sci Theor Appl (Dysc) (2020) 1847:012010. doi:10.1088/1742-6596/1847/1/012010
10. Safari M, Safari M. Analytical solution of two extended model equations for shallow water waves by He's variational iteration method. Am J Comput Math (2011) 1(4):235–9. doi:10.4236/ajcm.2011.14027
11. Safari M. Analytical solution of two extended model equations for shallow water waves by adomian's decomposition method. Adv Pure Math (2011) 1(4):238–42. doi:10.4236/apm.2011.14042
12. Bekir A, Aksoy E. Exact solutions of extended shallow water wave equations by exp-function method. Int J Numer Methods Heat Fluid Flow (2013) 23(2):305–19. doi:10.1108/09615531311293489
13. Mohand M, Mahgoub A. The new integral transform Mohand transform. Appl Math Sci (2017) 12(2):113–20.
14. Aggarwa S, Sharma N, Chauhan R. Solution of linear volterra integral equations of second kind using Mohand transform. Int J Res Advent Tech (2018) 6(11):3098–102.
15. Aggarwal S, Vyas A, Sharma SD. Mohand transform for handling convolution type volterra integro-differential equation of first kind. Int J Latest Tech Eng Manag Appl Sci (2020) IX(VII):78–84.
16. Nadeem M, He JH, Islam A. The homotopy perturbation method for fractional differential equations: Part 1 Mohand transform. Int J Numer Methods Heat Fluid Flow (2021) 31(11):3490–504. doi:10.1108/hff-11-2020-0703
17. Khandelwal R, Khandelwal Y. Solution of blasius equation concerning with Mohand transform. Int J Appl Comput Math (2020) 6(5):128. doi:10.1007/s40819-020-00871-w
18. Aggarwal S, Chaudhary R. A comparative study of Mohand and Laplace transforms. J Emerging Tech Innovative Res (2019) 6(2):230–40.
19. Aggarwal S, Sharma N, Chauhan R. Duality relations of kamal transform with Laplace, laplace-carson, Aboodh, Sumudu, Elzaki, Mohand and Sawi transforms. SN Appl Sci (2020) 2(1):135–8. doi:10.1007/s42452-019-1896-z
20. Fang JH, Nadeem M, Habib M, Akgül A. Numerical investigation of nonlinear shock wave equations with fractional order in propagating disturbance. Symmetry (2022) 14:1179. doi:10.3390/sym14061179
21. Althobaiti S, Dubey RS, Prasad JG. Solution of local fractional generalized fokker-planck equation using local fractional Mohand adomian decomposition method. Fractals (2022) 30(01):2240028. doi:10.1142/s0218348x2240028x
22. Shah R, Khan H, Farooq U, Baleanu D, Kumam P, Arif M. A new analytical technique to solve system of fractional-order partial differential equations. IEEE Access (2019) 7:150037–50. doi:10.1109/access.2019.2946946
23. He JH. Homotopy perturbation technique. Comp Methods Appl Mech Eng (1999) 178(3-4):257–62. doi:10.1016/s0045-7825(99)00018-3
24. Anjum N, He JH. Higher-order homotopy perturbation method for conservative nonlinear oscillators generally and microelectromechanical systems' oscillators particularly. Int J Mod Phys B (2020) 34(32):2050313. doi:10.1142/s0217979220503130
25. Yu DN, He JH, Garca AG. Homotopy perturbation method with an auxiliary parameter for nonlinear oscillators. J Low Frequency Noise, Vibration Active Control (2019) 38(3-4):1540–54. doi:10.1177/1461348418811028
26. He JH, El-Dib YO. Homotopy perturbation method with three expansions. J Math Chem (2021) 59:1139–50. doi:10.1007/s10910-021-01237-3
27. He JH. Application of homotopy perturbation method to nonlinear wave equations. Chaos Solitons and Fractals (2005) 26(3):695–700. doi:10.1016/j.chaos.2005.03.006
28. Hemeda AA. Homotopy perturbation method for solving systems of nonlinear coupled equations. Appl Math Sci (2012) 6(96):4787–800.
29. Madani M, Fathizadeh M, Khan Y, Yildirim A. On the coupling of the homotopy perturbation method and Laplace transformation. Math Comp Model (2011) 53:1937–45. doi:10.1016/j.mcm.2011.01.023
30. Mishra HK. A comparative study of variational iteration method and He-Laplace method. Appl Math (2012) 3:1193–201. doi:10.4236/am.2012.310174
31. He JH, Moatimid GM, Zekry MH. Forced nonlinear oscillator in a fractal space. Facta Universitatis Series: Mech Eng (2022) 20(1):001–20. doi:10.22190/fume220118004h
32. Anjum N, He JH, Ain QT, Tian D. LI-HE’S modified homotopy perturbation method for doubly-clamped electrically actuated microbeams-based microelectromechanical system. Ser Mech Eng (2021) 19(4):601–12. doi:10.22190/fume210112025a
33. Li XX, He CH. Homotopy perturbation method coupled with the enhanced perturbation method. J Low Frequency Noise Vibration Active Control (2018) 0(0):1399–403. doi:10.1177/1461348418800554
34. He JH, El-Dib YO. The enhanced homotoyp perturbation method for axxial vibration of strings. Facta Universitatis Ser Mech Eng (2021) 19(4):735–50. doi:10.22190/fume210125033h
Keywords: approximate solutions, shallow water wave equations, Mohand transform, homotopy perturbation method, water surface elevation
Citation: Liu Y, Zhang Y and Pang J (2023) Approximate solutions to shallow water wave equations by the homotopy perturbation method coupled with Mohand transform. Front. Phys. 10:1118898. doi: 10.3389/fphy.2022.1118898
Received: 08 December 2022; Accepted: 27 December 2022;
Published: 13 January 2023.
Edited by:
Chun-Hui He, Xi’an University of Architecture and Technology, ChinaReviewed by:
Dragan Marinkovic, Technical University of Berlin, GermanyChaolu Temuer, Shanghai Maritime University, China
Dan Tian, Xi’an University of Architecture and Technology, China
Copyright © 2023 Liu, Zhang and Pang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Yanni Zhang, NjQxOTkyMjY5QHFxLmNvbQ==; Jing Pang, cGFuZ19qQGltdXQuZWR1LmNu
 Yue Liu
Yue Liu Yanni Zhang
Yanni Zhang Jing Pang1,2*
Jing Pang1,2*