- Department of Physics, Indian Institute of Technology Delhi, New Delhi, India
Stern-Gerlach and/or matter-wave interferometry has garnered significant interest amongst members of the scientific community over the past few decades. Early theoretical results by Schwinger et al. demonstrate the fantastic precision capabilities required to realize a full-loop Stern-Gerlach interferometer, i.e., a Stern-Gerlach setup that houses the capability of recombining the split wave-packets in both, position and momentum space over a certain characteristic interferometric time. Over the years, several proposals have been put forward that seek to use Stern-Gerlach and/or matter-wave interferometry as a tool for a myriad of applications of general interest, some of which include tests for fundamental physics (viz., quantum wave-function collapse, stringent tests for the Einstein equivalence principle at the quantum scale, breaking the Standard Quantum Limit (SQL) barrier, and so forth), precision sensing, quantum metrology, gravitational wave detection and inertial navigation. In addition, a large volume of work in the existing literature has been dedicated to the possibility of using matter-wave interferometry for tests of quantum gravity. Inspired by the developments in this timely research field, this Perspective attempts to provide a general overview of the theory involved, the challenges that are yet to be addressed and a brief outlook on what lays ahead.
1 Introduction
Stern-Gerlach interferometry is considered to be by some, an ideal candidate for possibly testing theories of quantum gravity in simple table-top experiments. The realization of a so-called “full-loop” Stern-Gerlach interferometer almost arises as a general theme in this context. Unlike a conventional Stern-Gerlach apparatus that enables the splitting of particle wave functions into two spatially-separated wave-packets, each with a different spin projection following which the detector at the exit port of the SG apparatus records two distinct peaks that correspond to the two different spin eigenstates of the entrant particle beam, a full-loop Stern-Gerlach interferometer allows for the recombination of wave-packets following their splitting in both, position and momentum space. Recent proposals that seek to test theories of quantum gravity and fundamental physics using Stern-Gerlach interferometry regard this aspect of the interferometric procedure to be their starting point. A number of interesting ideas have emerged over the recent years that aim at exploiting the exciting prospects that Stern-Gerlach interferometry has to offer. For instance, one can make use of such an interferometric procedure to establish gravitationally-induced macroscopic spatial superpositions between heavy neutral test masses over relatively long time scales [1] and for realizing novel microgravity experiments [2]. In particular, microgravity environments enable long interferometric times with enhanced interferometric sensitivities. Such conditions are ideal for realizing fundamental tests of physics [2]. Of key importance is the realization of an interferometric setup that enables long observation and/or interrogation times and enhanced sensitivities. Amit et al. recently reported the first experimental realization of a T3 Stern-Gerlach interferometer [3], with T here being the total interferometric time or equivalently, the total time-of-flight of atoms in the interferometer. This in itself is a significant advance in this line of research, since it serves as an improvement over conventional T2-SG matter-wave interferometers, i.e., it has been shown that it is possible within the purview of currently existing technologies and experimental constraints to realize experimental schemes that enable longer interrogation times in Stern-Gerlach interferometers. Certain ideas seeking to provide tests for quantum gravity using matter-wave interferometry have emerged over the recent years. The authors in [4, 5] for instance, propose to do so through the implementation of a robust spin entanglement witness protocol in two adjacently-placed full-loop Stern-Gerlach interferometers. Much recently, the successful experimental realization of a full-loop SG interferometer was reported by Margalit et al. [6] based on magnetic field gradients originating from a novel atom-chip configuration. Most importantly, they demonstrate a high degree of control over the field gradients in their interferometric setup within experimental constraints imposed by previously published theoretical results and/or analyses. Although this topical review lays greater emphasis on Stern-Gerlach interferometry, the reader must be reminded that this area of research is vast and vibrant, with new and previously unexplored ideas emerging from time to time. Given the large volume of work that is dedicated exclusively to table-top quantum gravity, it is simply impossible to explore in depth, the motivations behind various proposals that have been put forward. Some that deserve a great deal of attention and careful thought nevertheless, include the conception of gedanken thought experiments [7] for tests of relativity (the authors in [7] for instance, demonstrate that any local experiment that distinguishes a coherent quantum superposition from a statistical mixture of quantum states involves a time scale that is proportional to the mass of the system under investigation), the realization of a novel Stern-Gerlach interferometer within which one considers the application of an unconventional magnetic field configuration [8] to probe magnetic field gradients at high sensitivities (the authors in [8] demonstrate that employing a butterfly-shaped configuration for the applied field in the interferometer ensures that a sufficiently strong interference signal strength be received towards the end of the interferometric scheme, even when the setup is subject to misalignments in position and momentum caused by the resulting field gradient), Mach-Zehnder matter-wave interferometry using Bose-Einstein condensates [9] and the measurement of the fundamental constants of nature and other quantities of interest [10, 11]. Moreover, in addition to gravity measurements, matter-wave interferometry is expected to find novel applications in a variety of other fields of interest, for instance quantum metrology, physics beyond the Standard Model, precision sensing and even core engineering disciplines, as we shall see in the subsequent sections. This Perspective is organized as follows: in Section 2, the basic theory behind Stern-Gerlach interferometry is laid out. In Section 3, a detailed discussion of the experimental protocol proposed by Bose et al. [5] for detecting quantum gravitational effects is presented. In Section 4, the entanglement dynamics of the two masses for the entanglement witness protocol in [5] is analyzed. In Section 5, a detailed discussion pertaining to the estimation of the interference signal in a general Stern-Gerlach interferometer based on a simple Stern-Gerlach model is presented; major drawbacks of such a model have been highlighted as well. In Section 6, a brief analysis of the coherent Stern-Gerlach momentum splitting scheme experimentally realized in [12] is presented. Section 7 discusses certain alternative proposals to test quantum gravitational effects that have been put forth over the recent years (a qualitative discussion of space-based approaches has been presented as well). Section 8 presents certain experimental considerations that one must account for when setting up table-top experiments for tests of quantum gravity. Section 9 discusses certain future directions for reseach in matter-wave interferometry (not limited to Stern-Gerlach interferometry). The Perspective comes to a close through Section 10, where strong emphasis is laid on the recent advances that have been made in this field and other fields that are closely-knit with matter-wave interferometry; an outlook of what lays ahead has been provided and some concluding remarks have been stated.
2 General Theory Behind Stern-Gerlach Interferometry—Important Analytical Results
A typical SG experiment involves the following: a particle beam is initially prepared in a pure spin state, say in the | + ⟩ eigenstate of Sx and it enters the Stern-Gerlach apparatus. One can regard Sz as a coherent superposition over the spin eigenstates of Sx. A key factor that comes into play in certain table-top gravity experiments involving Stern-Gerlach interferometry is the measurement of spin coherence or the visibility in the Stern-Gerlach interferometer. For instance, Bose et al. propose a scheme for establishing a robust spin-witness protocol for observing and/or detecting the quantum nature of gravity [5], a key aspect of which is performing spin correlation measurements at the exit ports of the Stern-Gerlach apparatus. Spin coherence essentially provides a measure of the degree to which the initial spin state of the entrant particle beam can be recovered following the recombination of the two spatially-separate wave-packets in both, position and momentum space. Schwinger et al. pioneered early works in Stern-Gerlach interferometry (see [13, 14]) and were fairly successful in developing a theoretical framework for performing spin correlation measurements by deriving important closed-form expressions for the interference signal strength in a general Stern-Gerlach interferometer. An in-depth analysis of the same calls for extreme mathematical rigor, hence we simply summarize their main results and/or conclusions in this Perspective.
To estimate spin coherence, one generally measures the x-component of the spin state to obtain the expectation value of the spin operator Sx. Consider a typical Stern-Gerlach apparatus. A couple of key assumptions that must be made before we proceed any further are as follows: the magnetic field gradient exists only along the z-direction and it is assumed that the applied field gradient is time-dependent. As a brief introduction to the Stern-Gerlach theory [13], we express the magnetic moment of the incoming particle beam (assumed to be spin-1/2 in our case) as
To proceed any further, we make an additional simplifying assumption: Maxwell’s equation
where ESG denotes the SG interaction energy. The Hamiltonian then assumes the form
where we define fSG as
and
where z0 and p0 indicate that the particle beam enters the SG apparatus at a spatial coordinate z0 with a non-zero momentum p0. The macroscopic displacements of the wave-packets in phase space, i.e., Δz(t) and Δpz(t) are given as
and
Alternatively, from Eqs 8, 9, it is possible to deduce the temporal evolution of the macroscopic displacements of the wave-packets in terms of their momentum splitting, as follows
Following a detailed mathematical analysis, Schwinger et al. were able to deduce a closed-form expression for the interference signal strength in a general Stern-Gerlach interferometer, expressed in terms of the overlap integral between the two spatially-separated wave-packets, as follows [13].
where ψi (z′) denotes the wave function of the initially prepared spatial state and z denotes the eigenvalue of the position operator z.
3 Stern-Gerlach Interferometry as a Tool to Potentially Detect Quantum Gravitational Effects
The possibility of detecting quantum gravitational effects using techniques such as matter-wave interferometry has gained much traction over the recent years. Consider now the proposal put forward by Bose et al. (see [5]), that suggests the use of two mesoscopic test masses initially trapped in two spatially-separated harmonic potential wells that are later released into two spatially-separated Stern-Gerlach interferometers, one corresponding to each harmonic trap. These masses each contain an embedded spin-1/2 (see [4]) that undergo spatial and momentum splitting once after entering the SG interferometers (i.e., in the presence of an applied magnetic field gradient). Considered here is a relativistic treatment of the scheme proposed in [5] (also see [15]). The quantum-split spins now exist in a quantum superposition of distinct spin states, denoted for the sake of the present discussion as | + ⟩ and | − ⟩ and are spatially separated from each other (say, they are located at positions x1 and x2 in space). We now obtain four interferometric paths in the two SG interferometers, each of which we can denote by the states | + + ⟩, | − − ⟩, | − + ⟩ and | + − ⟩, respectively. Further, we define the following tensor product state
To avoid complications, we assume that the two masses are spatially separated by a distance l in the interferometric path | − − ⟩ (as has been considered by the authors in [15]). Additionally, we assume that the gravitational time dilation in the other interferometric paths is negligible, given which the phase picked up by these interferometric paths can be effectively ignored in the analysis that follows. As the test masses propagate inside the SG interferometer, their quantum states pick up a time-dependent phase (we consider both masses to be of mass m), of the form
For the tensor product state of the two masses, we are left with
where the | − − ⟩ interferometric path picks up the phase given in Eq. 12. We arrive at Eq. 12 by noting that the phase is related to the gravitational time dilation as
where Tr denotes the trace. Upon diagonalizing
For different values of δβ, one obtains different measures of the entanglement entropy S. From Eqs 14, 15, we have for S
Repeated spin correlation measurements can thus be made to deduce the behavior of the accumulated phase δβ with S. One approach suggested in [15] is as follows: for a given time in the laboratory frame t and hence for a given phase difference δβ, one can discard the quantum state of one of the test masses and perform a quantum state tomography on the other test mass. A simple way to understand quantum state tomography is as follows: one performs repeated measurements on quantum systems that are characterised by the same density matrix. Frequency counts are then used to estimate probabilities, which when combined with Born’s probability rule can be used to ascertain a new density matrix that most appropriately conforms with the measurement observations. In this case, the new density matrix thus constructed can be diagonalized and used to obtain a new measure of the entanglement entropy S′ (using Eq. 14). It is assumed that all sources of error such as observational errors, apparatus imperfections, external noise sources, and so forth are accounted for. The behavior of S′ with δβ can be studied and consequently, compared to that predicted in Eq. 16 [15]. Differences between the behaviors of S and S′ could potentially point to a quantum gravitational effect at play.
To summarize then, the scheme proposed in [5] (using two adjacently-placed SG interferometric setups) entails the following steps: we take two test masses containing embedded spin-1/2 particles and split them spatially by exploiting the Stern-Gerlach effect (through the application of magnetic field gradients in the adjacently-placed SG interferometric setups). Consequently, we arrange one pair of interferometric paths such that the test masses in question interact via gravity (a phase shift thus arises for a certain combination of interferometric paths). This “gravitationally-induced phase gate” is then linked to the entanglement generated between the test masses (this again, is gravitationally-induced), which we then hope to test in some operational procedure (one such procedure being a quantum state tomographic-based approach, as outlined above; also see [5, 15] for more details).
Recent theoretical works have shown that given the current state-of-the-art, witnessing quantum features of the gravitational field is indeed a viable possibility. There is however a catch here. For instance, the authors in [17] employ a quantum information theoretic approach to show that it is in theory, possible to witness the quantum nature of the gravitational field by probing it with two test masses. Note however that for the quantum state of any one test mass, the fact that a gravitational phase is induced on it over the course of an experimental run does not necessarily imply that we witness quantum features of gravity. Instead, the salient feature of a table-top gravity experiment would be its capability to witness two non-commuting observables of the gravitational field (only then can its quantum nature be certified) [17]. To show conclusively that the gravitational field can exist in a quantum superposition of different values is of key importance here [17]. The scheme proposed in [5] in essence attempts to realize the idea that if two quantum systems (in our case, we have test masses whose spatial degrees of freedom exist in a quantum superposition) get entangled through the interaction with a third mediator (in our case, this is the gravitational field) [17], the third mediator then must be quantum in nature, for which the authors in [17] provide an explicit information theoretic proof.
4 Entanglement Dynamics in the Density Matrix Formalism
From an experimental point of view, it is essential to study the decoherence dynamics of the setup proposed in [5], when in contact with the environment. For this, we consider the two test masses (initially trapped in harmonic potential wells) to be spatially separated by a distance l. Upon release, the two masses split into a superposition of position states that are spatially separated by a distance D. Note here that we follow the arguments made by the authors in [1]; in essence, the authors in [1] consider the spatial splitting between the spin states to be in a direction orthogonal to the initial separation of the two masses. This is in slight contrast with the proposal put forward by Bose et al., where the spatial splitting between the spin states takes place in a direction that is parallel to their initial separation. One expects that the system will decohere primarily due to its interaction with the environment. The authors in [1] argue that given decoherence, the system in question collapses into a mixed state of positions, in which case it is compelling to consider the coupling of the environment with the position operator of the two test masses (σz in our case). The Hamiltonian thus assumes the form [1].
where k is a constant and
and
Note here that for dimensional consistency, the parameter t appearing in Eqs 18, 19 denotes the ratio of the physical time (measured in the laboratory frame) to the decoherence time of the system (t is hence dimensionless). For
where s is the dimensionless coupling strength between the two masses. To determine the entanglement dynamics of the system in question, one can compute the positive partial transposition of
One can use Eq. 21 to analyze the system’s entanglement dynamics for a range of cases, depending on the positivity of the eigenvalue λ for different s. Of key importance is the fact that for λ < 0, the quantum states of the two masses will be entangled [19]. Eq. 21 thus conclusively shows that the two masses can be entangled over a suitable time scale if the coupling strength s between them is sufficiently large (for which we have λ < 0) (Figure 1).
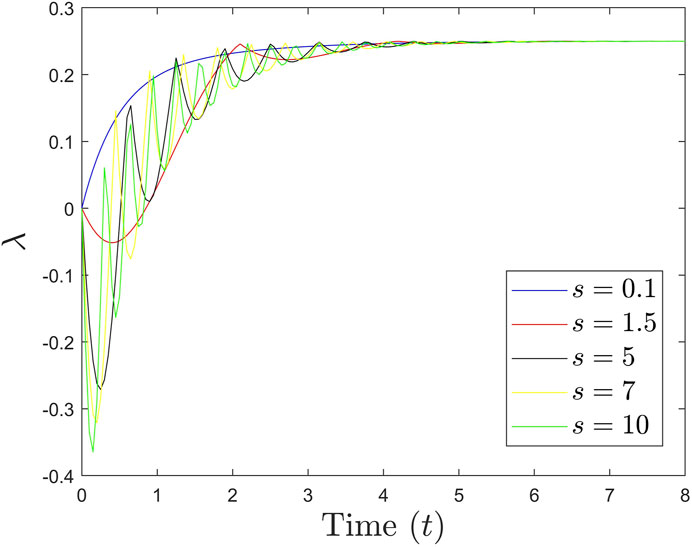
FIGURE 1. (Color outline) Plot for the eigenvalue λ vs. time (dimensionless). Note that as the coupling strength s increases, λ assumes negative values over a certain time scale, indicating that the quantum states of the test masses are entangled over this time scale. For small values of s, the entanglement is hardly visible and/or evident [98 and 99].
Utilizing a full state tomographic approach to witness quantum features of gravity is a viable approach, although difficult to implement in practice [20]. In essence, the experimental proposal in [5] is expected to yield a final quantum state consisting of entangled spin qubit states, so as long as the quantum nature of gravity manifests itself in the proposed experiment. The authors in [20] present two alternatives for measuring the entanglement entropy in the proposed QGEM (Quantum Gravity via Entanglement of Masses) experiment [5]: constructing an entanglement witness or employing an approach that involves measuring the concurrence of a general two qubit state [21] (which could either be pure qubit states (i.e., low entropic states) or mixed qubit states (i.e., high entropic states)).
In terms of spin states, the concurrence for a general two qubit state (herein denoted as C) can be measured as C(ρ) = max{0, λ1 − ∑j=2,3,4λj}, where the λ’s denote the square root of the eigenvalues of the matrix operator ρρ′, with ρ′ being given as ρ′ = (σy ⊗ σy)ρ*(σy ⊗ σy), σ being the usual Pauli spin operator, and * denoting complex conjugation [18]. Here, ρ can be constructed as a tensor product of the quantum states of each qubit state. The measure of the concurrence will attain its maximum value, i.e., 1, if one starts out in a maximally mixed state, such as a state associated with the reduced density matrix operator of a Bell state [20]. This approach however comes with the caveat that the density matrix operator of the full state must be known, making it practically hard to implement. To circumvent this, one could instead construct an entanglement witness. Owing to the trivial nature of the output state in the experimental proposal in [5], it is possible to construct such an entanglement witness that assumes the form [5, 20]
with (1) and (2) denoting test masses 1 and 2, respectively. The benefits of constructing an entanglement witness are two-fold: 1) only two measurements per test mass are required and 2) since spin correlation measurements involve only the two test masses, any entanglement generated will necessarily be between the two test masses, and not the environment [20]. The entanglement witness satisfies the unique property that
5 Estimation of the Interference Signal Strength in a Stern-Gerlach Interferometer Using a Simple Stern-Gerlach Model
In principle, it is possible to realize full-loop Stern-Gerlach interferometers using pure Bose-Einstein condensates (BECs). A possible arrangement is to have a BEC initially confined within a harmonic trap, which is then released and probed in a Stern-Gerlach interferometric setup. To this end, we consider one such case, as proposed and/or analyzed in Ref. [22]. We work under the crude assumption that interactions between atoms in the BEC are effectively negligible, in light of which the analysis will simply reduce to the singleparticle limit. Note here that a rapid free expansion of the BEC post-release is being assumed. The wave-packet of a BEC satisfies the Gross-Pitaevskii equation, as follows
where the Hamiltonian HMF(t) in the mean-field approximation assumes the form
where δz denotes the width of the initially prepared Gaussian wave-packet. The one-dimensional scaling factor assumes the form
and
where m is the mass of the atoms in the BEC,
The integral in Eq. 27 is a standard Gaussian integral, simplifying which we get
where δpz denotes the initial momentum uncertainty in the initially prepared BEC wave-packet (note: the Gaussian wave-packet is a minimum uncertainty state that saturates the uncertainty principle, for which δz δpz = ℏ/2). From Eq. 25, Eq. 26 and Eq. 28, one can deduce an approximate closed-form expression for ϕBEC.
To maximize the Stern-Gerlach interference signal strength, Eq. 28 suggests that the following conditions must hold1
and
A more robust analysis is however in order, for the following reasons. In an experimental setup, it is quite possible that the initial BEC wave-packet might not assume a Gaussian profile, in light of which Eqs. 27, 28 would not be sufficient to quantify the interference signal strength. Moreover, analyzing the model in the single-particle limit yields only approximate results1. It is in fact, necessary to consider a full quantum many-body treatment of a trapped impure BEC (i.e., by incorporating finite-temperature effects), which from an experimental point of view, seems more reasonable. Experimental realizations of the kind described here have already been reported in the literature. Ref. [23] for instance, reports the realization of a high stability Stern-Gerlach spatial fringe interferometer with pure BECs.
Using heavy neutral test masses instead of atomic clouds is another viable, yet formidable approach1. It is worth bearing in mind however that such an experiment would demand a delicate balance between several experimental parameters. A more realistic implementation of such a setup (more specifically, the quantification of the Stern-Gerlach interference signal strength) will have to take into account the effects of the field gradient present in the x − y plane (per Maxwell’s equations), in addition to the one applied along z1. This warrants a 2D analysis of such a setup [14]. In recent years, there have been attempts to address some of these issues. Marshman et al. not long ago analyzed a numerical model of a slightly modified version of an SG interferometric setup [24] by including the effects of the field gradient in the x − y plane (in addition to the one already existing along the z direction). Furthermore, they consider field gradients of intermediate strengths and the effect of the diamagnetic properties of the test mass in their analysis. Their results demonstrate that the introduction of a gradient-free region (see Ref. [24] for more details) along the wave-packet trajectories can facilitate the acceleration of micron-sized test masses in the interferometric setup, which in turn can help one realize more efficient splitting between the individual wave-packets.
6 Experimental Schemes for Realizing Wave-Packet Splitting in Atom Interferometers
Novel experimental schemes to achieve coherent momentum splitting of wave-packets in SG interferometers have been realized in certain experiments over the recent years. See for instance [23], wherein the authors provide a detailed analysis of a high-stability spatial fringe interferometer. The maximum spatial splitting between wave-packets thus achieved in such an interferometer exceeds their minimal spatial widths by at least an order of magnitude. This is enabled by the application of accurately-timed magnetic gradient pulses that are generated by a novel atom-chip configuration.
Machluf et al. demonstrated the experimental realization of a general splitting scheme to produce spatial interference fringes with measurable phase stabilities some years ago [12]. The authors in [12] demonstrate an operational procedure to achieve coherent momentum splitting between wave-packets in an SG interferometer on an atom-chip configuration. Their scheme makes use of two internal atomic states (we denote these as |1a⟩ and |1b⟩ for the purpose of discussion) between which it is possible to drive coherent atomic transitions. One must also keep in mind that these internal states undergo state-dependent interactions with the applied field gradient (in the presence of an external potential [12]). Initially, the atoms are present in internal state |1b⟩, which are subsequently released from a trap. Note also that the atomic cloud initially exists in an external state |p0, x0⟩ that represents a wave-packet, characterized by a central momentum p0 and a central position x0. Upon releasing the atomic cloud from the trap, a π/2 rotation pulse is applied that splits the wave-function of the atomic cloud into an equally weighted-superposition of the internal states |1a⟩ and |1b⟩. Given the presence of a time-dependent external potential Uk(x, t), a state-selective force (note that the internal states so chosen undergo state-dependent interactions with the applied field gradient) of the form F = − ∇Uk(x, t) is applied for a time τ which is typically shorter than the time the atoms spend moving in the applied force field [12]. Each internal state in question thus picks up a phase of the form − ∇(Uk(x, t)τ/ℏ), yielding Fk(x, t)τ/ℏ. The quantum state of the atoms is now
where the momentum states |p±⟩ are themselves a superposition over momentum states |p1⟩ and |p2⟩, each corresponding to a different wave-packet. From Eq. 31, we see that the internal states |1a⟩ and |1b⟩ get entangled with the wave-packet momenta states |p1⟩ and |p2⟩. With this, the momentum splitting operation concludes. The authors in [12] propose two more interferometry schemes to realize internal state interference in atom interferometers, both being interferometric techniques primarily based on the internal state population of atoms.
An alternative interferometry scheme that instead makes use of two magnetically insensitive atomic states for coherent SG momentum splitting of wave-packets is discussed in [12]. Precision interferometers based on internal state interference in the present day widely employ this approach. Typically, the two first-order magnetically insensitive substates |1a, 0⟩ and |1b, 0⟩ of two hyperfine states are chosen for this purpose [12]. As in the above scheme, the application of the first microwave π/2 rotation pulse generates an equally-weighted superposition of the two chosen magnetically insensitive states, following which one can split these into two distinct momentum states by the application of a magnetic gradient at a sufficiently strong magnetic field. The non-linear Zeeman shift of the transition energy between the two substates that occurs as a result is of the form ΔEZ = αB2, where B is the applied magnetic field strength. Given that the interferometric scheme is carried out in an atom-chip configuration, the atoms are exposed to a magnetic gradient
7 Alternative Proposals
Some works in the existing literature seek to study the quantum nature of gravity via alternate means. For instance, the authors in [15] propose a scheme for the experimental realization of the discreteness of time (this closely follows the proposal in [5]; an additional assumption here is that time itself assumes discrete values at the Planck scale). Using simple arguments, the authors in [15] demonstrate that the phase picked up by an interferometric path in the proposal by Bose et al. can be shown to assume only quantized values. Note here that one imposes no constraints on the observation time in the laboratory frame; it varies continuously over the course of the experiment. This has the effect that the behavior of S [see Eq. 16] with δβ is no longer of a continuous nature, but rather can be shown to be step-like. The authors however point out that the key assumption, i.e., the discretization of time at the Planck scale, might not hold true. Neither are the implications clear at the moment. That interference effects at the quantum scale depend on time scales on the order of the Planck time is nevertheless an idea that deserves greater scrutiny.
The weak equivalence principle, in its most general sense, establishes an equivalence between inertial and gravitational mass [25]. Over the years, there have been attempts to test the weak form of the equivalence principle in regimes wherein quantum effects become important. One of these experimental realizations employs the use of a Bragg-atom interferometer in a gravity-gradiometer configuration to test the equivalence principle at the quantum scale; in this case, for 87Rb atoms in a coherent superposition of internal (hyperfine) energy states [25]. Providing a detailed description of said experiment is not within the scope of this Perspective; nevertheless the key takeaway is that tests of the quantum aspects of the equivalence principle are in principle realizable and the use of quantum superpositions essentially allows one to probe the quantum aspects of fundamental laws and/or principles (which for many years have been thought to be purely classical, with possibly no quantum analogue) over suitably long time scales. The proposal in [5] can in effect, be extended beyond what it intends to achieve and/or demonstrate. The authors in [26] for instance, propose a novel thought experiment based on present-day quantum cryptographic concepts to potentially detect low-energy perturbative quantum gravity fluctuations in a setup that closely resembles the setup proposed in [5] (also see [27]) by experimentally revealing the notorious gravitational T3 phase term, which they then argue would allow one to test the Einstein equivalence principle. The hope is to detect gravitational field fluctuations from a rigorous analysis of the stochastic noise associated with an otherwise ideal output (one with a very high state-readout fidelity) of a measurement process of a quantum system (for more details regarding the operational principle of the proposed setup, see [26]). Future experimental works in this direction can turn out to be a promising venture, primarily because currently existing quantum technologies can in principle, as the authors in [26] point out, detect quantum gravitational effects through the direct measure of the gravitational T3 phase term.
Space-based experiments for tests of fundamental physics: Space-based approaches offer a unique opportunity to push our current understanding of the quantum nature of gravity and possibly numerous other areas to the very extreme. The very fundamentals of quantum mechanics, i.e., the superposition principle and wavefunction collapse models (see for instance, Chap. 15 in [28]; also see [29, 30]; for more recent experimental proposals and/or results that employ both interferometric and noninterferometric-based approaches, see [31–34] and the references listed therein) can be potentially tested and/or investigated using atom interferometry experiments in space environments. On this front [35], serves as an excellent current Perspective on the status of space-based approaches for quantum gravity measurements. In essence, space-based experiments (we primarily focus on the interferometric type here) offer certain advantages over their terrestrial counterparts, the most important of which is the possibility of achieving much longer coherence and/or interrogation times (more precisely, free-fall times of heavy neutral test masses), owing to low gravity. The authors in [35] lay great emphasis on the use of nano-particles for interferometry-based experiments in space environments and provide certain experimental constraints and/or estimates for the same. A detailed analysis of such approaches is certainly beyond the scope of this Perspective; rather, an attempt has been made to present and/or summarize the key ideas (the reader is encouraged to look beyond what this Perspective summarizes).
Long interferometric times, as has been emphasized in Section 1, are essential for matter-wave interferometry experiments. There are a few arguments that one can present in support of this claim: at first, atom and/or matter-wave interferometry experiments demand extreme experimental sensitivity. A long free-fall time, that one can potentially achieve in a space environment is crucial in this regard. Secondly, standard calculations reveal that the dependence of the wavefunction spread of masses prepared in a quantum superposition scales inversely with the magnitude of the masses, i.e., 1/m if we consider the two masses in question to be equal [35]. It is hence evident that one can facilitate longer interrogation times in these interferometric setups since the wavefunction spread for sufficiently large test masses will be low, thus effectively eliminating undesired dissipative effects. Another advantage that space-based approaches offer over ground-based interferometry experiments is the elimination of the need to vibrationally isolate the experimental setup from its immediate surroundings. Ground-based approaches must take into account all noise sources that can potentially render an experiment impossible to realize. Space-based approaches on the other hand, do not particularly suffer from such setbacks, especially in the low-frequency regime [35]. Additionally, concerning microgravity experiments on the ground, the possibility of running several trial runs within a dedicated span of time is virtually non-existent. The reason for this is simple to understand: each time an experimental run is scheduled, the test mass must be prepared through optomechanical means, following which it is released into the drop tower (this constitutes a single experimental run). The problem here is that test masses must be released into the drop towers one at a time. Moreover, preparing the test mass for an experimental run itself consumes a considerable amount of time, to the point that only say, 3–4 experimental trials can be practically run on a single day. Space-based approaches can easily circumvent this issue–the need to depressurize the experimental setup (this is essential, for reasons discussed in Section 8) is minimal, thus allowing for several more experimental runs to be realized within a particular span of time. This greatly aids in faster and more efficient data acquisition and subsequent analysis (see [35] for more details). The authors in [35] additionally discuss a number of experimental constraints that must be kept in mind to set up and run say, near-field interferometry-based experiments with heavy neutral masses (nano-particles for instance, serve as a viable candidate), which the reader is encouraged to look up. As to how near-field interferometry experiments are realized and how the experimental constraints can be optimized to achieve novel and useful results, the reader is yet once again directed to the arguments and/or approaches elucidated in [35] (also see [36]). To summarize, what is hoped eventually is that through the generation of gravitationally-induced macroscopic quantum superpositions of heavy neutral test masses, it would be possible to not only probe quantum gravitational effects, but also physics beyond the Standard Model, for instance. By this, we mean testing candidates for dark matter, investigating the regime of low-energy perturbative quantum gravity, and so forth [35]. Space-based approaches for the reasons discussed above, offer certain distinctive advantages in this regard, and all efforts in this direction deserve serious attention.
8 Experimental Considerations (With Regards to Ground-Based Interferometry Experiments)
The design of the Stern-Gerlach apparatus, particularly with regards to the ambient pressure that one must maintain inside the Stern-Gerlach interferometer must be given due attention. Collisions with gas and/or air molecules can lead to rapid and excessive decoherence effects [37]. To this end, the condition that the average collision time be much greater than the duration of an experiment must necessarily be satisfied. Preparing highly squeezed harmonic oscillator coherent states also poses a formidable challenge. For instance, the proposal conceived by Krisnanda et al. [38] involves using optomechanical oscillators to probe quantum gravitational effects (via entanglement of masses) over relatively long time scales. Achieving a high amount of squeezing in the initial position quadrature plays a crucial role in their scheme. Their calculations reveal that enabling this would lead to higher entanglement gain over time. In recent years, there have been proposals to address this aspect using efficient schemes [39–41] and significant progress has been made in this regard. Not only are table-top experiments susceptible to internal decoherence effects (i.e., collisions with air molecules or thermal effects) but also to external “noise,” such as seismic/tectonic vibrations or perhaps even vibrations caused in the ground due to a vehicle passing by. It is essential that these experiments be shielded from their immediate surroundings, as to minimize decoherence losses of all kinds, failing which the chances of probing any quantum effects are greatly diminished. In this regard, the design of an efficient vibration isolation system for atom and/or matter-wave interferometry experiments (at least for ground-based approaches) is currently the need of the hour. Stochastic fluctuations in the parameters used for setting up an experiment ought to be given due attention (see [1] for more details). Another important point that factors into the present discussion is the type of interferometer that one could use for the experimental realization of the proposals existing in the literature. In essence, one sees that the experimental protocol envisioned by Bose et al. could be successfully realized (whilst keeping in mind the experimental constraints) by using a transversal Stern-Gerlach interferometer, whereas the experimental realizations that [3, 42] report rely on the use of a longitudinal setup. Paraniak et al. recently analyzed a numerical model of a transversal Stern-Gerlach interferometry experiment without the usual simplifying assumptions [43]. The conclusions of their study suggest that a substantial loss of spin coherence is to be expected for interferometric path separations that are about 30–40 times larger than the initial wave-packet width. The proposal put forward by Bose et al. involves interferometric path separations that are about 200 times larger than the initial wave-packet width, thus hinting at the infeasibility of the same, at least in its present form.
9 Future Directions in Matter-Wave Interferometry
Having summarized some of the recent trends in matter-wave interferometry (specifically, Stern-Gerlach interferometry) and beyond, we now look towards the future. Of particular interest is the realization of three-dimensional matter-wave interferometers for heavy neutral test masses. Thus far, the experimental realization of a three-dimensional matter-wave interferometer for trapped ions has been reported [44]. It’d however be interesting to see if the same could be achieved for much larger masses (say, mesoscopic masses of the order of 10–14–10–15 kg that the proposal in [5] hopes to employ). The possibility of using degenerate Fermi gases for atom interferometry experiments also deserves some attention. Owing to their non-interacting nature, atoms present in the same internal state cannot undergo interactions (as per the Pauli exclusion principle), thereby effectively eliminating the possibility of any self-interactions. This in turn implies that the noise from uncontrolled phases in the system will be greatly suppressed [45]. The use of waveguides also forms an attractive choice for atom and/or matter-wave interferometry experiments. In particular, it can be argued that minimal dispersion in a direction transverse to the propagation axis can be achieved in waveguide structures. This can potentially lead to an enhanced performance for atom interferometers (see for instance [46]). Of particular importance is the ability to achieve much longer interferometric times in such structures. The transverse confinement allows for much less dispersion, given which the interference signal strength can be enhanced for much longer durations. One worry that however needs to be addressed in this regard is the thermal expansion of the atomic cloud within the waveguide, which can potentially lead to certain unwanted effects. A recent work by Pandey et al. attempts to address this issue (see [47]) by manipulating the spread in the momentum and density distributions of BECs and thermal atomic clouds in time-averaged adiabatic potential (TAAP) waveguides, to which end they demonstrate focusing and collimation of matter waves by using a series of gravito-magnetic matter-wave lenses (time-dependent). A fairly high suppression in the expansion energies of BECs and thermal atomic clouds can be achieved using this technique, thereby minimizing the dispersion of matter waves within the waveguide structure; nevertheless this open new avenues to research along these directions, i.e., the possibility of using atomtronic matter-wave lensing in conjunction with other novel techniques and/or schemes to further suppress the expansion energies of atomic clouds within waveguides is something that deserves greater scrutiny. Atomtronic matter-wave lensing can potentially in the future, find novel applications in the study of low-energy atomic collisions and precision measurements on ultracold thermal atomic ensembles (see [48] for further details on how matter-wave guides facilitating enhanced sensitivity can be implemented for say, gravity gradiometry and global navigation). Ring traps can be used for the purpose of countering noise effects in atom interferometers. An explanation for this can be found in [45], wherein the author argues that the phase noise arising in the two interferometric paths can be effectively canceled out if the interfering wave-packets are split such that they propagate in opposite directions around the ring structure with an integer number of rotations. Besides, there has been considerable interest in the implementation of different variants of time-orbiting potential and time-averaged adiabatic potential traps for atom interferometry experiments. These traps are capable of supporting atomic clouds against gravity whilst also providing weak axial symmetric confinement, as to minimize interatomic interaction effects [49], thus paving the way for high precision measurements on ultracold atomic systems and interferometry-enabled measurements on Bose-Einstein condensates (see [50–54] and the references listed therein). The geometric setup itself can play a key role in the realization of longer interferometric times in atom interferometers. Gochnauer et al. for instance, recently demonstrated the realization of a novel atom interferometer with ultracold Ytterbium BECs in a vertical geometry [55]. Not only does this setup provide an enhancement of interferometric times over horizontal interferometric setups, but also addresses certain experimental challenges associated with the realization of atom interferometers with heavy, non-magnetic atoms (in this case, Yb). Most importantly, the authors in [55] demonstrate the realization of a one-of-a-kind vertical atom interferometer in a double Mack-Zehnder configuration, which they argue is not only suited for precision sensing but also for gravity gradiometry measurements, owing to a stiff resistance to vibrational noise and/or perturbations. Future works could thus be aligned along these directions, namely the experimental realization of either atom interferometers with non-magnetic atomic species or atomic systems prepared in magnetically insensitive sublevels (in contrast to this, see [56] for the experimental realization of a multi-Zeeman state atom interferometer that exploits the coherence properties of Bose-Einstein condensates to facilitate enhanced sensitivities and generate interferometric signals with very sharp spatial interference fringes).
The determination of the precise value of Newton’s gravitational constant has been the subject of several works, ever since Cavendish first attempted to tackle this through his famous torsion pendulum and torsion balance experiment in 1798 [57]. More recently, there have been attempts to measure G using cold atoms and quantum interferometric techniques (see for instance [58, 59]), and these experiments have greatly aided in revealing the systematic errors that prevent one from discerning the value of G precisely. A more recent work by Asenbaum et al. demonstrates a very interesting realization of a long-time drift large momentum transfer atom interferometer with ultracold 87Rb atoms which can essentially be used as a gradiometer [60]. This gradiometric configuration can reach resolutions of down to 10–9 s−2 and the macroscopic separation realizable between the interfering atomic wavepackets allows the authors to probe the coupling between atomic recoil effects and the spacetime curvature induced by the presence of a Pb source mass [60]. Namely, the conclusions of their study indicate a 1 rad phase shift in the interference pattern of the interfering atomic wavepackets, caused by the gravitational influence of the nearby Pb source mass itself. Future experiments in the same spirit could in principle be tuned and/or tailored to perform more precise measurements of Newton’s gravitational constant.
Surpassing the measurement accuracy at quantum scales has been a subject of wide interest for several decades now. For an ensemble of ultracold atoms for instance, the noise that arises as a result of random outcomes (that are sampled from a certain probability distribution) of discrete measurements of the quantum states of individual atoms in the ensemble sets a limit on the accuracy achievable in the measurement of quantities that couple to the internal states of atoms [61]. To this end, Anders et al. report the first experimental realization of an entangled source of atoms that are compatible with current state-of-the-art atom interferometers [61]. Namely, they demonstrate the transfer of entanglement from the spin degree of freedom of a BEC (consisting of 87Rb atoms) to its momentum modes. In essence, it is possible to achieve complete control over the quantum state at the level of the ensemble itself, thereby minimizing the noise effects that would manifest as a result of discrete measurements being made on uncorrelated quantum states of atoms. Such studies can in principle, as the authors in [61] point out, serve as an excellent tool to realize entanglement-enhanced atom interferometry for more stringent tests of the equivalence principle at the quantum scale.
Inertial force-sensing and measurements of the fundamental constants of Nature: With the advent of light-pulse atom interferometry in recent years, there has been a considerable advance in the realization of precision interferometry-based approaches. It has become possible to design and/or construct quantum sensors and nanosphere matter-wave interferometers that enable inertial force-sensing at incredibly small length scales (for recent developments in this field, see [62–64]). An additional advantage that these sensors offer is the precise determination of the fundamental constants of Nature (see for instance [65]). The key experimental factors, as always, include long interferometric times and the implementation of large momentum transfer techniques [66]. As to what constitutes the current state-of-the-art, the figure of merit for these quantum sensing devices, the tools and techniques available to implement these devices in real time and certain experimental challenges that are yet to be addressed, the reader is encouraged to consult [66]. Of particular interest to the scientific community has been gravity measurements using cold-atom sensors. The possible applications span a major portion of geophysics and civil engineering; for instance, measuring changes in gravity at a particular location due to seismic effects, air pressure variations, melting polar ice-caps, and so forth [67]. The construction of navigation instruments based on cold-atom sensing technologies has also spurred up considerable interest amongst members of the engineering fraternity. There has been a continuous effort to realize more efficient devices of this kind by enhancing the currently achievable accuracy and sensitivity limits and the prospects as a whole look extremely promising. For a more recent Perspective on the real-world applications of atom interferometric quantum sensors (encompassing a wide range of fields such as oil and natural gas exploration, quantum metrology, space exploration, and so forth), see [68, 69].
10 Outlook and Conclusion
Despite several challenges, there is a lot to look forward to. Significant progress has been made in the area of optomechanical cavity cooling in recent years, thus making such sensitive experiments feasible [70–72] (for an extensive review of cavity optomechanics and its potential applications, see [73]). The construction of ultra-vacuum drop towers/tubes for microgravity experiments has proven to be a fruitful venture [74] and more recently, there have been successful attempts to implement matter-wave interferometry experiments using BECs in space [75, 76], ever since the realization of Bose-Einstein condensates aboard near-Earth orbit laboratories [77]. Of particular interest to the scientific community could be the realization of matter-wave interferometers with atoms in high Rydberg states [78, 79]. As the authors in [78] point out, experimental realizations of this kind could serve as a promising tool to study the acceleration of Rydberg atoms in the Earth’s gravitational field. Moreover, studies involving Rydberg atoms could aid in the better understanding of the atmospheric dynamics of relatively cold stars [80]. A few other applications of general interest include the study of molecular interactions at low temperatures and the possibility of using Rydberg atoms as “quantum sensors” for stray static RF electric fields (see for instance [81, 82]). The idea that Stern-Gerlach and/or matter-wave interferometry could be used as a tool for the detection of gravitational waves has seen much development over the recent years (for a brief introduction to the theoretical framework, see [83–86]). The key constraining factor in the realization of such detectors is their sensitivity to shot noise. A recent proposal by Marshman et al. seeks to develop a gravitational-wave detector that is much smaller than the ones currently in operation, the working principle of which is primarily based on Stern-Gerlach interferometry [87]. A further advantage that the detector proposed in [87] offers is that when compared to currently existing GW detectors, it is several times more sensitive and resilient to noise effects, which is typically the limiting factor in the realization of novel, state-of-the-art gravitational wave detectors. In a nutshell, the proposed GW detector will make use of N-doped diamonds containing an embedded spin-1/2 (the embedded spin-1/2 for instance, could be placed in Nitrogen-vacancy centers available in N-doped nanodiamonds) between which the hope is to generate quantum macroscopic spatial superpositions using a Stern-Gerlach interferometric setup. The authors in [87] find that a wide range of frequencies of gravitational waves is in theory, accessible to their proposed detector, which would otherwise not be accessible to current state-of-the-art laser interferometric setups, like the one at LIGO. A few experimental proposals, for instance the Matter-Wave Interferometric Gravitation Antenna (MIGA) experiment [88] and the Atomic Experiment for Dark Matter and Gravity Exploration in Space (AEDGE) [89] are already in place, and rapid developments in this area continue to take place (see [90] for more details). As to what dark matter and dark energy really are some of the most pressing mysteries of modern physics. Over the recent years, atom interferometric-based approaches have found novel applications in the probing of dark matter and dark energy. These experimental realizations are especially crucial, as they set tight bounds and/or constraints on a large class of dark energy theories [91]. While its true nature has eluded thus far, there are claims that dark energy consists of a light scalar field, in which case it is possible that it might couple to normal-matter objects and hence be detectable in the laboratory as a fifth force that is not currently known to us. A class of dark energy theories with so-called “screening” mechanisms have features within their framework that suppress their effects and/or influence in relatively high-density environments, facilitating in theory this coupling to normal-matter particles. Of particular interest is the theory of the chameleon field [91], which has the rather unique property of being able to mediate a long-range force in low-density environments, which in high-density environments assumes a short-range nature. This is precisely what makes its detection nearly impossible in Earth-based environments. Atom interferometric-enabled measurements find utility in this regard, in that it is possible to realize and/or simulate the low-density conditions of the cosmos using atoms contained in a UHV vacuum chamber [91]. This in turn has the effect that the long-range nature of the chameleon field will manifest itself, making its detection in theory, possible (see [91–93] for more details). The superposition principle is a powerful concept in fundamental physics and forms the backbone of quantum mechanics. Atom interferometric-based approaches have opened new avenues into realizing macroscopic spatial superpositions between quantum systems, thus making it possible to test the superposition principle in the macroscopic regime. Achieving macroscopic spatial superpositions between heavy test masses in interferometric setups is also crucial for realizing tests of quantum gravity, as has been discussed at length in the earlier sections (see [94–96] for an overview of some of the exciting developments in this line of research over the recent years). Interestingly enough, matter-wave interferometry can also find novel applications in quantum-assisted measurements on large biomolecules and biomolecular clusters [97]. Typical techniques seek to exploit the high sensitivity of matter-wave spatial interference fringes to circumvent the issues of dephasing and decoherence in such sensitive experiments (in the presence of external perturbative effects) [98] to measure and investigate the molecular properties of a large class of biomolecules.
These have been on the forefront of atom and/or matter-wave interferometry over the past few years and if successful, there is no denying that these will open new doors and avenues to previously unexplored regimes of cold-atom physics and quantum gravity. With growing interest amongst members of the scientific community, rapid developments in matter-wave interferometry and other areas such as optical levitodynamics and quantum optics are bound to occur. It is genuinely hoped that this Perspective will inspire and spearhead research along these directions in the coming years.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author Contributions
The author confirms being the sole contributor of this work and has approved it for publication.
Conflict of Interest
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Acknowledgments
The author YL would like to express his gratitude to his former mentors, A. Mazumdar and S. Bose, with whom he has had several useful and/or insightful discussions on matter-wave interferometry and related areas (in particular, realizing quantum gravity tests using Stern-Gerlach interferometry).
Footnotes
1Bose S, Mazumdar A. Private Communication. (2021).
References
1. Nguyen HC, Bernards F. Entanglement Dynamics of Two Mesoscopic Objects with Gravitational Interaction. Eur Phys J D (2020) 74:1–5. doi:10.1140/epjd/e2020-10077-8
2. Ufrecht C, Roura A, Schleich WP. Bose-Einstein Condensates in Microgravity and Fundamental Tests of Gravity (2021). arXiv. Available at: http://arxiv.org/abs/2107.037\\ (Accessed July 26, 2021).
3. Amit O, Margalit Y, Dobkowski O, Zhou Z, Japha Y, Zimmermann M, et al. T^{3} Stern-Gerlach Matter-Wave Interferometer. Phys Rev Lett (2019) 123:083601–6. doi:10.1103/PhysRevLett.123.083601
4. Wan C, Scala M, Morley GW, Rahman AA, Ulbricht H, Bateman J, et al. Free Nano-Object Ramsey Interferometry for Large Quantum Superpositions. Phys Rev Lett (2016) 117:143003–8. doi:10.1103/PhysRevLett.117.143003
5. Bose S, Mazumdar A, Morley GW, Ulbricht H, Toroš M, Paternostro M, et al. Spin Entanglement Witness for Quantum Gravity. Phys Rev Lett (2017) 119:240401–7. doi:10.1103/PhysRevLett.119.240401
6. Margalit Y, Zhou Z, Amit O, Japha Y, Moukouri S, Rohrlich D, et al. Realization of a Full-Loop Stern-Gerlach Interferometer. Sci Adv (2021) 7:22. doi:10.1126/sciadv.abg2879
7. Mari A, De Palma G, Giovannetti V. Experiments Testing Macroscopic Quantum Superpositions Must Be Slow. Sci Rep (2016) 6:22777–12. doi:10.1038/srep22777
8. Oh C, Kwon H, Jiang L, Kim MS. Field-gradient Measurement Using a Stern-Gerlach Atomic Interferometer with Butterfly Geometry. Phys Rev A (2020) 102:1–9. doi:10.1103/physreva.102.053321
9. Berrada T. Mach-Zehnder Interferometry with Interacting Bose-Einstein Condensates in a Double-Well Potential. Doctoral thesis. Vienna, Austria: Vienna University of Technology (2014). Available at: https://repositum.tuwien.at (Accessed July 26, 2021).
10. Peters A, Chung KY, Chu S. Measurement of Gravitational Acceleration by Dropping Atoms. Nature (1999) 400:849–52. doi:10.1038/23655
11. Santos JT, Li J, Ilvas J, Ockeloen-Korppi CF, Sillanpää M. Optomechanical Measurement of a Millimeter-Sized Mechanical Oscillator Approaching the Quantum Ground State. New J Phys (2017) 19:103014. doi:10.1088/1367-2630/aa83a5
12. Machluf S, Japha Y, Folman R. Coherent Stern-Gerlach Momentum Splitting on an Atom Chip. Nat Commun (2013) 4:2424. doi:10.1038/ncomms3424
13. Schwinger J, Scully MO, Englert B-G. Is Spin Coherence like Humpty-Dumpty? Z Phys D - Atoms, Mol Clusters (1988) 10:135–44. doi:10.1007/bf01384847
14. Englert B-G, Schwinger J, Scully MO. Is Spin Coherence like Humpty-Dumpty? I. Simplified Treatment. Found Phys (1988) 18(10):1045–56. doi:10.1007/bf01909939
15. Christodoulou M, Rovelli C. On the Possibility of Experimental Detection of the Discreteness of Time. Front Phys (2020) 8:207. doi:10.3389/fphy.2020.00207
16. Christodoulou M, Rovelli C. On the Possibility of Laboratory Evidence for Quantum Superposition of Geometries. Phys Lett B (2018) 792:64–8. doi:10.1016/j.physletb.2019.03.015
17. Marletto C, Vedral V. Gravitationally Induced Entanglement between Two Massive Particles Is Sufficient Evidence of Quantum Effects in Gravity. Phys Rev Lett (2017) 119:240402. doi:10.1103/physrevlett.119.240402
19. Horodecki M, Horodecki P, Horodecki R. Separability of Mixed States: Necessary and Sufficient Conditions. Phys Lett A (1996) 223:1–8. doi:10.1016/s0375-9601(96)00706-2
20. Marshman RJ, Mazumdar A, Bose S. Locality and entanglement in table-top testing of the quantum nature of linearized gravity. Phys Rev A (Coll Park) (2012) 101: 052110. doi:10.1088/1748-0221/7/03/P03012
21. Bose S, Mazumdar A, Schut M, Toros M. Mechanism for the quantum natured gravitons to entangle masses. Phys Rev D (2022) 105: 106028. doi:10.1103/physrevd.105.106028
22. Japha Y. Unified model of matter-wave-packet evolution and application to spatial coherence of atom interferometers. Phys Rev A (Coll Park) (2021) 104:053310. (Accessed July 26, 2021) doi:10.1103/physreva.104.053310
23. Margalit Y, Zhou Z, Machluf S, Japha Y, Moukouri S, Folman R. Analysis of a High-Stability Stern-Gerlach Spatial Fringe Interferometer. New J Phys (2019) 21:073040. doi:10.1088/1367-2630/ab2fdc
24. Marshman RJ, Mazumdar A, Folman R, Bose S. Constructing nano-object quantum superpositions with a Stern-Gerlach interferometer. Phys Rev Res (2022) 4:023087. (Accessed November 19, 2021) doi:10.1103/physrevresearch.4.023087
25. Rosi G, D'Amico G, Cacciapuoti L, Sorrentino F, Prevedelli M, Zych M, et al. Quantum Test of the Equivalence Principle for Atoms in Coherent Superposition of Internal Energy States. Nat Commun (2017) 8:15529–11. doi:10.1038/ncomms15529
26. Tamburini F, Licata I. Testing the Equivalence Principle and Discreteness of Spacetime through the T3 Gravitational Phase with Quantum Information Technology. Phys Lett B (2020) 810:135792. doi:10.1016/j.physletb.2020.135792
27. Marletto C, Vedral V. On the Testability of the Equivalence Principle as a Gauge Principle Detecting the Gravitational T3 Phase. Front Phys (2020) 8:176. doi:10.3389/fphy.2020.00176
28. Friedrich B. Molecular Beams in Physics and Chemistry Cham, Switzerland: Springer (2021). doi:10.1007/978-3-030-63963-1
29. Romero-Isart O. Quantum Superposition of Massive Objects and Collapse Models. Phys Rev A (2011) 84:29–31. doi:10.1103/physreva.84.052121
30. Romero-Isart O, Pflanzer AC, Blaser F, Kaltenbaek R, Kiesel N, Aspelmeyer M, et al. Large Quantum Superpositions and Interference of Massive Nanometer-Sized Objects. Phys Rev Lett (2011) 107:020405. doi:10.1103/PhysRevLett.107.020405
31. Vinante A, Mezzena R, Falferi P, Carlesso M, Bassi A. Improved Noninterferometric Test of Collapse Models Using Ultracold Cantilevers. Phys Rev Lett (2017) 119:110401. doi:10.1103/physrevlett.119.110401
32. Bassi A, Toroš M. Bounds on Collapse Models from Matter-Wave Interferometry: Calculational Details. J Phys A: Math Theor (2018) 51:115302.
33. Schrinski B, Nimmrichter S, Hornberger K. Quantum-classical Hypothesis Tests in Macroscopic Matter-Wave Interferometry. Phys Rev Res (2020) 2:033034. doi:10.1103/physrevresearch.2.033034
34. Gerlich S, Fein YY., Arndt M. Interferometric Tests of Wave-Function Collapse. In: V Allori, A Bassi, D Dürr, N Zanghiet al. editors. Do Wave Functions Jump? Fundamental Theories of Physics, 198. Cham: Springer (2021). doi:10.1007/978-3-030-46777-7_26
35. Gasbarri G, Belenchia A, Carlesso M, Donadi S, Bassi A, Kaltenbaek R, et al. Testing the Foundation of Quantum Physics in Space via Interferometric and Non-interferometric Experiments with Mesoscopic Nanoparticles. Commun Phys (2021) 4:1–13. doi:10.1038/s42005-021-00656-7
36. Bateman J, Nimmrichter S, Hornberger K, Ulbricht H. Near-field Interferometry of a Free-Falling Nanoparticle from a point-like Source. Nat Commun (2014) 5:4788. doi:10.1038/ncomms5788
37. van de Kamp TW, Marshman RJ, Bose S, Mazumdar A. Quantum Gravity Witness via Entanglement of Masses: Casimir Screening. Phys Rev A (2020) 102:062807. doi:10.1103/physreva.102.062807
38. Krisnanda T, Tham GY, Paternostro M, Paterek T. Observable Quantum Entanglement Due to Gravity. Npj Quan Inf (2020) 6:12. doi:10.1038/s41534-020-0243-y
39. Vahlbruch H, Mehmet M, Chelkowski S, Hage B, Franzen A, Lastzka N, et al. Observation of Squeezed Light with 10-dB Quantum-Noise Reduction. Phys Rev Lett (2008) 100:033602. doi:10.1103/PhysRevLett.100.033602
40. Vahlbruch H, Mehmet M, Danzmann K, Schnabel R. Detection of 15 dB Squeezed States of Light and Their Application for the Absolute Calibration of Photoelectric Quantum Efficiency. Phys Rev Lett (2016) 117:110801. doi:10.1103/physrevlett.117.110801
41. Schnabel R. Squeezed States of Light and Their Applications in Laser Interferometers. Phys Rep (2017) 684:1–51. doi:10.1016/j.physrep.2017.04.001
42. Palmer JE, Hogan SD. Electric Rydberg-Atom Interferometry. Phys Rev Lett (2019) 122:250404. doi:10.1103/physrevlett.122.250404
43. Paraniak MM, Englert B-G. Quantum Dynamical Simulation of a Transversal Stern-Gerlach Interferometer. Symmetry (2021) 13(9):1660. doi:10.3390/sym13091660
44. Shinjo A, Baba M, Higashiyama K, Saito R, Mukaiyama T. Three-Dimensional Matter-Wave Interferometry of a Trapped Single Ion. Phys Rev Lett (2021) 126:153604. doi:10.1103/physrevlett.126.153604
45. Robertson BI. High Contrast Measurements with a Bose-Einstein Condensate Atom Interferometer. Doctoral thesis. Glasgow, Scotland): University of Strathclyde (2016). Available at: https://eqop.phys.strath.ac.uk (Accessed September 25, 2021).
46. Navez P, Pandey S, Mas H, Poulios K, Fernholz T, von Klitzing W. Matter-wave Interferometers Using TAAP Rings. New J Phys (2016) 18:075014. doi:10.1088/1367-2630/18/7/075014
47. Pandey S, Mas H, Vasilakis G, von Klitzing W. Atomtronic Matter-Wave Lensing. Phys Rev Lett (2021) 126:170402. doi:10.1103/physrevlett.126.170402
48. Pandey S, Mas H, Drougakis G, Thekkeppatt P, Bolpasi V, Vasilakis G, et al. Hypersonic Bose-Einstein Condensates in Accelerator Rings. Nature (2019) 570:205–9. doi:10.1038/s41586-019-1273-5
49. Reeves JM, Garcia O, Deissler B, Baranowski KL, Hughes KS, Sackett CA. Time-orbiting Potential Trap for Bose Einstein Interferometry. Phys Rev A (2005) 72:051605. doi:10.1103/physreva.72.051605
50. Lesanovksy I, von Klitzing W. Time-Averaged Adiabatic Potentials: Versatile Matter-Wave Guides and Atom Traps. Phys Rev Lett (2007) 99:083001. doi:10.1103/PhysRevLett.99.083001
51. Garraway BM, Perrin H. Recent Developments in Trapping and Manipulation of Atoms with Adiabatic Potentials. J Phys B: Mol Opt Phys (2016) 49:172001. doi:10.1088/0953-4075/49/17/172001
52. Horne RA, Sackett CA. A Cylindrically Symmetric Magnetic Trap for Compact Bose-Einstein Condensate Atom Interferometer Gyroscopes. Rev Scientific Instr (2017) 88:013102. doi:10.1063/1.4973123
53. Hinton A, Perea-Ortiz M, Winch J, Briggs J, Freer S, Moustoukas D, et al. A Portable Magneto-Optical Trap with Prospects for Atom Interferometry in Civil Engineering. Philos Trans A Math Phys Eng Sci (2017) 375:20160238. doi:10.1098/rsta.2016.0238
54. Nivet-Dupont M, Demur R, Westbrook CI, Schwartz S. Experimental Study of the Role of Trap Symmetry in an Atom-Chip Interferometer above the Bose–Einstein Condensation Threshold. New J Phys (2018) 20:043051. doi:10.1088/1367-2630/aabc72
55. Gochnauer D, Rahman T, Wirth-Singh A, Gupta S. Interferometry in an Atomic Fountain with Ytterbium Bose-Einstein Condensates. Atoms (2021) 9:58. doi:10.3390/atoms9030058
56. Petrovic J, Herrera I, Lombardi P, Schäfer F, Cataliotti FS. A Multi-State Interferometer on an Atom Chip. New J Phys (2013) 15:043002. doi:10.1088/1367-2630/15/4/043002
57. Cavendish H. Experiments to Determine the Density of the Earth. Philos Trans R Soc Lond (1798) 88:469–526. doi:10.1098/rstl.1798.0022
58. Rosi G, Sorrentino F, Cacciapuoti L, Prevedelli M, Tino GM. Precision Measurement of the Newtonian Gravitational Constant Using Cold Atoms. Nature (2014) 510:518–21. doi:10.1038/nature13433
59. Rosi G, D’Amico G, Tino GM., Cacciapuoti L, Prevedelli M, Sorrentino F. Precision Measurement of the Newtonian Gravitational Constant by Atom Interferometry. Laser Spectrosc (2016) 61–70. doi:10.1142/9789813200616_0006
60. Asenbaum P, Overstreet C, Kovachy T, Brown DD, Hogan JM, Kasevich MA. Phase Shift in an Atom Interferometer Due to Spacetime Curvature across its Wave Function. Phys Rev Lett (2017) 118:183602. doi:10.1103/physrevlett.118.183602
61. Anders F, Idel A, Feldmann P, Bondarenko D, Loriani S, Lange K, et al. Momentum Entanglement for Atom Interferometry. Phys Rev Lett (2021) 127:140402. doi:10.1103/physrevlett.127.140402
62. Geraci A, Goldman H. Sensing Short-Range Forces with a NanosphereMatter-WaveInterferometer. Phys Rev D (2015) 92:062002. doi:10.1103/physrevd.92.062002
63. Schlippert D, Meiners C, Rengelink RJ, Schubert C, Tell D, Wodey É, et al. Matter-Wave Interferometry for Inertial Sensing and Tests of Fundamental Physics in Presented at the Eighth Meeting on CPT and Lorentz Symmetry, Bloomington, Indiana, May 12–16, 2019 (2020) 37–40.
64. Rademacher M, Millen J, Li YL. Quantum Sensing with Nanoparticles for Gravimetry: when Bigger Is Better. Adv Opt Tech (2020) 9(5):227–39. doi:10.1515/aot-2020-0019
65. Parker RH, Yu C, Zhong W, Estey B, Müller H. Measurement of the fine-structure Constant as a Test of the Standard Model. Science (2018) 360(6385):191–5. doi:10.1126/science.aap7706
66. Hensel T, Loriani S, Schubert C, Fitzek F, Abend S, Ahlers H, et al. Inertial Sensing with Quantum Gases: a Comparative Performance Study of Condensed versus thermal Sources for Atom Interferometry. Eur Phys J D (2021) 75:1–13. doi:10.1140/epjd/s10053-021-00069-9
67. Geiger R, Landragin A, Merlet S, Pereira Dos Santos F. High-accuracy Inertial Measurements with Cold-Atom Sensors. AVS Quan Sci. (2020) 2:024702. doi:10.1116/5.0009093
68. Bongs K, Holynski M, Vovrosh J, Bouyer P, Condon G, Rasel E, et al. Taking Atom Interferometric Quantum Sensors from the Laboratory to Real-World Applications. Nat Rev Phys (2019) 1:731–9. doi:10.1038/s42254-019-0117-4
69. Travagnin M. Cold Atom Interferometry Sensors: Physics and Technologies. A Scientific Background for EU Policymaking. EUR 30289EN. 978 -92-76-20405-3. Luxembourg: Publications Office of the European Union (2020). p. JRC121223. doi:10.2760/315209
70. Chang DE, Regal CA, Papp SB, Wilson DJ, Ye J, Painter O, et al. Cavity Opto-Mechanics Using an Optically Levitated Nanosphere. Proc Natl Acad Sci U S A (2010) 107(3):1005–10. doi:10.1073/pnas.0912969107
71. Xuereb A, Ulbricht H, Paternostro M. Optomechanical Interface for Probing Matter-Wave Coherence. Sci Rep (2013) 3:3378. doi:10.1038/srep03378
72. Vovrosh J, Rashid M, Hempston D, Bateman J, Paternostro M, Ulbricht H. Parametric Feedback Cooling of Levitated Optomechanics in a Parabolic Mirror Trap. J Opt Soc Am B (2017) 34:1421–8. doi:10.1364/josab.34.001421
73. Aspelmeyer M, Kippenberg TJ, Marquardt F. Cavity Optomechanics. Rev Mod Phys (2014) 86:1391–452. doi:10.1103/revmodphys.86.1391
74. Müntinga H, Ahlers H, Krutzik M, Wenzlawski A, Arnold S, Becker D, et al. Interferometry with Bose-Einstein Condensates in Microgravity. Phys Rev Lett (2013) 110:093602. doi:10.1103/PhysRevLett.110.093602
75. Schmitz K. LISA Sensitivity to Gravitational Waves from Sound Waves. Symmetry (2020) 12(9):1477. doi:10.3390/sym12091477
76. Lachmann MD, Ahlers H, Becker D, Dinkelaker AN, Grosse J, Hellmig O, et al. Ultracold Atom Interferometry in Space. Nat Commun (2021) 12:1317. doi:10.1038/s41467-021-21628-z
77. Aveline DC, Williams JR, Elliott ER, Dutenhoffer C, Kellogg JR, Kohel JM, et al. Observation of Bose-Einstein Condensates in an Earth-Orbiting Research Lab. Nature (2020) 582:193–7. doi:10.1038/s41586-020-2346-1
78. Palmer JE, Hogan SD. Matter-wave Interferometry with Atoms in High Rydberg States. Mol Phys (2019) 117:3108–19. doi:10.1080/00268976.2019.1607916
79. Tommey JDR, Hogan SD. Matter-wave Interferometry with Helium Atoms in Low-ℓ Rydberg States. Phys Rev A (2021) 104:033305. doi:10.1103/PhysRevA.104.033305
80. Gnedin YN, Mihajlov A-A, Ignjatović .LM, Sakan N, Srećković VA, Zakharov MY, et al. Rydberg Atoms in Astrophysics. New Astron Rev (2009) 53(issues 7-10):259–65. doi:10.1016/j.newar.2009.07.003
81. Facon A, Dietsche E-K, Grosso D, Haroche S, Raimond J-M, Brune M, et al. A Sensitive Electrometer Based on a Rydberg Atom in a Schrödinger-Cat State. Nature (2016) 535:262–5. doi:10.1038/nature18327
82. Fan H, Kumar S, Sedlacek J, Kübler H, Karimkashi S, et al. Atom Based RF Electric Field Sensing. J Phys B: Mol Opt Phys (2015) 48:202001. doi:10.1088/0953-4075/48/20/202001
83. Foffa S, Gasparini A, Papucci M, Sturani R. Sensitivity of a Small Matter-Wave Interferometer to Gravitational Waves. Phys Rev D (2006) 73:022001. doi:10.1103/physrevd.73.022001
84. Delva P, Angonin M -C, Tourrenc P A Comparison between Matter Wave and Light Wave Interferometers for the Detection of Gravitational Waves. Phys Lett A 357 (4-5): 249–54. (2006). doi:10.1016/j.physleta.2006.04.103
85. Dimopoulos S, Graham PW, Hogan JM, Kasevich MA, Rajendran S. Gravitational Wave Detection with Atom Interferometry. Phys Lett B (2009) 678(1):37–40. doi:10.1016/j.physletb.2009.06.011
86. Gao D, Ju P, Zhang B, Zhan M. Gravitational-wave Detection with Matter-Wave Interferometers Based on Standing Light Waves. Gen Relativ Gravit (2011) 43:2027–36. doi:10.1007/s10714-011-1173-y
87. Marshman RJ, Mazumdar A, Morley GW, Barker PF, Hoekstra S, Bose S. Mesoscopic Interference for Metric and Curvature & Gravitational Wave Detection. New J Phys (2020) 22:083012. doi:10.1088/1367-2630/ab9f6c
88. Canuel B, Bertoldi A, Amand L, Pozzo di Borgo E, Chantrait T, Danquigny C, et al. Exploring Gravity with the MIGA Large Scale Atom Interferometer. Sci Rep (2018) 8:14064–23. doi:10.1038/s41598-018-32165-z
89. El-Neaj YA, Alpigiani C, Amairi-Pyka S, Araújo H, Balaž A, Bathe-Peters L, et al. AEDGE: Atomic Experiment for Dark Matter and Gravity Exploration in Space. EPJ Quan Technol (2020) 7:6. doi:10.1140/epjqt/s40507-020-0080-0
90. Tino GM. Testing Gravity with Cold Atom Interferometry: Results and Prospects. Quan Sci. Technol. (2021) 6:024014. doi:10.1088/2058-9565/abd83e
91. Hamilton P, Jaffe M, Haslinger P, Simmons Q, Müller H, Khoury J. Atom-interferometry Constraints on Dark Energy. Science (2015) 349:849–51. doi:10.1126/science.aaa8883
92. Brax P, Davis A-C. Atomic Interferometry Test of Dark Energy. Phys Rev D (2016) 94:104069. doi:10.1103/physrevd.94.104069
93. Sabulsky DO, Dutta I, Hinds EA, Elder B, Burrage C, Copeland EJ. Experiment to Detect Dark Energy Forces Using Atom Interferometry. Phys Rev Lett (2019) 123:061102. doi:10.1103/PhysRevLett.123.061102
94. Romero-Isart O, Juan ML, Quidant R, Cirac JI. Toward Quantum Superposition of Living Organisms. New J Phys (2010) 12:033015. doi:10.1088/1367-2630/12/3/033015
95. Eibenberger S, Gerlich S, Arndt M, Mayor M, Tüxen J. Matter-wave Interference of Particles Selected from a Molecular Library with Masses Exceeding 10,000 Amu. Phys Chem Chem Phys (2013) 15:14696–700. doi:10.1039/c3cp51500a
96. Kovachy T, Asenbaum P, Overstreet C, Donnelly CA, Dickerson SM, Sugarbaker A, et al. Quantum Superposition at the Half-Metre Scale. Nature (2015) 528:530–3. doi:10.1038/nature16155
Keywords: Stern-Gerlach interferometry, matter-wave interferometers, entanglement entropy, density matrix, interference signal, precision sensing, quantum metrology
Citation: Lokare Y (2022) Stern-Gerlach Interferometry for Tests of Quantum Gravity and General Applications. Front. Phys. 10:785125. doi: 10.3389/fphy.2022.785125
Received: 28 September 2021; Accepted: 05 January 2022;
Published: 28 January 2022.
Edited by:
Lin Chen, Beihang University, ChinaReviewed by:
Ignazio Licata, Institute for Scientific Methodology (ISEM), ItalyPasquale Bosso, University of Lethbridge, Canada
Mingsheng Zhan, Innovation Academy for Precision Measurement Science and Technology (CAS), China
Copyright © 2022 Lokare. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Yash Lokare, cGgxMTgwODU3QGlpdGQuYWMuaW4=
 Yash Lokare
Yash Lokare