- 1College of Systems Engineering, National University of Defense Technology, Changsha, China
- 2College of Economy and Management, Changsha University, Changsha, China
- 3College of Liberal Arts and Sciences, National University of Defense Technology, Changsha, China
- 4Power China Zhongnan Engineering Corporation Limited, Changsha, China
- 5School of Software Engineering, Shenzhen Institute of Information Technology, Shenzhen, China
- 6Department of Global Public Health, Karolinska Institutet, Stockholm, Sweden
As a crucial technique for identifying irregular samples or outlier patterns, anomaly detection has broad applications in many fields. Convex analysis (CA) is one of the fundamental methods used in anomaly detection, which contributes to the robust approximation of algebra and geometry, efficient computation to a unique global solution, and mathematical optimization for modeling. Despite the essential role and evergrowing research in CA-based anomaly detection algorithms, little work has realized a comprehensive survey of it. To fill this gap, we summarize the CA techniques used in anomaly detection and classify them into four categories of density estimation methods, matrix factorization methods, machine learning methods, and the others. The theoretical background, sub-categories of methods, typical applications as well as strengths and limitations for each category are introduced. This paper sheds light on a succinct and structured framework and provides researchers with new insights into both anomaly detection and CA. With the remarkable progress made in the techniques of big data and machine learning, CA-based anomaly detection holds great promise for more expeditious, accurate and intelligent detection capacities.
1 Introduction
Anomalies are irregular items, events, or observations that differ significantly from the majority of the data and can translate into critical actionable information in various application domains [1–3]. For example, anomalous readings from the sensor of a large mechanical system could signify a fault in some components of the system.
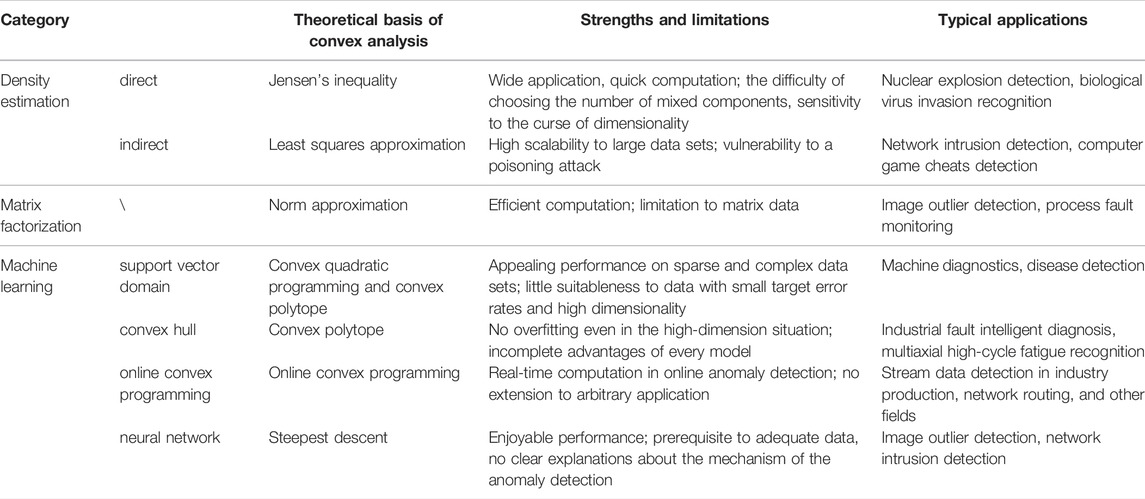
The problem of anomaly detection was raised as early as the 19th century [4], and has been extensively studied in various fields, such as network intrusion detection [5,6], process fault monitoring [7,8], image outlier detection [9,10], and other significant fields. Existing basic methods for anomaly detection can be generally classified into two categories [11], i.e., distance-based anomaly detection, such as K-nearest neighbor (KNN) [12], K-means [13] and DBSCAN [14], and model-based anomaly detection, such as rough set theory [15], Bayesian networks [16], Markov models [17], neural networks [18] and generative adversarial network [19]. To facilitate the settlement of the challenging problem that anomalies are low frequency, convex analysis (abbr.: CA in this paper), a branch of mathematics that studies convex sets and convex functions [20], has been widely applied to anomaly detection approaches, including linear-based, probabilistic-based, proximity-based, ensemble-based, and learning-based models [21,22].
With a wealth of practical techniques, CA is known as one of the fundamental techniques used to support solution and optimization in anomaly detection models. The superiority of the CA-based strategy can be summarized from the theoretical and practical perspectives. On the theoretical side, CA blends the advantages of providing efficient solutions with less complicated models. As to the applications, CA-based strategy has produced proverbially extensive applications in aviation, advertisement, finance and other fields. Specifically, compared with other kinds of strategies, CA plays a crucial role in anomaly detection for its robust approximation in algebra and geometry, efficient computation to a unique global solution, as well as mathematical optimization for modeling [23,24]. In addition, regarding the complex non-convex shape of the collected data in the real world, local convexity (a branch of CA) also shows outstanding performance in anomaly detection [25], and this paper can be equally practical as guidance for local convexity.
CA-based anomaly detection has been first proposed for studying the convex geometric approximation of subsurfaces and anomalies (i.e., seismic records) in 1966 [26], after which great efforts have been made to improve its accuracy and effectiveness. To date, convex analysis plays an essential role in anomaly detection, based on which a large number of anomaly detection algorithms have been developed. For example, density estimation is an indispensable method used for outlier detection, and matrix factorization is used to detect anomaly for the matrix data. Although CA plays an essential role in anomaly detection and evergrowing research has been conducted on CA-based anomaly detection algorithms (as described in Section 2.2), to the best of our knowledge, there is no survey paper which has addressed the anomaly detection methods based on CA, and little work has realized a comprehensive classification of it. In addition, the essential relationship between anomaly detection and CA has been rarely investigated [27,28].
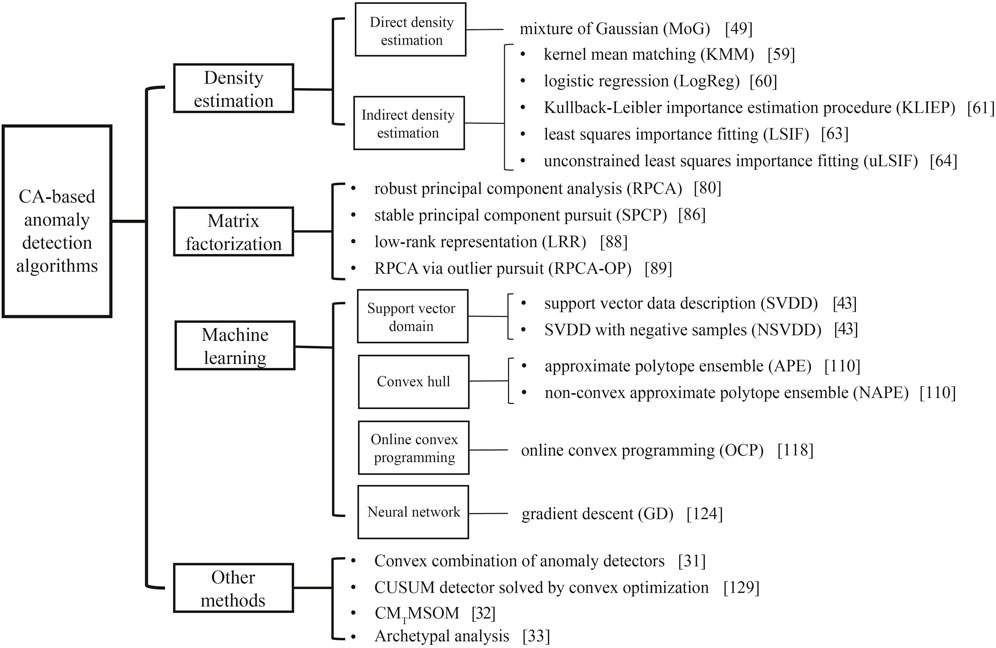
Therefore, in this paper, we aim to conduct an in-depth survey on the framework, principle, characteristics and applications of the CA-based anomaly detection methods, and to point out possible future research directions. Based on the function of CA in anomaly detection, we classify the CA-based anomaly detection methods into four categories: 1) Density estimation, a classic anomaly detection technique including direct density estimation and indirect density estimation, with CA optimizing or substituting the density estimation of samples; 2) Matrix factorization, a crucial branch of anomaly detection method by using CA to factorize the matrix data, which has received frequent usage in machine fault diagnosis and image outlier detection [10]; 3) Machine learning, a widely used technique for anomaly detection based on the functions of CA, including support vector domain method utilizing the solution and geometric approximation of CA, convex hull method utilizing the geometric approximation of CA, online convex programming method utilizing the quick optimization of CA, and neural network method utilizing the steepest descent of CA; and 4) Other CA-based anomaly detection methods. For each of the first three categories, the core CA-based anomaly detection techniques and their variants are both introduced. It should be emphasized that the function and contribution of CA in each algorithm are described, which demonstrates the multidisciplinary property of CA-based anomaly detection and provides new insights for understanding the association between anomaly detection and CA.
The rest of this paper is organized as follows: Section 2 introduces the fundamentals of CA-based anomaly detection; Section 3 reports the direct and indirect density estimation methods and presents the latest development trends; Section 4 reviews the techniques of matrix factorization used in anomaly detection and their applications; The machine learning-based anomaly detection algorithm in CA can be found in Section 5, composed of four sub-categories; Section 6 presents other CA-based anomaly detection methods not involved in the three mainstream categories; Section 7 summarizes this work and discusses the open challenges and future technological trends of anomaly detection based on CA.
2 Research Methodology and Statistics
2.1 Research Methodology
To collect theory and applications of anomaly detection algorithms based on CA, existing literatures are collected from eight authoritative library databases including Google Scholar, Web of Science, Elsevier, Springer, IEEE Xplore, Wiley, Annual Reviews and ProQuest Dissertations & Theses (PQDT). In order to guarantee the accuracy of the retrieval, search terms are divided into two parts: technique terms and application terms. Technique terms concern CA-based anomaly detection methods, in which “convex analysis” AND “anomaly detection” OR “outlier detection” is our primary candidate. Then the application terms are joint, e.g., “convex hull” AND “visual surveillance,” to construct a more comprehensive search string for their specific applications. Full text search is adopted and no restriction on publication type is set. Besides, considering some cornerstone and classic methods delivered earlier, there is also no limitation in publication time. However, we spotlight the latest research progress of CA-based anomaly detection methods since 2000 [29].
After executing each search operation, the filtering process of papers is implemented by reviewing each paper manually in our group. During the review, relevant cross-references are also searched by Google Scholar. If one paper satisfies CA-based anomaly detection algorithms, it is selected in this review for further introduction. Based on this kind of search strategy and criteria, appropriate publications are recorded and reviewed.
2.2 Statistical Analysis
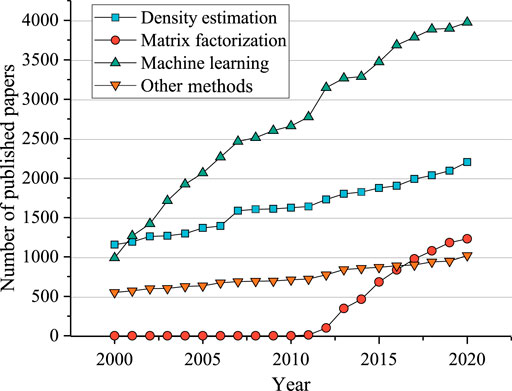
According to our searching results, the number of published papers and applications of CA-based anomaly detection algorithms are statistically analyzed. As shown in Figure 1, the development of the four CA-based anomaly detection categories presents a rapid growth trend in the past 2 decades. As a general and classic technique, density estimation has been employed with a steady upward trend, except a sharp rise in 2007 when the indirect density estimation method was produced. The curve of matrix factorization methods is flat until the emergence of its first model—robust principal component analysis (RPCA)—in 2011. After that, the growth of matrix factorization is steep initially and then slowed down, since this method is only appropriate for matrix data. In addition to the emergence of new sub-categories in 2003 and 2004, there was another rapid increase in the publication number of machine learning methods in 2012, probably because that ImageNet’s victory [30] has triggered the excitement of experts and scholars in deep learning and machine learning in this year. In recent decades, machine learning methods have been of essential importance in anomaly detection as a modern and advanced technique for managing big data generated from sophisticated realities. Besides the above three types of methods, there are many other CA-based anomaly detection methods, such as the convex combination of anomaly detectors [31], CMTMSOM algorithm [32], and archetypal analysis [33], and the number of corresponding researches is increasing every year.
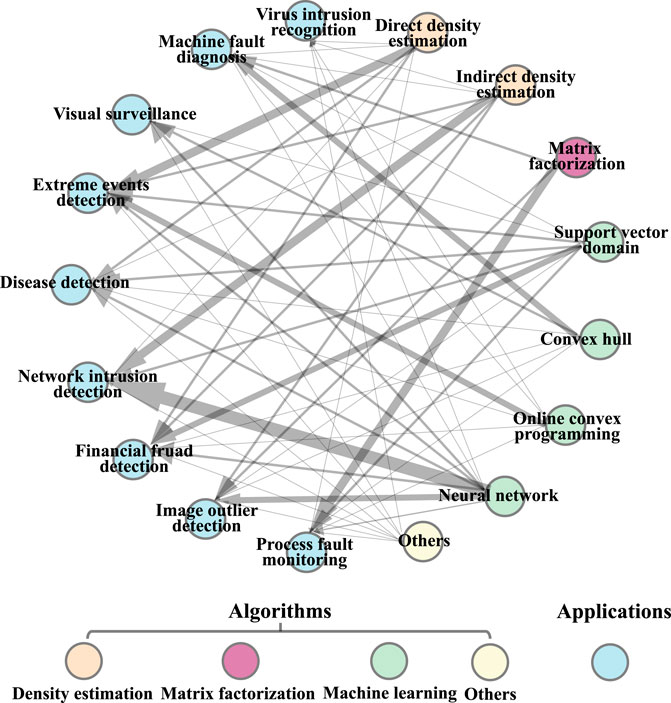
Refer to [34], we report the various real-world applications for CA-based anomaly detection methods in different fields, as shown in Figure 2. Among them, the arrow illustrates that the type of CA-based anomaly detection methods can resolve the corresponding problem of that application, and the line thickness is derived from the number of studies found in the literature search. We can see that the most proverbially extensive applications of CA-based anomaly detection methods are network intrusion detection, extreme events detection, and process fault mornitoring. The goal of the network intrusion detection is to identify unauthorized use, misuse, and abuse of computer systems by both system insiders and external penetrators [35,36]. The objectives of extreme events detection include neuclear explosion, extreme climate and epidemic [37]. And by early warning, manufacturing process-oriented process fault mornitoring is conductive to the prevention and control of dangerous malfunction and to reduce productivity loss [38].
3 Fundamentals of Convex Analysis
3.1 Theoretical Framework of Convex Analysis
Convex analysis (CA) is a branch of mathematics that studies the properties of convex sets and convex functions, often with applications in convex minimization, a subdomain of optimization theory [39]. We proceed to give a few vital and succinct foundations of CA that we used extensively in this review. In addition, we discuss the advantages of CA compared with other mathematical methods, which is the key to the algorithmic success.
3.1.1 Convex Sets
A set C is convex if the line segment between any two points in C lies in C, i.e., if ∀x1, x2 ∈ C and ∀θ ∈ [0, 1], we have
3.1.2 Convex Functions
A function
As a valuable property of convex functions, strong convexity can significantly speed-up the convergence of first order methods. We say that
A large value of α would lead to a faster convergence rate, since a point far from the optimum will have a large gradient, and thus gradient descent will produce large steps in this case.
3.1.3 Convex Optimization
As a significant subfield of CA, convex optimization studies the problem of minimizing convex functions over convex sets for mathematical optimization. A convex optimization problem in standard form is written as [40]:
where the optimization variable is
Convex optimization problem shows many beneficial properties. For example, every local minima is a global minima, and if the objective function is strictly convex, then the problem has at most one optimal point. Therefore, if a task can be formulated as a convex optimization problem, then it can be solved efficiently and reliably with effective and rapid optimization and solution, using interior-point methods or other special methods for convex optimization. General convex optimization focuses on problem formulation and modeling, more specifically, it is applied to find bounds on the optimal value, as well as approximate solutions. These solution methods are dependable enough to be embedded in computer-aided design or analysis tools, or even real-time automatic or reactive control systems.
3.1.4 Duality
The core design of the Lagrangian duality (or just duality) is to consider the constraints in the convex optimization problem Eq. 4 by constructing an objective function with a weighted sum of the constraint functions [42]. Then the Lagrangian
with dom
The associated dual problem of convex optimization problems could often produce an interesting interpretation regarding the original problem and lead to an efficient or distributed method for solving it. Therefore, it also reflects theoretical or conceptual advantages of convex optimization and CA [43].
3.2 Association Between Anomaly Detection and Convex Analysis
CA has substantially geometrical and computational advantages. Common techniques, such as the Karush-Kuhn-Tucker (KKT) optimality conditions [44], gradient descent method [45] and Jensen’s inequality [46], and common applications, such as norm approximation [40], geometric projection and maximum likelihood estimation in CA, are all devoted to typical anomaly detection algorithms. Such anomaly detection algorithms could benefit from CA in robust approximation in algebra and geometry, efficient computation to global unique solutions, and mathematical optimization. Therefore, CA is a valuable and intrinsic part and motivation for anomaly detection.
We review several architectures and methods of existing anomaly detection techniques based on CA and group them into four categories according to the underlying approach adopted by each technique. These include 1) density estimation methods based on the way how density directly or indirectly estimated, 2) matrix factorization methods, 3) machine learning methods based on the support vector domain algorithm, convex hull algorithm, online convex programming algorithm and neural network algorithm, and 4) other methods. The anatomy of CA-based anomaly detection methods and their cornerstone algorithms are illustrated in Figure 3.
4 Density Estimation
Density estimation is an indispensable method used for outlier detection, one of the most elementary issues of anomaly detection. There are two typical algorithms based on CA for which the density estimation is directly or indirectly used. In these methods, “density” describes the probability that the value of a random variable is generated by a certain distribution. Thresholds are set up for density estimation methods, and samples with a density below the threshold are outliers.
4.1 Direct Density Estimation
4.1.1 Model Description
In direct density estimation, abnormal data are defined as samples with a density less than the preset threshold. A probability density function for a continuous random variable is a non-negative Lebesgue-integrable function [47], and satisfies
where FX(x) is the cumulative distribution function of X.
Since the multivariate Gaussian distribution model (see Figure 4A) [48] is not capable of describing the situation where the data in the same set conform to multiple different distributions, the mixture of Gaussian (MoG) (see Figure 4B for instance, which is a linear combination of Gaussian distributions) was used to model the general data distribution [49]. Each Gaussian distribution in the MoG is defined as a component, and then the probability density of the target variable x, p(x), is defined in the MoG as:
where d represents the sample dimension, αk is a mixed coefficient, μk and ∑k are the mean and covariance matrix of the kth component, and γ is the number of mixed components. The Expectation-Maximization (EM) algorithm [50], a typical algorithm using CA, is adopted to optimize the parameter αk, μk and ∑k. The EM algorithm searches for the maximum likelihood estimation of parameters in a probability model that depends on unobservable hidden variables. For samples x1, x2, ..., xn, the hidden variables of each sample are assumed to be z(j), j ∈ [1, m]. Then, the algorithm finds the lower bound of the likelihood function through Jensen’s inequality [46].
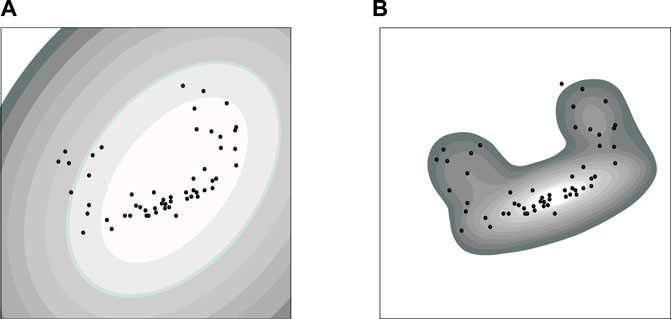
FIGURE 4. Gaussian model and the mixture of Gaussian model: (A) The Gaussian model imposes the ellipsoidal density model on the two-dimensional data; (B) the MoG model is a linear combination of Gaussian distributions. Apertures of diverse sizes are their transformations with different outlier detection errors.
In Eq. 9, L(θ) is the likelihood function, and Qi(z(j)) denotes the probability of xi belonging to class z(j). After parameter optimization through CA, samples with a density from the MoG model less than the preset threshold are outliers.
4.1.2 Systems and Applications
Inspired by the MoG model with the EM algorithm, Woodward and Sain [51] used the EM algorithm to identify outliers from a mixture of normal distributions when there is missing data. They confirmed through simulations and examples that using the EM algorithm on the entire dataset resulted in higher detection probabilities than using only the complete data vectors, which is the subset of the entire dataset that includes only data vectors for which all of the variables were observed. The MoG model with the EM algorithm, can detect nuclear explosions from a large number of background signals (such as earthquakes and mining explosions) using seismic signals (or any other discriminant) [52]. Carrying out outlier detection to recognize heart disease, biological virus invasion, and electrical power grid faults has also been explored [53–55].
4.1.3 Strengths and Limitations
By the Jensen’s inequality of the logarithmic function in the expectation format, the lower bound of the likelihood function L(θ) of parameters in direct density estimation was discovered rapidly, precisely, and effectively. However, the principal drawback of this method is that the number of mixed components is data-dependent due to the requirement such as weights ∑γαk = 1, so it is a tough choice, and the mixture of multiple Gaussian models requires more samples to overcome the curse of dimensionality [56].
4.2 Indirect Density Estimation
4.2.1 Model Description
Although direct density estimation method is adaptable to multiple different distributions estimation and efficient parametric optimization, it can not correctly reflect the pattern’s characteristics for most high-dimensional conditions, as multivariate functions are intrinsically difficult to estimate [57]. To solve this problem, indirect density estimation methods have been developed. The main reason for the name “indirect density estimation” is that it does not require density estimation. The goal of this method is to estimate the density ratio w(x), called importance, of the independent and identically distributed (i.i.d.) training samples
where pte(x) and ptr(x) are the probability density function [58] for the training data and test data, respectively. w(x) is non-negative because pte(x) ≥ 0 and ptr(x) > 0 for all x belonging to the data domain
With the key constraint of avoiding estimating densities pte(x) and ptr(x), adhoc studies have estimated the w(x) to detect the outlier by convex techniques, in which kernel mean matching (KMM) [59], logistic regression (LogReg) [60], the Kullback-Leibler importance estimation procedure (KLIEP) [61,62], least squares importance fitting (LSIF) [63], and unconstrained least squares importance fitting (uLSIF) [64] are popular. For the above-listed methods, the convex expressions for the estimation and their appraisal are summarized in Table 1; we describe the latest two methods in detail.
4.2.1.1 LSIF model
Through convex quadratic programming, Kanamori et al. estimated the w(x) of the sample, which did not involve density estimation by LSIF, and applied it to outlier detection in a toy dataset by considering w(x) as the index of abnormal degree [63]. The LSIF model hypothesizes that w(x) can be estimated by a linear model
In Eq. 11,
4.2.1.2 uLSIF Model
With convex quadratic programming, a unique global solution can be obtained using the LSIF method. However, it tends to suffer from a numerical problem, since the numerical errors tend to accumulate when tracking the regularization path; consequently, it is not practically reliable. Therefore, uLSIF, a practical alternative to LSIF, was developed to provide an approximate solution to LSIF in a computationally efficient and reliable way [64]. By ignoring the non-negativity constraint in the optimization problem in Eq. 11, Kanamori et al. derived the following unconstrained optimization problem:
In Eq. 12, a quadratic regularization term
in which Ib is the b-dimensional identity matrix. Due to the discarding of the non-negativity constraint, some of the learned parameters could be negative. To compensate for this approximation error, the solution was modified by Eq. 14 in an element-wise manner:
One advantage of the above-unconstrained formulation is that the closed-form solution can be computed simply by solving a system of linear equations. Consequently, its calculation can be stable when λ is not too small.
Afterward, several variants of the basic technique uLSIF model were developed, such as KuLSIF as a kernelized variant [66], and RuLSIF as a α-relative variant [67]. In addition, machine learning models like convolutional neural networks (CNN) [68], gradient boosting over decision trees (GBDT), and a one-layer neural network [69], can be trained with the uLSIF loss function to detect anomalies.
4.2.2 Systems and Applications
Since proposed, the uLSIF method has received widespread usage in outlier detection. For instance, based on the experimental results of 12 datasets available from Rätsch’s benchmark repository [70], the SMART disk-failure dataset, and the in-house financial dataset, Hido et al. concluded that the uLSIF-based method is a reliable and computationally efficient alternative to existing outlier detection methods [71]. Umer et al. also illustrated its superiority in the detection of malicious poisoning attacks in 2019 [6]. In addition, change-point detection in time series data such as smart home time series data [72,73], outlying image detection in hand-written digit image and face image data [68], outlier detection in both synthetic and benchmark datasets [74], and computer game cheats detection in game-traffic data [75], all proved its excellence.
4.2.3 Strengths and Limitations
Since estimating density is complex (especially in high-dimensional space), a convex heuristic enables indirect density estimation methods against the curse of dimensionality without going through density estimation. The outliers tend to have smaller importance values (close to zero) and then they emerge by a suitable threshold. Optimization methods, such as Newton’s method, the conjugate gradient method, the Broyden–Fletcher–Goldfarb–Shanno algorithm for a convex nonlinear problem, the gradient descent method, KKT conditions method [44], and the inexact augmented lagrange multiplier (IALM) method for unconstrained and constrained quadratic programs, are not only efficient, but could find the global minima. The uLSIF-based method is highly scalable to large datasets, which is of critical importance in practical applications.
The indirect density estimation method, however, is of well-documented vulnerability to a poisoning attack, even with a modest number of attack points inserted into the training data [6]. When an intelligent adversary (the one with full or partial access to the training data) injects well-crafted malicious samples into the training data, an incorrect estimation of the w(x) can occur.
5 Matrix Factorization
Matrix factorization is a series of methods used for anomaly detection when the data can be represented as a matrix, i.e., a significant representation of data in which columns generally represent linearly independent features and rows represent samples. The dominant mechanism of these methods is that convex programming is employed to factorize the matrix data. Among matrix factorization methods, robust principal component analysis (RPCA) methods consisting of RPCA and its relative extension and improvement, are mainstream and emerging. RPCA has the advantage of tolerance to high-amplitude sharp noise instead of the Gaussian distributed noise of its baseline PCA (or Singular Value Decomposition, SVD) [76]. In this method, a background dictionary is used to represent each pixel linearly, and the residual is taken as the pixel’s abnormal level.
A notable feature of the RPCA series is that there are different definitions and detection methods for anomalies in different applications, but all are based on matrix factorization. Therefore, the matrix factorization models, together with their systems and applications, strengths, and drawbacks, are provided in this section.
5.1 Model Description
The RPCA model and its relative extension and improvement have been widely applied in anomaly detection [77–79] after Candés et al. recovered a low-rank component and a sparse component from the original data matrix by a convenient convex programming, which achieved RPCA via principal component pursuit [80].
5.1.1 RPCA method
A data matrix
where
In Eq. 16, ∥L ∥* is the nuclear norm of the matrix L, obtained by the sum of the singular value of L. ∥E ∥1 is the norm of matrix E, i.e., the sum of absolute values of all elements in E. Also, the parameter λ provides the trade-off between the norm factor ∥L ∥* and ∥E ∥1, which can be calculated according to the standard Eq. 17
and then adjusted slightly according to prior knowledge of the solution.
The optimization problem in Eq. 16 is convex and linearly constrained, and several efficient algorithms are available, including the alternating direction method of multipliers (ADMM) [81], IALM [82], and singular value thresholding (SVT) [83]. Key steps of the RPCA problem solved by IALM are demonstrated in Algorithm 1.
Algorithm 1. RPCA problem using IALM

5.1.2 Stable principal component pursuit method.
After Isom and LaBarre [84] first applied RPCA in the monitoring of fuel cell power plants’ process fault detection, Zhang et al. [85] proposed an LRaSMD-based Mahalanobis distance (LSMAD) method for hyperspectral outlier detection. This algorithm dates to the SPCP model proposed by Zhou et al. [86], in which a noise item N (i.e., i.i.d. noise on each entry of the matrix) programming was
where ∥⋅∥F denotes its Frobenius norm and ∥N ∥F ≤ δ for some δ > 0, thus L* and E* can be estimated more stably.
5.1.3 Low-Rank representation method.
Xu et al. [87] suggested leveraging LRR [88] for anomaly detection in hyperspectral images (HSIs). The LRR model introduced a dictionary matrix D in the linear decomposition of the background matrix, and the convex optimization problem in Eq. 19 is solved for matrix factorization:
In Eq. 19, ∥⋅∥2,1 is defined to be the sum of ℓ2 norms of column vectors of a matrix, and ∥E ∥2,1 represents the ℓ2,1-norm to characterize the error term E. LRR could handle the data collected from multiple subspaces well.
In 2020, Su et al. [10] proposed an LRCRD method, and this model is primarily suitable for hyperspace. They employed another ℓ2 norm to collaborate the global background and anomaly feature as local representation process attribute on the foundation of LRR; thus, a functional outlier detection model with strong representation ability was built:
where ∥Z ∥* is still the nuclear norm of Z, convexly approximating the rank of Z, N is the number of pixels, β > 0 and λ > 0 are both regularization coefficients.
5.1.4 RPCA-OP method.
When it comes to strongly corrupted data, such that the columns of all entries are corrupted, the RPCA via outlier pursuit (RPCA-OP) method, an efficient convex optimization-based algorithm, should be employed for outlier detection [89]. Experiments have confirmed that the RPCA-OP method can even endure column-sparse or row-sparse errors. It recovers the correct column space of the uncorrupted matrix rather than the exact matrix itself like RPCA. Its convex optimization program is shown in Eq. 21:
where C is still a sparse matrix with some columns’ elements all be zero, ∥C ∥2,1 promotes column-wise sparsity. To ensure success, we could tune parameter λ to
5.2 Systems and Applications
Anomaly detection models with matrix facts are primarily applied in image outlier detection and process fault monitoring. Nevertheless, there are different definitions and detection methods for anomalies in these two applicable scenarios.
In image detection, the sparse matrix, one component, indicates outliers. Outlier detection can be simply done by finding the nonzero columns of E∗, when all or a fraction of the data samples are clean. For the cases where E∗ only approximately has sparse column supports, we can use threshold strategy (threshold τ > 0), that is, the ith data vector of X is discriminated to be an outlier if and only if
In process fault monitoring, the data may contain persistent process noise which weakly affect production. The noise may be caused by the sensor errors, the subjective control by operators with different experience, or the instability of the data transmission network. However, the faults, such as sudden changes in system behavior, should be paid more attention to and identified as anomalies.
In 2011, Isom and Labarre used the RPCA method for process monitoring for the first time by straightforward observation of the sparse matrix obtained [84]. Afterwards, powerful multivariate statistics were built for fault detection based on either component matrix. For example, the statistics L2 = xTZ (x is an online testing sample) [83] and Hotelling′s T2 [90] were built. If their value is greater than the threshold under a certain normal condition, a fault occurs.
Matrix factorization-based methods are extensively used in many applications of interest, including image outlier detection, especially in hyperspectral scenarios, video surveillance, and mechanical fault detection. Table 2 lists the applicable scenarios, models, and the improvement and application of the four sets of methods mentioned above, in which L denotes the low-rank component, E denotes the sparse component, N is the additional small dense noise, and Z is the (low-rank) coefficient matrix.
5.3 Strengths and Limitations
In the matrix factorization-based anomaly detection method, CA is of great significance in the fundamental linear factorization of the matrix. CA generally illuminates this method by norm approximation; nuclear norm minimization, as a convex surrogate, replaces the rank function, solves the original NP-hard problem, and makes it successful and efficiently computable. However, this method is only applicable when the sample can be represented as a matrix.
6 Machine Learning
CA has been adopted in many machine learning technologies, including logistic regression, support vector machines, and artificial neural networks. Therefore, these machine learning methods have inevitably and selectively been applied to anomaly detection [96]. In this review, we classified them into four sub-categories, i.e., support vector domain method, convex hull method, online convex optimization method, and neural network method, in conformity with the role of CA in anomaly detection in the machine learning field.
6.1 Support Vector Domain Method
6.1.1 Model Description
This method aims to discover a data description with a presupposed shape from the training dataset. A good description covers all target data but includes no superfluous space. Points outside the description in the test set will be detected as outliers.
Among the support vector domain methods, the support vector machine (SVM) [97] is a mainstream two-class classification method for fields such as text detection, human body recognition, and freight transportation [98]. The SVM separates two types of samples with a maximal margin by a hyperplane. For outlier detection, since there is often only the target sample in the training set due to the lack of negative examples, the original SVM is no longer applicable, and support vector data description (SVDD) was developed by Tax and Duin [43] for one-class classification. It looks for a spherical description as implicit mapping, as shown in Figure 5A. This description encloses most training samples xi and minimizes the volume (i.e., minimizes R) of the hypersphere (R, a), where R is the radius and a is its center.
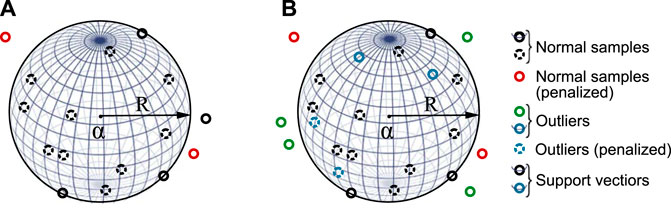
FIGURE 5. Support vector spherical description based on the training set: (A) SVDD and (B) NSVDD. The dashed circles represent samples in the description and the solid circles on and outside the description. The circles on the description are SVs (i.e., a solid circle crossed by a curve) containing both target samples and outliers in (B) NSVDD. The support vector domain method penalizes observations not in the correct position, i.e., red circles in (A) SVDD and (B) NSVDD because normal samples should be inside the description, and blue dashed circles in (B) NSVDD because outliers should fall outside the description.
SVDD adopts the soft-margin criterion [99], and a slack variable ξ is introduced to penalize training samples outside the sphere (i.e., the red point in Figure 5A, with square distance to the center of the sphere is greater than R2). It operates as Step 1 in the following SVDD algorithm to find the hypersphere with the penalty of ξi, where C is the regularization factor (i.e., the trade-off between the volume and the errors) for tighter description and higher accuracy. The detailed algorithm flow (SVDD by the Lagrange multiplier method) is presented as follows:
Step 1) min R2 + C∑iξi s.t. ∥xi − a ∥2 ≤ R2 + ξi, ξi ≥ 0, ∀i;
Step 2) L(R, a, αi, γi, ξi) = R2 + C∑iξi − ∑iαi{R2 + ξi − (∥xi ∥2 − 2a⋅xi + ∥a ∥2)} − ∑iγiξi is the loss function with the Lagrange multipliers αi ≥ 0 and γi ≥ 0;
Step 3) Setting partial derivatives to zero provides the following constraints:
Step 4) Extrapolate 0 ≤ αi ≤ C according to the last equation in Step 3) αi = C − γi and αi ≥ 0, γi ≥ 0;
Step 5) Resubstitute Step 3) into Step 2): L = ∑iαi(xi ⋅xi) − ∑i,jαiαj(xi ⋅xj) s.t. 0 ≤ αi ≤ C;
Step 6) R2 = (xk ⋅xk) − 2∑iαi(xi ⋅xk) + ∑i,jαiαj(xi ⋅xj), xk is the set of support vectors with 0 < αi < C;
Step 7) Test a new object z by the distance to the center of the sphere ∥z − a ∥2 = (z ⋅z) − 2∑iαi(z ⋅xi) + ∑i,jαiαj(xi ⋅xj), if this distance is larger than R2, then the object z is flagged as an anomalous object.
Applying the Lagrange multiplier method [44], the dual problem can be obtained by the KKT conditions, and the problem that both minimum volume and maximum samples are expected to be fulfilled can be transformed into the above convex quadratic programming problem in Step 1 of the SVDD algorithm. Besides, the duality a = ∑nαixi could generate the sparse center of the sphere, which improves its test performance.
Figure 5A is a visual representation of SVDD, and the points on the surface with 0 < αi < C are support vectors (SVs). The red circles are like the black ones (i.e., normal samples in the training set). However, the red circles are outside the hypersphere, so they are penalized.
To further enhance the flexibility of SVDD when negative examples are available, the following SVDD with negative samples (NSVDD) was also proposed by Tax and Duin [43]. NSVDD assumes that the target samples are in the hypersphere as much as possible (i.e., the black circle in Figure 5B), but the outliers are outside (i.e., the green circle in Figure 5B). Then, the normal points (i.e., the red circle) and the outliers (i.e., the blue dashed circle) should be penalized because they are not in the correct position. Eq. 23 describes how NSVDD works:
in which yi ∈ { − 1, 1} is the label of the training sample with “-1” denoting an outlier. NSVDD is identical to the normal SVDD when new variables
By employing two slack variables, NSVDD has shown higher classification accuracy with a varying radius of the hypersphere [100]. However, the outlier placed on the boundary of the description (i.e., the blue solid circle crossed by a curve in Figure 5B can not be distinguished from the SVs in the target class (i.e., black solid circle crossed by a curve) based on Step 7 in the SVDD algorithm. By applying kernel techniques, both SVDD and NSVDD can obtain a rigid hypersphere for nonlinear problems with greater flexibility and malleability.
SVDD is an unsupervised machine learning method for anomaly detection, while NSVDD is supervised. The related semi-supervised method [101] was developed in 2020 for rolling element bearings default detection by combining SVDD and cyclic spectral coherence (CSCoh) as domain indicators [102].
6.1.2 Systems and Applications
Although affected by noise and limited to hypersphere data, standard SVDD can be rated as a cornerstone in the field of anomaly detection. With its improvement, it has been explored for anomaly detection with high-dimensional and large-scale data [103], adversarial examples [104], contaminated data [105], and other anomaly detection situations. Furthermore, in 2020, Yuan et al. [106] demonstrated that this method can undertake robust process monitoring in over 20 real-life datasets, including vehicle evaluation, breast cancer, and process engineering.
6.1.3 Strengths and Limitations
By transforming the mini-volume and most-points problem into convex quadratic programming, convexity makes KKT conditions necessary and sufficient. The optimality of the convex program is adequate for solving the data description of the support vector domain method, which results in accuracy and efficiency for global outlier detection. This method ensures the accuracy of normal samples by minimizing the volume of the description and the error of outlier detection. Compared with other outlier detection methods, this method shows comparable or improved performance for sparse and complex datasets. However, for minuscule target error rates, the SVDD could break down, and this method is not preferred for high-dimensional samples.
6.2 Convex Hull Method
6.2.1 Model Description
The support vector domain method is a fundamental and special case of the convex hull method, in which the hypersphere is a convex hull (CH), and solutions are most provided by convex programming. The CH for a set of points
The convex hull CH(S) can be calculated according to Eq. 24:
Since the existence of outliers in the training set may lead to an overfitting decision model, the CH can be corrected by a parameter λ ∈ [0, + ∞), according to Eq. 25 [108]:
In Eq. 25, v incorporates the vertices of the original convex hull in Eq. 24 regarding their center
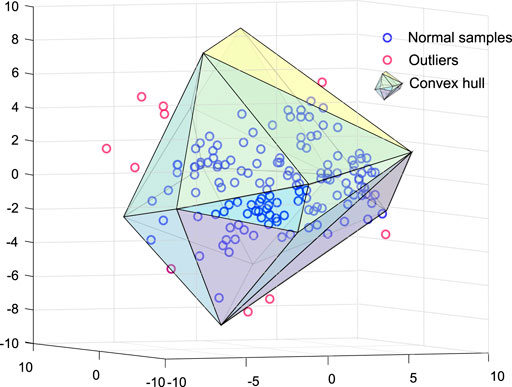
However, this approach shows two major drawbacks. First, the computation cost is high. And second, the training data’s boundary may not be well-modeled by a convex polytope. Calculating the CH of a high-dimension dataset requires a tremendous computational cost. If a dataset comprises N samples in
6.2.2 Systems and Applications
Outlier detection performance was investigated using this method on over 200 datasets [111–113], even in multi-modal distributions of automated visual surveillance detection [114]. All exhibited a trade-off between the detection rate (true positive rate) and false alarm rate (false positive rate), and AUC greater than 0.9. In practice, CHs are usually adopted in industrial intelligent fault diagnosis, multiaxial high-cycle fatigue recognition, and other anomaly detection applications, some of which are described in He et al. [115]’s and Scalet [116]’s studies.
6.2.3 Strengths and Limitations
As a flexible geometric model, a CH is typically a substantial approximation of the target region. It can approximate a polytope without overfitting, even in a high-dimension situation. The low computational and memory storage requirements allow the APE method to be used under limited resources. By the vertex of the CH of the training set, outliers can be relatively easily recognized. However, the boundaries of the training data may not be well modeled by APE in more general non-convex scenarios. Furthermore, due to its ability to manage strong non-convex distributions, NAPE, a more general extension than the APE algorithm, outperforms the rest of the outlier detection methods including APE in many cases [109,110]. Nevertheless, further efforts are needed to reduce the computational costs of building NAPE.
6.3 Online Convex Programming Method
6.3.1 Model Description
Unlike the CH method, which is largely an offline algorithm, the online convex programming (OCP) method can be explored in online anomaly detection methods for the data stream. OCP, such as the online gradient descent (OGD) algorithm [117], as defined by Zinkevich [118], features a sequence of convex programmings with feasible sets that are identical, but the cost functions are diverse. According to what has been learned, the algorithm should always choose a point for the lowest cumulative cost before observing the cost function. Whenever the anomaly score (i.e., probability, density, or other custom metrics) efficiently and simply calculated by the OCP for the current state falls below the dynamic threshold, we declare an anomaly.
OCP can be broadly viewed as a game between two opponents: the Forecaster and the Environment [74,119]. The Forecaster constantly predicts changes in a dynamic Environment, where the influence of the Environment is depicted by a sequence of convex cost functions with arbitrary variations over a given feasible set, and the Forecaster attempts to pick the next feasible point in such a way to reduce the cumulative cost as much as possible.
An OCP problem with horizon T can be outlined by a convex feasible set
Algorithm 2. Online convex programming

The Forecaster will minimize the difference between the actual cost incurred after T rounds of the game and the smallest cumulative cost that could be achieved in hindsight using a single feasible point. Given a strategy μT and a cost function tuple fT, the regret w.r.t. uT is defined as Eq. 26
where uT = (u1, ..., uT) ∈ UT, a time-varying tuple, is a comparison strategy distinguishing from the Forecaster’s observation-driven strategy μT and it does not depend on the previous points or cost functions but only on the time index t.Then the goal would be to select a suitably restricted subset
is sublinear in T. Whenever the anomaly score (i.e., probability, density, or other custom metrics) efficiently and simply calculated by the OCP for the current state falls below the dynamic threshold, we declare an anomaly.
6.3.2 Systems and Applications
Online anomaly detection based on OCP fulfills the needs of some fields, such as industrial production and network routing, where decisions should be made before the comprehension of true costs.
Inspired by recent developments in OCP, Raginsky et al. [120] designed and analyzed a so-called FHTAGN method consisting of assigning a belief (probability) and flagging potential anomalies according to the belief, exploring online anomaly detection methods with dynamic thresholding built on limited feedback. Nevertheless, classic statistical change point detection studies, such as this work [120], surveyed the transient outlier instead of the persistent change. Therefore, persistent change was considered for anomaly detection based on OCP. Further improvements have been made to achieve lower computational complexity [121] or higher anomaly detection accuracy [122].
6.3.3 Strengths and Limitations
Convex optimization provides a more versatile approach to tackling complex situations, especially sequential change point detection. Its efficiency and simplicity make it possible to perform computations in real-time. By the convex cost function of the Environment, schemes such as mirror descent for the OCP method are possible. It allows us to remarkably predict the extrinsic anomalous behavior for the next observation concerning the best model based on what we have seen in the past. However, this work has not been extended to any arbitrary anomaly detection method.
6.4 Neural Network Method
6.4.1 Model Description
In machine learning, especially deep learning, a neural network (NN) is also an essential algorithm that CA contributes to anomaly detection, with its core gradient descent method being the most significant technique in CA [123]. For anomaly detection, a NN extracts the characteristics of abnormal behavior by adaptive learning and learns the normal behavior pattern from the training set. Then, samples with anomalously-related labels in the test set will be anomalies [124].
The loss function to be minimized in a NN is:
where w is the weight of the network, X is the training set with labels and l(x, w) denotes the loss calculated by the sample x ∈ X and its label.
The gradient descent method is a first-order optimization algorithm usually applied to find the minima of a function. An iterative search is performed to the point with the specified step size from the current point along the opposite direction of the gradient (or approximate gradient), which is the direction of steepest descent. As the most common gradient descent method in NN, minibatch stochastic gradient descent [45] is usually called simply stochastic gradient descent (SGD) in recent literature even though it operates on mini-batches. It performs the following parameter update:
where
6.4.2 Systems and Applications
Many neural networks have been applied to specific fields of anomaly detection and have been investigated with appealing results. For example, Zenati et al. [125] leveraged bidirectional generative adversarial networks (BiGAN) for image and network intrusion detection, Gao et al. [126] applied CNN for time series anomaly detection in 367 public benchmark datasets from Yahoo, and Xu et al. [127] proposed a cluster-based deep adaptation network (CDAN) model that is adaptable for the spinning power consumption anomaly detection problem in the real-environment yarn spinning workshop. These studies have achieved a desirable performance and high speed.
6.4.3 Strengths and Limitations
As an unconstrained optimization in convex optimization theory, the gradient descent method achieves a rapid decline in the loss function by the convex path, contributing considerably to the behavior learning of normal samples and anomalies. NN is a non-parametric method that typically employs gradient descent. With the best architecture and an efficient training procedure, anomaly detection by a NN exhibits higher AUC and F1 scores than other state-of-the-art methods, such as LRR [88] and isolation forests (IF) [128]. Nevertheless, a NN generally desires adequate training data for convergence. Another critical drawback of this method may be that it can not provide the analyst with clear interpretability of why the system believes an entity is potentially anomalous.
7 Other Convex Analysis-Based Anomaly Detection Methods
In addition to the density estimation method, matrix factorization method, and machine learning method, there are also a number of other CA-based anomaly detection methods which still benefit from the geometrical and computational advantages of CA. Robust approximation, efficient computation, and mathematical optimization of CA make these techniques effective and reliable, which is a critical feature for deployment in practice.
In [31], a novel technique of finding a convex combination of outputs from anomaly detectors to maximize the number of true alarms in τ-fraction of most anomalies was proposed for security domain. In the experimental evaluation attack detections of NetFlow and HTTP network, this technique outperforms prior work, and it is also more robust to noise in labels of training data.
In [129], anomaly detector for control systems based on CUSUM was improved by breaking down the original nonlinearity into several convex optimization problems. In a simple example, it is shown that this anomaly detector could better diminish the attack impact and detect attacks.
In [32], CMTMSOM was proposed with the contributions of the powerful convex and continuous optimization techniques to diagnose Parkinson’s disease. Results on Parkinson telemonitoring dataset indicate that this method performs better than current parametric models.
In [130], CRO-FADALARA was proposed with a cleaning procedure and RO-FADALARA (Robust Outlier FADA for LARge Applications) to detect functional anomalies. This approach can not only return archetypoids but also output a set of outliers together with the importance that each variable had in the outlier detection. In [131], anomalous events during gameplay were detected through archetypal analysis (AA) with the reconstruction error distribution. In addition, archetypal analysis was explored to detect hyperspectral anomalies [132], anomalous flows in urban water networks [133], and so on.
8 Benchmark and Comparison
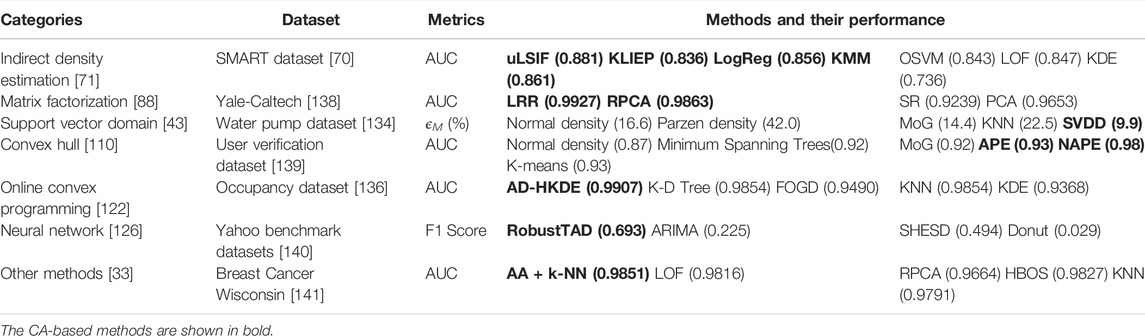
Based on the experiments introduced by several representative CA-based anomaly detection literatures, we summarize the performance of CA-based methods with other baseline methods in some golden-standard datasets. A comprehensive comparison is demonstrated in Table 3, in which the model with the best performance in the respective dataset is presented, and the CA-based methods are shown in bold. We introduce the support vector domain method and the online convex programming method in detail.
To investigate how the SVDD works in a real outlier detection problem, Tax and Duin focused on a machine diagnostics problem: the distinguishment of the pump with faulty operation conditions [43]. In the dataset of the submersible water pump [134], the outlier data contains pumping situations with loose foundation, imbalance and failure in loads and speeds of the pump. To see how well the SVDD performs, they compared it with a number of other methods, including the normal density, the MoG (optimized using EM), the Parzen density, and KNN. To make a more quantitative comparison, an error measure (ϵM) is derived from the ROC curves, as demonstrated in Eq. 31,
where ϵ1 is the error of the first kind and ϵΠ is the error of the second kind of the investigated interval (A, B) [135]. The methods were applied to number of features ranging from 3 up to 64, and Table 3 shows their overall best performances with 30 features. Results indicate that in almost all cases, the SVDD, which focuses on modeling the boundary, obtains a better performance than other methods, especially for higher dimensionalities.
In addition, with the latest progress of the online convex programming method, the anomaly detector with hierarchical kernel density estimators (AD-HKDE) method was applied to the Occupancy dataset [136], which consists of 10,808 data points whose labels correspond to occupied (normal) and unoccupied (anomalous) room states [122], and other seven real-world datasets. Using ROC and AUC, the performance of AD-HKDE was compared with that of KNN, K-D tree nearest neighbor search (K-D Tree), Fourier online gradient descent (FOGD) [137], and Kernel density estimation (KDE). As seen in Table 3, the AD-HKDE method achieves the highest AUC score, indicating that it has a stronger guarantee in relatively smaller false alarm regions (except a few cases). However, when the data size is small, AD-HKDE can not perfectly learn the bandwidths in all regions across time, thus yield relatively unsatisfactory anomaly detection results.
9 Conclusion and Discussion
Anomaly detection is a crucial technique used to identify abnormal samples with behavior or patterns conveying critical (usually harmful or even fatal) information. CA has been widely used in anomaly detection because of its ability to robustly approximate in algebra and geometry, efficiently compute to global unique solutions, and mathematically optimize. However, little work has realized a comprehensive classification of the CA-based anomaly detection. In this paper, we classify the existing CA-based anomaly detection techniques into four categories: density estimation, matrix factorization, machine learning, and other methods, according to the underlying principle of CA in anomaly detection. Models of wide application domains and data types from the general to the particular such as matrices and time series have been intensively investigated. The main methods discussed in this review are summarized in Table 4.
In summary, this paper presents an in-depth literature review of the CA-based anomaly detection techniques, including their latest progress, systems and applications, as well as strengths and limitations. Functions and contributions of CA in anomaly detection are underlined, demonstrating the multidisciplinary property of CA-based anomaly detection and providing new and succinct understanding of the association between anomaly detection and CA.
With the remarkable progress made in the techniques of big data and machine learning, CA-based anomaly detection shows great promise for more expeditious, accurate and intelligent detection capacities. In this field, further research should be conducted on the following open challenges to explore this promising domain:
1) Like the density estimation and matrix factorization techniques mentioned in this paper, they are popular and effective strategies for anomaly detection based on CA that declaring observations anomalous if their values deviate below or over some threshold. However, how to set this threshold with high efficiency remains in doubt, and this notoriously difficult problem should be resolved.
2) At present, the data streams generated in many industrial scenarios put forward higher requirements for anomaly detection algorithms, and real-time results should be generated without waiting for all inputs. Consequently, taking the support vector domain method as an example, future studies should explore how to utilize an online process to learn the hypersphere boundary of SVDD in streaming environments.
3) Incorporating prior rules for convex theory-based anomaly detection models, especially machine learning methods, could be investigated intensively to enhance their performance. For instance, mine the structural information of the data itself by norms, such as ℓ2,1 norm and ℓ2,0 norm.
4) Considering the data characteristics of the anomaly detection domain, where anomalies are few and two classes are extremely unbalanced, the generalization ability of machine learning methods, especially the gradient descent-based model, should be strengthened to be more suitable and applicable.
Author Contributions
Conceptualization: TW and XL; Methodology: TW and XO; Validation: MC and ZC; Formal analysis: MC and ZC; Investigation: MC and TC; Resources: XO and ZC; Writing—original draft: TW and XO; Writing—review and editing: TW and XL; Visualization: ZC; Supervision: XT; Project administration: XL; Funding acquisition: TC and XT. All authors contributed to the article and approved the submitted version.
Funding
This research was funded by the National Nature Science Foundation of China (72025405, 72088101, 91846301, 71790615, and 71774168), the Shenzhen Basic Research Project for Development of Science and Technology (JCYJ20200109141218676 and 202008291726500001) and the Hunan Science and Technology Plan Project (2020TP1013 and 2020JJ4673).
Conflict of Interest
ZC was employed by the Power China Zhongnan Engineering Corporation Limited.
The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Chandola V, Banerjee A, Kumar V. Anomaly Detection. ACM Comput Surv (2009) 41:1–58. doi:10.1145/1541880.1541882
2. Harrou F, Kadri F, Chaabane S, Tahon C, Sun Y. Improved Principal Component Analysis for Anomaly Detection: Application to an Emergency Department. Comput Ind Eng (2015) 88:63–77. doi:10.1016/j.cie.2015.06.020
3. Aryal S, Santosh KC, Dazeley R. Usfad: a Robust Anomaly Detector Based on Unsupervised Stochastic forest. Int J Mach Learn Cyber (2021) 12:1137–50. doi:10.1007/s13042-020-01225-0
4. Edgeworth FY. Xli. On Discordant Observations. The Lond Edinb Dublin Philosophical Mag J Sci (1887) 23:364–75. doi:10.1080/14786448708628471
5. Almiani M, AbuGhazleh A, Jararweh Y, Razaque A. Ddos Detection in 5g-Enabled Iot Networks Using Deep Kalman Backpropagation Neural Network. Int J Mach Learn Cyber (2021) 12:3337–49. doi:10.1007/s13042-021-01323-7
6. Umer M, Frederickson C, Polikar R. Vulnerability of Covariate Shift Adaptation against Malicious Poisoning Attacks. In: 2019 International Joint Conference on Neural Networks (IJCNN) (2019). p. 1–8. doi:10.1109/IJCNN.2019.8851748
7. Ahmed J, Gao B, Woo WL, Zhu Y. Ensemble Joint Sparse Low-Rank Matrix Decomposition for Thermography Diagnosis System. IEEE Trans Ind Electron (2021) 68:2648–58. doi:10.1109/TIE.2020.2975484
8. Eduardo S, Nazabal A, Williams CKI, Sutton C. Robust Variational Autoencoders for Outlier Detection and Repair of Mixed-type Data. In: S Chiappa, and R Calandra, editors. Proceedings of the Twenty Third International Conference on Artificial Intelligence and Statistics. Vol. 108 of Proceedings of Machine Learning Research. New York City, NY, USA: PMLR (2020). p. 4056–66.
9. Peng C, Chen Y, Kang Z, Chen C, Cheng Q. Robust Principal Component Analysis: A Factorization-Based Approach with Linear Complexity. Inf Sci (2020) 513:581–99. doi:10.1016/j.ins.2019.09.074
10. Su H, Wu Z, Zhu A-X, Du Q. Low Rank and Collaborative Representation for Hyperspectral Anomaly Detection via Robust Dictionary Construction. ISPRS J Photogrammetry Remote Sensing (2020) 169:195–211. doi:10.1016/j.isprsjprs.2020.09.008
11. Hu M, Feng X, Ji Z, Yan K, Zhou S. A Novel Computational Approach for Discord Search with Local Recurrence Rates in Multivariate Time Series. Inf Sci (2019) 477:220–33. doi:10.1016/j.ins.2018.10.047
12. Su M-Y. Using Clustering to Improve the Knn-Based Classifiers for Online Anomaly Network Traffic Identification. J Netw Computer Appl (2011) 34:722–30. doi:10.1016/j.jnca.2010.10.009
13. Muniyandi AP, Rajeswari R, Rajaram R. Network Anomaly Detection by Cascading K-Means Clustering and C4.5 Decision Tree Algorithm. Proced Eng (2012) 30:174–82. doi:10.1016/j.proeng.2012.01.849
14. Chen Z, Li YF. Anomaly Detection Based on Enhanced Dbscan Algorithm. Proced Eng (2011) 15:178–82. doi:10.1016/j.proeng.2011.08.036
15. Yao X-H, Fu J-Z, Chen Z-C. Intelligent Fault Diagnosis Using Rough Set Method and Evidence Theory for Nc Machine Tools. Int J Computer Integrated Manufacturing (2009) 22:472–82. doi:10.1080/09511920802537995
16. Mascaro S, Nicholso AE, Korb KB. Anomaly Detection in Vessel Tracks Using Bayesian Networks. Int J Approximate Reasoning (2014) 55:84–98. doi:10.1016/j.ijar.2013.03.012
17. Ren H, Ye Z, Li Z. Anomaly Detection Based on a Dynamic Markov Model. Inf Sci (2017) 411:52–65. doi:10.1016/j.ins.2017.05.021
18. Nagpal T, Brar YS. Artificial Neural Network Approaches for Fault Classification: Comparison and Performance. Neural Comput Applic (2014) 25:1863–70. doi:10.1007/s00521-014-1677-y
19. Yan K, Huang J, Shen W, Ji Z. Unsupervised Learning for Fault Detection and Diagnosis of Air Handling Units. Energy and Buildings (2020) 210:109689. doi:10.1016/j.enbuild.2019.109689
20. Rockafellar RT. Convex Analysis. Princeton, NJ, USA: Princeton University Press (1970). doi:10.1515/9781400873173
21. Wang H, Bah MJ, Hammad M. Progress in Outlier Detection Techniques: A Survey. IEEE Access (2019) 7:107964–8000. doi:10.1109/ACCESS.2019.2932769
22. Nachman B, Shih D. Anomaly Detection with Density Estimation. Phys Rev D (2020) 101:075042. doi:10.1103/PhysRevD.101.075042
23. Mordukhovich BS, Nam NM. An Easy Path to Convex Analysis and Applications. Synth Lectures Mathematics Stat (2013) 6:1–218. doi:10.2200/S00554ED1V01Y201312MAS014
24. Zhang W, Lu X, Li X. Similarity Constrained Convex Nonnegative Matrix Factorization for Hyperspectral Anomaly Detection. IEEE Trans Geosci Remote Sensing (2019) 57:4810–22. doi:10.1109/TGRS.2019.2893116
25. Li P, Niggemann O. Non-convex hull Based Anomaly Detection in Cpps. Eng Appl Artif Intelligence (2020) 87:103301. doi:10.1016/j.engappai.2019.103301
26. Pachman JM. Optimization of Seismic Reconnaissance Surveys in Petroleum Exploration. Management Sci (1966) 12:B–312. doi:10.1287/mnsc.12.8.b312
27. Goernitz N, Kloft M, Rieck K, Brefeld U. Toward Supervised Anomaly Detection. jair (2013) 46:235–62. doi:10.1613/jair.3623
28. Turchini F, Seidenari L, Del Bimbo A. Convex Polytope Ensembles for Spatio-Temporal Anomaly Detection. In: S Battiato, G Gallo, R Schettini, and F Stanco, editors. Image Analysis and Processing - ICIAP 2017. Cham: Springer International Publishing (2017). p. 174–84. doi:10.1007/978-3-319-68560-1_16
29. Wang Y, Yu Y, Cao S, Zhang X, Gao S. A Review of Applications of Artificial Intelligent Algorithms in Wind Farms. Artif Intell Rev (2020) 53:3447–500. doi:10.1007/s10462-019-09768-7
30. Krizhevsky A, Sutskever I, Hinton GE. Imagenet Classification with Deep Convolutional Neural Networks. Adv Neural Inf Process Syst (2012) 25:1097–105.
31. Grill M, Pevný T. Learning Combination of Anomaly Detectors for Security Domain. Computer Networks (2016) 107:55–63. doi:10.1016/j.comnet.2016.05.021
32. Taylan P, Yerlikaya-Özkurt F, Bilgiç Uçak B, Weber G-W. A New Outlier Detection Method Based on Convex Optimization: Application to Diagnosis of Parkinson's Disease. J Appl Stat (2021) 48:2421–40. doi:10.1080/02664763.2020.1864815
33. Cabero I, Epifanio I, Piérola A, Ballester A. Archetype Analysis: A New Subspace Outlier Detection Approach. Knowledge-Based Syst (2021) 217:106830. doi:10.1016/j.knosys.2021.106830
34. Tang J, Liu G, Pan Q. A Review on Representative Swarm Intelligence Algorithms for Solving Optimization Problems: Applications and Trends. Ieee/caa J Autom Sinica (2021) 8:1627–43. doi:10.1109/JAS.2021.1004129
35. Mukherjee B, Heberlein LT, Levitt KN. Network Intrusion Detection. IEEE Netw (1994) 8:26–41. doi:10.1109/65.283931
36. Hu N, Tian Z, Lu H, Du X, Guizani M. A Multiple-Kernel Clustering Based Intrusion Detection Scheme for 5g and Iot Networks. Int J Mach Learn Cyber (2021) 12:3129–44. doi:10.1007/s13042-020-01253-w
37. Peterson TC, Stott PA, Herring S. Explaining Extreme Events of 2011 from a Climate Perspective. Bull Amer Meteorol Soc. (2012) 93:1041–67. doi:10.1175/BAMS-D-12-00021.1
38. Saraeian S, Shirazi B. Process Mining-Based Anomaly Detection of Additive Manufacturing Process Activities Using a Game Theory Modeling Approach. Comput Ind Eng (2020) 146:106584. doi:10.1016/j.cie.2020.106584
39. Bubeck S. Convex Optimization: Algorithms and Complexity. FNT Machine Learn (2015) 8:231–357. doi:10.1561/2200000050
40. Boyd S, Vandenberghe L. Convex Optimization. Cambridge: Cambridge University Press (2004). doi:10.1017/CBO9780511804441
41. Liu N, Qin S. A Neurodynamic Approach to Nonlinear Optimization Problems with Affine equality and Convex Inequality Constraints. Neural Networks (2019) 109:147–58. doi:10.1016/j.neunet.2018.10.010
42. Boţ RI, Grad S-M, Wanka G. On strong and Total lagrange Duality for Convex Optimization Problems. J Math Anal Appl (2008) 337:1315–25. doi:10.1016/j.jmaa.2007.04.071
43. Tax DMJ, Duin RPW. Support Vector Data Description. Machine Learn (2004) 54:45–66. doi:10.1023/B:MACH.0000008084.60811.49
44. Li M. Generalized lagrange Multiplier Method and Kkt Conditions with an Application to Distributed Optimization. IEEE Trans Circuits Syst (2019) 66:252–6. doi:10.1109/TCSII.2018.2842085
45. Vaswani S, Mishkin A, Laradji I, Schmidt M, Gidel G, Lacoste-Julien S. Painless Stochastic Gradient: Interpolation, Line-Search, and Convergence Rates. In: H Wallach, H Larochelle, A Beygelzimer, F d’ Alché-Buc, E Fox, and R Garnett, editors. Advances in Neural Information Processing Systems, Vol. 32. Vancouver, Canada: Curran Associates, Inc. (2019).
46. Abramovich S, Jameson G, Sinnamon G. Refining Jensen’s Inequality. Bull Math Soc Sci Math Phys Répub Pop Roum (2004) 47(95):3–14.
47. Sayed WA, Darwish MA. On the Existence of Solutions of a Perturbed Functional Integral Equation in the Space of Lebesgue Integrable Functions on ℝ+. ZN PRz Mechanika (2018) 41:19–27. doi:10.7862/rf.2018.2
48. Ahrendt P. The Multivariate Gaussian Probability Distribution. Kongens Lyngby, Denmark: Tech. rep., Technical University of Denmark (2005).
49. Sain SR, Gray HL, Woodward WA, Fisk MD. Outlier Detection from a Mixture Distribution when Training Data Are Unlabeled. Bull Seismol Soc Am (1999) 89:294–304. doi:10.1785/BSSA0890010294
50. Sammaknejad N, Zhao Y, Huang B. A Review of the Expectation Maximization Algorithm in Data-Driven Process Identification. J Process Control (2019) 73:123–36. doi:10.1016/j.jprocont.2018.12.010
51. Woodward WA, Sain SR. Testing for Outliers from a Mixture Distribution when Some Data Are Missing. Comput Stat Data Anal (2003) 44:193–210. doi:10.1016/S0167-9473(03)00008-2
52. Scott DW, Sain SR. Multidimensional Density Estimation. In: C Rao, E Wegman, and J Solka, editors. Data Mining and Data Visualization. Vol. 24 of Handbook of Statistics. Amsterdam, Netherlands: Elsevier (2005). p. 229–61. doi:10.1016/S0169-7161(04)24009-3
53. Liu J, Miao Q, Sun Y, Song J, Quan Y. Fast Structural Ensemble for One-Class Classification. Pattern Recognition Lett (2016) 80:179–87. doi:10.1016/j.patrec.2016.06.028
54. Huang G, Yang Z, Chen X, Ji G. An Innovative One-Class Least Squares Support Vector Machine Model Based on Continuous Cognition. Knowledge-Based Syst (2017) 123:217–28. doi:10.1016/j.knosys.2017.02.024
55. De Santis E, Livi L, Sadeghian A, Rizzi A. Modeling and Recognition of Smart Grid Faults by a Combined Approach of Dissimilarity Learning and One-Class Classification. Neurocomputing (2015) 170:368–83. doi:10.1016/j.neucom.2015.05.112
56. Bach F. Breaking the Curse of Dimensionality with Convex Neural Networks. J Mach Learn Res (2017) 18:629–81.
57. van der Walt CM, Barnard E. Variable Kernel Density Estimation in High-Dimensional Feature Spaces. In: Thirty-first AAAI conference on artificial intelligence (2017). p. 2674–80.
58. Dobronets BS, A. Popova O, Popova OA. Improving the Accuracy of the Probability Density Function Estimation. J Sib Fed Univ Math Phys (2017) 10:16–21. doi:10.17516/1997-1397-2017-10-1-16-21
59. Huang J, Gretton A, Borgwardt K, Schölkopf B, Smola A. Correcting Sample Selection Bias by Unlabeled Data. Adv Neural Inf Process Syst (2006) 19:601–8.
60. Bickel S, Brückner M, Scheffer T. Discriminative Learning for Differing Training and Test Distributions. In: ICML ’07: Proceedings of the 24th International Conference on Machine Learning. New York, NY, USA: Association for Computing Machinery (2007). p. 81–8. doi:10.1145/1273496.1273507
61. Sugiyama M, Suzuki T, Nakajima S, Kashima H, von Bünau P, Kawanabe M. Direct Importance Estimation for Covariate Shift Adaptation. Ann Inst Stat Math (2008) 60:699–746. doi:10.1007/s10463-008-0197-x
62. Sugiyama M, Nakajima S, Kashima H, Von Buenau P, Kawanabe M. Direct Importance Estimation with Model Selection and its Application to Covariate Shift Adaptation. In: NIPS, Vol. 7. Princeton, NJ, USA: Citeseer (2007). p. 1433–40.
63. Kanamori T, Hido S, Sugiyama M. Efficient Direct Density Ratio Estimation for Non-stationarity Adaptation and Outlier Detection. In: Advances in Neural Information Processing Systems. Princeton, NJ, USA: Citeseer (2008). p. 809–16.
64. Kanamori T, Hido S, Sugiyama M. A Least-Squares Approach to Direct Importance Estimation. J Mach Learn Res (2009) 10:1391–445.
65. de Souza SVC, Junqueira RG. A Procedure to Assess Linearity by Ordinary Least Squares Method. Analytica Chim Acta (2005) 552:25–35. doi:10.1016/j.aca.2005.07.043
66. Kanamori T, Suzuki T, Sugiyama M. Statistical Analysis of Kernel-Based Least-Squares Density-Ratio Estimation. Mach Learn (2012) 86:335–67. doi:10.1007/s10994-011-5266-3
67. Yamada M, Suzuki T, Kanamori T, Hachiya H, Sugiyama M. Relative Density-Ratio Estimation for Robust Distribution Comparison. Neural Comput (2013) 25:1324–70. doi:10.1162/NECO_a_00442
68. Nam H, Sugiyama M. Direct Density Ratio Estimation with Convolutional Neural Networks with Application in Outlier Detection. IEICE Trans Inf Syst (2015) E98.D:1073–9. doi:10.1587/transinf.2014EDP7335
69. Hushchyn M, Ustyuzhanin A. Generalization of Change-point Detection in Time Series Data Based on Direct Density Ratio Estimation. J Comput Sci (2021) 53:101385. doi:10.1016/j.jocs.2021.101385
70. Rätsch G, Onoda T, Müller K-R. Soft Margins for Adaboost. Machine Learn (2001) 42:287–320. doi:10.1023/A:1007618119488
71. Hido S, Tsuboi Y, Kashima H, Sugiyama M, Kanamori T. Statistical Outlier Detection Using Direct Density Ratio Estimation. Knowl Inf Syst (2011) 26:309–36. doi:10.1007/s10115-010-0283-2
72. Liu S, Yamada M, Collier N, Sugiyama M. Change-point Detection in Time-Series Data by Relative Density-Ratio Estimation. Neural Networks (2013) 43:72–83. doi:10.1016/j.neunet.2013.01.012
73. Aminikhanghahi S, Wang T, Cook DJ. Real-time Change point Detection with Application to Smart home Time Series Data. IEEE Trans Knowl Data Eng (2019) 31:1010–23. doi:10.1109/TKDE.2018.2850347
74.[Dataset] Yamada M, Liu S, Kaski S. Interpreting Outliers: Localized Logistic Regression for Density Ratio Estimation. Arxiv preprint (2017). Available from: http://arxiv.org/abs/1702.06354 (Accessed December 5, 2021).
75. Islam MS, Dong B, Chandra S, Khan L, Thuraisingham BM. Gci: A Gpu Based Transfer Learning Approach for Detecting Cheats of Computer Game. IEEE Trans Dependable Secure Comput (2020) 2020:1. doi:10.1109/TDSC.2020.3013817
76. Zhang A, Han R. Optimal Sparse Singular Value Decomposition for High-Dimensional High-Order Data. J Am Stat Assoc (2019) 114:1708–25. doi:10.1080/01621459.2018.1527227
77.[Dataset] Chen X, Liu C, Li B, Lu K, Song D. Targeted Backdoor Attacks on Deep Learning Systems Using Data Poisoning. Arxiv preprint (2017). Available from: https://arxiv.org/abs/1712.05526 (Accessed December 5, 2021).
78. Bouwmans T, Javed S, Zhang H, Lin Z, Otazo R. On the Applications of Robust Pca in Image and Video Processing. Proc IEEE (2018) 106:1427–57. doi:10.1109/JPROC.2018.2853589
79. Ruff L, Kauffmann JR, Vandermeulen RA, Montavon G, Samek W, Kloft M, et al. A Unifying Review of Deep and Shallow Anomaly Detection. Proc IEEE (2021) 109:756–95. doi:10.1109/JPROC.2021.3052449
80. Candès EJ, Li X, Ma Y, Wright J. Robust Principal Component Analysis? J ACM (2011) 58:1–37. doi:10.1145/1970392.1970395
81. Candés E, Li X, Ma Y, Wright J. Robust Principal Component Analysis?: Recovering Low-Rank Matrices from Sparse Errors. In: 2010 IEEE Sensor Array and Multichannel Signal Processing Workshop (2010). p. 201–4. doi:10.1109/SAM.2010.5606734
82. Lin Z, Liu R, Su Z. Linearized Alternating Direction Method with Adaptive Penalty for Low-Rank Representation. In: NIPS’11: Proceedings of the 24th International Conference on Neural Information Processing Systems. Red Hook, NY, USA: Curran Associates Inc. (2011). p. 612–20.
83. Pan Y, Yang C, Sun Y, An R, Wang L. Fault Detection with Principal Component Pursuit Method. J Phys Conf Ser (2015) 659:012035. doi:10.1088/1742-6596/659/1/012035
84. Isom JD, LaBarre RE. Process Fault Detection, Isolation, and Reconstruction by Principal Component Pursuit. In: Proceedings of the 2011 American Control Conference (2011). p. 238–43. doi:10.1109/ACC.2011.5990849
85. Zhang Y, Du B, Zhang L, Wang S. A Low-Rank and Sparse Matrix Decomposition-Based Mahalanobis Distance Method for Hyperspectral Anomaly Detection. IEEE Trans Geosci Remote Sensing (2016) 54:1376–89. doi:10.1109/TGRS.2015.2479299
86. Zhou Z, Li X, Wright J, Candès E, Ma Y. Stable Principal Component Pursuit. In: 2010 IEEE International Symposium on Information Theory (2010). p. 1518–22. doi:10.1109/ISIT.2010.5513535
87. Xu Y, Wu Z, Li J, Plaza A, Wei Z. Anomaly Detection in Hyperspectral Images Based on Low-Rank and Sparse Representation. IEEE Trans Geosci Remote Sensing (2016) 54:1990–2000. doi:10.1109/TGRS.2015.2493201
88. Liu G, Lin Z, Yan S, Sun J, Yu Y, Ma Y. Robust Recovery of Subspace Structures by Low-Rank Representation. IEEE Trans Pattern Anal Mach Intell (2013) 35:171–84. doi:10.1109/TPAMI.2012.88
89. Xu H, Caramanis C, Sanghavi S. Robust Pca via Outlier Pursuit. IEEE Trans Inform Theor (2012) 58:3047–64. doi:10.1109/TIT.2011.2173156
90. Pan Y, Yang C, An R, Sun Y. Robust Principal Component Pursuit for Fault Detection in a Blast Furnace Process. Ind Eng Chem Res (2018) 57:283–91. doi:10.1021/acs.iecr.7b03338
91. Sun W, Yang G, Li J, Zhang D. Randomized Subspace-Based Robust Principal Component Analysis for Hyperspectral Anomaly Detection. J Appl Rem Sens (2018) 12:1–19. doi:10.1117/1.JRS.12.015015
92. Sun W, Liu C, Li J, Lai YM, Li W. Low-rank and Sparse Matrix Decomposition-Based Anomaly Detection for Hyperspectral Imagery. J Appl Remote Sens (2014) 8(1):083641. doi:10.1117/1.JRS.8.083641
93. Qu Y, Wang W, Guo R, Ayhan B, Kwan C, Vance S, et al. Hyperspectral Anomaly Detection through Spectral Unmixing and Dictionary-Based Low-Rank Decomposition. IEEE Trans Geosci Remote Sensing (2018) 56:4391–405. doi:10.1109/TGRS.2018.2818159
94. Zhou C, Paffenroth RC. Anomaly Detection with Robust Deep Autoencoders. In: KDD ’17: Proceedings of the 23rd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York, NY, USA: Association for Computing Machinery (2017). p. 665–74. doi:10.1145/3097983.3098052
95.[Dataset] Chalapathy R, Menon AK, Chawla S. Anomaly Detection Using One-Class Neural Networks. ArXiv preprint (2018). Available from: https://arxiv.org/abs/1802.06360 (Accessed December 5, 2021).
96. Cvitić I, Peraković D, Periša M, Gupta B. Ensemble Machine Learning Approach for Classification of Iot Devices in Smart home. Int J Mach Learn Cyber (2021) 12:3179–202. doi:10.1007/s13042-020-01241-0
97. Jan SU, Lee Y-D, Shin J, Koo I. Sensor Fault Classification Based on Support Vector Machine and Statistical Time-Domain Features. IEEE Access (2017) 5:8682–90. doi:10.1109/ACCESS.2017.2705644
98. Di Ciccio C, van der Aa H, Cabanillas C, Mendling J, Prescher J. Detecting Flight Trajectory Anomalies and Predicting Diversions in Freight Transportation. Decis Support Syst (2016) 88:1–17. doi:10.1016/j.dss.2016.05.004
99. Alam S, Sonbhadra SK, Agarwal S, Nagabhushan P, Tanveer M. Sample Reduction Using Farthest Boundary point Estimation (Fbpe) for Support Vector Data Description (Svdd). Pattern Recognition Lett (2020) 131:268–76. doi:10.1016/j.patrec.2020.01.004
100. Mu T, Nandi AK. Multiclass Classification Based on Extended Support Vector Data Description. IEEE Trans Syst Man Cybern B (2009) 39:1206–16. doi:10.1109/TSMCB.2009.2013962
101. Akcay S, Atapour-Abarghouei A, Breckon TP. Ganomaly: Semi-supervised Anomaly Detection via Adversarial Training. In: Asian Conference on Computer Vision. Berlin, Germany: Springer (2019). p. 622–37. doi:10.1007/978-3-030-20893-6_39
102. Liu C, Gryllias K. A Semi-supervised Support Vector Data Description-Based Fault Detection Method for Rolling Element Bearings Based on Cyclic Spectral Analysis. Mech Syst Signal Process (2020) 140:106682. doi:10.1016/j.ymssp.2020.106682
103. Erfani SM, Rajasegarar S, Karunasekera S, Leckie C. High-dimensional and Large-Scale Anomaly Detection Using a Linear One-Class Svm with Deep Learning. Pattern Recognition (2016) 58:121–34. doi:10.1016/j.patcog.2016.03.028
104. Ruff L, Vandermeulen R, Goernitz N, Deecke L, Siddiqui SA, Binder A, et al. Deep One-Class Classification. In: J Dy, and A Krause, editors. Proceedings of the 35th International Conference on Machine Learning. Vol. 80 of Proceedings of Machine Learning Research. New York City, NY, USA: PMLR (2018). p. 4393–402.
105. Wang K, Lan H. Robust Support Vector Data Description for novelty Detection with Contaminated Data. Eng Appl Artif Intelligence (2020) 91:103554. doi:10.1016/j.engappai.2020.103554
106. Yuan P, Mao Z, Wang B. A Pruned Support Vector Data Description-Based Outlier Detection Method: Applied to Robust Process Monitoring. Trans Inst Meas Control (2020) 42:2113–26. doi:10.1177/0142331220905951
107. Barber CB, Dobkin DP, Huhdanpaa H. The Quickhull Algorithm for Convex Hulls. ACM Trans Math Softw (1996) 22:469–83. doi:10.1145/235815.235821
108. Zhenbing Liu Z, Liu JG, Chao Pan C, Guoyou Wang G. A Novel Geometric Approach to Binary Classification Based on Scaled Convex Hulls. IEEE Trans Neural Netw (2009) 20:1215–20. doi:10.1109/TNN.2009.2022399
109. Jove E, Casteleiro-Roca J-L, Quintián H, Méndez-Pérez J-A, Calvo-Rolle JL. A New Method for Anomaly Detection Based on Non-convex Boundaries with Random Two-Dimensional Projections. Inf Fusion (2021) 65:50–7. doi:10.1016/j.inffus.2020.08.011
110. Casale P, Pujol O, Radeva P. Approximate Polytope Ensemble for One-Class Classification. Pattern Recognition (2014) 47:854–64. doi:10.1016/j.patcog.2013.08.007
111. Casale P, Pujol O, Radeva P. Approximate Convex Hulls Family for One-Class Classification. In: International Workshop on Multiple Classifier Systems. Berlin, Germany: Springer (2011). p. 106–15. doi:10.1007/978-3-642-21557-5_13
112. Fernández-Francos D, Fontenla-Romero O, Alonso-Betanzos A. One-class Convex hull-based Algorithm for Classification in Distributed Environments. IEEE Trans Syst Man Cybern, Syst (2020) 50:386–96. doi:10.1109/TSMC.2017.2771341
113. Jove E, Gonzalez-Cava JM, Casteleiro-Roca J-L, Quintián H, Méndez-Pérez JA, Calvo-Rolle JL. Anomaly Detection on Patients Undergoing General Anesthesia. In: International Joint Conference: 12th International Conference on Computational Intelligence in Security for Information Systems (CISIS 2019) and 10th International Conference on EUropean Transnational Education (ICEUTE 2019). Cham: Springer (2019). p. 141–52. doi:10.1007/978-3-030-20005-3_15
114. Turchini F, Seidenari L, Del Bimbo A. Convex Polytope Ensembles for Spatio-Temporal Anomaly Detection. In: International Conference on Image Analysis and Processing. Berlin, Germany: Springer (2017). p. 174–84. doi:10.1007/978-3-319-68560-1_16
115. He Z, Shao H, Cheng J, Yang Y, Xiang J. Kernel Flexible and Displaceable Convex hull Based Tensor Machine for Gearbox Fault Intelligent Diagnosis with Multi-Source Signals. Measurement (2020) 163:107965. doi:10.1016/j.measurement.2020.107965
116. Scalet G. A Convex hull‐based Approach for Multiaxial High‐cycle Fatigue Criteria. Fatigue Fract Eng Mater Struct (2021) 44:14–27. doi:10.1111/ffe.13318
117. Bartlett P, Hazan E, Rakhlin A. Adaptive Online Gradient Descent. Berkeley, California: Tech. rep., EECS Department, University of California (2007).
118. Zinkevich M. Online Convex Programming and Generalized Infinitesimal Gradient Ascent. In: Proceedings of the 20th international conference on machine learning (ICML-03). Washington, DC: ICML (2003). p. 928–36.
119. Shalev-Shwartz S. Online Learning and Online Convex Optimization. FNT Machine Learn (2011) 4:107–94. doi:10.1561/2200000018
120. Raginsky M, Willett RM, Horn C, Silva J, Marcia RF. Sequential Anomaly Detection in the Presence of Noise and Limited Feedback. IEEE Trans Inform Theor (2012) 58:5544–62. doi:10.1109/TIT.2012.2201375
121. Siddiqui MA, Fern A, Dietterich TG, Wright R, Theriault A, Archer DW. Feedback-guided Anomaly Discovery via Online Optimization. In: KDD ’18: Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining. New York, NY, USA: Association for Computing Machinery (2018). p. 2200–9. doi:10.1145/3219819.3220083
122. Kerpicci M, Ozkan H, Kozat SS. Online Anomaly Detection with Bandwidth Optimized Hierarchical Kernel Density Estimators. IEEE Trans Neural Netw Learn Syst. (2021) 32:4253–66. doi:10.1109/TNNLS.2020.3017675
123.[Dataset] Ruder S. An Overview of Gradient Descent Optimization Algorithms. ArXiv preprint (2016). Available from: https://arxiv.org/abs/1609.04747 (Accessed December 5, 2021).
124. Xu L, Davenport M. Dynamic Matrix Recovery from Incomplete Observations under an Exact Low-Rank Constraint. In: D Lee, M Sugiyama, U Luxburg, I Guyon, and R Garnett, editors. Advances in Neural Information Processing Systems, Vol. 29. Red Hook, NY, USA: Curran Associates, Inc. (2016).
125. Zenati H, Foo CS, Lecouat B, Manek G, Chandrasekhar VR. Efficient gan-based Anomaly Detection. arXiv preprint arXiv:1802.06222 (2018).
126.[Dataset] Gao J, Song X, Wen Q, Wang P, Sun L, Xu H. Robusttad: Robust Time Series Anomaly Detection via Decomposition and Convolutional Neural Networks. Arxiv preprint (2020). Available from: https://arxiv.org/abs/2002.09545 (Accessed December 5, 2021).
127. Xu C, Wang J, Zhang J, Li X. Anomaly Detection of Power Consumption in Yarn Spinning Using Transfer Learning. Comput Ind Eng (2021) 152:107015. doi:10.1016/j.cie.2020.107015
128. Hariri S, Kind MC, Brunner RJ. Extended Isolation forest. IEEE Trans Knowl Data Eng (2021) 33:1479–89. doi:10.1109/TKDE.2019.2947676
129. Umsonst D, Sandberg H, Cárdenas AA. Security Analysis of Control System Anomaly Detectors. In: 2017 American Control Conference (ACC) (2017). p. 5500–6. doi:10.23919/ACC.2017.7963810
130. Vinué G, Epifanio I. Robust Archetypoids for Anomaly Detection in Big Functional Data. Adv Data Anal Classif (2021) 15:437–62. doi:10.1007/s11634-020-00412-9
131. Sifa R, Drachen A, Block F, Moon S, Dubhashi A, Xiao H, et al. Archetypal Analysis Based Anomaly Detection for Improved Storytelling in Multiplayer Online Battle arena Games. In: 2021 Australasian Computer Science Week Multiconference (2021). p. 1–8. doi:10.1145/3437378.3442690
132. Zhao G, Li F, Zhang X, Laakso K, Chan JC-W. Archetypal Analysis and Structured Sparse Representation for Hyperspectral Anomaly Detection. Remote Sensing (2021) 13:4102. doi:10.3390/rs13204102
133. Millán-Roures L, Epifanio I, Martínez V. Detection of Anomalies in Water Networks by Functional Data Analysis. Math Probl Eng (2018) 2018:1–13. doi:10.1155/2018/5129735
134. Tax DMJ, Duin RPW. Support Vector Domain Description. Pattern recognition Lett (1999) 20:1191–9. doi:10.1016/S0167-8655(99)00087-2
135. Bradley AP. The Use of the Area under the Roc Curve in the Evaluation of Machine Learning Algorithms. Pattern recognition (1997) 30:1145–59. doi:10.1016/S0031-3203(96)00142-2
136. Candanedo LM, Feldheim V. Accurate Occupancy Detection of an Office Room from Light, Temperature, Humidity and CO 2 Measurements Using Statistical Learning Models. Energy and Buildings (2016) 112:28–39. doi:10.1016/j.enbuild.2015.11.071
137. Lu J, Hoi SC, Wang J, Zhao P, Liu Z-Y. Large Scale Online Kernel Learning. J Machine Learn Res (2016) 17:1.
138. Fei-Fei L, Fergus R, Perona P, Zekrifa D. Learning Generative Visual Models from Few Training Examples: An Incremental Bayesian Approach Tested on 101 Object Categories. Computer Vis Image Understanding (2007) 106:59–70. doi:10.1016/j.cviu.2005.09.012
139. Casale P, Pujol O, Radeva P. Personalization and User Verification in Wearable Systems Using Biometric Walking Patterns. Pers Ubiquit Comput (2012) 16:563–80. doi:10.1007/s00779-011-0415-z
140. Laptev N, Amizadeh S, Flint I. Generic and Scalable Framework for Automated Time-Series Anomaly Detection. In: Proceedings of the 21th ACM SIGKDD international conference on knowledge discovery and data mining (2015). p. 1939–47. doi:10.1145/2783258.2788611
Keywords: anomaly detection, convex analysis, density estimation, matrix factorization, machine learning
Citation: Wang T, Cai M, Ouyang X, Cao Z, Cai T, Tan X and Lu X (2022) Anomaly Detection Based on Convex Analysis: A Survey. Front. Phys. 10:873848. doi: 10.3389/fphy.2022.873848
Received: 11 February 2022; Accepted: 25 March 2022;
Published: 27 April 2022.
Edited by:
José Tadeu Lunardi, Universidade Estadual de Ponta Grossa, BrazilReviewed by:
Peng Li, Institute industrial IT, GermanyZhiwei Ji, Nanjing Agricultural University, China
Copyright © 2022 Wang, Cai, Ouyang, Cao, Cai, Tan and Lu. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Xu Tan, dGFueHVfbnVkdEB5YWhvby5jb20=; Xin Lu, eGluX2x5dUBzaW5hLmNvbQ==
†These authors have contributed equally to this work
 Tong Wang1†
Tong Wang1† Mengsi Cai
Mengsi Cai Xin Lu
Xin Lu