- 1School of Electrical Engineering–Physical Electronics, Center of Laser-Matter Interaction, Tel Aviv University, Ramat Aviv, Israel
- 2School of Electronic Information Engineering, Yangtze Normal University, Chongqing, China
- 3Fujian Key Laboratory of Quantum Information and Quantum Optics, Fuzhou University, Fuzhou, China
- 4Shenkar College of Engineering, Ramat Gan, Israel
- 5Schlesinger Family Accelerator Centre, Ariel University, Ariel, Israel
- 6California Institute of Technology, Pasadena, CA, United States
We present a fully quantum model for the excitation of a bound electron based on the “free-electron bound-electron resonant interaction” (FEBERI) scheme. The bound electron is modeled as a quantum two-level system (TLS) at any initial quantum (qubit) state, and the free electron is presented as a pre-shaped quantum electron wavepacket (QEW). In the case that the QEW is short or modulated at optical frequency, the TLS quantum state may be coherently controlled with multiple modulation-correlated QEWs. For this case, we derive the transition probability of the TLS due to interaction with a multi-particle beam based on an analytical approximate solution of the Schrodinger equation that amounts to using Born’s probabilistic interpretation of the quantum electron wavefunction. We verify the credibility of the analytical model at its validity ranges using a fully quantum density matrix computation procedure. It is shown that the transition probability can grow quadratically with the number of correlated QEWs and exhibit Rabi oscillation. The study indicates a possibility of engineering the quantum state of a TLS by utilizing a beam of shaped QEWs.
Introduction
Recent technological advances enable the shaping of free electron wavefunctions in the transverse [1–3] and longitudinal [4–6] dimensions in an electron microscope setup. In the longitudinal propagation direction of the electron (or in time dimension), the energy and density expectation values of the electron wavefunction can be modulated by a coherent laser beam at optical frequencies [7–9], utilizing the scheme of photo-induced near-field electron microscopy (PINEM) [10]. The modulation is made possible by a multiphoton emission/absorption process in the near field of a nanostructure [7], a foil [11], or a laser-beat (pondermotive potential) [12, 13]. After the PINEM interaction, the energy spectrum of a single quantum electron wavepacket (QEW) exhibits discrete energy sidebands spaced apart by the laser photon energy
Shaping and transfer of coherence and quantum properties from light to free electrons wavefunction have received recently significant research attention within an emerging new research field of “quantum electron optics”. It has been shown that the coherence and incoherence features of light, and even the quantum statistical states of light, can be transferred to the free-electron quantum electron wavefunction by means of the PINEM process [24, 25]. This paves the way for new applications of these emerging technologies for coherent control of quantum systems of light and matter using pre-shaped and optically modulated QEWs.
A simple example of coherent control of quantum states by electrons is the effect of free-electron bound-electron resonant interaction (FEBERI) proposed in Ref. [26]. In this process, a pre-shaped or pre-modulated beam of QEWs interacts with a bound electron modeled by a quantum two-level system (TLS). Such a TLS model is valid because, in general, in the linear response regime, the transition amplitude responds linearly to all possible transitions of quantum levels in matter with frequency-dependent amplitude. Therefore, targeting a single two-level transition does not reduce the generality of the model, even if the targets have multiple levels. The QEWs induce excitations of the TLS when passing in the vicinity of the TLS target. It has been suggested that a beam of probability-density modulation-correlated QEWs can interact resonantly with the TLS when the harmonic
Using a fully quantum-mechanical analysis (both free and bound electrons quantized) of the FEBERI interaction with a single arbitrarily shaped QEW [34, 35], we showed that the FEBERI effect can be applied for coherent control and interrogation of the qubit state of a target TLS. However, because the FEBERI effect is practically very weak for a single QEW and single TLS, it is necessary to consider the interaction of the TLS with multiple modulation-correlated QEWs. Such a beam of density modulation-correlated QEWs can be produced if all electrons are energy modulated in the PINEM process by the same coherent laser beam and then develop the same phase-correlated density bunching after drifting to the FEBERI interaction point. In this case, as proposed in the early paper of Gover and Yariv [32], based on a semi-classical model, a coherent build-up of the quantum state of the TLS may be possible, including full Rabi oscillation between the TLS quantum levels. Such a Rabi oscillation process that initially scales quadraticlly with the number of interacting electrons N, would be the analog of spontaneous superradiance (in the sense of Dicke [36]) by a density modulated electron beam, which is characterized by an emission rate proportional to
In this paper, we study the dynamics of a TLS excited by multiple finite size or modulation-correlated QEWs under the assumption that the interaction period is smaller than the relaxation time
The paper is organized as follows: In the first section we present the model and the theoretical framework of the FEBERI setup. In the subsequent two sections we apply the probabilistic model to interpret the excitation of a TLS with a single near point-particle (short size) QEW and with a beam of such QEWs. In the next two sections we present the excitation of a TLS with a single density modulated QEW and then, with a beam of such modulation correlated QEWs. All approximate analytical expressions are compared to the results of the quantum density matrix computations. Conclusions are presented in the final section.
System Model and Theoretical Framework
The setup of our system model is shown in Figure 1, in which a thin free-electron QEW propagates in proximity to a Hydrogen-like atom that is modeled as a TLS. The interaction of the free electron and bound electron is considered to be the Coulomb interaction. We denote the joint wavefunction of the free and bound electrons by
where
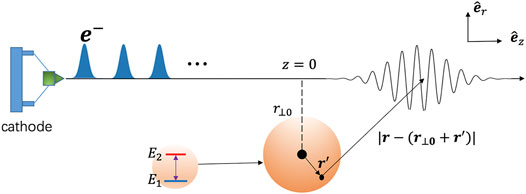
FIGURE 1. Setup of free-electron bound-electron resonant interaction. A beam of multiple finite size or modulation-correlated QEWs interacts with a bound electron which is modeled by a quantum two-level system.
This corresponds to second-order expansion of the relativistic energy dispersion of a free electron
For the simplified model where the spin is neglected, we assume that the free and bound electrons do not overlap spatially. Therefore, there are no exchange energy or spin-orbit interaction effects, and we can avoid the intricate second quantization of the many-body interaction theory [41]. For the Coulomb interaction in the near field and neglecting retardation [42], the interaction Hamiltonian is
Here we used Feynman’s expression for the Coulomb potential [43] in order to keep the analysis valid in the relativistic regime. A more accurate form would be to use the Darwin potential for relativistic Coulomb interaction between moving charged particles [44, 45]. However, for the parameters of the cases delineated here, the corrections due to this model are negligible.
Having the bound electron modeled as a TLS, the eigenfunction solutions of the Hamiltonian
where
The shape of the wavepacket is determined by the coefficients in momentum dimension -
The second case is a PINEM phase-modulated Gaussian wavepacket arriving at the FEBERI interaction point
Such a wavepacket represents in spatiotemporal space a density modulated finite-size QEW [14]. Here
During the interaction process, the expansion coefficients of the QEW
After substituting this expression into Eq. (
By multiplying by
where
where
Probabilistic Model for the Excitation of TLS With Single Free Electron
In order to describe the TLS dynamics analytically, we present in this section an iterative approach to solving the source equation (
on the RHS of (
With
This presentation is reminiscent of interaction with an unperturbed point-particle that arrives at time
The probability distribution of a single electron QEW of narrow width is:
where
where
and after integration
For a single Gaussian wavepacket at its longitudinal waist
Normalizing time to the transit time parameter
with the parameter
Defining Fourier transform
where
For a Gaussian QEW with
Therefore, the transition probability of TLS after the interaction is
where
where
where
The probabilistic model approximation is presumed to apply in the very short QEW regime
In order to check the validity of the analytical approximations, we have developed numerical computation codes for solving the FEBERI problem of interaction between a single finite-size QEW and a TLS at any initial state, starting from the Schrödinger equation (
where the evolution operator is
The transition probability to the TLS upper quantum state is defined as
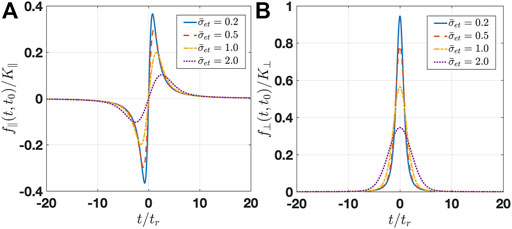
We first apply the quantum numerical computation to check the validity limits of the analytical expressions for the TLS transition probability for a single QEW (Eq. 24–Eq. 26). Figures 3A,B display the upper-level probability after interacting with a single QEW as a function of wave-packet size for the initial TLS in the ground state and superposition state, respectively. Numerical simulation results show that the transition probability is independent of the wave-packet size if the TLS starts from the ground state (blue curve), which contradicts the analytical result (Eq.
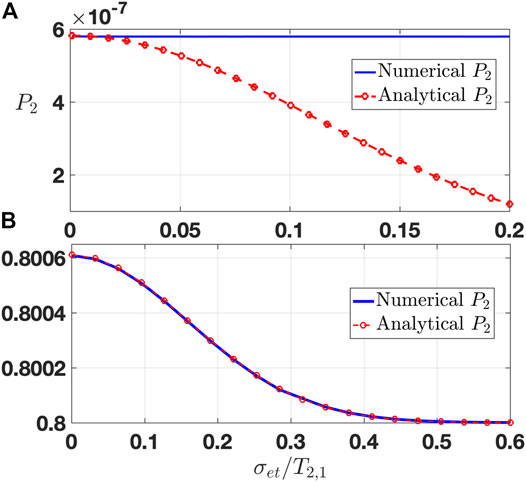
FIGURE 3. Numerical solution of Schrodinger equation (
Excitation of TLS With a Bunched Electron Beam
The excitation of a TLS with multiple QEWs is theoretically an intricate multi-particle quantum interaction problem that involves the entanglement of the free electron wavefunction with the states of TLS. Here, we resort again to the simple analytic approximate probabilistic model, in which we extend Eq. (
where
With change of variable
The incremental probability amplitude in this equation averages to zero for random
For a Gaussian QEW (
As we learned from the previous chapter, this approximate result may not be rigorous in the initial stage of the multiple electrons transition buildup from the ground state, when the phase of the dipole moment oscillation is not well-defined. We conjecture that when
This case of a periodically spaced train of near-point-particle QEWs may be realistic for low (microwave or THz) frequency TLS transitions, where classical Klystron-kind electron current modulation is available. It has thus been termed a “Quantum Klystron” in [30]. It can be comprehended as the quadratic approximation of the
It is instructive to compare the quadratic dependence of (
Figure 4 shows a simulation of the buildup of the TLS upper-level probability with
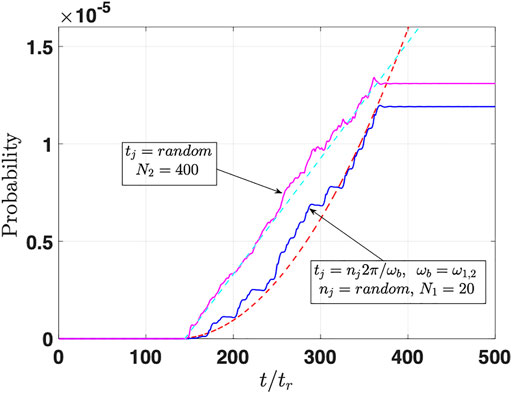
FIGURE 4. Simulation results of the TLS upper-level probability buildup by electrons arriving to the interaction point at random (magenta) and by electrons arriving in-phase with the modulating laser (modulo the bunching period
Excitation of a TLS With a Modulated Single Free Quantum Electron Wavepacket
Here we extend our Born’s probability interpretation of the electron wavefunction to model the case of a density modulated QEW. In Eq. (
where
We next derive the incremental excitation probabilities in Eq. (
We substitute this probability distribution of a modulated QEW in Eq. (
With a change of variables
Then the first-order incremental transition probability is.
If the envelope Gaussian distribution is a wide function -
under the condition that the QEW modulation phase is matched to the TLS initial dipole moment oscillation phase
Likewise, the second-order incremental transition probability can be calculated.
It can be seen that both first order and second-order expressions of the incremental probabilities are dependent on the QEW shape and modulation features and display resonant excitation characteristics around the condition
We check the results of the probabilistic model approximation by comparing it to the results of the quantum density matrix model numerical computation that is based on the solution of Schrodinger equation (
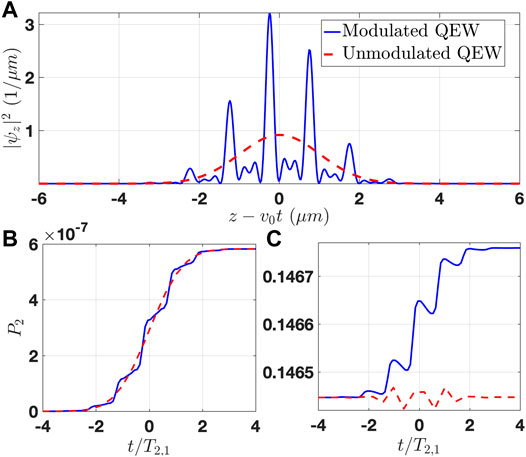
FIGURE 5. (A) Density distribution of a broad QEW (
Figures 5B,C present the dynamic buildup of the transition probability starting from the ground state
Excitation of a TLS With a Beam of Modulation-Correlated Quantum Electron Wavepackets
In this section, we extend our Born’s probability interpretation analytical model to the case of multiple modulation-correlated QEWs. Consider the case of multiple long-size QEWs, all phase- (energy-) modulated at a PINEM interaction point at the level of their quantum wavefunctions [14] by the same coherent laser beam of frequency
where
Then, substitution in Eq. (
Again, for broad Gaussian distribution
This averages to zero for random arrival times
And independently of the arrival times
This expression explicitly manifests the
To check the result of the probabilistic model approximation, we compare it to the results of the quantum model (Schrodinger equation) numerical computations (see details in appendix of Ref. [39]). For simulating the dynamics of multiple QEWs in interaction with the TLS, we consider a train of incoming QEWs, sequentially interacting with the TLS, and repeat the calculation for each electron passing by. Equation 7 is used to represent the initial quantum electron wavefunction of each electron upon arrival at the FEBERI interaction point. In Eq. 7 we use a random value
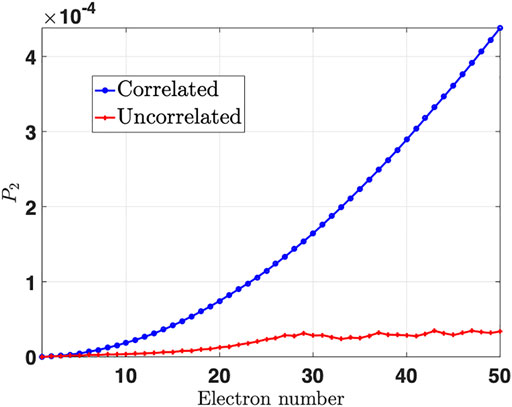
FIGURE 6. Numerical simulation results of the transition probability
Conclusion
We studied the excitation of a bound electron in an arbitrary initial quantum (qubit) state by a free electron beam, where the bound electron is modeled as a quantum two-level system (TLS) and the free electrons are represented as quantum electron wavepackets (QEWs). We developed an analytical model for the FEBERI interaction based on Born’s probabilistic interpretation of the quantum electron wavefunction and derived expressions for the transition probability of the TLS subject to interaction with a shaped QEW (finite size gaussian), optically modulated QEWs, and a beam of such QEWs. We tested the analytical results against the simulation results of an accurate quantum model of the FEBERI effect, based on the density matrix solution of the Schrodinger equation for the entangled free-bound electron wavefunctions.
The accurate quantum model simulations show quadratic growth of the TLS quantum transition probability as a function of the number of electrons in a train of modulation-correlated QEWs, when a harmonic of the QEW modulation frequency is resonant with the TLS quantum transition frequency, and the modulation initial phase of all electrons is the same (e.g., they are modulated by the same coherent laser beam in a PINEM process). This result confirms the prediction of the analytical approximation model based on Born’s probabilistic interpretation of the electron wavefunction and the earlier semiclassical analysis of the FEBERI effect [26].
The quadratic scaling of the TLS excitation build-up in the FEBERI process can be explained as the second-order expansion of the sinus-squared scaling of a Rabi oscillation process [26], where the optical frequency near-field of the beam of modulation-correlated QEWs play the same role as a laser beam in a conventional Rabi oscillation experiment. Another instructive observation that came out of the numerical simulations is that in the case of modulation-correlated QEWs beam, the temporal intervals between the probability-density micro bunches of the QEWs (Figure 5) are spaced apart at resonance an integral number of times the TLS transition period (
To test the surprising result of coherent transition probability buildup with a modulation-correlated electron beam independently of the random arrival times of the electrons to the FEBERI point, we show in Figure 6 (red curve) a simulation of interaction with a beam of modulated QEWs that are not modulation phase-correlated (random
We point out that coherent control and demonstration of Rabi oscillation of a single TLS with the proposed FEBERI effect is attractive in comparison to such operations with a laser beam, because of the atomic-scale resolution of an electron beam. However, the experimental realization of this scheme is challenging due to the very small value of the interaction coupling factor in typical TLS targets (
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.
Author Contributions
AG, AY, JS, and DR conceived the concept. BZ and DR performed the theoretical derivations and prepared the figures. BZ, DR, and AG wrote the paper with contributions from RI and AF All authors reviewed and discussed the manuscript and made significant contributions to it.
Funding
This work was supported by the Israel Science Foundation (ISF) under Grant No. 00010001000, the National Natural Science Foundation of China under Grant No. 12104068, and the Natural Science Foundation of Chongqing under Grant No. cstc2021jcyj-msxmX0684.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Acknowledgments
We acknowledge helpful communications with O. Kfir, Y. M. Pan, and F. J. Garcia de Abajo. DR acknowledges support by the PBC program of the Israel Council of Higher Education.
References
1. Verbeeck J, Tian H, Schattschneider P. Production and Application of Electron Vortex Beams. Nature (2010) 467(7313):301–4. doi:10.1038/nature09366
2. Voloch-Bloch N, Lereah Y, Lilach Y, Gover A, Arie A. Generation of Electron Airy Beams. Nature (2013) 494(7437):331–5. doi:10.1038/nature11840
3. Shiloh R, Lereah Y, Lilach Y, Arie A. Sculpturing the Electron Wave Function Using Nanoscale Phase Masks. Ultramicroscopy (2014) 144:26–31. doi:10.1016/j.ultramic.2014.04.007
4. Baum P. Quantum Dynamics of Attosecond Electron Pulse Compression. J Appl Phys (2017) 122(22):223105. doi:10.1063/1.5006864
5. Morimoto Y, Baum P. Single-cycle Optical Control of Beam Electrons. Phys Rev Lett (2020) 125(19):193202. doi:10.1103/physrevlett.125.193202
6. Vanacore GM, Madan I, Carbone F. Spatio-temporal Shaping of a Free-Electron Wave Function via Coherent Light-Electron Interaction. Riv Nuovo Cim (2020) 43(11):567–97. doi:10.1007/s40766-020-00012-5
7. Piazza L, Lummen TT, Quiñonez E, Murooka Y, Reed BW, Barwick B, et al. Simultaneous Observation of the Quantization and the Interference Pattern of a Plasmonic Near-Field. Nat Commun (2015) 6(1):6407–7. doi:10.1038/ncomms7407
8. Reinhardt O, Kaminer I. Theory of Shaping Electron Wavepackets with Light. ACS Photon (2020) 7(10):2859–70. doi:10.1021/acsphotonics.0c01133
9. Yalunin SV, Feist A, Ropers C. Tailored High-Contrast Attosecond Electron Pulses for Coherent Excitation and Scattering. Phys Rev Res (2021) 3(3):L032036. doi:10.1103/physrevresearch.3.l032036
10. Barwick B, Flannigan DJ, Zewail AH. Photon-induced Near-Field Electron Microscopy. Nature (2009) 462(7275):902–6. doi:10.1038/nature08662
11. Vanacore GM, Madan I, Berruto G, Wang K, Pomarico E, Lamb RJ, McGrouther D, Kaminer I, Barwick B, García de Abajo FJ, Carbone F. Attosecond Coherent Control of Free-Electron Wave Functions Using Semi-infinite Light fields. Nat Commun (2018) 9(1):2694–11. doi:10.1038/s41467-018-05021-x
12. Kozák M, Schönenberger N, Hommelhoff P. Ponderomotive Generation and Detection of Attosecond Free-Electron Pulse Trains. Phys Rev Lett (2018) 120(10):103203. doi:10.1103/physrevlett.120.103203
13. Kozák M, Eckstein T, Schönenberger N, Hommelhoff P. Inelastic Ponderomotive Scattering of Electrons at a High-Intensity Optical Travelling Wave in Vacuum. Nat Phys (2018) 14(2):121–5. doi:10.1038/nphys4282
14. Feist A, Echternkamp KE, Schauss J, Yalunin SV, Schäfer S, Ropers C. Quantum Coherent Optical Phase Modulation in an Ultrafast Transmission Electron Microscope. Nature (2015) 521(7551):200–3. doi:10.1038/nature14463
15. Priebe KE, Rathje C, Yalunin SV, Hohage T, Feist A, Schäfer S, et al. Attosecond Electron Pulse Trains and Quantum State Reconstruction in Ultrafast Transmission Electron Microscopy. Nat Photon (2017) 11(12):793–7. doi:10.1038/s41566-017-0045-8
16. Baum P. Quantum Dynamics of Attosecond Electron Pulse Compression. J Appl Phys (2017) 122(22):223105. doi:10.1063/1.5006864
17. Morimoto Y, Baum P. Single-cycle Optical Control of Beam Electrons. Phys Rev Lett (2020) 125(19):193202. doi:10.1103/physrevlett.125.193202
18. Gover A, Ianconescu R, Friedman A, Emma C, Sudar N, Musumeci P, et al. Superradiant and Stimulated-Superradiant Emission of Bunched Electron Beams. Rev Mod Phys (2019) 91(3):035003. doi:10.1103/revmodphys.91.035003
19. Gover A, Pan Y. Dimension-dependent Stimulated Radiative Interaction of a Single Electron Quantum Wavepacket. Phys Lett A (2018) 382(23):1550–5. doi:10.1016/j.physleta.2018.03.049
20. Black DS, Niedermayer U, Miao Y, Zhao Z, Solgaard O, Byer RL, et al. Net Acceleration and Direct Measurement of Attosecond Electron Pulses in a Silicon Dielectric Laser Accelerator. Phys Rev Lett (2019) 123(26):264802. doi:10.1103/physrevlett.123.264802
21. Schönenberger N, Mittelbach A, Yousefi P, McNeur J, Niedermayer U, Hommelhoff P. Generation and Characterization of Attosecond Microbunched Electron Pulse Trains via Dielectric Laser Acceleration. Phys Rev Lett (2019) 123(26):264803. doi:10.1103/physrevlett.123.264803
22. Pan Y, Gover A. Spontaneous and Stimulated Radiative Emission of Modulated Free-Electron Quantum Wavepackets-Semiclassical Analysis. J Phys Commun (2018) 2(11):115026. doi:10.1088/2399-6528/aae2ec
23. Pan Y, Gover A. Spontaneous and Stimulated Emissions of a Preformed Quantum Free-Electron Wave Function. Phys Rev A (2019) 99(5):052107. doi:10.1103/physreva.99.052107
24. Dahan R, Gorlach A, Haeusler U, Karnieli A, Eyal O, Yousefi P, Segev M, Arie A, Eisenstein G, Hommelhoff P, Kaminer I. Imprinting the Quantum Statistics of Photons on Free Electrons. Science (2021) 373(6561):eabj7128. doi:10.1126/science.abj7128
25. Kfir O, Di Giulio V, de Abajo FJG, Ropers C. Optical Coherence Transfer Mediated by Free Electrons. Sci Adv (2021) 7(18):eabf6380. doi:10.1126/sciadv.abf6380
26. Gover A, Yariv A. Free-Electron-Bound-Electron Resonant Interaction. Phys Rev Lett (2020) 124(6):064801. doi:10.1103/PhysRevLett.124.064801
27. de Abajo FJG. Comment on “Free-Electron–Bound-Electron Resonant Interaction”. Phys Rev Lett (2021) 126(1):019501. doi:10.1103/physrevlett.126.069902
28. de Abajo FJG. Erratum: Comment on “Free-Electron–Bound-Electron Resonant Interaction”[Phys. Rev. Lett. 126. Phys Rev Lett (20212021) 126(6):069902:019501. doi:10.1103/physrevlett.126.069902
29. Gover A, Yariv A. Gover and Yariv Reply. Phys Rev Lett (2021) 126(1):019502. doi:10.1103/physrevlett.126.019502
30. Rätzel D, Hartley D, Schwartz O, Haslinger P. Controlling Quantum Systems with Modulated Electron Beams. Phys Rev Res (2021) 3(2):023247. doi:10.1103/physrevresearch.3.023247
31. Zhao Z, Sun X-Q, Fan S. Quantum Entanglement and Modulation Enhancement of Free-Electron-Bound-Electron Interaction. Phys Rev Lett (2021) 126(23):233402. doi:10.1103/physrevlett.126.233402
32. García de Abajo FJ, Di Giulio V. Optical Excitations with Electron Beams: Challenges and Opportunities. ACS Photon (2021) 8(4):945–74. doi:10.1021/acsphotonics.0c01950
33. Ruimy R, Gorlach A, Mechel C, Rivera N, Kaminer I. Toward Atomic-Resolution Quantum Measurements with Coherently Shaped Free Electrons. Phys Rev Lett (2021) 126(23):233403. doi:10.1103/physrevlett.126.233403
34. Zhang B, Ran D, Ianconescu R, Friedman A, Scheuer J, Yariv A, et al. Quantum Wave-Particle Duality in Free-Electron-Bound-Electron Interaction. Phys Rev Lett (2021) 126(24):244801. doi:10.1103/physrevlett.126.244801
35. Zhang B, Ran D, Ianconescu R, Friedman A, Scheuer J, Yariv A, et al. Quantum States Interrogation Using a Pre-shaped Free Electron Wavefunction. Phys. Rev. Research (Forthcoming 2022).
36. Dicke RH. Coherence in Spontaneous Radiation Processes. Phys Rev (1954) 93(1):99–110. doi:10.1103/physrev.93.99
37. Gover A. Superradiant and Stimulated-Superradiant Emission in Prebunched Electron-Beam Radiators. I. Formulation. Phys Rev Spec Topics-Accelerators Beams (2005) 8(3):030701. doi:10.1103/physrevstab.8.030701
38. García de Abajo FJ, Di Giulio V. Optical Excitations with Electron Beams: Challenges and Opportunities. ACS Photon (2021) 8(4):945–74. doi:10.1021/acsphotonics.0c01950
39. Gover A, Zhang B, Ran D, Ianconescu R, Friedman A, Scheuer J, et al. Resonant Interaction of Modulation-Correlated Quantum Electron Wavepackets with Bound Electron States (2020). arXiv preprint arXiv:2010.15756.
40. Di Giulio V, Kociak M, de Abajo FJG. Probing Quantum Optical Excitations with Fast Electrons. Optica (2019) 6(12):1524–34. doi:10.1364/optica.6.001524
41. Bartlett RJ. Many-body Perturbation Theory and Coupled Cluster Theory for Electron Correlation in Molecules. Annu Rev Phys Chem (1981) 32(1):359–401. doi:10.1146/annurev.pc.32.100181.002043
42. García de Abajo FJ. Optical Excitations in Electron Microscopy. Rev Mod Phys (2010) 82(1):209–75. doi:10.1103/revmodphys.82.209
43. Feynman Richard P Mainly Electromagnetism and Matter, Feynman Lectures on Physics, Vol. 2. 33. Available at: https://www.feynmanlectures.caltech.edu/II_26.html.
44. Breit G. Dirac's Equation and the Spin-Spin Interactions of Two Electrons. Phys Rev (1932) 39(4):616–24. doi:10.1103/physrev.39.616
45. Lhuillier C, Faroux JP. Hamiltonian of a many-electron Atom in an External Magnetic Field and Classical Electrodynamics. J Phys France (1977) 38(7):747–55. doi:10.1051/jphys:01977003807074700
46. Robicheaux F, Noordam LD. Coherent Scattering with Pulsed Matter Beams. Phys Rev Lett (2000) 84(17):3735–9. doi:10.1103/physrevlett.84.3735
Keywords: quantum electron wavepackets, superradiance, coherent control, wavepackets size, electron-matter interaction
Citation: Ran D, Zhang B, Ianconescu R, Friedman A, Scheuer J, Yariv A and Gover A (2022) Coherent Excitation of Bound Electron Quantum State With Quantum Electron Wavepackets. Front. Phys. 10:920701. doi: 10.3389/fphy.2022.920701
Received: 14 April 2022; Accepted: 23 May 2022;
Published: 26 July 2022.
Edited by:
Giovanni Maria Vanacore, University of Milano-Bicocca, ItalyReviewed by:
Dawei Wang, Zhejiang University, ChinaJiteng Sheng, East China Normal University, China
Copyright © 2022 Ran, Zhang, Ianconescu, Friedman, Scheuer, Yariv and Gover. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Avraham Gover, Z292ZXJAZW5nLnRhdS5hYy5pbA==
†These authors have contributed equally to this work and share first authorship
 Du Ran
Du Ran Bin Zhang
Bin Zhang Reuven Ianconescu1,4
Reuven Ianconescu1,4