Cold atom inertial sensors for navigation applications

Quantum sensors based on atom interferometers can provide measurements of inertial quantities with unprecedented accuracy and precision. It has been suggested that this sea change in sensing could provide an inertial navigation capability that is comparable with current satellite based navigation systems. However, the accuracy of sensor measurements is not the only factor that limits the accuracy of inertial navigation systems. In this paper, we explore the fundamental limits to inertial navigation, and explain how quantum inertial sensors could be used to alleviate some of the problems encountered in current classical inertial navigation systems, but not to solve the fundamental instability inherent in inertial navigation methods.

1 Introduction

There has been a great deal of interest recently in cold atom sensors using quantum interferometry to provide inertial measurements of unprecedented accuracy [1–9]. The technologies rely on the fact that all atoms of the same isotope are identical and on the ability to place these atoms in superpositions of motional states using a sequence of laser pulses. Differences in the motion of these superposed states can then be measured by recombining the superpositions and detecting the interference between them. Such sensors are proving to be excellent candidates to probe fundamental physics associated with corrections to theories of gravity [10, 11] and verification of the equivalence principle [12–15]. However, the nature of these motional superposition states means that atom interferometers are ideal for measuring inertial quantities [1–9], and significant advances have been made to move these devices outside of the laboratory and into the real world [4, 7, 9, 16–19]. They are therefore potential candidates for use in inertial navigation systems (INSs), which use inertial measurements to estimate the motion of a moving vehicle relative to a fixed Earth reference frame [20–22]. This paper examines how the current and near future generations of atom interferometer sensors could be used to enhance conventional classical inertial navigation systems. In particular, we demonstrate how quantum sensors could be used to improve the calibration of a classical inertial systems.

Making measurements on superpositions of single atoms is very difficult, and multiple atoms are required to measure the phase of the interference between superpositions. Atom interferometry therefore uses a large number of atoms and forms superpositions of atoms within a cloud of atoms [1–9]. That is, each individual atom within a cloud is placed in a superposition of two motional states, and the number of atoms merely increases the signal that is being measured (the contrast of the interference fringes). To maximise the signal-to-noise ratio, an atom cloud needs to be generated, trapped in a vacuum, held, and cooled to low temperature before a measurement is made to reduce the thermal motion of the atoms obscuring the interferences arising from the superpositions.

The difficulties in making such measurements, and the trapping-cooling-measurement cycle, mean that the current generation of quantum sensors are limited to low operating frequencies compared to classical inertial sensors. Often quantum sensors are limited to a few Hz [23, 24] whereas classical sensors operate at several hundred Hz [20–22]. In addition, during the trapping-cooling part of the cycle, sensors are not able to respond to changes in the motion of a vehicle. During this ‘dead-time’, no useful information is provided. Quantum sensors often have limitations on their dynamic range, their ability to respond to signals that may cover several orders of magnitude. This property is not unique to cold atom systems, classical sensors also trade off sensitivity against dynamic range. However, the current generation of cold atom interferometers is more suited to the measurement of very small inertial quantities [12–15] than the variations experienced in most transport systems.

Sensors are improving. The efficiency and the time taken in the preparation of the atom clouds are being increased and reduced, respectively. Sensors that use multiple atom clouds are being developed [15, 25] to remove the dead time and increase the duty cycle. Other developments are focussed on reducing the size, weight and power (“SWaP”) requirements of the sensors through better design [9], integration of optical and laser technologies with the vacuum systems [26], and more complex laser pulse sequences [27]. However, the current technology does have potential uses in navigation. There have been studies of the full errors present in this type of sensor and the effect of these errors on navigation [28], and others have studied the ability of classical INS sensors to assist in the operation of cold atom sensors, as part of an integrated system [29, 30]. Here we focus on the ability of cold atom sensors operating at low frequency to assist in the calibration of classical inertial sensors to improve the overall performance of a purely inertial navigation system.

In Section 2, we review the problems associated with the use of inertial sensors for navigation and highlight some of the fundamental issues with such systems. Section 3 discusses the current and near future cold atom technologies that are being proposed for use for navigation systems. In Section 4, we review some of the more subtle aspects of the navigation problem, before presenting some test cases in Section 5, where we calculate examples of how cold atom sensors could be used to enhance current inertial navigation systems. We then summarise our conclusions in Section 6.

2 Navigation systems and inertial sensors

Navigation systems are based on two basic approaches [21]: position fixing or dead reckoning. Position fixing systems derive an estimate of the actual position of a navigation system from sensor measurements by referencing the measurements against a database of features with known positions. Dead reckoning systems measure aspects of motion, such as velocity or acceleration, and then infer the position of the system, or–more accurately–the changes in the position of a system, by integrating these quantities over time. Inertial navigation systems are examples of dead reckoning, where measured accelerations are integrated twice to obtain changes in position. Global Navigation Satellite Systems (GNSSs), such as the US Global Positioning System (GPS), are the most obvious form of position fixing system [21]. GNSS uses a constellation of satellites, which broadcast their positions at regular intervals, and receivers that measure the time between the satellite transmitting a signal and the receiver receiving it. GNSS also provides estimates for the velocity of the GNSS receiver by measuring the Doppler shift of each of the broadcast satellite signals, but it is primarily a position fixing system [21].

In addition to position information, most modern navigation systems are also required to provide orientation information [21]. The attitude of a vehicle (its orientation relative to an external reference frame¹) and its accuracy is critical in many aerospace applications, where such information may be used as part of a route planning or flight control system. As with position, the attitude of a vehicle can be derived via dead reckoning or direct measurement (fixing). Most modern inertial systems rely on the measurement of angle rates by rate gyroscopes; integrating the angle rates with respect to time to derive the attitude. However, like position, the integration only provides changes in attitude rather than a direct measurement. Similarly, direct measurements of attitude also rely on external references, such as the positions of known features (e.g. the horizon, stars), magnetic fields (a compass) or, when stationary, the local gravity vector and the Earth’s axis of rotation (called “gyro-compassing” [21], see Section 2.2 below).

Knowledge of the attitude is more important for modern ‘strapdown’ navigation systems [20, 21], which are physically mounted to the body of a vehicle and all measurements are made in Body-oriented axes. Older inertial navigation systems used platforms mounted on gimbals, which were free to move to maintain the orientation of the sensors to the local horizontal and local North, and the platforms were stabilised using mechanical gyroscopes [20]. Strapdown navigation systems do not require a stabilised platform, and are less complex mechanically and therefore tend to be smaller and cheaper. Strapdown navigation systems use knowledge of the INS attitude to resolve the motion into a stabilised Earth-oriented reference frame. This means that the accuracy of the gyroscopes in a strapdown navigation system is critical to the accuracy of the positioning solution. Inaccurate resolution of the motion into the stabilised frame causes significant errors in the other parts of the navigation solution.

The standard set of sensors for an inertial navigation system is three accelerometers and three gyroscopes; with the elements of each triad being mounted at right angles to one another. The accelerometers measure specific force, which is the acceleration experienced plus the effect of the local gravitation field [21], in Body axes. The gyroscopes measure angle rates about each of the axes in Body axes, which are not the time derivative of the Euler angles. The Euler angles are the angles relative to the local Earth-oriented axes. More specifically, inertial sensors measure specific force and angle rates in Sensor axes, which then need to be resolved into Body axes via a three-dimensional transformation, typically involving a translation (the “lever arm”, the offset of the sensor from the body centre of motion) and a rotation. Unlike the Body-to-Earth transformation, the Body-to-Sensor transformation is normally assumed to be constant. However, for flexible structures, this approximation is not always valid.

To find an inertial navigation solution incorporating a platform’s position, velocity and attitude, a number of different reference frames and corrections are required. The sensors measure inertial quantities in Sensor axes. These need to be transformed to Body axes, and then to a reference frame which is fixed relative to the Earth (see Section 4.1 below). The accelerometer measurements measure the effect of the acceleration of the platform and the gravitational acceleration experienced. Before integrating the specific force to find the change in velocity, the measurements must corrected for gravity. In addition, the Earth is moving and forms a non-inertial frame, which results in a velocity-dependent Coriolis term [20, 21], which must also be removed. Finally, when gyroscopes are moving relative to the local NED reference frame in which the Euler angles are defined, the Euler angles must be corrected so that they are consistent in the new local NED axes. This correction is called the “transport rate” [20, 21], and must be included in the calculations for the inertial navigation solution.

2.1 Inertial drift

Inertial navigation forms the basis for all high performance navigation systems. Conventional classical inertial systems normally operate at high frequencies (normally several hundred Hz [20–22]) and provide near continuous estimates for position, velocity and attitude. However, the navigation solution suffers from instabilities and it will drift way from the true values [21]. This is an inevitable consequence of using dead reckoning.

As has been noted above, the integration of an inertial quantity with respect to time provides a change in the quantity rather than a direct measurement of that quantity. If there are initial errors in the navigation solution provided when the INS is turned on, these will never be corrected using inertial measurements. An initial velocity error will be added to the position for every second of movement. An attitude error will produce a trajectory that moves off in the wrong direction. In addition, all sensor measurements contain some level of noise, and the integral of a noisy acceleration signal will provide incremental changes to the velocity that contain the integral of the noise. These incremental changes to velocity are then integrated to find the change in position. The estimated position therefore accumulates all of the integrated noise from the velocity increments, which themselves contain the integrated noise in the acceleration. If the acceleration noise is zero-mean, white, Gaussian noise, the velocity errors will be a Brownian random walk, which increases as the square root of time on average [21]. The position errors, being the integral of the velocity errors, will scale as the cube of the square root of time. Similarly for the attitude, the angular errors will be an accumulation of the noise in the angle rate measurements. At no stage does a purely inertial navigation system measure position or attitude directly, so this accumulation of errors will not be constrained and the navigation solution will naturally drift away from the true values.

In addition to this natural tendency of an INS to drift with a random walk, one needs to take into account possible systematic errors in each sensor, each transformation and each of the corrections applied in forming the solution. In addition to measurement noise, inertial sensors will normally have some systematic errors due to a small bias on each measurement. The biases in lower cost inertial sensors can be appreciable, and even the small biases found in higher cost systems will accumulate over time. Such errors, cause the navigation solution to drift faster than would be expected from a simple random walk. Other systematic errors include the alignment of each sensor to one another: non-orthogonality between the elements in a triad [20]. Small errors in the alignment of the sensors causes the outputs to be coupled and noise in one sensor can couple to another, so the errors arising from the noisiest sensor will couple to all of the other sensors over time. This is more important for strapdown systems, where the attitude values are used as an input into the velocity and position calculations.

Further errors are then caused by small errors in the transformations from sensor axes to body axes, and body axes to Earth-referenced axes, and–as with the measurement noise–these errors accumulate over time if they are not corrected by direct measurements of the velocity, position or attitude. The corrections applied in the calculation of the integrated quantities (gravity, Coriolis and transport rate) are also the source of errors. The local gravity is rarely known to a high degree of precision [31–34], and the accuracy of this correction will deteriorate further as the position errors grow because the wrong values of the gravitational acceleration will be used to convert the specific force to the acceleration. These errors in the gravitational corrections normally mean that the vertical position is the most unstable of all of the quantities. The Coriolis and transport rate terms are both functions of the platform’s velocity, and errors in the velocity will give rise to errors in these terms, which then effects the accuracy of other quantities. This cross-coupling of errors due to inertial corrections and the transformation between reference frames means that once one of the navigational states starts to drift, the others will follow.

Different types of INS have different inertial drift rates, with higher quality and higher SWaP systems being more accurate and more costly. Marine-grade inertial systems tend to have the lowest drift rate, with aviation-grade, intermediate grade, and then tactical grade systems having progressively higher drifts rates [21]. Typical accuracies for these systems range from several km per day for marine-grade INSs, and several km per hour for aviation-grade systems, to retaining a useful navigation solution for a few minutes in the lower grade systems [21]. Given the current stage of development of quantum sensors, the sizes and costs involved means that a comparison with marine and aviation-grade systems are the most useful.

2.2 Initialisation and calibration

For a given set of inertial sensors, the standard approach to reducing the drift of an INS is to improve the initial alignment of the system and to calibrate the sensors accurately so that systematic errors and biases can be corrected at every time step. Initial alignment sets the navigation states (position, velocity and orientation) of the platform and it is best achieved when the platform is stationary and time is available to obtain a good estimate of the attitude. Calibration can be done at manufacture, and can be assisted by adding environmental controls to stabilise the operating temperature and reduce the level of vibrations. However, even with the most sophisticated initialisation and calibration methods, there will still be residual errors that cannot be completely removed. And, even if sensors were perfect and transformations were calibrated exactly, an INS will still drift due to numerical errors arising from the finite measurement frequency of the sensors and any high frequency motion of the platform and residual vibrations in the structure on which the strapdown system sits.

Calibration of the inertial sensors can reduce drift errors dramatically. At manufacture, high quality inertial navigation systems undergo a multi-position test (also known as a “Savage test”) [35, 36]. In any mechanical system, there are tolerances for mounting sensors within the housing. Electrical and electronic systems have tolerances on the components that read out measured signals, giving rise to measurement biases and scaling inaccuracies. The multi-position test takes a series of measurements for up to 24 different sensor orientations and known rotation rates to estimate the non-orthogonality errors, scaling errors, and fixed bias errors. Some bias errors will vary with time and with environmental conditions (e.g. temperature), and there will be some errors that cannot be completely characterised because they are due to mechanical flexure in the sensor housing or in the sensors themselves.

Initialisation of an inertial navigation system for position and velocity is relatively straightforward as long as it is done at a known location and when the platform in stationary. Being stationary allows the initial velocity to be set to zero, and the errors in the initial position may be minimised using a pre-surveyed location. Attitude is slightly more difficult to initialise because a stationary platform may not be on level ground when the INS is initialised, and the platform orientation relative to North (Euler heading) may not be the same each time the system is initialised even if this is done in the same location. Typically, the attitude is initialised using the local gravity vector, which allow the platform pitch and roll to be fixed relative to the local vertical vector–although it should still be noted that gravity does vary in different locations and has very small time-dependent contributions from tidal effects, meaning that this can never be exact. Heading can be initialised using a compass or a landmark or, in the case of high performance gyroscopes, a process called gyrocompassing can be used [21]. Gyrocompassing uses the fact that a stationary gyroscope will experience a net rotation rate because of the rotation of the Earth, ≃ 7 × 10⁻⁵ rad s⁻¹, if the gyroscope is sensitive enough. An accuracy of $\sim 7\times 10^{-8}$rad s⁻¹ is a good benchmark figure [21], the North direction can be estimated well enough to initialise the navigation system. In all cases, the initialisation process requires a series of measurements to be taken over a reasonable period of time (often several minutes rather than seconds) to obtain accurate estimates for the initial navigation states.

Initialising an inertial navigation system can be achieved when moving using a process called “transfer alignment” [21], which often involves performing a series of predefined manoeuvres and referencing the navigation solution against another navigation system (parent-child). Transfer alignment can initialise the navigation system and, in some circumstances, can also calibrate some of the errors present in the sensors. However, calibration when moving requires a very accurate reference navigation system (the “parent” INS) to calibrate against.

2.3 Position fixing and augmentation

Given the natural tendency of dead reckoning navigation systems to drift, most navigation systems seek to augment a dead reckoning system with a position fixing solution. This augmentation is achieved by filtering the two solutions, dead reckoning and position fixing, together. A good filtered solution uses the position fixing system to correct and to limit the effect of the drift errors over a period of time. Position fixing systems rely on a database of features (e.g. terrain variations [37], ground features [38, 39]) or broadcast signals (from a constellation of satellites [40] or terrestrial broadcast antennas [41, 42]). These reference systems vary over time scales much longer than the operating frequencies of inertial navigation systems (around 1 Hz rather than several hundreds of Hz). As a result, their useful operating frequencies are limited because their position errors are highly correlated unless the features are changing significantly between updates.

Most inertial navigation systems will use a GNSS/GPS system as the main form of augmentation. GNSS is ubiquitous and position information is global and freely available. However, current satellite based systems do have significant vulnerabilities. The satellite broadcast signals have an extremely low signal-to-noise level [21], which means that they are relatively easy to disrupt with small, low cost jammers producing noise in the relevant wavebands [43]. Standard open GNSS signals are also sensitive to ‘spoofing’, the rebroadcasting of the signals with altered time delays to manipulate the position information generated [43]. Of course, more secure forms of encrypted GNSS signals are available [21], but these are typically only available for military applications.

Alternative methods for position fixing operate as back up systems where GNSS is not available or unreliable. Terrain matching [37] and visual feature matching [38] are both useable when travelling over land with sufficient suitable features. Terrestrial broadcast methods can use bespoke navigation signals [41] or standard radio broadcast signals [42]. Quantum gravity sensors have also been studied and appear to be viable candidates [44–49], including systems based on current cold atom technologies [49]. Typically, these systems are not as accurate as GNSS position updates, but they do still act to limit the drift of purely inertial navigation systems [50].

3 Cold atom sensing

Cold atom interferometers can be sensitive to accelerations [51] or rotations [9, 52, 53] or, more generally, both [3]. Possibly the simplest form of cold atom sensor is a one-dimensional (vertical) gravity sensor, where atoms are placed in a superposition of states, each corresponding to a slightly different trajectory within the local gravitational field. The phase of each of the states in the superposition depends on the trajectory that it has followed and when they are combined this gives rise to an interference pattern, and the phase of this interference pattern can be related to the gravitational acceleration experienced by the atoms. The superpositions are created by applying Raman π/2 pulses to place each atom in a superposition of its ground state and an excited state. The excitation changes the momentum of the atom in that state, thereby changing the rate that it falls in the gravitational field. After a period of time T, a π pulse then swaps the ground and excited state components and after another T seconds, another π/2 pulse is applied to allow the components to interfere. In its simplest form, the phase difference can be written as [54, 55],

${\varphi }_0=k_{\mathit{eff}}g{T}^2(1)$

where k_eff is the effective wave number of the π/2 interferometer pulses, T is the time between the π/2 and the π pulses, and g is the local gravitational acceleration. There are a number of errors sources even in such simple analysis. The number of atoms involved in the cloud varies from measurement to measurement, and each atom will be in a slightly different part of the laser field, so the π/2 and π pulses will have slightly different actions on each atom. The atoms will be at a small but finite temperature and there will be some thermal motion which will tend to reduce the signal S which is actually measured

$S=\eta \left(\bar{N}+\delta N\right)\sin \left({\varphi }_0+\delta \varphi \right)+s_0(2)$

where η is the measurement efficiency (or the contrast of the interference fringes), $\bar{N}$ is the average number of atoms in each cloud (normally $\bar{N}\sim 10^5-10^6$ for most systems), δN is the atom number shot noise on each measurement (where the standard deviation of δN is ${\sigma }_N=\sqrt{\bar{N}}$), δϕ is the measurement phase noise which is assumed to be Gaussian with a standard deviation σ_ϕ, and s₀ is a constant representing a signal bias. This is the simplest model for a one-dimensional atom interferometer but more complex models that describe higher order corrections to this model [56–58]. However, only a simple model is required here. When modelling the cold atom sensors to calibrate the classical inertial navigation sensor errors, we will only need to specify the final errors in the inertial measurements.

The signal to noise is maximised and the accuracy of the phase difference is improved by increasing the number of atoms used in each measurement, increasing the time of flight of the atoms (time$\sim 2T$), and maximising the momentum transfer of the π/2 pulses (increasing k_eff). There are practical limits to the number of atoms being used in the measurements, but these values are increasing as the trapping and cooling methods become more efficient. Increasing the time T is problematic because it increases the physical size of the vacuum chamber and reduces the measurement frequency. Increasing the momentum transfer is also being considered with system using multiple phonon excitations, where the numbers of photons and the momentum being exchanged is much larger [59, 60].

Although the technologies are advancing rapidly, there are some physical limitations in terms of the size of the devices, their operating frequencies, and the proportion of the measurement cycle when they are sensitive to the signal being measured (the duty cycle). To some extent, the last two of these are being addressed by using more than one atom species [13–15]. In effect, this approach is equivalent to running multiple interferometers in parallel, each with a different atom species. This makes the system more complex but it also offers significant benefits.

Other cold atom inertial sensors operate in similar ways, using laser pulses to create superposition states which are sensitive to horizontal as well as vertical accelerations, as well as rotation rates. Rotations are often sensed by defining different paths that enclose an area so that the interference phase becomes sensitive to rotations via the Sagnac effect [63, 64]. A key enabler for this type of device is the ability to use guiding potentials to move the atomic trajectories along well defined paths and allowing efficient recombination of the superposed paths [61, 62]. Current sensors tend to use vacuum and ballistic flight to define the atom trajectories, which is one reason that the dynamic range of cold atom sensors is relatively low. The motion of the atoms along the paths needs to be such that the paths are able to meet to interfere. Any very large rotation or large acceleration change will result in the paths not meeting correctly, or meeting outside the region of the sensor where the measurements can take place. Other systems try to reduce the effect of the residual thermal motion in the cloud of atoms by cooling the particle down to a point where they form a Bose-Einstein condensate (BEC) state, where the motion of the atoms is correlated and the fraction of the atoms in this BEC state are all in the same quantum motional state [65, 66].

The performance of current cold atom systems is improving rapidly, with a number of the methods outlined being used. Recent reviews of cold atom technologies [9, 24] provide useful comparisons of cold atom devices against classical systems. For example, cold atom gyroscopes demonstrate extremely good long time stability, with some example systems being able to demonstrate errors of 10⁻⁹rad over 10⁴ s, with a short term sensitivity of 100 nrad/s/$\sqrt{Hz}$ [6]. This compares well with the (high quality) iXBlue classical commercial fibre gyroscope with a sensitivity of 300 nrad/s/$\sqrt{Hz}$ or commercial navigation ring laser gyroscopes with sensitivities of tens of nrad/sec/$\sqrt{Hz}$ [9]. Other cold atom gyroscopes do offer comparable performance to commercial ring laser gyroscopes, but they also have significantly longer integration times [9]. For accelerometers, the performance over long integration times is impressive, with gravity/acceleration accuracies approaching 10⁻⁸ m/s² in some cases [24], which compares well with classical accelerometers used in inertial navigation systems [21].

Current cold atom technologies operate using superpositions of states, but future systems may be able to benefit from the use of entangled as well as superposed atom states. Theoretical investigations have demonstrated that the use of entanglement could provide several orders of magnitude better accuracy and precision than superpositions [67–69].

4 Inertial navigation

In this section, we outline the models that we have used to assess the accuracies achievable from quantum calibrated inertial navigation systems. Firstly, we outline the different frames of reference that we have used, all of which are standard navigation frames [21], and then define the simulated trajectories used in the paper, including the measurement error models. The navigation equations are given in the local NED frame, which are integrated numerically to form state estimates for the navigation solution. Comparing the estimated navigation solution to the true (simulated) trajectories provides the navigation drift, which can then be averaged over a set of examples (realisations of the noise/errors) to assess the navigation performance.

4.1 Frames of reference

The position of the platform is defined relative to the Earth using a standard ellipsoid which is, by convention, taken to be the WGS′84 ellipsoid [33]. We represent the platform’s location in terms of the latitude (Φ), longitude (Λ), and altitude above the ellipsoid mean sea level (h)². A number of global frames of reference are often used in navigation [21]. The Earth Centred Inertial (ECI) frame is a set of axes centred on the ellipsoid centre, within which the Earth rotates. It simplifies the physics by providing an inertial frame, but the transformations to/from this reference frame require small differences between large quantities, which can result in some numerical issues. Defining a reference frame where Earth is fixed, called Earth-Centred Earth-Fixed (ECEF), has similar numerical requirements. The Earth is fixed in this reference system but it is not an inertial reference frame, so the rotational non-inertial effects need to be included when calculating the navigation solution. In this paper, we use the local North-East-Down (NED) reference frame, which are Euclidian co-ordinates with a zero defined to be the current position, and oriented to the local North and local vertical (down) vector that is perpendicular to the local tangent plane to the ellipsoid³. Integrating the navigation equations requires that the local NED frame increments at each time step, which is numerically inefficient, but it does provide an intuitive representation of the motion.

Measurements are taken in the sensor axes, and the sensors are assumed to be fixed to the platform at the platform centre of navigation. This assumption simplifies the equations so that the transformation from sensor to body axes is a three-dimensional rotation matrix. It is not necessary, adding a translation to account for the effect of the level arm is straightforward but it does not add anything to the results presented in this paper. The sensor axes (x^(s), y^(s), and z^(s)) can be aligned to the body axes (x^(b), y^(b), and z^(b), representing Along (forward)-Across (right)-Down) without loss of generality as long as errors in this alignment can be included in the modelling, where the superscripts (s) and (b) indicate that the measurements are in sensor and body axes, respectively.

The alignment of the body axes to the local Earth NED axes (the platform attitude) are given by the three estimated Euler axes, heading $(\widehat{\psi })$, pitch $(\widehat{\theta })$, and roll $(\widehat{\phi })$, where the circumflexes indicate estimated quantities rather than quantum operators. Other representations for rotation are available, such as quaternions [21]. Quaternions are often used because they are more stable in numerical calculations and do not generate any infinities when the platform orientation is close to straight up or straight down. However, the Euler representation is more familiar and intuitive for most people and the trajectories have been defined to be benign and not to generate any numerical instabilities, so we use Euler angles in this paper.

4.2 Trajectories and measurements

The trajectories are selected to represent an aircraft following a simple straight line trajectory that starts above Brighton (Latitude 50.8374669^o, Longitude −0.1412091^o) and travels to Edinburgh (Latitude 55.9412846^o, Longitude −3.2753782^o) at a constant altitude of 3,000 m. This is a distance of 605 km and, fixing the speed as 100.0 m/s, the aircraft would cover this distance in around 100 min. An aircraft has been selected because it provides an environment that can accommodate the relatively large SWaP requirements of current quantum sensors and the operation of cold atom systems have already been demonstrated in an aircraft [4, 15]. The route has been defined to represent a benign trajectory that is long enough to require that the rotation and the non-spherical nature of the Earth must be taken into account when calculating the navigation solution.

We define a straight and level flight and generate appropriate specific forces and angle rates from this trajectory, using a standard uniform ellipsoid gravity model (the Somigliana gravity model [31]), and then add measurement noise and systematic biases according to the STANAG 4572 definition of errors [70]. The three-dimensional errors include: sensor biases for accelerometers b^(s,a) and for gyroscopes b^(s,g) (where the superscripts (., a) and (., g) indicate that the measurements are from the accelerometer or the gyroscope); non-orthogonalities in the alignment of individual accelerometers and gyroscopes, and scaling errors for each of these, represented by matrices M^(s,a) and M^(s,g) respectively; and random measurement noise w^(s,a)(t) and b^(w,g)(t). For simplicity, we do not consider vibrational or other acceleration dependent noise sources [21]. The simulated “real” values for the specific forces f^(s)(t) and angle rates ω^(s)(t) from the trajectory model are then modified using.

${\tilde{\mathbf{f}}}^{\left(s\right)}\left(t\right)=\left({\mathbf{I}}_3+{\mathbf{M}}^{\left(s,a\right)}\right){\mathbf{f}}^{\left(s\right)}\left(t\right)+{\mathbf{b}}^{\left(s,a\right)}+{\mathbf{w}}^{\left(s,a\right)}\left(t\right)(3)$

${\tilde{\mathit{\omega }}}^{\left(s\right)}\left(t\right)=\left({\mathbf{I}}_3+{\mathbf{M}}^{\left(s,g\right)}\right){\mathit{\omega }}^{\left(s\right)}\left(t\right)+{\mathbf{b}}^{\left(s,g\right)}+{\mathbf{w}}^{\left(s,g\right)}\left(t\right)(4)$

where ${\tilde{\mathbf{f}}}^{(s,a)}(t)$ and ${\tilde{\mathit{\omega }}}^{(s,a)}(t)$ are the measured quantities, and w^(s,a)(t) and w^(s,g)(t) are taken to be white Gaussian noise terms with standard deviations that are proportional to $\sqrt{\delta t}$. We assume values for the standard deviation of errors present in an aviation-grade inertial navigation system [21], see Table 1, and an INS integration frequency of 200 Hz.

TABLE 1

TABLE 1. Measurement errors for an aviation-grade inertial navigation system.

4.3 Navigation equations

To integrate the measurements to form a navigation solution, we take the accelerometer measurement data, ${\tilde{\mathbf{f}}}^{(s,a)}$ and convert from sensor axes to body axes, and from body axes to local NED axes using the current estimates for the Euler angles. The specific force is then corrected for the gravitational acceleration, which is a function of latitude, longitude and altitude,

${\tilde{\mathbf{a}}}^{\left(\widehat{E}\left(t\right)\right)}\left(t\right)={\tilde{\mathbf{f}}}^{\left(\widehat{E}\left(t\right),a\right)}\left(t\right)+\mathbf{g}\left(\widehat{\mathrm{\Phi }}\left(t\right),\widehat{\mathrm{\Lambda }}\left(t\right),\widehat{h}\left(t\right)\right)(5)$

where the superscript (E,.) indicates that the measurements are in the current local NED axes. The measured acceleration ${\tilde{\mathbf{a}}}^{(\widehat{E}(t))}(t)$ is then corrected for the rotation of the Earth and the transport rate,

${\tilde{\mathbf{a}}}_{+}^{\left(\widehat{E}\left(t\right)\right)}\left(t\right)={\tilde{\mathbf{a}}}^{\left(\widehat{E}\left(t\right)\right)}\left(t\right)-2\left({\widehat{\omega }}_E\times {\widehat{\mathbf{v}}}^{\left(\widehat{E}\left(t\right)\right)}\left(t\right)\right)-\left({\widehat{\omega }}_{tr}\left(t\right)\times {\widehat{\mathbf{v}}}^{\left(\widehat{E}\left(t\right)\right)}\left(t\right)\right)(6)$

where ${\widehat{\mathbf{v}}}^{(\widehat{E})(t)}$ is the current platform velocity in the (estimated) local Earth axes, the angular velocity vector for the rotation of the Earth is ${\widehat{\omega }}_E=7.2921159\times 10^{-5}{(\cos \widehat{\mathrm{\Phi }}(t),0.0,-\sin \widehat{\mathrm{\Phi }}(t))}^T$ rad/s, and T indicates a transpose, and the transport rate ${\widehat{\omega }}_{tr}(t)$ is given by,

${\widehat{\omega }}_{tr}\left(t\right)=\left(\begin{array}{c}\hfill {\widehat{v}}_2^{\left(\widehat{E}\left(t\right)\right)}\left(t\right)/\left(R_E\left(\widehat{\mathrm{\Phi }}\left(t\right),\widehat{\mathrm{\Lambda }}\left(t\right),\widehat{h}\left(t\right)\right)+\widehat{h}\left(t\right)\right)\hfill \\ \hfill -{\widehat{v}}_1^{\left(\widehat{E}\left(t\right)\right)}\left(t\right)/\left(R_N\left(\widehat{\mathrm{\Phi }}\left(t\right),\widehat{\mathrm{\Lambda }}\left(t\right),\widehat{h}\left(t\right)\right)+\widehat{h}\left(t\right)\right)\hfill \\ \hfill -{\widehat{v}}_2^{\left(\widehat{E}\left(t\right)\right)}\left(t\right)\tan \widehat{\mathrm{\Phi }}/\left(R_E\left(\widehat{\mathrm{\Phi }}\left(t\right),\widehat{\mathrm{\Lambda }}\left(t\right),\widehat{h}\left(t\right)\right)+\widehat{h}\left(t\right)\right)\hfill \end{array}\right)(7)$

where R_N and R_E are the local radii of curvature of the ellipsoid in the North and East directions at the current estimated position, $R_N=a(1-e^2)/({(1-e^2{\sin }^2\widehat{\mathrm{\Phi }})}^{3/2})$, $R_E=a/\sqrt{1-e^2{\sin }^2\widehat{\mathrm{\Phi }}}$, and e² = (a − b)²/a², where the equatorial radius and the polar radius of the Earth are a = 6378137.0 m and b = 6356752.314,245 m, respectively.

The corrected acceleration in the local NED axes (6) can then be integrated to provide an update to the estimated velocity

${\widehat{\mathbf{v}}}^{\left(\widehat{E}\left(t\right)\right)}\left(t\right)\to {\widehat{\mathbf{v}}}^{\left(\widehat{E}\left(t\right)\right)}\left(t+\delta t\right)={\widehat{\mathbf{v}}}^{\left(\widehat{E}\left(t\right)\right)}\left(t\right)+{\tilde{\mathbf{a}}}_{+}^{\left(\widehat{E}\left(t\right)\right)}\left(t\right)\delta t$

and the NED position

${\widehat{\mathbf{r}}}^{\left(\widehat{E}\left(t\right)\right)}\left(t\right)\to {\widehat{\mathbf{r}}}^{\left(\widehat{E}\left(t\right)\right)}\left(t+\delta t\right)={\widehat{\mathbf{r}}}^{\left(\widehat{E}\left(t\right)\right)}\left(t\right)+{\widehat{\mathbf{v}}}^{\left(\widehat{E}\left(t\right)\right)}\left(t\right)\delta t+\frac{1}{2}{\tilde{\mathbf{a}}}_{+}^{\left(\widehat{E}\left(t\right)\right)}\left(t\right)\delta t^2$

after each time step, δt.

The angle rate measurement is transformed to body axes ${\tilde{\mathit{\omega }}}^{(b,g)}(t)$ and is corrected in body axes by rotating the Earth’s rotation rate and the transport rate from Earth to body axes ${\omega }_E^{(b)}$ and ${\omega }_{tr}^{(b)}(t)$ and calculating

${\tilde{\mathit{\omega }}}_{+}^{\left(b,g\right)}\left(t\right)={\tilde{\mathit{\omega }}}^{\left(b,g\right)}\left(t\right)-{\widehat{\omega }}_E^{\left(b\right)}-{\widehat{\omega }}_{tr}^{\left(b\right)}\left(t\right)(8)$

The integration of the angle rates to find the new Euler angles requires that the Euler angle rates be calculated from the body angle rates. The Euler rates are given by,

$\frac{d\psi }{dt}\left(t\right)={\tilde{\omega }}_{2,+}^{\left(b,g\right)}\left(t\right)\sin \widehat{\phi }\left(t\right)/\cos \widehat{\theta }\left(t\right)+{\tilde{\omega }}_{3,+}^{\left(b,g\right)}\left(t\right)\cos \widehat{\phi }\left(t\right)/\cos \widehat{\theta }\left(t\right)(9)$

$\frac{d\theta }{dt}\left(t\right)={\tilde{\omega }}_{2,+}^{\left(b,g\right)}\left(t\right)\cos \widehat{\phi }\left(t\right)-{\tilde{\omega }}_{3,+}^{\left(b,g\right)}\left(t\right)\sin \widehat{\phi }\left(t\right)(10)$

$\frac{d\phi }{dt}\left(t\right)={\tilde{\omega }}_{1,+}^{\left(b,g\right)}\left(t\right)+{\tilde{\omega }}_{2,+}^{\left(b,g\right)}\left(t\right)\cos \widehat{\phi }\left(t\right)\tan \widehat{\theta }\left(t\right)+{\tilde{\omega }}_{23,+}^{\left(b,g\right)}\left(t\right)\cos \widehat{\phi }\left(t\right)\tan \widehat{\theta }\left(t\right)(11)$

The Euler rates can then be integrated to provide an incremental update for the Euler angles $(\widehat{\psi }(t),\widehat{\theta }(t),\widehat{\phi }(t))\to (\widehat{\psi }(t+\delta t),\widehat{\theta }(t+\delta t),\widehat{\phi }(t+\delta t))$, and keeping the periodic nature of each Euler angle in mind.

After updating each of the elements in the navigation solution, the NED position is converted back to latitude-longitude-altitude to maintain the correct local NED reference frame. The gravity correction term is often the dominant error present in high quality inertial navigation systems and it causes the vertical channel to become very unstable. To remove this effect, which may mask some of the more subtle effects, we assume that an altitude sensor is available to fix the altitude of the trajectory, and that this feeds in to the navigation solution to stabilise the vertical channel. This is not unreasonable since most aircraft will have a barometric or radar altimeter to augment the navigation system, and unlike a GNSS system, such altimeters cannot be easily jammed.

We have left an explicit time dependence in the equations above to emphasise where the estimated quantities, the frames of reference, and the associated errors vary with time. What is noticeable in these equations is that nearly all of the quantities in the transformations and the corrections applied to the measured quantities involve estimates taken from the navigation solution. The values for the transport rate and the Earth’s rotation rate in local NED coordinates are not sensitive to small errors in position, but it is sensitive on long timescales. As the navigational errors accumulate, these errors will grow and could start to have an effect on the navigational accuracy.

5 Online calibration of classical inertial navigation systems

In this section, we consider the performance of a conventional aviation-grade INS, where a cold atom sensor is used to perform online calibration of the sensor biases b^(s,a) and b^(s,g). Although conventional inertial systems have non-orthogonality and scaling errors, it is the biases that normally dominate the inertial drift so we focus on reducing the effect of these errors. All of the errors are contained in our classical INS models, but the other systematic errors would only become important and need calibration when the biases are sufficiently small that these other errors become the dominant contribution.

The current generation of cold atom sensors operate at low frequencies (0.5 Hz to a few Hz) and have a limited duty cycle (0.3–0.5). They can be assumed to integrate the inertial signals over a fraction of the operating period corresponding to the duty period. The integrated signal is then used to construct an estimate of the biases, ${\widehat{\mathbf{b}}}_q^{(s,a)}(t)$ and ${\widehat{\mathbf{b}}}_q^{(s,g)}(t)$, which can then be subtracted from the measurements to reduce the INS drift rate.

${\check{\mathbf{f}}}^{\left(s\right)}\left(t\right)={\tilde{\mathbf{f}}}^{\left(s\right)}\left(t\right)-{\widehat{\mathbf{b}}}_q^{\left(s,a\right)}\left(t\right)(12)$

${\check{\mathit{\omega }}}^{\left(s\right)}\left(t\right)={\tilde{\mathbf{f}}}^{\left(s\right)}\left(t\right)-{\widehat{\mathbf{b}}}_q^{\left(s,g\right)}\left(t\right)(13)$

Where the $\check{\mathit{o}}$ symbol indicates a calibrated value, and the subscript q indices that the quantity is derived from a quantum (cold atom) sensor.

Of course, there may be an error between the quantum sensor axes and the classical sensor axes, and this must be included in the analysis of errors. In Section 5.1, we start by considering cases where a perfect quantum sensor is used to calibrate the biases in a conventional aviation-grade INS when the sensors are perfectly aligned, so that the rotation matrix between the two sets of axes is known without errors–again we will ignore level arm effects arising from physical separation of the centres of each sensor from the platform’s centre of navigation and from each other. The lever arm effects are included in the model but the separations are set to zero for convenience. In practice, errors due to lever arm effects can be reduced by accurate calibration of the system and, in the absence of flexure in the structure and unlike the sensor biases, the errors generally do not change over time.

Section 5.1 considers cases of full calibration (accelerometers and gyroscopes are calibrated using quantum sensors), calibration of the accelerometers only, and calibration of the gyroscopes only. Section 5.2 then considers cases where the quantum sensors are still perfect but there are small misalignments between the axes of the quantum and conventional inertial sensors. Section 5.3 describes cases where there are sensor misalignments and the accuracy of the quantum sensor is limited. The aim is to assess the level of accuracy that would be required for a quantum sensor to provide a significant benefit in terms of the online calibration of a conventional inertial navigation systems. Finally, we consider other factors, such as the duty cycle of the sensor and the measurement frequencies of the cold atom systems.

5.1 Aviation-grade INS with perfect quantum sensors and perfect sensor alignment

In an ideal world, sensors would have minimal or zero noise and be perfectly aligned and calibrated. Unfortunately, this is never the case, but to examine the limiting performance of a coupled quantum-classical inertial navigation system, we start by assuming that the quantum sensor measurements have zero measurement noise and the sensor axes are perfectly aligned. For the cases presented, the quantum sensor is assumed to have a duty cycle of 0.5 and take measurements at 2 Hz. The quantum sensor model also has limits on its dynamic range, but these do not play a role for this analysis because the flight profile is benign and generally do not reach these limits. Outside this dynamic range, the sensors would produce a null measurement, and any benefit from having an online calibration sensor would be reduced or (in extreme cases) removed entirely.

Figure 1 shows the Brighton-Edinburgh trajectory and example navigation solutions for an unaided/uncalibrated classical INS and a classical INS that is calibrated during flight using a perfect quantum sensor. Figure 2 shows the mean horizontal position errors as a function of time. Calibration using a perfect sensor, albeit one with limited duty cycle and measurement frequency, is to reduce the drift rate by a factor of about two. The residual errors come from imperfect calibration due to the limited duty cycle of the quantum sensor, the integration of the motion over the measurement period at low frequency, and numerical errors in the integration of the navigation equations. In Figure 2, the errors contain an oscillatory term with a long oscillation period. This is the Schuler oscillation [21], which arises as a result of motion around the ellipsoid. This oscillation has a period of 87 min, which is approximately the period that a simple pendulum would have if it had a length equal to the radius of the Earth. The Schuler oscillation period is approximately fixed, and its amplitude is related to the size of the errors in the INS.

FIGURE 1

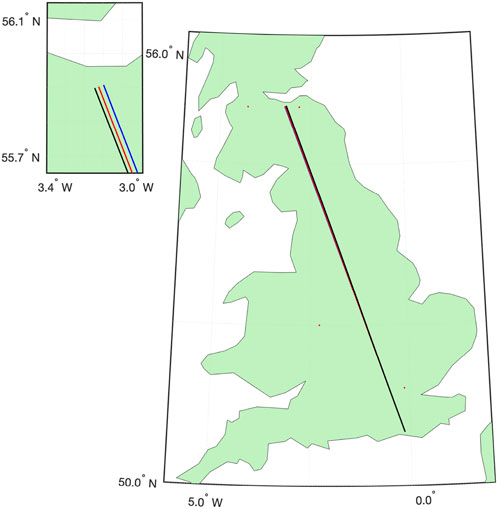
FIGURE 1. Map showing the true Brighton-Edinburgh trajectory (black), and an example of an uncalibrated aviation-grade INS solution (blue) and an aviation-grade INS with online calibration using a perfectly aligned set of perfect quantum sensors (red).

FIGURE 2

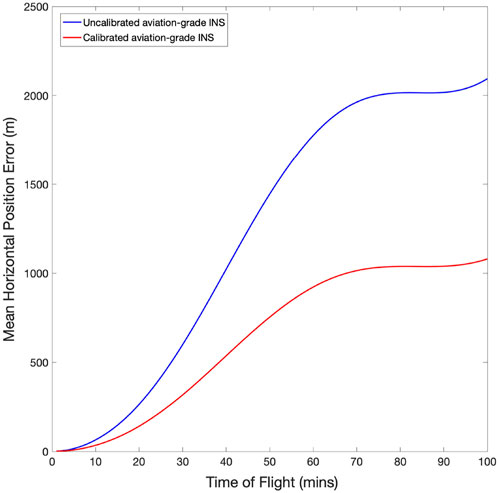
FIGURE 2. Mean horizontal error for route Brighton-Edinburgh for an uncalibrated aviation-grade INS solution (blue) and an aviation-grade INS that is calibrated online by a perfectly aligned set of perfect cold atom sensors (red)—mean is calculated over 50 realisations of the errors for the full trajectory.

The results shown are for a full suite of accelerometers and gyroscopes, but we have also run these trajectories for calibration using accelerometers only and gyroscopes only. We find that the main benefit comes from using quantum sensor for calibrating the gyroscopes rather than the accelerometers. Calibrating the errors in the accelerometers of an aviation-grade INS has little effect on the overall navigation performance, which is driven mainly by the errors in the gyroscopes. This is true for most or even all strapdown inertial systems because they rely on the accuracy of the gyroscopes and the attitude estimates to resolve the measured specific forces in the sensor/body frame into the navigation frame.

5.2 Aviation-grade INS with perfect quantum sensors and sensor misalignment

Moving away from a perfect sensor, one needs to take into account any misalignment of the quantum and the classical sensor axes. We do this by applying a three-dimensional rotation matrix, δR,

$\mathit{\delta }\mathbf{R}=\left(\begin{array}{ccc}\hfill 1\hfill & \hfill \delta \psi \hfill & \hfill -\delta \theta \hfill \\ \hfill -\delta \psi ,\hfill & \hfill 1\hfill & \hfill \delta \phi \hfill \\ \hfill \delta \theta \hfill & \hfill -\delta \phi \hfill & \hfill 1\hfill \end{array}\right)(14)$

with small angular errors in the Euler angles, δψ, δθ, δφ, to the measured quantities. The misalignment errors are Gaussian distributed and fixed for a given realisation of a trajectory with a given standard deviation. These errors represent any residual alignment errors after any alignment process that is performed to calibrate the sensors at manufacture/installation. These misalignments mean that the physical quantities being measured differ slightly and this introduces cross couplings between the different navigation errors.

The effect of these errors on navigation performance is shown in Figure 3. We see that misalignments of the sensors below 0.005^o lead to small deviations from the perfect case shown in Figure 2 and shown in Figure 3 as the solid red line. For alignment errors above 0.01^o, the errors increase significantly, and when the errors are significantly above this value, the navigation errors would be worse than the case of an uncalibrated classical INS.

FIGURE 3

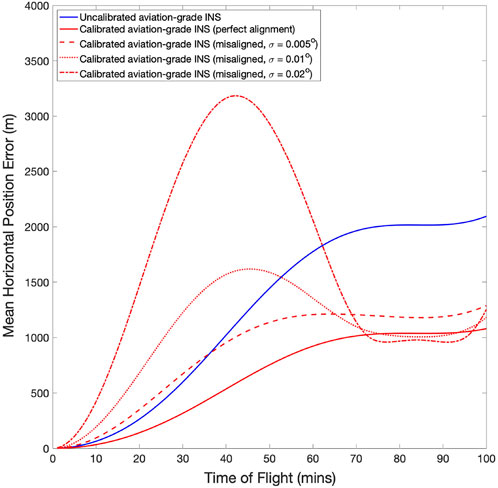
FIGURE 3. Mean horizontal error for an uncalibrated aviation-grade INS solution (blue), an online calibrated aviation-grade INS that is perfectly aligned to perfect cold atom sensors (red, solid), and an online calibrated aviation-grade INS that is misaligned with respect to the cold atom sensors: standard deviation of the misalignments in each axis σ =0.005^o (red, dash), σ =0.02^o (red, dotted), and σ =0.02^o (red, dot-dash). The means are calculated over 50 realisations of the errors for the full trajectory.

5.3 Aviation-grade INS with imperfect quantum sensors and sensor misalignment

Although cold atom sensors do have the potential to provide inertial measurements with unprecedented accuracy and precision, there are still errors due to phase noise in the laser systems, shot noise and reduced contrast in the interferometer phase measurements. As a result, one must also consider measurement noise in the cold atom signals. Adding measurement noise to the biases in (12) and 13 will degrade the ability of the quantum sensor to correctly calibrate the classical INS biases. Focussing on the performance of the gyroscopes (see Section 5.1), Figure 4 shows the navigation errors as a function of time for zero gyroscope noise, for 0.05μrad, 0.10μrad, and 0.20 μrad errors (1 standard deviation, 1σ) on each cold atom measurement. For errors at or below 0.10μrad, there is little or no degradation in the navigation performance. Only measurement errors at 0.20 μrad or above show a significant increase in the navigation errors. This is larger than the biases in the classical gyroscopes, which are 0.05 μrad (see Table 1). This can be can be attributed to the fact that the bias level only changes slowly relative to the measurements (both classical and quantum). The calibration of the classical gyroscopes should provide an improvement in navigation accuracy as long as the bias drift rate is very slow relative to the cold atom measurement errors averaged over an appropriate time interval (treated as a random walk since the quantum sensor should have little or no measurement bias).

FIGURE 4

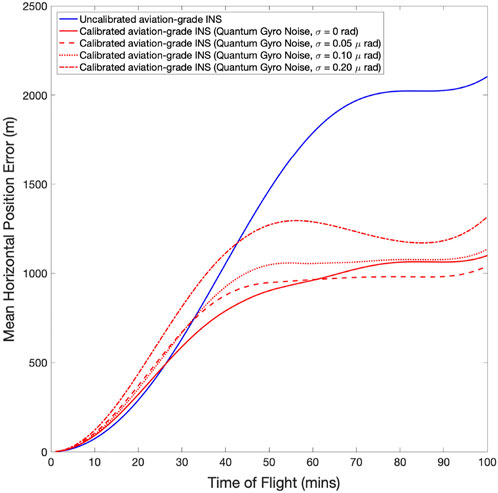
FIGURE 4. Mean horizontal error for an uncalibrated aviation-grade INS solution (blue), an online calibrated aviation-grade INS that is misaligned (σ =0.005^o) to perfect cold atom sensors (red, solid), and with gyroscope measurement noise σ =0.05 μrad (red, dash), σ =0.2 μrad (red, dotted), and σ =0.2 μrad (red, dot-dash). The means are calculated over 50 realisations of the errors for the full trajectory.

5.4 Sensor duty cycle and measurement frequency

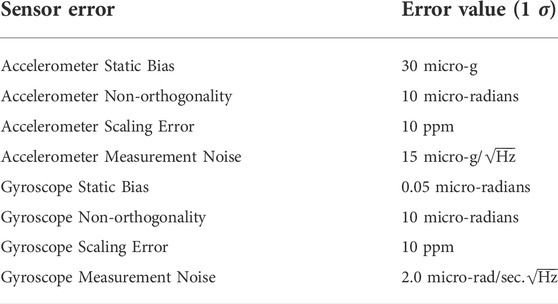
The results presented above are for a cold atom sensor with a duty cycle of 0.5 and a measurement frequency of 2 Hz. These values are based on the approximate parameter values for current cold atom sensors. However, as methods for preparing, trapping and cooling clouds of atoms are improved, and as more sophisticated methods of manipulating the atoms within the interferometer are developed (such as use of multiple atom species in a single interferometer), one would expect that the sensitivity of the sensors will improve, the duty cycle will improve, and the measurement frequency will increase. Improved measurement sensitivities can be encompassed in reduced measurement noise, as in the previous section. To reflect the other improvements, we have modelled the navigation performance of a calibrated classical INS for a range of duty cycles and for different measurement frequencies. We find that duty cycles above 0.4 provide a stable calibration solution for an aviation-grade INS, and duty cycles below 0.3 struggle to provide stable corrections to the classical biases. Measurement frequencies between 0.5 and 2 Hz do not affect the improvements in navigation performance significantly for the classical INS parameters in Table 1, but moving to frequencies between 4 and 5 Hz do provide significant improvements in the accuracy of the calibration methods described.

6 Summary and conclusion

In this paper, we have examined the potential for using current or near future cold atom inertial sensors for the online calibration of classical inertial navigation sensors. Classical inertial sensors contain significant measurement biases. Their use in dead reckoning navigation systems gives rise to significant drift rates in their navigation solutions. This is a fundamental property of dead reckoning navigation systems. Quantum inertial sensors will not remove this tendency to drift entirely, but they can reduce the rate at which drift occurs. Even with the low measurement frequencies and low duty cycles available in current cold atom sensors, we have demonstrated that using a quantum sensor to measure and to correct the biases in classical inertial sensors can provide improved navigation performance–for the examples shown, the drift rate of a classical inertial navigation system can be reduced by a factor of around two. Because of the relatively high size, weight and power requirements for current cold atom systems, we have concentrated attention on aviation-grade inertial navigation systems which are relatively high cost and have drifts rates approximately five to ten times larger than higher performance marine-grade inertial systems. However, some performance increases would also be expected for marine-grade inertial navigation systems. Although one might expect cold atoms sensors to improve in terms of size, weight, power and cost, it is unlikely that they will be compatible with the smaller and cheaper inertial navigation systems in the near future. In the case of aviation-grade systems, the biggest performance improvement is due to calibration of the classical gyroscope biases rather than the biases in the accelerometers. We find that these improvements are robust to the presence of sensor imperfections (such as sensor misalignments and measurement noise) and for a range of sensor parameters (including differing duty cycles and measurement frequencies).

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Footnotes

¹Attitude is conventionally expressed in terms of three Euler angles [21]—heading (ψ), pitch (θ), and roll (φ)—relative to the local Earth-oriented axes (North-East-Down, NED). These angles represent a sequence of rotations of ψ around the local Down axis, θ around the rotated axis Across-Right, and φ around the new rotated axis Along-Forward. The order of these operations is critical because of the non-commutativity of rotations in three-dimensions.

²Local mean sea level is related to the geiod, which reflects the local variations in gravity due to topology and density of the Earth locally. It can vary by tens and up to about one hundred metres from the global ellipsoid mean sea level [32].

³The local vertical defined by the local gravity will be different in general, due to the shape of the ellipsoid, and also different from the vertical vector defined as passing through the centre of the ellipsoid.

References

1. Gustavson TL, Bouyer P, Kasevich MA. Precision rotation measurements with an atom interferometer gyroscope. Phys Rev Lett (1997) 78:2046–9. doi:10.1103/physrevlett.78.2046

CrossRef Full Text | Google Scholar

2. Gustavson TL, Landragin A, Kasevich MA. Rotation sensing with a dual atom-interferometer Sagnac gyroscope. Class Quan Gravity (2000) 17:2385–98. doi:10.1088/0264-9381/17/12/311

CrossRef Full Text | Google Scholar

3. Canuel B, Leduc F, Holleville D, Gauguet A, Fils J, Virdis A, et al. Six-Axis inertial sensor using cold-atom interferometry. Phys Rev Lett (2006) 97:010402. doi:10.1103/physrevlett.97.010402

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Geiger R, Menoret V, Stern G, Zahzam N, Cheinet P, Battelier B, et al. Detecting inertial effects with airborne matter-wave interferometry. Nat Commun (2011) 2:474. doi:10.1038/ncomms1479

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Dickerson SM, Hogan JM, Sugarbaker A, Johnson DMS, Kasevich MA. Multiaxis inertial sensing with long-time point source atom interferometry. Phys Rev Lett (2013) 111:083001. doi:10.1103/physrevlett.111.083001

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Dutta I, Savoie D, Fang B, Venon B, Alzar CG, Geiger R, et al. Continuous cold-atom inertial sensor with1  nrad/secRotation stability. Phys Rev Lett (2016) 116:183003. doi:10.1103/physrevlett.116.183003

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Wu X, Zi F, Dudley J, Bilotta RJ, Canoza P, Muller H. Multiaxis atom interferometry with a single-diode laser and a pyramidal magneto-optical trap. Optica (2017) 4:1545–51. doi:10.1364/optica.4.001545

CrossRef Full Text | Google Scholar

8. Yankelev D, Avinadav C, Davidson N, Firstenberg O. Multiport atom interferometry for inertial sensing. Phys Rev A (Coll Park) (2019) 100:023617. doi:10.1103/physreva.100.023617

CrossRef Full Text | Google Scholar

9. Garrido Alzar CL. Compact chip-scale guided cold atom gyrometers for inertial navigation: Enabling technologies and design study. AVS Quan Sci (2019) 1:014702. doi:10.1116/1.5120348

CrossRef Full Text | Google Scholar

10. Biedermann GW, Wu DXL, Roy S, Mahadeswaraswamy C, Kasevich MA. Testing gravity with cold-atom interferometers. Phys Rev A (Coll Park) (2015) 91:033629. doi:10.1103/physreva.91.033629

CrossRef Full Text | Google Scholar

11. Tino GM. Testing gravity with cold atom interferometry: Results and prospects. Quan Sci Technol (2021) 6:024014. doi:10.1088/2058-9565/abd83e

CrossRef Full Text | Google Scholar

12. Overstreet C, Asenbaum P, Kovachy T, Notermans R, Hogan JM, Kasevich MA. Effective inertial frame in an atom interferometric test of the equivalence principle. Phys Rev Lett (2018) 120:183604. doi:10.1103/physrevlett.120.183604

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Zhou L, Long S, Tang B, Chen X, Gao F, Peng W, et al. Test of equivalence principle at 10⁻⁸ level by a dual-species double-diffraction Raman atom interferometer. Phys Rev Lett (2015) 115:013004. doi:10.1103/physrevlett.115.013004

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Bonnin A, Zahzam N, Bidel Y, Bresson A. Characterization of a simultaneous dual-species atom interferometer for a quantum test of the weak equivalence principle. Phys Rev A (Coll Park) (2015) 92:023626. doi:10.1103/physreva.92.023626

CrossRef Full Text | Google Scholar

15. Barrett B, Antoni-Micollier L, Chichet L, Battelier B, Leveque T, Landragin A, et al. Dual matter-wave inertial sensors in weightlessness. Nat Commun (2016) 7:13786–9. doi:10.1038/ncomms13786

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Bidel Y, Zahzam N, Blanchard C, Bonnin A, Cadoret M, Bresson A, et al. Absolute marine gravimetry with matter-wave interferometry. Nat Commun (2018) 9:627–9. doi:10.1038/s41467-018-03040-2

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Bongs K, Holynski M, Vovrosh J, Bouyer P, Condon G, Rasel E, et al. Taking atom interferometric quantum sensors from the laboratory to real-world applications. Nat Rev Phys (2019) 1:731–9. doi:10.1038/s42254-019-0117-4

CrossRef Full Text | Google Scholar

18. Bidel Y, Zahzam N, Bresson A, Blanchard C, Cadoret M, Olesen AV, et al. Absolute airborne gravimetry with a cold atom sensor. J Geod (2020) 94:20–9. doi:10.1007/s00190-020-01350-2

CrossRef Full Text | Google Scholar

19. Stray B, Lamb A, Kaushik A, Vovrosh J, Rodgers A, Winch J, et al. Quantum sensing for gravity cartography. Nature (2022) 602:590–4. doi:10.1038/s41586-021-04315-3

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Titterton DH, Weston JL. Strapdown inertial navigation technology”. London: IEE (1997).

Google Scholar

21. Groves PD. Principles of GNSS, inertial, and multisensor integrated navigation systems. 2nd ed. London: Artech House (2013).

Google Scholar

22. Nebylov AV, Watson J. Aerospace navigation systems”. Hoboken: Wiley (2016).

Google Scholar

23. Feng D. Review of quantum navigation IOP conference series: Earth and environmental science. IOP Conf Ser : Earth Environ Sci (2019) 237:032027. doi:10.1088/1755-1315/237/3/032027

CrossRef Full Text | Google Scholar

24. Geiger R, Landragin A, Merlet S, Pereira Dos Santos F. High-accuracy inertial measurements with cold-atom sensors. AVS Quan Sci (2020) 2:024702. doi:10.1116/5.0009093

CrossRef Full Text | Google Scholar

25. Bonnin A, Diboune C, Zahzam N, Bidel Y, Cadoret M, Bresson A. New concepts of inertial measurements with multi-species atom interferometry. Appl Phys B (2018) 124:181–8. doi:10.1007/s00340-018-7051-5

CrossRef Full Text | Google Scholar

26. Lee J, Ding R, Christensen J, Rosenthal RR, Ison A, Gillund DP, et al. A cold-atom interferometer with microfabricated gratings and a single seed laser, arXiv [preprint] (2021). Available at: arXiv:2107.04792. (Accessed September 15, 2022).

Google Scholar

27. Berg P, Abend S, Tackmann G, Schubert C, Giese E, Schleich WP, et al. Composite-light-pulse technique for high-precision atom interferometry. Phys Rev Lett (2015) 114:063002. doi:10.1103/physrevlett.114.063002

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Jekeli C. Navigation error analysis of atom interferometer inertial sensor. Navigation (2005) 52:1–14. doi:10.1002/j.2161-4296.2005.tb01726.x

CrossRef Full Text | Google Scholar

29. Cheiney P, Fouche L, Templier S, Napolitano F, Battelier B, Bouyer P, et al. Navigation-compatible hybrid quantum accelerometer using a Kalman filter. Phys Rev Appl (2018) 10:034030. doi:10.1103/physrevapplied.10.034030

CrossRef Full Text | Google Scholar

30. Wang X, Kealy A, Gilliam C, Haine S, Close J, Moran B, et al. Enhancing inertial navigation performance via fusion of classical and Quantum accelerometers, arXiv [preprint] (2018). Available at: arXiv:2103.09378 (Accessed September 15, 2022).

Google Scholar

31. Ardalan AA, Grafarend EW. Somigliana–pizzetti gravity: the international gravity formula accurate to the sub-nanoGal level. J Geodesy (2001) 75:424–37. doi:10.1007/pl00004005

CrossRef Full Text | Google Scholar

32. Pavlis NK, Holmes SA, Kenyon SC, Factor JK. The development and evaluation of the Earth GravitationalModel 2008 (EGM2008). J Geophys Res (2012) 117:B04406. doi:10.1029/2011jb008916

CrossRef Full Text | Google Scholar

33. Merrigan MJ, Swift ER, Wong RF, Saffel JT. A refinement to the World Geodetic System 1984 reference frame. In: Proceedings of the 15th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GPS 2002) (2002). p. 1519–29.

Google Scholar

34. Hirt C, Yang M, Kuhn M, Bucha B, Kurzmann A, Pail R. SRTM2gravity: An ultrahigh resolution global model of gravimetric terrain corrections. Geophys Res Lett (2019) 46:4618–27. doi:10.1029/2019gl082521

CrossRef Full Text | Google Scholar

35. Savage PG. Strapdown inertial navigation integration algorithm design part 1: Attitude algorithms. J Guidance, Control Dyn (1998) 21:19–28. doi:10.2514/2.4228

CrossRef Full Text | Google Scholar

36. Savage PG. Strapdown inertial navigation integration algorithm design part 2: Velocity and position algorithms. J Guidance, Control Dyn (1998) 21:208–21. doi:10.2514/2.4242

CrossRef Full Text | Google Scholar

37. Groves PD, Handley RJ, Runnalls AR. Optimising the integration of terrain referenced navigation with INS and GPS. J Navig (2006) 59:71–89. doi:10.1017/s0373463305003462

CrossRef Full Text | Google Scholar

38. Moreira EM, Camargo OAM, Duarte JC, Rosa PFF. Scene matching in GPS denied environments: A comparison of methods for orthophoto registration. In: 2019 IEEE International Conference on Mechatronics (ICM), (2019). p. 205–10.

CrossRef Full Text | Google Scholar

39. Bijjahalli S, Sabatini R, Gardi A. Advances in intelligent and autonomous navigation systems for small UAS. Prog Aerospace Sci (2020) 115:100617. doi:10.1016/j.paerosci.2020.100617

CrossRef Full Text | Google Scholar

40. Tan Z, Qin H, Cong L, Zhao C. New method for positioning using IRIDIUM satellite signals of opportunity. IEEE Access (2019) 7:83412–23. doi:10.1109/access.2019.2924470

CrossRef Full Text | Google Scholar

41. Son P-Y, Rhee JH, Seo J. Novel multichain-based Loran positioning algorithm for resilient navigation. IEEE Trans Aerosp Electron Syst (2017) 54:666–79. doi:10.1109/taes.2017.2762438

CrossRef Full Text | Google Scholar

42. Kapoor R, Ramasamy A, Gardi A, Sabatini R. UAV navigation using signals of opportunity in urban environments: A review. Energ Proced (2017) 110:377–83. doi:10.1016/j.egypro.2017.03.156

CrossRef Full Text | Google Scholar

43. Schmidt D, Radke K, Camtepe S, Foo E, Ren M. A survey and analysis of the GNSS spoofing threat and countermeasures. ACM Comput Surv (2017) 48:1–31. doi:10.1145/2897166

CrossRef Full Text | Google Scholar

44. Gleason DM. Passive airborne navigation and terrain avoidance using gravity gradiometry. J Guidance Control Dyn (1995) 18:1450–8. doi:10.2514/3.21567

CrossRef Full Text | Google Scholar

45. Jekeli C. Precision free-inertial navigation with gravity compensation by an onboard gradiometer. J Guidance Control Dyn (2006) 29:704–13. doi:10.2514/1.15368

CrossRef Full Text | Google Scholar

46. Welker TC, Pachter M, Huffman RE. Gravity gradiometer integrated inertial navigation. In: Proceedings of 2013 European Control Conference (ECC); July 17-19, 2013; Zurich, Switzerland (2013).

CrossRef Full Text | Google Scholar

47. Wang H, Wu L, Chai H, Hsu H, Wang Y. Technology of gravity aided inertial navigation system and its trial in South China Sea. IET Radar Sonar & Navigation (2016) 10:862–9. doi:10.1049/iet-rsn.2014.0419

CrossRef Full Text | Google Scholar

48. Wang H, Wu L, Chai H, Xiao Y, Hsu H, Wang Y. Characteristics of marine gravity anomaly reference maps and accuracy analysis of gravity matching-aided navigation. Sensors (2017) 17:1851. Paper 1851. doi:10.3390/s17081851

PubMed Abstract | CrossRef Full Text | Google Scholar

49. Phillips AM, Wright MJ, Kiss-Toth M, Read I, Riou I, Maddox S, et al. Augmented inertial navigation using cold atom sensing. Cold Atoms Quan Tech (2020) 11578:115780C. International Society for Optics and Photonics.

CrossRef Full Text | Google Scholar

50. Phillips AM, Wright MJ, Riou I, Maddox S, Maskell S, Ralph JF. Position fixing with cold atom gravity gradiometers. AVS Quan Sci (2022) 4:024404. doi:10.1116/5.0095677

CrossRef Full Text | Google Scholar

51. Janvier C, Ménoret V, Merlet S, Landragin A, Dos Santos FP, Desruelle B, A compact differential gravimeter at the quantum projection noise limit. arXiv [preprint] (2022). Available at: arXiv:2201.03345. (Accessed September 15, 2022).

Google Scholar

52. Gauguet A, Canuel B, Lévèque T, Chaibi W, Landragin A. Characterization and limits of a cold-atom sagnac interferometer. Phys Rev A (Coll Park) (2009) 80:063604. doi:10.1103/physreva.80.063604

CrossRef Full Text | Google Scholar

53. Tackmann G, Berg P, Schubert C, Abend S, Gilowski M, ErtmerRasel EM, et al. Self-alignment of a compact large-area atomic Sagnac interferometer. New J Phys (2012) 14:015002. doi:10.1088/1367-2630/14/1/015002

CrossRef Full Text | Google Scholar

54. McGuirk JM, Foster GT, Fixler JB, Snadden MJ, Kasevich MA. Sensitive absolute-gravity gradiometry using atom interferometry. Phys Rev A (Coll Park) (2002) 65:033608. doi:10.1103/physreva.65.033608

CrossRef Full Text | Google Scholar

55. Sorrentino F, Bertoldi A, Bodart Q, Cacciapuoti L, De Angelis M, Lien Y-H, et al. Simultaneous measurement of gravity acceleration and gravity gradient with an atom interferometer. Appl Phys Lett (2012) 101:114106. doi:10.1063/1.4751112

CrossRef Full Text | Google Scholar

56. Peters A, Chung KY, Chu S. High-precision gravity measurements using atom interferometry. Metrologia (2001) 38:25–61. doi:10.1088/0026-1394/38/1/4

CrossRef Full Text | Google Scholar

57. Sorrentino F, Bodart Q, Cacciapuoti L, Lien Y-H, Prevedelli M, Rosi G, et al. Sensitivity limits of a Raman atom interferometer as a gravity gradiometer. Phys Rev A (Coll Park) (2014) 89:023607. doi:10.1103/physreva.89.023607

CrossRef Full Text | Google Scholar

58. Bertoldi A, Minardi F, Prevedelli M. Phase shift in atom interferometers: Corrections for nonquadratic potentials and finite-duration laser pulses. Phys Rev A (Coll Park) (2019) 99:033619. doi:10.1103/physreva.99.033619

CrossRef Full Text | Google Scholar

59. Muller H, Chiow SW, Long Q, Herrmann S, Chu S. Atom interferometry with up to 24-photon-momentum-transfer beam splitters. Phys Rev Lett (2008) 100:180405. doi:10.1103/physrevlett.100.180405

PubMed Abstract | CrossRef Full Text | Google Scholar

60. Cadoret M, Zahzam N, Bidel Y, Diboune C, Bonnin A, Théron F, et al. Phase shift formulation for N-light-pulse atom interferometers: Application to inertial sensing. J Opt Soc Am B (2016) 33:1777–88. doi:10.1364/josab.33.001777

CrossRef Full Text | Google Scholar

61. Wu S, Su E, Prentiss M. Demonstration of an area-enclosing guided-atom interferometer for rotation sensing. Phys Rev Lett (2007) 99:173201. doi:10.1103/physrevlett.99.173201

PubMed Abstract | CrossRef Full Text | Google Scholar

62. Moukouri S, Japha Y, Keil M, David T, Groswasser D, Givon M, et al. Multi-pass guided atomic Sagnac interferometer for high-performance rotation sensing, arXiv [preprint] (2021). Available at: arXiv:2107.03446 (Accessed September 15, 2022).

Google Scholar

63. Schubert C, Abend S, Gersemann M, Gebbe M, Schlippert D, Berg P, et al. Multi-loop atomic Sagnac interferometry. Sci Rep (2021) 11:16121–9. doi:10.1038/s41598-021-95334-7

PubMed Abstract | CrossRef Full Text | Google Scholar

64. Savoie D, Altorio M, Fang B, Sidorenkov LA, Geiger R, Landragin A. Interleaved atom interferometry for high-sensitivity inertial measurements. Sci Adv (2018) 4:eaau7948. doi:10.1126/sciadv.aau7948

PubMed Abstract | CrossRef Full Text | Google Scholar

65. Debs JE, Altin PA, Barter TH, Doering D, Dennis GR, McDonald G, et al. Cold-atom gravimetry with a Bose-Einstein condensate. Phys Rev A (Coll Park) (2011) 84:033610. doi:10.1103/physreva.84.033610

CrossRef Full Text | Google Scholar

66. Hensel T, Loriani S, Schubert C, Fitzek F, Abend S, Ahlers H, et al. Inertial sensing with quantum gases: A comparative performance study of condensed versus thermal sources for atom interferometry. Eur Phys J D (2021) 75:108–13. doi:10.1140/epjd/s10053-021-00069-9

CrossRef Full Text | Google Scholar

67. Scully MO, Dowling JP. Quantum-noise limits to matter-wave interferometry. Phys Rev A (Coll Park) (1993) 48:3186–90. doi:10.1103/physreva.48.3186

PubMed Abstract | CrossRef Full Text | Google Scholar

68. Dowling JP. Correlated input-port, matter-wave interferometer: Quantum-noise limits to the atom-laser gyroscope. Phys Rev A (Coll Park) (1998) 57:4736–46. doi:10.1103/physreva.57.4736

CrossRef Full Text | Google Scholar

69. Szigeti SS, Hosten O, Haine SA. Improving cold-atom sensors with quantum entanglement: Prospects and challenges. Appl Phys Lett (2021) 118:140501. doi:10.1063/5.0050235

CrossRef Full Text | Google Scholar

70. Handley RJ, Stokes RF, Stevenson J, Owen JIR. Hardware-in-the-loop testing of the NATO standardisation agreement 4572 interface using high precision navigation equations. In: 2008 IEEE/ION Position, Location and Navigation Symposium (2008). p. 441–8.

CrossRef Full Text | Google Scholar