- 1Department of Physics, Dalian University of Technology, Dalian, China
- 2Department of Physics, Shanxi Vocational University of Engineering and Technology, Jinzhong, China
- 3DUT-BSU Joint Institute, Dalian University of Technology, Dalian, China
- 4State Key Laboratory of Molecular Reaction Dynamics, Dalian Institute of Chemical Physics, Chinese Academy of Sciences, Dalian, China
- 5Physics Department, Belarusian State University, Minsk, Belarus
- 6Department of Information Engineering and Electrical and Applied Mathematics/DIEM, University of Salerno, Fisciano, Salerno, Italy
By solving the full-dimensional time-dependent Schrödinger equation with the thermal-random-phase wavepacket method, we investigate the photoassociation (PA) process of hot (1000 K) magnesium atoms induced by two time-delayed femtosecond laser pulses. Driven by the 840 nm fs laser pulses, the Mg2 molecules can be formed on the four excited states, (1)1Πg, (1)1Πu, (2)1Πu, and
1 Introduction
Through the interaction of the external laser fields with the colliding atoms, the molecular bond can be formed by absorbing or stimulated emitting one or several photons. This process is named as photoassociation (PA). PA has been studied extensively by using different laser pulses such as ultrashort laser pulses [1, 2], shaped laser pulses [3–5], pulse trains [6–8], etc. Shaped laser pulses are used in many PA experiments because of the advantages of the controlling of phase [9], amplitude [10, 11] and polarization [12]. Compared with ultrashort laser pulses with symmetric time profiles, the shaped laser pulses can enhance the PA transition efficiency in both the resonant and non-resonant spectral ranges [13, 14]. Zhang et al. employed a slowly-turned-on and rapidly-turned-off (STRT) laser pulse to achieve the PA process of the Cs2 system [13]. The calculations indicated that the shaped STRT laser pulse has an obvious advantage over the unshaped pulses. The train of laser pulses is also a powerful way to transfer populations between different electronic states. Yang et al. investigated the effect of a train of ultrashort pulses on multiphoton transitions theoretically [6]. They found that the population accumulations are dependent on the relative phase between two adjacent pulses. It was proved that even higher PA efficiency can be achieved by using a train of STRT pulses [15]. They found that the population accumulations are dependent on the relative phase between two adjacent pulses. It was proved that even higher PA efficiency can be achieved by using a train of STRT pulses [16].
Many methods have been used to control the PA dynamics. Luc-Koenig et al. investigated the yield of molecules by using the theoretical framework of a Gaussian wavepacket as the initial state [16, 17]. Koch et al. found that molecules can be transferred directly from high-lying bound states to the ground vibrational level by using shaped femtosecond laser pulses [18]. de Lima et al. used a combination of two transition pathways to form molecules of the electronic ground state [19]. The first pathway is to use pump-dump time-delayed laser pulses to transfer populations to the electronic ground state. The second pathway applies a single far-infrared pulse to obtain electronic ground state molecules from free atoms directly. The interference between the pathways can be controlled by modifying the laser parameters, and the yields of the target ground state molecules can be enhanced.
With the development of laser techniques, researchers can achieve PA through ultrashort laser pulses such as femtosecond pulses. Ultrashort laser pulses are used to pump the free atom pairs to bound molecular states because of the broad bandwidth [20]. In previous studies, Salzmann et al. verified the PA of ultracold rubidium dimers using coherent femtosecond pulses and produced electronic excited rubidium molecules [2]. Merli et al. investigated the PA of ultracold rubidium atoms with shaped femtosecond laser pulses [4]. Vardi et al. calculated the radiative recombination of cold Na atoms by short laser pulses [21]. It was demonstrated that resonantly enhanced two-photon recombination of ultracold atoms is an efficient way to produce ultracold molecules.
Instead of forming ultracold molecules, PA also serves as another role in laser control of chemical reaction, i.e., the formation of chemical bonds in thermal atom gas. The PA of thermal atoms using femtosecond laser pulses and shaped pulses can lead to coherent control of thermal molecules [22, 23]. de Lima et al. used the non-perturbative laser pulse to produce molecules in a thermal atomic gas [24]. Levin et al. verified the coherent control of photoreactions in thermal conditions in experiment [25]. Wang et al. investigated the coherent control of the rovibrational dynamics of HF molecules by two-color pulses [26]. The population distributions oscillate with a period of π when the relative phase between the fundamental and the second-harmonic laser pulses varies.
In previous studies, many efforts have been devoted into the investigations of the effect of laser parameters, such as duration, amplitude, carrier envelope phase, etc., on PA process. And these laser pulse parameters are controllable and can also be used to enhance the PA efficiency in the pump-dump scheme [27]. Zhang et al. investigated the PA dynamics of Cs atoms system driven by a picosecond pulse with cubic phase modulation [28]. In the investigation of two-photon PA of 87Rb atoms system, Kallush et al. found that a frequency-chirped pulse can enhance the molecular formation rate [29]. Zhang et al. used a modulated two-color laser field to steer the PA of ultracold Cs atoms in theory and control the PA dynamics through changing the phase of envelope and the period of the laser field [30]. Some researchers also used optimal control theory to obtain laser pulses in population transfer studies. For instances, the shaped laser pulses with minimum intensity proposed by the optimal control theory can transfer the highly excited Na2 molecules to the ground vibrational level with a high efficiency of .99 [18]; and Ndong et al. used optimal control theory to drive the vibrational transfer from the dissociation limit to the vibrational ground state in the KRb system [31].
Compared to the single laser pulse, time-delayed pulses can introduce more various combination modes and be used in different ways in population transfer. There were reports on the formation of cold molecules by the PA process with consideration of the time delay of two laser pulses (see, e.g., Refs. [19, 24]). The dissociation process of the HD+ molecule driven by two overlapping THz and infrared laser pulses was reported recently [32]. The effect of 2 picosecond pulses on the adiabatic population transfer of the LiH molecule was also reported [33]. However, there is few report on the influence of the pulses’ delay time on the PA process in thermally hot atomic gas, except in Ref. [34].
Thus, we are motivated to investigate the influence of two time-delayed laser pulses on the PA process in thermally hot atomic gas. In this paper, the hot Mg atoms at 1000 K are taken as a model system, because it is a prototypical system for the study of PA processes in thermally hot atoms (see, e.g., Refs. [25, 34–36]). In thermal conditions, Mg2 molecules can be produced through the multiphoton PA process by using chirped femtosecond laser pulses [25]. Hu et al. proposed a full-dimensional thermal-random-phase wavefunction method to simulate the thermal PA process including rovibrational couplings [35]. By using this method, the detailed population transfer dynamics has been revealed by employing the five-electronic-state model [36]. Here, we use the same five-electronic-state model as the one used in Ref. [36], yet we consider the interaction of two time-delayed femtosecond laser pulses with the system instead. At different delay times and pulse durations, we simulate the final populations of the four excited states and investigate the feasibility of control the thermal PA process by manipulating the combination of two pulses.
This paper is organized as follows: In Section 2, we briefly introduce the theory. In Section 3, we discuss the effect of the delay time and pulse duration on the population transfer of PA process of Mg atoms at 1000 K. In Section 4, the conclusions are summarized.
2 Theoretical approach
The initial thermal ensemble of the numerous rovibrational eigenfunctions |n, j⟩ of the
where R is the internuclear distance and θ is the angle between the molecular axis and the z-axis of the space fix frame which is taken to be the polarization direction of the linear polarized laser pulses.
The laser field used in this work consists of 2 femtosecond Gaussian pulses with the same wavelength of 840 nm and with a specific delay time between each other. The total electric field of the two laser pulses can be expressed as,
where t01 and t02 represent the central time of the two Gaussian pulses. We define δt0 = t02 − t01 as the delay time. E0 = 5 × 1012 W/cm2 is the peak amplitude of the two Gaussian pulses.
In this paper, we focus on the influences of the delay time δt0 and the FWHM τ on the PA process. To compare the results with the variation of δt0, we set τ = 100 fs to be the time unit to present δt0. The envelope functions of the two pulses are shown in Figure 1A and the two pulses gradually separate from each other with the increase of δt0 from 0 to 2τ. Figure 1B presents the sum of the envelopes of the two Gaussian pulses, i.e., the total envelope function ftot(t), for different δt0.
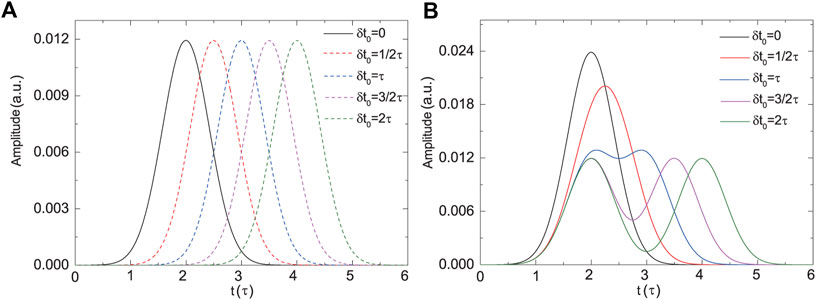
FIGURE 1. (A) The envelope functions of the two laser pulses at five different delay times, δt0 = 0, 1/2τ, τ, 3/2τ and 2τ, respectively. The solid and dashed curves denote f1(t) and f2(t), respectively. (B) The total envelope function of the two laser pulses according to the five different delay times. Here, τ = 100 fs.
The Hamiltonian that governs the propagation of the thermal-random-phase wavefunction is expressed as
where
The five-state time-dependent Schrödinger equation of the Mg2 system is shown as
where
We solve Eq. (4) by using the split-operator propagation method [39, 40]. At the critical time t = tf when the action of the laser pulses is over, the final population on the |ξ⟩ state is calculated by statistically averaging over the expectation values of all thermal-random-phase wavefunctions,
Note that Eq. (5) is the integral over R and θ, and we can also obtain the population distribution along R at any given time t, i.e., the propagation of the radial wavepacket, by performing integral only over θ,
3 Results and discussions
The initial temperature of the colliding Mg atoms system is set to be 1000 K. The potential energy curves of the five relevant electronic states of the Mg2 system are shown in Figure 2A. The relevant molecular datas, including the potentials, diabatic couplings, electric dipole moments, dynamic electronic polarizabilities, etc., are taken from Refs. [35, 37]. 1,024 and 250 grid points are used to express the radial range from 3 to 40 Bohr and the angular range from 0 to π, respectively. The time step is set to be .4 fs for the propagation of the wavepacket. These numerical parameters are kept the same as those used in Ref. [36] which have been checked to be able to provide the converged results.
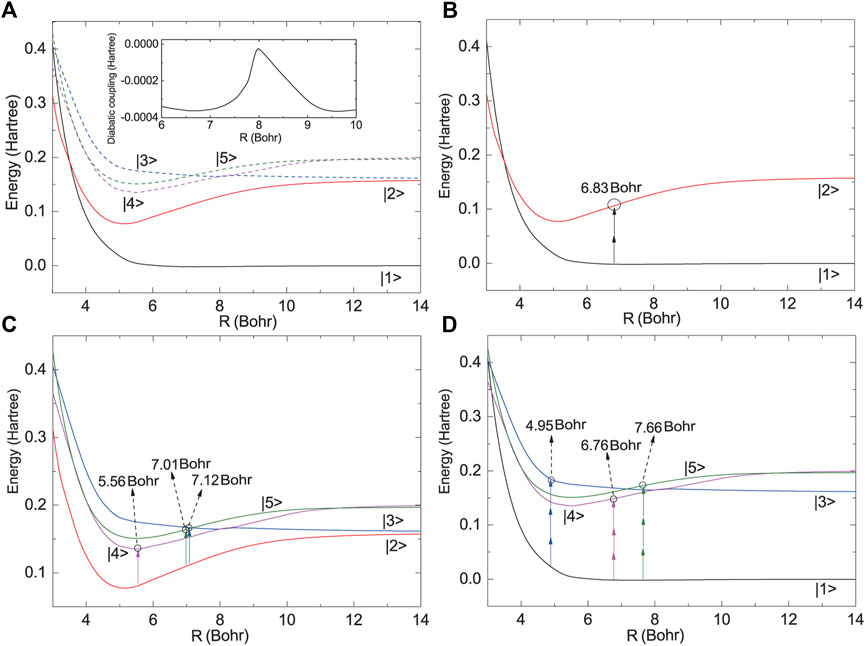
FIGURE 2. (A) The potential energy curves of the five-state-model of the Mg2 system. The diabatic coupling between the |3⟩ and |4⟩ states is shown in the inset. (B) The two-photon coupling between the states |1⟩ and |2⟩. (C) The one-photon couplings between the states |2⟩ and |u⟩. (D) The three-photon couplings between the states |1⟩ and |u⟩. Here, u = 3, 4, 5.
Driven by the 840 nm laser field, these electronic states can interact with each other via one-, two- or three-photon couplings. The two-photon transition, which have been considered extensively in the PA process of the titled system (see, e.g., Refs. [25, 34–37]), can occur between the two gerade states, |1⟩ and |2⟩. As shown in Figure 2B, the energy difference between the two potentials at R = 6.83 Bohr exactly equals to the energy of two photons. The other higher excited states, are all ungerade states and energetically close with each other. Thus, we use |u⟩ to denote the states |3⟩, |4⟩ and |5⟩ states, for simplicity. Via the one-photon interaction, the gerade |2⟩ state can couple with the ungerade |u⟩ state. Due to the different shapes of the potential energy curves, the critical internuclear distance for one-photon resonance between the two potentials of |2⟩ and |u⟩ varies with u. As shown in Figure 2C, for |2⟩ and |4⟩, the one-photon resonance may probably occur at R = 5.56 Bohr, while for |2⟩ and |3⟩ (or |5⟩), the one-photon resonance may probably occur in the vicinity of R ∼ 7 Bohr. Recent theoretical calculations demonstrated that the three-photon transition from |1⟩ to |u⟩ may also play an important role in the PA process [35, 36]. In Figure 2D, we illustrate those critical internuclear separations at which the potential energy gaps between |1⟩ to |u⟩ equal to three-photon energy, which also present variance.
The above different kinds of coupling interactions can construct several transition pathways for PA. As demonstrated in Ref. [36], with the action of the 840 nm fs laser pulse, the direct two-photon transition from |1⟩ to |2⟩ is much weaker than the three-photon transition from |1⟩ to |u⟩, because the three-photon transition between the gerade and ungerade states is electric dipole allowed, while the two-photon transition between the two gerade states is electric dipole forbidden. Thus, the major population transfer path is considered to be
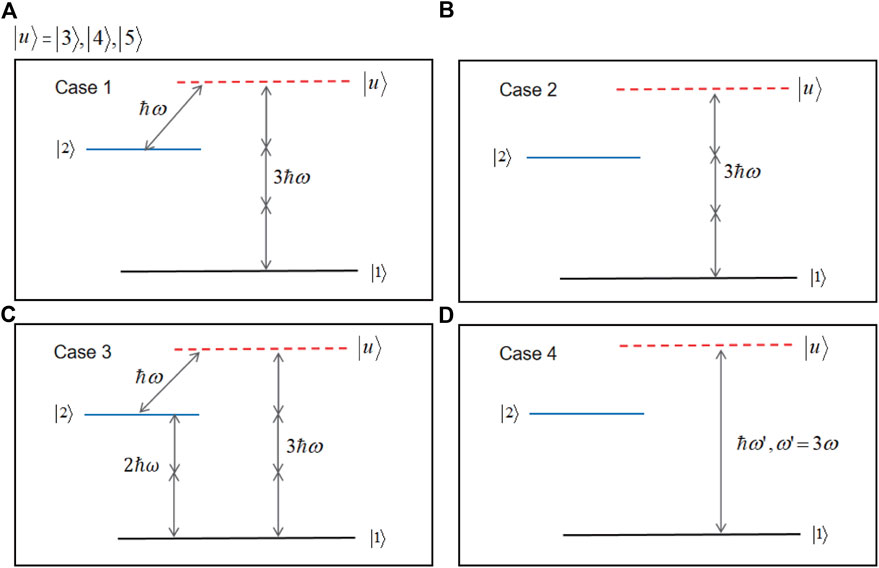
FIGURE 3. The four cases with the consideration of different coupling conditions. (A) Case 1: The one-photon coupling between |2⟩ and |u⟩ and the three-photon coupling between |1⟩ and |u⟩ are considered. (B) Case 2: Only the three-photon coupling between |1⟩ and |u⟩ is considered. (C) Case 3: All the one-, two- and three-photon couplings are taken into account. In Cases 1–3, the laser wavelength is 840 nm. (D) Case 4: The one-photon coupling between |1⟩ and |u⟩ is considered with the wavelength setting to be 280 nm.
In this paper, we mainly investigate the effect of the delay time δt0 and the FWHM τ of the laser pulses on the populations of the four excited states. Thus, we divide our discussion into different cases: Case 1, corresponds to the major population transfer path, as shown in Figure 3A where the two-photon transition is neglected, and W12 in Eq. 3 is set to be zero in the propagating; Case 2, only the three-photon transition between |1⟩ and |u⟩ is considered, and W12, W23, W24 and W25 in Eq. 3 are all set to be zero; Case 3, all the possible couplings have been taken into account, and the propagating is performed with the full Hamiltonian as presented in Eq. 3; Case 4 denotes the transition from |1⟩ to |u⟩ via one-photon resonant coupling with the central frequency corresponding to 280 nm wavelength instead, and the Hamiltonian is formally the same as the one used for Case 2 except that the central frequency for W13, W14 and W15 is changed accordingly. By comparing the calculation results of Cases 1 and 3, we can further confirm the major pathway for the PA process induced by the two time-delayed laser pulses. By comparing Cases 1 and 2, we can identify the enhancement of the one-photon coupling between |2⟩ and |u⟩ on the three-photon transition process. And by comparing Cases 1 and 4, we can demonstrate that the three-photon resonant transition and one-photon resonant transition depend on different laser-molecule interaction mechanism and that they behave differently with the laser parameters.
We first fix the FWHM of the two laser pulses to be τ = 100 fs and the delay time δt0 = 0 fs. Considering the major population transfer path, driven by the 840 nm laser pulses, i.e. Case 1, the formations and propagations of the radial wavepackets of the four excited states are shown in Figure 4. We can see that after the action of the laser pulses, the radial wavepackets oscillate periodically on the states |2⟩, |4⟩ and |5⟩, respectively. This indicates that several certain vibrational levels have been populated on these specific electronic states. The oscillation period of the radial wavepacket of |2⟩ is about 130 fs, which corresponds to a vibrational frequency of roughly 256 cm−1 which is quite comparable with the vibrational signal reported in experiment [34]. The radial wavepacket on |3⟩ actually contains both the vibrational-bound and the continuous states.
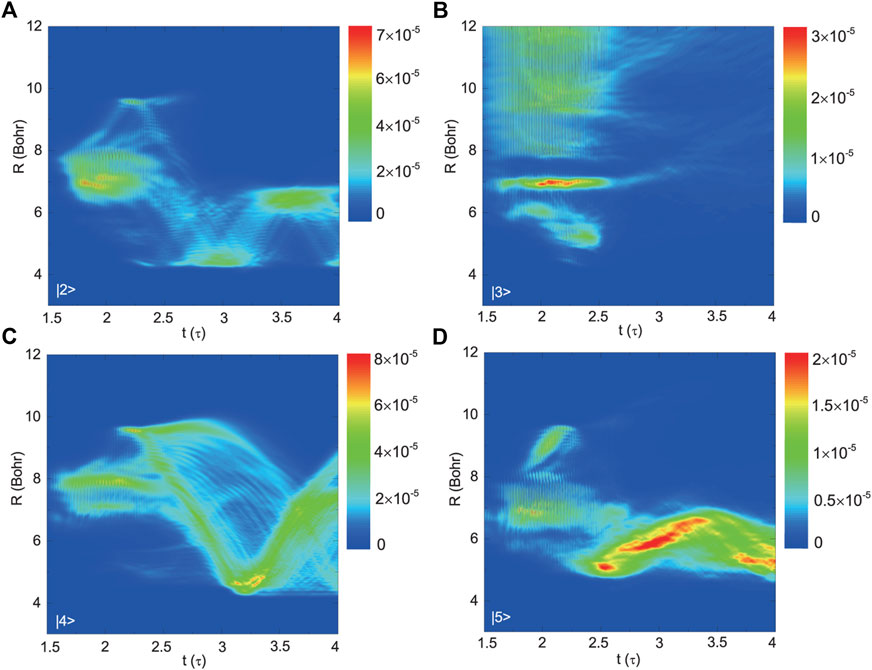
FIGURE 4. The propagations of the radial wavepackets for the four excited states, (A) |2⟩, (B) |3⟩, (C) |4⟩, and (D) |5⟩, in Case 1 with τ = 100 fs and δt0 = 0.
In Case 1, the one- and three-photon couplings are taken into account. Here, we correlate the R position at which the radial wavepacket is initially formed, with the one at which two different electronic states resonate with each other. Since the three-photon coupling between |u⟩ and |1⟩ plays a major role in the population transfer process [36], we first concern about the wavepackets formed on the three ungerade excited states. In Figure 4B, during the action of the laser pulses (mainly from t = 150 to 250 fs), the radial wavepacket on the |3⟩ is partly formed in the vicinity of R ∼ 5 Bohr, which is right around the resonant position between the potentials of |3⟩ and |1⟩ marked in Figure 2D. The other parts of the radial wavepacket on the |3⟩ are formed around R ∼ 6, 7 Bohr and in the large R region of over 8 Bohr. This can be ascribed to the diabatic coupling between the |3⟩ and |4⟩ states. As shown in the inset plot in Figure 2A, the diabatic coupling can influence the wavefunctions of the |3⟩ and |4⟩ in the range from roughly 6 to 10 Bohr. Thus, although |3⟩ and |1⟩ are not quite resonant with each other in this R region, once |4⟩ and |1⟩ are resonant or near resonant, then the |3⟩ state can be populated via diabatic coupling with the |4⟩ state. As shown in Figure 4C, the corresponding radial wavepacket on the |4⟩ state is initially in the R region from 6.5 to 8.5 Bohr which is in accordance with the above mentioned diabatic coupling region. Additionally, the resonance between the |4⟩ and |1⟩ states mainly occurs around 6.76 Bohr as shown in Figure 2D, which also falls in the diabatic coupling region between |4⟩ and |3⟩. Therefore, one can expect that the population is firstly transferred from |1⟩ to |4⟩ around 6.76 Bohr due to the three-photon resonance, and then redistributed between |4⟩ and |3⟩ in an even larger R region from 6 to 10 Bohr due to the diabatic coupling. Similarly, the radial wavepacket on |5⟩ is initially formed around 7 Bohr at t = 200 fs when the peak of the laser pulse occurs, as shown in Figure 4D. This is consistent with the three-photon resonant position between |5⟩ and |1⟩ shown in Figure 2D.
The one-photon coupling between |2⟩ and |u⟩ can additionally enhance the population transfer process from |1⟩ to |u⟩. As shown in Figure 2C, in the vicinity of 7 Bohr, the one-photon coupling between |2⟩ and |5⟩ (|3⟩) is strong. Thus, we can expect the three-photon transition from |1⟩ to |5⟩ (|3⟩) may be enhanced around R ∼ 7 Bohr. This can be verified from Figures 4B,D: When t varies from 200 to 250 fs, the distributions of the wavepackets on the |5⟩ and |3⟩ states have been enhanced around 7 Bohr. The similar circumstance occurs for the |4⟩ state. As seen in Figure 4C, when t varies from 200 to 250 fs, there is an enhancement of the wavepacket around 5 Bohr which is consistent with the resonant position, R ∼ 5.56 Bohr, between |4⟩ and |2⟩ shown in Figure 2C. The wavepacket on the |2⟩ completely results from the one-photon coupling between |2⟩ and |u⟩, and consequently, it can be found to be initially localized around R ∼ 5 and R ∼ 7 Bohr, as shown in Figure 4A.
Here, the two laser pulses are set to coincide with each other in time, and we further discuss the influence of the delay time between the two pulses, δt0, on the population transfer process. The thermally averaged final populations of the four excited states vary with δt0 for different cases are shown in Figure 5, where τ is still fixed at 100 fs.
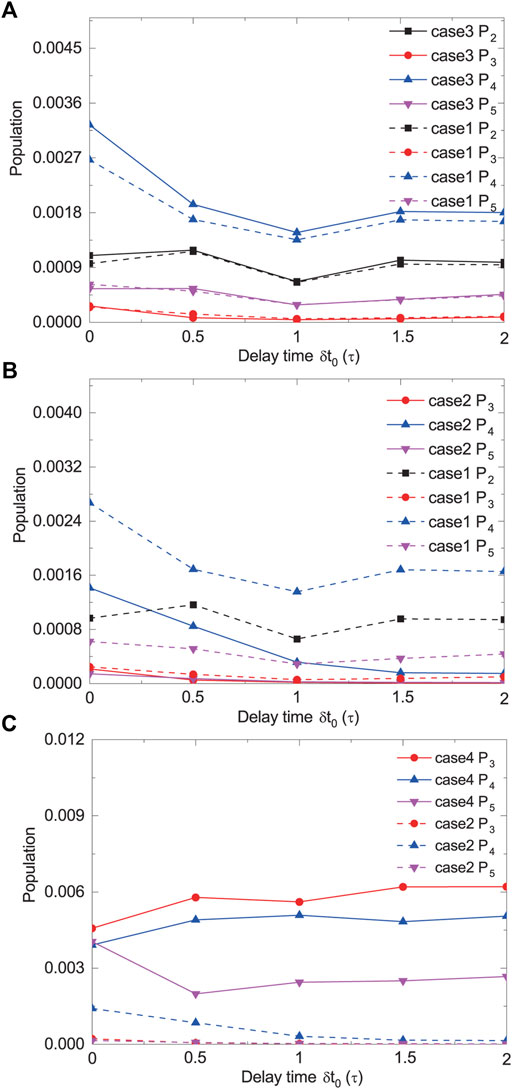
FIGURE 5. The comparisons of the final populations of the four excited states vary with δt0 between (A) Case 1 and Case 3, (B) Case 1 and Case 2, (C) Case 2 and Case 4. Here, τ = 100 fs.
One aspect shown in Figure 5 is that the population transfer process is dominated by the three-photon resonant transition from |1⟩ to |u⟩ which can be enhanced by the one-photon resonant coupling between |2⟩ and |u⟩. Specifically, in Figure 5A, we compare the final populations of the four excited states in Case 1 (dashed line) with those in Case 3 (solid line). It can be found that the population variations with δt0 in the two cases are almost the same. This illustrates that the two-photon coupling between |1⟩ and |2⟩ has little influence on the population transfer process, because Case 3 additionally includes the effect of two-photon coupling compared to Case 1. Figure 5B is then the comparison of the final populations of the four excited states between Case 1 (dashed line) and Case 2 (solid line). We can see that the final populations of the states |2⟩, |4⟩ and |5⟩ in Case 1 are higher than those in Case 2, while that of the state |3⟩ is not changed obviously from Case 1 to Case 2. This further indicates that the one-photon coupling between |u⟩ and |2⟩ can enhance three-photon transition from |1⟩ to |u⟩. These findings are consistent with the report in Ref. [36] based on the simulation of a single laser pulse action, and here we further extend it in the two time-delayed laser pulses condition.
The other aspect shown in Figure 5 is that the final populations of the four excited states can vary with δt0 to different extent. In Figure 5B, in Case 2 where only the three-photon coupling between |1⟩ and |u⟩ is taken into account, P3, P4, and P5 all decrease with the increase of δt0 from 0 to 100 fs? However, the absolute value of P5 is relatively small, which has been enhanced significantly by the one-photon coupling between |2⟩ and |5⟩. Therefore, the variation of P5 with δt0 in Case 1, as the dashed pink line shown in Figure 5B, can not duplicate its behavior in Case 2. To understand why the three-photon resonant transition probability decreases with the increase of δt0, we compare the final populations of the four excited states in Case 2 (dashed lines) with those in Case 4 (solid lines) in Figure 5C. Here, we find that in the |1⟩ → |u⟩ process, the resonance excitation of one-photon coupling is much higher than that of three-photon coupling. Moreover, the variation behavior of final population on a given state with δt0 in Case 2 is totally different from the one in Case 4. This is because the one-photon resonance excitation mainly depends on the pulse shape and area of the laser field, while the multiple-photon resonance excitation more greatly relies on the peak intensity of the laser field [41, 42]. As shown in Figure 1B, the shape and area of the total pulse envelope vary with δt0 which leads to the variations of P3, P4, and P5 in Case 4; while the peak intensity of the laser field first decreases dramatically from δt0 = 0 to 100 fs and then keeps almost unchanged from δt0 = 100 to 200 fs, which is consistent with the variation behaviors of P3, P4, and P5 in Case 2. Thus, the delay time between the pulses can be used as a good parameter for steering of the photoassociation process in the time area when the two pulses overlap with each other.
The FWHM of the laser pulse is another important laser parameter for steering molecular dynamics. To investigate its influence on the PA process, we first fix δt0 = 0 and decrease FWHM τ from 100 to 50 fs. The propagation dynamics of the wavepackets on the four excited states in Case 1 are shown in Figure 6. Obviously, the wavepacket dynamics and its corresponding excitation probability vary from those in Figure 4. The pulse with short duration can form wavepackets with more concentrative localization and the vibrational periods also vary a little. For instance, the period for |2⟩ decreases to roughly 100 fs which corresponds to an increase of the vibrational energy difference and suggests that some lower vibrational levels be populated. This can be ascribed to the relatively broader frequency domain of the τ = 50 fs pulse. Additionally, for the same peak intensity, the area of the τ = 50 fs pulse is smaller than that of the τ = 100 fs pulse. Thus, the final transition probability may also be influenced.
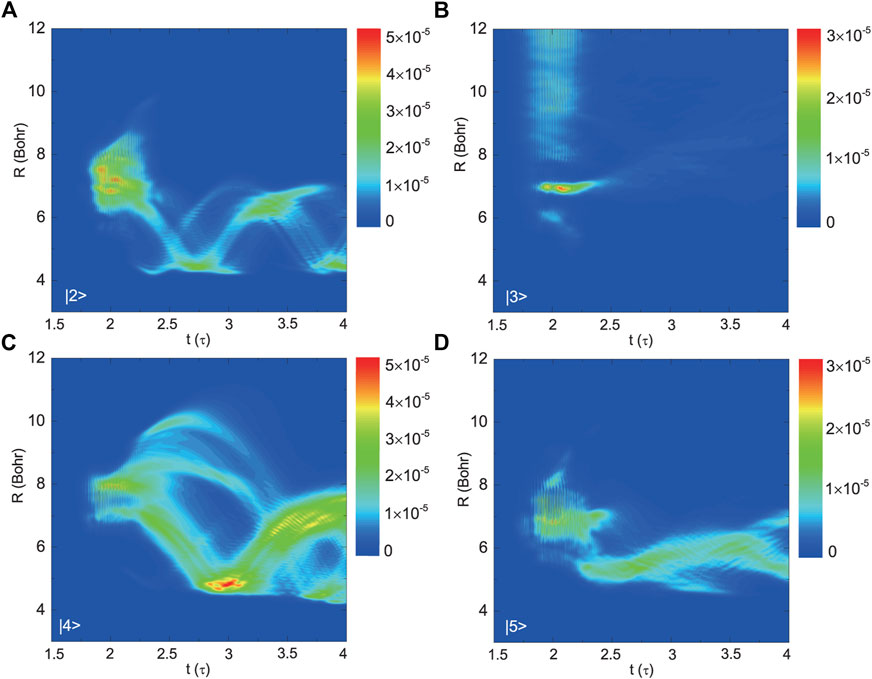
FIGURE 6. The propagations of the radial wavepackets for the four excited states, (A) |2⟩, (B) |3⟩, (C) |4⟩, and (D) |5⟩, in Case 1 with τ = 50 fs and δt0 = 0.
To further indicate the influence of τ and δt0 on the PA efficiency, we calculate the total population of the four excited states as a function of the delay time for different FWHMs, with consideration of Case 3 including all one-, two-, and three-photon couplings. As shown in Figure 7, the four lines related to different τ present the similar behavior with the variation of the delay time. The total population first exhibits a relatively maximal value at δt0 = 0, then decreases with the increase of the delay time from δt0 = 0 to δt0 = τ, and finally tends to be steady when the delay time further increases from δt0 = τ to δt0 = 2τ. This can be ascribed to the fact that the three-photon transition plays a dominant role in the PA process. And the three-photon transition heavily depends on the peak amplitude of the laser field. As shown in Figure 1, at δt0 = 0, the peak amplitude of the laser field is the strongest, and it decreases with the increase of δt0 and is unchanged when the two pulses separate from each other. Thus, it is good for us to use τ as the unit to define the delay time δt0.
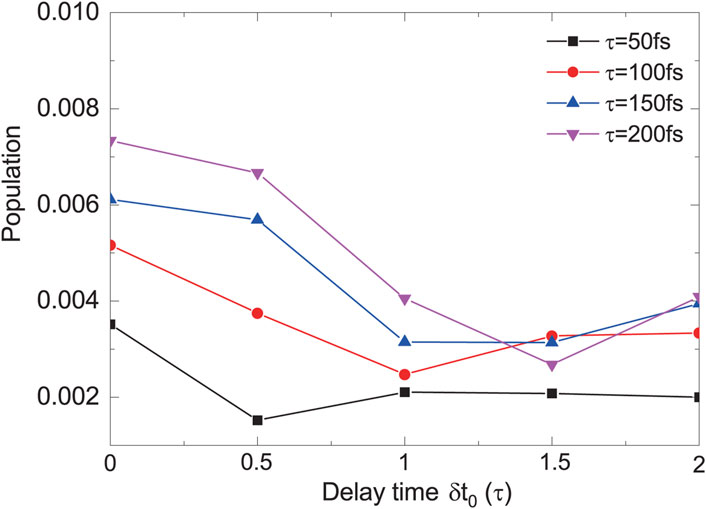
FIGURE 7. The total population of |2⟩, |3⟩, |4⟩ and |5⟩ as a function of the delay time in Case 3 for τ = 50, 100, 150, and 200 fs.
In Figure 7, it can be seen that the two parameters, τ and δt0 both strongly influence the final PA populations. We note that at δt0 = 0, the population for τ = 200 fs can reach .0073, while the one for τ = 50 fs decreases to roughly .0035. The former value is roughly 2 times larger than the latter one. At δt0 = 0.5τ, the total population for τ = 200 fs is roughly .0068, while the one for τ = 50 fs decreases to roughly .001. The former is about 6.8 times bigger than the latter. At δt0 = τ, the total population for τ = 200 fs is roughly .0041, while the one for τ = 50 fs decreases to roughly .002. At this point, the former is roughly 2 times greater than the latter. Thus, for a given δt0, the parameter τ can induce a significant variation (2 ∼ 6.8 times) for the population transfer of the PA process. Similarly, we can consider the influence of δt0 on the total final population for a given τ. For τ = 200 fs, we can obtain the minimal total population of roughly .0027 at δt0 = 1.5τ, compared to the maximal one (roughly .0073) at δt0 = 0. If we consider τ = 50 fs instead, the minimal value is roughly .001 at δt0 = 0.5τ, compared to the maximal one (roughly .0035) at δt0 = 0. Thus, it is also a significant variation (2.7 ∼ 3.5 times) which can be induced by δt0.
4 Conclusion
We have investigated theoretically the PA dynamics of hot Mg atoms induced by two time-delayed femtosecond laser pulses. In the typical five-electronic-state model, the molecules can be formed on the gerade excited state (1)1Πg and the three ungerade higher excited states (1)1Πu, (2)1Πu, and
Data availability statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding authors.
Author contributions
RZ performed research, analyzed data and wrote the paper; J-WH analyzed data and wrote the paper; Y-CH designed the research and wrote the paper; BF wrote the paper; MS wrote the paper.
Funding
The project is supported by the National Key R&D Program of China No. 2018YFA0306503; the National Natural Science Foundation of China under Grant Nos. 21873016, 12174044; International Cooperation Fund Project of DBJI No. ICR2105; the Fundamental Research Funds for the Central Universities (DUT21LK08).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Londono BE, Derevianko A, Mahecha JE, Crubellier A, Luc-Koenig E. Femtosecond pulses and dynamics of molecular photoexcitation: RbCs example. Phys Rev A (2012) 85:033419. doi:10.1103/PhysRevA.85.033419
2. Salzmann W, Mullins T, Eng J, Albert M, Wester R, Weidemüller M, et al. Coherent transients in the femtosecond photoassociation of ultracold molecules. Phys Rev Lett (2008) 100:233003. doi:10.1103/PhysRevLett.100.233003
3. Mullins T, Salzmann W, Götz S, Albert M, Eng J, Wester R, et al. Photoassociation and coherent transient dynamics in the interaction of ultracold rubidium atoms with shaped femtosecond pulses. I. Experiment. Phys Rev A (2009) 80:063416. doi:10.1103/PhysRevA.80.063416
4. Merli A, Eimer F, Weise F, Lindinger A, Salzmann W, Mullins T, et al. Photoassociation and coherent transient dynamics in the interaction of ultracold rubidium atoms with shaped femtosecond pulses. II. Theory. Phys Rev A (2009) 80:063417. doi:10.1103/PhysRevA.80.063417
5. Salzmann W, Poschinger U, Wester R, Weidemüller M, Merli A, Weber SM, et al. Coherent control with shaped femtosecond laser pulses applied to ultracold molecules. Phys Rev A (2006) 73:023414. doi:10.1103/PhysRevA.73.023414
6. Yang WF, Gong SQ, Li RX, Xu ZZ. Coherent population accumulations of multiphoton transitions induced by an ultrashort pulse train in polar molecules. Phys Rev A (2006) 74:013407. doi:10.1103/PhysRevA.74.013407
7. Yang J, Chen MD, Shu CC, Hu WH, Cong SL. Rovibrational manipulation of molecular quantum state by a train of ultrashort pulses. Chem Phys Lett (2010) 491:156–9. doi:10.1016/j.cplett.2010.04.019
8. Ban T, Aumiler D, Vdović S, Vujičić N, Skenderović H, Pichler G. Coherent population dynamics in rubidium atoms excited by resonant 0π pulses. Phys Rev A (2009) 80:023425. doi:10.1103/PhysRevA.80.023425
9. Weiner AM, Leaird DE, Patel JS, Wullert JR. Programmable femtosecond pulse shaping by use of a multielement liquid-crystal phase modulator. Opt Lett (1990) 15:326. doi:10.1364/OL.15.000326
10. Wefers MM, Nelson KA. Programmable phase and amplitude femtosecond pulse shaping. Opt Lett (1993) 18:2032. doi:10.1364/OL.18.002032
11. Wefers MM, Nelson KA. Generation of high-fidelity programmable ultrafast optical waveforms. Opt Lett (1995) 20:1047. doi:10.1364/OL.20.001047
12. Brixner T, krampert G, Niklaus P, Gerber G. Generation and characterization of polarization-shaped femtosecond laser pulses. Appl Phys B (2002) 74:s133–44. doi:10.1007/s00340-002-0911-y
13. Zhang W, Huang Y, Xie T, Wang GR, Cong SL. Efficient photoassociation with a slowly-turned-on and rapidly-turned-off laser field. Phys Rev A (2010) 82:063411. doi:10.1103/PhysRevA.82.063411
14. Han YC, Hu JW, Wang BB. Thermal-average effects on photoassociation with a slowly-turned-on and rapidly-turned-off laser pulse. Phys Rev A (2018) 98:043420. doi:10.1103/PhysRevA.98.043420
15. Zhang W, Wang GR, Cong SL. Efficient photoassociation with a train of asymmetric laser pulses. Phys Rev A (2011) 83:045401. doi:10.1103/PhysRevA.83.045401
16. Luc-Koenig E, Kosloff R, Masnou-Seeuws F, Vatasescu M. Photoassociation of cold atoms with chirped laser pulses: Time-dependent calculations and analysis of the adiabatic transfer within a two-state model. Phys Rev A (2004) 70:033414. doi:10.1103/PhysRevA.70.033414
17. Luc-Koenig E, Vatasescu M, Masnou-Seeuws F. Optimizing the photoassociation of cold atoms by use of chirped laser pulses. Eur Phys J D (2004) 31:239–62. doi:10.1140/epjd/e2004-00161-8
18. Koch CP, Palao JP, Kosloff R, Masnou-Seeuws F. Stabilization of ultracold molecules using optimal control theory. Phys Rev A (2004) 70:013402. doi:10.1103/PhysRevA.70.013402
19. Lima EF. Coherent control of the formation of cold heteronuclear molecules by photoassociation. Phys Rev A (2017) 95:013411. doi:10.1103/PhysRevA.95.013411
20. Ulmanis J, Deiglmayr J, Repp M, Wester R, Weidemüller M. Ultracold molecules formed by photoassociation: Heteronuclear dimers, inelastic collisions, and interactions with ultrashort laser pulses. Chem Rev (2012) 112:4890–927. doi:10.1021/cr300215h
21. Vardi A, Abrashkevich D, Frishman E, Shapiro M. Theory of radiative recombination with strong laser pulses and the formation of ultracold molecules via stimulated photo-recombination of cold atoms. J Chem Phys (1997) 107:6166–74. doi:10.1063/1.474282
22. Tannor DJ, Rice SA. Control of selectivity of chemical reaction via control of wave packet evolution. J Chem Phys (1985) 83:5013–8. doi:10.1063/1.449767
23. Tannor DJ, Kosloff R, Rice SA. Coherent pulse sequence induced control of selectivity of reactions: Exact quantum mechanical calculations. J Chem Phys (1986) 85:5805–20. doi:10.1063/1.451542
24. Lima EF, Ho TS, Rabitz H. Laser-pulse photoassociation in a thermal gas of atoms. Phys Rev A (2008) 78:063417. doi:10.1103/PhysRevA.78.063417
25. Levin L, Skomorowski W, Rybak L, Kosloff R, Koch CP, Amitay Z. Coherent control of bond making. Phys Rev Lett (2015) 114:233003. doi:10.1103/PhysRevLett.114.233003
26. Wang R, Niu YY, Qiu MH, Han YC. Rovibrational population transfer in the ground state controlled by two coherent laser pulses. Phys Rev A (2015) 91:013401. doi:10.1103/PhysRevA.91.013401
27. Dulieu O, Raoult M, Tiemann E. Cold molecules: A chemistry kitchen for physicists. J Phys B: Mol Opt Phys (2006) 39:E01. doi:10.1088/0953-4075/39/19/E01
28. Zhang W, Xie T, Huang Y, Cong SL. Enhancing photoassociation efficiency by using a picosecond laser pulse with cubic-phase modulation. Phys Rev A (2011) 84:065406. doi:10.1103/PhysRevA.84.065406
29. Kallush S, Carini JL, Gould PL, Kosloff R. Directional quantum-controlled chemistry: Generating aligned ultracold molecules via photoassociation. Phys Rev A (2017) 96:053613. doi:10.1103/PhysRevA.96.053613
30. Zhang W, Zhao ZY, Xie T, Wang GR, Huang Y, Cong SL. Photoassociation dynamics driven by a modulated two-color laser field. Phys Rev A (2011) 84:053418. doi:10.1103/PhysRevA.84.053418
31. Ndong M, Koch CP. Vibrational stabilization of ultracold KRb molecules: A comparative study. Phys Rev A (2010) 82:043437. doi:10.1103/PhysRevA.82.043437
32. Wang R, Niu YY. Control of photodissociation of the molecular ion HD+ with two completely overlapping laser pulses. Phys Lett A (2021) 409:127515. doi:10.1016/j.physleta.2021.127515
33. Niu YY, Wang R. Adiabatic population transfer between electronic states of LiH molecule in two picosecond laser pulses. AIP ADVANCES (2018) 8:115003. doi:10.1063/1.5052465
34. Rybak L, Amaran S, Levin L, Tomza M, Moszynski R, Kosloff R, et al. Generating molecular rovibrational coherence by two-photon femtosecond photoassociation of thermally hot atoms. Phys Rev Lett (2011) 107:273001. doi:10.1103/PhysRevLett.107.273001
35. Hu JW, Han YC. Investigation of photoassociation with full-dimensional thermal-random-phase wavefunctions. J Chem Phys (2021) 155:064108. doi:10.1063/5.0059543
36. Hu JW, Yu J, Han YC. Multi-path effect in population transfer dynamics of the photoassociation of hot Mg atoms by a femtosecond laser pulse. Chem Phys Lett (2022) 792:139405. doi:10.1016/j.cplett.2022.139405
37. Amaran S, Kosloff R, Tomza M, Skomorowski W, Pawlowski F, Moszynski R, et al. Femtosecond two-photon photoassociation of hot magnesium atoms: A quantum dynamical study using thermal random phase wavefunctions. J Chem Phys (2013) 139:164124. doi:10.1063/1.4826350
38. Marston CC, Balint-Kurti GG. The Fourier grid Hamiltonian method for bound state eigenvalues and eigenfunctions. J Chem Phys (1989) 91:3571–6. doi:10.1063/1.456888
39. Feit MD, Fleck JA. Solution of the Schrödinger equation by a spectral method II: Vibrational energy levels of triatomic molecules. J Chem Phys (1983) 78:301–8. doi:10.1063/1.444501
40. Kosloff RA, Kosloff D. Fourier method solution for the time dependent SchrOdinger equation: A study of the reaction H+ + H2, D++HD, and D++H2. J Chem Phys (1823) 79:1823–33. doi:10.1063/1.445959
41. Bergmann K, Theuer H, Shore BW. Coherent population transfer among quantum states of atoms and molecules. Rev Mod Phys (1998) 70:1003–25. doi:10.1103/RevModPhys.70.1003
Keywords: femtosecond (fs) laser, photoassociation, time-dependent schrodinger equation, thermal-random-phase wavepacket, multiphoton transition
Citation: Zhang R, Hu J-W, Han Y-C, Fu B and Shundalau M (2023) Steering thermal photoassociation of magnesium atoms by two time-delayed femtosecond laser pulses. Front. Phys. 11:1114719. doi: 10.3389/fphy.2023.1114719
Received: 02 December 2022; Accepted: 04 January 2023;
Published: 12 January 2023.
Edited by:
Yujun Zheng, Shandong University, ChinaReviewed by:
Chuancun Shu, Central South University, ChinaEmanuel De Lima, Federal University of São Carlos, Brazil
Copyright © 2023 Zhang, Hu, Han, Fu and Shundalau. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Jin-Wei Hu, aHVqaW53d0AxNjMuY29t; Yong-Chang Han, eWNoYW5AZGx1dC5lZHUuY24=
 Rong Zhang1
Rong Zhang1 Yong-Chang Han
Yong-Chang Han Maksim Shundalau
Maksim Shundalau