- 1Dipartimento di Scienze Matematiche, Fisiche e Informatiche, Università di Parma, Parma, Italy
- 2INFN, Gruppo Collegato di Parma, Parma, Italy
- 3PSH, UR 1115, French National Research Institute for Agriculture, Food, and the Environment (INRAE), Avignon, France
- 4Department of Sociology, Karlsruhe Institute of Technology, Karlsruhe, Germany
- 5Max Planck Institute for Dynamics and Self-Organization, Göttingen, Germany
- 6Dipartimento di Fisica, Politecnico di Milano, Milano, Italy
- 7Center for Nano Science and Technology@PoliMi, Istituto Italiano di Tecnologia, Milan, Italy
- 8Faculty of Basic Science, Van Lang University, Ho Chi Minh City, Vietnam
- 9John von Neumann Institute, Vietnam National University, Ho chi minh City, VietNam
- 10Institute of Fundamental and Applied Sciences, Duy Tan University, Ho Chi Minh City, Vietnam
- 11Faculty of Natural Sciences, Duy Tan University, Da Nang, Vietnam
Network science offers powerful tools to model complex social systems. Most social network science research focuses on topological networks by simply considering the binary state of the links, i.e., their presence or absence. Nonetheless, complex social systems present heterogeneity in link interactions (link weight), and accounting for this heterogeneity, it is mandatory to design reliable social network models. Here, we revisit the topic of weighted social networks (WSNs). By summarizing the main notions, findings, and applications in the field of WSNs, we outline how WSN methodology may improve the modeling of several real problems in social sciences. We are convinced that WSNs may furnish ideas and insights to open interesting lines of new research in the social sciences.
1 Introduction
Networks are prominent frameworks to model the functioning of complex social systems [1–4]. Social networks are composed of nodes (individual actors, people, or social organizations within the network) and the links (relationships or interactions) that connect them. Social networks have been used to describe patterns in friendship [5], science collaborations [6], criminal organizations [7, 8], and to model spreading dynamics involving, e.g., several real problems of interest, such as information diffusion [9, 10], social influence models [11–14], epidemic spreading [15, 16], and vaccination policies [17, 18].
Most of the social network science research has focused on the topological features of the networks by considering the binary state of the links only, i.e., presence or absence [19].
Nonetheless, complex social systems present heterogeneity in the interactions among nodes [4, 19, 20], and social networks should be specified not only by their topology but also by the importance of the links (link weights) that differentiate the interactions among nodes in terms of their strength, intensity, or capacity [2, 3, 21, 22]. For these reasons, considering the heterogeneity in the intensity of links/interactions is fundamental to understanding complex social systems [21].
This review focuses on social network research adopting a weighted network approach. We summarize the main notions, findings, and applications of weighted social networks (WSNs). Then, we outline how WSN methodology may improve the modeling of several complex social system problems and encourage new lines of research.
2 Basic notions
A binary network
3 The “strength of weak ties” hypothesis
The “weak link hypothesis” is probably the most influential sociological theory of networks. In the famous “The Strength of Weak Ties” research [23], Granovetter modeled the individual interpersonal relationships (links or ties) by quantifying the strength of the friendship (link weight) as “strong,” “weak,” or “absent.” Strong links represent friends, and weak links denote tenuous acquaintances. Granovetter stresses the importance of weak links involving secondary acquaintances outside the people community, which therefore represent preferential sources of new information and job opportunities [24].
The “weak link hypothesis” describes a specific social network structure in which strong links are located within dense communities (or groups) of similar individuals. In contrast, weaker links act as bridges between the different communities (Figure 1A). The weak acquaintance links play the important role of holding together groups with low levels of similarity, avoiding the segregation of different and disparate human communities, and thus preserving the cohesiveness of the social network. Consequently, social networks would be vulnerable to removing weak links since their removal would fragment the network into isolated communities [4, 23].
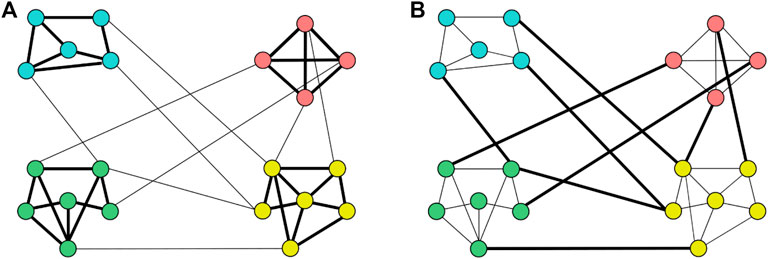
FIGURE 1. (A) Network structure underlying the “Granovetter weak link hypothesis” [23]. The thickness of the link indicates its weight, i.e., the intensity of the friendship between the nodes. Links of higher thickness are of higher weight (strong links), and links of lower thickness are of lower weight (weak links). Node color denotes different community memberships, and nodes of the same color are of the same community. The weak link hypothesis depicts a social network in which strong links denoting tight friendship generally occur within people communities, and weak acquaintance links connect distant individuals of different communities. Weak links are important to preserve the cohesiveness of the network. (B) The strong link hypothesis depicts a social network in which weak links generally occur within people communities, and strong friendship links connect individuals belonging to different communities. In this case, the strong links are the main players sustaining the cohesiveness of the social network.
In recent years, the “weak link hypothesis” has been confirmed in different real-world WSNs. In mobile phone call networks, longer phone calls (strong links) generally occur within communities, whereas shorter-duration calls (weak links) take place from nodes/individuals in different communities [25]. In a teenager criminal network, links, defined as friends of friends, join distant communities of individuals and have a positive impact on criminal activities [26]. In cinematic collaboration networks, in which the nodes represent actors and link weight indicates the number of movies in which they appeared together, weak links are the main ones responsible for supporting network cohesiveness. Their removal triggered the quickest network disconnection [27].
4 Node distance in weighted social networks
The distance among network nodes is a fundamental metric in social network science, and it is based on the notion of path [20]. A “path” is a set of distinct and connected nodes. The path of minimum length between two nodes is usually called the shortest path (SP) [19]. The “distance”
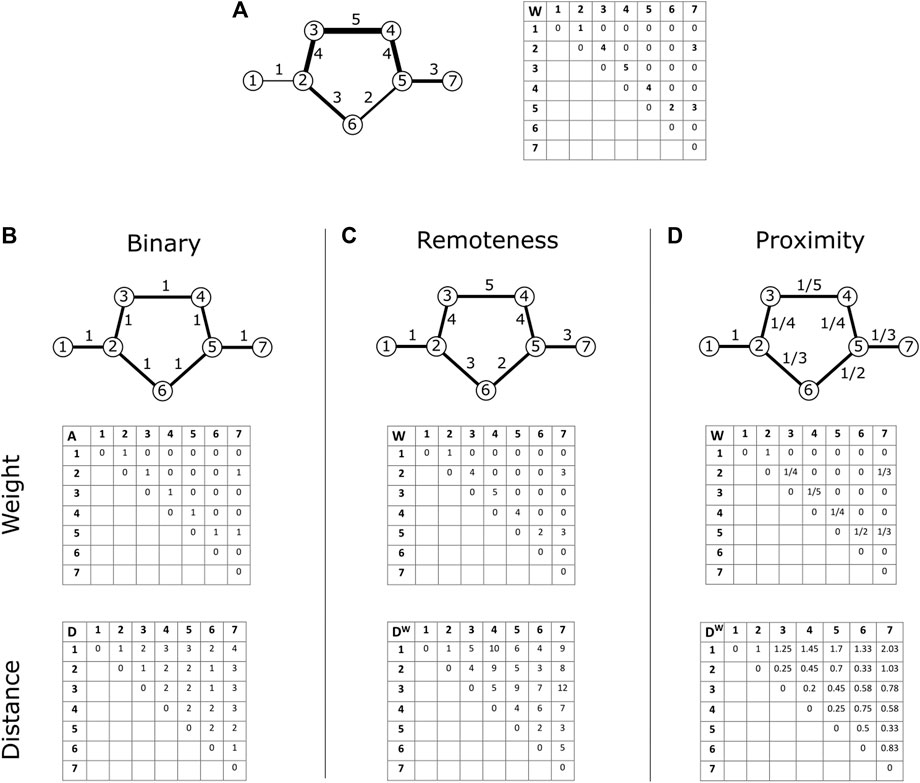
FIGURE 2. Binary and weighted node distance computational examples. (Top) Weighted network of seven nodes and seven links and its weight matrix
In the case of weighted networks, to compute the shortest path, it is necessary to distinguish, in advance, the link weight meaning [3, 29]. The link weight may assume different meanings in WSNs, and a higher link weight value may indicate that nodes are either closer or farther apart. Let us take the example of a social network of employees. The response time to emails among nodes/employees in this working network indicates how far the connected nodes are in the social network, thus denoting less important working relationships. On the contrary, the time two nodes/employees spend calling each other, calling time, indicates that the nodes are closer in this social network. From now on, we define “proximity” the link weight, if its increase denotes a closer relationship between the nodes, and we define “remoteness” the link weight in the opposite scenario. Proximity has been defined as a “flow or capacity” in the literature, and remoteness is also named “cost, distance, or resistance” [19]. Examples of link weights as remoteness in social networks can be computed from the physical distance among nodes/individuals in friendship networks [30], the response time to emails among nodes/employees in email networks, the number of troublesome among nodes/individuals in friendship networks [31], or the antagonism number in working relationship networks [32]. Conversely, examples of link weights as proximity in social networks are the duration of a call between nodes/individuals in telephone networks [25, 33], the number of co-authored papers between scholars in scientific collaboration networks [6, 34], the number of emails among nodes/employees [35, 36], and the declared strength of friendship among nodes/individuals in social networks [5, 37–39]. In Table 1, we list important types of real-world WSNs, indicating whether the link weight meaning is proximity or remoteness.
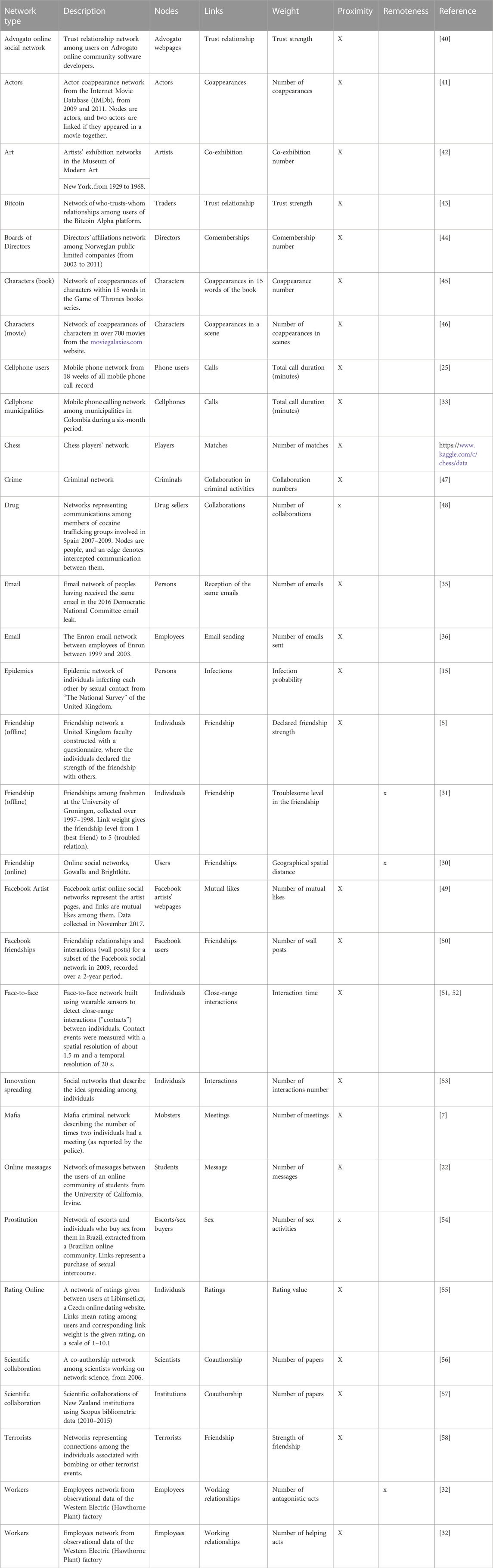
TABLE 1. Types of real-world weighted social networks. The “x” indicates if link weights are proximity or remoteness.
In weighted networks, we call the shortest path between two nodes the “weighted shortest path” (WSP). The “weighted distance”
While computing
In contrast, if the weights mean proximity, we first compute the reciprocal of the link weights, and then
Notably, while the interpretation of node distance is straightforward in binary, unweighted networks, whenever weights are reported, the meaning of the link weight must be considered to avoid wrong calculations and results. For example, Table 1 shows that since the link weights in most real-world WSNs present weights as proximity, the link weight is inversely proportional to the distance between network nodes. To correctly calculate the distances
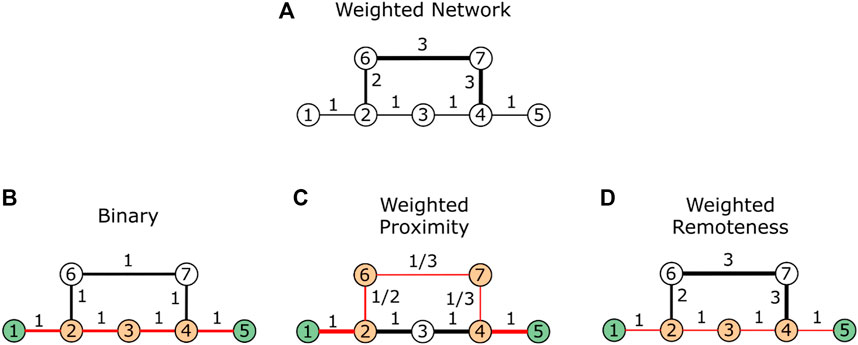
FIGURE 3. Finding the shortest path between nodes 1 and 5 in a weighted network. (A) The weighted network. (B) The binary shortest path. (C) Weighted “proximity” shortest path. (D) Weighted “remoteness” shortest path. The links forming the shortest path are in red, and nodes belonging to the shortest path are in orange. We can see how, by changing the methodology used to compute the distances among nodes in the social network, the shortest path between the nodes may change as well.
Mistakes in node distance computation in weighted networks may be more frequent than expected; it has been recently shown that in ecological network science, among 129 published research studies, 61% of these studies using shortest paths in weighted networks may contain errors in how WSPs are calculated [65].
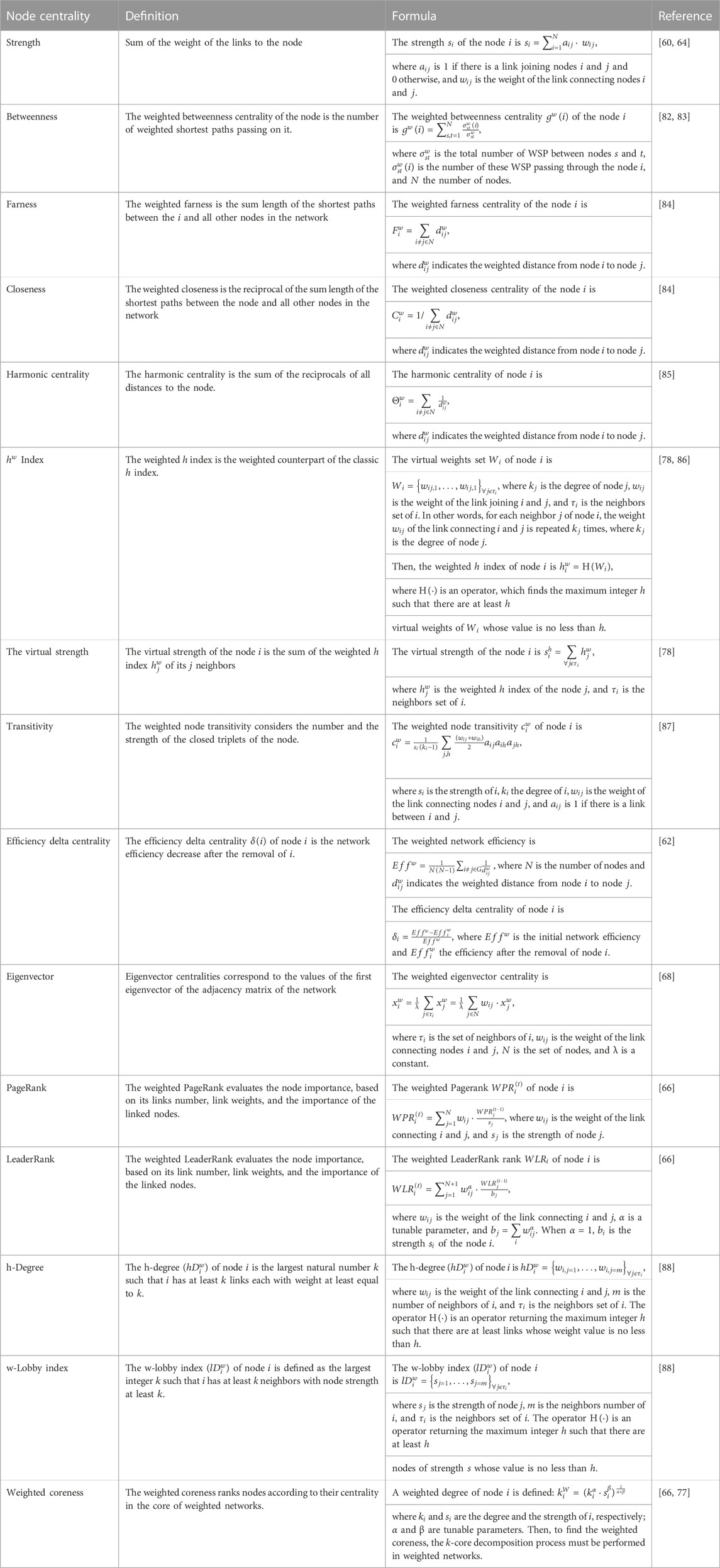
5 Measures of node centrality
In network science, measures (or indicators) of node centrality assign rankings to nodes within a network corresponding to their position in the network structure [1, 66]. Node centrality measures were first developed in social network analysis to identify influential persons in social networks [1, 67, 68]. Ranking network nodes according to their network structural embedding helps address a variety of problems in social networks, such as identifying the most influential persons in a friendship network [5], selecting the influential spreaders of news and information [69], and finding the most important nodes for vaccination to halt epidemic spreading, [17, 18, 70], etc [66]. Many node centrality measures conceived for binary networks were then adapted to rank nodes in WSNs.
The simplest measure of centrality is the node degree, i.e., the number of links to the node [1, 3].
The degree
where
The strength
where
The closeness centrality of node
where
The betweenness is another common measure of node centrality, accounting for how many shortest paths among nodes lie on a node [1].
The betweenness centrality
where
The weighted betweenness centrality
where
Passing from binary to node centrality measures accounting for the weight associated with the links might change the rank of node importance in social networks [3, 4, 19, 60]. In Figure 4, we show, on a simple network, how adopting the binary or the weighted version of the node centrality changes the node rank. Newman [6] showed that, by contrast, with the simple binary closeness measure, the list of scientists who are well-connected when ranking nodes with weighted closeness is no longer dominated by experimentalists, although the well-connected among them still score highly. The same has been proven true for other real-world social networks and different node rankings [60]. Therefore, for social network analyses, it is very important to adopt node centrality measures, considering the weight of the links.
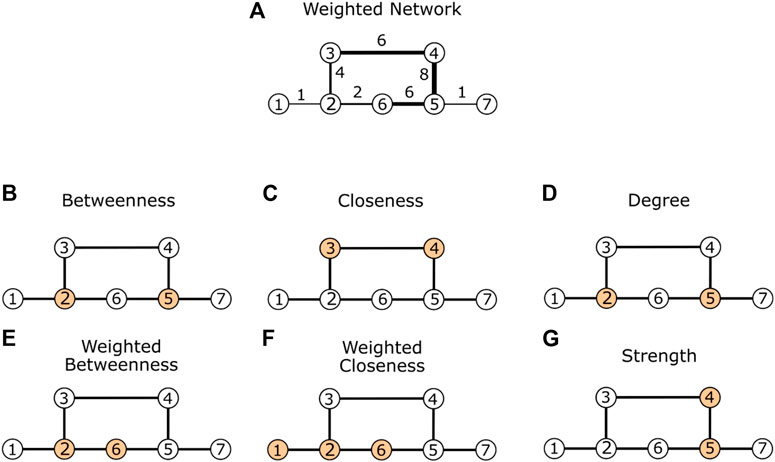
FIGURE 4. Node centrality ranking in binary and weighted networks. Orange nodes identify the highest centrality value nodes. (A) A weighted network with link weights as proximity. (B) First two nodes with a higher binary betweenness. (C) First two nodes with a higher binary closeness. (D) First two nodes with a higher degree. (E) First two nodes with higher weighted betweenness. (F) First three nodes with a higher weighted closeness. (G) First two nodes with higher strength. Passing from binary to weighted node centralities, the node rank changes as well.
Ranking important nodes is fundamental for finding influential spreaders in social networks [69, 75, 76], and most of the research investigating influential spreaders uses a binary network approach. In WSNs, Garas et al. [77] used a weighted SIR model to describe a general spreading process in networks of different natures and classified the nodes with a generalized method for calculating the weighted node coreness centrality. They show that the proposed weighted node coreness method places nodes with higher spreading potential closer to the network core, and it is more accurate in finding the best spreader nodes in WSNs [77]. With similar aims, Gao et al. [78] proposed a weighted version of the famous Hirsch index [79], usually called the H-index, to find influential spreader nodes. The authors defined the weighted h-index (
Finding influential spreader nodes is a pressing problem in case of a spreading epidemic [80, 81]. In this case, considering link weights and proper node centrality measures for weighted networks may be very important in selecting the best spreader node [4]. For example, let us take a social network where the link weights account for the face-to-face contact duration among people and consequently determine the probability that a susceptible person is infected after having been in contact with an infectious person. In this case, neglecting the link weights may hide the paths of higher infection probability, consequently selecting false influential spreader nodes and tracing unlikely infection trajectories (Figure 5).
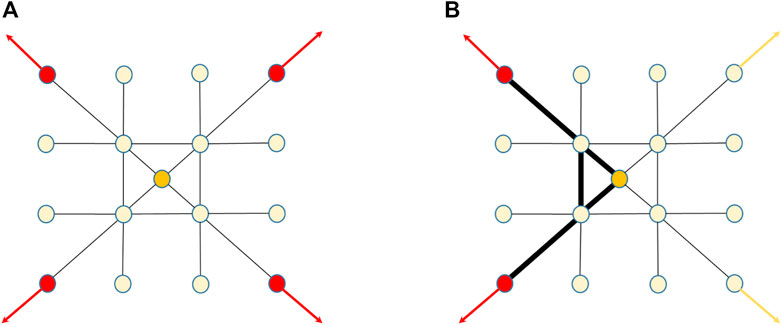
FIGURE 5. The paths of higher infection probability among nodes/individuals in a community. The orange node is the infected individual starting the epidemic; the red nodes are the individuals that may act as potential spreaders of infection outside the community, and the red arrows indicate the likely trajectories of the epidemic spreading outside the community. (A) A binary network where the four red nodes are all potential spreaders. (B) The weighted network counterpart of the binary network in (A), where the most significant channels of infection emerge; in this weighted network, the potential spreaders to consider are the two red nodes only, and the likely trajectories of infection outside the community are only two (red arrows).
In Table 2, we give a list of node centrality measures for WSNs with literature references.
6 Community structure in weighted social networks
The investigation of community structures in social networks is an important issue in many domains and disciplines since many real-world social networks present community structure [19, 61, 89]. Moreover, social networks offer a wide variety of possible community organizations: families, working and friendship circles, scholar collaborations, and social networking groups [90]. The classic weak link hypothesis is a paradigmatic example of social networks with community structure, in which densely connected communities of nodes/people are joined by sparsely weaker links (Figure 1).
The definition of community in binary networks is simple: a community is defined as a subset of nodes within the network such that the links among the nodes of the same community are denser than connections with the rest of the network [91]. In other words, communities are densely connected subgroups of network nodes with sparser connections among them. Synonyms of community are group, clique, module, class, and cluster.
In the following two paragraphs, we first describe node clustering, which can be viewed as the simple notion of the network community, and then the generalized community detection methodology.
6.1 Clustering coefficient
A simple method to investigate the presence of communities is to evaluate the network clustering coefficient [20]. In binary networks, (binary) clustering is a measure that counts node triplets in the network. A triplet (or triangle) is a set of three nodes. A closed triplet is a full network of three nodes, i.e., a set of three nodes in which each node is connected by a link with the others. In other terms, a triplet is three nodes that are connected by either two (open triplet) or three (closed triplet) links.
The binary “local clustering coefficient”
where
Alternatively, the binary “local clustering coefficient”
where
By computing the triplets over the whole network, we can define the binary global clustering coefficient by generalizing Eq. 6:
where
The binary clustering coefficient evaluates the local group cohesiveness, and it is defined for any node in the network as the fraction of connected neighbors. In other words, the binary clustering coefficient indicates the intensity with which nodes tend to form tightly knit communities characterized by a relatively high density of links, i.e., a likelihood that tends to be higher than the average probability of links randomly drawn among nodes [92, 93].
There are many generalizations of the binary clustering coefficient for weighted networks [22, 87, 94, 95]. Barrat et al. [87] proposed the most commonly used generalization, which defined a weighted version of the local clustering coefficient defined in Eq. 7 as:
where
Opsahl and Panzarasa [22] proposed another commonly used generalization of the global clustering coefficient in WSNs. Defining
where
The generalized weighted clustering coefficients proposed by Barrat et al. [87] and Opsahl and Panzarasa [22] are both measures of the local cohesiveness in weighted networks that take into account both the number of closed triplets in the neighborhood of a node and their total relative link weight with respect to the strength of the node. In Figure 6, we give examples of binary and weighted node clustering coefficient computation. As shown in Figure 6, the binary and weighted clustering coefficient values are different, and the weighted clustering provides additional information about the tightness of the node clustering.
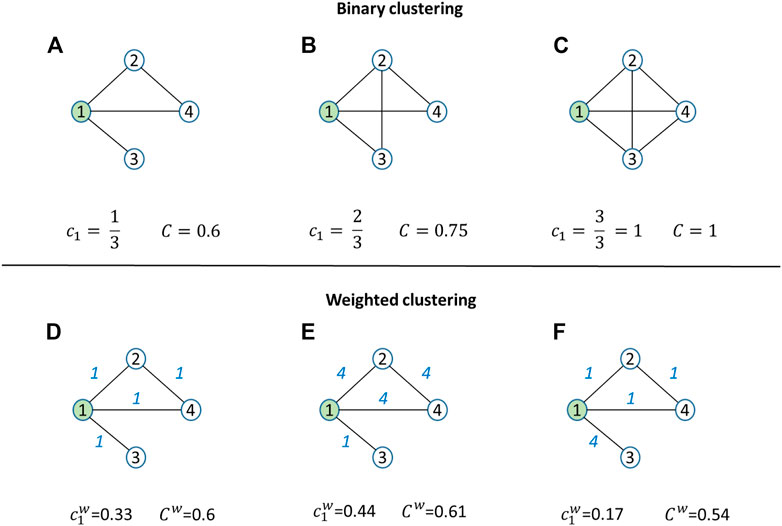
FIGURE 6. Clustering coefficients in binary and weighted networks. (A-B-C) The binary local clustering coefficient
The two measures described provide important results, and in all WSNs studied, the value of the weighted coefficient was greater than the value of the binary one [22]. These findings support Granovetter’s [23] claim that in social networks, strong ties are more likely to be part of transitive triplets than weak ones [22].
The clustering coefficient measures the community structure of the networks only considering the triadic closure, i.e., evaluating the tendency of the nodes to cluster in communities of three nodes.
6.2 Community detections in weighted social networks
Social network communities are often composed of several nodes, and the node’s propensity to cluster together in communities can be generalized to groups of any order.
The detection and characterization of community structure in social networks, meaning the appearance of densely connected groups of nodes with only sparser connections between groups, has increased in importance in the last decades [61, 96]. The node communities division can be performed by different methods of community detection, such as random walk searching [97], link betweenness [98], fast greedy modularity optimization [61], and spinning glass model [99] [90]. Proper indicators may then be used to evaluate the goodness of the communities division [90]. In the following, we describe the modularity
The modularity
The modularity indicators
where
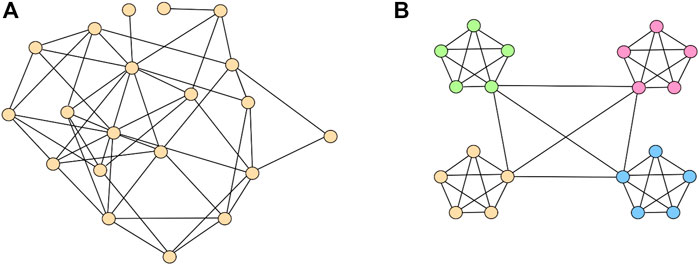
FIGURE 7. Community structure and the network modularity indicator
The modularity
The same rationale can be used to evaluate community structure in weighted networks. The modularity
The weighted modularity
where
The weighted modularity indicator considers both the binary presence of communities in the network and their total relative link weight. The weighted modularity
In Figure 8, we show that accounting link weights’ heterogeneity may change the detected community structure of the network. Figure 8A depicts a network with a strong binary community structure, i.e., nodes belonging to four distinct communities. Then, we associate link weights to the network based on the following two criteria: delivering strong links inside (Figure 8B) and outside the network communities (Figure 8C). Finally, we calculate the modularity indicator
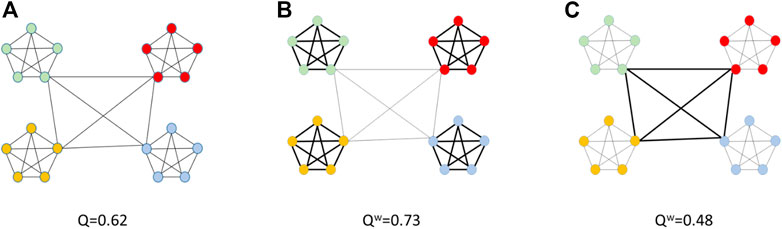
FIGURE 8. Community structure in weighted networks. (A) A binary network of
7 Robustness of weighted social networks
Understanding the causes of the robustness of social systems is of concern to social scientists, who explore the stability of human societies in the face of disrupting forces such as epidemics, criminal activities, social segregation, famine, war, and changes in social and economic order [104]. Social networks are prominent frameworks for analyzing the robustness of social systems [4, 27, 41, 73, 85, 105–107].
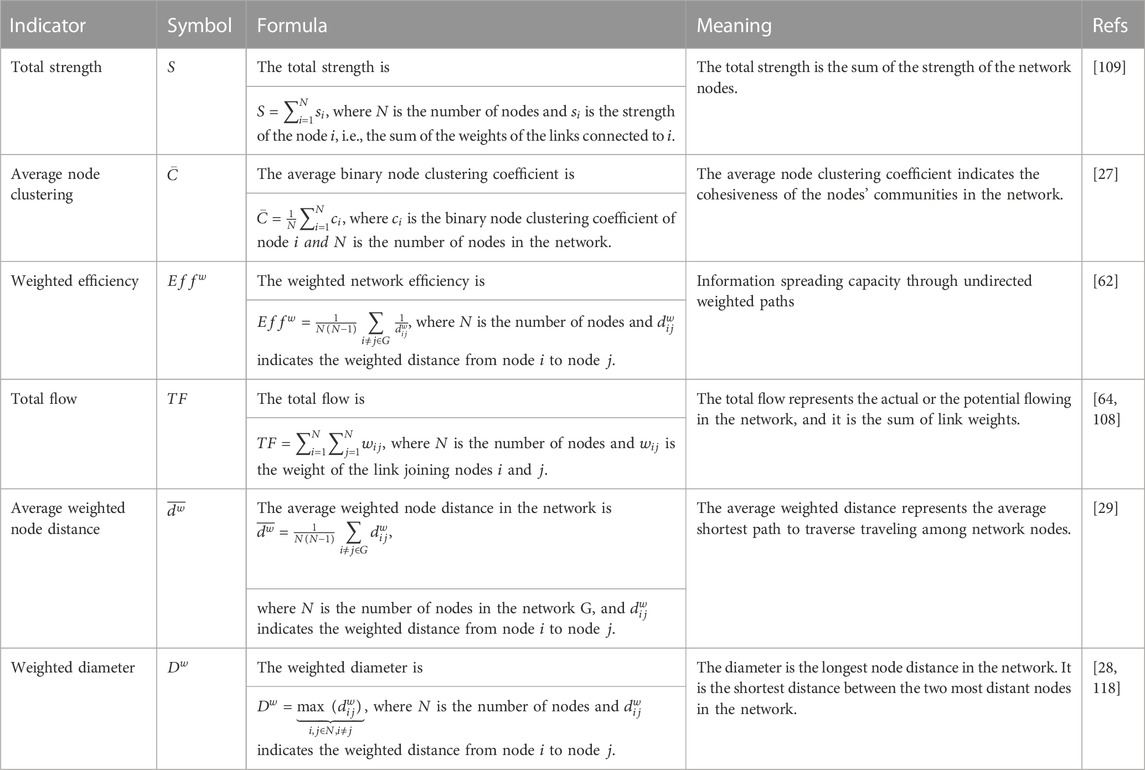
“Network robustness” can be defined as the functionality (capacity) of the system to maintain its functions after removing nodes or links [104, 108]. Usually, the decrease in network functionality is evaluated by focusing on the connectivity degradation after node or link removal. The two most common measures of network connectivity are the largest connected component (
The binary network efficiency
where
Other measures of network functioning have been proposed, such as the average node distance [112, 113], network diameter [114], algebraic connectivity [115], and others [116, 117]. In Table 3, we list network functioning measures for weighted networks.
Analyzing network robustness is also essential to determine the most important nodes and links in social networks, i.e., the nodes and links whose removal causes the greatest amount of damage in the social system, which reveal the links/nodes acting as key players for network functioning [110].
In the following, we review the main results and applications in the field of weighted social network robustness by focusing separately on link and node removal.
7.1 Link removal
Link removal (LR), also known as bond percolation [75], link attack [108, 119], or link pruning [120], studies how the robustness of networks decreases by removing links [108].
The “weak link hypothesis” [23, 24] can be viewed as one of the first applications of LR analysis in social networks. The “weak link hypothesis” describes a specific social network structure in which strong links are located within dense communities (or groups) of similar individuals. In contrast, weaker links act as bridges between different communities. As a consequence, social networks would be vulnerable to the removal of weak links since the removal of the weak link (acquaintances), which serve a cohesive function in social systems, may rapidly disconnect the
However, network science investigations have uncovered a seeming “paradox of weak ties,” suggesting that strong links (i.e., links of higher weight) may be more valuable than weak links to serve the cohesiveness and robustness of the system [4]. For example, science co-authorship networks are formed by nodes (scientists) and links weighted by the number of co-authored papers, presenting dense local neighborhoods mainly consisting of weaker links, while strong links connect senior scientists leading different research groups [27, 107]. In contrast to what occurred in other social networks, the
The aforementioned studies investigating the robustness of the social network to LR evaluated the robustness using the
Furthermore, Bellingeri et al. [64] found that removing a very small fraction of strong links of higher weight from science co-authorship and friendship social networks triggers an abrupt collapse of
LR may properly model various real problems in social systems, such as describing the effect of the interruption of friendship, work, or science collaboration relationships [4, 27]. Moreover, LR can be used to model social distancing and non-pharmaceutical interventions (NPIs) to curb epidemic spreading in complex social networks [124, 125]. In the simplest binary-topological model, LR may describe how reducing social interactions can fragment the social network, thus confining the epidemics to a small part of the network. On the other hand, coupling link removal and dynamical epidemiological models, i.e., SIR or SEIRS models [126], has the advantage of investigating important aspects of the NPIs, such as modeling how the NPIs affect the temporal dynamics of the infection [125, 127, 128]. Nonetheless, most research studies focusing on NPIs and social network epidemics fail to consider the weight of the links in the analyses. Including the weight heterogeneity in models describing the epidemic dynamics is fundamental in real-world social networks, such as face-to-face networks, which are highly promising frameworks to model epidemic spreading in real-world social systems [51]. Face-to-face networks describe the physical interactions among individuals, and the weight of the link accounts for the interaction time. Since longer interactions imply higher epidemic transmission probabilities, to properly model the epidemic dynamics in real-world WSNs, it is fundamental to develop models considering the link weight heterogeneity. For example, a correct description of the epidemic dynamics in face-to-face networks should assign higher infection probabilities to links with higher weights representing long interaction times.
7.2 Node removal
Node removal (NR), also known as node attack [74, 129] and site percolation [130], studies how the removal of nodes in the network affects its robustness [4]. The study of real-world network robustness after node removals has drawn great attention in recent years [73, 110, 131].
In social network analyses, NR may describe a variety of real problems. For example, in friendship networks, NR may be useful to individuate social hubs, i.e., more important individuals for the connectedness of the friendship networks [132]. In science co-authorship networks, it may be a tool to identify more important scholars for the connectedness of the scientific collaboration networks [133]. In criminal networks, NR may describe how arresting criminals affects the structure of interpersonal relationships in crime with the aim of developing policies to halt criminal activities [134]. Finally, in social contact networks within which a disease can spread, NR may simulate the effect of node vaccination [18] and quarantine [128] on the spread of the disease.
The majority of these studies focused on NR with a binary approach, failing to evaluate the difference in link weights. However, adopting a binary approach to NR may produce inaccurate modeling in real-world social networks. On the one hand, predicting the robustness of social networks when subjected to NR may be misleading. For example, removing a few nodes from WSNs may abruptly collapse the weighted network efficiency (
On the other hand, ignoring the weighted structure of the network may trigger an erroneous ranking of the node’s importance [60, 82, 109]. As explained in Figure 4, using weighted node centralities instead of the simple binary node centralities may change node rank. Therefore, in real-social networks presenting decoupling with binary and weighted node centralities, the inaccuracy in node ranking may be very high. For example, in real-world WSNs with a low correlation between the degree and the strength of the nodes, ranking nodes according to their degree would give more importance to nodes connected with several weak links than to nodes connected with a few stronger ones. This may induce many inaccurate models of real-world social systems. For example, in epidemic networks, such as face-to-face networks, neglecting the weighted structure may hide the important nodes to be vaccinated (Figure 9).
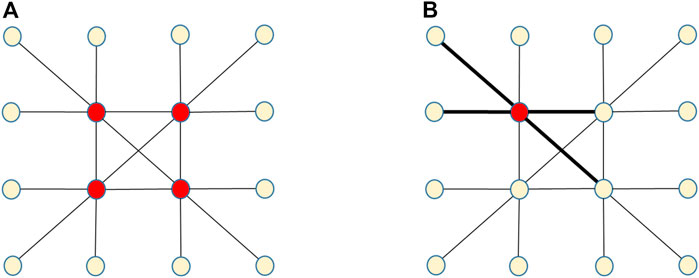
FIGURE 9. Node vaccination priority in social networks. (A) A binary network where the nodes to vaccinate (red nodes) are selected considering the node degree; in this network, the four red nodes show the same vaccination priority. (B) The weighted network counterpart of the binary network in (A); in this network, the nodes to be vaccinated are ranked considering their strength. The node in red has the highest strength and the highest priority for vaccination. In the case of face-to-face networks in which link weights indicate the contact time between individuals, vaccinating the node sharing strong links would eliminate the most significant channels of infection.
8 Conclusion
Network analysis is a promising tool for modeling and studying several problems in social systems. In many social networks, links have a naturally associated weight. We have shown that a more complete and proper view of WSNs is provided by considering the heterogeneity of the interactions defining the links between these social systems. On the one hand, this review aims to summarize the results of recent studies in WSNs. On the other hand, this review offers an overview of many open and pressing problems in social network science by outlining how adopting a weighted network perspective may improve the reality of social system descriptions. It is worth noting that artificial intelligence (AI) and data mining methodologies offer new and powerful tools to collect social systems information. For this reason, data are increasingly available, and they will permit the construction of new and well-resolved WSNs. Our review may prompt social science researchers to exercise social system analysis from a weighted network perspective.
Author contributions
MB and DC conceived the manuscript. All the authors wrote the manuscript.
Funding
This research is funded by a grant from the Italian Ministry of Foreign Affairs and International Cooperation. This project has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme [grant agreement no. (816313)]. This work is supported by the Vietnam’s Ministry of Science and Technology (MOST) under the Vietnam-Italy Scientific and Technological Cooperation Program for the period of 2021–2023. This work is supported by Vietnam National University Ho Chi Minh City (VNU-HCM), Ho Chi Minh City, Vietnam, under grant number B2018-42-01. We are greatly thankful to Van Lang University, Vietnam, for providing the budget for this study. This research is funded by the Ecosister project, funded under the National Recovery and Resilience Plan (NRRP), Mission 4 Component 2 Investment 1.5—Call for tender No. 3277 of December 30, 2021 of the Italian Ministry of University, and research funded by the European Union—NextGenerationEU. Award Number: Project Code ECS00000033, Concession Decree No. 1052 of June 23, 2022, adopted by the Italian Ministry. This work has been supported by Fondazione Cariplo, Grant No. 2018-0979.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Freeman HE. A set of measures of centrality based on betweenness. Sociometry (1977) 40:35. doi:10.2307/3033543
2. Wasserman S, Faust K. Social network analysis: Methods and applications. Cambridge, United Kingdom: Cambridge University Press (1994).
3. Opsahl T, Agneessens F, Skvoretz J. Node centrality in weighted networks: Generalizing degree and shortest paths. Soc Networks (2010) 32:245–51. doi:10.1016/j.socnet.2010.03.006
4. Bellingeri M, Bevacqua D, Scotognella F, Alfieri R, Nguyen Q, Montepietra D, et al. Link and node removal in real social networks: A review. Front Phys (2020) 8:8. doi:10.3389/fphy.2020.00228
5. Nepusz T, Petróczi A, Négyessy L, Bazsó F. Fuzzy communities and the concept of bridgeness in complex networks. Phys Rev E - Stat Nonlinear, Soft Matter Phys (2008) 77:016107–12. doi:10.1103/PhysRevE.77.016107
6. Newman MEJ. Scientific collaboration networks. II. Shortest paths, weighted networks, and centrality. Phys Rev E - Stat Physics, Plasmas Fluids Relat Interdiscip Top (2001) 64:016132. doi:10.1103/PhysRevE.64.016132
7. Ficara A, Cavallaro L, De Meo P, Fiumara G, Catanese S, Bagdasar O, et al. Social network analysis of Sicilian mafia interconnections. In: Studies in computational intelligence. Midtown Manhattan, New York City: Springer International Publishing (2020). p. 440–50. doi:10.1007/978-3-030-36683-4_36
8. Ficara A, Fiumara G, Catanese S, De Meo P, Liu X. The whole is greater than the sum of the parts: A multilayer approach on criminal networks. Futur Internet (2022) 14:1–21. doi:10.3390/fi14050123
9. Al-Taie MZ, Kadry S. Information diffusion in social networks. Python Graph Netw Anal (2017) 2017:165–84. doi:10.1007/978-3-319-53004-8_8
10. Li M, Wang X, Gao K, Zhang S. A survey on information diffusion in online social networks: Models and methods. Inf (2017) 8:118. doi:10.3390/info8040118
11. DeGroot M. Reaching a consensus. J Am Stat Assoc (1974) 69:118–21. doi:10.1080/01621459.1974.10480137
12. Friedkin N, Johnsen E. Social influence and opinions. J Math Sociol (1991) 15:193–206. doi:10.1080/0022250x.1990.9990069
13. Parisi D, Cecconi F, Natale F. Cultural change in spatial environments: The role of cultural assimilation and internal changes in cultures. J Conflict Resolut (2003) 47:163–79. doi:10.1177/0022002702251025
14. Deffuant G, Neau D, Amblard F, Weisbuch G. Mixing beliefs among interacting agents. Adv Complex Syst (2000) 03:87–98. doi:10.1142/s0219525900000078
15. Kamp C, Moslonka-Lefebvre M, Alizon S. Epidemic spread on weighted networks. Plos Comput Biol (2013) 9:e1003352. doi:10.1371/journal.pcbi.1003352
16. Bellingeri M, Bevacqua D, Turchetto M, Scotognella F, Alfieri R, Nguyen N-K-K, et al. Network structure indexes to forecast epidemic spreading in real-world complex networks. Front Phys (2022) 10:1–11. doi:10.3389/fphy.2022.1017015
17. Gallos LK, Liljeros F, Argyrakis P, Bunde A, Havlin S. Improving immunization strategies. Phys Rev E - Stat Nonlinear, Soft Matter Phys (2007) 75:045104–4. doi:10.1103/PhysRevE.75.045104
18. Sartori F, Turchetto M, Bellingeri M, Scotognella F, Alfieri R, Nguyen NKK, et al. A comparison of node vaccination strategies to halt SIR epidemic spreading in real-world complex networks. Sci Rep (2022) 12:21355–13. doi:10.1038/s41598-022-24652-1
19. Newman MEJ. Analysis of weighted networks. Phys Rev E - Stat Nonlinear, Soft Matter Phys (2004) 70:056131–9. doi:10.1103/PhysRevE.70.056131
20. Boccaletti S, Latora V, Moreno Y, Chavez M, Hwang DU. Complex networks: Structure and dynamics. Phys Rep (2006) 424:175–308. doi:10.1016/j.physrep.2005.10.009
21. Barthélemy M, Barrat A, Pastor-Satorras R, Vespignani A. Characterization and modeling of weighted networks. Phys A Stat Mech Its Appl (2005) 346:34–43. doi:10.1016/j.physa.2004.08.047
22. Opsahl T, Panzarasa P. Clustering in weighted networks. Soc Networks (2009) 31:155–63. doi:10.1016/j.socnet.2009.02.002
24. Rajkumar K, Saint-Jacques G, Bojinov I, Brynjolfsson E, Aral S. A causal test of the strength of weak ties. Science (2022) 377(80):1304–10. doi:10.1126/science.abl4476
25. Onnela JP, Saramäki J, Hyvönen J, Szabó G, Lazer D, Kaski K, et al. Structure and tie strengths in mobile communication networks. Proc Natl Acad Sci U S A (2007) 104:7332–6. doi:10.1073/pnas.0610245104
26. Patacchini E, Zenou Y. The strength of weak ties in crime. Eur Econ Rev (2008) 52:209–36. doi:10.1016/j.euroecorev.2007.09.002
27. Pajevic S, Plenz D. The organization of strong links in complex networks. Nat Phys (2012) 8:429–36. doi:10.1038/nphys2257
28. Buckley F, Harary F. Distance in graphs. Redwood City, CA: Addison-Wesley Publishing Company (1990). doi:10.1201/b16132-64
29. Bertagnolli G, Gallotti R, De Domenico M. Quantifying efficient information exchange in real network flows. Commun Phys (2021) 4:125. doi:10.1038/s42005-021-00612-5
30. Cho E, Myers SA, Leskovec J. Friendship and mobility: User movement in location-based social networks. Proc ACM SIGKDD Int Conf Knowl Discov Data Min (2011) 2011:1082–90. doi:10.1145/2020408.2020579
31. Van De Bunt GG, Duijn MAJV, Snijders TAB. Friendship networks through time: An actor-oriented dynamic statistical network model. Comput Math Organ Theor (1999) 52:167–92.
32. Dickson WJ, Roethlisberger FJ. Management and the worker. Econ J (2003) 51:306. doi:10.2307/2226267
33. Coscia M, Hausmann R. Evidence that calls-based and mobility networks are isomorphic. PLoS One (2015) 10:e0145091–15. doi:10.1371/journal.pone.0145091
34. De Domenico M, Lancichinetti A, Arenas A, Rosvall M. Identifying modular flows on multilayer networks reveals highly overlapping organization in interconnected systems. Phys Rev X (2015) 5:011027–11. doi:10.1103/PhysRevX.5.011027
35. Kunegis J. Konect - the koblenz network collection. In: WWW 2013 Companion - Proc 22nd Int Conf World Wide Web; May 13-17, 2013; Rio de Janeiro, Brazil (2013). p. 1343–50.
36. Klimt B, Yang Y. The enron corpus: A new dataset for email classification research. In: European Conference on Machine Learning; 19-23 September; Grenoble, France (2004). p. 217–26.
37. Moody J. Peer influence groups: Identifying dense clusters in large networks. Soc Networks (2001) 23:261–83. doi:10.1016/S0378-8733(01)00042-9
39. Freeman LC, Webster CM, Kirke DM. Exploring social structure using dynamic three-dimensional color images. Soc Networks (1998) 20:109–18. doi:10.1016/S0378-8733(97)00016-6
40. Massa P, Salvetti M, Tomasoni D. Bowling alone and trust decline in social network sites. 8th IEEE Int Symp Dependable, Auton Secur Comput DASC (2009) 2009:658–63. doi:10.1109/DASC.2009.130
41. Boldi P, Rosa M, Vigna S. Robustness of social networks: Comparative results based on distance distributions. Soc Inform (2011) 6984:8–21. doi:10.1007/978-3-642-24704-0_7
42. Braden LEA. Networks created within exhibition: The curators’ effect on historical recognition. Am Behav Sci (2021) 65:25–43. doi:10.1177/0002764218800145
43. Kumar S, Kumar M, Hooi B, Faloutsos C, Makhija D, Subrahmanian VS. REV2: Fraudulent user prediction in Rating platforms. In: WSDM 2018 - Proc 11th ACM Int Conf Web Search Data Min (2018); February 5-9, 2018; Marina Del Rey, CA, USA (2018). p. 333. doi:10.1145/3159652.3159729
44. Seierstad C, Opsahl T. For the few not the many? The effects of affirmative action on presence, prominence, and social capital of women directors in Norway. Scand J Manag (2011) 27:44–54. doi:10.1016/j.scaman.2010.10.002
45. Beveridge A, Shan J. Network of thrones. Math Horizons (2016) 23:18–22. doi:10.4169/mathhorizons.23.4.18
46. Kaminski J, Schober M, Albaladejo R, Zastupailo O, Hidalgo C. Moviegalaxies - social networks in movies. Harv Dataverse (2018) 3.
48. Framis AG-S. Illegal networks or criminal organizations. In: Crime and networks. England, UK: Routledge (2023). p. 17.
49. Rozemberczki B, Davies R, Sarkar R, Sutton C. GemSec: Graph embedding with self clustering. Proc 2019 Ieee/acm Int Conf Adv Soc Networks Anal Mining, ASONAM (2019) 2019:65–72. doi:10.1145/3341161.3342890
50. Viswanath B, Mislove A, Cha M, Gummadi KP. On the evolution of user interaction in Facebook. In: 2009 - Proc 2009 SIGCOMM Conf Co-Located Work Proc 2nd ACM Work Online Soc Networks; December 1 - 4, 2009; Rome Italy (2009). p. 37–42. doi:10.1145/1592665.1592675
51. Génois M, Barrat A. Can co-location be used as a proxy for face-to-face contacts? EPJ Data Sci (2018) 7:11–8. doi:10.1140/epjds/s13688-018-0140-1
52. Vanhems P, Barrat A, Cattuto C, Pinton JF, Khanafer N, Régis C, et al. Estimating potential infection transmission routes in hospital wards using wearable proximity sensors. PLoS One (2013) 8:e73970. doi:10.1371/journal.pone.0073970
53. Valente TW. Network models of the diffusion of innovations. Comput Math Organ Theor (1995) 2:163–4. doi:10.1007/bf00240425
54. Rocha LEC, Liljeros F, Holme P. Information dynamics shape the sexual networks of Internet-mediated prostitution. Proc Natl Acad Sci U S A (2010) 107:5706–11. doi:10.1073/pnas.0914080107
55. Kunegis J, Gröner G, Gottron T. Online dating recommender systems: The split-complex number approach. In: RSWeb’12 - Proceedings of the 4th ACM RecSys Workshop on Recommender Systems and the Social Web; September 9, 2012; Dublin, Ireland-book (2012). p. 37. doi:10.1145/2365934.2365942
56. Newman MEJ. Finding community structure in networks using the eigenvectors of matrices. Phys Rev E - Stat Nonlinear, Soft Matter Phys (2006) 74:036104–19. doi:10.1103/PhysRevE.74.036104
57. Aref S, Friggens D, Hendy S. Analysing scientific collaborations of New Zealand institutions using scopus bibliometric data. ACM Int Conf Proceeding Ser (2018) 2018. doi:10.1145/3167918.3167920
58. Gregori M, Merlone U. Comparing operational terrorist networks. Trends Organ Crime (2020) 23:263–88. doi:10.1007/s12117-020-09381-z
59. Marchiori M, Latora V. Harmony in the small-world. Physica A (2000) 285:539–46. doi:10.1016/s0378-4371(00)00311-3
60. Bellingeri M, Cassi D. Robustness of weighted networks. Phys A Stat Mech Its Appl (2018) 489:47–55. doi:10.1016/j.physa.2017.07.020
61. Clauset C, Newman MJ, Moore C. Finding community structure in very large networks. Phys Rev E (2004) 70:066111. doi:10.1103/physreve.70.066111
62. Latora V, Marchiori M. A measure of centrality based on network efficiency. New J Phys (2007) 9:188. doi:10.1088/1367-2630/9/6/188
63. Latora V, Marchiori M. Efficient behavior of small-world networks. Phys Rev Lett (2001) 87:198701. doi:10.1103/PhysRevLett.87.198701
64. Bellingeri M, Bevacqua D, Scotognella F, Cassi D. The heterogeneity in link weights may decrease the robustness of real-world complex weighted networks. Sci Rep (2019) 9:10692. doi:10.1038/s41598-019-47119-2
65. Costa A, Martín González AM, Guizien K, Doglioli AM, Gómez JM, Petrenko AA, et al. Ecological networks: Pursuing the shortest path, however narrow and crooked. Sci Rep (2019) 9:17826–13. doi:10.1038/s41598-019-54206-x
66. Lü L, Chen D, Ren XL, Zhang QM, Zhang YC, Zhou T. Vital nodes identification in complex networks. Phys Rep (2016) 650:1–63. doi:10.1016/j.physrep.2016.06.007
67. Moxley RL, Moxley NF. Determining point-centrality in uncontrived social networks. Sociometry (1974) 37:122. doi:10.2307/2786472
68. Bonacich P. Power and centrality: A family of measures. Am J Sociol (1987) 92:1170–82. doi:10.1086/228631
69. Kitsak M, Gallos LK, Havlin S, Liljeros F, Muchnik L, Stanley HE, et al. Identification of influential spreaders in complex networks. Nat Phys (2010) 6:888–93. doi:10.1038/nphys1746
70. Baharan M, Babaei M, Jalili M. Immunizing complex networks with limited budget. Europhys Lett (2012) 98:38004. doi:10.1209/0295-5075/98/38004
71. Borgatti SP. Identifying sets of key players in a social network. Comput Math Organ Theor (2006) 12:21–34. doi:10.1007/s10588-006-7084-x
72. Newman MEJ. The structure and function of complex networks. SIAM Rev (2003) 45:167–256. doi:10.1137/s003614450342480
73. Iyer S, Killingback T, Sundaram B, Wang Z. Attack robustness and centrality of complex networks. PLoS One (2013) 8:e59613. doi:10.1371/journal.pone.0059613
74. Nguyen Q, Pham HD, Cassi D, Bellingeri M. Conditional attack strategy for real-world complex networks. Phys A Stat Mech Its Appl (2019) 530:121561. doi:10.1016/j.physa.2019.121561
75. Hu Y, Ji S, Jin Y, Feng L, Eugene Stanley H, Havlin S. Local structure can identify and quantify influential global spreaders in large scale social networks. Proc Natl Acad Sci U S A (2018) 115:7468–72. doi:10.1073/pnas.1710547115
76. Pei S, Makse HA. Spreading dynamics in complex networks. J Stat Mech Theor Exp (2013) 2013:P12002. doi:10.1088/1742-5468/2013/12/P12002
77. Garas A, Schweitzer F, Havlin S. Ak-shell decomposition method for weighted networks. New J Phys (2012) 14:083030. doi:10.1088/1367-2630/14/8/083030
78. Gao L, Yu S, Li M, Shen Z, Gao Z. Weighted h-index for identifying influential spreaders. Symmetry (Basel) (2019) 11:1263–10. doi:10.3390/sym11101263
79. Hirsch JE. An index to quantify an individual’s scientific research output. Proc Natl Acad Sci U S A (2005) 102:16569–72. doi:10.1073/pnas.0507655102
80. Pastor-Satorras R, Vespignani A. Immunization of complex networks. Phys Rev E (2002) 65:036104. doi:10.1103/PhysRevE.65.036104
81. Wong F, Collins JJ. Evidence that coronavirus superspreading is fat-tailed. Proc Natl Acad Sci U S A (2020) 117:29416–8. doi:10.1073/pnas.2018490117
82. Nguyen Q, Nguyen NKK, Cassi D, Bellingeri M. New betweenness centrality node attack strategies for real-world complex weighted networks. Complexity (2021) 2021:2021–17. doi:10.1155/2021/1677445
83. Barthélemy M. Betweenness centrality in large complex networks. Eur Phys J B (2004) 38:163–8. doi:10.1140/epjb/e2004-00111-4
84. Bavelas A. Communication patterns in task-oriented groups. J Acoust Soc Am (1950) 22:725–30. doi:10.1121/1.1906679
85. Boldi P, Rosa M, Vigna S. Robustness of social and web graphs to node removal. Soc Netw Anal Min (2013) 3:829–42. doi:10.1007/s13278-013-0096-x
86. Lü L, Zhou T, Zhang QM, Stanley HE. The H-index of a network node and its relation to degree and coreness. Nat Commun (2016) 7:10168–7. doi:10.1038/ncomms10168
87. Barrat A, Barthélemy M, Pastor-Satorras R, Vespignani A. The architecture of complex weighted networks. Proc Natl Acad Sci U S A (2004) 101:3747–52. doi:10.1073/pnas.0400087101
88. Zhao SX, Rousseau R, Ye FY. H-Degree as a basic measure in weighted networks. J Informetr (2011) 5:668–77. doi:10.1016/j.joi.2011.06.005
89. Borgatti SP, Mehra A, Brass DJ, Labianca G. Network analysis in the social sciences. Science (2009) 323:892–5. doi:10.1126/science.1165821
90. Fortunato S. Community detection in graphs. Phys Rep (2010) 486:75–174. doi:10.1016/j.physrep.2009.11.002
91. Radicchi F, Castellano C, Cecconi F, Loreto V, Paris D. Defining and identifying communities in networks. Proc Natl Acad Sci U S A (2004) 101:2658–63. doi:10.1073/pnas.0400054101
92. Watts DJ, Strogatz SH. Collective dynamics of “small-world” networks. Nature (1998) 393:440–2. doi:10.1038/30918
93. Holland PW, Leinhardt S. Transitivity in structural models of small groups. Comp Gr Stud (1971) 2:107–24. doi:10.1177/104649647100200201
94. Doreian P. A note on the detection of cliques in valued graphs. Sociometry (1969) 32:237–42. doi:10.2307/2786266
95. Saramäki J, Kivelä M, Onnela JP, Kaski K, Kertész J. Generalizations of the clustering coefficient to weighted complex networks. Phys Rev E - Stat Nonlinear, Soft Matter Phys (2007) 75:027105–4. doi:10.1103/PhysRevE.75.027105
96. Red V, Traud AL, Kelsic ED, Mucha PJ, Porter MA. Comparing community structure to characteristics in online collegiate social networks. SIAM Rev (2011) 53:526–43. doi:10.1137/080734315
97. Pons P, Latapy M. Computing communities in large networks using random walks. In: Computer and Information Sciences - ISCIS; October 26 -- 28, 2005; Istanbul, Turkey (2005). p. 284–93.
98. Newman MEJ, Girvan M. Finding and evaluating community structure in networks. Phys Rev E - Stat Nonlinear, Soft Matter Phys (2004) 69:026113–5. doi:10.1103/PhysRevE.69.026113
99. Reichardt J, Bornholdt S. Statistical mechanics of community detection. Phys Rev E - Stat Nonlinear, Soft Matter Phys (2006) 74:016110–4. doi:10.1103/PhysRevE.74.016110
100. Brandes U, Delling D, Gaertler M, Görke R, Hoefer M, Nikoloski Z, et al. On modularity clustering. IEEE Trans Knowl Data Eng (2008) 20:172–88. doi:10.1109/TKDE.2007.190689
101. Salathe M, James J. Dynamics and control of diseases in networks with community structure. Plos Comput Biol (2010) 6:e1000736. doi:10.1371/journal.pcbi.1000736
102. Chen J, Zaïane OR, Goebel R. Detecting communities in social networks using max-min modularity. Soc Ind Appl Math - 9th SIAM Int Conf Data Min Proc Appl Math (2009) 2:973–84. doi:10.1137/1.9781611972795.84
103. Nguyen Q, Vu T, Dinh H, Cassi D, Scotognella F, Alfieri R, et al. Modularity affects the robustness of scale-free model and real-world social networks under betweenness and degree-based node attack. Appl Netw Sci (2021) 6:82. doi:10.1007/s41109-021-00426-y
104. Barabasi A-L. Network robustness. In: Network science. Cambridge, United Kingdom: Cambridge University Press (2021). p. 1–54.
105. Rockenbauch T, Sakdapolrak P. Social networks and the resilience of rural communities in the global south: A critical review and conceptual reflections. Ecol Soc (2017) 22:art10. doi:10.5751/ES-09009-220110
106. Moore JM, Small M, Yan G. Inclusivity enhances robustness and efficiency of social networks. Phys A Stat Mech Its Appl (2021) 563:125490. doi:10.1016/j.physa.2020.125490
107. Pan RK, Saramäki J. The strength of strong ties in scientific collaboration networks. Epl (2012) 97:18007. doi:10.1209/0295-5075/97/18007
108. Bellingeri M, Bevacqua D, Scotognella F, Alfieri R, Cassi D. A comparative analysis of link removal strategies in real complex weighted networks. Sci Rep (2020) 10:3911–5. doi:10.1038/s41598-020-60298-7
109. Dall’Asta L, Barrat A, Barthélemy M, Vespignani A. Vulnerability of weighted networks. J Stat Mech Theor Exp (2006) 2006:04006. doi:10.1088/1742-5468/2006/04/P04006
110. Wandelt S, Sun X, Feng D, Zanin M, Havlin S. A comparative analysis of approaches to network-dismantling. Sci Rep (2018) 8:13513–5. doi:10.1038/s41598-018-31902-8
111. Crucitti P, Latora V, Marchiori M, Rapisarda A. Error and attack tolerance of complex networks. Phys A Stat Mech Its Appl (2004) 340:388–94. doi:10.1016/j.physa.2004.04.031
112. Lekha DS, Balakrishnan K. Central attacks in complex networks: A revisit with new fallback strategy. Phys A Stat Mech Its Appl (2020) 549:124347. doi:10.1016/j.physa.2020.124347
113. Holme P, Kim BJ, Yoon CN, Han SK. Attack vulnerability of complex networks. Phys Rev E (2002) 65:056109. doi:10.1103/physreve.65.056109
114. Albert R, Jeong H, Barabasi A. Error and attack tolerance of complex networks. Nature (2000) 406:378–82. doi:10.1038/35019019
115. Martín-Hernández J, Wang H, Van Mieghem P, D’Agostino G. Algebraic connectivity of interdependent networks. Phys A Stat Mech Its Appl (2014) 404:92–105. doi:10.1016/j.physa.2014.02.043
116. Yang X, Zhu Y, Hong J, Yang LX, Wu Y, Tang YY. The rationality of four metrics of network robustness: A viewpoint of robust growth of generalized meshes. PLoS One (2016) 11:e0161077–13. doi:10.1371/journal.pone.0161077
117. Ellens W, Kooij RE. Graph measures and network robustness (2013). 1–13. Available at: http://arxiv.org/abs/1311.5064.
118. Divya PB, Lekha DS, Johnson TP, Balakrishnan K. Vulnerability of link-weighted complex networks in central attacks and fallback strategy. Phys A Stat Mech Its Appl (2022) 590:126667. doi:10.1016/j.physa.2021.126667
119. Sun S, Liu X, Wang L, Xia C. New link attack strategies of complex networks based on k-core decomposition. IEEE Trans Circuits Syst Express Briefs (2020) 67:3157–61. doi:10.1109/TCSII.2020.2973668
120. Mengiste SA, Aertsen A, Kumar A. Effect of edge pruning on structural controllability and observability of complex networks. Sci Rep (2015) 5:18145–14. doi:10.1038/srep18145
121. Onnela JP, Saramäki J, Hyvönen J, Szabó G, De Menezes MA, Kaski K, et al. Analysis of a large-scale weighted network of one-to-one human communication. New J Phys (2007) 9:179. doi:10.1088/1367-2630/9/6/179
122. Gee LK, Jones J, Burke M. Social networks and labor markets: How strong ties relate to job finding on Facebook’s social network. J Labor Econ (2017) 35:485–518. doi:10.1086/686225
123. Gee LK, Jones JJ, Fariss CJ, Burke M, Fowler JH. The paradox of weak ties in 55 countries. J Econ Behav Organ (2017) 133:362–72. doi:10.1016/j.jebo.2016.12.004
124. Kuhlman CJ, Tuli G, Swarup S, Marathe MV, Ravi SS. Blocking simple and complex contagion by edge removal. Proc - IEEE Int Conf Data Mining, ICDM (2013) 2013:399–408. doi:10.1109/ICDM.2013.47
125. Bellingeri M, Turchetto M, Bevacqua D, Scotognella F, Alfieri R, Nguyen Q, et al. Modeling the consequences of social distancing over epidemics spreading in complex social networks: From link removal analysis to SARS-CoV-2 prevention. Front Phys (2021) 9:1–7. doi:10.3389/fphy.2021.681343
126. Pastor-Satorras R, Castellano C, Van Mieghem P, Vespignani A. Epidemic processes in complex networks. Rev Mod Phys (2015) 87:925–79. doi:10.1103/RevModPhys.87.925
127. Thurner S, Klimek P, Hanel R. A network-based explanation of why most COVID-19 infection curves are linear. Proc Natl Acad Sci U S A (2020) 117:22684–9. doi:10.1073/pnas.2010398117
128. Amaral MA, Oliveira MMd., Javarone MA. An epidemiological model with voluntary quarantine strategies governed by evolutionary game dynamics. Chaos, Solitons and Fractals (2021) 143:110616. doi:10.1016/j.chaos.2020.110616
129. Albert R, Barabási A. Statistical mechanics of complex networks. Rev Mod Phys (2002) 74:47–97. doi:10.1103/revmodphys.74.47
130. Radicchi F, Castellano C. Breaking of the site-bond percolation universality in networks. Nat Commun (2015) 6:10196. doi:10.1038/ncomms10196
131. Bellingeri M, Cassi D, Vincenzi S. Efficiency of attack strategies on complex model and real-world networks. Phys A Stat Mech Its Appl (2014) 414:174–80. doi:10.1016/j.physa.2014.06.079
132. Jin L, James BD, Joshi MA. Mutual-friend based attacks in social network systems. Comput Secur (2013) 37:15–30. doi:10.1016/j.cose.2013.04.003
133. E Fonseca Bde PF, Sampaio RB, Fonseca MVde A, Zicker F. Co-authorship network analysis in health research: Method and potential use. Heal Res Pol Syst (2016) 14:34–10. doi:10.1186/s12961-016-0104-5
Keywords: social networks, weighted networks, weighted network analysis, network science, social physics
Citation: Bellingeri M, Bevacqua D, Sartori F, Turchetto M, Scotognella F, Alfieri R, Nguyen NKK, Le TT, Nguyen Q and Cassi D (2023) Considering weights in real social networks: A review. Front. Phys. 11:1152243. doi: 10.3389/fphy.2023.1152243
Received: 27 January 2023; Accepted: 13 March 2023;
Published: 28 March 2023.
Edited by:
Haroldo V. Ribeiro, State University of Maringá, BrazilReviewed by:
Divya Sindhu Lekha, Indian Institute of Information Technology, Kottayam, IndiaAyse Peker-Dobie, Istanbul Technical University, Türkiye
Copyright © 2023 Bellingeri, Bevacqua, Sartori, Turchetto, Scotognella, Alfieri, Nguyen, Le, Nguyen and Cassi. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: M. Bellingeri, bWljaGVsZS5iZWxsaW5nZXJpQHVuaXByLml0
 M. Bellingeri
M. Bellingeri D. Bevacqua3
D. Bevacqua3 F. Scotognella
F. Scotognella