A hybrid neural architecture search for hyperspectral image classification

Convolution neural network (CNN)is widely used in hyperspectral image (HSI) classification. However, the network architecture of CNNs is usually designed manually, which requires careful fine-tuning. Recently, many technologies for neural architecture search (NAS) have been proposed to automatically design networks, further improving the accuracy of HSI classification to a new level. This paper proposes a circular kernel convolution-β-decay regulation NAS-confident learning rate (CK-βNAS-CLR) framework to automatically design the neural network structure for HSI classification. First, this paper constructs a hybrid search space with 12 kinds of operation, which considers the difference between enhanced circular kernel convolution and square kernel convolution in feature acquisition, so as to improve the sensitivity of the network to hyperspectral information features. Then, the β-decay regulation scheme is introduced to enhance the robustness of differential architecture search (DARTS) and reduce the discretization differences in architecture search. Finally, we combined the confidence learning rate strategy to alleviate the problem of performance collapse. The experimental results on public HSI datasets (Indian Pines, Pavia University) show that the proposed NAS method achieves impressive classification performance and effectively improves classification accuracy.

1 Introduction

Hyperspectral sensing images (HSIs) collect rich spatial–spectral information in hundreds of spectral bands, which can be used to effectively distinguish ground cover. HSI classification is based on pixel level, and many traditional methods based on machine learning have been used, such as the K-nearest neighbor (KNN) [1] and support vector machine (SVM) [2]. The HSI classification method based on deep learning can effectively extract the robust features to obtain better classification performance [3–5].

Limited by the cost of computing resources and the workload of parameter adjustment, it is inevitable to promote the development of automatic design efficient neural network technology [6]. The goal of NAS (neural architecture search)is to select and combine different neural operations from predefined search spaces and to automate the construction of high-performance neural network structures. Traditional NAS work uses the reinforcement learning algorithm (RL) [7], evolutionary algorithm (EA) [8], and the gradient-based method to conduct architecture search.

In order to reduce resource consumption, one-shot NAS methods based on supernet are developed [9]. DARTS is a one-shot NAS method with a distinguishable search strategy [10]. By introducing Softmax function, it expands the discrete space into a continuous search optimization process. Specifically, it can reduce the workload of network architecture design and reduce the process of a large number of verification experiments [9].

The method based on the automatic design of convolutional neural network for hyperspectral image classification (CNAS) introduces DARTS into the HSI classification task for the first time. The method uses point-by-point convolution to compress the spectral dimensions of HSI into dozens of dimensions and then uses DARTS to search for neural network architecture suitable for the HSI dataset [11]. Subsequently, based on the method of 3D asymmetric neural architecture search (3D-ANAS), a classification framework from pixel to pixel was designed, and the redundant operation problem was solved by using the 3D asymmetric CNN, which significantly improved the calculation speed of the model [12].

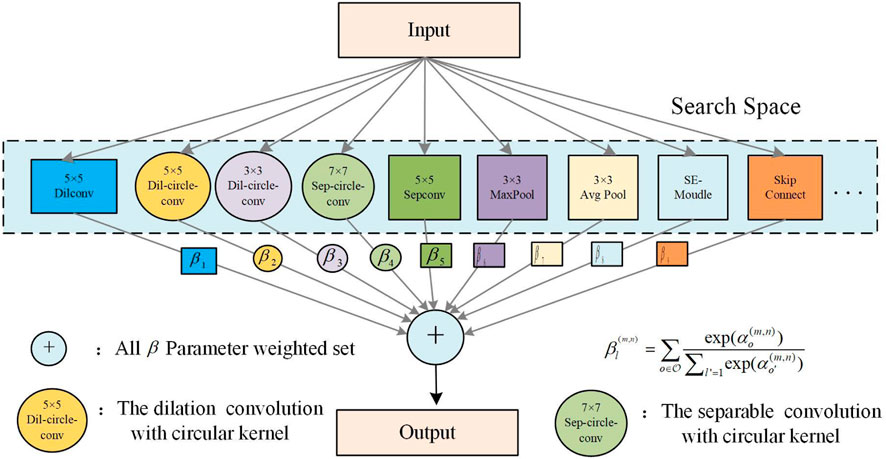
Traditional CNN design uses square kernel to extract image features, which brings significant challenges to the computing system because the number of arithmetic operations increases exponentially with the increase of network size. The features acquired by the square kernel are usually unevenly distributed [13] because the weights at the central intersection are usually large. Inspired by circular kernel (CK) convolution, this paper studies a new NAS paradigm to classify HSI data by automatically designing hybrid search space. The main contributions of this paper are as follows:

1) An effective framework is proposed to design the NAS, called CK-βNAS-CLR, which is composed of a hybrid search space of 12 operations of circular convolution with different convolution methods, different scales, and attention mechanism to effectively improve the feature acquisition ability.

2) β-decay regularization is introduced effectively to stabilize the search process and make the searched network architecture transferable among multiple HSI datasets.

3) We introduced the confident learning rate strategy to focus on the confidence level when updating the structure weight gradient and to prevent over-parameterization.

2 Materials and methods

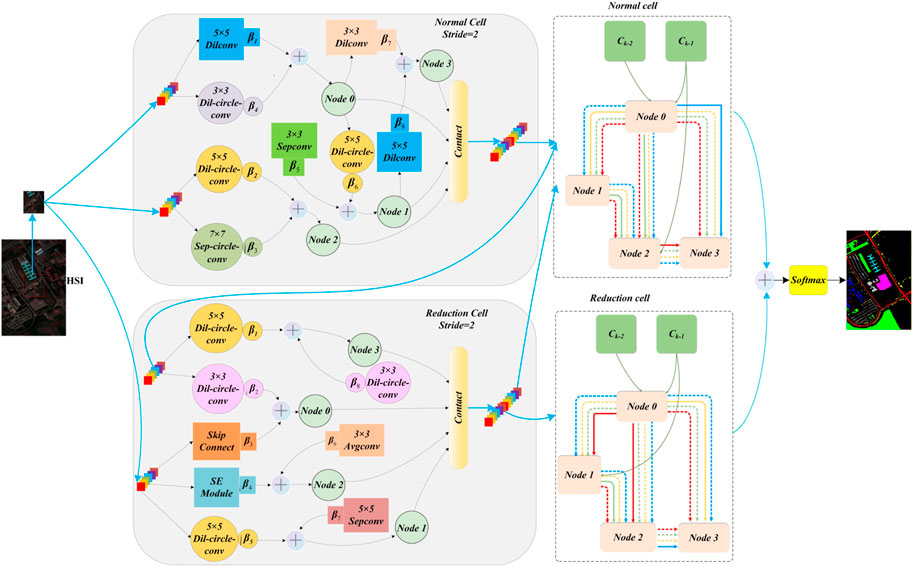
As shown in Figure 1, the NAS framework for HSI proposed is described, called as CK-βNAS-CLR. Compared with other HSI classification methods, this method aims to alleviate the shortcomings of traditional microNAS methods from three aspects of search space, search strategy, and architecture resource optimization and effectively improve the classification accuracy.

FIGURE 1

FIGURE 1. Overall framework of the proposed CK-βNAS-CLR model.

DARTS is a basic framework which adopts weight sharing and combines hypernetwork training with the search of the best candidate architecture to effectively reduce the waste of computing resources. First, the hyperspectral image is clipped into patch by sliding window as input. Then, the hybrid search space of CK convolution and attention mechanism is constructed, and the operation search between nodes is carried out in the hybrid search space to effectively improve the feature acquisition ability of the receptive field. At the same time, the architecture parameter set β, which represents the importance of the operator, is attenuated and regularized, effectively strengthening the robustness of DARTS and reducing the discretization differences in the architecture search process. After the search is completed, the algorithm stacks multiple normal cells and reduction cells to form the optimal neural structure, and then the classification results are obtained through Softmax operation. In addition, CLR is proposed to stack decay regularization to alleviate the performance crash of DARTS, improve memory efficiency, and reduce architecture search time.

2.1 The proposed NAS framework for HSI classification

2.1.1 Integrating circular kernel to convolution

The circular kernel is isotropic and can be realized from all directions. In addition, symmetric circular nuclei can ensure rotation invariance, which uses bilinear interpolation to approximate the traditional square convolution kernel to a circular convolution kernel, and uses matrix transformation to reparametrize the weight matrix, replacing the original matrix with the changed matrix to realize the offset of receptive field reception. Without considering the loss, the expression of receptive field H of standard 3 × 3 square convolution kernel with a dilation of 1 is written as follows:

$H=\left\{\left(-\mathrm{1,1}\right),\left(\mathrm{0,1}\right),\left(\mathrm{1,1}\right),\left(-\mathrm{1,0}\right),\left(\mathrm{0,0}\right),\left(\mathrm{1,0}\right),\left(-1,-1\right),\left(0,-1\right),\left(1,-1\right)\right\},(1)$

where $H$ represents the offset set of the neighborhood convolved on the center pixel. By convolution, the feature map is $R\in H^{\mathrm{S}\times \mathrm{S}}$ and kernel is $J\in H^{M\times N}$. The output feature map $\mathrm{U}\in H^{M\times N}$ can be obtained, and the coordinates of each position are shown in formula (2).

$U_{\mathrm{l}}\in {\displaystyle \sum }_{k\in H}{R}_k{J}_{\mathrm{l}+k}.(2)$

So, we get $U=R\otimes J$, where $\otimes$ represents the classical convolution operation used by the CNN. Therefore, the change of receptive field of nucleus circularis 3 × 3 is shown in formula(3).

$B=\left\{\left(-\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2}\right),\left(\mathrm{0,1}\right),\left(\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2}\right),\left(-\mathrm{1,0}\right),\left(\mathrm{0,0}\right),\left(\mathrm{1,0}\right),\left(-\frac{\sqrt{2}}{2},-\frac{\sqrt{2}}{2}\right),\left(0,-1\right),\left(\frac{\sqrt{2}}{2},-\frac{\sqrt{2}}{2}\right)\right\}.(3)$

For the sampling problem of circular convolution kernels, we selected the offset ($\left\{\Delta b\right\}$) of $k$ for different discrete kernel positions and resampled the offset to input $J$ to obtain circular receptive fields. Because the sampling receptive field of circular nucleus has a fraction, we use bilinear interpolation to approximate the sampling value of the receptive field.

$U_{\mathrm{l}}\in {\displaystyle \sum }_{k\in H}{R}_k{J}_{1+k+\Delta b},(4)$

$J_b={\displaystyle \sum }_{k\in H}\mathcal{V}\left(k,b\right)J_k,(5)$

where $b$ represents the grid position in the circular receptive field and $k$ represents all grid positions in the square receptive field, which is the kernel of two-dimensional bilinear interpolation. According to the bilinear interpolation, $\mathcal{V}$ can be divided into two one-dimensional cores.

$\mathcal{V}\left(k,b\right)=g\left(k_x,b_x\right)\cdot g\left(k_y,b_y\right),(6)$

$g\left(q,e\right)=\mathit{max}\left(\mathrm{0,1}-\left|q-e\right|\right).(7)$

Therefore, $\mathcal{V}\left(k,b\right)\ne 0$ and $\mathcal{V}\left(k,b\right)=1$ only correspond to the corresponding grid $k$ of receptive field $\mathrm{{\rm B}}$ with grid location $b$. Then, we let ${\widehat{J}}_{RF\left(l\right)}\in {\mathrm{{\rm B}}}^{S^2\times 1}$ and $\widehat{R}\in {\mathrm{{\rm B}}}^{S^2\times 1}$ represent the adjusted receptive field centered on position $i$ and nucleus, respectively. Generally, the standard convolution can be defined as shown in formula (8), so after replacing the circular convolution kernel, the circular convolution can be located as shown in formula (9).

$U_l\in {\widehat{R}}^T{\widehat{J}}_{RF\left(l\right),}(8)$

$U_l\in {\widehat{R}}^T\left(C{\widehat{J}}_{RF\left(l\right)}\right)=\left({\widehat{R}}^{T}C\right){\widehat{J}}_{RF\left(l\right),}(9)$

where ${C\in \mathrm{{\rm B}}}^{S^2\times S^2}$ is a fixed sparse coefficient matrix, so let ${J\in \mathrm{{\rm B}}}^{S^2\times S^2}$, ${U\in \mathrm{{\rm B}}}^{S^2\times S^2}$, and ${R\in \mathrm{{\rm B}}}^{S^2\times S^2}$ be the input feature map, output feature map, and kernel, respectively, so the corresponding definition of formula (9) can be written as formula (10).

$U_l\in R\otimes \left(C*J\right)=\left(R*C\right)\otimes J,(10)$

where $C*J$ is the convolution process of changing the square receptive field into a circular receptive field. Thus, we can calculate the core weight to achieve operation $C*J$. This calculation method can effectively avoid calculating the offset of multiple convolutions and reduce the cost of core operation. Next, we summarize the analysis of the actual effect of the transformation matrix. We let $\Delta R=R^{a+1}-R^a$, and the value of a change on the output is shown in formula (11). The squared value of a change on the output is shown in formula (12).

$\Delta U=U^{a+1}-U^a,(11)$

$\begin{array}{c}{‖\Delta U‖}^2={\left(C*J\right)}^T\otimes \Delta R^T\Delta R\otimes \left(\mathrm{C}*J\right).\\ =J^T\otimes \left(C^T*{\Delta R}^T\Delta R*C\right)\otimes J\end{array}(12)$

In contrast, $\Delta U$ of the traditional convolution layer is defined by ${\Delta R}^T\Delta R$ . Therefore, it can be concluded that the transformation matrix $C$ caused by the circular core can provide a better choice for the gradient descent path of DARTS.

2.1.2 β-decay regularization scheme

In order to alleviate unfair competition in DARTS, we introduced the β-decay regulation scheme [14] so as to improve its robustness and generalization ability and effectively reduce the search memory and the search cost to find the best architecture as shown in Figure 2.

FIGURE 2

FIGURE 2. β-decay regularization scheme.

${\alpha }_o^{\left(m,n\right)}$ converts the discretization operation of the optional operation set $\mathcal{O}$ in the search space into an operable continuous set. After implementing Softmax operation, the architecture parameter set ${\beta }_l^{\left(m,n\right)}$ is obtained, which is attenuated and regularized.

${\beta }_l^{\left(m,n\right)}={\displaystyle \sum }_{o\in \mathcal{O}}\frac{\mathit{exp}\left({\alpha }_o^{\left(m,n\right)}\right)}{{\sum }_{l^{\prime }=1}\mathit{exp}\left({\alpha }_{o^{\prime }}^{\left(m,n\right)}\right)},(13)$

where ${\beta }_l^{\left(m,n\right)}$ is the combination of architecture parameters between node m and node n and $l$ is the number of optional operations. Each cell can have up to N nodes, and ${\alpha }_o^{\left(m,n\right)}$ represents the architecture parameters. A special coefficient for each candidate operation ${\beta }_o^{\left(m,n\right)}$ is defined.

${\beta }_o^{\left(m,n\right)}=\frac{\mathit{exp}\left({\alpha }_o^{\left(m,n\right)}\right)}{{\sum }_{o^{\prime }\in \mathcal{O}}\exp \left({\alpha }_{o^{\prime }}^{\left(m,n\right)}\right)}.(14)$

Starting from the default setting of regularization, consider the one-step update of architecture parameter $\alpha$, where ${\varsigma }_{\alpha }$ represents the learning rate a of architecture parameters.

${\alpha }_l^{t+1}\leftarrow {\alpha }_l^t-{\eta }_{\alpha }.{\nabla }_{\alpha }{\mathcal{L}}_{valid}.(15)$

For the special gradient descent algorithm of DARTS, these regularized gradients need to be normalized ($\mathcal{N}\mathcal{L}$) through the sum size and to realize the average distribution of the total gradient without normalization.

${\alpha }_l^{t+1}\leftarrow {\alpha }_l^t-{\eta }_{\alpha }.{\nabla }_{\alpha }{\mathcal{L}}_{valid}-{\varsigma }_{\alpha }\delta \mathcal{N}\mathcal{L}\left({\alpha }_l^t\right),(16)$

${\alpha }_l^{t+1}\leftarrow {\alpha }_l^t-{\eta }_{\alpha }.{\nabla }_{\alpha }{\mathcal{L}}_{valid}-{\varsigma }_{\alpha }\delta \left({\alpha }_k^y\right).(17)$

In the DARTS search process, the architecture parameter set, β, is used to express the importance of all operators. The research on explicit regularization of β can more clearly standardize the optimization of architecture parameters so as to improve the robustness and architecture universality of DARTS. We use the $\chi$ function with $\alpha$ as the independent variable to express the total impact of attenuation regularization.

${\overline{\beta }}_l^{t+1}={\chi }_l^{t+1}\left({\alpha }_l^t\right){\beta }_l^{t+1},(18)$

${\alpha }_l^{t+1}\leftarrow {\alpha }_l^t-{\eta }_{\alpha }.{\nabla }_{\alpha }{\mathcal{L}}_{valid}-{\varsigma }_{\alpha }\delta R\left({\alpha }_k^t\right),(19)$

where the $\chi$ function ($R$ is the independent variable) represents the overall influence of β attenuation regularization and $R$ is the mapping function. We can iterate for dividing the single-step update parameter value ${\beta }_l^{t+1}$ and parameter value weighted sum ${\overline{\beta }}_l^{t+1}$ of β.

$\frac{{\overline{\beta }}_l^{t+1}}{{\beta }_l^{t+1}}=\frac{{\sum }_{l^{\prime }=1}^{\left|\mathcal{O}\right|}\mathit{exp}\left({\alpha }_{l^{\prime }}^{t+1}\right)}{{\sum }_{l^{\prime }=1}^{\left|\mathcal{O}\right|}{\left[\mathit{exp}\left(R\left({\alpha }_l^t\right)-R\left({\alpha }_{l^{\prime }}^t\right)\right)\right]}^{\delta {\varsigma }_{\alpha }}\mathit{exp}\left({\alpha }_{l^{\prime }}^{t+1}\right)}.(20)$

It can be found that mapping function $R$ determines the impact of $\alpha$ on β. To avoid excessive regularization and optimization difficulties, Softmax is used to normalize $\alpha$.

$R\left({\alpha }_l\right)=\frac{\mathit{exp}\left({\alpha }_l\right)}{{\sum }_{l^{\prime }=1}^{\left|\mathcal{O}\right|}\mathit{exp}\left({{\alpha }_l}^{\prime }\right).}(21)$

We can obtain the impact and effect of our method.

${\chi }_l^{t+1}\left({\alpha }_l^t\right)=\frac{{\sum }_{l^{\prime }=1}^{\left|\mathcal{O}\right|}\mathit{exp}\left({\alpha }_{l^{\prime }}^{t+1}\right)}{{\sum }_{l^{\prime }=1}^{\left|\mathcal{O}\right|}{\left[\mathit{exp}\left(\frac{exp\left({\alpha }_l^t\right)-\mathit{exp}\left({\alpha }_{l^{\prime }}^t\right)}{{\sum }_{l^{″}=1}^{\left|\mathcal{O}\right|}\mathit{exp}\left({\alpha }_{l^{″}}^t\right)}\right)\right]}^{\delta {\varsigma }_{\alpha }}\mathit{exp}\left({\alpha }_{l^{\prime }}^{t+1}\right)}{\chi }_l^{t+1}\left({\alpha }_l^t\right).(22)$

2.1.3 Confident learning rate strategy

When the NAS method is used to classify hyperspectral datasets, a large number of parameters will be generated. When the training samples are limited, the performance of the network may be reduced due to the over-fitting phenomenon, which will lead to low memory utilization during the training process. CLR is used to alleviate these two problems [15].

After applying the Softmax operation, the structure is relaxed. The gradient descent algorithm is used to optimize the $\alpha =\left\{{\alpha }^{\left(m,n\right)}\right\}$ matrix, and the original weight of the network is called $w$. Then, the cross-entropy formula is used to calculate the loss value in the training stage and the parameters ${\mathcal{L}}_{train}$ and ${\mathcal{L}}_{valid}$ are updated.

In order to enable both to achieve the optimization strategy at the same time, it is necessary to fix the value of $\alpha =\left\{{\alpha }^{\left(m,n\right)}\right\}$ matrix on the training set, update $w$ using the gradient descent algorithm, fix the $w$ value on the verification set, update the $\alpha =\left\{{\alpha }^{\left(m,n\right)}\right\}$ value using the gradient descent algorithm, and obtain the best parameter value repeatedly. Stop the optimization after finding the best architecture neural architecture ${\alpha }_{\mathrm{o}}^{*}$ and minimize the verification loss ${\mathcal{L}}_{valid}\left(w^{*},{\alpha }^{*}\right)$.

$\underset{\mathrm{\alpha }}{\mathit{min}}{\mathcal{L}}_{val\text{id}}\left(w^{*}\left(\alpha \right),\alpha \right),(23)$

$\mathrm{s}.\mathrm{t}.w^{*}\left(\alpha \right)=\mathit{arg}\underset{w}{\mathit{min}}{\mathcal{L}}_{train}\left(w,\alpha \right).(24)$

NAS architecture parameters will be over-parameterized with the increase of training time. Therefore, the gradient confidence obtained from the parameterized DARTS should increase with the training time of the architecture weight update.

$L{R}_{Confident}\left(a\right)={\left(\frac{a}{A}\right)}^{\tau }\times L{R}_{\alpha },(25)$

where $\alpha$ represents the number of epochs currently trained, $A$ represents the preset total epochs, and $\tau$ is the confidence factor of CLR. Through the update of the confidence learning rate, the network obtains ${\mathcal{L}}_{valid}$ and uses it for gradient update.

$gra{d}_{\alpha }={\nabla }_{\alpha }{\mathcal{L}}_{val\text{id}}\left(w-\xi {\nabla }_w{\mathcal{L}}_{train}\left(\omega ,\alpha \right),\alpha \right).(26)$

The confidence learning rate is established in the process of architecture gradient update.

$gra{d}_{\alpha }=L{R}_{confident}*{\nabla }_{\alpha }{\mathcal{L}}_{val\text{id}}\left(w-\xi {\nabla }_w{\mathcal{L}}_{train}\left(w,\alpha \right),\alpha \right).(27)$

3 Results

Our experiments are conducted using Intel (R) Xeon (R) 4208 CPU@2.10GHz Processor and Nvidia GeForce RTX 2080Ti graphics card. We selected the average of 10 experiments to compute the overall accuracy (OA), average accuracy (AA), and Kappa coefficient (K).

3.1 Comparison with state-of-the-art methods

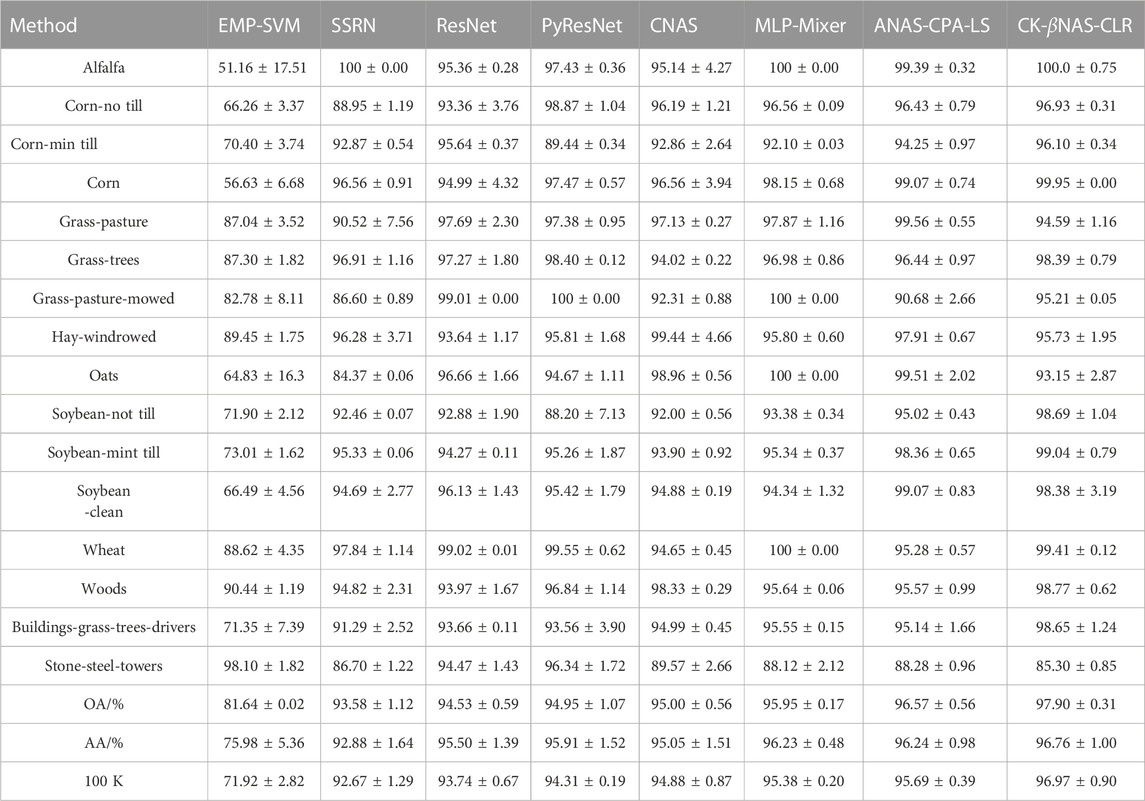
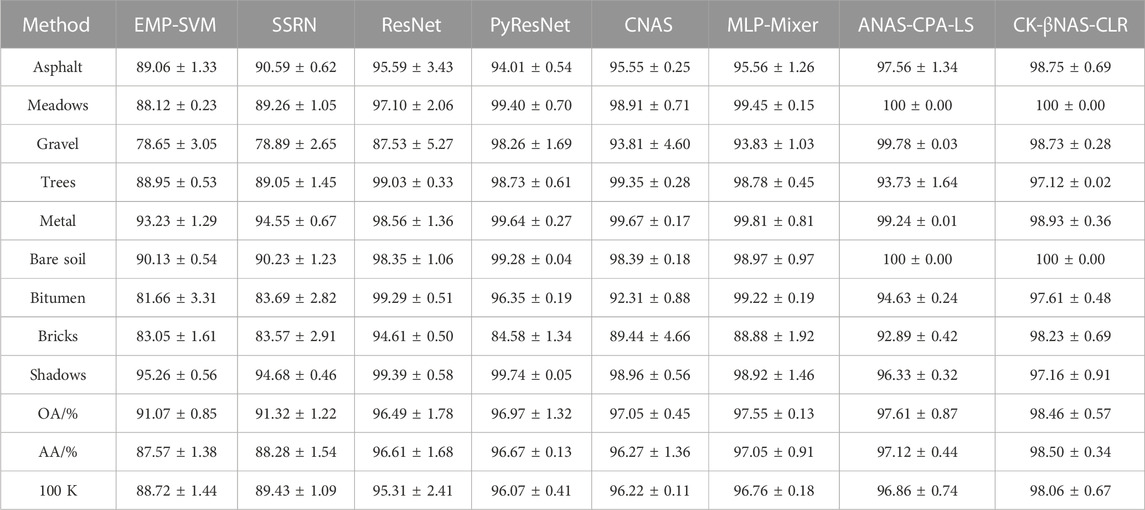
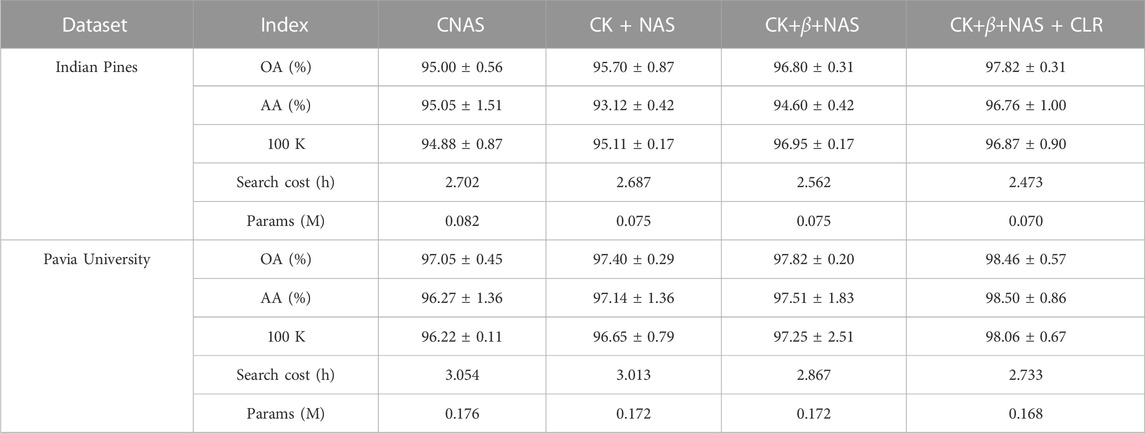
In this section, we select some advanced methods to make comparison so as to evaluate the classification performance, which include extended morphological profile combined with support vector machine (EMP-SVM) [16], spectral spatial residual network (SSRN) [17], residual network (ResNet) [18], pyramid residual network (PyResNet) [19], multi-layer perceptron mixer (MLP Mixer) [20], CNAS [11], and efficient convolutional neural architecture search (ANAS-CPA-LS) [21]. All experimental results are shown in Tables 1, 2. The sample is clipped by using the sliding window strategy size of 32 × 32, and the overlap rate is set to 50%. We randomly selected 30 samples as the training dataset and 20 samples as the validation dataset. The training time is set to 200, and the learning rate of the three data sets is set to 0.001.

TABLE 1

TABLE 1. Performance comparison of different methods of the Indian Pines dataset.

TABLE 2

TABLE 2. Performance comparison of different methods of the Pavia University dataset.

In Table 1, compared with EMP-SVM, SSRN, ResNet, PyResNet, CNAS, MLP Mixer, and ANAS-CPA-LS, OA obtained by our proposed method is increased by 16.26%, 4.32%, 3.37%, 2.95%, 2.9%, 1.95%, and 1.33%, respectively, on the Indian Pines dataset. Figures 3, 4 shows the classification diagram obtained from a visual perspective. By comparing the classification diagrams obtained, we can draw a conclusion that our algorithm achieves better performance. Compared with CNAS, our method uses a hybrid search space, which can effectively expand the receptive field acquired by pixels, improve the flexibility of different convolution kernel operations to process spectrum and space, and achieve higher classification accuracy.

FIGURE 3

FIGURE 3. Classification results of the Indian pines dataset. (A) Ground-truth map, (B) EMP-SVM, (C) SSRN, (D)ResNet, (E) PyResNet, (F) CNAS, (G) MLP-Mixer, (H) ANAS-CPA-LS, and (I) (I) CK-βNAS-CLR.

FIGURE 4

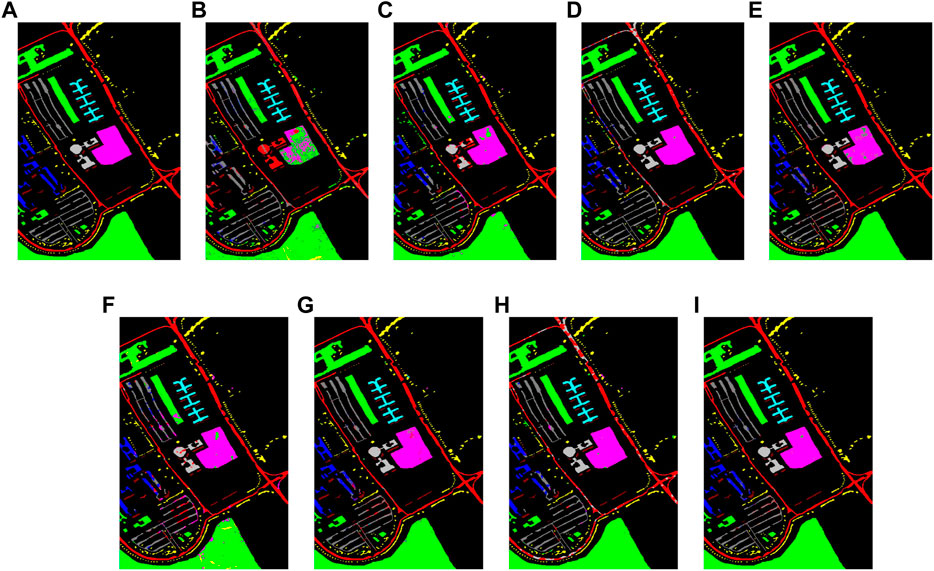
FIGURE 4. Classification results of the Pavia University dataset. (A) Ground-truth map, (B) EMP-SVM, (C) SSRN, (D)ResNet, (E) PyResNet, (F) CNAS, (G) MLP-Mixer, (H) ANAS-CPA-LS, and (I) CK-βNAS-CLR.

4 Discussion

The ablation study results are provided in Table 3. When CNAS is combined with hybrid search space, OA increases by 0.70%, 0.35%, and 0.54%, which proves that the hybrid search space can improve the sensitivity of the network to hyperspectral information features and slightly improve the classification performance of the model. Compared with CNAS, CK-NAS has no time change in the search time on the three datasets but has achieved better classification accuracy. CK-βNAS-CLR search gets better results with fewer parameters and involves less computational complexity.

TABLE 3

TABLE 3. Ablation results on the two datasets.

5 Conclusion

In this paper, the neural network structure CK-βNAS-CLR is proposed. First of all, we introduce a hybrid search space with circular kernel convolution, which can not only enhance the robustness of the model and the ability of receptive field acquisition but also achieve a better role in optimizing the path. Second, we quoted the β-decay regulation scheme, which reduced the discretization difference and the search time. Finally, the confidence learning rate strategy is introduced to improve the accuracy of model classification and reduce computational complexity. The experiment was conducted on two HSI datasets, and CK-βNAS-CLR is compared with seven methods, and the experimental results show that our method achieves the most advanced performance while using less computing resources. In future, we will use an adaptive subset of the data even when training the final architecture, which may lead to faster runtime and lower regularization term.

Data availability statement

Publicly available datasets were analyzed in this study. These data can be found here: https://www.ehu.eus/ccwintco/index.php?%20title=Hyperspectral-Remote-Sensing-Scenes.

Author contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Funding

This work was funded by the Reserved Leaders of Heilongjiang Provincial Leading Talent Echelon of 2021, high and foreign expert’s introduction program (G2022012010L), and the Key Research and Development Program Guidance Project (GZ20220123).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Chandra B, Sharma RK. On improving recurrent neural network for image classification. In: Proceeding of the International Joint Conference on Neural Networks. Alaska, USA: IJCNN (2017). p. 1904–7. doi:10.1109/IJCNN.2017.7966083

CrossRef Full Text | Google Scholar

2. Samadzadegan F, Hasani H, Schenk T. Simultaneous feature selection and SVM parameter determination in classification of hyperspectral imagery using Ant Colony Optimization. Remote Sens (2012) 38:139–56. doi:10.5589/m12-022

CrossRef Full Text | Google Scholar

3. Hu W, Huang Y, Wei L, Zhang F, Li H. Deep convolutional neural networks for hyperspectral image classification. J Sensors (2015) 2015:1–12. doi:10.1155/2015/258619

CrossRef Full Text | Google Scholar

4. Makantasis K, Karantzalos K, Doulamis A, Doulamis N. Deep supervised learning for hyperspectral data classification through convolutional neural networks. In: 2015 IEEE International Geoscience and Remote Sensing Symposium (IGARSS). Milan, Italy: IGARSS (2015). p. 4959–62.

CrossRef Full Text | Google Scholar

5. Li W, Wu G, Zhang F, Du Q. Hyperspectral image classification using deep pixel-pair features. IEEE Trans Geosci Remote Sensing (2017) 55(2):844–53. doi:10.1109/tgrs.2016.2616355

CrossRef Full Text | Google Scholar

6. Kaifeng B, Lingxi X, Chen X, Longhui W, Tian Q. GOLD-NAS: Gradual,one-level, differentiable (2020). p. 03331. arXiv:2007.

Google Scholar

7. Real E, Aggarwal A, Huang Y, Le QV, “Regularized evolution for image classifier architecture search,” in Proc. AAAI Conf. Artif. Intell (2019) 33, 4780–9. doi:10.1609/aaai.v33i01.33014780

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Tan M, Chen B, Pang R, V asudevan V, Sandler M, Howard A, et al. MnasNet: Platform-aware neural architecture search for mobile. Long Beach, CA, USA: CVPR (2019). 2820–8.

Google Scholar

9. Liang H. DARTS+: Improved differentiable architecture search with early stopping (2020). arXiv:1909.06035. [Online]. Available: https://arxiv.org/abs/1909.06035 (Accessed October 20, 2020).

Google Scholar

10. Guo Z, “Single path one-shot neural architecture search with uniform sampling,” in Proc. IEEE Eur. Conf. Comput. Vis (2020), 544–60.

CrossRef Full Text | Google Scholar

11. Chen Y, Zhu K, Zhu L, He X, Ghamisi P, Benediktsson JA. Automatic design of convolutional neural network for hyperspectral image classification. IEEE Trans Geosci Remote Sensing (2019) 57(9):7048–66. doi:10.1109/tgrs.2019.2910603

CrossRef Full Text | Google Scholar

12. Zhang H, Gong C, Bai Y, Bai Z, Li Y. 3d-anas: 3d asymmetric neural architecture search for fast hyperspectral image classification (2021). arXiv preprint arXiv:2101.04287, 2021.[Online]. Available: https://arxiv.org/abs/2101.04287 (Accessed Janunary 12, 2021).

Google Scholar

13. Li G, Qian G, Delgadillo IC, Muller M, Thabet A, Ghanem B. Sgas: Sequential greedy architecture search. In: Proc. IEEE Conf. Comput. Vis. Pattern Recognit (2020). p. 1620–30.

CrossRef Full Text | Google Scholar

14. Ye P, Li B, Li Y, Chen T, Fan J, Ouyang W, et al. beta$-DARTS: Beta-Decay regularization for differentiable architecture search, in Proceeding of the 2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), New Orleans, LA, USA (2022), 10864–73.

Google Scholar

15. Ding Z, Chen Y, Li N, Zhao D. BNAS-v2: Memory-Efficient and performance-collapse-prevented broad neural architecture search. IEEE Trans Syst Man, Cybernetics: Syst (2022) 52(10):6259–72. doi:10.1109/TSMC.2022.3143201

CrossRef Full Text | Google Scholar

16. Melgani F, Bruzzone L. Classification of hyperspectral remote sensing images with support vector machines. IEEE Trans Geosci Remote Sensing (2004) 42(8):1778–90. doi:10.1109/tgrs.2004.831865

CrossRef Full Text | Google Scholar

17. Zhong Z, Li J, Luo Z, Chapman M. Spectral–spatial residual network for hyperspectral image classification: A 3-D deep learning framework. IEEE Trans Geosci Remote Sensing (2018) 56(2):847–58. doi:10.1109/tgrs.2017.2755542

CrossRef Full Text | Google Scholar

18. Liu X, Meng Y, Fu M, "Classification research based on residual network for hyperspectral image,"In, Proceeding of the 2019 IEEE 4th International Conference on Signal and Image Processing (IC) (2019). 911–5.

CrossRef Full Text | Google Scholar

19. Paoletti ME, Haut JM, Fernandez-Beltran R, Plaza J, Plaza AJ, Pla F. Deep pyramidal residual networks for spectral–spatial hyperspectral image classification. IEEE Trans Geosci Remote Sensing (2019) 57(2):740–54. doi:10.1109/TGRS.2018.2860125

CrossRef Full Text | Google Scholar

20. He X, Chen Y. Modifications of the multi-layer Perceptron for hyperspectral image classification. Remote Sensing (2021) 13(17):3547. doi:10.3390/rs13173547

CrossRef Full Text | Google Scholar

21. Wang A, Xue D, Wu H, Gu Y. Efficient convolutional neural architecture search for LiDAR DSM classification. IEEE Trans Geosci Remote Sensing (2022) 60:1–17. Art no. 5703317. doi:10.1109/TGRS.2022.3171520

CrossRef Full Text | Google Scholar