- 1Science Institute, University of Iceland, Reykjavík, Iceland
- 2Peter Grünberg Institute and Institute for Advanced Simulation, Forschungszentrum Jülich and JARA, Jülich, Germany
- 3Department of Physics, RWTH Aachen University, Aachen, Germany
- 4Department of Physics and Astronomy, Uppsala University, Uppsala, Sweden
- 5Independent Scholar, St Petersburg, Russia
Cubic chiral magnets exhibit a remarkable diversity of two-dimensional topological magnetic textures, including skyrmions. However, the experimental confirmation of topological states localized in all three spatial dimensions remains challenging. In this paper, we investigate a three-dimensional topological state called a heliknoton, which is a hopfion embedded into a helix or conic background. We explore the range of parameters at which the heliknoton can be stabilized under realistic conditions using micromagnetic modeling, harmonic transition state theory, and stochastic spin dynamics simulations. We present theoretical Lorentz TEM images of the heliknoton, which can be used for experimental comparison. Additionally, we discuss the stability of the heliknoton at finite temperatures and the mechanism of its collapse. Our study offers a pathway for future experimental investigations of three-dimensional topological solitons in magnetic crystals.
1 Introduction
Cubic chiral magnets have attracted significant theoretical and experimental attention due to the vast diversity of experimentally observed topological magnetic solitons. These materials include various Si- and Ge-based alloys with B20-type crystal structures, such as Fe1−xCox[1]; [2], [3]; [4]; [5]; [6], [7], and others [8]. The competition between the Heisenberg exchange interaction and the chiral Dzyaloshinskii-Moriya interaction [9]; [10] (DMI) stabilizes topological solitons in these materials. The most extensively studied types of magnetic solitons in these systems are magnetic skyrmions [11]; [12]. Skyrmions are vortex-like strings or tubes characterized by a topological index Q = −1. Experimental observations have revealed that clusters of skyrmion tubes can form complex three-dimensional superstructures, such as skyrmion braids [13]. Additionally, the skyrmion antiparticle, antiskyrmions, with topological charge Q = +1, have been observed in thin films of FeGe [14]. Skyrmion bags with arbitrary topological charge and skyrmions with chiral kinks are other solitons that have been reported [15]; [16]; [17]. Recently, the experimental observation of skyrmion bags with positive topological charge and their current-induced motion has been reported by Tang et al. [18].
Skyrmions, antiskyrmions, and skyrmion bags are two-dimensional (2D) topological solitons that are localized in the plane of the sample and confined by the free surfaces of the sample in the third dimension. The homotopy classification of these solitons is based on the continuous mapping between two spheres,
where the vector field
is the curvature vector of the vector field n and is frame-invariant, meaning it does not depend on the choice of coordinate frame [20,21]. For an unambiguous definition of Q, the direction of the z-axis should be chosen consistently with the magnetization n0 around the region of texture localization such that
Three-dimensional (3D) topological magnetic solitons belong to a distinct class of solutions that are localized in all three spatial dimensions. The classification of 3D magnetic solitons is based on the mapping
where V is a vector potential satisfying ∇ ×V = F. For localized 3D magnetic textures without singularities, the Hopf index H is an integer that has the following meaning: two morphologically distinct magnetic textures with identical H can be continuously transformed into each other without the appearance of singularities, whereas continuous transformations between magnetic configurations with different H are impossible. Statically stable structures with non-zero Hopf index are commonly referred to as Hopf solitons or hopfions. It should be noted that the topological charge Q is zero for any hopfion cross-section. An example of a hopfion texture with H = 1 is depicted in the first column of Figure 1.
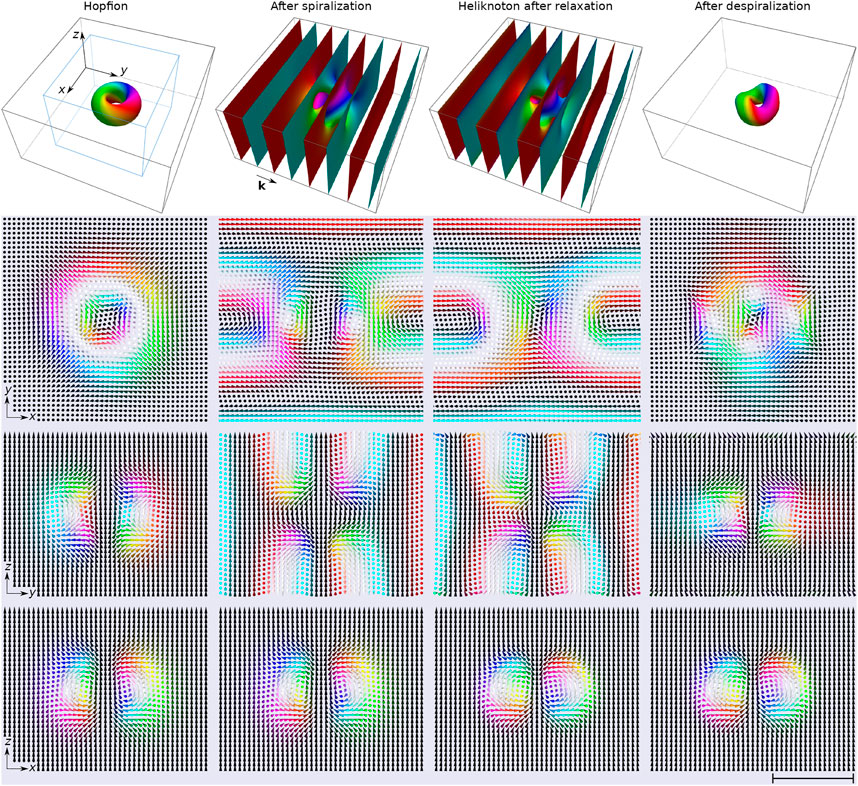
FIGURE 1. The images illustrate the spin texture inside the simulated box of the size 4LD × 4LD in the xy-plane and thickness of 2LD along the z-axis. The first column of images correspond to the hopfion anzatz (5). The second column represents the hopfion ansatz after applying the spiralization (6) with the k-vector of the spiral parallel to the y-axis, |k| = 2π/LD. The third column of images corresponds to the spin texture after the energy minimization assuming periodical boundary conditions in the xy-plane and free boundaries along the z-axis. The fourth column illustrates the relaxed spin texture after applying despiralization. The first row of images shows the isosurfaces nz = 0. The images depicted in the second, third, and fourth rows illustrate the magnetization field in the middle planes. For illustrative purposes, these images are bounded by the blue box of the size 2.5LD × 2.5LD × 2LD depicted in the top left image. The scale bar in the bottom right image corresponds to 1LD.
Theoretical studies of hopfions in various models of magnetic crystals began in the 1970s and continue to the present day [26]; [27]; [28]; [29]; [30]; [31]; [32]; [33]; [34]. There is also some limited experimental evidence for direct observation of such magnetic textures [35]; [23]. An intriguing type of hopfion has been predicted in cubic chiral magnets [31], but has not been observed so far. This hopfion is embedded not in a collinear ferromagnetic state but in a helical spin spiral state. We refer to it as a heliknoton following the terminology used in Refs.[36]; [31].
The primary goal of this study is to investigate the stability of the heliknoton under realistic conditions, taking into account the demagnetizing field effects, and estimate its stability range in films of different thicknesses. Additionally, we explore how the contrast in theoretical Lorentz transmission electron microscopy (TEM) images changes with film thickness and suggest optimal conditions for experimental observations of the heliknoton. Furthermore, we estimate the stability of the heliknoton at finite temperatures using two complementary methods: harmonic transition state theory (HTST) [37]; [38] and stochastic spin dynamics [39].
2 Model
To estimate the stability of heliknoton in the films of finite thickness, we use a micromagnetic model, which contains the Heisenberg exchange term, the DMI, the Zeeman interaction, and the self-energy of the demagnetizing field [13]; [40]:
where n(r) is the magnetization unit vector field, Ms is the saturation magnetization,
The static equilibrium heliknoton was obtained by numerically minimizing (4) with respect to the pair of fields n and A using a nonlinear conjugate gradient method (for details, see Ref. [13]). The simulated domain was discretized on a regular mesh with 256 × 256 × 181 nodes along the x, y, and z axes, respectively. To simulate an extended film, periodic boundary conditions were applied in the xy-plane. The results presented below for the micromagnetic calculations were obtained using GPU-accelerated software Excalibur [41]. Additionally, the results were verified with the publicly available software MuMax3 [42]. For definiteness, we used the material parameters for FeGe [43]:
3 Results
3.1 Initial guess
The initial configuration for heliknoton can be obtained in two steps. First, we insert in the simulated domain the classical hedgehog-based ansatz [24]; [44] for a hopfion in the ferromagnetic background:
where function G = G(r) with
In the second step, we implemented the spiralization procedure, which involves rotating all spins by an angle dependent on their coordinate along the wavevector k of the spiral. This transforms the ferromagnetic background into a helical one. Note that we applied this procedure to the entire volume, including the area containing the hopfion. For the case k‖ey the spiralization procedure can be written as
where n corresponds to the ansatz (5) and n′ is the ansatz for the hopfion in the helical background. The second column in Figure 1 illustrates the spin texture obtained after applying the spiralization (6) to the initial hopfion ansatz (5). The spin texture after energy minimization is shown in the third column of Figure 1. The quality of our ansatz is seen from the comparison of the spin textures before and after energy minimization. To better visualize the spin texture of the heliknoton, we utilize the despiralization procedure, which is illustrated in the last column of Figure 1. This procedure serves as the inverse of the spiralization operation (6). After the energy minimization or capturing a snapshot of the magnetic texture, we apply the transformation (6) with φ↦ − φ to obtain the despiralized spin texture. By using this procedure, one can gain a better understanding of the heliknoton’s spin texture.
3.2 Demagnetizing field effect
To estimate the demagnetizing field effect on the stability of heliknoton in a film of finite thickness, we performed systematic energy minimization at different external magnetic fields and film thickness starting with the ansatz (5)-(6). The results of these calculations performed with and without demagnetizing fields are presented in Figure 2. In these calculations, we keep the size of the simulated domain in xy-plane fixed, 4LD × 4LD, and vary only the film thickness between 0.5LD and 3.5LD. We have checked the interaction between heliknotons due to the periodic boundary conditions and found that it is relatively weak for this size of the simulation domain and does not significantly affect the heliknoton stability. Since the absolute values of the critical fields for the cases with and without demagnetizing fields are very different, we provide the critical fields in reduced units with respect to the saturation field of conical phase, Bc. This approach objectively estimates the range of heliknoton stability in both cases.
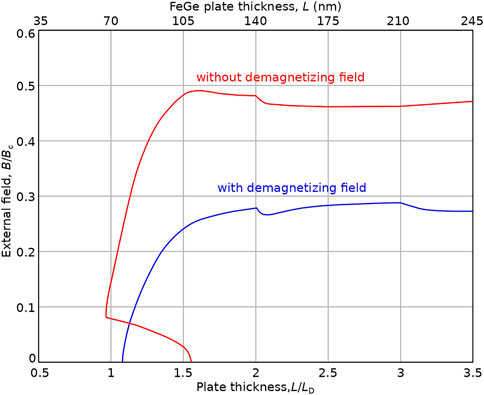
FIGURE 2. The diagram of stability for heliknoton in extended film calculated with and without demagnetizing field. For consistency, the external fields for both cases are given in reduced units with respect to the saturation field of the cone phase, Bc = BD + μ0Ms and Bc = BD, for the case with and without demagnetizing filed, respectively. For B20-type FeGe, Bc = BD + μ0Ms = 0.682 T and LD = 70 nm, see the top axis.
As follows from the diagram in Figure 2, taking into account the demagnetizing fields reduces the heliknoton stability range down to
At the film thickness below LD, the heliknoton does not fit the size of the film and becomes unstable in both cases, with and without demagnetizing fields. With increasing thickness, the critical heliknoton fields tend to saturate in both cases. Near the thicknesses commensurate to the period of helical modulations, e.g., L/LD = 2, the critical fields show minor picks. Similar but less pronounced pick is also seen at L/LD = 3 for the case with demagnetizing field only. We attribute the non-monotonic behavior of the collapse field to the chiral surface twist effect [45]. This effect manifests as an additional twist of magnetization near the free edges of the sample, which can penetrate into the volume of the sample. In the case of thin films with L/LD ≲ 3, these twists can distort the magnetic texture of the heliknoton. It is worth noting that the twist of magnetization near the free edges of the sample is also supported by the demagnetizing fields. The major difference is that the demagnetizing field does not favor a particular chirality of the surface twist, while the chiral surface twist gains energy only for the chirality favorable by the DMI. Thus, when we take into account the demagnetizing field, these two effects exhibit a cumulative effect. The most distinguishing is the behavior of the heliknoton in the thickness range between 1LD and 1.5LD. In this range, without demagnetizing fields, the solution remains stable only in the presence of the external field. Such anomaly in the stability of heliknoton in this case can be explained as the absence of cumulative effect from the chiral surface twist and demagnetizing fields. At realistic conditions, with demagnetizing fields, however, it is not the case, and the heliknoton is stable in the whole range of L > 1.1LD even at zero magnetic fields. The thickness of
3.3 Theoretical analysis of Lorentz TEM contrast
According to the diagram shown in Figure 2, there is no upper bound limit for the sample thickness, and even in a bulk crystal, a heliknoton can exist. However, the thickness of the sample plays a crucial role in experimental observation. In particular, the sample’s thickness is a significant factor for the applicability of Lorentz TEM. In our previous studies [13], we estimated the upper limit for the thickness of the FeGe sample to be approximately 300 nm. Above this thickness, the sample becomes no longer transparent for electrons. In the case of thicker samples beyond 300 nm, one must use a TEM setup with an acceleration voltage above 300 kV, the standard voltage for the most modern TEM instruments. Besides that, it is well known that for some magnetic textures, the Lorentz deflection forces can be completely canceled and thus give no contrast in non-tilted samples [46]; [47].
Since the heliknoton is the texture localized in all three dimensions, it is natural to expect that the contrast it produces in Lorentz TEM is thickness dependent. Figure 3 shows the Lorentz TEM contrast provided by the heliknoton in films of different thicknesses, which we calculated assuming material parameters for FeGe. For these calculations, we used a well-established method based on the phase object approximation [48]. For details of implementation, see Ref. [13].
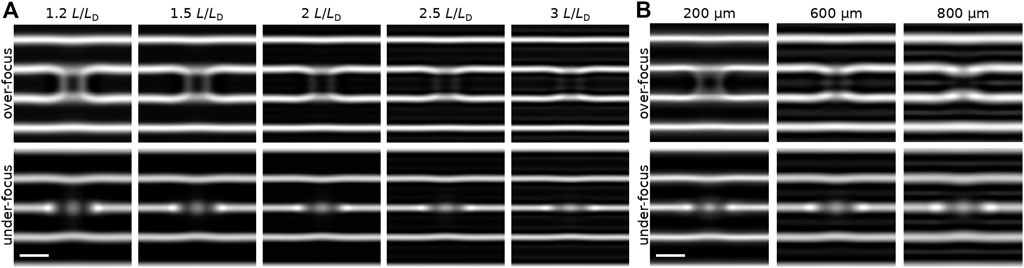
FIGURE 3. (A) The theoretical Lorentz TEM images of heliknoton at zero external field in the plate of different thicknesses. The thicknesses in reduced units with respect to the period of helical modulations LD are indicated on the top of each pair of over-focus and under-focus images. The defocus distance is 400 μm. (B) The over-focus and under-focus Lorentz TEM images of heliknoton in the film of thickness 2LD calculated for different defocus distances. The scale bar in (A, B) corresponds to 70 nm.
As seen from Figure 3A, above the thickness of
3.4 Minimum energy path calculations and HTST analysis
To estimate the stability of heliknoton at finite temperature within HTST, we use an effective atomistic spin Hamiltonian defined on a simple cubic lattice:
were ni is the unit vector along the magnetic moment at the lattice site i, J and
Here we ignore the demagnetizing field effect and introduce characteristic parameters LD = 2πJa/D and BD = D2/(Jμ) for the atomistic model (7), where a is the lattice constant. The calculations for heliknoton energy barriers and lifetime provided below were performed at zero external magnetic field, Bext = 0.
First, we apply HTST to estimate the lifetime of a particular magnetic state and the possible mechanisms of its collapse. Within the HTST, the rate of transition between states X and Y at temperature T is described by the Arrhenius law,
where the energy barrier ΔEX→Y can be computed knowing the minimal energy path (MEP) connecting X and Y states on the energy surface as the energy difference between the highest point along the MEP—The first-order saddle point (SP) on the energy surface of the system—And the minimum at X. The pre-exponential factor νX→Y incorporates dynamical νdyn and entropic νent contributions to the transition rate
Within the harmonic approximation, the energy of the system in the vicinity of a stationary state is approximated by a quadratic form that allows the prefactors to be determined explicitly [49]. The quadratic forms for the minimum nX and the saddle point nSP are determined by the corresponding Hessian matrices
where the Hessians are restricted to subspaces consisting of non-zero modes.
The dynamical prefactor is expressed in terms of the negative eigenvalue ζ of the Hessian
The index i numbers the lattice sites.
The heliknoton in bulk has at least two zero modes corresponding to translations in directions orthogonal to the helical axis. We eliminate one of the zero modes by pinning the spins at the boundaries x = const and y = const in such a way that the direction of the magnetic moments coincides with one of the helix. The pinned spins were not affected by the optimization procedures and were not included as degrees of freedom to the Hessians. On the surfaces z = const the boundary conditions are free, which allows us to simulate the escape through the boundary. Translation along the z-axis becomes a quasi-zero mode because of the effect of the boundary.
The computation of MEP was performed in Cartesian coordinates with constraints on the magnetic moments length taking into account by introduction of Lagrange multipliers, which allows us to avoid singularities and the necessity to transform coordinates while changing the map in the atlas [50]. The string method [51] with stable tangent estimate [52] was used for MEP calculation.
The most challenging part of the computation of the transition rate is the calculation of the determinants. When a standard LU or QR decomposition is used, the complexity of the problem is
To find the optimal mesh density, we calculated the MEPs at different mesh densities of LD equal to.
To find the optimal mesh density, we calculated the MEPs at different mesh densities of LD equal to 12a, 24a, 36a, and 48a. While the coarsest grid of 12a gives significantly different values of both the Heliknoton energy and the activation barrier, the results for the three densest grids (with 24a, 36a, and 48a) are only slightly different (see right inset in Figure 4A). Therefore, we used the discretization density LD = 24a for the transition rate computation.
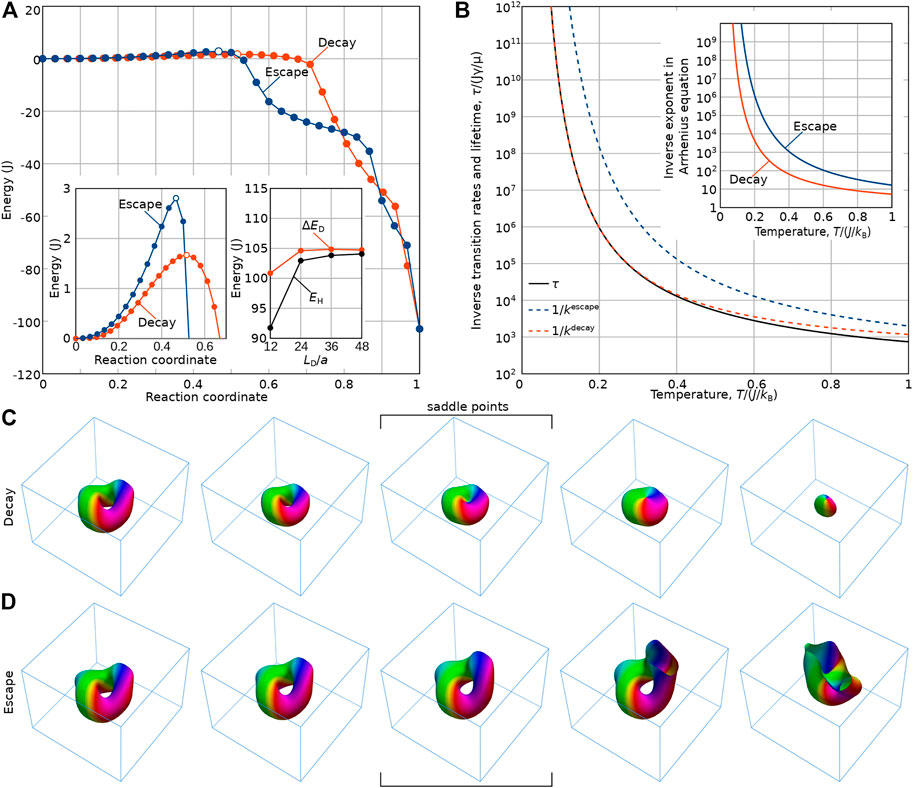
FIGURE 4. (A) The minimum energy paths for two distinct mechanisms for heliknoton collapse in the film: the escape through the free edges of the plate (blue curve) and the decay inside the film via the nucleation of a pair of Bloch points (red curve). The saddle points are indicated by hollow symbols. The right inset illustrates the convergence of the energies of the heliknoton, EH, and the energy barrier for the decay, ΔED, to the micromagnetic limits with increasing mesh density, LD/a. (B) The lifetime of heliknoton as a function of temperature. The escape mechanism (blue line) is less probable than the decay mechanism for all temperatures. Insets in (B) show the contributions of the exponent (activation barrier) in Arrhenius law to the lifetime. (C) Snapshots of the system along the minimum energy path for heliknoton decay. The spin texture after despiralization is represented by the isosurfaces mz = 0. The number above each image corresponds to the reaction coordinate, r. Similar to Figure 1, the images show the volume confined by the blue box of the size 2.5LD × 2.5LD × 2LD—The quarter of the whole simulated domain of the size 5LD × 5LD × 2LD. (D) Snapshots of the system along the minimum energy path for heliknoton escape through the free surface. The field of view and notations are the same as in (C). In (C, D), the images in the middle correspond to the saddle points of corresponding MEPs.
The results of the HTST analysis are summarized in Figure 4. The MEPs presented in Figure 4A correspond to two distinct mechanisms for heliknoton collapse, which we refer to as decay and escape. The decay mechanism is similar to the collapse of hopfions in a model of a frustrated magnet [33]; [34]. In this case, the heliknoton collapses via the emergence of a pair of magnetic singularities, namely Bloch points of opposite signs. Representative images along the MEP corresponding to heliknoton decay are shown in Figure 4C.
As seen from the images in Figure 4D, when the heliknoton escapes through the boundary, magnetic singularities do not appear at any point along the MEP. Surprisingly, the escape mechanism for the heliknoton collapse is characterized by a higher energy barrier compared to heliknoton decay for sufficiently dense lattices. Thereby, unlike the case of hopfions in the model of frustrated magnets [32], the escape through the boundary for the heliknoton requires overcoming some activation barrier, which we attribute to the emergence of the chiral surface twist effect [53]. The latter suggests that the heliknoton in a thin plate of a chiral magnet may be more promising for experimental observations due to its finite energy barrier for escape.
The total transition rate for a metastable state is the sum of transition rates for all mechanisms of the collapse. The main contributions to the mean lifetime (inverse to the transition rate) of the heliknoton are the decay and escape mechanisms, with decay dominating:
The dependence of the heliknoton lifetime on temperature is shown in Figure 4B. The inverse to the transition rate for the decay mechanism gives an estimate of the lifetime of the heliknoton in thick films because the escape transition rate is inversely proportional to the film thickness.
Overall, our HTST analysis sheds light on the decay mechanisms of the heliknoton and highlights potential avenues for its experimental observation, especially at low temperatures. For instance, at T = 0.455J/kB (or 0.35Tc), the lifetime for heliknoton is τ ∼ 106 in dimensionless time units scaled by Jγμ−1, see Figure 4B. For J = 112 meV and μ = 1030μB, we obtain the heliknoton lifetime of
3.5 Stochastic LLG dynamics
The stochastic LLG equation can be written as
where t is a dimensionless time scaled by Jγμ−1, with γ being the gyromagnetic ratio, α is the Gilbert damping parameter,
To visualize the heliknoton isosurface nz = 0 in the presence of strong thermal fluctuations, we first apply Fourier filtering as described in Ref. [57]. After that, we apply the despiralization procedure as introduced above, Figure 5. Among the few independent runs of the LLG simulations, we chose the two most representative examples illustrated in Figures 5A, B; Supplementary Movies S1, S2. In agreement with the results of HTST presented in the previous section, we observe two mechanisms of heliknoton collapse. In particular, Figure 5A shows the snapshots of the systems during the heliknoton collapse via the decay, accompanied by the Bloch points nucleation. Figure 5B illustrates the case when heliknoton collapses via escape through the top free surface of the plate. These are the only two mechanisms observed in stochastic LLG simulations. In the first case, the heliknoton shrinks until the tor hole completely disappears. At this moment, a pair of Bloch points of the opposite charge appears, and we see the transition from the heliknoton to the dipole string or toron [57]. The dipole string represents a non-stable state at these parameters and collapses through shrinking. In the second case, we observe the shifting of the heliknoton to the open surface as a result of its Brownian motion. The escaping happens if the distance between the heliknoton and the surface is smaller than the critical one. It is worth noting that despite the temporal fluctuations, the escape through the free surface represents a smooth transition. Remarkably, the heliknoton remains stable near the surface of the plate for a noticeably long time. That might indicate the existence of a metastable state resembling surface modulations. Details of the investigation of such localized states will be provided elsewhere.
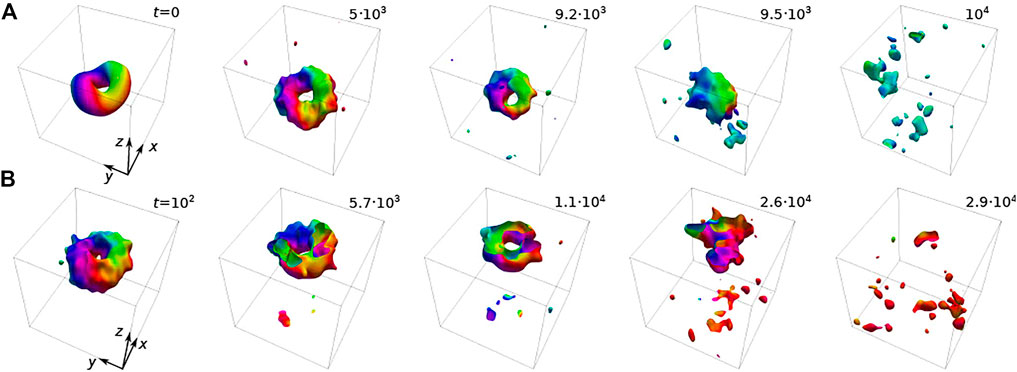
FIGURE 5. Snapshots of the system in two different stochastic LLG simulations are shown. The set of images in row (A) corresponds to the heliknoton collapse through the nucleation of Bloch points, while images in row (B) correspond to its escaping through the free surface of the plate. The shown box has size 2LD in each dimension.
Among ten independent simulations, we observed the collapse of the heliknoton in the times range between 2 × 104 to 8 × 104 in reduced time units. Using these results, we estimated the lifetime of the heliknoton at T = 1.0J/kB to be approximately τ ∼ 104. This result agrees with the findings of the HTST calculations presented in Figure 4B, which suggest a lifetime of τ ∼ 103 for this temperature. The limited sampling (only ten independent runs) may account for the observed discrepancy. However, given the variation of the heliknoton’s lifetime by ten orders of magnitude for different temperatures, we consider the agreement between the simulations and HTST calculations to be satisfactory.
4 Conclusion
In this study, we investigated the stability and decay mechanisms of the heliknoton in realistic conditions using direct energy minimization, stochastic LLG simulations, and HTST calculations. Our results showed that the heliknoton is stable in a wide range of magnetic fields and plate thicknesses, as demonstrated by the stability diagram calculated at zero temperature. However, our calculations indicated that for plate thicknesses above 2.5LD, the magnetic contrast in Lorentz TEM becomes too weak for reliable observations.
Based on our findings, we estimate the optimal plate thickness for heliknoton observations to be 2LD ± 0.5LD (140 ± 35 nm for FeGe parameters). Our analysis using the GNEB method revealed two main mechanisms of heliknoton decay: collapse via the formation of Bloch points and escape through the plate surface. The LLG simulations at finite temperatures supported these observations and showed reasonable agreement with the estimation of heliknoton lifetime, at least at elevated temperatures. Moreover, the HTST calculations allowed us to estimate heliknoton lifetimes at different temperatures. Overall, our results suggest that the heliknoton should be stable with a reasonably long lifetime at the standard measurement temperature of liquid nitrogen (T = 95 K) used in TEM experiments. We anticipate that these findings will stimulate further experimental observations of heliknotons in magnetic systems.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding authors.
Author contributions
VK, NK, and FR performed micromagnetic and LLG simulations, IL performed minimum energy path and lifetime calculations. NK wrote the first draft of the manuscript. SB and VU participated in the interpretation of the results, review and editing, supervision. All authors contributed to the manuscript writing. All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication. All authors contributed to the article and approved the submitted version.
Funding
VK acknowledges financial support from the Icelandic Research Fund (Grant No. 217750). This project has received funding from the European Research Council under the European Union’s Horizon 2020 Research and Innovation Programme (Grant No. 856538—Project “3D MAGiC”). NK and SB acknowledge financial support from the Deutsche Forschungsgemeinschaft through SPP 2137 “Skyrmionics”, Grant No. KI 2078/1-1 and Grant No. BL 444/16, respectively. FR acknowledges support from the Swedish Research Council.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2023.1201018/full#supplementary-material
References
1. Yu XZ, Onose Y, Kanazawa N, Park JH, Han JH, Matsui Y, et al. Real-space observation of a two-dimensional skyrmion crystal. Nature (2010) 465:901–4. doi:10.1038/nature09124
2. Park HS, Yu X, Aizawa S, Tanigaki T, Akashi T, Takahashi Y, et al. Observation of the magnetic flux and three-dimensional structure of skyrmion lattices by electron holography. Nat Nanotechnology (2014) 9:337–42. doi:10.1038/nnano.2014.52
3. Yu XZ, Kanazawa N, Onose Y, Kimoto K, Zhang WZ, Ishiwata S, et al. Near room-temperature formation of a skyrmion crystal in thin-films of the helimagnet FeGe. Nat Mater (2010) 10:106–9. doi:10.1038/nmat2916
4. Kovács A, Caron J, Savchenko AS, Kiselev NS, Shibata K, Li Z-A, et al. Mapping the magnetization fine structure of a lattice of bloch-type skyrmions in an FeGe thin film. Appl Phys Lett (2017) 111:192410. doi:10.1063/1.5004394
5. Du H, Zhao X, Rybakov FN, Borisov AB, Wang S, Tang J, et al. Interaction of individual skyrmions in a nanostructured cubic chiral magnet. Phys Rev Lett (2018) 120:197203. doi:10.1103/PhysRevLett.120.197203
6. Yu X, Morikawa D, Yokouchi T, Shibata K, Kanazawa N, Kagawa F, et al. Aggregation and collapse dynamics of skyrmions in a non-equilibrium state. Nat Phys (2018) 14:832–6. doi:10.1038/s41567-018-0155-3
7. Yu X, Kikkawa A, Morikawa D, Shibata K, Tokunaga Y, Taguchi Y, et al. Variation of skyrmion forms and their stability in mnsi thin plates. Phys Rev B (2015) 91:054411. doi:10.1103/PhysRevB.91.054411
8. Shibata K, Yu XZ, Hara T, Morikawa D, Kanazawa N, Kimoto K, et al. Towards control of the size and helicity of skyrmions in helimagnetic alloys by spin–orbit coupling. Nat Nanotechnology (2013) 8:723–8. doi:10.1038/nnano.2013.174
9. Dzyaloshinsky I A thermodynamic theory of “weak” ferromagnetism of antiferromagnetics. J Phys Chem Sol (1958) 4:241–55. doi:10.1016/0022-3697(58)90076-3
10. Moriya T Anisotropic superexchange interaction and weak ferromagnetism. Phys Rev (1960) 120:91–8. doi:10.1103/PhysRev.120.91
11. Bogdanov AN, Yablonskii DA Thermodynamically stable “vortices” in magnetically ordered crystals. the mixed state of magnets. Sov Phys JETP (1989) 68.
12. Tokura Y, Kanazawa N Magnetic skyrmion materials. Chem Rev (2020) 121:2857–97. doi:10.1021/acs.chemrev.0c00297
13. Zheng F, Rybakov FN, Kiselev NS, Song D, Kovács A, Du H, et al. Magnetic skyrmion braids. Nat Commun (2021) 12:5316. doi:10.1038/s41467-021-25389-7
14. Zheng F, Kiselev NS, Yang L, Kuchkin VM, Rybakov FN, Blügel S, et al. Skyrmion–antiskyrmion pair creation and annihilation in a cubic chiral magnet. Nat Phys (2022) 18:863–8. doi:10.1038/s41567-022-01638-4
15. Rybakov FN, Kiselev NS Chiral magnetic skyrmions with arbitrary topological charge. Phys Rev B (2019) 99:064437. doi:10.1103/PhysRevB.99.064437
16. Foster D, Kind C, Ackerman PJ, Tai J-SB, Dennis MR, Smalyukh II Two-dimensional skyrmion bags in liquid crystals and ferromagnets. Nat Phys (2019) 15:655–9. doi:10.1038/s41567-019-0476-x
17. Kuchkin VM, Barton-Singer B, Rybakov FN, Blügel S, Schroers BJ, Kiselev NS Magnetic skyrmions, chiral kinks, and holomorphic functions. Phys Rev B (2020) 102:144422. doi:10.1103/PhysRevB.102.144422
18. Tang J, Wu Y, Wang W, Kong L, Lv B, Wei W, et al. Magnetic skyrmion bundles and their current-driven dynamics. Nat Nanotechnology (2021) 16:1086–91. doi:10.1038/s41565-021-00954-9
19. Dubrovin BA, Fomenko AT, Novikov SP Modern geometry – methods and applications. Part II. The geometry and topology of manifolds. New York: Springer-Verlag (1985). doi:10.1007/978-1-4612-1100-6
20. Aminov JA. Sources of curvature of a vector field. Mathematics USSR-Sbornik (1969) 9:199–211. doi:10.1070/sm1969v009n02abeh001128
22. Rybakov P Topological excitations in field theory models of superconductivity and magnetism. Ph.D. thesis. Stockholm: KTH Royal Institute of Technology (2021).
23. Zheng F, Kiselev NS, Rybakov FN, Yang L, Blügel S, Dunin-Borkowski RE Hopfion rings in a cubic chiral magnet. Preprint Res Square (2023). doi:10.21203/rs.3.rs-2681064/v1
24. Hopf H Über die abbildungen der dreidimensionalen sphäre auf die kugelfläche. Mathematische Annalen (1931) 104:637–65. doi:10.1007/bf01457962
25. Whitehead JHC An expression of hopf's invariant as an integral. Proc Natl Acad Sci (1947) 33:117–23. doi:10.1073/pnas.33.5.117
26. Dzyloshinskii IE, Ivanov BA Localized topological solitons in a ferromagnet. JETP Lett (1979) 29:540.
27. Bogolubsky I Three-dimensional topological solitons in the lattice model of a magnet with competing interactions. Phys Lett A (1988) 126:511–4. doi:10.1016/0375-9601(88)90049-7
28. Cooper NR Propagating magnetic vortex rings in ferromagnets. Phys Rev Lett (1999) 82:1554–7. doi:10.1103/PhysRevLett.82.1554
29. Sutcliffe P Skyrmion knots in frustrated magnets. Phys Rev Lett (2017) 118:247203. doi:10.1103/physrevlett.118.247203
30. Liu Y, Lake RK, Zang J Binding a hopfion in a chiral magnet nanodisk. Phys Rev B (2018) 98:174437. doi:10.1103/PhysRevB.98.174437
31. Voinescu R, Tai J-SB, Smalyukh II Hopf solitons in helical and conical backgrounds of chiral magnetic solids. Phys Rev Lett (2020) 125:057201. doi:10.1103/PhysRevLett.125.057201
32. Rybakov FN, Kiselev NS, Borisov AB, Döring L, Melcher C, Blügel S Magnetic hopfions in solids. APL Mater (2022) 10:111113. doi:10.1063/5.0099942
33. Sallermann M, Jónsson H, Blügel S Stability of hopfions in bulk magnets with competing exchange interactions. Phys Rev B (2023) 107:104404. doi:10.1103/PhysRevB.107.104404
34. Lobanov IS, Uzdin VM Lifetime, collapse, and escape paths for hopfions in bulk magnets with competing exchange interactions. Phys Rev B (2023) 107:104405. doi:10.1103/PhysRevB.107.104405
35. Kent N, Reynolds N, Raftrey D, Campbell ITG, Virasawmy S, Dhuey S, et al. Creation and observation of hopfions in magnetic multilayer systems. Nat Commun (2021) 12:1562. doi:10.1038/s41467-021-21846-5
36. Tai J-SB, Smalyukh II Three-dimensional crystals of adaptive knots. Science (2019) 365:1449–53. doi:10.1126/science.aay1638
37. Bessarab PF, Uzdin VM, Jónsson H Harmonic transition-state theory of thermal spin transitions. Phys Rev B (2012) 85:184409. doi:10.1103/PhysRevB.85.184409
38. Bessarab PF, Uzdin VM, Jónsson H Potential energy surfaces and rates of spin transitions. Z für Physikalische Chem (2013) 130708000310008. doi:10.1524/zpch.2013.0403
39.D ter Haar, editor. Collected papers of L.D. Landau (pergamon). Chap. 18 - on the theory of the dispersion of magnetic permeability in ferromagnetic bodies (1965). p. 101–14. doi:10.1016/B978-0-08-010586-4.50023-7
40. Di Fratta G, Muratov CB, Rybakov FN, Slastikov VV Variational principles of micromagnetics revisited. SIAM J Math Anal (2020) 52:3580–99. doi:10.1137/19M1261365
41. Rybakov FN, Babaev E Excalibur software (2020). URL: http://quantumandclassical.com/excalibur/.
42. Vansteenkiste A, Leliaert J, Dvornik M, Helsen M, Garcia-Sanchez F, Van Waeyenberge B The design and verification of mumax3. AIP Adv (2014) 4:107133. doi:10.1063/1.4899186
43. Zheng F, Rybakov FN, Borisov AB, Song D, Wang S, Li Z-A, et al. Experimental observation of chiral magnetic bobbers in b20-type FeGe. Nat Nanotechnology (2018) 13:451–5. doi:10.1038/s41565-018-0093-3
44. Skyrme THR A non-linear field theory. Proc R Soc Lond Ser A. Math Phys Sci (1961) 260:127–38. doi:10.1098/rspa.1961.0018
45. Rybakov FN, Borisov AB, Blügel S, Kiselev NS New spiral state and skyrmion lattice in 3D model of chiral magnets. New J Phys. IOP Publishing (2016) 18 (4):045002. doi:10.1088/1367-2630/18/4/045002
46. Denneulin T, Caron J, Hoffmann M, Lin M, Tan H, Kovács A, et al. Off-axis electron holography of néel-type skyrmions in multilayers of heavy metals and ferromagnets. Ultramicroscopy (2021) 220:113155. doi:10.1016/j.ultramic.2020.113155
47. Denneulin T, Caron J, Müller-Caspary K, Boulle O, Kovács A, Dunin-Borkowski RE Visibility and apparent size of néel-type magnetic skyrmions in fresnel defocus images of multilayer films. Microsc Microanalysis (2021) 27:1356–65. doi:10.1017/s1431927621012927
48. Graef MD 2. lorentz microscopy: Theoretical basis and image simulations. In: Experimental methods in the physical sciences. Elsevier (2001). p. 27–67. doi:10.1016/s1079-4042(01)80036-9
49. Lobanov IS, Uzdin VM The lifetime of micron scale topological chiral magnetic states with atomic resolution. Comp Phys Commun (2021) 269:108136. doi:10.1016/j.cpc.2021.108136
50. Lobanov IS, Potkina MN, Uzdin VM Stability and lifetimes of magnetic states of nano-and microstructures (brief review). JETP Lett (2021) 113:801–13. doi:10.1134/S0021364021120109
51. E W, Ren W, Vanden-Eijnden E Simplified and improved string method for computing the minimum energy paths in barrier crossing events. J Chem Phys (2007) 126:164103. doi:10.1063/1.2720838
52. Henkelman G, Jónsson H Improved tangent estimate in the nudged elastic band method for finding minimum energy paths and saddle points. J Chem Phys (2000) 113:9978–85. doi:10.1063/1.1323224
53. Rybakov FN, Borisov AB, Blügel S, Kiselev NS New type of stable particlelike states in chiral magnets. Phys Rev Lett (2015) 115:117201. doi:10.1103/PhysRevLett.115.117201
54. Mentink JH, Tretyakov MV, Fasolino A, Katsnelson MI, Rasing T Stable and fast semi-implicit integration of the stochastic landau–lifshitz equation. J Phys Condensed Matter (2010) 22:176001. doi:10.1088/0953-8984/22/17/176001
55. Kiselev NS Magnoom software (2016). URL: https://github.com/n-s-kiselev/magnoom.
56. Savchenko AS, Kuchkin VM, Rybakov FN, Blügel S, Kiselev NS Chiral standing spin waves in skyrmion lattice. APL Mater (2022) 10:071111. doi:10.1063/5.0097651
Keywords: heliknoton, hopfion, topological magnetic soliton, chiral magnets, stochastic LLG dynamics, micromagnetic simulations, minimum energy path calculations, lifetime calculations
Citation: Kuchkin VM, Kiselev NS, Rybakov FN, Lobanov IS, Blügel S and Uzdin VM (2023) Heliknoton in a film of cubic chiral magnet. Front. Phys. 11:1201018. doi: 10.3389/fphy.2023.1201018
Received: 05 April 2023; Accepted: 02 May 2023;
Published: 10 May 2023.
Edited by:
Jamal Berakdar, Martin Luther University of Halle-Wittenberg, GermanyReviewed by:
Jianbao Zhao, Canadian Light Source, CanadaMaciej Krawczyk, Faculty of Physics, Adam Mickiewicz University, Poland
Copyright © 2023 Kuchkin, Kiselev, Rybakov, Lobanov, Blügel and Uzdin. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Vladyslav M. Kuchkin, dmt1Y2hraW5AaGkuaXM=; Nikolai S. Kiselev, bi5raXNlbGV2QGZ6LWp1ZWxpY2guZGU=
 Vladyslav M. Kuchkin
Vladyslav M. Kuchkin Nikolai S. Kiselev
Nikolai S. Kiselev Filipp N. Rybakov4
Filipp N. Rybakov4 Stefan Blügel
Stefan Blügel Valery M. Uzdin
Valery M. Uzdin