- 1Department of Mathematics, Faculty of Science, Beijing University of Technology, Beijing, China
- 2Chemical Engineering Department, College of Engineering, King Khalid University, Abha, Saudi Arabia
- 3Interdisciplinary Research Centre for Renewable Energy and Power System (IRC-REPS), Research Institute, King Fahd University of Petroleum and Minerals (KFUPM), Dhahran, Saudi Arabia
- 4Department of Mathematics, University of Kotli AJ and K Pakistan, Kotli, Pakistan
- 5Mechanical Engineering, Future University in Egypt, Cairo, Egypt
- 6Faculty of Materials and Manufacturing, College of Mechanical Engineering and Applied Electronics Technology, Beijing University of Technology, Beijing, China
- 7Center of Research, Faculty of Engineering, Future University in Egypt New Cairo, Cairo, Egypt
This communication analyzes the dual convection regime of Newtonian fluid flow in a Y shaped porous enclosure with heat and mass distribution, using a mathematical model of dimensionless PDEs and an effective finite element method. The top curved wall of the enclosure is assumed hot and side walls are cold while the bottom wall is assumed adiabatic. The problem is discretized using
1 Introduction
The interaction between mass and heat transfer is a common occurrence observed in both natural and industrial settings. An interesting consequence of this interplay arises when a fluid experiences simultaneous gradients in both temperature and concentration, resulting in the emergence of a complex and intricate fluid flow pattern, referred to as double diffusive convection. This phenomenon has long fascinated the scientific and engineering communities, owing to its far-reaching implications in numerous fields, such as oceanography, geophysics, energy transport, and materials science. To obtain a more comprehensive understanding of this phenomenon, delving into some of the crucial foundational works is imperative [1–3]. Later on several authors had noticed the occurrence of doubly diffusive natural convection (DDNC) [4] effects of a fluid within a porous material [5, 6] with a high Rayleigh number [7] and transition between oscillatory and steady convection [8]. The transport of heat and mass in double diffusive natural convection is closely linked, as the fluid flow induced by the temperature and concentration gradients affects the transport of both heat and mass. Kumar etal [9]. Conducted a numerical investigation to examine the transport of flow, heat, and mass in a rectangular cavity with partially heated walls. He employed the Lattice Boltzmann Method (LBM) as a numerical technique to solve the fluid flow problems involving single and multi-phase systems. Furthermore, he recommended conducting additional experiments to visualize the application of LBM in heat and mass transfer. The phenomenon of double diffusive convection has been studied extensively by various researcher AA Farooq [10]. The phenomenon of double diffusive convection has been studied extensively by various researchers. Han and Kuehn [11] looked at how the temperature and concentration gradients applied horizontally would affect a vertical rectangular cavity. They concluded that a complicated temporary multi-structural formation can be seen during the concurrent transfer of heat and mass in a rectangular container under both supporting and opposing buoyancy circumstances. The study conducted by Beghein et al. [12] focused on exploring the consequences of steady-state thermosolutal convection in a square cavity, while Mamou et al. [13] analyzed a numerical and analytical model for natural convection in a rectangular cavity containing a double-diffusive fluid, with uniform heat and mass flux along the vertical sides. Nikbakhti and Rahimi [14] conducted a computational analysis of the fluid dynamics, thermal dynamics, and mass transfer in a rectangular chamber where the walls were heated partially. He obtained results for different heating conditions and parameters, also measured the heat and mass transfer rates to determine the mean Sherwood and Nusselt numbers. The researchers discussed DDNC in a rectangular [15], trapezoidal [16, 17], irregular [18], trapezoidal with fillets [19], and hexagonal [20, 21] enclosure. While Walker and Homsy [22] investigated natural convection driven by buoyancy in a porous square cavity where one of the horizontal sides was differentially heated. The study concluded that non-uniform heating of the bottom wall produces a higher heat transfer rate at the centre of the bottom wall compared to the uniform heating case. Furthermore, the study determined that conduction is the primary mechanism for heat and mass transfer, and established critical Rayleigh numbers for dominant cases, as well as a correlation between average Nusselt number and Rayleigh numbers.
Porous media have found wide-ranging applications in different fields, owing to their exceptional characteristics and features. Even though Mamou et al. [23] analyzed the commencement of the double-diffusive convection phase inside a rectangular porous channel, while Karimfard et al. [24] analyzed the occurrence of double-diffusive natural convection in a squared porous cavity. Some of the fluid-flow models that the researchers looked into were the Forchheimer and Brinkman additions, the Darcy flow, and the extended flow. In a similar way, Nithiarasu et al. [25] used analytical methods to study double-diffusive flow in a rectangular cavity, while Bennacer and others [26] used numerical simulation methods to study how soaked asymmetrical porous materials affect this kind of convection. Anand Rao et al. [27] cast-off the finite element method to study the flow of a rotating fluid across an infinite flat porous plate when a magnetic field and Hall current were present. He found that fluid flows in plate at constant angular velocity and the primary and secondary velocity fields are in non-dimensional form. Researchers [28–31] have used the finite element method to explore the influence of mass and heat transfer on the dynamics of suction-driven, vertically oscillating plates in unstable magneto hydrodynamic flows. Ramana Murthy et al. [32]. Looked at the effects of mass and heat transmission on instable MHD regular convection stream over an infinite vertical plate in a porous environment warmed by thermal radiation. A well-known author [33] examined the transfer of heat and mass while discussing the blood flow through a narrow artery with stenosis. He investigated that the presence of gold (Au) nanoparticles (NPs) in Oldroyd-B nanoliquid flow affects stenosis arteries under the influence of MHD. Taklifi and Aliabadi [34] did an analytical study of the stream of a non-Newtonian fluid over a permeable layer when the magneto hydrodynamic (MHD) conditions were unstable. Taza et al. [35] presented a numerical model that investigates and compares the behavior of simple and hybrid nanoparticles on a spreading surface. The work on stretching surface was discussed by zahr shah [36, 37]. Abdullah et al. [38] studied about ceramic materials, i.e., Alumina. As a result, the author has developed a mathematical equation to describe the mixed convective flow of nanofluid contain Alumina nanoparticles past a stretching surface in three dimensions under magnetohydrodynamic condition.
Rashad and El-Kabeir [39] studied a diverse flow of convection over a vertically strained sheet immersed inside a fluid-saturated porous media under the impact of a chemical reaction effect to study the associated mass and temperature transport processes under transient conditions. Noor Fadiya et al. [40] used the Adomian decomposition method along with Padé approximants to solve the magneto hydrodynamic boundary-layer stream caused by a transparent stretching sheet submerged in a porous material. The problem was effectively and precisely solved using this method. An analysis of Co-current convection and radiation phenomena around an impermeable inclined plate, subject to magneto and thermal radiation effects in a porous medium, was performed by Orhan and Ahmet [41]. Zahir et al. [42] studied irreversibility in steady water-based nanofluid flows between two rotating disks using the Darcy–Forchheimer relation, constant temperatures/velocities, and a radial/tangential magnetic field. They proved that the radial velocity component is increased with the Reynolds number and decreased with the porosity parameter and inertial coefficient, while the tangential velocity component and temperature profile are reduced with the Reynolds number and increased with the Hartmann number and nanoparticle volume fraction. Mukesh Kumar Sharma et al. [43] examined a non-Darcian permeable material containing an electrically charged, viscous, and appropriate solvent trapped between two indefinitely long, horizontal, impermeable plates and the relatively stable magneto hydrodynamic flow and heat exchange properties of this system. Both viscous as well as Joule absorption characteristics were taken into account in the analysis. The mixed convective stream along an inclined surface inside a permeable material filled with Newtonian fluid was analyzed by Mansour et al. [44]. The magneto hydrodynamic circulation of an incompressible level commensurate over porous materials was studied by Masood Khan et al. [45], who found perfect solutions to the problem. Hayat et al. [46] looked at magneto hydrodynamic flow, utilizing Laplace as well as Fourier sine transform techniques to derive steady-state and transient solutions. Das et al. [47]. Studied the effects of Hall and thermal radiation on an unsteady magneto hydrodynamic convective flow that vibrates via a porous medium contained in a vertical plate. Its effect of mass transport upon the magneto hydrodynamic circulation of two compressible fluids under the influence of a chemical reaction as they flow across a translucent stretching sheet in a porous medium was studied by Abbas et al. [48]. The unsteady, oscillatory flow of a magneto hydrodynamic flow through a rectangular channel packed with an absorbent medium that is flooded, as well as the accompanying thermal transfer properties, were studied by Ahmer et al. [49]. The effect of a wall’s temperature that is not consistent with the rest of the surface was also taken into account in the study. Ahmet and Sezer [50]. Provided an analytical solution for the constant, two-dimensional, turbulent, forced magneto hydrodynamic Hiemenz flow that occurs against a flat board with a changing wall temperature in a permeable material. The study employed the homotopic perturbation method to arrive at the solution. Well-known author Mahmood [51] incorporated a variety of visual representations, including 2D plots, to illustrate the acquired solutions Based on an assessment of the previously mentioned scientific studies, the spreading occurrence in non-newtonian fluid as a result of thermal and solutal buoyancy propelled forces has not been explored. Moreover, in spite of the significant increase of magnetic fields in numerous contemporary engineering systems, such characteristics are rarely analyzed collectively. Consequently, the aim of this undertaking is to address this deficiency by introducing non-newtonian fluid with thermal and solutal limitations on the right wall of the cavity. In order to achieve this, the mathematical formulation of the problem is represented as a partial differential equation, and subsequently, similarity parameters are utilized to transform PDEs [52] into ODEs. A numerical solution to the formulated problem is obtained through the utilization of finite element methodology in simulation. Ultimately, crucial parameters’ impacts on associated distributions are illustrated in a visual and tabulated layout.
In the initial section of this paper, the inspiration and rationale behind the research are explained, along with an extensive discussion of the relevant references and literature. In Section 2 of the paper, the mathematical equation that governs DDNC in fluid-saturated porous media is thoroughly described. This section offers a detailed explanation of the underlying physical phenomena that drive the DDNC process. The dimensionless form of the Navier-Stokes equations is solved using FEM. In Section 3 of the paper, the proposed method’s accuracy and effectiveness are showcased through a detailed presentation of the numerical approach and validation methodology. In Section 4, the outcomes are visually presented through streamlines, isoconcentration and isotherms plots, depicting the influence of the variables on the heated and cooled regions. Section 5 summarizes the results of the analysis conducted in this study.
2 Mathematical model
2.1 Problem description
We have considered the fluid flow that is laminar, uniform, incompressible, and flowing in two dimensions inside a Y-shaped cavity with circular cylinder inside. When the left and right side cavity wall is affected by cooling temperature
2.2 Governing equations
The non-dimensional governing equations for two-dimensional incompressible and steady flow is defined through Eqs. 1–7 (for ref see [53])
Where
The dimensionless boundary conditions are defined as
The local and average Nusselt and Sherwood numbers are calculated on the heated wall using Eqs. 11–14,
3 Numerical scheme
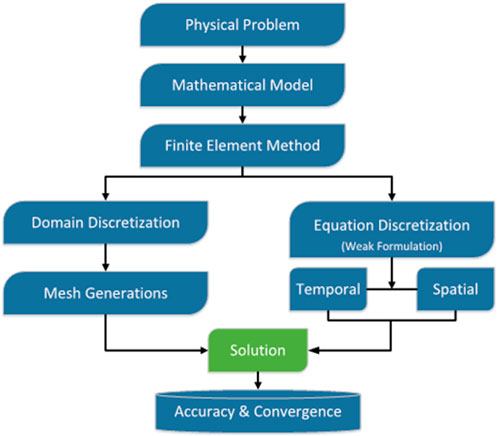
Exact procedures are useful for dealing with fluid flow behavior in the absence of limited barriers, but it is challenging to find the solution in a closed cavity with obstacles of varying forms and sizes using only those approaches. Hence, most researchers use numerical systems to publish their findings, with FEM, FDM, and FVM among the most common approaches. One of the most flexible of these numerical methods is the FEM, which is used to discrete elements to simulate complicated and irregular geometries on a flat domain. Fluid, heat and mass transfer movement inside of enclosures have served as the focus of a significant amount of research using computational methods. Using the finite-element method (FEM), the above leading Eqs. 1–10 are discretized. Then Newton’s Raphson iteration approach is applied to the nonlinear algebraic equations. The flowchart in Figure 2 shows FEM’s basic process.
3.1 Weak formulation
The Eqs. 1–5 can be written in the weak form as follows
In order to obtain a numerical approximation, we compare the solutions obtained from continuous and discrete methods within finite dimensional sub-spaces.
Using Eq. 22 into above equation the discrete version is as follow
For discrete solution the basic function is as follow
The parameters retain their typical definitions, and in order to obtain the solution, the non-linear system is iteratively processed until a certain threshold of tolerance is reached.
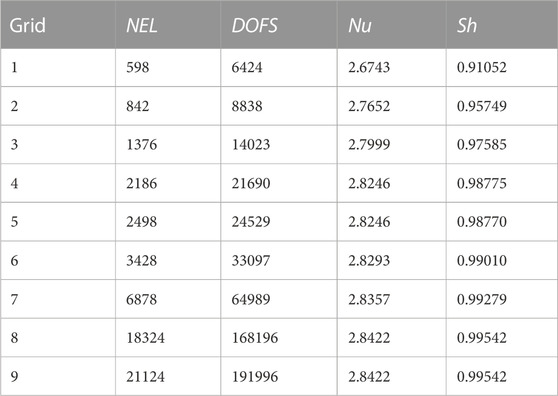
3.2 Verification and investigation of grid dependency
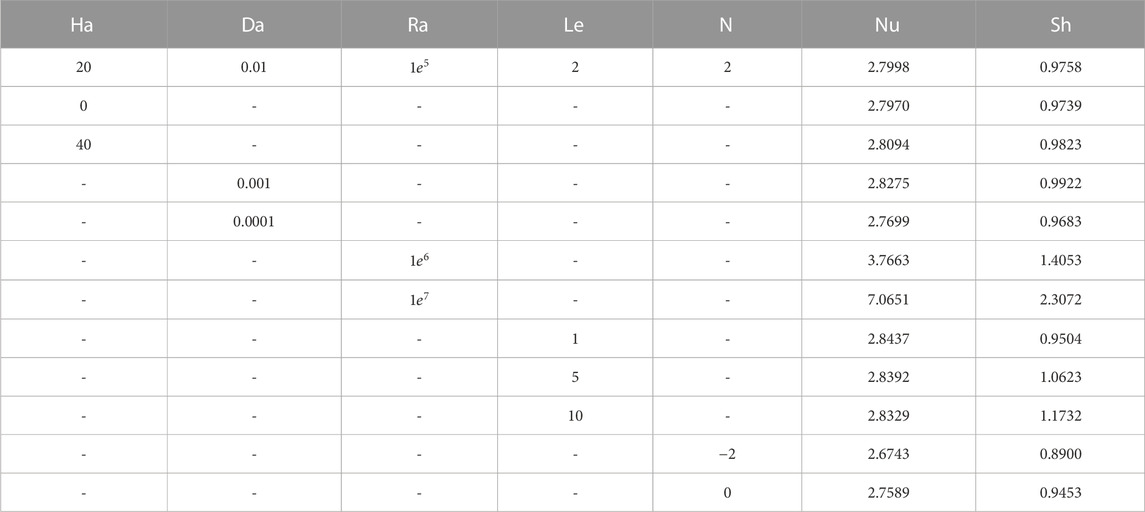
To validate the efficiency of the achieved consequences, Table 1 displays the results of using several grids with the parameters
4 Result and discussion
In this section, we will compare the findings of the study in the form of streamlines, temperature profile, and isoconcentration patterns to a variety of physical parameters. This involves Ra (Rayleigh number), N (buoyancy ratio), Ha (Hartmann number), Le (Lewis number) and Da (Darcy number). The obtained mass flux coefficients (Sherwood numbers) and heat flux coefficients (Nusselt numbers) are of significant importance, in terms of their wider applicability and their local relevance.
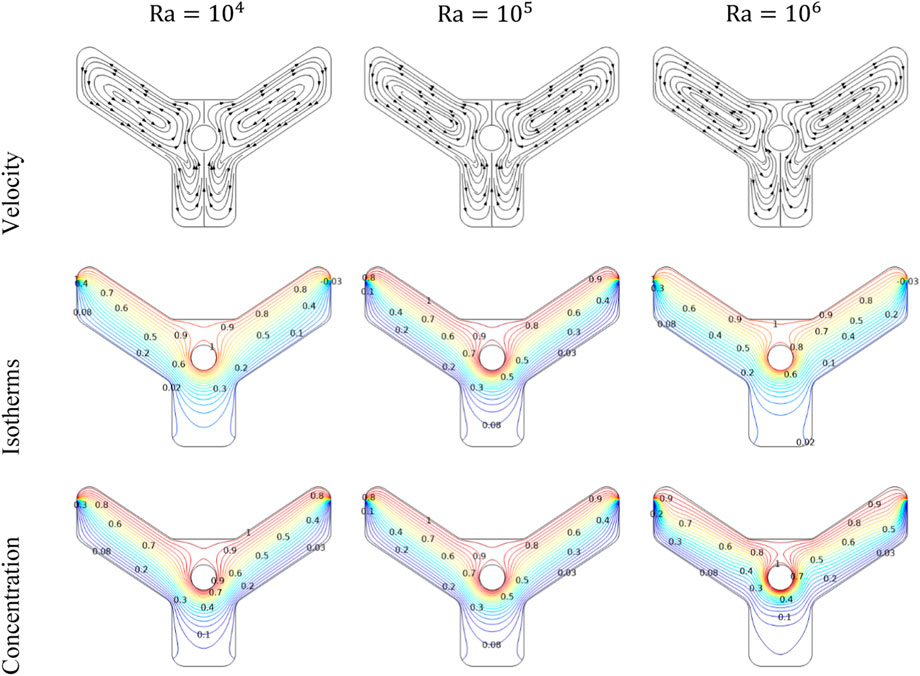
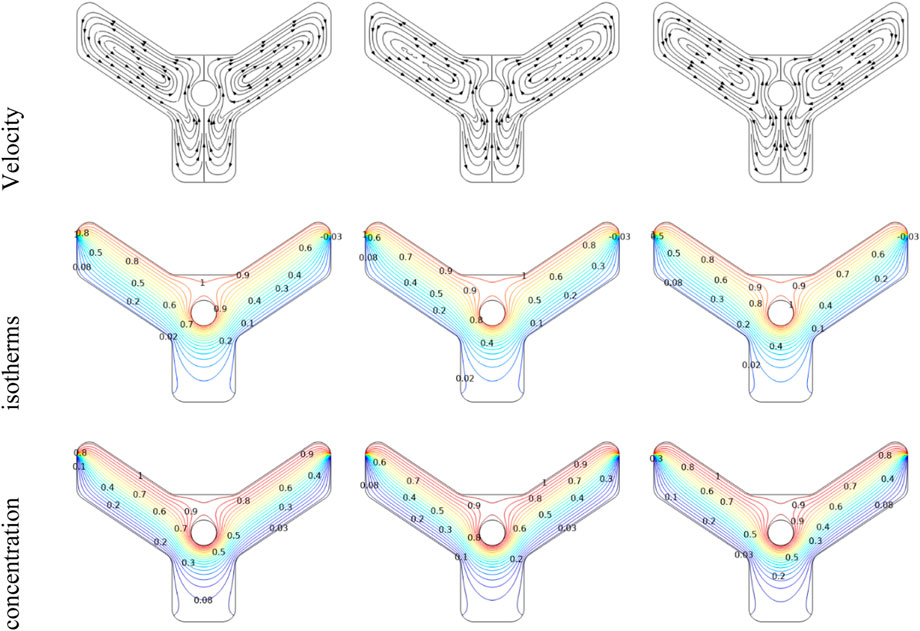
The dispersion of streamlines, temperature profile, and isoconcentrations at different Ra are shown in Figure 3. The results show that an increase in the Ra results in a stronger natural convection, causing notable changes in fluid velocities, temperature, and concentration distributions. The impact of the Rayleigh number on natural convection and its related heat and mass transfer properties is noticeable. Due to the temperature gradient between the top, left, and right walls, the fluid within the system circulates from the region with higher temperature to the cooler areas.
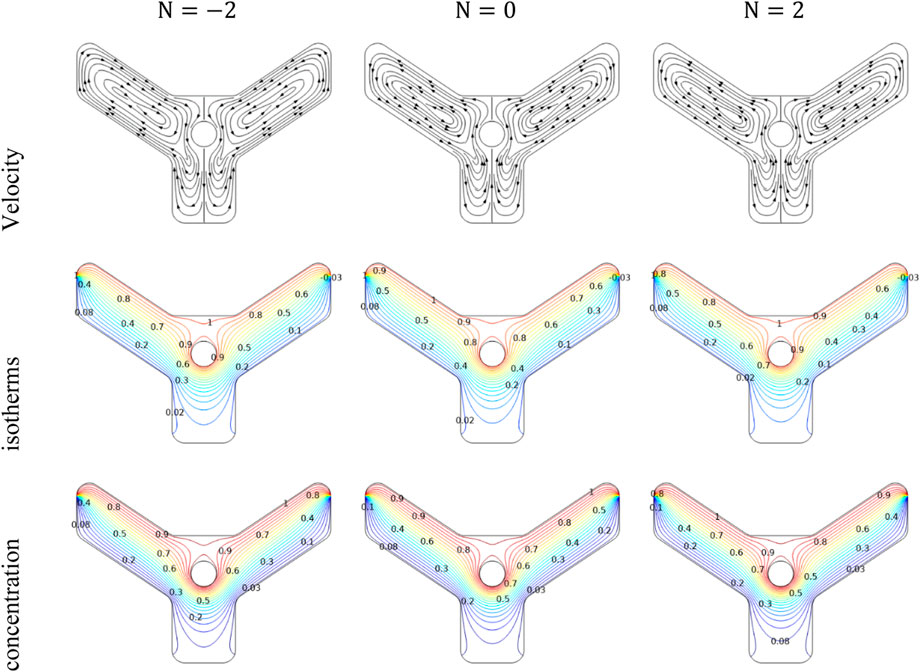
Figure 4 displays the streamlines for varying buoyancy ratios. Natural convection and the related flow dynamics are seen to be significantly affected by the buoyancy ratio. When buoyancy ratio is negative (concentration dominated counter flow), fluid flows mostly from the warm to the cool side of the cavity, creating two convection cells. As the buoyancy ratio approaches zero (thermal convection dominated flow), the 2 cells become increasingly symmetric, and the flow becomes more uniform. At higher buoyancy ratios (concentration dominated assisting flow), the flow pattern becomes more complex, with extra vortices forming in the cavity. So when buoyancy ratio becomes negative, as seen in part 2 of Figure 4, the fluid closest to the top wall heats up, while the fluid near its bottom wall cools down. As buoyancy ratio approaches zero, the temperature distribution becomes increasingly symmetric, and the heat transfer becomes more uniform. At higher buoyancy ratios, the temperature distribution becomes more uniform. In the third part the Isoconcentration behave same as Isotherms.
Figure 5 shows how Da affects the mass as well as heat transmission properties of natural convection. As can be seen in this diagram, Da has a major impact on the distributions of both temperature as well as concentration. When Darcy’s number goes down, its temperature closest to hot wall goes up, while the temperature close to the cold wall falls down. The same is true for concentration, which gets better as it gets closer to the top of the wall and worse as it gets closer to the bottom. Moreover, the concentration distribution becomes more uniform as the Darcy number decreases.
In Figure 6, we see how the streamlines, isotherms, and concentrations vary for various Hartmann numbers. When the Hartmann number rises, its magnetic field becomes stronger, resulting in increased suppression of fluid motion, and hence reduced rates of thermal and mass transfer. The figure reveals this phenomenon as the streamlines start pointing in the same direction as the magnetic field and the fluid flow is restricted to the bottom of the cavity. Further it also shows that the temperature and concentration distributions become more uniform as the Hartmann number increases, which is caused by suppressed temperature and concentration gradients and decreased fluid velocity.
Figure 7 shows the relationship between the Nusselt number and the Sherwood number as a function of the Rayleigh number for a range of Darcy numbers. When the Darcy number goes down, the rate of heat and mass transfer goes down. For all Darcy numbers, it is seen that a rise in the Rayleigh number results in a corresponding increase in the Nusselt number.
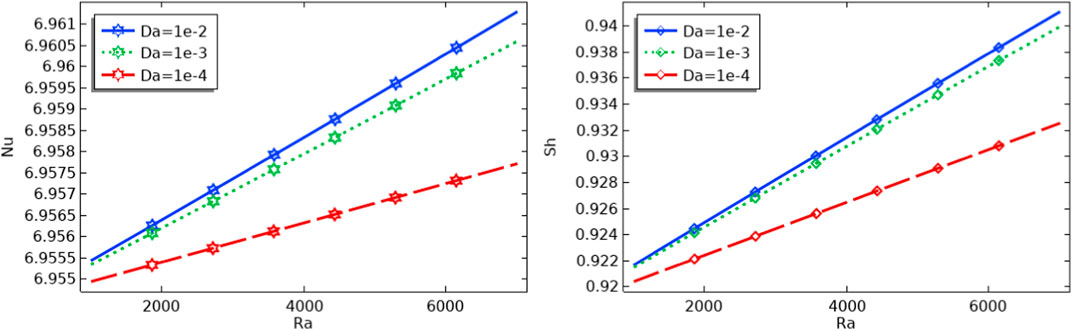
FIGURE 7. Effect of Da and Ra on the mean Nusselt number and mean Sherwood number for Pr = 6.8, Ha = 20, N = 2.
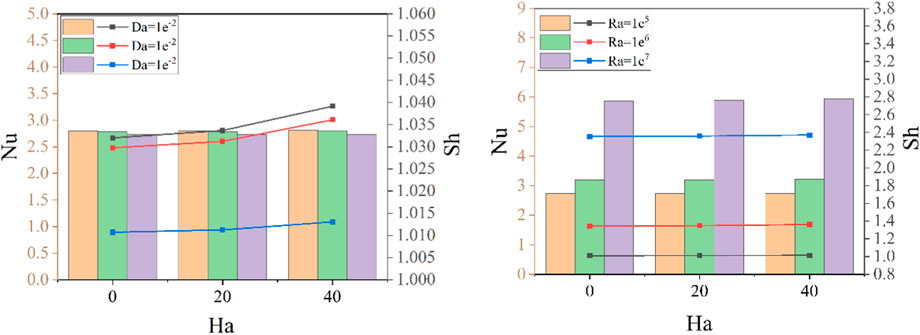
Figure 8 illustrates how the Rayleigh number affects the heat and mass transfer for variation of Hartmann numbers. Heat and mass transfer rate is minimum for pure hydrodynamic case (
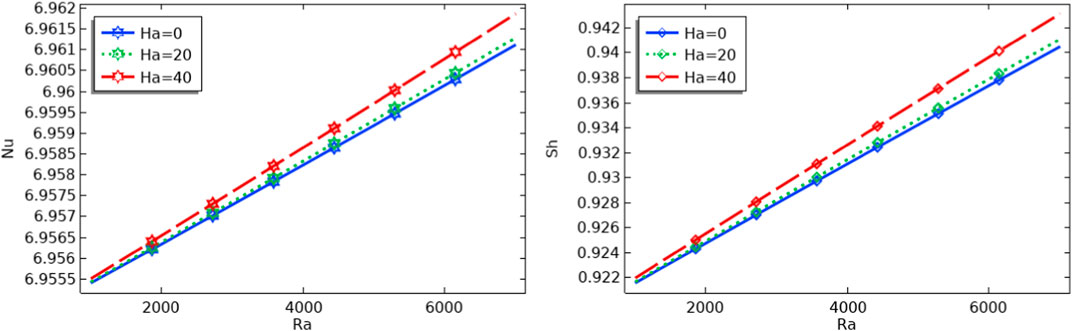
FIGURE 8. Effect of Ha and Ra on the mean Nusselt number and mean Sherwood number for Pr = 6.8, Ha = 20, N = 2.
Figure 9 is a chart that illustrates the Sherwood and Nusselt numbers as a consequence of the Rayleigh number for a variety of buoyancy ratios (−2, 0, 2). Heat and mass transfer rate is minimum for concentration dominated counter flow (
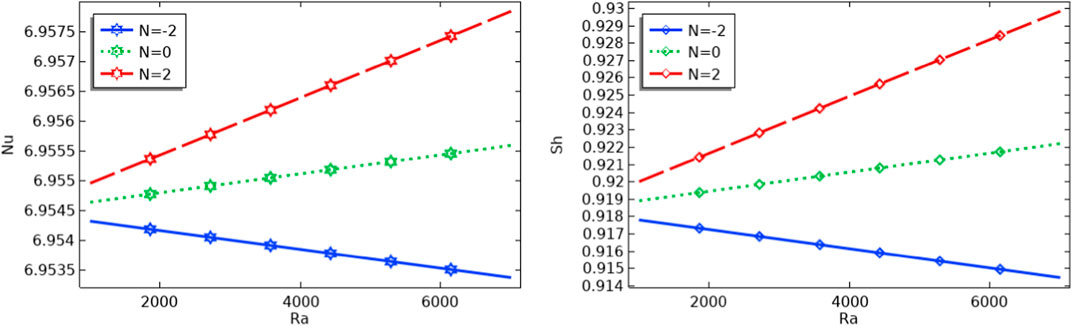
FIGURE 9. Effect of N and Ra on the mean Nusselt number and mean Sherwood number for Pr = 6.8, Ha = 20, N = 2.
Figure 10 presents a statistical analysis of the relationship between heat and mass transfer considering variation in the Darcy number and Rayleigh number. The heat transfer rate is visually represented by blocks, whereas the variation in mass transfer is illustrated by lines. The result indicates a discernible increase in both heat and mass transfer for higher values of the Darcy number (Da) and Rayleigh number (Ra), as visually observed in the figure.
Table 2 presents numerical data on the Hartmann number (
5 Conclusion
The purpose of the present investigation is to demonstrate the flow characteristics of a viscous fluid inside of a Y shaped porous cavity containing a circular cylinder. The problem is formulated mathematically using system of dimensionless PDEs. An effective FEM is used to handle modified partial differential systems. The domain is discretized using quadrilateral and triangular elements at multiple level. The LBB-stable element provides as close approximation of the velocity, temperature and concentration. These results could be used to improve the design of heat transfer systems, cooling systems, and other engineering parts.
• Increase in the Hartmann number, Buoyancy ratio and Rayleigh numbers amplifies both the heat and mass transfer rates.
• The natural convection becomes stronger as the Rayleigh number increases, leading to higher fluid velocities and significant changes in the temperature and concentration distributions.
• The Darcy number significantly affects the temperature and concentration distributions, with decreasing Darcy number resulting in increased temperature near the hot wall and increased concentration near the top wall.
• For concentration dominated counter flow heat and mass transfer rate decreases for the variation in
• For concentration dominated assisting flow mass and heat transfer rate increases for the variation in Rayleigh number.
Data availability statement
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
Author contributions
All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.
Funding
Funded by Deanship of Scientific Research (Project no. RGP. 2/108/43), King Khalid University, Abha, KSA.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Huppert HE, Turner JS. Double-diffusive convection. J Fluid Mech (1981) 106:299–329. doi:10.1017/s0022112081001614
2. Huppert HE, Sparks RSJ. Double-diffusive convection due to crystallization in magmas. Annu Rev Earth Planet Sci (1984) 12(1):11–37. doi:10.1146/annurev.ea.12.050184.000303
3. Schmitt RW. Double diffusion in oceanography. Annu Rev Fluid Mech (1994) 26(1):255–85. doi:10.1146/annurev.fl.26.010194.001351
4. Uddin M, Rasel S, Adewole JK, Al Kalbani KS. Finite element simulation on the convective double diffusive water-based copper oxide nanofluid flow in a square cavity having vertical wavy surfaces in presence of hydro-magnetic field. Results Eng (2022) 13:100364. doi:10.1016/j.rineng.2022.100364
5. Griffiths R. Layered double-diffusive convection in porous media. J Fluid Mech (1981) 102:221–48. doi:10.1017/s0022112081002619
6. Gumir FJ, Al-Farhany K, Jamshed W, Tag El Din ESM, Abd-Elmonem A. Natural convection in a porous cavity filled (35% MWCNT-65% Fe3O4)/water hybrid nanofluid with a solid wavy wall via Galerkin finite-element process. Scientific Rep (2022) 12(1):17794. doi:10.1038/s41598-022-22782-0
7. Linden P, Shirtcliffe T. The diffusive interface in double-diffusive convection. J Fluid Mech (1978) 87(3):417–32. doi:10.1017/s002211207800169x
8. Curry JH, Herring JR, Loncaric J, Orszag SA. Order and disorder in two-and three-dimensional Bénard convection. J Fluid Mech (1984) 147:1–38. doi:10.1017/s0022112084001968
9. Kumar S, Gangawane KM, Oztop HF. Applications of lattice Boltzmann method for double-diffusive convection in the cavity: A review. J Therm Anal Calorim (2022) 147(20):10889–921. doi:10.1007/s10973-022-11354-z
10. Farooq A, Shah Z, Shutaywi M, Bonyah E, Roy P. Axisymmetric mixed convective propulsion of a non-Newtonian fluid through a ciliated tubule. AIP Adv (2020) 10(5):055214. doi:10.1063/5.0003671
11. Han H, Kuehn TH. Double diffusive natural convection in a vertical rectangular enclosure—II. Numerical study. Int J Heat mass transfer (1991) 34(2):461–71. doi:10.1016/0017-9310(91)90265-g
12. Beghein C, Haghighat F, Allard F. Numerical study of double-diffusive natural convection in a square cavity. Int J Heat Mass Transfer (1992) 35(4):833–46. doi:10.1016/0017-9310(92)90251-m
13. Mamou M, Vasseur P, Bilgen E. Analytical and numerical study of double diffusive convection in a vertical enclosure. Heat Mass Transfer (1996) 32(1):115–25. doi:10.1007/s002310050100
14. Nikbakhti R, Rahimi AB. Double-diffusive natural convection in a rectangular cavity with partially thermally active side walls. J Taiwan Inst Chem Eng (2012) 43(4):535–41. doi:10.1016/j.jtice.2012.02.010
15. Moraveji MK, Hejazian M. Natural convection in a rectangular enclosure containing an oval-shaped heat source and filled with Fe3O4/water nanofluid. Int Commun Heat mass transfer (2013) 44:135–46. doi:10.1016/j.icheatmasstransfer.2013.03.011
16. Esfe MH, Abbasian Arani AA, Yan WM, Ehteram H, Aghaie A, Afrand M. Natural convection in a trapezoidal enclosure filled with carbon nanotube–EG–water nanofluid. Int J Heat Mass Transfer (2016) 92:76–82. doi:10.1016/j.ijheatmasstransfer.2015.08.036
17. Khan ZH, Khan WA, Haq R, Usman M, Hamid M. Effects of volume fraction on water-based carbon nanotubes flow in a right-angle trapezoidal cavity: FEM based analysis. Int Commun Heat Mass Transfer (2020) 116:104640. doi:10.1016/j.icheatmasstransfer.2020.104640
18. Mohammadi M, Nassab SG. Double-diffusive convection flow with Soret and Dufour effects in an irregular geometry in the presence of thermal radiation. Int Commun Heat Mass Transfer (2022) 134:106026. doi:10.1016/j.icheatmasstransfer.2022.106026
19. Shahzad H, Ain QU, Pasha AA, Irshad K, Shah IA, Ghaffari A, et al. Double-diffusive natural convection energy transfer in magnetically influenced Casson fluid flow in trapezoidal enclosure with fillets. Int Commun Heat Mass Transfer (2022) 137:106236. doi:10.1016/j.icheatmasstransfer.2022.106236
20. Shah IA, Bilal S, Noeiaghdam S, Fernandez-Gamiz U, Shahzad H. Thermosolutal natural convection energy transfer in magnetically influenced casson fluid flow in hexagonal enclosure with fillets. Results Eng (2022) 15:100584. doi:10.1016/j.rineng.2022.100584
21. Khan Y, Majeed AH, Shahzad H, Awan FJ, Iqbal K, Ajmal M, et al. Numerical computations of non-Newtonian fluid flow in hexagonal cavity with a square obstacle: A hybrid mesh–based study. Front Phys (2022) 10:336. doi:10.3389/fphy.2022.891163
22. Basak T, Roy S, Paul T, Pop I. Natural convection in a square cavity filled with a porous medium: Effects of various thermal boundary conditions. Int J Heat Mass Transfer (2006) 49(7-8):1430–41. doi:10.1016/j.ijheatmasstransfer.2005.09.018
23. Mamou M, Vasseur P, Bilgen E. Multiple solutions for double-diffusive convection in a vertical porous enclosure. Int J Heat Mass Transfer (1995) 38(10):1787–98. doi:10.1016/0017-9310(94)00301-b
24. Karimi-Fard M, Charrier-Mojtabi M, Vafai K. Non-Darcian effects on double-diffusive convection within a porous medium. Numer Heat Transfer, A: Appl (1997) 31(8):837–52. doi:10.1080/10407789708914067
25. Nithiarasu P, Seetharamu K, Sundararajan T. Double-diffusive natural convection in an enclosure filled with fluid-saturated porous medium: A generalized non-Darcy approach. Numer Heat Transfer, A Appl (1996) 30(4):413–26. doi:10.1080/10407789608913848
26. Bennacer R, Tobbal A, Beji H, Vasseur P. Double diffusive convection in a vertical enclosure filled with anisotropic porous media. Int J Therm Sci (2001) 40(1):30–41. doi:10.1016/s1290-0729(00)01185-6
27. Anand RJ, Srinivasa RR, Sivaiah S. Finite element solution of MHD transient flow past an impulsively started infinite horizontal porous plate in a rotating fluid with Hall current. J Appl Fluid Mech (2012) 5:105–12. doi:10.36884/JAFM.5.03.19452
28. Mahmood R, Hussain Majeed A, Ain Q, Awrejcewicz J, Siddique I, Shahzad H. Computational analysis of fluid forces on an obstacle in a channel driven cavity: Viscoplastic material based characteristics. Materials (2022) 15(2):529. doi:10.3390/ma15020529
29. Wang X, Shahzad H, Chen Y, Kanwal M, Ullah Z. Mathematical modelling for flexible blade coater with magnetohydrodynamic and slip effects in blade coating process. J Plast Film Sheeting (2020) 36(1):38–54. doi:10.1177/8756087919848807
30. Shahzad H, Wang X, Raizah Z, Riaz A, Majeed AH, Anwar MA, et al. Fluid-structure interaction study of bio-magnetic fluid in a wavy bifurcated channel with elastic walls. Front Phys (2022) 10:1147. doi:10.3389/fphy.2022.999279
31. Anand RJ, Srinivasa RR, Sivaiah S. Finite element solution of heat and mass transfer in MHD flow of a viscous fluid past a vertical plate under oscillatory suction velocity. J Appl Fluid Mech (2012) 5:1–10. doi:10.36884/JAFM.5.03.19435
32. Murthy MR, Raju RS, Rao JA. Heat and mass transfer effects on MHD natural convective flow past an infinite vertical porous plate with thermal radiation and Hall current. Proced Eng (2015) 127:1330–7. doi:10.1016/j.proeng.2015.11.491
33. Tang TQ, Rooman M, Shah Z, Asif Jan M, Vrinceanu N, Racheriu M. Computational study and characteristics of magnetized gold-blood Oldroyd-B nanofluid flow and heat transfer in stenosis narrow arteries. J Magnetism Magn Mater (2023) 569:170448. doi:10.1016/j.jmmm.2023.170448
34. Taklifi A, Aliabadi A. Analytical solution of unsteady MHD periodic flow of a non-Newtonian fluid through a porous channel. J Porous Media (2012) 15(11):1051–9. doi:10.1615/jpormedia.v15.i11.50
35. Gul T, Khan A, Bilal M, Alreshidi NA, Mukhtar S, Shah Z, et al. Magnetic dipole impact on the hybrid nanofluid flow over an extending surface. Scientific Rep (2020) 10(1):8474–13. doi:10.1038/s41598-020-65298-1
36. Shah Z, Rooman M, Shutaywi M. Computational analysis of radiative engine oil-based Prandtl–Eyring hybrid nanofluid flow with variable heat transfer using the Cattaneo–Christov heat flux model. RSC Adv (2023) 13(6):3552–60. doi:10.1039/d2ra08197k
37. Deebani W, Lund LA, Chandio AF, Yashkun U, Shah Z, Alshehri A. Convective micropolar fluid over inclined surface with thermal radiation and velocity slip condition effects: Duality and stability. Int J Mod Phys B (2023) 2023:2450114. doi:10.1142/s0217979224501145
38. Dawar A, Thumma T, Islam S, Shah Z. Optimization of response function on hydromagnetic buoyancy-driven rotating flow considering particle diameter and interfacial layer effects: Homotopy and sensitivity analysis. Int Commun Heat Mass Transfer (2023) 144:106770. doi:10.1016/j.icheatmasstransfer.2023.106770
39. Rashad AM, El-Kabeir S. Heat and mass transfer in transient flow by mixed convection boundary layer over a stretching sheet embedded in a porous medium with chemically reactive species. J porous media (2010) 13(1):75–85. doi:10.1615/jpormedia.v13.i1.70
40. Prasad DK, Chaitanya GK, Raju RS. Double diffusive effects on mixed convection Casson fluid flow past a wavy inclined plate in presence of Darcian porous medium. Results Eng (2019) 3:100019. doi:10.1016/j.rineng.2019.100019
41. Aydin O, Kaya A. Effects of thermal radiation on steady MHD mixed convective heat transfer flow over an impermeable inclined plate embedded in a porous medium. J Porous Media (2011) 14(7):617–25. doi:10.1615/jpormedia.v14.i7.50
42. Shah Z, McCash LB, Dawar A, Bonyah E. Entropy optimization in Darcy–Forchheimer MHD flow of water based copper and silver nanofluids with Joule heating and viscous dissipation effects. AIP Adv (2020) 10(6):065137. doi:10.1063/5.0014952
43. Sharma M, Singh K, Kumar A. MHD flow and heat transfer through non-Darcy porous medium bounded between two parallel plates with viscous and joule dissipation. Spec Top Rev Porous Media: Int J (2014) 5(1):1–11. doi:10.1615/specialtopicsrevporousmedia.v5.i1.10
44. Mansour M, El-Anssary NF, Aly AM, Gorla RSR. Chemical reaction and magnetohydrodynamic effects on free convection flow past an inclined surface in a porous medium. J porous Media (2010) 13(1):87–96. doi:10.1615/jpormedia.v13.i1.80
45. Khan M, Fetecau C. On the exact solutions for oscillating flow of a MHD second-grade fluid through porous media. Spec Top Rev Porous Media: Int J (2012) 3(1):13–22. doi:10.1615/specialtopicsrevporousmedia.v3.i1.20
46. Hayat T, Afzaal MF, Asghar S, Hendi AA. A comparative study on MHD flow by two different transform methods. J Porous Media (2011) 14(12):1105–13. doi:10.1615/jpormedia.v14.i12.50
47. Das S, Jana RN, Makinde OD. An oscillatory MHD convective flow in a vertical channel filled with porous medium with Hall and thermal radiation effects. Spec Top Rev Porous Media: Int J (2014) 5(1):63–82. doi:10.1615/specialtopicsrevporousmedia.v5.i1.60
48. Abbas Z, Sheikh M, Sajid M. Mass transfer in two MHD viscoelastic fluids over a shrinking sheet in porous medium with chemical reaction species. J Porous Media (2013) 16(7):619–36. doi:10.1615/jpormedia.v16.i7.40
49. Mehmood A, Ali A, Mahmood T. Unsteady magnetohydrodynamic oscillatory flow and heat transfer analysis of a viscous fluid in a porous channel filled with a saturated porous medium. J Porous Media (2010) 13(6):573–7. doi:10.1615/jpormedia.v13.i6.70
50. Yildirim A, Sezer SA. Analytical solution of MHD stagnation-point flow in porous media by means of the homotopy perturbation method. J Porous Media (2012) 15(1):83–94. doi:10.1615/jpormedia.v15.i1.70
51. Abdelrahman MA, Almatrafi MB, Alharbi A. Fundamental solutions for the coupled KdV system and its stability. Symmetry (2020) 12(3):429. doi:10.3390/sym12030429
52. Alharbi A, Abdelrahman MA, Almatrafi M. Analytical and numerical investigation for the DMBBM equation. Comput Model Eng Sci (2020) 122(2):743–56. doi:10.32604/cmes.2020.07996
53. Qiu G, Wang J, Zhang Y. Double-diffusive natural convection of low Prandtl number liquids with soret and dufour effects. Front Heat Mass Transfer (2018) 10:24. doi:10.5098/hmt.10.24
Nomenclature
Keywords: mixed convection, finite element analysis (FEM), irregular cavity, viscus fluid, porous media
Citation: Aslam MA, Yao H, Al Mesfer MK, Irshad K, Chuhan IS, Danish M, Hassan AM, Shahzad H and Eldin SM (2023) Finite element modeling of dual convection in a Y shaped porous cavity containing viscus fluid. Front. Phys. 11:1207462. doi: 10.3389/fphy.2023.1207462
Received: 17 April 2023; Accepted: 20 June 2023;
Published: 04 July 2023.
Edited by:
Chuang-Yao Zhao, Xi’an University of Architecture and Technology, ChinaReviewed by:
Ebenezer Bonyah, University of Education, GhanaMahmoud Abdelrahman, Mansoura University, Egypt
Copyright © 2023 Aslam, Yao, Al Mesfer, Irshad, Chuhan, Danish, Hassan, Shahzad and Eldin. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Hasan Shahzad, aGFzYW5zaGFoemFkOTlAaG90bWFpbC5jb20=
†ORCID: Sayed M. Eldin, orcid.org/0000-0002-0229-0705
 Muhammad Aqib Aslam
Muhammad Aqib Aslam Hailou Yao1
Hailou Yao1 Imran Shabir Chuhan
Imran Shabir Chuhan Hasan Shahzad
Hasan Shahzad