Bound states at disclinations: an additive rule of real and reciprocal space topology

Focusing on the two-dimensional (2D) Su-Schrieffer-Heeger (SSH) model, we propose an additive rule between the real-space topological invariant s of disclinations (related to the Burgers vector B) and the reciprocal-space topological invariant p of bulk wave functions (the vectored Zak phase). The disclination-induced bound states in the 2D SSH model appear only if (s + p/2π) is nonzero modulo the lattice constant. These disclination-bound states are robust against perturbations respecting C₄ point group symmetry and other perturbations within an amplitude determined by p. Besides the disclination-bound states, the proposed additive rule also suggests that a half-bound state extends over only half of a sample and a hybrid-bound state, which always have a nonvanishing component of s + p/2π.

1 Introduction

Topology studies the properties of a geometric or physical system under continuous transformations in parameter spaces. Its application in condensed matter physics has, in the past few years, renewed our understanding of energy band structures of crystalline systems [1–4]. As a cornerstone, the so-called bulk-edge correspondence principle [5–9] requires that robust quantum states appear at the boundaries of samples possessing topologically nontrivial band structures [10–13]. This principle links the reciprocal-space topology (i.e., energy band structure) to real-space profiles of quantum states. It provides a foundation for potentially transformative applications in spintronics and other practical areas. Recently [14–22], the bulk-edge correspondence has been extended to higher-order topological phases, culminating in the discovery of topologically protected corner states [23–28]. Applications such as laser cavity and quantum computation have been proposed based on these corner states [29, 30].

Unlike edge states, topological corner states usually appear as bound states in the continuum of bulk spectra, which complicates their experimental detection [31–34]. However, at a disclination center of crystallographic defects, nontrivial higher-order topology induces bound states accompanied by fractional charges, which have been experimentally observed in artificial crystalline systems recently [35–38].

The correlation between the appearance of fractional charges carried by bound states at disclination centers and the reciprocal topological invariant of bulk wave functions is framed as the bulk-disclination correspondence, which offers us a general principle of detecting higher-order topological phases [39–45]. Inspired by these observations of bulk-disclination correspondence, we look into the correlation between these anomalous bound states and the real-space topology of disclinations. Focusing on a typical higher-order topological model–the two-dimensional (2D) Su-Schrieffer-Heeger (SSH) model, we propose an additive rule between the real-space topological invariant s and the reciprocal topological invariant p. The SSH model is one fundemental model of topological insulators, and its extension to higher dimensions has resulted higher-order topological insulators. Especially, because the SSH model is spinless, it is suitable for the realization of the 2D SSH model and its higher-dimensional counterparts in various artifical crystalline systems, which leads to fruitiful experimental observations of topological corner states and accompanying fractional charges. These higher-order topological states are useful in fields such as laser cavity and quantum computation [46–53]. Thus, focusing on the 2D SSH model as an example, it would be helpful for understanding the general relation between the real-space topological defects and the reciprocal topological invariant. Furthermore, our proposal gives a possible explanation for the emergence of disclination-bound states, which may fertilize interesting physical phenomena and applications in the interdisciplinary field of the classical real-space topology of crystallographic defects and the reciprocal-space topology of wave functions, especially in designing disclination-induced bound states in artificial crystalline systems, such as photonic, phononic crystals, and metamaterials [54].

The remaining parts of the paper are organized as follows. In Sec. 2.1, we introduce the topological defect–disclination, the 2D SSH model, and their topological invariants s and p. In Sec.2.2 we explain the proposed additive rule in terms of s and p. In Sec. 2.3, we numerically show that when s + p/2π is nontrivial, bound states appear at centers of disclinations and discuss the specific symmetry protecting them for the 2D SSH model. In Secs. 2.4 and 2.5, we show that half-bound states and hybrid-bound states appear in the centers of disclinations that have s = (0, 1/2) and s = (1/2, 0). In Sec. 3, we discuss the generalization of the additive rule to other lattices and give conclusions of our study.

2 Results

2.1 Disclinations and 2D SSH model

Being global crystallographic defects, local operations cannot remove disclinations [55]. One may use the Volterra method [56] to construct a disclination. An example is depicted in Figure 1A, where a sample is cut into a few identical wedge portions, and one (marked in yellow) is removed to form a disclination after gluing the remaining sections without lattice mismatch. According to the homotopy theory, a disclination is characterized by two parameters (Ω, B). Here Ω is the Frank angle, whose magnitude is the wedge angle and whose sign indicates adding or removing a wedge, and B is the Burgers vector, which measures the lattice distortion induced by the defect [57, 58]. Choosing a start point, B can be evaluated by comparing the loop path around the disclination core and the loop path in a defect-free sample. For more details of the calculation of the Buregers vector, please refer to the Supplementary Material. For a square lattice respecting C₄ point group symmetry, Ω can only be a multiple of π/2. The group of non-equivalent classes of B is isomorphic to the discrete group Z₂ and Z₂ ⊗ Z₂ for Ω = ±π/2 and ± π, respectively [42]. The details of equivalenece classes of B is discussed in the Supplementary Material.

FIGURE 1

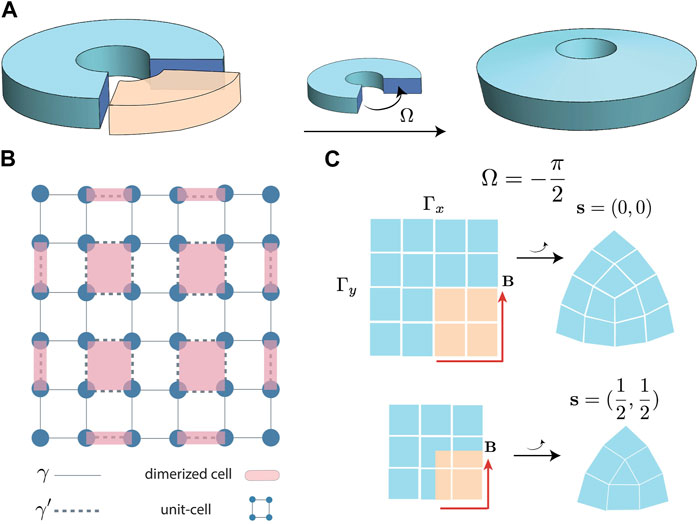
FIGURE 1. Construction and characteristic of a disclination. (A). Schematic of Volterra process for constructing a disclination. A wedge part spanning angle |Ω| is cut off from a symmetric sample, and the remaining sections are glued without any lattice mismatch. The wedge center is located at the point of rotation symmetry of the sample. The resulting disclination has a negative Frank angle Ω =−|Ω|. Alternatively, one may insert an extra wedge instead of removing the wedge, resulting in a disclination with positive Ω =|Ω|. (B). Sample of the 2D SSH model in the case of |γ|<|γ′| that respects C₄ point group symmetry, where solid/dashed line indicates the intra/inter-cell hopping of strength γ/γ′, and square/shade indicates the unit/dimerized cell. (C). Two types of disclinations with Ω =−π/2 allowed for samples with C₄-point group symmetry characterized by s. Each square represents a unit cell, and the lighter ones are the wedges being removed. s is determined by the parity of the numbers of unit cells on the x- and y-boundaries as $\mathbf{s}=\frac{1}{2}[({\mathrm{\Gamma }}_x,{\mathrm{\Gamma }}_y)\text{mod}2]$, which forms a bijection of the homotopy group of the Burgers vectors.

To concrete our study, we consider the 2D SSH model [59, 60], one of the typical models that admit topological corner states [26, 27, 60–62]. A sample of the 2D SSH model is depicted in Figure 1B, where the unit cell consists of four sub-lattices forming a square Bravais lattice. There are two types of hopping, namely, the intra-cell hopping γ and the inter-cell hopping γ′. Depending on the ratio of |γ/γ′|, the 2D SSH model can be in the atomic insulator phase or the atomic-obstructed phase. For the atomic insulator phase, its Wannier center coincides with the atomic lattice, for the atomic-obstructed phase, its Wannier center locates at the middle of two unit-cells. It is noted that for the atomic-obstructed phase, the Wannier center cannot be changed untill the band gaps close. For the detials of the band structure and fractional charge of the 2D SSH model, please refer to the Supplementary Material. For |γ| < |γ′| as in Figure 1B, the lowest energy band is inverted at (π/a, 0) and (0, π/a) in the reciprocal-space (with a the lattice constant) and becomes topologically nontrivial accompanying with corner states [59]. The appearance of topological corner states in the 2D SSH model is owing to the shift of dimerized cells as displayed by the light magenta square in Figure 1B, whose centers are related to the vectored Zak’s phase p = (p_x, p_y) by a factor of $\frac{a}{2\pi }$ [63–66]. Constrained by the periodicity of Bravais lattice, p_x/y is defined within $\left[\right.\mathrm{0,2}\pi \left.\right)$ and becomes a quantization of π when inversion symmetry is present, as determined by the parity of the bulk wave function at (0,0) and (π/a, 0)/(0, π/a) in the reciprocal space. Upon shifting the center of dimerized cells as well as Wannier states, the lowest energy band accommodates less than one electron in the unit cells located at the edges and corners, known as the filling anomaly that results in topological edge and corner states carrying 1/2 and 1/4 fractional charges, respectively [7].

Figure 1C displays two distinct disclinations with Ω = −π/2 for the 2D SSH model, where the square represents the unit cell, and the intra-cell and inter-cell hoppings are omitted. Depending on the unfolded Burgers vector B in undistorted space (indicated by red vectors in Figure 1C), the disclinations of Ω = −π/2 are classified into two topologically distinct types as labeled by s = (0, 0) and s = (1/2, 1/2), respectively. The relation between B and s is given as $\mathbf{s}=\frac{1}{2}\left[(2\mathbf{B})\text{mod}2\right]$, which forms a bijection to the homotopy group of B and thus is a real-space topological invariant. For a finite sample with full point-group symmetry, s can also be determined by counting the number of unit cells along the boundaries of the sample, i.e., $\mathbf{s}=\frac{1}{2}[({\mathrm{\Gamma }}_x,{\mathrm{\Gamma }}_y)\text{mod}2]$, where Γ_x and Γ_y denote the numbers of unit cells on x- and y-boundaries, respectively. It is noted that s forms a one-to-one mapping to nonequivalent disclination centers. For well-localized bound states without resonance, we focus on the cases that |γ − γ′| > min (|γ|, |γ′|), i.e., γ, γ′ = 1.0, 3.0 and γ, γ′ = 3.0, 1.0, where band gaps form between the first and the second bands, and the third and the fourth bands.

2.2 Proposed additive rule

Considering that the removal or addition of the wedge part resolves the filling anomaly at the disclination center, we expect a concurrent action of the real-space topological invariant s and the reciprocal topological invariant p, which we propose as an additive rule between them. In Table 1, s is tabulated for all possible values of Ω for the 2D SSH model. The integers inside Table 1 are the numbers of bound states at the different types of disclination centers for both trivial and nontrivial reciprocal topologies. From Table 1, we see that even for the trivial reciprocal topology, bound states exist as s + p/2π is nontrivial, whereas for the nontrivial p bound state is missing if s + p/2π is trivial. We define the net topology of real-space and reciprocal topology as $\mathcal{P}=(\mathbf{s}+\mathbf{p}/2\pi )\text{mod}1$, and discuss three unique manifestations of the proposed additive rule in the follows, which embody the content in Table 1. Extending the additive rule to other lattice models is possible, and we discuss it in the latter part.

TABLE 1

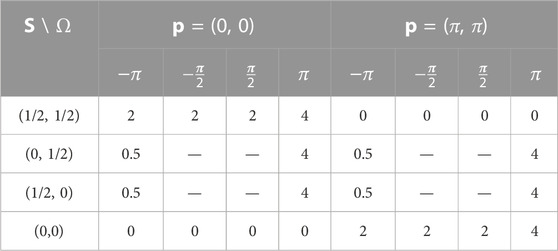
TABLE 1. Number of bound states for different disclination types and reciprocal topology. The disclination is characterized by the real space topological invariant s and the Frank angle Ω. Ω takes the value of −π, $-\frac{\pi }{2}$, $\frac{\pi }{2}$ and π. The reciprocal topological invariant, namely, the vectored Zak phase p, is (0,0) for the trivial topological phase and (π, π) for the nontrivial topological phase. “0.5” indicates a half-bound mode. “—” indicates such a type of disclination does not exist.

Previous studies suggest that the relationship between real and reciprocal spaces should be multiplicative [21, 36, 67, 68]. We obtain the additive rule because we focus on the bound states rather than the fractional charge. As discussed in Ref. [36], the fractional charge at the disclination core is given by the formula $Q=\frac{\mathrm{\Omega }}{2\pi }(n_b+2n_c)+\mathbf{T}\cdot \mathbf{p}$, where Q is the fractional charge at the disclination center, n_b, n_c are the numbers of the inverted band at high symmetric k points, and T = a₁d₁ + a₂d₂ with d_i ⋅e_j = δ_ij. As suggested by the formula, Q always appears as finite no matter the real-space topology if nontrivial p exists, which is considered the bulk-disclination correspondence. As demonstrated below, the bound state can appear at the disclination core even for trivial p and disappear for nontrivial p. In other words, the disclination-bound states and trapped fractional charge are dissociated.

2.3 Bound states and fractional charges

The first phenomenon of the proposed additive rule is the dissociation of fractional charges from bound states. The construction of disclination lattices and the caculation of fractional charge is discussed in the Methods section. We consider the samples with $\left(-\frac{\pi }{2}\right)$-disclinations. Figures 2A–C show the fractional charges and bound states for the $\left(-\frac{\pi }{2}\right)$-disclinations with three distinct additive conditions between the real and reciprocal topological invariants s and p. In the left panels of Figures 2A–C, each unit-cell’s numerical datum of charge distribution are written as digits. The bound states are indicated by the dark magenta shades (circles and triangles), and the fractional charges with ±1/4 are marked with the cyan crescents. In the middle panels of Figures 2A–C, we have also displayed the numerical datum of eigenfunctions when electrons are mostly localized for the corresponding left samples at disclination centers. In the right panels of Figures 2A–C, the eigenenergies distributions for samples of left panels are displayed.

FIGURE 2

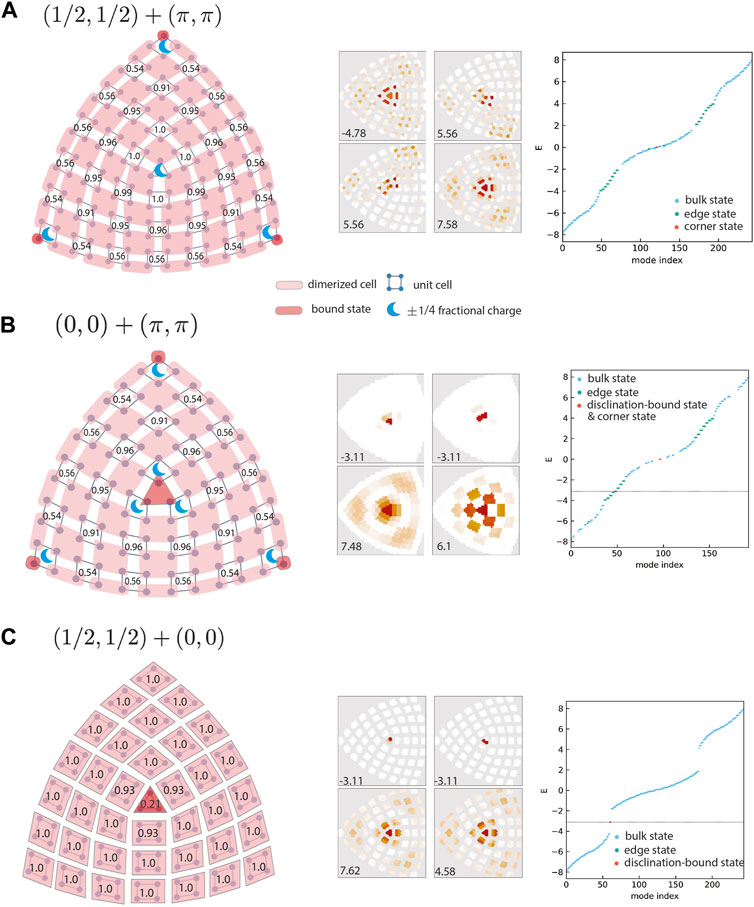
FIGURE 2. Fractional charge and bound state dissociation for $(-\frac{\pi }{2})$-disclinations. In left panels, a unit cell consists of 4 sites joined by thin lines, and a dimerized cell consists of sites in the same shade. A crescent indicates unit cells carrying 1/4 fractional charge; the number indicates the numerical results of charge distribution in each unit cell. The charge is calculated with the lowest energy band filled. Middle panels are the most concentrating four eigenstates at the disclination center, with their eigenenergies indicated on the left corners. The right panels are the eigenenergies distribution, where a dashed line indicates the eigenenergy of disclination-bound states. (A). s =(1/2,1/2) and p =(π, π), and $\mathcal{P}$ is trivial. Hence, no bound state exists, while fractional charge appears at the disclination center due to nonvanishing p. (B). s =(0,0) and p =(π, π), giving a nontrivial $\mathcal{P}$. As a result, bound states appear at the disclination center along with fractional charges. (C). $\mathbf{s}=(\frac{1}{2},\frac{1}{2})$ and p =(0,0), and hence, $\mathcal{P}$ is also nontrivial, leading to both bound state and fractional charge at the disclination center like in (B).

As can be seen in the left panel of Figure 2A, fractional charges appear at the disclination center and the sample corners, but bound states are absent at the center (see also the right panel of Figure 2A) even with the nontrivial reciprocal topology p. This result can be intuitively understood using the dimerization of sites as shown by lighter magenta squares in the left panel of Figure 2A. As explained earlier, the corner state accompanying with 1/4 fractional charge appears due to dimerized cells shifting from the original Bravais lattice and the resulting filling anomaly. However, here in Figure 2A, the filling anomaly at the disclination center that is supposed to be induced by nontrivial p is canceled out by the nontrivial real-space topological invariant s. As a result, no fractionally filled dimerized cell is isolated from the bulk states, as suggested by the additive rule between s and p.

Figure 2B shows the disclination with trivial s = (0, 0) but non-trivial p = (π, π). Since the additive rule gives nontrivial $\mathcal{P}$, both the bound states and fractional charges simultaneously appear at the disclination center together with the corner state, as seen in Figure 2B. The eigenenergies distributions are gapless in Figures 2A, B owing to the nontrivial p, where edge states appear within the band gaps. Figure 2C shows a complementary example, where the real-space topology is nontrivial, and the reciprocal space topology is trivial. The additive rule gives nontrivial $\mathcal{P}$. Thus, the bound state appears at the center of disclination without corner states, as shown in Figure 2C. A pseudo fractional charge is just located at the disclination center. We shall note that this fractional charge at the disclination center is further smeared out beyond the fractionally filled dimerized cell as seen in the left panel of Figure 2C, unlike those in Figures 2A, B. It is also noted that in the right panel of Figure 2C, the disclination-bound state appears in the middle of the first energy band gap.

As the emergence of disclination-bound states is due to the dimerization at the disclination core, it is worth discussing the robustness of these bound states. Here we consider two types of perturbations. One is the perturbation without respecting the C₄ point group symmetry, and another is the perturbation respecting the C₄ point group symmetry. For the first type of perturbation, we consider three possibilities: onsite potential on the disclination center sites, a dangling bond in the disclination center, and inter-cell hopping connecting sites belonging to the same sub-lattice. As detailed in the Supplementary Material, for the perturbations without C₄ point group symmetry, the amplitude of perturbations cannot go beyond |γ − γ′|; otherwise, the disclination-bound states disappear. For the second type of perturbations respecting C₄ point group symmetry, the amplitude of perturbations can go beyond |γ − γ′|. This is because of the unique real-space structure in the disclination core, where one sublattice is missing in the central dimer of disclinations that disclination-bound states cannot mix with bulk states respecting C₄ point group symmetry. It is noted that the disclination-bound states are not located at zero energy, which suggests the absence of chiral symmetry in the formation of disclination-bound states [45, 69, 70].

2.4 Half-bound states

The second phenomenon of the proposed additive rule is the formation of half-bound states, which decay on one side of the sample but extend over the other. Here we consider a disclination structure with a unsymmetric s index, i.e., (s_x, s_y) = (0, 1/2) for Ω = −π as displayed in Figure 3. A bound state can be viewed as a wave function with a purely imaginary wavenumber for all independent real-space directions. Because of the unsymmetric disclination structure between k_x and k_y directions, a half-bound state can be expected. As displayed in Figures 3A, B, we find such half-bound states in our numerical calculations. Interestingly, the decaying direction for the half-bound states depends on the summation value of s + p/2π. As displayed in Figure 3A, when s_y + p_y/2π is nontrivial, the half-bound state decays along the x side. While s_x + p_x/2π is nontrivial, the half-bound state decays along the y side, as displayed in Figure 3B. This is perhaps because of the spatial distortion induced by the disclination structure.

FIGURE 3

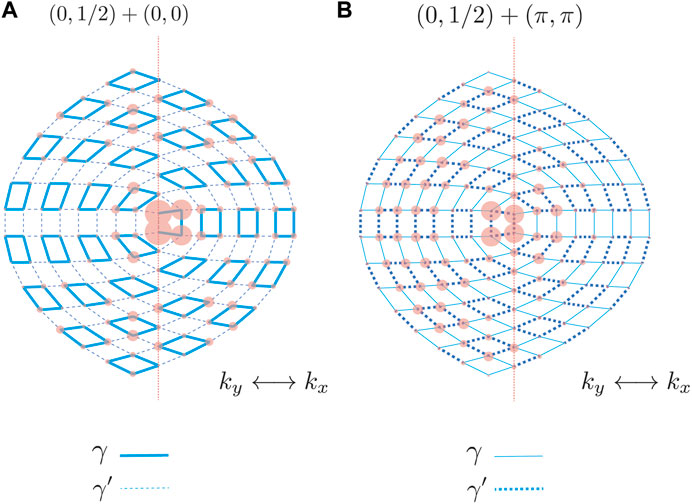
FIGURE 3. Existence of half-bound states. The disclinations have Ω =−π and s =(0,1/2). (A). p =(0,0), the state decays on the x-side but extends over the y-side. (B). p =(π, π), it decays on the y-side but extends over the x-side on the other hand. A dashed line passes through the center of the disclination, which divides the sample into x- (perpendicular to k_y direction of the reciprocal space) and y- (perpendicular to k_x direction of the reciprocal space) parts.

It is noted that the formation of half-bound states seems analogous to edge states due to the second-order topology. In the 2D SSH model, if the systems have p_xp_y = 0 but p_x + p_y ≠ 0, only edge states exist but no corner state. In the present case, this may be paraphrased: For two-sided systems with s_xs_y = 0 but s_x + s_y ≠ 0, only a half-bound state exists but not a bound state. This half-bound state can potentially control wave propagation using artificial crystalline structures such as photonic crystals. These states are impervious to the system size as shown in the Supplemntal Material. For the practical realization of the half-bound state, the hopping amplitude should depend on the distance between the two sites. In this case, the lattice distortion induced by the disclination cannot be ignored. The site’s position should be carefully tuned to achieve a situation similar to the tight-binding model.

2.5 Hybrid-bound states

The third phenomenon of the proposed additive rule is the hybrid-bound state, which can be numerically observed in any disclination with Ω ≥ π and s_x ≠ s_y. Figure 4A shows a disclination with Ω = π and s = (1/2, 0). This disclination is formed by inserting two extra π/2 blocks into the sample. Considering there are only two-independent directions in two dimensions, we can regard there are three x-parts and three y-parts arranged alternately in Figure 4A. For the sample of Figure 4A, we only observe bound states rather than half-bound states. This is because there are multiple x-parts, unlike the case in Figure 3, which only has one x-part. Furthermore, $\mathcal{P}$ is nontrivial regardless of p being trivial or nontrivial. We call this type of disclination-bound state hybrid-bound states because of their unsymmetrical s index. Figure 4B displays the energy spectrum for the disclination in Figure 4A with p = (0, 0), where a doubly degenerate bound state emerges within the band gap. Interestingly, for p = (π, π), the bound state is robust to the onsite potential perturbation as shown in the Supplementary Material, which may be useful for constructing cavities. A full spectrum of parameter pumping for such a hybrid-bound state is also given in Supplementary Material.

FIGURE 4

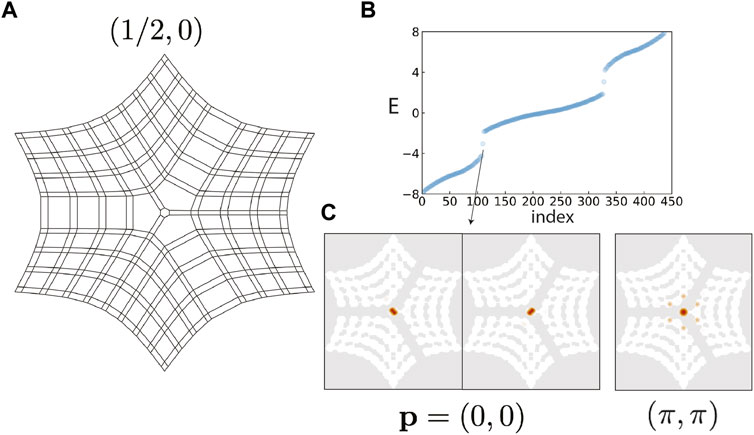
FIGURE 4. Real-space topology protected bound states and reciprocal-space topology protected ones. (A). The disclination has Ω = π and s =(1/2,0), and hence a nontrivial s + p/2π irrespective of p. (B)–(C), Topologically stable bound states invariably emerge at the disclination center. The energy levels are displayed for p =(0,0) in (B), where doubly degenerate in-gap bound states to appear. However, for p =(π, π), a symmetric charge distribution appears inside the bulk band gaps, as shown in (C).

3 Discussion

Finally, we discuss the generalization of the additive rule to other lattices. As the real-space topological invariant s is injective to nonequivalent disclination centers, and the reciprocal space topological invariant p/2π yields the Wannier center, it is intuitive to regard the additive rule as a result of the combination of disclination centers and Wannier centers. For example, for the C₄-symmetric lattice, there are two and four non-equivalent disclination centers for Ω = ±π/2 and Ω = ±π, respectively, and two possible Wannier centers. Their combinations give the afore-discussed dissociation of fractional charges from bound states, half-bound states, and hybrid-bound states in the 2D SSH model. Generalizing the additive rule to other C₄-symmetric is possible, which we remain as a future study.

To summarize, we proposed an additive rule between the real space and the reciprocal space topology by observing the cancellation of charge filling anomaly at the disclination core indicated by Burgers vector and the Zak phase. To support our proposal, we consider a typical higher-order topological model, the 2D SSH model, and show three pieces of evidence by numerical calculations: the dissociation of fractional charges from bound states, half-bound states, and hybrid-bound states. All those numerical calculations demonstrate the applicability of the proposed additive rule for the typical 2D SSH model.

4 Methods

For the disclination of −π/2, it can be constructed by removing the quarter of the 2D SSH lattice that is spanned by θ ∈ [0, π/2], and then changing the position of the remaining lattices according to θ → 4/3θ. The topological invariant s determines the center of the removing section and the corresponding 2D SSH model sample as displayed in Figure 1C, For other Ω, the construction of disclinations can be done following a similar process, i.e., for Ω = −π, the removing section should be half of the 2D SSH lattice, and the remaining lattices change position according to θ → 2θ. The fractional charge is calculated by solving the tight-binding model of the corresponding disclination lattice and integrating the charge density |ψ|² up to the first band gap and summing up in each unit cell. The Python package KWANT does this numerical simulation of tight-binding [71].

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

FL conceived the idea and conducted the research project. All authors contributed to the article and approved the submitted version.

Funding

This work is supported by the Research Starting Funding of Ningbo University, NSFC Grant No. 12074205, and NSFZP Grant No. LQ21A040004. KW acknowledges the financial support by JSPS KAKENHI (Grant Nos. 22H05473, JP21H01019, JP18H01154) and JST CREST (Grant No. JPMJCR19T1).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2023.1213158/full#supplementary-material

References

1. Hasan MZ, Kane CL. Colloquium: Topological insulators. Rev Mod Phys (2010) 82:3045–67. doi:10.1103/RevModPhys.82.3045

CrossRef Full Text | Google Scholar

2. Qi XL, Zhang SC. Topological insulators and superconductors. Rev Mod Phys (2011) 83:1057–110. doi:10.1103/RevModPhys.83.1057

CrossRef Full Text | Google Scholar

3. Ando Y. Topological insulator materials. J Phys Soc Jpn (2013) 82:102001. doi:10.7566/JPSJ.82.102001

CrossRef Full Text | Google Scholar

4. Bansil A, Lin H, Das T. Colloquium: Topological band theory. Rev Mod Phys (2016) 88:021004. doi:10.1103/RevModPhys.88.021004

CrossRef Full Text | Google Scholar

5. Hatsugai Y. Chern number and edge states in the integer quantum hall effect. Phys Rev Lett (1993) 71:3697–700. doi:10.1103/PhysRevLett.71.3697

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Fu L, Kane CL. Time reversal polarization and a Z₂ adiabatic spin pump. Phys Rev B (2006) 74:195312. doi:10.1103/PhysRevB.74.195312

CrossRef Full Text | Google Scholar

7. Hwang Y, Ahn J, Yang BJ. Fragile topology protected by inversion symmetry: Diagnosis, bulk-boundary correspondence, and Wilson loop. Phys Rev B (2019) 100:205126. doi:10.1103/PhysRevB.100.205126

CrossRef Full Text | Google Scholar

8. Bouhon A, Black-Schaffer AM, Slager RJ. Wilson loop approach to fragile topology of split elementary band representations and topological crystalline insulators with time-reversal symmetry. Phys Rev B (2019) 100:195135. doi:10.1103/PhysRevB.100.195135

CrossRef Full Text | Google Scholar

9. Wang Z, Dong L, Xiao C, Niu Q. Berry curvature effects on quasiparticle dynamics in superconductors. Phys Rev Lett (2021) 126:187001. doi:10.1103/PhysRevLett.126.187001

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Fujita M, Wakabayashi K, Nakada K, Kusakabe K. Peculiar localized state at zigzag graphite edge. J Phys Soc Jpn (1996) 65:1920–3. doi:10.1143/JPSJ.65.1920

CrossRef Full Text | Google Scholar

11. Delplace P, Ullmo D, Montambaux G. Zak phase and the existence of edge states in graphene. Phys Rev B (2011) 84:195452. doi:10.1103/PhysRevB.84.195452

CrossRef Full Text | Google Scholar

12. Kane CL, Lubensky TC. Topological boundary modes in isostatic lattices. Nat Phys (2013) 10:39–45. doi:10.1038/nphys2835

CrossRef Full Text | Google Scholar

13. Hafezi M, Mittal S, Fan J, Migdall A, Taylor JM. Imaging topological edge states in silicon photonics. Nat Photon (2013) 7:1001–5. doi:10.1038/nphoton.2013.274

CrossRef Full Text | Google Scholar

14. Fu L. Topological crystalline insulators. Phys Rev Lett (2011) 106:106802. doi:10.1103/PhysRevLett.106.106802

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Slager RJ, Mesaros A, Juričić V, Zaanen J. The space group classification of topological band-insulators. Nat Phys (2013) 9:98–102. doi:10.1038/nphys2513

CrossRef Full Text | Google Scholar

16. Shiozaki K, Sato M. Topology of crystalline insulators and superconductors. Phys Rev B (2014) 90:165114. doi:10.1103/PhysRevB.90.165114

CrossRef Full Text | Google Scholar

17. Benalcazar WA, Bernevig BA, Hughes TL. Quantized electric multipole insulators. Science (2017) 357:61–6. doi:10.1126/science.aah6442

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Langbehn J, Peng Y, Trifunovic L, von Oppen F, Brouwer PW. Reflection-symmetric second-order topological insulators and superconductors. Phys Rev Lett (2017) 119:246401. doi:10.1103/PhysRevLett.119.246401

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Song Z, Fang Z, Fang C. (d − 2)-dimensional edge states of rotation symmetry protected topological states. Phys Rev Lett (2017) 119:246402. doi:10.1103/PhysRevLett.119.246402

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Qian S, Liu CC, Yao Y. Second-order topological insulator state in hexagonal lattices and its abundant material candidates. Phys Rev B (2021) 104:245427. doi:10.1103/PhysRevB.104.245427

CrossRef Full Text | Google Scholar

21. Takahashi R, Zhang T, Murakami S. General corner charge formula in two-dimensional C_n-symmetric higher-order topological insulators. Phys Rev B (2021) 103:205123. doi:10.1103/PhysRevB.103.205123

CrossRef Full Text | Google Scholar

22. Tan Y, Huang ZH, Liu XJ. Two-particle berry phase mechanism for Dirac and majorana kramers pairs of corner modes. Phys Rev B (2022) 105:L041105. doi:10.1103/PhysRevB.105.L041105

CrossRef Full Text | Google Scholar

23. Peterson CW, Benalcazar WA, Hughes TL, Bahl G. A quantized microwave quadrupole insulator with topologically protected corner states. Nature (2018) 555:346–50. doi:10.1038/nature25777

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Imhof S, Berger C, Bayer F, Brehm J, Molenkamp LW, Kiessling T, et al. Topolectrical-circuit realization of topological corner modes. Nat Phys (2018) 14:925–9. doi:10.1038/s41567-018-0246-1

CrossRef Full Text | Google Scholar

25. Serra-Garcia M, Peri V, Süsstrunk R, Bilal OR, Larsen T, Villanueva LG, et al. Observation of a phononic quadrupole topological insulator. Nature (2018) 555:342–5. doi:10.1038/nature25156

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Ota Y, Liu F, Katsumi R, Watanabe K, Wakabayashi K, Arakawa Y, et al. Photonic crystal nanocavity based on a topological corner state. Optica (2019) 6:786–9. doi:10.1364/OPTICA.6.000786

CrossRef Full Text | Google Scholar

27. Xie BY, Su GX, Wang HF, Su H, Shen XP, Zhan P, et al. Visualization of higher-order topological insulating phases in two-dimensional dielectric photonic crystals. Phys Rev Lett (2019) 122:233903. doi:10.1103/PhysRevLett.122.233903

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Xue H, Ge Y, Sun HX, Wang Q, Jia D, Guan YJ, et al. Observation of an acoustic octupole topological insulator. Nat Commun (2020) 11:2442. doi:10.1038/s41467-020-16350-1

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Harari G, Bandres MA, Lumer Y, Rechtsman MC, Chong YD, Khajavikhan M, et al. Topological insulator laser: Theory. Science (2018) 359:eaar4003. doi:10.1126/science.aar4003

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Wu Y, Jiang H, Liu J, Liu H, Xie XC. Non-abelian braiding of Dirac fermionic modes using topological corner states in higher-order topological insulator. Phys Rev Lett (2020) 125:036801. doi:10.1103/PhysRevLett.125.036801

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Hsu CW, Zhen B, Stone AD, Joannopoulos JD, Soljačić M. Bound states in the continuum. Nat Rev Mater (2016) 1:16048. doi:10.1038/natrevmats.2016.48

CrossRef Full Text | Google Scholar

32. Benalcazar WA, Cerjan A. Bound states in the continuum of higher-order topological insulators. Phys Rev B (2020) 101:161116. doi:10.1103/PhysRevB.101.161116

CrossRef Full Text | Google Scholar

33. Cerjan A, Jürgensen M, Benalcazar WA, Mukherjee S, Rechtsman MC. Observation of a higher-order topological bound state in the continuum. Phys Rev Lett (2020) 125:213901. doi:10.1103/PhysRevLett.125.213901

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Liu F, Wakabayashi K. Higher-order topology and fractional charge in monolayer graphene. Phys Rev Res (2021) 3:023121. doi:10.1103/PhysRevResearch.3.023121

CrossRef Full Text | Google Scholar

35. Benalcazar WA, Li T, Hughes TL. Quantization of fractional corner charge in C_n-symmetric higher-order topological crystalline insulators. Phys Rev B (2019) 99:245151. doi:10.1103/PhysRevB.99.245151

CrossRef Full Text | Google Scholar

36. Li T, Zhu P, Benalcazar WA, Hughes TL. Fractional disclination charge in two-dimensional C_n-symmetric topological crystalline insulators. Phys Rev B (2020) 101:115115. doi:10.1103/PhysRevB.101.115115

CrossRef Full Text | Google Scholar

37. Peterson CW, Li T, Jiang W, Hughes TL, Bahl G. Trapped fractional charges at bulk defects in topological insulators. Nature (2021) 589:376–80. doi:10.1038/s41586-020-03117-3

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Liu Y, Leung S, Li FF, Lin ZK, Tao X, Poo Y, et al. Bulk–disclination correspondence in topological crystalline insulators. Nature (2021) 589:381–5. doi:10.1038/s41586-020-03125-3

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Rüegg A, Coh S, Moore JE. Corner states of topological fullerenes. Phys Rev B (2013) 88:155127. doi:10.1103/PhysRevB.88.155127

CrossRef Full Text | Google Scholar

40. de Juan F, Rüegg A, Lee DH. Bulk-defect correspondence in particle-hole symmetric insulators and semimetals. Phys Rev B (2014) 89:161117. doi:10.1103/PhysRevB.89.161117

CrossRef Full Text | Google Scholar

41. Slager RJ, Mesaros A, Juričić V, Zaanen J. Interplay between electronic topology and crystal symmetry: Dislocation-line modes in topological band insulators. Phys Rev B (2014) 90:241403. doi:10.1103/PhysRevB.90.241403

CrossRef Full Text | Google Scholar

42. Teo JC, Hughes TL. Topological defects in symmetry-protected topological phases. Annu Rev Condens Matter Phys (2017) 8:211–37. doi:10.1146/annurev-conmatphys-031016-025154

CrossRef Full Text | Google Scholar

43. Slager RJ. The translational side of topological band insulators. J Phys Chem Sol (2019) 128:24–38. doi:10.1016/j.jpcs.2018.01.023

CrossRef Full Text | Google Scholar

44. Roy B, Juričić V. Dislocation as a bulk probe of higher-order topological insulators. Phys Rev Res (2021) 3:033107. doi:10.1103/PhysRevResearch.3.033107

CrossRef Full Text | Google Scholar

45. Geier M, Fulga IC, Lau A. Bulk-boundary-defect correspondence at disclinations in rotation-symmetric topological insulators and superconductors. Scipost Phys (2021) 10:092. doi:10.21468/SciPostPhys.10.4.092

CrossRef Full Text | Google Scholar

46. Watanabe H, Po HC. Fractional corner charge of sodium chloride. Phys Rev X (2021) 11:041064. doi:10.1103/PhysRevX.11.041064

CrossRef Full Text | Google Scholar

47. Jung M, Yu Y, Shvets G. Exact higher-order bulk-boundary correspondence of corner-localized states. Phys Rev B (2021) 104:195437. doi:10.1103/PhysRevB.104.195437

CrossRef Full Text | Google Scholar

48. Zhang SB, Rui WB, Calzona A, Choi SJ, Schnyder AP, Trauzettel B. Topological and holonomic quantum computation based on second-order topological superconductors. Phys Rev Res (2020) 2:043025. doi:10.1103/PhysRevResearch.2.043025

CrossRef Full Text | Google Scholar

49. Zhang SB, Calzona A, Trauzettel B. All-electrically tunable networks of majorana bound states. Phys Rev B (2020) 102(R):100503. doi:10.1103/PhysRevB.102.100503

CrossRef Full Text | Google Scholar

50. Pahomi TE, Sigrist M, Soluyanov AA. Braiding majorana corner modes in a second-order topological superconductor. Phys Rev Res (2020) 2:032068. doi:10.1103/PhysRevResearch.2.032068

CrossRef Full Text | Google Scholar

51. Li L, Zhu W, Gong J. Direct dynamical characterization of higher-order topological phases with nested band inversion surfaces. Sci Bull (2021) 66:1502–10. doi:10.1016/j.scib.2021.04.006

CrossRef Full Text | Google Scholar

52. Pan XH, Luo XJ, Gao JH, Liu X. Detecting and braiding higher-order majorana corner states through their spin degree of freedom. Phys Rev B (2022) 105:195106. doi:10.1103/PhysRevB.105.195106

CrossRef Full Text | Google Scholar

53. Wu J, Wang Z, Biao Y, Fei F, Zhang S, Yin Z, et al. Non-abelian gauge fields in circuit systems. Nat Electron (2022) 5:635–42. doi:10.1038/s41928-022-00833-8

CrossRef Full Text | Google Scholar

54. Deng Y, Benalcazar WA, Chen ZG, Oudich M, Ma G, Jing Y. Observation of degenerate zero-energy topological states at disclinations in an acoustic lattice. Phys Rev Lett (2022) 128:174301. doi:10.1103/PhysRevLett.128.174301

PubMed Abstract | CrossRef Full Text | Google Scholar

55. Gopalakrishnan S, Teo JCY, Hughes TL. Disclination classes, fractional excitations, and the melting of quantum liquid crystals. Phys Rev Lett (2013) 111:025304. doi:10.1103/PhysRevLett.111.025304

PubMed Abstract | CrossRef Full Text | Google Scholar

56. Kleman M, Friedel J. Disclinations, dislocations, and continuous defects: A reappraisal. Rev Mod Phys (2008) 80:61–115. doi:10.1103/RevModPhys.80.61

CrossRef Full Text | Google Scholar

57. Azevedo S, Moraes F. Topological aharonov-bohm effect around a disclination. Phys Lett A (1998) 246:374–6. doi:10.1016/S0375-9601(98)00527-1

CrossRef Full Text | Google Scholar

58. Alexander GP, Chen BGG, Matsumoto EA, Kamien RD. Colloquium: Disclination loops, point defects, and all that in nematic liquid crystals. Rev Mod Phys (2012) 84:497–514. doi:10.1103/RevModPhys.84.497

CrossRef Full Text | Google Scholar

59. Liu F, Wakabayashi K. Novel topological phase with a zero berry curvature. Phys Rev Lett (2017) 118:076803. doi:10.1103/PhysRevLett.118.076803

PubMed Abstract | CrossRef Full Text | Google Scholar

60. Liu F, Deng HY, Wakabayashi K. Helical topological edge states in a quadrupole phase. Phys Rev Lett (2019) 122:086804. doi:10.1103/PhysRevLett.122.086804

PubMed Abstract | CrossRef Full Text | Google Scholar

61. Xu K, Zhang X, Luo K, Yu R, Li D, Zhang H. Coexistence of topological edge states and skin effects in the non-hermitian su-schrieffer-heeger model with long-range nonreciprocal hopping in topoelectric realizations. Phys Rev B (2021) 103:125411. doi:10.1103/PhysRevB.103.125411

CrossRef Full Text | Google Scholar

62. Tang S, Xu Y, Ding F, Liu F. Continuously tunable topological defects and topological edge states in dielectric photonic crystals. Phys Rev B (2023) 107:L041403. doi:10.1103/PhysRevB.107.L041403

CrossRef Full Text | Google Scholar

63. Zak J. Berry’s phase for energy bands in solids. Phys Rev Lett (1989) 62:2747–50. doi:10.1103/PhysRevLett.62.2747

PubMed Abstract | CrossRef Full Text | Google Scholar

64. Vanderbilt D, King-Smith RD. Electric polarization as a bulk quantity and its relation to surface charge. Phys Rev B (1993) 48:4442–55. doi:10.1103/PhysRevB.48.4442

PubMed Abstract | CrossRef Full Text | Google Scholar

65. Resta R. Macroscopic polarization in crystalline dielectrics: The geometric phase approach. Rev Mod Phys (1994) 66:899–915. doi:10.1103/RevModPhys.66.899

CrossRef Full Text | Google Scholar

66. Fang C, Gilbert MJ, Bernevig BA. Bulk topological invariants in noninteracting point group symmetric insulators. Phys Rev B (2012) 86:115112. doi:10.1103/PhysRevB.86.115112

CrossRef Full Text | Google Scholar

67. Teo JCY, Hughes TL. Existence of majorana-fermion bound states on disclinations and the classification of topological crystalline superconductors in two dimensions. Phys Rev Lett (2013) 111:047006. doi:10.1103/PhysRevLett.111.047006

PubMed Abstract | CrossRef Full Text | Google Scholar

68. Benalcazar WA, Teo JCY, Hughes TL. Classification of two-dimensional topological crystalline superconductors and majorana bound states at disclinations. Phys Rev B (2014) 89:224503. doi:10.1103/PhysRevB.89.224503

CrossRef Full Text | Google Scholar

69. Geier M, Trifunovic L, Hoskam M, Brouwer PW. Second-order topological insulators and superconductors with an order-two crystalline symmetry. Phys Rev B (2018) 97:205135. doi:10.1103/PhysRevB.97.205135

CrossRef Full Text | Google Scholar

70. Day IA, Akhmerov AR, Varjas D. Topological defects in a double-mirror quadrupole insulator displace diverging charge. Scipost Phys Core (2022) 5:053. doi:10.21468/SciPostPhysCore.5.4.053

CrossRef Full Text | Google Scholar

71. Groth CW, Wimmer M, Akhmerov AR, Waintal X. Kwant: A software package for quantum transport. New J Phys (2014) 16:063065. doi:10.1088/1367-2630/16/6/063065

CrossRef Full Text | Google Scholar