- 1Department of Physics and Astronomy, Purdue University, West Lafayette, IN, United States
- 2Quantum Science and Engineering Institute, Purdue University, West Lafayette, IN, United States
While many phenomena in cold atoms and other Bose–Einstein condensate (BEC) systems are often described using the mean-field approaches, understanding the kinetics of BECs requires the inclusion of particle scattering via the collision integral of the quantum Boltzmann equation. A rigorous approach for many problems in the dynamics of the BEC, such as the nucleation of the condensate or the decay of the persistent current, requires, in the presence of factors making a symmetry breaking possible, considering collisions with thermal atoms via the collision integral. These collisions permit the emergence of vorticity or other signatures of long-range order in the nucleation of the BEC or the transfer of angular momentum to thermal atoms in the decay of persistent current, due to corresponding terms in system Hamiltonians. Here, we also discuss the kinetics of spin–orbit-coupled BEC. The kinetic equation for the particle spin density matrix is derived. Numerical simulations demonstrate significant effects of the collision integral on the dynamics of the spin–orbit-coupled BEC upon quenching of the Raman coupling that generates synthetic electric and magnetic fields.
1 Introduction
Bose–Einstein condensation [1–3] was observed for atoms cooled in magnetic traps to low temperatures [4, 5]. Many phenomena in condensed matter physics, e.g., in superfluid He [6, 7], in exciton systems in semiconductors [8–13], in bilayer quantum Hall effect systems [14–16], and in superconductors with preformed Cooper pairs [17–22], are directly related to Bose–Einstein condensation. Atomic BECs have also been formed in other systems, such as microelectronic chips [23], and they may play a role in quantum information processing [24].
Mean-field theory provides a framework for understanding the main features of condensation and the role of interactions between particles [25]. The mean-field approach, in which the total Bose system field is divided into the condensate field and the field of excitations, was suggested by Bogoliubov [26]. When the field of excitations is small compared with the condensate field, the latter is described by Gross–Pitaevskii equations for the wavefunction of the BEC [27, 28]. However, over the years, it has been understood that in many problems, the mean-field Gross–Pitaevskii equation for BEC wavefunction is insufficient for understanding the whole spectrum of the properties of BEC systems and that excitations themselves and correlations beyond the Gross–Pitaevskii equation must be included.
In this paper, after a brief review of examples of BEC systems and properties requiring approaches beyond the mean-field approximation, the author discusses the kinetic equation approach to an investigation of the relaxation of the spin current and other transport properties of the spin–orbit-coupled Bose–Einstein condensates. A kinetic equation for the particle spin density matrix is derived using an approach similar to that of [29], extending it to non-uniform atomic BECs with spin–orbit interactions. Then, a symmetry-based approach will be used for the qualitative discussion of the relaxation of various modes in the condensate, as well as the relaxation of its excitations. Numerical calculation in a 1D model system shows that collision integral due to particle–particle interactions leads to a significant effect on relaxation in the spin–orbit BEC.
This article is partly a review and partly a report of the original results on the quantum Boltzmann equation for the spin density matrix of a spin–orbit-coupled Bose–Einstein condensate. Due to the limited size of the article, it does not provide a comprehensive overview of many of the important recent developments. I present my sincere apology for the inevitable omission of key contributions in the field.
2 Beyond the mean-field approach to BEC systems
While many properties of BEC systems have been successfully predicted and explained by using the Bogoliubov mean-field approach, in particular, the Gross–Pitaevskii equations for the Bose condensate wavefunction, the investigation of many BEC systems and properties requires going beyond mean-field studies. In this section, we will review two such examples: (1) nucleation of Bose–Einstein condensates and (2) decay of the current-carrying state.
2.1 Kinetics of Bose–Einstein condensation
The kinetics of Bose–Einstein condensation and nucleation of the condensate, in which the initial state does not contain the condensate itself, is an obvious example of the necessity to consider the BEC beyond mean-field approaches. In [29], it was observed that the whole process of BEC can be separated into three stages: restructuring of the Bose system before condensation, nucleation of the condensate itself or a phase transition stage, and then the growth of the emerged condensate. The first and the third stages can be approached using the kinetic Boltzmann-like equation, which includes real fluctuations and collisions. In the first stage, the energy relaxation in thermally populated Bose gas is needed to populate the ground state. Energy relation, e.g., in a uniform Bose system, can be treated using the Boltzmann equation [30].
The phase transition stage was studied in the 1980s [31–34]. The attempts to apply the Boltzmann-like equation via the inclusion of scattering of particles or coupling to a thermal bath to this stage led to the conclusion that the condensate density can only increase if the condensate already exists [35]. The important observation made in this latter work is that merely populating the ground state with Bose particles does not lead to an actual phase transition that requires coherence of the condensate faction. To address this question, the Keldysh approach to Green’s function of the Bose system combined with the path integral approach was developed in [35]. However, the conclusion that the nucleation of coherent condensate occurs on a time scale much smaller than the lifetime of the sample defined by interactions and that a quantum phase transition is needed to create coherence in the condensate was criticized, e.g., in [36]. Many authors attempted to treat this phase transition stage using the Gross–Pitaevskii equations, often applying them to local Bose fields [36–40]. Efforts beyond the regime of applicability of the GPE equations in the high-density limit were undertaken in [41]. Quantum corrections to the mean-field approximation were studied in [42]. A full kinetic equation approach beyond the Gross–Pitaevskii equation was undertaken in a series of papers [43–47]. Similarly, a quantum master equation was used in [48, 49]. In [50], the dynamics of condensation in a bimodal trap, consisting of a large reservoir region and a dimple, were modeled. The depth of the “dimple” can be controlled, and experimental investigations, see, e.g., [51, 52] have shown that such traps provide an efficient means of achieving condensation. It was shown that it is important for kinetic equations to include both two- and three-body processes.
In [53], a four-stage process was suggested for BEC kinetics. In this scenario, the phase transition stage is divided into two substages. The first corresponds to the creation of the local quasicondensates, with domain structure and without long-range order. Each domain has a specific phase, but phase correlation between different domains is absent. The second substage of the phase transition is the actual Bose condensation, accompanied by the emergence of a vorticity structure. It was suggested in [40] that the numerical solution of the non-linear Schrodinger equations, essentially a version of the Gross–Pitaevskii equation for classical Bose fields, shows the emergence of vorticity. However, the emergence of vorticity requires the presence of circulation, or its higher-order correlators, in such a final condensed phase, containing, e.g., a vortex ring. These correlators or vorticity are not present on the first substage of incoherent local condensate domains and must somehow be generated. The non-dissipative Schrodinger equations do not provide mechanisms to generate these vorticities. Hence, numerical simulations in [40] must have introduced some relaxation mechanisms on the second substage.
It was suggested in [36] that, generally, symmetry breaking can occur only as a result of introducing a small term of the Hamiltonian violating the conservation of particles. The most likely source of the term allowing the relaxation of vorticity is the interaction that would make non-condensed atoms serve as a reservoir for vorticity and energies. All quantum simulations of the Bose system have to be treated rigorously via the equations for the correlator (the order parameter) describing such vorticity. A quantum approach to BEC kinetics beyond the Gross-Pitaevskii equation was undertaken in [54]. The approach was based on associating the quantum-field density matrix in the coherent state representation with a correlator of a pair of classical fields, whose evolution is governed by a system of two coupled non-linear equations with stochastic terms. The Hamiltonian used in [54] included a localized absorber that removed the neutral atoms via collisions with foreign atoms. Such an absorber term designs a reservoir of non-condensed atoms, which can potentially absorb vorticity. The presence of vortex states in [54] was analyzed on the basis of angular momentum states, and the angular momentum distribution was calculated. Still, in order to generate average angular momentum or its correlators in the BEC ground state, the absorber term ought to design the reservoir for angular momentum via coupling of the condensate with the non-condensed gas. Thus, consideration beyond the mean-field equations or their analogs, exclusively in terms of the condensate variables, is required for analysis of the BEC nucleation stage, when Bose particles occupying the ground state acquire coherence and long-range order.
In the final stage of the Bose–Einstein condensation, the growth of the condensate can be described by the Boltzmann equation [55, 56]. The collision integral in such an equation can possibly include both the two-body and three-body processes, coupling the emerged Bose condensate faction with all other particles, including particle- and phonon-like excitations [57].
2.2 Decay of the current-carrying states
In systems with a complex (vectorial) order parameter, the ground state in a superfluid sample can have a non-zero persistent current [58, 59]. However, even for an ordinary scalar order parameter, superfluids can carry metastable currents. The ability to support current-carrying states in multiply-connected settings is one of the prime signatures of superfluidity and superconductivity. Such states in trapped Bose condensed alkali gases were investigated theoretically in [60]. Of particular interest are the kinetics of such a state and the rate at which persistent currents decay via thermal fluctuations. While the current-carrying states are not truly eternal, they can have extraordinarily long lifetimes. Their decay requires the occurrence of certain relatively infrequent but nevertheless topologically accessible (quantum or thermal) collective fluctuations [61–63].
For the condensate to be able to undergo the free-energy (and angular-momentum) changing fluctuation necessary for current dissipation, the condensate must not be isolated. In order to achieve this, the condensate in [60] was studied at temperatures not far below the critical temperature Tc, in which case, the non-condensed atoms can serve to provide an energy and angular momentum reservoir.
To find the decay rate, one needs to analyze the events in which the system decays from some metastable current-carrying states (which is a local minimum of the free energy) to a lower-energy (and typically more stable) state via a thermal fluctuation. The current decays through a dissipative process during which the condensate density decreases in magnitude over a region whose length is comparable to healing length ξ, which depends on the maximal density of particles and the strength of interactions.
In [60], the toroidal sample was assumed to have a circumference much larger than ξ, which leads to the possibility of locally stable current-carrying states. The healing length was also assumed larger than the radius of the torus cross-section, which results in suppression of the complex relaxation processes, such as the nucleation of vortex rings [64], and leads to simpler relaxation mechanisms, such as angular momentum relaxation. Dynamically, this process occurs via the passage of a vortex across the sample. For this event, a free-energy barrier must be overcome. The height of this barrier δF is given by the difference between the free energy of the metastable state Ψm and that of the transition state Ψt, i.e., the lowest possible free-energy high point en route through configuration space between the initial and final metastable states. This thermally activated process should occur at a rate of ω0e−δF/kT. The energies of both metastable and transition states are determined using the Gross–Pitaevskii equation, and so is the barrier height for transition between these states. However, for BECs undergoing a transition between those states, the term that permits an increase or decrease in the angular momentum of the system must be present in the system’s Hamiltonian. The attempt frequency and kinetics of this process must be defined by collisions between the condensate and thermal atoms and the solution of the Boltzmann equation, which defines microscopic relaxation times.
Experimentally, relaxation processes in a BEC system with the persistent current in a toroidal sample were investigated in [65, 66], where phase slips are observed between quantized persistent current states around a toroidal atomic 23Na Bose–Einstein condensate. However, these phase slips are induced by a weak link (a localized region of reduced superfluid density) rotated slowly around the ring. This is analogous to the behavior of a superconducting loop with a weak link in the presence of an external magnetic field. When the weak link is rotated rapidly, well-defined phase slips do not occur, and vortices enter into the bulk of the condensate. The presence of artificially created weak links changes the dynamics compared to the case ofpersistent currents flowing around a uniform torus. Nevertheless, the principles of relaxation remain the same: it is necessary to implement a mechanism by which the angular momentum of the persistent flow will be transferred to a bath of non-condensate atoms when the current changes. This is relevant both to the phase slip mechanism and the mechanism due to the production of vortices. Therefore, theoretical modeling of these effects must include coupling to non-condensate atoms within the quantum kinetics equation and cannot be solely restricted to the consideration of the condensate wavefunction within the Gross–Pitaevskii formalism.
Ring-shaped BEC samples carrying persistent currents were experimentally probed in the time-of-flight evolution experiments in [67]. However, the evolution time was sufficiently small and decay most probably did not occur in these experiments. In the experiment, the initial condensate was stirred to generate an angular momentum that leads to circulation. The experiment for observation of the decay of persistent current can be set with the generation of angular momentum 1, which produces a hole in the released condensate, and observation of the disappearance of that hole when there is a sufficient window of observation in the time-of-flight evolution experiments.
Recently, it was proposed that using linear and Laguerre–Gaussian Raman beams, which have been used to create spin–momentum coupling [68] and spin–angular momentum coupling [69], it is possible to realize a synthetic torus penetrated by a net effective magnetic flux [70]. It will be of considerable interest to investigate current-carrying states and their dynamics and decay in such configurations.
3 Kinetic approach to transport in Bose–Einstein condensate systems
The transport properties of Bose–Einstein condensates requiring an approach beyond the Gross–Pitaevskii equations can be discussed in terms of the kinetic equation. The kinetic approach has historically already been applied to superfluid He-4 by Landau and Khalatnikov [71, 72]. In the early work on kinetic equations in Bose systems, two fluid hydrodynamic non-linear equations for the condensate and normal fluid were derived using the distribution function method, starting from the Liouville equation and leading to a kinetic equation for the distribution function of quasiparticles in a dilute spatially inhomogeneous Bose gas below the helium λ point. Such a kinetic equation describes a state close to a local equilibrium state. Hohenberg and Martin [73] used the time-correlation function approach and considered a relaxation of a fluctuation about an equilibrium state. They obtained linearized two-fluid equations and Kubo-type equations for transport coefficients. As discussed in [55], the results obtained by these two methods for transport coefficients are identical. In [55, 56], the solution of the kinetic equation, as well as the distribution functions of quasiparticles, was used to derive the equations of motion for superfluid velocity.
The derivation of kinetic equations for quasiparticles is most convenient in the reference frame where the superfluid is at rest, allowing the separation of the condensate part of the Bose field operators and the application of the Bogoliubov transformation [74], which leads to a description of the system in terms of quasiparticles. In a system with a single-spin ground state, or a singlet-order parameter, a rigorous description includes both consideration of the condensate and quasiparticle densities and inclusion of the off-diagonal terms due to the presence of anomalous Green’s functions [72]. For usual singlet superconductors, the kinetic equation approach was developed by Betbeder–Matibet and Nozieres [75] and by Aronov and co-authors [76].
The matrix kinetic equation for a system with a spin-triplet order parameter, superfluid 3-He, which is an anisotropic Fermi superfluid, was developed by Wolfle [77, 78]. Using the matrix equation, one can determine deviations from equilibrium for particle number density, spin, and superfluid and normal currents. The collision integral for Bogoliubov quasiparticles and their relaxation rates in this case were derived in [79]. Furthermore, the kinetic equation can be used to determine the spin diffusion and intrinsic spin relaxation times. In the case of the anisotropic He3-A phase, anisotropic viscosity and orbital relaxation were also calculated [7]. A hydrodynamic description of the spin systems in A-phases can involve three fluids, and superfluid velocities are defined for the total phase and a difference of phases for the two spin components. Due to the presence of spin, and as a result of the presence of anomalous averages, a full kinetic description of the He-3 spin system involves a 4 × 4 matrix equation.
In much the same way as for superfluid He-3 with orbital angular momentum and spin vector order parameters, for spin-1 Bose–Einstein systems, the full kinetic equation generally constitutes the equation for a 6 × 6 density (Green’s function) matrix. For Raman beam-induced spin–orbit-coupled Bose–Einstein condensates with a state for one of the spin projections much higher in energy than the two lower spin projection states, thus becoming effectively a spin 1/2 system, the kinetic equation for quasiparticles should be an equation for a 4 × 4 matrix.
The question emerges as to whether a simpler approach is possible. Indeed, even for regular superconductors, the 2 × 2 matrix kinetic equation for quasiparticles with non-zero off-diagonal elements is rather intricate, and still, is not capable of describing many of the potential phenomena of interest [80]. However, for Bardeen–Cooper–Schrieffer (BCS) superconductors, such a kinetic equation is likely the simplest microscopic model allowing the treatment of transport phenomena. The nature of the BCS superconducting transition is superconducting pairing, i.e., the creation of bosons in a fermion system. The important aspect is the role of the off-diagonal Green’s function
where N is the number of particles,
Therefore, for the Bose–Einstein condensates, a simpler approach to kinetic phenomena appears to be possible [29, 81]. In these works, a simpler kinetic equation, a kinetic equation for particles only, was derived. In this approach, particles are divided into condensate particles and excited particles, and corresponding distribution functions and particle densities are evaluated. While quasiparticles are not introduced, many of the scattering processes between the condensate particles and excited particles are taken into account by the collision integral of the kinetic equation. It was shown in [29, 81] that if the characteristic energy of excited particles ∼ p2/m exceeds the characteristic energy from the interaction ∼ gn, then the results of the simplified approach coincide with the results of [55] that have included all quasiparticle effects. On the intuitive level, when excitations are primarily particle-like, one can use the description in terms of particles. However, for phonon-like collective excitations, quasiparticle description must be applied [57].
Furthermore, we are interested in comparing the mean-field consideration of interactions, and their effect on the system via fluctuations and dissipative processes, introduced as scattering accounted by the collision integral in the kinetic equation. We will apply a simple kinetic equation for particles to illustrate that collision integral consideration strongly affects the dynamics of the spin–orbit Bose–Einstein condensates.
4 Spin–orbit-coupled BEC condensates
Cold atomic gases provide a clean and highly controllable [82] platform for simulating and exploring many condensed matter phenomena [83], in particular those associated with spin [84]. Spin, an internal quantum degree of freedom of particles, is central to many condensed matter phenomena such as topological insulators and superconductors [85] and technological applications such as spintronics [86, 87] and spin-based quantum computation [88].
The generation of synthetic electric [89] and magnetic [90] fields, artificial gauge fields in general [91], makes neutral atoms behave like charged particles. The synthetic magnetic and spin-dependent magnetic fields have been realized to demonstrate, respectively, the superfluid Hall [92] and spin Hall effects [93] in BECs.
Spin–orbit-coupled Bose–Einstein condensates (BECs) offer a unique experimental system. The creation of spin–orbit-coupled synthetic BECs in systems of bosonic [68] and fermionic [94] atoms further paves the way to explore diverse phenomena such as topological states [95] and exotic condensates and superfluids [96] Using counter-propagating Raman beams, an effective two-level system can be set up using the atoms’ internal degrees of freedom, thus creating a spin–orbit-coupled spin-1/2 BEC. By controlling the Raman beam coupling strength, Ω, the BEC can be driven between a miscible phase, where the two spin states are mixed in momentum space, and an immiscible phase, where the two spin states are well-separated in momentum space.
In [97], experiments were performed exploring how the BEC responds to non-adiabatic shifts in Ω. The effects of one-dimensional synthetic spin–orbit coupling on the spin relaxation in a disorder-free atomic BEC were explored using a condensate collider, in which the spin dipole mode of two BECs of different spin states constitutes an alternating spin current. The spin dipole mode [98] is initiated by applying a spin-dependent synthetic electric field to the BEC. This is done via quenching, i.e., non-adiabatically changing the Raman coupling Ω, which generates the spin–orbit-coupled band structure. It should be noted that interactions in 87Rb have a repulsive characteristic so that collapse phenomena [99] do not emerge in such spin–orbit-coupled BECs.
The shifts in Ω make the BEC oscillate in momentum space, with the oscillations being dependent upon the size of the shift, Figure 1. Theoretically, these oscillations can be reproduced using the Gross–Pitaevskii equation [97]. The Gross–Pitaevskii equation was used also for consideration of a spin–orbit BEC in a moving trap [100]. However, oscillations of the spin–orbit BEC due to quenching of the Raman coupling are associated with a change in the ground state and reconstruction of a new BEC state and, therefore, require interactions of the condensate and thermal atoms, i.e., dissipative in nature. The mean-field theory, like the Gross–Pitaevskii equation, lacks dissipative processes; therefore, an accurate description of these oscillations must go beyond mean-field theory. Here, we explore the oscillations of the BEC caused by non-adiabatic shifts in Ω using a kinetic equation that includes a collision integral for a trapped one-dimensional BEC. As discussed in the previous section, we will use a simplified scheme with the kinetic equations for particles. In the following section, we derive the quantum Boltzmann equation for a 2 × 2 particle spin density matrix in a spin–orbit-coupled BEC and qualitatively analyze the relaxation processes. We, then, will make a numerical comparison of the dynamics of the 1D BEC under quenching of Ω between cases where the atoms are non-interacting, where only mean-field terms are included, as well as when the collision integral effects are considered. We will see that the mean-field effects are either less or similar in importance compared to the effect of collision integral terms. Thus, a mean-field theory is incapable of describing the evolution of the spin–orbit-coupled BEC after such a non-adiabatic quenching, and it is necessary to include correlations via the collision integral in the kinetic equation.
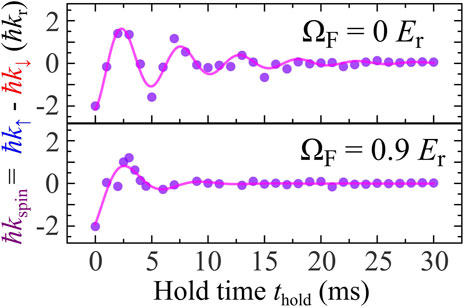
FIGURE 1. Adopted from [97]. Relative momentum oscillations in a spin-dipole mode. Solid lines are fits for damped sinusoidal oscillations.
4.1 Spectra and the spin density matrix of the spin–orbit BEC
The BEC in [97] is contained in a three-dimensional anisotropic harmonic trap with frequencies ωi, i = x, y, z, with the trap potential
Counter-propagating Raman beams are coupled to the system with a strength Ω, detuning δ, and recoil momentum kr and generate synthetic spin–orbit interaction. The single-particle Hamiltonian is given as follows:
where x is the direction of Raman-induced one-dimensional spin–orbit coupling, equivalent to the case of equal Rashba and Dresselhaus couplings of the two-dimensional electron gas in III–V semiconductor heterostructures [101], k⊥ = (ky, kz), and the σi are the Pauli 2 × 2 spin matrices on the basis of spin states of projections mF = 0, − 1 of the total spin F = 1 in the BEC. The third state is shifted out of resonance by a quadratic Zeemann splitting. At δ = 0, the single particle eigenenergies are given by the following equation [68, 102].
Depending on magnitudes of
The quantity
constitutes the effective vector potential acting on BEC particles in the double-minima structure at Ω < 4Er. Changing Ω in time results in the time-dependent electric field. This form of the effective spin–orbit vector potential is specific for the spin–orbit interaction of a one-dimensional type and is different from the spin–orbit effects in two dimensions [103–105]. Furthermore, non-Abelian effects of the spin–orbit-induced effective vector potential can emerge when the BECs with a higher angular momentum (or spin) are studied, similarly to the charge carrier hole system in [106].
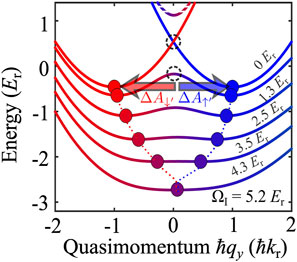
FIGURE 2. Adopted from [97]. The ground band (solid lines) of the synthetic spin–orbit-coupled condensate calculated for several Ω at δ = 0. A higher band calculated for Ω = 1.3Er is shown as dashed lines. The colors indicate the spin compositions, with red for |↑⟩ and blue for |↓⟩. The ground band minima in quasimomentum marked by dots are identified with the spin-dependent vector potentials Aσ, which shift the minima in opposite directions as Ω is lowered into the double minima band. This generates spin-dependent synthetic electric fields Eσ = dAσ/dt and thus excites the spin-dipole mode and an alternating spin current along the direction of the spin–orbit vector potential in a trapped BEC. The upper (lower) dashed circle represents the region around qy = 0 in the double minima band, from which the two (dressed) spin components of the BEC roll down toward the corresponding band minima in response to the application of the spin electric field.
Introducing interactions, we restrict collisions to two-body collisions in our system and use a spin-dependent contact potential of the
where Vi,j is a matrix of the form
with c0 and c2 parametrizing the interaction, while
We now study how this system evolves when Ω suddenly changes, going beyond mean-field corrections. This is done by using the Hamiltonian (3) and a standard Keldysh diagrammatic technique. Starting from the Keldysh matrix Green’s function G(r1, r2, t1, t2), the equations are derived for the 2 × 2 one-particle spin density matrix describing the distribution of particles, ρ(p, r, ϵ, t), where r = (r1 + r2)/2 are the center of mass coordinates, time t = (t1 + t2)/2, and p and ϵ are the kinematic momentum and energy arising in the Fourier transforms over the differences of coordinates and times, correspondingly. The equation for the particle density matrix is as follows:
where V = ∂H1/∂p is the spin-dependent velocity operator and curly brackets denote the anticommutator of operators A and B,
is the spin-dependent part of the single-particle Hamiltonian, leading to spin precession of the Bose particles. Rectangular brackets [A, B] = AB − BA denote the commutator of operators A and B, which describes the spin precession. Sint includes both a spin-independent contribution and a spin operator component that defines the precession caused by the mean field of polarized bosons,
where the Trace is taken over the spin indices of the particle colliding with another particle. Here, Hint is the interaction Hamiltonian of the system given by Eq. 7. Furthermore, the second term in Eq. 9 containing a spatial derivative describes the effects of the BEC quantum pressure in terms of the evolution of the spin density matrix. Moreover, F is the force acting on bosons. For atomic gases in traps, the force has two sources:
where Utrap(r) is the oscillator potential of the trap and Sint is determined by the sum of interactions of a single boson with all other bosons. The quantity Sint depends on the single-particle density matrix and is a Boltzmann equation counterpart of the interaction term in the Gross–Pitaevskii equation. Finally, Ic(ρ(1)) is the collision integral given by the following equation:
where indices p and p′ of ρ(1) and k and k′ of ρ(2) correspond to momenta before and after scattering for two interacting particles, respectively, and the direct product of spin matrices
Hamiltonian H0 in the expression for collision integral defines the energy of particles and corresponding equilibrium density matrices that make the collision integral 0. H0 in the density matrix equation includes kinetic energy, potential energy, spin–orbit coupling, and other effective magnetic field spin precession terms, as well as the mean-field interaction energy.
While we restricted our consideration of the relaxation of the BEC to two-body collision processes, three-body interactions can introduce many important effects. It was recently discussed, for example, that in addition to density losses, three-body interactions may result in internal pressure, resulting in repulsive potential [107]. A rigorous treatment of three-body interactions must account for both coherent effects, such as forces and spin precession, and fluctuation and relaxation effects via collision integral. The collision integral (14) takes into account only part of the contributions associated with the effect of oscillations of the trap, via the δ-function describing the conservation of energy. To fully include the trap effects on the collision of particles, a procedure similar to that used for considering the effects of disorder and magnetic field on electron collision integral in [108] must be implemented.
In electron systems, the quantum kinetic Boltzmann equation for the spin-dependent 2 × 2 density matrix was derived in [109–111]. For cold Fermi-gases, the collision integral in simulations of spin–orbit dynamics was introduced phenomenologically in [112]. A major feature of Eq. 9 for bosons is that it is written for particles, like in [29]. The density matrix in this case, as will be discussed in the next subsection, will include both the condensate and thermal parts. Excitations included in the collision integral for particles represent particle-like excitations and do not account for phonon-like excitations appearing in a quasiparticle description. However, spin current relaxation, as we consider in the next sections, is primarily due to elastic processes in the presence of the effective magnetic field due to spin–orbit interactions and precession field stemming from Raman beam coupling. Therefore, the approach in terms of particles largely captures the spin current relaxation effects.
4.2 Qualitative analysis of the evolution of the spin density matrix
The time-dependent evolution of the density matrix depends on the evolution of the parameters of the system. We are interested in the evolution of the BEC system due to the change in Rabi frequency Ω from ΩI to ΩF. The initial particle density matrix is ρi(r, p, t), and the final particle density matrix ρf(r, p, t) depends on the structure of the condensate at Ωi and ΩF, correspondingly. It has been shown [102, 113]that the interaction of particles dictates that below Ω ∼ 0.2Er, the condensate occupies both spectral minima of the single-particle spectrum, and above that, the condensate occupies only one of the two spectral minima (provided Ω < 4Er and results in two minima). Therefore, for small Ω, the condensate part of the density matrix has a two-minima structure. This results in two Gaussians in diagonal representation. At Ω ≥ 0.2Er, there is one Gaussian in diagonal representation. However, in this case, experiments can be interpreted as two projected Gaussians comprised in terms of bare spin states.
Our goal is to attempt to understand the relaxation of the spin–orbit-coupled BEC system starting from the initial state. To do this, we will first use symmetry considerations. The BEC system in a harmonic trap is a finite system, in which particle states are localized. Density matrix equations are usually applied to infinite systems, in which particles’ momenta are good quantum numbers. However, scattering in the considered BEC system is rather strong and occurs on a spatial scale less than the characteristic harmonic trap size. Therefore, in order to understand the symmetry properties and which components of the density matrix are subject to relaxation, it is sufficient to consider the particles’ momenta, treating the trap as an external force. In this case, the initial density matrix is given by the following equation:
and final state density matrices at small Ω (for two different cases depending on whether Ω ≥ 0.2Er or Ω < 0.2Er) are approximately given by the following expression:
for Ω ≥ 0.2Er and
for Ω < 0.2Er, where ±p0 are the momenta at the energy dispersion minima, and where fBs are the Bose matrix distribution function for thermal excitations.
The evolution of the system naturally depends on how fast Ω is being switched between initial and final values. In the case of adiabatic switching, the system in the first approximation gradually evolves between states described by density matrices in the initial and final states. Matrices in initial and final states are at equilibrium, and when they are substituted into the collision integral, it vanishes. In fact, for adiabatic switching, all intermediate states of the system (and the corresponding condensates) lead to vanishing collision integrals, which is a consequence of the energy conservation law described by the δ-function of energy. If the density matrix is a function of energy only, it cannot lead to currents or spin currents. As a result, no spin current arises or exists in the initial, intermediate, and final states of the BEC system for adiabatic switching.
In the case of abrupt switching between the initial and final state, after switching, the initial density matrix is no longer at equilibrium and is subject to relaxation, a symmetry consideration allows us to determine which components of this density matrix relax. The number of particles in the condensate decreases because of collisions with non-condensate particles and due to the effects of the fields corresponding to a new equilibrium. In addition to the variation in the equilibrium (Bose–Einstein) non-condensate part, non-equilibrium components of the density matrix also arise due to fields. The primary scattering mechanism is spin-independent (characterized by c0). Spin-dependent effects, however, arise because of particle spin precession in Hs fields.
It is important to recognize that the collision integral vanishes for the density matrix components describing the current (flux) of particles. This term represents the first excited ‘sloshing’ dipole mode and is described by the first Legendre polynomial. The collision term vanishes because of momentum conservation in binary collisions between particles of the same spin, which is described by the δ-function of momenta in the expression for collision integrals. Let us assume that the component of a non-equilibrium density matrix has the form
where pi is the projection of the particle momentum, and the dependence of the coefficient κ1 characterizing the distribution, which depends on equilibrium Hamiltonian H0, indicates that the symmetry of this non-equilibrium density matrix component is determined by the momentum vector. We then observe that due to the δ-function of momenta in the collision integral, the collision integral vanishes, manifesting the well-known property of BECs that dipole moment and flux of particles are conserved in binary collisions.
However, binary collisions do result in the decay of a breathing mode. Consider, e.g., the momentum distribution
For a harmonic trap, this density matrix component, characterized by the second Legendre polynomial in particle momentum, can be used for analyzing the breathing mode. By inserting δρ2 into the collision integral, we observe that energy and momentum conservation does not make the collisional integral vanish, so the decay of this mode is governed by spin-independent scattering constant c0 and is significant.
Furthermore, we observe that the spin current also decays due to binary collisions between atoms with different spins. The corresponding density matrix component is characterized by the product of one of the spin Pauli operators and the first Legendre polynomial in momentum. Expanding the density matrices in the collision integral, we obtain that spin current relaxation is defined by the quantity
where
We further observe that spin polarization decays due to binary collisions despite no spin-flipping terms being present in the scattering matrix (once the original spin 1 scattering operator is projected onto 0 and –1 projections manifold). However, due to spin-current decay, spin polarization is damped via spin–orbital precession in the presence of the effective magnetic field due to Raman beam coupling. This mechanism is analogous to the Dyakonov–Perel spin relaxation mechanism in non-centrosymmetric conductors [114] and can also be interpreted as dephasing in the presence of a random spin–orbit-induced vector potential [115].
4.3 Numerical simulations in the 1D case
The full numerical simulation of the 3D atomic BEC is outside the scope of the present work, but we present a simulation of a 1D case in order to demonstrate the importance of including a collision integral term [116]. Here, we assume and define the harmonic oscillator frequency by ωx = ω = 2.5kHz so that ℏω = 0.1Er, where the recoil energy Er = 25 × 10−24 erg and ℏkr = 10–22 g cm/s is the recoil momentum of the Raman beams. Similar to the experiments studying the quench of spin–orbit-coupled BECs through non-adiabatic changes in Ω, we start with large Ω = 10Er. For these initial conditions, the two bare spin states of the BEC are equally populated and are in a miscible state. Assuming T = 0, the atoms of the BEC are all then in the lowest state of the harmonic trap. This then gives us the starting Wigner distribution.
On the basis of the bare spin states, the Wigner distribution of each spin state has its maximum in momentum space shifted away from p = 0 in opposite directions.
In the first case under consideration, the condensate is quenched by shifting Ω = 10 → Ω = 0. The final state in the case of this quench has a singular property among all possible final states: if the system is infinite, the gauge potential Aσ would be removed by a gauge transformation, so that the ground state of the condensate is p = 0 for both bare spin projections. In a finite system with finite confinement, this transformation leaves spin–orbit interaction acting near the boundary of the condensate, due to changes in boundary conditions. In the numerical study, similarly to the experimentally investigated three-dimensional case, this quench gives rise to large oscillations in momentum space, where the two spin states oscillate around their equilibrium positions as shown in Figure 3. As the oscillations continue to evolve, the BEC begins to spread out in momentum space, with an increasing number of particles remaining at the equilibrium position.
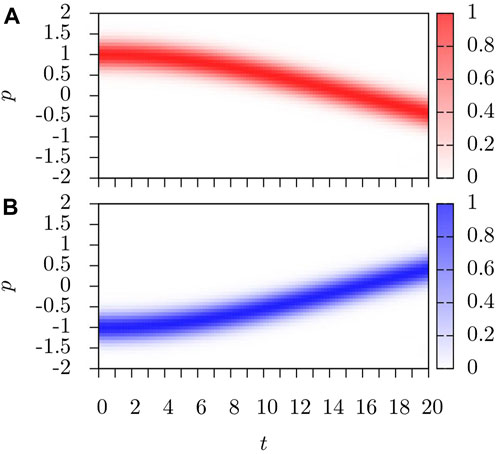
FIGURE 3. Evolution of (A) n11(p, t) and (B) n22(p, t) after Ω = 10Er → Ω = 0 for non-interacting particles. The change in Ω shifts the ground state minima from
To visualize the effects of the interaction, we look at differences in the calculated BEC density with different corrections added. To simplify our analysis of these differences, we will introduce the following notation: for the case when there are no interactions included, the density in momentum space will be
We first consider the effects of the mean-field and collision integral corrections in the case Ω = 10Er → Ω = 0. In Figure 4A, we look at the effects of the mean-field corrections denoted by
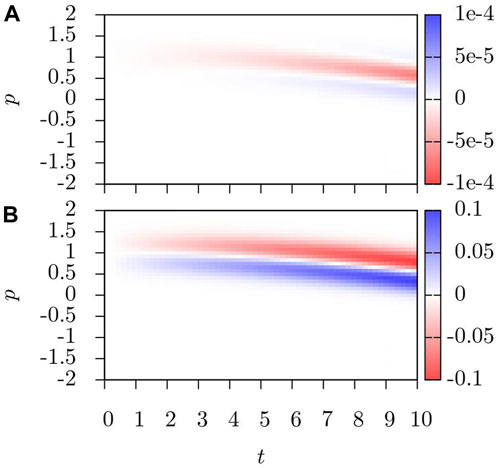
FIGURE 4. (A)
Let us now consider the case Ω = 10Er → Ω = 1, as shown in Figure 5. The gauge (Galilean) transformation can also be applied in this case, making p = 0 the location of minima in transformed momentum space; however, this transformation generates a new precessional term due to the presence of Ω = Er in the final state. Here, the simulation shows that the shift in the Raman coupling causes small oscillations in the BEC about the initial equilibrium state. These oscillations, however, begin to quickly lose cohesion as particles begin to move toward the new equilibrium at p = 0.
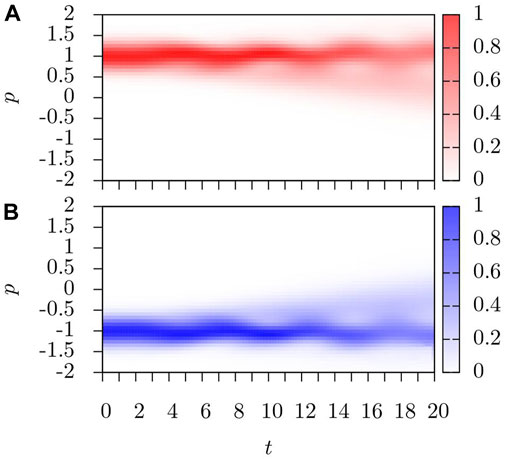
FIGURE 5. Evolution of (A) n11(p, t) and (B) n22(p, t) after Ω = 10Er → Ω = Er for non-interacting particles. The shift excites small oscillations about p = ±1, which are quickly weakened as the density peak disintegrates as particles move toward the new equilibrium position.
Next, let us consider the effects of the interaction corrections, which are shown in Figure 6. First, the mean-field corrections now have a substantially larger effect, acting to push the BEC toward equilibrium, as can be seen from the
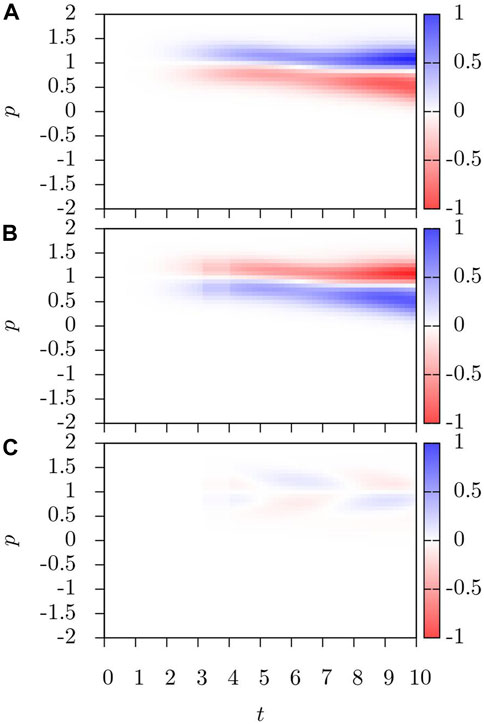
FIGURE 6. (A)
Interestingly, oscillations between assisting and restricting the expansion of the BEC are reminiscent of effective localization that emerged in the hydrodynamic simulation of spin–orbit-coupled BEC released from harmonic trap [117]. However, the effect in our simulations of the quenching of Raman coupling in spin–orbit BEC emerges from the competition of the mean-field and collision integral contribution to the kinetics of BEC, while the approach of [117] to the dynamics of the condensate released from the trap is based on Gross–Pitaevskii equations and considers only the mean-field interaction effects. We note that in [118], it was shown that localization effects in 1D BEC can lead to fluid-to-insulator transition. Consideration of such transitions involves analysis of thermal excitations of quasiparticles and understanding the diffusion coefficient of a cloud of atoms and requires going beyond the mean-field approximations.
5 Conclusion
While the mean-field approaches and the Gross–Pitaevskii equation are capable of explaining many experimental observations in atomic BEC and other BEC systems, the quantum Boltzmann equation for the density matrix is required to fully understand the kinetics of the evolution of the Bose–Einstein condensates. Nucleation of the Bose–-Einstein condensates and the decay of persistent currents are among the problems where the kinetic approach is necessary for full understanding. There is an important common symmetry principle characterizing these two phenomena. In order to describe the nucleation of the Bose–Einstein condensates, the Hamiltonian of the system has to include interactions, possibly small, capable of non-conserving the particles and resulting in generation (relaxation) of the vorticity. In the decay of persistent currents, the kinetics must take into account interactions capable of transferring angular momentum from the condensate to thermal atoms. Recently, the decay of spin currents was studied in spin–orbit-coupled Bose–Einstein condensates. While the time-dependent Gross–Pitaevskii approach allows for explaining certain features of experimental data, a full understanding of dissipative processes requires an account of interactions via the collision integral in the Boltzmann equation. We derived the quantum Boltzmann equation for the spin density matrix in a spin–orbit-coupled BEC and examined the evolution of the spin–orbit BEC removed from equilibrium. We used a simplified approach of the kinetic equation for particles that leads to a 2 × 2 matrix kinetic equation. The effects of the mean field and the collision integral terms on the dynamics of the condensate are strongly influenced by how the Raman coupling is changed. This correlates with different evolutions of the BEC depending on the characteristics of change in the Raman coupling in the experiment. Two types of behavior are observed in 1D simulation. In one kind, the mean-field and collision integral contribution may have similar effects, acting to dampen the oscillations by causing the spread of the cold atoms away from the minimum energy. The collision integral-induced relaxation, however, is observed to have a stronger effect than the mean-field contributions. Another type of behavior is collision integral contribution, which dampens the effects of all of the coherent forces, including the mean-field interaction effect, so that the mean-field interactions and collision integral acting together lead to an overall small effect that oscillates between supporting and restricting the expansion of the BEC, with oscillations gradually damping. It is of interest to see if these patterns of behavior will also emerge in full 3D treatment. However, as already observed from the present results, it is clear that the non-equilibrium dynamics of the BEC are strongly influenced by the collision integral relaxation effects. Thus, proper treatment of these systems requires going beyond the mean-field approach.
Author contributions
YL-G: investigation and writing–original manuscript.
Funding
The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This work has been supported by the U.S. Department of Energy, Office of Basic Energy Sciences, Division of Materials Sciences and Engineering under Award DE-SC0010544.
Acknowledgments
The author is grateful to Yong Chen, Chris Greene, and Qi Zhou for useful discussions and to Anthony Tylan-Tyler for performing numerical simulations of the kinetics of the 1D spin–orbit-coupled BEC.
Conflict of interest
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Einstein A. Quantum theory of the monatomic ideal gas. In: Sitzungsberichte der Preussischen akademie der Wissenschaften, 261. Physikalisch-mathematische Klasse (1924).
2. Einstein A. Quantum theory of mono-atomic ideal gas. Second paper. In: Sitzunberichte der Preussichen akademie der Wissenshchaften, 3. Physikalisch-mathematische Klasse (1925).
3. Bose SN. Plancks gesetz und lichtquantenhypothese. Z Physik (1924) 26:178–81. doi:10.1007/bf01327326
4. Anderson MH, Ensher JR, Matthews MR, Wieman CE, Cornell EA. Observation of bose-einstein condensation in a dilute atomic vapor. Science (1995) 269:198–201. doi:10.1126/science.269.5221.198
5. Davis KB, Mewes M-O, Andrews MR, van Druten NJ, Durfee DS, Kurn DM, et al. Bose-Einstein condensation in a gas of sodium atoms. Phys Rev Lett (1995) 75:3969–73. doi:10.1103/physrevlett.75.3969
6. Kapitza P. Viscosity of liquid helium below the λ-point. Nature (1938) 141:74. doi:10.1038/141074a0
8. Blatt M, Boer JKW, Brandt W. Bose-Einstein condensation of excitons. Phys Rev (1962) 126:1691–2. doi:10.1103/physrev.126.1691
9. Keldysh LV, Kopaev YV. Possible instability of the semimetallic state with respect to Coulombic interaction. Fiz Tverd Tela (1965) 6:2791.
10. Wolfe JP, Lin JL, Snoke DW. Bose-Einstein condnesation of a nearly idea gas: excitons in Cu2O. In: DW Snoke, A Griffin, and S Stringari, editors. Bose-Einstein condensation. Cambridge: Cambridge University Press (1995). p. 281.
11. Lozovik YE, Yudson VI. Novel mechanism of superconductivity - pairing of spatially separated electrons and holes. Zh Eksp Teor Fiz (1976) 71:738.
13. Butov LV. Exciton condensation in coupled quantum wells. Solid State Comm (2003) 127:89–98. doi:10.1016/s0038-1098(03)00312-0
14. Eisenstein JP, Boebinger GS, Pfeiffer LN, West KW, Song H. New fractional quantum Hall state in double-layer two-dimensional electron systems. Phys Rev Lett (1992) 68:1383–6. doi:10.1103/physrevlett.68.1383
15. Wen XG, Zee A. Neutral superfluid modes and “magnetic” monopoles in multilayered quantum Hall systems. Phys Rev Lett (1992) 69:1811–4. doi:10.1103/physrevlett.69.1811
16. Eisenstein JP, MacDonald AH. Bose-Einstein condensation of excitons in bilayer electron systems. Nature (2004) 432:691–4. doi:10.1038/nature03081
17. Anderson PW, Baskaran G, Zou Z, Hsu T. Resonating valence bond theory of phase transitions and superconductivity in La2CuO4 -based compounds. Phys Rev Lett (1987) 58:2790–3. doi:10.1103/physrevlett.58.2790
19. Leggett AJ. Cooper pairing in spin-polarized Fermi system. J. Phys. Colloques (1980) 41:19–26. doi:10.1051/jphyscol:1980704
20. Geshkenbein VB, Ioffe LB, Larkin AI. Superconductivity in a system with preformed pairs. Phys Rev B (1997) 55:3173–80. doi:10.1103/physrevb.55.3173
21. Nozieres P, SchmittRink S. Bose condensation in an attractive fermion gas: from weak to strong coupling superconductivity. J Low Temp Phys (1985) 59:195–211. doi:10.1007/bf00683774
22. Emery VJ, Kivelson SA. Importance of phase fluctuations in superconductors with small superfluid density. Nature (1995) 374:434–7. doi:10.1038/374434a0
23. Hansel W, Hommelhoff P, Hansch TW, Reichel J. Bose-Einstein condensation on a microelectronic chip. Nature (2001) 413:498–501. doi:10.1038/35097032
24. Byrnes T, Wen K, Yamamoto Y. Macroscopic quantum computation using Bose-Einstein condensates. Phys Rev A (2012) 85:(R):040306. doi:10.1103/physreva.85.040306
25. Dalfovo F, Giorgini S, Pitaevskii LP, Stringari S. Theory of Bose-Einstein condensation in trapped gases. Rev Mod Phys (1999) 71:463–512. doi:10.1103/revmodphys.71.463
27. Gross EP. Structure of a quantized vortex in boson systems. Nuovo Simento (1961) 20:454–77. doi:10.1007/bf02731494
29. Semikoz DV, Tkachev II. Kinetics of bose condensation. Phys Rev Lett (1995) 74:3093–7. doi:10.1103/physrevlett.74.3093
30. Zakharov VE. Kolmogorov spectra in weak turbulence problems. In: AA Galeev, and RN Sudan, editors. Basic plasma physics, Vol. 2. Amsterdam: North-Holland (1984).
31. Inoue M, Hanamura E. Population dynamics of excitons and excitonic molecules. J Phys Soc Jpn (1976) 41:771–81. doi:10.1143/jpsj.41.771
32. Levich E, Yakhot V. Time evolution of a Bose system passing through the critical point. Phys Rev B (1977) 15:243–51. doi:10.1103/physrevb.15.243
33. Levich E, Yakhot V. Time development of coherent and superfluid properties in the course of a λ-transition. J Phys A (1978) 11:2237–54. doi:10.1088/0305-4470/11/11/011
34. Tikhodeev SG. Bose-condensation of finite-lifetime particles with excitons as an example. Zh Eksp Teor Fiz (1990) 97:681.
35. Stoof HTC. Formation of the condensate in a dilute Bose gas. Phys Rev Lett (1991) 66:3148–51. doi:10.1103/physrevlett.66.3148
36. Kagan Y, Svistunov BV. Evolution of correlation properties and appearance of broken symmetry in the process of Bose-Einstein condensation. Phys Rev Lett (1997) 79:3331–4. doi:10.1103/physrevlett.79.3331
37. Bijlsma M, Stoof HTC. Variational approach to the dilute Bose gas. Phys Rev A (1997) 55:498–512. doi:10.1103/physreva.55.498
38. Damle K, Majumdar SN, Sachdev S. Phase ordering kinetics of the Bose gas. Phys Rev A (1996) 56:5037–41. doi:10.1103/physreva.54.5037
39. Perez-Garcia VM, Michinel H, Lewenstein JIM, Zoller P. Dynamics of Bose- Einstein condensates: variational solutions of the Gross-Pitaevskii equations. Phys Rev A (1997) 56:1124. doi:10.1103/PhysRevA.56.1424
40. Berloff NG, Svistunov BV. Scenario of strongly nonequilibrated Bose-Einstein condensation. Phys Rev A (2002) 66:013603. doi:10.1103/physreva.66.013603
41. Ziegler K, Shukla A. Bose-Einstein condensation in a trap: the case of a dense condensate. Phys Rev A (1997) 56:1438–42. doi:10.1103/physreva.56.1438
42. Braaten E, Nieto A. Quantum corrections to the ground state of a trapped Bose-Einstein condensate. Phys Rev B (1997) 56:14745–65. doi:10.1103/physrevb.56.14745
43. Gardiner CW, Zoller P. Quantum kinetic theory: a quantum kinetic master equation for condensation of a weakly interacting Bose gas without a trapping potential. Phys Rev A (1997) 55:2902–21. doi:10.1103/physreva.55.2902
44. Jaksch D, Gardiner CW, Zoller P. Quantum kinetic theory. II. Simulation of the quantum Boltzmann master equation. Phys Rev A (1997) 56:575–86. doi:10.1103/physreva.56.575
45. Gardiner CW, Zoller P. Quantum kinetic theory. III. Quantum kinetic master equation for strongly condensed trapped systems. Phys Rev A (1998) 58:536–56. doi:10.1103/physreva.58.536
46. Jaksch D, Gardiner CW, Gheri K, Zoller P. Quantum kinetic theory. IV. Intensity and amplitude fluctuations of a Bose- Einstein condensate at finite temperature including trap loss. Phys Rev A (1998) 58:1450–64. doi:10.1103/physreva.58.1450
47. Gardiner CW, Zoller P, Ballagh RJ, Davis MJ. Kinetics of bose-einstein condensation in a trap. Phys Rev A (1997) 79:1793–6. doi:10.1103/physrevlett.79.1793
48. Holland M, Williams J, Cooper J. Bose-Einstein condensation: kinetic evolution obtained from simulated trajectories. Phys Rev A (1997) 55:3670–7. doi:10.1103/physreva.55.3670
49. Plimak LI, Walls DF. Nonclassical spatial and momentum distributions in a Bose-condensed gas. Phys Rev A (1996) 54:652–5. doi:10.1103/physreva.54.652
50. Dutta S, Mueller EJ. Kinetics of Bose-Einstein condensation in a dimple potential. Phys Rev A (2015) 91:013601. doi:10.1103/physreva.91.013601
51. Pinkse PWH, Mosk A, Weidemuller M, Reynolds MW, Hijmans TW, Walraven JTM. Adiabatically changing the phase-space density of a trapped Bose gas. Phys Rev Lett (1997) 78:990–3. doi:10.1103/physrevlett.78.990
52. Stamper-Kurn DM, Miesner H-J, Chikkatur AP, Inouye S, Stenger J, Ketterle W, et al. Optical confinement of a Bose-Einstein condensate. Phys Rev Lett (1998) 80:2027–30. doi:10.1103/physrevlett.80.2027
53. Kagan YM. Formation kinetics of the Bose condensate and long-range order. Physics-Uspekhi (2008) 51:603. doi:10.1070/pu2008v051n06abeh006544
54. Drummond PD, Corney JF. Quantum dynamics of evaporatively cooled Bose-Einstein condensates. Phys Rev A (1962) 60:R2661–4. doi:10.1103/physreva.60.r2661
55. Kirkpatrick TR, Dorfman JR. Transport in a dilute but condensed nonideal bose gas: kinetic equations. J Low Temp Phys (1962) 58:301–31. doi:10.1007/bf00681309
56. Eckern U. Relaxation processes in a condensed Bose gas. J Low Temp Phys (1984) 54:333–59. doi:10.1007/bf00683281
57. Reichl LE, Tran M-B. A kinetic equation for ultra-low temperature Bose–Einstein condensates. J Phys A: Math Theor (2019) 52:063001. doi:10.1088/1751-8121/aaf7b3
58. Lyanda-Geller Y, Goldbart PM, Loss D. Quantization of superflow circulation and magnetic flux with a tunable offset. Phys Rev B (1996) 53:12395–9. doi:10.1103/physrevb.53.12395
59. Lyanda-Geller Y, Goldbart PM. Mesoscopic phenomena in Bose-Einstein systems: persistent currents, population oscillations, and quantal phases. Phys Rev A (2000) 61:043609. doi:10.1103/physreva.61.043609
60. Mueller EJ, Goldbart PM, Lyanda-Geller Y. Multiply connected Bose-Einstein-condensed alkali-metal gases: current-carrying states and their decay. Phys Rev A (1998) 57:R1505–8. doi:10.1103/physreva.57.r1505
61. Little WA. Decay of persistent currents in small superconductors. Phys Rev (1967) 156:396–403. doi:10.1103/physrev.156.396
62. Langer J, Ambegaokar V. Intrinsic resistive transition in narrow superconducting channels. Phys Rev (1967) 164:498–510. doi:10.1103/physrev.164.498
63. McCumber DE, Halperin BI. Time scale of intrinsic resistive fluctuations in thin superconducting wires. Phys Rev B (1970) 1:1054–70. doi:10.1103/physrevb.1.1054
64. Langer JS, Fisher ME. Intrinsic critical velocity of a superfluid. Phys Rev Lett (1967) 19:560–3. doi:10.1103/physrevlett.19.560
65. Ramanathan A, Wright KC, Muniz SR, Zelan M, Hill WT, Lobb CJ, et al. Superflow in a toroidal Bose-Einstein condensate: an atom circuit with a tunable weak link. Phys Rev Lett (2011) 106:130401. doi:10.1103/physrevlett.106.130401
66. Wright KC, Blakestad RB, Lobb CJ, Phillips WD, Campbell GK. Driving phase slips in a superfluid atom circuit with a rotating weak link. Phys Rev Lett (2013) 110:025302. doi:10.1103/physrevlett.110.025302
67. Murray N, Krygier M, Edwards M, Wright KC, Campbell GK, Clark CW. Probing the circulation of ring-shaped Bose-Einstein condensates. Phys Rev A (2013) 88:053615. doi:10.1103/physreva.88.053615
68. Lin Y-J, Jiménez-García K, B Spielman I. Spin-orbit-coupled bose-einstein condensates. Nature (2011) 471:83–6. doi:10.1038/nature09887
69. Sun K, Qu C, Zhang C. Spin orbital-angular-momentum coupling in Bose-Einstein condensates. Phys Rev A (2015) 91:063627. doi:10.1103/physreva.91.063627
70. Yan Y, Zhang SL, Chaudhury S, Qi Z. Emergent periodic and quasiperiodic lattices on surfaces of synthetic Hall tori and synthetic Hall cylinders. Phys Rev Lett (2019) 123:260405. doi:10.1103/physrevlett.123.260405
73. Hohenberg PC, Martin PC. Microscopic theory of superfluid helium. Ann Phys (1965) 34:291–359. doi:10.1016/0003-4916(65)90280-0
75. Betbeder-Matibet O, Nozieres P. Transport equations in clean superconductors. Ann Phys (1969) 51:392–417. doi:10.1016/0003-4916(69)90136-5
76. Aronov AG, Gal’perin Y. M, Gurevich VL, Kozub VI. The Boltzmann-equation description of transport in superconductors. Adv Phys (1981) 30:539–92. doi:10.1080/00018738100101407
77. Wolfle P. Kinetic theory of anisotropic Fermi superfluids. J Low Temp Phys (1976) 22:157–83. doi:10.1007/bf00655220
78. Wolfle P. Theory of sound propagation in pair-correlated Fermi liquids-application to He3-B. Phys Rev B (1976) 14:89–113. doi:10.1103/physrevb.14.89
79. Einzel D, Wolfle P. Transport and relaxation properties of superfluid 3He. I. Kinetic equation and Bogoliubov quasiparticle relaxation rate. J Low Temp Phys (1978) 32:19–37. doi:10.1007/bf00116904
81. Semikoz DV, Tkachev II. Condensation of bosons in the kinetic regime. Phys Rev D (1997) 55:489–502. doi:10.1103/physrevd.55.489
82. Bloch I, Dalibard J, Zwerger W. Many-body physics with ultracold gases. Rev Mod Phys (2008) 80:885–964. doi:10.1103/revmodphys.80.885
83. Goldman N, Juzeliunas G, Oehberg P, Spielman IB. Light-induced gauge fields for ultracold atoms. Rep Prog Phys (2014) 77:126401. doi:10.1088/0034-4885/77/12/126401
84. Zhai H. Degenerate quantum gases with spin-orbit coupling: a review. Rep Prog Phys (2015) 61:026001. doi:10.1088/0034-4885/78/2/026001
85. Qi X-L, Zhang S-C. Topological insulators and superconductors. Rev Mod Phys (2011) 83:1057–110. doi:10.1103/revmodphys.83.1057
86. Zutic I, Fabian J, Das Sarma S. Spintronics: fundamentals and applications. Rev Mod Phys (2004) 76:323–410. doi:10.1103/revmodphys.76.323
87. Lyanda-Geller Y. Spin-related phenomena in spin 3/2 charge carrier holes systems. Solid State Commun (2022) 322:114815. doi:10.1016/j.ssc.2022.114815
88. Awschalom DD, Bassett LC, Dzurak AS, Hu EL, Petta JR. Quantum spintronics: engineering and manipulating atom-like spins in semiconductors. Science (2013) 339:1174–9. doi:10.1126/science.1231364
89. Lin YJ, Compton RL, Jimenez-Garcia K, Phillips WD, Porto JV, Spielman IB. A synthetic electric force acting on neutral atoms. Nat Phys (2011) 7:531–4. doi:10.1038/nphys1954
90. Lin Y-J, Compton RL, Jiménez-García K, Porto JV, Spielman IB. Synthetic magnetic fields for ultracold neutral atoms. Phys Rev A (2009) 462:628–32. doi:10.1038/nature08609
91. Galitski V, Juzeliunas G, Spielman IB. Artificial gauge fields with ultracold atoms. Phys Today (2019) 72:39. doi:10.1063/pt.3.4111
92. LeBlanc LJ, Jiménez-García K, Williams RA, Beeler MC, Perry AR, Phillips WD, et al. Observation of a superfluid Hall effect. Proc Natl Acad Sci USA (2012) 109:10811–4. doi:10.1073/pnas.1202579109
93. Beeler MC, Williams RA, Jimenez-Garcia K, LeBlanc LJ, Perry AR, Spielman IB. The spin Hall effect in a quantum gas. Nature (2013) 498:201–4. doi:10.1038/nature12185
94. Wang P, Yu ZQ, Fu Z, Miao J, Huang L, Chai S, et al. Spin-orbit coupled degenerate Fermi gases. Phys Rev Lett (2012) 109:095301. doi:10.1103/physrevlett.109.095301
95. Goldman N, Budich JC, Zoller P. Topological quantum matter with ultracold gases in optical lattices. Nat Phys (2016) 12:639–45. doi:10.1038/nphys3803
96. Stringari S. Diffused vorticity and moment of inertia of a spin-orbit coupled Bose-Einstein condensate. Phys Rev Lett (2017) 118:145302. doi:10.1103/physrevlett.118.145302
97. Li CH, Qu C, Niffenegger RJ, Wang SJ, He M, Blasing DB, et al. Spin current generation and relaxation in a quenched spin-orbit-coupled Bose-Einstein condensate. Nat Comm (2019) 10:375. doi:10.1038/s41467-018-08119-4
98. Zhang JY, Ji SC, Chen Z, Zhang L, Du ZD, Yan B, et al. Collective dipole oscillations of a spin-orbit coupled Bose-Einstein condensate. Phys Rev Lett (2012) 109:115301. doi:10.1103/physrevlett.109.115301
99. Modugno M, Sherman EY. Collapse inhibition in three-dimensional Bose-Einstein condensates: internal repulsion and particle loss. Chaos, Solitons and Fractals (2022) 163:112502. doi:10.1016/j.chaos.2022.112502
100. Chen X, Jiang RL, Li J, Ban Y, Sherman EY. Inverse engineering for fast transport and spin control of spin-orbit-coupled Bose-Einstein condensates in moving harmonic traps. Phys Rev A (2018) 97:013631. doi:10.1103/physreva.97.013631
101. Miller JB, Zumbuhl D, Marcus CM, Lyanda-Geller Y, Goldhaber-Gordon D, Campman K, et al. Gate-controlled spin-orbit quantum interference effects in lateral transport. Phys Rev Lett (2003) 90:076807. doi:10.1103/physrevlett.90.076807
102. Ho T-L, Zhang S. Bose-einstein condensates with spin-orbit interaction. Phys Rev Lett (2011) 107:150403. doi:10.1103/physrevlett.107.150403
103. Aronov AG, Lyanda-Geller YB. Spin-orbit Berry phase in conducting rings. Phys Rev Lett (1993) 70:343–6. doi:10.1103/physrevlett.70.343
104. Lyanda-Geller YB. Topological transitions in Berry’s phase interference effects. Phys Rev Lett (1993) 71:657–61. doi:10.1103/physrevlett.71.657
105. Lyanda-Geller YB, Aleiner IL, Goldbart PM. Domain walls and conductivity of mesoscopic ferromagnets. Phys Rev Lett (1998) 81:3215–8. doi:10.1103/physrevlett.81.3215
106. Arovas DP, Lyanda-Geller YB. Non-Abelian geometric phases and conductance of spin-3/2 holes. Phys Rev B (1998) 57:12302–5. doi:10.1103/physrevb.57.12302
107. Li J, Malomed BA, Li W, Chen X, Sherman EY. Coupled density-spin Bose-Einstein condensates dynamics and collapse in systems with quintic nonlinearity. Comm Nonlinear Schence Numerical Simulation (2020) 82:105045. doi:10.1016/j.cnsns.2019.105045
108. Zala G, Narozhny BN, Aleiner IL. Interaction corrections at intermediate temperatures: longitudinal conductivity and kinetic equation. Phys Rev B (2001) 64:214204. doi:10.1103/physrevb.64.214204
109. Ivchenko EL, Lyanda-Geller YB, Pikus GE. Current of thermalized spin-oriented photocarriers. Sov Phys JETP (1990) 71:550.
110. Aronov AG, Lyanda-Geller YB, Pikus GE. Spin polarization of electrons by an electric current. Sov Phys JETP (1991) 73:537.
111. Glazov MM, Ivchenko EL. Effect of electron–electron interaction on spin relaxation of charge carriers in semiconductors. Sov Phys JETP (2004) 99:1279–90. doi:10.1134/1.1854815
112. Tokatly IV, Sherman EY. Spin dynamics of cold fermions with synthetic spin-orbit coupling. Phys Rev A (2013) 87:(R):041602. doi:10.1103/physreva.87.041602
113. Zheng W, Li Z. Collective modes of a spin-orbit-coupled Bose-Einstein condensate: a hydrodynamic approach. Phys Rev A (2011) 85:053607. doi:10.1103/physreva.85.053607
114. Dyakonov MI, Perel VI. Spin orientation of electrons associated with interband absorption of light in semiconductors. JETP (1971) 33:1053.
115. Lyanda-Geller YB. Quantum interference and electron-electron interactions at strong spin-orbit coupling in disordered systems. Phys Rev Lett (1998) 80:4273–6. doi:10.1103/physrevlett.80.4273
116. Tylan-Tyler A, Lyanda-Geller Y. Evolution of a quenched spin-orbit coupled Bose-Einstein condensate beyond the Gross-Pitaevskii equation. (unpublished).
117. Qu C, Pitaevskii LP, Stringari S. Spin orbit coupling induced localization in the expansion of an interacting Bose–Einstein condensate. New Journ Phys (2017) 19:085006. doi:10.1088/1367-2630/aa7e8c
Keywords: Bose–Einstein condensation, kinetic equation, spin–orbit-coupled Bose–Einstein condensate, ring-shaped Bose–Einstein systems, decay of current-carrying states, spin current decay, spin current oscillations
Citation: Lyanda-Geller Y (2023) Evolution of Bose–Einstein condensate systems beyond the Gross–Pitaevskii equation. Front. Phys. 11:1257370. doi: 10.3389/fphy.2023.1257370
Received: 12 July 2023; Accepted: 02 November 2023;
Published: 23 November 2023.
Edited by:
Evgeny Sherman, University of the Basque Country, SpainReviewed by:
Vitalii Dugaev, Rzeszów University of Technology, PolandLeonid Golub, University of Regensburg, Germany
Copyright © 2023 Lyanda-Geller. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Yuli Lyanda-Geller, eXVsaUBwdXJkdWUuZWR1
 Yuli Lyanda-Geller
Yuli Lyanda-Geller