Across the stages: a multiscale extension of the generalized stochastic microdosimetric model (MS-GSM2) to include the ultra-high dose rate

Ultra-high dose rate (UHDR) irradiations with different types of radiation have shown a larger sparing of normal tissue and unchanged tumor control with respect to conventional delivery. In recent years, there has been an accumulation of experimental evidence related to the so-called FLASH effect. However, the underpinning mechanism remains, to date, extremely debated and largely unexplained, while the involvement of multiple scales of radiation damage has been suggested. Since it is believed that the chemical environment plays a crucial role in the FLASH effect, this work aims to develop a multi-stage tool, the multiscale generalized stochastic microdosimetric model (MS-GSM²), that can capture several possible effects on DNA damage at the UHDR regime, such as reduction of DNA damage yield due to organic radical recombination, damage fixation due to oxygenation, and spatial and temporal dose deposition effects, allowing us to explore most of the candidate mechanisms for explaining the FLASH effect. The generalized stochastic microdosimetric model (GSM²) is a probabilistic model that describes the time evolution of DNA damage in a cell nucleus using microdosimetric principles, accounting for different levels of spatio-temporal stochasticity. In particular, the GSM² describes radiation-induced DNA damage formation and kinetic repair in the case of protracted irradiation without considering the Poissonian assumption to treat the number of radiation-induced DNA damage. In this work, we extend the GSM², coupling the evolution of DNA damage to fast chemical reaction kinetics, described by a system of ordinary differential equations, accounting for an additional level of stochasticity, i.e., in chemistry. We simulate energy deposition by particles in a microscopic volume, which mimics the cell nucleus, in order to examine the combined effects of several chemical species and the time evolution of DNA damage. We assume that UHDR modifies the time evolution of the peroxyl radical concentration, with a consequent reduction in the yield of the indirect DNA damage. This damage reduction emerges only at UHDR and is more pronounced at high doses. Moreover, the indirect damage yield reduction depends on the radiation quality. We show that the MS-GSM² can describe the empirical trend of dose- and dose rate-dependent cell sensitivity over a broad range, particularly the larger sparing of healthy tissue occurring at the FLASH regime. The complete generality of the MS-GSM² also allows us to study the impact of different dose delivery time structures and radiation qualities, including high LET beams.

1 Introduction

1.1 Ultra-high dose rate irradiation: general context

Ultra-high dose rate (UHDR) irradiation, sometimes also referred to in the literature as FLASH irradiation, is a novel technique based on fast beam delivery, with a total irradiation time $<$ 100 ms and an overall dose rate $>$ 40 Gy/s for a single high enough dose, usually exceeding 10 Gy. It has been extensively demonstrated experimentally [1–5] that FLASH irradiation allows obtaining a higher sparing of normal tissue, e.g., a decrease in memory loss [6, 7] or less intestine necrosis [8], and, at the same time, an unchanged tumor control, e.g., an indistinguishable tumor response for HBCx-12A xenografts [1], with respect to conventional dose rate irradiation (CONV), characterized by a dose rate of 0.03–0.1 Gy/s. Many other experiments confirmed this sparing effect appearing at FLASH regimes, such as in animals, for example, no severe fibro-necrotic lesions on mini pig skin were observed [2] or even in humans, as in the first patient with cutaneous lymphoma, treated using electron beams [9].

In addition to that, the FLASH effect was observed for different radiation qualities [10], i.e., for different particle types, energies, and linear energy transfer (LET): (i) studies with electrons, such as in [11] with a 6 MeV electron beam LINAC, showed the same delayed glioblastoma growth in both CONV and the FLASH regime, while only the FLASH regime significantly spared animals from cognitive deficits in learning and memory; (ii) with protons, as demonstrated in [12], where using IBA Proteus Plus at 203 MeV at the FLASH regime, a significant reduction in the loss of proliferating cells in intestinal crypts was observed compared to the CONV regime, or in [13], where a reduction in normal tissue damage (in particular, acute skin damage and radiation-induced fibrosis) was observed for the same tumor control in the case of FLASH with respect to CONV using proton PBS (ProBeam, Varian Medical Systems) at 244 MeV for CONV and 250 MeV for FLASH; and, more recently, (iii) also with carbon ions [14, 15], both in vitro at the Heidelberg Ion-Beam Therapy Center (HIT) synchrotron and in vivo at the GSI Helmholtz Center in Darmstadt. Moreover, the first clinical trial with protons has already started [16]. Clinical translation is a fundamental step since FLASH radiotherapy, in principle, should allow for an enhancement of the therapeutic window because it should reduce the normal tissue toxicity for the same tumor control probability.

In recent years, numerous experimental efforts [3] have been dedicated to confirming the FLASH effect. However, the mechanism underlying this effect remains, to date, extremely debated and largely unexplained [5]. Several possible explanations of the FLASH effect have been proposed in the last few years [17], such as (i) transient hypoxia due to O₂ depletion [18], (ii) organic radical recombination [19], (iii) intertrack effects [20], or (iv) the immune system-driven effect [21].

(i) The transient hypoxia speculation [18] stems from the well-known effect that O₂ is locally consumed due to chemical reactions induced by the interaction between the ionizing radiation and the medium. Although the re-oxygenation phenomenon happens in milliseconds, the oxygen depletion is probably not enough to prompt radiobiological resistance. Therefore, it is not sufficient to explain the differential effect between healthy tissue and tumor, as described in [22]. (ii) The radical recombination hypothesis is based on the concept that a specific radical could accumulate differently between normal tissue and tumor under the UHDR regime. In particular, in [19], it was suggested that the different temporal evolution of the peroxyl radical concentration [ROO^•] at a high dose rate could explain the sparing effect. The peroxyl radical ROO^• is generated from the reaction between the alkyl radical R^• and O₂, and it is known to be an important source of adverse effects on lipids and DNA [19, 23, 24]. (iii) The conjecture of the intertrack effect arises from the fact that, at a high dose rate, particles could arrive close enough in time and space before heterogeneous chemical reactions end, and this may affect the chemical stage of water radiolysis [20] and, in turn, the chemical environment of the cell. (iv) The last main hypothesis, the immune system-driven effect [21], postulates that UHDR irradiation may change the expression level of immune factors and active immune cells or, in general, influence the immune response.

To date, there are no experimental data that can validate or completely reject only one of these hypotheses; however, the involvement of a combination of multiple scales of radiation damage has been suggested [25]. If we compare the typical time scale to deliver 10 Gy CONV or 10 Gy FLASH with protons, it can be seen that the spatio-temporal window between the homogeneous chemical and biochemical stages of radiation damage could play a crucial role in the FLASH effect [25, 26].

1.2 An overview of mechanistic models and the contribution of this work

In the last 3–4 years, several mechanistic models have been developed to understand the underlying mechanism of the FLASH effect, using several different approaches such as molecular dynamics, Monte Carlo methods (e.g., track structure codes), analytical models, and mixed techniques [19, 27–31]. Despite the huge effort of the community, which succeeded in providing several insights into this complex picture, e.g., stressing the minor role of some proposed hypotheses, none of the proposed models seem to be able to fully describe the mechanism at the origin of the FLASH effect. Furthermore, the aforementioned models focus on a single possible mechanism and, thus, do not provide a mechanistically driven interpretation of the FLASH effect that fully includes an interplay of several potential pathways and spatio-temporal scales. This work extends a recently developed stochastic radiobiological model, the Generalized Stochastic Microdosimetric Model (GSM²) [32–36].

The GSM² is a comprehensive mathematical model that encompasses numerous stochastic effects that arise during the creation, repair, and kinetics of radiation-induced DNA damage [34]. The GSM², based on microdosimetric principles, describes the formation and kinetic repair of two types of DNA lesions, namely, X and Y, which represent lesions that are reparable and lesions that result in cell inactivation, respectively. The GSM² assumes that lethal and sub-lethal lesions can undergo three different pathways, namely, r, a, and b, which represent, respectively, the repair of a sub-lethal lesion, the conversion of a sub-lethal lesion to a lethal lesion, and the pairwise interaction of two sub-lethal lesions to become a lethal one [32, 33].

Due to the significant role that the chemical environment is believed to play in the FLASH effect, in the present work, we expanded the GSM² by coupling fast chemical reaction kinetics, as described in [19], to the slow evolution of DNA damage. This led to the development of a multiscale version of the GSM² (MS-GSM²), which can capture various potential impacts on DNA damage within the UHDR regime. The multiscale nature of the MS-GSM² emerges from the driving equations, where the slow biological processes are described by discrete stochastic differential equations, whereas the chemical kinetics are continuous ordinary differential equations. Following [19], we hypothesize that the different temporal evolution of the peroxyl radical concentration [ROO^•] at a high dose rate is at the origin of the FLASH effect. In contrast to [19], we directly link [ROO^•] to the biological damage as follows: we split the creation of biological damage by an energy deposition into direct and indirect damage. As standard in the literature, we assume that the number of direct damages is proportional to the imparted energy. On the contrary, indirect damage is linked to the chemical environment. In particular, we conjecture that the number of lethal and sub-lethal damages depends on the local peroxyl radical concentration [ROO^•], since the contribution of [ROO^•] to the damage of biological structures, including DNA, is well known [19]. Therefore, we show how UHDR regimes that modify the [ROO^•] evolution can, in turn, change the indirect damage yield that eventually leads to a cell survival reduction. Similar to the approach described in [37], energy depositions are described via a Monte Carlo sampling of particle tracks hitting the target, while the radial dose distribution is described via an amorphous track model [38]. The target considered is bigger than the cell nucleus, so the energy deposited by tracks passing near the cell nucleus, i.e., the ionization penumbra of the tracks, is also accounted for by the MS-GSM². The resulting model is an extremely general biophysical model, able to provide a mechanistically grounded description of several effects of random processes in space and time [34, 39].

In addition to introducing the MS-GSM², the present paper investigates the effect of radiation quality on the onset of the FLASH effect. The latter issue is presently largely debated [25], and it is still largely unknown how LET can affect the typical normal tissue sparing encountered in FLASH. For this reason, we consider protons of 18.6 MeV and carbon ions of 149 MeV/u, studying how the different spatio-temporal stochastic patterns of energy deposition affect the damage yield and, in turn, the resulting cell survival.

The main contributions of the present work are as follows:

(i) Introducing a general stochastic model able to provide a unified framework encompassing physics, chemistry, and biology;

(ii) Proposing a mechanism underpinning the manifestation of the FLASH effect, which includes three of the major potential mechanistic pathways commonly considered for explaining that effect, i.e., organic radical–radical recombination, damage fixation due to oxygenation, and spatial and temporal dose deposition effects;

(iii) Showing how the interplay of the aforementioned different mechanisms can, in turn, produce cell survival sparing at a sufficiently high dose and dose rate.

2 Theory and calculations

2.1 Generalized stochastic microdosimetric model

The GSM² is a fully probabilistic model that accurately describes the stochastic nature of energy deposition in volumes of interest for cellular systems. The final goal is to overcome existing models, which most assume a Poissonian distribution of the number of radiation-induced DNA damages, to provide a better prediction of biological endpoints relevant to radiotherapy applications. The GSM² was first introduced in [32], where a detailed description of its structure can be found. The model assumes that the cell nucleus is divided into N_d independent domains d. Within each domain, it is assumed that two types of DNA lesions can be formed: lethal and sub-lethal lesions. The former represents damage that cannot be repaired, leading to cell inactivation, while the latter can be either repaired or become a lethal lesion, leading to cell inactivation.

For modeling the time evolution of the number of lethal and sub-lethal lesions, we will denote the state of the system by $\left(Y(t),X(t)\right)$ at time t, where X and Y are two $\mathbb{N}-$valued random variables representing the number of lethal and sub-lethal lesions, respectively.

A sub-lethal lesion can evolve in three different ways: (i) it can become a lethal lesion at a rate a, (ii) it can be repaired at a rate r, or (iii) it can combine with another sub-lethal lesion to become a lethal lesion at a rate b. This scheme can be represented by the following equations:

$\begin{array}{cc}\hfill & X\stackrel{a}{\to }Y,\hfill \\ \hfill & X\stackrel{r}{\to }\varnothing ,\hfill \\ \hfill & X+X\stackrel{b}{\to }Y,\hfill \end{array}(1)$

where ∅ represents the ensemble of healthy cells.

Based on Eq. 1, we developed the microdosimetric master equation (MME) as follows [32]:

$\begin{array}{cc}\hfill \frac{\partial }{\partial t}p\left(t,y,x\right)& =\left(E^{-\mathrm{1,2}}-1\right)\left[x\left(x-1\right)bp\left(t,y,x\right)\right]+\left(E^{-\mathrm{1,1}}-1\right)\left[xap\left(t,y,x\right)\right]+\left(E^{\mathrm{0,1}}-1\right)\left[xrp\left(t,y,x\right)\right]\hfill \\ \hfill & ={\mathcal{E}}^{-\mathrm{1,2}}\left[x\left(x-1\right)bp\left(t,y,x\right)\right]+{\mathcal{E}}^{-\mathrm{1,1}}\left[xap\left(t,y,x\right)\right]\hfill \\ \hfill & +{\mathcal{E}}^{\mathrm{0,1}}\left[xrp\left(t,y,x\right)\right],\hfill \end{array}(2)$

where the creation operator is defined as

${\mathcal{E}}^{i,j}\left[f\left(y,x\right)\right]≔\left(E^{i,j}-1\right)\left[f\left(y,x\right)\right]≔f\left(y+i,x+j\right)-f\left(y,x\right),$

which signifies a transition in the state, defining the number of sub-lethal and lethal damages.

The MME is coupled with an initial damage distribution derived from microdosimetric spectra, providing a comprehensive description of the radiation field quality [40–42]. The single-event distribution of energy deposition on a domain d, referred to as f_1;d(z) [43], can either be computed numerically with a Monte Carlo code or measured experimentally. Given a cell nucleus domain d, the probability that ν events deposit energy z follows a Poissonian distribution with the mean denoted by ${\lambda }_n≔\frac{z_n}{z_F}$, where z_n represents the mean energy deposition on the nucleus domain and z_F is the first moment of the single-event distribution f_1;d. Then, assuming a Poissonian probability that a domain registers ν events, the energy deposition distribution is given by

$f_d\left(z|z_n\right)≔{\displaystyle \sum _{\nu =0}^{\infty }}\frac{e^{-\frac{z_n}{z_F}}}{\nu !}{\left(\frac{z_n}{z_F}\right)}^{\nu }{f}_{\nu ;d}\left(z\right),(3)$

where f_ν;d(z) is the energy deposition distribution resulting from ν depositions. We conventionally assumed that f_0;d(z) = δ₀(z), indicating that no event will result in the deposition specific energy.

Using p_z (x, y|z) to denote the initial joint distributions for the number of sub-lethal and lethal lesions for a given energy deposition z, we obtain

$p_0\left(x,y\right)={\displaystyle \sum _{\nu =0}^{\infty }}{\int }_0^{\infty }\dots {\int }_0^{\infty }{p}_z\left(x,y|z_1,\dots ,z_{\nu }\right)\frac{e^{-\frac{z_n}{z_F}}}{\nu !}{\left(\frac{z_n}{z_F}\right)}^{\nu }{\times f}_{\nu ;d}\left(z_1,\dots ,z_{\nu }\right)d{z}_1\dots d{z}_{\nu }.(4)$

In particular, assuming the events to be statistically independent, the distribution resulting from ν events can be computed by convolving the single-event distribution ν times [43]. Therefore, the distribution f_ν;d of the imparted energy z is computed iteratively as

$\begin{array}{cc}\hfill f_{2;d}\left(z\right)& ≔{\int }_0^{\infty }{f}_{1;d}\left(\bar{z}\right)f_{1;d}\left(z-\bar{z}\right)d\bar{z},\hfill \\ \hfill & \dots ,\hfill \\ \hfill f_{\nu ;d}\left(z\right)& ≔{\int }_0^{\infty }{f}_{1;d}\left(\bar{z}\right)f_{\nu -1;d}\left(z-\bar{z}\right)d\bar{z}.\hfill \end{array}.$

It is considered that the quantity p_z (x, y|z₁, … , z_ν) gives the probability of observing x sub-lethal lesions and y lethal lesions resulting from the energy depositions z₁, … , z_ν. The average yields of sub-lethal and lethal lesions are denoted by κ(z₁, … , z_ν) and λ(z₁, … , z_ν), respectively, for the energy depositions z₁, … , z_ν. The formation of lesions by different deposition events is statistically independent because the events are independent. The formation of lesions by a single energy deposition event is approximately statistically independent. It follows that the distribution of the number of lesions that result from the i-th deposition event is approximately Poissonian, i.e.,

$p_z\left(x_{\nu },y_{\nu }|z_1,\dots ,z_{\nu }\right)≔e^{-\kappa \left(z_1,\dots ,z_{\nu }\right)}\frac{{\left(\kappa \left(z_1,\dots ,z_{\nu }\right)\right)}^{x_{\nu }}}{x_{\nu }!}{\times e}^{-\lambda \left(z_1,\dots ,z_{\nu }\right)}\frac{{\left(\lambda \left(z_1,\dots ,z_{\nu }\right)\right)}^{y_{\nu }}}{y_{\nu }!}.$

The probability that x and y total lesions will be produced if energy depositions z₁, … , z_ν occur is

$p_z\left(x,y|z_1,\dots ,z_{\nu }\right)≔{\displaystyle \sum _{\begin{array}{c}{x}_1,\dots ,x_{\nu }\\ y_1,\dots ,y_{\nu }\end{array}}}{p}_z^X\left(x_1,y_1|z_1\right)p_z^X\left(x_2,y_2|z_1,z_2\right)\dots {\times p}_z^X\left(x_{\nu },y_{\nu }|z_1,\dots ,z_{\nu }\right),$

where the aforementioned summation runs over x₁, … , x_ν and y₁, … , y_ν such that x₁ + ⋯ + x_ν = x and y₁ + ⋯ + y_ν = y. In short, we can denote as

$\bar{\kappa }\left(z_1,\dots ,z_{\nu }\right)≔{\displaystyle \sum _{i=1}^{\nu }}\kappa \left(z_1,\dots ,z_i\right),\bar{\lambda }\left(z_1,\dots ,z_{\nu }\right)≔{\displaystyle \sum _{i=1}^{\nu }}\lambda \left(z_1,\dots ,z_i\right),$

and the probability of x and y lesions is given by

$p_z\left(x,y|z_1,\dots ,z_{\nu }\right)=e^{-\bar{\kappa }\left(z_1,\dots ,z_{\nu }\right)}\frac{{\left(\bar{\kappa }\left(z_1,\dots ,z_{\nu }\right)\right)}^x}{x!}{e}^{-\bar{\lambda }\left(z_1,\dots ,z_{\nu }\right)}\frac{{\left(\bar{\lambda }\left(z_1,\dots ,z_{\nu }\right)\right)}^y}{y!}.$

The standard assumption is that the average yield of lesions is proportional to the dose, i.e.,

$\bar{\kappa }\left(z_1,\dots ,z_{\nu }\right)=\kappa \left(z_1+\cdots +z_{\nu }\right)=\kappa z,\bar{\lambda }\left(z_1,\dots ,z_{\nu }\right)=\lambda \left(z_1+\cdots +z_{\nu }\right)=\lambda z,$

for positive constants κ > 0 and λ > 0. In [32, 33], the same choice has been made, implying that the average yield of the lesion for a given dose D is given by

${\displaystyle \sum _{x\ge 0}}x{p}_0\left(x,y\right)=\kappa D.$

The quantity κ(z₁, … , z_ν) is generally taken to be either a linear or quadratic function that summarizes several physical, chemical, and biological effects. It is a function of the type of ionizing particle, LET, details of the track structure, radical diffusion and reaction rates, the phase in the cell cycle, and the chemical environment of the cell. Additionally, as it is widely acknowledged that the temporal and spatial distribution of various particle tracks and energy deposition significantly influence the emergence of the FLASH effect, our forthcoming approach is geared toward explicitly incorporating both temporal and spatial stochasticity. This will be achieved by closely coupling the energy deposition with a rapid chemical characterization of the surrounding environment. We will formally introduce a fast component that describes the evolution of the chemical environment. To further explicitly model the dose rate effect, we will assume that the function κ depends on the chemical environment modified by radiation.

2.2 Multiscale GSM²

In order to generalize the GSM² to the multiscale GSM² (MS-GSM²), including the fast chemical reactions, as schematized in Figure 1, we first reformulate the model along two main directions: on one side, we provide a general multi-domain cell nucleus description along the lines of [32], and on the other side, we give a pathwise description for the MME (2) in terms of jump-type stochastic differential equations (SDEs).

FIGURE 1

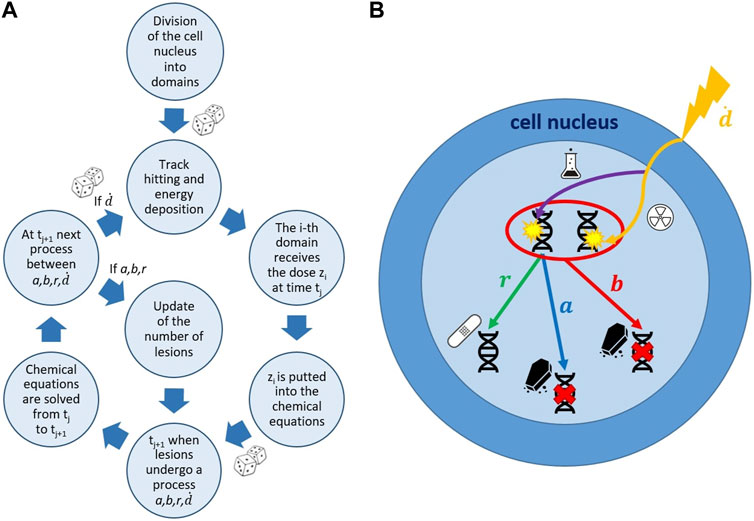
FIGURE 1. Schematic representation of the MS-GSM² workflow. (A) Simulation steps of the MS-GSM². Energy deposition according to microdosimetry, dose z distributed with the amorphous track model; joint evolution of slow biological and fast chemical processes. (B) Possible evolution of DNA lesions in a cell nucleus. a, b, r, and $\dot{d}$ are the death, pairwise death, repair, and dose rates, respectively. Both direct and indirect damage actions of ionizing radiation are taken into account.

In particular, it can be seen [44, Chapter 13] that Eq. 2 describes the time evolution for the probability density function associated with the following SDE for the domain d of the cell c:

${\mathrm{\Sigma }}^c:\left\{\begin{array}{cc}{Y}^{\left(c,d\right)}\left(t\right)\hfill & =Y_0^{\left(c,d\right)}+{\mathrm{P}}_a^{\left(c,d\right)}\left({\int }_0^{t}a{X}^{\left(c,d\right)}\left(s\right)ds\right)+{\mathrm{P}}_b^{\left(c,d\right)}\left({\int }_0^{t}b{X}^{\left(c,d\right)}\left(s\right)\left(X^{\left(c,d\right)}\left(s\right)-1\right)ds\right),\hfill \\ X^{\left(c,d\right)}\left(t\right)\hfill & =X_0^{\left(c,d\right)}-{\mathrm{P}}_a^{\left(c,d\right)}\left({\int }_0^{t}a{X}^{\left(c,d\right)}\left(s\right)ds\right)-{\mathrm{P}}_r^{\left(c,d\right)}\left({\int }_0^{t}r{X}^{\left(c,d\right)}\left(s\right)ds\right)+\hfill \\ \hfill & -2{\mathrm{P}}_b^{\left(c,d\right)}\left({\int }_0^{t}b{X}^{\left(c,d\right)}\left(s\right)\left(X^{\left(c,d\right)}\left(s\right)-1\right)ds\right),\hfill \\ d\hfill & =1,\dots ,N_d.\hfill \end{array}\right.(5)$

In Eq. 5, the terms ${\mathrm{P}}_h^{(c,d)}$, with h ∈ {a, b, r}, are independent unitary Poisson jump processes [45]. In order to include the effect of UHDR in the GSM², as briefly mentioned above, we will suitably modify here how the energy depositions z create lethal and sub-lethal lesions. In particular, we introduce several improvements to the presently available version of GSM². First, as already carried out in [32], (i) we include a protracted dose-rate term that accounts for the energy deposition events and subsequent lesion creation; such a term explicitly models the series of energy depositions in the whole cell nucleus z₁, … , z_ν, where ν, in this case, is the number of events on the nucleus. Then, (ii) we split the creation of direct and indirect DNA damage, where the former happens instantaneously at the energy deposition and the latter depends on the chemical environment and how organic radicals recombine in a suitable time interval [0, T_I]. At last, (iii) to describe the formation of indirect DNA damage, following [19], we include a set of differential equations that model the time evolution and reaction of radicals and other molecular species.

Thus, we get to the following MS-GSM² system of equations:

${\mathrm{\Sigma }}_{\text{MS}}^c:\left\{\begin{array}{cc}{Y}^{\left(c,d\right)}\left(t\right)\hfill & ={\mathrm{P}}_a^{\left(c,d\right)}\left({\int }_0^{t}a{X}^{\left(c,d\right)}\left(s\right)ds\right)+{\mathrm{P}}_b^{\left(c,d\right)}\left({\int }_0^{t}b{X}^{\left(c,d\right)}\left(s\right)\left(X^{\left(c,d\right)}\left(s\right)-1\right)ds\right)+\hfill \\ \hfill & +Z_{Y;d}^{\left(c,d\right)}{\mathrm{P}}_{\dot{d}}^{\left(c\right)}\left({\int }_0^t\dot{d}ds\right)+Z_{Y;i}^{\left(c,d\right)}{\mathrm{P}}_{\rho }^{\left(c,d\right)}\left({\int }_0^t\rho \left({\xi }_s\right)ds\right)\hfill \\ X^{\left(c,d\right)}\left(t\right)\hfill & =-{\mathrm{P}}_a^{\left(c,d\right)}\left({\int }_0^{t}a{X}^{\left(c,d\right)}\left(s\right)ds\right)-{\mathrm{P}}_r^{\left(c,d\right)}\left({\int }_0^{t}r{X}^{\left(c,d\right)}\left(s\right)ds\right)+\hfill \\ \hfill & -2{\mathrm{P}}_b^{\left(c,d\right)}\left({\int }_0^{t}b{X}^{\left(c,d\right)}\left(s\right)\left(X^{\left(c,d\right)}\left(s\right)-1\right)ds\right)+\hfill \\ \hfill & +Z_{X;d}^{\left(c,d\right)}{\mathrm{P}}_{\dot{d}}^{\left(c\right)}\left({\int }_0^t\dot{d}ds\right)+Z_{X;i}^{\left(c,d\right)}{\mathrm{P}}_{\rho }^{\left(c,d\right)}\left({\int }_0^t\rho \left({\xi }_s\right)ds\right),\hfill \\ \frac{d}{dt}{\left[{\mathrm{e}}_{\mathrm{a}\mathrm{q}}^{-}\right]}^d\left(t\right)\hfill & =f_{{\mathrm{e}}_{\mathrm{a}\mathrm{q}}^{-}}\left({\xi }^d\left(t\right)\right)+c_{\text{e}}{\dot{z}}^d,\hfill \\ \frac{d}{dt}{\left[{\mathrm{O}}_2\right]}^d\left(t\right)\hfill & =f_{{\text{O}}_2}\left({\xi }^d\left(t\right)\right),\hfill \\ \frac{d}{dt}{C}_{{\mathrm{H}}_{\mathrm{2}}{\mathrm{O}}_2}^d\left(t\right)\hfill & =f_{{\mathrm{H}}_{\mathrm{2}}{\mathrm{O}}_2}\left({\xi }^d\left(t\right)\right)+c_{{\mathrm{H}}_{\mathrm{2}}{\mathrm{O}}_2}{\dot{z}}^d,\hfill \\ \frac{d}{dt}{C}_{\text{O}{\mathrm{H}}^{•}}^d\left(t\right)\hfill & =f_{\text{O}{\mathrm{H}}^{•}}\left({\xi }^d\left(t\right)\right)+c_{\text{O}{\mathrm{H}}^{•}}{\dot{z}}^d,\hfill \\ \frac{d}{dt}{\left[{\mathrm{H}}^{•}\right]}^d\left(t\right)\hfill & =f_{{\text{H}}^{•}}\left({\xi }^d\left(t\right)\right)+c_{{\text{H}}^{•}}{\dot{z}}^d,\hfill \\ \frac{d}{dt}{\left[{\mathrm{H}}_{\mathrm{2}}\right]}^d\left(t\right)\hfill & =f_{{\mathrm{H}}_{\mathrm{2}}}\left({\xi }^d\left(t\right)\right)+c_{{\mathrm{H}}_{\mathrm{2}}}{\dot{z}}^d,\hfill \\ \frac{d}{dt}{C}_{{\text{O}}_2^{•-}}^d\left(t\right)\hfill & =f_{{\text{O}}_2^{•-}}\left({\xi }^d\left(t\right)\right),\hfill \\ \frac{d}{dt}{\left[{\mathrm{R}}^{•}\right]}^d\left(t\right)\hfill & =f_{{\mathrm{R}}^{•}}\left({\xi }^d\left(t\right)\right)+c_{{\mathrm{R}}^{•}}{\dot{z}}^d,\hfill \\ \frac{d}{dt}{\left[{\mathrm{R}\mathrm{O}\mathrm{O}}^{•}\right]}^d\left(t\right)\hfill & =f_{{\mathrm{R}\mathrm{O}\mathrm{O}}^{•}}\left({\xi }^d\left(t\right)\right),\hfill \\ {\xi }^d\left(t\right)\hfill & =\left({\left[{\mathrm{e}}_{\mathrm{a}\mathrm{q}}^{-}\right]}^d,{\left[{\mathrm{O}}_2\right]}^d,C_{{\mathrm{H}}_{\mathrm{2}}{\mathrm{O}}_2}^d,C_{{\mathrm{O}\mathrm{H}}^{•}}^d,{\left[{\mathrm{H}}^{•}\right]}^d,{\left[{\mathrm{H}}_{\mathrm{2}}\right]}^d,C_{{\text{O}}_2^{•-}}^d,{\left[{\mathrm{R}}^{•}\right]}^d,{\left[{\mathrm{R}\mathrm{O}\mathrm{O}}^{•}\right]}^d\right)\left(t\right),\hfill \\ d\hfill & =1,\dots ,N_d.\hfill \end{array}\right..$

(6)

The reaction network is schematized in Figure 1 of [19], while the specific reactions and the rate constants considered in this work are reported in Sections S.1 and S.2 of [19].

The key aspects worth highlighting regarding the MS-GSM² (6) are the following:

(i) Compared to the system Σ^c in Eq. 5, the MS-GSM² system ${\mathrm{\Sigma }}_{\text{MS}}^c$ in Eq. 6 is driven by two more unitary Poisson processes: ${\mathrm{P}}_{\dot{d}}^{(c)}$ and ${\mathrm{P}}_{\rho }^{(c,d)}$. It should be noted that ${\mathrm{P}}_{\rho }^{(c,d)}$ is similar to ${\mathrm{P}}_h^{(c,d)}$, where h ∈ {a, b, r}, and it is a Poisson process acting on a single domain, whereas ${\mathrm{P}}_{\dot{d}}^{(c)}$ accounts for energy deposition and is, therefore, an inter-domain process that can affect more than one domain at once. Each single energy deposition can induce a random number $Z_{Y;d}^{(c,d)}$ and $Z_{X;d}^{(c,d)}$ of direct lethal and sub-lethal lesions, respectively, on each domain d = 1, … , N_d; a similar argument holds for $Z_{Y;i}^{(c,d)}$ and $Z_{X;i}^{(c,d)}$ concerning indirect damages.

(ii) The Poisson jump process ${\mathrm{P}}_{\rho }^{(c,d)}$ describes the formation of indirect damages. It depends explicitly on the chemical environment and energy depositions. In doing so, we assume that the effect of the chemical environment on the creation of DNA damage is not instantaneous but depends on the concentration of radicals in a time interval [t − T_I, t]. Therefore, we employed the short-hand notation ξ_t to denote

${\xi }_t≔{\int }_{-T_I}^0\xi \left(t+\theta \right)d\theta .$

In the present work, we choose the rate

$\rho \left({\xi }_t\right)≔\varrho {\int }_{-T_I}^0{e}^{-T_{\mathit{irr}}}\xi \left(t+\theta \right)d\theta ,(7)$

for a suitable constant ϱ > 0, where T_irr is the irradiation time.

(iii) The random variables $Z_{Y;d}^{(c,d)}$ and $Z_{X;d}^{(c,d)}$ describe the number of direct lethal and sub-lethal lesions, respectively, created on each domain d = 1, … , N_d, whereas $Z_{Y;i}^{(c,d)}$ and $Z_{X;i}^{(c,d)}$ are random variables describing the number of indirect lethal and sub-lethal lesions, respectively, created on each domain d = 1, … , N_d. As mentioned previously, the distinction has been made to account for the UHDR effects. According to the aforementioned description, we first assume that, given an energy deposition z subsequent to a track deposition, a certain number of direct DNA damages are created within the cell nucleus, $Z_Y^{(c,d)}$ and $Z_X^{(c,d)}$. These random variables follow a distribution

$\begin{array}{cc}\hfill p\left(x|z\right)& =e^{-\kappa \left(z\right)}\frac{{\left(\kappa \left(z\right)\right)}^x}{x!}\hfill \\ \hfill p\left(y|z\right)& =e^{-\lambda \left(z\right)}\frac{{\left(\lambda \left(z\right)\right)}^y}{y!}.\hfill \end{array}(8)$

Thus, we explicitly include in the functions κ(z) and λ(z) the effects that the chemical environment and LET have on the number of damages created. In particular, we assume that the average yield of sub-lethal lesions per unit Gy under the conventional dose rate is κ > 0. Then, we assume that a fraction q ∈ [0, 1] of κ is due to indirect damage, i.e., radical-mediated. In contrast, the remaining 1 − q is due to direct damages, and this fraction depends on LET, according to several experimental data such as in [46]; we assume that only the number of indirect damages created depends on the chemical environment. Summarizing, after an energy deposition event z is registered at a certain time t, we assume first that a random number of direct sub-lethal or lethal lesions can be created at rates κ(1 − q)z and λ(1 − q)z, respectively.

(iv) The chemical system ξ evolves according to [19]; nonetheless, in contrast to [19], we do not assume a continuous dose-rate effect, but the effect of energy deposition is modulated by the track’s arrival time as prescribed by ${\mathrm{P}}_{\dot{d}}^{(c)}$. In particular, ${\dot{z}}^d$ is a purely discontinuous jump process that describes the energy deposition in the domain d. This allows extreme flexibility in the modelization of the effect of dose rate so that any dose-rate structure can be implemented into the MS-GSM².

2.3 Stepwise construction of the MS-GSM²

In Algorithm 1, we describe in detail how to construct and simulate stepwise the solution of the MS-GSM² (6), as also summarized in Figure 1. Such construction is based on the joint usage of a standard stochastic simulation algorithm (SSA) [45], together with a solver of ordinary differential equations (ODEs) for the chemical system. In the following, we assume irradiation in the time interval [0, T_irr] so that we have $\dot{d}=0$ for t > T_irr and a terminal time T > T_irr + T_I sufficiently large so that the system ${\mathrm{\Sigma }}_{\text{MS}}^c$ reaches convergence.

Algorithm 1.The MS-GSM².

 1:  Notation:

$\begin{array}{cc}\hfill & h_{1+4\left(d-1\right)}\left(x,\xi \right)=r{x}^d,h_{2+4\left(d-1\right)}\left(x,\xi \right)=a{x}^d,h_{3+4\left(d-1\right)}\left(x,\xi \right)=b{x}^d\left(x^d-1\right),\hfill \\ \hfill & h_{4+4\left(d-1\right)}\left(x,\xi \right)=\rho \left({\xi }^d\right),h_{1+4N_d}\left(x,\xi \right)=\dot{d},h\left(x,\xi \right)≔{\displaystyle \sum _{i=1}^{1+4N_d}}{h}_i\left(x,\xi \right).\hfill \end{array}$

 2: Start with an initial chemical environment ξ(t) = ξ₀, biological system X(t) = Y(t) = 0, and initial time t = 0;

 3:  set T_i = 0, for i = 1, …, 1 + 4N_d;

 4:  while t < T do

 5:   for all h_i, i = 1, … , 1 + 4N_d do

 6: generate a random number R_i ∼ U (0, 1) and set $U_i≔\log \frac{1}{R_i}$;

 7:    compute τ_i solving

${\int }_t^{t+{\tau }_i}{h}_i\left(X\left(s\right),{\xi }_s\right)ds=S_i-T_i.$

        We use the convention that if h_i (X(t), ξ_s) = 0, then τ_i = ∞;

 8:   end for

 9:   select $\tau ≔{\min }_{(i=1,\dots ,1+4N_d)}{\tau }_i$;

 10:   select the corresponding rate h_i at which the minimum is attained;

 11:   solve the chemical system for ξ in the time interval [t, t + τ];

 12:   for all h_i, i = 1, … , 1 + 4N_d do

 13:    set

$T_i=T_i+{\int }_t^{t+\tau }{h}_i\left(X\left(s\right),{\xi }_s\right)ds,$

 14:   update t = t + τ;

 15:   if i = 1 + 4 (d − 1), for some d = 1, … , N_d, then

 16:    update X(t) = X(t) − 1, Y(t) = Y(t), and ξ(t) = ξ(t);

 17:   else if i = 2 + 4 (d − 1), for some d = 1, … , N_d, then

 18: update X(t) = X(t) − 1, Y(t) = Y(t) + 1, and ξ(t) = ξ(t);

 19:   else if i = 3 + 4 (d − 1), for some d = 1, … , N_d, then

 20:    update X(t) = X(t) − 2, Y(t) = Y(t) + 1, and ξ(t) = ξ(t);

 21:   else if i = 4 + 4 (d − 1), for some d = 1, … , N_d, then

 22:    simulate $Z_{Y;i}^{(c,d)}$ and $Z_{X;i}^{(c,d)}$;

 23:   update $X(t)=X(t)+Z_{X;i}^{(c,d)}$, $Y(t)=Y(t)+Z_{Y;i}^{(c,d)}$, and ξ(t) = ξ(t);

 24:   else if i = 4N_d, then

 25:    simulate the position where the track hits;

 26:    compute the total specific energy deposition z according to microdosimetric spectra;

 27:    for d = 1 to N_d do

 28:     compute the specific energy deposition z^d according to an amorphous track model;

 29:     simulate $Z_{Y;d}^{(c,d)}$ and $Z_{X;d}^{(c,d)}$ according to Eq. 8;

 30:     update $X(t)=X(t)+Z_{X;d}^{(c,d)}$, $Y(t)=Y(t)+Z_{Y;d}^{(c,d)}$, and ξ(t) = ξ(t) + G_ξρz^d;

 31:    end for

 32:   end if

 33:   end for

 34:  end while

 35:  end the system.

2.4 MS-GSM² simulations

We consider a microscopic volume consisting of a water cylinder of radius R_N = 8 μm (xy-plane) and length 2R_N (z-direction), divided into N_d = 64 × 8 cubic domains to mimic a cell nucleus. The impact point of the particle is simulated by sampling randomly from a uniform distribution on a circle of radius R_N + R₈₀ on the xy-plane, where

$R_{80}=R_c\exp \left(\frac{0.8\left(1+2\ln \left(R_p/R_c\right)-1\right)}{2}\right)$

is the radius corresponding to 80% of the dose deposited by the track, according to the amorphous track model description mentioned in [25]. The choise of R_N + R₈₀ is made in such a way as to take into account for dose depositions due to particles passing outside the cell nucleus but delivering a significant contribution inside it. We use the following parameters: R_c = 0.01 μm is the core radius and R_p = 0.05 (E/A)^1.7 is the penumbra radius of the track, according to [47], where E/A is the energy per nucleon. The choice of approximating the penumbra radius R_p with R₈₀ is a compromise between the accuracy of the description of the amorphous track and computational reasons (long time and large memory consumption). The average number of simulated particles N_p is defined by the dose–LET relation, considering $\pi {(R_N+R_{80})}^2$ as the hitting surface. The actual number of simulated particles is obtained by summing the number of deposition events up to the irradiation time $T_{\mathit{irr}}=D/\dot{D}$ according to Algorithm 1, where D is the imparted macroscopic dose and $\dot{D}$ is the mean dose rate. The time τ between one deposition and the next is sampled as described in Algorithm 1. The absorbed dose of a single event z is distributed on the N_d domains of the xy-plane according to the amorphous track model described in [47], i.e.,

$\begin{array}{c}\hfill D_c=\frac{1}{\pi R_c^2}\left(\frac{LET}{\rho \left(1+2\ln \left(R_p/R_c\right)\right)}\right)\\ \hfill D_p\left(r\right)=\frac{1}{\pi r^2}\left(\frac{LET}{\rho \left(1+2\ln \left(R_p/R_c\right)\right)}\right)\end{array},$

where r is the track radius and ρ is the water density. The path of the ion is considered parallel to the cylinder axis, and variations in trajectory and speed are neglected along the z-direction, i.e., the LET is constant within the cylinder (“track-segment conditions”), in analogy to [38].

The chemical system is described by a set of nine ordinary differential equations (Eq. 6), considering the reactions and their rate constants and initial concentrations according to [19]. The evolution of the chemical species is followed up to a time T = T_irr + T_off > 500 s, where T_off is the time for the relaxation of the chemical system once the irradiation is finished, i.e., $\dot{d}=0$. The indirect DNA damage yield κ, described in the previous paragraph (i.e., in Eq. 8), is modulated, in particular, by the time evolution of the peroxyl radical concentration [ROO^•], according to Eq. 7. This organic radical is crucial for DNA damage, as described in [19]. The number of sub-lethal and lethal lesions is calculated from Eq. 6, while the cell survival fraction is estimated according to [32, 33], considering common values for the pathway rates, i.e., a = 0.01, b = 0.01, and r = 4.

Given a certain particle, characterized by type, energy, and LET, the simulation is repeated over a wide range of macroscopic doses D, from 1 Gy to 30 Gy, and the average dose rate $\dot{D}$, from 0.03 Gy/s (CONV) to 100 Gy/s (UHDR). The time evolution of the instantaneous dose rate depends on the deposition time structure described previously. The simulation is also repeated for different radiation qualities; specifically, we report the results for protons at 18.6 MeV and carbon ions at 149 MeV/u.

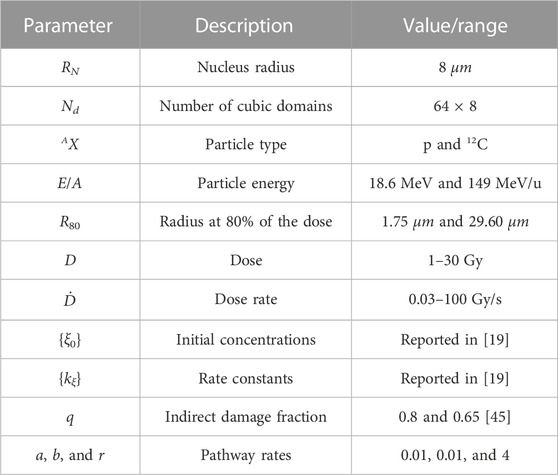
To summarize, all the parameters considered in our simulations are shown in Table 1. Moreover, as mentioned previously, the MS-GSM² accounts for several stages of radiation damage, including the physical, homogeneous chemical, and biological stages, as well as different levels of stochasticity, particularly in ionizing radiation, chemistry, and DNA damage formation and time evolution, as reported in Table 2. Finally, following Algorithm 1, all the simulations reported in this work were performed using MATLAB; specifically, we used the function ode15s.m for the numerical integration of the ODEs that describe the chemical system shown in Eq. 6.

TABLE 1

TABLE 1. Summary of the parameters considered in this work.

TABLE 2

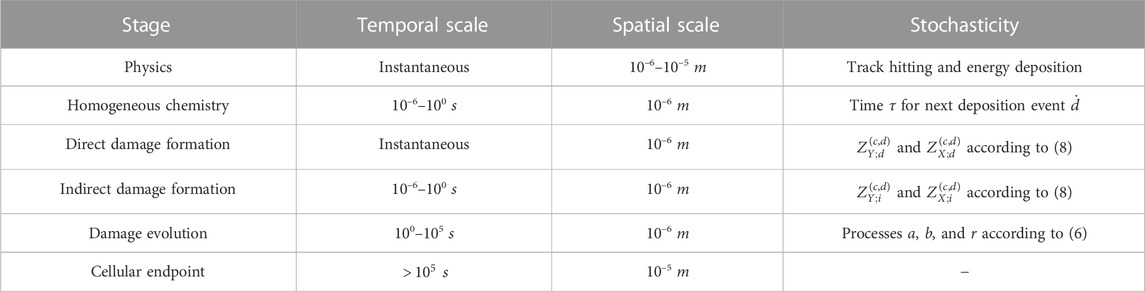
TABLE 2. Stages and corresponding spatio-temporal scales of radiation damage considered in this work and related levels of stochasticity taken into account by the MS-GSM².

3 Results

Figure 2 shows the microscopic absorbed dose for protons at 18.6 MeV over the cell nucleus in different domains for different (macroscopic) average doses: the top row reports 1 Gy, the bottom row reports 30 Gy, the left column reports 0.03 Gy/s (CONV), and the right column reports 100 Gy/s (UHDR). Figure 3 shows the same results for the case of carbon ions at 149 MeV/u. Both Figures 2, 3 highlight how the case of 1 Gy is characterized by a more spatially heterogeneous dose distribution over the cell nucleus; on the contrary, at 30 Gy, the dose distribution is more homogeneously distributed. Furthermore, differences in the absorbed dose over cell domains are more significant in the case of carbon ions, characterized by high local energy deposition in a single domain even at 30 Gy, with a non-uniform dose distribution. Specifically, in the case of 1 Gy, the impact of the energy deposited by a single track depositing almost 3 Gy in a single domain is evident, as opposed to an overall dose deposition of 1 Gy in the cell nucleus. Furthermore, it is clear from both figures that the dose rate has no impact on the total dose distribution, as expected.

FIGURE 2

FIGURE 2. Domain distribution of the absorbed dose by the cell nucleus for protons of 18.6 MeV at 1 Gy (top row) and 30 Gy (bottom row) and overall doses for rates of 0.03 Gy/s (left column) and 100 Gy/s (right column).

FIGURE 3

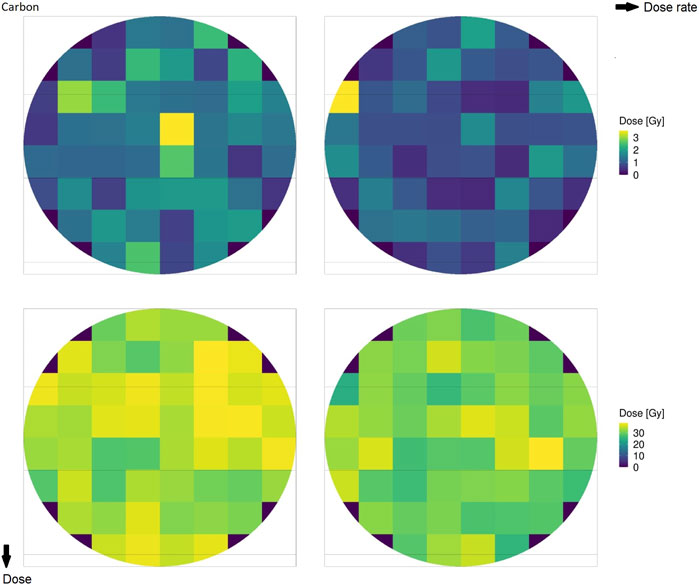
FIGURE 3. Absorbed dose by the cell nucleus for carbon ions of 149 MeV/u at 1 Gy (top row) and 30 Gy (bottom row) for rates of 0.03 Gy/s (left column) and 100 Gy/s (right column).

Figure 4 shows the cumulative absorbed dose in a single domain over time for different dose rates. Both panels report the case of a total dose of 1 Gy in the domain; the top panel shows the case of protons at 18.6 MeV, whereas the bottom panel considers the case of carbon ions at 149 MeV/u. The figure shows how the pattern of local energy deposition is different for the two ions considered. Protons are characterized by a higher amount of energy deposition, each of which releases a small amount of energy. On the contrary, carbon ions exhibit fewer depositions, with a clear impact of single tracks hitting the nucleus. Jumps in the cumulative absorbed dose due to high energy depositions are clearly visible.

FIGURE 4

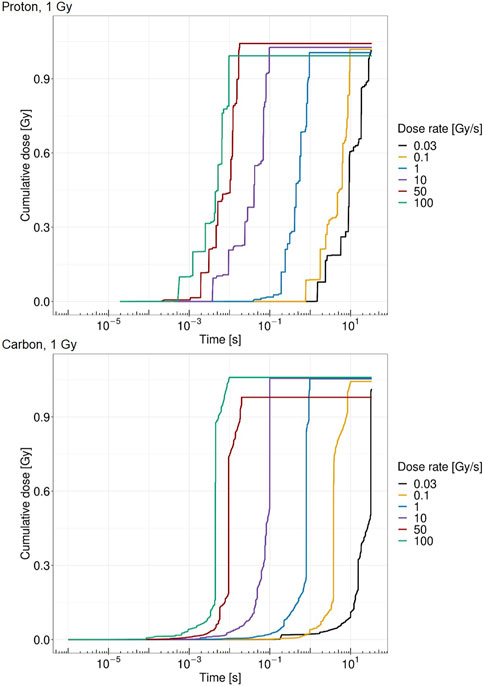
FIGURE 4. Cumulative absorbed dose by the cell nucleus for protons of 18.6 MeV over time for a single domain at 1 Gy (top panel) and carbon ions of 149 MeV/u over time for a single domain at 1 Gy (bottom panel) at 0.03 Gy/s (black), 0.1 Gy/s (yellow), 1 Gy/s (blue), 10 Gy/s (purple), 50 Gy/s (red), and 100 Gy/s (green).

Figure 5 shows the ROO^• concentration over time for a single domain for proton at 18.6 MeV at 1 Gy (top panel) and 30 Gy (bottom panel) for different dose rates. From Figure 5, it is visible how both dose and dose rate play a crucial role in the peroxyl radical concentration evolution. The higher-dose case is characterized by a higher concentration of ROO^•. In addition, high dose rates show an almost continuous pattern of energy deposition, whereas on the contrary, low dose rates are characterized by more jagged behavior due to the longer time elapsing between consecutive energy depositions. Moreover, ROO^• concentrations at 1 Gy are more similar for the different dose rates, while in the 30 Gy case, there is a clearly different time evolution of [ROO^•] for the dose rates considered, both in terms of maximum concentration and in terms of growth and relaxation rate of the chemical species.

FIGURE 5

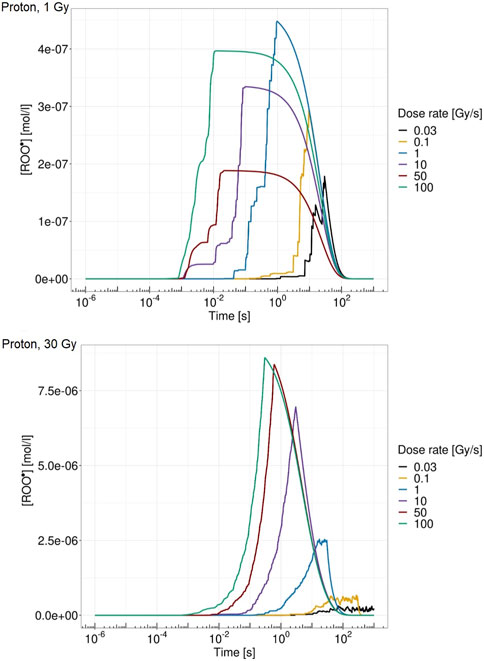
FIGURE 5. ROO^• concentration over time for a single domain for proton of 18.6 MeV at 1 Gy (top panel) and 30 Gy (bottom panel) at 0.03 Gy/s (black), 0.1 Gy/s (yellow), 1 Gy/s (blue), 10 Gy/s (purple), 50 Gy/s (red), and 100 Gy/s (green).

Figure 6 reports the relative reduction in indirect damage per unit Gy versus dose rate for different doses. The top panel shows the case of protons at 18.6 MeV, whereas the bottom panel shows the case of carbon ions at 149 MeV/u. A more severe reduction is evident in the case of protons, where at 30 Gy and 100 Gy/s, the indirect damage yield is reduced to 30% compared to the conventional dose rate of 0.03 Gy/s. In the case of carbon ions, the relative reduction reaches at most 12% in the same situation. This is consistent with what was predicted in [25], pointing to a lower entity of the FLASH effect for higher-LET beams. Furthermore, in both ions considered, there is a clear pattern of reversed behavior, where increasing the imparted dose up to 10 Gy/s yields a higher amount of indirect damage, whereas after this dose rate, the pattern is the opposite. For dose rates exceeding 50 Gy/s, higher doses are associated with less damage induced. In general, low doses are characterized by a steady low reduction of damage yields, whereas high doses show almost no reduction up to 10 Gy/s, followed by a sharp fall-off with high indirect damage yield reduction.

FIGURE 6

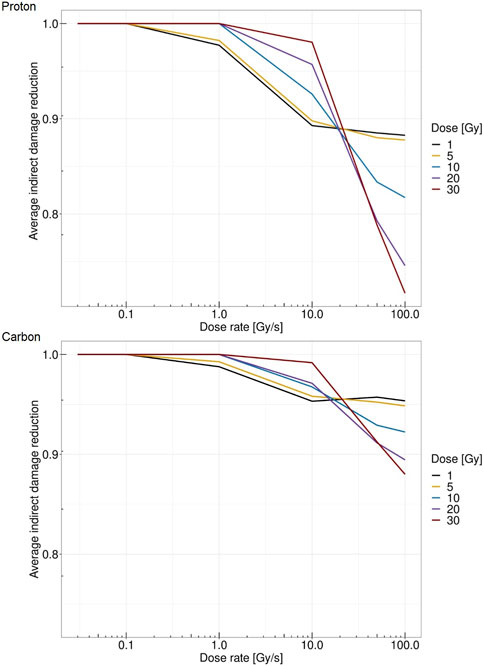
FIGURE 6. Dose rate versus average relative reduction in indirect damage per unit Gy for protons of 18.6 MeV (top panel) and for carbon ions of 149 MeV/u (bottom panel) at 1 Gy (black), 5 Gy (yellow), 10 Gy (blue), 20 Gy (purple), and 30 Gy (red).

Figure 7 shows the survival fraction of the human salivary gland (HSG) cells computed with the MS-GSM² versus dose rate at different doses in the case of protons at 18.6 MeV. Figure 8 reports the same result in the case of carbon ions at 149 MeV/u. Both figures are characterized by a steady, flat surviving fraction from the conventional dose rates up to 10 Gy/s, after which an increase in the surviving fraction is visible. The sparing effect emerges only at high doses: for protons, this effect is slightly visible at 10 Gy and severe at 30 Gy, whereas for carbon ions, the effect clearly emerges after 20 Gy and is more attenuated.

FIGURE 7

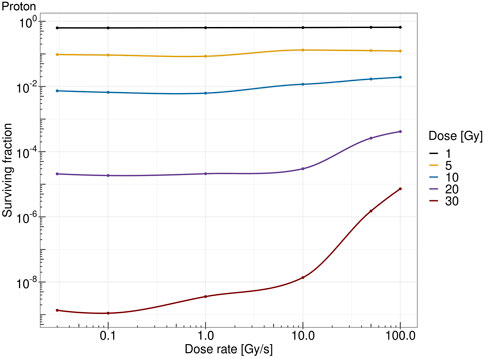
FIGURE 7. Dose rate versus survival fraction for protons of 18.6 MeV at 1 Gy (black), 5 Gy (yellow), 10 Gy (blue), 20 Gy (purple), and 30 Gy (red).

FIGURE 8

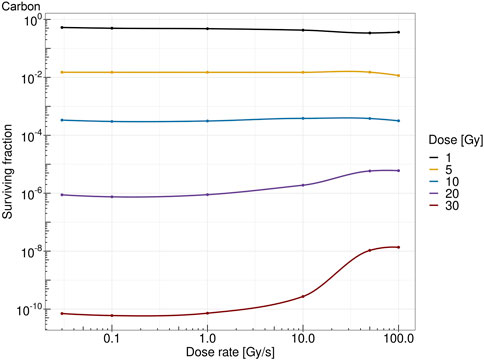
FIGURE 8. Dose rate versus survival fraction for carbons ion of 149 MeV/u at 1 Gy (black), 5 Gy (yellow), 10 Gy (blue), 20 Gy (purple), and 30 Gy (red).

4 Discussion

4.1 Analysis of the results

It is worth stressing, first, how different stochastic effects and time scales are included in the MS-GSM² derived in this study, as summarized in Table 2. The MS-GSM² construction highlights the several stochasticities that are taken into account in the MS-GSM². First, the time between consecutive energy depositions is stochastic, so both the evolution of the chemical environment and the yield of DNA damage depend on the time elapsing between two consecutive energy deposition events. Furthermore, the spatial position of the track hitting the biological target, which, in complete generality, is larger than the cell nucleus, is again stochastic; consequently, each domain of the cell nucleus experiences a different amount of energy imparted at any deposition event. It is worth noticing that, mostly in the case of high-LET radiation, some domains could also have null energy deposited. Then again, both the chemical environment and the damage yield are affected by stochastic energy deposition; this implies that not only the time elapsed between consecutive tracks is stochastic but also the actual energy imparted is a random variable. Moreover, the indirect damage yield depends on the chemical environment, thus accounting for a further stochasticity. At last, after the chemical environment reaches stability after irradiation, only the biological pathways of repair and clustering, as described by the GSM² via r, a, and b, remain, which allows for the computation of the predicted cell survival probability.

The obtained results, summarized in Figures 7, 8, show a cell survival increase with a consequent tissue sparing at sufficiently high doses and dose rates; specifically, it is worth highlighting how both the dose and the dose rate play a crucial role in the sparing effect at the UHDR regime, consistent with most preclinical literature, interestingly collected as a general trend in [48]. In this regard, in the proposed model, several results point toward the conclusion that the dose and the dose rate play a different role in inducing the FLASH effect: (i) a sufficiently high dose rate allows for close enough energy depositions over time so that the chemical environment is modified appropriately, whereas (ii) a sufficiently high dose permits spatial interaction of subsequent energy depositions. Relevant enough, as expected, the ion and its energy play a role in both dose- and dose rate-related effects, and as shown in the results in Figures 7, 8, the dose and dose rate at which the FLASH effect emerges and the magnitude of the sparing shown depend strongly on the quality of the radiation considered. For both ions considered and more clearly in the case of carbon ions (Figures 2, 3), it is evident that high local dose deposition is not sufficient to trigger the FLASH effect, whereas on the contrary, a uniform dose must be reached over the cell nucleus in order to give rise to the FLASH effect. In other words, enough domains must be above a certain dose threshold to have a significant response, since the FLASH effect is not linear. Energy depositions happen not only due to the direct hit of tracks of the cell nucleus but also due to tracks passing nearby. This translates into more localized energy deposition for high LET and a more spatially homogeneous dose pattern for lower LET. This is evident in Figures 2, 3, where carbon ions are characterized by high local energy deposition. The same effect emerges in Figure 4, with sudden jumps in the cumulative deposited dose due to tracks hitting the cell nucleus.

Regarding the chemical environment, again, it emerges from Figure 5 how both dose and dose rate concur to trigger the FLASH effect. Heuristically speaking, the main idea of the proposed model is, following the main mechanism already proposed in [19], to relate cell survival sparing to the peroxyl radical concentration ROO^• evolution. Therefore, the dose rate concurs to increase [ROO^•] in a short time so that, if the absorbed dose is sufficiently high, causing [ROO^•] to be high enough, organic radical–radical recombination during the chain termination in the homogeneous chemical stage is more likely to happen with a consequently lower probability of interaction with the DNA. This reduced radical interaction probability with the DNA has a consequent DNA damage yield reduction, as emerges in Figure 6. This combined effect of dose and dose rate is also coherent with the inversion of the indirect damage yield pattern that emerges between 10 Gy/s and 50 Gy/s. At a chemical level, a higher dose corresponds to a higher production of ROO^•, which is more marked at high dose rates. Indeed, only the combined effect of high dose and high dose rate leads to a different temporal evolution of [ROO^•]; specifically, the high dose rate allows faster growth of [ROO^•] but, at the same time, also a more rapid decrease due to the recombination of these chemical species. At high dose rates, the dose deposition events are much closer to each other in time, and therefore, this leads to competition with radical recombination effects. On the contrary, if the dose rate is not high enough, increasing the dose would only increase the rate of damage induction per unit Gy, i.e., the standard trend of damage dependence on the dose, which, due to the well-known linear quadratic behavior, will result in an increasing derivative at a larger dose. This is because at a low dose rate, the cell exposure to a high concentration of this harmful organic radical takes place for a prolonged time; this effect is similar to what occurs with drugs [44], as described in [19]. On the contrary, if a sufficiently high dose is imparted over a short time, organic radical–radical recombination is favored over interaction with DNA. This leads to cell tissue sparing, implying that a high dose rate will trigger an additional quenching effect on the dose, in addition to the previously described standard effect, while with conventional radiation, this latter effect will not occur. Again, the sparing effect is more pronounced in the low-LET case, whereas as the LET increases, the highly localized dose deposition pattern implies that a local disappearance of some harmful chemical species occurs. However, this process does not happen on the whole cell, i.e., a higher dose is required to reach the sufficiently spatially uniform dose needed to trigger the FLASH effect.

The aforementioned points also highlight some key differences between the originally proposed model in [19] and the generalization proposed in the current research. The main novelty, compared to [19], is to provide a more direct link from the chemical environment to its biological effect. Radical concentration is, thus, related to indirect damage induction. Therefore, the general linear or quadratic relation between energy deposition and damage yield, already proposed decades ago in [49], is generalized in the present work so that a more direct link between the concentration of the radical and the consequent damage yield is considered. In addition, the multiscale nature of the proposed model clearly emerges in several plots (Figures 4, 5). A purely discontinuous time pattern in energy deposition is evident. This translates into highly jagged radical concentrations at low dose rates, which naturally turn continuous as the dose rate increases, differing from what is considered in [19].

Therefore, with the proposed approach, we can directly link the radical concentration, which is directly modified by the energy deposition pattern depending on both dose and dose rate, to the DNA damage formation. It should be noted that conventional dose rates do not provide any changes in the indirect damage yield, whereas as the dose rates increase, a reduction in the damage occurs. The magnitude of damage reduction depends on the absorbed dose. Moreover, the overall pattern of indirect damage yield reduction strongly depends on the radiation quality. In this regard, it is worth stressing that, Figure 6 reports the relative reduction in the indirect damage yield per unit Gy. Therefore, since the proportion of indirect damage compared to direct damage in the high-LET radiation is lower than in the low-LET case, the overall reduction in the total damage yields would be even higher.

All the previously mentioned discussions eventually emerge in the different sparing at the cell survival level. Both Figures 7, 8 show that a sufficiently high dose and dose rate result in cell survival sparing. Furthermore, the highly localized energy deposition of high LET results in a less sparing at 30 Gy compared to protons. The magnitude of the sparing of carbon ions at FLASH dose rates at 30 Gy is in the order of the sparing at FLASH dose rates for protons at 20 Gy. This is in agreement with the discussion that emerged previously, considering how the local pattern of energy deposition affects the chemical environment. It is worth stressing that the surviving fraction remains almost constant up to 10 Gy/s, after which there is an increase in the surviving fraction. For protons, a slight increase in the surviving fraction emerges at 10 Gy, and it is clear at higher doses, such as 30 Gy; this is in agreement with what was experimentally observed in [48]. On the contrary, carbon ions require a higher dose to observe the FLASH effect, which is in agreement with [25]. Differently from the results derived in [29], where the predicted surviving fraction steadily decreases in the conventional dose rate regimes, reaching a minimum of approximately 1 Gy/s, the predicted surviving fraction of the MS-GSM² remains almost unchanged in the range below 10 Gy/s, after which the FLASH effect is triggered.

4.2 Current limitations of the MS-GSM² and future perspectives

Although the presently developed model is general enough in the sense that it includes several effects of random processes in space and time inherent to three different domains, such as physics, chemistry, and biology, it also presents some limitations. Subsequently, we discuss some possible future lines of research to strengthen the developed model.

It is worth stressing that 100 Gy/s represents a limit for the proposed model. Above 100 Gy/s, the time elapsed by two consecutive energy depositions significantly overlaps with the heterogeneous chemical stage. Therefore, accurately considering high dose rates would require a more sophisticated chemical treatment that goes beyond the homogeneous chemical stage as considered in the current approach, e.g., including diffusion during the heterogeneous chemical stage. Finally, as previously described, this model allows us to consider single deposition events. This, in principle, would allow us to consider any temporal structure of dose delivery to study the effect that an intra-pulse dose rate could have on the triggering of the FLASH effect. Both of these aspects are currently under investigation and will be analyzed in future work.

As is well known, the FLASH biological effect can be described by two different and presently unexplained aspects, i.e., the sparing effect of healthy tissues and the differential effect between normal tissues and tumors. In this work, we chose to focus on the first aspect of UHDR irradiation, i.e., the higher sparing of healthy tissues at high doses and high dose rates with respect to conventional irradiation; nevertheless, our model is not in contradiction with some of the most accredited hypotheses that try to explain the differential effect between normal tissues and tumors. The first hypothesis is based on a combination of two mechanisms linked to DNA damage, i.e., a different damage formation due to the reduction of a specific oxygen-dependent DNA damage, which is consistent with a decrease in the organic peroxyl radical concentration, and a defective repair process, such as pathologic chromosome rearrangements due to an aberrant DNA double-strand break (DSB) repair, as described in [19]. The second conjecture postulates that a different accumulation of a specific chemical species between normal tissue and tumor is the basis for the differential effect, as proposed in [50]. Specifically, this hypothesis states that normal tissues have a greater ability to detoxify from reactive oxygen species, reducing oxidative injury with respect to tumors, as described in [23]. In fact, normal cells have a more rapid elimination, mediated by enzymes, of peroxidized compounds compared to tumor cells [50]. We may test these hypotheses in future work.

Last, a critical aspect that we decided not to address in this work is the experimental validation of our model. As stated at the beginning of this paper, the aim of this work is to develop a multiscale model, merging the homogeneous chemical stage, described by a reaction kinetic model, with the formation and time evolution of DNA damage, accounted for by the GSM². The aim of this study is to show the mathematical framework of this novel tool that allows, among many biological effects of radiation, to capture possible effects of DNA damage during UHDR irradiation. The goal of the calculations that we report here is to show how, in principle, this tool is able to describe the sparing effect of healthy tissues at high doses and high dose rates—an effect contradicting conventional radiobiological modeling outcomes, which typically may explain larger damage in occurrence on a more temporally dense dose-delivery basis—and not explain the FLASH effect. For this reason, considering the great importance of this aspect and the complexity due to the presence of several parameters that play a role in this context, we decided to dedicate a specific future work regarding the comparison with the experimental data. At this stage, we want to underline how the trend of the survival curves that we obtained is, in any case, in agreement with the few experimental in vitro data currently available, such as in [14].

5 Conclusion

In this paper, we extended the GSM² by coupling biological DNA damage repair and kinetics to the radiation-induced chemical environment. Specifically, by introducing a proper mathematical formulation of the homogeneous chemical stage, we establish a link between the organic radical concentration and the formation of indirect damage. The resulting model is a universal multiscale stochastic model able to treat in a complete general formulation the stochastic effects inherent to physics, chemistry, and biology. Different temporal and spatial scales are efficiently included in the model. We showed how the proposed model is able to describe the normal tissue sparing arising at ultra-high dose rates. Relevant enough, this sparing typical of the FLASH effect emerges at the interplay of many mechanisms: oxygen concentration is involved in driving the effect so that spatial and temporal dose deposition effects favor organic radical–radical recombination, such as R^• and ROO^•, during the homogeneous chemical stage, that eventually reduces the indirect damage yield, causing tissue sparing. A natural generalization of the model developed will be to include the heterogeneous chemical stage in order to provide a more mechanistically grounded analysis of the phenomena involved in the FLASH effects, opening up further investigation of higher dose rates than the one considered in the current research. Such a generalization will require a more advanced spatial description of the physical, chemical, and biological processes involved, thus abandoning a domain-like formulation in favor of a true full spatial description [35]. Such a model, adequately tuned with in vitro and in vivo experimental data and coupled with advanced biologically driven treatment plan optimization [51], can, on the one hand, help understand the main biological mechanism underlying the FLASH effect and, on the other hand, favor the full exploitation of such an effect in clinical practice.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

MB: conceptualization, data curation, formal analysis, investigation, methodology, software, validation, writing–original draft, and writing–review and editing. MM: conceptualization, methodology, and writing–review and editing. AA: conceptualization, writing–review and editing. FT: conceptualization, writing–review and editing. CLT: funding acquisition and writing–review and editing. FGC: conceptualization, data curation, formal analysis, investigation, methodology, supervision, writing–original draft, and writing–review and editing. ES: conceptualization, formal analysis, funding acquisition, methodology, supervision, validation, writing–original draft, and writing–review and editing.

Funding

The authors declare that financial support was received for the research, authorship, and/or publication of this article. This work was partially supported by the INFN CSN5 project FRIDA.

Acknowledgments

Rudi Labarbe and Lucian Hotoiu are gratefully acknowledged for multiple fruitful discussions and for providing their code. Martina Fuss, Michael Krämer, Gianmarco Camazzola, and Daria Boscolo are thanked for inspiring discussions.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Favaudon V, Caplier L, Monceau V, Pouzoulet F, Sayarath M, Fouillade C, et al. Ultrahigh dose-rate flash irradiation increases the differential response between normal and tumor tissue in mice. Sci Transl Med (2014) 6:245ra93. doi:10.1126/scitranslmed.3008973

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Vozenin M, De Fornel P, Petersson K, Favaudon V, Jaccard M, Germond J, et al. The advantage of flash radiotherapy confirmed in mini-pig and cat cancer patients. Clin Cancer Res (2019) 25:35–42. doi:10.1158/1078-0432.CCR-17-3375

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Schüler E, Acharya M, Montay-Gruel P, Loo BW, Vozenin M-C, Maxim PG. Ultra-high dose rate electron beams and the flash effect: from preclinical evidence to a new radiotherapy paradigm. Med Phys (2022) 49:2082–95. doi:10.1002/mp.15442

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Adrian G, Ruan J-L, Paillas S, Cooper CR, Petersson K. In vitro assays for investigating the flash effect. Expert Rev Mol Med (2022) 24:e10. doi:10.1017/erm.2022.5

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Limoli CL, Vozenin M-C. Reinventing radiobiology in the light of flash radiotherapy. Annu Rev Cancer Biol (2023) 7:1–21. doi:10.1146/annurev-cancerbio-061421-022217

CrossRef Full Text | Google Scholar

6. Montay-Gruel P, Petersson K, Jaccard M, Boivin G, Germond J, Petit B, et al. Irradiation in a flash: unique sparing of memory in mice after whole brain irradiation with dose rates above 100gy/s. Radiother Oncol (2017) 124:365–9. doi:10.1016/j.radonc.2017.05.003

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Montay-Gruel P, Acharya M, Petersson K, Alikhani L, Yakkala C, Allen B, et al. Long-term neurocognitive benefits of flash radiotherapy driven by reduced reactive oxygen species. Proc Natl Acad Sci USA (2019) 116:10943–51. doi:10.1073/pnas.1901777116

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Loo B, Schuler E, Lartey F, Rafat M, King G, Trovati S, et al. (P003) delivery of ultra-rapid flash radiation therapy and demonstration of normal tissue sparing after abdominal irradiation of mice. Int J Radiat Oncol Biol Phys (2017) 98:E16. doi:10.1016/j.ijrobp.2017.02.101

CrossRef Full Text | Google Scholar

9. Bourhis J, Sozzi WJ, Jorge PG, Gaide O, Bailat C, Duclos F, et al. Treatment of a first patient with flash-radiotherapy. Radiother Oncol (2019) 139:18–22. doi:10.1016/j.radonc.2019.06.019

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Bourhis J, Montay-Gruel P, Jorge PG, Bailat C, Petit B, Ollivier J, et al. Clinical translation of flash radiotherapy: why and how? Radiother Oncol (2019) 139:11–7. doi:10.1016/j.radonc.2019.04.008

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Montay-Gruel P, Acharya MM, Gonçalves Jorge P, Petit B, Petridis IG, Fuchs P, et al. Hypofractionated flash-rt as an effective treatment against glioblastoma that reduces neurocognitive side effects in mice. Clin Cancer Res (2021) 27:775–84. doi:10.1158/1078-0432.CCR-20-0894

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Diffenderfer ES, Verginadis II, Kim MM, Shoniyozov K, Velalopoulou A, Goia D, et al. Design, implementation, and in vivo validation of a novel proton flash radiation therapy system. Int J Radiat Oncology*Biology*Physics (2020) 106:440–8. doi:10.1016/j.ijrobp.2019.10.049

CrossRef Full Text | Google Scholar

13. Sørensen BS, Sitarz MK, Ankjærgaard C, Johansen JG, Andersen CE, Kanouta E, et al. Pencil beam scanning proton flash maintains tumor control while normal tissue damage is reduced in a mouse model. Radiother Oncol (2022) 175:178–84. doi:10.1016/j.radonc.2022.05.014

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Tinganelli W, Sokol O, Quartieri M, Puspitasari A, Dokic I, Abdollahi A, et al. Ultra-high dose rate (flash) carbon ion irradiation: dosimetry and first cell experiments. Int J Radiat Oncology*Biology*Physics (2022) 112:1012–22. doi:10.1016/j.ijrobp.2021.11.020

CrossRef Full Text | Google Scholar

15. Tinganelli W, Weber U, Puspitasari A, Simoniello P, Abdollahi A, Oppermann J, et al. Flash with carbon ions: tumor control, normal tissue sparing, and distal metastasis in a mouse osteosarcoma model. Radiother Oncol (2022) 175:185–90. doi:10.1016/j.radonc.2022.05.003

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Daugherty E, Mascia A, Zhang Y, Lee E, Xiao Z, Sertorio M, et al. Flash radiotherapy for the treatment of symptomatic bone metastases (fast-01): protocol for the first prospective feasibility study. JMIR Res Protoc (2023) 12:e41812. doi:10.2196/41812

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Friedl AA, Prise KM, Butterworth KT, Montay-Gruel P, Favaudon V. Radiobiology of the flash effect. Med Phys (2022) 49:1993–2013. doi:10.1002/mp.15184

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Wilson JD, Hammond EM, Higgins GS, Petersson K. Ultra-high dose rate (flash) radiotherapy: silver bullet or fool’s gold? Front Oncol (2020) 9:1563–12. doi:10.3389/fonc.2019.01563

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Labarbe R, Hotoiu L, Barbier J, Favaudon V. A physicochemical model of reaction kinetics supports peroxyl radical recombination as the main determinant of the flash effect. Radiother Oncol (2020) 153:303–10. doi:10.1016/j.radonc.2020.06.001

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Ramos-Méndez J, Domínguez-Kondo N, Schuemann J, McNamara A, Moreno-Barbosa E, Faddegon B. Let-dependent intertrack yields in proton irradiation at ultra-high dose rates relevant for flash therapy. Radiat Res (2020) 194:351–62. doi:10.1667/RADE-20-00084.1

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Zhou G. Mechanisms underlying flash radiotherapy, a novel way to enlarge the differential responses to ionizing radiation between normal and tumor tissues. Radiat Med Prot (2020) 1:35–40. doi:10.1016/j.radmp.2020.02.002

CrossRef Full Text | Google Scholar

22. Boscolo D, Scifoni E, Durante M, Krämer M, Fuss MC. Oxygen depletion explain the flash effect? a chemical track structure analysis. Radiother Oncol (2021) 162:68–75. doi:10.1016/j.radonc.2021.06.031

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Favaudon V, Labarbe R, Limoli CL. Model studies of the role of oxygen in the flash effect. Med Phys (2022) 49:2068–81. doi:10.1002/mp.15129

PubMed Abstract | CrossRef Full Text | Google Scholar

24. von Sonntag C. The chemical basis of radiation biology. Taylor & Francis (1987).

Google Scholar

25. Weber UA, Scifoni E, Durante M. Flash radiotherapy with carbon ion beams. Med Phys (2022) 49:1974–92. doi:10.1002/mp.15135

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Wardman P. Radiotherapy using high-intensity pulsed radiation beams (flash): a radiation-chemical perspective. Radiat Res (2020) 194:607–17. doi:10.1667/RADE-19-00016

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Abolfath R, Grosshans D, Mohan R. Oxygen depletion in flash ultra-high-dose-rate radiotherapy: a molecular dynamics simulation. Med Phys (2020) 47:6551–61. doi:10.1002/mp.14548

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Abolfath R, Peeler C, Mirkovic D, Mohan R, Grosshans D. A dna damage multiscale model for ntcp in proton and hadron therapy. Med Phys (2020) 47:2005–12. doi:10.1002/mp.14034

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Liew H, Mein S, Dokic I, Haberer T, Debus J, Abdollahi A, et al. Deciphering time-dependent dna damage complexity, repair, and oxygen tension: a mechanistic model for flash-dose-rate radiation therapy. Int J Radiat Oncology* Biology* Phys (2021) 110:574–86. doi:10.1016/j.ijrobp.2020.12.048

CrossRef Full Text | Google Scholar

30. Petersson K, Adrian G, Butterworth K, McMahon SJ. A quantitative analysis of the role of oxygen tension in flash radiation therapy. Int J Radiat Oncology* Biology* Phys (2020) 107:539–47. doi:10.1016/j.ijrobp.2020.02.634

CrossRef Full Text | Google Scholar

31. Abolfath R, Baikalov A, Rahvar S, Fraile A, Bartzsch S, Schüler E, et al. Differential tissue sparing of flash ultra high dose rates: an in-silico study (2022). arXiv preprint arXiv:2210.03565.

Google Scholar

32. Cordoni F, Missiaggia M, Attili A, Welford S, Scifoni E, La Tessa C. Generalized stochastic microdosimetric model: the main formulation. Phys Rev E (2021) 103:012412. doi:10.1103/PhysRevE.103.012412

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Cordoni FG, Missiaggia M, Scifoni E, La Tessa C. Cell survival computation via the generalized stochastic microdosimetric model (gsm2); part i: the theoretical framework. Radiat Res (2022) 197:218–32. doi:10.1667/RADE-21-00098.1

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Cordoni FG, Missiaggia M, La Tessa C, Scifoni E. Multiple levels of stochasticity accounted for in different radiation biophysical models: from physics to biology. Int J Radiat Biol (2022) 1:807–22. doi:10.1080/09553002.2023.2146230

CrossRef Full Text | Google Scholar

35. Cordoni FG. A spatial measure-valued model for radiation-induced dna damage kinetics and repair under protracted irradiation condition (2023). arXiv preprint arXiv:2303.14784.

Google Scholar

36. Missiaggia M, Cordoni FG, Scifoni E, La Tessa C. Cell survival computation via the generalized stochastic microdosimetric model (gsm2); part ii: numerical results (2023). (submitted).

Google Scholar

37. Manganaro L, Russo G, Cirio R, Dalmasso F, Giordanengo S, Monaco V, et al. A Monte Carlo approach to the microdosimetric kinetic model to account for dose rate time structure effects in ion beam therapy with application in treatment planning simulations. Med Phys (2017) 44:1577–89. doi:10.1002/mp.12133

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Kase Y, Kanai T, Matsufuji N, Furusawa Y, Elsässer T, Scholz M. Biophysical calculation of cell survival probabilities using amorphous track structure models for heavy-ion irradiation. Phys Med Biol (2007) 53:37–59. doi:10.1088/0031-9155/53/1/003

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Cordoni FG. On the emergence of the deviation from a Poisson law in stochastic mathematical models for radiation-induced dna damage: a system size expansion. Entropy (2023) 25:1322. doi:10.3390/e25091322

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Missiaggia M, Cartechini G, Scifoni E, Rovituso M, Tommasino F, Verroi E, et al. Microdosimetric measurements as a tool to assess potential in-field and out-of-field toxicity regions in proton therapy. Phys Med Biol (2020) 65:245024. doi:10.1088/1361-6560/ab9e56

PubMed Abstract | CrossRef Full Text | Google Scholar

41. Missiaggia M, Pierobon E, Castelluzzo M, Perinelli A, Cordoni F, Centis Vignali M, et al. A novel hybrid microdosimeter for radiation field characterization based on the tissue equivalent proportional counter detector and low gain avalanche detectors tracker: a feasibility study. Front Phys (2021) 8:578444. doi:10.3389/fphy.2020.578444

CrossRef Full Text | Google Scholar

42. Missiaggia M, Cartechini G, Tommasino F, Scifoni E, La Tessa C. Investigation of in-field and out-of-field radiation quality with microdosimetry and its impact on relative biological effectiveness in proton therapy. Int J Radiat Oncology* Biology* Phys (2023) 115:1269–82. doi:10.1016/j.ijrobp.2022.11.037

CrossRef Full Text | Google Scholar

43. Zaider M, Rossi BHH, Zaider M. Microdosimetry and its applications. Springer (1996).

Google Scholar

44. Scheff JD, Almon RR, Dubois DC, Jusko WJ, Androulakis IP. Assessment of pharmacologic area under the curve when baselines are variable. Pharm Res (2011) 28:1081–9 (2022) 114:1032–44. doi:10.1007/s11095-010-0363-8

PubMed Abstract | CrossRef Full Text | Google Scholar

45. Weinan E, Li T, Vanden-Eijnden E. Applied stochastic analysis, 199. American Mathematical Soc. (2019).

Google Scholar

46. Hirayama R, Ito A, Tomita M, Tsukada T, Yatagai F, Noguchi M, et al. Contributions of direct and indirect actions in cell killing by high-let radiations. Radiat Res (2009) 171:212–8. doi:10.1667/RR1490.1

PubMed Abstract | CrossRef Full Text | Google Scholar

47. Scholz M, Kraft G. Track structure and the calculation of biological effects of heavy charged particles. Adv Space Res (1996) 18:5–14. doi:10.1016/0273-1177(95)00784-C

PubMed Abstract | CrossRef Full Text | Google Scholar

48. Böhlen TT, Germond J-F, Bourhis J, Vozenin M-C, Ozsahin EM, Bochud F, et al. Normal tissue sparing by flash as a function of single-fraction dose: a quantitative analysis. Int J Radiat Oncology*Biology*Physics (2022) 114:1032–44. doi:10.1016/j.ijrobp.2022.05.038

CrossRef Full Text | Google Scholar

49. Kellerer AM, Rossi HH. A generalized formulation of dual radiation action. Radiat Res (1978) 75:471–88. doi:10.2307/3574835

CrossRef Full Text | Google Scholar

50. Spitz DR, Buettner GR, Petronek MS, St-Aubin JJ, Flynn RT, Waldron TJ, et al. An integrated physico-chemical approach for explaining the differential impact of flash versus conventional dose rate irradiation on cancer and normal tissue responses. Radiother Oncol (2019) 139:23–7. doi:10.1016/j.radonc.2019.03.028

PubMed Abstract | CrossRef Full Text | Google Scholar

51. Battestini M, Schwarz M, Krämer M, Scifoni E. Including volume effects in biological treatment plan optimization for carbon ion therapy: generalized equivalent uniform dose-based objective in trip98. Front Oncol (2022) 12:826414. doi:10.3389/fonc.2022.826414

PubMed Abstract | CrossRef Full Text | Google Scholar