- 1Instituto de Física Interdisciplinar y Sistemas Complejos IFISC (CSIC-UIB), Palma de Mallorca, Spain
- 2Complex Systems Group, Universidad Rey Juan Carlos, Madrid, Spain
- 3G.I.S.C, Universidad Rey Juan Carlos, Madrid, Spain
We discuss the core principles underpinning the concept of identifiability, providing an overview of relevant literature concerning this phenomenon within the domain of complex networks. We delve into the potentialities and inherent constraints associated with the analysis of identifiability in real networked systems. Through this exploration, we establish a comprehensive classification scheme for network identifiability, distinguishing i) structural, ii) functional, and iii) meta-identifiability categories. We explain the principal conceptual distinctions characterising each category. Finally, we deliberate upon the contextual frameworks where system identifiability can be achieved, also highlighting the factors that impede structural, functional, and meta-identifiability.
1 Introduction
The identifiability of complex systems stands as a foundational challenge in the realm of scientific inquiry, spanning disciplines ranging from physics and biology, to engineering and economics [1–4]. In this context, identifiability refers to the ability to uniquely determine the parameters and characteristics of a system based on observed data. The concept holds paramount importance as it directly influences the precision and reliability of modelling and analysis efforts, ultimately shaping our understanding of the underlying mechanisms governing complex phenomena. Generally speaking, a real system is said to be identifiable when its parameters can be uniquely determined from observations of either its structure or its dynamics. Therefore, identifiability is strongly related with the concept of parameter identification, which consists on the estimation of a system’s parameters based on the observation of its dynamics [5]. Certainly, the three key factors constraining the ability to determine a system’s parameters are i) the complexity of the system’s dynamics, ii) the ability of recording, with enough resolution, all variables describing the dynamical state of a system and iii) the presence of noise in the observation [6]. In the field of nonlinear dynamical systems, the challenge lies in automatically uncovering the governing equations of complex systems [7]. Nonparametric methods that assume linearity or produce numerical models fail to reveal the full internal structure of these systems [7]. However, by perturbing and observing the system in intelligent ways, it is possible to uncover the function (s) governing the dynamics of the system and even the parameters that univocally determine this function [7]. An alternative methodology relies on the use of synchronisation phenomena as the proxy to adjust adaptive parameter estimation. Under this framework, the output signal of the observable system is used as an input of a receiver system whose parameters are modified to maximise synchronisation until the dynamics of the receiver matches the one of the driver [8]. More recently, the use of machine learning has been proposed as a successful tool to extract model parameters in spatiotemporal systems [9]. In this case, an unsupervised learning method (variational auto-encoders) is used to determine the relevant parameters of the system without requiring information of its partial differential equations.
However, when the system consists of a complex network connecting a diversity of dynamical units, identifiability goes beyond the estimation of the single unit parameters, and focuses on the quantification of the connections between the nodes of the network. Under this framework, one can further distinguish between i) structural (a priori) and ii) functional identifiabilities, the former being an intrinsic (objective) property of the system (i.e., its structure), while the latter depends on subjective criteria based on the observable data or the behaviour of the system [10].
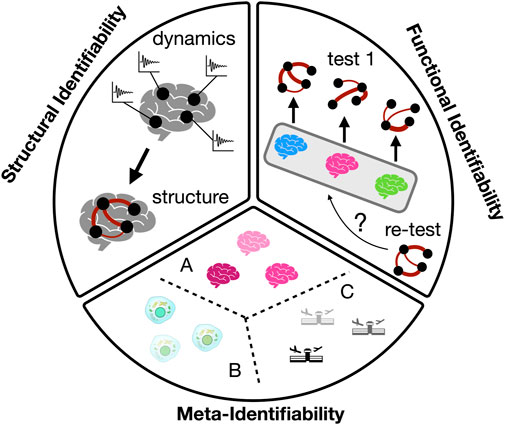
The analysis of if -and when-a complex network is identifiable is still an open problem in the statistical physics community, since complex networks present characteristics that make this analysis challenging. For example, their structure and dynamics manifest over multiple scales, with macro-scale dynamics emerging (in non trivial ways) from the micro-scale interactions. As a consequence, in order for a complex network to be structurally identifiable, we must recover the whole connectivity structure, i.e., its complete adjacency matrix. However, such reconstruction at the micro-scale level usually has to be performed without having access to its fully resolved dynamics and, frequently, macro-scale observables are the only sources of information. Despite these limitations, there is still space for complex networks to be identified when certain system requirements are fulfilled and, on top of that, under the presence of non-negligible levels of noise and complexity in the networks, or without having access to all variables of the system. The goal of this paper is to delve into the conceptual and methodological intricacies of identifiability in complex networks. We aim to provide a comprehensive survey of the theoretical underpinnings and practical challenges associated with identifying the structure of real networks from observed data. We begin defining three different types of identifiability -functional, structural and meta-identifiability (see Figure 1)- and continue discussing the interplay between the identifiability of complex networks and their underlying structures, seeking to shed light on the strategies and techniques employed to address this pervasive issue.
2 Structural identifiability
The first type of identifiability is related with the interplay between structure and dynamics. The structural identifiability of a complex network refers to the capacity of correctly recovering the existence (and weight) of all links connecting its nodes. In general terms, it implies the reconstruction of the network adjacency matrix, no matter if it is weighted or unweighted. The most extended approach is to recover the structural adjacency matrix from the functional adjacency matrix, the latter being extracted from evaluating the amount of coordination between nodes thanks to the analysis of their dynamics. Therefore, the most desirable situation would imply to have access to the dynamics of all variables describing the dynamical state of the nodes and, then, quantifying the level of coordination between each pair and assigning the probability of link existence accordingly. A diversity of methodologies have been proposed to infer the network structure from its dynamics. In [11], the author proposes a method based on response dynamics, where the response of a node to different perturbations is used to infer the connectivity patterns. The study demonstrates the effectiveness of this approach in inferring network connectivity in various types of networks, including random, scale-free, and modular ones. The method is shown to outperform traditional correlation-based approaches in certain scenarios. When a prior understanding of the functional form of the dynamical components and the coupling functions between them is at hand, it is also possible to reconstruct a network’s connection topology from the observation of the collective dynamical trajectories [12]. This approach eliminates the need for external interventions or driving forces, and it accommodates diverse types of dynamics with minimal constraints, with successful results when dynamics exhibit various characteristics, including complexity, stationarity, invariance, transience, synchronicity, asynchronicity, chaos, or periodicity. Statistical similarity analysis of time-series to infer the connectivity of coupled oscillators has also been tested as a way to recovery the structure of a network from the observation of its dynamics [13]. Introducing a Kuramoto oscillator into each node of a complex network and analysing the resulting synchronisation properties of the whole system allows, under certain conditions, to accurately infer the network links given an appropriate choice of the observed variables, the interaction strength, and thresholding of the similarity matrix [13]. Interestingly, the performance of linear statistical similarity measures can overcome, in many cases, the nonlinear ones [13]. Furthermore, it is also possible to determine the existence of unidirectional links in the network structure using statistical similarity measures, such as cross-correlation (CC) and mutual information (MI) [14].
It is worth noting that structural identifiability is a concept strongly connected to reproducibility [15, 16]. Supposing the underlying system’s structure does not change, one can only recover the same or similar networks if such reconstructions are accurate; reproducibility is thus a necessary condition for achieving structural identifiability. On the contrary, if the dynamics is not reproducible, the resulting reconstructed networks will not be the same and systems may not be identifiable. One can also adopt a more macroscale perspective, and assess the identifiability of topological metrics. This is especially relevant in the case of brain networks, for which it is accepted that individual links have a high degree of variability. The question then becomes whether the topology of the networks is identifiable; or, in other words, whether the values of the topological metrics from them extracted are constant, and do not depend on the individual measurement [17].
3 Functional identifiability
We can also identify systems without paying attention to their structural connectivity. Functional identifiability refers to the ability of distinguishing the “owner” of a functional network without necessarily recovering the underlying structure of connections. This would be the case, for example, of functional brain networks: if they were identifiable we would be able to know which person generated a given functional network just by analyzing its dynamics and without reconstructing the underlying anatomical connections. Importantly, to assess which system is behind a given functional network, we require previous observations of the functional network, which, in turn, should be univocally assigned to its underlying complex system—i.e., it has to be labelled. In other words, in the context of brain networks, we first need to know that a given functional network
• Classification identifiability [21], i.e., when the complex system behind a functional network can be associated with one or more predefined groups -or profiles-of functional networks.
• Recognition identifiability [21], i.e., when a unique functional network can be associated to each complex system belonging to the subset of functional networks being compared.
In this way, classification identifiability is responsible for the success in the classification of complex systems by means of the analysis of their corresponding functional networks. For example, functional brain networks are used to discriminate between healthy controls and patients suffering from a neurological condition thanks to the fact that the class of their functional networks is identifiable. Uncountable examples are available in the literature, as such identifiability is the basis of any diagnostic application [22–26]. Additionally, the capacity of discriminating between two sets of subjects has been used as a way of validating the usefulness of a given network representation [27]. Note that classification identifiability is equivalent to the classification tasks in machine learning [28], where the starting point is the network structure.
Under the same framework, recognition identifiability refers to the ability of detecting when a set of networks are describing the same object, being this an individual, if we are dealing with brain networks, or any other complex system in a more general context. It is thus one step beyond classification identifiability, since a unique label is assigned to each system or, in other words, where each group is composed of only one system. In the case of brain networks, this implies being able to discriminate one person from another by analysing their functional networks, and it is conceptually similar to the problem of identity assurance [29]. In recent years, it has been shown that such recognition identifiability can be achieved by observing characteristics of either the connectome [18, 30] or functional networks [31–34]. The same concept can also be applied to other contexts. To illustrate, one can assess the identifiability of football teams by analyzing the passing networks between their players, i.e., recognition identifiability can evaluate how unique the passing patterns of a given team are, and therefore how easy it is to differentiate the playing styles of one team from another one [35, 36]; identify account identities in crypto-currency transaction networks [37]; or identify users across multiple social networks [38].
4 Meta-identifiability
Finally, meta-identifiability refers to how unique a class of complex systems is with respect to other classes. Let us consider the scale-free network structure of some complex systems to illustrate the specificities of this kind of identifiability. It is well known that functional brain networks organise according to scale-free topologies [39–41]. Scale-freeness [42] is nevertheless not unique to the brain, but has instead been observed in a plethora of natural and man-made systems, from cells [43] to earthquakes [44] or air transportation networks [45]. Therefore, we can then conclude that brain networks are not identifiable (from other classes of complex networks) with regard to their scale-free organisation. From a practical perspective, if we observe a scale-free topology in a network of unknown origin, little to no information can be derived on the type of system it is describing. This also applies to other fundamental complex network concepts, as e.g., small-worldness or modularity [46].
The lack of meta-identifiability of complex systems may in principle be due to two causes. On one hand, it may be the unavoidable result of describing a system through -only- its observed macro-scale dynamics; its individuality may be lost in this coarse-graining. On the other hand, this may be the result of a bias, as the scientific community has hitherto considered more relevant to identify what are the universal properties of a system complex, than describing what makes a complex system different from its peers [47].
Why should the scientific community be interested in meta-identifiability? We here argue that such level of identifiability can be used to assess the relevance of a (macro-scale) representation of a complex system. Following the previous example, the human brain is unique in several aspects, as it is, e.g., the only intelligent and self-aware system we know. On the other hand, air transport is clearly neither intelligent nor self-aware. If we mix a group of brain networks with a group of air-transportation network and the resulting network representations are not meta-identifiable, they do not represent the uniqueness of each system, indicating that we are disregarding key aspects of the underlying complex systems such as, in this example, the level of intelligence and self-awareness. This is something well known when studying diseases and conditions: if a given brain network reconstruction yields the same brain networks for, e.g., a group of control subjects and a second group of Alzheimer’s patients, clearly such procedure is ill-design to describe the effects of the disease [27].
5 Discussion
We have seen that identifiability emerges as a fundamental precondition for sound scientific inquiry, raising questions about the uniqueness, stability, and robustness of parameter estimates in the face of inherent uncertainties and limitations in measurement. Structural identifiability of a complex system relies on the extraction of the structural pattern of connections of its individual components from the observation of the system dynamics and it is akin to classical parameter estimation. Importantly, structural identifiability can be defined for a single system without comparing it to other ones. On the contrary, functional and meta-identifiabilities imply having a subset of complex systems and comparing a single system (or a class of systems) to the rest. Consequently, identifiability becomes a pairwise or relative characteristic, contingent on both the specific complex system under consideration and its counterparts within the group. In essence, a complex system may be (functional and meta) identifiable when scrutinized within a designated subgroup of other complex systems, yet this identifiability might not persist within a different subgroup.
Given the context of group comparison, functional and meta-identifiabilities are intertwined with how differences are computed, akin to a classification task. This poses the question of which methodologies are most suitable for discerning disparities between functional networks and which network parameters encapsulate the distinct attributes of the underlying complex system. In addition, the underlying system may evolve with time at multiple time scales, as is the case of the human brain [48]; and may be further be represented through interactions boing beyond pair-wise ones, giving birth to multiplex [49], multilayer [50, 51] or higher-order networks [52–54]. At present, there is no solution that can universally be applied across diverse complex networks, and, to the best of our knowledge, the problem of the identifiability of higher-order networks has never been tackled. Each analysis must then systematically compare different approaches to identify the most effective discriminants between complex systems. With this regard, deep learning is expected to offer a valuable tool in determining optimal indicators tailored to each specific study. Concerning the value of N, i.e., the size of the group of systems to be identified, there are no studies analyzing the system size. Intuitively, one may think that the larger the value of N, the higher of the probability of finding similar systems in the group and, as a consequence, to reduce identifiability. However, the heterogeneity of the group seems to be more relevant than the system size, since the more heterogenous the group is, the more identifiable its units will be. Therefore, further analysis should focus on the interplay between the system size N and the heterogeneity of the group.
On the other hand, it is pertinent to note that both the diversity within the group of complex systems under comparison and the presence of noise play a pivotal role in determining identifiability [19]. While comparing functional networks within a group of complex systems, the need for divergent behaviour requires distinct patterns of functional connections. Hence, the degree of coordination among individual components assumes significance. As elucidated in (19), the ability to identify a complex system based on its functional networks is hindered when these networks are fundamentally random (due to minimal coordination) or excessively regular (due to high coordination). Intermediate levels of coordination between complex network units have demonstrated to enhance system identifiability, even in the face of moderate noise levels [19]. Notably, the intrinsic noisy perturbations inherent to real systems do not preclude identifiability, as evident in various contexts [19, 55].
Lastly, the interplay between the consistency of a complex system and its identifiability merits emphasis. Consistency quantifies a system’s ability to exhibit uniform behaviour under identical circumstances, irrespective of initial conditions. Evidently, a complex system displaying different functional networks for the same task could be characterised as non-identifiable. However, this issue introduces potential applications of functional and meta-identifiability. In cases where a complex system lacks consistency, could we raise the question of what are the features of its corresponding functional networks that change and what are being maintained? We believe that adaptations of the identifiability framework could be used to evaluate a system’s consistency level, facilitating the identification of essential conditions governing a system’s behaviour.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary material, further inquiries can be directed to the corresponding author.
Author contributions
MZ: Conceptualization, Writing–original draft, Writing–review and editing. JB: Conceptualization, Writing–original draft, Writing–review and editing.
Funding
The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This project has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement No. 851255). This work has been partially supported by the María de Maeztu project CEX2021-001164-M funded by the MCIN/AEI/10.13039/501100011033. JB is funded by Ministerio de Ciencia e Innovación (project PID2020-113737GB-I00).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Koopmans TC. Identification problems in economic model construction. Econometrica, J Econometric Soc (1949) 17:125–44. doi:10.2307/1905689
2. Bellman R, Åström KJ. On structural identifiability. Math biosciences (1970) 7:329–39. doi:10.1016/0025-5564(70)90132-x
3. Anstett-Collin F, Denis-Vidal L, Millérioux G. A priori identifiability: an overview on definitions and approaches. Annu Rev Control (2020) 50:139–49. doi:10.1016/j.arcontrol.2020.10.006
4. Wieland FG, Hauber AL, Rosenblatt M, Tönsing C, Timmer J. On structural and practical identifiability. Curr Opin Syst Biol (2021) 25:60–9. doi:10.1016/j.coisb.2021.03.005
5. Åström KJ, Eykhoff P. System identification - a survey. Automatica (1971) 7:123–62. doi:10.1016/0005-1098(71)90059-8
6. Voss HU, Timmer J, Kurths J. Nonlinear dynamical system identification from uncertain and indirect measurements. Int J Bifurcation Chaos (2004) 14:1905–33. doi:10.1142/s0218127404010345
7. Vapnik V. The nature of statistical learning theory. Berlin, Germany: Springer science & business media (1999).
8. Chen S, Lü J. Parameters identification and synchronization of chaotic systems based upon adaptive control. Phys Lett A (2002) 299:353–8. doi:10.1016/s0375-9601(02)00522-4
9. Lu PY, Kim S, Soljačić M. Extracting interpretable physical parameters from spatiotemporal systems using unsupervised learning. Phys Rev X (2020) 10:031056. doi:10.1103/physrevx.10.031056
10. Saccomani MP, Thomaseth K. Dynamics of mathematical models in biology. Berlin, Germany: Springer (2016). p. 31–41.Structural vs practical identifiability of nonlinear differential equation models in systems biology
11. Timme M. Revealing network connectivity from response dynamics. Phys Rev Lett (2007) 98:224101. doi:10.1103/physrevlett.98.224101
12. Shandilya SG, Timme M. Inferring network topology from complex dynamics. New J Phys (2011) 13:013004. doi:10.1088/1367-2630/13/1/013004
13. Tirabassi G, Sevilla-Escoboza R, Buldú JM, Masoller C. Inferring the connectivity of coupled oscillators from time-series statistical similarity analysis. Scientific Rep (2015) 5:10829. doi:10.1038/srep10829
14. Rubido N, Martí AC, Bianco-Martínez E, Grebogi C, Baptista MS, Masoller C. Exact detection of direct links in networks of interacting dynamical units. New J Phys (2014) 16:093010. doi:10.1088/1367-2630/16/9/093010
15. Deuker L, Bullmore ET, Smith M, Christensen S, Nathan PJ, Rockstroh B, et al. Reproducibility of graph metrics of human brain functional networks. Neuroimage (2009) 47:1460–8. doi:10.1016/j.neuroimage.2009.05.035
16. Telesford QK, Morgan AR, Hayasaka S, Simpson SL, Barret W, Kraft RA, et al. Reproducibility of graph metrics in fmri networks. Front neuroinformatics (2010) 4:117. doi:10.3389/fninf.2010.00117
17. Welton T, Kent DA, Auer DP, Dineen RA. Reproducibility of graph-theoretic brain network metrics: a systematic review. Brain connectivity (2015) 5:193–202. doi:10.1089/brain.2014.0313
18. Amico E, Goñi J. The quest for identifiability in human functional connectomes. Scientific Rep (2018) 8:8254–14. doi:10.1038/s41598-018-25089-1
19. Vera-Ávila V, Sevilla-Escoboza R, Goñi J, Rivera-Durón R, Buldú J. Identifiability of structural networks of nonlinear electronic oscillators. Scientific Rep (2020) 10:14668. doi:10.1038/s41598-020-71373-4
20. Uchida A, McAllister R, Roy R. Consistency of nonlinear system response to complex drive signals. Phys Rev Lett (2004) 93:244102. doi:10.1103/physrevlett.93.244102
22. Bassett DS, Bullmore ET. Human brain networks in health and disease. Curr Opin Neurol (2009) 22:340–7. doi:10.1097/wco.0b013e32832d93dd
23. Bullmore E, Sporns O. The economy of brain network organization. Nat Rev Neurosci (2012) 13:336–49. doi:10.1038/nrn3214
24. Stam CJ. Modern network science of neurological disorders. Nat Rev Neurosci (2014) 15:683–95. doi:10.1038/nrn3801
25. de Vico Fallani F, Richiardi J, Chavez M, Achard S. Graph analysis of functional brain networks: practical issues in translational neuroscience. Phil Trans R Soc B: Biol Sci (2014) 369:20130521. doi:10.1098/rstb.2013.0521
26. Fornito A, Zalesky A, Breakspear M. The connectomics of brain disorders. Nat Rev Neurosci (2015) 16:159–72. doi:10.1038/nrn3901
27. Zanin M, Sousa P, Papo D, Bajo R, García-Prieto J, Pozo F, et al. Optimizing functional network representation of multivariate time series. Scientific Rep (2012) 2:630–6. doi:10.1038/srep00630
28. Kotsiantis SB, Zaharakis I, Pintelas P. Supervised machine learning: a review of classification techniques In: I. G. Maglogiannis editors. Emerging Artificial Intelligence Applications in Computer Engineering. IOP Press (2007) 160:3–24.
29. Bertino E, Takahashi K. Identity management: concepts, technologies, and systems. New Jersey: Artech House (2010).
30. Tian Y, Yeo BT, Cropley V, Zalesky A. High-resolution connectomic fingerprints: mapping neural identity and behavior. NeuroImage (2021) 229:117695. doi:10.1016/j.neuroimage.2020.117695
31. Finn ES, Shen X, Scheinost D, Rosenberg MD, Huang J, Chun MM, et al. Functional connectome fingerprinting: identifying individuals using patterns of brain connectivity. Nat Neurosci (2015) 18:1664–71. doi:10.1038/nn.4135
32. Satterthwaite TD, Xia CH, Bassett DS. Personalized neuroscience: common and individual-specific features in functional brain networks. Neuron (2018) 98:243–5. doi:10.1016/j.neuron.2018.04.007
33. Horien C, Shen X, Scheinost D, Constable RT. The individual functional connectome is unique and stable over months to years. Neuroimage (2019) 189:676–87. doi:10.1016/j.neuroimage.2019.02.002
34. Van De Ville D, Farouj Y, Preti MG, Liégeois R, Amico E. When makes you unique: temporality of the human brain fingerprint. Sci Adv (2021) 7:eabj0751. doi:10.1126/sciadv.abj0751
35. Garrido D, Antequera D, Busquets J, López Del Campo R, Resta Serra R, Jos Vielcazat S, et al. Consistency and identifiability of football teams: a network science perspective. Scientific Rep (2020) 10:19735–10. doi:10.1038/s41598-020-76835-3
36. Gong B, Zhou C, Gómez MÁ, Buldú J. Identifiability of Chinese football teams: a complex networks approach. Chaos, Solitons & Fractals (2023) 166:112922. doi:10.1016/j.chaos.2022.112922
37. Wang Y, Liu Z, Xu J, Yan W. Heterogeneous network representation learning approach for ethereum identity identification. IEEE Trans Comput Soc Syst (2022) 10:890–9. doi:10.1109/tcss.2022.3164719
38. Zhou X, Liang X, Du X, Zhao J. Structure based user identification across social networks. IEEE Trans Knowledge Data Eng (2017) 30:1178–91. doi:10.1109/tkde.2017.2784430
39. Eguiluz VM, Chialvo DR, Cecchi GA, Baliki M, Apkarian AV. Scale-free brain functional networks. Phys Rev Lett (2005) 94:018102. doi:10.1103/physrevlett.94.018102
40. van den Heuvel MP, Stam CJ, Boersma M, Pol HH. Small-world and scale-free organization of voxel-based resting-state functional connectivity in the human brain. Neuroimage (2008) 43:528–39. doi:10.1016/j.neuroimage.2008.08.010
41. He BJ. Scale-free properties of the functional magnetic resonance imaging signal during rest and task. J Neurosci (2011) 31:13786–95. doi:10.1523/jneurosci.2111-11.2011
42. Barabási AL. Scale-free networks: a decade and beyond. science (2009) 325:412–3. doi:10.1126/science.1173299
43. Albert R. Scale-free networks in cell biology. J Cel Sci (2005) 118:4947–57. doi:10.1242/jcs.02714
44. Abe S, Suzuki N. Scale-free network of earthquakes. EPL (Europhysics Letters) (2004) 65:581–6. doi:10.1209/epl/i2003-10108-1
45. Guimera R, Mossa S, Turtschi A, Amaral LN. The worldwide air transportation network: anomalous centrality, community structure, and cities’ global roles. Proc Natl Acad Sci (2005) 102:7794–9. doi:10.1073/pnas.0407994102
46. Vértes PE, Nicol RM, Chapman SC, Watkins NW, Robertson DA, Bullmore ET. Topological isomorphisms of human brain and financial market networks. Front Syst Neurosci (2011) 5:75. doi:10.3389/fnsys.2011.00075
47. Achard S, Delon-Martin C, Vértes PE, Renard F, Schenck M, Schneider F, et al. Hubs of brain functional networks are radically reorganized in comatose patients. Proc Natl Acad Sci (2012) 109:20608–13. doi:10.1073/pnas.1208933109
48. Zalesky A, Fornito A, Cocchi L, Gollo LL, Breakspear M. Time-resolved resting-state brain networks. Proc Natl Acad Sci (2014) 111:10341–6. doi:10.1073/pnas.1400181111
49. Battiston F, Nicosia V, Latora V. Structural measures for multiplex networks. Phys Rev E (2014) 89:032804. doi:10.1103/physreve.89.032804
50. Kivelä M, Arenas A, Barthelemy M, Gleeson JP, Moreno Y, Porter MA. Multilayer networks. J complex networks (2014) 2:203–71. doi:10.1093/comnet/cnu016
51. Boccaletti S, Bianconi G, Criado R, Del Genio CI, Gómez-Gardenes J, Romance M, et al. The structure and dynamics of multilayer networks. Phys Rep (2014) 544:1–122. doi:10.1016/j.physrep.2014.07.001
52. Benson AR, Gleich DF, Leskovec J. Higher-order organization of complex networks. Science (2016) 353:163–6. doi:10.1126/science.aad9029
53. Battiston F, Cencetti G, Iacopini I, Latora V, Lucas M, Patania A, et al. Networks beyond pairwise interactions: structure and dynamics. Phys Rep (2020) 874:1–92. doi:10.1016/j.physrep.2020.05.004
54. Bick C, Gross E, Harrington HA, Schaub MT. What are higher-order networks? SIAM Rev (2023) 65:686–731. doi:10.1137/21m1414024
Keywords: identifiability, complex networks, network inference, parameter identification, network classification
Citation: Zanin M and Buldú JM (2023) Identifiability of complex networks. Front. Phys. 11:1290647. doi: 10.3389/fphy.2023.1290647
Received: 07 September 2023; Accepted: 20 October 2023;
Published: 03 November 2023.
Edited by:
Linlin Fei, ETH Zürich, SwitzerlandReviewed by:
Jonathan Crofts, Nottingham Trent University, United KingdomYuting Xu, Johns Hopkins University, United States
Copyright © 2023 Zanin and Buldú. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: M. Zanin, bWFzc2ltaWxpYW5vLnphbmluQGdtYWlsLmNvbQ==
 M. Zanin
M. Zanin J. M. Buldú
J. M. Buldú