A fermionic portal to a non-abelian dark sector

We introduce a new class of renormalizable models for dark matter with a minimal particle content, consisting of a dark SU(2)_D gauge sector connected to the standard model through a vector-like fermion mediator, not requiring a Higgs portal, in which a massive vector boson is the dark matter candidate. These models are labeled fermion portal vector dark matter (FPVDM). Multiple realizations are possible, depending on the properties of the vector-like partner and scalar potential. One example is discussed in detail. Fermion portal vector dark matter models have a large number of applications in collider and non-collider experiments, with their phenomenology depending on the mediator sector.

The nature of DM, whose existence has been established beyond any reasonable doubt by several independent cosmological observations, is one of the greatest puzzles of contemporary particle physics. Models with a vector DM, especially in the non-abelian case, are the least explored but well-motivated, as the gauge principle offers guidance and constraints limiting the possible theoretical constructions (see, e.g., [1–26], for a discussion of non-abelian DM in different setups, in particular using non-renormalizable kinetic mixing terms or Higgs portal scenarios). In this article, we develop a new minimal framework that extends the gauge sector of the standard model (SM) by a new non-abelian gauge group for which no renormalizable kinetic mixing terms are allowed¹ and under which all SM particles are singlets. The full model structure, Lagrangian, and particle content are presented in the following sections, along with the main results and immediate prospects for experimental testing, while more technical details can be found in [27].

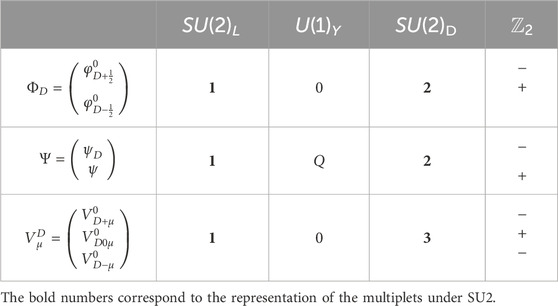
The simplest non-abelian group is SU(2), which in the following will be labeled SU(2)_D as it connects the SM to the dark sector. The gauge bosons associated with SU(2)_D are labeled as $V_{\mu }^D=\left(V_{D+\mu }^0{V}_{D0\mu }^0{V}_{D-\mu }^0\right)$, where, here and in the following, the electric charge is specified in the field superscripts, while the isospin under SU(2)_D (D-isospin) is specified in the field subscripts. The covariant derivative associated with SU(2)_D is

$D_{\mu }={\partial }_{\mu }-\left(i\frac{g_D}{\sqrt{2}}{V}_{D\pm \mu }^0{T}_D^{\pm }+i{g}_D{V}_{D0\mu }^0{T}_{3\text{D}}\right),(1)$

where g_D is the SU(2)_D coupling constant and T_3D is the D-isospin.

The fields responsible for breaking the gauge symmetries are two scalar doublets:

$\begin{array}{ccccccc}\hfill {\mathrm{\Phi }}_H\hfill & \hfill =\hfill & {\left({\varphi }^{+}{\varphi }^0\right)}^T\hfill & \hfill ⇝\hfill & \hfill \langle {\mathrm{\Phi }}_H\rangle \hfill & \hfill =\hfill & \frac{1}{\sqrt{2}}{\left(0v\right)}^T,\hfill \\ \hfill {\mathrm{\Phi }}_D\hfill & \hfill =\hfill & {\left({\phi }_{D+\frac{1}{2}}^0{\phi }_{D-\frac{1}{2}}^0\right)}^T\hfill & \hfill ⇝\hfill & \hfill \langle {\mathrm{\Phi }}_D\rangle \hfill & \hfill =\hfill & \frac{1}{\sqrt{2}}{\left(0v_D\right)}^T,\hfill \end{array}(2)$

where the first is breaking SU(2)_L × U(1)_Y, while the second is breaking SU(2)_D via their respective vacuum expectation values (VEVs) v and v_D.

The scalar potential for Φ_H and Φ_D reads

$\begin{array}{ll}\hfill V\left({\mathrm{\Phi }}_H,{\mathrm{\Phi }}_D\right)& =-{\mu }^2{\mathrm{\Phi }}_H^{†}{\mathrm{\Phi }}_H-{\mu }_D^2{\mathrm{\Phi }}_D^{†}{\mathrm{\Phi }}_D+\lambda {\left({\mathrm{\Phi }}_H^{†}{\mathrm{\Phi }}_H\right)}^2\hfill \\ \hfill & +{\lambda }_D{\left({\mathrm{\Phi }}_D^{†}{\mathrm{\Phi }}_D\right)}^2+{\lambda }_{{\mathrm{\Phi }}_H{\mathrm{\Phi }}_D}{\mathrm{\Phi }}_H^{†}{\mathrm{\Phi }}_H{\mathrm{\Phi }}_D^{†}{\mathrm{\Phi }}_D,\hfill \end{array}(3)$

which was introduced in [2] and ensures that the gauge bosons of SU(2)_D are degenerate and stable because of the custodial symmetry of the scalar Lagrangian. Although the operator ${\mathrm{\Phi }}_H^{†}{\mathrm{\Phi }}_H{\mathrm{\Phi }}_D^{†}{\mathrm{\Phi }}_D$ is not protected by any symmetry and cannot thus be removed from the potential, coupling ${\lambda }_{{\mathrm{\Phi }}_H{\mathrm{\Phi }}_D}$ can have any value. If it is small enough, the dark sector would be effectively decoupled from the SM and only observable through gravitational effects. Moreover, the Higgs portal induces scalar mixing, which modifies Higgs–SM couplings and generates Higgs–DM interactions, all of which are strongly constrained [28]. Here, we suggest a different mechanism of communication between the dark and visible sectors via a fermion doublet Ψ = (ψ_D ψ), vector-like (VL) under SU(2)_D, and both elements of which are singlets under SU(2)_L, sharing the same hypercharge as one of the SM right-handed fermions². The mass and Yukawa interaction terms of Ψ read

$-{\mathcal{L}}_f=M_{\mathrm{\Psi }}\bar{\mathrm{\Psi }}\mathrm{\Psi }+\left(y^{\prime }{\bar{\mathrm{\Psi }}}_L{\mathrm{\Phi }}_D{f}_R^{\text{SM}}+h.c\right),(4)$

where $f_R^{\text{SM}}$ generically denotes an SM right-handed singlet and y′ is a new Yukawa coupling connecting the SM fermion with ${\mathrm{\Psi }}_L=\frac{(1-{\gamma }_5)}{2}\mathrm{\Psi }$ through the Φ_D doublet. At this point, it would be possible to write an additional Yukawa term $y^{\prime \prime }{\bar{\mathrm{\Psi }}}_L{\mathrm{\Phi }}_D^c{f}_R^{\text{SM}}$, which would violate the stability of DM due to the simultaneous mixing of ψ_D and ψ with SM fermions and would induce a direct coupling $V_{D\pm }^0{\bar{f}}^{\text{SM}}{f}^{\text{SM}}$. The appearance of such y′′ term and the respective stability of DM can be avoided by imposing an unbroken continuous global symmetry $U{(1)}_D\equiv e^{i\mathrm{\Lambda }{Y}_D}$, unrelated to local SU(2)_D.

Without this symmetry, such a term would be compulsory since the scalar doublet, Φ_D, is in the pseudo-real representation. The symmetry-breaking pattern is $SU{(2)}_D\times U{(1)}_D\to U{(1)}_D^d$. With U(1)_D phase assignments $Y_D=\frac{1}{2}$ for dark doublets and Y_D = 0 for triplets, there is still an invariance under the subgroup ${\mathbb{Z}}_2\equiv {(-1)}^{Q_D}$, where $Q_D=T_D^3+Y_D$. The new particles are summarized in Table 1.

Table 1

Table 1. Quantum numbers of the new particles under the electro-weak (EW) and SU(2)_D gauge groups.

The lightest ${\mathbb{Z}}_2$-odd particle is stable and could be either $V_{D\pm }^0$ or ψ_D, with very different consequences from a cosmological point of view [27]. We consider the case where the lightest ${\mathbb{Z}}_2$-odd particle is $V_{D\pm }^0$, which we label fermion portal vector dark matter (FPVDM). The theory contains six massive gauge bosons (Z, W^±, $V_{D0}^0$, and $V_{D\pm }^0$), and therefore, six Goldstone bosons correspond to their longitudinal components. The remaining two degrees of freedom correspond to physical scalars, which include the SM Higgs boson and another CP-even scalar. By denoting the neutral scalars in terms of their components in the unitary gauge as ${\varphi }^0=\frac{1}{\sqrt{2}}(v+h_1)$ and ${\phi }_{D-1/2}^0=\frac{1}{\sqrt{2}}(v_D+{\phi }_1)$, the mass terms of the scalar Lagrangian reads

${\mathcal{L}}_m^{\mathcal{S}}=\left(h_1{\phi }_1\right)\left(\begin{array}{cc}\hfill \lambda v^2\hfill & \hfill \frac{{\lambda }_{{\mathrm{\Phi }}_H{\mathrm{\Phi }}_D}}{2}v{v}_D\hfill \\ \hfill \frac{{\lambda }_{{\mathrm{\Phi }}_H{\mathrm{\Phi }}_D}}{2}v{v}_D\hfill & \hfill {\lambda }_D{v}_D^2\hfill \end{array}\right)\left(\begin{array}{c}\hfill h_1\hfill \\ \hfill {\phi }_1\hfill \end{array}\right).(5)$

Upon diagonalization, the mass eigenvalues read

$m_{h,H}^2=\lambda v^2+{\lambda }_D{v}_D^2\mp \sqrt{{\left({\lambda }_D{v}_D^2-\lambda v^2\right)}^2+{\lambda }_{{\mathrm{\Phi }}_H{\mathrm{\Phi }}_D}^2{v}^2{v}_D^2},(6)$

with the mixing angle $\sin {\theta }_S=\sqrt{2\frac{m_H^2{v}^2\lambda -m_h^2{v}_D^2{\lambda }_D}{m_H^4-m_h^4}}$.

In the fermion sector, the component with T_3D = +1/2 gets only a VL mass; therefore, $m_{{\psi }_D}=M_{\mathrm{\Psi }}$. However, the other fermion masses are generated after both scalars acquire a VEV. The fermionic mass Lagrangian reads

${\mathcal{L}}_m^f=\left({\bar{f}}_L^{\text{SM}}{\bar{\psi }}_L\right)\left(\begin{array}{cc}\hfill y\frac{v}{\sqrt{2}}\hfill & \hfill 0\hfill \\ \hfill y^{\prime }\frac{v_D}{\sqrt{2}}\hfill & \hfill M_{\mathrm{\Psi }}\hfill \end{array}\right)\left(\begin{array}{c}\hfill f_R^{\text{SM}}\hfill \\ \hfill {\psi }_R\hfill \end{array}\right).(7)$

The mass eigenvalues are

$m_{f,F}^2=\frac{1}{4}\left[\mathrm{\Delta }\mp \sqrt{{\mathrm{\Delta }}^2-8y^2{v}^2{M}_{\mathrm{\Psi }}^2}\right],(8)$

where $\mathrm{\Delta }=y^2{v}^2+y^{\prime 2}{v}_D^2+2M_{\mathrm{\Psi }}^2$, f identifies the SM fermion, and F identifies its heavier partner. The mass hierarchy is $m_f<m_{{\psi }_D}\le m_F$.

The Yukawa couplings and mixings can be expressed in terms of the masses of the physical fermions. The new fermion sector is completely decoupled in the limit $m_F=m_{{\psi }_D}$, for which y = y_SM and y′ = 0. When the full flavor structure of the SM is taken into consideration, different possibilities can be considered. A VL fermion can interact with one or more SM flavors, and there can be multiple VL fermions. The Cabibbo–Kobayashi–Maskawa (CKM) matrix of the SM might also receive contributions from new physics induced by the mixing of SM and VL quarks.

The masses of the SM gauge bosons are not altered by the presence of Φ_D. The gauge bosons of SU(2)_D are all degenerate in mass at the tree level: $m_{V_D}\equiv m_{V_{D\pm }^0}=m_{V_{D0}^0}=\frac{g_D}{2}{v}_D$. This degeneracy is broken by kinetic mixing in the broken EW and dark gauge symmetry phases and by the different fermionic loop corrections associated with the opposite ${\mathbb{Z}}_2$ parities of the SU(2)_D gauge bosons. Such different contributions might also affect loop corrections to Z and W masses, addressing the CDF anomaly [32]. In the following, to simplify notation, we will label $V_D\equiv V_{D\pm }^0$, with mass $m_{V_D}$, and $V^{\prime }\equiv V_{D0}^0$, with mass m_V′. The leading contribution to the radiative mass split of V′ and V_D bosons, $\mathrm{\Delta }{m}_V=m_{V_D}-m_{V^{\prime }}$, is determined by F and ψ_D loops and reads

$\mathrm{\Delta }{m}_V=\frac{{ϵ}^2{g}_D^2{m}_F^2}{32{\pi }^2{m}_{V_D}}+o\left({ϵ}^2\right),\text{\hspace{0.17em}\hspace{0.17em}where\hspace{0.17em}\hspace{0.17em}}ϵ=\frac{m_F^2-m_{{\psi }_D}^2}{m_F^2}.(9)$

In the following, we assume that new VL fermions interact only with one flavor of the SM. Six independent input parameters are thus necessary to describe the new physics sector of the model, namely, g_D, $m_{V_D}$, m_H, sin θ_S, m_F, and $m_{{\psi }_D}$.

Let us now discuss a specific realization of the model, assuming only one VL partner interacting exclusively with the SM top quark and no mixing between h and H, i.e., θ_S = 0. This choice significantly simplifies the Lagrangian: the Higgs sector of the SM is not affected by the new physics at the tree level, and the potential of Φ_D has the very same structure as the Higgs potential. A mixing between h and H is induced only by fermionic loops and will be neglected in the following. Therefore, in this case, the model is described by the following five parameters: g_D, $m_{V_D}$, m_H, m_F = m_T, and $m_{{\psi }_D}=m_{t_D}$.

The hierarchy between the masses in the fermion sector is $m_t<m_{t_D}\le m_T$, while H can have any mass allowed by experimental bounds, even being lighter than the SM Higgs boson.

In our study, we tested this realization of the model against multiple observables from cosmology, DM direct, and indirect detection (DD and ID) experiments and LHC searches. For this purpose, the Lagrangian has been implemented in LanHEP [33] and FeynRules [34], while model files have been generated in CalcHEP [35], UFO [36], as well as FeynArts [37] formats and are available on the HEPMDB [38]. This implementation has been used in micrOMEGAs v5.2.7 [39] for the evaluation of various DM observables and for extracting the respective limits. The model implementation in UFO format has been used in MG5_aMC [40] for the determination of the LHC constraints. Collider simulations have been performed at LO using the NNPDF3.0 LO set [41] through the LHAPDF6 library [42] (LHA index 262400). A simplified version of the model has been implemented to calculate cross-sections at one loop in MG5_aMC and FormCalc9.8 [43].

The amount of relic density is determined by the interplay of annihilation and co-annihilation processes, a subset of which is shown in Figure 1A. ID constraints are associated with DM annihilation rates at CMB time, excluding regions of parameter space where the injection into SM-plasma in the early universe is too large to be consistent with CMB data. Both the relic density and ID processes are tested against PLANCK data [44]. DD processes arise from diagrams such as those shown in Figure 1B and are tested against limits from XENON 1T [45].

Figure 1

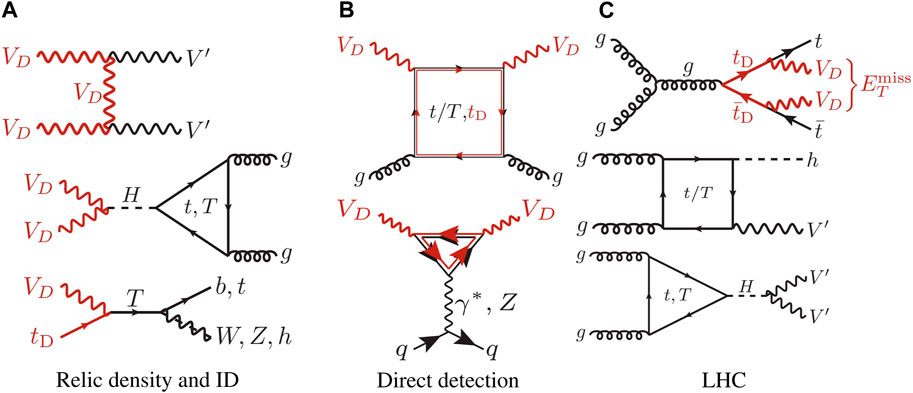
Figure 1. Representative diagrams for (A) t-channel and resonant contributions to DM annihilation and DM-mediator co-annihilation processes; (B) DD processes; (C) production processes at the LHC: $t\bar{t}$ + $E_T^{\text{miss}}$, hV′, and V′V′.

The LHC bound has been obtained via testing of t_D pair production with subsequent decay into V_D and top quarks against CMS searches for top squark pair production decaying into DM [46]. The relevant limit from $T\bar{T}$ of even partners of the SM top quark from the respective ATLAS and CMS searches is approximately 1.5 TeV for m_T [47, 48]. Single T production is less constrained, as it is driven by the small T − t mixing.

We also estimated the relevance of V′ pair production and associate production of V′ with the Higgs boson, occurring at LO via fermion loops. Representative topologies for the tested processes are shown in Figure 1C.

The complementarity of cosmological and collider constraints has been studied by performing a comprehensive scan over the parameter space (excluding the fixed parameter sin θ_S = 0) projected onto the $(g_D,m_{V_D})$ plane, as shown in Figure 2. The allowed parameter space is indicated by the green, cyan, and blue regions, presenting generic DM annihilation, dominated by the t-channel diagram of Figure 1A, resonance (H) and DM-t_D co-annihilation regions, respectively, which satisfy the relic density constraint from PLANCK within 5%. The allowed regions of the parameter space are superimposed on top of the forbidden ones to provide their best visualization in this projection of the five-dimensional scan into the two-dimensional plane.

Figure 2

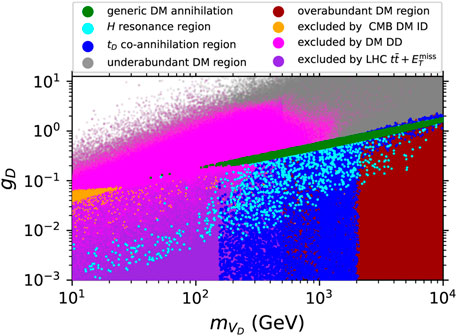
Figure 2. Excluded and allowed region of the parameter space of the model from the full five-dimensional scan (sin θ_S = 0) of the parameter space projected into a $(g_D,m_{V_D})$ plane. White areas represent non-perturbative regions.

The generic DM annihilation determines a lower limit on g_D as a function of $m_{V_D}$. At the same time, the H-resonant region allows for the reduction of g_D values by up to two orders of magnitude, while the strong DM-t_D co-annihilation channel allows for even lower values of g_D for not-so-heavy DM. For $m_{V_D}$ above 2 TeV, however, the co-annihilation mechanism saturates, while H-resonant annihilation requires larger g_D coupling for higher DM mass to provide the right amount of relic density. Therefore, the region with $m_{V_D}\gtrsim 1$ TeV has an over-abundant relic density, as indicated by the dark red color, except the space with large values of g_D couplings, corresponding to the bulk V_DV_D → V′V′ annihilation and H-resonant annihilation presented in Figure 2 by green and light-blue colors, respectively. Notice also that the regions with $m_{V_D}\lesssim 1$ TeV values are partly excluded by DD and/or ID experiments, as indicated by magenta and orange points, respectively. The region of DM masses that can be tested and excluded by the LHC is $m_{V_D}\lesssim 400\mathrm{G}\mathrm{e}\mathrm{V}$, represented by the violet region.

To assess the relative role of the different constraints, we identify representative benchmarks characterized by different gauge couplings, g_D = 0.05 and g_D = 0.5, and fixed values for the masses, m_T = 1,600 GeV and m_H = 1,000 GeV. For these points, gauge coupling is small enough to allow a perturbative treatment in a region of parameter space, which can be tested by both collider and cosmological observables.

We show in Figure 3 the exclusion regions in the $\{m_{t_D},m_{V_D}\}$ and $\{m_{t_D},1-m_{V_D}/m_{t_D}\}$ planes to highlight the low $m_{V_D}$ or low $m_{t_D}-m_{V_D}$ regions, respectively. The masses of the DM candidate V_D and mediator t_D are left as free parameters.

Figure 3

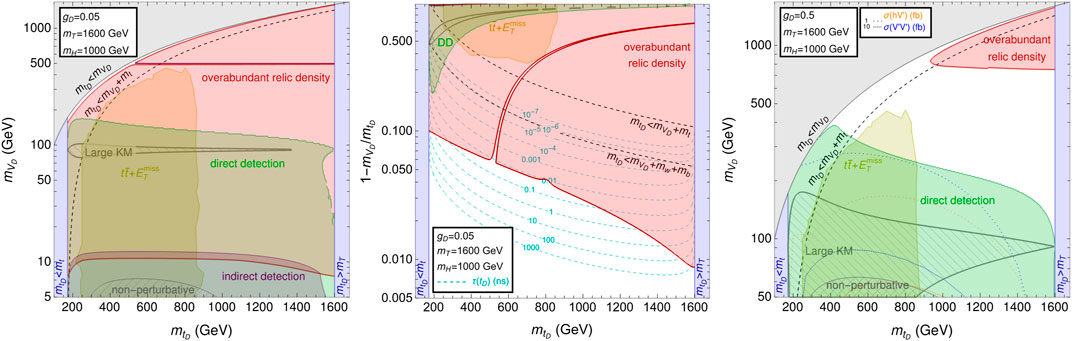
Figure 3. Combination of constraints from LHC, relic density, DD, and ID for the benchmark points in the $\{m_{t_D},m_{V_D}\}$ (left and right panels) and $\{m_{t_D},1-m_{V_D}/m_{t_D}\}$ (center panel) planes. The colored regions are excluded. For relic density, the under-abundant region is considered allowed and the borders of the excluded region correspond to the measured relic density value. The non-perturbative region corresponds to one-loop corrections to gauge boson masses larger than 50%. An estimate of the region of large kinetic mixing is shown as a hatched area. Contours corresponding to different t_D lifetimes are shown for the small mass splitting region. Cross-sections for collider processes that are at one-loop at LO are shown as orange and blue contours.

The predicted relic density is consistent with PLANCK results only in specific regions: for g_D = 0.05 (left and central panels of Figure 3), most of the parameter space predicts an over-abundant relic density, except for an area where the mass difference between t_D and DM is less than $\sim 10\%$ of the mediator mass (where t_D-t_D and DM-t_D co-annihilation processes dominate), a small area around $m_{V_D}=m_H/2$ (DM annihilation via resonant H), and $m_{V_D}\lesssim 10\mathrm{G}\mathrm{e}\mathrm{V}$. For larger values of g_D (right panel of Figure 3), annihilation processes become more effective, reducing the size of the excluded area in the lower $m_{V_D}$ region and eventually extending the under-abundant relic density region. The enhancement of the V_DV_D → V′V′ process, due to Δm_V > 0, affects the relic density and ID signals. The complementarity of various constraints is especially evident for small values of g_D in the low $m_{V_D}$ region. The region excluded by ID corresponds to small values of $m_{V_D}$ for g_D = 0.05, largely overlapping with the region excluded by relic density, and rapidly vanishes as g_D increases. The large region excluded by DD is mainly determined by processes (see Figure 1B) with sizable kinetic mixing or DM multipole moment contributions, taking place in the regions with low $m_{V_D}$ values (i.e., below few hundreds GeV).

The LHC bound is almost independent of the mass of t_D until its mass difference with the DM reaches the top-quark threshold: in that region, $E_T^{\text{miss}}$ decreases and the sensitivity of the CMS search reduces, allowing a small mass-gap region. As the process is QCD-initiated, the bound is also almost independent of other parameters of the model. Processes of V′ pair production and associated production of V′ with the Higgs boson would only be potentially testable in a region already excluded by DD constraints (see orange and blue contours in the right panel of Figure 3). The model has an important feature, especially for small values of g_D in the small DM-t_D mass-gap region where the correct relic density is reproduced. In this region, t_D is long-lived (its lifetime in the small mass-gap region is shown in the central panel, Figure 3³) and can be probed by dedicated searches at the LHC or future colliders. Different T or H masses would not modify this qualitative picture.

The FPVDM scenario introduced in this paper connects a vectorial DM candidate from a non-abelian SU(2)_D gauge group to the fermionic sector of the SM without the necessity of a Higgs portal at the tree level, and the mechanism is realized in the most economical way, with a minimal set of new parameters and new particles. Even the simplest realization of FPVDM, involving interactions of the dark sector with only one SM fermion, has great potential to explain DM phenomena and has several important implications for collider and non-collider DM searches. Minimal FPVDM realizations involving other SM fermions can be used to explain outstandingly observed anomalies. For example, if the VL fermion interacts with the leptonic sector of the SM, new contributions might explain (g − 2)_μ [49] and, at the same time, provide novel physics cases for future e⁺e⁻ colliders [50–53]. Non-minimal realizations, including mixing in the scalar sector, further VL partners, or additional interactions of the same VL representation, would open up a vast range of possibilities for future studies, both phenomenological and experimental, and would allow one to explore the complementarity between collider and non-collider observables in multiple scenarios.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

AB: writing–original draft and investigation. LP: writing–original draft and investigation. AD: writing–original draft and investigation. SM: writing–original draft and investigation. DR: writing–original draft and investigation. NT: investigation and writing–original draft.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. AB and SM acknowledge support from the STFC Consolidated Grant ST/L000296/1 and are partially financed through the NExT Institute. AB also acknowledges support from Soton-FAPESP and Leverhulme Trust RPG-2022-057 grants. LP’s work is supported by the Knut and Alice Wallenberg Foundation under the SHIFT project (grant KAW 2017.0100). AD is grateful to the LABEX Lyon Institute of Origins (ANR-10-LABX-0066) for its financial support within the program “Investissements d’Avenir”. AD acknowledges partial support from the National Research Foundation in South Africa. NT is supported by the scholarship from the Development and Promotion of Science and Technology Talents Project (DPST).

Acknowledgments

All authors acknowledge the use of the IRIDIS High-Performance Computing Facility and associated support services at the University of Southampton in completing this work.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Footnotes

¹Contributions to gauge kinetic mixing may arise at the loop level, depending on the structure of the Higgs sector, but they correspond to suppressed higher operator terms.

²VL portals have also been explored in [29, 30], but for scalar DM candidates, and in [26, 31] for vector dark matter, but with either the simplifying assumptions of setting the new Yukawa coupling to zero [31] or with a much larger, hence non-minimal, particle content [26].

³t_D decay can only occur through the t_D → V_Dt⁽*⁾ process, as it is ${\mathbb{Z}}_2$-odd. The decays of V′ and H can be into different final states if kinematically allowed: $V^{\prime }\to t\bar{t}/ZZ/WW$ and $H\to t_D{\bar{t}}_D/t\bar{t}/T\bar{T}/V^{\prime }V/V_D{V}_D$.

References

1. (2012). A Multi-TeV Linear Collider Based on CLIC Technology: CLIC Conceptual Design Report, SLAC-R-985, SLAC National Accelerator Lab, Menlo Park, CA, United States, doi:10.5170/CERN-2012-007

CrossRef Full Text | Google Scholar

2. Aaltonen T., et al. High-precision measurement of the W boson mass with the CDF II detector. Science (2022) 376:170–176. doi:10.1126/science.abk1781

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Abada A., et al. FCC-ee: the lepton collider: future circular collider conceptual design report volume 2. Eur. Phys. J. ST (2019) 228:261–623. doi:10.1140/epjst/e2019-900045-4

CrossRef Full Text | Google Scholar

4. Abe T., Fujiwara M., Hisano J., Matsushita K., A model of electroweakly interacting non-abelian vector dark matter. JHEP (2020) 07:136. doi:10.1007/JHEP07(2020)136

CrossRef Full Text | Google Scholar

5. Abi B., et al. Measurement of the positive muon anomalous magnetic moment to 0.46 ppm. Phys. Rev. Lett. (2021) 126:141801. doi:10.1103/PhysRevLett.126.141801

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Aghanim N., et al. Planck 2018 results. VI. cosmological parameters. Astron. Astrophys. (2020) 641:A6. doi:10.1051/0004-6361/201833910

CrossRef Full Text | Google Scholar

7. Alloul A., Christensen N. D., Degrande C., Duhr C., Fuks B., FeynRules 2.0 - A complete toolbox for tree-level phenomenology. Comput. Phys. Commun. (2014) 185:2250–2300. doi:10.1016/j.cpc.2014.04.012

CrossRef Full Text | Google Scholar

8. Alwall J., Frederix R., Frixione S., Hirschi V., Maltoni F., Mattelaer O., et al. The automated computation of tree-level and next-to-leading order differential cross sections, and their matching to parton shower simulations. JHEP (2014) 07:079. doi:10.1007/JHEP07(2014)079

CrossRef Full Text | Google Scholar

9. An F., et al. Precision higgs physics at the CEPC. Chin. Phys. C (2019) 43:043002. doi:10.1088/1674-1137/43/4/043002

CrossRef Full Text | Google Scholar

10. Aprile E., et al. Dark matter search results from a one ton-year exposure of XENON1T. Phys. Rev. Lett. (2018) 121:111302. doi:10.1103/PhysRevLett.121.111302

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Arcadi G., Djouadi A., Kado M., The Higgs-portal for vector dark matter and the effective field theory approach: A reappraisal. Phys. Lett. B (2020) 805:135427. doi:10.1016/j.physletb.2020.135427

CrossRef Full Text | Google Scholar

12. ATLAS Collaboration. Search for pair-production of vector-like quarks in pp collision events at $\sqrt{s}=13$˜TeV with at least one leptonically-decaying Z˜boson and a third-generation quark with the ATLAS detector (2021). https://arxiv.org/abs/2210.15413.

Google Scholar

13. Babu K. S., Jana S., Thapa A., Vector boson dark matter from trinification. JHEP (2022) 02:051. doi:10.1007/JHEP02(2022)051

CrossRef Full Text | Google Scholar

14. Baek S., Ko P., Park W.-I., Senaha E., Higgs portal vector dark matter : revisited. JHEP (2013) 05:036. doi:10.1007/JHEP05(2013)036

CrossRef Full Text | Google Scholar

15. Baek S., Ko P., Wu P., Heavy quark-philic scalar dark matter with a vector-like fermion portal. JCAP (2018) 07:008. doi:10.1088/1475-7516/2018/07/008

CrossRef Full Text | Google Scholar

16. Baer H., et al. The international linear collider technical design report - volume 2: physics (2013). https://arxiv.org/abs/1306.6352.

Google Scholar

17. Ball R. D., et al. Parton distributions for the LHC Run II. JHEP 04 (2015) 040. doi:10.1007/JHEP04(2015)040

CrossRef Full Text | Google Scholar

18. Baouche N., Ahriche A., Faisel G., Nasri S., Phenomenology of the hidden SU(2) vector dark matter model. Phys. Rev. D (2021) 104:075022. doi:10.1103/PhysRevD.104.075022

CrossRef Full Text | Google Scholar

19. Barman B., Bhattacharya S., Patra S. K., Chakrabortty J., Non-abelian vector boson dark matter, its unified route and signatures at the LHC. JCAP (2017) 12:021. doi:10.1088/1475-7516/2017/12/021

CrossRef Full Text | Google Scholar

20. Barman B., Bhattacharya S., Zakeri M., Multipartite dark matter in SU(2)_N extension of Standard Model and signatures at the LHC. JCAP (2018) 09:023. doi:10.1088/1475-7516/2018/09/023

CrossRef Full Text | Google Scholar

21. Barman B., Bhattacharya S., Zakeri M., Non-abelian vector boson as fimp dark matter. JCAP (2020) 02:029. doi:10.1088/1475-7516/2020/02/029

CrossRef Full Text | Google Scholar

22. Belanger G., Mjallal A., Pukhov A., Recasting direct detection limits within micrOMEGAs and implication for non-standard Dark Matter scenarios. Eur. Phys. J. C (2021) 81:239. doi:10.1140/epjc/s10052-021-09012-z

CrossRef Full Text | Google Scholar

23. Belyaev A., Christensen N. D., Pukhov A., CalcHEP 3.4 for collider physics within and beyond the Standard Model. Comput. Phys. Commun. (2013) 184:1729–1769. doi:10.1016/j.cpc.2013.01.014

CrossRef Full Text | Google Scholar

24. Belyaev A., Deandrea A., Moretti S., Panizzi L., Thongyoi N., A fermionic portal to vector dark matter from a new gauge sector. Phys. Rev. D (2022) 108.

Google Scholar

25. Bhattacharya S., Diaz-Cruz J., Ma E., Wegman D., Dark vector-gauge-boson model. Phys. Rev. D (2012) 85:055008. doi:10.1103/PhysRevD.85.055008

CrossRef Full Text | Google Scholar

26. Bondarenko M., Belyaev A., Blandford J., Basso L., Boos E., Bunichev V., et al. High Energy Physics Model Database: Towards decoding of the underlying theory (within Les Houches 2011: Physics at TeV Colliders New Physics Working Group Report) (2012). https://hepmdb.soton.ac.uk/index.php?mod=user&act=reference.

Google Scholar

27. Buckley A., Ferrando J., Lloyd S., Nordström K., Page B., Rüfenacht M., et al. LHAPDF6: parton density access in the LHC precision era. Eur. Phys. J. C (2015) 75:132. doi:10.1140/epjc/s10052-015-3318-8

CrossRef Full Text | Google Scholar

28. Buttazzo D., Di Luzio L., Ghorbani P., Gross C., Landini G., Strumia A., et al. Scalar gauge dynamics and Dark Matter. JHEP (2020) 01:130. doi:10.1007/JHEP01(2020)130

CrossRef Full Text | Google Scholar

29. Chen F., Cline J. M., Frey A. R., Nonabelian dark matter: Models and constraints. Phys. Rev. D (2009) 80:083516. doi:10.1103/PhysRevD.80.083516

CrossRef Full Text | Google Scholar

30. Chowdhury T. A., Saad S., Non-Abelian vector dark matter and lepton g-2. JCAP (2021) 10:014. doi:10.1088/1475-7516/2021/10/014

CrossRef Full Text | Google Scholar

31. CMS. Search for pair production of vector-like quarks in leptonic final states in proton-proton collisions at $\sqrt{s}$ = 13 TeV (2022). https://arxiv.org/abs/2209.07327.

Google Scholar

32. Colucci S., Fuks B., Giacchino F., Lopez Honorez L., Tytgat M. H. G., Vandecasteele J., Top-philic Vector-Like Portal to Scalar Dark Matter. Phys. Rev. D (2018) 98:035002. doi:10.1103/PhysRevD.98.035002

CrossRef Full Text | Google Scholar

33. Degrande C., Duhr C., Fuks B., Grellscheid D., Mattelaer O., Reiter T., UFO - the universal feynrules output. Comput. Phys. Commun. (2012) 183:1201–1214. doi:10.1016/j.cpc.2012.01.022

CrossRef Full Text | Google Scholar

34. Diaz-Cruz J., Ma E., Neutral SU(2) Gauge Extension of the Standard Model and a Vector-Boson Dark-Matter Candidate. Phys. Lett. B (2011) 695:264–267. doi:10.1016/j.physletb.2010.11.039

CrossRef Full Text | Google Scholar

35. DiFranzo A., Fox P. J., Tait T. M. P., Vector dark matter through a radiative higgs portal. JHEP (2016) 04:135. doi:10.1007/JHEP04(2016)135

CrossRef Full Text | Google Scholar

36. Farzan Y., Akbarieh A. R., VDM: a model for vector dark matter. JCAP (2012) 10:026. doi:10.1088/1475-7516/2012/10/026

CrossRef Full Text | Google Scholar

37. Fraser S., Ma E., Zakeri M., SU(2)_N model of vector dark matter with a leptonic connection. Int. J. Mod. Phys. A (2015) 30:1550018. doi:10.1142/S0217751X15500189

CrossRef Full Text | Google Scholar

38. Gross C., Karamitsos S., Landini G., Strumia A., Gravitational vector dark matter. JHEP (2021) 03:174. doi:10.1007/JHEP03(2021)174

CrossRef Full Text | Google Scholar

39. Gross C., Lebedev O., Mambrini Y., Non-abelian gauge fields as dark matter. JHEP (2015) 08:158. doi:10.1007/JHEP08(2015)158

CrossRef Full Text | Google Scholar

40. Hahn T., Generating feynman diagrams and amplitudes with FeynArts 3. Comput. Phys. Commun. (2001) 140:418–431. doi:10.1016/S0010-4655(01)00290-9

CrossRef Full Text | Google Scholar

41. Hahn T., Paßehr S., Schappacher C., FormCalc 9 and extensions. PoS LL2016 (2016) 068. doi:10.1088/1742-6596/762/1/012065

CrossRef Full Text | Google Scholar

42. Hambye T., Hidden vector dark matter. JHEP (2009) 01:028. doi:10.1088/1126-6708/2009/01/028

CrossRef Full Text | Google Scholar

43. Hisano J., Ibarra A., Nagai R., Direct detection of vector dark matter through electromagnetic multipoles. JCAP (2020) 10:015. doi:10.1088/1475-7516/2020/10/015

CrossRef Full Text | Google Scholar

44. Hu Z., Cai C., Tang Y.-L., Yu Z.-H., Zhang H.-H., Vector dark matter from split SU(2) gauge bosons. JHEP (2021) 07:089. doi:10.1007/JHEP07(2021)089

CrossRef Full Text | Google Scholar

45. Huang W.-C., Ishida H., Lu C.-T., Tsai Y.-L. S., Yuan T.-C., Signals of new gauge bosons in gauged two higgs doublet model. Eur. Phys. J. C (2018) 78:613. doi:10.1140/epjc/s10052-018-6067-7

CrossRef Full Text | Google Scholar

46. Huang W.-C., Tsai Y.-L. S., Yuan T.-C., G2HDM : gauged two higgs doublet model. JHEP (2016) 04:019. doi:10.1007/JHEP04(2016)019

CrossRef Full Text | Google Scholar

47. Hubisz J., Meade P., Phenomenology of the littlest Higgs with T-parity. Phys. Rev. D (2005) 71:035016. doi:10.1103/PhysRevD.71.035016

CrossRef Full Text | Google Scholar

48. Ko P., Park W.-I., Tang Y., Higgs portal vector dark matter for GeV scale γ-ray excess from galactic center. JCAP (2014) 09:013. doi:10.1088/1475-7516/2014/09/013

CrossRef Full Text | Google Scholar

49. Ko P., Tang Y., Residual non-abelian dark matter and dark radiation. Phys. Lett. B (2017) 768:12–17. doi:10.1016/j.physletb.2017.02.033

CrossRef Full Text | Google Scholar

50. Koorambas E., Vector gauge boson dark matter for the SU(N) gauge group model. Int. J. Theor. Phys. (2013) 52:4374–4388. doi:10.1007/s10773-013-1756-3

CrossRef Full Text | Google Scholar

51. Lebedev O., Lee H. M., Mambrini Y., Vector higgs-portal dark matter and the invisible Higgs. Phys. Lett. B (2012) 707:570–576. doi:10.1016/j.physletb.2012.01.029

CrossRef Full Text | Google Scholar

52. Semenov A., Lanhep—a package for the automatic generation of feynman rules in field theory. version 3.0. Computer Physics Communications (2009) 180:431–454. doi:10.1016/j.cpc.2008.10.012

CrossRef Full Text | Google Scholar

53. Sirunyan A. M., et al. Search for top squarks and dark matter particles in opposite-charge dilepton final states at $\sqrt{s}=$ 13 TeV. Phys. Rev. D (2018) 97:032009. doi:10.1103/PhysRevD.97.032009

CrossRef Full Text | Google Scholar