- 1Faculty of Physics, University of Warsaw, Warsaw, Poland
- 2Systems Research Institute, Polish Academy of Sciences, Warsaw, Poland
- 3Center for Theoretical Physics, Polish Academy of Sciences, Warsaw, Poland
We analyze the results of the test of π/2 qubit rotations on a public quantum computer provided by IBM. We measure a single qubit rotated by π/2 about a random axis, and we accumulate vast statistics of the results. The test performed on different devices shows systematic deviations from the theoretical predictions, which appear at level 10–3. Some of the differences, beyond 5 standard deviations, cannot be explained by simple corrections due to nonlinearities of pulse generations. The magnitude of the deviation is comparable with the randomized benchmarking of the gate, but we additionally observe a pronounced parametric dependence. We discuss other possible reasons for the deviations, including states beyond the single-qubit space. The deviations have a similar structure for various devices used at different times, so they can also serve as a diagnostic tool to eliminate imperfect gate implementations and a faithful description of the involved physical systems.
1 Introduction
Recent progress in the operation of quantum devices offered by IBM enables many researchers to perform quantum computations in a realistic setup [1–6]. The fragility of the operating devices, user-defined actions, and readouts deserve constant diagnostic checks. The paradigm for operating these systems relies on the quantum description of a few-level Hilbert space and the unitary evolution controlled by a programmed sequence of gates. The devices and operations are not perfect in reality: the deviations come from the decoherence, environment noise, inaccuracy of the gate parameters, and presence of additional states. To diagnose the realistic implementation of the ideal model, one can perform various control tests, including gate set tomography [7, 8], where the outcome statistics reveal the nature of such deviations, their possible sources, and hints for countermeasures [9].
In this paper, we propose to perform a simple experiment as a diagnostic test of the reliability of the rotation of single-qubit quantum gates. Quantum computers usually offer a limited set of basic operations (gate), but they can be controlled by a continuous parameter, the rotation angle. It means that the interlevel transition amplitudes are multiplied by e±iθ, with θ being a control angle. In short, the test compares the outcome probability of the qubit in a specific state with the standard cos2θ, with θ being the phase shift of a given gate. Deviations from the fit to the combination of 1, cos, and sin beyond the statistical error mean corrupt rotation. Taking a list of angles, shuffled randomly, and repeating the test sufficiently many times, one can reveal potential deviations. There exist other testing approaches based on the state dimension [10]. The specifics of our test are minimalistic circuit complexity, a single control parameter (angle θ), and robustness to many sources of noise, which makes it a convenient diagnostic tool to be run whenever the accuracy of the gate is critical. The test is also linear, being robust against drifts and calibration changes as long as the relaxation and decoherence are phase-independent. Our test goes beyond the standard randomized benchmarking [11], as we systematically monitor the dependence of the deviations on a control parameter.
The public quantum computer by IBM offers the possibility to perform such a test with sufficiently large statistics as the rotation is performed virtually by shifting the phase of the gate [12]. We were able to run the experiment on several different devices, including a single-qubit one. The statistics we collected were sufficiently large to make confident conclusions. We found deviations at the relative level 10–3 and far beyond 5 standard deviations. Our observations show that the deviations are not accidental, and corrections to the ideal model are necessary to explain them. We also tested the nonlinearities of the waveform generators [13] as the possible cause, and they only partially explain the data. The remaining discrepancies are still beyond 5 standard deviations, and their cause is still unknown. We encourage readers to investigate possible causes. There may be subtle technical reasons, but extraordinary models such as involving a larger Hilbert space [14] or more exotic concepts such as interacting many copies [15, 16] should also be considered. We perform additional benchmarking tests to show that the deviations are independent of the inevitable decoherence caused by subsequent gates.
This paper is organized as follows. We start by describing the test of the π/2 rotation on a qubit, repeated n times, then explain implementation on IBM cloud computing, and next, discuss the obtained results and their significance, including the analysis of n = 1, 5 and n = 1, 5, 9 cases. We discuss the benchmark tests and conclude with the general summary. We present the calculation of model-based deviations in Supplementary Appendixes.
2 Materials and methods
2.1 Test of a rotated gate on a qubit
We consider the two-level Hilbert space of a qubit, i.e., spun by states, |0⟩, |1⟩. We assume a θ-dependent quantum operation (gate) of a general form (Eq. 1):
with the angle-dependent rotation (phase shift) around the z-axis on the Bloch sphere [17] (Eq. 2),
written in the basis |0⟩, |1⟩. It is motivated by the implementation of qubit gates, e.g., in the IBM quantum computer, as explained in the following.
The operation Sθ can be applied n times, resulting in the total operation

FIGURE 1. Quantum circuit used to test the rotation of the gate S. The bare gate S acts on the initial state
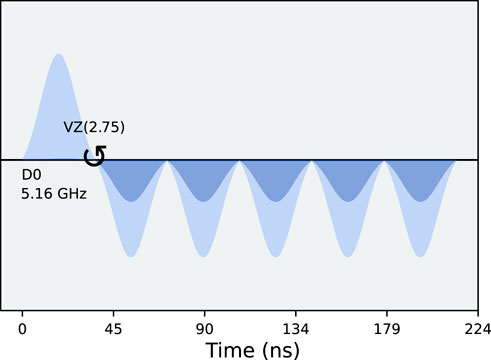
FIGURE 2. Actual waveform of the pulse on the IBM quantum computer (Perth), first S and then n = 5 gates Sθ for θ = 7π/8 ≈ 2.75. The discretization unit time is dt = 0.222 ns. Driving (level gap) frequency is denoted by D0. The light/dark shading corresponds to the in-phase/out-of-phase amplitude component, respectively. The element VZ(2.75) is a zero-duration virtual gate, a part of native Sθ.
We perform a dichotomic diagonal measurement M = α|0⟩⟨0| + β|1⟩⟨1| on the prepared state ρ, which gives the mutually exclusive outcomes 1, 0. A general form for the probability of 1, given some initial ρ and some given S, is (Eq. 3):
with some constants An, Bn, Cn, which are independent of θ. This is the simplest possible test of the phase shift to run on a generic quantum computer. Due to linearity, even changes in the gate S (e.g., due to a different calibration) do not affect the test’s validity. Only the A, B, and C constants will change.
Of course, this prediction will no longer be valid if (a) the actual Hilbert state is larger, with, e.g., an additional state |2⟩, (b) M, S, or ρ depend on θ, and (c) M is not diagonal.
Only such effects can lead to deviations from (3). For (c), only a second harmonics occurs. We discuss these possibilities in detail in Section 3, focusing on potential perturbative corrections.
2.2 π/2 rotation gate
The operations we use conform to native gates [18] provided by IBM quantum cloud computing, realized by microwave pulses. The perfect operation corresponding to our particular choice is given by M = |1⟩⟨1|, ρ = S|0⟩⟨0|S†, and
An ideal π/2 rotation has eigenvalues ± i and 1, and the probability reads as follows (Eq. 5):
We test (A) the fit from (3) against the measured outcome of the preparation sequence for a specific n and (B) if p1 − p5 = 0 and p1 − 2p5 + p9 = 0 for an arbitrary θ. The rotation Zθ is virtual and is performed together with S [12], resulting in a single operation Sθ. The actual effect of the Z gate is the rotation of in-phase and out-of-phase pulse components, not the gate pulse itself. Z gates (phase shifts) are a standard method to parameterize the native gates in the easiest possible way. The drive (interlevel) frequency is, in practice, much higher than the inverse time scale of the gate pulse. Therefore, the application of the Z gate reduces to a phase shift of the original gate pulse with the driving microwave field. It remains independent of the shape of the pulse as long as the shift is correct. It should be noted that an ideal gate S gives A = 0, but we do not have to assume it. On the contrary, keeping all three fit parameters, our test is robust against global phase shifts and decoherence. The great advantage of these tests is the usage of only a single qubit, partial independence of unknown properties of the environment and quantum operations, and universality. It applies to any two-level system. In practical implementation, it is helpful to eliminate memory effects of its repetitions by picking a random θ from a range uniformly covering any interval of length 2π. The result of the test should not change if adding a definite number of operations, S, at the end. It should be noted that in the ideal case, an even number of Ss after Zθ gives the probability 1/2, while for an odd case, the probabilities of 0 and 1 get swapped every two Ss.
2.3 Implementation on the quantum computer
The IBM Quantum Platform cloud computing offers several devices, working as a collection of qubits, which can be manipulated by gates from a limited set—either single-qubit or two-qubit operations. The rotation Z is not a real but an instantaneous virtual gate VZ(θ) added to the next gate [12]. In particular, the sequence of gates Zθ and S, shown in Figure 1, is realized by the native Sθ.
The names of the devices we tested are Armonk, Lagos, Lima, Jakarta, Perth, Nairobi, and Bogota. The collected statistics depend on the number of jobs, circuits, and shots, see Supplementary Appendix SA1. The linearity of the fit (3) makes the test robust against calibrations. Probabilities from different jobs can be simply averages, and so do the fitting parameters. The fitting has been performed by least squares. We compared the outcome statistics, the measured rate of occurred value 1, with the fit to (3). We also ran the circuits consisting of two and three gates Sθ instead of one to compare the possible deviations. For a benchmark, to estimate an error per gate, we used up to 70 Sθ. We made our scripts and collected data publicly available [19].
3 Results
3.1 General results
We present the results in Figures 3, 4. The standard deviation is calculated for the independent Bernoulli statistics, i.e.,
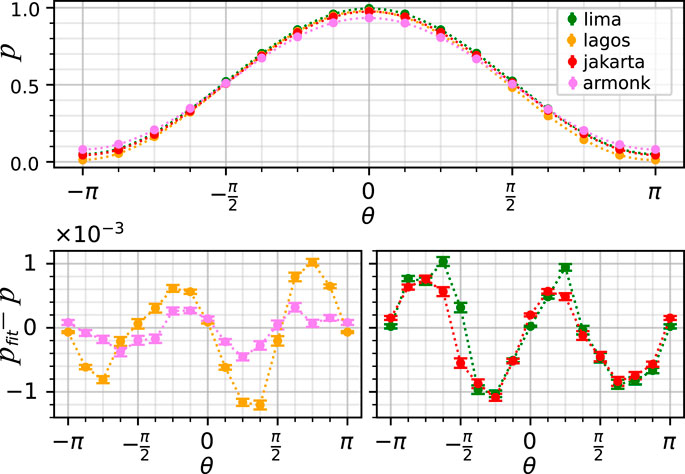
FIGURE 3. Results of the tests on IBM quantum devices for n = 1 with 8,192 shots per job with 56 circuits per angle per job and 100 jobs, except Armonk with 4 circuits per angle and 1,556 jobs. The probability of registering 1 is fitted by least squares to (3) in the upper figure, while the lower figure presents the deviation from the fit. On the vertical axis, p denotes the probability of 1, while pfit is the fit of p to (3).
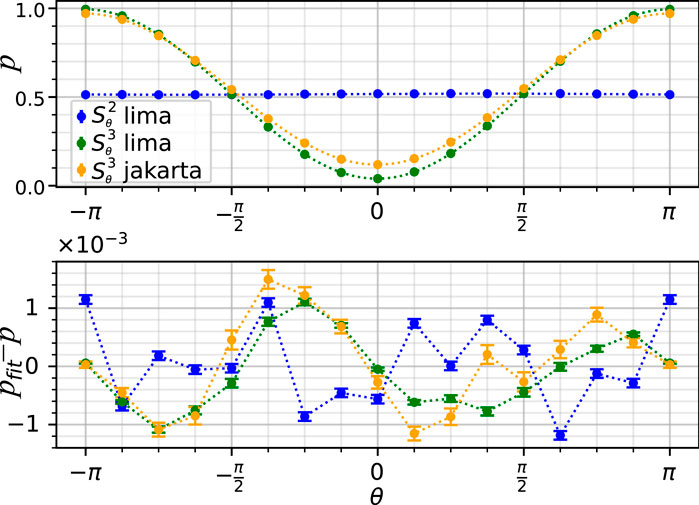
FIGURE 4. Results of tests as in Figure 2 but with n = 2, 3. It should be noted that the ideal angle dependence for n = 3 is reversed with respect to Figure 2, as the two Sθ swap the states |0⟩ and |1⟩.
3.2 Analysis of deviations
We analyze a possible explanation of the deviations by non-ideal execution of the gates under the following four assumptions:
1. The two-dimensional Hilbert space of the quantum system
2. The identical subsequent Sθ gates
3. Decoherence independent of the θ-parameter
4. The small deviations, i.e., dominating the first-order correction
The standard realization of the gate S, including generic deviations in the actual pulse, can be described as (Eq. 6):
for some complex ϵ(θ, ϕ) = ϵr + iϵi describing the parameter-dependent imperfection of the gate, including over/under-rotations and other coherent errors, where
At first sight, the model above could, in principle, explain the deviations because most of the deviations cross 0 at θ = 0, π in Figures 3, 4 (taking into account a general shift of the angle on Bogota) and the deviations for a single and three Sθ sum approximately to zero if the symmetry ϵ(ϕ) = ϵ(π/2 − ϕ) is assumed. Nevertheless, this must be confirmed by tracing down to the actual pulse formation. The results for
3.3 Additional tests
To fully test the model in Eq. 7, we re-run the tests to compare the results from 1 to 5 gates Sθ, which should give identical deviations, according to the model, i.e., p1 − p5 = 0 in the first order. We performed the tests on Lagos (qubits 0 and 6), Lima (qubit 0), and Perth (qubit 0), running with shuffled angles to avoid memory effects. The results show extraordinary deviations for Lagos qubit 0 in the first run in February 2022 (however, we found such large deviations already in November 2021 in the benchmark test), but repeating the test in May 2022 gave much smaller deviations, see Figure 5. The deviation from the first run is large,
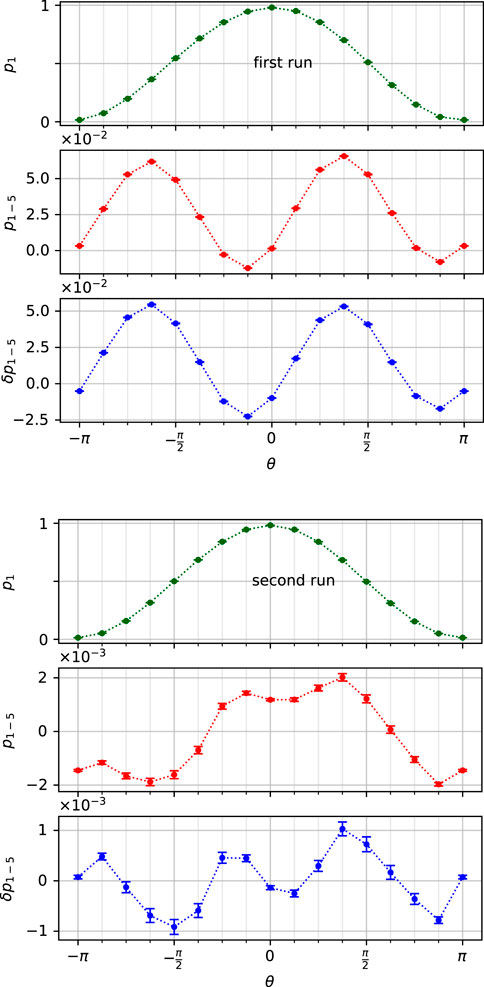
FIGURE 5. Comparison between 1 and 5 gates, p1−5 = p1 − p5 with the fit to (3) subtracted in δp, for Lagos qubit 0, using 32,000 shots each and 9 repetitions for each case angle for 43 jobs in the first run in February and 80 jobs in the second run in May 2022; each data point is a result of 43 ⋅ 32,000 ⋅ 9 or 80 ⋅ 32,000 ⋅ 9 runs. The very large reversal deviation in the first run, reversed between 1 and 5, should be noted.
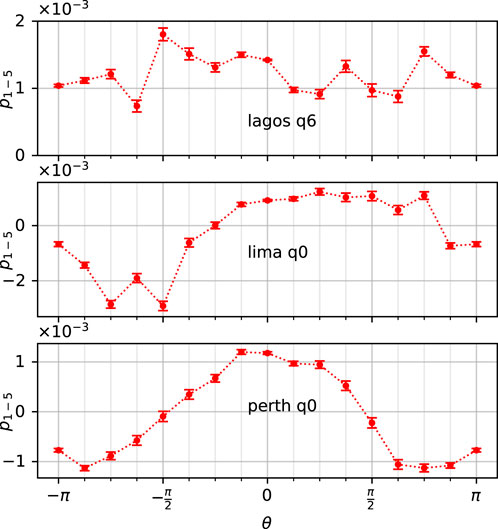
FIGURE 6. Comparison between n = 1 and n = 5, p1 − p5, for Lagos qubit 6 with 195 jobs with 32,000 shots each and 9 repetitions for each case angle, (top), Lima qubit 0 with 290 jobs, 20,000 shots, and 3 repetitions (middle), and Perth qubit 0 with 53 jobs, 100,000 shots each, and 9 repetitions (bottom).
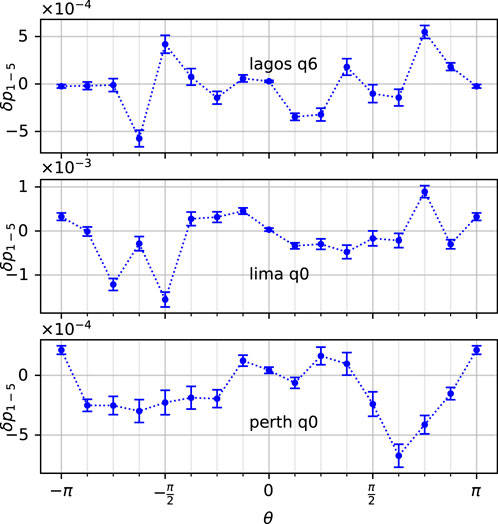
FIGURE 7. Results for n = 1 and n = 5, as in Figure 5, after removing the fit to (3).
Standard models of decoherence do not depend on gate parameters (θ in our work). Benchmarking the decoherence rate at
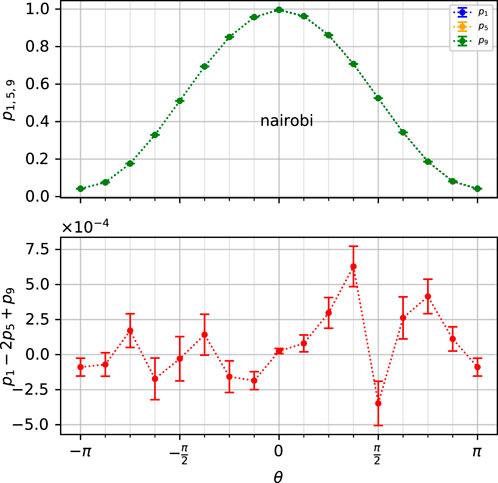
FIGURE 8. Comparison between n = 1, n = 5, and n = 9, p1 − 2p5 + p9, for Nairobi qubit 0, with 100 jobs with 100,000 shots each and 6 repetitions. The actual probabilities almost overlap each other, but the combination gives a deviation over 4 standard deviations.
A higher state [14] as an alternative explanation seems unlikely due to different transition frequencies and the fact that it is a second-order correction (see the analysis in Supplementary Appendix SA6). A simple in-phase/quadrature (I/Q) imbalance [12] cannot explain the dominating second harmonic in the deviations, as it would give only third harmonics (see Supplementary Appendix SA7). An even more complicated description, like a considerable extension of the Hilbert space [15, 16], would be the last option.
4 Conclusion
We observed the deviation from the ideal π/2 rotation on several devices available at the IBM Quantum Platform. The deviations are significant, systematic, and with the amplitude exceeding 5 standard deviations. They exist in a similar form on different devices, different qubits within a device, tested over a long period. The deviations are smaller but persistent for a single-qubit Armonk. Our test is robust against non-idealities of the gates as long as the relaxation and decoherence are phase-independent as they do not affect the difference p1 − p5 in the first order. The benchmark test rules out the possibility of accumulation of decoherence error by many identical gates. Also, the angle-dependent contribution from higher states should remain negligible in the lowest order. The most likely solution, the imperfection of I/Q-mixers and waveform generators, close to sin 2θ (except Bogota), fails to reproduce equal deviations in the case of 1 and 5 gates Sθ, so it is, at best, insufficient. The additional test of 1, 5, and 9 gates resulted in a deviation beyond 4 standard deviations, which deserves confirmation in a larger statistics collected within a relatively short time (in our case, below 2 months). Nevertheless, the systematic occurrence of the deviation should serve as a diagnostic test to enhance the calibration of the gates and find the correct description of the qubit. Due to our assumptions on the identical pulses and restricted Hilbert space, we cannot claim the deviations to be a signature of fundamental problems with the description of the tested qubits. However, we believe that the robustness of such tests will motivate further exploration of qubits diagnostics, an alternative to gate set tomography [7, 8].
We used standard gates available at the IBM Quantum Platform, but one can continue the tests using OpenPulse API [22], which allows fine-tuning the gates or using more complicated tests to reveal the relevant dimensionality of transmon Hilbert space. Dimension tests based on equality can be used to determine the dimensionality [23]. One can also similarly test two-qubit gates with two independent angles for each qubit. In any case, we believe that further improvement of quantum computers from IBM or other public providers will allow even more stringent tests of quantum predictions in the case of low-level systems.
Data availability statement
The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found at: https://zenodo.org/record/7538941.
Author contributions
TB: writing–review and editing, data curation, and software. TR: software and writing–review and editing. JT: writing–review and editing and writing–original draft. AB: writing–original draft and writing–review and editing.
Funding
The authors declare that financial support was received for the research, authorship, and/or publication of this article. TR acknowledges the financial support by the TEAM-NET project co-financed by the EU within the Smart Growth Operational Programme (contract no. POIR.04.04.00-00-17C1/18-00).
Acknowledgments
The authors acknowledge the use of the IBM Quantum Platform for this work. The views expressed are those of the authors and do not reflect the official policy or position of IBM or the IBM Quantum Platform team.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2024.1360080/full#supplementary-material
References
1. Alsina D, Latorre JI. Experimental test of Mermin inequalities on a five-qubit quantum computer. Phys Rev A (2016) 94:012314. doi:10.1103/physreva.94.012314
2. Hebenstreit M, Alsina D, Latorre JI, Kraus B. Compressed quantum computation using a remote five-qubit quantum computer. Phys Rev A (2017) 95:052339. doi:10.1103/physreva.95.052339
3. Simon J. Performing quantum computing experiments in the cloud. Devitt, Phys Rev A (2016) 94:032329. doi:10.1103/physreva.94.032329
4. Huffman E, Mizel A. Violation of noninvasive macrorealism by a superconducting qubit: implementation of a Leggett-Garg test that addresses the clumsiness loophole. Phys Rev A (2017) 95:032131. doi:10.1103/physreva.95.032131
5. Rundle RP, Mills PW, Todd T, Samson JH, Everitt MJ. Simple procedure for phase-space measurement and entanglement validation. Phys Rev A (2017) 96:022117. doi:10.1103/physreva.96.022117
6. Berta M, Wehner S, Wilde MM. Entropic uncertainty and measurement reversibility. New J Phys (2016) 18:073004. doi:10.1088/1367-2630/18/7/073004
7. Rudinger K, Kimmel S, Lobser D, Maunz P. Experimental demonstration of a cheap and accurate phase estimation. Phys Rev Lett (2017) 118:190502. doi:10.1103/physrevlett.118.190502
8. Nielsen E, Gamble JK, Rudinger K, Scholten T, Young K, Blume-Kohout R. Gate set tomography. Quantum (2021) 5:557. doi:10.22331/q-2021-10-05-557
9. Carvalho ARR, Ball H, Biercuk MJ, Hush MR, Thomsen F. Error-robust quantum logic optimization using a cloud quantum computer interface. Phys Rev Appl (2021) 15:064054. doi:10.1103/physrevapplied.15.064054
10. Sun Y-N, Liu ZD, Bowles J, Chen G, Xu XY, Tang JS, et al. Experimental certification of quantum dimensions and irreducible high-dimensional quantum systems with independent devices. Optica (2020) 7:1073. doi:10.1364/optica.396932
11. Garion S, Kanazawa N, Landa H, McKay DC, Sheldon S, Cross AW, et al. Experimental implementation of non-Clifford interleaved randomized benchmarking with a controlled-S gate. Phys Rev Res (2021) 3:013204. doi:10.1103/physrevresearch.3.013204
12. McKay DC, Wood CJ, Sheldon S, Jerry MC, Jay M. Efficient Z gates for quantum computing. Gambetta Phys Rev A (2017) 96:022330. doi:10.1103/physreva.96.022330
13. Chaves KR, Wu X, Rosen YJ, DuBois JL. Nonlinear signal distortion corrections through quantum sensing. Appl Phys Lett (2021) 118:014001. doi:10.1063/5.0035712
14. Strikis A, Datta A, Knee GC. Quantum leakage detection using a model-independent dimension witness. Phys Rev A (2019) 99:032328. doi:10.1103/physreva.99.032328
15. Plaga R. On a possibility to find experimental evidence for the many-worlds interpretation of quantum mechanics. Found Phys (1997) 27:559–77. doi:10.1007/bf02550677
16. Bednorz A. Objective realism and joint measurability in quantum many copies. Annalen D Physik (2018) 530:201800002. doi:10.1002/andp.201800002
17. Nielsen M, Chuang I. Quantum computation and quantum information. Cambridge: Cambridge University Press (2010).
18. Maldonado TJ, Flick J, Krastanov S, Galda A. Error rate reduction of single-qubit gates via noise-aware decomposition into native gates. Sci Rep (2022) 12:6379. doi:10.1038/s41598-022-10339-0
19. European Organization For Nuclear Research and Open AIRE. Zenodo. CERN (2021). Available at: https://zenodo.org/record/7538941 (Accessed February 19, 2024).
20. Riste D, Bultink CC, Tiggelman MJ, Schouten RN, Lehnert KW, DiCarlo L. Millisecond charge-parity fluctuations and induced decoherence in a superconducting transmon qubit. Nat Commun (2013) 4:1913. doi:10.1038/ncomms2936
21. Chen Z, Kelly J, Quintana C, Barends R, Campbell B, Chen Y, et al. Measuring and suppressing quantum state leakage in a superconducting qubit. Phys Rev Lett (2016) 116:020501. doi:10.1103/physrevlett.116.020501
22. McKay DC, Alexander T, Bello L, Biercuk MJ, Bishop L, Chen J, et al. Qiskit backend specifications for OpenQASM and OpenPulse experiments (2018). arXiv:1809.03452 [quant-ph] Available at: https://arxiv.org/abs/1809.03452 (Accessed February 19, 2024).
Keywords: qubit, quantum computer, Hilbert space, Bloch sphere, quantum gate
Citation: Białecki T, Rybotycki T, Tworzydło J and Bednorz A (2024) Testing the accuracy of qubit rotations on a public quantum computer. Front. Phys. 12:1360080. doi: 10.3389/fphy.2024.1360080
Received: 22 December 2023; Accepted: 08 February 2024;
Published: 06 March 2024.
Edited by:
Jonas Maziero, Federal University of Santa Maria, BrazilReviewed by:
Prasanta Panigrahi, Indian Institute of Science Education and Research Kolkata, IndiaShashi Prabhakar, Physical Research Laboratory, India
Copyright © 2024 Białecki, Rybotycki, Tworzydło and Bednorz. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Adam Bednorz, YWRhbS5iZWRub3J6QGZ1dy5lZHUucGw=
 Tomasz Białecki1
Tomasz Białecki1 Adam Bednorz
Adam Bednorz