- 1Department of Chemistry, Paderborn University, Paderborn, Germany
- 2Bionics and Materials Development, Department Lippstadt 1, Hamm-Lippstadt University of Applied Sciences, Hamm, Germany
- 3Bruker Optik GmbH, Ettlingen, Germany
- 4Department Microstructure Physics and Alloy Design, Max-Planck-Institut für Eisenforschung GmbH, Düsseldorf, Germany
Leaky mode resonances of the setae of Cataglyphis bombycina are found to enhance the thermal emission of the animals by near field coupling to the chitinous exoskeleton. This is remarkable, as the setae are also an adaption to enhance the reflectivity in the visible wavelength range. Both effects are dependent on morphology, dimensions and spatial arrangement. These parameters were experimentally characterized and simulated by finite difference time domain simulations to elucidate the optical impact of the setae in the mid infrared range and the contribution of leaky mode resonances. This mode of action and the setae’s optical properties in the visible range explain evolutionary strains that led to the actual morphology and size of the setae.
1 Introduction
Cataglyphis bombycina is a highly heat-tolerant ant species living in desert areas with extreme insolation. Since they forage during the hottest hours of the day, they have to sustain temperatures that are close to their critical thermal limit [1]. For survival, this species has evolved several traits, including long legs, heat shock proteins, visual orientation, and a dense coverage with hair-like setae [1–3]. These setae have been shown to have amazing optical properties, helping the ant to deal with a wide spectrum of electromagnetic waves from sunlight. Nano-ribs on their upper surface in combination with a central canal efficiently scatter ultraviolet (UV) light [4]. The setae have cross sections in the shape of an isosceles right triangle with a hypothenuse of (3.4 ± 0.4) μm [4]. Because of this cross-sectional shape, they reflect visible light by total internal reflection [5, 6] and scatter light in the visible range by higher order Mie-resonances [4, 6]. In the mid infrared (MIR) the setae are suggested to form an antireflection layer, which enhances the radiative cooling of their body [6]. However, the size of the setae in that wavelength range is large enough to cause scattering due to low-order Mie-resonances [4]. Since the setae have an elongated shape, these resonances resemble resonances in optical wires. In optical wires these resonances are eigenmodes, that can be perfectly linked with Mie-resonances in dielectric structures [7]. These eigenmodes are also named leaky mode resonances (LMRs), since their electric field decays in the surrounding of the structure. Leaky modes determine optical properties of dielectric structures including absorption, scattering and emission. These properties can be engineered by changing, e.g., morphological details as well as substrate and superstrate [7]. In the natural system represented by the ant’s integument, the distances between the setae and the cuticle are small compared to the wavelength of the thermal radiation. In this case, near field effects may play a role for radiative cooling [8, 9]. Reid et al. showed that the radiative heat transfer between patterned and between un-patterned slabs increases by orders of magnitude if they are brought in close proximity, where
2 Materials and methods
2.1 Measurements of the distances between setae and cuticle
The spatial arrangement of the setae of the ants was investigated on cross-sectional samples of the cuticle. For this, small parts of the abdominal tergites were dissected and fixed in a mixture of 2.5% glutaraldehyde and 2% paraformaldehyde in H2O (pH 7.8). After washing the cuticle pieces 3 times in bi-distilled water (10 min) they were post-fixed for 60 min in an aqueous solution of 1% OsO4 and 0.8% K4 [Fe(CN)6]. Subsequently, the samples were washed a second time in bi-distilled water and dehydrated in a series of isopropanol solutions. After a final washing step in 100% acetone (4 min), the cuticle pieces were embedded in EPON-resin. Cross-sectional block faces of the resin embedded cuticle were polished using a Leica RM 2155 Ultramicrotome and a diamond knife (Diatome, Switzerland). The polished cross sections were analyzed using a confocal laser scanning microscope (Olympus LEXT OLS3100) with a MPLAPON ×10 plan apochromat objective lens.
2.2 Estimating emission via FDTD reflectance simulations of the setae-covered cuticle
The emissivity can be investigated via simulations of the reflection R. Since the absorption A and the emission E are correlated via Kirchhoff’s Law, the following holds for an opaque body:
The reflection of the ant’s setae-cuticle system at an angle of incidence of 90° was simulated with a classical 2D-FDTD approach using Meep [10] to investigate the influence of the setae in the MIR. The simulations were carried out with both TE and TM polarization. TE represents the case where the electric field is transversal to the long axis of the setae, while TM represents the case where the magnetic field is transversal to the long axis of the setae. The simulations were reduced to two dimensions with the assumption that the dimension of the setae’s cross section is much smaller compared to its length. Therefore, the results represent the case of infinitely long setae.
Three scenarios were compared by simulating a plane wave pulse incident perpendicular to the cuticle surface to obtain the reflection. As first reference, the pulse was simulated in empty space for normalization purposes. As second reference, the pulse was directed towards a plain cuticle surface without setae. The reflection of the cuticle was calculated by the ratio of the results of these two simulations. The third scenario includes a layer of setae on top of the cuticle to simulate the reflection of the entire setae-cuticle system. Comparing these results with the plain cuticle can be used to investigate the influence of the setae on the reflection.
To investigate the influence of the gap between setae and cuticle as accurately as possible, randomized setups with 40 setae at five different mean distances dmean to the cuticle were created (0 μm, 0.38 µm, 0.63 µm, 1.0 µm, and 2.5 µm). The simulation results of 32 arrangements for each mean distance were averaged. The simulation parameters are summarized after the next section.
2.3 Simulation of the angle resolved emission of the setae covered cuticle
The emissive properties were additionally investigated by directly simulating the black body radiation of the ant with FDTD following the approach in [11]. The thermal radiation was simulated as a random noise
In Meep, the random noise in the polarization is realized via a noisy Lorentzian susceptibility. Therefore, the complex material dispersion must be considered. For this, the absorption of chitin was experimentally determined and fitted with a Lorentzian dispersion function (see Supplementary Material). The results are summarized in Table 1 together with additional noise amplitudes simulating the respective emission temperature. These have been weighted by the Planck radiation of a black body at 53°C. The electrical fields are created by the random material polarization. Therefore, no other electro-magnetic source was specified in these simulations.
The electric field
Where the integration boundaries are defined by the unit cell size p and the simulation time
The unit cell must be large enough to prevent a time correlation between the left and the right boundary of the simulation cell. A schematic of the computation cell and the utilized geometry is given in Figure 1. The simulation size was chosen to cover at least 40 randomly distributed setae (the randomization is summarized in the next section) on top of the cuticle, so the unit cell is large enough to employ periodic boundaries and make use of the equations above. The random thermal noise prevents a time correlation between corresponding points in neighboring unit cells. The incoherent thermal sources are thus advantageous for simulating the angle dependent emission.
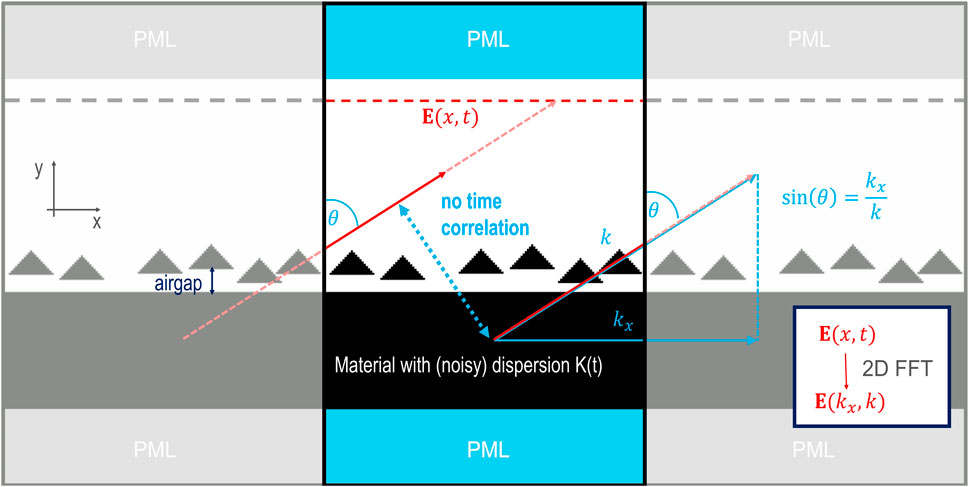
Figure 1. Sketch of the computation cell for the simulation of the angle resolved emission in Meep, with grey shaded copys of itself on the left and right to illustrate the periodic boundary conditions.
For the correct emission, a Lorentzian susceptibility is necessary. The absorption of chitin was fitted with the same Lorentz-oscillator model used for the reflection simulations. The thermal noise amplitudes of each Lorentz oscillator in
Where the most relevant temperature is the maximum temperature, the ant can survive T = 326,15 K = 53°C [3]. An average of 800 simulations with just the plain cuticle were used as reference. Since these simulations are based on thermal noise, longer simulation times are employed and up to 430 different runs with randomized setae arrangements were averaged. The emission enhancement caused by the setae is calculated by dividing the emission with setae by the reference without setae.
2.3.1 Simulation parameters
The size of the computation cell was 16 μm × 60 µm bordered above and below by two perfect matching layers (PML) of 20 µm thickness. In Y-direction, periodic boundaries were employed. The cuticle has a thickness of 30 µm and the setae are represented as right-angled triangles with a hypotenuse of 3.5 µm length and a ribbed surface.
The randomization of the setae positions was realized by multiplication of the ordered coordinates with normal distributed random factors ϕx and ϕy, one for the X and one for the Y coordinate of the setae positions. The X coordinate determines the distance between adjacent setae and is always randomized. The Y coordinate determines the distance of each seta to the cuticle. Its randomization depends on the mean size of the gap dmean multiplied with ϕy. The dimensions of the triangular setae cross sections were adapted from experimental measurements [4]. The complex refractive index of the seta material was experimentally determined [4] and fitted with a complex absorption function including 8 Lorentz resonance frequencies (see Supplementary Material).
One unit in Meep was defined to represent 10 µm. For the reflection simulations a broadband planewave pulse and a resolution of 128 was used. For the emission simulations, only the noisy material dispersion was used as source. The computation cell and the number of simulations was increased; therefore, the resolution was reduced to 32. This is still reasonable, since the maximum frequency of an emitting body at 53°C is lower than the maximum frequency of the pulse used for the reflectance simulations.
The imaginary part of the refractive index was fitted with a sum of 8 Lorentzian susceptibilities:
Where
3 Results
3.1 Distribution of the setae on top of the cuticle
The distances between the cuticle and 42 setae distributed over 250 µm were measured on confocal laser scan images using the software ImageJ [15]. An exemplary section is shown in Figure 2. The section shows the layered structure of the cuticle with the triangular setae distributed above in embedding resin. The cuticle and the embedding resin material are separated by a black area above the cuticle, which is a gap that opened up during microtome sectioning of the samples. Since the delamination of the embedding material and the cuticle happened after sectioning of the sample, the distances between individual setae were measured from the center of the hypothenuse to the cuticle surface and the delamination width was not included in the resulting distances.
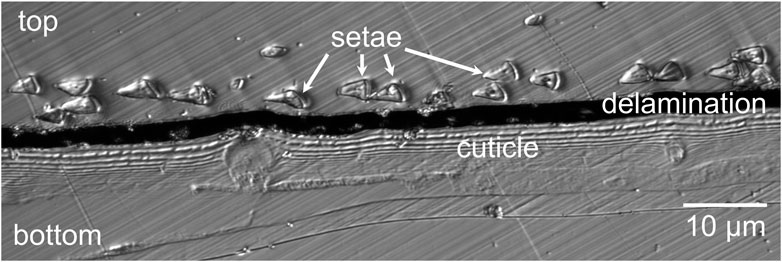
Figure 2. Confocal laser-scanning microscopic image of the embedded cross sectioned cuticle of Cataglyphis bombycina with setae.
The measured distances are summarized in the histogram in Figure 3. Since the distance represents a positive random variable, it can be represented with a log-normal distribution (black curve). The according mean value is dmean = (0.68 ± 0.72) µm.
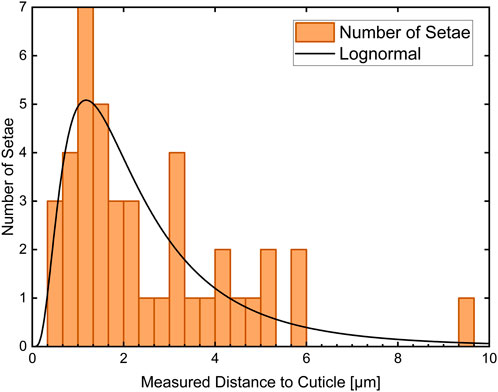
Figure 3. Histogram of the measured distances between 42 setae and the cuticle surface. The histogram has three classes per micrometer. The according lognormal distribution is plotted in black and results in a mean value of dmean = (0.68 ± 0.72) µm.
3.2 FDTD reflection simulations using Kirchhoff’s law for emission
First insights of the influence of the setae on the emissive properties of the ant are gathered by the reflection simulations under perpendicular incidence. In Figures 4A, C the simulated reflection is plotted in the range from 0–7,000 cm−1, in (A) for TM polarization (electric field parallel to the setae’s long axis) and in (C) for TE polarization (electric field perpendicular to the setae’s long axis). The data is averaged from simulations of 32 randomized setae arrangements for each mean gap to the cuticle.
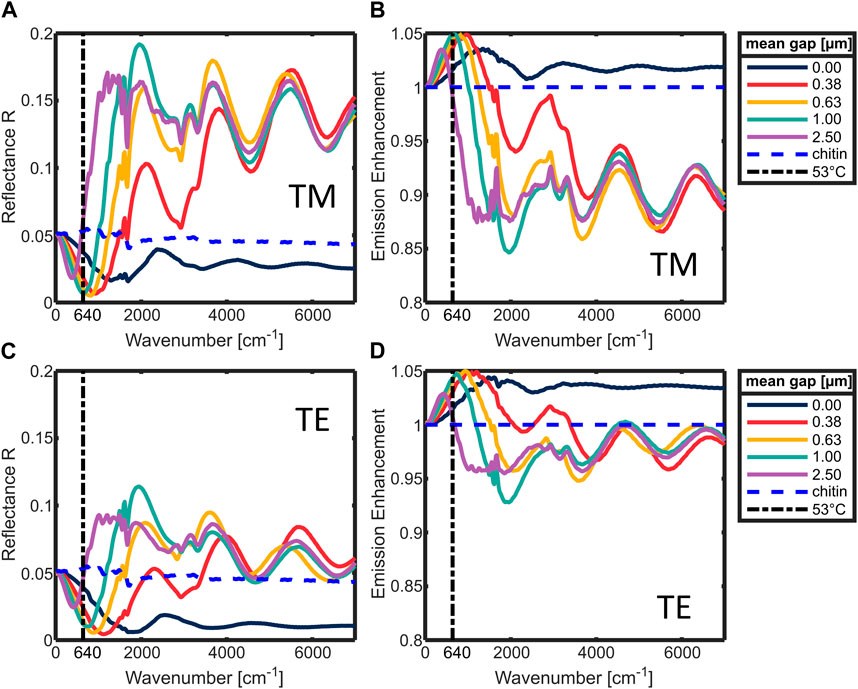
Figure 4. (A,C) Simulated reflectance of a cuticle covered with setae [polarization: (A) TM; (C) TE], with different mean gaps between setae and cuticle. (B,D) The according emission enhancement [polarization: (B) TM; (D) TE]. In all graphs for comparison: simulated chitin reference without setae (blue dashed curve), wavenumber of the maximum of the Planck radiation at 53°C (black dash-dot vertical line).
The trends of both polarizations are comparable. They mostly differ in magnitude. The reflectance for TM polarization is generally higher than for TE. At 0 cm−1, the reflection is independent of the gap around 5% reflectance, which is the same reflectance as without presence of setae. With increasing wavenumbers all graphs undergo a minimum which is shifted to smaller wavenumbers the larger the gap between setae and cuticle becomes. At larger wavenumbers the reflection beyond this minimum increases the larger the gap between setae and cuticle is, and the absorption becomes more pronounced, e.g., around 1,600–1,700 cm−1. Towards even larger wavenumbers, Fabry-Perot-like fringes form when a gap larger than 0 µm is present. The transition from low reflectance to the fringes, where all graphs with gaps coincide, takes place at larger wavenumbers the smaller the gap is. Interestingly, when using the formula to determine a film thickness from Fabry-Perot fringes:
With Eq. 1 the emission can be calculated from the reflection, by assuming that E = A via the reciprocity of light and Kirchhoff’s law. In Figures 4B, D the respective emission curves are plotted. The emission is normalized to the emission of the plain cuticle without setae. This results in an emission enhancement due to the coverage with setae. The minimum in the reflection is now a maximum depending on the gap size. The strongest enhancement can be found for the gap of 0.63 µm (orange) in the range between 0 and 1,500 cm−1 in both polarizations. Interestingly, both polarizations have similar enhancement values in this range.
For the first three resonances found in Figures 4A, B (at wavenumbers of
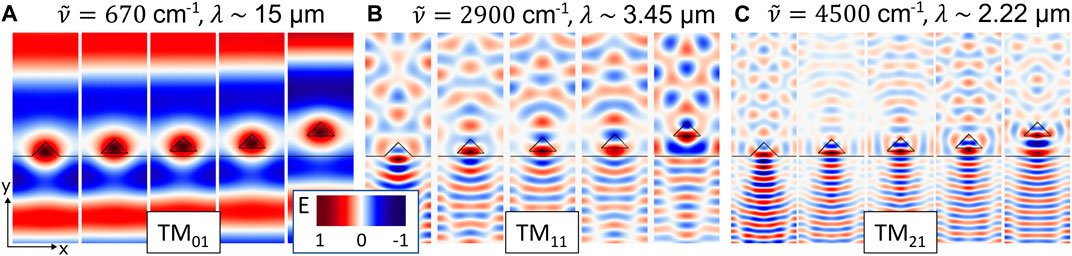
Figure 5. Field distribution of the LMRs of the setae. Plotted is the scattering electric field of single setae on top of a cuticle with periodic boundaries in x-direction for TM-polarized light:
3.3 FDTD simulations of the thermal emission of the ant
The simulations with a plane wave only represent the case for perpendicular incidence. Since the thermal emission occurs in all directions, the hemispherical emissivity of the ant has to be considered. This would require multiple simulations for many angles and wavelengths with the conventional FDTD simulation of the reflectivity. Therefore, a different and more direct approach was used to simulate the angle-resolved emission of the ant. Figure 6 shows three simulations of the angle resolved emission with mean gaps of 0 μm, 0.63 µm, and 1.56 µm. The data is integrated over the frequency and normalized by reference simulations of a plain cuticle. Therefore, the results can be interpreted as an emission enhancement by the setae. Each graph is the average of 430 randomized setae arrangements and 800 reference runs were done. The according standard deviation is shown as confidence interval by the shaded areas around the graphs. As additional information the angle integrated values of the enhancement are listed in the legend entries, these can be seen as the amplification of the hemispherical emissivity of the ant through the presence of setae.
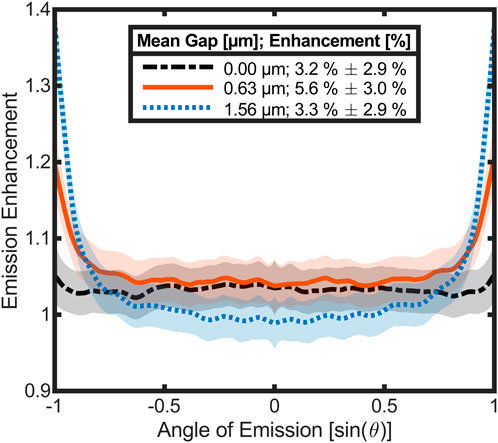
Figure 6. Simulation of the angle dependent emission enhancement for three different mean gaps between setae and cuticle. Data was integrated over the simulated wavelength range (0–4,000 cm−1) and averaged over 430 randomized setae arrangements each. The graphs are normalized by the reference of a plain chitin surface that was averaged over 800 runs to reduce the confidence interval. The emission enhancement over all angles is given in percent within the legend.
The emission enhancement with a gap of zero is meant to compare the natural setup of the ant with a typical anti-reflection coating. The emission enhancement of the surface coating at a gap size of 0 µm amounts to around 3% over the full angle range with little fluctuation and a slight trend to increase towards large angles. At a gap size of 0.63 µm, the emission of the ant increases over the whole angle of emission. Towards large exit angles, the enhancement is strongly elevated. Increasing the gap to 1.56 µm reduces the emission for small angles close to normal incidence compared to the previous two cases. The increase of the emission at large exit angles starts at slightly lower angle values and is even more pronounced than in the other simulations. Integrating the angle-resolved emission enhancement values results in an overall increase of the ant’s emission of 3.2% if there is no gap between setae and cuticle, whereas the emission increases to 5.6% for a gap of 0.63 µm. Increasing distances between setae and cuticle further lowers the overall emission enhancement to 3.3%.
To verify the dependence of emission enhancement from setae-cuticle distance, further simulations were performed in a broader range of gap sizes up to 2.5 µm. To reduce computational efforts, only 72 randomized arrangements were simulated per gap size. This increases the confidence interval of these simulations, but the data is reproducible, and the trend of the emission enhancement is continuous. The integrated data with the according confidence intervals is plotted in Figure 7A together with the data used for Figure 6 (smaller confidence intervals). The emission enhancement reaches a maximum of about 5.6% at a mean gap size of 0.63 µm. At smaller gap sizes, the emission enhancement drops to a value of around 3% at 0 µm gap size. Gap sizes over 0.63 µm reduce emission enhancement continuously down to a value close to 0% at 2.5 µm. In a second set of simulations, the dependence of the emission enhancement on the gap size was investigated for different setae dimensions.
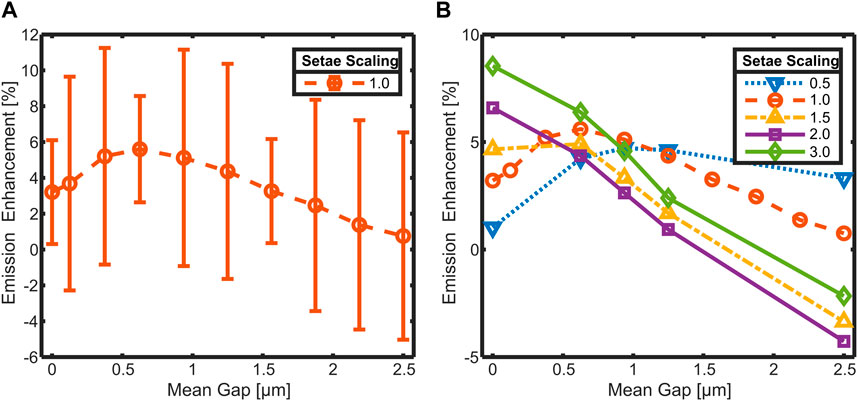
Figure 7. Hemispherical emission enhancement in dependence of the average gap size between setae and cuticle. Simulated with various randomized setae arrangements (numerically integrated over emission angle and wavenumber) for (A): setae with the natural size of Cataglyphis bombycina with confidence intervals and (B): setae of different sizes.
The results are shown in Figure 7B. Each data point is an average of 72 randomized setae arrangements with the according mean gap. The confidence intervals are around ± 6% for all shown data points. For clarity reasons, they are not displayed as error bars. The data of the setae with natural dimensions (scaling factor 1.0; Figure 7A) is included in the same color (orange; Figure 7B). The emission enhancement of the system with smaller sized setae (scaling factor 0.5; blue dashed) has a maximum which is shifted to larger gaps compared to the original setae. For systems with larger setae (scaling factors 1.5, 2.0 and 3.0) this maximum is shifted to smaller gaps ultimately ending up at 0 µm and the classical behavior of an anti-reflection coating for scaling factors larger than 2. Comparison of the curves at a mean gap of 1 µm shows that the enhancement is highest for the original sized system. In the gap size range from 0.5 µm to 1 μm, only the largest of the simulated setae (scaling factor 3.0) shows a better enhancement.
4 Discussion
Since the setae of C. bombycina have a very anisotropic aspect ratio, it is still a challenge to simulate them with reasonable computational efforts. Therefore, the setae-cuticle system was assumed to extend infinitely along the setae’s long axis. The simulations can then be reduced to a 2D computation cell. Therefore, the emission can only be investigated along angles perpendicular to the setae’s long axes. In this study, hemispherical is thus defined only via the angle
The angle resolved emission was simulated for three different systems with increasing gap sizes between setae and cuticle (Figure 6). To demonstrate the effect of the setae on the emission, the three curves are normalized to a cuticle without setae (emission enhancement = 1). In the first simulated case the setae are directly attached to the cuticle without any gap (black dashed, gap = 0 µm). This already leads to an average increase in emission of about 3%. At small angles the emission enhancement is constant and only increases slightly at large angles. This mode of action corresponds to a classical anti-reflection surface [19]. In the second case the emission was simulated with a mean gap of 0.63 µm between setae and cuticle (orange solid) which corresponds closely to the geometry present in the ants with a mean distance of (0.68 ± 0.72) µm [determined by experimental measurements (Figures 2, 3)]. At small angles, the emission enhancement is almost like in the case without a gap, but at large angles it strongly increases. This results in an average emission enhancement of about 6%, which is almost twice as much as if there was no gap between setae and cuticle. If the gap is enlarged to more than double the size of the natural setup (blue dotted, gap = 1.56 µm), the overall average emission enhancement decreases to about 3%. This is a similar value as in the first case, but the curves show different trajectories in similar angle ranges. At small angles, the emission enhancement is lower and at larger angles [sin(θ) > 0.7] it is much higher and rises with an even larger slope than in case two. The enhanced emission at large angles in case two and three can be explained by much better outcoupling of evanescent waves than in case one.
The lower emission enhancement at small angles in case three shows that when the distance between setae and the cuticle would be too large, the setae would become a hindrance for the thermal radiation. This is also supported by the reflectance simulations under perpendicular incident light (Figures 4A, C).
The reflectance of the setup without a gap between setae and cuticle (dark blue; gap = 0 µm) is lower than that of the plain cuticle (dashed blue) over the full displayed wavenumber range for both polarizations. Thus, the zero-gap case shows the typical behavior of an anti-reflection coating [19]. The situation is different if a gap between cuticle and the setae is present. In those cases, resonances occur, especially at large wavenumbers (e.g., between 4,000–7,000 cm−1). These resonances increase the reflectance of TM as well as TE polarized light (Figures 4A, C). In the spectral range below 2,000 cm−1 however, the presence of setae results in a lower reflectance compared to a plain cuticle. Depending on the gap size between setae and cuticle, there is a spectral region where the reflectance is lower than if the setae were attached to the cuticle without gap. The larger the gap size, the narrower the respective region with low reflectivity. Additionally, the minimum in the reflectance is also shifted to lower wavenumbers. The larger the gap, the stronger is the influence of the absorption bands of chitin. They originate from the material dispersion included in the simulation, which is summarized in Table 1. The strongest ones occur between 1,500 and 2,000 cm−1.
An opaque body with a higher reflectance has by Eq. 1 a lower absorption. By the reciprocity of light, a lower absorption also leads to lower emission. Thus, a higher reflectance would cause a lower emission for the ant. Therefore, all gaps between setae and cuticle reduce the emission enhancement in the spectral range between 4,000–7,000 cm−1 (Figure 4B). In this range, all curves of the simulations with a gap show a higher reflectance and similar resonances. This indicates that these resonances are independent of gap size and the randomized spatial arrangement of the setae. Therefore, it is safe to assume that the resonances originate solely from the setae and correspond to their leaky modes (LMR) or Mie-resonances. Interestingly, deriving a Fabry-Perot thickness from the periodicity of these resonances leads to a value d ∼ 1.75 µm, which corresponds very well to the height of the setae [4]. The presence of similar resonances was confirmed before with experimental FTIR transmission measurements of single setae [4]. Since the Planck radiation of a black body at 53°C is almost zero in the wavenumber range of 4,000–7,000 cm−1, the resonances in this region do not contribute to the thermal emission of the ant. For the thermal emission and resulting possible radiative cooling effects the range between 0–1,500 cm−1 is much more relevant. In the range of 0–1,500 cm−1, the reflectance for all gap sizes decreases below the reflectance of the hypothetical anti-reflection coating represented by the zero-gap case. In this spectral region the emission is strongly influenced by the distance between cuticle and setae. Increasing these gap sizes shifts the maximum of the emission enhancement towards smaller wavenumbers. This effect can be explained by near field coupling of the LMRs. Three examples of these LMRs of setae in different distances to the cuticle are illustrated in Figure 5.
Figure 5A shows the LMR TM01 of a seta. Interestingly, it corresponds very well to the TM01 of a cylinder, as demonstrated for a thin Germanium wire in [17]. Even the resonance frequency correlates very well to this literature example when considering the larger dimensions of the seta and the lower refractive index of chitin compared to the Germanium wire. Due to the lower refractive index of the seta, the leaky mode covers a broader wavenumber range (Figure 4) and extends further into the surrounding space. Therefore, the LMR can couple to the cuticle and to neighboring setae even if the gap between seta and cuticle becomes quite large. Similar coupling effects have been measured on Si-nanowires, too [20].
In terms of optics, enhancing the thermal emission of the ant for its survival is a problem which is comparable to maximizing the absorption in nanowire antennas for harvesting solar radiation, although different wavelengths are involved. Cao et al. showed that there would be better structures than triangular prisms for enhancing the absorption, at least at resonances of higher order than TM01 [17]. To maximize the photocurrent inside their nanowires, they optimized the absorption of the TM21/TE11 resonances rather than TM01, because these are less sensitive on illumination angle. The TM01 LMR of silicon nanowires has a low absorption cross section (Qabs) [17], which limits the absorption in the wires, a disadvantage that would lower the photocurrent. Cao et al. theoretically showed that the TM01 LMR would have the largest potential to enhance the photocurrent compared to unstructured silicon with the same thickness, at least for certain illumination angles [17]. However, a wire that could use TM01 LMR would require a diameter of around 10 nm, which is experimentally not feasible.
Despite the absorption bands in the MIR, which increase the refractive index of the chitinous setae, the optical nanowire antennas investigated by Cao have a much higher refractive index. Thus, the TM01 LMR of the setae have an even lower Qabs [4] compared to the nanowires. This turns into an advantage for the thermal emission problem of the ant. The setae cannot be treated as isolated antennas, since the underlying cuticle is an integral part of the body that always plays a role for the optical system of the ant. Thus, a large Qabs is not necessary for the setae to enhance the outcoupling of the emitted thermal radiation of the cuticle. In this, the ant differs fundamentally from the nanowire antennas, where the substrate does not play an optical role. Therefore, near field heat transfer and near field coupling effects are much more relevant for the ant [9, 20]. For such coupling, the TM01 of the setae is beneficial, because of its larger spatial extension compared to higher order resonances or to TM01 resonances of high refractive index materials like Ge.
In this study, the TM01 LMR was only investigated for angles of emission perpendicular to the setae’s long axis. However, for angles parallel to the long axis Cao et al. [17] experimentally characterized the LMRs of an isotropic nanowire and theoretically showed that there are only minor differences in the low order LMRs for nanowires of round, rectangular, hexagonal, and triangular cross-sectional shapes. The results in [17] show that the absorption cross section Qabs is largest at normal incidence and decreases at larger angles of incidence. Especially the TM01 resonance strongly decreases beyond 40° to normal incidence and disappears at parallel incidence. The incidence angle on the setae in the setae-cuticle system is limited by the angle of total internal reflection at the cuticle-air surface, which is about 40°; larger angles result in evanescent waves, which lead to parallel incidence on the setae. Since the TM01 resonance of wire shaped objects (including objects with triangular cross sections like the setae of C. bombycina) is not excitable from these angles [17] the respective electric fields can no longer couple to the LMR. Thus, this scenario plays a minor role for the emission enhancement of the ant cuticle. Therefore, we focus on angles of emission perpendicular to the setae’s long axis, thus avoiding expensive 3D-simulations of the complex architecture of the natural setae-cuticle system and still gaining the most important information on its mode of action in the MIR. The LMRs of the triangular setae, illustrated in Figure 5A, are almost cylindrical even near the cuticle. Therefore, the TM01 LMR is excitable over a broad illumination angle and the LMR can radiate into all the seta’s azimuthal angles in free space. Thus, the coupled LMR extends the angle of emission of the ant cuticle. Thereby, the thermal emission of the ant is enhanced by outcoupling of evanescent waves. The TM01 intercoupling of the randomly arranged setae and its coupling to the cuticle causes the system to act like an array of low-Q optical antennas [20] that emit in the MIR and offload thermal radiation, which helps to keep the ant cool.
Figures 5B, C show the higher order resonances (TM11 and TM21). TM11 corresponds well to simulations of triangular nanowires published by [17]. Since higher order resonances like TM21 occur at shorter wavelengths, they are more confined to the seta. Therefore, they cannot couple that efficiently to the cuticle or neighboring setae like lower order resonances. Backscattering effects may occur and therefore the setae become a hinderance for the emitted radiation in these wavelength ranges. This is the reason why the emission depicted in Figures 4B, D decreases in these wavelength ranges compared to the zero-gap situation.
The simulations shown in Figures 4A, B reveal a certain wavenumber range where the near field-coupled TM01 LMR have a lower reflectance than a classical anti-reflection coating. If the peak wavenumber of the Planck radiation at 53°C (
The dependence of the emission on the gap size suggests that it results from the coupling of the setae’s LMR to the cuticle. If this is the case, the trajectory of the curve in Figure 7A should be significantly influenced by variations in setae dimensions as this would shift the resonances and influence their coupling to the cuticle and between each other. Since the setae of C. bombycina are also adapted to reflect incoming sunlight [4–6], their dimensions are playing a crucial role in the visible and ultraviolet (UV) range [4]. Previous investigations have shown that the reflectance in the visible and the UV becomes better if the setae would be larger than their actual size [4]. The ability of the setae to enhance the emission in the MIR could be a possible evolutionary strain for their size restriction. To verify this, simulations of the emission of the setae-cuticle system were also done with varying setae sizes. This was done with a reduced number of simulations and only for a subset of gaps used for the data in Figure 7A to limit the computational effort. In Figure 7B the results of these simulations are summarized together with the curve from Figure 7A. The results indicate that the maximum enhancement for smaller setae (scaling factor = 0.5, blue dotted) would be localized at larger gaps, whereas for larger setae, the local maximum would be achieved at smaller gaps. At setae scaling factors of 2 (purple) and 3 (green) the emission enhancement decreases almost linearly with increasing gap size, similar to an anti-reflection coating, where the maximum of the emission enhancement is located at 0 µm gap size and leaky mode resonances play a minor role. This compellingly suggests that the setae-cuticle system represents an anti-reflection structure in the MIR through nearfield coupling resonant leaky-modes of the setae to the cuticle.
5 Conclusion
The detailed simulations presented in this paper lead to the conclusion, that the setae enhance the thermal emission of the ant in a more complex way then forming an effective medium. The setae not only form a Mie-resonant structure in the visible [4, 6], but also in the MIR. Thus, they do not only shield the ant from visible and UV-light, but also enhance their ability for radiative cooling. This is crucial for the survival of the animals in their extreme desert habitat, where the body of the ants is heated up by solar radiation and the surrounding sand and air. This heat radiates from the body to the environment. Without setae, the emission angle is limited by the total internal reflection inside the cuticle. This leads to evanescent waves that are trapped inside the body. Through the presence of the setae, these waves can now couple to the first order LMRs of neighboring setae, thereby radiating the energy to the full hemispherical angle range. This leads to a thermal emission enhancement of about 6% compared to the plain cuticle. Varying the setae’s size and their distances to the cuticle in our simulations shows, that the parameters realized by the ant are evolutionary optimized for enhancing the thermal emission. Considering the optical effects of the setae in the visible and UV range shows that dimensions, shape, surface structure, and average distance from the cuticle are evolutionary compromises to fulfill a large variety of functions that help this ant species to survive in its environment.
Although the optical functions described for visible and UV-light would be more efficient with larger setae [4], their actual size might be evolutionary restricted through their ability to enhance their thermal emission. The MIR effects are resonant-based, where the size is crucial and larger setae would become a hinderance for radiative cooling. LMRs in, e.g., nanowires have been shown to be an efficient way to enhance the absorption and the emission of light [7]. Radiative cooling does not require energy and is therefore a promising concept for a number of technical applications in the energy sector [21]. Here we show that a concept of radiative cooling based on near field coupled LMRs is realized in a biological system, which mainly differs from technical applications by consisting of low refractive index materials. Such systems can also combine high reflectance in the visible range with a high emittance in the MIR within a single structure. This type of structure has not been considered yet and might provide inspiration for new ways to use passive radiative cooling as a sustainable energy source.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Ethics statement
Ethical approval was not required for the studies involving animals in accordance with the local legislation and institutional requirements because the specimens used were obtained from a laboratory that rear this ant species for their studies. The specimens used died of natural causes (age).
Author contributions
BS: Conceptualization, Investigation, Methodology, Visualization, Writing–original draft, Writing–review and editing. XW: Writing–review and editing. MT: Writing–review and editing. H-OF: Conceptualization, Supervision, Writing–review and editing.
Funding
The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This study was supported by the DFG (Deutsche Forschungsgemeinschaft) Priority Program 1839 “Tailored Disorder—A science- and engineering-based approach to materials design for advanced photonic applications” within project 12 “Broadband reflecting fibers with tailored structures inspired by desert ants”.
Acknowledgments
H-OF thanks Prof. Dr.-Ing. Dierk Raabe and the entire team of the Department Microstructure Physics and Alloy Design at the Max-Planck-Institut für Eisenforschung GmbH for hosting this research and their continuous support. We thank Dr. Matthias Wittlinger and Prof. Dr. Harald Wolf from the Department Neurobiology of the University of Ulm for providing dead C. bombycina workers from their cultures.
Conflict of interest
Author XW was employed by Bruker Optik GmbH.
The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2024.1393279/full#supplementary-material
References
1. Lenoir A, Aron S, Cerdá X, Hefetz A. Cataglyphis desert ants: a good model for evolutionary biology in Darwin’s anniversary year - a review. Isr J Entomol (2009) 39:1–32.
2. Pfeffer SE, Wahl VL, Wittlinger M, Wolf H. High-speed locomotion in the Saharan silver ant, Cataglyphis bombycina. J Exp Biol (2019) 222:jeb198705. doi:10.1242/jeb.198705
3. Wehner R, Marsh AC, Wehner S. Desert ants on a thermal tightrope. Nature (1992) 357:586–7. doi:10.1038/357586a0
4. Schwind B, Wu X, Tiemann M, Fabritius H-O. Broadband Mie scattering effects by structural features of setae from the Saharan silver ant Cataglyphis bombycina. J Opt Soc Am B (2023) 40:B49. doi:10.1364/JOSAB.474899
5. Willot Q, Simonis P, Vigneron J-P, Aron S. Total internal reflection accounts for the bright color of the saharan silver ant. PLoS ONE (2016) 11:e0152325. doi:10.1371/journal.pone.0152325
6. Shi NN, Tsai C-C, Camino F, Bernard GD, Yu N, Wehner R. Keeping cool: enhanced optical reflection and radiative heat dissipation in Saharan silver ants. Science (2015) 349:298–301. doi:10.1126/science.aab3564
7. Huang L, Xu L, Powell DA, Padilla WJ, Miroshnichenko AE. Resonant leaky modes in all-dielectric metasystems: fundamentals and applications. Phys Rep (2023) 1008:1–66. doi:10.1016/j.physrep.2023.01.001
8. Rodriguez AW, Ilic O, Bermel P, Celanovic I, Joannopoulos JD, Soljačić M, et al. Frequency-selective near-field radiative heat transfer between photonic crystal slabs: a computational approach for arbitrary geometries and materials. Phys Rev Lett (2011) 107:114302. doi:10.1103/PhysRevLett.107.114302
9. Reid MTH, Rodriguez AW, Johnson SG. Fluctuation-induced phenomena in nanoscale systems: harnessing the power of noise. Proc IEEE (2013) 101:531–45. doi:10.1109/JPROC.2012.2191749
10. Oskooi AF, Roundy D, Ibanescu M, Bermel P, Joannopoulos JD, Johnson SG. Meep: a flexible free-software package for electromagnetic simulations by the FDTD method. Comput Phys Commun (2010) 181:687–702. doi:10.1016/j.cpc.2009.11.008
11. Luo C, Narayanaswamy A, Chen G, Joannopoulos JD. Thermal radiation from photonic crystals: a direct calculation. Phys Rev Lett (2004) 93:213905. doi:10.1103/PhysRevLett.93.213905
12. Kolle M Theoretical aspects of photonic structures. In: M Kolle, editor. Photonic structures inspired by nature springer theses. Berlin, Heidelberg: Springer (2011). p. 5–27. doi:10.1007/978-3-642-15169-9_2
13. Sproull RL, Phillips WA Modern physics: the quantum physics of atoms, solids, and nuclei. 3d ed. New York: Wiley (1980).
14. Leertouwer HL, Wilts BD, Stavenga DG. Refractive index and dispersion of butterfly chitin and bird keratin measured by polarizing interference microscopy. Opt Express (2011) 19:24061. doi:10.1364/OE.19.024061
15. Schneider CA, Rasband WS, Eliceiri KW. NIH Image to ImageJ: 25 years of image analysis. Nat Methods (2012) 9(9):671–5. doi:10.1038/nmeth.2089
16. Cao L, White JS, Park J-S, Schuller JA, Clemens BM, Brongersma ML. Engineering light absorption in semiconductor nanowire devices. Nat Mater (2009) 8:643–7. doi:10.1038/nmat2477
17. Cao L, Fan P, Vasudev AP, White JS, Yu Z, Cai W, et al. Semiconductor nanowire optical antenna solar absorbers. Nano Lett (2010) 10:439–45. doi:10.1021/nl9036627
18. Liu T, Xu R, Yu P, Wang Z, Takahara J. Multipole and multimode engineering in Mie resonance-based metastructures. Nanophotonics (2020) 9:1115–37. doi:10.1515/nanoph-2019-0505
19. Boden SA, Bagnall DM. Optimization of moth-eye antireflection schemes for silicon solar cells. Prog Photovoltaics (2010) 18:195–203. doi:10.1002/pip.951
20. Cao L, Fan P, Brongersma ML. Optical coupling of deep-subwavelength semiconductor nanowires. Nano Lett (2011) 11:1463–8. doi:10.1021/nl1040429
Keywords: Cataglyphis bombycina, leaky mode resonance, near field coupling, thermal emission enhancement, low refractive index materials, anti-reflection structures, FDTD
Citation: Schwind B, Wu X, Tiemann M and Fabritius H-O (2024) Natural near field coupled leaky-mode resonant anti-reflection structures: the setae of Cataglyphis bombycina. Front. Phys. 12:1393279. doi: 10.3389/fphy.2024.1393279
Received: 28 February 2024; Accepted: 23 April 2024;
Published: 22 May 2024.
Edited by:
Sébastien Robert Mouchet, University of Exeter, United KingdomReviewed by:
Branko Kolaric, University of Mons, BelgiumDiana Skigin, University of Buenos Aires, Argentina
Copyright © 2024 Schwind, Wu, Tiemann and Fabritius. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Bertram Schwind, YmVydHJhbS5zY2h3aW5kQGhzaGwuZGU=
 Bertram Schwind
Bertram Schwind Xia Wu1,3
Xia Wu1,3