Filament simulations for stellarators; a review of recent progress

Shanahan, Brendan

doi:10.3389/fphy.2024.1399287

REVIEW article

Front. Phys., 30 May 2024

Sec. Fusion Plasma Physics

Volume 12 - 2024 | https://doi.org/10.3389/fphy.2024.1399287

This article is part of the Research Topic Transport in the Scrape-Off Layer of Magnetically Confined Fusion Plasmas View all 4 articles

Filament simulations for stellarators; a review of recent progress

Brendan Shanahan*

Max-Planck-Institut für Plasmaphysik, Greifswald, Germany

A review of recent advances in simulations of turbulent filaments with relevance to stellarators is presented. Progress in performing global edge turbulence simulations is discussed as well as results from seeded filament simulations with applications to the unique environment of a stellarator island divertor–including abrupt changes in connection length and highly-nonuniform curvature drive. It is determined that the motion of filaments generally follows the average curvature, but strong nonuniform perturbations can shear a filament and reduce the overall transport. The coherence of filament transport is also determined to be influenced by the collisionality and electron plasma beta. By simplifying the simulation geometries, large parameter scans can be performed which accurately reflect the macroscopic transport of filaments observed in Wendelstein 7-X. Comparisons to experiments are discussed, and a the develeopment of a synthetic diagnostic has been able to inform experimental measurements by quantifying potential sources of error in filament propagation measurements. A discussion of the necessary extension to more complex multifluid models, and the scope for near-term filament simulations in stellarators, is provided.

1 Introduction

Large, coherent, field-aligned structures–often called blobs or filaments–can be responsible for substantial transport in the scrape-off-layer (SOL) of magnetic fusion devices. A significant amount of theoretical, numerical, and experimental research has been devoted to the nature of blobs, providing an understanding of the basic propagation and generation mechanisms. A thorough review of blob dynamics is given in References [1–3]. The basic mechanism of filament propagation is as follows: a separation of charge is induced via diamagnetic drifts, resulting in a dipolar potential structure. The resultant motion is then governed by the mitigation of this charge separation; where there is a large connection length to the sheath, the potential is dissipated via perpendicular currents within the filament. If, however, the connection to the sheath is short enough (or the filament has a large enough perpendicular size), then the potential is resolved via currents through the sheath at the plasma facing components. The resistivity within the filament, and any sort of nonuniformity in the filament structure can thereby also result in altered propagation. The propagation of filaments is therefore governed by three components: the polarizing force (curvature, in a toroidal device), currents within the filament, and magnetic shear. The scrape-off layer of stellarators provides a novel environment for filament dynamics due to the unique SOL parameters; namely, nonuniform magnetic field strength in the toroidal direction and a strongly discontinuous connection length profile. The former provides a nontrivial polarizing force, and the latter complicates the mitigation of the current separation due to this polarizing force.

The SOL of stellarators similarly provides unique challenges in numerical simulation. Fluid simulations often utilize a field-aligned coordinate system, and often invoke a symmetry direction. The SOL of stellarators can however include magnetic islands and chaotic field lines, thereby inhibiting fluid turbulence simulations. As such, the investigation of filaments in stellarators has until recently been limited to experimental analysis [3–13]. The utilization of alternative numerical approaches, such as the Flux-Coordinate-Independent (FCI) approach [14–22] or direct approach [23, 24] to parallel derivatives has facilitated the global simulation of turbulent structures in the stellarator SOL [21, 25, 26]. Simultaneously, simulations in simplified geometries have allowed for a more detailed analysis of the relevant mechanisms.

Here we provide a brief overview of recent work simulating plasma filaments in stellarators, using both global (Section 2) and local simulations and the subsequent comparison to experiment, Section 3. A brief discussion of some open questions and the prospects for future studies will be presented in Section 4.

2 Global simulations

The high collisionality of the edge and SOL of fusion devices facilitates a fluid approach to simulations. While recent work has simulated blobs using a gyrokinetic treatment [27], the majority of blob simulations are performed using a fluid approach due to the efficiency of the calculations. In general, these simulation codes utilize a field-aligned coordinate system, where one of the coordinates is aligned to the magnetic field. This approach becomes untenable for stellarators, due to the existence of magnetic islands and chaotic field lines in the stellarator edge. As such, other methods must be employed; either a non-aligned coordinate system [23–25, 28], or a locally-aligned approach, such as the Flux-Coordinate-Independent method for parallel derivatives [14, 16, 18, 19, 21]. Global fluid turbulence simulations have been performed in analytic [25, 26] and experimentally-relevant geometries [28], although a consistent picture of the dynamics within these systems is as yet undetermined.

In Reference [25], global nonlinear simulations are performed in an analytic geometry. It is determined that the system is ballooning unstable, and would in principle be suitable to filament generation. There exists, however, no broadband turbulence or recognizable filaments. Rather, the system is dominated by a single coherent mode, whose fluctuation amplitude is highest on the inboard (“good” curvature) side of the configuration. This geometry is again studied in [26] with a more simplified model and a broader-range of turbulent fluctuations are found, although again no distinct filaments are observed. Rather, broadband turbulence is observed with increased fluctuation amplitudes on the outboard side of the torus, see Figure 1.

Figure 1

Figure 1. Standard deviation of density fluctuations at the last closed flux surface in an analytical stellarator with an island divertor. Fluctuation amplitudes increase on the outboard side of the torus. Reproduced under the Creative Commons CC BY 4.0 license from [26].

More insight is found in Reference [28], which compares global simulations in the TJ-K [29] stellarator to experimental measurements. The simulations recover low poloidal mode number oscillations, as seen in experiment. The E × B turbulent flux is found to be similar to experiment at some toroidal angles, but different in others. An area is found in simulations where coherent structures enter the SOL from the confined region, which could indicate a region of filament generation similar to what was found in previous experimental measurements [10].

The global simulations cited above do not focus on any particular aspects relevant for filament propagation. However, global simulations of seeded plasma filaments in an analytic stellarator geometry have also been performed in Reference [21], marking the first nonlinear simulations of filaments in a global stellarator geometry. In this work, it was determined that filaments propagate nonuniformly due to the long parallel connection lengths which allow the development of parallel gradients which cannot sufficiently resolve the charge separation due to the nonuniform curvature drive. It was determined that hotter filaments propagate more uniformly, but determined that this could not be an Alfvénic effect. This work inspired later work which examined the role of nonuniform curvature drive in simplified geometries, which will be discussed in the following section.

3 Local simulations

Due to the complexity in interpreting data from global simulations, it is often advantageous to isolate physics for a more complete understanding. Here, we will focus on the work which has been done to understand the effects unique to stellarators; namely, nonuniform curvature drive and a highly-discontinuous connection length profile.

3.1 Nonuniform curvature

A nonuniform curvature drive is inherent in any toroidal magnetic geometry with a rotational transform, as field lines will traverse poloidally, experiencing varying magnetic field strengths and curvature drive. In stellarators, however, this effect is exacerbated due to the nonaxisymmetric nature of the equilibrium. Simulations in slab geometry [30, 31] have determined, among other effects, that the propagation of filaments generally follows the average curvature drive. The work in Reference [31] also confirmed the assertion from global simulations that filaments with a higher electron temperature propagate more uniformly. If, however, this nonuniformity is too drastic, the filaments can be sheered apart. Reference [32] explores the parameters relevant for the coherence of filaments in scenarios with nonuniform drive, and determines that the filament coherence is governed by the collisionality and the electron plasma beta, see Eq 1.

Δ / δ_{⊥} \sim (\frac{β_{e} L_{κ}}{2} + \frac{ν L_{κ} τ_{b}}{n δ_{⊥}^{2}}) j_{‖} ≔ (β^{'} + ν^{'}) j_{‖} . (1)

where Δ is the filament displacement, δ_⊥ is the perpendicular size of the filament, L_k is the curvature length scale, τ_b = δ_⊥/v_b is the advection timescale, and j_‖ is the parallel current. Simulations were then performed in scenarios with sinusoidal curvature, while varying the electron plasma beta and the collisionality, and the coherence of filaments was plotted in Figure 2.

Figure 2

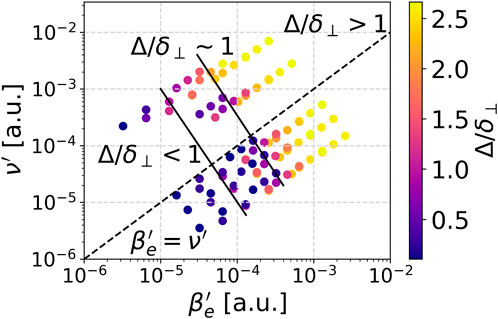
Figure 2. Normalized filament displacement as a function of electron plasma beta $(β_{e}^{'})$ and collisionality (ν′) for a filament polarized by a sinusoidal curvature drive. Reproduced under the Creative Commons CC BY 4.0 license from [32].

The simulations shown in Figure 2, reproduced here from Reference [32], confirmed the assertion in Eq 1, namely, that the displacement of filaments scales linearly with electron plasma beta and collisionality.

3.2 Discontinuous connection length profile

Another unique aspect of stellarators, particularly those with an island divertor [33–35] such as Wendelstein 7-X [36], is the discontinuous connection length profile where the connection length to the sheath can abruptly change in a short perpendicular distance. This is due to the divertor targets intersecting the magnetic islands at discrete toroidal locations, resulting in discrete field line lengths to the sheath. Since connection length determines the current distribution within a filament, these abrupt changes can alter filament dynamics. The dynamics in such situations was explored in Reference [37], where it was determined that filaments can be accelerated or decelerated when entering areas of higher or lower connection length, respectively. Furthermore, it was determined that the filaments in W7-X will have a predominantly poloidal trajectory due to the large radial electric field and relatively small curvature drive; an assertion which was later confirmed by experimental measurements [38].

3.3 Experimental comparison

Having established from the global and local simulations mentioned above that filaments propagate according to the average curvature, drift-plane simulations were performed with parameters gleaned from measurements in Wendelstein 7-X. These drift-plane simulations where then compared to experimental probe measurements [38]. Despite the drift-plane approximation which removes any sort of geometry in the curvature drive apart from the average major radius, the experimental filament scaling of radial propagation velocity vs. filament size was captured by seeded filament simulations, see Figure 3. Furthermore, the filaments were determined to have a small radial velocity, as predicted previously in Reference [37], and therefore were not a cause of turbulent spreading.

Figure 3

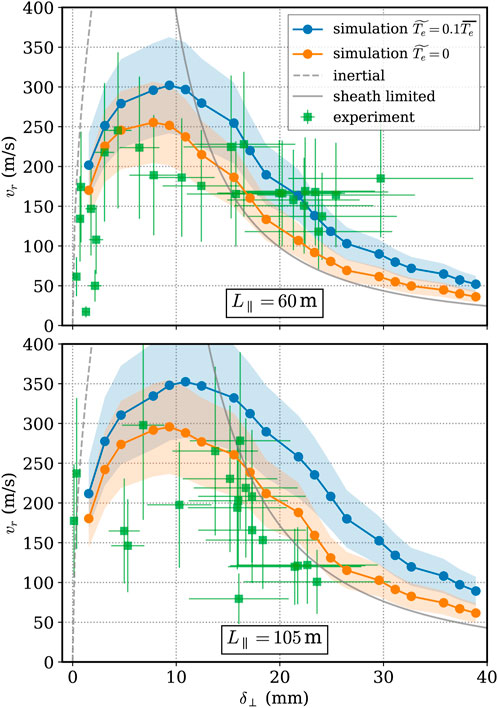
Figure 3. Comparison of experimental probe measurements and drift-plane simulations for the filament scaling within Wendelstein 7-X, for two distinct connection length regimes. The shaded region around the simulation results indicates different ellipticities (which is unknown from experimental measurements). Reproduced under the Creative Commons CC BY 4.0 license from [38].

This experimental comparison in turn inspired the work in Reference [39], where the sources of error in the filament characteristics via probe measurement in the Wendelstein 7-X SOL were quantified. The primary source of error was the one dimensional, conditionally-averaged measurement which systematically underestimated the filament size. It is determined analytically that the measured filament diameter will be 79% of the true diameter. Furthermore, filament velocities can be inaccurately measured due to misalignment of the probe head relative to the poloidal trajectories of the filaments, and an optimal probe spacing relative to the filament size was determined. To visualize the total contribution of all error sources, a synthetic filament scaling was performed to mimic the measurements shown in Figure 3 [38]. Filaments were randomly seeded with a diameter and pressure within experimental parameters, and their resultant trajectories were measured using the synthetic diagnostic. The synthetic scaling is reproduced in Figure 4 [39], where the solid green circles indicate the filament properties measured by the synthetic diagnostic, and the hollow green circles indicate the actual properties determined from simulation. The green bar which connects these dots, then, indicates the total error associated with probe measurements. This work then provides context for Figure 3, as filament velocities and diameters are systematically underestimated by probe measurements.

Figure 4

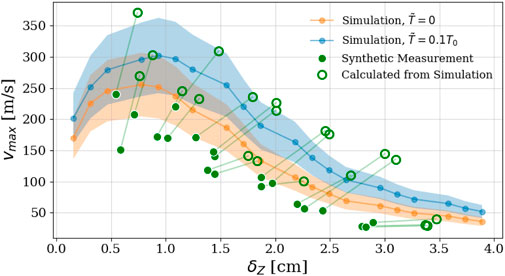
Figure 4. A comparison of filament scaling for randomly-generated filaments as measured by the synthetic diagnostic (filled green circles), as extracted directly from simulation (hollow green circles), and the simulated results (with constant pressure perturbation) from [?] in orange and blue. Reproduced under the Creative Commons CC BY 4.0 license from [39].

4 Open questions

While the dynamics of filaments in stellarators are largely similar to those in other geometries, there remain several unique aspects where novel research has begun to provide insight. Nevertheless, several questions remain. In Reference [38], it was determined that due to the low radial velocity of filaments, they remain close to a flux surface and cannot contribute to turbulence spreading. If this is the case, the question remains as to where and how the filaments are generated. Typically, blobs originate in areas of higher pressure near the separatrix and carry heat and particles into the separatrix. Without any sort of ballistic motion in Wendelstein 7-X, it remains to be seen how and where these filaments are generated. While there has been some research into blob generation mechanisms [40–42], very little research has been devoted to blob generation mechanisms in stellarators.

Furthermore, the magnetic islands create a region of complicated topology which will influence filament dynamics. In tokamaks, filaments can be distorted near the X-point [43, 44], which disconnects them from the midplane and causes a quiescent zone at the strike point. Indeed, the work in Reference [38] indicates that the filaments extend to the target, but this is only true for the target closest to the probe measurements; no data is available at the other end of the field line. The complicated edge topology in Wendelstein 7-X, which includes a magnetic island chain and a nonaxisymmetric equilibrium with substantial toroidal flux expansion is certain to significantly distort filaments.

Global simulations of fluid turbulence experimentally-relevant geometries with an island divertor should enable a thorough examination of these phenomena. The recent development of SOL turbulence codes for complicated magnetic geometries [21, 25, 26, 28], including nonaxisymmetric island chains, has in principle enabled such studies, although global simulations in Wendelstein 7-X geometries remain as yet unrealized due to the considerable numerical expense of such simulations. As such, simulations of smaller-scale experiments, like that which is done in [26, 28] or in [45], could also ascertain such dynamics.

Local simulations can also provide novel insight. Filaments will spin about their parallel axis When a filament’s temperature differs from the background plasma [46], or when there is a parallel nonunformity of blob characteristics [47–50]. This mechanism has been proposed to reduce filament velocity [51], and could also be seen in stellarators. However, there exists no explicit research into filament spin dynamics in stellarators. The strong nonuniformity of plasma parameters along a stellarator SOL field line should induce novel spin dynamics.

Finally, the influence of target interactions, such as the role of neutrals and impurities, on filament dynamics has been investigated in tokamak contexts [52–55]. While many of these effects are also applicable to stellarators, impurity transport is fundamentally different in stellarators due to the lack of any temperature screening [56] (although recent work has suggested this impurity accumulation might not be so drastic as previously thought [57]). Therefore, the development of global fluid turbulence codes for stellarator geometries should look to include impurity and neutral species, a mechanism which is already available for axisymmetric geometries [58, 59].

Author contributions

BS: Writing–original draft, Writing–review & editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work has been carried out within the framework of the EUROfusion Consortium, funded by the174 European Union via the Euratom Research and Training Programme (Grant Agreement No 101052200 -175 EUROfusion). Views and opinions expressed are however those of the author(s) only and do not necessarily reflect those of the European Union or the European Commis.

Acknowledgments

The author recognizes the brilliant work of the colleagues cited within.

Conflict of interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Krasheninnikov S, Ryutov D, Yu G. Large plasma pressure perturbations and radial convective transport in a tokamak. J Plasma Fusion Res (2004) 6.

Google Scholar

2. Krasheninnikov SI, D’Ippolito DA, Myra JR. Recent theoretical progress in understanding coherent structures in edge and sol turbulence. J Plasma Phys (2008) 74:679–717. doi:10.1017/S0022377807006940