Reverse degree-based topological indices study of molecular structure in triangular ϒ-graphyne and triangular ϒ-graphyne chain

Hakeem, Abdul; Katbar, Nek Muhammad; Shaikh, Hisamuddin; Tolasa, Fikadu Tesgera; Abro, Oshaque Ali

doi:10.3389/fphy.2024.1422098

ORIGINAL RESEARCH article

Front. Phys., 14 August 2024

Sec. Atomic and Molecular Physics

Volume 12 - 2024 | https://doi.org/10.3389/fphy.2024.1422098

Reverse degree-based topological indices study of molecular structure in triangular ϒ-graphyne and triangular ϒ-graphyne chain

Abdul Hakeem¹*

Nek Muhammad Katbar¹

Hisamuddin Shaikh²

Fikadu Tesgera Tolasa³

Oshaque Ali Abro⁴

¹School of Mathematics and Statistics, Central South University, Changsha, China
²Deparment of Mathematics, Shah Abdul Latif University, Khairpur, Pakistan
³Deparment of Mathematics, Dambi Dollo University, Dambi Dollo, Ethiopia
⁴Dawood University of Engineering and Technology Karachi, Karachi, Pakistan

Topological indices are mathematical descriptors of the structure of a molecule that can be used to predict its properties. They are derived from the graph theory, which describes the topology of a molecule and its connectivity. The main objective is mathematical modeling and topological properties of ϒ-graphyne. Current research focuses on two structures made from hexagonal honeycomb graphite lattices named triangular ϒ-graphyne and triangular ϒ-graphyne chains. The authors have simultaneously computed the first and second Reverse Zagreb indices, reverse hyper-Zagreb indices, and their polynomials. This research also derives mathematical closed-form formulas for some of its fundamental degree-based molecular descriptors. Researchers have been trying to synthesize a novel carbon form called Graphyne. For over a decade but with no success. Recently, some researchers have made a breakthrough in generating Carbons elusive allotrope and solved a long-standing problem in carbon materials. This wonder material is created to rival the conductivity of graphene but with control. These results opened new ways of research in the fields of semiconductors, electronics and optics. Furthermore, graphical and tabular results will help to investigate the structure-property relationships in γ-graphyne.

1 Introduction

Graph theory has been utilized extensively in the modeling of chemical structures, and their mathematical modeling is referred to as chemical graph theory. This notion has a significant impact on the advancement of chemical science. The study of topological indices that can describe and predict organic molecules’ physicochemical and pharmacological properties is novel and active research in chemical graph theory. The topological index calculates the properties of interesting compounds, and it remains invariant. In cheminformatics, if we want to study compounds’ properties and chemical bioactivity, we must utilize the Quantitative structure-property relationships (QSPR) together with topological indices. The selection of topological indices is based on previous validations by researchers, where these indices were correlated with certain physico-chemical properties in molecules; hence, they are applied to model the considered structures. Numerous applications of the topological indices are found in the Quantitative structure-activity relationship (QSAR), which is used to forecast the physio-chemical characteristics of chemical compounds [1–7]. Topological indices are the numbers that belong to a chemical’s structure and are supposed to show how it relates to other structures. The study of molecular descriptors assists in compensating for the lack of chemical experiments by giving a theoretical base for making chemical materials [8–14]. In the structure-activity relationship, the topological architecture of the chemical structure and the simple connectivity between neighboring atoms are more important than the nature of chemical bonds. This is because the nature of chemical bonds is not seen as a significant factor in the biological activity of the chemical compound [12, 15–19]. Harold Wiener, a chemist, used a topological index for the first time in 1947 when chemists and mathematicians defined 100 topological indices and investigated many chemical structural features [19, 20]. Gutman described Zagreb indices as degree-based topological indices more than 40 years ago [21]. Topological indices like these were proposed to quantify the degree to which the carbon atom skeleton is branched [22]. A molecule’s topological index is a non-empirical numerical value [23]. Topological indices are molecular graph invariants that can be employed to create QSPR/QSAR as numerical descriptors [24]. These can be shaped with a distance matrix and the chemical graph (hydrogen-suppressed graph). Notations and terminology not defined here can be found in refs [25–30] except if otherwise stated.

The Weiner index [31]. and the Gutman defined and formulated The first and second Zagreb indices as in 1972 [32].

M_{1} (G) = \sum_{u v \in E (G)} (d_{u} + d_{v})

M_{2} (G) = \sum_{u v \in E (G)} (d_{u} . d_{v})

Harold et al. [33] examined the connection between the Zagreb indices and the overall energy of π-electrons, as indicated by references [34–37] for more results related to Zagreb indices. After Gutman, Shirdel et al [38] first and second hyper-Zagreb indices such as

{H M}_{1} (G) = \sum_{u v \in E (G)} {(d_{u} + d_{v})}^{2}

{H M}_{2} (G) = \sum_{u v \in E (G)} {(d_{u} \times d_{v})}^{2}

More see Reference [39–41]. Chemical graph theory has applications in predicting molecular properties, such as boiling points and solubilities. It also aids in understanding chemical reactions and exploring molecular databases. Overall, chemical graph theory provides a foundation for the analysis and prediction of chemical structures and properties using graph theory principles [42–47].

Graph Theory is widely used in real-world phenomena. For communication networks, computational devices, and data organization, a graph is extensively used in computer science and the study of the properties of molecules in chemistry, physics, and biology.

1.1 γ-graphyne

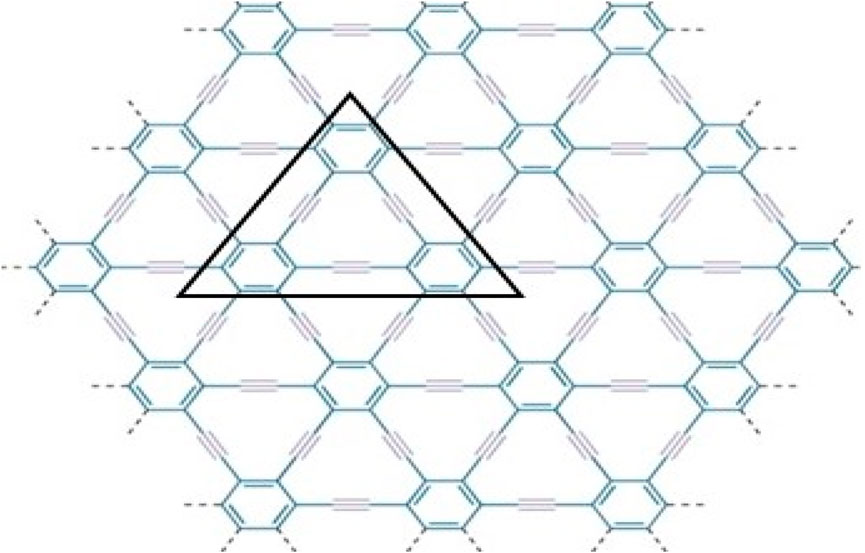
γ-graphyne is a two-dimensional carbon allotrope that belongs to the graphyne family. It is a highly intriguing material because of having unique structure and exceptional properties. Gamma graphyne has shown promising potential as a catalyst for various chemical reactions, demonstrating its usefulness in energy conversion and storage. Researchers actively explore its properties, synthesizing methods, and applications to harness its full potential. The importance of (2D) derivatives of graphite structures like graphyne is rising due to their promising properties like band tunable gaps, charge carrier mobilities, etc. Hexagons and sp² hybridized (the mixing of one s and two p atomic orbitals) carbon atoms make up the two-dimensional sheet known as graphene. Its significance and novelty are due to its remarkable physical, mechanical, chemical, and electrical properties [48]. Recently, increasing interest in graphene-based material achieved the Nobel Prize in Physics in 2010 for groundbreaking experiments in 2D substance graphene [49]. The states of sp² atoms remain similar when carbyne chains [50]. Acetylenic connections are added to a honeycomb structure made of carbon (C) atoms that have undergone sp hybridization to create graphyne, two-dimensional materials developed from graphene. Due to acetylene groups, these structures exhibit a diverse spectrum of electrical, optical, and mechanical properties [51]. Various graphene ganoscroll (GN) derivatives are under study, and their crystal structures are shown in [52]. Because of their high heat storage capacity on adsorption and negligible change in computed activation barriers, graphyne has been suggested by Swathi et al. for use as substrates with graphene in practical devices [53]. M. Kando et al. verified from vibrational investigations that practically all oligomer model planar configurations are at least local energy minima [54]. The fascinating and distinctive mechanical and electron-conducting properties of graphyne were predicted [55–58] optical characteristics. In particular, like in graphene, the electron conduction in graphynes would be incredibly rapid. Unlike graphene’s multidirectional conduction, some graphynes’ electron conduction can be regulated in a specific direction because triple bonds can bend Dirac cones [55, 56]. Although the topological descriptors for the structures of the graphene nanoscroll (GNs) have not yet been investigated, due to the importance in applications of structures, the study of the topological indices of these distinct networks to compare and contrast the complexity of these structures is necessary aspect [59–61]. Molecular descriptors for the structure of γ-graphyne have not investigated before, as given in Figures 1, 2. Consequently, the authors in [62] have shown its significance. The reverse vertex degree, which focuses on less-connected nodes, can illuminate various physical and chemical phenomena. For example, in catalysis, active sites often occur at low-degree vertices where unique reactions happen. Similarly, in material science, defects and irregularities frequently reside at these less-connected nodes, impacting properties like conductivity and strength. In biological networks, reverse vertex degree analysis reveals crucial nodes in protein interactions or metabolic pathways, often associated with rare but significant interactions. By examining these less-connected vertices, we uncover insights into reactivity, stability, and functionality, demonstrating the practical significance of topological indices in real-world applications.

Figure 1

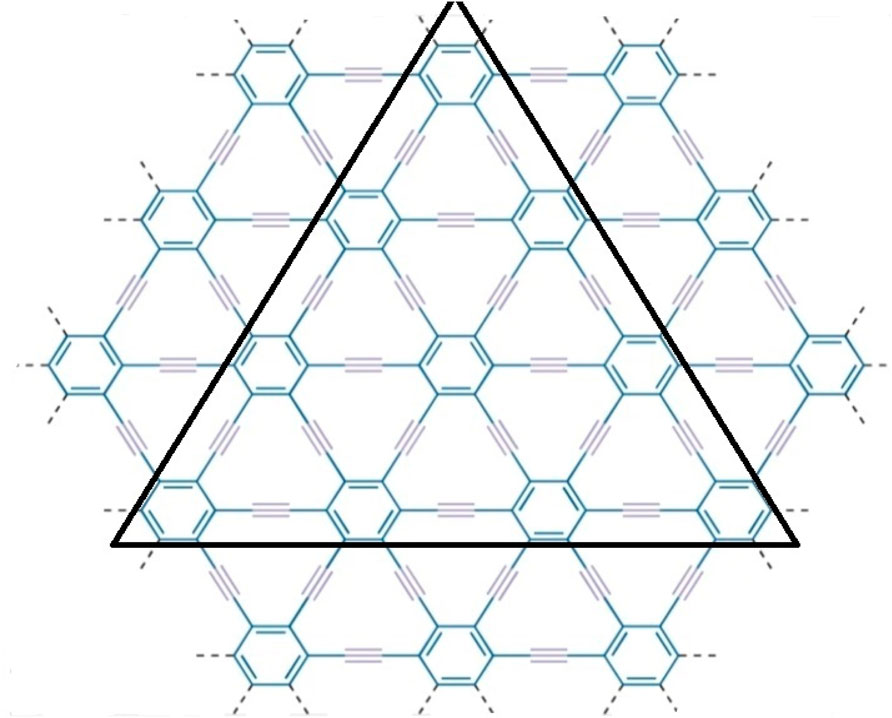
Figure 1. Molecular graph $γ$ -graphyne [62].

Figure 2

Figure 2. Graphical representation of triangular γ-graphyne.

ϒ-Graphyne, with its tunable band gap and high electron mobility, is promising for electronics, semiconductors, and energy storage devices. It enhances supercapacitors, batteries, and hydrogen storage. Additionally, it is valuable in sensors, catalysis, optoelectronics, and composite materials due to its unique structure and properties.

2 Calculation method

A molecular graph is a simple graph in which vertices and edges reflect atoms and bonds [63–65]. The number of edges that a vertex is associated with determines its degree. A graph’s maximum vertex degree is represented by the symbol (G). Kulli introduces the concept of reverse vertex degree with the formula as

C_{v} = ∆ (G) - d_{g} (V) + 1

Where C_v is denoted by the reverse degree, $∆ (G)$ is the maximum degree $a n d$ $d_{g} (V)$ shows the minimum vertices adjacent to v [12, 66].

Gutman (1972) defined and formulated the first and second Zagreb indices [32]. We defined the ${C M}_{1} (G)$ and ${C M}_{2} (G)$ reverse Zagreb index.

{C M}_{1} (G) = \sum_{u v є E (G)} (c_{u} + c_{v})

{C M}_{2} (G) = \sum_{u v є E (G)} (c_{u} {\times c}_{v})

Ivan Gutman introduced the first and second hyper-Zagreb indice [32, 38, 67]. We defined the ${H C M}_{1} (G)$ and ${H C M}_{2} (G)$ reverse Zagreb index.

{H C M}_{1} (G) = \sum_{u v є E (G)} {(c_{u} + c_{v})}^{2}

{H C M}_{2} (G) = \sum_{u v є E (G)} {(c_{u} {\times c}_{v})}^{2}

The first and second Zagreb polynomials were introduced by Ivan Gutman [11]. We defined the ${C M}_{1} (G . x)$ and ${C M}_{2} (G . x)$ reverse Zagreb index.

{C M}_{1} (G . x) = \sum_{u v є E (G)} x^{(c_{u} + c_{v})}

{C M}_{2} (G . x) = \sum_{u v є E (G)} x^{(c_{u} \times c_{v})}

The same paper first and second hyper-Zagreb indices [38]. We defined the ${H C M}_{1} (G . x)$ and ${H C M}_{2} (G . x)$ reverse Zagreb index.

{H C M}_{1} (G . x) = \sum_{u v є E (G)} x^{{(c_{u} + c_{v})}^{2}}

{H C M}_{2} (G . x) = \sum_{u v є E (G)} x^{{(c_{u} \times c_{v})}^{2}}

Similarly, many other indices are essential in relationship QSPR/QSAR analysis. Review topological indices and further information in an in-depth review of references [68–74].

3 Results and discussion

3.1 Triangular γ-graphyne

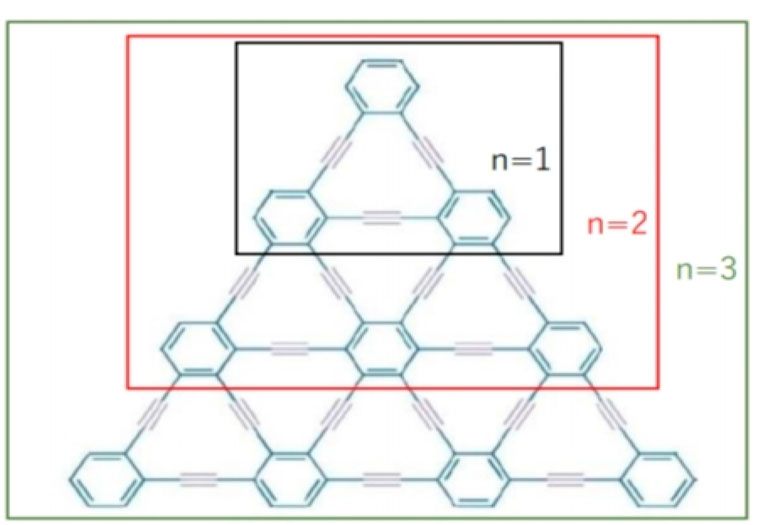
We have discussed molecular structure, edge partitioning technique, and robust computational results. In this study, as the focus is on the mathematical modeling of graphyne, we deliberately treat the π bonds within the benzene rings and the acetylene bonds bridging the benzene rings as equivalent despite their believed different chemical characteristics. We applied topological indices on the triangular γ-graphyne structure and obtained novel and new findings. Using the edge partitioning technique and topological indices, each row of the system given in Figure 3 contains $3 n^{2} + 9 n + 6$ vertices and $\frac{9}{2} n^{2} + \frac{21}{2} n + 6$ edges, where n is the number of the rows, and the number of edges that are incident on vertex u and vertex v governs their degrees denoted by the $d_{u} (G) o r d_{v} (G)$ .In our graph model, the notation d_uv = d₂₂ represents an edge connecting two vertices, with each vertex having two edges (or a degree of 2).

Figure 3

Figure 3. Triangular γ-graphyne.

Similarly, 'd₂₃' refers to an edge connecting two vertices, where one vertex has two edges, and the other has three. Lastly, 'd₃₃' indicates an edge connecting vertices that each have three edges. These notations are crucial for understanding the edge-vertex relationships and their degrees in our graph-theoretical framework.

E_{1} = \{u v є E (G) | d_{G} (u) = 2, d_{G} (v) = 2\}, |E_{1}| = 3 n + 6

Where $|E_{1}|$ denotes the number (elements of) of edges

E_{2} = \{u v є E (G) | d_{G} (u) = 2, d_{G} (v) = 3\}, |E_{2}| = 6 n

E_{3} = \{uv є E (G) | d_{G} (u) = 3, d_{G} (v) = 3\}, |E_{3}| = \frac{1}{2} ({9 n}^{2} + 3 n)

Clearly. We have $c_{u} = Δ (G) - d_{G} (u) + 1 = 4 - d_{G} (u),$

We know that there are three different types of reverse edges.

{C E}_{1} = \{u v є E (G) | c_{u} = 2, c_{v} = 2\}, |E_{1}| = 3 n + 6

{C E}_{2} = \{u v є E (G) | c_{u} = 2, c_{v} = 1\}, |E_{2}| = 6 n

{CE}_{3} = \{uv є E (G) | c_{u} = 1, c_{v} = 1\}, |E_{3}| = \frac{1}{2} ({9 n}^{2} + 3 n)

Theorem 3.1.1. If G is a graph of the Triangular $γ$ - graphyne. Then, we have the

i. ${C M}_{1} (G) = {9 n}^{2} + 33 n + 24$

ii. ${C M}_{2} (G) = \frac{1}{2} ({9 n}^{2}) + \frac{1}{2} (51 n) + 24$

iii. $H C M_{1} (G) = {18 n}^{2} + 108 n + 96$

iv. $H C M_{2} (G) = \frac{1}{2} {9 n}^{2} + \frac{1}{2} 147 n + 96$

Proof: our results using the reverse edge partition of the triangular - $γ$ graphyne;

C M_{1} (G) = \sum_{u v є E (G)} (c_{u} {+ c}_{v})

= 4 (3 n + 6) + 3 (6 n) + 2 (\frac{1}{2} ({9 n}^{2} + 3 n))

= {9 n}^{2} + 33 n + 24

C M_{2} (G) = \sum_{u v є E (G)} (c_{u} {\times c}_{v})

= 4 (3 n + 6) + 2 (6 n) + 1 (\frac{1}{2} ({9 n}^{2} + 3 n))

= \frac{1}{2} ({9 n}^{2}) + \frac{1}{2} (51 n) + 24

H C M_{1} (G) = \sum_{u v є E (G)} {(c_{u} {+ c}_{v})}^{2}

= 16 (3 n + 6) + 9 (6 n) + 4 (\frac{1}{2} ({9 n}^{2} + 3 n))

= {18 n}^{2} + 108 n + 96

H C M_{2} (G) = \sum_{u v є E (G)} {(c_{u} {\times c}_{v})}^{2}

= 16 (3 n + 6) + 4 (6 n) + (1) \frac{1}{2} ({9 n}^{2} + 3 n)

= \frac{1}{2} {9 n}^{2} + \frac{1}{2} 147 n + 96

Theorem 3.1.2. If G is a graph of the Triangular $γ$ - graphyne. Then, we have then.

I. $C M_{1} (G . x) = (3 n + 6) x^{4} + (6 n) x^{3} + (\frac{1}{2} ({9 n}^{2} + 3 n)) x^{2}$

II. $C M_{2} (G . x) = (3 n + 6) x^{4} + (6 n) x^{2} + (\frac{1}{2} ({9 n}^{2} + 3 n)) x$

III. $H C M_{1} (G . x) = (3 n + 6) x^{16} + (6 n) x^{9} + (\frac{1}{2} ({9 n}^{2} + 3 n)) x^{4}$

IV. $H C M_{2} (G . x) = (3 n + 6) x^{16} + (6 n) x^{4} + (\frac{1}{2} ({9 n}^{2} + 3 n)) x$

Proof: our results using the reverse edge partition of the triangular - γ-graphyne;

C M_{1} (G . x) = \sum_{u v є E (G)} x^{(c_{u} + c_{v})}

= (3 n + 6) x^{4} + (6 n) x^{3} + (\frac{1}{2} ({9 n}^{2} + 3 n)) x^{2}

C M_{2} (G . x) = \sum_{u v є E (G)} x^{(c_{u} {\times c}_{v})}

= (3 n + 6) x^{4} + (6 n) x^{2} + (\frac{1}{2} ({9 n}^{2} + 3 n)) x

H C M_{1} (G . x) = \sum_{u v є E (G)} x^{{(c_{u} + c_{v})}^{2}}

= (3 n + 6) x^{16} + (6 n) x^{9} + (\frac{1}{2} ({9 n}^{2} + 3 n)) x^{4}

H C M_{2} (G . x) = \sum_{u v є E (G)} x^{{(c_{u} {\times c}_{v})}^{2}}

= (3 n + 6) x^{16} + (6 n) x^{4} + (\frac{1}{2} ({9 n}^{2} + 3 n)) x

3.2 Triangular chain γ-graphyne

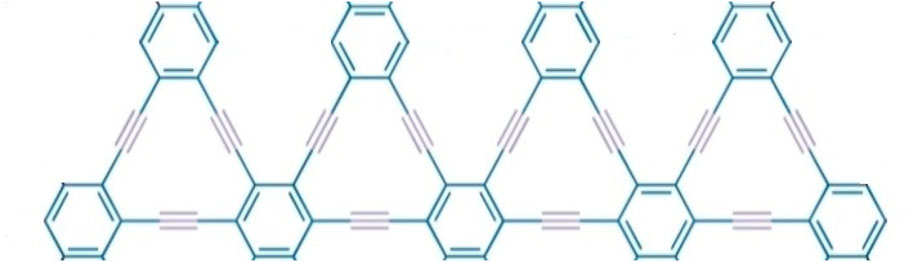
We have discussed molecular structure, edge partitioning technique, and robust computational results. We applied topological indices on the triangular γ-graphyne chain structure and obtained novel and new findings from Figure 4. Using the edge partitioning technique and topological indices, each column of the system given in Figure 4 having $12 n + 6$ vertices and $15 n + 6$ edges, where n is the number of the column, and the number of edges that are incident on vertex u and vertex v governs their degrees denoted by the $d_{u} (G) d_{v} (G),$ where the notation d_uv = d₂₂ represents an edge connecting two vertices, with each vertex having two edges (or a degree of 2). Similarly, d₂₃' refers to an edge connecting two vertices, where one vertex has two edges, and the other has three. Lastly, 'd₃₃' indicates an edge connecting vertices that each have three edges. These notations are crucial for understanding the edge-vertex relationships and their degrees in our graph-theoretical framework.

E_{1} = \{u v є E (G) | d_{G} (u) = 2, d_{G} (v) = 2\}, |E_{1}| = 4 n + 5

E_{2} = \{u v є E (G) | d_{G} (u) = 2, d_{G} (v) = 3\}, |E_{2}| = 4 n + 2

E_{3} = \{u v є E (G) | d_{G} (u) = 3, d_{G} (v) = 3\}, |E_{3}| = 7 n - 1

Figure 4

Figure 4. Graphical representation of Triangular γ-graphyne chain.

Clearly. We have $c_{u} = Δ (G) - d_{G} (u) + 1 = 4 - d_{G} (u),$

We know that there are three different types of reverse edges.

{C E}_{1} = \{u v є E (G) | c_{u} = 2, c_{v} = 2\}, |E_{1}| = 4 n + 5

{C E}_{2} = \{u v є E (G) | c_{u} = 2, c_{v} = 1\}, |E_{2}| = 4 n + 2

{C E}_{3} = \{u v є E (G) | c_{u} = 1, c_{v} = 1\}, |E_{3}| = 7 n - 1

Theorem 3.2.1. If G is a graph of the triangular chain γ-graphyne chain. Then, we have the

i. ${C M}_{1} (G) = 42 n + 24$

ii. ${C M}_{2} (G) = 31 n + 23$

iii. $H C M_{1} (G) = 128 n + 94$

iv. $H C M_{2} (G) = 87 n + 87$

Proof: our results using the reverse edge partition triangular chain γ-graphyne;

C M_{1} (G) = \sum_{u v є E (G)} (c_{u} {+ c}_{v})

= 4 (4 n + 5) + 3 (4 n + 2) + 2 (7 n - 1)

= 42 n + 24

C M_{2} (G) = \sum_{u v є E (G)} (c_{u} {\times c}_{v})

= 4 (4 n + 5) + 2 (4 n + 2) + 1 (7 n - 1)

= 31 n + 23

H C M_{1} (G) = \sum_{u v є E (G)} {(c_{u} {+ c}_{v})}^{2}

= 16 (4 n + 5) + 9 (4 n + 2) + 4 (7 n - 1)

= 128 n + 94

H C M_{2} (G) = \sum_{u v є E (G)} {(c_{u} {\times c}_{v})}^{2}

= 16 (4 n + 5) + 4 (4 n + 2) + 1 (7 n - 1)

= 87 n + 87

Theorem 3.2.2. If G is a graph of the triangular chain γ-graphyne chain. Then, we have the

i. $C M_{1} (G . x) = (4 n + 5) x^{4} + (4 n + 2) x^{3} + (7 n - 1) x^{2}$

ii. $C M_{2} (G . x) = (4 n + 5) x^{4} + (4 n + 2) x^{2} + (7 n - 1) x$

iii. $H C M_{1} (G . x) = (4 n + 5) x^{16} + (4 n + 2) x^{9} + (7 n - 1) x^{4}$

iv. $H C M_{2} (G . x) = (4 n + 5) x^{16} + (4 n + 2) x^{4} + (7 n - 1) x$ partition triangular chain γ- graphyne;

C M_{1} (G . x) = \sum_{u v є E (G)} x^{(c_{u} {+ c}_{v})}

= (4 n + 5) x^{4} + (4 n + 2) x^{3} + (7 n - 1) x^{2}

C M_{2} (G . x) = \sum_{u v є E (G)} x^{(c_{u} {\times c}_{v})}

= (4 n + 5) x^{4} + (4 n + 2) x^{2} + (7 n - 1) x

H C M_{1} (G . x) = \sum_{u v є E (G)} x^{{(c_{u} {+ c}_{v})}^{2}}

= (4 n + 5) x^{16} + (4 n + 2) x^{9} + (7 n - 1) x^{4}

H C M_{2} (G . x) = \sum_{u v є E (G)} x^{{(c_{u} {\times c}_{v})}^{2}}

= (4 n + 5) x^{16} + (4 n + 2) x^{4} + (7 n - 1) x

4 Numerical and graphical results and discussions

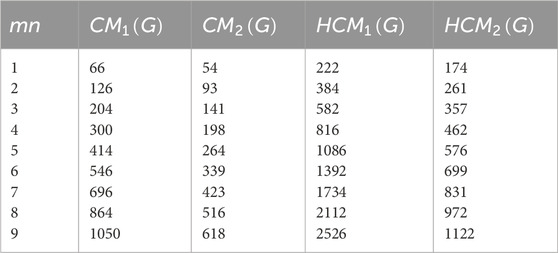
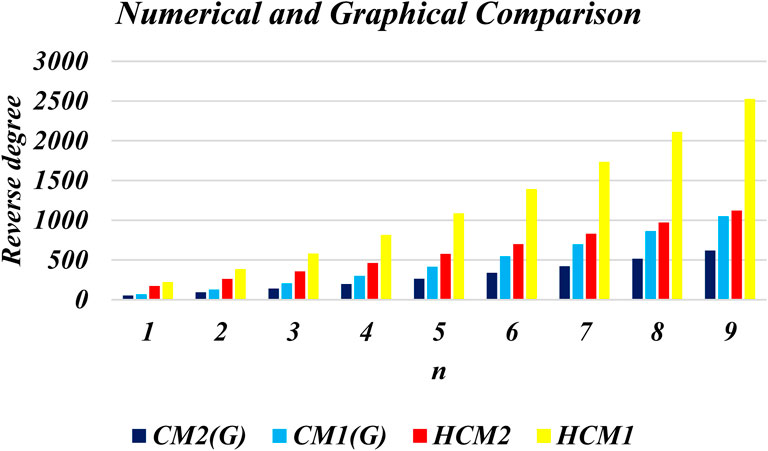
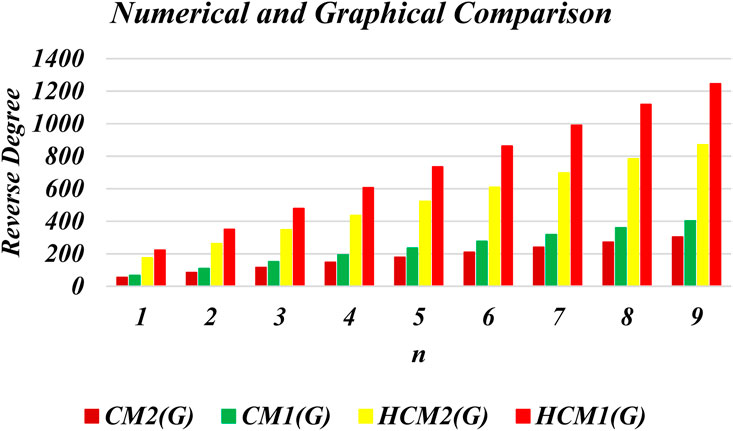
This section presents numerical and graphical results for the triangular γ-graphyne and triangular chain γ-graphyne via reverse degree-based topological indices. We compute numerical values for the first and second reverse Zagreb indices, as well as the first and second hyper-reverse Zagreb indices at different values of n, as seen in Tables 1, 2. Furthermore, we have plotted bar graphs to investigate the behavior of these topological indices at different n values, as given in Figures 5, 6. Additionally, we observed that the reverse first hyper Zagreb index has the highest value while the reverse second Zagreb index has the lowest value.

Table 1

Table 1. Numerical results of CM₁ (G), CM₂ (G), HCM₁ (G), and HCM₂ (G) for triangular γ-graphyne.

Table 2

Table 2. Numerical results of CM₁ (G), CM₂ (G), HCM₁ (G), HCM₂ (G) triangular chain γ-graphyne.

Figure 5

Figure 5. Graphical representation of triangular γ- graphyne.

Figure 6

Figure 6. Graphical representation of triangular γ-graphyne chain.

5 Conclusion

An edge partitioning technique based on graph theory is used on the molecular topology of γ–graphyne. Mathematical closed-form formulas are derived for several of its significant degree-based molecular descriptors. The results show that the reverse first hyper Zagreb index has the highest value. It is observed that the reverse first hyper Zagreb index has high predictive performance among all the other computed molecular descriptors. These numerical values signify various physicochemical properties of triangular γ-graphyne and chain triangular γ-graphyne. The results obtained in this study will help to investigate the structure-property relationships in γ-graphyne. In future research, we plan to calculate entropy, Mpolynomial indices, Zagreb connections, and distancebased topological indices to further characterise the molecular structure of Triangular γ–Graphyne and Triangular γ–Graphyne chain. Such analysis will provide additional insight into the properties and behaviour of these materials, and may contribute to their potential applications in various fields.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

AH: Conceptualization, Investigation, Software, Writing–original draft, Writing–review and editing. NK: Data curation, Methodology, Supervision, Writing–original draft. HS: Formal Analysis, Project administration, Validation, Writing–original draft. FT: Funding acquisition, Resources, Writing–review and editing. OA: Methodology, Validation, Visualization, Writing–review and editing.

Funding

The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Balaban AT, Devillers J. Topological indices and related descriptors in QSAR and QSPAR. CRC Press (2014).

Google Scholar

2. Dobrynin AA, Kochetova AA. Degree distance of a graph: a degree analog of the Wiener index. J Chem Inf Computer Sci (1994) 34(5):1082–6. doi:10.1021/ci00021a008