- 1Department of Physics, Institute for Fusion Studies, University of Texas at Austin, Austin, TX, United States
- 2Oak Ridge National Laboratory, Oak Ridge, TN, United States
- 3Department of Physics, Universidad Carlos III de Madrid, Madrid, Spain
The development of reduced models provide efficient methods that can be used to perform short term experimental data analysis or narrow down the parametric range of more sophisticated numerical approaches. Reduced models are derived by simplifying the physics description with the goal of retaining only the essential ingredients required to reproduce the phenomena under study. This is the role of the gyro-fluid code FAR3d, dedicated to analyze the linear and nonlinear stability of Alfvén Eigenmodes (AE), Energetic Particle Modes (EPM) and magnetic-hydrodynamic modes as pressure gradient driven mode (PGDM) and current driven modes (CDM) in nuclear fusion devices. Such analysis is valuable for improving the plasma heating efficiency and confinement; this can enhance the overall device performance. The present review is dedicated to a description of the most important contributions of the FAR3d code in the field of energetic particles (EP) and AE/EPM stability. FAR3d is used to model and characterize the AE/EPM activity measured in fusion devices as LHD, JET, DIII-D, EAST, TJ-II and Heliotron J. In addition, the computational efficiency of FAR3d facilitates performing massive parametric studies leading to the identification of optimization trends with respect to the AE/EPM stability. This can aid in identifying operational regimes where AE/EPM activity is avoided or minimized. This technique is applied to the analysis of optimized configurations with respect to the thermal plasma parameters, magnetic field configuration, external actuators and the effect of multiple EP populations. In addition, the AE/EPM saturation phase is analyzed, taking into account both steady-state phases and bursting activity observed in LHD and DIII-D devices. The nonlinear calculations provide: the induced EP transport, the generation of zonal structures as well as the energy transfer towards the thermal plasma and between different toroidal/helical families. Finally, FAR3d is used to forecast the AE/EPM stability in operational scenarios of future devices as ITER, CFETR, JT60SA and CFQS as well as possible approaches to optimization with respect to variations in the most important plasma parameters.
1 Introduction
Substantial efforts have been dedicated to analysis of the effects of energetic particle components (EP) on plasma stability over several decades, leading to a reasonably good understanding of the phenomena in present day devices. Nevertheless, some open questions still remain with respect to the EP driven instability in burning plasmas, especially with multiple EP populations, as will be present in future fusion reactors. Future fusion regimes will deviate from existing experiments, such as the last Deuterium-Tritium JET campaign, which had only a negligible density of alpha particles. In addition, the consequences of Alfvén Eigenmodes (AE) on the transport of fusion produced alpha particles, energetic hydrogen neutral beams or particle heated using ion cyclotron resonance heating (ICRF) is not well understood yet [1–3]. Experiments in tokamaks as TFTR, JET and DIII-D or stellarators as LHD and W7-AS measured the excitation of AE, leading to a drop of the device performance [4–9]. The resonance of energetic particles with velocities similar or a fraction of the Alfvén velocity can destabilize the plasma driving instabilities that enhance particle losses, leading to a lower heating efficiency, more restrictive operation requirement for plasma ignition and also an enhancement of the EP losses [10–14]. Future fusion devices will require extrapolations to energetic particle distributions that may deviate from present day experiments, with a special attention to the EP gyroradius/minor radius, Alfvén Mach number
The frequency of EP-driven modes depends on the drive induced by the gradients of the EP distribution function, particularly the density gradient; the dispersion relation of EP-driven instabilities can be expressed by an implicit equation for
Alfvén Eigenmodes are driven in the spectral gaps of the shear Alfvén continua [32, 33], destabilized by super-Alfvénic alpha particles and energetic particles from external sources (e.g., beams, ICRF tails). AE activity has been observed in several different discharge regimes and configurations [34–37]. The different Alfvén eigenmode families (
There are different strategies to improve the AE/EPM stability in nuclear fusion devices. Towards that goal, the destabilizing effect of the EPs can be analyzed with respect to the EP population features, the thermal plasma parameters and the magnetic field configuration. An example is the application of external actuators such as neutral beams (NBI) that can alter the magnetic field topology through the generation of non inductive currents [54, 55]. Neutral beam current drive (NBCD) can be used to achieve steady state operation in advanced tokamaks [56–58] or to modify the magnetic field configuration [59–62]. NBCD can also affect the stability of AEs [63, 64]. Another technique is the injection of ECW [65, 66] that also generate non inductive currents in the plasma. In particular, the electron cyclotron current drive (ECCD) [67–71] can improve the stability of the pressure/current gradient driven modes and AEs in tokamaks [72–77] and stellarators [78–82]. Regarding the thermal plasma parameters, a modification of the thermal ion density changes the plasma Alfvén velocity (defined as
The coexistence of multiple EP species also affects the AE stability of fusion devices. This effect was originally observed in early DT experiments on the TFTR device, which had both fusion alpha populations that coexisted with the neutral beam ions used for heating. Alpha particle driven AEs were stabilized by the presence of NBI driven EP species through Landau damping on the lower energy NBI ions. Alpha-drive AEs were only measured at the end of the discharge after the beam injection was turned off [93–95]. Numerical studies using the TAEFL gyrofluid model were used to develop an optimization strategy for the TFTR DT plasma by increasing
The present review is dedicated to summarizing the different strategies that have been used to improve the AE stability in nuclear fusion devices based on comparisons between experiment and numerical models. In particular, the discussion is based on the simulations performed by the gyro-fluid FAR3d code [97, 105–109]. The numerical model, with the appropriate Landau closure relations, solves the reduced non-linear resistive MHD equations including the linear wave-particle resonance effects required for Landau damping/growth [110]. The code follows the evolution of MHD and Alfvén frequency instabilities, based on starting from equilibria, calculated by the VMEC or EFIT codes [111, 112].
The main motivation of performing the analysis with the gyro-fluid code FAR3d is the computational efficiency; this is due to its reduction of selected kinetic effects to a set of 3D fluid-like equations rather than more complex approaches, for example initial value gyrokinetic codes as EUTERPE [113], GEM [114], GYRO [115], GTC [116], ORB5 [117] and GENE [118] or kinetic-MHD hybrid codes as MEGA [119] and M3d-C1 [120]. FAR3d can be used for rapid parameter/profile scans in order to perform optimization/design studies, which are facilitated by the efficient evaluation of physics target functions. Also, the code can be used to identify AE stability trends since critical fast ion characteristics, such as the density profile often cannot directly be measured. It should be noted that the Landau closure model used in the FAR3d code leads to an eigenmode equation, which can be analyzed in similarity to the linear gyrokinetic code LIGKA [121] and the linear kinetic-MHD code MARS-K [122]. Finally, in comparison to particle-based methods, this approach has the advantages of zero noise levels, exact implementation of boundary conditions and an improved ability to include extended mode coupling effects. On the other hand, the simplification of the kinetic effects can lead to a deviation of FAR3d results compared to more complete approaches, although a methodology has been developed for calibrating the Landau-closure against more complete kinetic models through optimization of the closure coefficients [110]. A detailed comparison between FAR3d and other gyro-fluid, gyro-kinetic and hybrid codes was recently performed [123]. Consequently, FAR3d is a tool that complements more complex numerical models by providing a first estimate of AE/EPM linear and non-linear stability, helping to narrow down the parameter selection for the resonance identification with respect to the experimental observations [124]. In addition, the computationally efficient analysis that FAR3d offers can provide a new tool for fast experimental data interpretation and aid in the design of future devices.
This paper is organized as follows. First, a description of the numerical model and simulation parameters is given in Section 2. A description of the research methodology is included in Section 3. The analysis of the AE/EPM activity in different devices is discussed in Section 4. Optimization strategies to minimize the AE/EPM activity is introduced in Section 5. The analysis of the nonlinear AE/EPM saturation phase is done in Section 6. Predictions of the AE/EPM stability in future fusion devices is mentioned in Section 7. The main finding of the FAR3d research lines, the discussion of advantage and drawback of the model and bench-marking with other codes are introduced in Section 8. Next, the conclusions of this paper are presented in Section 9. Finally, ongoing and future research topics as well as projected code updates are commented in Section 10.
2 Numerical model
This section is dedicated to discuss the main features of the FAR3d code. Details of the main model equations, EP distribution function, damping effects and trapped EP operator are introduced. Moreover, the numerical method used to solve FAR3d model is briefly discussed. For a further detailed discussion of the FAR3d code equations and derivation.
2.1 Model equations
The model is based on reduced MHD with acoustic couplings for the thermal plasma and a two-pole (two moments) energetic ion closure model, leading to a six evolution equations for the perturbed poloidal magnetic flux
The model formulation assumes high aspect ratio, medium
where
The evolution equations of the perturbed quantities are:
Equation 2 is derived from Ohm’s law coupled with Faraday’s law, Equation 3 is obtained from the toroidal component of the momentum balance equation multiplied by the operator
Here the
We also define the parallel gradient, perpendicular gradient squared (lowest order) and curvature operators as
with the Jacobian of the transformation,
with
Equations 4, 5 introduce the parallel momentum response of the thermal plasma. These are required for coupling to the geodesic acoustic waves, accounting for the geodesic compressibility in the frequency range of the geodesic acoustic mode (GAM) [110]. The coupling between the equations of the EP and thermal plasma is done in the equation of the perturbation of the toroidal component of the vorticity (Equation 3) introducing the EP destabilizing effect caused by the gradient of the fluctuating EP density/pressure.
Equilibrium flux coordinates
Two versions of the FAR3d code have been developed: nonlinear and linear. The linear version is designed to solve the linearized system of equations, facilitating the study of linear phases of different instabilities and phenomena (e.g., determining growth rates, spatial scales, and frequencies), and enabling rapid parametric studies to explore the parameter space associated with each magnetic equilibrium computed via equilibrium codes. The nonlinear version is dedicated to study the instabilities saturation phase and their long-term behavior, providing information of the EP transport induced by AEs and thermal plasma instabilities, the generation of zonal structures as well as nonlinear couplings between perturbations and thermal plasma, different toroidal mode families and EP species. The nonlinear version utilizes MPI parallelization over toroidal mode groups for the linear solver and over radial domains for the nonlinear convolution products coupled with OpenMP parallelization over loops; a GPU-based version has also been recently developed.
Two numerical schemes to solve the linear equations can be used in the code: a semi-implicit initial value or an eigenvalue solver. The initial value solver calculates the mode with the largest growth rate (dominant mode) and the eigen-solver provides both the stable and unstable modes (sub-dominant modes). The eigensolver uses a Jacobi-Davidson algorithm, which allows solutions near targeted values of frequency/growth rate. The analysis of the sub-dominant modes is required to calculate the growth rate of the multiple AE families that can be unstable or marginally unstable during the discharge. In addition, the study of the sub-dominant modes is motivated by the fact that the equilibrium profiles are not known precisely from the experiment. This can result in a more close correspondence of sub-dominant modes with the experimentally observed modes than the fastest growing mode. In this way, the eigenmode can provide an uncertainty characterization both in the modeling and the measurements.
A finite difference method is applied for the radial discretization, while Fourier expansions are used for poloidal and toroidal directions. The numerical scheme employs semi-implicit discretization for linear terms and explicit one for nonlinear terms using a two semi-step method to ensure
2.2 Trapped EP approximation
The effect of helically or toroidally trapped EPs are introduced in the model through modification of the average drift velocity operator normally designed to model passing EP average drifts). Using the expressions 6.72, 6.77 and 6.83 of the Ref. [127], the trapped EP trajectory can be derived in the
Here,
The bounce length of the guiding center
Here,
fixed the canonical and magnetic momentum of the trapped EP participating in the resonance. The bounce velocity and distance are linked to the parallel canonical and magnetic momentum as:
with the pitch angle of the trapped EP defined as
Now, the expression of the bounce length is replaced in the Equations 14, 15, extracted from the integral by assuming, as first order approximation, no radial or angular dependency of the bounce length is included in the model, thus:
defining the bounce velocity of the guiding center as
Next, the Jacobian is extracted from the integral because it is an equilibrium variable independent of the time. Consequently:
The modified operator to describe the averaged drift velocity of the trapped particles
thus, the modified operator of the drift velocity of the trapped particles is (after normalization):
The new drift velocity operator includes information of the bounce frequency and length of the guiding center of the trapped EP. Using the correct set of bounce frequency and length values the resonance induced by barely or deeply trapped EP can be approximated. In addition, a first order estimation of the resonance caused by EPs with different pitch angles can be obtained.
2.3 EP distribution function
The FAR3d two-moment gyro-fluid model is based on a two-pole approximation to the resonant response function (equivalent to a Lorentzian distribution function) that can be approximately matched to a Maxwellian or to a slowing-down distribution by choosing an equivalent average energy. The EP distribution in the model is a Maxwellian which has the same second moment, the effective EP temperature, as that of the equivalent slowing-down distribution defined below [128, 129]:
and the Maxwellian distribution as:
where
with
The assumption of the model is that the averaged Maxwellian energy can be matched to the thermalized energy of the EP, thus:
with
with
Here,
2.4 Damping effects
EP FLR effects in the gyrokinetic equation and gyro-Landau closure model enter in through the functions
here,
These operators can be inverted by identifying
Then, after multiplying through by
that define the functions W and Q in terms of the evolving dynamical variable
with
The EP FLR term in the parallel velocity moment equation is:
with
The contribution of the electron-ion Landau damping effect is included in the vorticity equation through a term of the form:
with
2.5 Simulation equilibria and parameters
FAR3d can use equilibria calculated by either the VMEC or EFIT codes [111, 112]. VMEC and EFIT data is first transformed to Boozer coordinates; then, the metric elements and various combinations of equilibrium magnetic data are produced as input to FAR3d.
The main profiles of the model require an initial input that can be introduced using analytical expressions or experimental data, particularly the thermal electron/ion density and temperature, EP density and energy as well as the equilibrium toroidal plasma rotation (Doppler effect).
The dynamic and equilibrium toroidal and poloidal modes used in the simulations are chosen to resolve the range of surfaces that characterize the instability of interest. In linear simulations, the equilibrium modes (
The dynamic variables add both mode parities because the moments of the gyro-kinetic equation break the MHD symmetry. The convention used by the code for the Fourier decomposition is, taking the example of the pressure:
The same way, the eigenfunction can be also expressed in terms of real (R) and imaginary (I) components:
Equilibrium variables also may include both parities if up-down asymmetric configurations are analyzed (e.g., a tokamak with a single-null divertor).
It should be noted that for all of the cases discussed it is assumed that the AE/EPM are destabilized by passing EP, that is to say, the pitch angle of the EPs is assumed to be zero. The only exception is the analysis of the EIC in LHD plasma including the trapped EP approximation. A detail analysis of the EP-driven mode stability with respect to the EP bounce distance and frequency is performed in Ref. [131]. The analysis identifies a resonance leading to the destabilization of a
3 Analysis methodology
Fast tools dedicated to analyze the AE/EPM stability are required to provide timely support/interpretation during and in between experimental campaigns. It is well know there is a time gap between theoretical analysis and experimental results caused by the large computational demand of gyro-kinetic and hybrid codes as well as the accuracy of the input data (profiles, equilibrium, realistic EP distributions, etc), leading to a time-lag between experimental group observations and theory attainments. Reduced models can cover this gap providing a first characterization of the AE/EPM activity observed in the experiment as well as useful information of the AE/EPM stability trend with respect to the main operation parameters of the device.
The FAR3d code is routinely used in several research institutions as a means to provide theoretical support for experimental groups in the analysis of the AE/EPM activity. FAR3d studies consist in identifying the EP resonance that causes the destabilization of the AE/EPM by comparing code output and experimental data. A successful instability identification requires the dominant modes, frequency range, radial location and eigenfunction structure obtained in the linear simulations must be consistent with the experimental observations. Towards that aim, the simulation results are compared with the magnetic fluctuations measured by Mirnov coils or Langmuir probes
Once the AE/EPM activity in the experiment is reproduced, the next step of the analysis consist in the identification of operation scenarios with reduced AE/EPM activity. On that aim, parametric studies are performed to identify optimization trends with respect to different simulation variables directly connected to experimental parameters. The analysis provides information about configurations that may show improved AE/EPM stability. Promising operational scenarios that can be explored in the device are suggested and dedicated experiments are performed. Some examples of these studies are discussed in Section 5.
Linear simulations are useful to identify the instabilities that can be triggered in a given configuration but not how such perturbations will evolve in time, that is to say, no information of the instability saturation is provided. Consequently, it is mandatory performing nonlinear simulations to study the saturation phase of AE/EPM, in particular the induced EP transport, the energy exchange between different toroidal/helical families and the thermal plasma as well as the generation of zonal structures. There is experimental evidence of the important effects of the AE/EPM saturation on the confinement of nuclear fusion devices, in particular the bursting activity which is characterized by transitory strong magnetic fluctuations and large EP losses. Such instabilities are caused by presence of a wide single AE/EPM or the overlapping of individual AEs/EPMs. This kind of analysis is included in Section 6.
Another topic to study is forecasting possible AE/EPM stability issues of future devices, in particular if the device is able to explore reactor relevant configurations. This is the case of devices as JT60SA, ITER or DEMO. In addition, smaller devices dedicated to explore interesting magnetic field symmetries are also explored, identifying the benefits of such symmetries on the plasma AE/EPM stability. Such studies are introduced in Section 7.
4 Identification of AE/EPM
The first applications of the FAR3d code were dedicated to analyze the AE stability in the stellarators LHD and TJ-II. These devices use tangential NBIs to heat the plasma by injecting neutrals up to 180 keV in the case of LHD and 40 keV in the case of the TJ-II plasma [133, 134]. In addition, LHD can also heat the plasma periphery using perpendicular NBIs by injecting 32 keV neutrals. Strong NBI injection leads to the destabilization of AE/EPM in LHD [53, 135–137] and in TJ-II discharges [138, 139]. In the following, a mode is identified as a AE if the perturbation eigenfunction is fully located in the frequency range and radial location of an Alfvén gap. On the other hand, a mode is identified as an EPM if the perturbation eigenfunction crosses the continuum and the maximum of the mode amplitude is located inside the continuum.
4.1 Stellarator: large helical device
The EP resonance is particularly intense in LHD operation scenarios with low magnetic field and density, leading to the destabilization of AEs if the plasma is strongly heated by the tangential NBIs. Particularly, high thermal
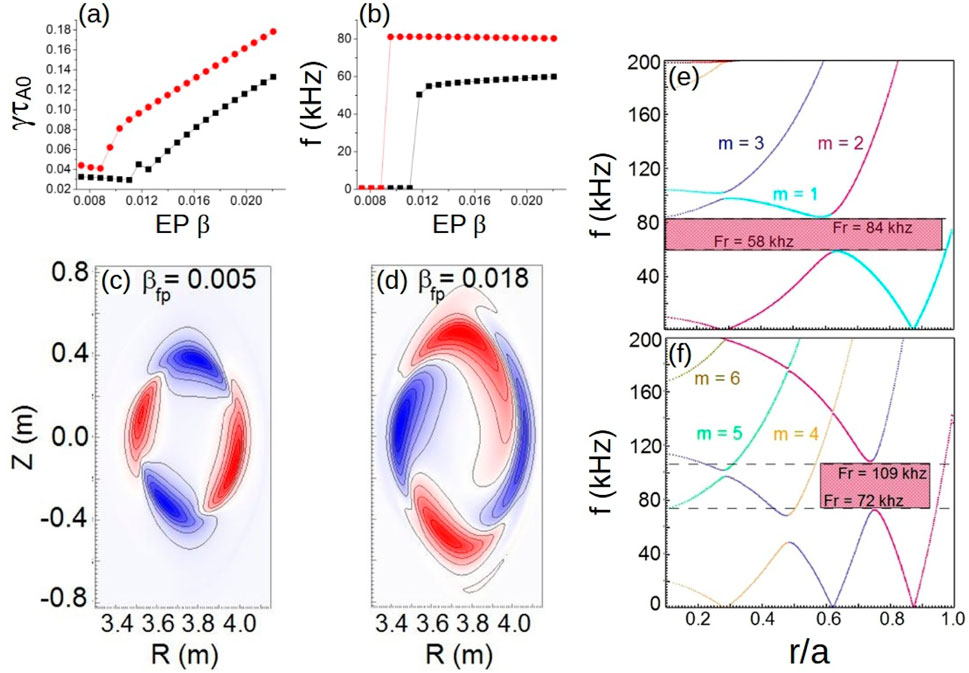
Figure 1. Analysis of TAE stability in LHD plasma. Growth rate (A) and frequency (B) of
Another dangerous instability observed in LHD plasma is the energetic-ion-driven resistive interchange mode (EIC), destabilized in discharges with low density and high ion temperature if the plasma is heated by perpendicular and tangential NBIs; these show magnetic fluctuations similar to the fishbone oscillations [84, 145]. In these discharges, the
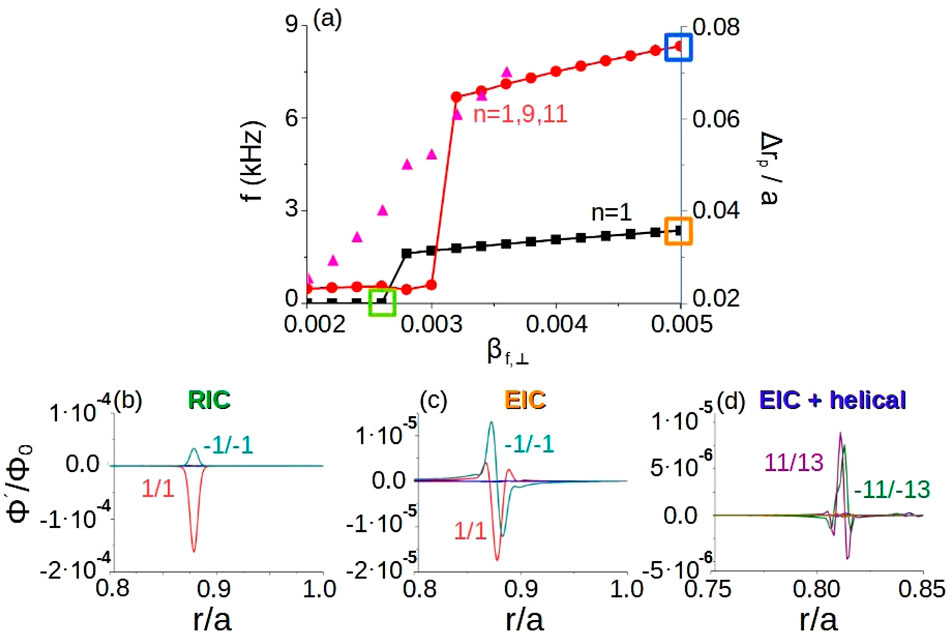
Figure 2. Analysis of the EIC stability in the LHD plasma. (A) Perturbation frequency for different values of the EP
4.2 Stellarator: TJ-II
TJ-II plasmas heated by “co-/counter-” injected NBI along/against the toroidal field show an increase/decrease of the rotational transform by the NBI driven currents. The NBIs destabilize multiple AEs in the range of 150–300 kHz, resulting in frequency sweeps that are connected to the evolution of the iota profile [138, 139]. The FAR3d code was used to analyze the AE destabilization by EPs in different TJ-II configurations, comparing simulation results and experimental observations, reproducing the AE frequency sweeping as the rotational transform profile is modified by the current induced by the NBI [152]. Figure 3, panels a, indicates that the dominant mode in the simulation changes as the iota profile is modified, showing an anti-correlation between the growth rate of different helical families. Panel b shows the sweeping of the mode frequency as the iota profile is displaced, similar to the experiment observations. Panels c to f indicate the radial displacement, frequency range variation and opening/closing of the Alfvén continuum gaps as the iota profile is displaced. The evolution of the gaps may explain the modification of the AE stability observed in the experiment. Panels g to i show the destabilization of
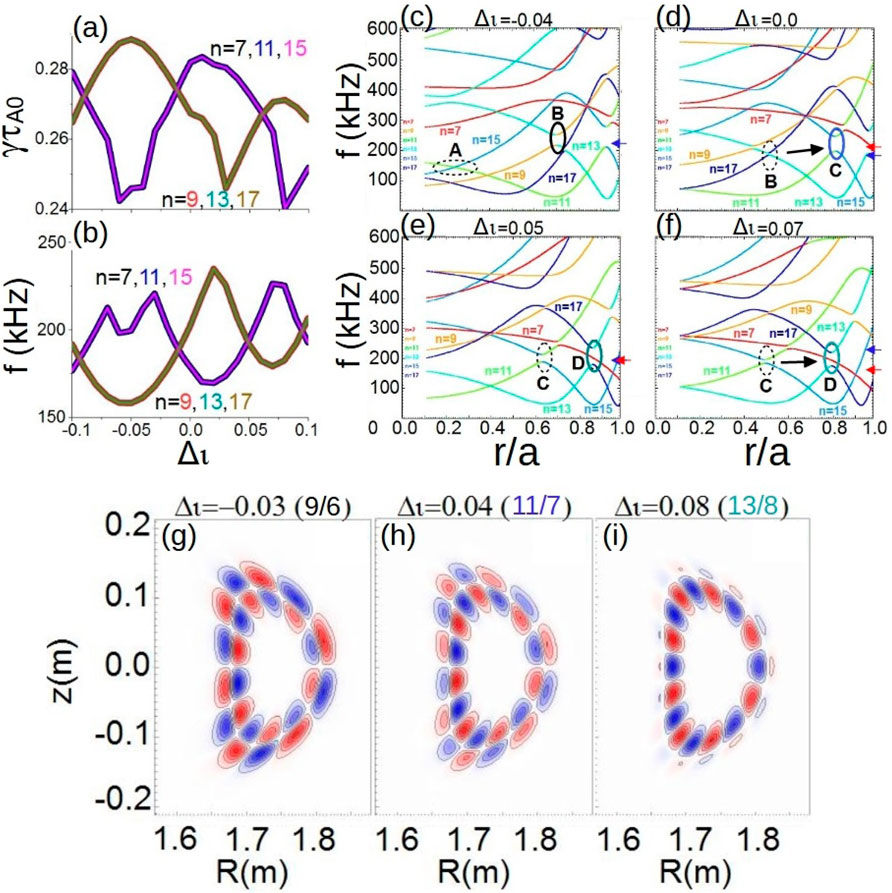
Figure 3. Analysis of HAE stability in the TJ-II plasma. (A) Growth rate and (B) frequency of the simulation dominant modes if the iota profile is displaced by
The combination of NBI heating with electron cyclotron heating (ECH) and electron cyclotron current drive (ECCD) in TJ-II plasma lead to a modification of the AE activity observed in the experiments [153]. Several TJ-II operational scenarios are explored using FAR3d to identify and characterize the unstable AEs for discharges combining NBI with ECH/ECCD injection. Figure 4, panels a to d, shows the AE activity measured in the discharge 44,257 heated only by the NBI. AEs are triggered in a rather narrow frequency range around 100 and 200 kHz as well as chirping AE activity between 160 and 210 kHz observed from
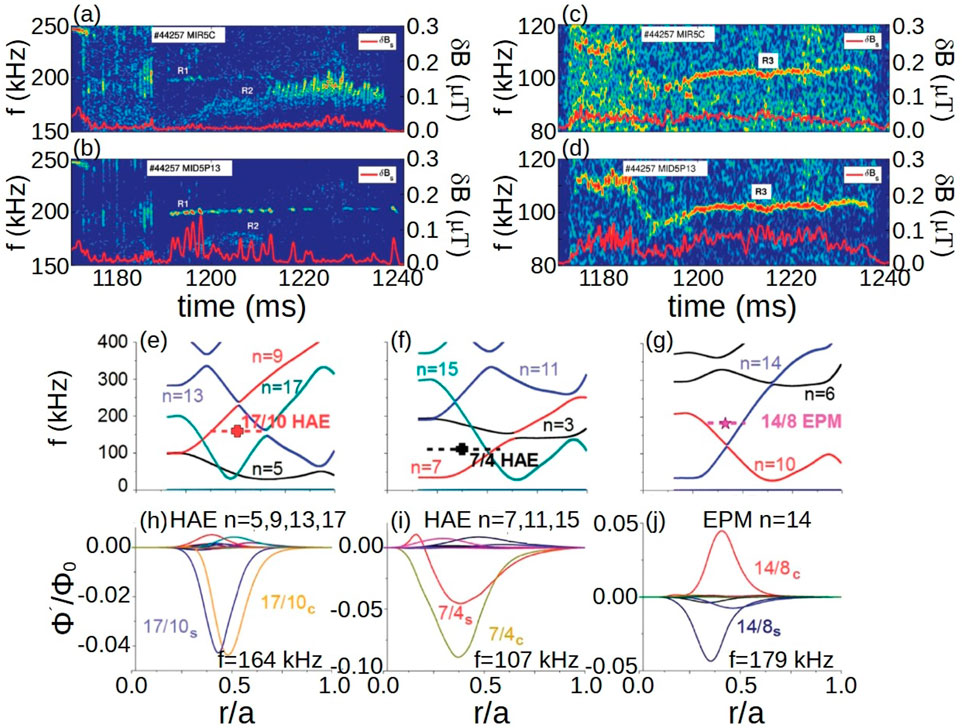
Figure 4. Analysis of AEs destabilized in NBI heated TJ-II plasma. Magnetic fluctuations spectrograms in the
The effect of the iota profile evolution on the AE stability is further analyzed in TJ-II plasma by modifying the current flowing in the vertical field coils of the device, performing experiments that show oscillating patterns of the AE frequency [154]. FAR3d is used to reproduce the AE frequency sweeping as the current in the vertical field coils changes and modifys the iota profile. Figure 5, panel a, shows the sweeping of the measured AE frequency along the discharge as successive maxima and minima correlated with the up or down-shift of the iota profile. Panel b indicates the AE frequency sweeping calculated by FAR3d approximately reproduces the experimental observation. Panel c shows the
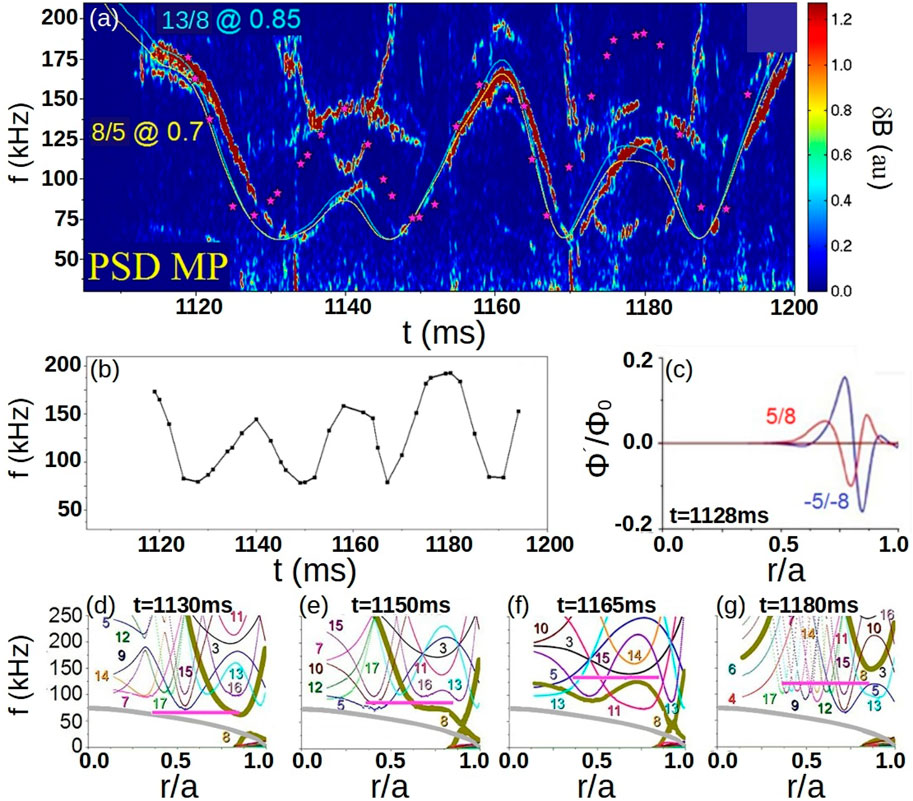
Figure 5. Analysis of AEs frequency sweeping in TJ-II plasma. (A) Power spectrogram of magnetic fluctuations measured by the Mirnov probes. The blue and yellow lines indicate the analytical prediction of
4.3 Tokamak: DIII-D
The FAR3d code is also used for analyzing AE instabilities in tokamak devices. AE activity induced by strong NBI heating has been extensively studied in the DIII-D device, detecting a large variety of Alfvénic instabilities as GAE [159], TAE [160], RSAE [161], BAE [162], EAE [163] and NAE [32]. The NBI system in DIII-D can provide up to 20 MW of injection heating power with EPs in the energy range of 40–85 keV. AE instabilities caused by the NBIs reduce DIII-D performance, increasing the EP transport and enhancing energetic particle losses [164–166]. FAR3d was applied to study the AEs destabilized at the DIII-D pedestal during transient thermal
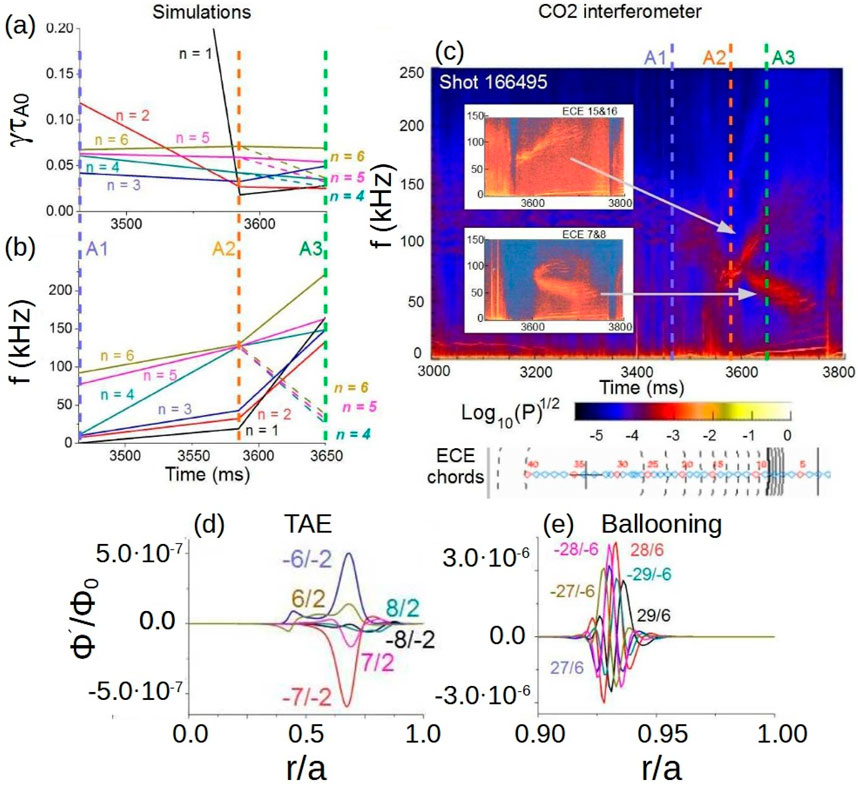
Figure 6. Analysis of the AEs destabilized in DIII-D high poloidal
AE destabilization in advanced DIII-D high poloidal
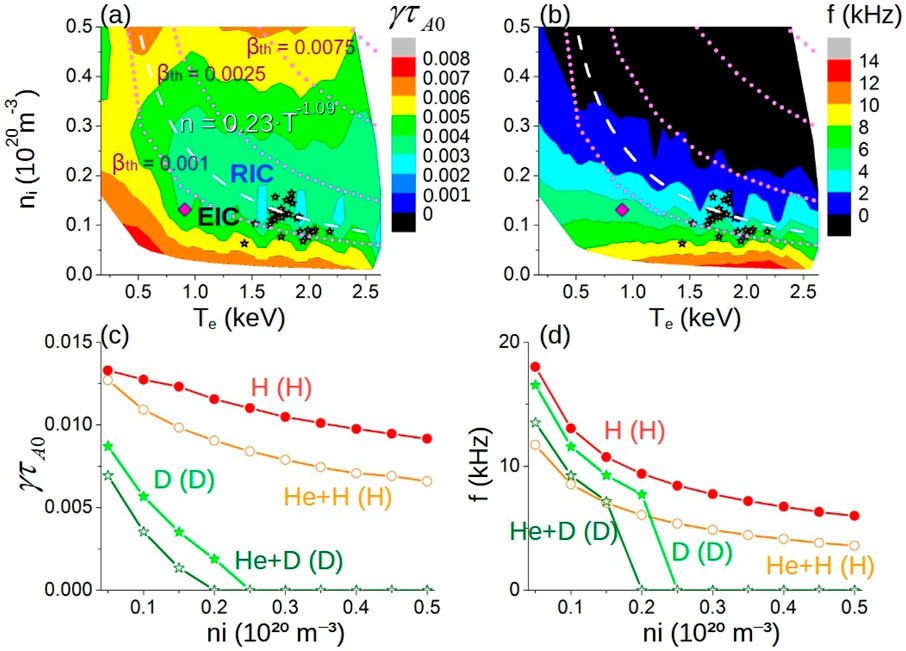
Figure 7. Analysis of EIC stability trends in LHD plasma. (A) Growth rate and (B) frequency of the instabilities in simulations with different values of the thermal plasma ion density and electron temperature at the
4.4 Tokamak: EAST
Another example dedicated to tokamaks is the study of the AE activity in the Experimental Advanced Superconducting tokamak (EAST) discharges with high thermal
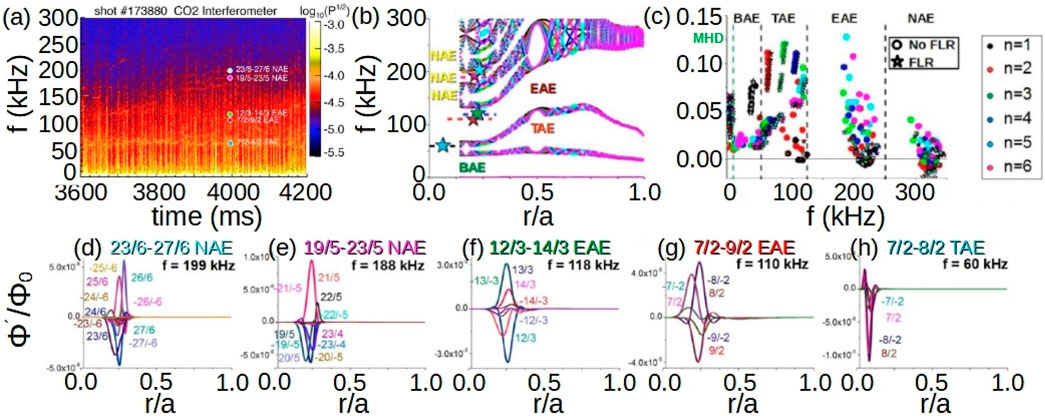
Figure 8. Analysis of the AE stability in DIII-D high poloidal
FAR3d has also participated in other research efforts dedicated to identify AE activity in the LHD [92, 187], TJ-II [188, 189], JET [190], EAST [191] and Heliotron J [192] plasmas; the simulations show a reasonable agreement with the experimental data. Once the AE activity is validated with the code, optimization studies can be performed to identify operational scenarios resulting in reduced AE activity which may lead to reduced EP transport and improved plasma heating performance. Such analysis is the topic of the next section.
5 Optimization studies
There are different techniques to reduce the AE/EPM activity in fusion devices, for example, modifying the properties of the thermal plasma and magnetic field configuration, applying external actuators (NBI, ECH, ECCD) or the interaction between different EP species present in the plasma [193]. This section is dedicated to a discussion of the application of FAR3d to explore different optimization strategies.
5.1 Effect of the thermal plasma
Modifying the thermal plasma properties can influence AE stability through various channels. A change of the thermal plasma density and temperature modifies the EP resonance energy (through changes in the Alfvén velocity), EP slowing down time, plasma resistivity as well as continuum, FLR and electron-ion Landau damping effects. Consequently, an optimized selection of the thermal plasma properties may lead to configurations with reduced AE activity. It must be recalled the EP resonance associated with EPM destabilization is not affected by a modification of the thermal plasma density/temperature; however, the Alfvén gap structure, FLR and electron-ion Landau damping effects will change. For this reason the EPM growth rate and frequency can also depend on thermal plasma properties.
In the LHD stellarator, several stabilization strategies to mitigate the
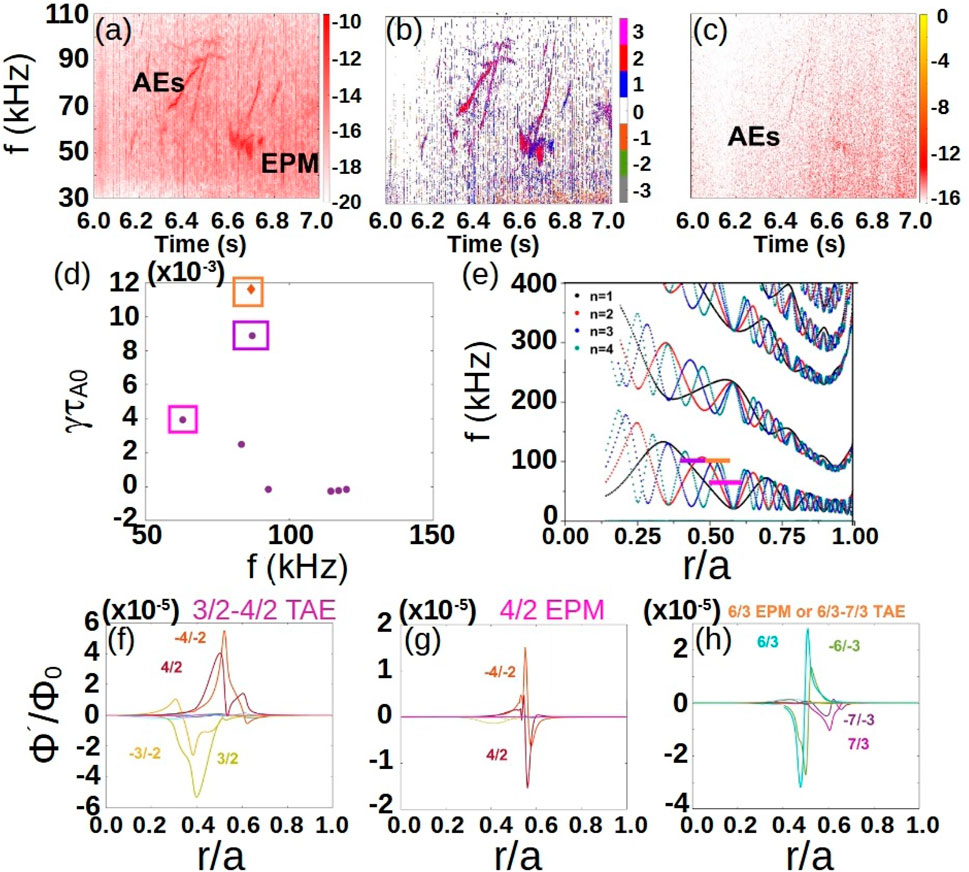
Figure 9. Analysis of AE/EPM destabilization in EAST after Tungsten plasma contamination. (A) Magnetic perturbations measured by Mirnov coils, (B) toroidal mode number of the instability and (C) ECE diagnostic data at
5.2 Effect of the magnetic field configuration
The analysis of the plasma and EP stability for stellarator fusion devices with different magnetic field configurations (i.e., types of quasi-symmetry) is essential for the design and optimization of future stellarator reactors. Examples of devices taking advantage of quasi-symmetries are the Chinese First Quasi-Axisymmetric stellarator (CFQS) [195–197] and National Compact stellarator Experiment (NCSX) [198], the Quasi Poloidal stellarator (QPS) [199] and the Helically Symmetric Experiment (HSX) [200]. In addition, there are generalized symmetries such as omnigenity where the mean radial collisionless guiding center magnetic drift is minimized, leading to good collisionless orbit confinement [201]. The optimization of the AE stability in these configurations is important in order to attain efficient plasma heating, reduce operational power requirements and improve the economic viability of reactor devices.
The CFQS plasma will be heated by a tangential neutral beam injector (NBI) with an injection energy of 30 keV and a power of 0.9 MW that may lead to the destabilization of AEs [202]. FAR3d was applied to study the AE destabilization threshold of
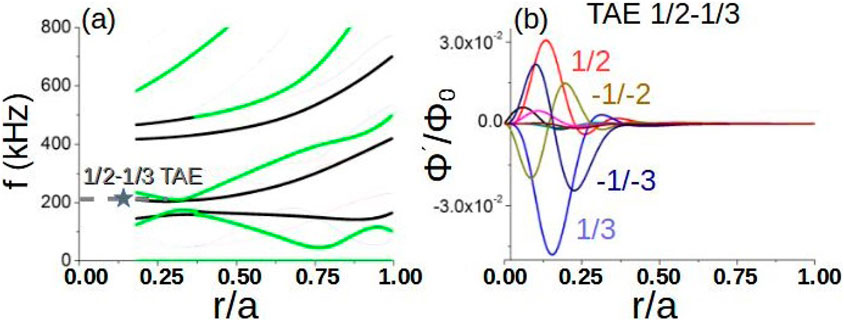
Figure 10. Analysis of the AE stability of CFQS plasma. (A) Alfvén continuum for the CFQS configurations if the thermal
Another example is the QPS design that combines quasipoloidal symmetry and low aspect ratio [204, 205] to achieve particle and energy confinement at high
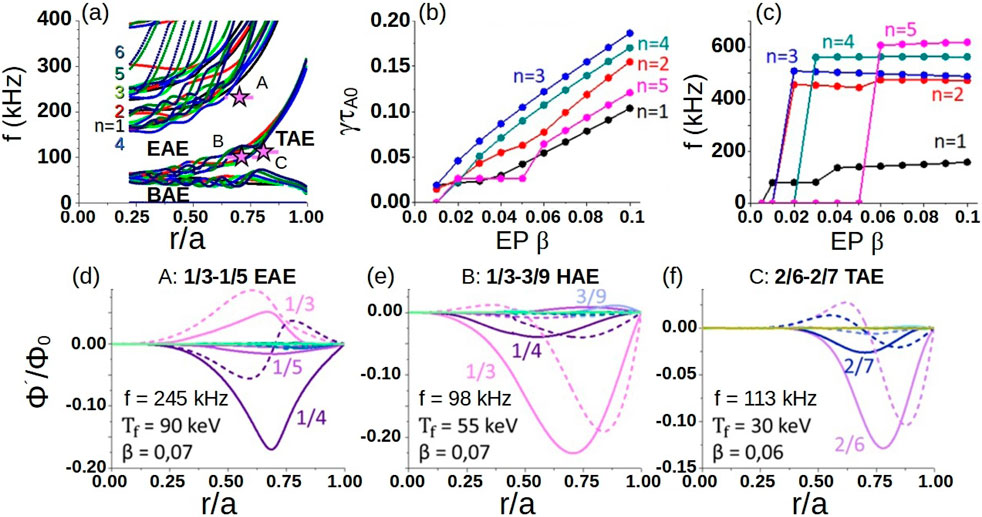
Figure 11. Analysis of the AE stability in QPS plasma. (A) Alfvén continuum of the configuration with two magnetic field periods and finite thermal
Advanced tokamak operation scenarios can be attained by modifying the magnetic field configuration, for example generating wide reverse magnetic shear regions in the plasma [210, 211]. Nevertheless, AE stability in such configurations could be unfavorable for an efficient plasma heating. Reverse magnetic shear discharges are extensively studied in the DIII-D device [212–214] showing a large fraction of bootstrap current [215, 216] and improved MHD stability [217–219]. These configurations have been selected as a base line scenario for ITER and DEMO [220–222], although an enhancement of the energetic particle transport by unstable AEs was measured [42, 165, 223]. FAR3d is used to explore optimization pathways to improve thermal plasma and AE linear stability of DIII-D reverse magnetic shear discharges [224]. It has identified configurations that minimize the growth rate of AE/thermal plasma instabilities for DIII-D discharges with different magnetic configurations and NBI operation regimes. This approach can be useful for optimizing device performance. Figure 12, panel a, indicate AE activity throughout the discharge measured by CO2 interferometry: burst activity at M10, constant frequency AE at M1A, up-sweeping frequency AE at M1B and weaker steady frequency AEs at M1C. In addition, magnetic diagnostic data in panel b shows
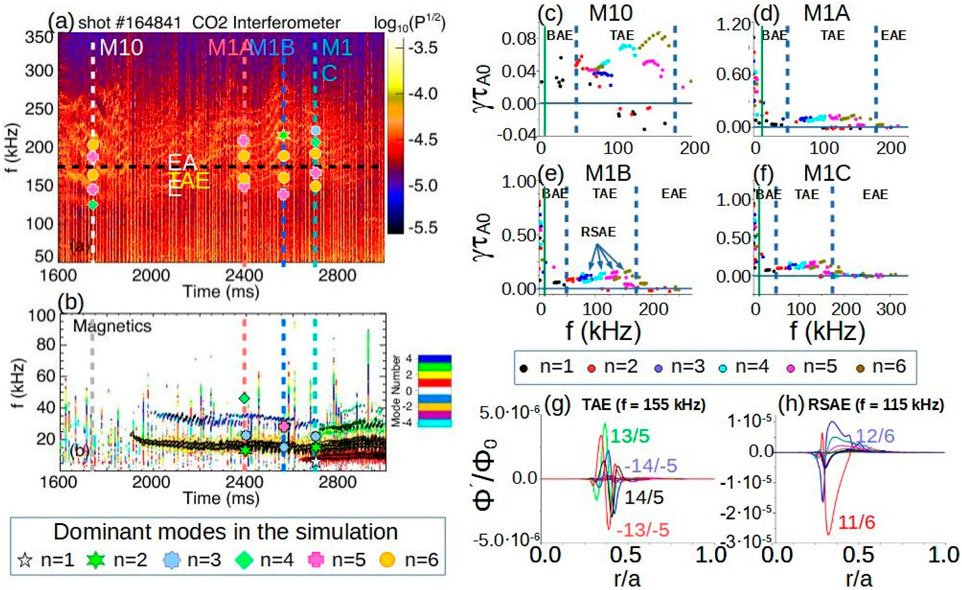
Figure 12. Stability of AEs in DIII-D reverse shear configurations. Instabilities measured along the shot 164,841 by (A) CO2 interferometer and (B) Mirnov coils: M10 (
Another example of optimization in tokamak devices are operational scenarios using negative triangularity plasma shaping (NT). NT configurations can reach a rather large thermal
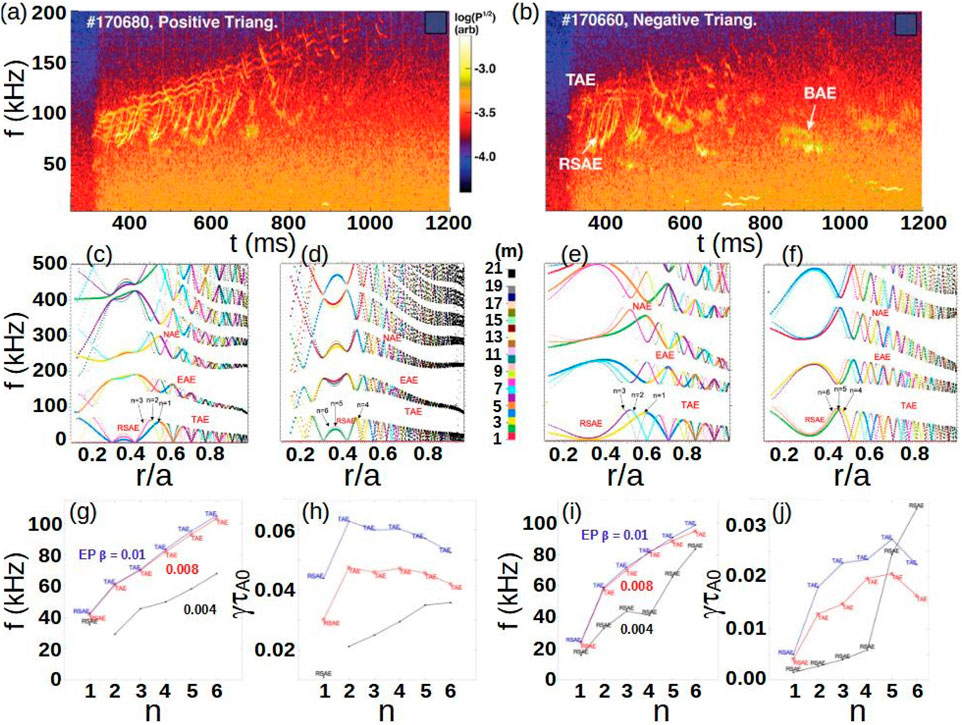
Figure 13. Stability of AEs in DIII-D negative triangularity discharges. ECE spectrogram of DIII-D (A) PT discharge 170,660 and (B) NT discharge 170,680. Alfvén continuum plots of PT discharge (no sound wave coupling) for (C)
5.3 Effect of external actuators
Neutral beam injectors or RF wave launchers required to heat the plasma can cause the destabilization of AEs. Nevertheless, the operational regime of any external actuators can be adapted to minimize such destabilizing effects. For example, AEs can be stabilized by modifying the actuator injected power to keep EP populations in the plasma below the AE destabilization threshold. Other options are weakening the EP resonance by modifying the EP energy or optimizing the NBI deposition to reduce the EP density gradients. In addition, the generation of non inductive currents can reduce the AE activity by locally modifying the magnetic field helicity, e.g., by increasing the magnetic shear and closing/narrowing the continuum gaps. Such mechanisms can be active with NBCD and ECCD. Additionally, actuators as ECW can locally modify the thermal plasma profiles leading to a reduction of the AE activity.
A set of experiments were performed in DIII-D investigating the NBI destabilizing effect by keeping the injected power fixed while changing the NBI voltage and current. This is equivalent to varying the EP energy and density, respectively [231–233]. This method provides a path to modify the EP distribution and reduce AE activity without requiring a change in the NBI injection geometry. FAR3d is used to calculate the AE stability as a function of the NBI voltage by analyzing the destabilizing effect of EP populations with different energies [87]. Figure 14, panels a and b, indicate a larger AE activity in the discharge 169,129 compared to the discharge 169,128 for the same total beam power. The NBI voltage increases in the discharge 169,128 from 60 to 80 keV although decreases in the discharge 169,129 from 80 to 60 keV. That implies that the higher NBI energy at the beginning of the discharge 169,129 causes a stronger EP resonance and larger AE activity. Panels c and d indicate
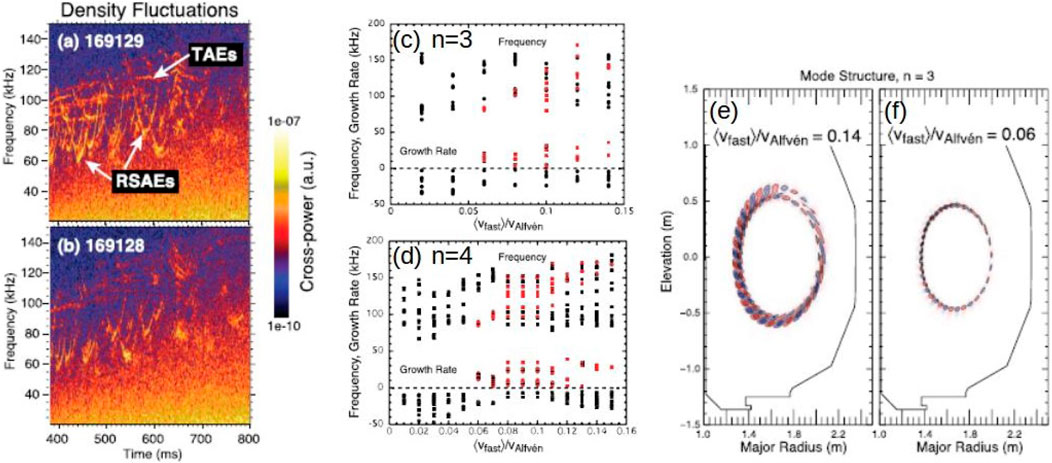
Figure 14. Stability of AEs in DIII-D plasma with respect to the NBI voltage and current. Cross-power of density fluctuations from two interferometer chords for the shots (A) 169,129 and (B) 169,128. Frequency and growth rates of (C)
Non inductive current drive generated by ECCD and NBCD locally modifies the magnetic field configuration, affecting the stability of pressure gradient and current driven modes [72–75, 234] as well as AEs [63, 64]. There are several examples of ECCD injection in stellarators [69, 70, 235, 236] leading to an improved stability of pressure gradient driven modes and AE [78, 79, 237, 238]. In particular, the effect of the ECCD and the NBCD was analyzed in LHD and Heliotron J plasmas [239, 240] which attained a stabilization of TAE, GAE and EPM [71] as well as pressure gradient driven modes [241, 242]. The FAR3d code was used to study the stability of pressure gradient driven modes and AEs in LHD configurations for different locations of the vacuum magnetic axis
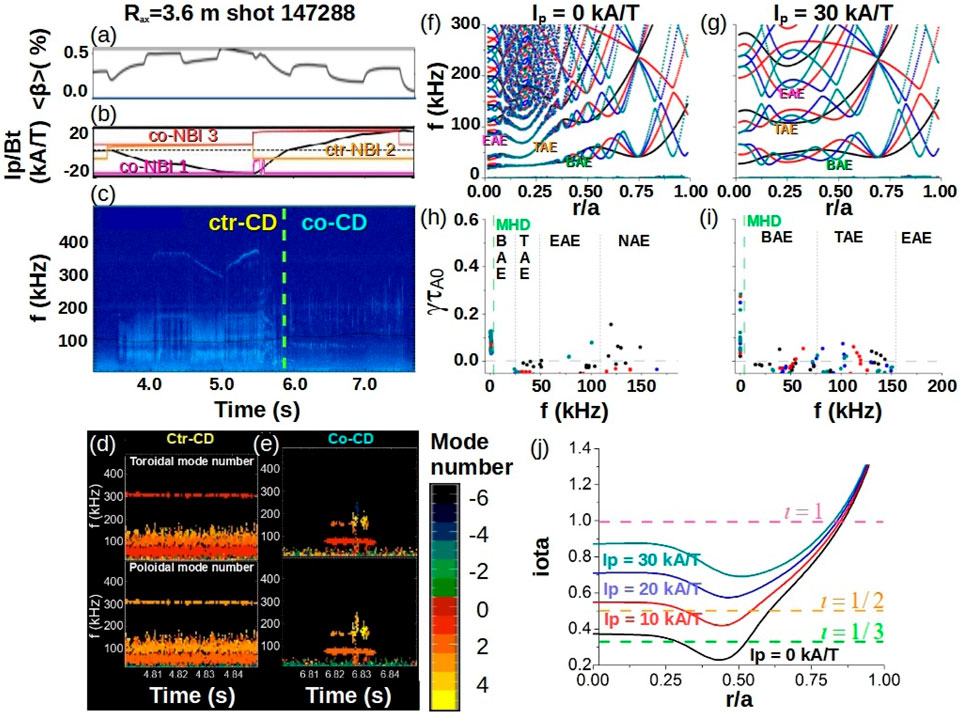
Figure 15. AE stability in LHD plasma with respect to the NBI current drive. Shot 147,288. (A) Averaged
Another example is the analysis of the ECCD effect on LHD and Heliotron J plasmas performed using FAR3d [192]. Figure 16, panels a and b, indicates a larger AE activity in the co-ECCD discharge compared to the counter-ECCD case even though other plasma parameters such as the thermal plasma density and NBI heating pattern are the same. Panels c and e show the ctr-ECCD case has slender gaps with respect to the co-ECCD case, leading to a stronger effect of the continuum damping and the stabilization of the modes observed in the co-ECCD case, particularly a
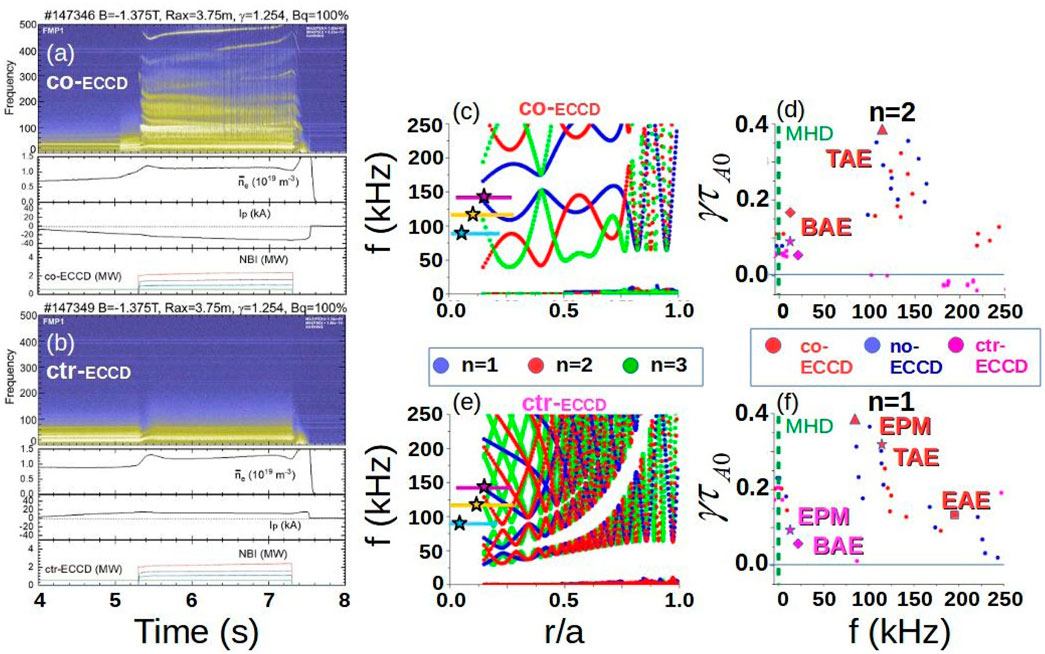
Figure 16. AE stability in LHD plasma with respect to the ECCD injection. Time evolution of magnetic spectrogram, electron density, plasma current and heating power in LHD discharged with (A) co-ECCD and (B) counter-ECCD. Alfvén gaps in the (C) co-ECCD and (E) ctr-ECCD cases.
Another option to modify the AE activity in fusion devices is increasing the plasma temperature using ECH. This locally affects the EP slowing-down distribution function and the AE damping effects as the thermal
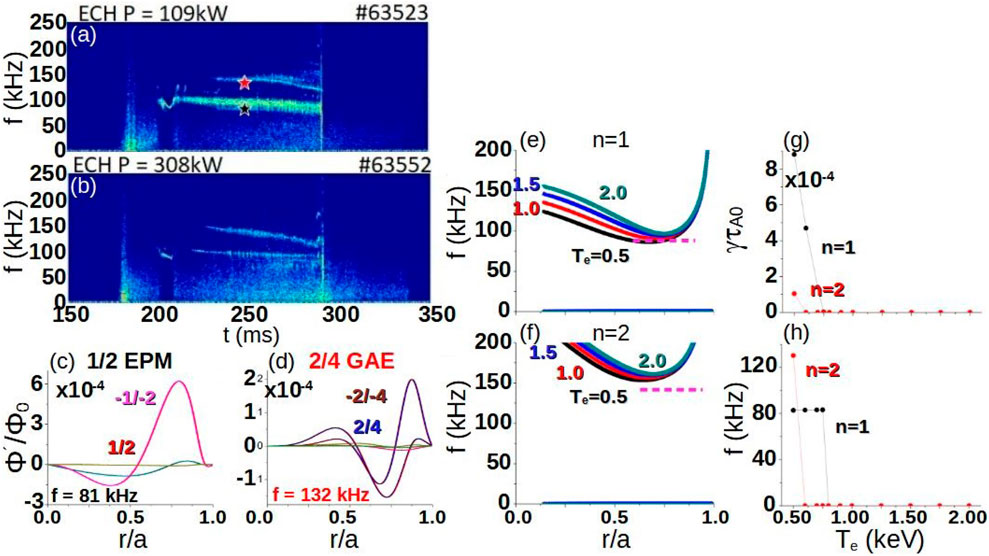
Figure 17. AE stability in Heliotron J plasma with respect to the ECH injection power. Magnetic spectrogram of discharges with an ECH injection power of (A) 100 kW and (B) 300 kW. The colored stars indicate the frequency range of the modes calculated by FAR3d (black
5.4 Effect of multiple EP populations
The AE/EPM stability in reactor relevant plasmas must be analyzed considering all the EP species that are present, including fusion born alpha particles as well as the EPs generated for plasma heating from NBI and ICRH. The closest examples of a reactor relevant plasma to date are the experiments performed during the second Deuterium Tritium campaign in JET, in particular for the so called 3-ion radio-frequency (RF) heating scenario [247–250]. This has revealed that the AE/EPM stability and EP transport measured in these discharges can be only reproduced using numeric models if the contribution of all the EP populations is included in the analysis [99, 190].
There are several examples of multiple EP population effects that have been analyzed using FAR3d code. For example, predicting the consequences on the AE stability for ITER, DIII-D and CFETR plasma [101, 103, 104] require multiple EP species, as well as in reproducing experimental observations in LHD and JET plasmas [179, 190]. Figure 18, panels a and b, show the growth rate and frequency of the dominant modes calculated by FAR3d for the ITER reverse shear operation scenario considering only the destabilizing effect of the NBI EP (black line), only alpha particles (red line) and simulations with both NBI EP + alpha particles (blue line). The AE growth rate in the simulation with NBI EP + alpha particles is
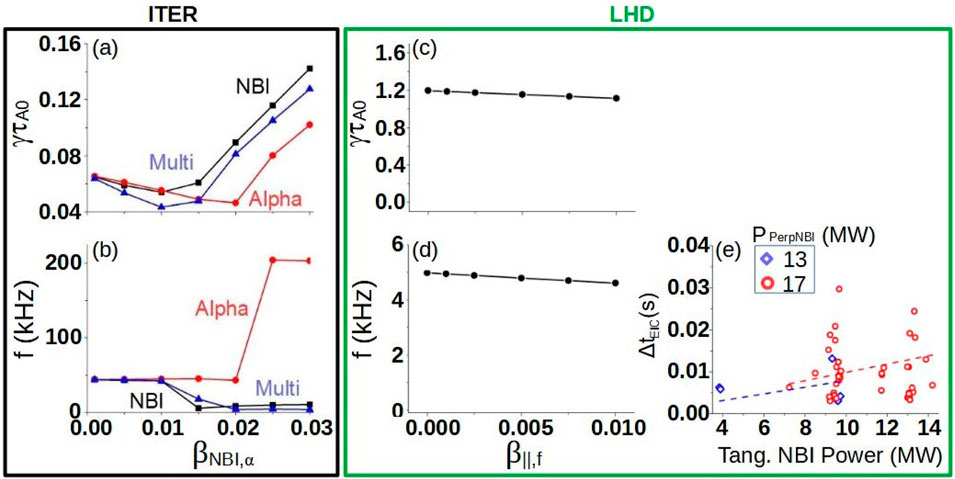
Figure 18. AE stability in ITER and LHD plasmas with multiple EP populations. Growth rate (A) and frequency (B) of the dominant
6 Saturation of AE/EPM
The analysis of the nonlinear saturation phase of AE/EPM provides information about the induced EP transport, energy transfer towards the thermal plasma and redistribution between different toroidal or helical mode families, generation of zonal structures as shear flows and zonal current, nonlinear interaction between the electromagnetic fields linked to different EP populations in addition to other effects. It is mandatory to study the saturation phase of AE/EPM to fully understand the effect of EP driven modes on the plasma heating performance and thermal plasma confinement. Nonlinear simulations performed using FAR3d can explore the saturation phase of AE/EPM potentially tracking the plasma evolution for dozens of milliseconds, providing information of the late AE/EPM saturation phase that is rarely analyzed by more sophisticated numerical models due to the large computational cost.
There are several examples in LHD and DIII-D experiments showing an important decrease of the devices performance measured during the saturation phase of AE/EPM. In particular, bursting events are linked to large EP losses and a deterioration of the plasma heating efficiency. In the following, several examples that have been analyzed using FAR3d are discussed.
The saturation of
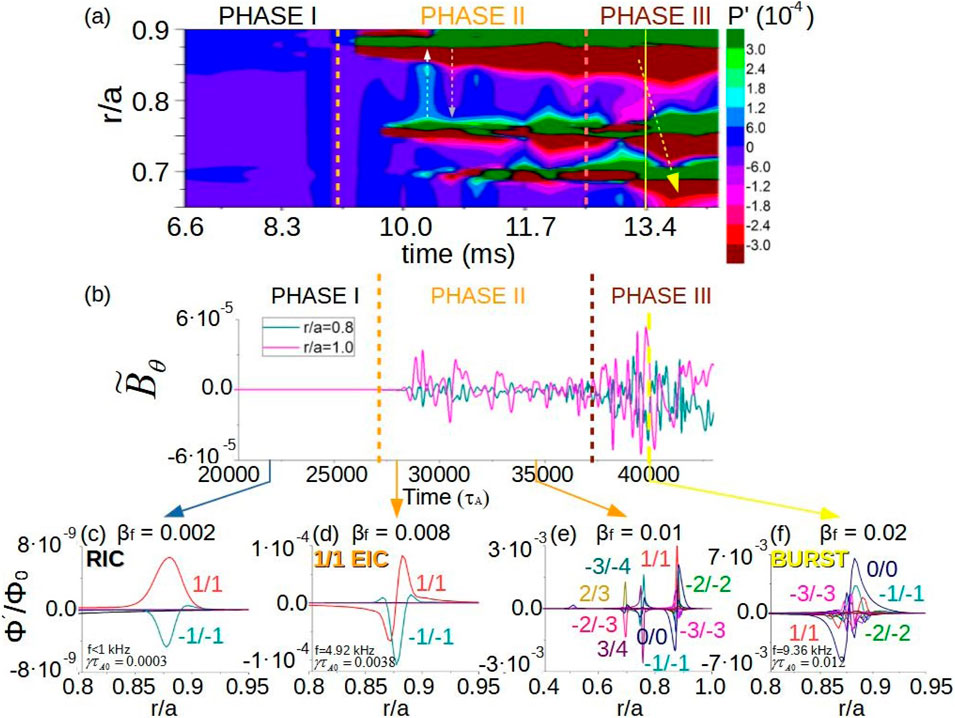
Figure 19. Analysis of the saturation phase of EIC in LHD plasma. (A) Evolution of the pressure perturbation between
Another example is the MHD burst observed in the LHD plasma [140]. The linear study discussed in previous sections is extended to analyze the TAEs saturation phase and the mechanism leading to the MHD burst destabilization [253]. Figure 20, panels a, indicates FAR3d nonlinear simulation reproduces the frequency range of the TAE activity observed in the experiment during the MHD burst (see Figure 10 of Ref. [140]), between
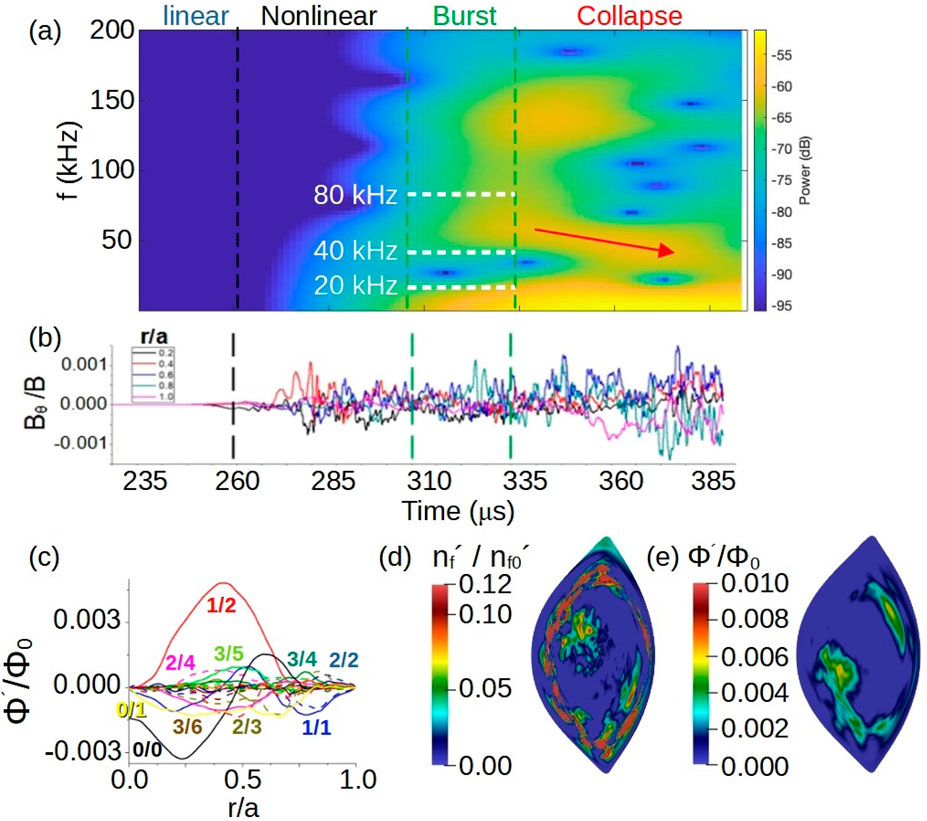
Figure 20. Analysis of the MHD burst in LHD plasma. (A) Spectrogram of the poloidal component of the magnetic field perturbation during the nonlinear simulation. (B) Evolution of the poloidal component of the magnetic field perturbation (C) Eigenfunction of the electrostatic potential perturbation during the MHD burst. Poloidal contour of the perturbations of the (D) EP density and (E) electrostatic potential during the MHD burst. Reproduced courtesy of IAEA, IOPScience, Nuclear Fusion journal. Figure adapted from [253]. Copyright (2021) IAEA.
FAR3d has also been used to study the saturation phase of AEs in tokamak devices, for example, pulsed beam discharges in DIII-D [254]. The DIII-D plasma in the discharge 176,523 is heated using a pulsed tangential NBI leading to the periodic destabilization of AEs [255]. The analysis of an isolated pulse has several advantages from the point of view of modeling because the simulations do not require source/sinks and the decay of the instability amplitude can be directly compared with the experimental data. Figure 21, panels a, shows the instability measured in the experiment at the frequency range of 105 kHz. Panel b indicates the saturation of an AE with
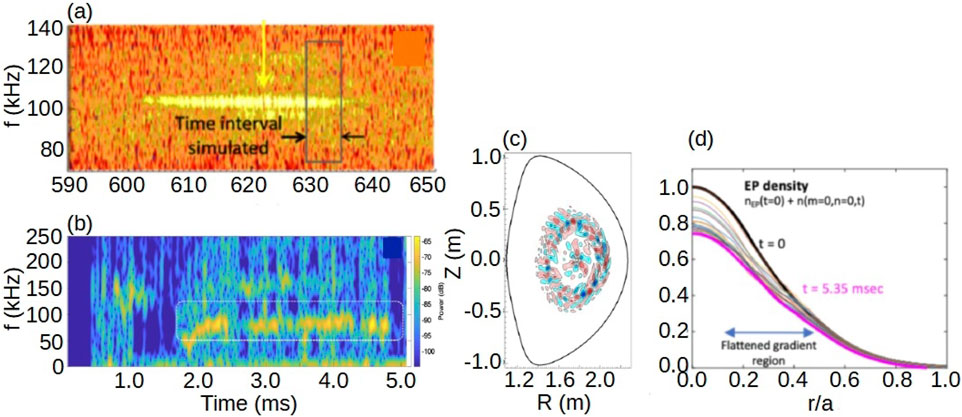
Figure 21. Analysis of the AEs saturation phase in DIII-D plasma heated using a pulsed tangential NBI. (A) Frequency vs. time spectrogram of magnetic probe
Optimization studies with respect to the AE saturation phase for different NBI operational regimes were performed for the DIII-D plasma using the FAR3d code, emphasizing the analysis of bursting events [256]. External actuators are used in DIII-D plasma to improve the AE stability, for example ECH [64, 257, 258], and ECCD [63, 259], or by optimizing the NBI operational regime [87, 260–262]. Nevertheless, bursting activity is detected in DIII-D EP diagnostics above a given threshold of the NBI injection power linked to avalanche-like events [263]. Figure 22, panels a, shows a chain of burst events triggered during the saturation phase of the simulation observed as a local maximum of the poloidal magnetic field perturbation. Panels b to g indicate that the burst events are correlated with a maximum of
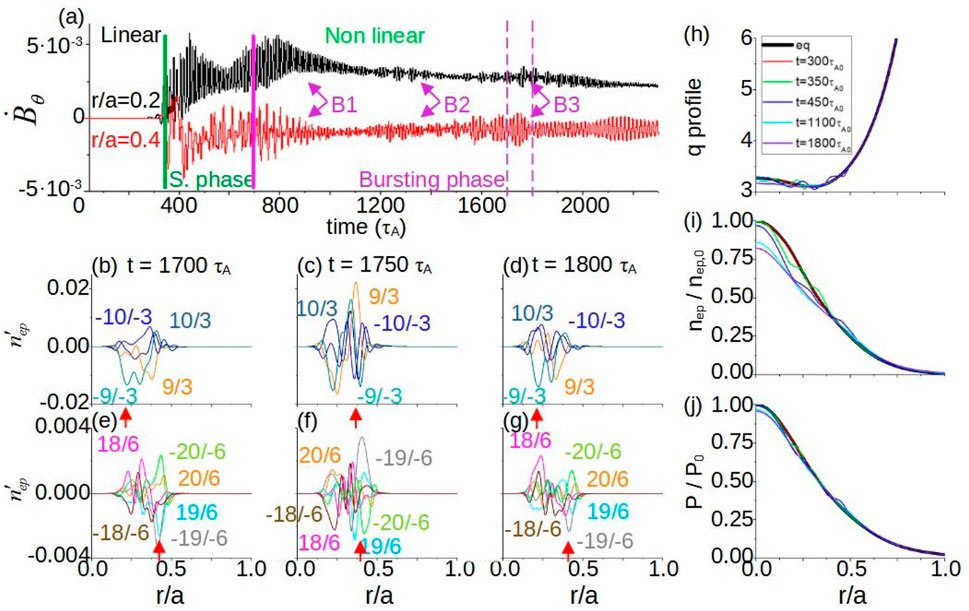
Figure 22. Analysis of the bursting activity in DIII-D plasma. (A) Perturbation of the poloidal component of the magnetic field in the nonlinear simulations with an EP
The analysis of shear flows induced by AE/EPM is also performed in LHD and JET plasmas; in particular such shear flows can have consequences on the thermal plasma confinement and plasma turbulence level. Numerical studies may indicate that the plasma turbulence could be modified during the AEs saturation phase although there are only indirect experimental evidences of the shear flows generated by AEs [265–271]. For example, shear flows induced by RSAEs in EAST experiments may help in the generation of electron-internal transport barriers, reducing the requirements for the L-H transition [272]. In the JET experiment, shear flows induced by AE/EPMs may improve the thermal plasma confinement [190]. FAR3d is applied to investigate the generation of shear flows and the effect on the plasma turbulence and confinement in LHD, JET and DIII-D devices [254, 273, 274]. Regarding LHD plasmas, the analysis shows reasonable similarities between simulations and experiments, reproducing at the same radial location shear flows measured during EIC and MHD bursts by the charge exchange spectroscopy diagnostic. Simulations dedicated to JET DT discharges indicate shear flows linked to the saturation of TAEs and fishbones may improve the thermal plasma confinement.
7 Predictions
Another contribution of FAR3d is in the forecasting of AE/EPM stability for future nuclear fusion devices, particularly ITER, CFETR or reactor relevant experiments in JT60SA. Predicting the AE/EPM stability may help to improve the plasma heating performance by identifying unfavorable configurations or regimes that should be avoided, as well as anticipating efficient methods for reducing AE/EPM destabilization.
The ITER plasma will be heated by two NBIs providing 33 MW of power, injecting a Deuterium beam with an energy of 1 MeV or a Hydrogen beam of 0.85 MeV [275]. Extrapolations from present experiments and numerical simulations predict the destabilization of AE/EPM by the NBI as well as fusion born alpha particles [276–284]. FAR3d is used to calculate the linear stability of the ITER plasma with respect to the NBI and alpha particle destabilizing effects on reverse shear, hybrid and steady state configurations [101]. Figure 23 shows an example of the analysis dedicated to the reverse shear scenario. Panel a indicates the Alfvén continuum of the
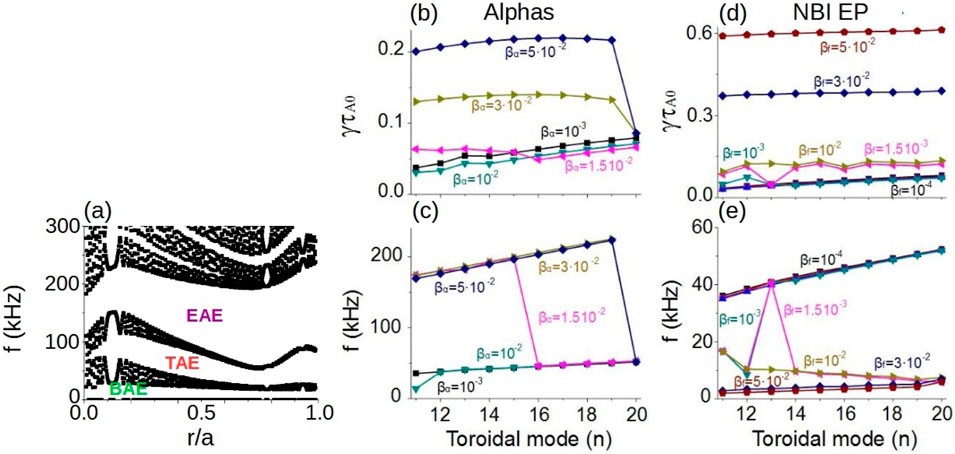
Figure 23. AE stability in ITER plasma including the effect of multiple EP populations (NBI EP + alpha particles). (A) Alfvén gaps of
CFETR high poloidal
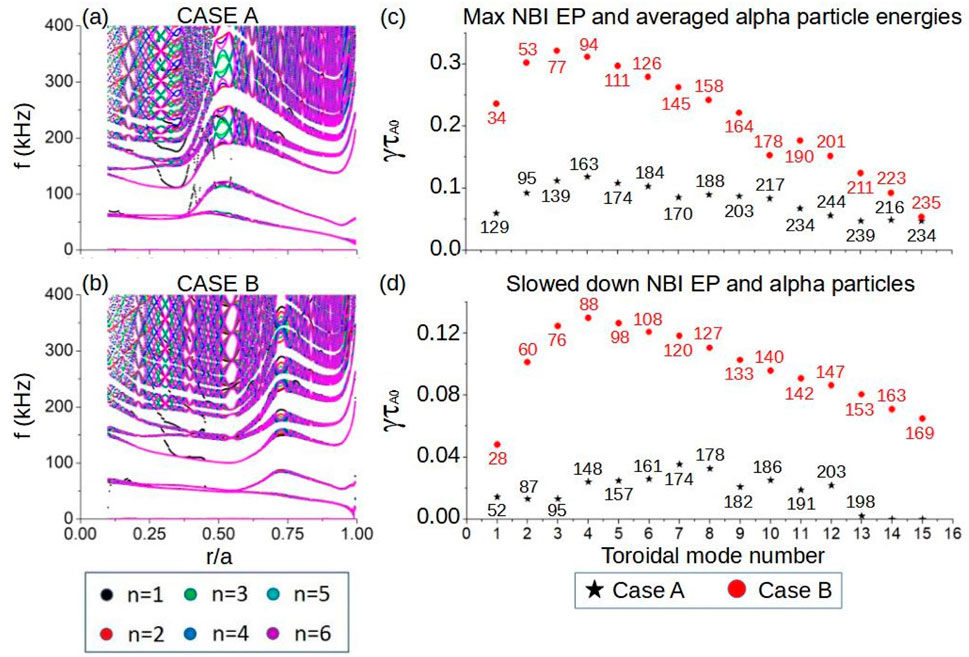
Figure 24. AE stability in CFETR plasma considering multiple EP populations (NBI EP + alpha particles). Continuum gaps of cases (A) A and (B) B for
JT-60SA is a critical milestone in nuclear fusion research, designed to test ITER and DEMO operational scenarios [289–292], for example the ITER-like inductive scenario [293]. The JT-60SA plasma will be heated using 34 MW of NBI power, including 12 positive-ion-based and 2 negative-ion-based NBIs (N-NBI). The N-NBI will inject a power of 10 MW using Deuterium with an energy of 500 keV; injectors will be aimed at the magnetic axis and middle plasma region [294, 295]. The destabilizing effect of the N-NBI EP may cause a triggering of AEs in the JT-60SA plasma [296–298]. FAR3d is used to forecast the AE activity in the JT-60SA ITER-like inductive scenario [299]. Figure 25, panel a, shows rather wide TAE and EAE gaps covering main part of the plasma radius. Panels b to g show
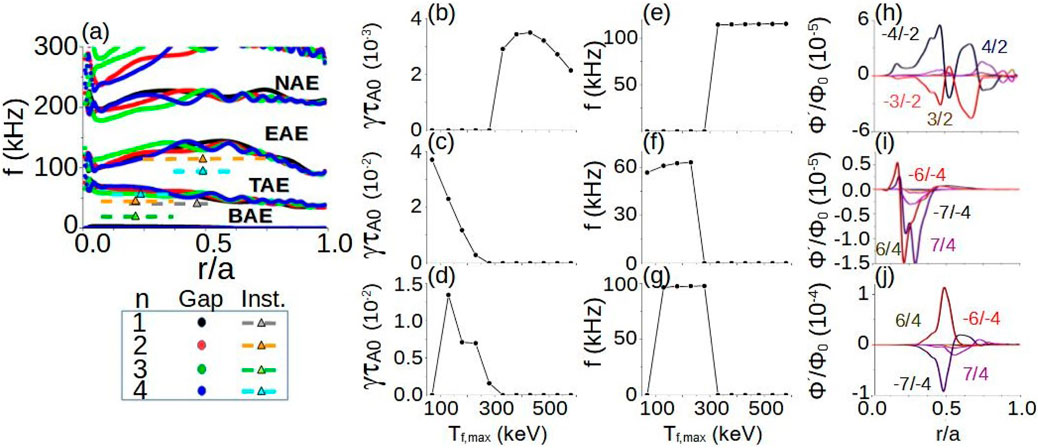
Figure 25. AE stability in JT60SA ITER-like inductive scenario. (A) Alfvén gaps of JT60SA ITER-like inductive scenario. The dashed lines indicate the width of the unstable AEs and the triangles the eigenfunction maxima. (B) Growth rate and (E) frequency of
8 Discussion
In this section the main findings of FAR3d are discussed and contextualized. In addition, the main advantages and drawbacks of the model are commented on. Next, FAR3d bench-marking studies with other codes are summarized.
8.1 Summary of main findings
One of the early applications of FAR3d code was to reproduce the AE activity measured in different devices, for example TAEs and EIC in LHD, HAEs in TJ-II or GAE and EPM in Heliotron J plasma. Some of these instabilities were reproduced for the first time. These analyses also introduced parametric studies as a new tool to analyze the AE/EPM stability with respect to the EP resonance features (as determined by variations in the input EP profiles/parameters used in the model).
Follow up studies were then dedicated to reproduce the AE activity in high poloidal
It is important to mention FAR3d simulations were also used to calibrate the EP profiles obtained from other codes. This technique was applied to reproduce the AE activity measured in EAST discharges after Tungsten plasma contamination and AE/EPM observed in Heliotron J discharges. This implies that FAR3d can be also used to calibrate the EP input profiles of more sophisticated models, providing a first guess of the EP characteristics that are consistent with the AE/EPM activity observed in the experiment. Through this approach, FAR3d can reduce the parametric range and the computational cost of studies performed by gyro-kinetic and hybrid codes.
Another topic covered by FAR3d simulations was reproducing the AE/EPM/interchange mode stability trends observed in LHD, Heliotron J and TJ-II discharges if external actuators as ECCD, ECH or NBCD are applied. The reasonable success in reproducing such trends opens the possibility of using the FAR3d code to predict operational scenarios for future devices as JT60SA, ITER and DEMO with optimized AE/EPM stability with assistance from the application of external actuators.
Bursting activity in LHD and DIII-D plasmas was analyzed by performing long term nonlinear simulation with the FAR3d code, analyzing the AE/EPM saturation phase. The simulations show that the destabilization of bursts may have common features in both devices; these events could be triggered due to the overlapping of resonances induced by different toroidal mode families. Moreover, the analysis may indicate the bursting activity is a universal feature of plasma systems undergoing a transition from the soft MHD limit, with local relaxations, to the hard MHD limit, with global relaxations. Another important conclusion comes from the EP transport enhancement in the simulation bursting phase, reproducing the critical gradient behaviour proposed to explain the EP loss measurements in DIII-D bursting plasma. Furthermore, nonlinear simulations dedicated to analyze the saturation phase of interchange modes in LHD plasma may indicate, internal collapse and sawtooth-like events are also caused by a transition from the soft to the hard MHD limit, leading to a partial stochastization of the magnetic field due to overlapping magnetic islands [300–302]. In summary, operational scenarios with plasma in the hard MHD limit must be avoided in future fusion reactors, leading to an important reduction of the heating performance by massive EP losses and damage to plasma facing components.
A crucial topic for fusion reactors explored by FAR3d linear and nonlinear simulations is the AE/EPM stability in plasma with multiple EP species. The analysis indicates the experimental observation in the second JET DT campaign can only be explained if multiple EP effects are included in the simulations, in particular the alpha particle losses measured once fish-bones are destabilized. Efficient plasma heating in future fusion reactors requires the minimizing alpha particle losses, thus the nonlinear destabilization of the alpha particle population by NBI and ICRH EPs below the
FAR3d analysis dedicated to study shear flows generated during the AE/EPM saturation phase may indicate important consequences for thermal plasma confinement. The trends identified in simulations comparing the intensity of the shear flows for different JET DT discharges may support this possibility, reproducing the improved thermal plasma confinement measured in the experiments. This result may indicate that the thermal plasma confinement in ITER and DEMO could be better than expected.
Another contribution of the FAR3d studies is to forecast the AE/EPM stability in ITER, JT60SA and CFETR for different operational scenarios. In addition, the AE/EPM stability has been studied in stellarator devices exploring different magnetic configurational symmetries. Operational scenarios and magnetic configurations with strong AE/EPM activity could lead to fusion reactors with poor plasma heating efficiency and must be avoided.
The analysis of the linear and nonlinear interaction between EPs and and interchange, ballooning, kink and tearing modes may indicate, EPs have a stabilizing effect below the
8.2 Advantages and drawbacks of the FAR3d gyro-fluid model
The main motivation of developing gyro-fluid models is the computational efficiency. Thus, FAR3d allows the rapid characterization of the AE/EPM activity measured experimental studies. Examples of a reasonable agreement between simulations and experimental observations has been obtained in studies dedicated to JET, DIII-D, EAST, LHD, TJ-II and Heliotron J discharges.
Developing reduced models while retaining the key elements for a first order characterization of the AE/EPM linear and nonlinear stability, opens the possibility of performing massive parametric studies, providing useful information for optimization studies. Such improved scenarios can be tested in experiments dedicated to confirm theoretical optimization trends. These kind of experiments were performed in LHD, leading to promising results. Additionally, the model simplifications enable analysis of the AE/EPM late nonlinear saturation phase including multiple EP species and toroidal families, approaching the stability of reactor relevant plasma. These studies may provide relevant information about the induced EP transport, zonal structure generation and nonlinear interactions between EP populations, thermal plasma and different toroidal mode families in ITER and DEMO plasmas.
Besides these advantages of the FAR3d model, the limitations on the model can be explicitly stated. The FAR3d two moment version can only explore parallel and velocity-specific trapped resonances induced by Maxwellian EP distribution functions. Introducing a slowing down EP distribution function requires, at least a three moment version of the code, including an evolution equation for the EP energy moment perturbation. The three moment Landau closure, that requires five parameters, is able to fit the gyro-kinetic response function for an EP slowing down distribution function, although benchmarking of the three moments version of FAR3d against the two moments version is still underway. Further development and testing of both the three and a four moment version of FAR3d (adds the parallel EP heat flux moment) is ongoing. Additionally, versions of FAR3d are under development based on perpendicular and parallel perturbed EP pressure moments. This moment hierarchy should be especially appropriate for anisotropic EP populations. It also allows a more accurate treatment of the resonance contributions of the drift (also know as toroiddal) resonances. In the meanwhile, the resonance induced by a slowing down EP distribution function can be approximated performing parametric studies using multiple Maxwellian distributions, fitted to the EP populations and encompassing the key resonances in the experiment. It should be noted that the results of the parametric studies must be analyzed with care because not all the resonances identified reproduce the real resonances in the experiment. On top of that, the Maxwellian is a symmetric distribution function, thus FAR3d simulations cannot at this time distinguish between co- and ctr-passing EPs.
The trapped EP approximation should be considered a first order step in the analysis of resonances induced by toroidal and helically trapped EP, thus the code predictions may deviate from the parametric ranges of the experiment. An improved approximation requires introducing the parallel and perpendicular components of the pressure tensor, an active research topic in the FAR3d project. However, the present trapped EP module provides a reasonable approximation of the resonance induced by trapped helical particles that can destabilize the EIC in the LHD device. The resonance induced by particles with different pitch angles can be also approximated by adapting the bounce distance and frequency of the trapped EP in the model.
EP resonance effects and destabilization are approximated by the parallel Landau closure coupled with the average drift velocity and diamagnetic drift frequency operators. In addition, the fitted Maxwellian EP distribution function used in the simulations is allowed to deviate with respect to the real EP distribution in the experiment. This is motivated by the hypothesis that the drive for AE instabilities from configuration space gradients may dominate over that from velocity space gradients (which may be resolved by higher frequency activity). For this reason the analysis of the AE/EPM stability trends can deviate from the experimental observations if the parametric range of the resonance is not correctly identified. As a consequence, the EP
FAR3d results shows a large sensitivity to the EP configuration introduced in the model. In general, EP profiles obtained from other codes as TRANSP, ASCOT, ONETWO/NUBEAM or MORH have to be calibrated by performing parametric studies to identify the optimal configuration that better reproduces the EP resonance and AE/EPM stability in the experiments.
The present version of the model does not include the parallel magnetic field perturbation, leading to an artificial stabilizing effect on ideal current driven modes and low frequency AEs [303–305]. This limitation causes the inability of the model to study ideal internal kinks. Thus, an improved description of the fish-bone stability requires introducing the parallel magnetic field perturbation. The analysis of fish-bones is possible using FAR3d code by including the effect of the resistivity in the simulations, leading to the destabilization of resistive internal kink modes. The growth rate of the mode is not as large as the ideal internal kink calculated by full MHD codes as MISHKA [306] for the case of JET discharges, although the simulation provides a first approach of the phenomena. The consequence is, the EP
Neoclassical effects are not included in the model, consequently the stability of neoclassical tearing mode cannot be analyzed. Introducing the highly anisotropic thermal plasma heat transport required for a correct description of the current depletion in the island regions is a numerically challenging problem. A future FAR3d module will explore possible implementations.
The numerical stability of nonlinear FAR3d simulations can pose a limitation in configurations with strong drive, particularly if rather large perturbations induced by multiple EP resonances and pressure gradient/currents develop at the same time. Such simulations show a strong overshot in the transition from the linear to the saturation phase, leading to a large decrease of the time step of the simulation, required by the code to channel the energy/information flows in the system, leading eventually to ending the run. In such circumstances, diffusive and damping terms must be enhanced to reduce the free energy of the model and force a smoother transition to the saturation phase. The other possible strategy consists in including a larger number of stable toroidal mode families that provides an energy sink at short wavelengths.
FAR3d simulations exploring the late saturation phase of AE/EPM may show the destabilization of modes not observed in the experiment or an overestimation of marginal unstable modes. This is caused by an inaccurate nonlinear energy redistribution from the dominant perturbation towards different toroidal mode families, other EP populations and the thermal plasma. This is explained by the role of the high n modes in the simulations, stabilized by the FLR effects, that should participate as energy sinks. If the high n modes are not included, the fraction of the free energy that should be dissipated by the non linearly energy cascade to high n modes is still available to trigger instabilities. This issue is minimized by including a larger number of toroidal modes families, equilibrium poloidal modes and EP species with a non negligible population in the plasma.
The FAR3d model is based on perfect conducting fixed boundary conditions at the plasma edge. Consequently, the calculation of ballooning modes and AE/EPM at the pedestal of tokamak plasma is problematical; free boundary conditions are mandatory to avoid an overestimation of the growth rates for such modes.
Single fluid models can only reproduce the stability of plasma in the slow reconnection regime, that is to say, plasma with a non negligible effect of the resistivity. Consequently, FAR3d simulations do not make accurate descriptions of plasma relaxations induced in the fast reconnection regime. For example, the plasmoid instability cannot be reproduced, or events that significantly reduce the free energy available to trigger other instabilities. Consequently, single fluid simulations overestimate the growth rate of perturbations triggered in high temperature plasma with low resistivity, that is to say, instabilities triggered in the core of fusion devices. This limitation particularly affects pressure gradient and current driven modes, although the impact is smaller for AE/EPM. Two fluid modes are required for an improved description of the system stability.
FAR3d studies performed for tokamaks including the pedestal can show artificial modes with rather large growth rates at the plasma edge. This is caused by spurious currents that can appear in equilibria generated by the VMEC code nearby the outer model boundary. This issue can be avoided in linear simulation using the eigen-solver version of the code by excluding spurious modes and retaining only the physically relevant modes. In addition, it is also well known that the VMEC code provides a poor description of the magnetic surfaces near the magnetic axis. This issue can be partially resolved by the interpolations used nearby the magnetic axis. That may cause an incorrect identification of the perturbation mode number in the inner plasma region.
Non linear simulations performed using a large number of toroidal modes families including multiple EP populations and FLR damping effects require a large amount of RAM memory due to the size of the matrix generated by the numerical model. Thus, the range of poloidal modes must be limited by removing fluid and wave-EP resonances that may not have an important impact on the instability analyzed, for example, ignoring peripheral resonances if the target modes are located in the inner plasma region.
The MPI parallelization of the nonlinear FAR3d version is performed with respect to the number of toroidal/helical mode families included in the simulation. Consequently, inputs keeping the same range of resonances for low
Thermal and EP FLR effects must be used with care because activating these modules can lead to the destabilization of artificial AEs if the Larmor radius is too large and the target mode is marginally unstable. This issue is linked to the mathematical expression used to implement the FLR effects, a power series expansion for the thermal ion FLR terms and a Pade approximation for EP FLR. If the effective
It must be noted the correct use of FAR3d code requires a training period, particularly if the user wants to perform nonlinear simulations. The FAR3d distribution includes a user guide and several basic examples to speed up the learning process.
8.3 Bench-marking FAR3d with other codes
Bench-marking reduced models with more sophisticated codes is mandatory to demonstrate the reliability of the approximations. Towards that aim, the FAR3d code has been compared with five initial value gyrokinetic codes (EUTERPE, GEM, GTC, GYRO, ORB5), the initial value gyrokinetic-MHD code MEGA, and the perturbative eigenvalue code NOVA-K [307] for a reference DIII-D discharge 159,243 [123].
Figure 26, panels a and b, shows the destabilization of multiple RSAEs with up-sweeping frequency from
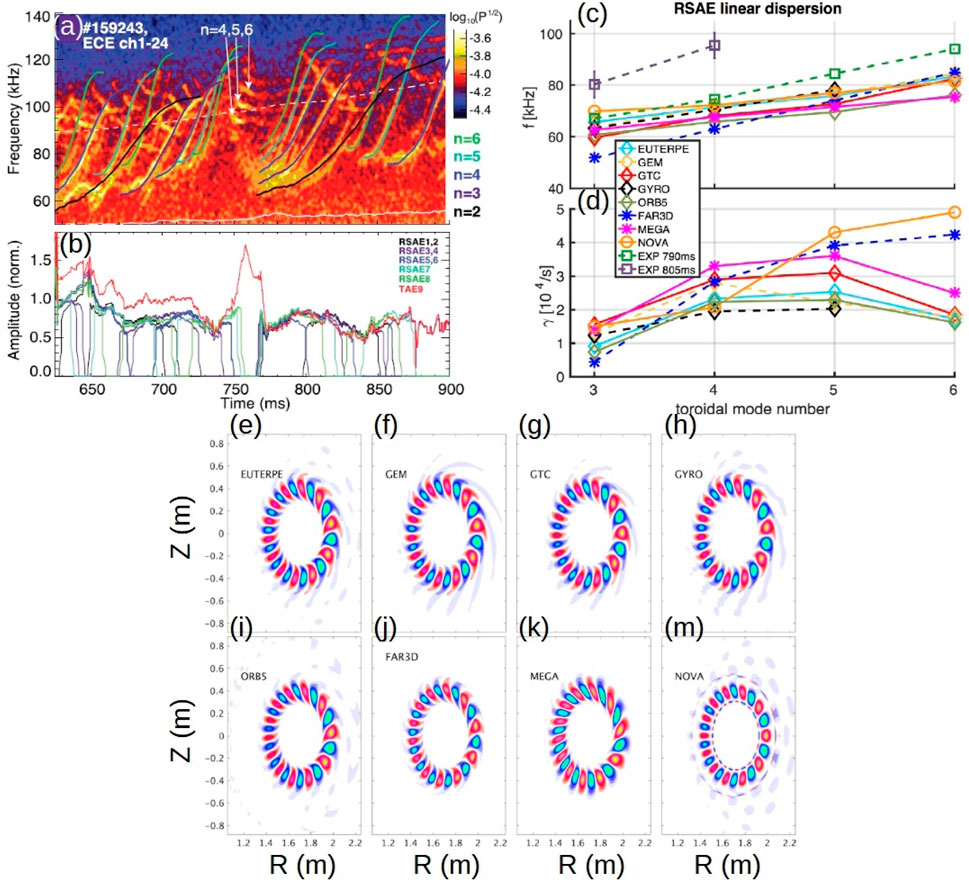
Figure 26. (A) ECE power spectrum with RSAE time evolution fits from an ad hoc model [40] and calculated GAM (solid white line) and TAE frequencies (dashed white line, in plasma frame). (B) Time evolution of amplitudes determined from the kick model for DIII-D shot 159,243. Figures adapted from [88]. Copyright (2017) IAEA. Linear dispersion relation calculation for RSAE in DIII-D shot 158243 at 805 m. (C) Real frequencies. (D) Growth rates. The plot markers are diamond, star, and circle for the gyrokinetic, kinetic-MHD hybrid, and perturbative eigenvalue codes, respectively. (E–M)
The analysis of MHD bursts in LHD plasma was also performed using the MEGA code [143]. Both models show important EP losses induced during the bursting phase of the instability. MEGA analysis can track the evolution of the EP slowing down distribution function along the simulation, providing useful information about the resonance evolution that cannot be obtained by gyro-fluid simulations, providing a more accurate description of the EP losses during the bursting event.
The destabilization of EPM/GAE in Heliotron J discharges was also explored using MEGA code in the linear and saturation phases [64, 308]. MEGA and FAR3d simulations show a good agreement with the experimental measurements, reproducing the same mode structure, dominant mode number and frequency range. In addition, MEGA simulations also reported the importance of performing free boundary simulations to avoid the underestimation of the linear growth rate by fixed boundary condition. This issue is partially compensated in FAR3d simulations by adapting the EP profiles in the plasma periphery, particularly the gradient of the EP density profile. The MEGA code was also applied to analyze the effect of ECCD injection on the AE stability of Heliotron J plasma, leading to qualitatively similar results compared to the FAR3d linear simulations and the experimental observations [309].
The study of AE/EPMs triggered in the EAST discharge 93,910 after Tungsten plasma contamination was first explored using the M3D-K/GTAW codes [184]. Both FAR3d and M3D-K/GTAW codes simulations obtain consistent results, reproducing the measure AE activity. The main discrepancy is the identification of the
Simulations performed for JT60SA using the codes MEGA [296, 298] and MISHKA/CASTOR-K [297, 310–312] indicate the destabilization of AE/EPM in different operational scenarios. FAR3d simulations also identified unstable AEs in JT60SA ITER-like inductive scenario.
Simulations dedicated to forecast the AE stability in ITER operation scenarios indicate TAEs of toroidal mode families between
9 Conclusions
The gyro-fluid code FAR3d is a computationally efficient tool to analyze the AE/EPM stability in nuclear fusion devices, filling the gap between the short term analysis required during experimental campaigns and long term studies complementing more sophisticated gyrokinetic and kinetic-MHD hybrid codes.
FAR3d has been applied to reproduce the AE/EPM activity in tokamaks such as JET, DIII-D and EAST as well as stellarators such as LHD, TJ-II and Heliotron J, showing reasonable similarities between simulations and experimental observations by identifying the same radial location, dominant mode numbers, frequency range and eigenfunction structure. In particular, the stability of TAEs and EICs in LHD, HAEs and GAEs in TJ-II, TAEs and RSAEs in DIII-D, TAEs and EPMs in EAST, GAEs and EPMs in Heliotron J and TAEs and fish-bones in JET has been analyzed.
The rapid turn-around time of FAR3d simulations allow one to perform parametric studies dedicated to the analysis of the linear and non-linear stability of AE/EPM for different device configurations. This opens up the possibility optimization studies that can identify configurations with reduced AE/EPM activity. Towards that goal, FAR3d analysis can explore optimal configurations with respect to the thermal plasma properties, magnetic field geometry, the effect of external actuators and the impact of multiple EP populations. Such improved operational scenarios were validated in dedicated experiments in devices as LHD, TJ-II, Heliotron J, DIII-D and EAST.
The combination of experimental observations and FAR3d optimization studies provided valuable information in the search for optimal operational conditions to stabilize EICs in LHD with respect to the thermal plasma configuration, the effect of AEs on ITB for EAST discharges, as well as the impact of the magnetic field topology on the AE stability for reverse shear and negative triangularity discharges in DIII-D. In addition, the AE stability in quasi-poloidal and quasi-axysymmetric stellarators has been explored.
The effect of external actuators on the AE/EPM activity in LHD, Heliotron J and DIII-D plasmas has also been analyzed. FAR3d can reproduce and account for the effects of the application of ECCD, the induction of currents by the NBI or the injection of ECH leading to the stabilization or further destabilization of AE/EPMs in different device configurations, providing useful information to develop reliable techniques dedicated to improve the performance of future nuclear fusion reactors.
The analysis of multiple EP population effects in LHD and JET discharges provides a first approach to the AE/EPM stability issues in reactor relevant plasmas, indicating its essential role in the analysis of the EP transport. Linear and nonlinear feedback between different EP population must be included in the studies for a correct analysis of experimental observations. In addition, multiple EP effects in future devices such as ITER and CFETR are explored.
The analysis of the AE/EPM nonlinear saturation phase is required to reproduce the experimental observation, in particular the induced EP transport, profile flattening, generation of zonal structures and the energy cascades between different toroidal or helical families. In addition, nonlinear simulations can be used to analyze the bursting phenomena observed in multiple fusion devices, linked to an important deterioration of the operational performance and large EP losses. FAR3d analysis suggests EIC and MHD bursting activity in LHD as well as burst events in DIII-D could be caused by resonance overlapping effects, leading to a transition from the soft MHD limit (local plasma relaxation) to the hard MHD limit (global plasma relaxation), inducing large EP losses due to an abrupt increase of the EP transport. On top of that, the shear flows caused by AE/EPM instabilities may have an important role on the thermal plasma confinement and plasma turbulent level as it is observed in LHD, JET, DIII-D and EAST discharges and FAR3d simulations.
FAR3d can also provide a first approach of the AE/EPM linear and nonlinear stability for future devices as ITER, CFETR and JT60SA. Forecasting resonances that may induce the destabilization of AE/EPM will be helpful to constrain the parametric space leading to operational scenarios with an efficient plasma heating and optimal performance. In addition, future analysis will be dedicated to explore how external actuators may improve the AE/EPM stability in unfavorable configurations, for example, by the injection of ECCD, ECH or due to the generation of NBCD. Also, optimization trends with respect to the thermal plasma parameters and external actuators operational regime will be explored. On top of that, the saturation phase of AE/EPM will be analyzed to predict the EP transport induced and the generation of zonal structures.
10 Prospects and future plans
This section is dedicated to show ongoing and future research topics of the FAR3d project. Also, future upgrades of the code are discussed.
10.1 Ongoing research lines
The main topics of present FAR3d research lines are dedicated to studies of the EP transport and the generation of zonal structures during the AE/EPM nonlinear saturation phase. A set of dedicated experiments were performed in LHD device to measure shear flows using charge exchange spectroscopy, comparing the radial electric field and thermal plasma poloidal rotation with the output of nonlinear FAR3d simulations [274]. The generation of shear flows by TAE and fish-bones is also explored in the DT JET discharge 99,896. Demonstrating the generation of shear flows during the saturation phase of AE/EPM and their potential effect on the thermal plasma confinement is a key topic for ITER and future fusion reactors [318]. The instability-driven EP transport rates are also an important consideration for future fusion reactors, and can be inferred directly from profile flattening effects.
The study of the JET DT plasma is extended to analyze the EP populations leading to the destabilization of TAEs and fish-bones in the discharge 99,896. In addition, multiple EP nonlinear simulations including ICRH EP + alpha particles are performed to investigate the alpha particle losses induced by fish-bone. Understanding multiple EP effects and the nonlinear destabilization of the alpha particle population by NBI and ICRH EP populations is essential to forecast correctly the alpha particle confinement in ITER and future fusion reactors [273].
Another research line is dedicated to analyze the effect of the EPs on the linear and nonlinear stability of kink, interchange and tearing modes. In particular, such stability trends are analyzed in multiple EP plasma including NBI EP and alpha particles. The analysis of cross stabilizing/destabilizing effects between thermal plasma instabilities and AE/EPM are important to predict the confinement of both, thermal plasma and alpha particles, in ITER and fusion reactors [319].
The saturation phase and extinction of EPMs in tokamak and stellarator can be explored doing FAR3d nonlinear simulations. In particular, the fish-bones and EIC frequency down-sweeping observed in JET and LHD plasma have been analyzed, as well as the destabilization of kink and interchange modes, respectively, after fish-bones and EIC stabilize. This analysis is important to evaluate how the EP losses affect the stability of EPMs and thermal plasma instabilities in fusion devices.
A set of experiments in the LHD device were performed during 2021 and 2022 campaigns dedicated to identify operational scenarios with improved performance by minimizing, at the same time, the activity of AEs and interchange modes. On that aim, discharges with different heating patterns, magnetic field configurations and thermal plasma parameters are tested, measuring the AE and interchange mode activity with respect to the NBCD, thermal plasma density and NBI operational regime. The optimization trends obtained in the experiments were analyzed and reproduced by linear simulations performed using the FAR3d code. Exploring operational scenarios with reduced AE/interchange mode activity is important to optimize the LHD device performance, improving the thermal plasma confinement and the plasma heating efficiency [320].
The tracer code TAPAS has been coupled with FAR3d to study the EP transport generated in DIII-D, JET and ITER plasmas using self-consistent AE/EPM perturbations calculated by FAR3d non linear simulations. The TAPAS/FAR3d model will be validated by comparing simulation results and EP losses measured in DIII-D and JET discharges. The next step is applying the model to forecast the alpha particle transport in different operational scenarios of ITER [321].
10.2 Future research lines
The analysis of the linear and nonlinear stability of AEs measured in TJ-II plasma using HIBP will be one of the next research lines for the FAR3d project. HIBP is a diagnostic that provides unique information of the electrostatic potential perturbation induced by AEs. Such data can be directly compared with the FAR3d output, providing an excellent framework to test the accuracy of the simulations and analyze in detail the saturation phase of AEs [82, 322–324].
The analysis of zonal structures generation during the AE/EPM saturation phase will be extended to TJ-II, Heliotron J and DIII-D devices by performing dedicated experiments that will be compared to nonlinear FAR3d simulations.
A set of experiments were performed in 2024 LHD campaign dedicated to analyze the bursting activity induced in discharges combining tangential and perpendicular NBI injection with ICRH. Multiple EP linear simulations will be performed to analyze the AEs observed in the discharges, and how multiple EP effects can modify the AE stability in LHD plasma.
Parametric studies will be performed to analyze the EP transport in the DIII-D plasma using the nonlinear version of FAR3d. The aim of the study is reproducing the EP losses measured in DIII-D discharges as the NBI power increases. In particular, the abrupt increase of the EP transport during bursting events will be main target of the study, providing support to the soft to hard transition caused by the overlapping of multiple resonances.
The linear stability of AEs in ITER plasma configuration including RMPs will be analyzed. Forecasting the AE stability in ITER configurations with and without RMPs is an essential topic to understand the effect of the RMPs on plasma heating efficiency of ITER plasma.
A set of linear and nonlinear studies will be dedicated to study the AE stability in different KSTAR configurations. The methods developed by KSTAR team to improve the AE stability and the plasma heating efficiency are important to improve the performance of ITER operation scenarios.
The linear and nonlinear stability of AE/EPM in different configurations of JT60SA, ITER and DEMO will be explored, emphasizing the analysis of the alpha particle transport and zonal structure generation in multiple EP plasma. In addition, the possibility of soft to hard transitions in reactor relevant plasma and the consequences on the device performance will be studied. Another part of the analysis will be dedicated to predict the effects of external actuators to reduce or avoid the AE/EPM activity.
The linear stability of AEs and thermal plasma instabilities with respect to the EP population at the plasma periphery of tokamak plasma will be explored. Keeping aware of the FAR3d model limitations for providing a correct description of modes destabilized at the pedestal, the analysis will be limited to identify stability trends. That means, FAR3d cannot provide the stability threshold of peripheral modes but it is possible to explore configurations showing reduced mode growth rates for optimization studies.
Another research line consists in analyzing the linear and nonlinear AE/EPM stability in new designs of optimized stellarators. This information may be useful to select the magnetic configurations with optimal plasma heating efficiency with respect to an improved AE/EPM stability.
FAR3d will be added to integrated modelling frameworks dedicated to the design of fusion reactors. FAR3d may provide information of the NBI EP, ICRH EP and alpha particle destabilizing effects on reactor relevant plasma configurations, EP density transport fluxes, identifying the parametric range with optimal plasma heating. Integrated modeling workflows such as IMAS (proposed) [312] and FREDA (ongoing) [325] are examples of FAR3d implementations dedicated to explore AE/EPM stability and EP transport [328, 329].
Future studies will be dedicated to compare the FAR3d and GENE code simulations, analyzing the AE/EPM stability of different devices.
Finally, AI applications based on FAR3d nonlinear simulations will be developed to predict the EP transport in different fusion devices.
10.3 Next code updates
A major updated version of the FAR3d distribution, the open source version of the code, will be released during 2024. The FAR3d 2.0 distribution will include the linear and nonlinear versions of the code allowing simulations with up to 3 EP populations at the same time. This distribution will also include a new add-on dedicated module to transform EFIT data to the FAR3d equilibrium input.
The implementation of GPU parallelization is ongoing. An early version including GPU parallelization is being tested.
Different methods to introduce neoclassical effects into the model are under review. Updating the code to analyze NTMs is one of the priorities of the core development team.
Introduce the perturbation of the magnetic field along the magnetic field line is another of the developing team priorities, required to model ideal internal kinks, EPMs and low frequency AEs in tokamak plasmas.
The development of the four moments version of the code continues, with the goal of resolving issues identified in the version with moments of the EP energy and EP parallel heat flux, as well as the version with parallel ad perpendicular components of the pressure tensor.
A new equation describing the evolution of the thermal plasma density perturbation will be included in the nonlinear version of the code. This upgrade will enable the analysis of ion temperature gradient instabilities (ITGs) during the saturation phase of AE/EPM, providing further information of the thermal plasma turbulence and anomalous transport and their coupling with the AE turbulence. ITGs are connected to the grad
Author contributions
JV: Conceptualization, Data curation, Formal Analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization, Writing–original draft, Writing–review and editing. DS: Conceptualization, Data curation, Formal Analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization, Writing–original draft, Writing–review and editing. LG: Conceptualization, Data curation, Formal Analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization, Writing–original draft, Writing–review and editing. YG: Conceptualization, Data curation, Formal Analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization, Writing–original draft, Writing–review and editing. JO: Conceptualization, Data curation, Formal Analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization, Writing–original draft, Writing–review and editing.
FAR3d contributors
D. C. Pace, M. Murakami, M. A. Van Zeeland, X. Du (General Atomics, P.O. Box 85608, San Diego, California 92186-5608, United States), J. Huang, C. Jiale, X. H. Wang, Y. Sun (Institute of Plasma Physics, Chinese Academy of Science, Hefei, China), S. Ohdachi, K. Y. Watanabe, Y. Todo, K. Nagaoka, A. Azegami, K. Ida, K. Tanaka, K. Ogawa, M. Osakabe, P. Adulsiriswad, Y. Takemura, M. Yoshinuma, T. Tokuzawa, M. Idouakass (National Institute for Fusion Science, National Institute of Natural Science, Toki, 509-5292, Japan), R. Seki (SOKENDAI, Department of Fusion Science, Toki/Gifu and National Institute for Fusion Science, National Institute of Natural Science), S. Taimourzadeh (University of California, Irvine, CA, 92697, United States of America), W. A. Cooper (Ecole Polytechnique de Lausanne (EPFL), Centre de Recherches en Physique des Plasma (CRPP), CH-1015 Lausanne, Switzerland), A. Cappa, E. Ascasíbar, J. M. García-Regaña, M. Ochando, C. Hidalgo, P. Pons-Villalonga, F. Papousek, B. Ph. Van Milligen, U. Losada (Laboratorio Nacional de Fusion CIEMAT, Madrid, Spain), S. Yamamoto, K. Shinohara, H. Yang, J. Shiraishi, M. Honda, Y. Kamada, N. Aiba (National Institutes for Quantum and Radiological Science and Technology, Naka, Ibaraki 311-0193, Japan), K. Nagasaki, S. Kobayashi, (Institute of Advanced Energy, Kyoto University, Uji, Japan), A. Melnikov, L. G. Eliseev (National Research Centre “Kurchatov Institute”, Moscow, Russian Federation), Y. Suzuki (Graduate School of Advanced Science and Engineering, Hiroshima University, 1-4-1 Kagamiyama, Higashi-Hiroshima 739-8527, Japan), B. Breizman, F. L. Waelbroeck (Institute for Fusion Studies, Department of Physics, University of Texas at Austin, Austin, Texas 78712, United States), Y. Zou, (University of Science and Technology of China, Hefei, China), Y. Zou, (Southwestern Institute of Physics, Chengdu 610041, China), A. Wingen, D. del-Castillo-Negrete (Oak Ridge National Laboratory, Oak Ridge, Tennessee 37831-8071, US), D. Zarzoso, H. Betar (Aix-Marseille Université, CNRS, Centrale Marseille, M2P2 UMR 7340 Marseille, France), R. Sanchez, V. Tribaldos, J. M. Reynolds-Barredo, L. Herrera (Universidad Carlos III de Madrid, 28911 Leganes, Madrid, Spain), A. Bader (Type One Energy, 40 New York Ave. 200, Oak Ridge, TN 37830), D. Monseev (Max-Planck-Institut für Plasmaphysik, Wendelsteinstr. 1, Greifswald 17,491, Germany), J. Garcia, S. Mazzi (CEA, IRFM, F-13108 Saint Paul-lez-Durance, France), Y. Kazakov (Laboratory for Plasma Physics, LPP-ERM/KMS, TEC Partner, 1000 Brussels, Belgium), S. Sharapov (CCFE, Culham Science Centre, Oxfordshire OX14 3DB, United Kingdom), Z. Stancar (United Kingdom Atomic Energy Authority, Culham Science Centre, Abingdon, United Kingdom), M. Baruzzo (Consorzio RFX, Corso Stati Uniti 4, Padova, Italy), J. Ongena (Plasma Physics Laboratory – Royal Military Academy, Renaissancelaan 30, 1000 Brussels, Belgium), M. Poradzinski (Institute of Plasma Physics and Laser Microfusion, Hery str. 23, 01-497, Warsaw, Poland), N. Gorelenkov, F. Poli, J. Breslau, M. Podesta (Princeton Plasma Physics Laboratory, Princeton University, Princeton, NJ, 08543, United States), A. Di Siena, F. Jenko (Max-Planck-Institut für Plasmaphysik, D-85748 Garching, Germany), I. Holod (Lawrence Livermore National Laboratory, Livermore, CA 94550, United States), A. Melnikov (National Research Nuclear University MEPhI, Moscow, Russia 115409), A. Melnikov (Moscow Institute of Physics and Technology, Moscow Region, Dolgoprudny, Russia 141700), H. Betar (Renaissance Fusion, 38600 Fontaine, France).
Funding
The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work was supported by the Comunidad de Madrid under the project 2019-T1/AMB-13648, US DOE under grant DE-FG02-04ER54742, U.S. Department of Energy Office Contract DE-AC05-00OR22725 with UT-Battelle LLC and NIFS07KLPH004.
Acknowledgments
The authors would like to thanks LHD, Heliotron J, TJ-II, CFQS, DIII-D, JET and EAST technical staff for their contributions in the operation and maintenance of devices. The authors want to thanks the collaboration with S. A. Lazerson, A. Bierwage, V. Chan, W. W. Heidbrink, R. Fitzpatrick, S. M. Mahajan, D. Hatch.
Conflict of interest
FAR3d contributor XD was employed by the company General Atomics. FAR3d contributor AB was employed by the company Type One Energy. FAR3d contributor HB was employed by the company Renaissance Fusion.
The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2024.1422411/full#supplementary-material
References
1. Toi K, Ohdachi S, Yamamoto S, Nakajima N, Sakakibara S, Watanabe K, et al. MHD instabilities and their effects on plasma confinement in Large Helical Device plasmas. Nucl Fusion (2004) 44:217–25. doi:10.1088/0029-5515/44/2/001
2. Yamamoto S, Toi K, Ohdachi S, Nakajima N, Sakakibara S, Nührenberg C, et al. Experimental studies of energetic-ion-driven MHD instabilities in Large Helical Device plasmas. Nucl Fusion (2005) 45:326–36. doi:10.1088/0029-5515/45/5/003
3. Phillips CK, Fredrickson E, Hammett G, Hosea J, McGuire K, Stevens J, et al. ICRF Heating on TFTR. AIP Conf Proc (1992) 244:89–95. doi:10.1063/1.41652
4. Wong KL, Fonck R, Paul S, Roberts D, Fredrickson E, Nazikian R, et al. Excitation of toroidal Alfvén eigenmodes in TFTR. Phys Rev Lett (1991) 66:1874–7. doi:10.1103/PhysRevLett.66.1874
5. Sharapov SE, Borba D, Fasoli A, Kerner W, Eriksson LG, Heeter R, et al. Stability of alpha particle driven Alfvén eigenmodes in high performance JET DT plasmas. Nucl Fusion (1999) 39:373–88. doi:10.1088/0029-5515/39/3/307
6. Heidbrink WW, Strait E, Doyle E, Sager G, Snider R. An investigation of beam driven Alfvén instabilities in the DIII-D tokamak. Nucl Fusion (1992) 31:1635–48. doi:10.1088/0029-5515/31/9/002
7. Duong HH, Heidbrink W, Strait E, Petrie T, Lee R, Moyer R, et al. Loss of energetic beam ions during TAE instabilities. Nucl Fusion (1993) 33:749–65. doi:10.1088/0029-5515/33/5/i06
8. Kusama Y, Kramer G, Kimura H, Saigusa M, Ozeki T, Tobita K, et al. Characteristics of Alfvén eigenmodes, burst modes and chirping modes in the Alfvén frequency range driven by negative ion based neutral beam injection in JT-60U. Nucl Fusion (1999) 39:1837–43. doi:10.1088/0029-5515/39/11y/324
9. Shinohara K, Takechi M, Ishikawa M, Kusama Y, Morioka A, Oyama N, et al. Recent progress of Alfvén eigenmode experiments using N-NB in JT-60U tokamak. Nucl Fusion (2002) 42:942–8. doi:10.1088/0029-5515/42/8/302
10. Ross DW, Chen GL, Mahajan SM. Kinetic description of Alfvén wave heating. Phys Fluids (1982) 25:652–67. doi:10.1063/1.863789
11. Mahajan SM, Ross DW, Chen GL. Discrete Alfvén eigenmode spectrum in magnetohydrodynamics. Phys Fluids (1983) 26:2195–9. doi:10.1063/1.864404
12. Mahajan SM. Kinetic theory of shear Alfvén waves. Phys Fluids (1984) 27:2238–47. doi:10.1063/1.864878
13. Evans TE, Valanju PM, Benesch JF, Bengtson RD, Li YM, Mahajan SM, et al. Direct observation of the structure of global Alfvén eigenmodes in a tokamak plasma. Phys Rev Lett (1984) 53:1743–6. doi:10.1103/physrevlett.53.1743
14. Li YM, Mahajan SM, Ross DW. Destabilization of global Alfvén eigenmodes and kinetic Alfvén waves by alpha particles in a tokamak plasma. Phys Fluids (1987) 30:1466–84. doi:10.1063/1.866260
15. Coppi B, Migliuolo S, Pegoraro F, Porcelli F. Global modes and high-energy particles in ignited plasmas. Fluids B (1990) 2:927–43. doi:10.1063/1.859240
16. Rosenbluth MN, Tsai ST, Van Dam JW, Engquist MG. Energetic particle stabilization of ballooning modes in tokamaks. Phys Rev Lett (1983) 51:1967–70. doi:10.1103/physrevlett.51.1967
17. White RB, Bussac M, Romanelli F. High-beta, sawtooth-free tokamak operation using energetic trapped particles. Phys Rev Lett (1989) 62:539–42. doi:10.1103/PhysRevLett.62.539
18. Porcelli F. Fast particle stabilisation. Plasma Phys Control Fusion (1991) 33:1601–20. doi:10.1088/0741-3335/33/13/009
19. Chen L, White RB, Rosenbluth MN. Excitation of internal kink modes by trapped energetic beam ions. Phys Rev Lett (1984) 52:1122–5. doi:10.1103/physrevlett.52.1122
20. Coppi B, Porcelli F. Theoretical model of fishbone oscillations in magnetically confined plasmas. Phys Rev Lett (1986) 57:2272–5. doi:10.1103/physrevlett.57.2272
21. Biglari H, Chen L. Unified theory of resonant excitation of kinetic ballooning modes by energetic ions and alpha particles in tokamaks. Phys Rev Lett (1991) 67:3681–4. doi:10.1103/physrevlett.67.3681
22. Garcia-Munoz M, Classen I, Geiger B, Heidbrink W, Van Zeeland M, Äkäslompolo S, et al. Fast-ion transport induced by Alfvén eigenmodes in the ASDEX Upgrade tokamak. Nucl Fusion (2011) 51:103013. doi:10.1088/0029-5515/51/10/103013
23. Darrow DS, Zweben S, Chang Z, Cheng C, Diesso M, Fredrickson E, et al. Observations of neutral beam and ICRF tail ion losses due to Alfven modes in TFTR. Nucl Fusion (1997) 37:939–54. doi:10.1088/0029-5515/37/7/i03
24. Marashek M, Günter S, Kass T, Scott B, Zohm H, ASDEX Upgrade Team. Observation of toroidicity-induced alfvén eigenmodes in ohmically heated plasmas by drift wave excitation. Phys Rev Lett (1997) 79:4186–9. doi:10.1103/physrevlett.79.4186
25. Melnikov AV, Markovic T, Eliseev LG, Adámek J, Aftanas M, Bilkova P, et al. Quasicoherent modes on the COMPASS tokamak. Plasma Phys Control Fusion (2015) 57:065006. doi:10.1088/0741-3335/57/6/065006
26. Markovic T, Markovicˊ A, Melnikov J, Seidl L, Eliseev J, Havlicek A, et al. 44th European Physical Society Conference on Plasma Physics. Queen's University: Belfast, North. Ireland (2017) 41:P5.140.
27. Valovič M, Lloyd B, McClements K, Warrick C, Fielding S, Morris A, et al. Quasi-stationary high plasmas and fast particle instabilities in the COMPASS-D tokamak with ECRH and LHCD. Nucl Fusion (2000) 40:1569–73. doi:10.1088/0029-5515/40/9/101
28. Wong KL, Chu M, Luce T, Petty C, Politzer P, Prater R, et al. Internal kink instability during off-axis electron cyclotron current drive in the DIII-D tokamak. Phys Rev Lett (2000) 85:996–9. doi:10.1103/PhysRevLett.85.996
29. Deng CB, Brower DL, Breizman BN, Spong DA, Almagri AF, Anderson DT, et al. Energetic-electron-driven instability in the helically symmetric experiment. Phys Rev Lett (2009) 103:025003. doi:10.1103/PhysRevLett.103.025003
30. Isobe M, Toi K, Yoshimura Y, Shimizu A, Akiyama T, Ida K, et al. Energetic-particle modes driven by suprathermal electrons produced by off-axis second harmonic ECRH in compact helical system (CHS). Nucl Fusion (2010) 50:084007. doi:10.1088/0029-5515/50/8/084007
31. Melnikov AV, Eliseev LG, Ochando MA, Nagaoka K, Ascasibar E, Cappa A, et al. A quasi-coherent electrostatic mode in ECRH plasmas on TJ-II. Plasma Fusion Res (2011) 6:2402030. doi:10.1585/pfr.6.2402030
32. Heidbrink WW. Basic physics of Alfvén instabilities driven by energetic particles in toroidally confined plasmas. Plasma Phys (2008) 15:055501. doi:10.1063/1.2838239
33. Todo Y. Introduction to the interaction between energetic particles and Alfven eigenmodes in toroidal plasmas. Rev Mod Plasma Phys (2019) 3:1. doi:10.1007/s41614-018-0022-9
34. Weller A, Spong DA, Jaenicke R, Lazaros A, Penningsfeld FP, Sattler S. Neutral beam driven global Alfvén eigenmodes in the Wendelstein W7-AS stellarator. Phys Rev Lett (1994) 72:1220–3. doi:10.1103/physrevlett.72.1220
35. Van Zeeland MA, Kramer GJ, Austin ME, Boivin RL, Heidbrink WW, Makowski MA, et al. Radial structure of Alfvén eigenmodes in the DIII-D tokamak through electron-cyclotron-emission measurements. Phys Rev Lett (2006) 97:135001. doi:10.1103/PhysRevLett.97.135001
36. Nazikian R, Gorelenkov NN, Alper B, Berk HL, Borba D, Budny RV, et al. Excitation of Alfvén eigenmodes by low energy beam ions in the DIII-D and JET tokamaks. Phys Plasmas (2008) 15:056107. doi:10.1063/1.2839286
37. Van Zeeland MA, Heidbrink W, Nazikian R, Austin M, Cheng C, Chu M, et al. Measurements, modelling and electron cyclotron heating modification of Alfvén eigenmode activity in DIII-D. Nucl Fusion (2009) 49:065003. doi:10.1088/0029-5515/49/6/065003
38. Kieras CE, Tataronis JA. The shear Alfvén continuous spectrum of axisymmetric toroidal equilibria in the large aspect ratio limit. J Plasma Phys (1982) 28:395–414. doi:10.1017/s0022377800000386
39. Wang Z, Lin Z, Deng W, Holod I, Heidbrink WW, Xiao Y, et al. Properties of toroidal Alfvén eigenmode in DIII-D plasma. Phys Plasmas (2015) 22:022509. doi:10.1063/1.4908274
40. Van Zeeland M, Heidbrink W, Sharapov S, Spong D, Cappa A, Chen X, et al. Electron cyclotron heating can drastically alter reversed shear Alfvén eigenmode activity in DIII-D through finite pressure effects. Nucl Fusion (2016) 56:112007. doi:10.1088/0029-5515/56/11/112007
41. Turnbull AD, Strait EJ, Heidbrink WW, Chu MS, Duong HH, Greene JM, et al. Global alfvén modes: theory and experiment*. Phys Fluids B (1993) 5:2546–53. doi:10.1063/1.860742
42. Deng W, Lin Z, Holod I, Wang Z, Xiao Y, Zhang H. Linear properties of reversed shear Alfvén eigenmodes in the DIII-D tokamak. Nucl Fusion (2012) 52:043006. doi:10.1088/0029-5515/52/4/043006
43. Kimura H, Kusama Y, Saigusa M, Kramer G, Tobita K, Nemoto M, et al. Alfvén eigenmode and energetic particle research in JT-60U. Nucl Fusion (1998) 38:1303–14. doi:10.1088/0029-5515/38/9/304
44. Betti R, Freidberg JP. Stability of Alfvén gap modes in burning plasmas. Phys Fluids B (1992) 4:1465–74. doi:10.1063/1.860057
45. Kramer GJ, Saigusa M, Ozeki T, Kusama Y, Kimura H, Oikawa T, et al. Noncircular triangularity and ellipticity-induced alfvén eigenmodes observed in jt-60u. Phys Rev Lett (1998) 80:2594–7. doi:10.1103/physrevlett.80.2594
46. Betti R, Freidberg JP. Ellipticity induced Alfvén eigenmodes. Phys Fluids B (1991) 3:1865–70. doi:10.1063/1.859655
47. Bass EM, Waltz RE. Gyrokinetic simulation of global and local Alfvén eigenmodes driven by energetic particles in a DIII-D discharge. Phys Plasmas (2013) 20:012508. doi:10.1063/1.4773177
48. Yamamoto S, Toi K, Nakajima N, Ohdachi S, Sakakibara S, Watanabe KY, et al. Observation of helicity-induced Alfvén eigenmodes in large-helical-device plasmas heated by neutral-beam injection. Phys Rev Lett (2003) 91:245001. doi:10.1103/PhysRevLett.91.245001
49. Chen L. Theory of magnetohydrodynamic instabilities excited by energetic particles in tokamaks*. Phys Plasmas (1994) 1:1519–1522. doi:10.1063/1.870702
50. Ido T, Osakabe M, Shimizu A, Watari T, Nishiura M, Toi K, et al. Identification of the energetic-particle driven GAM in the LHD. Nucl Fusion (2015) 55:083024. doi:10.1088/0029-5515/55/8/083024
51. Wang H, Todo Y, Ido T, Osakabe M. Simulation study of high-frequency energetic particle driven geodesic acoustic mode. Phys Plasmas (2015) 22:092507. doi:10.1063/1.4930130
52. Wang H, Todo Y, Ido T, Suzuki Y. Chirping and sudden excitation of energetic-particle-driven geodesic acoustic modes in a large helical device experiment. Phys Rev Lett (2018) 120:175001. doi:10.1103/PhysRevLett.120.175001
53. Ogawa K, Isobe M, Toi K, Shimizu A, Spong D, Osakabe M, et al. A study on the TAE-induced fast-ion loss process in LHD. Nucl Fusion (2013) 53:053012. doi:10.1088/0029-5515/53/5/053012
54. Murakami M, Park J, Giruzzi G, Garcia J, Bonoli P, Budny R, et al. Integrated modelling of steady-state scenarios and heating and current drive mixes for ITER. Nucl Fusion (2011) 51:103006. doi:10.1088/0029-5515/51/10/103006
55. Pengxiang C, Wu B, Wang J, Li Y, Wang X, Xu H, et al. The influence of neutral beam injection on the heating and current drive with electron cyclotron wave on EAST. Plasma Sci Technol (2016) 18:1064–8. doi:10.1088/1009-0630/18/11/02
56. Murakami M, Greenfield C, Wade M, Luce T, Ferron J, John HS, et al. 100% noninductive operation at high beta using off-axis ECCD in DIII-D. Nucl Fusion (2005) 45:1419–26. doi:10.1088/0029-5515/45/11/024
57. Takenaga H, JT-60 Team. Overview of JT-60U results for the development of a steady-state advanced tokamak scenario. Nucl Fusion (2007) 47:S563–78. doi:10.1088/0029-5515/47/10/s06
58. Voitsekhovitch I, Alper B, Brix M, Budny R, Buratti P, Challis C, et al. Non-inductive current drive and transport in high βN plasmas in JET. Nucl Fusion (2009) 49:055026. doi:10.1088/0029-5515/49/5/055026
59. Chapman IT, La Haye R, Buttery R, Heidbrink W, Jackson G, Muscatello C, et al. Sawtooth control using electron cyclotron current drive in ITER demonstration plasmas in DIII-D. Nucl Fusion (2012) 52:063006. doi:10.1088/0029-5515/52/6/063006
60. Murakami M, Park J, Petty C, Luce T, Heidbrink W, Osborne T, et al. Off-axis neutral beam current drive for advanced scenario development in DIII-D. Nucl Fusion (2009) 49:065031. doi:10.1088/0029-5515/49/6/065031
61. Isayama A, Matsunaga G, Kobayashi T, Moriyama S, Oyama N, Sakamoto Y, et al. Neoclassical tearing mode control using electron cyclotron current drive and magnetic island evolution in JT-60U. Nucl Fusion (2009) 49:055006. doi:10.1088/0029-5515/49/5/055006
62. Oikawa T, Ushigusa K, Forest C, Nemoto M, Naito O, Kusama Y, et al. Heating and non-inductive current drive by negative ion based NBI in JT-60U. Nucl Fusion (2000) 40:435–43. doi:10.1088/0029-5515/40/3y/301
63. Sharapov SE, Garcia-Munoz M, Van Zeeland MA, Bobkov B, Classen IGJ, Ferreira J, et al. The effects of electron cyclotron heating and current drive on toroidal Alfvén eigenmodes in tokamak plasmas. Plasma Phys Control Fusion (2018) 60:014026. doi:10.1088/1361-6587/aa90ee
64. Adulsiriswad P, Todo Y, Yamamoto S, Kado S, Kobayashi S, Ohshima S, et al. Magnetohydrodynamic hybrid simulation of Alfvén eigenmodes in Heliotron J, a low shear helical axis stellarator/heliotron. Nucl Fusion (2020) 60:096005. doi:10.1088/1741-4326/ab9c4b
65. Silva Rosa PR, Giruzzi G. RF current drive by electron cyclotron waves in the presence of magnetic islands. Plasma Phys Control Fusion (2000) 42:755–69. doi:10.1088/0741-3335/42/7/302
66. Prater R. Heating and current drive by electron cyclotron waves. Phys Plasma (2004) 11:2349–76. doi:10.1063/1.1690762
67. Sauter O, Henderson MA, Hofmann F, Goodman T, Alberti S, Angioni C, et al. Steady-state fully noninductive current driven by electron cyclotron waves in a magnetically confined plasma. Phys Rev Lett (2000) 84:3322–5. doi:10.1103/PhysRevLett.84.3322
68. Suzuki T, Ide S, Hamamatsu K, Isayama A, Fujita T, Petty CC, et al. Heating and current drive by electron cyclotron waves in JT-60U. Nucl Fusion (2004) 44:699–708. doi:10.1088/0029-5515/44/7/002
69. Motojima G, Nagasaki K, Nosaku M, Okada H, Watanabe K, Mizuuchi T, et al. Control of non-inductive current in Heliotron J*. Nucl Fusion (2007) 47:1045–52. doi:10.1088/0029-5515/47/8/039
70. Fernandez A, Cappa A, Castejón F, Fontdecaba JM, Nagasaki K. ECCD experiments in the TJ-II stellarator. Fusion Sci Technol (2008) 53:254–60. doi:10.13182/fst08-a1670
71. Yamamoto S, Nagasaki K, Nagaoka K, Varela J, Cappa Á, Ascasíbar E, et al. Effect of ECH/ECCD on energetic-particle-driven MHD modes in helical plasmas. Nucl Fusion (2020) 60:066018. doi:10.1088/1741-4326/ab7f13
72. Nagasaki K, Isayama A, Hayashi N, Ozeki T, Takechi M, Oyama N, et al. Stabilization of neoclassical tearing mode by ECCD and its evolution simulation on JT-60U tokamak. Nucl Fusion (2005) 45:1608–17. doi:10.1088/0029-5515/45/12/016
73. Prater R, Haye RL, Luce T, Petty C, Strait E, Ferron J, et al. Stabilization and prevention of the 2/1 neoclassical tearing mode for improved performance in DIII-D. Nucl Fusion (2007) 47:371–7. doi:10.1088/0029-5515/47/5/001
74. Fasoli A, Borba D, Gormezano C, Heeter R, Jaun A, Jacquinot J, et al. Alfvén eigenmode experiments in tokamaks and stellarators Plasma Phys. Control. Fusion (1997) 39:B287. doi:10.1088/0741-3335/39/12B/022
75. Felici F, Goodman T, Sauter O, Canal G, Coda S, Duval B, et al. Integrated real-time control of MHD instabilities using multi-beam ECRH/ECCD systems on TCV. Nucl Fusion (2015) 52:074001. doi:10.1088/0029-5515/52/7/074001
76. Petty CC, Nazikian R, Park J, Turco F, Chen X, Cui L, et al. Advances in the steady-state hybrid regime in DIII-D—a fully non-inductive, ELM-suppressed scenario for ITER. Nucl Fusion (2017) 57:116057. doi:10.1088/1741-4326/aa80ab
77. Kim J, Kang J, Rhee T, Jo J, Han H, Podestà M, et al. Suppression of toroidal Alfvén eigenmodes by the electron cyclotron current drive in KSTAR plasmas. Nucl Fusion (2022) 62:026029. doi:10.1088/1741-4326/ac3e39
78. Sallander E, Weller A, Team WA. Effects of non-vanishing toroidal current densities on stability in the Wendelstein 7-AS stellarator. Nucl Fusion (2000) 40:1499–509. doi:10.1088/0029-5515/40/8/308
79. Castejon F, Fujisawa A, Ida K, Talmadge JN, Estrada T, López-Bruna D, et al. Influence of magnetic topology on transport and stability in stellarators. Plasma Phys Control Fusion (2005) 47:B53–69. doi:10.1088/0741-3335/47/12b/s05
80. Nagaoka K, Ido T, Ascasíbar E, Estrada T, Yamamoto S, Melnikov A, et al. Mitigation of NBI-driven Alfvén eigenmodes by electron cyclotron heating in the TJ-II stellarator. Nucl Fusion (2013) 53:072004. doi:10.1088/0029-5515/53/7/072004
81. Garcia L, Ochando MA, Carreras BA, Carralero D, Hidalgo C, van Milligen BP. Effect of fast electrons on the stability of resistive interchange modes in the TJ-II stellarator. Phys Plasma (2016) 23:062319. doi:10.1063/1.4954826
82. Melnikov AV, Krupnik L, Eliseev L, Barcala J, Bravo A, Chmyga A, et al. Heavy ion beam probing—diagnostics to study potential and turbulence in toroidal plasmas. Nucl Fusion (2017) 57:072004. doi:10.1088/1741-4326/aa5382
83. Stix TH. Generation and thermalization of plasma waves. Phys Fluids (1958) 1(4):308–17. doi:10.1063/1.1705889
84. Du XD, Toi K, Osakabe M, Ohdachi S, Ido T, Tanaka K, et al. Resistive interchange modes destabilized by helically trapped energetic ions in a helical plasma. Phys Rev Lett (2015) 114:155003. doi:10.1103/PhysRevLett.114.155003
85. Du XD, Toi K, Ohdachi S, Osakabe M, Ido T, Tanaka K, et al. Resistive interchange mode destabilized by helically trapped energetic ions and its effects on energetic ions and bulk plasma in a helical plasma. Nucl Fusion (2016) 56:016002. doi:10.1088/0029-5515/56/1/016002
86. Du XD, Toi K, Ohdachi S, Watanabe KY, Takahashi H, Yoshimura Y, et al. Suppression of trapped energetic ions driven resistive interchange modes with electron cyclotron heating in a helical plasma. Phys Rev Lett (2017) 118:125001. doi:10.1103/PhysRevLett.118.125001
87. Pace DC, Austin ME, Bardoczi L, Collins CS, Crowley B, Davis E, et al. Dynamic neutral beam current and voltage control to improve beam efficacy in tokamaks. Phys Plasmas (2018) 25:056109. doi:10.1063/1.5016160
88. Collins C, Heidbrink W, Podestà M, White R, Kramer G, Pace D, et al. Phase-space dependent critical gradient behavior of fast-ion transport due to Alfvén eigenmodes. Nucl Fusion (2017) 57:086005. doi:10.1088/1741-4326/aa720c
89. Van Zeeland MA, Heidbrink WW, Fisher RK, García Muñoz M, Kramer GJ, Pace DC, et al. Measurements and modeling of Alfvén eigenmode induced fast ion transport and loss in DIII-D and ASDEX Upgrade. Phys Plasmas (2011) 18:056114. doi:10.1063/1.3574663
90. Fenstermacher ME, Abbate J, Abe S, Abrams T, Adams M, Adamson B, et al. DIII-D research advancing the physics basis for optimizing the tokamak approach to fusion energy. Nucl Fusion (2022) 62:042024. doi:10.1088/1741-4326/ac2ff2
91. Kramer GJ, Bortolon A, Ferraro NM, Spong DA, Crocker NA, Darrow DS, et al. Mitigation of Alfvénic activity by 3D magnetic perturbations on NSTX. Plasma Phys Control Fusion (2016) 58:085003. doi:10.1088/0741-3335/58/8/085003
92. Ida K, Yoshinuma M, Kobayashi M, Kobayashi T, Kenmochi N, Nespoli F, et al. Overview of Large Helical Device experiments of basic plasma physics for solving crucial issues in reaching burning plasma conditions. Nucl Fusion (2024) 64:112009. doi:10.1088/1741-4326/ad3a7a
93. Fu GY, Cheng C, Budny R, Chang Z, Darrow D, Fredrickson E, et al. Stability analysis of toroidicity-induced Alfvén eigenmodes in TFTR deuterium-tritium experiments. Phys Rev Lett (1995) 75:2336–9. doi:10.1103/PhysRevLett.75.2336
94. Fu GY, Cheng CZ, Budny R, Chang Z, Darrow DS, Fredrickson E, et al. Analysis of alpha particle-driven toroidal Alfvén eigenmodes in Tokamak Fusion Test Reactor deuterium–tritium experiments. Plasma Phys (1996) 3:4036–4045. doi:10.1063/1.871537
95. Nazikian R, Fu GY, Batha SH, Bell MG, Bell RE, Budny RV, et al. Alpha-particle-driven toroidal Alfvén eigenmodes in the tokamak fusion test reactor. Phys Rev Lett (1997) 78:2976–9. doi:10.1103/physrevlett.78.2976
96. Spong DA, Carreras BA, Hedrick CL. Linearized gyrofluid model of the alpha-destabilized toroidal Alfvén eigenmode with continuum damping effects. Phys.Fluids B (1992) 4:3316–28. doi:10.1063/1.860386
97. Spong DA, Hedrick C, Carreras B. Strategies for modifying alpha driven TAE thresholds through q profile and ion temperature control. Nucl Fusion (1995) 35:1687–96. doi:10.1088/0029-5515/35/12/i33
98. Fitzgerald M, Sharapov S, Siren P, Tholerus E, Dreval M, Szepesi G, et al. Toroidal Alfvén eigenmode stability in JET internal transport barrier afterglow experiments. Nucl Fusion (2022) 62:106001. doi:10.1088/1741-4326/ac84ee
99. Fitzgerald M, Dumont R, Keeling D, Mailloux J, Sharapov S, Dreval M, et al. Stability analysis of alpha driven toroidal Alfvén eigenmodes observed in JET deuterium-tritium internal transport barrier plasmas. Nucl Fusion (2023) 63:112006. doi:10.1088/1741-4326/acee14
100. Porcelli F, Stankiewicz R, Kerner W, Berk HL. Solution of the drift-kinetic equation for global plasma modes and finite particle orbit widths. Plasmas (1994) 1:470–80. doi:10.1063/1.870792
101. Varela J, Spong D, Garcia L. Analysis of Alfven eigenmode destabilization in ITER using a Landau closure model. Nucl Fusion (2019) 59:076036. doi:10.1088/1741-4326/ab1ebe
102. Huang J, Garofalo A, Qian J, Gong X, Ding S, Varela J, et al. Progress in extending high poloidal beta scenarios on DIII-D towards a steady-state fusion reactor and impact of energetic particles. Nucl Fusion (2020) 60:126007. doi:10.1088/1741-4326/abaf33
103. Varela J, Huang J, Spong D, Chen J, Chan V, Garcia L, et al. Theoretical study of the Alfven eigenmode stability in CFETR steady state discharges. Nucl Fusion (2022) 62:036005. doi:10.1088/1741-4326/ac4778
104. Varela J, Spong DA, Garcia L, Todo Y, Huang J, Murakami M. Study of Alfven eigenmodes stability in plasma with multiple NBI driven energetic particle species. Phys.Plasmas (2019) 26:062502. doi:10.1063/1.5098347
106. Charlton LA, Holmes J, Hicks H, Lynch V, Carreras B. Numerical calculations using the full MHD equations in toroidal geometry. J Comp. Phys (1986) 63:107–29. doi:10.1016/0021-9991(86)90086-0
107. Charlton LA, Holmes J, Lynch V, Carreras B, Hender T. Compressible linear and nonlinear resistive MHD calculations in toroidal geometry. J Comp. Phys (1990) 86:270–93. doi:10.1016/0021-9991(90)90102-7
108. Hedrick CL, Leboeuf JN, Spong DA. Alpha-Alfvén local dispersion relation and solutions. Phys.Fluids B (1992) 4:3869–82. doi:10.1063/1.860344
109. Varela J, Spong D, Garcia L. Analysis of Alfvén eigenmode destabilization by energetic particles in Large Helical Device using a Landau-closure model. Nucl Fusion (2017) 57:046018. doi:10.1088/1741-4326/aa5d04
110. Spong DA. Simulation of Alfvén frequency cascade modes in reversed shear-discharges using a Landau-closure model. Nucl Fusion (2013) 53:053008. doi:10.1088/0029-5515/53/5/053008
111. Hirshman SP, Whitson JC. Steepest-descent moment method for three-dimensional magnetohydrodynamic equilibria. Phys Fluids (1983) 26:3553–3568. doi:10.1063/1.864116
112. Brix M, Hawkes NC, Boboc A, Drozdov V, Sharapov SE, JET-EFDA Contributors. Accuracy of EFIT equilibrium reconstruction with internal diagnostic information at JET. Rev Sci Instrum (2008) 79:10F325. doi:10.1063/1.2964180
113. Mishchenko A, Cole M, Kleiber R, Könies A. New variables for gyrokinetic electromagnetic simulations. Plasmas (2014) 21:092110. doi:10.1063/1.4880560
114. Chen Y, Parker SE. A δf particle method for gyrokinetic simulations with kinetic electrons and electromagnetic perturbations. J Comp. Phys (2003) 189:463–75. doi:10.1016/s0021-9991(03)00228-6
115. Candy J, Waltz R. An Eulerian gyrokinetic-Maxwell solver. J Comp. Phys (2003) 186:545–81. doi:10.1016/s0021-9991(03)00079-2
116. Lin Z, Hahm TS, Lee WW, Tang WM, White RB. Turbulent transport reduction by zonal flows: massively parallel simulations. Science (1998) 281:1835–7. doi:10.1126/science.281.5384.1835
117. Bottino A, Peeters AG, Hatzky R, Jolliet S, McMillan BF, Tran TM, et al. Nonlinear low noise particle-in-cell simulations of electron temperature gradient driven turbulence. Phys Plasmas (2007) 14:010701. doi:10.1063/1.2428280
118. Citrin J, Garcia J, Görler T, Jenko F, Mantica P, Told D, et al. Electromagnetic stabilization of tokamak microturbulence in a high-βregime. Plasma Phys Control Fusion (2015) 57:014032. doi:10.1088/0741-3335/57/1/014032
119. Todo Y, Shinohara K, Takechi M, Ishikawa M. Nonlocal energetic particle mode in a JT-60U plasma. Plasmas (2005) 12:012503. doi:10.1063/1.1828084
120. Breslau J, Ferraro N, Jardin S. Some properties of the M3D-C1 form of the three-dimensional magnetohydrodynamics equations. Plasmas (2009) 16:092503. doi:10.1063/1.3224035
121. Lauber P, Günter S, Könies A, Pinches S. LIGKA: a linear gyrokinetic code for the description of background kinetic and fast particle effects on the MHD stability in tokamaks. J Comput Phys (2007) 226:447–65. doi:10.1016/j.jcp.2007.04.019
122. Liu Y, Chu MS, Chapman IT, Hender TC. Publisher’s Note: “Third harmonic generation of a short pulse laser in a plasma density ripple created by a machining beam” [Phys. Plasmas 15, 023106 (2008)]. Plasmas (2008) 15:112503. doi:10.1063/1.3008045
123. Taimourzadeh S, Bass E, Chen Y, Collins C, Gorelenkov N, Könies A, et al. Verification and validation of integrated simulation of energetic particles in fusion plasmas. Nucl Fusion (2019) 59:066006. doi:10.1088/1741-4326/ab0c38
124. Chen L, Zonca F. Physics of Alfvén waves and energetic particles in burning plasmas. Rev Mod Phys (2016) 88:015008. doi:10.1103/revmodphys.88.015008
125. Boozer AH. Establishment of magnetic coordinates for a given magnetic field. Phys Fluids (1982) 25:520–1. doi:10.1063/1.863765
128. Stix TH. Fast-wave heating of a two-component plasma. Nucl Fusion (1975) 15:737–54. doi:10.1088/0029-5515/15/5/003
129. Wilkie GJ. Analytic slowing-down distributions as modified by turbulent transport. J Plasma Phys (2018) 84:745840601. doi:10.1017/s0022377818001058
130. Hedrick CL, Leboeuf JN. Landau fluid equations for electromagnetic and electrostatic fluctuations. Phys.Fluids B (1992) 4:3915–34. doi:10.1063/1.860348
131. Varela J, Spong D, Garcia L, Ohdachi S, Watanabe K, Seki R. Analysis of the MHD stability and energetic particles effects on EIC events in LHD plasma using a Landau-closure model. Nucl Fusion (2019) 59:046008. doi:10.1088/1741-4326/aaff80
132. Suzuki Y, Yamada H, Nakajima N, Watanabe K, Nakamura Y, Hayashi T. Theoretical considerations of doublet-like configuration in LHD. Nucl Fusion (2006) 46:123–32. doi:10.1088/0029-5515/46/1/014
133. Nagaoka K, Ida K, Yoshinuma M, Takeiri Y, Yokoyama M, Morita S, et al. Heat and momentum transport of ion internal transport barrier plasmas on the Large Helical Device. Nucl Fusion (2011) 51:083022. doi:10.1088/0029-5515/51/8/083022
134. Ascasíbar E, Alba D, Alegre D, Alonso A, Alonso J, de Aragón F, et al. Overview of recent TJ-II stellarator results. Nucl Fusion (2019) 59:112019. doi:10.1088/1741-4326/ab205e
135. Ido T, Shimizu A, Nishiura M, Nakamura S, Kato S, Nakano H, et al. Potential fluctuation associated with the energetic-particle-induced geodesic acoustic mode in the Large Helical Device. Nucl Fusion (2011) 51:073046. doi:10.1088/0029-5515/51/7/073046
136. Toi K, Watanabe F, Tokuzawa T, Ida K, Morita S, Ido T, et al. Observation of reversed-shear Alfvén eigenmodes excited by energetic ions in a helical plasma. Phys Rev Lett (2010) 105:145003. doi:10.1103/PhysRevLett.105.145003
137. Toi K, Yamamoto S, Nakajima N, Ohdachi S, Sakakibara S, Osakabe M, et al. Energetic ion driven Alfvén eigenmodes in Large Helical Device plasmas with three-dimensional magnetic structure and their impact on energetic ion transport. Plasma Phys Control Fusion (2004) 46:S1–S13. doi:10.1088/0741-3335/46/7/s01
138. Melnikov AV, Eliseev L, Ascasibar E, Chmyga A, Hidalgo C, Ido T, et al. Alfvén eigenmode properties and dynamics in the TJ-II stellarator. Nucl Fusion (2012) 52:123004. doi:10.1088/0029-5515/52/12/123004
139. Melnikov AV, Ochando M, Ascasibar E, Castejon F, Cappa A, Eliseev L, et al. Effect of magnetic configuration on frequency of NBI-driven Alfvén modes in TJ-II. Nucl Fusion (2014) 54:123002. doi:10.1088/0029-5515/54/12/123002
140. Osakabe M, Yamamoto S, Toi K, Takeiri Y, Sakakibara S, Nagaoka K, et al. Experimental observations of enhanced radial transport of energetic particles with Alfvén eigenmode on the LHD. Nucl Fusion (2006) 46:S911–7. doi:10.1088/0029-5515/46/10/s07
141. Kamio S, Fujiwara Y, Nagaoka K, Ogawa K, Seki R, Yamaguchi H, et al. Observation of clump structure in transported particle orbit using an upgraded neutral particle analyzer during TAE burst in LHD. Nucl Fusion (2020) 60:112002. doi:10.1088/1741-4326/ab7890
142. Todo Y, Seki R, Spong DA, Wang H, Suzuki Y, Yamamoto S, et al. Comprehensive magnetohydrodynamic hybrid simulations of fast ion driven instabilities in a Large Helical Device experiment. Plasma Phys (2017) 24:081203. doi:10.1063/1.4997529
143. Seki R, Todo Y, Suzuki Y, Spong D, Ogawa K, Isobe M, et al. Comprehensive magnetohydrodynamic hybrid simulations of Alfvén eigenmode bursts and fast-ion losses in the Large Helical Device. Nucl Fusion (2019) 59:096018. doi:10.1088/1741-4326/ab266e
144. Spong DA, Sanchez R, Weller A. Shear Alfvén continua in stellarators. Plasma Phys (2003) 10:3217–24. doi:10.1063/1.1590316
145. Nave MFF, Campbell D, Joffrin E, Marcus F, Sadler G, Smeulders P, et al. Fishbone activity in JET. Nucl Fusion (1991) 31:697–710. doi:10.1088/0029-5515/31/4/007
146. Toi K, Ohdachi S, Yamamoto S, Sakakibara S, Narihara K, Tanaka K, et al. Observation of the low to high confinement transition in the large helical device. Phys Plasmas (2005) 12:020701. doi:10.1063/1.1843122
147. Watanabe KY, Masamune S, Takemura Y, Funaba H, Sakakibara S, Watanabe F, et al. Effect of pressure-driven MHD instabilities on confinement in reactor-relevant high-beta helical plasmas. Phys Plasmas (2011) 18:056119. doi:10.1063/1.3592675
148. Ueda R, Watanabe KY, Matsumoto Y, Itagaki M, Sato M, Oikawa S. Characteristics of magnetic island formation due to resistive interchange instability in helical plasma. Phys Plasmas (2014) 21:052502. doi:10.1063/1.4875340
149. Sakakibara S, Watanabe KY, Suzuki Y, Narushima Y, Ohdachi S, Nakajima N, et al. MHD study of the reactor-relevant high-beta regime in the Large Helical Device. Plasmas Phys Control Fusion (2008) 50:124014. doi:10.1088/0741-3335/50/12/124014
150. Ogawa K, Isobe M, Kawase H, Nishitani T, Seki R, Osakabe M. Observation of enhanced radial transport of energetic ion due to energetic particle mode destabilized by helically-trapped energetic ion in the Large Helical Device. Nucl Fusion (2018) 58:044001. doi:10.1088/1741-4326/aaab18
151. Ogawa K, Isobe M, Kawase H, Nishitani T, Seki R, Osakabe M, et al. Effect of the helically-trapped energetic-ion-driven resistive interchange modes on energetic ion confinement in the Large Helical Device. Plasma Phys Control Fusion (2018) 60:044005. doi:10.1088/1361-6587/aaab1f
152. Varela J, Spong D, Garcia L. Analysis of Alfven eigenmodes destabilization by energetic particles in TJ-II using a Landau-closure model. Nucl Fusion (2017) 57:126019. doi:10.1088/1741-4326/aa83c4
153. Cappa A, Varela J, López Bruna D, Ascasíbar E, Liniers M, Eliseev L, et al. Stability analysis of TJ-II stellarator NBI driven Alfvén eigenmodes in ECRH and ECCD experiments. Nucl Fusion (2021) 61:066019. doi:10.1088/1741-4326/abf74b
154. Eliseev LG, Melnikov AV, Ascasibar E, Cappa A, Drabinskiy M, Hidalgo C, et al. Experimental observation of the geodesic acoustic frequency limit for the NBI-driven Alfvén eigenmodes in TJ-II. Phys Plasmas (2021) 28:072510. doi:10.1063/5.0049225
155. Eliseev LG, Melnikov AV, Lysenko SE. Study of Alfvén eigenmodes with heavy ion beam probing in the TJ-II stellarator. Rev Mod Plasma Phys (2022) 6:25. doi:10.1007/s41614-022-00088-y
156. Melnikov AV, Hidalgo C, Chmyga AA, Dreval NB, Eliseev LG, Khrebtov SM, et al. Plasma Potential Measurements by the Heavy Ion Beam Probe Diagnostic in Fusion Plasmas: Biasing Experiments in the TJ-II Stellarator and T-10 Tokamak. Fusion Sci Technol (2004) 46:299–311. doi:10.13182/FST04-A568
157. Melnikov AV, Alonso A, Ascasíbar E, Balbin R, Chmyga AA, Dnestrovskij YN, et al. Plasma potential evolution study by HIBP diagnostic during NBI experiments in the TJ-II stellarator. Fusion Sci.Technol. (2007) 51:31–7. doi:10.13182/fst07-a1284
159. Turnbull AD, Chu MS, Strait EJ, Lao LL, Greene JM, Taylor TS, et al. Global Alfven eigenmodes in DIII-D. San Diego, CA: General Atomics (1992).
160. Strait EJ, Heidbrink W, Turnbull A, Chu M, Duong H. Stability of neutral beam driven TAE modes in DIII-D. Nucl Fusion (1993) 33:1849–70. doi:10.1088/0029-5515/33/12/i07
161. Heidbrink W, Van Zeeland M, Austin M, Bass E, Ghantous K, Gorelenkov N, et al. The effect of the fast-ion profile on Alfvén eigenmode stability. Nucl Fusion (2013) 53:093006. doi:10.1088/0029-5515/53/9/093006
162. Heidbrink W, Strait EJ, Chu MS, Turnbull AD. Observation of beta-induced Alfvén eigenmodes in the DIII-D tokamak. Phys Rev Lett (1993) 71:855–8. doi:10.1103/physrevlett.71.855
163. Van Zeeland MA, Austin M, Carlstrom T, Deterly T, Finkenthal D, Holcomb C, et al. Internal Alfvén eigenmode observations on DIII-D. Nucl Fusion (2006) 46:S880–7. doi:10.1088/0029-5515/46/10/s03
164. Pace DC, Fisher RK, García-Muñoz M, Heidbrink WW, Van Zeeland MA. Convective beam ion losses due to Alfvén eigenmodes in DIII-D reversed-shear plasmas. Plasma Phys Control Fusion (2011) 53:062001. doi:10.1088/0741-3335/53/6/062001
165. Van Zeeland MA, Gorelenkov N, Heidbrink W, Kramer G, Spong D, Austin M, et al. Alfvén eigenmode stability and fast ion loss in DIII-D and ITER reversed magnetic shear plasmas. Nucl Fusion (2012) 52:094023. doi:10.1088/0029-5515/52/9/094023
166. Heidbrink W. Energetic ion experiments in DIII-D. Fusion Sci Technol (2017) 48:945–53. doi:10.13182/fst05-a1050
167. Varela J, Spong D, Garcia L, Huang J, Murakami M, Garofalo A, et al. Analysis of Alfven eigenmode destabilization in DIII-D high poloidal β discharges using a Landau closure model. Nucl Fusion (2018) 58:076017. doi:10.1088/1741-4326/aac33f
168. Ding S, Garofalo AM, Qian J, Cui L, McClenaghan JT, Pan C, et al. Confinement improvement in the high poloidal beta regime on DIII-D and application to steady-state H-mode on EAST. Phys Plasmas (2017) 24:056114. doi:10.1063/1.4982058
169. Garofalo AM, Gong X, Qian J, Chen J, Li G, Li K, et al. Development of high poloidal beta, steady-state scenario with ITER-like tungsten divertor on EAST. Nucl Fusion (2017) 57:076037. doi:10.1088/1741-4326/aa7186
170. Ding S, Xu G, Wang Q, Solomon W, Zhao Y, Gong X, et al. Scenario development for high βp low torque plasma with qmin above 2 and large-radius internal transport barrier in DIII-D. Nucl Fusion (2017) 57:022016. doi:10.1088/0029-5515/57/2/022016
171. Litaudon X, B coulet A, Crisanti F, Wolf R, Baranov Y, Barbato E, et al. Progress towards steady-state operation and real-time control of internal transport barriers in JET. Nucl Fusion (2003) 43:565–72. doi:10.1088/0029-5515/43/7/309
172. Qian JP, Garofalo A, Gong X, Ren Q, Ding S, Solomon W, et al. Advances in the high bootstrap fraction regime on DIII-D towards theQ = 5 mission of ITER steady state. Nucl Fusion (2017) 57:056008. doi:10.1088/1741-4326/aa626a
173. Huang J, et al. Collaborative research: the evolution of magnetic skeletons during 3D reconnection. APS division Plasma Phys Meet San Jose (2016).
174. Huang J, Qian J, Garofalo A, Gong X, Wu C, Chang J, et al. Improved high-performance fully non-inductive discharge by optimizing the fast-ion confinement on EAST. Nucl Fusion (2020) 60:016002. doi:10.1088/1741-4326/ab443a
175. McClenaghan J, Garofalo A, Lao L, Weisberg D, Meneghini O, Smith S, et al. Transport at high βp and development of candidate steady state scenarios for ITER. Nucl Fusion (2020) 60:046025. doi:10.1088/1741-4326/ab74a0
176. Wan YX, Li J, Liu Y, Wang X, Chan V, Chen C, et al. Overview of the present progress and activities on the CFETR. Nucl Fusion (2017) 57:102009. doi:10.1088/1741-4326/aa686a
177. Zhuang G, Li G, Li J, Wan Y, Liu Y, Wang X, et al. Progress of the CFETR design. Nucl Fusion (2019) 59:112010. doi:10.1088/1741-4326/ab0e27
178. Huang J., Garofalo AM, Qian JP, Gong XZ, Ding SY, Varela J, et al. Progress in extending high poloidal beta scenarios on DIII-D towards a steady-state fusion reactor and impact of energetic particles. Nucl Fusion (2020) 60:126007. doi:10.1088/1741-4326/abaf33
179. Varela J, Ohdachi S, Watanabe K, Spong D, Garcia L, Seki R. Theoretical analysis of energetic-ion-driven resistive interchange mode stabilization strategies using a Landau closure model. Nucl Fusion (2020) 60:046013. doi:10.1088/1741-4326/ab7213
180. Li J, Guo HY, Wan BN, Gong XZ, Liang YF, Xu GS, et al. A long-pulse high-confinement plasma regime in the Experimental Advanced Superconducting Tokamak. Nat Phys (2013) 9:817–821. doi:10.1038/nphys2795
181. Hu C, Xie Y, Xie Y, Liu S, Xu Y, Liang L, et al. Overview of development status for EAST-NBI system. Plasma Sci Technol (2015) 17:817–25.
182. Hu Y, Todo Y, Pei Y, Li G, Qian J, Xiang N, et al. Simulation of fast-ion-driven alfvén eigenmodes on the experimental advanced superconducting tokamak. Phys Plasmas (2016) 23:022505. doi:10.1063/1.4941970
183. Pei Y, Xiang N, Shen W, Hu Y, Todo Y, Zhou D, et al. Simulations of toroidal alfvén eigenmode excited by fast ions on the experimental advanced superconducting tokamak. Phys Plasmas (2018) 25:052503. doi:10.1063/1.5023538
184. Liqing X, Wei S, Zhenzhen R, Tianfu Z, Yifeng W, Lian H, et al. Investigation of Alfvén eigenmodes and energetic particle modes in EAST with neutral beam injection Nucl Fusion (2021) 61:076005. doi:10.1088/1741-4326/abf2e2
185. Wang XH, Huang J, Varela J, Zhao H, Spong D, Xu L, et al. Analysis of beam ion driven Alfvén eigenmode stability induced by Tungsten contamination in EAST. Nucl Fusion (2024) 64:016028. doi:10.1088/1741-4326/ad0f5e
186. Chu N, Sun Y, Gu S, Wang H, Hu Y, Shi T, et al. Observation of toroidal Alfvén eigenmode excited by energetic electrons induced by static magnetic perturbations in the EAST tokamak. Nucl Fusion (2018) 58:104004. doi:10.1088/1741-4326/aad70c
187. Osakabe M, Takahashi H, Yamada H, Tanaka K, Kobayashi T, Ida K, et al. Recent results from deuterium experiments on the large helical device and their contribution to fusion reactor development. Nucl Fusion (2022) 62:042019. doi:10.1088/1741-4326/ac3cda
189. Ortiz J, Varela J, Spong D, Garcia L, Ghai Y. Study of Alfvén eigenmode stability in Quasi-Poloidal Stellarator (QPS) plasma using a Landau closure model. Nucl Fusion (2024) 63:056010. under review, Analysis of the HAE activity in the TJII using Landau closure model. doi:10.1088/1741-4326/acc25f
190. Garcia J, Kazakov Y, Coelho R, Dreval M, de la Luna E, Solano ER, et al. Stable Deuterium-Tritium burning plasmas with improved confinement in the presence of energetic ions instabilities. Sci Adv (2024). under review.
191. Sun Y, Benmhammed H, Al Abdullatif S, Habara A, Fu E, Brady J, et al. PGC-1α agonism induces fetal hemoglobin and exerts antisickling effects in sickle cell disease. Sci Adv (2024) 10:eadn8750. under review, Fast ion studies in the extended high-performance high βp plasma on EAST. doi:10.1126/sciadv.adn8750
192. Varela J, Nagasaki K, Nagaoka K, Yamamoto S, Watanabe KY, Spong DA, et al. Modeling of the ECCD injection effect on the Heliotron J and LHD plasma stability. Nucl Fusion (2020) 60:112015. doi:10.1088/1741-4326/abad84
193. Garcia-Munoz M, Sharapov SE, Van Zeeland MA, Ascasibar E, Cappa A, Chen L, et al. Active control of Alfvén eigenmodes in magnetically confined toroidal plasmas. Plasma Phys Control Fusion (2019) 61:054007. doi:10.1088/1361-6587/aaef08
194. Ohdachi S, Takahashi Y, Suzuki M, Osakabe T, Morisaki T, Bando K, et al. 27 th IAEA fusion energy conference (2018). EX/1-3Rb. Available at: https://www.iaea.org/sites/default/files/18/10/cn-258-abstracts.pdf
195. Liu H, Shimizu A, Isobe M, Okamura S, Nishimura S, Suzuki C, et al. Magnetic configuration and modular coil design for the Chinese first quasi-axisymmetric stellarator. Plasma Fusion Res (2018) 13:3405067. doi:10.1585/pfr.13.3405067
196. Shimizu A, Liu H, Kinoshita S, Isobe M, Okamura S, Ogawa K, et al. Consideration of the influence of coil misalignment on the Chinese first quasi-axisymmetric stellarator magnetic configuration. Plasma Fusion Res (2019) 14:3403151. doi:10.1585/pfr.14.3403151
197. Yang L, Liu H, Shimizu A, Xu Y, Wang X, Liu H, et al. Local axisymmetry-breaking–induced transition of trapped-particle orbit and loss channels in quasi-axisymmetric stellarators. Europhysics Lett (2020) 129:35001. doi:10.1209/0295-5075/129/35001
198. Zarnstorff MC, Berry LA, Brooks A, Fredrickson E, Fu GY, Hirshman S, et al. Physics of the compact advanced stellarator NCSX. Plasma Phys Control Fusion (2001) 43:A237–49. doi:10.1088/0741-3335/43/12a/318
199. Nelson BE. Design of the quasi-poloidal stellarator experiment (QPS). Fusion Eng Des (2003) 66:205.
200. Nuhrenberg J, Zille R. Quasi-helically symmetric toroidal stellarators. Phys Lett A (1988) 129:113–7. doi:10.1016/0375-9601(88)90080-1
201. Landreman M, Catto PJ. Omnigenity as generalized quasisymmetry. Plasmas (2012) 19:056103. doi:10.1063/1.3693187
202. Ogawa K, Seki R, Yamaguchi H, Murakami S, Isobe M, Shimizu A, et al. Feasibility study of neutral beam injection on Chinese first quasi-axisymmetric stellarator (CFQS). Plasma Fusion Res (2019) 14:3402067. doi:10.1585/pfr.14.3402067
203. Varela J, Shimizu A, Spong D, Garcia L, Ghai Y. Study of the Alfven eigenmodes stability in CFQS plasma using a Landau closure model. Nucl Fusion (2021) 61:026023. doi:10.1088/1741-4326/abd072
204. Strickler DJ, Hirshman SP, Spong DA, Cole MJ, Lyon JF, Nelson BE, et al. Development of a robust quasi-poloidal compact stellarator. Sci Technol (2004) 45:15–26. doi:10.13182/fst04-a421
205. Spong DA, Harris JH. New QP/QI symmetric stellarator configurations. Plasma Fusion Res (2010) 5:S2039. doi:10.1585/pfr.5.s2039
206. Hudson SR, Hegna CC, Torasso R, Ware A. Marginal stability diagrams for infinite-nballooning modes in quasi-symmetric stellarators. Plasma Phys Control Fusion (2004) 46:869–76. doi:10.1088/0741-3335/46/5/009
207. Spong DA Generation and damping of neoclassical plasma flows in stellarators. Phys Plasmas (2005) 12:056114. doi:10.1063/1.1887172
208. Rewoldt G, Ku LP, Tang WM. Comparison of microinstability properties for stellarator magnetic geometries. Plasmas (2005) 12:102512. doi:10.1063/1.2089247
209. Ortiz J, Varela J, Spong D, Garcia L, Ghai Y. Study of Alfvén eigenmode stability in Quasi-Poloidal Stellarator (QPS) plasma using a Landau closure model. Nucl Fusion (2023) 63:056010. doi:10.1088/1741-4326/acc25f
210. Wolf RC, Hobirk J, Conway G, Gruber O, Gude A, Günter S, et al. Performance, heating and current drive scenarios of ASDEX Upgrade advanced tokamak discharges. Nucl Fusion (2001) 41:1259–71. doi:10.1088/0029-5515/41/9/315
211. Wolf RC, Biel W, de Bock MFM, Finken KH, Günter S, Hogeweij GMD, et al. 20th IAEA fusion energy conference, paper IAEA-CN-116/EX/6-5 conference symposium papers CD ROM, IAEA-CSP25/CD. IAEA Vienna (2005). ISBN 92-0-100405-2, ISSN 1562-4153.
212. Murakami M, John HS, Casper T, Chu M, DeBoo J, Greenfield C, et al. Status of advanced tokamak scenario modelling with off-axis electron cyclotron current drive in DIII-D. Nucl Fusion (2000) 40:1257–65. doi:10.1088/0029-5515/40/6/320
213. Wade MR, Murakami M, Luce T, Ferron J, Petty C, Brennen D, et al. Integrated, advanced tokamak operation on DIII-D. Nucl Fusion (2003) 43:634–46. doi:10.1088/0029-5515/43/7/318
214. Wade MR. Development in the DIII-D tokamak of advanced operating scenarios and associated control techniques for ITER. Nucl Fusion (2007) 47:S543–62. doi:10.1088/0029-5515/47/10/s05
215. Garofalo AM, Gong X, Grierson B, Ren Q, Solomon W, Strait E, et al. Compatibility of internal transport barrier with steady-state operation in the high bootstrap fraction regime on DIII-D. Nucl Fusion (2015) 55:123025. doi:10.1088/0029-5515/55/12/123025
216. Ren H. The residual zonal flows in anisotropic tokamak plasmas. Phys Plasmas (2016) 23:062511. doi:10.1063/1.4954914
217. Ferron JR, Casper TA, Doyle EJ, Garofalo AM, Gohil P, Greenfield CM, et al. Optimization of DIII-D advanced tokamak discharges with respect to the β limit. Phys Plasmas (2005) 12:056126. doi:10.1063/1.1871247
218. Holcomb CT, Ferron JR, Luce TC, Petrie TW, Politzer PA, Challis C, et al. Optimizing stability, transport, and divertor operation through plasma shaping for steady-state scenario development in DIII-D. Phys Plasmas (2009) 16:056116. doi:10.1063/1.3125934
219. Piovesan P, Igochine V, Turco F, Chrystal I, Classen M, Dunne NM, et al. Impact of ideal MHD stability limits on high-beta hybrid operation. Plasma Phys Control Fusion (2017) 59:014027. doi:10.1088/0741-3335/59/1/014027
220. Doyle EJ, DeBoo J, Ferron J, Jackson G, Luce T, Murakami M, et al. Demonstration of ITER operational scenarios on DIII-D. Nucl Fusion (2010) 50:075005. doi:10.1088/0029-5515/50/7/075005
221. Litaudon X, Voitsekhovitch I, Artaud J, Belo P, João PS, Bizarro JP, et al. Modelling of hybrid scenario: from present-day experiments towards ITER. Nucl Fusion (2013) 53:073024. doi:10.1088/0029-5515/53/7/073024
222. Hill DN, et al. DIII-D research towards resolving key issues for ITER and steady-state tokamaks. Nucl Fusion (2013) 53:104001. doi:10.1088/0029-5515/53/10/104001
223. Chen Y, Munsat T, Parker SE, Heidbrink WW, Van Zeeland MA, Tobias BJ, et al. Gyrokinetic simulations of reverse shear Alfvén eigenmodes in DIII-D plasmas. Phys Plasmas (2013) 20:012109. doi:10.1063/1.4775776
224. Varela J, Spong D, Murakami M, Garcia L, D’Azevedo E, Van Zeeland M, et al. Subdominant modes and optimization trends of DIII-D reverse magnetic shear configurations. Nucl Fusion (2019) 59:046017. doi:10.1088/1741-4326/ab0052
225. Marinoni A, Brunner S, Camenen Y, Coda S, Graves JP, Lapillonne X, et al. The effect of plasma triangularity on turbulent transport: modeling TCV experiments by linear and non-linear gyrokinetic simulations. Plasma Phys Control Fusion (2009) 51:055016. doi:10.1088/0741-3335/51/5/055016
226. Camenen Y, Pochelon A, Behn R, Bottino A, Bortolon A, Coda S, et al. Impact of plasma triangularity and collisionality on electron heat transport in TCV L-mode plasmas. Nucl Fusion (2007) 47:510–6.
227. Austin ME, Marinoni A, Walker ML, Brookman MW, deGrassie JS, Hyatt AW, et al. Achievement of reactor-relevant performance in negative triangularity shape in the DIII-D tokamak. Phys Rev Lett (2019) 122:115001. doi:10.1103/PhysRevLett.122.115001
228. Marinoni A, Austin ME, Hyatt AW, Walker ML, Candy J, Chrystal C, et al. H-mode grade confinement in L-mode edge plasmas at negative triangularity on DIII-D. Phys Plasmas (2019) 26:042515. doi:10.1063/1.5091802
229. Van Zeeland MA, Collins C, Heidbrink W, Austin M, Du X, Duarte V, et al. Alfvén eigenmodes and fast ion transport in negative triangularity DIII-D plasmas. Nucl Fusion (2019) 59:086028. doi:10.1088/1741-4326/ab2488
230. Ghai Y, Spong D, Varela J, Garcia L, Van Zeeland M, Austin M. Effects of negative triangularity shaping on energetic particle driven Alfvén eigenmodes in DIII-D *. Nucl Fusion (2021) 61:126020. doi:10.1088/1741-4326/ac2bc0
231. Pawley C, Crowley B, Pace D, Rauch J, Scoville J, Kellman D, et al. Advanced control of neutral beam injected power in DIII-D. Fusion Eng Des (2017) 123:453–7. doi:10.1016/j.fusengdes.2017.02.106
232. Rauch J, Pace DC, Crowley B, Johnson RD, Kellman DH, Pawley CJ, et al. Upgrade to DIII-D National Fusion Facility PCS and Neutral Beam Systems: In-Shot Variation of Neutral Beam Particle Energy. Fusion Sci Technol (2017) 72:500–504. doi:10.1080/15361055.2017.1333845
233. Pace DC, Collins C, Crowley B, Grierson B, Heidbrink W, Pawley C, et al. Control of power, torque, and instability drive using in-shot variable neutral beam energy in tokamaks. Nucl Fusion (2017) 57:014001. doi:10.1088/0029-5515/57/1/014001
234. Hegna CC, Callen JD. On the stabilization of neoclassical magnetohydrodynamic tearing modes using localized current drive or heating. Phys Plasma (1997) 4:2940–6. doi:10.1063/1.872426
235. Erckmann V, Gasparino U. Electron cyclotron resonance heating and current drive in toroidal fusion plasmas. Plasma Phys Control Fusion (1994) 36:1869. doi:10.1088/0741-3335/36/12/001
236. Nagasaki K, Motojima G, Fernández AC, Cappa ÁA, Fontdecaba JM, Yoshimura Y, et al. ECCD experiments in heliotron J, TJ-II, CHS, and LHD. J.Plasca Fusion Res (2008) 3:S1008. doi:10.1585/pfr.3.s1008
237. Hegna CC, Callen JD. Stability of bootstrap current-driven magnetic islands in stellarators. Phys Plasma (1994) 1:3135–7. doi:10.1063/1.870505
238. Yamamoto S, Nagasaki K, Kobayashi S, Nagaoka K, Cappa A, Okada H, et al. Suppression of fast-ion-driven MHD instabilities by ECH/ECCD on Heliotron J. Nucl Fusion (2017) 57:126065. doi:10.1088/1741-4326/aa8f04
239. Takeiri Y, Nakamura Y, Noda N, Osakabe M, Kawahata K, Oka Y, et al. Plasma characteristics of long-pulse discharges heated by neutral beam injection in the Large Helical Device. Plasma Phys Control Fusion (2000) 42:147–59. doi:10.1088/0741-3335/42/2/307
240. Shimozuma T, Kubo S, Yoshimura Y, Igami H, Nagasaki K, Notake T, et al. Progress on electron cyclotron heating and electron cyclotron current drive experiments in LHD. Fusion Sci Technol (2006) 50:403–11. doi:10.13182/fst06-a1262
241. Notake T, Shimozuma T, Kubo S, Idei H, Ida K, Watanabe K, et al. First demonstration of rotational transform control by electron cyclotron current drive in large helical device. Plasma Fusion Res (2008) 3:S1077. doi:10.1585/pfr.3.s1077
242. Yoshimura Y, Kubo S, Shimozuma T, Igami H, Takahashi H, Nishiura M, et al. ECCD experiment using an upgraded ECH system on LHD. Plasma Fusion Res (2012) 7:2402020. doi:10.1585/pfr.7.2402020
243. Varela J, Cooper W, Nagaoka K, Watanabe K, Spong D, Garcia L, et al. Effect of the tangential NBI current drive on the stability of pressure and energetic particle driven MHD modes in LHD plasma. Nucl Fusion (2020) 60:026016. doi:10.1088/1741-4326/ab60cf
245. Kobayashi S, Okada M, Kaneko Y, Suzuki T, Mizuuchi K, Nagasaki Y, et al. 20th IAEA fusion energy conference (2004). EX/P4-41.
246. Varela J, Nagasaki K, Kobayashi S, Nagaoka K, Adulsiriswad P, Cappa A, et al. Analysis of the ECH effect on EPM/AE stability in Heliotron J plasma using a Landau closure model. Nucl Fusion (2023) 63:026009. doi:10.1088/1741-4326/aca98e
247. Kazakov YO, Van Eester D, Dumont R, Ongena J. On resonant ICRF absorption in three-ion component plasmas: a new promising tool for fast ion generation. Nucl Fusion (2015) 55:032001. doi:10.1088/0029-5515/55/3/032001
248. Kazakov YO, Ongena J, Wright JC, Wukitch SJ, Lerche E, Mantsinen MJ, et al. Efficient generation of energetic ions in multi-ion plasmas by radio-frequency heating. Nat Phys (2017) 13:973–8. doi:10.1038/nphys4167
249. Kazakov YO, Nocente M, Mantsinen M, Ongena J, Baranov Y, Craciunescu T, et al. Plasma heating and generation of energetic D ions with the 3-ion ICRF + NBI scenario in mixed H-D plasmas at JET-ILW. Nucl Fusion (2020) 60:112013. doi:10.1088/1741-4326/ab9256
250. Nocente M, Kazakov Y, Garcia J, Kiptily V, Ongena J, Dreval M, et al. Generation and observation of fast deuterium ions and fusion-born alpha particles in JET D-3 He plasmas with the 3-ion radio-frequency heating scenario. Nucl Fusion (2020) 60:124006. doi:10.1088/1741-4326/abb95d
251. Varela J, Spong D, Garcia L, Ohdachi S, Watanabe K, Seki R, et al. Theoretical analysis of the saturation phase of the 1/1 energetic-ion-driven resistive interchange mode. Nucl Fusion (2021) 61:126016. doi:10.1088/1741-4326/ac26a0
252. Todo Y, Van Zeeland M, Heidbrink W. Fast ion profile stiffness due to the resonance overlap of multiple Alfvén eigenmodes. Nucl Fusion (2016) 56:112008. doi:10.1088/0029-5515/56/11/112008
253. Varela J, Spong D, Todo Y, Garcia L, Ghai Y, Ortiz J, et al. Simulation of the TAEs’ saturation phase in the large helical device: MHD burst. Nucl Fusion (2022) 62:126020. doi:10.1088/1741-4326/ac8f5a
254. Spong D, Van Zeeland M, Heidbrink W, Du X, Varela J, Garcia L, et al. Nonlinear dynamics and transport driven by energetic particle instabilities using a gyro-Landau closure model *. Nucl Fusion (2021) 61:116061. doi:10.1088/1741-4326/ac2990
255. Van Zeeland MA, Bardoczi L, Gonzalez-Martin J, Heidbrink W, Podesta M, Austin M, et al. Beam modulation and bump-on-tail effects on Alfvén eigenmode stability in DIII-D. Nucl Fusion (2021) 61:066028. doi:10.1088/1741-4326/abf174
256. Varela J, Spong DA, Garcia L, Ghai Y, Zarzoso D, del-Castillo-Negrete D, et al. Effect of the neutral beam injector operational regime on the Alfven eigenmode saturation phase in DIII-D plasma. Plasma Phys Control Fusion (2023) 65:125004. doi:10.1088/1361-6587/ad05d4
257. Van Zeeland MA, Heidbrink WW, Nazikian R, Solomon WM, Austin ME, Berk HL, et al. Reversed shear Alfvén eigenmode stabilization by localized electron cyclotron heating. Plasma Phys Control Fusion (2008) 50:035009. doi:10.1088/0741-3335/50/3/035009
258. Hu W, Olofsson K, Welander A, Heidbrink W, Van Zeeland M, Austin M, et al. Active real-time control of Alfvén eigenmodes by neutral beam and electron cyclotron heating in the DIII-D tokamak. Nucl Fusion (2018) 58:124001. doi:10.1088/1741-4326/aaddaf
259. Petty CC, et al. Impact of central ECCD on steady-state hybrid scenario in DIII-D. AIP Conf Proc (2015) 1689:090002.
260. Mantsinen M, Ingesson LC, Johnson T, Kiptily VG, Mayoral ML, Sharapov SE, et al. Controlling the profile of ion-cyclotron-resonant ions in JET with the wave-induced pinch effect. Phys Rev Lett (2002) 89:115004. doi:10.1103/PhysRevLett.89.115004
261. Tobias B, Bass E, Classen I, Domier C, Grierson B, Heidbrink W, et al. Alfvén eigenmode structure during off-axis neutral beam injection. Nucl Fusion (2012) 52:103009. doi:10.1088/0029-5515/52/10/103009
262. Tang SX, Carter TA, Crocker NA, Heidbrink WW, Lestz JB, Pinsker RI, et al. Stabilization of alfvén eigenmodes in DIII-D via controlled energetic ion density ramp and validation of theory and simulations. Phys Rev Lett (2021) 126:155001. doi:10.1103/PhysRevLett.126.155001
263. Collins CS, Heidbrink WW, Austin ME, Kramer GJ, Pace DC, Petty CC, et al. Observation of critical-gradient behavior in alfvén-eigenmode-induced fast-ion transport. Phys Rev Lett (2016) 116:095001. doi:10.1103/PhysRevLett.116.095001
264. Heidbrink WW, Collins CS, Podestà M, Kramer GJ, Pace DC, Petty CC, et al. Fast-ion transport by Alfvén eigenmodes above a critical gradient threshold. Phys Plasma (2017) 24:056109. doi:10.1063/1.4977535
265. Chen L, Zonca F. Nonlinear excitations of zonal structures by toroidal Alfvén eigenmodes. Phys Rev Lett (2012) 109:145002. doi:10.1103/PhysRevLett.109.145002
266. Qiu Z, Chen L, Zonca F. Nonlinear excitation of finite-radial-scale zonal structures by toroidal Alfvén eigenmode. Nucl Fusion (2017) 57:056017. doi:10.1088/1741-4326/aa6413
267. Ge W, Wang ZX, Wang F, Liu Z, Xu L. Multiple interactions between fishbone instabilities and internal transport barriers in EAST plasmas. Nucl Fusion (2023) 63:016007. doi:10.1088/1741-4326/aca10c
268. Mazzi S, Garcia J, Zarzoso D, Kazakov YO, Ongena J, Dreval M, et al. Enhanced performance in fusion plasmas through turbulence suppression by megaelectronvolt ions. Nat Phys (2022) 18:776–82. doi:10.1038/s41567-022-01626-8
269. Brochard G, Liu C, Wei X, Heidbrink W, Lin Z, Gorelenkov N, et al. Saturation of fishbone instability by self-generated zonal flows in tokamak plasmas. Phys Rev Lett (2024) 132:075101. doi:10.1103/PhysRevLett.132.075101
270. Falessi MV, Zonca F. Transport theory of phase space zonal structures. Phys Plasmas (2019) 26:022305. doi:10.1063/1.5063874
271. Falessi MV, Chen L, Qiu Z, Zonca F. Nonlinear equilibria and transport processes in burning plasmas. New J Phys (2023) 25:123035. doi:10.1088/1367-2630/ad127d
272. Han X, Liu Y, Zhou T, Zhang T, Shi T, Li Y, et al. Dynamics of electron internal transport barrier formation at the H–L transition on EAST. Nucl Fusion (2022) 62:064005. doi:10.1088/1741-4326/ac5c75
273. Varela J, Garcia J, Mazzi S, Kazakov Y, Stancar Z, Burazzo M, et al. Simulation of the AE activity in JET D-T discharges using a Landau closure model*. 65th Annual Meeting of the APS Division of Plasma Physics; 2023 Oct 30-Nov 3; Denver, CO, United States (2023). Available online at: https://meetings.aps.org/Meeting/DPP23/Session/KI02.2.
274. Varela J, Hidalgo C, Tokuzawa T, Nagaoka K, Nagasaki K, Ohdachi S, et al. Shear flows induced by AE / EPM in LHD plasma. 7th Asia-Pacific Conference on Plasma Physics; 2023 Nov 12-17; Nagoya, Japan (2023). Available online at: https://www.aappsdpp.org/DPP2023/html/3contents/pdf/5577.pdf.
275. Hemsworth RS, Boilson D, Blatchford P, Palma MD, Chitarin G, de Esch HPL, et al. Overview of the design of the ITER heating neutral beam injectors. New J Phys (2017) 19:025005. doi:10.1088/1367-2630/19/2/025005
276. Putvinski SV, et al. Physics of energetic particles in ITER. Nucl Fusion (1998) 38:1275–81. doi:10.1088/0029-5515/38/9/302
277. Fasoli A, Gormenzano C, Berk H, Breizman B, Briguglio S, Darrow D, et al. Chapter 5: physics of energetic ions. Nucl Fusion (2007) 47:S264–84. doi:10.1088/0029-5515/47/6/s05
278. Albergante M, Graves JP, Fasoli A, Jenko F, Dannert T. Anomalous transport of energetic particles in ITER relevant scenarios. Plasma Phys (2009) 16:112301. doi:10.1063/1.3257913
279. Todo Y, Bierwage A. Large-scale simulation of energetic particle driven magnetohydrodynamic instabilities in ITER plasmas. Plasma Fusion Res (2014) 9:3403068. doi:10.1585/pfr.9.3403068
280. Pinches SD, Chapman IT, Lauber PW, Oliver HJC, Sharapov SE, Shinohara K, et al. Energetic ions in ITER plasmas. Plasma Phys (2015) 22:021807. doi:10.1063/1.4908551
281. Lauber P. Local and global kinetic stability analysis of Alfvén eigenmodes in the 15 MA ITER scenario. Plasma Phys Control Fusion (2015) 57:054011. doi:10.1088/0741-3335/57/5/054011
282. Schneller M, Lauber P, Briguglio S. Nonlinear energetic particle transport in the presence of multiple Alfvénic waves in ITER. Plasma Phys Control Fusion (2016) 58:014019. doi:10.1088/0741-3335/58/1/014019
283. Brochard G, Dumont R, Lütjens H, Garbet X, Nicolas T, Maget P. Nonlinear dynamics of the fishbone-induced alpha transport on ITER. Nucl Fusion (2020) 60:126019. doi:10.1088/1741-4326/abb14b
284. White RB, Chance MS. Hamiltonian guiding center drift orbit calculation for plasmas of arbitrary cross section. Fluids B (1984) 27:2455–67. doi:10.1063/1.864527
285. Chen J, Jian X, Chan VS, Li Z, Deng Z, Li G, et al. Self-consistent modeling of CFETR baseline scenarios for steady-state operation. Plasma Phys Control Fusion (2017) 59:075005. doi:10.1088/1361-6587/aa6d20
286. Shi N, Chan VS, Jian X, Li G, Chen J, Gao X, et al. Study of impurity effects on CFETR steady-state scenario by self-consistent integrated modeling. Nucl Fusion (2017) 57:126046. doi:10.1088/1741-4326/aa79d1
287. Shi N, Kessel C, Chan V, Guo Y, Chen J, Jian X, et al. The time-dependent simulation of CFETR baseline steady-state scenarios. Nucl Fusion (2018) 58:096009. doi:10.1088/1741-4326/aacb3c
288. Zou Y, Chan VS, Chen W, Wang Y, Hou Y, Zhu Y. Energetic particle transport prediction for CFETR steady state scenario based on critical gradient model. Chin Phys. Lett. (2021) 38:045203. doi:10.1088/0256-307x/38/4/045203
289. Ishida S, Barabaschi P, Kamada Y. Overview of the JT-60SA project. Nucl Fusion (2011) 51:094018. doi:10.1088/0029-5515/51/9/094018
290. Kamada Y, Barabaschi P, Ishida S, Ide S, Lackner K, Fujita T, et al. Plasma regimes and research goals of JT-60SA towards ITER and DEMO. Nucl Fusion (2011) 51:073011. doi:10.1088/0029-5515/51/7/073011
291. Sips ACC, Giruzzi G, Ide S, Kessel C, Luce TC, Snipes JA, et al. Phys Plasma (2015) 22:021804. doi:10.1063/1.4904015
292. Giruzzi G, Yoshida M, Artaud J, Asztalos Ö, Barbato E, Bettini P, et al. Physics and operation oriented activities in preparation of the JT-60SA tokamak exploitation. Nucl Fusion (2017) 57:085001. doi:10.1088/1741-4326/aa7962
293. Casper T, Gribov Y, Kavin A, Lukash V, Khayrutdinov R, Fujieda H, et al. Development of the ITER baseline inductive scenario. Nucl Fusion (2015) 54:013005. doi:10.1088/0029-5515/54/1/013005
294. Hanada M, Kojima A, Tanaka Y, Inoue T, Watanabe K, Taniguchi M, et al. Progress in development and design of the neutral beam injector for JT-60SA. Fusion Eng Des (2011) 86:835–838. doi:10.1016/j.fusengdes.2011.04.068
295. Kojima A, Umeda N, Hanada M, Yoshida M, Kashiwagi M, Tobari H, et al. Progress in long-pulse production of powerful negative ion beams for JT-60SA and ITER. Nucl Fusion (2015) 55:063006. doi:10.1088/0029-5515/55/6/063006
296. Bierwage A, Toma M, Shinohara K. MHD and resonant instabilities in JT-60SA during current ramp-up with off-axis N-NB injection. Plasma Phys Control Fusion (2017) 59:125008. doi:10.1088/1361-6587/aa8ae8
297. Coelho R, Vincenzi P, Vallar M, Rodrigues P, Tholerus E, Särkimäki K, et al. Predictive modeling of Alfvén eigenmode stability in inductive scenarios in JT-60SA. Front Phys (2023) 11:063006. doi:10.3389/fphy.2023.1267696
298. Adulsiriswad P, Todo Y, Sato M, Aiba N, Narita E, Wang H, et al. Simulation study of interaction between energetic particles and magnetohydrodynamic modes in the JT-60SA inductive scenario with a flat q≈1 profile. Nucl Fusion (2023) 63:126030. doi:10.1088/1741-4326/acfcca
299. Varela J, Watanabe K, Shinohara K, Honda M, Suzuki Y, Shiraishi J, et al. MHD stability of JT-60SA operation scenarios driven by passing energetic particles for a hot Maxwellian model. Nucl Fusion (2020) 60:096009. doi:10.1088/1741-4326/ab9dd1
300. Varela J, Watanabe KY, Ohdachi S. The internal disruption as hard Magnetohydrodynamic limit of 1/2 sawtooth like activity in large helical device. Phys Plasmas (2012) 19:082512. doi:10.1063/1.4747534
301. Varela J, Watanabe KY, Ohdachi S, Narushima Y. Hard magnetohydrodynamic limit in 1/3 sawtooth like activity in LHD. Phys Plasmas (2014) 21:032501. doi:10.1063/1.4867066
302. Varela J, Watanabe KY, Ohdachi S, Narushima Y. Magnetic turbulence and pressure gradient feedback effect of the 1/2 mode soft-hard magnetohydrodynamic limit in large helical device. Phys Plasmas (2014) 21:092505. doi:10.1063/1.4895499
303. Breizman BN, Arefiev AV, Fomyts’kyi MV. Publisher’s Note: “Nonlinear physics of laser-irradiated microclusters” [Phys. Plasmas 12, 056706 (2005)]. Plasmas (2005) 12:112506. doi:10.1063/1.2008263
304. Graves JP, Coste-Sarguet M, Wahlberg C. Pressure driven long wavelength MHD instabilities in an axisymmetric toroidal resistive plasma. Plasma Phys Control Fusion (2022) 61:014001. doi:10.1088/1361-6587/ac3496
305. Brochard G, Bao J, Liu C, Gorelenkov N, Choi G, Dong G, et al. Verification and validation of linear gyrokinetic and kinetic-MHD simulations for internal kink instability in DIII-D tokamak. Nucl Fusion (2022) 62:036021. doi:10.1088/1741-4326/ac48a6
306. Mikhailovskii AB, Huysmans GTA, Kerner WOK, Sharapov SE Optimization of computational MHD normal-mode analysis for tokamaks. Plasma Phys Rep (1997) 23:844. doi:10.1063/1.3224035
307. Cheng CZ, Chance MS Low-n shear Alfvén spectra in axisymmetric toroidal plasmas. Phys Fluids (1986) 29:3695–701.
308. Adulsiriswad P, Todo Y, Kado S, Yamamoto S, Kobayashi S, Ohshima S, et al. Numerical investigation into the peripheral energetic-particle-driven MHD modes in Heliotron J with free boundary hybrid simulation. Nucl Fusion (2021) 61:116065. doi:10.1088/1741-4326/ac2779
309. Adulsiriswad P, Todo Y, Yamamoto S, Kado S, Kobayashi S, Ohshima S, et al. Effects of the resonance modification by electron cyclotron current drive on the linear and nonlinear dynamics of energetic particle driven magnetohydrodynamics modes in Heliotron J. Nucl Fusion (2024) 64:016036. doi:10.1088/1741-4326/ad0a0c
310. Duarte B, Kerner W. CASTOR-K: stability analysis of Alfvén eigenmodes in the presence of energetic ions in tokamaks. J Comput Phys (1999) 153:101–38.
311. Borba D, Berk HL, Breizman BN, Fasoli A, Nabais F, Pinches SD, et al. Modelling of Alfvén waves in JET plasmas with the CASTOR-K code*. Nucl Fusion (2002) 42:1029–38.
312. Imbeaux F, Pinches S, Lister J, Buravand Y, Casper T, Duval B, et al. Design and first applications of the ITER integrated modelling and analysis suite. Nucl Fusion (2015) 55:123006. doi:10.1088/0029-5515/55/12/123006
313. Gorelenkov NN, Berk H, Budny R. Beam anisotropy effect on Alfvén eigenmode stability in ITER-like plasmas. Nucl Fusion (2005) 45:226–37. doi:10.1088/0029-5515/45/4/002
314. Chen Y, Parker SE, Lang J, Fu GY. Linear gyrokinetic simulation of high-n toroidal Alfvén eigenmodes in a burning plasma. Phys Plasmas (2010) 17:102504. doi:10.1063/1.3490213
315. Figueiredo ACA, Rodrigues P, Borba D, Coelho R, Fazendeiro L, Ferreira J, et al. Comprehensive evaluation of the linear stability of Alfvén eigenmodes driven by alpha particles in an ITER baseline scenario. Nucl Fusion (2016) 56:076007. doi:10.1088/0029-5515/56/7/076007
316. Bass EM, Waltz R. Prediction of Alfvén eigenmode energetic particle transport in ITER scenarios with a critical gradient model. Nucl Fusion (2020) 60:016032. doi:10.1088/1741-4326/ab54fb
317. Hayward-Schneide T, Lauber P, Bottino A, Lu Z. Global linear and nonlinear gyrokinetic modelling of Alfvén eigenmodes in ITER. Nucl Fusion (2021) 61:036045. doi:10.1088/1741-4326/abdca2
318. Varela J, Garcia J, Mazzi S, Kazakov Y, Štancar Ž, Baruzzo M, et al. 31st meeting of ITPA topical group on energetic particle physics EP20 - id51. contibuted talk; Apr 16–18; Daejeon, South Korea (2024).
319. Varela J, et al. FY’24 US-Japan MHD workshop 43rd ITPA MDC TG meeting (2024). In: contributed talk.
320. Varela J, Nagaoka K, Takemura Y, Watanabe KY, Ida K, Yoshinuma M, et al. MHD stability trends and improved performance of LHD inward shifted configurations: the role of the neutral beam current drive and thermal plasma density. Phys Plasmas (2024) 31. under review. doi:10.1063/5.0206400
321. Betar H, et al. Transport and losses of energetic particles in tokamaks in the presence of Alfvén activity using the new full orbit TAPaS code coupled to FAR3d. Nucl Fusion (2024). under review.
322. Melnikov AV, Eliseev L, Jiménez-Gómez R, Ascasibar E, Hidalgo C, Chmyga A, et al. Internal measurements of Alfvén eigenmodes with heavy ion beam probing in toroidal plasmas*. Nucl Fusion (2010) 50:084023. doi:10.1088/0029-5515/50/8/084023
323. Melnikov AV, Eliseev L, Castejón F, Hidalgo C, Khabanov P, Kozachek A, et al. Study of NBI-driven chirping mode properties and radial location by the heavy ion beam probe in the TJ-II stellarator. Nucl Fusion (2016) 56:112019. doi:10.1088/0029-5515/56/11/112019
324. Melnikov AV, Ascasibar E, Cappa A, Castejón F, Eliseev L, Hidalgo C, et al. Detection and investigation of chirping Alfvén eigenmodes with heavy ion beam probe in the TJ-II stellarator. Nucl Fusion (2018) 58:082019. doi:10.1088/1741-4326/aabcf8
325. Collins CS. Fusion REactor Design and Assessment (FREDA): enabling whole facility modeling and optimization via advanced simulation of integrated physics and engineering. Oak Ridge National Laboratory ORNL (2023).
326. Leboeuf JN, Lynch VE, Carreras BA, Alvarez JD, Garcia L. Full torus Landau fluid calculations of ion temperature gradient-driven turbulence in cylindrical geometry. Phys Plasmas (2000) 7:5013–22. doi:10.1063/1.1323757
327. Johnson JL, Oberman CR, Kulsrud RM, Frieman EA. Some stable hydromagnetic equilibria.Phys.Plasmas (1958) 1:281–296.
328. Mukhovatov VS, Shafranov V. Plasma equilibrium in a tokamak. Nucl Fusion (1971) 11:605–33. doi:10.1088/0029-5515/11/6/005
329. Anania G, Johnson JL. Application of the stellarator expansion for plasma stability studies in stellarators. Phys.Fluids (1983) 26:3070–8. doi:10.1063/1.864031
330. Dimits AM, Joseph I, Umansky MV. A fast non-Fourier method for Landau-fluid operators. Phys Plasmas (2014) 21:055907. doi:10.1063/1.4876617
Keywords: Alfv én Eigenmodes, gyro-fluid, optimization, FAR3d, stability
Citation: Varela J, Spong D, Garcia L, Ghai Y, Ortiz J and FAR3d project collaborators (2024) Stability optimization of energetic particle driven modes in nuclear fusion devices: the FAR3d gyro-fluid code. Front. Phys. 12:1422411. doi: 10.3389/fphy.2024.1422411
Received: 24 April 2024; Accepted: 12 August 2024;
Published: 16 September 2024.
Edited by:
Massimo Nocente, University of Milano-Bicocca, ItalyReviewed by:
Guillaume Brochard, ITER, FranceRuirui Ma, Southwestern Institute of Physics, China
Yao Yao, Southwestern Institute of Physics, China
Copyright © 2024 Varela, Spong, Garcia, Ghai, Ortiz and FAR3d project collaborators. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: J. Varela, amFjb2JvLnJvZHJpZ3VlekBhdXN0aW4udXRleGFzLmVkdQ==
 J. Varela
J. Varela D. Spong
D. Spong L. Garcia3
L. Garcia3 Y. Ghai
Y. Ghai