The polychromatic retrigger: a new tool to mitigate pileup in spectral photon-counting computed-tomography

High photon rates, like the ones required in clinical computed tomography, can generate pulse pileup in photon-counting detectors, and in extreme cases induce system paralysis. The instant retrigger technology has been developed by DECTRIS Ltd. to counteract such phenomena, effectively making detectors non-paralyzable. The instant retrigger behavior is regulated by a quantity named retrigger time, which originally was the same for all the energy thresholds of the detector. We developed a new ASIC that features an improved version of the instant retrigger (polychromatic retrigger) that allows different retrigger times for each of the four energy thresholds. In this work, we investigate how this feature can be exploited in computed tomography to mitigate pileup artifacts. Using a Monte Carlo method, we modeled a full computed tomography system with four energy thresholds (20, 50, 70 and 90 keV), and we simulated head scans from low (1$\times$10⁷ cps/mm²) to high (1$\times$10⁹ cps/mm²) photon count rates for different values of the retrigger time. The quality of the resulting images generally degrades when increasing the photon rates (pileup artifacts) and, at the same time, it becomes strongly dependent on the retrigger time. We show how, even at high incoming rates, it is possible to identify for each energy threshold a retrigger time value that restores almost completely the image quality obtained in the low count-rate scenario. The analysis indicates that the higher the energy threshold, the longer the retrigger time has to be set.

1 Introduction

Photon-counting (PC) detectors are currently used for Computed Tomography (CT) applications and, compared to conventional energy-integrating detectors, have been proven to provide better spatial resolution and contrast-to-noise ratio at the same radiation dose [1–3]. Besides improving image quality, PC detectors also intrinsically provide spectral information thanks to their multiple and adjustable energy thresholds. This, in combination with novel contrast agents [4] and K-edge imaging techniques [5, 6], can add diagnostic value to CT images and provide new tools to clinicians and researchers [7–9].

One of the main challenges that PC detectors have to face in a clinical environment is the high photon rate, up to 1$\times$10⁹ cps/mm² (counts per second per squared millimeter) before the bow tie filter [10], that is required for specific applications, like cardiac imaging. The counting process takes place if a photon is absorbed by the sensor and the generated signal exceeds the pre-set threshold value. If the incoming photon rate is too high, the signals of the individual photons will pileup, and the overall signal might stay above the threshold for a long time. During this time, the detector is insensitive to new arriving photons and is considered paralyzed. Technologies like the instant retrigger [11] have been developed to address such scenarios, making the detector work in a specific type of non-paralyzable counting mode. Another approach that can be followed in parallel is the one of improving the pulse shaping time of the detector front-end. This would effectively provide faster detectors capable of better discerning individual photons. However, this approach has to face the physical limitation of charge collection and signal rising time, and it constitutes a technical challenge for all PC-detector manufacturers [12]. Other strategies to cope with pileup and induced spectral distortion involve the development of post-processing algorithms or on-chip solutions [12,13].

Recently, a new application-specific integrated circuit (ASIC), called LYNX, was developed at DECTRIS Ltd. The LYNX ASIC was designed specifically for CT applications, and it features four energy thresholds and an improved version of the instant-retrigger technology. The retrigger time of the LYNX chip can be tuned for every energy threshold individually, hence the name polychromatic retrigger. In this work, we deeply investigate this new feature through Monte-Carlo simulations and characterise how it can be exploited to mitigate the pileup artifacts that are associated with the high photon rates required in the clinic. In this way, we gain a better understanding of the relation between energy threshold, retrigger time, detected count-rate and image quality.

2 Materials and methods

2.1 The LYNX ASIC and the polychromatic retrigger

The LYNX (Figure 1) was specifically designed for photon counting CT applications and its development was focused on low power consumption, count rate capability, gapless packaging and cost-effectiveness. The ASIC is intended for sensors with 330 µm pixel pitch. A total number of 648 pixels are arranged in a $24\times 27$ pixel matrix. In its current iteration, LYNX measures 8.84 mm × 10 mm and offers four discrete energy thresholds per pixel. Read/Write operations are carried out through a Serial Peripheral Interface (SPI). Image data is retrieved through a single LVDS line operating at 100–150 MHz. Selecting only a single threshold for readout, we achieve 19.2–28.8 kHz frame rate. Activating all four thresholds drops the frame rate down to 4.8–7.2 kHz. A Dead-time-free readout is achieved with two 16 bit counters per threshold: while one counter is being exposed, the other counter is being read and subsequently reset. LYNX is equipped with an internal readout logic and all-internal DACs, minimizing the pinout. The power consumption is around 95 µW/pixel (85 mW/cm²) when idling, and 130 µW/pixel (115 mW/cm²) at 2.8$\times$10⁷ cps/pixel with all four thresholds active. All four thresholds have an energy range of −200 to 200 keV and a full-width half maximum of 4–5 keV. Last but not least, due to a simple front-end and high DC current tolerance of up to 160 nA/pixel (140 μA/cm²), LYNX does not need leakage current compensation, further simplifying its operation and calibration routines.

Figure 1

Figure 1. A single LYNX ASIC wirebonded to a readout board for testing.

A tunable non-paralyzable model is realized through the polychromatic retrigger, an improved version of the proven instant retrigger technology. The instant retrigger by DECTRIS Ltd. is a technology developed to counteract detector paralysis in counting systems [11]. A pixel equipped with the instant retrigger evaluates the output of the comparator periodically after the signal goes above the threshold. The time period between evaluations is called retrigger time $(t_R)$ and can be programmed within a certain range. At every evaluation, if the signal is still above the threshold, the relative counter will be increased by one, and the process will be repeated. If the signal is found to be below the threshold, the periodic evaluation stops. This operating principle ensures a detected count rate that monotonically increases with increasing incoming count rates until it eventually saturates. The theoretical upper limit for the detected count rate is $1/t_R$, therefore a shorter retrigger time will lead to a higher count-rate limit. Nonetheless, a too-short retrigger time (shorter than the time-over-threshold of a photon’s pulse) would lead to spurious multiple counting. Up to now, during an acquisition, the retrigger time has to be set to the same value for all the energy thresholds. The new feature introduced with the polychromatic retrigger allows one to set different retrigger times for each of the four thresholds of the chip. This provides an additional degree of freedom during measurements, which might be particularly beneficial in polychromatic environments like clinical ones. In the following, we investigate through simulations the influence of the threshold energy and the retrigger time on the recorded count rate and on CT reconstructions.

2.2 Monte Carlo method

The Monte Carlo method used in this work was already mentioned in [14] and it is herein described more in detail.

Based on the geometry and features of the new LYNX ASIC, a detector element is modeled as a square pixel with a size of 330 µm bump-bonded to a 1.5 mm thick CdTe sensor operated at a bias voltage of −1,000 V. Given the spectrum impinging on a pixel, the detected spectrum is obtained by convolving the impinging spectrum with the spectral response of the detector, which was previously calculated for the specific pixel geometry and materials [14] using FLUKA (program version 2005), a Monte Carlo software for the simulation of particle transport and interaction [15–17]. To emulate the X-ray sources used in clinical CT practice, a 120 kV polychromatic spectrum prefiltrated with 6.8 mm of aluminum was chosen as the incoming spectrum. In Figure 2 left, the incoming spectrum and the spectrum detected by a detector element are visible. The detected spectrum is used to randomly sample the energy of the photons impinging a pixel. The time of arrival of each photon is randomly sampled with 1 ns resolution from a uniform distribution over the acquisition time-interval. The duration of the acquisition $\mathrm{\Delta }t$ is calculated as $\mathrm{\Delta }t=n/r$, where $r$ is the desired incoming photon-rate and $n$ is the amount of incoming photons we want to simulate. Therefore, 1$\times$10⁴ photons at 1$\times$10⁶ cps/pixel will be distributed over a time interval of 10 ms, whereas the same amount of photons at a rate of 1$\times$10⁸ cps/pixel will simulated within a time interval of 0.1 ms. The analog signal shape resulting from the pixel front-end electronics was modeled as an asymmetric Gaussian with 6 ns of rise time, 24 ns of decay time, and height equal to the photon energy. The time-ordered sum of the different pulses generates a waveform. In Figure 2 right, two waveforms for the same detected spectrum and time interval are displayed: one at a low rate of 1$\times$10⁶ cps/pixel and one at a high rate of 5$\times$10⁷ cps/pixel. At a high rate, it is clearly visible how the signals of different photons can pileup and generate signals at energies higher than the ones of the initial spectrum. The waveform is then fed to the four ideal comparators set to 20, 50, 70 and 90 keV. Finally, the output of each comparator is fed into the counter logic, which, according to the chosen retrigger time, evaluates the counts-over-threshold.

Figure 2

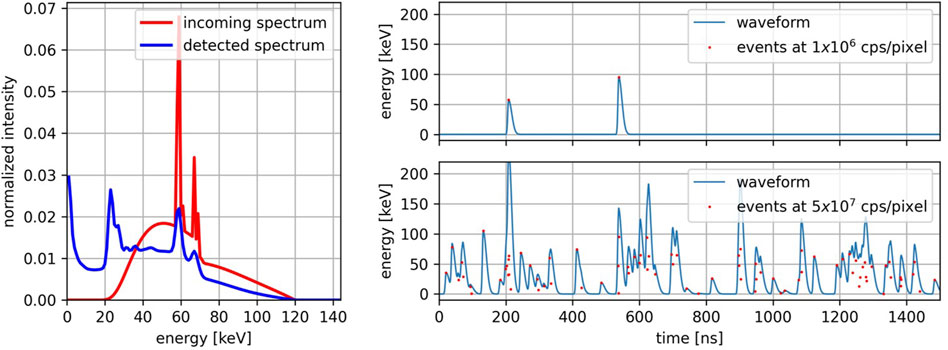
Figure 2. Left: Incoming X-ray spectrum at 120 kV (red) and the same spectrum detected by a CdTe sensor with a pixel size of 330 μm, a thickness of 1.5 mm, and a bias voltage of −1,000 V (blue). Right: Waveforms at different incoming photon rates (top: 1$\times$10⁶ cps/pixel, bottom: 5$\times$10⁷ cps/pixel). The photon energies are sampled from the detected spectrum. The coordinates (photon energy VS arrival time) of the individual events are plotted as red dots.

At a pixel level, the described simulations were used to calculate the count-rate curves and the detected integral spectrum for retrigger times between 10 ns and 1,000 ns, and count-rates between 1$\times$10⁶ cps/pixel and 1$\times$10⁸ cps/pixel. By disabling the instant retrigger capability of the comparator, such quantities were calculated for a conventional paralyzable model as well.

2.3 CT simulation and image analysis

To assess the dependency of the image quality on the retrigger time, CT images were simulated using the MC method described in the previous section. A CT scanner was modeled using a simple parallel beam geometry. As x-ray source, the aforementioned 120 kV spectrum prefiltered with 6.8 mm of aluminum was used (Figure 2, left). To avoid saturation in the line of flight not intersecting the phantom, the incoming spectrum was attenuated by a bow tie filter. The phantom (Figure 3, left) consists of a head-sized water cylinder (160 mm diameter) with high-Z inserts. The attenuated spectrum transmitted through the phantom was calculated for every detector pixel (500 pixels of 330 µm) and every projection angle (360 projections, 0.5$◦$ apart). The pixel-wise attenuated spectrum was fed to the MC method to obtain the corresponding recorded counts. This process was repeated for incoming photon-rates between 1$\times$10⁶ cps/pixel and 1$\times$10⁸ cps/pixel (equivalent to 1$\times$10⁷ cps/mm² and 1$\times$10⁹ cps/mm², respectively), four energy thresholds (20, 50, 70 and 90 keV) and 11 retrigger times between 10 and 1,000 ns. The projection acquisition time was scaled to keep the total number of incoming photons per pixel constant at 1$\times$10⁴ for all photon rates. This ensures that all images are simulated at iso-dose level. To obtain the sinogram (Figure 3, right) for each scenario, the required flat field image was simulated in the same way but omitted the phantom. Once the sinograms had been obtained, the CT images were reconstructed with a filtered-back projection algorithm.

Figure 3

Figure 3. Left: Head-sized phantom (160 mm diameter) used for the CT simulations. Six 20 cm vials filled with 10 mg/mL high-Z material solution are placed close to the periphery. Right: example sinogram of the phantom in parallel beam geometry.

For each reconstructed image $\mu$, the root mean square relative error (RMSRE) was evaluated as:

$RMSRE=\sqrt{\frac{1}{N}{\displaystyle \sum _{n=0}^N}{\left(\frac{{\mu }_n-{\mu }_n^{GT}}{{\mu }_n^{GT}}\cdot 100\right)}^2},(1)$

where $N$ are the pixels within the phantom, and ${\mu }^{GT}$ is the ideal reconstruction obtained for an ideal detector. The error on the RMSRE was evaluated as the root of the standard deviation of the square relative error within the phantom. For the ideal images, the counts-over-threshold were obtained by integrating the attenuated detected spectrum, without feeding the spectrum to the Monte Carlo method. Therefore, the resulting ideal images are pileup- and noise-free.

3 Results

3.1 Count-rate curves

The Monte Carlo method described in Section 2.2 was used to simulate the count-rate curves for a single pixel exposed to a photon rate between 1$\times$10⁶ cps/pixel and 1$\times$10⁹ cps/pixel. For this investigation, the detected spectrum was used without further filtration by the bow tie filter nor attenuation by the phantom. The count-rate curves for energy thresholds at 1, 20, 50, and 90 keV are displayed in Figure 4. The retrigger time was varied between 10 ns and 1,000 ns. The ideal curve and the paralyzable model curve are displayed as well. As expected, a shorter retrigger time leads to a higher maximum count rate. At the same time, low values of the retrigger time lead to spurious multiple-counting (or multiplicity). This is clearly visible at 1 keV and 20 keV: before saturation, multiplicity results in a scaling factor¹ of the measured curve compared to the ideal curve. The scaling factor is evident even at low photon rates, aligning with the observation that if the retrigger time is shorter than the time-over-threshold of a photon pulse, the counter will be triggered multiple times by a single photon. Since the time-over-threshold of a pulse decreases with increasing threshold, the contribution of multiplicity is less visible at 50 keV, and almost absent at 90 keV. The contribution of pileup is mostly present at high energy thresholds, like 90 keV, and consists of an increase in the recorded counts compared to the ideal curve. The surplus of counts persists and grows as the incoming photon rate increases, eventually reaching saturation. This occurs because at higher photon rate, it is more likely for multiple photon pulses to overlap and be recorded as a photon of higher energy. The pileup behavior is also dependent on the retrigger time: the longer the retrigger time, the less count excess is recorded.

Figure 4

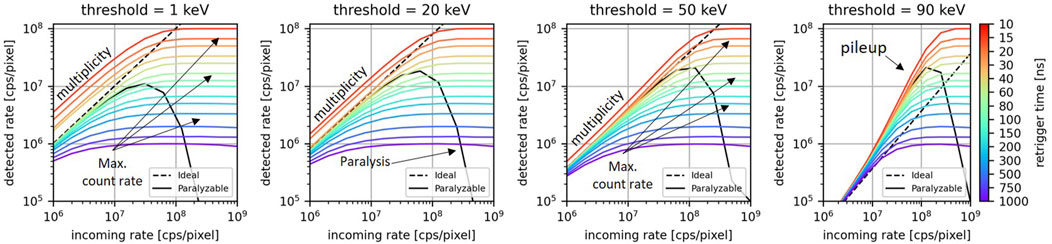
Figure 4. For different values of the retrigger time, the count-rate curves for energy thresholds at 1, 20, 50, and 90 keV. The count-rate curves for the ideal model and the paralyzable are displayed as dashed lines and continuous lines, respectively.

3.2 Integral spectra

In Figure 5, the detected integral spectra are displayed for an incoming photon rate of 1$\times$10⁶ cps/pixel and 5$\times$10⁷ cps/pixel. For this investigation, the detected spectrum was used without further filtration by the bow tie filter nor attenuation by the phantom. The counts-over-threshold were evaluated at each photon rate for all thresholds between 1 keV and 144 keV, and for retrigger times between 10 ns and 1,000 ns. The ideal and the paralyzable model spectra are displayed as well.

Figure 5

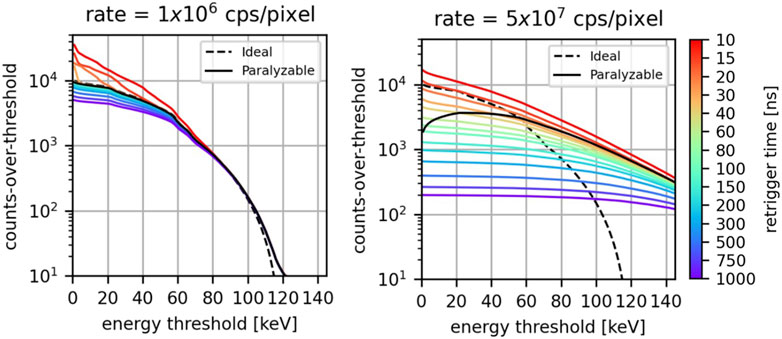
Figure 5. For different values of the retrigger time, the detected integral-spectra at 1$\times$10⁶ cps/pixel and 5$\times$10⁷ cps/pixel photon incoming rate. The integral spectra for the ideal model and the paralyzable are displayed as dashed lines and continuous lines, respectively.

At low photon rates, the ideal spectrum, the paralyzable model, and the retrigger model exhibit approximately the same behavior. The main differences are found for the retrigger model at low energies for low values of the retrigger time: consistent with what was found in the previous section, in this scenario there is an excess of detected counts due to spurious multiple-counting. Minor deviations are also found at low energies for high values of the retrigger time because of early count-rate saturation.

At a high photon rate, the difference among the various models is more significant. Firstly, due to pileup both the paralyzable and the retrigger model count photons at energies higher than the maximum photon energy contained in the incoming spectrum. This phenomenon is expected at high photon rates and was already described by [14]. Secondly, the paralyzable model does not exhibit anymore a monotonically decreasing behavior. Instead, it has a count peak between 20 and 40 keV. This undesired behavior is due to the paralysis, which becomes more pronounced as the energy threshold decreases, and will result in negative counts once the differential spectrum is calculated. On the other hand, the retrigger model always exhibits a monotonically decreasing behavior which will ensure no negative counts once energy bins are taken into account. The longer the retrigger, the fewer counts are recorded and the flatter the integrated spectrum is. For retrigger times above 15 ns, the retrigger model curves intersect the ideal curve at different energies. This means that for a specific energy threshold, a retrigger time can be chosen such that the retrigger model provides the same counts of the ideal scenario. The coordinates of the intersection points (retrigger time vs. energy threshold) suggests that the higher the energy threshold one wants to use, the higher the retrigger time has to be set. Also the paralyzable model curve intersects the ideal curve between 50 and 60 keV.

3.3 CT reconstructions

Figure 6 displays the RMSRE of the CT images simulated for an incoming photon-rate of 1$\times$10⁶, 1$\times$10⁷, 5$\times$10⁷, and 1$\times$10⁸ cps/pixel. The RMSRE is plotted as a function of the retrigger time for the different energy thresholds. The RMSRE for the paralyzable model is shown as well, as a dashed line.

Figure 6

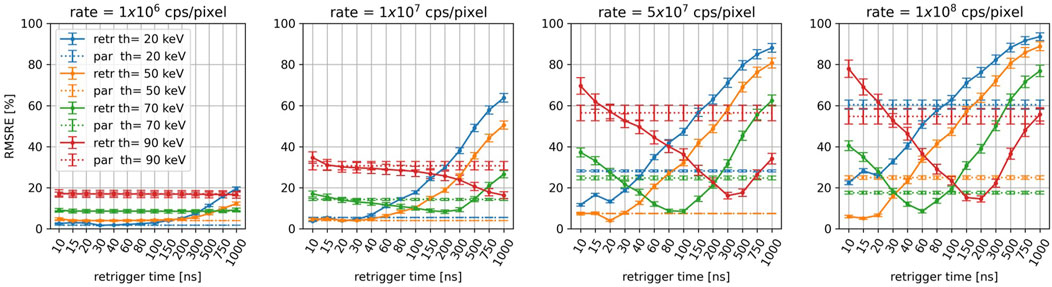
Figure 6. For the different energy thresholds and incoming photon-rates, RMSRE of the reconstructions as a function of the retrigger time. The RMSRE for the paralyzable model is plotted as a dashed line.

At 1$\times$10⁶ cps/pixel, the RMSRE is below 20% for all thresholds for both models and almost constant in the interval of investigated retrigger times. This is consistent with the fact that at a low count rate, there is barely any pileup. Furthermore, it is possible to see how the photon starvation taking place at high energy results in an RMSRE that increases as the threshold energy increases. Only the reconstructions at the two lowest thresholds (20 and 50 keV) deviate from the constant regime for retrigger times above 100 ns. This is due to saturation which takes place prematurely for low-energy threshold and long retrigger times (see Section 3.1). For the different thresholds, the mean RMSRE in the constant regime is 2% (20 keV), 4% (50 keV), 9% (70 keV), and 17% (90 keV). Interestingly, the spurious multiple-counting that takes place for the threshold at 20 keV and retrigger times lower than 20 ns (see Section 3.1) does not result in significant deviation of the RMSRE. This is likely explained by the fact that multiple-counting takes place in the acquisitions of both the projections and the flat field image. Then, the flat-field normalization needed to calculate the sinograms counteracts the count multiplicity introduced by the short retrigger time.

As the count rate increases, the average RMSRE increases as well. For incoming rates above 1$\times$10⁶ cps/pixel, the RMSRE of the images simulated with the Monte-Carlo method strongly depends on the retrigger time, and a minimum of the RMSRE becomes visible. The results for the paralyzable and polychromatic retrigger models are summarized in Table 1. For example, at 5$\times$10⁷ cps/pixel, the minima are 12% at 10 ns (20 keV), 4% at 20 ns (50 keV), 9% at 100 ns (70 keV), and 16% at 300 ns (90 keV). This provides proof that for specific acquisition settings, the retrigger time can be optimized in order to improve the image fidelity. For every threshold, by comparing these minima to the ones obtained at low photon rate, it is possible to see that the deviation from the ideal case is almost restored. By comparing these results to the ones of the paralyzable model (dashed lines in Figure 6) it is possible to assess that the best performance of the retrigger model always outperforms the ones of the paralyzable model. Interestingly, at 5$\times$10⁷ cps/pixel for an energy threshold value of 50 keV, the paralyzable model provides an RMSRE similar to the best one provided by the retrigger model for a retrigger time of 20 ns. This is consistent with what was already found in Section 3.2, where it was shown that for values of the energy threshold around 50 and 60 keV, the paralyzable model provides the same counts of the ideal model.

Table 1

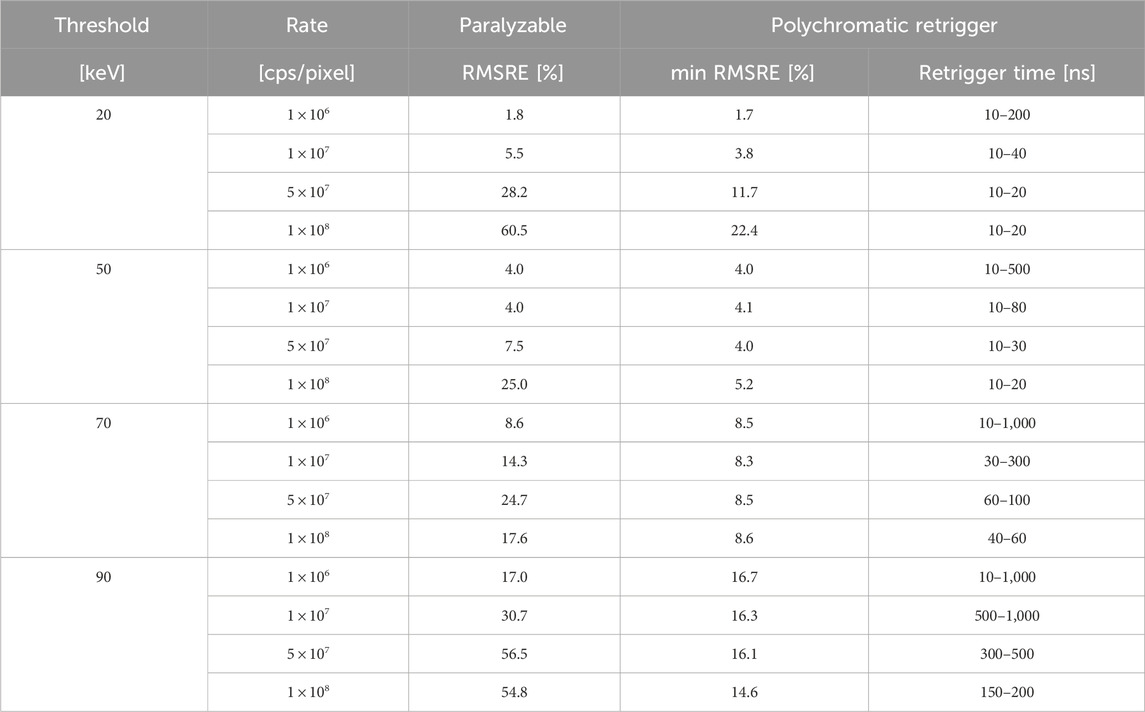
Table 1. For the investigated photon rates and energy thresholds, RMSRE of the CT images simulated with the paralyzable and polychromatic retrigger models. For the polychomatic retrigger, the minimum RMSRE is listed together with the range of retrigger times providing the minimum RMSRE within 5%.

For visual comparison, Figure 7 shows the CT reconstructions for the ideal, paralyzable, and retrigger models with 20, 70 and 90 keV energy threshold, at low (1$\times$10⁶ cps/pixel) and high (5$\times$10⁷ cps/pixel) incoming photon-rates. As already shown quantitatively in Figure 6, at a low photon rate the image quality is similar for the two realistic models, there is barely any dependence on the retrigger time, and no major artifacts are visible, except for the image noise. At a high rate instead, pileup artifacts appear in the form of mild cupping² and change in the attenuation value of the sample. The paralyzable model underestimates or overestimates the attenuation value of the phantom compared to the ideal images. The images obtained with the instant retrigger become highly dependent on the retrigger time. While the artifacts are unavoidable for the paralyzable model, they can be mitigated if the proper retrigger time is chosen. Specifically, the highest fidelity to the ideal image is reached for a retrigger time between 10 and 20 ns for the 20 keV threshold, 100 ns for the 70 keV threshold, and 300 ns for the 90 keV threshold.

Figure 7

Figure 7. Example of the CT images for the three simulated models: ideal, paralyzable, and instant retrigger for different values of the retrigger time. The reconstructions are shown for energy threshold at 20 keV (blue box), 70 keV (green box), and 90 keV (red box), for two values of the incoming photon rate: 1$\times$10⁶ cps/pixel and 5$\times$10⁷ cps/pixel. Window settings: C = 0.03 mm⁻¹, W = 0.02 mm⁻¹.

4 Discussion

The results have shown how the count-rate curves, the detected spectra, and the image quality depend on the retrigger time, and how this dependency becomes more significant as the incoming photon rate increases. In Figure 5 right, it was shown that at high rates, the ideal integral spectrum intersects with the spectra obtained with retrigger model. This means that for a specific energy threshold, there is a retrigger time that provides the same counts-over-threshold of the ideal model. It was found that the higher the desired energy threshold, the longer the retrigger time has to be set. This is consistent with what found in Figure 4, where it was shown that a longer retrigger time can mitigate the pileup counts recorded at high energies.

This first optimization attempt was carried out at a pixel level, without any attenuation by a sample or patient, meaning that it was performed with only one detected spectrum. A second characterization of the polychromatic retrigger was performed with a real-world CT application. In such scenario, the bow tie filter and imaged object attenuate the incoming spectrum according to their material composition and intersection lengths. Therefore by simulating a CT system and by evaluating the quality of the final reconstructed image, a global optimization process could be performed, without individually investigate all the slightly different spectra detected by each pixel in the 2D detector matrix. The characterization of the RMSRE of the CT reconstructions is summarized in Table 1. The results have shown that the RMSRE as a function of the retrigger time exhibits a global minimum, proving that the retrigger time can optimize the image quality even in a real-world application. The value of the best retrigger time depends on the energy threshold and incoming photon rate, and it is expected to change also with the tube voltage and the thickness of the imaged object. These dependencies do not limit the applicability of the polychromatic retrigger in clinical settings, where the different acquisition protocols are defined according to the body region to be scanned. Therefore, the optimal retrigger times can be calibrated in advance for each acquisition protocol. The pile-up artifact reduction provided by the polychromatic retrigger might offer benefits in multiple clinical domains like cardiovascular imaging, early tumor detection, implant visualization, and pediatric imaging. Furthermore, the enhanced image fidelity is expected to improve the accuracy of K-edge imaging, which is used to quantify the concentration of specific contrast agents or molecular markers within tissues. This has potential applications in both research and clinical settings for tracking disease progression and response to therapy. Lastly, the polychromatic retrigger might be beneficial to other imaging modalities where accurate photon counting is required [18].

Figure 8 compares the best results obtained with the polychromatic retrigger with the ones obtained with the paralyzable model (left), and with the conventional instant retrigger (equal for all thresholds) fixed at 20 ns (center) and 300 ns (right). In all three scenarios, it is possible to see how all models perform similarly at the lowest photon rate of 1$\times$10⁶ cps/pixel. As the photon rate increases, the RMSRE provided by the paralyzable and instant retrigger models increases. On the other hand, the polychromatic retrigger model is able to provide an almost constant RMSRE over the full range of photon rates by adjusting the retrigger time as a function of the energy threshold and the photon rate. A limitation is encountered at the lowest energy threshold where the amount of counts-over-threshold is so high that no retrigger time can restore the RMSRE achieved at low photon rates, and the detector inevitably saturates. However, this is not a limitation of the polychromatic retrigger per se, but a limitation of the realistic detector modeled and its finite pulse-shape duration.

Figure 8

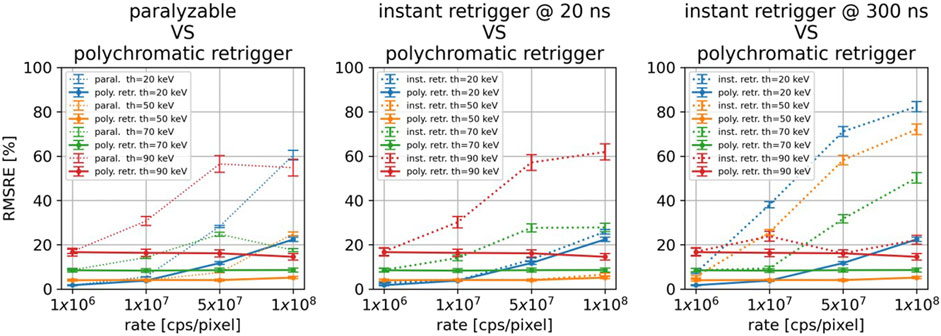
Figure 8. For all the investigated energy thresholds and incoming photon rates, comparison between the polychromatic retrigger and the paralyzable model (left), with the instant retrigger fixed at 20 ns (center), and with the instant retrigger fixed at 300 ns (right).

The main benefit of the polychromatic retrigger over the instant retrigger is highlighted in Figure 8 center and right. With the conventional instant retrigger, only one retrigger time can be set for all thresholds. If 20 ns is set (Figure 8 center, dashed lines), the threshold images at 20 and 50 keV will provide the best RMSRE achievable even at high photon rates. Conversely, the image quality at 70 and 90 keV will decrease. On the other hand, if a retrigger time of 300 ns is set (Figure 8 right, dashed lines), the threshold images at 90 keV will have almost constant RMSRE, whereas the RMSRE will increase for the other energy thresholds. By using the polychromatic retrigger instead, it is possible to optimize the retrigger time for each threshold individually and obtain the best achievable RMSRE for every incoming photon rate. While the current results are promising, we acknowledge that experimental validation is necessary to fully confirm our findings and we will pursue this in future work.

5 Conclusion

In the framework of photon-counting CT applications, we have investigated how pulse pileup at high photon rates can degrade the quality of the reconstructed images and how the polychromatic retrigger can mitigate this. In general, the deviation of realistic images from the ideal ones increases when the incoming photon rate increases from 1$\times$10⁶ cps/pixel (1$\times$10⁷ cps/mm²) to 1$\times$10⁸ cps/pixel (1$\times$10⁹ cps/mm²). At low incoming rates, both the paralyzable model and all retrigger models provide deviations below 20%. As photon rate increases, the deviation for the paralyzable model can reach values up to 60%. For the retrigger model, the deviation-increase highly depends on the energy threshold and on the retrigger time. We have shown how it is possible to optimize the retrigger time for every energy threshold independently and by doing so, it is possible to keep the image deviation below 23% even at high incoming rates. The results indicate that the optimal retrigger times increase with higher energy thresholds. For example, at 1$\times$10⁸ cps/pixel (1$\times$10⁹ cps/mm²) incoming rate, the optimal retrigger time is 10 ns for 20 keV, 20 ns for 50 keV, 100 ns for 70 keV, and 300 ns for 90 keV. A longer retrigger time implies also a lower maximum detectable count rate, but this is not a limitation since the number of available photons decreases with increasing energy threshold.

The deviation provided by the polychromatic retrigger is almost constant for all the different incoming photon rates, meaning that the polychromatic retrigger can enable CT acquisitions at higher photon rates, with only a marginal loss of image quality. The polychromatic retrigger constitutes an additional degree of freedom for image quality optimization. For a specific acquisition protocol like the ones implemented in clinics, the value of the optimal retrigger time can be evaluated in advance through standardized calibrations and phantoms, and tabulated. An example of an optimization process was provided in this work for a head-sized phantom. Working with the proper retrigger time is especially relevant for applications requiring short acquisition times (cardiac imaging) and/or high image fidelity at high energy thresholds (K-edge, multi-contrast imaging).

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

CA: Conceptualization, Data curation, Formal Analysis, Investigation, Methodology, Software, Writing–original draft, Writing–review and editing. CD: Conceptualization, Software, Writing–review and editing. PZ: Resources, Writing–review and editing.

Funding

The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.

Conflict of interest

Authors CA, CD, and PZ were employed by DECTRIS Ltd.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Footnotes

¹In log-log scale, the scaling factor is visualized as an offset.

²Cupping is an artifact where the periphery of an object has a different attenuation value than its center.

References

1. Mannil M, Hickethier T, Von Spiczak J, Baer M, Henning A, Hertel M, et al. Photon-counting CT: high-resolution imaging of coronary stents. Invest Radiol (2018) 53:143–9. doi:10.1097/RLI.0000000000000420

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Klein L, Dorn S, Amato C, Heinze S, Uhrig M, Schlemmer HP, et al. Effects of detector sampling on noise reduction in clinical photon-counting whole-body computed tomography. Invest Radiol (2020) 55:111–9. doi:10.1097/RLI.0000000000000616

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Sawall S, Klein L, Amato C, Kachelrieß M. Iodine contrast-to-noise ratio improvement at unit dose and contrast media volume reduction in a whole-body photon-counting CT. Eur J Radiol (2020) 1675:1–26. doi:10.1016/j.ejrad.2020.108909

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Amato C, Klein L, Wehrse E, Rotkopf LT, Sawall S, Maier J, et al. Potential of contrast agents based on high-Z elements for contrast-enhanced photon-counting computed tomography. Med Phys (2020) 47:6179–90. doi:10.1002/mp.14519

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Roessl E, Proksa R. K-edge imaging in x-ray computed tomography using multi-bin photon counting detectors. Phys Med Biol (2007) 52:4679–96. doi:10.1088/0031-9155/52/15/020

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Schlomka JP, Roessl E, Dorscheid R, Dill S, Martens G, Istel T, et al. Experimental feasibility of multi-energy photon-counting K-edge imaging in pre-clinical computed tomography. Phys Med Biol (2008) 53:4031–47. doi:10.1088/0031-9155/53/15/002

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Symons R, Krauss B, Sahbaee P, Cork TE, Lakshmanan MN, Bluemke DA, et al. Photon-counting CT for simultaneous imaging of multiple contrast agents in the abdomen: an in vivo study. Med Phys (2017) 44:5120–7. doi:10.1002/mp.12301

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Ren L, Rajendran K, McCollough CH, Yu L. Quantitative accuracy and dose efficiency of dual-contrast imaging using dual-energy CT: a phantom study. Med Phys (2020) 47:441–56. doi:10.1002/mp.13912

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Amato C, Susenburger M, Lehr S, Kuntz J, Gehrke N, Franke D, et al. Dual-contrast photon-counting micro-CT using iodine and a novel bismuth-based contrast agent. Phys Med and Biol (2023) 68:135001. doi:10.1088/1361-6560/ACDB42

CrossRef Full Text | Google Scholar

10. Taguchi K, Srivastava S, Kudo H, Barber WC. Enabling photon counting clinical x-ray CT. In: IEEE Nuclear Science Symposium Conference Record; 24 October 2009 - 01 November 2009; Orlando, FL, USA (2009). p. 3581–5. doi:10.1109/NSSMIC.2009.5401823

CrossRef Full Text | Google Scholar

11. Loeliger T, Bronnimann C, Donath T, Schneebeli M, Schnyder R, Trub P. The new PILATUS3 ASIC with instant retrigger capability. In: IEEE Nuclear Science Symposium Conference Record; 27 October 2012 - 03 November 2012; Anaheim, CA, USA (2012). p. 610–5doi. doi:10.1109/NSSMIC.2012.6551180

CrossRef Full Text | Google Scholar

12. Hsieh SS, Iniewski K. Improving paralysis compensation in photon counting detectors. IEEE Trans Med Imaging (2021) 40:3–11. doi:10.1109/TMI.2020.3019461

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Hsieh SS. Coincidence counters for charge sharing compensation in spectroscopic photon counting detectors. IEEE Trans Med Imaging (2020) 39:678–87. doi:10.1109/TMI.2019.2933986

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Zambon P, Amato C. Pulse pileup model for spectral resolved X-ray photon-counting detectors with dead time and retrigger capability. Front Phys (2023) 11. doi:10.3389/fphy.2023.1205638

CrossRef Full Text | Google Scholar

15. Ferrari A, Sala PR, Fasso A, Ranft J. FLUKA: a multi-particle transport code. Cern-2005-010, Infn/Tc_05/11, Slac-R-773 (2005). doi:10.5170/CERN-2005-010

CrossRef Full Text | Google Scholar

16. Battistoni G, Cerutti F, Fassò A, Ferrari A, Muraro S, Ranft J, et al. The FLUKA code: description and benchmarking. AIP Conf Proc (2007) 896:31–49. doi:10.1063/1.2720455

CrossRef Full Text | Google Scholar

17. Böhlen TT, Cerutti F, Chin MP, Fassò A, Ferrari A, Ortega PG, et al. The FLUKA code: developments and challenges for high energy and medical applications. Nucl Data Sheets (2014) 120:211–4. doi:10.1016/J.NDS.2014.07.049

CrossRef Full Text | Google Scholar

18. Moskal P, Dulski K, Chug N, Curceanu C, Czerwiński E, Dadgar M, et al. Positronium imaging with the novel multiphoton PET scanner. Sci Adv (2021) 7:4394–407. doi:10.1126/sciadv.abh4394

CrossRef Full Text | Google Scholar