Ground-state β-feeding determination using total-absorption spectrometers

The determination of the $\beta$ intensity probability between the ground states of parent and daughter nuclei has traditionally been a difficult task with standard $\gamma$-spectroscopy approaches due to the lack of the associated $\gamma$ emission. In the last years, the total absorption $\gamma$-ray spectroscopy technique has successfully proven its ability to deal with this problem by means of different procedures. This article discusses the potential of these methods, and a new approach for segmented total-absorption $\gamma$-ray spectrometers is also introduced. An overview of applications is presented based on past, present, and future $\beta$-decay experiments.

1 Introduction

The study of $\beta$-decay properties provides valuable information for our understanding of the nuclear structure. Among these properties, the determination of the $\beta$-decay probabilities to populate each level in the daughter nucleus is typically accomplished with $\gamma$-spectroscopy techniques. The traditional approach relies on HPGe detectors for the measurement of the individual $\gamma$-rays de-exciting the levels fed in the daughter nucleus. One difficulty arises when dealing with the probability to populate the ground state (g.s.), $I_{\beta }^{g.s.}$, because of the absence of the $\gamma$-ray emission. For this reason, $I_{\beta }^{g.s.}$ is typically obtained indirectly as the difference between the total number of decays and the number of decays feeding excited states in the daughter nucleus. The latter are evaluated from $\gamma$-ray intensity imbalances using absolute $\gamma$ intensities per $\beta$ decay. A drawback of this method is the limited efficiency of HPGe detectors, especially for high-energy $\gamma$-rays, which translates into an underestimation of the probability to feed levels at high excitation energies in the daughter nucleus. This effect, known as pandemonium [1], generally becomes more severe with larger $\beta$-decay energy windows and when the number of levels potentially fed in the daughter nucleus is large.

The total-absorption $\gamma$-ray spectroscopy (TAGS) technique allows us to avoid the pandemonium effect by means of high-efficiency $\gamma$ calorimeters made of scintillation crystals. Such a detector, called total-absorption spectrometer (TAS), detects the full $\gamma$ cascade de-exciting each level populated in the daughter nucleus. A TAS is usually employed in coincidence with an ancillary detector for $\beta$-particles (typically plastic or Si $\mathrm{\Delta }$E detectors at ISOL facilities and Si implantation detectors at fragmentation facilities) in order to reject the environmental background. Examples of active TAS setups are Lucrecia [2], SuN [3], Rocinante [4], MTAS [5], DTAS [6], and HECTOR [7]. The feasibility of using TAS detectors for the determination of $I_{\beta }^{g.s.}$ is discussed in Section 2, highlighting some exciting applications in Section 3 and discussing the future perspective of this kind of measurements in Section 4.

2 Methods for the determination of $I_{\beta }^{g.s.}$ using a TAS

2.1 Deconvolution

The traditional method employed in the TAGS analysis to determine the $\beta$-intensities from experimental spectra is based on applying a deconvolution method for the solution of the inverse problem in Equation 1 [8]:

$d_i={\displaystyle \sum _j^{\mathit{levels}}}{R}_{ij}\left(B\right)f_j+C_i,(1)$

where $f_j$ represents the number of decay events feeding level $j$ in the daughter nucleus, $d_i$ is the number of counts in channel $i$ of the experimental TAGS spectrum, $C_i$ accounts for all contaminants in the experimental channel $i$ (electronic pileup, activity of descendants, etc.), and $R_{ij}$ is the response function of the TAS detector to the $\beta$-decay under analysis. This response function, in turn, depends on the branching ratios $(B)$ de-exciting the states populated in the daughter nucleus [9, 10]. The response function is calculated with Monte Carlo (MC) simulations, carefully validated with standard radioactive sources by comparing experimental and simulated spectra [9]. As part of $R_{ij}$, the response to the g.s.-to-g.s. transition is also calculated, and it gets involved in the deconvolution process. The associated $\beta$ particles emitted penetrate the scintillation material of the TAS detector if no absorbers are placed on purpose to stop them. In the case of ${\beta }^{-}$ decays, it produces a clear fingerprint with a tailing spectrum peaking at low energies, as shown in Figure 2. For ${\beta }^{+}$ decays, the g.s.-to-g.s. response includes the positron annihilation fingerprint with the detection of two 511-keV $\gamma$-rays, which enhances the efficiency for the g.s. branch. Note that in this case, as in the general case of the response associated with feeding to an excited state, the $\beta$ penetration effect introduces a high-energy tail in the spectrum when summed to the corresponding $\gamma$-ray detection.

2.2 4$\pi \gamma -\beta$ counting method

The $4\pi \gamma -\beta$ method is complementary but independent to the deconvolution of TAGS spectra presented in the previous section. It was proposed by Greenwood et al. 30 years ago [11] and applied to the study of the $\beta$-decays of several fission fragments. Recently, it was revisited, corrected, and extended for the case of $\beta$-delayed neutron emitters [12].

This method relies on the determination of the experimental ratio $R=N_{\beta \gamma }/N_{\beta }$, where $N_{\beta }$ is the number of counts detected in the ancillary $\beta$ detector and $N_{\beta \gamma }$ is the number of counts registered in coincidence in both the TAS and the $\beta$ detector. For the decay of interest, both numbers of counts must be corrected by subtracting all possible contaminants: electronic pileup, activity of descendants, etc. The same contaminants with the same normalization factors are taken into account in the TAGS deconvolution, as discussed in the previous section.

In addition, this method requires the computation of three correction factors, $a$, $b$, and $c$, that are ratios of $\beta$ efficiencies computed by means of MC simulations. The detailed definition of these terms is given in [12]. The response function $R_{ij}$ used for the TAGS deconvolution can be used for the evaluation of these correction factors.

With all these ingredients, the $\beta$ intensity probability to populate the g.s. in the daughter nucleus can be calculated as in Equation 2 [12].

$I_{\beta }^{g.s.}=\frac{1-aR}{1+bR-c}.(2)$

The main advantage of this method with respect to the TAGS deconvolution is that it does not depend on the features of the TAS spectrum, but only on the integral number of counts. This minimizes the impact of the branching ratio matrix $(B)$, which plays a crucial role in the reproduction of the structures of peaks found in the TAS spectrum when using the TAGS deconvolution method. Additionally, this reduces the associated uncertainty of this method, as discussed by [12].

2.3 Asymmetry in segmented spectrometers

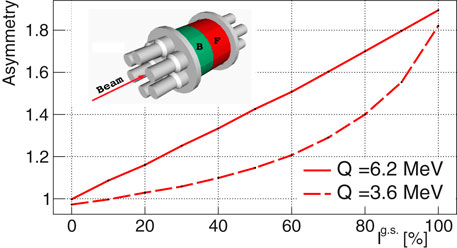
This novel method, introduced here for the first time, relies on the fact that for g.s.-to-g.s. ${\beta }^{-}$ transitions, the coincidence between an ancillary $\beta$ detector and a segmented TAS detector is not symmetric with respect to the beam direction and the placement of the $\beta$ detector. At ISOL facilities, the beam is typically implanted on a movable tape for the accumulation of the radioactive sample of interest and subsequent removal of the activity of the descendants. The ancillary detector for $\beta$ tagging is placed in front of the implantation tape, normally covering less than half of the total solid angle subtended at its center. Before depositing energy in the modules of the segmented TAS (referred before as $\beta$ penetration), $\beta$ electrons emitted from the tape leave some energy in the $\beta$ detector. For this reason, TAS modules placed behind the $\beta$ detector (in forward direction with respect to the beam) will register more coincidences for g.s.-to-g.s. transitions than those modules placed in front of the $\beta$ detector (in backward direction with respect to the beam). A schematic view is shown in the inset of Figure 1 for the 12-fold segmented Rocinante detector [4].

Figure 1

Figure 1. Simulated asymmetry coefficient as a function of the $I_{\beta }^{g.s.}$ for two $\beta$ decays with different $Q_{\beta }$. In the simulation, the Rocinante detector [4] was used in coincidence with a 0.5-mm-thick Si detector. A schematic view of the detector is shown in the inset with forward (F) and backward (B) modules highlighted in red and green, respectively.

For each event, the module multiplicity $M_m$ in a segmented TAS represents the number of modules that register a signal above the threshold. The probability of $\beta$ penetration in more than one module depends on the dimensions of the crystals, the material, and the energy of the $\beta$ electron, but in normal conditions, events associated with g.s. feeding can be assumed to have mostly $M_m$=1.

For the coincidence spectrum between a segmented TAS and the corresponding ancillary $\beta$ detector with the $M_m$=1 condition, the following asymmetry coefficient A in Equation 3 can be defined:

$A=\frac{F}{0.5\left(F+B\right)},(3)$

where $F$ is the number of counts in the forward TAS modules and $B$ is the number of counts in the backward TAS modules after subtraction of all contaminants (one again electronic pileup, activity of descendants etc.). The coefficient thus defined is ideally 1 when $\gamma$-rays are emitted isotropically together with $\beta$ electrons, and it is larger than 1 for g.s.-to-g.s. transitions. For a certain decay with the $\beta$-energy window $Q_{\beta }$, the asymmetry coefficient can be computed as a function of the $I_{\beta }^{g.s.}$ value by means of MC simulations. The experimentally obtained asymmetry coefficient can be then employed for the determination of $I_{\beta }^{g.s.}$ by linear interpolation. Figure 1 shows the asymmetry coefficient evaluated for two different $\beta$ decays simulated by means of the Geant4 package [13]. The DECAYGEN event generator [10] served as input with different $I_{\beta }^{g.s.}$ values and realistic feeding distributions and branching ratio matrices for the remaining parts of the decay schemes. Increasing sensitivity of the asymmetry coefficient is observed with increasing $Q_{\beta }$.

As in the case of the 4$\pi \gamma -\beta$ counting method, the use of the asymmetry coefficient is complementary but independent of the deconvolution of TAGS spectra. It relies on carefully validated MC simulations and needs normalized contributions for all contaminants, but this method is also expected to be less influenced by the branching ratio matrix $(B)$.

3 Applications

Proper knowledge of the $\beta$ feeding probabilities, which carry information about the overlap between parent and daughter nuclear wave functions, is essential for the understanding of the underlying nuclear structure through comparisons between experimental values and theoretical calculations. As discussed in Section 1, in practical terms, the $I_{\beta }^{g.s.}$ value acts as a normalization for the rest of $\beta$ intensity probabilities, and it may play a crucial role in many $\beta$ decays, with a great variety of applications: environmental dose evaluation, reactor calculations, isospin symmetry studies, double $\beta$-decay systems, electro-weak tests, nuclear astrophysics, etc. In this section, three stimulating applications will be featured.

3.1 Reactor physics: decay heat and reactor antineutrinos

In nuclear reactors, due to the radioactivity of fission fragments, an average of six $\beta$ decays occur per fission. The energy released by this $\beta$-decay radioactivity, commonly known as decay heat, mainly involves the emission of electrons, antineutrinos, and $\gamma$-rays de-exciting levels populated in the daughter nucleus. The decay heat is thus associated with the $\beta$-intensity probabilities of each of such decays, and its evolution depends on the activity of each fission fragment, shaped by the corresponding half-life, and fission yield (FY). For a recent review, see Ref. [14]. The same applies for the understanding of reactor antineutrino spectra in the field of neutrino oscillation experiments as shown by [15] and references therein. Due to the commonly large $Q_{\beta }$ of these cases, the TAGS technique is especially suitable in order to avoid the Pandemonium effect [16]. Following priority lists established by the International Atomic Energy Agency (IAEA) [17], the TAGS measurements of the most relevant $\beta$ decays to the reactor decay heat and the reactor antineutrino spectrum have been carried out in the last 20 years [14, 15].

A significant part of the $\beta$ decays that contribute the most both to the reactor decay heat and the reactor antineutrino spectrum, because of their significant FY, exhibit large $I_{\beta }^{g.s.}$ values. Some examples are ⁹²Rb [95.2(7)%, 4.82(7)%], ⁹³Rb [35(3)%, 3.55(4)%], ⁹⁴Y [41(4)%, 6.45(6)%], ⁹⁵Sr [55.7(25)%, 5.27(7)%], ^96gsY [95.5(5)%, 6.0(10)%], ¹⁴⁰Cs [35.9(17)%, 5.72(8)%], and ¹⁴²Cs [56(5)%, 2.72(8)%], where $I_{\beta }^{g.s.}$ values and cumulative FY for ²³⁵U, both from ENDF [18], are, respectively, quoted in brackets. Note that all these g.s.-to-g.s. branches are forbidden $\beta$ transitions.

In the past years, the shape of forbidden $\beta$ transitions has attracted a lot of attention since it carries information about fundamental properties of the weak interaction, such as the ratio between the vector and the axial–vector coupling constants [19], and they may serve as proofs of non-standard model components [20]. In addition, the shape of forbidden $\beta$ transitions plays a crucial role in the understanding of the discrepancies found between calculated and measured reactor antineutrino spectra [21–25]. In this context, an important effort is being taken to study the $\beta$ spectral shapes of the most relevant $\beta$ decays for the reactor antineutrino spectrum, both from a theoretical point of view [26–29] and with novel experimental approaches [30].

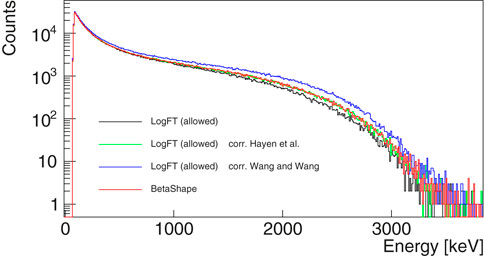
In the near future, it will be of great interest to study the impact of theoretical and experimental shape factors for forbidden transitions in the application of the TAGS technique, in particular with the deconvolution method. In some particular cases, the shape of the emitted $\beta$ spectrum may affect the response function of the TAS detector for the g.s.-to-g.s. branch. This is something already shown by the MTAS collaboration for the first forbidden unique transition ⁸⁸Rb$\left(2^{-}\right)$ $\to$ ⁸⁸Sr$\left(0^{+}\right)$ [31]. Analogously, Figure 2 shows Geant4 MC simulations of the response of DTAS to the $\beta$ electrons of the $2^{-}\to 0^{+}$ g.s.-to-g.s. first forbidden unique transition from the decay of ⁹⁴Y into ⁹⁴Zr ($Q_{\beta }$ of 49,18(6) keV [32]). As input for these simulations, we have used 1) a $\beta$ spectrum assuming an allowed shape calculated with the subroutines from the logFT program of NNDC based on Ref. [33]; 2) the allowed $\beta$ spectrum from 1) multiplied by the reference shape factor from shell model calculations by Hayen et al. [26, 27]; 3) the allowed $\beta$ spectrum from 1) multiplied by the reference shape factor from projected shell model calculations by [28]; and 4) a $\beta$ spectrum calculated using the BetaShape code [34] considering all available corrections. The different β-shape factors clearly affect the response to the g.s.-to-g.s. branch, as shown in Figure 2. The impact on the experimental determination of $I_{\beta }^{g.s.}$ is still under evaluation, pointing to the importance of verifying the influence and systematic uncertainty introduced by different sets of corrections in those cases, where these calculated shape corrections are large and the g.s.-to-g.s. branch is expected to be strong.

Figure 2

Figure 2. MC simulated response of the DTAS detector in coincidence with a 3-mm thick $\beta$ plastic detector for the g.s.-to-g.s. first forbidden unique transition ⁹⁴Y$(2^{-}){\to }^{94}$Zr$0^{+}$. Different theoretical $\beta$ spectra are used as input for the simulation of emitted electrons (see text for details).

3.2 Astrophysics: the Urca cooling mechanism

The Urca cycle is a neutrino cooling process considered in different astrophysical scenarios (neutron stars, presupernova stars, white dwarfs, and type-Ia supernovae), where a pair of nuclei cool down the environment by means of sequential electron capture (EC) and ${\beta }^{-}$ decays [35]. This process becomes possible for some nuclear pairs when the chemical potential of the electron gas in the astrophysical environment is larger than $Q_{EC}$, in order to allow the EC from the $(Z,A)$ nucleus to the $(Z-1,A)$ partner, but does not exceed it by more than $\sim$100 keV for typical temperatures, in order not to block the phase space for electron emission back to the $(Z,A)$ nucleus via ${\beta }^{-}$ decay. In practical terms, this implies that g.s.-to-g.s. transitions are the most important ones contributing to this process, although it was recently shown that considering also transitions to low-lying excited states has a non-negligible influence in the neutrino luminosities of Urca pairs for neutron stars [36]. The cooling rate associated with the Urca process depends on the $ft$ values of the transitions involved, where $f$ is the statistical rate function and $t$ is the partial half-life, determined from the total half-life, $T_{1/2}$ and the $\beta$ intensity probability of this transition. The $I_{\beta }^{g.s.}$ value is thus essential to evaluate the impact of each Urca pair. The first TAGS experiment in this line has been performed by the SuN collaboration at the National Superconducting Cyclotron Laboratory (NSCL), measuring the ${\beta }^{-}$ decay of ⁶¹V [37], the Urca partner of ⁶¹Cr. It would be very interesting for the understanding of the Urca cooling mechanism in different astrophysical environments to perform new TAGS measurements of the most relevant Urca pairs, as the ones identified for neutron stars by [38, 39]. In particular, Urca pairs in the crust of neutron stars have larger $Q_{EC}$ windows than ocean Urca pairs [39], and they are expected to be affected by larger uncertainties due to the Pandemonium effect.

3.3 Weak-interaction studies: superallowed transitions

In order to improve our understanding of the electro-weak interaction, pure Fermi superallowed $0^{+}\to 0^{+}\beta$ transitions have been employed for more than 50 years to test the conservation of the vector weak current (CVC) and provide us with a precise value of the $V_{ud}$ element of the Cabibbo–Kobayashi–Maskawa (CKM) quark mixing matrix [40]. An independent determination of $V_{ud}$ has been recently proposed based on superallowed mirror $\beta$ transitions between analog $T=1/2$ states in mirror nuclei (mixture of Fermi and Gamow–Teller) [41]. The $ft$ values for these superallowed transitions, and, thus, the corresponding g.s.-to-g.s. $\beta$-intensity probabilities, are key ingredients for precision tests. In many cases, $I_{\beta }^{g.s.}$ is not known experimentally or does not have enough precision to be considered for weak-interaction tests. In addition, for those that are currently included in such tests, 15 pure Fermi transitions [40] and 8 mirror transitions [42], the limitations in determining $I_{\beta }^{g.s.}$ with traditional approaches may bias the adopted values. In particular, the possible Pandemonium effect in the determination of these superallowed branching ratios was raised by Hardy and Towner [43], and it is expected to be particularly important in medium–heavy nuclei, where there may be a competition between the superallowed branch and numerous weak allowed branches populating excited states at higher excitation energies. A recent letter of intent at ISOLDE proposes the use of the Lucrecia TAS to determine superallowed branching ratios of medium nuclei free from the Pandemonium effect [44]. TAGS studies for these cases will also allow the validation of the procedures employed to precisely estimate the missing $\beta$ intensity in experiments with HPGe detectors, based on the $\gamma$ intensity going through low-lying collector states combined with theoretical calculations [45–47].

As we approach the drip line for $N=Z$ nuclei, the number of superallowed decays accessible at ISOL facilities is limited, and in-flight production techniques are needed. The role of the most advanced fragmentation facilities, FRIB, GANIL/Spiral-2, FAIR/GSI, and RIKEN, will be crucial for the extension of the number of studied superallowed decays. Some cases without known superallowed branching ratios have already been produced in these laboratories, such as ⁹⁸In and ⁹⁴Ag at RIKEN [48] and ⁸²Nb, ⁸⁶Tc, and ⁹⁰Rh at GSI [49]. The presence of isomers and the energetically possible $\beta$-delayed proton(s) emission will complicate the determination of the g.s. feeding probability in these cases.

4 Discussion

Inthis work, the ability of TAS detectors to obtain the $\beta$-feeding probability to the g.s. was discussed on the basis of three independent methods. The deconvolution method is linked to the standard application of the TAGS technique and has been proven to successfully determine $I_{\beta }^{g.s.}$ in many ${\beta }^{-}$ cases [4, 27, 31, 37, 50–62] and in a few ${\beta }^{+}/EC$ decays such as ⁵⁸Cu [63] and recently in ⁶⁴Ga [64]. The revisited $4\pi \gamma -\beta$ method has only been applied experimentally with the DTAS detector for ${\beta }^{-}$ decays [12, 60] and successfully tested with MC simulations for Lucrecia in the superallowed ${\beta }^{+}/EC$ decay of ⁶²Ga [44]. It will be crucial to verify its potential to improve the precision with respect to the deconvolution method by using other TAS detectors and studying more $\beta$-decaying cases. The novel method based on the asymmetry coefficient proposed here for segmented spectrometers calls for an experimental validation with an uncertainty survey. Due to their complementarity, a deep comparison of the three methods and their associated uncertainties would be of great interest. Given that all these methods rely on MC simulations, it would also be desirable to test the systematic uncertainties and limitations introduced by the electron/positron models implemented in commonly used simulation codes such as Geant4. The MC validation of experimental measurements of pure $\beta$ emitters, such as ⁹⁰${\mathrm{S}\mathrm{r}-}^{90}$Y or ³²P, would be helpful. In connection with this, the aforementioned impact of the $\beta$ shape corrections also needs a careful investigation. These technical advances would boost the robustness of future high-impact results such as those outlined in Section 3. In the coming years, the well-consolidated reactor physics application will benefit from ongoing $\beta$ spectral studies [65] and from the measurement of the remaining $\beta$ decays with strong g.s. branches in nuclear reactors. The recently proposed application for Urca cycle studies [37] evinces a direct impact of g.s. branches in nuclear astrophysics, suggesting an exciting opportunity for future measurements. Finally, future work linking $I_{\beta }^{g.s.}$ with fundamental properties of the weak interaction represents a novel approach for these studies and for the TAGS technique. The feasibility of such a proposition for the extraction of precise enough results for weak-interaction validations needs to be verified in the coming years.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

VG: conceptualization, data curation, funding acquisition, investigation, methodology, visualization, writing–original draft, and writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work has been funded by the National Science Center, Poland, under Grant Nos 2019/35/D/ST2/02081 and 2020/39/B/ST2/02346.

Conflict of interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Hardy J, Carraz L, Jonson B, Hansen P. The essential decay of pandemonium: a demonstration of errors in complex beta-decay schemes. Phys Lett B (1977) 71:307–10. doi:10.1016/0370-2693(77)90223-4

CrossRef Full Text | Google Scholar

2. Rubio B, Gelletly W, Algora A, Nacher E, Tain JL. Beta decay studies with total absorption spectroscopy and the lucrecia spectrometer at isolde. J Phys G: Nucl Part Phys (2017) 44:084004. doi:10.1088/1361-6471/aa797f

CrossRef Full Text | Google Scholar

3. Simon A, Quinn S, Spyrou A, Battaglia A, Beskin I, Best A, et al. Sun: summing nai(tl) gamma-ray detector for capture reaction measurements. Nucl Instr Methods Phys Res Section A: Acc Spectrometers, Detectors Associated Equipment (2013) 703:16–21. doi:10.1016/j.nima.2012.11.045

CrossRef Full Text | Google Scholar

4. Valencia E, Tain JL, Algora A, Agramunt J, Estevez E, Jordan MD, et al. Total absorption γ-ray spectroscopy of the β-delayed neutron emitters ⁸⁷Br, ⁸⁸Br, and ⁹⁴Rb. Phys Rev C (2017) 95 (2):024320. doi:10.1103/PhysRevC.95.024320

CrossRef Full Text | Google Scholar

5. Karny M, Rykaczewski K, Fijałkowska A, Rasco B, Wolińska-Cichocka M, Grzywacz R, et al. Modular total absorption spectrometer. Nucl Instr Methods Phys Res Section A: Acc Spectrometers, Detectors Associated Equipment (2016) 836:83–90. doi:10.1016/j.nima.2016.08.046

CrossRef Full Text | Google Scholar

6. Tain J, Algora A, Agramunt J, Guadilla V, Jordan M, Montaner-Pizá A, et al. A decay total absorption spectrometer for DESPEC at FAIR. Nucl Instr Methods Phys Res Section A: Acc Spectrometers, Detectors Associated Equipment (2015) 803:36–46. doi:10.1016/j.nima.2015.09.009

CrossRef Full Text | Google Scholar

7. Reingold CS, Olivas-Gomez O, Simon A, Arroyo J, Chamberlain M, Wurzer J, et al. High efficiency total absorption spectrometer HECTOR for capture reaction measurements. The Eur Phys J A (2019) 55:77. doi:10.1140/epja/i2019-12748-8

CrossRef Full Text | Google Scholar

8. Tain JL, Cano-Ott D. Algorithms for the analysis of -decay total absorption spectra. Nucl Instrum Methods A (2007) 571:728–38. doi:10.1016/j.nima.2006.10.098

CrossRef Full Text | Google Scholar

9. Cano-Ott D, Tain J, Gadea A, Rubio B, Batist L, Karny M, et al. Monte Carlo simulation of the response of a large NaI(Tl)total absorption spectrometer for β-decay studies. Nucl Instrum Methods A (1999) 430:333–47. doi:10.1016/s0168-9002(99)00217-x

CrossRef Full Text | Google Scholar

10. Tain JL, Cano-Ott D. The influence of the unknown de-excitation pattern in the analysis of -decay total absorption spectra. Nucl Instrum Methods A (2007) 571:719–27. doi:10.1016/j.nima.2006.09.084

CrossRef Full Text | Google Scholar

11. Greenwood RC, Struttmann DA, Watts KD. Use of a total absorption gamma-ray spectrometer to measure ground-state β−-branching intensities. Nucl Instrum Methods Phys Res A (1992 (1):175–184. doi:10.1016/0168-9002(92)90607-6

CrossRef Full Text | Google Scholar

12. Guadilla V, Tain JL, Algora A, Agramunt J, Jordan D, Monserrate M, et al. Determination of β-decay ground state feeding of nuclei of importance for reactor applications. Phys Rev C (2020) 102:064304. doi:10.1103/PhysRevC.102.064304

CrossRef Full Text | Google Scholar

13. Agostinelli S, Allison J, Amako K, Apostolakis J, Araujo H, Arce P, et al. Geant4—a simulation toolkit. Nucl Instrum Methods A (2003) 506:250. doi:10.1016/S0168-9002(03)01368-8

CrossRef Full Text | Google Scholar

14. Nichols AL, Dimitriou P, Algora A, Fallot M, Giot L, Kondev FG, et al. Improving fission-product decay data for reactor applications: part I—decay heat. Eur Phys J (2023) 59:78. doi:10.1140/epja/s10050-023-00969-x

CrossRef Full Text | Google Scholar

15. Zhang C, Qian X, Fallot M. Reactor antineutrino flux and anomaly. Prog Part Nucl Phys (2024) 136:104106. doi:10.1016/j.ppnp.2024.104106

CrossRef Full Text | Google Scholar

16. Algora A, Tain JL, Rubio B, Fallot M, Gelletly W. Beta-decay studies for applied and basic nuclear physics. The Eur Phys J A (2021) 57:85. doi:10.1140/epja/s10050-020-00316-4

CrossRef Full Text | Google Scholar

17. Dimitriou P, Nichols AL. IAEA report No. INDC(NDS)-0676. Vienna, Austria: IAEA (2015).

Google Scholar

18. Chadwick M, Herman M, Obložinský P, Dunn M, Danon Y, Kahler A, et al. ENDF/B-VII.1 Nuclear Data for Science and Technology: cross sections, covariances, fission product yields and decay data. Nucl Data Sheets (2011) 112:2887–996. doi:10.1016/j.nds.2011.11.002

CrossRef Full Text | Google Scholar

19. Haaranen M, Srivastava PC, Suhonen J. Forbidden nonunique β decays and effective values of weak coupling constants. Phys Rev C (2016) 93:034308. doi:10.1103/PhysRevC.93.034308

CrossRef Full Text | Google Scholar

20. Severijns N. Correlation and spectrum shape measurements in β-decay probing the standard model. J Phys G: Nucl Part Phys (2014) 41:114006. doi:10.1088/0954-3899/41/11/114006

CrossRef Full Text | Google Scholar

21. Hayes AC, Friar JL, Garvey GT, Jungman G, Jonkmans G. Systematic uncertainties in the analysis of the reactor neutrino anomaly. Phys Rev Lett (2014) 112:202501. doi:10.1103/PhysRevLett.112.202501

CrossRef Full Text | Google Scholar

22. Fang D-L, Brown BA. Effect of first-forbidden decays on the shape of neutrino spectra. Phys Rev C (2015) 91:025503. doi:10.1103/PhysRevC.91.025503

CrossRef Full Text | Google Scholar

23. Mougeot X. Reliability of usual assumptions in the calculation of β and ν spectra. Phys Rev C (2015) 91:055504. doi:10.1103/PhysRevC.91.055504

CrossRef Full Text | Google Scholar

24. Li Y-F, Zhang D. New realization of the conversion calculation for reactor antineutrino fluxes. Phys Rev D (2019) 100:053005. doi:10.1103/PhysRevD.100.053005

CrossRef Full Text | Google Scholar

25. Ramalho M, Suhonen J, Kostensalo J, Alcalá GA, Algora A, Fallot M, et al. Analysis of the total β-electron spectrum of ⁹²Rb: implications for the reactor flux anomalies. Phys Rev C (2022) 106:024315. doi:10.1103/PhysRevC.106.024315

CrossRef Full Text | Google Scholar

26. Hayen L, Kostensalo J, Severijns N, Suhonen J. First-forbidden transitions in reactor antineutrino spectra. Phys Rev C (2019) 99:031301. doi:10.1103/PhysRevC.99.031301

CrossRef Full Text | Google Scholar

27. Hayen L, Kostensalo J, Severijns N, Suhonen J. First-forbidden transitions in the reactor anomaly. Phys Rev C (2019) 100:054323. doi:10.1103/PhysRevC.100.054323

CrossRef Full Text | Google Scholar

28. Wang B-L, Wang L-J. First-forbidden transition of nuclear β decay by projected shell model. Phys Lett B (2024) 850:138515. doi:10.1016/j.physletb.2024.138515

CrossRef Full Text | Google Scholar

29. Ramalho M, Suhonen J. gA-sensitive β spectral shapes in the mass a=86--99 region assessed by the nuclear shell model. Phys Rev C (2024) 109:034321. doi:10.1103/PhysRevC.109.034321

CrossRef Full Text | Google Scholar

30. Guadilla V, Algora A, Estienne M, Fallot M, Gelletly W, Porta A, et al. First measurements with a new β-electron detector for spectral shape studies. J Instrumentation (2024) 19:P02027. doi:10.1088/1748-0221/19/02/P02027

CrossRef Full Text | Google Scholar

31. Shuai P, Rasco BC, Rykaczewski KP, Fijałkowska A, Karny M, Woli ńska Cichocka M, et al. Determination of β-decay feeding patterns of ⁸⁸Rb and ⁸⁸Kr using the modular total absorption spectrometer at ORNL HRIBF. Phys Rev C (2022) 105:054312. doi:10.1103/PhysRevC.105.054312

CrossRef Full Text | Google Scholar

32. Wang M, Huang W, Kondev F, Audi G, Naimi S. The AME 2020 atomic mass evaluation (II). tables, graphs and references. Chin Phys C (2021) 45:030003. doi:10.1088/1674-1137/abddaf

CrossRef Full Text | Google Scholar

33. Gove N, Martin M. Log-f tables for beta decay. At Data Nucl Data Tables (1971) 10:205–19. doi:10.1016/S0092-640X(71)80026-8

CrossRef Full Text | Google Scholar

34. Mougeot X. Betashape: a new code for improved analytical calculations of beta spectra. EPJ Web Conf (2017) 146:12015. doi:10.1051/epjconf/201714612015

CrossRef Full Text | Google Scholar

35. Gamow G, Schoenberg M. Neutrino theory of stellar collapse. Phys Rev (1941) 59:539–47. doi:10.1103/PhysRev.59.539

CrossRef Full Text | Google Scholar

36. Wang L-J, Tan L, Li Z, Misch GW, Sun Y. Urca cooling in neutron star crusts and oceans: effects of nuclear excitations. Phys Rev Lett (2021) 127:172702. doi:10.1103/PhysRevLett.127.172702

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Ong W-J, Brown EF, Browne J, Ahn S, Childers K, Crider BP, et al. Decay of ⁶¹V and its role in cooling accreted neutron star crusts. Phys Rev Lett (2020) 125:262701. doi:10.1103/PhysRevLett.125.262701

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Schatz H, Gupta S, Möller P, Beard M, Brown EF, Deibel AT, et al. Strong neutrino cooling by cycles of electron capture and β-decay in neutron star crusts. Nature (2014) 505:62–5. doi:10.1038/nature12757

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Deibel A, Meisel Z, Schatz H, Brown EF, Cumming A. Urca cooling pairs in the neutron star ocean and their effect on superbursts. The Astrophysical J (2016) 831:13. doi:10.3847/0004-637X/831/1/13

CrossRef Full Text | Google Scholar

40. Hardy JC, Towner IS. Superallowed 0⁺→0⁺ nuclear β decays: 2020 critical survey, with implications for V_ud and ckm unitarity. Phys Rev C (2020) 102:045501. doi:10.1103/PhysRevC.102.045501

CrossRef Full Text | Google Scholar

41. Naviliat-Cuncic O, Severijns N. Test of the conserved vector current hypothesis in t=1/2 mirror transitions and new determination of V_ud. Phys Rev Lett (2009) 102:142302. doi:10.1103/PhysRevLett.102.142302

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Severijns N, Hayen L, De Leebeeck V, Vanlangendonck S, Bodek K, Rozpedzik D, et al. Ft values of the mirror β transitions and the weak-magnetism-induced current in allowed nuclear β decay. Phys Rev C (2023) 107:015502. doi:10.1103/PhysRevC.107.015502

CrossRef Full Text | Google Scholar

43. Hardy JC, Towner IS. Superallowed beta decay of nuclei with A ≥ 62: the limiting effect of weak gamow-teller branches. Phys Rev Lett (2002) 88:252501. doi:10.1103/PhysRevLett.88.252501

PubMed Abstract | CrossRef Full Text | Google Scholar

44. Guadilla V. Direct measurement of superallowed β transitions with lucrecia (2023). Available at: https://cds.cern.ch/record/002872373.

Google Scholar

45. Dunlop R, Ball GC, Leslie JR, Svensson CE, Towner IS, Andreoiu C, et al. High-precision branching-ratio measurement for the superallowed β⁺ emitter ⁷⁴Rb. Phys Rev C (2013) 88:045501. doi:10.1103/PhysRevC.88.045501

CrossRef Full Text | Google Scholar

46. Morales AI, Algora A, Rubio B, Kaneko K, Nishimura S, Aguilera P, et al. Simultaneous investigation of the T = 0(J^π=0⁺) and T = 0(J^π=9⁺) decays in ⁷⁰Br. Phys Rev C (2017) 95:064327. doi:10.1103/PhysRevC.95.064327

CrossRef Full Text | Google Scholar

47. MacLean AD, Laffoley AT, Svensson CE, Ball GC, Leslie JR, Andreoiu C, et al. High-precision branching ratio measurement and spin assignment implications for ⁶²Ga superallowed β decay. Phys Rev C (2020) 102:054325. doi:10.1103/PhysRevC.102.054325

CrossRef Full Text | Google Scholar

48. Moschner K, Blazhev A, Warr N, Boutachkov P, Davies P, Wadsworth R, et al. Study of ground and excited state decays in N ≈ Z Ag nuclei. EPJ Web of Conferences (2015) 93:01024. doi:10.1051/epjconf/20159301024

CrossRef Full Text | Google Scholar

49. Garnsworthy AB, Regan PH, Pietri S, Sun Y, Xu FR, Rudolph D, et al. Isomeric states in neutron-deficient A∼80–90 nuclei populated in the fragmentation of ¹⁰⁷Ag. Phys Rev C (2009) 80:064303. doi:10.1103/PhysRevC.80.064303

CrossRef Full Text | Google Scholar

50. Jordan D, Algora A, Taín JL, Rubio B, Agramunt J, Perez-Cerdan AB, et al. Total absorption study of the β decay of ^102,104,105Tc. Phys Rev C (2013) 87:044318. doi:10.1103/PhysRevC.87.044318

CrossRef Full Text | Google Scholar

51. Zakari-Issoufou A-A, Fallot M, Porta A, Algora A, Tain JL, Valencia E, et al. Total absorption spectroscopy study of ⁹²Rb decay: a major contributor to reactor antineutrino spectrum shape. Phys Rev Lett (2015) 115:102503. doi:10.1103/PhysRevLett.115.102503

PubMed Abstract | CrossRef Full Text | Google Scholar

52. Rasco BC, Woli ńska Cichocka M, Fijałkowska A, Rykaczewski KP, Karny M, Grzywacz RK, et al. Decays of the three top contributors to the reactor ν^–_e high-energy spectrum, ⁹²Rb, ^96gsY, and ¹⁴²Cs, studied with total absorption spectroscopy. Phys Rev Lett (2016) 117:092501. doi:10.1103/PhysRevLett.117.092501

PubMed Abstract | CrossRef Full Text | Google Scholar

53. Rasco BC, Rykaczewski KP, Fijałkowska A, Karny M, Wolińska-Cichocka M, Grzywacz RK, et al. Complete β-decay pattern for the high-priority decay-heat isotopes ¹³⁷ I and ¹³⁷Xe determined using total absorption spectroscopy. Phys Rev C (2017) 95:054328. doi:10.1103/PhysRevC.95.054328

CrossRef Full Text | Google Scholar

54. Rice S, Algora A, Tain JL, Valencia E, Agramunt J, Rubio B, et al. Total absorption spectroscopy study of the β decay of ⁸⁶Br and ⁹¹Rb. Phys Rev C (2017) 96:014320. doi:10.1103/PhysRevC.96.014320

CrossRef Full Text | Google Scholar

55. Guadilla V, Algora A, Tain JL, Agramunt J, Jordan D, Montaner-Pizá A, et al. Experimental study of ¹⁰⁰Tc β decay with total absorption γ-ray spectroscopy. Phys Rev C (2017) 96:014319. doi:10.1103/PhysRevC.96.014319

CrossRef Full Text | Google Scholar

56. Guadilla V, Algora A, Tain JL, Agramunt J, Äystö J, Briz JA, et al. Total absorption γ-ray spectroscopy of niobium isomers. Phys Rev C (2019) 100:024311. doi:10.1103/PhysRevC.100.024311

CrossRef Full Text | Google Scholar

57. Guadilla V, Tain JL, Algora A, Agramunt J, Jordan D, Monserrate M, et al. Total absorption γ-ray spectroscopy of the β-delayed neutron emitters ¹³⁷I and ⁹⁵Rb. Phys Rev C (2019) 100:044305. doi:10.1103/PhysRevC.100.044305

CrossRef Full Text | Google Scholar

58. Dombos AC, Spyrou A, Naqvi F, Quinn SJ, Liddick SN, Algora A, et al. Total absorption spectroscopy of the β-decay of ^101,102Zr and ¹⁰⁹Tc. Phys Rev C (2021) 103:025810. doi:10.1103/PhysRevC.103.025810

CrossRef Full Text | Google Scholar

59. Gombas J, DeYoung PA, Spyrou A, Dombos AC, Algora A, Baumann T, et al. β-decay feeding intensity distributions for ^103,104mNb. Phys Rev C (2021) 103:035803. doi:10.1103/PhysRevC.103.035803

CrossRef Full Text | Google Scholar

60. Guadilla V, Le Meur L, Fallot M, Briz JA, Estienne M, Giot L, et al. Total absorption γ-ray spectroscopy of the β decays of ^96gs,mY. Phys Rev C (2022) 106:014306. doi:10.1103/PhysRevC.106.014306

CrossRef Full Text | Google Scholar

61. Rasco BC, Rykaczewski KP, Fijałkowska A, Karny M, Woli ńska Cichocka M, Grzywacz RK, et al. Deciphering ⁹⁸Nb β decay with the modular total absorption spectrometer at ornl. Phys Rev C (2022) 105:064301. doi:10.1103/PhysRevC.105.064301

CrossRef Full Text | Google Scholar

62. von Seeger WW, DeYoung PA, Spyrou A, Karampagia S, Brown EF, Ahn S, et al. β-decay feeding intensity distribution of ⁶⁴Mn. Phys Rev C (2024) 109:044312. doi:10.1103/PhysRevC.109.044312

CrossRef Full Text | Google Scholar

63. Janas Z, Karny M, Fujita Y, Batist L, Cano-Ott D, Collatz R, et al. Total absorption spectroscopy of ⁵⁸Cu decay. Eur. Phys. J. A - Hadrons and Nuclei (2001) 12 (2):143–145. doi:10.1007/s100500170021

CrossRef Full Text | Google Scholar

64. Nácher E, Parra S, Briz JA, Aguilera P, Agramunt J, Algora A, et al. Beta decay along the N=Z line and its relevance in rp-process and X-ray bursts. EPJ Web Conf (2023) 279:12004. doi:10.1051/epjconf/202327912004

CrossRef Full Text | Google Scholar

65. Alcalá GA, Algora A, Fallot M, Estienne M, Guadilla V, Gelletly W, et al. Beta spectrum shape studies for the predictions of the antineutrino spectrum from reactors. EPJ Web of Conferences (2023) 284:08001. doi:10.1051/epjconf/202328408001

CrossRef Full Text | Google Scholar