State-of-the-art analysis of quantum cryptography: applications and future prospects

Quantum computing provides a revolution in computational competences, leveraging the principles of quantum mechanics to process data in fundamentally novel ways. This paper explores the profound implications of quantum computing on cryptography, focusing on the vulnerabilities it introduces to classical encryption methods such as RSA and ECC, and the emergence of quantum-resistant algorithms. We review the core principles of quantum mechanics, including superposition and entanglement, which underpin quantum computing and cryptography. Additionally, we examine quantum encryption algorithms, particularly Quantum Key Distribution (QKD) protocols and post-quantum cryptographic methods, highlighting their potential to secure communications in the quantum era. This analysis emphasizes the urgent need for developing robust quantum-resistant cryptographic solutions to safeguard sensitive information against the imminent threats posed by advancing quantum technologies.

1 Introduction

By applying quantum mechanics to handle information in completely new ways, quantum computing represents a revolutionary development in computational technology. Quantum computers use quantum bits, or qubits, as opposed to conventional computers, which use bits. Qubits are capable of being in several states at once because of superposition and entanglement. This allows quantum computers to execute complex calculations at extraordinary speeds, potentially solving problems that classical computers find impossible [1]. The idea of quantum computing was introduced in the early 1980s by physicists like Richard Feynman and David Deutsch. In recent decades, considerable strides have been made in quantum hardware and algorithms, with major tech companies and research institutions heavily investing in this arena [2]. As quantum computing progresses, it is expected to significantly impact various industries, including cryptography, material science, and pharmaceuticals.

In today’s digital world, encryption is crucial for safeguarding sensitive information from unauthorized access and cyber threats. With the use of a key, encryption algorithms transform readable data into an unreadable format, guaranteeing that only those with the proper authorization can decrypt and gain access to the data [3]. This is essential for securing communication, financial transactions, personal data, and confidential government information. Rivest-Shamir-Adleman (RSA) and Elliptic Curve Cryptography (ECC) are two examples of classical encryption techniques [4, 5]. These techniques rely on the computational complexity of particular mathematical problems, such as factoring huge numbers or computing discrete logarithms. The advent of quantum computing poses a threat to conventional cryptography systems, as quantum algorithms, like Shor’s algorithm, have the ability to effectively resolve these issues, rendering conventional encryption vulnerable [6].

Quantum computing introduces new challenges for cryptography. Shor’s algorithm, created by Peter Shor in 1994, can factorize large integers and compute discrete logarithms exponentially faster than the best classical algorithms [4–6]. This capability compromises the security of widely-used public-key cryptosystems like RSA and ECC, which are foundational to many secure communication protocols. Moreover, Grover’s algorithm, another quantum algorithm, can perform unstructured search problems quadratically faster than classical algorithms. This threatens symmetric key cryptography by lowering the effective security level of encryption schemes like the Advanced Encryption Standard (AES). For example, Grover’s algorithm can reduce the security of AES-128 to an effective security of 64 bits, necessitating larger key sizes to maintain security [7]. Given the imminent threat that quantum computing poses to classical encryption methods, it is crucial to develop and understand quantum-resistant encryption algorithms. This research seeks to advance the understanding and development of secure communication methods in the quantum era, ensuring that information remains protected as quantum technologies evolve.

2 Fundamentals of quantum computing and cryptography

2.1 Basic principles of quantum mechanics

Quantum mechanics introduces several principles that are crucial for understanding and leveraging quantum computing and quantum cryptography. Here, we analyze the core principles of quantum mechanics that are foundational to these advanced technologies: superposition, entanglement, and the nature of quantum bits (qubits).

2.1.1 Superposition

One of the foundations of quantum mechanics is superposition. It asserts that, up until it is measured, a quantum system can be present in several states concurrently. In contrast, anything in a classical system can only exist in one state at a time [8]. In quantum mechanics, the state of a particle is described by a wave function, denoted as |ψ⟩. For a qubit, the wave function can be represented as a linear combination of its basis states |0⟩ and |1⟩:

$\left|\mathrm{\psi }\right.〉=\mathrm{\alpha }\left|0\right.〉+\mathrm{\beta }\left|1\right.〉$

with the requirement that,

${\left|\mathrm{\alpha }\right|}^2+{\left|\mathrm{\beta }\right|}^2=1$

Here, α and β are complex numbers that represent the probability amplitudes of the qubit being in the state |0⟩ and |1⟩, respectively. The probabilities are given by |α|² and |β|².

In a classical computer, a bit can be either 0 or 1. However, a qubit in superposition can be 0, 1, or any quantum superposition of these states [9]. This allows quantum computers to process a vast amount of information in parallel, offering exponential speedup for certain types of calculations compared to classical computers.

2.1.2 Entanglement

A phenomenon known as entanglement occurs when two or more quantum elements link up in a way that, independent of their distance from one another, the state of one particle instantly affects the state of the other. In quantum mechanics, this non-local correlation is one of the most mysterious and important concepts [10].

For a pair of qubits in an entangled state, such as the Bell state:

$\left|\mathrm{\Phi }\right.〉=\frac{1}{\surd 2}\left(\left|00\right.〉+\left|11\right.〉\right)$

This state indicates that if one qubit is measured and found to be in the state |0⟩, the other qubit will also be in the state |0⟩, and if one qubit is found to be in the state |1⟩, the other will be in the state |1⟩, with no regard to the spatial separation between them.

Entanglement is crucial for quantum key distribution (QKD) protocols like E91, where entangled particles are used to generate secure cryptographic keys. The correlation between entangled particles ensures that any eavesdropping attempt will disturb the system, revealing the presence of the eavesdropper.

2.1.3 Quantum bits (qubits)

Qubits are the basic units of information in quantum computing, analogous to bits in classical computing. However, qubits have unique properties that enable the advanced capabilities of quantum computers. Qubits can be physically realized in various ways, including:

(i) Trapped Ions: Ions confined in electromagnetic traps, where quantum states are manipulated using lasers [11].

(ii) Superconducting Circuits: Electrical circuits operating at near absolute zero temperatures, where current flows without resistance, forming qubits based on Josephson junctions [12].

(iii) Quantum Dots: Semiconductor particles that confine electrons, using their spin states as qubits [13].

(iv) Photonic Qubits: Qubits represented by the polarization states of photons, widely used in quantum communication [14].

Quantum operations, or quantum gates, manipulate the state of qubits. Sequences of quantum gates applied to qubits form quantum circuits, which are the basis for quantum algorithms. Quantum circuits can perform complex computations by exploiting superposition and entanglement.

2.1.4 Measurement in quantum mechanics

In quantum physics, measurement is very crucial because it collapses a qubit’s superposition into one of the basic states, |0⟩ or |1⟩. The outcome of a measurement is probabilistic, governed by the probability amplitudes.

Upon measurement, the wave function |ψ⟩ collapses to the measured state, and the superposition is lost. This collapse is irreversible and fundamentally different from classical measurement [15]. The basis in which the measurement is performed affects the outcome. For example, measuring a qubit in the computational basis (|0⟩, |1⟩) will yield different probabilities than measuring in the Hadamard basis (|+⟩, |-⟩).

2.1.5 No-cloning theorem

The fundamental principles of quantum mechanics underpinning quantum cryptography include superposition, entanglement, and uncertainty principle. The No-Cloning Theorem, which states that it is impossible to create an identical copy of an arbitrary unknown quantum state, is a critical implication of these principles but not a fundamental principle itself.

According to the quantum no-cloning theorem, any given unique quantum state cannot be replicated exactly. The security of quantum cryptography protocols depends on this concept. The theorem asserts that no unitary operation or quantum circuit can transform a single qubit |ψ⟩ into two qubits |ψ⟩⊗|ψ⟩ without destroying the original state. The no-cloning theorem ensures that an eavesdropper cannot perfectly copy qubits without detection, providing a fundamental layer of security in quantum key distribution [16].

By understanding these basic principles of quantum mechanics, we can appreciate how they enable the unique capabilities of quantum computing and cryptography. These principles form the foundation for developing advanced quantum algorithms and secure communication protocols, paving the way for the quantum era.

2.2 Overview of classical cryptography

Classical cryptography encrypts data by converting it into a format that is unreadable through the use of complex mathematical equations. Classical cryptography relies on computationally hard problems to provide security, which becomes a concern with the advent of quantum computing. Here, we explore the main types of classical cryptography: symmetric cryptography and asymmetric cryptography. A general classification of classical cryptography is represented in Figure 1.

Figure 1

Figure 1. An overview of classical cryptography.

2.2.1 Symmetric cryptography

The same key is used for both encryption and decryption in symmetric cryptography, commonly referred to as secret-key cryptography. This method is simple and effective in terms of computation, but it needs a safe way to distribute keys. In symmetric cryptography, the message is converted from plaintext to ciphertext by the sender using a secret key. The recipient decrypts the ciphertext back into the original plaintext using the same secret key [17]. A significant obstacle in symmetric cryptography is distributing the secret key securely. The private nature of the encrypted message is jeopardized if the key is intercepted during transmission. Various methods, such as manual key exchange and Diffie-Hellman key exchange, are used to address this issue.

2.2.1.1 Common algorithms

(i) Advanced Encryption Standard (AES): One of the most commonly used symmetric encryption techniques is AES. It handles key sizes of 128, 192, and 256 bits and runs on fixed block sizes of 128 bits. AES is known for its efficiency and robustness against attacks [18].

(ii) Data Encryption Standard (DES): DES was one of the earliest symmetric encryption standards. It operates on 64-bit blocks and uses a 56-bit key. Due to its shorter key length, DES is now considered insecure and has been largely replaced by AES and its variant, Triple DES (3DES), which applies the DES algorithm three times with different keys for enhanced security [18].

(iii) Blowfish: Blowfish is a symmetric key block cipher designed to be fast and secure. It operates on 64-bit blocks and supports variable key lengths from 32 to 448 bits. Blowfish is widely used in various applications due to its flexibility and performance [19].

2.2.2 Asymmetric cryptography

Two keys are used in asymmetric cryptography: a private key is used for decryption while a public key is used for encryption. This technique deals with the symmetric cryptography’s fundamental key distribution issue. Every user in asymmetric cryptography has a private key in addition to a public key. While the private key is kept confidential, the public key is shared with everyone. To ensure that only the intended recipient has access to a message encrypted with a public key, it can only be decoded with that recipient’s matching private key [20].

2.2.2.1 Common algorithms

(i) Rivest-Shamir-Adleman (RSA): RSA is one of the first public-key cryptosystems and remains widely used for secure data transmission. Its security is based on the difficulty of factoring large composite numbers. RSA keys are typically 2048 or 4096 bits long [4].

(ii) Elliptic Curve Cryptography (ECC): ECC uses the mathematics of elliptic curves over finite fields to provide security. It offers similar levels of security to RSA but with shorter key lengths, making it more efficient. ECC is increasingly popular for applications requiring high security with limited computational resources, such as mobile devices and IoT [5].

(iii) Diffie-Hellman Key Exchange: Without actually transferring the key, two parties can create a shared secret key across an unsecure channel using the Diffie-Hellman protocol. Symmetric encryption can subsequently be performed with this key [21].

2.2.3 Challenges

Both symmetric and asymmetric cryptography face challenges related to key distribution and management. In Symmetric Cryptography the secure distribution of secret keys remains a fundamental challenge. Methods like the Diffie-Hellman key exchange provide solutions, but they also come with their own vulnerabilities and require secure initial exchanges. While asymmetric systems solve many key distribution problems, they introduce new challenges, such as the need for a public key infrastructure (PKI) to manage and authenticate public keys. PKI systems must be robust and secure to prevent attacks.

The security of classical cryptographic algorithms relies on the computational infeasibility of certain mathematical problems. The security of symmetric algorithms depends on the key length and the complexity of the algorithm. Although longer keys are more secure, they also need more processing power. The complexity of tasks like factoring big integers or calculating discrete logarithms determines the security of asymmetric algorithms like RSA and ECC. These presumptions are threatened by developments in quantum computing.

2.3 Introduction to quantum cryptography

Using the ideas of quantum mechanics, quantum cryptography builds secure communication systems which are essentially distinct from those built using classical techniques. Quantum cryptography gets its security from the principles of physics, as opposed to classical encryption, which depends on the computational challenge of specific mathematical problems [22]. Quantum Key Distribution (QKD), the most well-known use of quantum cryptography, allows two parties to create a shared secret key with security provided by quantum mechanics. QKD is the primary application of quantum cryptography and aims to securely distribute encryption keys between two parties, commonly referred to as Alice (the sender) and Bob (the receiver). The security of QKD is based on the fundamental principles of quantum mechanics, ensuring that any eavesdropping attempt by a third party (Eve) will be detectable.

Quantum Cryptography encompasses various techniques that leverage the principles of quantum mechanics to secure communication. While Quantum Key Distribution (QKD) is the most well-known application, providing secure key exchange, Quantum Encryption extends beyond QKD, incorporating methods that utilize quantum states to encrypt data directly. This includes advanced protocols such as Quantum Homomorphic Encryption and Quantum Secure Direct Communication [23].

2.3.1 Advantages of quantum cryptography

Various advantages of the quantum cryptography are:

(i) Unconditional Security: As QKD relies on the core concepts of quantum mechanics, so its security is theoretically unbreakable. Any attempt to intercept or measure the quantum states used in QKD will introduce detectable disturbances.

(ii) Future-Proof Security: Unlike classical cryptographic methods, which can be compromised by advances in computing power (e.g., quantum computers breaking RSA or ECC), quantum cryptographic protocols are secure against future technological developments due to their reliance on physical principles.

(iii) Tamper Detection: QKD inherently provides a mechanism for detecting eavesdropping. Any unauthorized observation or measurement of the quantum channel will introduce errors in the key, which can be detected during the reconciliation phase.

2.3.2 Use of quantum superposition in quantum cryptography

Quantum superposition allows a qubit to be in a combination of states |0⟩ and |1⟩ simultaneously, which is leveraged in various quantum cryptographic protocols. For example, in the BB84 protocol, superposition states are used to encode information into the polarization of photons, ensuring secure key distribution. This principle ensures that any measurement of the qubit collapses it to one of the basis states, thereby revealing any eavesdropping attempts.

2.3.3 Challenges

While QKD holds great promise, its practical implementation poses several challenges:

(i) Photon Loss and Noise: Quantum channels, such as optical fibers, are subject to photon loss and noise, which can degrade the signal and reduce the effective communication distance. Current QKD systems typically operate over distances up to several hundred kilometers, with efforts ongoing to extend this range.

(ii) Quantum Repeaters: To overcome distance limitations, quantum repeaters are being developed. These devices can extend the range of quantum communication by entangling photons over long distances, allowing the secure transmission of keys across much larger networks.

(iii) Integration with Classical Networks: Integrating QKD with existing classical communication networks requires sophisticated hardware and protocols. Hybrid systems that combine classical and quantum cryptographic techniques are being explored to provide practical and scalable solutions.

(iv) Cost and Infrastructure: The specialized equipment required for QKD can be expensive and complex to deploy. Efforts are underway to develop more cost-effective and robust quantum communication technologies.

3 Quantum encryption algorithms

Using the ideas of quantum mechanics, quantum encryption algorithms offer secure encryption techniques that are immune against both classical as well as quantum threats. These algorithms are designed to ensure the confidentiality, integrity, and authenticity of information, even in the face of adversaries with quantum computing capabilities. This section explores the core concepts and prominent quantum encryption algorithms that exemplify the potential of quantum cryptography. Quantum encryption uses quantum states to encode information, making it inherently secure against eavesdropping and quantum computing attacks. These algorithms can be divided into two main categories:

(i) Quantum Key Distribution (QKD)-Based Encryption: These methods use QKD to securely distribute encryption keys, which are then used with classical encryption algorithms to encrypt and decrypt messages.

(ii) Fully Quantum Encryption: These methods involve direct encryption and decryption of information using quantum states and quantum operations, without relying on classical cryptographic techniques.

3.1 Quantum key distribution (QKD)-based encryption

3.1.1 BB84 protocol

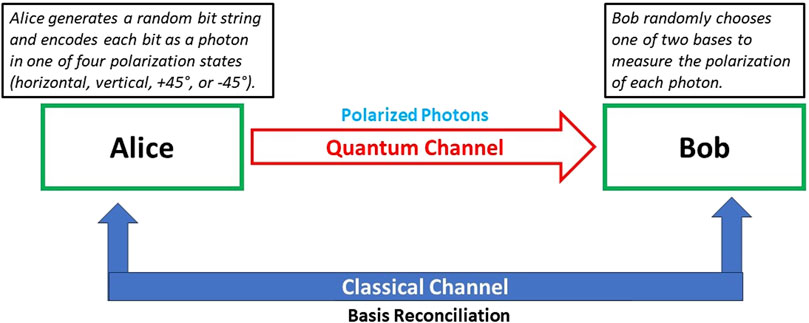
The BB84 protocol is the first and most well-known QKD protocol, designed by Charles Bennett and Gilles Brassard. It utilizes the polarization states of photons to securely exchange encryption keys between two parties. Figure 2 represents the basics of BB84 protocol in a simple block diagram form [24].

Figure 2

Figure 2. Basic principle of BB84 protocol.

The process begins with Key Generation, where Alice generates a random bit string. Each bit in this string is then encoded as a photon in one of four possible polarization states: horizontal, vertical, +45°, or −45°. This encoding ensures that the information is securely embedded in the quantum states of the photons. Next, in the Transmission step, Alice sends these polarized photons to Bob over a quantum channel. This channel is designed to preserve the quantum properties of the photons, making it possible for Bob to receive the photons in the same polarization states that Alice sent them. Upon receiving the photons, Bob engages in the Measurement step. Here, he randomly selects one of two bases, either rectilinear (horizontal/vertical) or diagonal (+45°/−45°), to measure the polarization of each incoming photon. The randomness in Bob’s choice of measurement basis is crucial for the security of the protocol, as it ensures that any potential eavesdropper cannot predict the basis in which the photons will be measured. Following the measurement, Alice and Bob move to the Basis Reconciliation stage. Over a classical channel, they publicly compare the bases they used for encoding and measuring the photons. They do not reveal the actual bit values, only the bases. They discard the bits where their basis choices do not match and retain only those bits where their bases coincide. This process results in a shared string of bits known as the raw key. The final step involves Error Correction and Privacy Amplification. During error correction, Alice and Bob compare portions of their raw keys over the classical channel to identify and correct any discrepancies. This step ensures that their keys are perfectly aligned. Afterward, they perform privacy amplification. By applying specific mathematical functions, they distill a shorter, more secure key from the raw key. The result of these processes is the final secret key, which Alice and Bob can then use for secure communication. This comprehensive protocol ensures that any attempt to eavesdrop on the quantum channel can be detected, maintaining the integrity and confidentiality of the key distribution process. The secret key generated by BB84 is used with a classical symmetric encryption algorithm, such as AES, to encrypt and decrypt messages. The security of the encrypted communication relies on the fact that any eavesdropping attempt on the quantum channel will introduce detectable disturbances.

3.1.2 E91 protocol

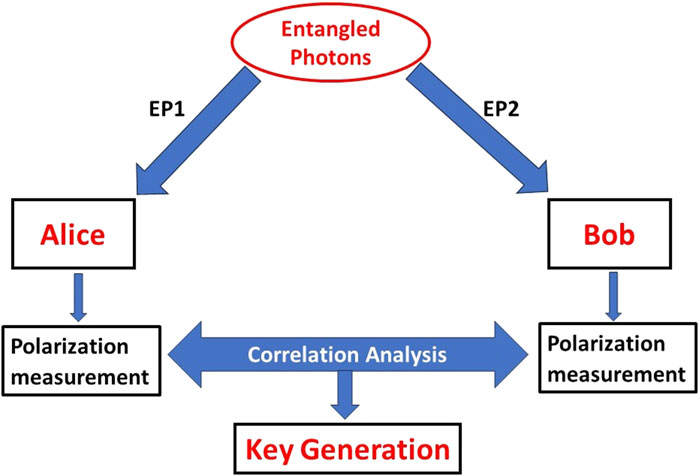
The E91 protocol, proposed by Artur Ekert, uses quantum entanglement to securely exchange encryption keys. This protocol leverages the non-local correlations of entangled particles to detect eavesdropping [25]. The basic principles of E91 protocol have been represented in a block diagram in Figure 3.

Figure 3

Figure 3. Basic principle of E91 protocol.

The protocol steps for generating a secure key using the E91 protocol, which leverages entangled photon pairs, are meticulously designed to ensure security. The process begins with Entangled Photon Pairs, where a source generates pairs of entangled photons. One photon from each pair is sent to Alice, and the other is sent to Bob. This entanglement ensures that the state of one photon is intrinsically linked to the state of the other, regardless of the distance between them. Then in the Measurement step, both Alice and Bob independently measure the polarization of their photons using randomly chosen bases. The randomness in their choice of measurement bases is crucial for maintaining the security of the protocol, as it prevents any eavesdropper from predicting the measurements. Following the measurements, the protocol proceeds to Correlation Analysis. Alice and Bob publicly compare their measurement bases and results over a classical channel, without revealing the actual bit values. They only retain the bits where their measurement bases match, resulting in a correlated string of bits known as the raw key.

The next stage is Key Generation, where the correlated measurement outcomes from the matched bases form the raw key. This raw key, however, may still contain some errors due to noise in the transmission or measurement process. To address these errors and enhance security, Alice and Bob perform Error Correction and Privacy Amplification. Error correction involves comparing portions of their raw keys to identify and correct any discrepancies, ensuring that their keys are perfectly aligned. Privacy amplification then follows, where they apply specific mathematical functions to distill a shorter, more secure key from the raw key.

Once the secure key is established, it can be used for Encryption. Similar to the BB84 protocol, the secret key generated by the E91 protocol is employed with a classical encryption algorithm to secure communication. This integration of quantum key distribution with classical encryption techniques provides a robust method for ensuring the confidentiality and integrity of the transmitted information, making any eavesdropping attempt detectable through disturbances in the quantum correlations.

3.1.3 SARG04 protocol

The SARG04 protocol was proposed by Andrew J. Shields, Robert J. Young, and Paul D. Townsend. It is an extension of the BB84 protocol, utilizing six quantum states instead of four to enhance key generation rates and security [26].

In the SARG04 protocol, the steps unfold systematically to ensure secure key distribution. First, in the state preparation phase, Alice prepares photons in one of six polarization states: horizontal (|H⟩), vertical (|V⟩), +45° (|+⟩), −45° (|-⟩), circular right (|R⟩), or circular left (|L⟩). Next, Alice transmits these prepared photons to Bob over a quantum channel. Upon receiving the photons, Bob randomly selects one of three measurement bases: rectilinear, diagonal, or circular -to measure the polarization of each photon. Following this, during basis reconciliation, Alice and Bob compare their measurement bases over a classical channel and discard the results where they used different bases. The remaining bits, where both used the same basis, form the raw key in the key distillation step. Finally, Alice and Bob perform privacy amplification by hashing and reducing the key length to distill a secure key. The SARG04 protocol enhances the efficiency and security of key distribution compared to the BB84 protocol by utilizing additional polarization states and measurement bases.

3.1.4 Twin-field QKD

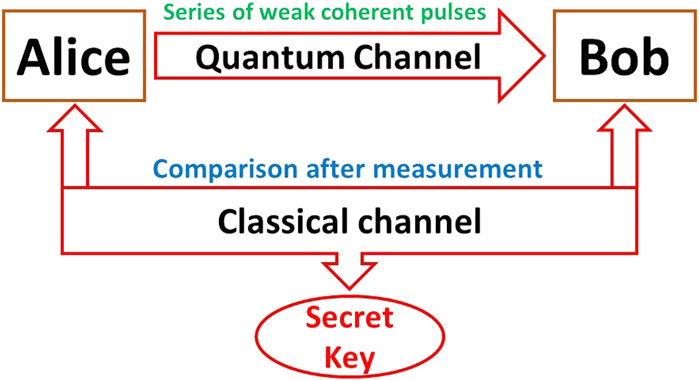
Twin-Field QKD is a protocol that utilizes two independent optical channels to distribute quantum keys, proposed by Feihu Xu et al. in 2015. Figure 4 shows the basic concept of twin field QKD.

Figure 4

Figure 4. Basic principle of twin field QKD protocol.

In the Twin-Field Quantum Key Distribution (QKD) protocol, the process begins with key preparation. Alice prepares a pair of photons, one in a weak coherent pulse (WCP) and the other in a strong coherent pulse (SCP). She then sends these photons to Bob over two separate optical channels: the WCP channel and the SCP channel. Once Bob receives the photons, he measures their polarization states in both channels. After the measurement, Alice and Bob compare their measurement bases over a classical communication channel. They discard any results where they used different bases, keeping only the measurements made with the same bases. These shared measurements form the raw key, which is then processed to create a secure key. The Twin-Field QKD protocol has notable advantages. It increases the secure key rate and is less affected by channel loss, making key distribution more efficient and reliable [27].

3.1.5 Coherent-one-way (COW) QKD

In the Coherent-One-Way (COW) QKD protocol, introduced by Yoshihisa Doi et al. in 2016, the process of secure key distribution is carried out through a series of well-defined steps. Figure 5 represents the block diagram of COW QKD.

Figure 5

Figure 5. Overview of coherent-one-way QKD.

First, in the photon preparation phase, Alice prepares a series of weak coherent pulses. These pulses form a coherent pulse train, which is essential for the subsequent steps of the protocol. Next, in the transmission phase, Alice sends this coherent pulse train to Bob over a quantum channel, ensuring that the pulses maintain their integrity during transit. Upon receiving the pulses, Bob measures their phases in the measurement phase. Finally, in the key distillation phase, Alice and Bob compare their measurement results to distill a secure key. This process involves sifting through the measurements to identify a shared secret key.

The COW QKD protocol offers several advantages. It is particularly suitable for long-distance key distribution, as the coherent pulse train can travel over extended distances with minimal degradation. Additionally, the protocol has the potential for high-speed key generation rates, making it an efficient and practical solution for secure communication in various applications [28].

3.1.6 Continuous-variable QKD (CV-QKD)

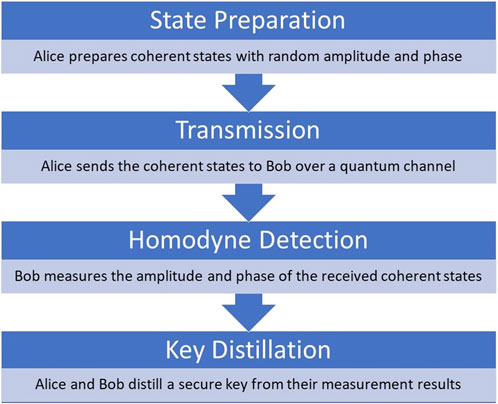
Continuous-Variable QKD is a protocol that encodes quantum information in the amplitude and phase of electromagnetic waves, rather than discrete quantum states, proposed by Nicolas J. Cerf et al. in 2002. Figure 6 shows the steps involved in Continuous-Variable QKD.

Figure 6

Figure 6. Steps of continuous-variable QKD.

The Continuous-Variable Quantum Key Distribution (CV-QKD) protocol involves a series of steps to ensure secure key distribution using coherent states. First, in the state preparation phase, Alice prepares coherent states with random amplitude and phase. This randomness is crucial for the security of the protocol. Next, during the transmission phase, Alice sends these coherent states to Bob over a quantum channel, typically an existing fiber optic network. After receiving the coherent states, Bob performs homodyne detection, where he measures the amplitude and phase of the received states. This measurement step is essential for determining the key values. Finally, in the key distillation phase, Alice and Bob use their measurement results to distill a secure key. They compare their results and perform necessary error correction and privacy amplification to ensure the key is secure.

CV-QKD offers significant advantages. It can operate over existing fiber optic networks, making it practical for integration with current communication infrastructure. Additionally, it has the potential for high-speed key distribution rates, enhancing its efficiency and applicability for secure communication [29].

3.1.7 Challenges and future directions

Despite their advantages, QKD protocols face several challenges and areas for improvement:

(i) Distance and Loss Tolerance: Improving the distance over which QKD can operate and increasing tolerance to channel loss are critical for practical deployment.

(ii) Security Proofs: Providing rigorous security proofs and ensuring resilience against emerging attacks are essential for verifying the security of QKD protocols.

(iii) Integration and Scalability: Integrating QKD protocols into existing communication infrastructures and scaling them for large-scale networks are key challenges.

(iv) Technological Advancements: Advancing quantum technologies, like quantum repeaters and quantum memories, will enhance the efficiency and practicality of QKD protocols.

3.2 Fully quantum encryption

Fully quantum encryption methods involve direct manipulation of quantum states for encryption and decryption, bypassing the need for classical cryptographic algorithms. These methods are still in the experimental and theoretical stages but offer a glimpse into the future of quantum-secure communication.

3.2.1 Quantum one-time pad

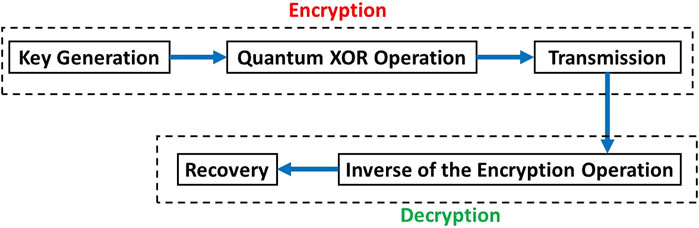
The quantum one-time pad (QOTP) is an advanced cryptographic technique that extends the principles of the classical one-time pad by employing quantum states for encryption. This method leverages the unique properties of quantum mechanics to provide theoretically unbreakable security. The encryption process begins with the generation of a secret key composed of random qubits. These qubits form the basis of the encryption and ensure the randomness and unpredictability crucial to the QOTP’s security. The plaintext message, which is encoded as a quantum state, is then subjected to a quantum XOR operation. This operation is performed using a series of controlled-NOT (CNOT) gates, where each qubit of the plaintext is XORed with a corresponding qubit from the quantum key. This creates a quantum ciphertext, a complex and highly secure form of the original message. Once the quantum ciphertext is generated, it is transmitted to the intended receiver. The transmission of quantum information is delicate and must be handled with precision to maintain the integrity of the quantum states. Upon receiving the quantum ciphertext, the receiver, who possesses an identical quantum key, begins the decryption process. This involves applying the inverse of the encryption operation, effectively reversing the quantum XOR operation. By doing so, the receiver can recover the original plaintext, as the process restores the quantum state to its initial form. The security of the QOTP is rooted in the fundamental principles of quantum mechanics. If an eavesdropper tries to intercept the quantum ciphertext, the act of measurement would alter the quantum states. Such a disturbance would be detectable, thus alerting the legitimate parties to the presence of an eavesdropper and ensuring the security of the communication.

Figure 7 gives the basic operations of Quantum one time pad. The QOTP combines the randomness and secrecy of the classical one-time pad with the added security benefits of quantum mechanics. By utilizing quantum states for encryption and decryption, it achieves a level of security that is theoretically unbreakable, making it a powerful tool for secure communication in the quantum age [30].

Figure 7

Figure 7. An overview of quantum one time pad.

3.2.2 Quantum homomorphic encryption

QHE preserves privacy by enabling computations on encrypted quantum information without ever having to decrypt it. Figure 8 shows the process of Quantum Homomorphic Encryption.

Figure 8

Figure 8. An overview of Quantum Homomorphic Encryption.

In the encryption phase, QHE begins with the generation of a quantum key composed of entangled qubits. This key forms the basis for encrypting the plaintext quantum data, utilizing quantum operations such as sequences of controlled quantum gates that interact with the key. These operations ensure that the data is securely encoded into an encrypted quantum state. The unique feature of QHE lies in its ability to perform computations directly on the encrypted data. This means that once the data is encrypted, arbitrary quantum computations can be applied to manipulate and process the encrypted quantum information. This capability is achieved through specialized quantum algorithms and protocols designed to operate within the constraints of encrypted quantum states. Decryption in QHE involves the receiver, who possesses the corresponding decryption key, applying the inverse quantum operation to the processed encrypted data. This operation effectively reverses the encryption process, allowing the original quantum data to be retrieved without compromising its privacy. The applications of QHE are diverse and significant, particularly in fields like secure cloud computing where sensitive quantum data needs to be processed while maintaining confidentiality. By enabling computations on encrypted data, QHE enhances data security and privacy [31].

3.2.2.1 Technical difficulties in quantum homomorphic encryption

Implementing Quantum Homomorphic Encryption (QHE) faces several technical challenges:

(i) Error Rates: Quantum computations are prone to errors due to decoherence and noise, which significantly affect the reliability of QHE.

(ii) Resource Requirements: QHE requires a substantial amount of quantum resources, including a large number of qubits and quantum gates, making it currently impractical with existing quantum hardware.

(iii) Complexity of Quantum Operations: The complexity of quantum operations involved in QHE increases the computational overhead, thus demanding more advanced quantum error correction methods.

3.3 Security considerations in quantum encryption

Quantum encryption algorithms provide robust security based on the laws of quantum mechanics, but several practical considerations must be addressed:

(i) Error Rates and Noise: Quantum channels are susceptible to noise and errors, which can affect the integrity of the encrypted data. Techniques like error correction and entanglement purification are used to mitigate these issues.

(ii) Key Management: Efficient management of quantum keys, including generation, distribution, and storage, is crucial for the practical deployment of quantum encryption systems.

(iii) Scalability: Scaling quantum encryption systems to support large-scale networks and high data throughput requires advancements in quantum hardware and protocols.

(iv) Interoperability: Ensuring compatibility between quantum and classical systems is essential for the seamless integration of quantum encryption into existing communication infrastructures.

3.4 Future directions and challenges

The development of quantum encryption algorithms is an ongoing area of research, with several challenges and future directions:

(i) Quantum Hardware Development: Improving quantum hardware, such as single-photon sources, detectors, and quantum repeaters, is essential for the practical implementation of quantum encryption.

(ii) Standardization: Establishing standards and protocols for quantum encryption to ensure interoperability and security across different implementations and platforms.

(iii) Quantum-Resistant Classical Algorithms: Developing classical cryptographic algorithms that are resistant to quantum attacks to complement quantum encryption methods.

(iv) Regulatory and Ethical Considerations: Addressing regulatory, ethical, and privacy concerns associated with the deployment of quantum encryption technologies.

4 Post quantum cryptography (PQC)

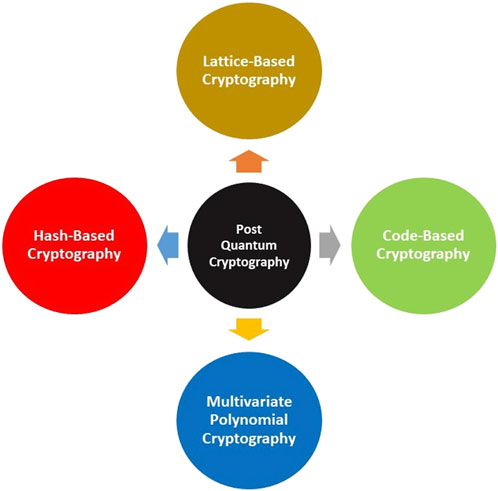
PQC describes cryptographic techniques that are built to withstand attacks from quantum computing systems [32]. Figure 9 provides an overview of post-quantum cryptographic algorithms.

Figure 9

Figure 9. Classification of post quantum cryptography.

PQC focuses on developing cryptographic algorithms resistant to threats from quantum computers, which threaten traditional schemes like RSA and ECC due to algorithms such as Shor’s algorithm that can very easily factor large numbers and solve discrete logarithm problems on quantum computers. There are several main categories of post-quantum cryptographic algorithms, each with distinct approaches to achieving quantum-resistant security.

Lattice-Based Cryptography relies on the difficulty of finding short vectors in high-dimensional lattices [33]. Key algorithms include NTRUEncrypt, NTRUSign, and variants of lattice signature schemes. These schemes leverage lattice problems that are believed to be hard to solve even with quantum algorithms, making them promising candidates for post-quantum security. Code-Based Cryptography, exemplified by the McEliece cryptosystem, operates on the complexity of decoding linear error-correcting codes. The security of these schemes is grounded in the presumed difficulty of decoding such codes, which remains challenging for quantum computers despite their potential computational power [34]. Multivariate Polynomial Cryptography, using schemes like HFE and Rainbow, relies on the complexity of solving systems of multivariate polynomial equations. These equations are designed to be hard for both classical and quantum algorithms, thus enhancing security against potential quantum attacks [35]. Hash-Based Cryptography utilizes cryptographic hash functions as the basis for schemes such as Merkle’s Tree-Based Signature Schemes (MSS) and Winternitz One-Time Signature Scheme. These schemes derive their security from the collision resistance of hash functions, which is a property not easily undermined by quantum algorithms [36].

Quantum-resistant algorithms typically require larger key sizes compared to RSA and ECC for equivalent security levels. They may also involve higher computational costs for key generation, encryption, and decryption. Memory usage varies among algorithms, impacting their suitability for different devices and applications. Ongoing cryptanalysis is essential to verify their security and to identify potential vulnerabilities. Efficient and secure implementation is crucial for the adoption of quantum-resistant algorithms in real-world applications.

5 Applications of quantum cryptography

Quantum cryptography introduces revolutionary approaches to ensuring secure communication. Various current application areas of quantum cryptography are mentioned below.

(i) Secure Communications: Quantum Key Distribution (QKD) is revolutionizing secure communications, particularly in government and military applications. QKD enables the exchange of cryptographic keys with provable security based on the principles of quantum mechanics. Governments and military organizations prioritize the use of QKD to protect classified information and secure their communication channels against eavesdropping and cyber espionage. The ability to detect any interception attempts ensures the integrity and confidentiality of sensitive data, making QKD an indispensable tool in national security.

(ii) Research and Development (R&D): Ongoing efforts focus on advancing QKD protocols to enhance their resilience against emerging threats, including quantum computing-based attacks. Research institutions and private companies collaborate to develop practical QKD systems suitable for deployment in real-world networks.

(iii) Commercial Applications: Industries such as finance, defence, and telecommunications are increasingly adopting quantum cryptography to safeguard sensitive information. Quantum secure communication networks offer robust protection against eavesdropping and data breaches, critical for securing financial transactions and confidential communications.

(iv) IoT Security: Quantum cryptography addresses vulnerabilities in IoT devices by providing secure communication channels between sensors, actuators, and central control systems. Quantum-resistant algorithms and protocols are being developed to mitigate potential threats posed by quantum computing advancements.

(v) Smart Grids: Quantum cryptography enhances the security of smart grid infrastructures by securing data transmission within energy distribution networks. Protecting against cyber threats and ensuring the integrity of metering and control signals are critical for maintaining grid stability and reliability.

(vi) Financial Transactions: Quantum cryptographic techniques secure online banking transactions, digital payments, and stock market transactions against sophisticated cyber threats. Quantum-resistant cryptographic algorithms are being researched to future-proof financial systems against quantum computing attacks.

(vii) Government and Military: Quantum-secure communication systems safeguard classified information and enable secure military operations and diplomatic communications. Quantum-resistant cryptography is critical for national security initiatives and defence against state-sponsored cyber threats.

(viii) Aerospace and Satellite Communications: Quantum cryptography ensures secure data transmission in satellite networks, protecting telemetry data, remote sensing information, and satellite-to-ground communications. Quantum-enhanced navigation and timing systems enhance the resilience and accuracy of aerospace applications.

(ix) Telecommunications: Telecommunication companies are integrating QKD into their infrastructure to enhance the security of their networks. As the volume of data transmitted over telecommunications networks continues to grow, so does the risk of cyber-attacks. By incorporating QKD, telecommunication providers can secure data transmission channels against eavesdropping and unauthorized access. This ensures the privacy and security of customer data, which is essential for maintaining the trust of users in an increasingly connected world. Additionally, QKD can be used to secure the communication between different nodes in a telecommunication network, further enhancing overall network security.

(x) Healthcare Data: The protection of healthcare data is of paramount importance due to the sensitive nature of medical records and patient information. Quantum cryptographic methods are being researched to safeguard healthcare data from cyber threats. By implementing QKD and other quantum-based encryption techniques, healthcare providers can ensure the confidentiality and integrity of patient data. This is especially critical as the healthcare industry continues to digitize medical records and embrace telemedicine, which increases the vulnerability of sensitive information to cyber-attacks.

6 Future prospects

As we look ahead, several promising avenues for future research and development emerge:

(i) Integration with Quantum Computing: The synergy between quantum cryptography and quantum computing offers unprecedented opportunities. Future studies could explore the practical implications of quantum computing in enhancing cryptographic protocols, particularly in scaling up secure key distribution and encryption processes.

(ii) Advancements in QKD Protocols: Continued research is needed to refine and optimize existing QKD protocols. Novel approaches such as measurement-device-independent QKD and post-quantum cryptography solutions need further exploration to enhance security guarantees and operational efficiency [37].

(iii) Real-World Implementation and Standardization: Moving beyond theoretical frameworks, future efforts should focus on real-world deployment of quantum cryptographic systems. This includes addressing practical challenges such as compatibility with existing infrastructure, standardization of protocols, and regulatory frameworks to facilitate widespread adoption.

(iv) Quantum Network Development: The establishment of quantum networks capable of transmitting quantum information over long distances is a critical area for future development. This involves not only technological advancements but also addressing fundamental challenges in quantum repeater technology and quantum memory [38].

(v) Security and Post-Quantum Era: Future research should focus on exploring alternative cryptographic primitives and transitioning towards quantum-resistant standards [39].

6.1 Emerging directions in quantum cryptography

Recent advancements in quantum cryptography include the development of quantum and semi-quantum private comparison protocols [40]. These protocols enable secure comparison of private data without revealing the actual data, which is crucial for applications like secure voting and confidential data comparison. For business negotiations or competitive analysis, these protocols allow organizations to compare sensitive information without exposing their confidential details, protecting their competitive advantages. Leveraging principles such as superposition and entanglement, quantum private comparison protocols perform secure computations and ensure that any attempt to eavesdrop would disturb the quantum states and be detectable. While offering enhanced security and privacy preservation, these protocols face challenges such as the need for reliable quantum hardware and efficient algorithms. Future research aims to address these challenges to make quantum private comparison practical and scalable [41].

6.2 Ethical and legal issues in quantum cryptography

6.2.1 Privacy

The unbreakable nature of quantum cryptography ensures unmatched data security, but it could also be misused for complete anonymity, complicating law enforcement efforts. Balancing privacy for legitimate users with the need for lawful access to investigate illegal activities is crucial.

6.2.2 Regulation

The deployment of quantum cryptographic systems requires new regulatory frameworks to ensure responsible use and public safety. Governments and regulatory bodies need to establish guidelines for the certification, management, and use of quantum cryptographic technologies to address potential misuse.

6.2.3 Access and equity

Ensuring equitable access to quantum cryptographic technologies is essential to prevent a technological divide. Policies and initiatives should promote broader accessibility, supporting smaller entities and developing countries to enhance global cybersecurity resilience.

6.2.4 Ethical considerations

Quantum cryptography must balance confidentiality with the need for transparency and accountability. Ethical principles should guide the development and deployment of these technologies, prioritizing societal wellbeing and promoting trust and security.

7 Conclusion

Quantum cryptography, underpinned by the fundamental principles of quantum mechanics, represents a paradigm shift in securing communication networks against both classical and quantum threats. This paper has explored the vulnerabilities that quantum computing introduces to classical cryptographic methods such as RSA and ECC, highlighting the urgency of developing quantum-resistant solutions. We have reviewed the essential concepts of quantum mechanics, including superposition and entanglement, and how they are leveraged in quantum cryptography. The analysis has shown that quantum key distribution (QKD) protocols, offer unparalleled security by utilizing the inherent properties of quantum mechanics. These protocols ensure that any attempt at eavesdropping introduces detectable disturbances, thus maintaining the integrity and confidentiality of the communication. Furthermore, post-quantum cryptographic algorithms are being developed to secure data against the capabilities of future quantum computers. However, the practical implementation of quantum cryptography faces challenges such as photon loss, noise in quantum channels, and the need for quantum repeaters to extend communication distances. Integrating quantum cryptographic systems with existing classical networks also presents significant technical and infrastructural hurdles. Despite these challenges, ongoing advancements in quantum technology and cryptographic research are paving the way for more robust and scalable solutions. The transition to quantum cryptography is not only a defensive measure against the looming threat of quantum computing but also a proactive step towards future-proofing our cryptographic systems. As research and development continue to progress, it is imperative for governments, industries, and academia to collaborate and invest in quantum technologies to safeguard sensitive information in the coming quantum era. The future of secure communication lies in harnessing the unique capabilities of quantum mechanics to build resilient and impenetrable cryptographic frameworks.

Author contributions

SS: Conceptualization, Methodology, Writing–original draft, Writing–review and editing. KM: Conceptualization, Methodology, Writing–original draft, Writing–review and editing.

Funding

The authors declare that no financial support was received for the research, authorship, and/or publication of this article.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Rieffel E, Polak W. An introduction to quantum computing for non-physicists. ACM Comput Surv (Csur) (2000) 32(3):300–35. doi:10.1145/367701.367709

CrossRef Full Text | Google Scholar

2. Ladd TD, Jelezko F, Laflamme R, Nakamura Y, Monroe C, O’Brien JL. Quantum computers. nature (2010) 464(7285):45–53. doi:10.1038/nature08812

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Hiroka T, Morimae T, Nishimaki R, Yamakawa T. Quantum encryption with certified deletion, revisited: public key, attribute-based, and classical communication. In: InAdvances in cryptology–ASIACRYPT 2021: 27th international conference on the theory and application of cryptology and information security, Singapore, december 6–10, 2021, proceedings, Part I 27 2021. Springer International Publishing. p. 606–36.

Google Scholar

4. Rachmawati D, Budiman MA. On using the first variant of dependent rsa encryption scheme to secure text: a tutorial. InJournal Phys Conf Ser (2020) 1542(1):012024. doi:10.1088/1742-6596/1542/1/012024

CrossRef Full Text | Google Scholar

5. Khan MA, Quasim MT, Alghamdi NS, Khan MY. A secure framework for authentication and encryption using improved ECC for IoT-based medical sensor data. IEEE Access (2020) 8:52018–27. doi:10.1109/access.2020.2980739

CrossRef Full Text | Google Scholar

6. Wong HY. Shor’s algorithm. In: InIntroduction to quantum computing: from a layperson to a programmer in 30 steps, 21. Cham: Springer International Publishing (2023). p. 289–98. doi:10.1007/978-3-031-36985-8_29

CrossRef Full Text | Google Scholar

7. Preston RH. Applying Grover's algorithm to hash functions: a software perspective. IEEE Trans Quan Eng (2022) 3:1–10. doi:10.1109/tqe.2022.3233526

CrossRef Full Text | Google Scholar

8. Zhou R, Marshman RJ, Bose S, Mazumdar A. Catapulting towards massive and large spatial quantum superposition. Phys Rev Res (2022) 4(4):043157. doi:10.1103/physrevresearch.4.043157

CrossRef Full Text | Google Scholar

9. Burkard G, Ladd TD, Pan A, Nichol JM, Petta JR. Semiconductor spin qubits. Rev Mod Phys (2023) 95(2):025003. doi:10.1103/revmodphys.95.025003

CrossRef Full Text | Google Scholar

10. Erhard M, Krenn M, Zeilinger A. Advances in high-dimensional quantum entanglement. Nat Rev Phys (2020) 2(7):365–81. doi:10.1038/s42254-020-0193-5

CrossRef Full Text | Google Scholar

11. Krutyanskiy V, Galli M, Krcmarsky V, Baier S, Fioretto DA, Pu Y, et al. Entanglement of trapped-ion qubits separated by 230 meters. Phys Rev Lett (2023) 130(5):050803. doi:10.1103/physrevlett.130.050803

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Vepsäläinen AP, Karamlou AH, Orrell JL, Dogra AS, Loer B, Vasconcelos F, et al. Impact of ionizing radiation on superconducting qubit coherence. Nature (2020) 584(7822):551–6. doi:10.1038/s41586-020-2619-8

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Saraiva A, Lim WH, Yang CH, Escott CC, Laucht A, Dzurak AS. Materials for silicon quantum dots and their impact on electron spin qubits. Adv Funct Mater (2022) 32(3):2105488. doi:10.1002/adfm.202105488

CrossRef Full Text | Google Scholar

14. Niemietz D, Farrera P, Langenfeld S, Rempe G. Nondestructive detection of photonic qubits. Nature (2021) 591(7851):570–4. doi:10.1038/s41586-021-03290-z

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Mercier de Lépinay L, Ockeloen-Korppi CF, Woolley MJ, Sillanpää MA. Quantum mechanics–free subsystem with mechanical oscillators. Science (2021) 372(6542):625–9. doi:10.1126/science.abf5389

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Chen YC, Gong M, Xue P, Yuan HD, Zhang CJ. Quantum deleting and cloning in a pseudo-unitary system. Front Phys (2021) 16:53601–7. doi:10.1007/s11467-021-1063-z

CrossRef Full Text | Google Scholar

17. Bellizia D, Bronchain O, Cassiers G, Grosso V, Guo C, Momin C, et al. Mode-level vs. implementation-level physical security in symmetric cryptography: a practical guide through the leakage-resistance jungle. In: Advances in cryptology–CRYPTO 2020: 40th annual international cryptology conference, CRYPTO 2020, santa barbara, CA, USA, august 17–21, 2020, proceedings, Part I 40. Springer International Publishing (2020). p. 369–400.

CrossRef Full Text | Google Scholar

18. Hamza A, Kumar B. A review paper on DES, AES, RSA encryption standards. In: 2020 9th international conference system modeling and advancement in research trends (SMART). IEEE (2020). p. 333–8.

CrossRef Full Text | Google Scholar

19. Alotaibi M. Improved blowfish algorithm-based secure routing technique in IoT-based WSN. IEEE Access (2021) 9:159187–97. doi:10.1109/access.2021.3130005

CrossRef Full Text | Google Scholar

20. Merkepci M, Abobala M. On some novel results about split-complex numbers, the diagonalization problem, and applications to public key asymmetric cryptography. J Maths (2023) 2023(1):1–12. doi:10.1155/2023/4481016

CrossRef Full Text | Google Scholar

21. Sahu SK, Mazumdar K. Exploring security threats and solutions Techniques for Internet of Things (IoT): from vulnerabilities to vigilance. Front Artif Intelligence (2024) 7:1397480. doi:10.3389/frai.2024.1397480

CrossRef Full Text | Google Scholar

22. Portmann C, Renner R. Security in quantum cryptography. Rev Mod Phys (2022) 94(2):025008. doi:10.1103/revmodphys.94.025008

CrossRef Full Text | Google Scholar

23. Zhou NR, Hua TX, Gong LH, Pei DJ, Liao QH. Quantum image encryption based on generalized Arnold transform and double random-phase encoding. Quan Inf Process (2015) 14:1193–213. doi:10.1007/s11128-015-0926-z

CrossRef Full Text | Google Scholar

24. Lee C, Sohn I, Lee W. Eavesdropping detection in BB84 quantum key distribution protocols. IEEE Trans Netw Serv Manage (2022) 19(3):2689–701. doi:10.1109/tnsm.2022.3165202

CrossRef Full Text | Google Scholar

25. Escánez-Expósito D, Caballero-Gil P, Martín-Fernández F. Study and implementation of an interactive simulation of quantum key distribution using the E91 cryptographic protocol. In: InInternational conference on ubiquitous computing and ambient intelligence, 21. Cham: Springer International Publishing (2022). p. 965–70. doi:10.1007/978-3-031-21333-5_96

CrossRef Full Text | Google Scholar

26. Sekga C, Mafu M. Security of quantum-key-distribution protocol by using the post-selection technique. Phys Open (2021) 7:100075. doi:10.1016/j.physo.2021.100075

CrossRef Full Text | Google Scholar

27. Liu Y, Zhang WJ, Jiang C, Chen JP, Zhang C, Pan WX, et al. Experimental twin-field quantum key distribution over 1000 km fiber distance. Phys Rev Lett (2023) 130(21):210801. doi:10.1103/physrevlett.130.210801

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Lavie E, Lim CC. Improved coherent one-way quantum key distribution for high-loss channels. Phys Rev Appl (2022) 18(6):064053. doi:10.1103/physrevapplied.18.064053

CrossRef Full Text | Google Scholar

29. Zhang Y, Bian Y, Li Z, Yu S, Guo H. Continuous-variable quantum key distribution system: past, present, and future. Appl Phys Rev (2024) 11(1). doi:10.1063/5.0179566

CrossRef Full Text | Google Scholar

30. Sharma K, Wakakuwa E, Wilde MM. Conditional quantum one-time pad. Phys Rev Lett (2020) 124(5):050503. doi:10.1103/physrevlett.124.050503

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Zeuner J, Pitsios I, Tan SH, Sharma AN, Fitzsimons JF, Osellame R, et al. Experimental quantum homomorphic encryption. npj Quan Inf (2021) 7(1):25. doi:10.1038/s41534-020-00340-8

CrossRef Full Text | Google Scholar

32. Kumar M, Pattnaik P. Post quantum cryptography (pqc)-an overview. In: In2020 IEEE high performance extreme computing conference (HPEC). IEEE (2020). p. 1–9.

Google Scholar

33. Zheng Z. Lattice-based cryptography. In: InModern cryptography volume 1: a classical introduction to informational and mathematical principle 2022 apr 17. Singapore: Springer Singapore. p. 253–351.

Google Scholar

34. Balamurugan C, Singh K, Ganesan G, Rajarajan M. Post-quantum and code-based cryptography—some prospective research directions. Cryptography (2021) 5(4):38. doi:10.3390/cryptography5040038

CrossRef Full Text | Google Scholar

35. Dey J, Dutta R. Progress in multivariate cryptography: systematic review, challenges, and research directions. ACM Comput Surv (2023) 55(12):1–34. doi:10.1145/3571071

CrossRef Full Text | Google Scholar

36. Sahraneshin T, Malekhosseini R, Rad F, Yaghoubyan SH. Securing communications between things against wormhole attacks using TOPSIS decision-making and hash-based cryptography techniques in the IoT ecosystem. Wireless Networks (2023) 29(2):969–83. doi:10.1007/s11276-022-03169-5

CrossRef Full Text | Google Scholar

37. Stanley M, Gui Y, Unnikrishnan D, Hall SR, Fatadin I. Recent progress in quantum key distribution network deployments and standards. In J Phys Conf Ser 2022 (Vol. 2416, No. 1, p. 012001). doi:10.1088/1742-6596/2416/1/012001

CrossRef Full Text | Google Scholar

38. Kozlowski W, Dahlberg A, Wehner S. Designing a quantum network protocol. In: Proceedings of the 16th international conference on emerging networking experiments and technologies (2020). p. 1–16.

CrossRef Full Text | Google Scholar

39. Malina L, Dzurenda P, Ricci S, Hajny J, Srivastava G, Matulevičius R, et al. Post-quantum era privacy protection for intelligent infrastructures. IEEE Access (2021) 9:36038–77. doi:10.1109/access.2021.3062201

CrossRef Full Text | Google Scholar

40. Gong LH, Li ML, Cao H, Wang B. Novel semi-quantum private comparison protocol with Bell states. Laser Phys Lett (2024) 21(5):055209. doi:10.1088/1612-202x/ad3a54

CrossRef Full Text | Google Scholar

41. Gong LH, Ye ZJ, Liu C, Zhou S. One-way semi-quantum private comparison protocol without pre-shared keys based on unitary operations. Laser Phys Lett (2024) 21(3):035207. doi:10.1088/1612-202x/ad21ec

CrossRef Full Text | Google Scholar