- Mathematics Department, Jamoum University College, Umm Al-Qura University, Jamoum, Saudi Arabia
This work introduces a novel mathematical framework for examining the thermal conduction characteristics of a viscothermoelastic, isotropic micro-circular ring. The foundation of the model is Kirchhoff’s theory of love plates. The governing equations have been developed by using Lord and Shulman’s generalized thermoelastic model. For a viscothermoelasticity material, Young’s modulus incorporates an additional fractional derivative consideration such as the classical Caputo and Caputo-Fabrizio types, alongside the normal derivative. The outer bounding plane is thermally loaded by ramp-type heating. Laplace transform has been applied and its inverse has been obtained numerically. Graphical comparisons between the definitions of the ordinary derivative and the fractional derivatives were incorporated into the study. The objective was to study the impacts of the fractional derivative order on the vibration distribution of a ceramic micro-circular ring and obtain novel results. It is ascertained that the fractional derivative order and resonator thickness have no discernible effect on the distribution of thermal waves; nevertheless, the ramp heat parameter is identified as having a significant impact. The order of the fractional derivatives and the resonator’s thickness, have a significant impact on the mechanical wave. It has been demonstrated that the ramp heat parameter effectively regulates the energy damping in ceramic resonators.
Introduction
Micro-circular rings and plates have substantial uses in MEMS (Micro-Electro-Mechanical Systems). They may be used in sensors for accurate measurement, such as the detection of pressure or acceleration. Actuators facilitate the attainment of regulated motions. Their small size and distinctive mechanical characteristics render them optimal for tiny devices, augmenting the performance and utility of MEMS across diverse domains like as electronics and biomedicine [1, 2]. Many researchers introduced many applications of micro-circular rings and plates due to their importance in the construction of various electromechanical micro-resonators. Hao conducted a study on the reduction of vibrations in micro/nanoelectromechanical systems by investigating thermoelastic attenuation using circular thin-plate resonators [3]. A study on thermoelastic damping of circular-plate resonators, with a special emphasis on the axisymmetric out-of-plane vibration has been conducted by Sun and Tohmyoh [4]. The influence of thermoelastic damping on the vertical oscillation of circular plate resonators has been investigated by Sun and Saka [5]. The damping of vibrations that occur out-of-plane for a circular thin plate with generalized viscothermoelastic properties has been computed by Grover [6]. The dual-phase-lag (DPL) model has been employed by Guo et al. to develop the thermoelastic damping theory for micro and nanomechanical resonators [7, 8]. When studying the behaviour of materials that change over time, it is crucial to consider the properties of viscoelastic materials or mechanical relaxation. Biot has analyzed the ideas of viscothermoelasticity and the principles of vibration in the field of thermodynamics [9, 10]. Drozdov constructed a mathematical model to describe the behaviour of polymers when subjected to the combined influences of viscosity, temperature variations, and deformation under high stresses [11]. Ezzat and El-Karmany employed an innovative thermo-viscoelastic model to investigate how volumetric characteristics impact the thermoelastic behaviour of viscoelastic materials [12]. Carcione et al. employed computer methodology to study the transmission of waves in a solid substance, utilizing the mechanical model of Kelvin-Voigt [13]. Grover conducted research on transverse vibrations in small-scale viscothermoelastic beam resonators [6, 14]. The mathematical equations that depict the lateral vibrations of a slender beam composed of homogeneous thermoelastic material, which has minuscule voids at a microscopic level have been analyzed by Sharma and Grover [15]. The inclusion of memory in fractional systems offers a legitimate justification for this generalization, as the formation of romantic relationships is fundamentally affected by memory [16, 17]. The fractional derivative is a powerful technique for understanding the origins and lineage of different materials and processes. Research has demonstrated that using fractional derivatives in real-world modelling is more appropriate than using typical integer derivatives [18–20]. A multitude of scholars have dedicated their efforts to the advancement of a groundbreaking concept, beginning with the works of Riemann–Louville and Caputo, in the field of fractional derivatives [21–23]. Youssef developed a theory of thermoelasticity that integrates the notion of fractional heat conductivity and expands upon preexisting thermoelasticity theories [24, 25]. Sherief et al. introduced a different theory of thermoelasticity by employing the methodology of fractional calculus [26].
The fractional calculus models demonstrate more consistency in comparison to classic models due to their precise prediction of delayed effects. Researchers have shown that new fractional derivatives might potentially solve the issue of exceptional or non-singular kernels by providing an exponential solution to the problem of a single kernel in fractional derivatives concepts. There exist three distinct categories of fractional derivatives, namely Liouville-Caputo, Riemann-Liouville, and Caputo-Fabrizio [27, 28]. Consequently, several innovative thermoelastic models were introduced, all of which depended on the fundamental notion of fractional calculus. Magin and Royston developed a model that utilized the fractional deformation derivative to describe the behaviour of the material [29]. A Hookean solid is a substance that demonstrates zero-order derivative behaviour, while a Newtonian fluid is a substance that demonstrates first-order derivative behaviour. The heat exchanges at an intermediate level and the splitting process for viscothermoelastic material are described in the spectrum [29]. A new theory of generalized thermoelasticity, which relied on the strain resulting from factional order derivative has been proposed by Youssef. The stress-strain relation has been considered based on a new and distinct addition to the Duhamel-Neumann framework by Youssef [30]. Youssef has effectively solved the issue of thermoelasticity in a one-dimensional system by addressing the fractional order strain. More precisely, he has examined an application where half of the space is involved, based on the frameworks proposed by Biot, Green-Lindsay, Lord-Shulman, and Green-Naghdi type-II [30]. Awad et al. investigated the occurrence condition for the thermal resonance phenomenon during the electron-phonon interaction process in metals based on the hyperbolic two-temperature model [31]. Awad presented the mathematical description of a two-dimensional unsteady magneto-hydrodynamics slow flow with thermoelectric properties (TEMHD) on an infinite vertical partially hot porous plate [32].
This paper introduces a novel mathematical framework for analyzing the heat conduction of a viscothermoelastic, isotropic micro-circular ring. The notion is based on Kirchhoff’s plate hypothesis. The governing equations were constructed based on Lord and Shulman’s extended thermoelastic model. This model incorporates Young’s modulus, which encompasses the normal derivative as well as the fractional derivative definitions of classical Caputo and Caputo-Fabrizio. The study report utilizes a micro-circular ring to illustrate the concept of scaled viscothermoelasticity. The micro-circular ring’s outer bounding plane was subjected to heating using a ramp-type method. Numerical methods were employed to compute the inverse of the Laplace transform. The investigation involved doing visual comparisons between normal and fractional derivative definitions. The objective was to investigate the effects of the fractional order of the derivatives on the vibration of ceramic micro-circular rings and obtain new results.
Generalized viscothermoelastic based on Lord and Shulman model
We assume an isotropic, viscothermoelastic, and homogeneous, micro-circular ring based on the plate theory of Kirchhoff’s Love. The origin is at the centre of the plate with a uniform thickness
At the beginning, the plate is in a state of no tension, no strain, and is at a consistent room temperature
Hence, the components of the displacement have the following form [6]:
where
The temperature increment based on the reference temperature
According to Hook’s solid state, the stress components are [4, 29–33]:
The strain components take the following formulations:
The equation of motion is [33]:
where
In the Equations 3–13,
In the context of Lord-Shulman theory based on the viscothermoelastic definition, the generalized heat conduction equation is given by [7, 33]:
where
By inserting Equations 10–12 into the Equation 9, we obtain the equation of motion as follows:
For the viscothermoelastic material based on the fractional order derivative, Young’s modulus has the following form [34, 35]:
where
Therefore, the equation of motion Equation 15 takes the following form:
The formula of the heat conduction Equation 14 will be in the following form:
The formulations of the stress components Equations 4–6 will be in the following forms:
and
Now, for the axisymmetric circular micro-ring, the displacement components Equation 2 are as follows [6]:
Hence, from Equations 20–22, the components of the strain Equations 7, 8 are as follows:
and from Equations 23, we obtain:
where
Because no heat flux exists across the two sides of the circular beam
For the very thin circular micro-beam
Thus, by inserting Equation 26 into the equation of motion Equation 18 it will be changed to the following form:
After executing the integration in the second term of Equation 27, we obtain:
By using the Equations 14, 24, 26, the heat conduction Equation 19 could be written in the form:
where
The following dimensionless variables will be used to simplify the governing Equations 28, 29 as following [44, 45]:
Hence, we obtain:
and
where
For simplicity, all the primes have been removed.
The Laplace transform will be used, which is given as:
For the fractional derivative, the Laplace transforms Equation 34 which is defined in Equation 17 and given by [27, 36–38]:
The initial conditions have been considered as follows:
After applying the Laplace transform and the initial conditions Equation 36, the three types of derivatives in Equation 35 will be in the following form:
To use the formula in Equation 37, we must add a first-order derivative concerning time for the Equation 30 to be in the following form:
and re-write the Equations 31–33 in the following form:
and
After applying Laplace transform, we obtain:
where
Equations 38, 39 give:
and
where
Equations 44, 45 after elimination, give the following equation:
The solutions of the Equation 46 where
and
where
We consider the micro-circular ring to be simply supported, moreover, it is thermally loaded on the outer surface
and
By applying the Laplace transform defined above on the boundary conditions Equations 50, 51, we obtain:
and
where
By applying the given boundary conditions Equations 52, 53 in the Equations 47, 48, we obtain the following system of linear equations:
By solving Equation 49 and the above system of linear equations in Equations 54–59 by using MAPLE-21 software, we obtain the parameters (see the Appendix 1).
Regarding the function of the thermal loading, we consider the micro-circular ring to be subjected to a ramp-type heat with ramp-time heat parameter
In the Laplace transform domain, the thermal loading function in Equation 60 will take the form:
From Equations 40–42, it is available to obtain the average stress distribution as follows:
where ω is defined in Equation 43. After inserting the Equation 61 in the solutions, we obtain the complete solutions in the Laplace transform domain.
Numerical results and discussion
In the following numerical calculations and to obtain the numerical results, a micro-circular ring made of ceramic (Si3N4) has been considered. Thus, the mechanical and thermal material properties will take the following values [6, 33]:
The Laplace transform inversions could be calculated for the Equations 47, 48, 62 by using the following Riemann-sum approximation method of Tzou [46]:
“Re” denotes the real part, while “
To get convergence with faster steps, the value “
The mathematical software MAPLE 21 is suitable to compute the inversions of the Laplace transform by applying the formula in the iteration Equation 63.
For the non-dimensional values of the parameters
Figure 2 is the first group and contains four Figures 2A–D, the results have been figured for four following cases:
(a) The non-viscous case (N-V) in black lines when
(b) The normal-derivative (N-D) and viscothermelastic case in blue lines when
(c) The Classical-Caputo (C-C) of fractional viscothermelastic case in red lines when
(d) The Caputo-Fabrizio (C-F) of fractional viscothermelasticity case in green lines when
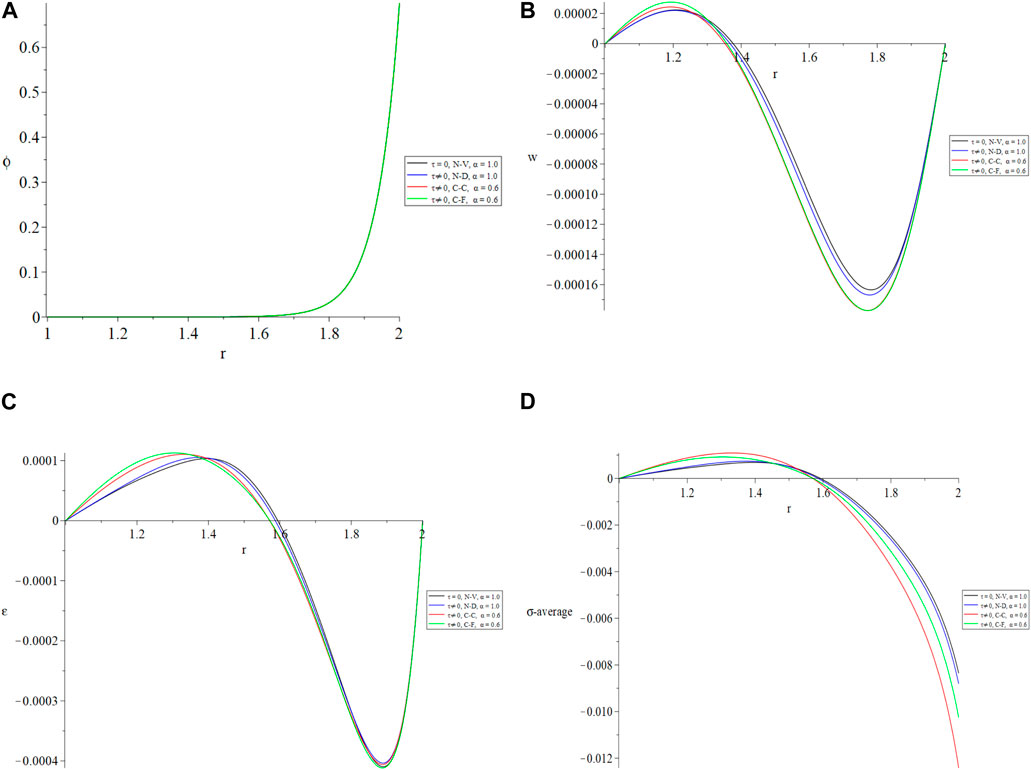
Figure 2. The studied function distributions are based on different types of derivatives. (A) The temperature increment. (B) The lateral deflection (vibration). (C) The deformation. (D) The average stress.
Figure 2A shows that the fractional derivatives do not impact the temperature increment distribution and all the studied cases give the same value even the non-visco case.
The lateral deflection of the resonator is shown in Figure 2B. The fractional order parameter plays a significant role in the vibration of the resonator, and the absolute values of the peak points of the lateral deflection distributions have been arranged in the following order in Equation 64:
The resonator vibration reaches its maximum amplitude in the classical Caputo definition before it reaches its maximum amplitude in the non-viscous definition. Furthermore, the magnitudes of the vibration in the setting of the two definitions, classical-Caputo and Caputo-Fabrizo, exhibit a higher degree of similarity compared to the other two scenarios.
Figure 2C illustrates the deformation of the resonator, where the fractional order parameter significantly influences its vibration. The deformation’s maximum points are ordered based on the absolute values as in Equation 65:
Accordingly, the non-viscus definition yields the least deformation value while the classical-Caputo definition yields the largest. The deformation values are also more closely packed in the setting of the two classical Caputo and Caputo-Fabrizo formulations compared to the other two instances.
As seen in Figure 2D, the average value of the stress components is significantly affected by the fractional order parameter. In addition, the average stress’s absolute values follow this sequence as in Equation 66:
Figure 3 is the third group and contains four Figures 2A–D in which the impacts of the ramp-time heat parameter have been studied in the context of the four studied cases of the derivatives as in the first group of figures but for two different values of the ramp-time heat parameter
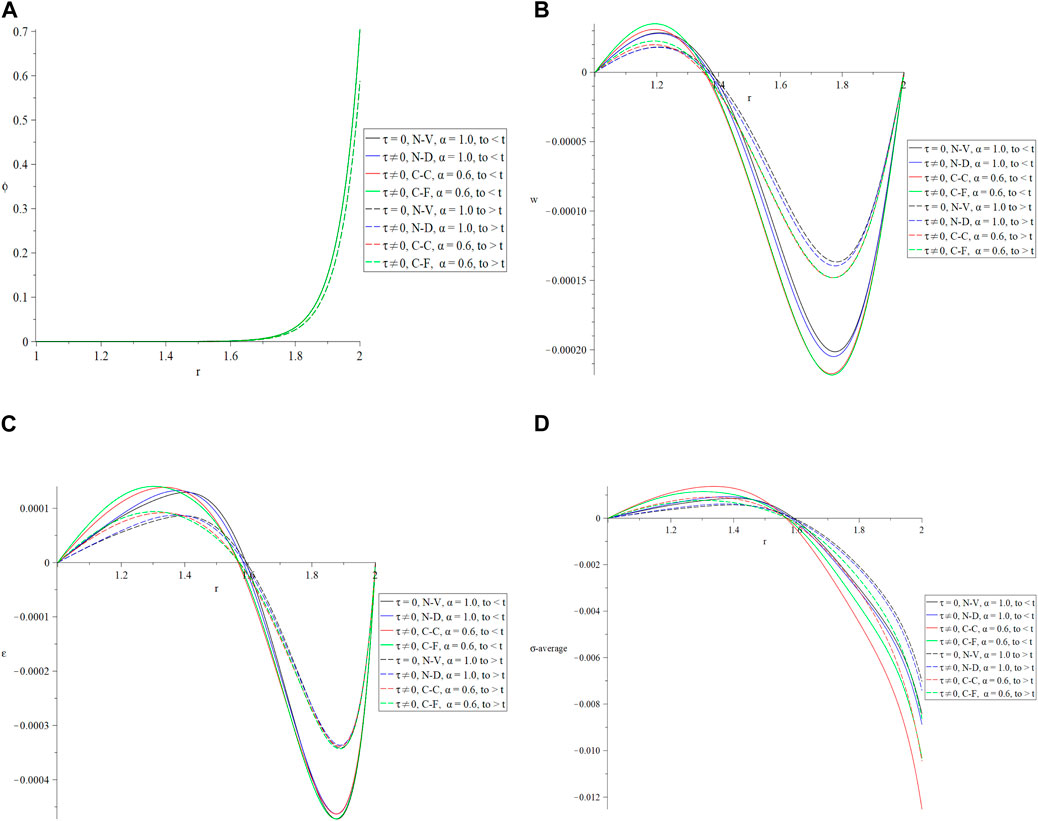
Figure 3. The studied function distributions are based on different types of fractional derivatives with different values of ramp-time heat parameter. (A) The temperature increment. (B) The lateral deflection (vibration). (C) The deformation. (D) The average stress.
The ramp-time heat parameter has a pronounced effect on the temperature rise, vibration, absolute deformation value, and absolute average stress distributions shown in the figures. The values of all these distributions, including the outer border of the micro-circular ring resonator, drop as the ramp-time heat parameter’s value increases.
Figure 4 is the fourth group which contains Figures 4A–D, in which the results have been figured for the studied functions in the context of the Caputo-Fabrizo fractional derivatives for four values of fractional order parameter
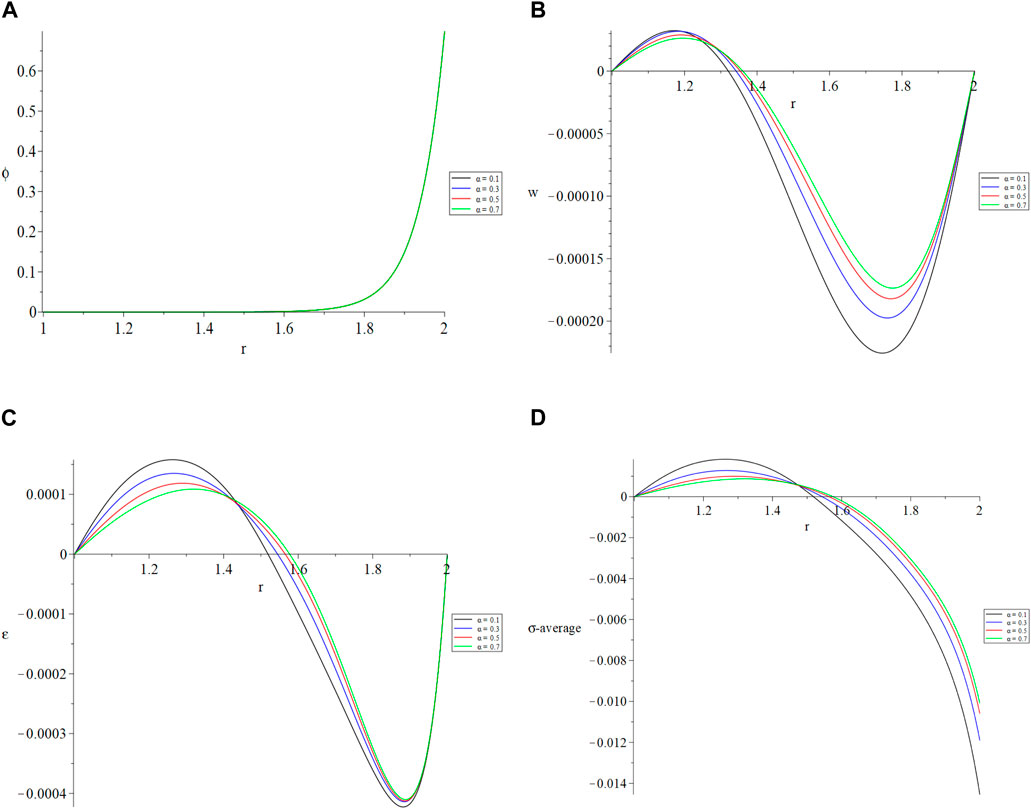
Figure 4. The studied function distributions based on Caputo-Fabrizo (C-F) of fractional derivatives with different order. (A) The temperature increment. (B) The lateral deflection (vibration). (C) The deformation. (D) The average stress.
Figure 4A shows that the fractional order parameter does not affect the distribution of temperature increments. Nevertheless, it has a major impact on the vibration, deformation, and stress distributions, as seen in Figures 4B–D. Specifically, as the fractional order parameter rises, the magnitude of deformation, vibration, and average stress decreases.
Figure 5 is the fifth group which contains Figures 5A–D, in which the results have been figured for the studied functions in the context of the classical-Caputo fractional derivatives for four values of fractional order parameter
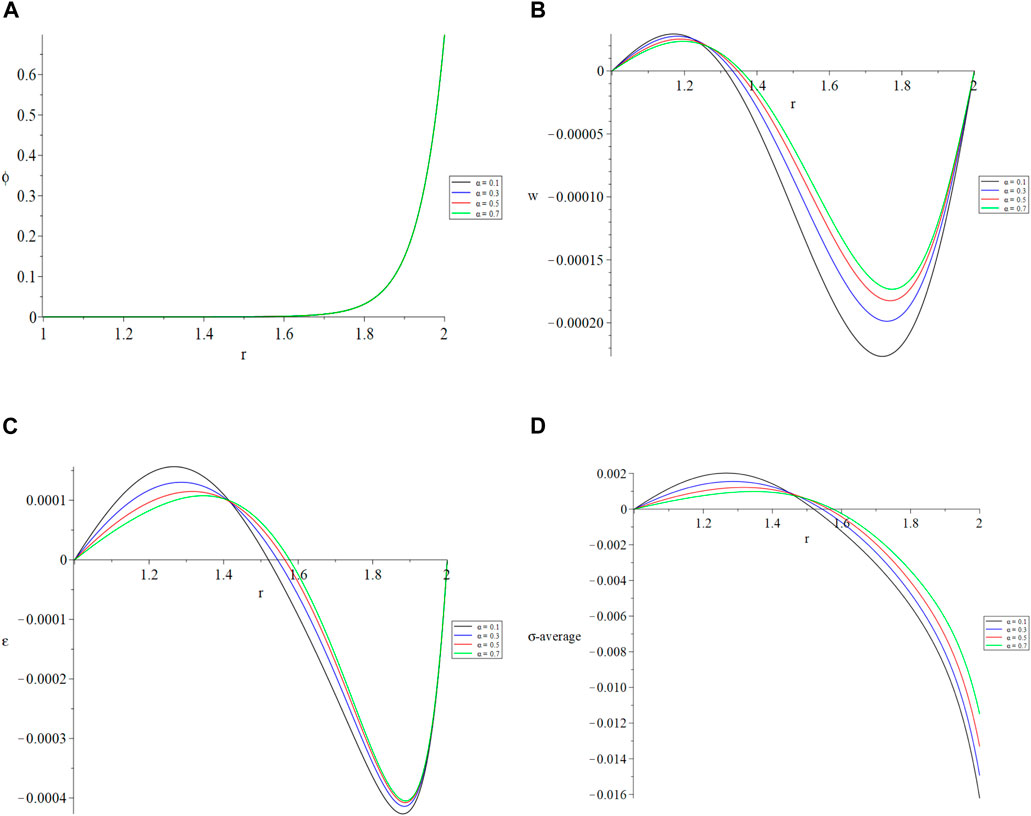
Figure 5. The studied function distributions based on classical-Caputo (C-C) of fractional derivatives with a different order. (A) The temperature increment. (B) The lateral deflection (vibration). (C) The deformation. (D) The average stress.
Figure 5A shows that the distribution of temperature increase remains unchanged regardless of the fractional order parameter. Nonetheless, it has a substantial impact on the vibration, deformation, and stress distributions, as seen in Figures 5B–D: as the value of the fractional order parameter increases, the magnitude of deformation, vibration, and average stress diminishes.
Figure 6 is the last group which contains Figures 6A–D in which the results have been figured for the studied functions in the context of the Caputo-Fabrizo fractional derivatives for four values of the micro-circular ring’s thickness
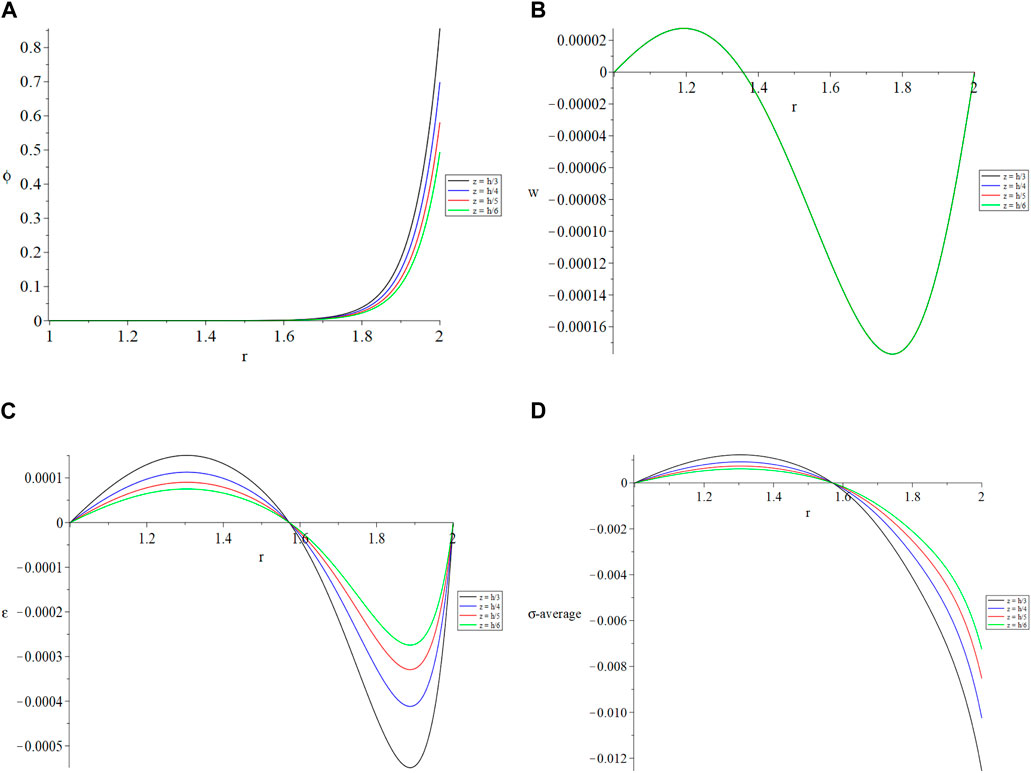
Figure 6. The studied function distributions based on Caputo-Fabrizo (C-F) of the fractional derivative with different thickness z when
The value of
Conclusion
The conclusions can be drawn from the analysis of the vibration of the simply supported micro-circular ring resonator made of viscothermoelastic ceramic: The fractional order parameter and the ratio of the plate’s radius to its thickness do not have a significant impact on the distribution of temperature increment. This conclusion is based on the definitions of viscothermoelasticity, classical Caputo, and Caputo-Fabrizo of the fractional derivative were taken into consideration.
The distribution of the temperature increase is significantly affected by the ramp-time heat parameter.
The fractional order parameter in the context of the two studied definitions of fractional derivatives does not affect the thermal wave while it has significant effects on the mechanical waves.
The distribution of the temperature increase is significantly affected by the thickness of the micro-circular ring resonator.
The mechanical relaxation time parameter has significant effects on the mechanical waves while it does not affect the thermal wave in the context of the two studied definitions of the fractional derivatives.
The vibration, deformation, and stress distributions of the micro-circular ring resonator are significantly influenced by the fractional order, thickness of the resonator, and the ramp-time heat parameters.
The ramp-type heat parameter serves as a regulator for the energy dissipation process inside the micro-circular ring resonator.
The studied functions are significantly influenced by the ramp-type heat parameter, which plays a crucial role in determining the amount of energy created by the resonator’s material.
Data availability statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.
Author contributions
EA-L: Conceptualization, Data curation, Formal Analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization, Writing–original draft, Writing–review and editing.
Funding
The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. He J-H, He C-H, Qian M-Y, Ali Alsolami A. Piezoelectric Biosensor based on ultrasensitive MEMS system. Sensors Actuators A: Phys (2024) 376:115664. doi:10.1016/j.sna.2024.115664
2. He J-H. Periodic solution of a micro-electromechanical system. Facta Universitatis, Ser Mech Eng (2024) 187–98. doi:10.22190/fume240603034h
3. Hao Z. Thermoelastic damping in the contour-mode vibrations of micro-and nano-electromechanical circular thin-plate resonators. J Sound Vibration (2008) 313:77–96. doi:10.1016/j.jsv.2007.11.035
4. Sun Y, Tohmyoh H. Thermoelastic damping of the axisymmetric vibration of circular plate resonators. J Sound Vibration (2009) 319:392–405. doi:10.1016/j.jsv.2008.06.017
5. Sun Y, Saka M. Thermoelastic damping in micro-scale circular plate resonators. J Sound Vibration (2010) 329:328–37. doi:10.1016/j.jsv.2009.09.014
6. Grover D. Damping in thin circular viscothermoelastic plate resonators. Can J Phys (2015) 93:1597–605. doi:10.1139/cjp-2014-0575
7. Guo F, Song J, Wang G, Zhou Y. Analysis of thermoelastic dissipation in circular micro-plate resonators using the generalized thermoelasticity theory of dual-phase-lagging model. J Sound Vibration (2014) 333:2465–74. doi:10.1016/j.jsv.2014.01.003
8. Guo F, Wang G, Rogerson G. Analysis of thermoelastic damping in micro-and nanomechanical resonators based on dual-phase-lagging generalized thermoelasticity theory. Int J Eng Sci (2012) 60:59–65. doi:10.1016/j.ijengsci.2012.04.007
9. Biot MA. Theory of stress-strain relations in anisotropic viscoelasticity and relaxation phenomena. J Appl Phys (1954) 25:1385–91. doi:10.1063/1.1721573
10. Biot MA. Variational principles in irreversible thermodynamics with application to viscoelasticity. Phys Rev (1955) 97:1463–9. doi:10.1103/physrev.97.1463
11. Drozdov A. A constitutive model in finite thermoviscoelasticity based on the concept of transient networks. Acta mechanica (1999) 133:13–37. doi:10.1007/bf01179008
12. Ezzat MA, El-Karamany AS. The relaxation effects of the volume properties of viscoelastic material in generalized thermoelasticity. Int J Eng Sci (2003) 41:2281–98. doi:10.1016/s0020-7225(03)00108-3
13. Carcione JM, Poletto F, Gei D. 3-d wave simulation in anelastic media using the kelvin–voigt constitutive equation. J Comput Phys (2004) 196:282–97. doi:10.1016/j.jcp.2003.10.024
14. Grover D. Viscothermoelastic vibrations in micro-scale beam resonators with linearly varying thickness. Can J Phys (2012) 90:487–96. doi:10.1139/p2012-044
15. Sharma J, Grover D. Thermoelastic vibrations in micro-/nano-scale beam resonators with voids. J Sound Vibration (2011) 330:2964–77. doi:10.1016/j.jsv.2011.01.012
16. Ahmad WM, El-Khazali R. Fractional-order dynamical models of love. Chaos, Solitons and Fractals (2007) 33:1367–75. doi:10.1016/j.chaos.2006.01.098
17. Sur A, Mondal S. Effect of non-locality in the vibration of a micro-scale beam under two-temperature memory responses. Waves in Random and Complex Media (2020) 32:2368–95. doi:10.1080/17455030.2020.1851069
18. Colinas-Armijo N, Di Paola M, Di Matteo A. Fractional viscoelastic behaviour under stochastic temperature process. Probabilistic Eng Mech (2018) 54:37–43. doi:10.1016/j.probengmech.2017.06.005
19. Xu J. A pdem based new methodology for stochastic dynamic stability control of nonlinear structures with fractional-type viscoelastic dampers. J Sound Vibration (2016) 362:16–38. doi:10.1016/j.jsv.2015.09.040
20. Xu J, Wang D, Dang C. A marginal fractional moments based strategy for points selection in seismic response analysis of nonlinear structures with uncertain parameters. J Sound Vibration (2017) 387:226–38. doi:10.1016/j.jsv.2016.10.008
21. Khalil R, Al Horani M, Yousef A, Sababheh M. A new definition of fractional derivative. J Comput Appl Mathematics (2014) 264:65–70. doi:10.1016/j.cam.2014.01.002
22. Baleanu D, Fernandez A. On some new properties of fractional derivatives with mittag-leffler kernel. Commun Nonlinear Sci Numer Simulation (2018) 59:444–62. doi:10.1016/j.cnsns.2017.12.003
23. Atangana A. On the new fractional derivative and application to nonlinear Fisher’s reaction–diffusion equation. Appl Mathematics Comput (2016) 273:948–56. doi:10.1016/j.amc.2015.10.021
24. Youssef HM. Theory of fractional order generalized thermoelasticity. J Heat Transfer (2010) 132. doi:10.1115/1.4000705
25. Youssef HM. Theory of generalized thermoelasticity with fractional order strain. J Vibration Control (2016) 22:3840–57. doi:10.1177/1077546314566837
26. Sherief HH, El-Sayed A, Abd El-Latief A. Fractional order theory of thermoelasticity. Int J Sol structures (2010) 47:269–75.
27. Podlubny I. Fractional differential equations: an introduction to fractional derivatives, fractional differential equations, to methods of their solution and some of their applications. Elsevier (1998).
28. Caputo M, Fabrizio M. A new definition of fractional derivative without singular kernel. Progr Fract Differ Appl (2015) 1:1–13.
29. Magin RL, Royston TJ. Fractional-order elastic models of cartilage: a multi-scale approach. Commun nonlinear Sci Numer simulation (2010) 15:657–64. doi:10.1016/j.cnsns.2009.05.008
30. Youssef HM. Theory of generalized thermoelasticity with fractional order strain. J Vibration Control (2015):1077546314566837.
31. Awad E, Dai W, Sobolev S. Thermal oscillations and resonance in electron–phonon interaction process. Z für Angew Mathematik Physik (2024) 75(4):143. doi:10.1007/s00033-024-02277-w
32. Awad E, Abo-Dahab SM, Abdou MA. Exact solutions for a two-dimensional thermoelectric MHD flow with steady-state heat transfer on a vertical plate with two instantaneous infinite hot suction lines. arXiv preprint arXiv:2212.01665 (2022).
33. Grover D, Seth R. Generalized viscothermoelasticity theory of dual-phase-lagging model for damping analysis in circular micro-plate resonators. Mech Time-Dependent Mater (2019) 23:119–32. doi:10.1007/s11043-018-9388-x
36. Samko SG, Kilbas AA, Marichev OI. Fractional integrals and derivatives. Yverdon Yverdon-les-Bains, Switzerland: Gordon and Breach Science Publishers (1993).
38. Saad KM. New fractional derivative with non-singular kernel for deriving legendre spectral collocation method. Alexandria Eng J (2019) 59:1909–17. doi:10.1016/j.aej.2019.11.017
39. Sherief HH, Hussein EM. The effect of fractional thermoelasticity on two-dimensional problems in spherical regions under axisymmetric distributions. J Therm Stresses (2020) 43:440–55. doi:10.1080/01495739.2020.1724219
40. Youssef HM, El-Bary AA. Generalized fractional viscothermoelastic nanobeam under the classical caputo and the new caputo–fabrizio definitions of fractional derivatives. Waves in Random and Complex Media (2023) 33:545–66. doi:10.1080/17455030.2021.1883767
41. Youssef HM, El-Bary AA, Al-Lehaibi EA. Characterization of the quality factor due to the static prestress in classical caputo and caputo–fabrizio fractional thermoelastic silicon microbeam. Polymers (2020) 13:27. doi:10.3390/polym13010027
42. Marin M, Hobiny A, Abbas I. The effects of fractional time derivatives in porothermoelastic materials using finite element method. Mathematics (2021) 9:1606. doi:10.3390/math9141606
43. Abbas IA. Generalized thermoelastic interaction in functional graded material with fractional order three-phase lag heat transfer. J Cent South Univ (2015) 22:1606–13. doi:10.1007/s11771-015-2677-5
44. Alghamdi N. Dual-phase-lagging thermoelastic damping vibration in micro-nano scale beam resonators with voids. Int J Multidisciplinary Curr Res (2017) 5.
45. Al-Lehaibi EA, Youssef HM. Vibration of gold nano-beam with variable young’s modulus due to thermal shock. World J Nano Sci Eng (2015) 5:194–203. doi:10.4236/wjnse.2015.54020
46. Tzou D. Macro-to microscale heat transfer: the lagging behavior. Washington: Taylor Francis (1997).
Appendix 1
Keywords: fractional derivative, micro-circular ring, resonator, viscothermoelasticity, ceramic, Kirchhoff’s Love plate, ramp-type heat
Citation: Al-Lehaibi EAN (2025) The vibration of micro-circular ring of ceramic with viscothermoelastic properties under the classical Caputo and Caputo-Fabrizio of fractional-order derivative. Front. Phys. 12:1490664. doi: 10.3389/fphy.2024.1490664
Received: 03 September 2024; Accepted: 26 November 2024;
Published: 06 January 2025.
Edited by:
Kateryna Buryachenko, Humboldt University of Berlin, GermanyReviewed by:
Emad Awad, Alexandria University, EgyptGuangqing Feng, Henan Polytechnic University, China
Copyright © 2025 Al-Lehaibi. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Eman A. N. Al-Lehaibi, ZWFsZWhhaWJpQHVxdS5lZHUuc2E=
†ORCID: Eman A. N. Al-Lehaibi, orcid.org/0000-0002-4480-0793
 Eman A. N. Al-Lehaibi
Eman A. N. Al-Lehaibi