1 Introduction
Nowadays, traditional incandescent light bulbs have largely been replaced by LED lamps, mainly because LEDs are highly energy efficient and last for long duration. However, to create a desired light output with LEDs, optical systems are required. Therefore, in the illumination optics industry, a lot of research is carried out on the design of optical systems for a myriad of applications.
The industry standard in optical design is (quasi-)Monte Carlo ray tracing. These are forward methods, which compute the target light distribution for a given source, typically LED, and a given optical system, tracing a large collection of rays from the source to target. Convergence of ray tracing is slow and requires millions or, maybe, even billions of rays to accurately compute the target distribution; see ([1], Chapter3). Moreover, to realize the desired target distribution, these methods have to be embedded in an iterative procedure, adjusting system parameters. More specifically to update these parameters, sophisticated design methods combine an iterative gradient-based optimization method, to minimize a suitably chosen merit function, with differentiable ray tracing to compute the required gradient. These methods are efficient and broadly applicable; see e.g., [31, 32]
A promising alternative are inverse methods. These methods compute the shape/location of the optical surface(s) in one go, given a source distribution and a desired target distribution. The surfaces are referred to as freeform since they have no imposed symmetries. Mathematical models for inverse methods are based on the principles of geometrical optics and conservation of luminous flux. Our models contain the following: a geometrical equation describing the shape/location of the optical surface(s), an (implicit) relation between the location of an optical surface and the optical map, which expresses target coordinates as a function of source coordinates, a matrix equation for the optical map, a conservation law of luminous flux, and a constraint on the luminous flux. The geometrical equation can be derived evaluating one of Hamilton’s characteristic functions and has multiple solutions. The optical map satisfies the luminous flux balance, which is a Jacobian equation, and a matrix equation, which has to be supplemented with the unconventional transport boundary condition. Our models are restricted to zero-étendue sources; more specifically, we consider only planar sources emitting a parallel beam of light or point sources.
In mathematics, the abstract theory of optimal transport is the correct framework to formulate optical design problems. The subject of optimal transport theory is to compute a transport plan (mapping) that transforms a given density function into another one, minimizing the transportation cost and subject to a(n) (integral) conservation law; see [2]. One of the governing equations is precisely the geometrical equation, containing a so-called cost function in the right hand side. The transportation cost is then a cost functional (an integral of the cost function). The analogy with optical design is obvious, the two density functions correspond to the source and target distributions, the transport plan to the optical map, the cost functional can be associated with the optical path length, and the conservation law applies to the luminous flux.
Based on the analogy with optimal transport theory, we can distinguish three mathematical models of increasing complexity. First, in the simplest model, the geometrical equation contains a quadratic cost function, and the Jacobian equation reduces to the standard Monge–Ampère (MA) equation, which is a second-order, non-linear, elliptic partial differential equation (PDE) [3], defining the location of an optical surface. In the next model, the cost function is no longer quadratic and the Jacobian equation corresponds to a generalized Monge–Ampère (GMA) equation. Finally, the most complicated model does not allow a description in terms of a cost function anymore; instead, a so-called generating function is required. The Jacobian equation now corresponds to a generated Jacobian (GJ) equation.
The procedure to derive our mathematical models consists of the following steps:
1. By applying principles of geometrical optics, derive the geometrical equation.
2. Formulate the luminous flux balance, which is a Jacobian equation for the optical map.
3. Based on optimal transport theory, select a uniquely defined solution from the geometrical equation.
4. Derive the necessary (zero-gradient) condition for this solution to define a unique relation between the location of an optical surface and the optical map.
5. Derive from the zero-gradient condition the matrix equation for the Jacobi matrix of the optical map.
6. Combine the luminous flux balance with the matrix equation to derive a constraint on the luminous flux.
There are many numerical methods available for inverse freeform optical design; for a detailed survey, see [4], Chapter 5. Without trying to be complete, a possible categorization is as follows: first, numerical methods for (G)MA equations governing the shape/location of an optical surface; second, optimization methods; third, geometrical construction methods; and fourth, ray mapping methods. In the first category are methods that directly solve the second-order PDE of MA type by discretization and subsequent iteration for the resulting algebraic system. Examples of these are reported in papers by Froese [5], using a wide-stencil finite difference scheme, Benamou et al. [6], using finite differences, Brix et al. [35], using B-spline collocation, and Kawecki et al. [7], using finite elements, to just name a few examples. Methods in the second category are based on optimal transport theory and determine the optical surface(s) by minimizing the cost functional subject to conservation of luminous flux, see, e.g., [33, 34] Next, based on the work of Caffarelli and Oliker [8], geometrical construction methods for optical surfaces with paraboloids have been investigated by Kitagawa et al. [9] and Mérigot and Thibert [10] for the GMA equation, and by Galouët et al. [11] for the GJ equation. Finally, in ray mapping methods, the computation of the optical surface(s) is split into two parts, i.e., first, an estimate of the optical map is computed from an optimal transport problem, and subsequently, the optical surface is computed employing the law of reflection/refraction; see e.g., [36–38]
Our methods are of the first category. The publication that inspired us to develop our numerical solvers is by Caboussat et al. [12]. In this paper, the authors present a least-squares method to solve the Dirichlet problem for the standard MA equation. Prins adjusted their method to include the transport boundary condition; see [13]. In a series of papers, Yadav and Romijn extended the method for the GMA equation, corresponding to a non-quadratic cost function; see [14], [15, 16]. Romijn further extended our least-squares methods to deal with the GJ equation; see [17, 18]. Specifically, for the cost function models, we have developed a two-stage algorithm, i.e., we first compute the optical map and subsequently the shape/location of the optical surface(s). For both stages, we apply a least-squares method. For the generating function model, the optical map and the optical surface(s) have to be computed simultaneously, also in a least-squares fashion.
In this paper, we present a systematic derivation of all models and outline numerical simulation methods. The content is then as follows. First, in Section 2, we introduce Hamilton’s characteristic functions needed to derive the geometrical equations. In Section 3, we give an outline of optimal transport theory, needed to select a uniquely defined solution of the geometrical equation. A generic conservation law for luminous flux is presented in Section 4. Next, in Section 5, we apply the results of the previous sections to present a hierarchy of models based on three example systems. A concise description of our numerical methods is presented in Section 6. To demonstrate the performance of our methods, we present a few challenging examples in Section 7. Concluding remarks are given in Section 8, and the paper is concluded with a nomenclature list.
2 Hamilton’s characteristic functions
In this section, we introduce Hamilton’s characteristic functions which are needed for the derivation of the geometrical equations in Section 5; see, e.g., [19], pp. 94–107; [20], Section 4.1 for a more detailed account. Our starting point is the eikonal equation given by
where
is the phase of an electromagnetic wave and
is the refractive index field as functions of the (three-dimensional) position vector (or coordinates)
of a typical point. A surface
is a wavefront. We denote three-dimensional vectors in bold font with an underbar
, to distinguish them from two-dimensional vectors, which are only written in bold font. Equation 1 describes free propagation of light waves and no longer holds when a light wave is reflected or refracted at an optical surface. The eikonal Equation 1 is a first-order non-linear PDE, which has the characteristic strip equations
See, e.g., Kevorkian [21]. The curves
, parameterized by the arc length
, are the characteristics of (1). The system of ordinary differential equations in (2) determines the location of the characteristics and the solution along the characteristics, from which the solution of (1) can be reconstructed. From the first equation in (2), we conclude that the characteristics are orthogonal trajectories to the wavefronts, i.e., characteristics are light rays; see, e.g., [20], p. 114.
Hamilton’s characteristic functions are related to the optical path length of a ray, which we, therefore, introduce next. We assume that
is piecewise continuous, with jumps at lens surfaces; consequently, rays are continuous and consist of piecewise differentiable curve segments; cf. Equation 2. In this setting, we define the optical path length (OPL) between the points
(position vector
) and
(position vector
), connected by a light ray along the curve
, as
A consequence of Fermat’s principle is that the optical path length
is stationary with respect to variations in the curve
; see, e.g., [20], p. 740.
Consider an optical system consisting of a source, located in a plane
(source plane), emitting light which via a sequence of reflectors and/or lenses arrives at a plane
(target plane). The
-axis is referred to as the optical axis. In this paper, we use the subscripts
and
for variables/vectors to denote their value at the source and target, respectively. Let
denote the unit tangent vector of a ray; thus,
; cf. Equation 2. Unit vectors are denoted with a hat
. Let
(position vector
) and
(position vector
) be two points on the source and target plane, respectively; then, from Equation 3, we obtain
Note that reversing the direction of integration yields the symmetry property of
, i.e.,
as one would expect from the definition in Equation 3. Observe that
is a metric since
, with equality only if
, and it satisfies the triangle inequality due to Fermat’s principle. The symmetry of
is stated in Equation 5.
For ease of presentation, we use the shorthand notation
and
. Straightforward differentiation of the expression for
in Equation 4 gives
where
denotes the gradient with respect to the source coordinates
and likewise for
. From these relations, we readily conclude that
i.e.,
satisfies the eikonal equation in both source and target coordinates.
A ray is completely determined by its position and direction coordinates. Position coordinates
are defined as the projection on a plane
of the position vector
of a typical point on the ray. Position coordinates in the source and target planes are denoted by
and
, respectively. Thus,
, with position vector
, will denote the point at which a light ray is emitted from the source plane, and
, with the position vector
, as the point at which it arrives at the target plane. Next, selecting the first two components from the equation
, we introduce the momentum vector
as
Thus, the momentum vector is the projection of
on a plane
and determines the direction of a light ray. Momentum vectors at the source and target are denoted with
and
, respectively. The variables
and
are referred to as phase-space coordinates and together constitute phase space.
In the remainder of this paper, we assume that
is piecewise constant, with possible discontinuities at optical interfaces, and consequently, a light ray consists of piecewise straight line segments. Below, we define four characteristic functions which relate the optical path length to phase-space coordinates at the source and target.
Point characteristic
As a function of the position coordinates
and
, the point characteristic
is the optical path length of the ray connecting the points
and
, i.e.,
From Equation 4, we conclude that
. Combining this relation with the equations in Equation 6, selecting the first two components in both equations, we find for the directional derivatives
and
the following expressions:
cf. Equation 7. Typically, Equations 8, 9 are used to derive a geometrical equation for optical systems described in terms of the position coordinates
and
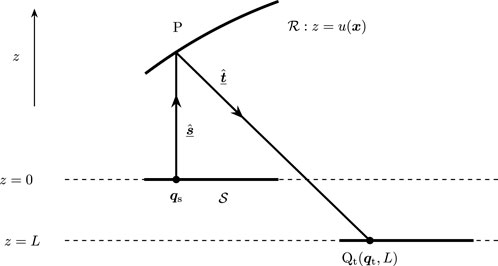
. An example is the parallel-to-near-field reflector, discussed in Section 5.3.
Mixed characteristic of the first kind
Let a light ray connect the points
and
with momentum
and
, respectively; then, the mixed characteristic of the first kind
is defined as
Straightforward differentiation yields
and
; cf. Equation 9, second relation. Consequently,
indeed. Moreover, we readily verify that
can be interpreted as a modification of
, which we show as follows. Assume that
and define the point
as the intersection of the ray segment arriving at
, parameterized by
, and the plane passing through the origin
of the target plane (position vector
) perpendicular to this ray, given by the normal equation
; see Figure 1. The intersection point is given by
. Since the third component of
vanishes, this can be rewritten as
; cf. Equation 7 or Equation 9. For the
-component of
, we have
with
since the ray is directed toward the target plane
. From this, we conclude that
if
, i.e.,
is located behind the target plane as seen from the source, and
otherwise. Obviously, the distance
since
is a unit vector. If
, then
, implying that
and
; cf. Equation 3. Analogously, if
, then
. Finally, we can easily verify that
; thus,
can be interpreted as
The characteristic function
is convenient to describe optical systems in terms of
and
. An example is the parallel-to-far-field reflector, as described in Section 5.1.
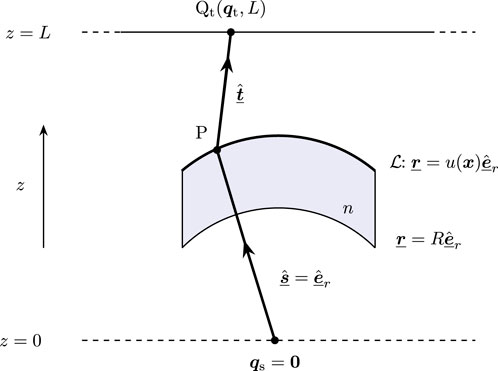
Mixed characteristic of the second kind
Under the same setting, the mixed characteristic of the second kind
is defined as
In this case, using the first relation in Equation 9, we readily verify that
and
, so
is a function of
and
indeed. Furthermore, straightforward differentiation yields
In addition,
can be interpreted as a modified OPL. We assume again that
and introduce the point
as the intersection of the ray segment emitted from
, parameterized by
, and the plane passing through the origin
of the source plane (position vector
) perpendicular to this ray, given by
; see Figure 1. Analogous to the previous derivation, we obtain
. The
-component of
is given by
with
. Thus, if
, then
; otherwise,
. Following the same line of reasoning as before, we find that
with
. Therefore, the second mixed characteristic can be interpreted as
Note that
, i.e., the mixed characteristic of the second kind of the ray in reversed direction equals the mixed characteristic of the first kind of the original ray. The function
can be used to characterize optical systems in terms of
and
. An example is the point-to-near-field reflector.
Angular characteristic
The angular characteristic
is another modification of
and is a function of the momenta
and
. Its definition and interpretation (for
) are given by
From Equations 9, 11, we readily verify that
and
, implying that
. Moreover, it is evident that
Note that
, i.e., the angular characteristic is invariant if the direction of the ray is reversed. This function is used to describe optical systems in terms of
and
, such as the point-to-far-field lens; see Section 5.2.
3 Geometrical description of optical systems: an optimal transport point of view
To derive a geometrical description of an optical system, i.e., an algebraic relation defining the location and shape of the optical surface(s), we have to evaluate one of the four Hamilton’s characteristic functions. However, this geometrical equation does not have a unique solution. In this section, we discuss how to select a uniquely defined solution from this equation. Subsequently, we derive an equation for the optical map.
First, we introduce some notation. We denote with
and
the (physical) source and target domain, respectively. The source and target domain are parameterized by
and
, respectively, i.e.,
and
are the parameter domains for the source and target. We assume that
and
are compact, i.e., bounded and closed, and consequently, any continuous function defined on one of these domains assumes a minimum and a maximum. The key in the following discussion is the optical map
, defining how a point on the source domain (specified by
) is connected via a light ray with a point on the target domain (specified by
). Given source and target domains, the optical map has to satisfy the condition
, i.e.,
is the image of
under the mapping
.
We consider optical systems having one or two freeform optical surfaces, i.e., surfaces without any symmetry. Consider an arbitrary ray connecting the source and target, for which
. Evaluation of the appropriate Hamilton’s characteristic function for such a ray leads to either one of the two algebraic equations:
which we refer to as geometrical equations, where
defines the location of (one of) the optical surface(s) and
is either an auxiliary variable or defines the location of the other surface. We like to emphasize that in Equation 12, source and target coordinates are related via
. In Section 5, we will derive geometrical equations for several optical systems. Note that in Equation 12a, source and target coordinates are separated in the left-hand side. This equation occurs in the theory of optimal transport, where
and
are referred to as Kantorovich potentials and
as the cost function; see, e.g., [2] for a rigorous mathematical account. In Equation 12b, source and target coordinates are no longer separated. It will turn out that for fixed
and
, the function
has a unique inverse
, referred to as the generating function; see [22]. Thus, the following holds:
Obviously, Equation 12a is a special case of Equation 12b if we choose
. Nevertheless, for the sake of completeness, we discuss both cases separately.
-convex analysis
Equation 12a has multiple solution pairs
. From the theory of optimal transport, we know that a possible solution of Equation 12a is given by
which implicitly defines the optical map as an alternative to a geometrical optics derivation. To be more precise, for any
, its image
is the maximizer in Equation 13a. In addition, for any
, we have that
such that
is the maximizer in Equation 13b, which is possible since
. Under certain conditions, to be specified shortly, the maxima in (13) are unique, which we henceforth assume. The solution in (13) is referred to as a
-convex pair; see [23]. The proof of the equivalence of (Equation 13a) and (Equation 13b) proceeds as follows. Suppose, Equation 12a and the expression for
in Equation 13a hold, then we have to derive the expression for
in Equation 13b. From Equation 13a we conclude
or equivalently, swapping
and
,
Since the latter inequality holds for all
, we can take the maximum over all
to obtain
Recall that
. Let
, then
for some
. From Equation 12a, we conclude that
Combining both inequalities, we obtain the expression for
in Equation 13b and conclude that
is the (unique) maximizer of
. Thus, the expression for
in Equation 13a combined with Equation 12a implies the expression for
in Equation 13b. Conversely, given the expression for
in Equation 13b and Equation 12a, we can derive in a similar manner the expression for
defined in Equation 13a.
Alternatively, Equation 12a has a
-concave solution pair, for which the maxima in Equation 13 are replaced by minima, defining another mapping
. In either case, a necessary condition is that
is a stationary point of
for all
, i.e.,
where
is the gradient of
with respect to the source coordinates
. A sufficient condition for the
-convex pair (max/max solution) in (Equation 13) is that
be symmetric negative definite (SND) for all
, where
and
are the Hessian matrices of
(with respect to
) and
, respectively. The function
is then concave, guaranteeing a unique maximum in Equation 13b. Alternatively, for a
-concave pair (min/min solution), the sufficient condition is that
be symmetric positive definite (SPD) for all
. Then,
is convex and has a unique minimum.
According to the implicit function theorem, the optical map
is well-defined by Equation 14, provided the mixed derivative matrix
is regular in
for all
, the so-called twist condition. However, for many optical systems, the actual computation of
from Equation 14 is quite complicated, if not impossible. Therefore, to derive an equation for the optical map, we differentiate the zero-gradient condition in Equation 14 to obtain the equation
where
is the Jacobi matrix of the optical map. We refer to Equation 15 as the matrix-Jacobi equation. Note that the matrix
is either SPD, for a
-convex, or SND for a
-concave solution pair.
Equation 15 has to be supplemented with the so-called transport boundary condition
stating that the boundary of the source domain
is mapped to the boundary of the target domain
. This condition is a consequence of the edge-ray principle of geometrical optics [24] and guarantees that all light emitted from the source arrives at the target.
For some basic optical systems
, implying that
and
; see Section 5.1. The
-convex solution pair in (13a) reduces to a conjugate pair of Legendre–Fenchel transforms, see e.g., [4], for which the necessary condition (14) reduces to
. The sufficient condition for the
-convex solution pair is that
is SPD for all
, i.e.,
is a convex function. Likewise, for the
-concave solution pair,
has to be SND for all
, and
is then concave. In both cases,
has a unique extremum.
In our numerical algorithm, the matrix-Jacobi (Equation 15), subject to the transport boundary condition (16), is employed to compute the optical map, and subsequently,
is reconstructed from Equation 14. If needed,
is computed from Equation 12a. From
and possibly
, the shape of the optical surface(s) is computed. A concise account of the numerical algorithm is given in Section 6.
-convex analysis
Next, we consider the geometrical Equation 12b, which can always be formulated such that
for all
and
, implying that
has an inverse. Also, Equation 12b has multiple solution pairs
. In analogy with (Equation 13), a possible solution reads
implicitly defining the optical map as follows:
is the maximizer in Equation 17a and
such that
is the minimizer in Equation 17b. Provided a condition on
holds, which we specify shortly, the extrema in Equation 17 are unique, which we henceforth assume. The functions
and
are referred to as a
-convex
-concave solution pair; see [4]. We prove that (Equation 17a) together with (Equation 12b) implies (Equation 17b); the implication in the reverse order proceeds in a similar way. Assume that the expression for
in (Equation 17a) holds, then
Applying the inverse
and using that
, we obtain
Since this inequality holds for all
, we can take the minimum and find
Let
for some
. Then, by virtue of Equation 12b.
Combining both inequalities, we arrive at the expression for
in Equation 17b with
the unique minimizer. Conversely, given the expression for
in Equation 17b, we can derive in a similar manner the expression for
in Equation 17a.
Equation 12b also has a
-concave
-convex (min/max) solution pair. The necessary condition for both solutions is that
is a stationary point of
, i.e.,
A sufficient condition for the max/min pair is that
be SPD for all
. Alternatively, for the min/max pair, the Hessian matrix
should be SND for all
. In both cases, the solution pair is unique.
Equation 18 implicitly defines the optical map
, provided the mixed derivative matrix
is regular in
for all
, but the actual computation of the optical map from Equation 18 is virtually impossible for most optical systems. So, we differentiate the zero-gradient condition in Equation 18 and recover the matrix-Jacobi equation in Equation 15; however, with matrices
and
given by
Notice, there is one difficulty, i.e., the function
depends on
, and consequently, also the matrices
and
do. Therefore, the computation of the optical map and the function
can no longer be decoupled; see Section 6 for more details. Finally, also, in this case, the transport boundary condition (16) applies.
4 Conservation of luminous flux
In the previous section, we presented equations describing the geometry of an optical system, more specifically (Equation 12) for the shape/location of the optical surface(s), the zero-gradient conditions (Equations 14, 18), and the matrix-Jacobi equation for the optical map, defined in Equations 15, 19. To close the model, we have to formulate the conservation law of luminous flux.
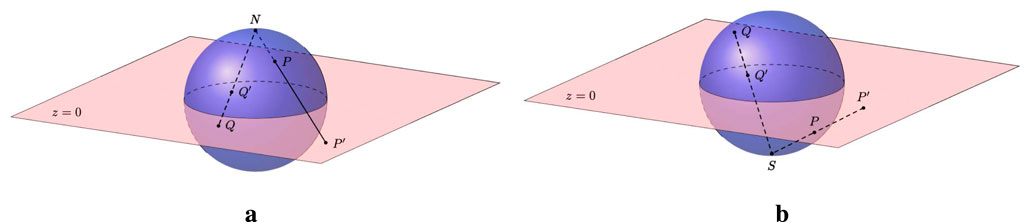
We first introduce stereographic projections of a unit vector
, needed in some of the flux balances. A unit vector
can be represented by a point
or
on the unit sphere; see Figure 2. There are two stereographic projections of
, i.e., the projection from the north pole and from the south pole. To compute the stereographic projection from the north pole
, we have to compute the intersection of the line through
and
, given by
with the equator plane
. In this way, we obtain the stereographic projection
given by
which is defined for
. The latter condition means that
and
should not coincide. Using the relations
and
, we can compute the inverse
and find
In a similar manner, we can determine the stereographic projection from the south pole and its inverse. These are given by
and are defined for
. Both projections are parameterizations of
, and in either case, an area element
on
generated by
is given by
The choice for the stereographic projection depends on the direction of
. If
, a suitable choice is the projection from the south pole; since then, the domain for
is included in the interior of the disc
. The projection from the north pole gives a domain outside this disc; see Figure 2. Likewise, if
, the projection from the north pole is the proper choice.
Assuming there is no energy lost, the most generic form of the luminous flux balance reads
for every subset
and image set
, where
and
are the flux densities, to be specified shortly, at the source and target, respectively. Here,
denotes an area element on the (curved) surface
describing the source and parameterized by
. Analogously,
is an area element on the target surface
, parameterized by
. Equation 23 should hold for any subsets
and
, so also for
and
, giving the global luminous flux balance. This implies that an inverse design problem can only have a solution if
and
satisfy this global flux balance.
The precise form of the flux balance depends on the source and target. For the source, we consider two options: first, a planar source located in
and emitting a parallel beam of light with
, and second, a point source located in the origin and emitting a conical beam of light with
. Both are zero-étendue (English: zero-extent) sources, meaning that the emitted beam has either a spatial or angular extent, but in the embedding four-dimensional phase space, it has zero volume; see Chaves [25]. For the planar source
,
are spatial coordinates (Cartesian/polar),
, the area element in the source plane, and
, the emittance, i.e., the luminous flux per unit area emitted by the source. The point source has no spatial extent but emits light rays in an angular domain, specified by
. As parameterization, we choose a stereographic projection, either from the north or south pole, the area element
, cf. Equation 22, and
, the intensity of the source, i.e., the emitted luminous flux per unit solid angle. We can express both flux densities in the form
, where
and
, the trivial projection from
to
, for the planar source and
and
or
for the point source.
For the target, we consider the following cases; first, a near-field target located on a curved surface
, and second, a far-field target. For the near-field target,
are spatial coordinates in a reference plane
, the area element
and
, the illuminance, i.e., the luminous flux per unit area incident on the target surface. The domain of a far-field target is an angular domain, determined by the transmitted rays with
. Therefore, we choose for
one of the two stereographic projections, for which
; cf. Equation 22. However,
, the intensity in the target domain as a function of
, the unit direction vector directed straight from source to target domain, skipping all optical surfaces, rather than a function of
. In the far-field approximation, the distance from the source to target is large compared to the size of the optical system, specifically
, where
is the distance from the optical surface to target, measured along a reflected ray; see, e.g., [4], pp. 59–60. The optical system is considered a point contracted at the origin, so we simply consider
. In addition, for the target, both flux densities can be unified in the expression
, where for the near field
and
is the orthogonal projection from
to
, and where for the far-field target,
and either
or
.
5 Reflector and lens equations: a hierarchy of mathematical models
We present a hierarchy of mathematical models for optical systems with a zero-étendue source, based on three example systems, i.e., a parallel-to-far-field reflector, point-to-far-field lens, and parallel-to-near-field reflector. These example systems are selected based on the mathematical model (quadratic cost function, non-quadratic cost function, and generating function) but are otherwise arbitrary. Other choices like a parallel-to-far-field-lens (quadratic cost function) or point-to-near-field reflector (generating function) would be equally appropriate. In this section, we combine the geometrical equations with the conservation law for luminous flux.
5.1 Parallel-to-far-field reflector
We consider a light source located in the plane
emitting a parallel beam of light, for which
. Light rays strike the reflector
defined by
,
, and are reflected off in the direction
. The reflected rays intersect an auxiliary plane
, which we introduce to be able to determine an optical distance; see Figure 3. More precisely, to derive a geometrical equation for the reflector surface, we determine from Equation 10 the mixed characteristic of the first kind
for an arbitrary ray with
and
, connecting the source with the plane
. The point characteristic
involved is given by
where
is the distance between the points
and
, which are the points where the reflected ray hits the reflector and target plane, respectively, loosely referred to as intersection points. For the direction vector
of the reflected ray, we have
Moreover,
since
is perpendicular to the source plane, implying that
. Elaborating the expression for
, using the relations in Equations 24, 25, we find
To separate the variables
(source) and
(target), we bring all terms that solely depend on
to the left-hand side, and we obtain
Note that
since rays cannot pass straight through the reflector. Using the expressions for
and
, we can show that
from which we readily conclude that the left-hand side in Equation 26 is independent of
, which makes sense since a far-field target domain should not depend on the choice of a particular plane
. As stated in Section 4, the proper choice to parameterize the target
is the stereographic projection from the north pole; thus,
and
; cf. Equation 20. Substituting the expression for
in Equation 26, we arrive at the geometrical equation
where
and
.
Referring to Section 3, a possible solution of Equation 27 is the max/max solution in Equation 13, which is a conjugate pair of Legendre–Fenchel transforms since
. The necessary condition in Equation 14 and the matrix equation for the optical map in Equation 15 reduce to
Recall that Equation 28b has to be supplemented with the transport boundary condition (Equation 16).
To close the model, we elaborate the flux balance in Equation 23. Substituting
,
,
, and
, we obtain
for arbitrary
and
. Substituting
and the expression for
, replacing
by
in Equation 22, we can rewrite the integral in the right-hand side and find
where we used that
, which is correct because
is either SPD or SND. Since Equation 29 should hold for arbitrary
, we obtain the differential form
referred to as the Jacobian equation. Substituting
, this equation reduces to the standard MA equation
; see, e.g., Gutiérrez [3].
5.2 Point-to-far-field lens
We consider a point source located in the origin
(position vector given by
and
), emitting upward a conical beam of light with the direction vector
. Light rays hit a lens of refractive index
; see Figure 4. The first (entrance) surface is spherical with center
and radius
; hence, rays are not refracted there; however, the second (exit) surface is freeform and given by the parameterization
. Rays are refracted at the exit surface and arrive at an auxiliary plane
. To derive a geometrical equation for the freeform surface, we evaluate the angular characteristic
defined in Equation 11 for an arbitrary ray connecting the source with the plane
. The point characteristic
needed to evaluate
is given by
where
is the distance between the points
and
, which are the intersection points of the refracted ray with exit surface and target screen, respectively. The direction vector
of the refracted ray is given by
Note that
, implying that
. Evaluating the expression for
in Equation 11 using the relations in Equations 30, 31, we obtain
To derive the last expression for
in Equation 32, we substituted the relation
. Next, we move all terms that solely depend on
and the constant
to the left-hand side and find
Differentiating the first expression in Equation 32 with respect to
and combining the expression for
with Equation 31, we obtain
from which we readily see that the left-hand side in Equation 33 is independent of
, as anticipated.
To separate source and target coordinates, analogous to Equation 27, we have to take the logarithm of the left- and right-hand sides of Equation 33. Note that
and
; consequently, the left-hand side is positive as well, and we can take the logarithms. In addition, we substitute the stereographic projections (from the south pole)
of
and
of
since both
and
are directed upward; cf. Equation 21. In this way, we obtain
where the variables
and
and the cost function
are defined by
Formulated in terms of stereographic coordinates, the cost function reads
which is no longer quadratic. A possible solution of Equation 34a is the
-convex pair in Equation 13, for which the necessary condition (Equation 14) holds. For the optical map, matrix Equation 15 accompanied with the transport boundary condition (Equation 16) is given.
Referring to Section 4, in the far-field approximation, the luminous flux balance reads
for arbitrary
and image set
. To derive the differential form, we substitute the expressions for
and
, according to Equation 22, and subsequently substitute
. Assuming
, we obtain
Combining this equation with the matrix equation in Equation 15, we obtain the GMA equation
.
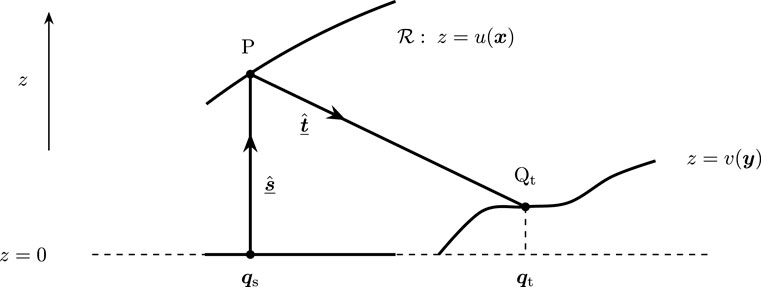
5.3 Parallel-to-near-field reflector
The last example concerns a planar source, located in
, emitting a parallel beam of light rays in the direction
, consequently
, which hits a reflector
given by
, with
spatial coordinates in the source domain, and are reflected off in the direction
and lands at a target surface given by
, with
spatial coordinates in the reference plane
. Thus, source and target planes coincide; see Figure 5. We evaluate Hamilton’s point characteristic and find
where
is the distance between the intersection points
and
of the reflected ray with the reflector and the target surface, respectively. Since
, we find that
. In this case, it is no longer possible to separate the source and target coordinates
and
like in Equation 27 or (Equation 34a). Instead, we write
where
and
. Straightforward differentiation gives
, implying that for fixed
, the inverse
exists. Therefore, we can explicitly determine
from Equation 36, and we obtain
A possible solution of Equations 36, 37 is the
-convex
-concave pair in Equation 17, for which the necessary condition (18) holds. The matrix equation for
is given in Equation 15 with matrices
and
defined in Equation 19. Recall that these matrices explicitly depend on
. Obviously, also the transport boundary condition (16) holds.
Making the proper choices for the flux densities and area elements, the flux balance (23) reduces to
for an arbitrary set
and image set
, where
and
denote the emittance and illuminance of the source and target, respectively. Substituting
, assuming
, we obtain
Combining this equation with Equation 15 and the matrices
and
defined in Equation 19, we obtain the equation
, referred to as the GJ equation.
5.4 Summary of mathematical models
All mathematical models considered consist of a geometrical equation, a (zero-gradient) condition for a stationary point, a matrix equation for the optical map coupled to the transport boundary condition, and a luminous flux balance
. The conditions for the stationary point read
Substituting the optical map
and differentiating with respect to
gives the matrix equation
, where the matrices
and
are given by
Combining the matrix equation for
with the flux balance gives
which we refer to as the luminous flux constraint. Note that for the cost-function model, the matrices
and
explicitly depend on
and
; on the other hand, for the generating-function model, both matrices in addition depend on
. In [26], we have given a similar overview of mathematical models of 16 base optical systems.
In the next section, we outline numerical methods to compute the optical map
and the auxiliary variable
. The shape/location of the optical surface is then reconstructed from a simple algebraic equation, i.e.,
for the parallel-to-far-field and parallel-to-near-field reflectors and
for the parallel-to-far-field lens.
6 Iterative least-squares methods
In this section, we outline iterative least-squares methods for the models presented in the previous section, starting with the base scheme for the cost-function models and adding modifications for the generation-function model. A detailed account of these methods is presented in a series of theses—see [27]; [23]; [4]—and papers—see [13]; [28]; [14, 29]; [15–18]; [26].
Base scheme for cost function
To compute the layout of the optical system, we apply a two-stage method, i.e., we first compute the optical map
and subsequently, the auxiliary variable
and possibly
, from which we trivially can compute the shape/location of the optical surface(s). We employ a uniform rectangular grid covering the parameter space of the source domain.
We iteratively compute a symmetric matrix
as approximation of the symmetric part of
, satisfying
, and a vector field
, from which we subsequently compute
. Our solution strategy is then to minimize the functionals
where
denotes the Frobenius norm. The minimization of
is to enforce the transport boundary condition (16). Given an initial guess
, the iteration scheme then reads
where the corresponding function spaces are given by
In common parlance,
is the space of
matrix functions that are continuously differentiable on
, are symmetric, and satisfy the luminous flux constraint.
is the space of continuous vector functions that map the boundary
to the boundary
.
The minimization of
to compute
can be performed point-wise and requires the solution of a constrained minimization problem.
has to be either SPD or SND, which can be enforced by a constraint on
. The minimization of
to compute
is a piecewise projection of
on
. For the minimization of
, we impose the first variation with respect to
to vanish, i.e.,
for arbitrary
. Evaluating this limit, applying Gauss’s theorem and the fundamental lemma of calculus of variations ([30], p. 185), we derive the following coupled boundary value problem (BVP) for
:
where
is the unit outward normal on
. The divergence of a
matrix function
is defined as
. For discretization of the BVP in (Equation 45), we employ the standard finite volume method ([4], pp. Appendix B).
Next, upon convergence of the iteration (42), we compute
from (Equation 39a) by minimizing the functional
Analogous to the derivation of (Equation 45), we set the first variation
for arbitrary
, to obtain the Neumann problem
We employ standard finite differences for the BVP in 46.
is determined up to an additive constant, which translates in an additive constant in the location of the parallel-to-far-field reflector and a multiplicative constant for the location of the point-to-far-field lens. To compute a unique solution from 46 we either fix the distance from the source to optical surface along a specific ray, or prescribe an average for
.
Extension to generating function
The optical map
and the variable
have to be computed simultaneously since the matrices
and
depend on both variables. Like in the previous case, the optical map satisfies the equation
, with the matrices
and
defined in Equation 40c, and the luminous flux balance
. Consequently, the functional
remains the same, albeit with different matrices
and
. The variable
has to be computed from Equation 39b, for which we introduce the functional
To minimize the functional in Equation 47, we require
for arbitrary
, with
the first variation in
with respect to
, defined analogously to Equation 44. This way we can derive the BVP
We employ the standard finite volume method for discretization. We can show that also the solution of the BVP in Equation 48 is determined up to an additive constant and compute a unique solution prescribing the average value of
; see ([4], pp. 166–167) for more details. Finally, given an initial guess
and
, the iteration scheme then reads
with
, where we have included
in the argument list of
and
to denote their implicit dependence on
via the matrix
.
7 Numerical examples
We present two numerical examples, viz. the point-to-far-field lens discussed in Section 5.2 and the parallel-to-near-field reflector from Section 5.3.
7.1 Point-to-far-field lens
We consider a point source, located in the origin
of the source plane
, emitting upward a beam of light with uniform intensity
on the circular stereographic source domain
. In terms of spherical coordinates
, this corresponds to the domain
and
with
and
as the polar and azimuthal angle, respectively, i.e., the emitted conical light beam has an opening angle of
. For the target, we choose the stereographic domain
and intensity
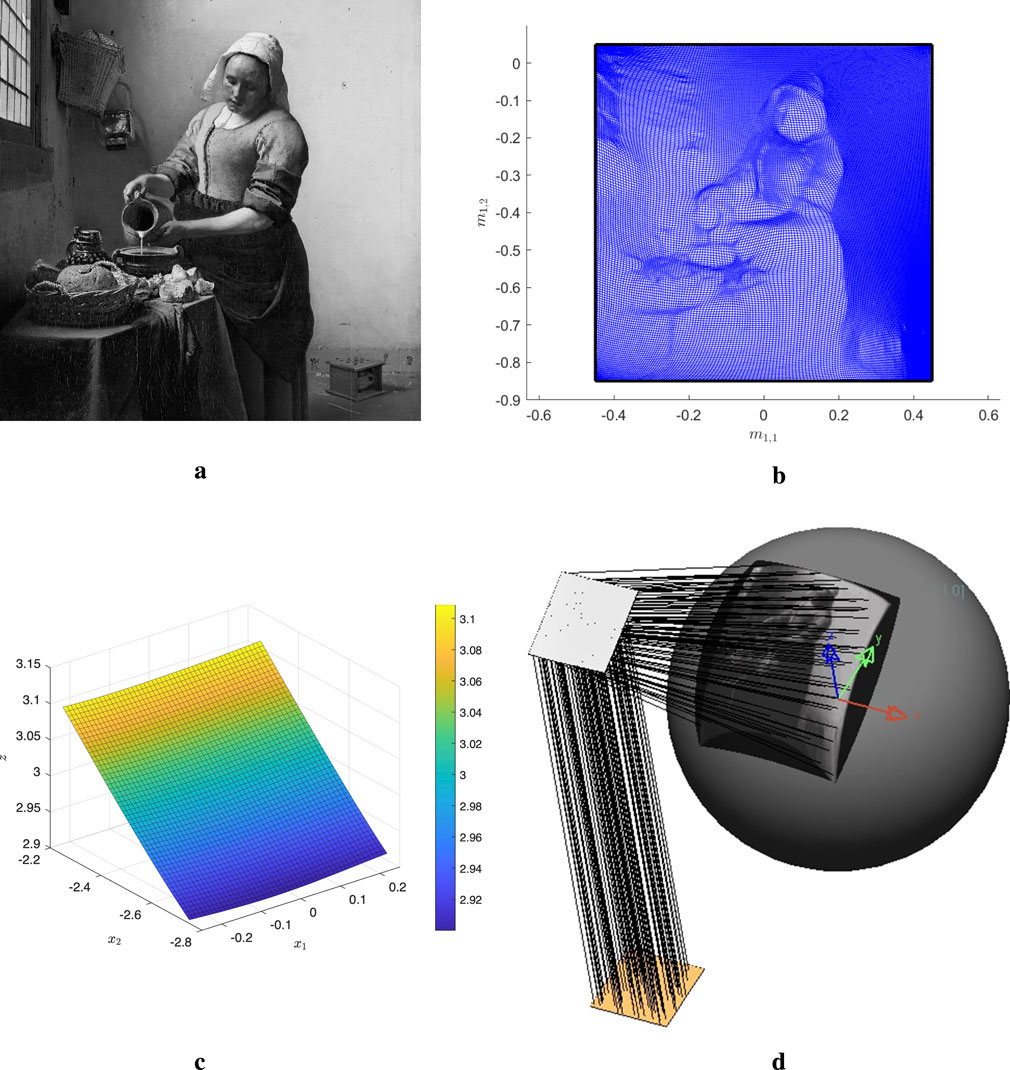
corresponding to the gray-scale image of the TU/e logo given in Figure 6a. Both intensities are scaled such that the global luminous flux balance holds, i.e., Equation 35 for
and
. Both stereographic coordinates are projections from the south pole; cf. Equation 21. The refractive index of the lens
, and we enforce a unique solution for the lens surface by setting
, and therefore,
, corresponding to the central light ray with stereographic source coordinate
and direction vector
; cf. Equation 34b.
For space discretization of the BVPs in (45) and (46), we cover the source domain with a uniform
grid and evaluate 500 iterations of scheme (42)–(43), where the associated functionals are defined in Equation 41. We choose
. The computational time, on a laptop with Intel Core i7 - 11800 H 2.30 GHz processor and a RAM of 16.0 GB, is
s (7.39 min). The optical mapping, computed as an image of the source grid, is shown in Figure 6b, and clearly exhibits the TU/e-logo. The computed freeform lens with a ray traced target intensity pattern is shown in Figure 6c. This intensity pattern is computed with the commercial software code LightTools using
rays and clearly resembles the desired intensity. The corresponding (normalized) 3D illuminance distribution, projected on the plane
, is shown in Figure 6d.
7.2 Parallel-to-near-field reflector
We consider a reflector that converts a uniform source emittance
into the illuminance
corresponding to the gray-scale image of the painting ‘the Milkmaid’ by Johannes Vermeer as shown in Figure 7a, projected on a spherical target surface. The source domain
and the target domain is located on the northern hemisphere of the unit sphere given by
with
. The parameters
and
are both Cartesian coordinates. The emittance and illuminance are scaled such that the global flux balance holds, i.e., Equation 38 for
and
. We enforce a unique solution for the location of the reflector by setting
, where
is the center point of the source domain
.
To discretize the BVPs in Equations 45, 48, we cover the source domain
with a uniform
grid and 500 times apply the iteration scheme defined in Equations 49, 43. The associated functionals are defined in Equation 41, where we choose
, and Equation 47. On the same laptop/processor, the computational time is 496.63 s (8.28 min). The optical map as image of the uniform rectangular source grid is shown in Figure 7b. Clearly, the girl shown in Figure 7a is recognizable in optical mapping as grid points come closer together in regions of high contrast, showing her contours. The sag map of the reflector is shown in Figure 7c.
To verify the reflector computed by the least-squares algorithm, we used LightTools. Implementing the reflector coordinates into this code and specifying the uniformly distributed rectangular source along with the curved target surface, we obtained the reflector system illustrated in Figure 7d, where only 50 rays are shown. The resulting target intensity was obtained tracing
rays. The image of the ‘Milkmaid’ is clearly visible, confirming the validity of the reflector computed by the least-squares algorithm.
8 Concluding remarks
We have presented a systematic and generic derivation of the governing equations for inverse optical design. Using Hamilton’s characteristic functions, we could derive a geometrical equation defining the shape/location of the optical surface(s). From this equation, applying concepts from optimal transport theory, we derived equations for the optical map. To close the model, we presented a generic conservation law of luminous flux. Combining all equations, we derived the luminous flux constraint. Subsequently, we elaborated the generic model in three different models of increasing complexity, on the basis of three example optical systems. We briefly outlined numerical least-squares methods for all models and demonstrated their performance for a few examples.
We intend to expand our research on inverse methods along the following lines. First, we will adjust our numerical methods to incorporate two target distributions; second, we will develop mathematical models and numerical methods for catadioptric systems, where light rays propagate via different paths from the source to target, and finally, and probably the most challenging, we intent to generalize our models and numerics to optical systems with finite sources, as opposed to zero-étendue sources.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.
Author contributions
JT: writing–original draft and writing–review and editing. KM: writing–original draft and writing–review and editing. MA: writing–review and editing. LK: writing–review and editing. PB: writing–review and editing. WI: writing–review and editing.
Funding
The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work was partially supported by the Dutch Research Council (Dutch: Nederlandse Organisatie voor Wetenschappelijk Onderzoek–NWO) through the (grants P15-36 and P21-20).
Acknowledgments
The authors would like to thank R. Beltman from Signify for executing all LightTools simulations.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Generative AI statement
The author(s) declare that no Generative AI was used in the creation of this manuscript.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Filosa C. Phase space ray tracing for illumination optics. Eindhoven: Eindhoven University of Technology (2018). PhD Thesis.
Google Scholar
2. Santambrogio F. Optimal transport for applied mathematicians. Birkäuser, New York: Springer (2015).
Google Scholar
3. Gutiérrez C. The Monge-Ampère equation. 2nd ed. Switzerland: Birkhäuser: Springer International Publishing AG (2016).
Google Scholar
4. Romijn L. Generated Jacobian equations in freeform optical design. Eindhoven: Eindhoven University of Technology (2021). PhD Thesis.
Google Scholar
5. Froese B. A numerical method for the elliptic Monge–Ampère equation with transport boundary conditions. SIAM J Scientific Comput (2012) 34:A1432–59. doi:10.1137/110822372
CrossRef Full Text | Google Scholar
6. Benamou J, Froese B, Oberman A. Numerical solution of the optimal transportation problem using the Monge–Ampère equation. J Comput Phys (2014) 260:107–26. doi:10.1016/j.jcp.2013.12.015
CrossRef Full Text | Google Scholar
7. Kawecki E, Lakkis O, Pryer T. A finite element method for the Monge-Ampère equation with transport boundary conditions. arXiv preprint arXiv:1807 (2018).
Google Scholar
8. Caffarelli L, Oliker V. Weak solutions of one inverse problem in geometric optics. J Math Sci (2008) 154:39–49. doi:10.1007/s10958-008-9152-x
CrossRef Full Text | Google Scholar
9. Kitagawa J, Mérigot Q, Thibert B. Convergence of a Newton algorithm for semi-discrete optimal transport. J Eur Math Soc (2019) 21:2603–51. doi:10.4171/jems/889
CrossRef Full Text | Google Scholar
11. Gallouet A, Mérigot Q, Thibert B. A damped Newton algorithm for generated Jacobian equations. Calculus of Variations and Partial Differential Equations (2021) 61:49–59. doi:10.1007/s00526-021-02147-7
CrossRef Full Text | Google Scholar
12. Caboussat A, Glowinski R, Sorensen D. A least-squares method for the numerical solution of the Dirichlet problem for the elliptic Monge − Ampère equation in dimension two. ESAIM: Control, Optimisation and Calculus of Variations (2013) 19:780–810. doi:10.1051/cocv/2012033
CrossRef Full Text | Google Scholar
13. Prins C, Beltman R, ten Thije Boonkkamp J, IJzerman W, Tukker T. A least-squares method for optimal transport using the Monge-Ampère equation. SIAM J Scientific Comput (2015) 37:B937–61. doi:10.1137/140986414
CrossRef Full Text | Google Scholar
14. Yadav N, ten Thije Boonkkamp J, IJzerman W. A Monge-Ampère problem with non-quadratic cost function to compute freeform lens surfaces. J Sci Comput (2019) 80:475–99. doi:10.1007/s10915-019-00948-9
CrossRef Full Text | Google Scholar
16. Romijn L, ten Thije Boonkkamp J, IJzerman W. Inverse reflector design for a point source and far-field target. J Comput Phys (2020) 408:109283. doi:10.1016/j.jcp.2020.109283
CrossRef Full Text | Google Scholar
17. Romijn L, Anthonissen M, ten Thije Boonkkamp J, IJzerman W. The generating function approach for double freeform lens design. J Opt Soc Am A (2021) 38:356–68. doi:10.1364/OE.438920
PubMed Abstract | CrossRef Full Text | Google Scholar
18. Romijn L, ten Thije Boonkkamp J, Anthonissen M, IJzerman W. An iterative least-squares method for generated Jacobian equations in freeform optical design. SIAM J Scientific Comput (2021) 43:B298–B322. doi:10.1364/OE.438920
CrossRef Full Text | Google Scholar
19. Luneburg R. Mathematical theory of optics. Berkeley and Los Angeles: University of California Press (1966).
Google Scholar
20. Born M, Wolf E. Principles of optics: electromagnetic theory of propagation, interference and diffraction of light. 5th ed. Oxford: Pergamon Press (1975).
Google Scholar
21. Kevorkian J. Partial differential equations: analytical solution techniques. Pacific Grove, California: Brooks/Cole (1990).
Google Scholar
22. Guillen N. A primer on generated Jacobian equations: geometry, optics, economics. Notices Am Math Soc (2019) 66:1401–11. doi:10.1090/noti1956
CrossRef Full Text | Google Scholar
23. Yadav N. Monge-Ampère problems with non-quadratic cost function: application to freeform optics. Eindhoven: Eindhoven University of Technology (2018). PhD Thesis.
Google Scholar
26. Anthonissen M, ten Thije Boonkkamp J, IJzerman W. Unified mathematical framework for a class of fundamental freeform optical systems. Opt Express (2021) 29:31650–64. doi:10.1364/OE.438920
PubMed Abstract | CrossRef Full Text | Google Scholar
27. Prins C. Inverse methods for illumination optics. Eindhoven: Eindhoven University of Technology (2014). PhD Thesis.
Google Scholar
28. Beltman R, ten Thije Boonkkamp J, IJzerman W. A least-squares method for the inverse reflector problem in arbitrary orthogonal coordinates. J Comput Phys (2018) 367:347–73. doi:10.1016/j.jcp.2018.04.041
CrossRef Full Text | Google Scholar
29. Yadav N, Romijn L, ten Thije Boonkkamp J, IJzerman W. A least-squares method for the design of two-reflector optical systems. J Phys Photon (2019) 1:034001. doi:10.1088/2515-7647/ab2db3
CrossRef Full Text | Google Scholar
30. Courant R, Hilbert D. Methods of mathematical physics, 2. New York: John Wiley and Sons (1989). doi:10.1002/9783527617210
CrossRef Full Text | Google Scholar
31. Wang C, Luo Y, Li H, Zang Z, Xu Y, Han Y, et al. Extended ray-mapping method based on differentiable ray-tracing for non-paraxial and off-axis freeform illumination lens design. Optics Express (2023) 31:30066–30078.
PubMed Abstract | CrossRef Full Text | Google Scholar
32. Heemels A, de Koning B, Möller M, Adam A. Optimizing freeform lenses for extended sources with algorithmic differentiable ray tracing and truncated hierarchical B-splines. Optics Express (2024) 32:9730–9746.
PubMed Abstract | CrossRef Full Text | Google Scholar
33. Doskolovich L, Bykov D, Andreev E, Bezus E, Oliker V. Designing double freeform surfaces for collimated beam shaping with optimal mass transportation and linear assignment problems. Optics Express (2018) 26:24602–24613.
PubMed Abstract | CrossRef Full Text | Google Scholar
34. Doskolovich L, Bykov D, Mingazov A, Bezus E. Optimal mass transportation and linear assignment problems in the design of freeform refractive optical elements generating far-field irradiance distributions. Optics Express (2019) 27:13083–13097.
PubMed Abstract | CrossRef Full Text | Google Scholar
Nomenclature
Scalar variables
cost function
distance between the points
and
optical distance, i.e., optical path length
as function of the position vectors
and
illuminance at a near-field target
generic flux density of the source
generic flux density of the target
generating function
inverse of generating function
intensity of the point source
intensity of the far-field target
factor in the area element
on
generated by
and parameterized by
emittance of the planar source
refractive index field
arc length along a curve
representing a ray
angular characteristic (function)
Kantorovich potential for source domain
Kantorovich potential for target domain
point characteristic (function)
mixed characteristic (function) of the first kind
mixed characteristic (function) of the second kind
coordinate along the optical axis
phase of an electromagnetic wave
optical path length between the points
and
Vectors
2D momentum vector of a ray
2D position vector of a ray
3D position vector of an arbitrary point
3D unit direction/tangent vector of a ray at the source plane
3D unit direction/tangent vector of a ray at the target plane
3D unit direction/tangent vector at an arbitrary point of a ray
2D vector parameterizing the source domain
2D vector parameterizing the target domain

 J. H. M. ten Thije Boonkkamp
J. H. M. ten Thije Boonkkamp K. Mitra1
K. Mitra1 M. J. H. Anthonissen
M. J. H. Anthonissen