Systematic study of the propagation of uncertainties to transfer observables

A systematic study of parametric uncertainties in transfer reactions is performed using the recently developed uncertainty quantified global optical potential (KDUQ). We consider reactions on the doubly-magic spherical nucleus ⁴⁸Ca and explore the dependence of the predicted $(d,p)$ angular distribution uncertainties at different beam energies and for different properties of the final single-particle state populated by the reaction. Our results show that correlations between the uncertainties associated with the bound state potential and with the optical potentials may be important for correctly determining the uncertainty in the transfer cross sections (in our case, these do not add in quadrature). In general, we find small uncertainties in the predicted transfer observables: half-width of the 68% credible interval is roughly $5-10$%, which is comparable to the experimental error on the transfer data. Finally, our results show that the relative magnitude of the parametric uncertainty in transfer observables increases with the beam energy and does not depend strongly on the properties of the final state.

1 Introduction

Transfer reactions are widely used in nuclear experimental studies, either for extracting astrophysical information that cannot be obtained directly or for studying properties of the nucleus of interest (e.g., Refs. [1–11]). However, reaction theory is essential to interpret transfer reactions measurements [12, 13]. The properties we wish to extract from transfer reactions, such as spectroscopic factors (SF), asymptotic normalization coefficients (ANC) or neutron capture rates, depend strongly on the normalization of the transfer cross section while the model used to describe the reaction carries uncertainties that affect the normalization [12]. Thus, for a reliable interpretation of transfer measurements, it is crucial that we understand the uncertainties associated with the theory.

In this work we focus on $(d,p)$ reactions. The preferred model for interpreting single-nucleon $(d,p)$ transfer reactions is the adiabatic wave approximation (ADWA) [14, 15]. This model has the advantage that it includes deuteron breakup non-perturbatively, without increasing the computational cost as compared to the Distorted Wave Born Approximation (DWBA). It has also been shown to fare well compared to the state-of-the-art models in the field [16, 17]. In ADWA, the input interactions are nucleon optical potentials, in addition to potentials that bind the deuteron and the final state. From all the studies performed so far, optical potentials are the dominant source of uncertainty in ADWA predictions for transfer $(d,p)$ cross sections. It is important not only to quantify those uncertainties but also understand how they may change with beam energy and specific properties of the final state being produced.

In the last few years, many studies have been performed to quantify the uncertainty in $(d,p)$ reactions using Bayesian statistics [18–21]. These studies use optical potentials fitted for one projectile-target combination, at a specific beam energy, constrained with a single or a couple data sets. Typically, proton or neutron elastic scattering data at the relevant beam energies are used in a Bayesian calibration to obtain parameter posterior distributions for the optical potentials. The uncertainties in the $(d,p)$ cross sections for the reaction are then obtained by sampling these posterior distributions, which are then propagated using the ADWA framework. Uncertainties obtained in [18–21] are large, in part due to the choice of the likelihood function [22]. By propagating uncertainties from each optical potential independently, no correlations between the neutron and proton optical potentials in the entrance channel are included, nor between those and the proton optical potential in the exit channel. Recent work on charge-exchange reactions has shown that the inclusion of such correlations can make a significant difference in the uncertainty estimate [23, 24].

Moreover, Ref. [21] studies the uncertainties coming from the single-particle potential that binds the neutron in the final state in $(d,p)$ reactions, in addition to the uncertainties in the optical potential. By constraining the geometry of the binding potential with the asymptotic normalization coefficient, one can greatly reduce the uncertainties (see Figure 2 of Ref; [21]). If the ANC squared is poorly known the uncertainties in the $(d,p)$ cross section are very large. If the ANC squared is known to say 10% then the uncertainties in the cross section are greatly reduced.

The recent development of an uncertainty-quantified global optical model (KDUQ) [25], based on the original work [26], provides another avenue to study the uncertainties in reactions. Propagating the parametric uncertainties from KDUQ to reaction observables has been done for specific cases (e.g., for knockout and transfer [27, 28] and charge-exchange [24]). In general, the uncertainties due to optical potentials in reaction observables can be influenced by many different details of the reaction process [29, 30]. Due to strong non-linearities in the reaction model, it is important to study these uncertainties more systematically to understand the impact of correlations in optical potential parameters and whether there are general features that emerge. KDUQ provides a unified effective framework to perform this study.

This work is a systematic study of the uncertainties associated with the optical potentials in transfer $(d,p)$ observables. We use ⁴⁸Ca${(d,p)}^{49}$Ca to set up the problem and consider a range of beam energies as well as a variety of final bound states with different properties. In Section 2, we briefly describe the reaction and statistical models used. In Section 3.1, we compare the predictions obtained with KDUQ to existing elastic scattering and transfer data, to establish our framework for a realistic case. In the rest of Section 3, we vary beam energies and final bound state properties (separation energy, angular momentum, nodes, etc.) and analyze the dependencies of the resulting uncertainties. Section 4 presents the conclusions of this work.

2 A brief summary of the theory used

2.1 Reaction theory

The finite-range ADWA [14] starts out by considering a full three-body picture for the transfer reaction $A(d,p)B$. As detailed in Ref. [14], it uses Weinberg states to then simplify the T-matrix to

$T^{\mathit{ADWA}}=\langle {\varphi }_{nA}{\chi }_{pB}^{\left(-\right)}|V_{np}|{\varphi }_{np}{\chi }_d^{ad}\rangle .(1)$

In Equation 1, ${\varphi }_{np}$ and ${\varphi }_{nA}$ correspond to the deuteron bound state and single-particle state of the final nucleus B, $V_{np}$ is the neutron-proton interaction and ${\chi }_{pB}$ is the outgoing distorted wave of the proton relative to the final nucleus $B$, obtained with the optical potential $U_{pB}$ at the energy of the outgoing proton. The adiabatic distorted wave ${\chi }_d^{ad}$ is generated from the effective adiabatic potential:

$U_{Ap}^{\text{eff}}=-\langle {\varphi }_o|V_{np}\left(U_{nA}+U_{pA}\right)|{\varphi }_o\rangle ,$

where $U_{nA}$ and $U_{pA}$ are the nucleon optical potentials between neutron/proton and the target evaluated at half the deuteron incoming energy. The wave function ${\varphi }_o$ is the first Weinberg basis state, which is directly proportional to the deuteron bound state [14]. The T-matrix of Equation 1 assumes that the remnant term $(U_{nA}-U_{pB})$ is negligible. In ADWA calculations, the sources of parametric uncertainties are therefore the optical potentials used to generate the scattering states and the single-particle potentials used to model bound states.

More details about the ADWA and how to obtain numerical solutions for bound and scattering states can be found in Ref. [31]. In this work, we use the code NLAT [15] to perform all ADWA transfer calculations and the code FRESCO [32] to perform the elastic scattering calculations.

2.2 Statistical model

As mentioned in Section 1, we use the global optical potentials KDUQ [25] for all nucleon-nucleus interactions needed in the reaction model of Section 2.1, which is valid for $24\le A\le 209$ and 1 keV $\le E\le 200$ MeV. In this work, we chose the democratic version of KDUQ which weighs every data point equally¹. By performing a Bayesian calibration using a large set of reaction data (including nucleon elastic scattering angular distributions and analyzing powers, neutron total cross sections and proton reaction cross sections, all on stable nuclei), the authors of KDUQ obtained parameter posterior distributions and correlations for the 46 parameters of their global optical model. In this work, we use the 416 samples of their posterior distributions, published in Ref. [25], to compute the uncertainties in the transfer cross sections. We quantify the uncertainty in the transfer angular distribution in terms of the relative half-width of the $1\sigma$ credible interval at the peak of the angular distributions (corresponding to a scattering angle ${\theta }_{\mathit{max}}$):

${\epsilon }_{68\%}=\frac{{\sigma }_{\mathit{max}}^{68\%}\left({\theta }_{\mathit{max}}\right)-{\sigma }_{avg}^{68\%}\left({\theta }_{\mathit{max}}\right)}{{\sigma }_{avg}^{68\%}\left({\theta }_{\mathit{max}}\right)}(2)$

$\text{with}{\sigma }_{avg}^{68\%}\left({\theta }_{\mathit{max}}\right)=\frac{{\sigma }_{\mathit{max}}^{68\%}\left({\theta }_{\mathit{max}}\right)+{\sigma }_{\mathit{min}}^{68\%}\left({\theta }_{\mathit{max}}\right)}{2}$

The test case we focus on is based on the ⁴⁸Ca${(d,p)}^{49}$Ca (g.s) reaction. Our choice is mainly motivated by the availability of elastic and transfer data. Moreover, since no ⁴⁸Ca data were included in the KDUQ corpus, the analysis performed in this work share similar challenges as the ones on transfer data populating exotic nuclei. All optical potentials are taken consistently from KDUQ and evaluated at the relevant energies, i.e., all three nucleon-nucleus optical potentials are derived from the same KDUQ sample. This consistent treatment hence includes correlations between the various optical potential parameters. For describing the final state of the neutron, we take a standard radius and diffuseness $r_R=1.25$ fm and $a_R=0.65$ fm (STD) or we take the geometry of the real part of the KDUQ interaction (KDUQ-real). In both cases, we adjust the depth to reproduce the neutron separation energy and the parameters in the spin orbit term for the final bound-state potential are fixed: the depth is $V_{so}=6$ MeV, the radius is $r_{so}=1.25$ fm and the diffuseness is $a_{so}=0.65$ fm. In the physical ⁴⁹Ca ground state, the neutron is in a $1p3/2$ orbital, bound by $S_n=5.146$ MeV. We also consider in Section 3.3 other configurations for the final state being populated in the $(d,p)$ reaction.

It must be underlined that KDUQ posterior distributions contain no constraints from bound state data. Our assumption is to consider that the geometry of the mean field generated by the target nucleus does not change considerably from bound to scattering states. This is consistent with the KDUQ assumption, since it uses an energy-independent parametrization for the radius and diffuseness of the real term, and these parameters are well constrained by the Bayesian calibration. When using 416 samples for the real radius and diffuseness of KDUQ and refitting the real depth to reproduce the correct neutron separation energy (KDUQ-real). The resulting ANC-squared ${\mathcal{C}}^2$ distribution (not shown) is slightly multimodal and is well constrained: its half-width is about 5%. Interestingly, the value predicted by KDUQ-real ${\mathcal{C}}^2=28.6\pm 1.3$ ${\text{fm}}^{-1}$ is consistent with the value ${\mathcal{C}}^2=32.1\pm 3.2$ ${\text{fm}}^{-1}$ [33] determined from the analysis of various ⁴⁸Ca${(d,p)}^{49}$Ca (g.s.) datasets at various energies, i.e., 2 MeV, 13 MeV, 19 MeV, 30 MeV and 56 MeV [34–36]. This surprising agreement seems fortuitous, as ANCs for states of ⁸⁷Kr, ⁸B and ¹⁰B predicted by KDUQ do not match the values extracted from transfer and breakup data [37–39]. The KDUQ-real posteriors obtained in this way will also be used to quantify uncertainties from the neutron singe-particle interaction in ${\varphi }_{nA}$.

3 Results

3.1 The physical ⁴⁸Ca (d,p)⁴⁹Ca (g.s) reaction

Optical potentials are determined primarily from observables that are sensitive to the on-shell T-matrix. Transfer observables are also sensitive to properties of the T-matrix off-shell. It is thus not guaranteed, even if the optical potentials reproduce the corresponding elastic channels, that they describe the transfer data. Using the reaction ⁴⁸Ca${(d,p)}^{49}$Ca (g.s) at 19 MeV, for which there is data [35].² We compare predictions using KDUQ with the corresponding data to assess the quality of the uncertainty quantification. We select nucleon elastic scattering data that is close to the energies relevant to the transfer reaction of interest ($E_n=9.5$ MeV and $E_p=9.5$ MeV in the entrance channel and $E_p=21.9$ MeV in the exit channel) and compare the credible intervals generated from the KDUQ parameter posteriors with the actual data (with the quoted experimental error bars) [40–42]. The corresponding angular distributions are shown in Figure 1: (a) neutron elastic scattering for $E_{\mathit{lab}}=12$ MeV, (b) proton elastic scattering for $E_{\mathit{lab}}=14$ MeV, (c) proton elastic scattering for $E_{\mathit{lab}}=25$ MeV. Note that the KDUQ global optical potential was not fitted on these data sets. The dark (light) shade corresponds to the 68% (95%) credible intervals³.

Figure 1

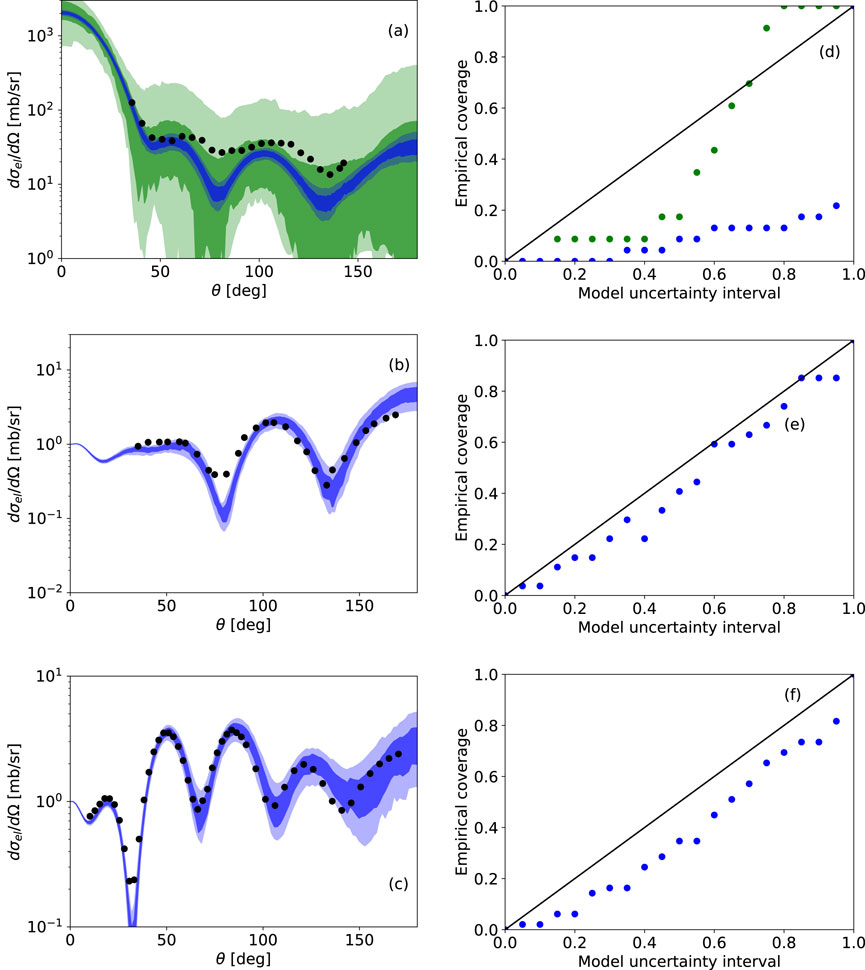
Figure 1. Angular distributions for the elastic scattering of (A) $n{+}^{48}$Ca at 12 MeV, (B) $p{+}^{48}$Ca at 14 MeV and (C) $p{+}^{48}$Ca at 25 MeV. The dark and light shaded blue bands correspond respectively to the 68% and 95% credible intervals obtained with optical potentials derived from the KDUQ posterior distribution. The green bands are obtained with rescaled KDUQ posterior distributions (referred as KDUQ-n) in the text. These predictions are compared with data from Refs. [40–42]. (D–F) Corresponding empirical coverage for elastic-scattering data.

The empirical coverage provides a sanity check for uncertainty quantification. Our empirical coverages for a x% model uncertainty are calculated as the number of data points, including a x% experimental error, that fall into the theoretical x% credible interval divided by the total number of data points in an angular distribution. These are shown in Figures 1D–F for the corresponding three elastic scattering examples. In an ideal situation, the predicted empirical coverage should line up with the black diagonal line⁴. In our calculations for proton elastic scattering, empirical coverages calculated at the high-confidence level are only slightly underestimated. However, for neutron scattering, there is a severe mismatch. This suggests that, in this case, the error on the data [40] and/or on the KDUQ parameters are seriously under-reported. To include unaccounted-for uncertainties, we have inflated the width of the posterior distributions of the depths, radii and diffuseness of the neutron-target potential, so that we can reproduce the correct empirical coverage specifically for $1\sigma$. We do this by approximating the parameter distributions of the neutron-target potential $U_{nA}$ to a multivariate Gaussian. We then rescale the covariance matrix by a factor: it turns out that we need to rescale these by 38, effectively rescaling uncertainties by a factor of $\sqrt{38}\sim 6$. Note that such approach, although simplistic, allows to keep the correlations between the optical potentials parameters informed by the large KDUQ corpus. We refer to this as KDUQ-n. Replacing KDUQ by KDUQ-n for $U_{nA}$ results in the green bands in Figure 1A and the green dots in Figure 1D. As can be seen, the empirical coverage obtained for the 68% is now exactly 68%.

We now use these parameter posterior distributions and propagate the uncertainties to the ⁴⁸Ca${(d,p)}^{49}$Ca (g.s.) reaction at beam energy $E_{\mathit{lab}}=19$ MeV. In Figure 2, we show the predicted credible intervals for the corresponding transfer angular distributions: we compare the results obtained with the original KDUQ (blue bands) and those obtained when the neutron interaction is replaced by KDUQ-n (green bands). In these calculations, we fix the neutron bound state using the STD geometry (discussed in Section 2.2). Figure 2 already includes the scaling by the SF, taking into account both the optical potential parameter uncertainties propagated in the ADWA model and the experimental error on the transfer data. This is done by adding in quadrature the errors ${\epsilon }_{\mathit{opt}}$ associated with the optical potential and ${\bar{\epsilon }}_{SF}$ resulting from the fitting procedure to the transfer data. The uncertainty ${\epsilon }_{\mathit{opt}}$ is the standard deviation of the 416 SFs minimizing the ${\chi }^2$ obtained from the transfer data and the theoretical predictions, e.g., obtained with each KDUQ sample. The variance ${\bar{\epsilon }}_{SF}^2$ is calculated by averaging the variances on the SFs associated with each of the 416 fits. Further tests have shown that the total uncertainty on the SF is completely dominated by ${\epsilon }_{\mathit{opt}}$ for transfer data errors $\lesssim 10\%$, i.e., the total errors on the SFs are the same regardless of we include ${\bar{\epsilon }}_{SF}$ or not.

Figure 2

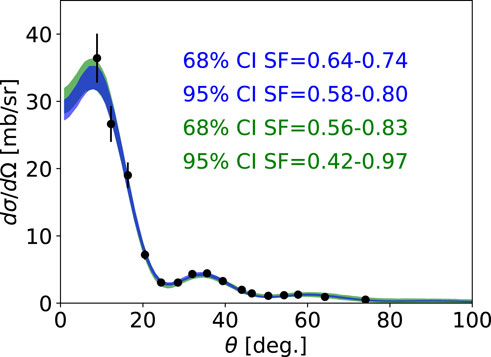
Figure 2. Angular distribution for ⁴⁸Ca${(d,p)}^{49}$Ca (g.s.) at 19 MeV scaled to reproduce the first four forward data point, with the corresponding scaling factors (SFs) and their uncertainties. The shaded blue band corresponds to the 68% credible intervals respectively obtained with optical potentials derived from the same sample of the KDUQ posterior distribution. The green band is obtained using the KDUQ-n posterior distribution for $U_{nA}$ and KDUQ posterior distribution for $U_{pA}$ and $U_{pB}$. These predictions are compared with data from Ref. [35].

The theoretical predictions for $\frac{d\sigma }{d\mathrm{\Omega }}$ agree well with the data. At the $1\sigma$ level, the relative half-width ${\epsilon }_{68\%}$ Equation 2 is 5% (16%) when using KDUQ (KDUQ-n). These uncertainties can be compared with the 20% full-width uncertainty shown in green in Figure 3 of [21] for the same reaction, at slightly higher beam energy. Note that the work in [21] uses local potentials with mock data (with 10% error) and systematically renormalizes the likelihood, effectively increasing the error on both proton and neutron optical potentials. These results demonstrate the benefit of a global parametrization: although there are no ⁴⁸Ca elastic angular distributions in the data corpus used to calibrate the KDUQ parameters, the uncertainties on the transfer predictions are reliable (of the Ca isotopes, the KDUQ data corpus includes only ⁴⁰Ca elastic angular distributions).

Figure 3

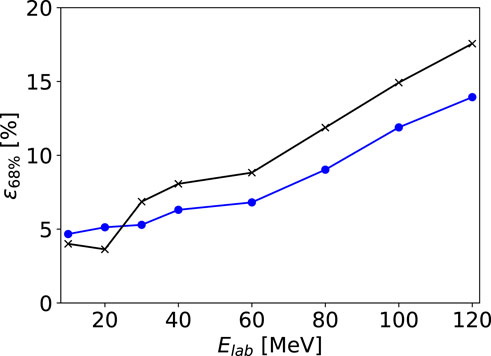
Figure 3. Relative half-width ${\epsilon }_{68\%}$ Equation 2 for ⁴⁸Ca${(d,p)}^{49}$Ca (g.s.), as a function of the beam energy. In blue are the results obtained with nucleon-nucleus interactions needed for the ADWA calculations derived consistently from the same KDUQ sample. The black line corresponds to the situation where all three interactions are derived from different KDUQ samples.

To complement our analysis, we also study the uncertainties associated with the single-particle potential used to generate the final bound state. We quantify its uncertainties using the geometry of the real part of the KDUQ interaction (KDUQ-real), as discussed in Section 2.2. We consider various cases in Table 1 for which we compute the relative half-widths of the transfer angular distribution ${\epsilon }_{68\%}$ and of the extracted SF, which also account for the errors on the experimental transfer data. Specifically, we investigate if the geometry of the single-particle potentials, used to generate the final state, has an impact on the relative uncertainties due to the optical potentials in transfer observables. First, we include only uncertainties in the optical potential, for two choices of single-particle potentials. In the first two lines of Table 1, we compare the results obtained when using the STD single-particle potential ($r_R=1.25$ fm and $a_R=0.65$ fm) and the mean values of the real radius and diffuseness of KDUQ-real ($r_R=1.17$ fm and $a_R=0.689$ fm). One can see that the relative uncertainties stay rather constant, showing that the magnitude of relative uncertainties due to the optical potentials do not depend strongly on the geometry of the single-particle potential in the final state.

Table 1

Table 1. Relative half-width ${\epsilon }_{68\%}$ Equation 2 for⁴⁸Ca${(d,p)}^{49}$Ca (g.s.) at 19 MeV and, in parentheses, the corresponding relative half-width of the $1\sigma$ credible interval of the extracted SFs using the data from Ref. [35]. We consider the KDUQ original samples and the rescaled KDUQ posterior KDUQ-n (discussed in the text). Results are obtained when propagating only the uncertainties due to the optical potentials (first two lines), only the uncertainties due to the single-particle potential (third line) and both uncertainties (last line).

Then, we evaluate the uncertainties due to the choice of single-particle potentials, using the geometry of the real volume term of 416 KDUQ and KDUQ-n samples. In the KDUQ case, the uncertainty half-widths ${\epsilon }_{68\%}$ are below 4% for both the peak of the distribution and the extracted SF, indicating that the KDUQ posterior distributions for $r_R$ and $a_R$ are quite constrained. The magnitude of the uncertainties on the peak of the transfer cross sections are similar to those on the ANC squared (see Section 2.2), suggesting that this reaction is quite peripheral. As expected, the uncertainties when using the KDUQ-n samples are larger. Interestingly, they are scaled by roughly the same factor $\sqrt{38}\sim 6$, as the one used to scale the KDUQ uncertainties (compare left and right column of the third line). This suggests that the uncertainties in the single-particle radius and diffuseness seem to propagate linearly to transfer observables. Finally, we include both the uncertainties due to the single-particle potential and the optical potentials (last line). Contrary to what was found in [21], in both cases KDUQ original and KDUQ-n, the total uncertainties cannot be deduced simply by summing in quadrature the two source uncertainties, hinting at the presence of strong correlations. These correlations are due to the interplay between the extension of the single-particle wavefunction, and the range of the real part of the neutron-target optical potential. Although in [21] the ANC-squared is explicitly used as a constrain, the single-particle potential parameter sampling is independent of the sampling of the optical potential parameters, whereas in this work, KDUQ-real used for the single-particle potential is perfectly correlated to KDUQ (or KDUQ-n) used for the optical potentials.

Having established a realistic foundation for the uncertainty estimates of the angular distributions of the ⁴⁸Ca${(d,p)}^{49}$Ca (g.s.) reaction at $E_{\mathit{lab}}=19$ MeV, for which we can compare to experimental data, we now explore how these uncertainties change with beam energy and how they evolve with various properties of the final bound state. In this exploration, no uncertainty quantification is included for the bound state interactions - the mean field that binds the neutron in the final state is kept fixed. We vary either the kinematics or the structure of the final state, and take the optical potential parameters from the same original KDUQ posterior distributions. This is done in order to show how the same parameter posteriors for optical potentials propagate through the model differently, depending on the details of the reaction. Obviously, because we are not including the additional error in KDUQ-n, nor the uncertainty in the bound state interaction, the overall magnitude of the uncertainty estimates shown in Sections 3.2 and 3.3 are underestimated. It is their variation with beam energy or single-particle properties that matters.

3.2 Uncertainties in transfer reactions with beam energy

We first analyze the dependence of the uncertainties on the beam energy. For this study, we keep the final bound state fixed using the STD single-particle geometry as described in Section 3.1, and take all optical potential posteriors from the original KDUQ parametrization. The relative half-width ${\epsilon }_{68\%}$ Equation 2, evaluated at the peak of the transfer angular distribution for ⁴⁸Ca${(d,p)}^{49}$Ca (g.s.), are shown in Figure 3. There is no convolution with the experimental error on the transfer data in this plot; only the theoretical uncertainties are considered.

We first consider ADWA calculations using all three optical potentials derived consistently from the same KDUQ sample (blue line). We find that the relative half-width ${\epsilon }_{68\%}$ Equation 2 increases with the beam energy⁵. This can be explained by the fact that at higher beam energy, transfer observables become more sensitive to the short-range part of scattering wave functions, which are typically less constrained by observables used to calibrate optical potentials. This explanation was verified by comparing the relative uncertainties obtained when computing the short-range contribution to the radial integral of the T-matrix Equation 1, i.e., considering only $d$-⁴⁸Ca distances smaller than $R<r_R\ast 48^{1/3}$, to the uncertainties associated with the long-range contribution to the T-matrix.

To investigate the importance of correlations in the uncertainties of the optical potentials, we consider ADWA calculations using optical potentials derived from different KDUQ samples (black line). For almost all beam energies, the relative uncertainties are slightly larger than in the previous results, where all potentials were derived consistently from the same KDUQ sample. At the highest beam energies studied, the shift in ${\epsilon }_{68\%}$ is about 25%.

3.3 Dependence on the properties of the final bound state

Next, we consider the effects of different properties of the final bound state, namely, the dependence of the uncertainty with the r.m.s Radius squared $⟨r^2⟩$, the angular momentum $l$, the number of nodes $n_r$ and the separation energy $S_n$.

We first consider the effect of the single-particle potential radius $r_R$ used to generate the final bound state wave function on the reaction ⁴⁸Ca${(d,p)}^{49}$Ca (g.s) at 23 MeV. We take the original $n$-⁴⁸Ca bound wave function, in a $1p3/2$ orbital, and vary the mean field radius parameter in STD in the range $r_R=1.0-1.4$ fm, along with the depth to reproduce the same separation energy. The results are shown in Figure 4: the transfer angular distributions for a range of single-particle potential radii are shown (on the left, panels a–e) and the relative half-width ${\epsilon }_{68\%}$ Equation 2 as a function of the r.m.s Single-particle radius squared (on the right, panel f). The same message is relayed when plotting the uncertainty estimates as a function of the ANC squared.

Figure 4

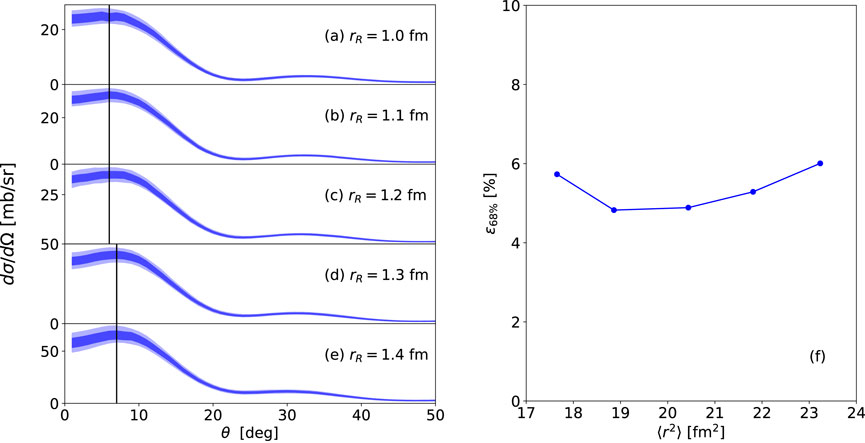
Figure 4. (a–e) Transfer angular distributions for ⁴⁸Ca${(d,p)}^{49}$Ca (g.s.) at 23 MeV for a range of single-particle radii and (f) the relative half-width ${\epsilon }_{68\%}$ Equation 2 as a function of the squared of the single-particle r.m.s radius $⟨r^2⟩$. The vertical black lines in panels (a–e) represent the position of the peaks of the transfer distribution ${\theta }_{\mathit{max}}$.

We find that the diffraction pattern of the transfer angular distributions do not change significantly with radius. Expectedly, the magnitude of the transfer cross section increases with the single-particle potential radius $r_R$. Since these reactions are primarily peripheral, they scale with the ANC squared, which in turn is directly related to the r.m.s radius squared. However, the percent uncertainty remains roughly constant and small, similar to what was observed in Table 1. Further tests have shown that the same conclusions, i.e., independence of the shape, larger magnitude, small and constant uncertainties for the transfer cross sections, can be drawn when increasing the diffuseness $a_R$.

Next, we consider the dependence on the separation energy of the final state, of the uncertainty for the transfer cross section due to the optical potentials. We fix the STD geometry for the neutron single-particle potential to the original values ($=1.25$ fm and $a_R=0.65$ fm) and adjust the depth of this interaction to reproduce the neutron separation energies $S_n=1.146$-15.146 MeV in the $1p3/2$ wave. We repeat the procedure considering a bound state in a $0p3/2$ orbital. The corresponding wave functions are shown in Figures 5A,B. The lower the separation energy, the more extended is the single-particle wave function. The resulting $(d,p)$ angular distributions in Figure 6, panels (a-h) (resp. (i-n)) are obtained with a final bound state in the $1p3/2$ (resp. $0p3/2$) wave. In both cases, the peak of the angular distribution shifts to large angles for larger separation energy, as this directly increases the Q-value for the reaction and the momentum matching. The magnitude of the cross section is also affected: the cross sections are larger for bound states with smaller separation energies. This is due to the spatial extension of the final bound-state wave function.

Figure 5

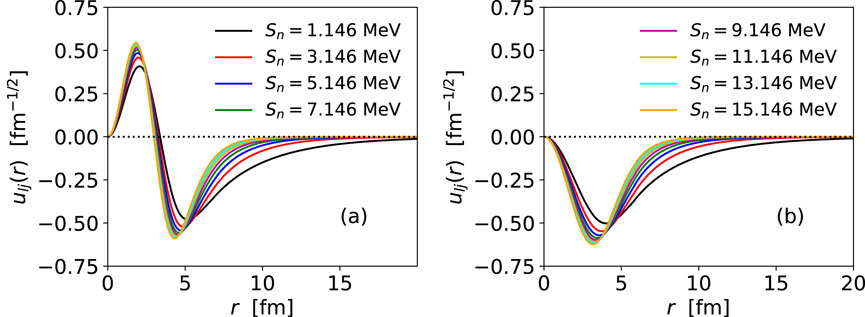
Figure 5. ⁴⁸Ca s. p. Wave function for a $n$ in a (a) $1p3/2$ and (b) $0p3/2$ states reproducing various separation energies $S_n=1.146$-15.146 MeV.

Figure 6

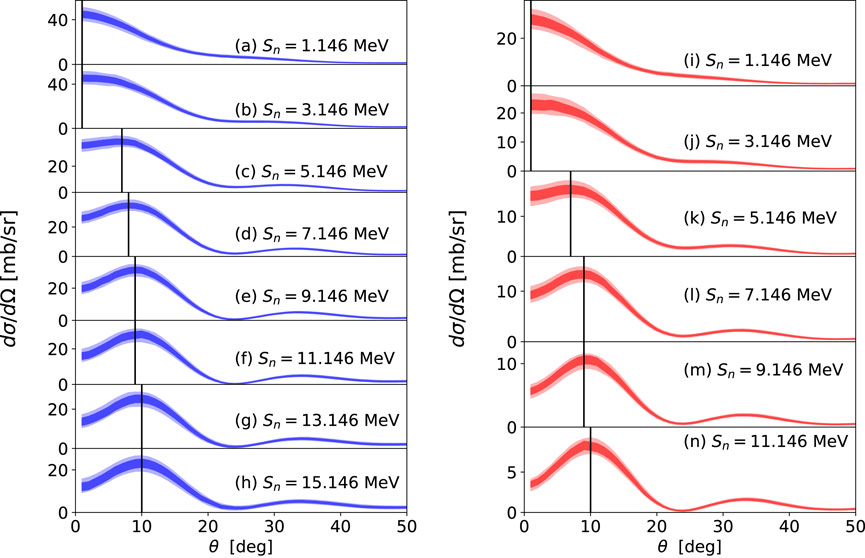
Figure 6. Transfer angular distributions for ⁴⁸Ca${(d,p)}^{49}$Ca (g.s.) at 23 MeV, for different wave function shown in Figure 5. Panels (a–h) (resp. (i–n)) are obtained with ⁴⁸Ca s. p. Wave function for a $n$ in a $1p3/2$ (resp. $0p3/2$). The vertical black lines in panels (a–h) represent the position of the peaks of the transfer distribution ${\theta }_{\mathit{max}}$.

The resulting relative half-width ${\epsilon }_{68\%}$ Equation 2 are summarized in Figure 7. Here we include not only the uncertainties due to the optical potentials for transfer observables populating a bound state in the $1p3/2$ orbital (blue) and in the $0p3/2$ orbital (red), but also in the $1s1/2$ orbital (magenta). The uncertainties remain small (below 10%), regardless of separation energy, the number of nodes $n_r$ and the angular momentum $l$ of the neutron orbital in the final state.

Figure 7

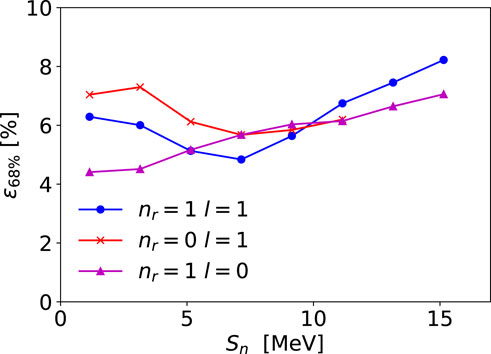
Figure 7. Relative half-widths ${\epsilon }_{68\%}$ Equation 2 for various cases: the blue dots correspond to transfer cross sections populating a $1p3/2$ state, the red crosses to the population of a $0p3/2$ state and the magenta triangles to the population of a $1s1/2$ state. The corresponding single-particle wave functions and transfer observables are plotted in Figures 5, 6.

4 Conclusion

In this work, we perform a systematic study of parametric uncertainties in $(d,p)$ reactions, and their sensitivity to the kinematics of the reaction, as well as to the properties of the final bound state. The results were obtained using the posterior distribution of the global optical potential KDUQ, enabling us to study the impact of optical potential correlations on transfer observables.

By first analyzing a realistic case, we show that for proton scattering off the doubly-magic spherical nucleus ⁴⁸Ca, the elastic-scattering cross sections predicted with the KDUQ global optical potential reproduce well the available scattering data. The empirical coverage lies close to the ideal case, i. e., the diagonal, demonstrating the reliability of the uncertainty estimates of the KDUQ optical potential. However, KDUQ does not reproduce well the neutron scattering data on ⁴⁸Ca, suggesting that either the error on the data are seriously under-reported or the uncertainties of KDUQ are unrealistically small. To account for this, we rescale the KDUQ posterior to obtain an ideal empirical coverage at the $1\sigma$ level. By propagating the posterior distributions in a ADWA model, we find that the relative half-width of the $1\sigma$ credible interval at the peak of the transfer angular distributions is about $5\%$ when using the KDUQ parameters, and 25$\%$ when using the rescaled KDUQ-n parameters. Moreover, we note that the uncertainties due to the single-particle binding potentials are below 5% when using KDUQ and 25% for the rescaled KDUQ-n. Interestingly, our results also show that, in transfer observables, the two uncertainties (from the single-particle binding potential and from the optical potentials) do not add in quadrature. This suggests the impact of correlations between the single-particle binding potential and the optical potential parameters is significant.

Then fixing the geometry of the single-particle potentials and considering the same KDUQ posterior distribution, we investigate how the uncertainties in transfer observables are influenced by the beam energy of the reaction and the properties of the final bound state. Since the same KDUQ posterior parameters are taken in all cases, the different uncertainties do not come from the evolution of KDUQ uncertainties across nuclei or with the beam energy, but are a direct consequence on how uncertainties propagate through the model differently, depending on the details of the reaction.

We show that at higher beam energy, the uncertainties in transfer observables increase. This is a direct consequence of the radial range probed by transfer reactions at various beam energies: transfer reactions at higher beam energies are more sensitive to the short-range part of the T-matrix, which is not well constrained for optical potentials fitted on elastic observables. We find that the correlations in the optical potentials used to generate the scattering states can change the uncertainty estimate by $20-25$%.

We also investigate how uncertainties due to optical potentials depend on the properties of the final bound state: we vary the geometry of the single-particle potential, the binding energy, the orbital angular momentum and the number of nodes. As expected, the magnitude and the shape of the transfer cross sections change, as they are influenced by the spatial extension of the bound-state wave function, its orbital angular momentum and the $Q$-value of the reaction. Nevertheless, the relative half-widths ${\epsilon }_{68\%}$ Equation 2 remain below 10% for all the cases covered in this study. When using KDUQ, the magnitude of the optical model uncertainties on transfer observables is not strongly dependent on the properties of the bound state.

Although our results are quite general, there were important simplifying assumptions that should be kept in mind. First, our analysis does not account for uncertainties associated with the ADWA approximation to the three-body dynamics. In particular, the neglect of the remnant term is likely to become inaccurate for reactions on light nuclei or populating halo final states. Second, we use the same KDUQ posterior distributions for all cases. This assumption likely leads to an underestimation of parametric uncertainties for transfer reactions at higher beam energies, since KDUQ’s relative uncertainties are larger at higher energy (as illustrated in the volume integral in Figure 13 of Ref; [25]). Finally, the KDUQ posterior distribution we chose is likely unrealistic for nuclei with low separation energies, since these isotopes are far from the valley of stability. No data on unstable nuclei or deformed nuclei were included in the calibration of KDUQ and, therefore, one expects the uncertainties to grow substantially as we move to more exotic territory.

This systematic study enables us to draw three important take-away points. First, for well constrained potentials, such as KDUQ, small uncertainties in transfer observables can be expected, typically around 5%–10%. Second, there are significant correlations between the single-particle potential and optical potential parameters that impact the estimated uncertainties on the transfer. This argues for a framework where bound state data and scattering data can both be used to constrain the same interaction consistently, something that is obtained by imposing the dispersive relation [43]. We should expect that, because in the dispersive optical model bound state data is used to the potential, it may lead to a better constrained off-shell part of the T-matrix, hence reducing the uncertainties on reaction observables that do not solely depend on the on-shell properties (such as elastic scattering). Third, our results show that the relative uncertainty estimates of transfer angular distributions are not sensitive to detailed properties of the neutron orbital in the final state populated by the transfer reaction.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

CH: Conceptualization, Data curation, Formal analysis, Investigation, Software, Visualization, Writing – original draft, Writing – review and editing. FN: Conceptualization, Formal analysis, Investigation, Writing – original draft, Writing – review and editing.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. The work of FN was in part supported by the U.S. Department of Energy grant DE-SC0021422 and National Science Foundation CSSI program under award No. OAC-2004601 (BAND Collaboration).

Acknowledgments

CH and FN. thank Kyle Beyer, Manuel Catacora-Rios, Garrett King and other members of the few-body reaction group at MSU for their careful reading of the manuscripts and their comments. CH thanks Cole Pruitt and Gregory Potel for interesting discussions regarding the results of this work. We gratefully acknowledge computational support from iCER at Michigan State University.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The handling editor BK declared a past co-authorship with the author CH.

Generative AI statement

The author(s) declare that no Gen AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Footnotes

¹We also consider the federal version of KDUQ [25], in which each data type is given equal weight on the overall likelihood. Using the federal KDUQ, we obtained transfer angular distributions exhibiting similar uncertainties as the ones obtained with the democratic KDUQ

²The uncertainties of this data set are not clearly reported. We consider a 10% relative error per data point, which is a typical error for transfer data on stable nuclei

³The x% credible intervals are computed as the smallest interval that include x% of the cross section predicted by the 416 samples of KDUQ

⁴All results in blue in Figure 1 correspond to the uncertainties from KDUQ when the data protocol is democratic [25].

⁵We do not compute transfer cross sections beyond $E_b=120$ MeV as the cross sections then become forbiddingly small to measure

References

1. Kay BP, Schiffer JP, Freeman SJ. Quenching of cross sections in nucleon transfer reactions. Phys Rev Lett (2013) 111:042502. doi:10.1103/physrevlett.111.042502

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Avila ML, Rogachev GV, Koshchiy E, Baby LT, Belarge J, Kemper KW, et al. Constraining the 6.05 MeV 0⁺ and 6.13 MeV 3⁻ cascade transitions in the ¹²C(α,γ)¹⁶O reaction using the asymptotic normalization coefficients. Phys Rev Lett (2015) 114:071101. doi:10.1103/physrevlett.114.071101

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Walter D, Pain SD, Cizewski JA, Nunes FM, Ahn S, Baugher T, et al. Constraining spectroscopic factors near the r-process path using combined measurements: ⁸⁶Kr (d,p)⁸⁷Kr. Phys Rev C (2019) 99:054625. doi:10.1103/physrevc.99.054625

CrossRef Full Text | Google Scholar

4. Salathe M, Crawford HL, Macchiavelli AO, Kay BP, Hoffman CR, Ayangeakaa AD, et al. Search for the 1/2⁺ intruder state in ³⁵P. Phys Rev C (2020) 102:064317. doi:10.1103/physrevc.102.064317

CrossRef Full Text | Google Scholar

5. Lalanne L, Sorlin O, Assié M, Hammache F, de Séréville N, Koyama S, et al. Evaluation of the ³⁵K(p,γ)³⁶Ca reaction rate using the ³⁷Ca(p,d)³⁶Ca transfer reaction. Phys Rev C (2021) 103:055809. doi:10.1103/PhysRevC.103.055809

CrossRef Full Text | Google Scholar

6. Hammache F, de Sereville N. Transfer reactions as a tool in nuclear astrophysics. Front Phys (2021) 8:2020. doi:10.3389/fphy.2020.602920

CrossRef Full Text | Google Scholar

7. Kay BP, Tang TL, Tolstukhin IA, Roderick GB, Mitchell AJ, Ayyad Y, et al. Quenching of single-particle strength in A = 15 nuclei. Phys Rev Lett (2022) 129:152501. doi:10.1103/physrevlett.129.152501

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Lalanne L, Sorlin O, Poves A, Assié M, Hammache F, Koyama S, et al. Structure of ³⁶Ca under the coulomb magnifying glass. Phys Rev Lett (2022) 129:122501. doi:10.1103/physrevlett.129.122501

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Jones KL, Bey A, Burcher S, Allmond JM, Galindo-Uribarri A, Radford DC, et al. Neutron transfer reactions on the ground state and isomeric state of a ¹³⁰Sn beam. Phys Rev C (2022) 105:024602. doi:10.1103/physrevc.105.024602

CrossRef Full Text | Google Scholar

10. Bennett SA, Garrett K, Sharp DK, Freeman SJ, Smith AG, Wright TJ, et al. Direct determination of fission-barrier heights using light-ion transfer in inverse kinematics. Phys Rev Lett (2023) 130:202501. doi:10.1103/physrevlett.130.202501

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Hebborn C, Avila ML, Kravvaris K, Potel G, Quaglioni S. Impact of the ⁶Li asymptotic normalization constant onto α-induced reactions of astrophysical interest. Phys Rev C (2024) 109:L061601. doi:10.1103/physrevc.109.l061601

CrossRef Full Text | Google Scholar

12. Nunes F, Potel G, Poxon-Pearson T, Cizewski J. Nuclear reactions in astrophysics: a review of useful probes for extracting reaction rates. Annu Rev Nucl Part Sci (2020) 70:147–70. doi:10.1146/annurev-nucl-020620-063734

CrossRef Full Text | Google Scholar

13. Timofeyuk NK, Johnson RC. Theory of deuteron stripping and pick-up reactions for nuclear structure studies. Prog Part Nucl Phys (2020) 111:103738. doi:10.1016/j.ppnp.2019.103738

CrossRef Full Text | Google Scholar

14. Johnson RC, Tandy PC. An approximate three-body theory of deuteron stripping. Nucl Phys A (1974) 235:56–74. doi:10.1016/0375-9474(74)90178-x

CrossRef Full Text | Google Scholar

15. Titus LJ, Ross A, Nunes FM. Transfer reaction code with nonlocal interactions. Comput Phys Commun (2016) 207:499–517. doi:10.1016/j.cpc.2016.06.022

CrossRef Full Text | Google Scholar

16. Nunes FM, Deltuva A. Adiabatic approximation versus exact faddeev method for (d, p) and (p, d) reactions. Phys Rev C (2011) 84:034607. doi:10.1103/physrevc.84.034607

CrossRef Full Text | Google Scholar

17. Upadhyay NJ, Deltuva A, Nunes FM. Testing the continuum-discretized coupled channels method for deuteron-induced reactions. Phys Rev C (2012) 85:054621. doi:10.1103/physrevc.85.054621

CrossRef Full Text | Google Scholar

18. Lovell AE, Nunes FM. Constraining transfer cross sections using bayes’ theorem. Phys Rev C (2018) 97:064612. doi:10.1103/physrevc.97.064612

CrossRef Full Text | Google Scholar

19. King GB, Lovell AE, Nunes FM. Uncertainty quantification due to optical potentials in models for (d, p) reactions. Phys Rev C (2018) 98:044623. doi:10.1103/physrevc.98.044623

CrossRef Full Text | Google Scholar

20. Lovell AE, Nunes FM, Catacora-Rios M, King GB. Recent advances in the quantification of uncertainties in reaction theory. J Phys G: Nucl Part Phys (2020) 48:014001. doi:10.1088/1361-6471/abba72

CrossRef Full Text | Google Scholar

21. Catacora-Rios M, Lovell AE, Nunes FM. Complete quantification of parametric uncertainties in (d, p) transfer reactions. Phys Rev C (2023) 108:024601. doi:10.1103/physrevc.108.024601

CrossRef Full Text | Google Scholar

22. Pruitt CD, Lovell AE, Hebborn C, Nunes FM. The role of the likelihood for elastic scattering uncertainty quantification. Phys Rev C (2024) 110:064606. doi:10.1103/PhysRevC.110.064606

CrossRef Full Text | Google Scholar

23. Whitehead TR, Poxon-Pearson T, Nunes FM, Potel G. Prediction for (p, n) charge-exchange reactions with uncertainty quantification. Phys Rev C (2022) 105:054611. doi:10.1103/physrevc.105.054611

CrossRef Full Text | Google Scholar

24. Smith AJ, Hebborn C, Nunes FM, Zegers RGT. Uncertainty quantification in (p, n) reactions. Phys Rev C (2024) 110:034602. doi:10.1103/physrevc.110.034602

CrossRef Full Text | Google Scholar

25. Pruitt CD, Escher JE, Rahman R. Uncertainty-quantified phenomenological optical potentials for single-nucleon scattering. Phys Rev C (2023) 107:014602. doi:10.1103/physrevc.107.014602

CrossRef Full Text | Google Scholar

26. Koning A, Delaroche J. Local and global nucleon optical models from 1 keV to 200 MeV. Nucl Phys A (2003) 713:231–310. doi:10.1016/s0375-9474(02)01321-0

CrossRef Full Text | Google Scholar

27. Hebborn C, Nunes FM, Lovell AE. New perspectives on spectroscopic factor quenching from reactions. Phys Rev Lett (2023) 131:212503. doi:10.1103/physrevlett.131.212503

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Hebborn C, Nunes FM, Lovell AE. Erratum: new perspectives on spectroscopic factor quenching from reactions. Phys Rev Lett (2024) 132:139901. doi:10.1103/physrevlett.132.139901

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Hebborn C, Whitehead TR, Lovell AE, Nunes FM. Quantifying uncertainties due to optical potentials in one-neutron knockout reactions. Phys Rev C (2023) 108:014601. doi:10.1103/PhysRevC.108.014601

CrossRef Full Text | Google Scholar

30. Hebborn C, Nunes FM, Potel G, Dickhoff WH, Holt JW, Atkinson MC, et al. Optical potentials for the rare-isotope beam era. J Phys G: Nucl Part Phys (2023) 50:060501. doi:10.1088/1361-6471/acc348

CrossRef Full Text | Google Scholar

31. Thompson IJ, Nunes FM. Nuclear reactions for astrophysics. Cambridge University Press (2009).

Google Scholar

32 . Thompson IJ. Coupled reaction channels calculations in nuclear physics. Comp Phys Rep (1988) 7:167–212. doi:10.1016/0167-7977(88)90005-6

CrossRef Full Text | Google Scholar

33. Mukhamedzhanov AM, Nunes FM, Mohr P. Benchmark on neutron capture extracted from (d, p) reactions. Phys Rev C (2008) 77:051601. doi:10.1103/PhysRevC.77.051601

CrossRef Full Text | Google Scholar

34. Rapaport J, Sperduto A, Salomaa M. Analysis of the 48Ca(d,p)49Ca reaction for incident energies below and above the coulomb barrier. Nucl Phys A (1972) 197:337–51. doi:10.1016/0375-9474(72)91015-9

CrossRef Full Text | Google Scholar

35. Metz WD, Callender WD, Bockelman CK. Forbidden transitions in the ⁴⁸Ca(d,p)⁴⁹Ca reaction. Phys Rev C (1975) 12:827–44. doi:10.1103/PhysRevC.12.827

CrossRef Full Text | Google Scholar

36. Uozumi Y, Iwamoto O, Widodo S, Nohtomi A, Sakae T, Matoba M, et al. Single-particle strengths measured with 48Ca(d,p)49Ca reaction at 56 mev. Nucl Phys A (1994) 576:123–37. doi:10.1016/0375-9474(94)90740-4

CrossRef Full Text | Google Scholar

37. Walter D, Pain SD, Cizewski JA, Nunes FM, Ahn S, Baugher T, et al. Constraining spectroscopic factors near the r-process path using combined measurements: ⁸⁶Kr (d,p)⁸⁷Kr. Phys Rev C (2019) 99:054625. doi:10.1103/PhysRevC.99.054625

CrossRef Full Text | Google Scholar

38. Sürer O, Nunes FM, Plumlee M, Wild SM. Uncertainty quantification in breakup reactions. Phys Rev C (2022) 106:024607. doi:10.1103/PhysRevC.106.024607

CrossRef Full Text | Google Scholar

39. Fernandes JC, Crespo R, Nunes FM. How unique is the asymptotic normalization coefficient method? Phys Rev C (2000) 61:064616. doi:10.1103/PhysRevC.61.064616

CrossRef Full Text | Google Scholar

40. Mueller JM, Charity RJ, Shane R, Sobotka LG, Waldecker SJ, Dickhoff WH, et al. Asymmetry dependence of nucleon correlations in spherical nuclei extracted from a dispersive-optical-model analysis. Phys Rev C (2011) 83:064605. doi:10.1103/physrevc.83.064605

CrossRef Full Text | Google Scholar

41. Lombardi JC, Boyd RN, Arking R, Robbins AB. Nuclear sizes in ^40,44,48Ca. Nucl Phys A (1972) 188:103–14. doi:10.1016/0375-9474(72)90186-8

CrossRef Full Text | Google Scholar

42. McCamis RH, Nasr TN, Birchall J, Davison NE, van Oers WTH, Verheijen PJT, et al. Elastic scattering of protons from ^40,42,44,48Ca from 20 to 50 MeV and nuclear matter radii. Phys Rev C (1986) 33:1624–33. doi:10.1103/physrevc.33.1624

PubMed Abstract | CrossRef Full Text | Google Scholar

43. Dickhoff W, Charity R. Recent developments for the optical model of nuclei. Prog Part Nucl Phys (2019) 105:252–99. doi:10.1016/j.ppnp.2018.11.002

CrossRef Full Text | Google Scholar