Direct reactions for astrophysical p-capture rates with ORRUBA and GODDESS

Understanding the nucleosynthesis and energy generation in quiescent and explosive stellar burning requires a detailed understanding of reaction rates on many unstable nuclides. Such reaction rates are often governed by the properties of low-lying, isolated proton resonances. Though direct measurements of resonance strengths are ultimately desired, and are a focus of rare isotope beam facilities worldwide, such tour-de-force experiments must be guided by indirect techniques, in order to know resonance energies, ${\text{J}}^{\pi }$ assignments, and estimated widths, to inform targeted measurements. Furthermore, some important low-lying resonances may be too weak for direct measurements with radioactive beams, and indirect techniques provide the only practical constraints. Additionally, there has been growing interest in the astrophysical role of isomeric states, which can influence the reaction flow in nucleosynthetic reaction networks, and hence impact the quantitative interpretation of astronomical observables, such as $\gamma$-ray signatures, and elemental and isotopic ratios. Properties of single-proton resonances can be obtained by exploiting the selectivity of direct reactions, such as single-nucleon transfer and charge-exchange reactions. Constraining proton-capture rates via direct reactions has been a focus of the astrophysics program at ORNL for over two decades, spurring the development of the ORRUBA and GODDESS detector systems. Herein, a review of recent developments in instrumentation and radioactive beam delivery (including isomeric beam experiments) is presented, along with some specific examples of astrophysically interesting $sd$-shell nuclides, which have been a target of recent ORRUBA and GODDESS experiments.

1 Introduction

Astrophysical radiative proton-capture reaction rates are often governed by the properties of low-lying discrete proton resonances. In order to constrain the astrophysical reaction rate, the location and strengths of these resonances must be known. However, as the reaction network typically involves short-lived nuclides, complete measurements of proton excitation functions over the astrophysically-important energy range on many important nuclides are not within reach. Consequently, only the most important resonances must be targeted for direct measurement of their strengths. To this end, recoil separators optimized for measuring radiative-capture reactions from isolated resonances in inverse kinematics have been developed across the globe, including the DRAGON recoil separator at TRIUMF, the Daresbury Recoil Separator at the (now closed) Holifield Radioactive Ion Beam Facility (HRIBF), the St George separator at the Nuclear Science Laboratory at Notre Dame, and most recently the SECAR recoil separator at the nascent Facility for Rare Isotope Beams (FRIB).

Though ultimately such direct measurements of resonance strengths are desired, indirect techniques are needed to initially locate and constrain the resonances, so that the most important resonances can be identified. Furthermore, in some cases, important low-energy resonances are too weak for direct radiative-capture reaction measurements with radioactive beams in the foreseeable future; in these cases, indirect techniques are the only way of ascertaining these resonance strengths. Various direct reactions, such as single-particle transfer and charge-exchange reactions, have long been employed for this purpose. The reaction can be chosen to selectively populate certain states (such as states of strong single-particle character, or those of low spin). Such reactions can provide resonance energies, determine the proton orbital angular momenta $({\ell }_p)$ and $J^{\pi }$ assignments (determining barrier penetrabilities) and in some cases spectroscopic factors (informing the single-particle width of the resonance) that are critical to determining the resonance strengths and hence the astrophysical reaction rate.

In recent years, as focus shifted toward reactions of radioactive nuclides, which dominate the reaction network in explosive nucleosynthesis, instrumentation and techniques for performing direct reactions in inverse kinematics with radioactive beams have been advanced. There have been a number of excellent reviews of recent progress [1–4]. Herein, some specific developments are reviewed in the context of the silicon detector array ORRUBA (Section 3.1), encompassing the GODDESS coupling to the large germanium detector arrays Gammasphere and GRETINA (Section 3.2), and utilization of new opportunities in rare isotope beam delivery enabling reaction measurements on beams in isomeric states (Section 5).

The manuscript is organized as follows. In Section 2, the formalism of radiative-capture reactions though isolated resonances is outlined. In Section 3, the ORRUBA/GODDESS instrumentation for the measurement of direct reactions is discussed. Following this, Section 4 details some methods by which direct reactions can be used to constrain resonance strengths. Section 5 outlines recent efforts and opportunities aimed at constraining reactions on nuclei in isomeric states. Finally, in Section 6, a number of astrophysically-motivated cases are discussed, pertaining to proton-induced nucleosynthesis in massive stars, novae and x-ray bursts. These cases all involve odd-odd $N$ = $Zsd$-shell nuclides, which have been a focus of the ORRUBA and GODDESS physics program over the past two decades.

2 Radiative-capture reactions through isolated resonances

Though direct measurements of radiative-capture reactions on radioactive nuclides are ultimately desired, the limited intensities and high cost associated with radioactive beams makes the measurement of complete excitation functions across the Gamow window unfeasible. However, at the low temperatures associated with quiescent stellar burning, and the hot CNO cycle and breakout into the rp process in novae, radiative-capture rates are often dominated by capture through isolated low-lying discrete resonances. In an astrophysical environment of temperature $T$, the reaction rate per-particle-pair for radiative capture through an isolated resonance is given by

$<\sigma v>\hspace{0.17em}={\left(\frac{2\pi }{\mu kT}\right)}^{2/3}\exp \left(\frac{-E_r}{kT}\right)\omega \gamma ,(1)$

where $\mu$ is the reduced mass for the entrance channel. This reaction rate is proportional exponentially to the resonance energy $E_r$, and linearly to the resonance strength $(\omega \gamma )$, where

$\omega \gamma =\frac{2J_f+1}{\left(2J_t+1\right)\left(2J_p+1\right)}\frac{{\mathrm{\Gamma }}_p{\mathrm{\Gamma }}_{\gamma }}{\mathrm{\Gamma }}.(2)$

Here, $\mathrm{\Gamma }$ represents the total width of the resonance for all open channels $(\mathrm{\Gamma }={\mathrm{\Gamma }}_p+{\mathrm{\Gamma }}_{\gamma }+\cdots )$, and $J_p$, $J_t$ and $J_f$ are respectively the spins of the proton, “target” nucleus, and the resonance through which the reaction proceeds.

Rather than measure the complete excitation function over the Gamow window, it is therefore possible to target only the most important resonances, and sum their contributions as a function of temperature, to obtain the total reaction rate. Though this substantially reduces amount of experimental data needed, to just measurements of the strength of a handful of important resonances, it introduces a problem that the resonances (and hence the bombarding energies at which to measure) are not known a priori. It is therefore critical that the energies and approximate strengths of resonances in the vicinity of the Gamow window must first be identified, such that direct measurements can subsequently target only those resonances anticipated to contribute appreciably to the astrophysical reaction rate.

It can be seen from Equation 2 that determining the energies of resonances in the proximity of the Gamow window is the most crucial component, as this highlights which states may contribute, and constrains their contribution due to the exponential dependence on resonance energy. Having determined resonance energies, further constraints on $\omega \gamma$ can stem from determining the spins of the states, or constraining the widths from scattering or branching ratio measurements. For low-energy resonances, where the barrier penetrability dominates, constraints on energies and spins can be substantially constraining on $\omega \gamma$.

Though there are numerous ways in which resonances can be identified and their strengths constrained, direct reactions, such as transfer and charge-exchange reactions, provide a number of benefits [1, 3], including being able to constrain energies, spins, and ultimately strengths of multiple resonances in a single measurement. Level energies can be determined, either through two-body reaction kinematics or, often more precisely, via the detection of de-excitation $\gamma$ rays. $J^{\pi }$ assignments can be made by measurement of the angular distributions of reaction ejectiles, which are characteristic of the angular momentum of the transferred particle. Furthermore, if a reaction can be selected which populates the states of interest via transfer of the same particle as is captured in the astrophysical reaction, cross sections from the transfer reaction can be used to constrain the resonant-capture cross section. This is usually undertaken by gaining insight into the overlap of the many-body wavefunction of the state with a pure single-particle state: i.e., the extraction of single-particle spectroscopic factors. This is discussed further in Section 4.3.

3 Direct reaction instrumentation

Using direct reactions with radioactive beams to constrain astrophysical reaction rates has been a major focus of the astrophysics program at Oak Ridge National Laboratory over the last two decades. Stemming from the astrophysics program at the HRIBF, charged-particle detectors for radioactive-beam experiments have been developed in collaborations based at ORNL, including silicon detector arrays optimized for inverse-kinematics experiments (the SIDAR array of YY1 detectors [5], based on the LEDA design [6], followed by the development of ORRUBA [7, 8]), and fast ionization chambers for the detection and identification of beam-like recoils [9]. Since the closure of the HRIBF over a decade ago, these detectors have been deployed at various facilities across the US, coupled to the large semiconductor $\gamma$-ray arrays (Gammasphere and GRETINA) and large recoil separators (S800, FMA, and, in future, SECAR) and the JENSA gas-jet target. Below, some basic details of these detectors are discussed.

3.1 ORRUBA

ORRUBA [7] is a high-solid-angle silicon detector array designed for the measurement of charged-particle reactions with radioactive beams. The position sensitivity of the array, which amounts to approximately 1$°$ resolution in polar angle, was designed around the requirements of inverse-kinematics experiments with radioactive beams at Coulomb-barrier energies ($\sim$5 MeV/u). The design was initially optimized for measuring (d,p) reactions on heavy fission fragment beams, which were a focus of the research program at the HRIBF at ORNL. The original array comprised two 12-fold rings of custom-designed resistive-strip X3 detectors from Micron Semiconductor, covering angles from $\sim$ 45$°$ to 135$°$. In the downstream ring, detector telescopes were deployed (using 65-$\mu$m-thick BB10 detectors) backed by 1000-$\mu$m-thick X3 detectors) for particle identification. For the upstream barrel, which typically only detects particles lighter than the target (i.e., protons), a single layer of 1000-$\mu$m-thick X3 detectors were deployed. Angles further upstream were subtended, when needed, by the SIDAR array of YY1 detectors, typically in a lampshade configuration.

In more recent years, the X3 detectors have been replaced with sX3 detectors (Figure 1), which include 4-fold non-resistive segmentation on the Ohmic contact, for improved energy resolution. Concurrently, the YY1 lampshade was replaced by an annular QQQ5 detector endcap to the sX3 barrel [8, 10], resulting in a more compact array, with near seamless polar angular coverage, enabling the array to be mounted inside major $\gamma$-ray detector arrays (see Section 3.2). The design of the QQQ5 detectors involves radial segmentation which is graded in pitch, placing increasingly finer segmentation away from the beam axis, to match the steepness of the kinematic shifts from either pickup or stripping reactions in inverse kinematics, in order to optimize resolution and channel count.

ORRUBA operates as a standalone detector using a fast ionization chamber as a recoil detector (Section 3.3), coupled to recoil separators such as the S800 at FRIB, and operates as the main particle detector for the JENSA gas-jet target [11, 12].

3.2 GODDESS

For many direct-reaction measurements, the detection of $\gamma$ rays in coincidence with charged particles is either necessary (Coulomb-excitation measurements, for instance) or highly advantageous. For measurements such as particle transfer reactions, $\gamma$ rays aid significantly in separating closely-spaced states populated in the reaction. In addition to the improved energy resolution of $\gamma$-ray detection, in many cases neighboring levels decay to different states, leading to better separation in $\gamma$-ray energy than the difference in excitation energy. Furthermore, $\gamma$ rays carry additional information on the states populated (their decay paths, angular distributions, lifetimes, etc.) and can provide information on states not populated directly in the transfer reaction, but fed by decay.

Motivated by these advantages, there has been much investment across the globe in couplings of high-resolution and high-efficiency charged-particle and $\gamma$-ray detectors, with a focus on measuring direct reactions on radioactive beams in inverse kinematics. These include TIARA [13] coupled to EXOGAM (GANIL), the SHARC array [14] coupled to the TIGRESS (TRIUMF), TREX [15] and more recently HI-TREX [16] coupled to Miniball (ISOLDE), MUGAST coupled to AGATA [17] (GANIL), and the GODDESS coupling [18] of ORRUBA [7] to Gammasphere [19] and GRETINA [20–24].

GODDESS [18] (Pain et al., forthcoming) is a coupling of an upgraded version of ORRUBA to the large semiconductor $\gamma$-ray detector arrays in the US: Gammasphere and GRETINA (and, in the near future, GRETA [25]). GODDESS has been in routine operation with GRETINA since 2019 (see Figure 2), following its original deployment with Gammasphere in 2015. To date, GODDESS campaigns have been performed at ATLAS (2015, 2019, 2021, 2025), and FRIB (2024). In its default configuration, GODDESS provides near-seamless charged-particle coverage from $\sim 15°$ to $\sim 165°$, with $\sim 1°$ of polar angular resolution and $\sim 80\%$ azimuthal coverage throughout this range, with particle identification in the forward hemisphere. GODDESS can be operated with a compact ionization chamber (Section 3.3) that mounts at zero degrees, or coupled to recoil separators such as the FMA and the S800.

Figure 1

Figure 1. Photograph of ORRUBA, showing two complete rings of sX3 Si detectors, deployed at ReA (beam direction right-to-left). The Si signals are taken out of vacuum immediately to air-cooled preamplifier boxes (removed in photo), mounted from the preamplifier ring in the downstream direction.

Figure 2

Figure 2. Photograph of GODDESS, deployed with GRETINA at ATLAS at Argonne National Laboratory (beam direction left-to-right). The 720-channels of Si signals are taken out of vacuum immediately to air-cooled preamplifier boxes, in the downstream direction. The beam-right hemisphere of GRETINA is retracted for access.

In preparation for the deployment of GRETA at FRIB, at the time of writing GODDESS is being upgraded. A slightly smaller configuration, with new endcap detectors and a new vacuum chamber, will allow compatibility with the nearly full implementation of GRETA. This will provide a quasi-4$\pi$ particle-$\gamma$ spectrometer with semiconductor resolution for FRIB.

3.3 MAGIC

For inverse-kinematics experiments with radioactive beams, detection and identification of the beam-like recoil is often desirable. Firstly, RIBs are often delivered with contaminants, so event-by-event identification of the recoil is needed to associate reaction ejectiles with the beam constituent of interest. Secondly, reactions are often performed on targets with undesired elements (such as the carbon component of polyethylene and deuterated polyethylene targets). Reactions on these nuclides, such as fusion-evaporation reactions, result in substantially different recoils (both nuclide and energy), which can be readily separated by measurement of the beam-like recoil downstream of the target.

Though recoil separators provide numerous benefits for recoil detection, they are not always available, or necessary. Furthermore, their use is complicated in many cases by the energy, angle and charge-state distributions of beam-like recoils after the reaction target. Alternatively, for beam intensities below $\sim 10^6$ ions/second, a zero-degree detector that sees the entire beam flux can often be used. Ionization chambers can be very effective as such detectors. They can be segmented along the stopping axis, and easily tuned in pressure to match the required stopping power to the energy and charge of the incoming ion, to optimize particle identification via $\mathrm{\Delta }$E-E. They are radiation hard, and can deliver good (typically a few percent) resolution at reasonable count rates ($<10^{4-6}$, depending on design).

Conventional transverse-field gridded ionization chambers have been used as zero-degree detectors (e.g., [26]), but they are rate limited to $\sim 10^4$ ions/second, due to the long drift times. More recently, a number of axial-field ionization chambers have been developed with increased count-rate capability. The TEGIC detector [27], was designed for high-energy ions ($\sim$100 MeV/u), using a series of aluminized Mylar foils, stacked along the beam axis, to form parallel transmission electrodes, alternately biased to form a series of anodes and cathodes. In this manner, the electron and ion drift distance can be substantially reduced (typically to 1–2 cm) compared to a more conventional transverse-field gridded ionization chamber (where drifts are typically 5–10 cm). The TEGIC electrodes are tilted from the beam axis at 30$°$, to help reduce recombination. The reduced drift distance results in substantially increased counting rate capacity, enabling this detector to operate at up to $10^6$ ions/second.

Because the foils provide too much dead material for this design to be used for low-energy ions (such as in the 5–10 MeV/u direct-reaction experiments discussed herein), an axial-field ionization chamber was built in support of the ORRUBA program. This detector was based upon the concept of the TEGIC detector, but replaced the foils with a series of high-transmission wire grids (using $\sim$18 $\mu$m diameter wires, spaced by 2 mm, giving $>99\%$ transmission per grid) [9], so that the ions do not traverse dead material between electrodes (instead, a few percent of the ions stop prematurely, by hitting a wire as they traverse the detector). In this detector, groups of anodes were electrically connected together and read out via charge-sensitive preamplifiers to provide $\mathrm{\Delta }$E and residual energy signals, while the cathodes were grounded. This provided particle identification at rates up to $10^6$ ions/second [9].

Subsequently, a number of other axial-field ionization chamber detectors have been built upon the wire-grid design, incorporating various improvements. A more compact tilted-grid ionization chamber was built, to operate in the much more confined space of GODDESS [18]. An ionization chamber for ANASEN [28] simplified the design by removing the tilt from the grids, and along with it broadening due to tilted windows and asymmetric dead gas lengths, with minimal impact on resolution or count rate capacity [29]. This larger detector also introduced individual wire readout on the entrance anodes, with the rotation of the grids oriented for XY measurement of position of the ion as it enters the detector, with 3 mm resolution. The TRIFIC detector [30] was developed at TRIUMF, using the tilted-grid approach, but biasing the anodes and cathodes symmetrically (rather than grounding the cathodes) for reduced fringe-field effects and enabling operation at higher electric fields.

The most recent detector in this series, MAGIC (Multi Axial-field Gridded Ionization Chamber), is purposefully built for GODDESS (Pain et al., forthcoming). In order to operate in the small space available, while maintaining maximum acceptance and easy reconfiguration, the perpendicular grids are self-supporting and stacked using electric headers (see Figure 3), which provide both mechanical support, and electrical connections from each of the grids to the back flange, where signals are brought out of vacuum. This design makes the detector easily adjustable and serviceable. In this detector, the front two anodes use individual wire readout, for XY position measurement, with 2 mm resolution. The remaining anode signals are brought out of vacuum individually, and can easily be recombined (via a custom preamplifier motherboard) to optimize the anode groupings for particle identification. Furthermore, this is the first detector that provides readout of the cathode signal in addition to the anodes, which facilitates gain matching and improved sensitivity (Pain et al., forthcoming).

Figure 3

Figure 3. Photograph of the self-supporting grids of the MAGIC detector (see text). The wires (2 mm pitch) of the first two anodes are read out individually, for XY position measurement of incident ions.

4 Using transfer reactions to constrain resonance strengths

This section highlights some manners in which direct reactions can be utilized to constrain resonance strengths, illustrated by some specific examples from ORRUBA/GODDESS experiments.

4.1 Constraining resonance strengths by determination of resonance energies

To constrain the reaction rate from a single isolated low-lying resonance, three things are needed: the resonance energy $E_r$, the $J^{\pi }$ of the resonance, and its resonance strength $\omega \gamma$. Determination of the energy of the resonance is most critical; for a given resonance strength, it impacts the reaction rate exponentially (Equation 1). It also impacts the resonance strength itself (along with the $J^{\pi }$ of the resonance, which constrains the orbital angular momentum of the captured particle) by impacting barrier penetrabilities; at low energies, the barrier penetrabilities, and hence resonance strength, also exhibit an exponential dependence on resonance energy.

The combination of high resolution charged-particle and $\gamma$-ray detection can enable the use of transfer reactions as a mechanism to populate states of astrophysical interest, using high-resolution $\gamma$-ray spectroscopy to obtain precise energies of the states populated. In such measurements, the detection, identification and energy measurement of the outgoing ejectile can give unambiguous determination of the nucleus populated, and the approximate formation energy. By detecting angle of the outgoing proton not only helps with the kinematic reconstruction of the two-body reaction, but also enables determination of the momentum vector of the recoiling nucleus, which can be used for a more-precise Doppler correction to the $\gamma$ rays, and can provide angular distributions that can be used for $J^{\pi }$ assignments.

In this approach, it is not important whether the reaction proceeds via the component of the wavefunction important for the capture reaction; that is, the resonance strength is not constrained from the cross sections, only by the energy and $J^{\pi }$ assignments derived from the analysis. This can often reduce uncertainties on resonance strength from experiments with relatively simple analyses, without the concerns pertaining to efficiencies, acceptances, deadtime and normalization that must be addressed in order to extract reaction cross sections for spectroscopic factors (as discussed in Section 4.2). To this end, a series of (³He,t) experiments have been performed with GODDESS; examples of such experiments are given in Sections 6.1 and 6.6.

4.2 Constraining resonance strengths by measuring spectroscopic factors

For low-lying resonances, ${\mathrm{\Gamma }}_p$ is a particularly important parameter for determining $\omega \gamma$. Indeed, in very low-lying resonances (below $\sim$500 keV), ${\mathrm{\Gamma }}_p$ is generally much smaller than ${\mathrm{\Gamma }}_{\gamma }$. In this case, the resonance strength can be approximated as:

$\omega \gamma =\frac{2J_f+1}{\left(2J_t+1\right)\left(2J_p+1\right)}{\mathrm{\Gamma }}_p,$

where ${\mathrm{\Gamma }}_p$ depends critically on $E_r$ and $J^{\pi }$ of the resonance.

In the absence of further information, the maximum strength of a pure single-particle resonance at $E_r$ and with $J^{\pi }$ can be calculated. At such low energies, the value of this width, ${\mathrm{\Gamma }}_{sp}$, is dominated by the penetrability of the Coulomb and angular-momentum barriers, so is strongly dependent on $E_r$ and $J^{\pi }$ (or, more strictly, the orbital angular momentum of the proton, ${\ell }_p$). The single-proton width can be determined by calculating single-particle wavefunctions corresponding to the elastic scattering of a proton by a realistic diffuse potential, such as a Woods-Saxon well [31], at the resonance energy of interest [32, 33]. Tuned by adjusting the potential depth, the width of the pure single-proton resonance is determined by the energy dependence of the phase shift $\delta$, and can be calculated by codes such as DWUCK and WSPOT [34, 35].

The proton width of a given resonance is further dependent on the overlap between the many-body nuclear wavefunction of the resonance and the pure single-proton wavefunction - i.e., the proton spectroscopic factor, $C^{2}S$:

${\mathrm{\Gamma }}_p=C^{2}S{\mathrm{\Gamma }}_{sp}.(3)$

The many-body wavefunction is, a priori, unknown for a given resonance. However, it can be constrained by a nuclear structure model, such as shell-model calculations, or ideally by experimental data, such as from a transfer reaction [3].

The proportionality between cross sections (i.e., spectroscopic factors) from proton-transfer reactions and radiative proton direct-capture [36] and resonant capture reactions [33, 37, 38] is documented. It is important to note that in the extraction of resonance strengths from transfer reactions, the same potential should be used for the calculation of the transfer-reaction cross sections as for the calculation of the single-particle proton widths, as was suggested by the late John Schiffer [32]. Particularly, a strong dependency between the geometry of the single-particle binding potential and reaction cross sections is well known; providing a consistent potential is employed between the two reactions, much of the uncertainty associated with this potential choice cancels [32, 39–41].

The use of transfer reactions to obtain resonance strengths has a number of advantages. Firstly, it can be used to study multiple resonances in a single measurement. Secondly, because the transfer reactions are measured at energies above the Coulomb barrier (typically, several MeV/u upward), the cross sections are not hindered by barrier penetrability. This allows transfer reactions to be used to study very low-lying resonances that are out of reach for direct measurements in the foreseeable future.

4.3 Benchmarking resonance strengths from (d,p) against direct (p,$\gamma$) measurements

Though proton-transfer reactions, such as (³He,d) and (d,n), are the reactions of choice for extracting proton spectroscopic factors, the application of these reactions to experiments in inverse kinematics with radioactive beams remains a challenge. Both (³He,d) and (d,n) reactions are experimentally complicated, by target requirements and the complexities of spectroscopic neutron detection, respectively. Recently, the technique of measuring angle-integrated cross sections by γ-ray tagging the final state, such as a number of recent measurements using GRETINA and the S800 [42, 43], has been employed. Though this approach can be effective, it relies on knowledge of proton-$\gamma$ branching ratios, corrections for feeding, and on the spins of the final states being known in order to infer ${\ell }_p$. Furthermore, for transfer onto states with non-zero spins, even knowledge of $J^{\pi }$ assignments of final states is insufficient for a conclusive interpretation, as the total angle-integrated cross section for a given final $J^{\pi }$ can be composed of a sum of multiple proton orbital angular momentum couplings. Without a method to deconvolve these components, it is impossible to assign more than limits on spectroscopic factors for the individual orbital angular components, which inherently have vastly different contributions to the astrophysical reaction rate, due to barrier penetrabilities. Combining these experiments with neutron detection helps address this issue, at the cost of efficiency and the complexity of neutron detection.

However, the isospin independence of the nuclear force can be exploited to constrain proton spectroscopic factors from their neutron counterparts, by using the mirrored reaction (for example, the (d,p) reaction) to extract neutron spectroscopic factors for the equivalent state in the mirror system. There are several experimental advantages to using this technique of measuring (d,p) on proton-rich nuclei, including simple targets, high particle-detection efficiency that is well understood, a compact setup that can be fielded with large germanium detector arrays, and positive Q values which reduce kinematic compression in inverse-kinematic stripping reactions. This approach has been benchmarked for a number of astrophysically-interesting cases in the $sd$ shell, finding general systematic agreement between proton and neutron spectroscopic factors (extracted from (³He,d) and (d,p) reactions, respectively), and associated direct measurements of proton resonance strengths, to within about 30$\%$ [37]. The (d,p) reaction has recently exploited using isobaric analog states in neighboring isobars, at the NSCL using the ²⁶Si(d,p$\gamma$)²⁷Si to constrain the ^26mAl(p,$\gamma$)²⁷Si reaction [44], and at TRIUMF using the ²³Ne(d,p$\gamma$)²⁴Ne reaction to constrain the ²³Al(p,$\gamma$)²⁴Ne reaction [45].

Furthermore, a number of astrophysically-interesting nuclides for proton capture lie on or close to the $N$ = $Z$ line (See Section 6). The technique described above is further simplified in the case of the $N$ = $Z$ nuclides, as the ‘target’ nucleus is self-conjugate, and hence identical for the two mirror systems. ²⁶Al represents an important testing ground for this approach, as it is a radioactive $N$ = $Z$ nuclide with strong astrophysical interest [46], yet the ground state (^26gAl) has a long enough lifetime that it can be fabricated into target. Consequently, numerous resonances in the ^26gAl(p,$\gamma$) reaction have been well studied in both normal [47] and inverse [48] kinematics, as well as with indirect techniques such as ^26gAl (³He,d) [47, 49] using an ^26gAl target, and inverse kinematics (d,p) measurements using beams of ²⁶Al [50–52]. The lowest resonance for which there have been direct measurements of the resonance strength via ^26gAl(p,$\gamma$) is the 189-keV resonance. This has been measured [47] using an ^26gAl target to be 0.055 (9) meV [47] and, via inverse kinematics using a $10^9$ ions/s radioactive beam at TRIUMF using the DRAGON recoil separator to be 0.035 (7) meV [48]. An indirect measurement of the ^26gAl(³He,d)²⁷Si reaction using an ^26gAl target and a Q3D spectrograph yielded a resonance strength of 0.064 for an ${\ell }_p=1$ transfer, with unreported uncertainty (statistical errors on the differential cross section amount to $\sim 20\%$)¹. This experiment was unable to probe lower-energy resonances due to the strong backgrounds from the ²⁷Al component of the target.

More recently (d,p) experiments using radioactive ²⁶Al beams have been used to determine the strengths of resonances out of current reach of direct (p,$\gamma$) measurements [50, 51], which are unconstrained by target impurities that limited the ^26gAl(³He,d)²⁷Si experiment. These experiments are described in Section 6.3. Concurrently, as a benchmarking of the (d,p) technique, spectroscopic factors for the mirrors to high-lying resonances were extracted, and resonance strengths determined and compared to direct measurements using (p,$\gamma$) reactions [50].

When constraining resonance strengths via mirror symmetry, it is important to note that the mirror states in the two systems lie at different energies with respect to the separation energy. For example, the low-lying resonances in the ²⁶Al + p system lie hundreds of keV above $S_p$ in ²⁷Si, whereas the mirror states in the ²⁶Al + n system lie 2–3 MeV below $S_n$ in ²⁷Al. Though the wavefunctions of the mirror states are of a highly similar structure, there are differences due to the effects of different couplings to the continuum. In some studies (e.g., [51]), the spectroscopic factors are assumed to be equal in the two systems to about $30\%$, which is often a reasonable approximation, compared to other uncertainties in the experiments, and certainly to the potential orders of magnitude uncertainty in resonance strengths prior to experimental constraint. However, a rigorous approach is to explicitly account for the systematic difference in spectroscopic factors in the two systems due to coupling to the continuum. In [50], spectroscopic factors were calculated for bound ²⁷Al states and unbound ²⁷Si in the Shell Model Embedded in the Continuum (SMEC) formalism [53, 54], using the USDb interaction [55]. The ratio of spectroscopic factors between the two mirror systems was then used to scale the experimentally-determined spectroscopic factors between ²⁷Al and ²⁷Si. This scaling, which is dependent on the energies of the states with respect to their separation energies, and the orbital angular momentum, is typically of the order 10–40$\%$.

5 Opportunities with isomeric beams

There is a growing understanding of the importance that isomers play in astrophysical reaction networks (astromers) [46, 56–62], impacting reaction flow and effective lifetimes, in scenarios ranging from massive stars, to novae, supernovae, and r-process nucleosythesis [44, 46, 63, 64]. For example, many odd-odd $N$ = $Z$ nuclides in the sd and fp shells are of substantial astrophysical interest (see Section 6), affecting reaction flow, and impacting astronomical observables such as isotopic ratios and prompt $\gamma$-ray signatures [46]). Many also have low-lying spin isomers which must be incorporated into the reaction network (see Table 1; Figure 4).

Table 1

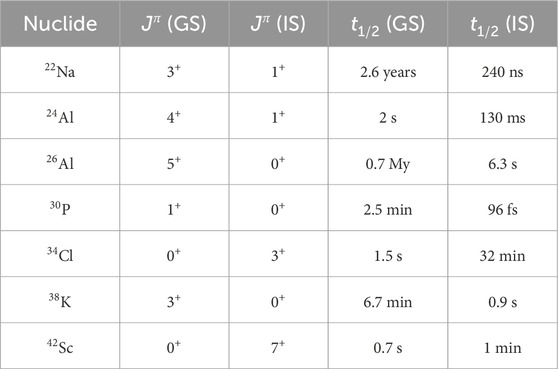
Table 1. Properties of the ground and isomeric states in odd-odd nuclides in the $sd$ shell and lower $fp$ shell. In most cases, either the ground state or isomer has a lifetime of comparable duration to the possible range of holdup times (10s of ms to seconds) in the ReA system, potentially enabling the employment of the hold-up technique (see text) to manipulate the GS:IS content of the beam.

Figure 4

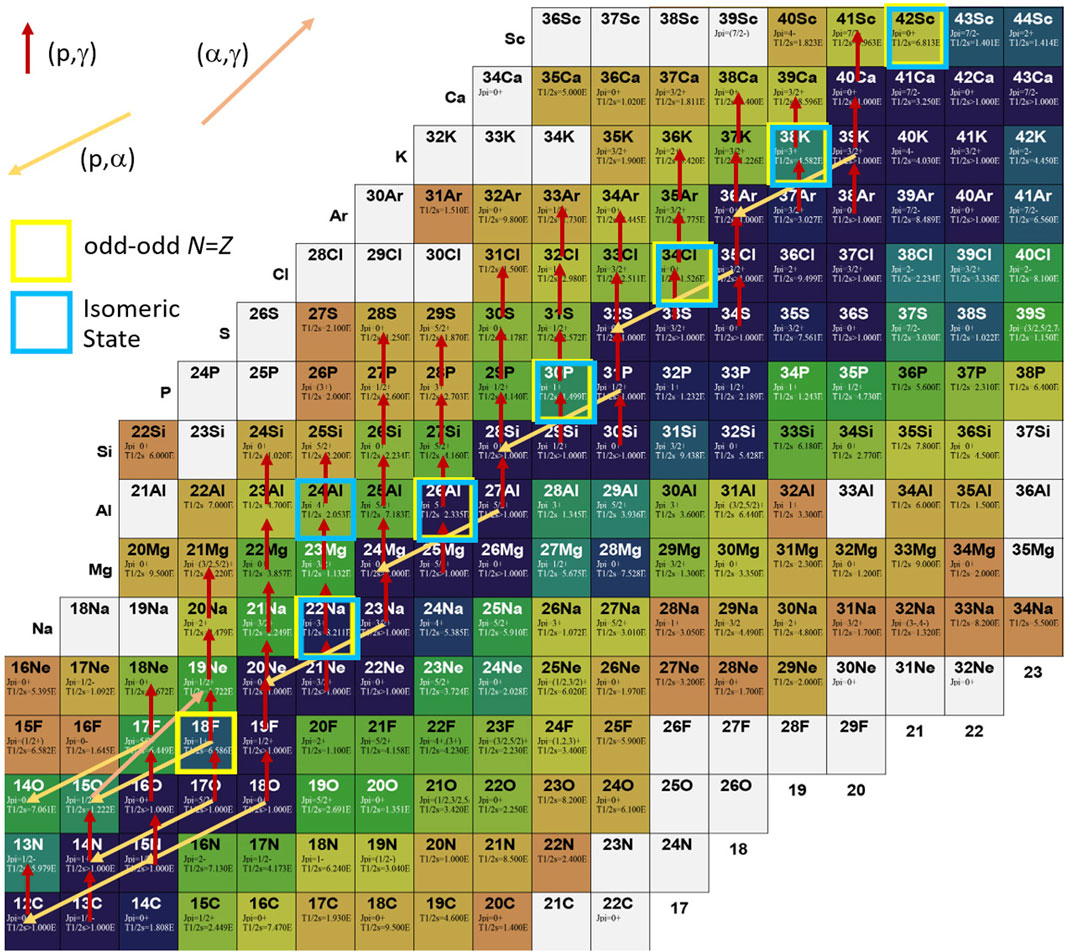
Figure 4. Simplified reaction network for nova nucleosythesis, omitting $\beta$ decays and photodissociation reactions for clarity. The odd-odd $N$ = $Z$ nuclides, which are all of particular astrophysical interest (see text), are highlighted, along with nuclides with isomeric states (see Table 1) on which capture cross sections are needed.

The lack of information on reaction cross sections on isomers in radioactive nuclides presents a particular challenge. Beam production techniques typically populate both the ground state (GS) and isomeric state (IS) of such nuclides. However, in general, the ratio is difficult to predict or control without undesired impacts on other beam properties.

5.1 Production and control of mixed GS:IS beams at FRIB

Recent developments at the ReA facility at FRIB are enabling the delivery of beams containing isomeric states in which the GS:IS composition can be controlled without impact on the other properties of the reaccelerated beam [65, 66]. This is achieved by completely stopping the fragmentation beam, and reaccelerating it to energies appropriate for either direct measurements at astrophysical energies, or to Coulomb-barrier energies that are appropriate for indirect techniques for constraining astrophysical reaction rates, such as direct reactions. The GS:IS ratio of the reaccelerated beam can be controlled by two mechanisms. Firstly, the tuning of the fragment separator can be employed to change the GS:IS content of the fragmentation beam before stopping and reacceleration. Secondly, if the lifetimes of the two states are conducive, the adjustable hold-up times in the reacceleration system can be used to further modify the GS:IS composition of the reaccelerated beam. Crucially, because of the stopping and reacceleration, the final beam properties (energy, emittance, etc.) are largely isolated from these adjustments to the GS:IS ratio. These two mechanisms are discussed in Section 5.1.1 and Section 5.1.2.

5.1.1 Selection by fragment momentum

In general, projectile fragmentation populates nuclei in an ensemble of excited states, which subsequently $\gamma$ decay in-flight; in nuclides with isomers, this can result in feeding of the isomer as well as the ground state. If that isomer has a comparable lifetime to the flight-time of the beam, a beam can be delivered with a mixed GS:IS composition. Due to the differences in spin between the GS and IS, some control over GS:IS ratio can be achieved by selectively tuning the fragment separator to transmit a subset of the fragmentation momentum distribution. In two studies, performed at the NSCL prior to FRIB operations, the production of mixed GS:IS beams of ³⁸K [65] and ³⁴Cl [66] were investigated. In both cases, the beams were produced via the 1p-1n removal channel of the fragmentation of a primary beam (⁴⁰Ca and ³⁶Ar, respectively), incident at similar energies (140 and 150 MeV/u) on a beryllium production target. It is noteworthy that both nuclides have the same GS and IS spins (though reversed ordering), and comparable lifetimes (see Table 1). In both studies, the GS and IS were populated in the fragmentation reaction with approximately equal proportions. Tuning the fragment separator to transmit the low-momentum tail of the fragmentation distribution (which stems from smaller-impact-parameter fragmentation events with on-average larger momentum transfer) was found to enhance the fractional population of the higher-spin state (the 3⁺ GS in ³⁸K, and the $3^{+}$ IS in ³⁴Cl) [65, 66], albeit at the cost of total production yields.

5.1.2 Selection by lifetime

In addition to the spin selectivity obtainable by the tuning of the fragment separator, the content of the reaccelerated beam is subject to the holdup times inherent to the ReA system. If one or both of the lifetimes of GS or IS is comparable to the range of available hold-up times, the content of the reaccelerated beam can be manipulated by adjusting the hold-up time. The reacceleration process involves stopping the fragmentation beam in a gas stopper, preparing the ions in a cooler-buncher trap, and charge-breeding the ions in an electron-beam ion trap (EBIT), before reacceleration in the ReA linac. In this process, the ions spend an equal amount of time in the cooler-buncher and EBIT; this time is adjustable, in the range of 10s of ms to seconds. By setting this holdup time based on the lifetime of the ground and/or isomeric states involved, the composition of the beam can be adjusted by controlling how much of each species is allowed to $\beta$ decay before reacceleration. The advantages of this approach are several-fold:

• Beams at ReA can be delivered at energies spanning direct astrophysics measurements (100s of keV/u to a few MeV/u) to transfer-reactions (5–15 MeV/u).

• The high-quality reaccelerated beam emittance ($<0.5\%$ energy spread, $\sim$2-mm beam spot size) is critical to recoil-separator acceptance for radiative-capture measurements, and to resolution in kinematic reconstruction in direct reactions, such as transfer reactions or inelastic scattering.

• Data can be acquired with two different GS:IS beam compositions without affecting other properties of the reaccelerated beam. This enables a straightforward deconvolution of the GS and IS yields, without having to account for additional changes to the experimental response.

5.1.3 Production of pure isomeric beams

In addition, it is possible to produce certain beams almost entirely in one either of isomeric state or ground state, by taking advantage of the selectivity of $\beta$ decay, which often very preferentially populates just one of the of two states in a nuclide, and the lifetimes of the nuclides involved. For example, the $\beta$ decay of ²⁶Si results almost entirely in population of the isomeric state of ²⁶Al$(>99.9\%)$. So, rather than tuning the fragment separator for ²⁶Al in the method described above, which would produce a beam of ²⁶Al in both the ground and isomeric states, the fragment separator can instead be tuned for the $\beta$-decay parent, ²⁶Si. The ²⁶Si can then be held up in the ReA system for long enough that a substantial fraction $\beta$ decays to ²⁶Al, exclusively in the IS, which can then be reaccelerated. The resultant beam is then a mix of ²⁶Si and ²⁶Al, with the ²⁶Al component exclusively in the IS. Though the beam is not isobarically pure, the contaminant is a different element, rather than a different state in the same nuclide, which is much easier to handle in experiments due the Z difference, either by identification of recoils in a zero degree detector (such as an ionization chamber, discussed in Section 3.3) or a recoil separator. The first experiment using this approach has been approved for beam time at FRIB [67]. This experiment will measure the ^26mAl($\alpha$,p) reaction using the JENSA gas-jet target and ORRUBA, and is currently awaiting scheduling.

6 The odd-odd N = Z sd-shell nuclides

This section highlights the usage of the techniques and instrumentation described above to determine astrophysical reaction rates due to isolated proton resonances, on nuclides in ground and isomeric states. These examples are located within a region of the nuclear chart (the odd-odd $N$ = $Z$ nuclides in the $sd$ shell) which has been a focus of the ORRUBA/GODDESS program, highlighting some experiments which have been performed, and some which are planned for the near future.

Figure 4 shows a simplified reaction network for nova nucleosynthesis, including the hot CNO cycle and breakout reactions into the rp process. The odd-odd $N$ = $Z$ nuclides are highlighted, as these are of elevated astrophysical interest. The ¹⁸F(p,$\gamma$)¹⁸Ne reaction competes with the ¹⁸F(p,$\alpha$) reaction, governing breakout from the hot CNO cycle and the synthesis of heavier elements. The radioisotope ²²Na is anticipated to be produced in sufficient quantities that the 1.275-MeV $\gamma$-ray from its decay may be a prompt observable from nova explosions, yet its abundance is subject to uncertainties on the astrophysical rate of the ²²Na(p,$\gamma$)²²Na destruction reaction. ²⁶Al is the most-studied radionuclide, with the 1.8 MeV $\gamma$-ray line associated with its $\beta$ decay being the subject of years of data collected with the HEAO [68, 69], the COMPTEL and INTEGRAL satellite $\gamma$-ray telescopes [70–73], and is used to map regions of star formation and to trace stellar ejecta in the interstellar medium [74]. However, the destruction reaction ²⁶Al(p,$\gamma$)²⁷Si impacts the quantitative interpretation of this signal. The rate of the ³⁰P(p,$\gamma$)³¹S reaction is crucial for classical nova nucleosynthesis, bottle-necking the reaction flow into the A = 30–40 mass range. The ³⁴S/³²S isotopic ratio in pre-solar grains, which is believed to be a strong indicator of nova origin, is impacted by the ³⁴Cl(p,$\gamma$)³⁵Ar reaction rate, which governs the reaction flow due to the unbound nature of ³⁴K. The ³⁸K(p,$\gamma$)³⁹Ca reaction likewise bottlenecks the reaction flow to higher masses due to the unbound nature of ³⁹Sc.

The situation is further complicated because many of these $N$ = $Z$ nuclides have low-lying isomers with sufficiently long lifetimes that they can contribute to the reaction network. At low temperatures, the ground and isomeric states can be independently populated and destroyed by capture reactions and $\beta$ decay, so are typically treated as independent species in reaction networks. However, at elevated temperatures they can be connected, via thermal excitations to higher levels. In the limit of high-enough temperature, the two states are in thermal equilibrium, and can be treated as a single effective species. At intermediate temperatures, there is a transition between these two scenarios, resulting in strongly temperature-dependent effective properties [57, 75]. For the reaction network, proton-capture cross sections are required on both ground state and isomer. With new techniques of isomeric beam production (such as those outlined in Section 5), indirect techniques are being used to unambiguously study resonances that are sensitive to the overlap in the many-body wavefunction to single-particle resonances on both ground states and isomers. Examples of such experiments are described in Sections 6.3, 6.5, and 6.6.

6.1 The ¹⁸F(p,$\gamma$)¹⁹Ne reaction

Understanding the reaction flow breaking out of the hot CNO cycle, and the abundance of ¹⁸F produced in novae (a major source of 511-keV radiation, and hence a potential prompt $\gamma$-ray observable), is influenced by the strengths of resonances in ¹⁹Ne, which impact the ¹⁸F(p,$\alpha$)¹⁵O and ¹⁸F(p,$\gamma$)¹⁹Ne reactions. An experiment was performed to measure the ¹⁸F(d,p)¹⁹F reaction to determine spectroscopic factors in the mirror system, to constrain the proton widths in ¹⁹Ne [76]. An isotopically-pure ¹⁸F beam was from the HRIBF was impinged at 6 MeV/u upon a 160 $\mu$g/cm² deuterated polyethylene target. In this pioneering experiment using a (d,p) reaction in inverse-kinematics with a radioactive beam, and an application of the mirror-symmetry approach, proton ejectiles were detected at backward angles in the SIDAR array. In coincidence, the very forward-focused ¹⁹Ne recoils were detected in coincidence at the focal plane of the Daresbury Recoil Separator, while the ¹⁵N recoils from the $\alpha$ emission channel were detected in an annular silicon detector at forward angles. Angular distributions for the protons were measured, and spectroscopic factors extracted from a DWBA analysis, from which proton widths were determined using mirror symmetry. These were used to calculate the astrophysical rate of the ¹⁸F(p,$\alpha$)¹⁵O reaction, which was found to be reduced by approaching an order of magnitude over the temperature range of classical novae [76, 77]. However, systematic uncertainties remained pertaining to the precise mirror assignments between ¹⁹Ne and ¹⁹F.

More recently, uncertainties in this reaction rate stemming from uncertainties in the energies of low-lying resonances ¹⁹Ne have been addressed, using the ¹⁹F(³He,$t\gamma$)¹⁹Ne reaction, measured using GODDESS at ATLAS [10, 78]. The experiment used a 30-MeV ³He beam incident on a $\sim$1 mg/cm² ${\text{CaF}}_2$ target, and outgoing tritons were detected and identified in the ORRUBA silicon detectors. De-excitation $\gamma$ rays were measured in coincidence in the Gammasphere array of Compton-suppressed HPGe detectors. Over forty decays from 21 energy levels were identified. In particular, the positions of two 3/2⁺ states near the proton threshold were determined, and the location of an 11/2⁺ state, previously thought to be unbound, was found to be sub-threshold. This reduced the upper limit to the ¹⁸F(p,$\alpha$)¹⁵O reaction rate by a factor of 1.5–17 across the nova temperature range, reducing the nova detection probability uncertainty by a factor of two [10, 78].

6.2 The ²²Na(p,$\gamma$)²³Na reaction

The radioisotope ²²Na is one of the most promising targets of discrete $\gamma$-ray astronomy, producing a 1.275 MeV $\gamma$-ray line with a lifetime ($t_{1/2}$ = 2.6 years) that is sufficiently short to maintain spatial correlation with localized sources, yet long enough to last beyond the opaque conditions at the peak of a nova explosion. ²²Na is predicted to be produced in sufficient quantity in novae to be detectable, and therefore ²²Na is a leading candidate for a prompt $\gamma$-ray signature for nova nucleosynthesis in our galaxy. Current and previous instruments may be close in sensitivity to detecting the ²²Na line [79–82], and planning has begun for future missions with greater sensitivity [83]. Understanding the quantity of ²²Na produced in a typical nova explosion is crucial to informing such missions, by predicting the number of novae that are within detectable distance, and enabling a quantitative interpretation of this potential signature, should it be detected. This requires reliable models of nova nucleosynthesis, including reaction rates which affect the ²²Na abundance ejected.

The ²²Na(p,$\gamma$)²³Mg reaction is one of the main destruction mechanisms affecting ²²Na yields in nova models. Despite decades of direct and indirect study of the proton resonances important for ²²Na(p,$\gamma$), there is no consensus on the resonance strengths for this important reaction. The resonance believed to be most important at nova temperatures is the 205 keV (7/2)⁺ resonance. There have been two absolute determinations of the strength of this resonance through direct measurements of the (p,$\gamma$) reaction [84–86], performed in 1990 and 2010.² These experiments differ in resonance strength by about a factor of about 2.5, resulting in a discrepancy in ²²Na yields from novae, and hence the possibility of prompt $\gamma$ detection, of a factor of 1.4–2.0. It should be noted that all of these challenging direct (p,$\gamma$) measurements utilized ²²Na-implanted targets. Such measurements are subject to possible systematic uncertainties associated with beam/target overlap due to non-uniformities of implanted ²²Na ions (in both depth and transverse profiles) and the beam profile, and uncertainties in the stopping power of the target. This is further complicated by target degradation from irradiation with intense proton beams (typically tens of $\mu$A), and backgrounds from the mCi-activity of the targets.

Because of this, and its astrophysical importance, the 205-keV (7/2)⁺ resonance has also been the subject of a number of indirect studies, based on measurements of branching ratios of this state, fed by $\beta$ decay. However, rather than resolving the situation, these indirect studies yield resonance strengths with even greater disagreement, spanning over an order of magnitude, and typically with lower strengths than the direct measurements. A recent result yields the lowest number yet [88]. This stems from an experiment using the new gas-filled detector GADGET [89], which is designed to substantially suppress $\beta$ backgrounds compared to silicon-based setups, to aid in measuring low-energy $\beta$-delayed protons. This experiment yielded a substantially smaller proton branching ratio for the 205-keV resonance, despite being in agreement with previous results for the 275-keV and 583-keV resonances [90]. Nominally, the result from the GADGET measurement suggests a resonance strength that is a factor of 7 and 22 below the two direct measurements.

However, in all the $\beta$-delayed proton experiments, the branching ratios obtained must be combined with the absolute lifetime of the state in order to determine a resonance strength, and it has been suggested that the lifetime of the state be revisited [91]. The universally-adopted value for the lifetime of the 205-keV (7/2)⁺ resonance is 10 (3) fs, stemming from a fusion-evaporation measurement using Gammasphere [92, 93], in which the lifetime was determined from the fractional Doppler-shift technique. A more recent measurement at TRIUMF has placed a 3$\sigma$ upper limit on the lifetime of 12 fs [94] using the Doppler-shift Attenuation Method. However, shell-model calculations suggest a shorter lifetime (0.6–1.7 fs) [91, 95], which would systematically raise all the resonance strengths from indirect measurements by about an order of magnitude.

A detailed systematic study of the spectroscopic strengths of single-proton states in ²³Mg would considerably enlighten the situation, as the large variations in resonance strengths correspond to equally large variations in proton spectroscopic factors for these states, as in Equation 3. Though some proton spectroscopic factors have been determined using the ²²Na(³He,d)²³Mg reaction [96] in an experiment using an implanted ²²Na target and a Q3D spectrometer, only upper limits were obtained for most of the resonances in the astrophysically interesting region. Despite the excellent resolution afforded by the spectrometer, the experiment was hampered by strong background lines and less distinct angular distribution shapes from (³He,d), and the need for substantial shielding to cope with the activity of the ²²Na target.

To address this, the GODDESS collaboration undertook a measurement of the ²²Na(d,p)²³Na reaction in inverse kinematics, to determine single-particle spectroscopic factors of the neutron mirror states, and thereby inform the resonance strengths in ²³Mg independently of the systematics of the previous measurements. Spectroscopic strengths in $N$ = $Z$ mirror systems are typically preserved to $\sim$20%–30% level, a considerably smaller uncertainty than the discrepancies in the resonance strengths, and the differences in mirror systems can further be addressed by SMEC calculations [50] (see Section 4.3). The measurement utilized a 10-MeV/A²²Na beam produced by the ²¹Ne(d,p)²²Na reaction at 10 MeV/A using the RAISOR facility at ATLAS at Argonne National Laboratory. The beamline was tuned for ²²Na($q=11+$), providing suppression of Ne (fully stripped Ne ions have $q=10+$), with further suppression of scattered beam by the RF sweeper. This energy is well-suited to the population of the astrophysically-important low-angular-momentum states, and produces distinctive angular distributions. Such measurements in inverse kinematics involve substantially smaller quantities of ²²Na, thereby avoiding the radiological complications of experiments with ²²Na targets. As with a many $sd$-shell $N$ = $Z$ nuclei, ²²Na has a 1⁺ isomer a few hundred keV above the ground state. Though the ²¹Ne(d,n)²²Na reaction populates both the ground state and isomer, the ²²Na isomer $\gamma$ decays with a 243 ns half life to the ²²Na ground state. The flight path between the production target and the experimental target is $\sim$150 feet - which is equivalent to $\sim$5 half lives. Therefore, 97% of the isomeric component of the beam decayed to the ground state by the time the ions reached the experimental target.

The GODDESS position-sensitive fast ionization chamber provided real-time beam diagnostics, including beam composition, rates by particle type, and mm-precision spatial feedback, to aid in tuning of the beamline and optimization of the RF sweeper phase. Protons emitted in the ²²Na(d,p$\gamma$)²³Na reaction were detected in the ORRUBA silicon detectors, and de-excitation $\gamma$ rays in GRETINA. The data from this experiment are currently under analysis.

6.3 The ²⁶Al(p,$\gamma$)²⁷Si reaction

The 1.8 MeV $\gamma$-ray line from the decay of ²⁶Al is a major target of $\gamma$-ray astronomy. Its distribution in galactic coordinates has been extensively mapped, and its Doppler shift studied, indicating that it is co-rotating with, and hence pervasive across, the galaxy. Though it is likely that multiple sites contribute to the 1.8-MeV signature, clues to possible sources can be garnered from its correlation with other signatures that have also been directionally-mapped [97]. Notably, the 1.8-MeV $\gamma$ ray shows strong correlation with 53 GHz free-free microwave emission, which is an indicator of ionized dust clouds, and hence regions of massive star formation [98]. It is likely that massive stars contribute substantially to the ²⁶Al signature, and the rate ^26gAl(p,$\gamma$)²⁷Si reaction at stellar temperatures impacts the net production of ²⁶Al. Although many direct measurements constraining ^26gAl (p,$\gamma$) resonance strengths have been performed, at such low temperatures ($<$ 0.1 GK) the main resonances within the Gamow window for massive stars are out of reach. As discussed in Section 4.3, the lowest energy for which a direct (p,$\gamma$) measurement has been possible is the 189-keV resonance, studied in both normal [47] and inverse kinematics [48].

A 9/2⁺ resonance at 127 keV is likely to dominate in massive stars, which can be populated via ${\ell }_p=0$ proton capture on the 5^{+ 26g}Al. However, due to the lower energy, this resonance is several orders of magnitude weaker than the 189-keV resonance, and hence out of reach for direct measurements. An indirect measurement of the ^26gAl(³He,d)²⁷Si reaction [49] using an ^26gAl target and a Q3D spectrograph was unable to provide more than an upper limit on this resonance, due to the strong backgrounds from reactions on the ²⁷Al component of the target. More recently, (d,p) experiments using radioactive ²⁶Al beams have been used to determine the strengths of resonances out of current reach of direct (p,$\gamma$) measurements [50, 51], which are unconstrained by target impurities that limited the ^26gAl(³He,d)²⁷Si experiment. These experiments, performed at the HRIBF with ORRUBA [50] and at TRIUMF [51], are in remarkable agreement, constraining the strength of the 127-keV resonance ($\omega \gamma$ = ${2.6}_{-0.9}^{+0.7}\times 10^{-5}$ meV [50] and 2.5 (5) $\times 10^{-5}$ meV [51]). The resonance strength was found to be 4 times higher than the previously adopted upper limit, and to dominate the reaction rate at temperatures between 0.04 GK and 0.1 GK [50]. The experiments also placed upper limits on the strength of the even lower-lying 68 keV resonance ($\omega \gamma \le 3.0\times 10^{-12}$ meV [50] and 8 $\times 10^{-13}$ meV [51]).

6.4 The ³⁰P(p,$\gamma$)³¹S reaction

³⁰P is of particular interest for understanding classical nova nucleosynthesis on ONe white dwarfs [99], due in part to the long lifetime of ³⁰P ($\sim$2.5 min) with respect to the timescale of a nova outburst. The ³⁰P(p,$\gamma$)³¹S reaction is a potential bottleneck, affecting the reaction flow into the A = 30–40 mass range during the nova [100]. As a consequence, the rate affects the abundances of isotopes of phosphorus, sulphur and silicon - critical elements for observational constraints on novae. The ³⁰P(p,$\gamma$)³¹S reaction rate directly affects the isotopic ratio of ³⁰Si/²⁸Si, which is an important nova identifier in the analysis of pre-solar grains [101]. Furthermore, the O/S, S/Al, O/P and P/Al elemental ratios have recently been shown to be particularly sensitive probes of nova peak temperatures, with final abundance ratios varying by 2–3 orders of magnitude due to peak temperature changes between $\sim$230 and $\sim$310 MK. In this detailed study, in which these ratios were found to be one-to-two orders of magnitude more sensitive than ratios solely of elements lighter than phosphorus [102], the impact of various reaction rates on the ratios was examined. The uncertainty in the ³⁰P(p,$\gamma$)³¹S rate was highlighted as the major nuclear physics uncertainty in interpreting these ratios, currently hampering the use of these ratios to constrain the energetics of novae.

The rate of this reaction depends critically on the spectroscopic strengths of levels between 6 and 7 MeV excitation in ³¹S. The ³⁰P(d,p$\gamma$)³¹P reaction was measured with GODDESS in inverse kinematics, using mirror symmetry to inform state in ³¹S. An 8 MeV/u beam of ³⁰P ($\sim 80\%$ pure) was produced via the ²⁹Si(d,p)³⁰P reaction, using the RAISOR facility at ATLAS, and delivered to the GODDESS particle-$\gamma$ spectrometer.

The protons emitted from the ³⁰P (d,p)³¹S reaction on a $\sim$600 $\mu$g/cm² ${\text{C}}_2{\text{D}}_4$ target were measured in the ORRUBA detectors. The GODDESS position-sensitive ionization chamber was used to identify P recoils, and aid in the kinematic reconstruction using the recoil position to help account for the large in-flight beam spot. Using coincident $\gamma$ rays to aid in resolution, angular distributions were measured and spectroscopic factors determined. As in the case of ²⁶Al, states of a particular ${\text{J}}^{\pi }$ can be populated via multiple ${\ell }_n$ transfers, due to the 1⁺ ground-state spin. A manuscript on these results is currently in preparation (Ghimire et al., forthcoming).

6.5 The ³⁴Cl(p,$\gamma$)³⁵Ar reaction

The elemental and isotopic composition of dust grains formed during the cooling of nova outflows can provide a signature of the nova origin of these grains, and furthermore provide metrics against which nova models can be tested. Such pre-solar grains can be found in primitive meteorites within the solar system [103]. However, the majority of grains originate from supernovae and massive stars and, although a number of isotopic ratios (including C, N and Si isotopes) are indicators of nova origins, none provide an unambiguous nova signature. A promising candidate for pre-solar grain classification is the ³⁴S/³²S ratio, which recent studies have suggested is constrained to a narrow range in nova grains [101], limit its usefulness. The ³⁴Cl(p,$\gamma$) reaction impacts the nucleosynthetic flow in the sulfur region; if the rate proceeds fast enough with respect to ³⁴Cl $\beta$ decay, the reaction flow bypasses ³⁴S. However, the ³⁴Cl(p,$\gamma$) reaction rate is subject to substantial uncertainties. In nova sensitivity studies [100], a statistical Hauser-Feshbach calculation is adopted for the ³⁴Cl(p,$\gamma$) reaction rate, and assigned factor of 100 uncertainty due to the lack of experimental constraint, resulting in $\times 5$ variations of final ³⁴S abundance. However, in addition to the 0^{+ 34}Cl ground state ($t_{1/2}$ = 1.53 s), the uncertainties are compounded by a low-lying long-lived $3^{+}$ isomer at 146 keV ($t_{1/2}$ = 32 min), which can both be produced directly via the nucleosynthesis network, and by thermal population at nova temperatures [57, 75]. Notably, the reaction network in [100] did not treat the isomer explicitly. It is necessary to assess the reaction rate on both ^34gCl and ^34mCl, and include both explicitly in network calculations.

A recent spectrograph measurement [104] located levels in ³⁵Ar but was unable to constrain the $J^{\pi }$ or widths relevant to the ³⁴Cl(p,$\gamma$)³⁵Ar reaction rate. A theoretical study of rp-process nuclei with low-lying isomers [105] used shell-model calculations of spectroscopic factors and $\gamma$ widths to estimate stellar enhancement factors for radiative capture rates on the isomeric states due to thermal population. For ³⁴Cl(p,$\gamma$), an enhancement factor of $10^3$ was found, peaked at 0.2 GK. As calculations were performed using the USD interaction [106], only positive-parity states were included. However, in other mid $sd$-shell nuclei, substantial spectroscopic strength is expected for ${\ell }_p=1$ resonances, as the lowest states from the $fp$-shell are typically located close to the proton separation energy in these nuclei [50, 52, 107–109]. A more recent (2020) study [107] in $(0+1\hslash \omega )$ space using the $sdpf$-$mu$ interaction [110] predicted negative parity states in the astrophysically interesting energy range. However, with no experimental constraint on these levels, 200-keV uncertainties were assumed on excitation energies, and factor 2 uncertainties on spectroscopic factors (partial widths), leading to large uncertainties in the reaction rate. As the authors note: ‘In a study by Fry et al., 17 ³⁵Ar levels have been detected in the energy region Ex = 5.9–6.7 MeV and their excitation energies have been determined, but not spins, parities, widths, or branching ratios. Because of the paucity of such information, it is not yet possible to derive meaningful experimental ^34g,mCl(p,$\gamma$)³⁵Ar reaction rates’ [107].

A systematic experimental determination of the distribution of single-proton spectroscopic strengths as a function of excitation energy in ³⁵Ar, for both ^34gCl and ^34mCl, would considerably enlighten the situation. A^34g,mCl(d,p)³⁵Cl experiment has been approved by the FRIB PAC [111], using the techniques outlined in Sections 5 and 6.6, and is awaiting scheduling at the time of writing.

6.6 The ³⁸K(p,$\gamma$)³⁹Ca reaction

The ³⁸K(p,$\gamma$)³⁹Ca reaction is an important bottleneck to the end-point of the rp-process chain. The reaction rate has been estimated to be uncertain by a factor of ${10}^4$ [100], leading to large uncertainties in abundances from novae [100, 112]. Further, in Type I x-ray bursts on neutron stars, the rp process branches and proceeds either via ³⁶K (${\beta }^{+}$, $t_{1/2}$ = 0.342 s)³⁶Ar(p,$\gamma$)³⁷K(p,$\gamma$)³⁸Ca or ³⁶K(p,$\gamma$)³⁷Ca(${\beta }^{+}$, $t_{1/2}$ = 0.175 s)³⁷K(p,$\gamma$)³⁸Ca. Since ³⁹Sc is almost proton unbound, the rp flow must wait for ³⁸Ca(${\beta }^{+}$, $t_{1/2}$ = 0.440 s)³⁸K(p,$\gamma$)³⁹Ca [113, 114]. The ³⁸K(p,$\gamma$)³⁹Ca reaction is thus an important path to the formation of heavier elements. However, there is limited experimental constraint; the current rate widely used for nucleosynthesis calculations (JINA REACLIB v2.0) is a theoretical rate based on a Hauser-Feshbach statistical model calculation [115]. Furthermore, the relatively short-lived ($t_{1/2}$ = 924.3 ms) ³⁸K isomer is important, as it is the endpoint of 76.5$\%$ of the ³⁸Ca decays [116] and the rise times of x-ray bursts typically fall in the range of 1–10 s. As such, capture on both ground (^38gK, ${\text{J}}^{\pi }$ = $3^{+}$) and isomeric (^38mK, ${\text{J}}^{\pi }$ = $0^{+}$) states plays an important role in the astrophysical network, and needs experimental constraint.

Though a direct measurement of the ^38gK(p,$\gamma$)³⁹Ca reaction has been reported in recent papers [112, 117], many significant questions remain open. This experiment targeted three known $5/2^{+}$ states (at 386$\pm$10 keV, 515$\pm$10 keV, and 689$\pm$10 keV) in ³⁹Ca, assumed to be populated by $\ell$ = 0 protons coupled to the 3^{+ 38}K ground state. Only upper limits were set for the lower two resonances. A strength for the 689-keV resonance was extracted, but its energy was found to lie 10 keV lower than the adopted energy, at 679 keV. This reaction rate has been addressed by two recent ORRUBA/GODDESS experiments, as detailed in Sections 6.6.1 and 6.6.2.

6.6.1 Constraining ³⁸K(p,$\gamma$)³⁹Ca reaction via the ⁴⁰Ca(³He,$\alpha \gamma$)³⁹Ca reaction

GODDESS was deployed at ATLAS to search for resonances in ³⁹Ca, utilizing the ⁴⁰Ca(³He,$\alpha \gamma$)³⁹Ca reaction [118], and in particular to better constrain the energies of these three 5/2⁺ states. The (³He,$\alpha$) reaction channel was cleanly selected by particle-identification and two-body reaction kinematics of outgoing $\alpha$ particles in ORRUBA. The coincident de-excitation $\gamma$ rays were used to determine 23 new transitions, corresponding to three 5/2⁺ states in ³⁹Ca. The $\gamma$ decay of the 386-keV 5/2⁺ resonance was observe via a direct ground-state transition of 6156.7 (16) keV. This level had previously been measured via the same ⁴⁰Ca(³He,$\alpha$)³⁹Ca reaction, detecting the alphas in a split-pole spectrograph, as 6154 (5) keV [119]. Reducing the uncertainty on this resonance energy alone reduced the uncertainty on this resonance contribution from a factor of $\sim$3 to $\sim$1.6.

The second of these resonances was first reported in 1993 to be at 6286 (10) keV by a spectrograph measurement of the ⁴⁰Ca(p,d)³⁹Ca reaction at 65 MeV [120], giving a resonance energy of 515 (13) keV. This state was not been confirmed in subsequent measurements, such as the ⁴⁰Ca(³He,$\alpha$)³⁹Ca measurement of [119], and was non-observed (i.e., an upper limit reported) in the direct ^38gK(p,$\gamma$)³⁹Ca [112, 117]. In the GODDESS experiment, a direct to ground-state transition of 6268.8 (22) keV was observed, giving a resonance energy of 498 (2) keV - barely over 1$\sigma$ away from the energy of [120]. If this is the same state, not only does this energy difference impact the reaction rate, it also impacts the interpretation of the direct ^38gK(p,$\gamma$)³⁹Ca experiment of [112, 117], in which the gas target covered resonance energies of 515$\pm$13 keV; a 498 (2) keV would not have been located in the gas target.

The third resonance, placed at 679 (2) keV in the ^38gK(p,$\gamma$)³⁹Ca, likely corresponds to previous observations at 6450 (30) keV [121] and 6467 (10) keV [120]. However, the ⁴⁰Ca(³He,$\alpha$)³⁹Ca experiment of [119] placed this state at 6472.2 (24) keV. The GODDESS experiment measured a ground-state transition of 6470.8 (19) keV, in agreement with [119]. This would place this resonance even higher in energy, at 701 (2) keV, which would have been located at the entrance (rather than the center) of the target, which covered 689$\pm$13 keV. This leads to questions as the absolute normalization of the yields from this experiment if these are the same resonance. It is noteworthy that capture at this beam energy on the $0^{+}$ isomer (which comprised $\sim 5\%$ of the beam composition [112, 117]), corresponds exactly to a known state at 6580 keV [120].

In total, from this experiment, by locating the energies of states more precisely, the upper limit on the ³⁸K(p,$\gamma$)³⁹Ca was reduced over the temperature range of novae [118]. Furthermore, such experiments highlight the importance of high-resolution experiments, such as $\gamma$-ray spectroscopy, for precise determination of resonance energies, which are crucial to guiding the planning and interpretation of direct (p,$\gamma$) measurements with radioactive beams.

6.6.2 Constraining ³⁸K(p,$\gamma$)³⁹Ca reaction via the ³⁸K (d,p)³⁹K reaction

Despite substantial progress, many open questions remain pertaining to the ³⁸K(p,$\gamma$)³⁹Ca reaction rate. Firstly, these direct measurements provided no explicit constraint on proton capture on ^38mK. Furthermore, in addition to the ${\ell }_p=0$ resonances that have been the subject of much focus, important ${\ell }_p=1$ resonances are anticipated in this region, as the $2p$ orbitals are mostly vacant in ³⁸K, the $2s$ orbital is full, and the $3s$ orbital lies much higher in energy. No information constraining the precise location and strength of these resonances currently exists. Proton capture through higher-$\ell$ orbitals is suppressed due to the larger barrier (Section 4.3).

Indeed, there are two known $3/2^{-}$ states in ³⁹Ca that are just above the ³⁸K + p threshold at 5.771 MeV, and there are several levels in ³⁹K in the same region that are potential mirrors to these ³⁹Ca states [122]. One or both of these states might be formed with a 2$p_{3/2}$ proton coupled to either the 3^{+ 38g}K or the 0^{+ 38m}K(130.4 keV), but those structures have not been studied. Determining the location, spins and strengths of these resonances is crucial for an accurate and robust description of the ³⁸K(p,$\gamma$) rate, and to identify the most important resonances to be targeted with direct measurements.

To inform the properties of the relevant proton resonances near the ³⁸K + p threshold, a proton transfer reaction, such as ³⁸K(³He,d)³⁹Ca or ³⁸K(d,n)³⁹Ca, would ideally be performed on both ground and isomeric states of ³⁸K. However, as ³⁹K and ³⁹Ca are mirror nuclei, the technique of measuring the mirror ³⁸K(d,p)³⁹K reaction can be applied. Furthermore, due to the advances in delivering beams of nuclides in their ground and isomeric states, and controlling their ratio (as described in Section 5), a simultaneous measurement of ^38g,mK (d,p)³⁹K was undertaken at the ReA facility.

The 4.57 MeV/u beam, at a total intensity of $\sim$50k ions/second, comprised a 60:40 composition of ³⁸K and ³⁸Ar. The beam was delivered to a 420 $\mu$g/cm² ${\text{C}}_2{\text{D}}_4$ target. Proton ejectiles following the (d,p) reaction were measured between $\sim$ 45$°$ and $\sim$ 175$°$ using ORRUBA. The GODDESS position-sensitive fast ionization chamber MAGIC (Pain et al., forthcoming) was used to identify events corresponding to K or Ar induced reactions. Two charge-breeding settings were employed for the experiment to manipulate the ³⁸K GS:IS content of the beam. A short setting of 150 ms charge-breeding time (corresponding to a total hold-up time of $\sim$ 300 ms) produced a³⁸K GS:IS composition of $\sim$5:4. A long setting, allowing most of the IS to decay, resulted in a GS:IS composition of $\sim$9:1.

The reactions on the GS and isomer are deconvolved by scaling the data with the long holdup time to the short-holdup-time data by the number of incident GS ions. The difference between the two spectra therefore results entirely from reactions on the isomer. This deconvolution is straightforward, as the beam, target and detector properties, and hence experimental response, are identical for the two data sets. These data are currently under analysis to extract angular distributions, $J^{\pi }$ assignments and spectroscopic factors for states built on both ^38gK and ^38mK.

7 Conclusion and outlook

Recent years have seen substantial investments in radioactive beam production, in the US (with the nascent US flagship facility, FRIB, and nuCARIBU at ATLAS at Argonne National Laboratory), and globally. With these investments come opportunities for constraining radiative-capture cross sections via direct measurements of resonance strengths, consequently spurring the development of new instrumentation, such as recoil separators such as SECAR at FRIB, and the JENSA gas-jet target.

However, to make use of these advances, indirect techniques, including various direct reactions (such as (d,p), (³He,t) and (³He,$\alpha$) reactions highlighted herein) using stable and radioactive beams, are crucial in guiding the direct measurements. Techniques for constraining astrophysically-important proton-capture reactions via direct reactions has been a major focus of the ORRUBA program for approaching two decades. To this end, new developments in instrumentation have been undertaken, such as the GODDESS coupling to the flagship HPGe arrays (Gammasphere, GRETINA and GRETA), and improved recoil detectors, to improve the sensitivity and resolution of direct reaction measurements.

With the increased complexity of RIB facilities, and competition for beam time, such indirect measurements will be increasingly critical for guiding direct measurements of radiative capture reactions, and in some cases remain the only way of constraining lower-lying resonances that are too weak for direct measurements with radioactive beams in the foreseeable future.

Author contributions

SP: Writing – original draft, Writing – review and editing.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. This work was supported by the U.S. Department of Energy, Office of Science, Office of Nuclear Physics under Contract No. DE-AC05-00OR22725 (ORNL).

Acknowledgments

Thanks are owed to the members of the ORRUBA and GODDESS collaborations, and the operations staff at the HRIBF, ATLAS and ReA (NSCL/FRIB). The mentorship, friendship, collaboration, and pioneering contributions of the late Ray Kozub to the (d,p) experimental program discussed herein, stemming from the ¹⁸F(d,p) experiment, are remembered with fondness and gratitude.

Conflict of interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Gen AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Footnotes

¹Note that in this experiment, the statistics in differential cross sections (see Figure 6 of [49]) were insufficient to constrain ${\ell }_p$, and for many years this state was assigned positive parity. Recent (d,p) data (see below) indicate an ${\ell }_p=1$ transfer to the mirror of this state.

²A third study of direct ²²Na(p,$\gamma$)²³Mg measurement [87], performed at Bochum, extended measurements to lower energy resonances, but measured relative yields only, using the 274-keV and 583-keV resonances to normalize the their data to the Münster experiment [84], so provide no independent constraint on the absolute value of the strength of the 205-keV resonance

References

1. Bardayan DW. Transfer reactions in nuclear astrophysics. J.Phys.(London) (2016) G43:043001. doi:10.1088/0954-3899/43/4/043001

CrossRef Full Text | Google Scholar

2. Brune CR, Davids B. Radiative capture reactions in astrophysics. Annu Rev Nucl Part Sci (2015) 65:87–112. doi:10.1146/annurev-nucl-102014-022027

CrossRef Full Text | Google Scholar

3. Hammache F, de Séréville N. Transfer reactions as a tool in nuclear astrophysics. Front Phys (2021) 8. doi:10.3389/fphy.2020.602920

CrossRef Full Text | Google Scholar

4. Catford WN. What can we learn from transfer, and how is best to do it? Berlin, Heidelberg: Springer Berlin Heidelberg (2014). 67–122. doi:10.1007/978-3-642-45141-6_3

CrossRef Full Text | Google Scholar

5. Bardayan DW, Blackmon JC, Brune CR, Champagne AE, Chen AA, Cox JM, et al. Observation of the astrophysically important 3⁺ state in¹⁸ne via elastic scattering of a radioactive¹⁷f beam from¹h. Phys Rev Lett (1999) 83:45–8. doi:10.1103/PhysRevLett.83.45

CrossRef Full Text | Google Scholar

6. Davinson T, Bradfield-Smith W, Cherubini S, DiPietro A, Galster W, Laird A, et al. Louvain–edinburgh detector array (leda): a silicon detector array for use with radioactive nuclear beams. Nucl Instr Methods Phys Res Section A: Acc Spectrometers, Detectors Associated Equipment (2000) 454:350–8. doi:10.1016/S0168-9002(00)00479-4

CrossRef Full Text | Google Scholar

7. Pain SD, Cizewski JA, Hatarik R, Jones KL, Thomas JS, Bardayan DW, et al. Development of a high solid-angle silicon detector array for measurement of transfer reactions in inverse kinematics. Nuclear Instruments and Methods in Physics Research Section B: Beam Interactions with Materials and Atoms (2007). 261:1122–1125. doi:10.1016/j.nimb.2007.04.289

CrossRef Full Text | Google Scholar

8. Pain SD. Advances in instrumentation for nuclear astrophysics. AIP Adv (2014) 4:041015. doi:10.1063/1.4874116

CrossRef Full Text | Google Scholar

9. Chae K, Ahn S, Bardayan D, Chipps K, Manning B, Pain S, et al. Construction of a fast ionization chamber for high-rate particle identification. Nucl Instr Methods Phys Res Section A: Acc Spectrometers, Detectors Associated Equipment (2014) 751:6–10. doi:10.1016/j.nima.2014.03.016

CrossRef Full Text | Google Scholar

10. Hall MR, Bardayan DW, Baugher T, Lepailleur A, Pain SD, Ratkiewicz A, et al. ¹⁹Ne level structure for explosive nucleosynthesis. Phys Rev C (2020) 102:045802. doi:10.1103/PhysRevC.102.045802

CrossRef Full Text | Google Scholar

11. Chipps K, Greife U, Bardayan D, Blackmon J, Kontos A, Linhardt L, et al. The jet experiments in nuclear structure and astrophysics (jensa) gas jet target. Nucl Instr Methods Phys Res Section A: Acc Spectrometers, Detectors Associated Equipment (2014) 763:553–64. doi:10.1016/j.nima.2014.06.042

CrossRef Full Text | Google Scholar

12. Schmidt K, Chipps KA, Ahn S, Bardayan DW, Browne J, Greife U, et al. Status of the JENSA gas-jet target for experiments with rare isotope beams. Nucl Inst.s Meth.in Phys Res A (2018). 911:1–9. doi:10.1016/j.nima.2018.09.052

CrossRef Full Text | Google Scholar

13. Labiche M, Catford W, Lemmon R, Timis C, Chapman R, Orr N, et al. Tiara: a large solid angle silicon array for direct reaction studies with radioactive beams. Nucl Instr Methods Phys Res Section A: Acc Spectrometers, Detectors Associated Equipment (2010) 614:439–48. doi:10.1016/j.nima.2010.01.009

CrossRef Full Text | Google Scholar

14. Diget CA, Fox SP, Smith A, Williams S, Porter-Peden M, Achouri L, et al. SHARC: silicon highly-segmented array for reactions and coulex used in conjunction with the tigress γ-ray spectrometer. J Instrumentation (2011) 6:P02005. doi:10.1088/1748-0221/6/02/p02005

CrossRef Full Text | Google Scholar

15. Bildstein V, Gernhauser R, Kroll T, Krucken P, Wimmer P, Van Duppen P, et al. T-rex a new setup for transfer experiments at rex-isolde. Eur.Phys.J. (2012) 48:85. doi:10.1140/epja/i2012-12085-6

CrossRef Full Text | Google Scholar

16. Berner C, Werner L, Gernhäuser R, Kröll T. Hi-trex—a highly integrated transfer setup at rex-(hie)isolde. Nucl Instr Methods Phys Res Section A: Acc Spectrometers, Detectors Associated Equipment (2021) 987:164827. doi:10.1016/j.nima.2020.164827

CrossRef Full Text | Google Scholar

17. Assié M, Clément E, Lemasson A, Ramos D, Raggio A, Zanon I, et al. The mugast-agata-vamos campaign: set-up and performances. Nucl Instr Methods Phys Res Section A: Acc Spectrometers, Detectors Associated Equipment (2021) 1014:165743. doi:10.1016/j.nima.2021.165743

CrossRef Full Text | Google Scholar

18. Pain SD, Ratkiewicz A, Baugher T, Febbraro M, Lepailleur A, Ayangeakaa AD, et al. Direct reaction measurements using GODDESS. Phys Proc (2017) 90:455. doi:10.1016/j.phpro.2017.09.051

CrossRef Full Text | Google Scholar

19. Lee IY. The gammasphere. Nucl Struct Nineties 520 (1990) c641–55. doi:10.1016/0375-9474(90)91181-P

CrossRef Full Text | Google Scholar

20. Vetter K, Kuhn A, Lee I, Clark R, Cromaz M, Deleplanque M, et al. Performance of the greta prototype detectors. Nucl Instr Methods Phys Res Section A: Acc Spectrometers, Detectors Associated Equipment (2000) 452:105–14. doi:10.1016/S0168-9002(00)00431-9

CrossRef Full Text | Google Scholar

21. Descovich M, Lee I, Cromaz M, Clark R, Deleplanque M, Diamond R, et al. GRETINA status and recent progress: The effect of neutron damage on energy and position resolution of the GRETINA detector. Nucl Instr Methods Phys Res Section B: Beam Interactions Mater Atoms (2005) 241:931–4. doi:10.1016/j.nimb.2005.07.150

CrossRef Full Text | Google Scholar

22. Paschalis S, Lee I, Macchiavelli A, Campbell C, Cromaz M, Gros S, et al. The performance of the gamma-ray energy tracking in-beam nuclear array GRETINA. Nucl Instr Methods Phys Res Section A: Acc Spectrometers, Detectors Associated Equipment (2013) 709:44–55. doi:10.1016/j.nima.2013.01.009

CrossRef Full Text | Google Scholar

23. Fallon P, Gade A, Lee IY. GRETINA and its early science. Annu Rev Nucl Part Sci (2016) 66:321–39. doi:10.1146/annurev-nucl-102115-044834

CrossRef Full Text | Google Scholar

24. Weisshaar D, Bazin D, Bender P, Campbell C, Recchia F, Bader V, et al. The performance of the γ -ray tracking array GRETINA for γ -ray spectroscopy with fast beams of rare isotopes. Nucl Instr Methods Phys Res Section A: Acc Spectrometers, Detectors Associated Equipment (2017) 847:187–98. doi:10.1016/j.nima.2016.12.001

CrossRef Full Text | Google Scholar

25. GRETA final design report. Lawrence Berkeley National Laboratory (2020).

Google Scholar

26. Thomas JS, Bardayan DW, Blackmon JC, Cizewski JA, Greife U, Gross CJ, et al. First study of the level structure of the r-process nucleus ⁸³Ge. Phys Rev C (2005) 71:021302. doi:10.1103/PhysRevC.71.021302

CrossRef Full Text | Google Scholar

27. Kimura K, Izumikawa T, Koyama R, Ohnishi T, Ohtsubo T, Ozawa A, et al. High-rate particle identification of high-energy heavy ions using a tilted electrode gas ionization chamber. Nucl Instr Methods Phys Res Section A: Acc Spectrometers, Detectors Associated Equipment (2005) 538:608–14. doi:10.1016/j.nima.2004.08.100

CrossRef Full Text | Google Scholar

28. Koshchiy E, Blackmon J, Rogachev G, Wiedenhöver I, Baby L, Barber P, et al. Anasen: the array for nuclear astrophysics and structure with exotic nuclei. Nucl Instr Methods Phys Res Section A: Acc Spectrometers, Detectors Associated Equipment (2017) 870:1–11. doi:10.1016/j.nima.2017.07.030

CrossRef Full Text | Google Scholar

29. Lai J, Afanasieva L, Blackmon J, Deibel C, Gardiner H, Lauer A, et al. Position-sensitive, fast ionization chambers. Nucl Instr Methods Phys Res Section A: Acc Spectrometers, Detectors Associated Equipment (2018) 890:119–125. doi:10.1016/j.nima.2018.01.010

CrossRef Full Text | Google Scholar

30. Chester A, Smallcombe J, Henderson J, Berean-Dutcher J, Bernier N, Bhattacharjee S, et al. Trific: the triumf fast ion counter. Nucl Instr Methods Phys Res Section A: Acc Spectrometers, Detectors Associated Equipment (2019) 930:1–7. doi:10.1016/j.nima.2019.03.075

CrossRef Full Text | Google Scholar

31. Woods RD, Saxon DS. Diffuse surface optical model for nucleon-nuclei scattering. Phys Rev (1954) 95:577–578. doi:10.1103/PhysRev.95.577

CrossRef Full Text | Google Scholar

32. Schiffer JP. Proton widths in a diffuse well. Nucl Phys (1963) 46:246–250. doi:10.1016/0029-5582(63)90586-8

CrossRef Full Text | Google Scholar

33. Iliadis C. Proton single-particle reduced widths for unbound states. Nucl Phys A (1997) 618:166. doi:10.1016/s0375-9474(97)00065-1

CrossRef Full Text | Google Scholar

34. Author anonymous (2024). Available online at: https://orruba.org/software (Accessed December 2024).

Google Scholar

35. Author anonymous (2024). Available online at: https://people.frib.msu.edu/brown/reaction-codes (Accessed December 2024).

Google Scholar

36. Iliadis C, Wiescher M. Spectroscopic factors from direct proton capture. Phys Rev C (2004) 69:064305. doi:10.1103/PhysRevC.69.064305

CrossRef Full Text | Google Scholar

37. Iliadis C, Endt PM, Prantzos N, Thompson WJ. Explosive hydrogen burning of 27si, 31s, 35ar, and 39ca in novae and x-ray bursts. Astrophysical J (1999) 524:434–53. doi:10.1086/307778

CrossRef Full Text | Google Scholar

38. Iliadis C. Nuclear Physics of Stars. Wiley-VCH (2007).

Google Scholar

39. Kozub RL, Youngblood DH. Single-particle strengths for quasibound levels in ³³Cl. Phys Rev C (1972) 5:413–9. doi:10.1103/PhysRevC.5.413

CrossRef Full Text | Google Scholar

40. Hale SE, Champagne AE, Iliadis C, Hansper VY, Powell DC, Blackmon JC. Investigation of the ²²Ne(p,γ)²³Na reaction via (³He, d) spectroscopy. Phys Rev C (2001) 65:015801. doi:10.1103/PhysRevC.65.015801

CrossRef Full Text | Google Scholar

41. Harrouz DS, de Séréville N, Adsley P, Hammache F, Longland R, Bastin B, et al. Experimental study of the ³⁰Si(³He, d)³¹P reaction and thermonuclear reaction rate of ³⁰Si(p,γ)³¹P. Phys Rev C (2022) 105:015805. doi:10.1103/PhysRevC.105.015805

CrossRef Full Text | Google Scholar

42. Kankainen A, Woods PJ, Nunes F, Langer C, Schatz H, Bader V, et al. Angle-integrated measurements of the ²⁶Al (d, n)²⁷Si reaction cross section: a probe of spectroscopic factors and astrophysical resonance strengths. Eur Phys J (2016). 52:6. doi:10.1140/epja/i2016-16006-5

CrossRef Full Text | Google Scholar

43. Kankainen A, Woods PJ, Schatz H, Poxon-Pearson T, Doherty DT, Bader V, et al. Measurement of key resonance states for the ³⁰p(p,γ)³¹s reaction rate, and the production of intermediate-mass elements in nova explosions. Phys Lett B (2017) 769:549. doi:10.1016/j.physletb.2017.01.084

CrossRef Full Text | Google Scholar

44. Hallam S, Lotay G, Gade A, Doherty DT, Belarge J, Bender PC, et al. Exploiting isospin symmetry to study the role of isomers in stellar environments. Phys Rev Lett (2021) 126:042701. doi:10.1103/physrevlett.126.042701

PubMed Abstract | CrossRef Full Text | Google Scholar

45. Lotay G, Henderson J, Catford WN, Ali FA, Berean J, Bernier N, et al. Single neutron transfer on ²³ne and its relevance for the pathway of nucleosynthesis in astrophysical x-ray bursts. Phys Lett B (2022) 833:137361. doi:10.1016/j.physletb.2022.137361

CrossRef Full Text | Google Scholar

46. Laird AM, Lugaro M, Kankainen A, Adsley P, Bardayan DW, Brinkman HE, et al. Progress on nuclear reaction rates affecting the stellar production of ²⁶al. J.Phys.(London) (2023). G50:033002. doi:10.1088/1361-6471/ac9cf8

CrossRef Full Text | Google Scholar

47. Vogelaar RB. The ²⁶Al(p,γ) ²⁷Si reaction: stellar origins of galactic ²⁶Al. Pasadena, CA: California insitute of Technology. Ph.D Thesis (1989).

Google Scholar

48. Ruiz C, Parikh A, José J, Buchmann L, Caggiano JA, Chen AA, et al. Measurement of the Ec.m. = 184 keV resonance strength in the 26gAl (p, gamma)27 Si reaction. Phys Rev Lett (2006) 96:252501. doi:10.1103/PhysRevLett.96.252501

PubMed Abstract | CrossRef Full Text | Google Scholar

49. Vogelaar RB, Mitchell LW, Kavanagh RW, Champagne AE, Magnus PV, Smith MS, et al. Phys Rev C (1996). 53:1945–9. doi:10.1103/PhysRevC.53.1945

PubMed Abstract | CrossRef Full Text | Google Scholar

50. Pain SD, Bardayan DW, Blackmon JC, Brown SM, Chae KY, Chipps KA, et al. Constraint of the astrophysical ^26gAl(p,γ)²⁷ Si destruction rate at stellar temperatures. Phys Rev Lett (2015) 114:212501. doi:10.1103/PhysRevLett.114.212501

PubMed Abstract | CrossRef Full Text | Google Scholar

51. Margerin V, Lotay G, Woods PJ, Aliotta M, Christian G, Davids B, et al. Inverse kinematic study of the (26g)Al(d,p)(27)Al reaction and implications for destruction of (26)Al in wolf-rayet and asymptotic giant branch stars. Phys Rev Lett (2015) 115:062701. doi:10.1103/PhysRevLett.115.062701

PubMed Abstract | CrossRef Full Text | Google Scholar

52. Lotay G, Woods PJ, Moukaddam M, Aliotta M, Christian G, Davids B, et al. High-resolution radioactive beam study of the ²⁶al(d, p) reaction and measurements of single-particle spectroscopic factors. Eur Phys J (2020) A 56:3. doi:10.1140/epja/s10050-019-00008-8

CrossRef Full Text | Google Scholar

53. Okołowicz J, Płoszajczak M, Rotter I. Dynamics of quantum systems embedded in a continuum. Phys Rep (2003) 374:271–383. doi:10.1016/S0370-1573(02)00366-6

CrossRef Full Text | Google Scholar

54. Okołowicz J, Michel N, Nazarewicz W, Płoszajczak M. Asymptotic normalization coefficients and continuum coupling in mirror nuclei. Phys Rev C (2012) 85:064320. doi:10.1103/PhysRevC.85.064320

CrossRef Full Text | Google Scholar

55. Brown BA, Richter WA. New usd Hamiltonians for the sd shell. Phys Rev C (2006) 74:034315. doi:10.1103/physrevc.74.034315

CrossRef Full Text | Google Scholar

56. Ward R, Fowler WA. Thermalization of long-lived nuclear isomeric states under stellar conditions. Astrophys J (1980) 238:266–86. doi:10.1086/157983

CrossRef Full Text | Google Scholar

57. Coc A, Porquet MG, Nowacki F Lifetimes of ²⁶Al and ³⁴Cl in an astrophysical plasma. Phys Rev C (1999) 61:015801. doi:10.1103/PhysRevC.61.015801

CrossRef Full Text | Google Scholar

58. Gupta SS, Meyer BS. Internal equilibration of a nucleus with metastable states: ²⁶Al as an example. Phys Rev C (2001) 64:025805. doi:10.1103/PhysRevC.64.025805

CrossRef Full Text | Google Scholar

59. Misch GW, Ghorui SK, Banerjee P, Sun Y, Mumpower MR. Astromers: nuclear isomers in astrophysics^*. Astrophysical J Suppl Ser (2020) 252:2. doi:10.3847/1538-4365/abc41d

CrossRef Full Text | Google Scholar

60. Misch GW, Sprouse TM, Mumpower MR. Astromers in the radioactive decay of r-process nuclei. Astrophysical J Lett (2021) 913:L2. doi:10.3847/2041-8213/abfb74

CrossRef Full Text | Google Scholar

61. Misch GW, Sprouse TM, Mumpower MR, Couture AJ, Fryer CL, Meyer BS, et al. Sensitivity of neutron-rich nuclear isomer behavior to uncertainties in direct transitions. Symmetry (2021) 13:1831. doi:10.3390/sym13101831

CrossRef Full Text | Google Scholar

62. Misch GW, Mumpower MR Astromers: status and prospects. Eur Phys J Spec Top (2024) 233:1075–99. doi:10.1140/epjs/s11734-024-01136-z

CrossRef Full Text | Google Scholar

63. Lotay G, et al. Radiative Capture on Nuclear Isomers: Direct Measurement of the ^26mAl(p, γ) ²⁷Si Reaction. Phys Rev Lett (2022). 128:042701. doi:10.1103/PhysRevLett.128.042701

PubMed Abstract | CrossRef Full Text | Google Scholar

64. Almaraz-Calderon S, Rehm KE, Gerken N, Avila ML, Kay BP, Talwar R, et al. Study of the ²⁶Al^m(d,p)_27AI reaction and the influence of the ²⁶Al 0⁺ isomer on the destruction of ²⁶Al in the galaxy. Phys Rev Lett (2017) 119:072701. doi:10.1103/PhysRevLett.119.072701

PubMed Abstract | CrossRef Full Text | Google Scholar

65. Chipps KA, Kozub RL, Sumithrarachchi C, Ginter T, Baumann T, Lund K K 38 isomer production via fast fragmentation. Phys Rev Accel Beams (2018). 21:121301. doi:10.1103/PhysRevAccelBeams.21.121301

CrossRef Full Text | Google Scholar

66. Shehu OA, Crider BP, Ginter T, Hoffman CR, Ogunbeku TH, Xiao Y, et al. Experimental study of the ^34mCl beam production at intermediate energies. Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment (2022). 1035:166789. doi:10.1016/j.nima.2022.166789

CrossRef Full Text | Google Scholar

67. Pain S. FRIB Proposal 23079 Approved; awaiting scheduling (2023).

Google Scholar

68. Mahoney WA, Ling JC, Jacobson AS, Lingenfelter RE. Diffuse galactic gamma-ray line emission from nucleosynthetic Fe-60, Al-26, and Na-22 - preliminary limits from HEAO 3. Astrophys J (1982) 262:742. doi:10.1086/160469

CrossRef Full Text | Google Scholar

69. Share GH, Kinzer RL, Kurfess JD, Forrest DJ, Chupp EL, Rieger E. Detection of galactic Al-26 gamma radiation by the SMM spectrometer. Astrophys J (1985) 292:L61–L65. doi:10.1086/184473

CrossRef Full Text | Google Scholar

70. Schoenfelder V, Aarts H, Bennett K, de Boer H, Clear J, Collmar W, et al. Instrument description and performance of the imaging gamma-ray telescope COMPTEL aboard the Compton gamma-ray observatory. Astrophys J Supp Ser (1993) 86:657–92. doi:10.1086/191794

CrossRef Full Text | Google Scholar

71. Diehl R, Dupraz C, Bennett K, Bloemen H, de Boer H, Hermsen W, et al. COMPTEL observations of the 1.809 MeV gamma-ray line from galactic Al (1994). 26:429–32. doi:10.1086/191990

CrossRef Full Text | Google Scholar

72. Diehl R, Halloin H, Kretschmer K, Lichti GG, Schönfelder V, Strong AW, et al. Radioactive ²⁶Al from massive stars in the Galaxy. Nature (2006) 439:45–7. doi:10.1038/nature04364

PubMed Abstract | CrossRef Full Text | Google Scholar

73. Diehl R, Lang M, Kretschmer K, Wang W. ²⁶Al emission throughout the galaxy. New Astron Rev 52 (2008). 440–4. doi:10.1016/j.newar.2008.06.024

CrossRef Full Text | Google Scholar

74. Voss R, Diehl R, Hartmann D, Kretschmer K. Population synthesis models for 26al production in starforming regions. New Astron Rev (2008) 52:436–9. doi:10.1016/j.newar.2008.06.022

CrossRef Full Text | Google Scholar

75. Banerjee P, Misch GW, Ghorui SK, Sun Y Effective stellar β-decay rates of nuclei with long-lived isomers: ²⁶Al and ³⁴Cl. Phys Rev C (2018) 97:065807. doi:10.1103/PhysRevC.97.065807

CrossRef Full Text | Google Scholar

76. Kozub RL, Bardayan DW, Batchelder JC, Blackmon JC, Brune CR, Champagne AE, et al. New constraints on the¹⁸F(p,α)¹⁵O rate in novae from the (d, p) reaction. Phys Rev C (2005) 71:032801. doi:10.1103/PhysRevC.71.032801

CrossRef Full Text | Google Scholar

77. Kozub RL, Bardayan DW, Batchelder JC, Blackmon JC, Brune CR, Champagne AE, et al. Neutron single particle strengths from the reaction on ¹⁸F. Phys Rev C 73 (2006) 044307. doi:10.1103/PhysRevC.73.044307

CrossRef Full Text | Google Scholar

78. Hall MR, Bardayan DW, Baugher T, Lepailleur A, Pain SD, Ratkiewicz A, et al. Key¹⁹Ne states identified affecting γ-ray emission from¹⁸F in novae. Phys Rev Lett (2019) 122:052701. doi:10.1103/PhysRevLett.122.052701

PubMed Abstract | CrossRef Full Text | Google Scholar

79. Iyudin AF, Bennett K, Bloemen H, Diehl R, Hermsen W, Lichti GG, et al. COMPTEL search for 2̂2N̂a line emission from recent novae. Astron Astrophys (1995) 300:422.

Google Scholar

80. Jean P, Hernanz M, Gomez-Gomar J, Jose J. Galactic 1.275-MeV emission from ONe novae and its detectability by INTEGRAL/SPI. Mon Not R Astron Soc (2000) 319:350–64. doi:10.1046/j.1365-8711.2000.03587.x

CrossRef Full Text | Google Scholar

81. Siegert T, Coc A, Delgado LG, Diehl R, Greiner J, Hernanz M, et al. Gamma-ray observations of nova sgr 2015 no. 2 with integral, 292 (2018).

Google Scholar

82. Siegert T, Coc A, Delgado LG, Diehl R, Greiner J, Hernanz M, et al. Gamma-ray observations of nova sgr 2015 no. 2 with integral. Astron Astrophys (2018) 615:A107. doi:10.1051/0004-6361/201732514

CrossRef Full Text | Google Scholar

83. Fryer CL, Timmes F, Hungerford AL, Couture A, Adams F, Aoki W, et al. Catching element formation in the act (2019).

Google Scholar

84. Seuthe S, Rolfs C, Schroder U, Schulte W, Somorjai E, Trautvetter H, et al. Resonances in the 22Na(p,γ)23mg reaction. Nucl Phys A (1990) 514:471–502. doi:10.1016/0375-9474(90)90153-D

CrossRef Full Text | Google Scholar

85. Sallaska AL, Wrede C, García A, Storm DW, Brown TAD, Ruiz C, et al. Direct measurements of ²²Na(p,γ) ²³Mg resonances and consequences for ²²Na production in classical novae. Phys Rev Lett (2010) 105:152501. doi:10.1103/PhysRevLett.105.152501

PubMed Abstract | CrossRef Full Text | Google Scholar

86. Sallaska AL, Wrede C, García A, Storm DW, Brown TAD, Ruiz C, et al. Absolute determination of the²²Na(p, γ)²³Mg reaction rate in novae. Phys Rev C (2011) 83:034611. doi:10.1103/PhysRevC.83.034611

CrossRef Full Text | Google Scholar

87. Stegmüller F, Rolfs C, Schmidt S, Schulte WH, Trautvetter HP, Kavanagh RW. ²²Na(p,γ) ²³Mg resonant reaction at low energies. Nucl Phys A (1996) 601:168–80. doi:10.1016/0375-9474(96)00084-X

CrossRef Full Text | Google Scholar

88. Friedman M, Budner T, Pérez-Loureiro D, Pollacco E, Wrede C, José J, et al. Low-energy ²³-delayed proton decay and ²²Na destruction in novae. Phys Rev C 101 (2020) 052802. doi:10.1103/PhysRevC.101.052802

CrossRef Full Text | Google Scholar

89. Friedman M, Perez-Loureiro D, Budner T, Pollacco E, Wrede C, Cortesi M, et al. Gadget: a gaseous detector with germanium tagging. Nucl Instr Methods Phys Res Section A: Acc Spectrometers, Detectors Associated Equipment (2019) 940:93–102. doi:10.1016/j.nima.2019.05.100

CrossRef Full Text | Google Scholar

90. Saastamoinen A, Trache L, Banu A, Bentley MA, Davinson T, Hardy JC, et al. Experimental study of β-delayed proton decay of ²³Al for nucleosynthesis in novae. Phys Rev C (2011) 83:045808. doi:10.1103/PhysRevC.83.045808

CrossRef Full Text | Google Scholar

91. Friedman M, Budner T, Perez-Loureiro D, Pollacco E, Wrede C, Jose J, et al. Low-energy ²³Al β-delayed proton decay and ²²Na destruction in novae. arXiv (2019).

Google Scholar

92. Jenkins DG, Lister CJ, Janssens RVF, Khoo TL, Moore EF, Rehm KE, et al. Reevaluation of the ²²Na(p, γ) reaction rate: implications for the detection of ²²Na gamma rays from novae. Phys Rev Lett (2004) 92:031101. doi:10.1103/PhysRevLett.92.031101

PubMed Abstract | CrossRef Full Text | Google Scholar

93. Jenkins DG, Bouhelal M, Courtin S, Freer M, Fulton BR, Haas F, et al. γ-ray spectroscopy of the a = 23, t = 1/2 nuclei ²³Na and ²³Mg: high-spin states, mirror symmetry, and applications to nuclear astrophysical reaction rates. Phys Rev C (2013) 87:064301. doi:10.1103/PhysRevC.87.064301

CrossRef Full Text | Google Scholar

94. Kirsebom OS, Bender P, Cheeseman A, Christian G, Churchman R, Cross DS, et al. Measurement of lifetimes in ²³Mg. Phys Rev C (2016) 93:025802. doi:10.1103/PhysRevC.93.025802

CrossRef Full Text | Google Scholar

95. Jin SJ, Wang YB, Su J, Yan SQ, Li YJ, Guo B, et al. Resonant scattering of ²²na + p studied by the thick-target inverse-kinematic method. Phys Rev C (2013) 88:035801. doi:10.1103/PhysRevC.88.035801

CrossRef Full Text | Google Scholar

96. Schmidt S, Rolfs C, Schulte WH, Trautvetter HP, Kavanagh RW, Hategan C, et al. ²²Na(³He,d)²³Mg reaction studies of states near the proton threshold and hydrogen burning of ²²Na. Nucl Phys A (1995). 591:227. doi:10.1016/0375-9474(95)00164-V

CrossRef Full Text | Google Scholar

97. Knödlseder J, Bennett K, Bloemen H, Diehl R, Hermsen W, Oberlack U, et al. A multiwavelength comparison of COMPTEL 1.8 MeV {(26)} line data, 344 (1999). 68–82.

Google Scholar

98. Knödlseder J. On the origin of galactic ²⁶AL. Astrophys Lett Comm (1999) 38:379. doi:10.48550/arXiv.astro-ph/9902281

CrossRef Full Text | Google Scholar

99. Wrede C. The ³⁰P(p,γ)³¹S reaction in classical novae: progress and prospects. A.I.P Adv (2014) 4:041004. doi:10.1063/1.4864193

CrossRef Full Text | Google Scholar

100. Iliadis C, Champagne A, José J, Starrfield S, Tupper P. Ap J Suppl Ser (2002) 142:105. doi:10.1086/341400

CrossRef Full Text | Google Scholar

101. José J, Hernanz M, Amari S, Lodders K, Zinner E. The Imprint of Nova Nucleosynthesis in Presolar Grains. Astrophys J (2004) 612:414. doi:10.1086/422569

CrossRef Full Text | Google Scholar

102. Downen LN, Iliadis C, Josè J, Starrfield S. Nuclear Thermometers for Classical Novae. Astrophys J (2013) 762:105. doi:10.1088/0004-637X/762/2/105

CrossRef Full Text | Google Scholar

103. Hynes K, Gyngard F. The presolar grain database. Lunar Planet Sci (2009) 40:1198.

Google Scholar

104. Fry C, Wrede C, Bishop S, Brown BA, Chen AA, Faestermann T, et al. Discovery of ^34g,mCl(p,γ)³⁵Ar resonances activated at classical nova temperatures. Phys Rev C (2015) 91:015803. doi:10.1103/PhysRevC.91.015803

CrossRef Full Text | Google Scholar

105. Grineviciute J, Brown BA, Schatz H. The role of excited states in rp-process for sd shell nuclei. arXiv [Preprint]. arXiv:1404.7268 (2014). Available online at: https://arxiv.org/abs/1404.7268 (Accessed April 29, 2025).

Google Scholar

106. Brown BA, Wildenthal WDM. Status of the nuclear shell model. Ann Rev Nucl Part Sci (1988) 38:29–66. doi:10.1146/annurev.ns.38.120188.000333

CrossRef Full Text | Google Scholar

107. Richter WA, Brown BA, Longland R, Wrede C, Denissenkov P, Fry C, et al. Shell-model studies of the astrophysical rp-process reactions ³⁴S(p,γ)³⁵Cl and ^34g,mCl(p,γ)³⁵Ar. Phys Rev C (2020) 102:025801. doi:10.1103/PhysRevC.102.025801

CrossRef Full Text | Google Scholar

108. Brown BA, Richter WA, Wrede C. Shell-model studies of the astrophysical rapid-proton-capture reaction ³⁰P(p,γ)³¹S. Phys Rev C (2014) 89:062801R. doi:10.1103/physrevc.89.062801

CrossRef Full Text | Google Scholar

109. Pain SD (2018). Proposal to the NSCL PAC, e18037.

Google Scholar

110. Utsuno Y, Otsuka T, Brown BA, Honma M, Mizusaki T, Shimizu N. Shape transitions in exotic si and s isotopes and tensor-force-driven jahn-teller effect. Phys Rev C (2012) 86:051301. doi:10.1103/PhysRevC.86.051301

CrossRef Full Text | Google Scholar

111. Pain S. FRIB Proposal 21067 (2021). Approved; awaiting scheduling.

Google Scholar

112. Lotay G, Christian G, Ruiz C, Akers C, Burke DS, Catford WN, et al. Direct measurement of the astrophysical ³⁸K(p,γ)³⁹Ca reaction and its influence on the production of nuclides toward the end point of nova nucleosynthesis. Phys Rev Lett (2016) 116:132701. doi:10.1103/PhysRevLett.116.132701

PubMed Abstract | CrossRef Full Text | Google Scholar

113. Fisker JL, Brown EF, Liebendörfer M, Thielemann FK, Wiescher M, et al. The reactions and ashes of thermonuclear explosions on neutron stars. Nucl.Phys. (2005). A752:604c. doi:10.1016/j.nuclphysa.2005.02.063

CrossRef Full Text | Google Scholar

114. Fisker JL, Schatz H, Thielemann FK. Explosive hydrogen burning during type I X-ray bursts. Astrophys J Supp Ser (2008) 174:261–76. doi:10.1086/521104

CrossRef Full Text | Google Scholar

115. Cyburt RH, Amthor AM, Ferguson R, Meisel Z, Smith K, Warren S, et al. The jina reaclib database: its recent updates and impact on type-i x-ray bursts. Astrophysical J Suppl Ser (2010) 189:240–52. doi:10.1088/0067-0049/189/1/240

CrossRef Full Text | Google Scholar

116. Cameron JA, Singh B. Nuclear data sheets for a = 38. Nucl Data Sheets (2008) 109:1–170. doi:10.1016/j.nds.2007.12.001

CrossRef Full Text | Google Scholar

117. Christian G, Lotay G, Ruiz C, Akers C, Burke DS, Catford WN, et al. Direct measurement of astrophysically important resonances in ³⁸K(p,γ)³⁹Ca. Phys Rev C (2018) 97:025802. doi:10.1103/PhysRevC.97.025802

CrossRef Full Text | Google Scholar

118. Hall MR, Bardayan DW, Baugher T, Lepailleur A, Pain SD, Ratkiewicz A, et al. γ-ray spectroscopy of astrophysically important states in ³⁹Ca. Phys Rev C (2020) 101:015804. doi:10.1103/PhysRevC.101.015804

CrossRef Full Text | Google Scholar

119. Setoodehnia K, Marshall C, Kelley JH, Liang J, Portillo Chaves F, Longland R. Excited states of ³⁹Ca and their significance in nova nucleosynthesis. Phys Rev C (2018) 98:055804. doi:10.1103/PhysRevC.98.055804

CrossRef Full Text | Google Scholar

120. Matoba M, Iwamoto O, Uozumi Y, Sakae T, Koori N, Fujiki T, et al. ⁴⁰Ca(p,d)³⁹ca reaction at 65 mev. Phys Rev C (1993) 48:95–104. doi:10.1103/PhysRevC.48.95

PubMed Abstract | CrossRef Full Text | Google Scholar

121. Doll P, Wagner G, Knöpfle K, Mairle G. The quasihole aspect of hole strength distributions in odd potassium and calcium isotopes. Nucl Phys A (1976) 263:210–36. doi:10.1016/0375-9474(76)90169-X

CrossRef Full Text | Google Scholar

122. Singh B, Cameron JA. Nuclear data sheets for a = 39. Nucl Data Sheets (2006) 107:225–354. doi:10.1016/j.nds.2006.01.001

CrossRef Full Text | Google Scholar