Social dynamics and stability of human society

Sociophysics involves the use of physical models to describe human society. This makes it possible to simplify the construction of social models and use concepts, equations, and consequences from them, already well-known in physics. In this work, a system of equations is proposed that describes the dynamics of human society in an N-dimensional social space, introduced on the basis of a widely used survey method. The proposed system of equations links such parameters as social density, velocity of social flows, gradient of social pressure, and social potential, as well as their derivatives with respect to social coordinates and time. The constructed system of equations is similar to multidimensional Navier-Stokes equations for a fluid with variable density, viscosity, and non-stationary temperature distribution. This excludes the possibility of an analytical solution of the system in the general case and leaves a door open only for numerical simulations with the prediction of future behavior at short time intervals in a common way in meteorology. Proposed simple model of social dynamics is based on the assumptions of metricity and continuity of the N-dimensional social space, the presence of potential forces of paired interaction of social particles both among themselves and with the field of things, which is the main factor of indirect attraction of people to each other. The model is built in a sequence similar to the structure of classical fluid mechanics and thermodynamics. The purpose of this article is to point out the main qualitative results to which this model leads.

1 Introduction

Ideas and concepts of physics have previously been repeatedly used to create mathematical models of human society [1], despite the lack of a rigorous justification for such actions. Physical space easily lends itself to the introduction of numerical scales and distances between objects, which makes it possible to apply the rich apparatus of mathematical analysis in physics and write down mathematical formulations of physical laws. On the path to implementing a similar approach in relation to society and individuals, the first step should be the development and introduction of some similar system of coordinates. This paper proposes a social space metric that allows each person to assign a certain set of coordinates in social space $\overline{X}$ = {x_i}, and every pair of people {x_i} and {y_i} – a social distance d = | $\overline{X}$-$\overline{Y}$ |. Following this, we can introduce the strength of human interaction as a function of distance $\overline{F}$ = f(d) and write down the equations of social mechanics in mathematical form, by analogy with physical mechanics.

Previously, social interactions have been analyzed using Social Network Analysis (SNA) [2], but this discrete approach makes it difficult to use mathematical analysis in continuous space. Social Force Models are similar to particle interaction models in physics, but have previously been used only to describe pedestrian dynamics or crowd behavior in physical 3D space [3], whereas in our model we expand the space under study to include all social interactions and consider the dynamics in it (N-dimensional space).

There is also a common “template” approach, where an already well-developed physical theory is transferred and applied to the life of society. Examples include all sorts of spin models of the Ising type with phase transitions [4]. Such an approach lacks a step-by-step consideration of the simplest concepts of social dynamics, and the authors quickly encounter the problem of understanding, unambiguously defining and calculating the basic parameters of society, such as thermodynamic temperature.

Metric social space has probably been introduced by many authors before without further consideration of social dynamics in such space. For example, similar ideas were expressed by Terziyan [5], but the more complex mathematical expression for the distance between social particles (e.g., as in [6]) made it difficult to further study social dynamics in such spaces.

The structure of this work is as follows: in Sections 1, 2 we introduce the basic concepts of social coordinates and velocities by analogy with known physical quantities; in Sections 3–5 we introduce the forces of social interaction and consider the balance of these forces, including the forces of attraction of people to material wealth; in Sections 6–8 we move on to continuous social coordinates, which allows us to write the corresponding equations of the dynamics of a continuous medium, introduce social viscosity, reflecting an array of micro-conflicts between individuals. Finally, in Sections 9–11 we go beyond the framework of classical mechanics as we encounter the dissipation of social energy and its emergence in the process of the birth of new social particles.

This work is primarily a theoretical study, not aimed at immediate practical application. However, as we will see in the last sections, the proposed approach allows us to draw two main practically important conclusions.

(A) The introduction of even the simplest metric Euclidean social space leads to dynamics described by equations of the Navier-Stokes type, which even in the uncomplicated cases do not have analytical solutions and are extremely sensitive to initial conditions.

(B) As in any system with internal friction, social flows in a human society fade away over time. Only the birth of new social particles leaves society a chance to exist.

2 Results

2.1 Coordinates in a social space

The concept of a sociological survey, which is carried out using certain questionnaires, is well known. Let’s imagine that we have a questionnaire with a fairly large number N ∼100–1,000 independent questions from a variety of areas, the answers to which do not correlate with each other and to which a continuous range of answers can be given ([1, 0]) between +1 (yes), 0.5 (do not know), 0 (no). Moreover, these answers must be confirmed by the daily practical actions of a person and are not just words, but correspond to real actions.

Then if i–is a serial number of the question, the list of answers of a specific person X can be represented as a set of numbers {x_i}, where every x_i lies between 0 and 1. Then the vector in N-dimensional space $\overline{X}$ = {x_i} will be the social coordinate of this person in society. To use the apparatus of mathematical analysis, we need the answer scale to be continuous. To carry out ordinary measurements in such a space, we need to make it metric.

A metric space is a set in which between any pair of elements a distance is defined that satisfies certain conditions [7]. Let us consider human society as such a set. For any pair of people currently existing on Earth, we can determine how much they agree or differ in their views, since we can virtually transport them to one place and force them to interact, talk, discuss something, or act together. They can learn each other’s language, or some third language, or action language or non-verbal communication. The nature of their interaction will be determined by the social distance between them. Thus, the idea of introducing social distance, indicating the possible degree of interaction between people, is very natural.

Conditions that the social distance between people must satisfy in order to determine the metric social space [7].

1.d($\overline{\mathit{X}}$, $\overline{\mathit{Y}}$) = 0 only when $\overline{X}$ = $\overline{Y}$. This means that there are no two indistinguishable people in the society. This condition is satisfied for sufficiently large questionnaires (N >> 1). It is violated if the questionnaire contains an insufficient number of questions. Then the distance will be determined between groups of like-minded people who give the same answers to all questions.

2.d($\overline{\mathit{X}}$, $\overline{\mathit{Y}}$) = d($\overline{\mathit{Y}},\overline{\mathit{X}}$), that is, the distance must be a symmetrical form: if X considers himself far from the views of Y, then Y will, under the same conditions, consider himself far from the views of X, when the provided the information is the same. If people communicate long enough and openly, this condition is met.

3.d($\overline{\mathit{X}}$, $\overline{\mathit{Z}}$) ≤ d($\overline{\mathit{X}}$, $\overline{\mathit{Y}}$) + d($\overline{\mathit{Y}},\overline{\mathit{Z}}$), that is, if there are three acquaintances, where X and Y, as well as Y and Z, are friends, then X and Z cannot be in hostile relationships. In the language of social relations, this will sound like “my friend’s friend is my friend, my friend’s enemy is my enemy.” In society this is done quite often, but not always.

4.Continuity of change of social coordinates. Social coordinates cannot change abruptly, but are a continuous function of time. Without this condition, we would not be able to construct differential equations for social coordinates.

One of the most well-studied and widely used metrics is the Euclidean distance [8],

$d\left(\overline{X,}\overline{Y}\right)=\sqrt{{\displaystyle \sum _{i=1}^N}{\left(x_i-y_i\right)}^2}(1)$

widely used in physics. Equation 1 is a symmetric form for which all three above mentioned criteria are fulfilled. Already here, building an analogy with physics, we have to simplify the model and limit ourselves to considering only societies with full awareness (criterion #2) and absence of ambiguous relations (criterion #3).

Considering those societies for which criteria 1-4 are true, we determine the coordinates of people in society and the social distance between them by analogy with the way it is done in physics, namely, with the help of a kind of “ruler”, which is a social questionnaire with N independent questions. Unlike the physical world, where the dimensionality of space is 3, the dimensionality of social space (N) is large (∼100–1,000), depends on the stage of development of society and changes over time. For simple communities, for example, for animals, a significant part of this social dimensionality should be just physical coordinates of an individual. But the more complex a society is organized, the less role physical proximity plays.

2.2 Movement in a social space

Coordinates are introduced in physics to describe the motion of objects using time derivatives of coordinates [9]. Similarly, social coordinates change with time, as people’s beliefs and their answers to questionnaire questions, confirmed by their daily actions, change with age. The task of social mechanics is to predict the future state of society from known initial conditions.

Social movement is closely related to interactions in society. If we completely isolate any individual from society, his or her opinion on all issues will never change. This can be formulated using the first derivative of time: d $\overline{X}$/dt = 0. If we now take into account that the society that creates social questionnaires for measurements does not stand still, we come to the conclusion that even in the absence of interaction $\overline{V}=$ d $\overline{X}$/dt ≠ 0. This means that the relative rate of change in the social position of an isolated person will not be zero. If society changes at a constant social speed, we come to the “law of social inertia”, similar to the one known from classical mechanics [10].

• The absence of a person’s social interaction leads to an unchanged social position (d $\overline{X}$/dt = 0) with the precision of a change in the questionnaire system. Only social interaction can change one’s position in the social space.

Indeed, since our social coordinate is a rather rigid thing, depending on our psychological profile, we cannot expect our behavior, character, beliefs to change without any external influence. Thus, ‘social inertia’ turns out to be a rather plausible assumption. Only thanks to the social inertia we get a picture of the character (psychological portrait) of a particular person and a certain profile of his actions. If social inertia did not exist, then we could expect any action from any person at any time.

How to determine the social velocity? It is necessary to conduct two social surveys with some short time interval (Δt → 0) and compare the results (Equation 1a)

$d\overline{X}/dt\approx \left(\overline{X}\left(t+∆t\right)-\overline{X}\left(t\right)\right)/\Delta \mathrm{t}(\mathrm{1a})$

The introduction of social interaction forces $\overline{F}$ changes the situation and causes people’s beliefs to change over time. Since we cannot relate $\overline{V}$ directly to $\overline{F}$ because of social inertia (social forces cannot change people’s opinions instantly), let us do what is done in classical mechanics using an analogy. Let us take as the origin the center ($\overline{X_C}$) of public opinion in a society of M members (j is an index denoting a particular person) on each ith question of the questionnaire (Equation 2)

$x_i^C=\frac{1}{M}{\displaystyle \sum _{j=1}^M}{x}_{i,j}and\overline{X_C}=\left\{x_i^C\right\},(2)$

and write the acceleration of the social movement of a particular person $\overline{X}$ as (Figure 1)

$\frac{d\overline{V}}{dt}=\frac{d^2\left(\overline{X}-{\overline{X}}_C\right)}{{dt}^2}=\overline{F}\left(d\left(\overline{X},\dots \right)\right)=\overline{F}\left(x_{i,j}\right),(3)$

Figure 1

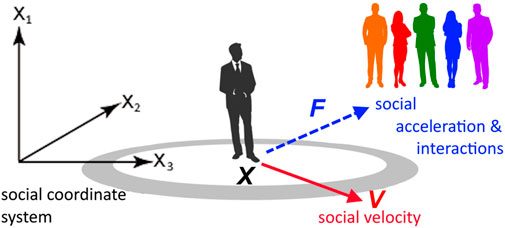
Figure 1. Basic concepts of social mechanics: a coordinate system introduced through a social survey, a person’s social coordinate (X), his social movement (V) and social acceleration, which is achieved through social interaction with other people.

where all interaction between people is contained in a function $\overline{F}\left(x_{i,j}\right)$, which, in the most general case, depends on the distances between $\overline{X}$ and all other people in society. In this Equation 3, we simplify the consideration and exclude the analysis of additional coefficients (for example, mass, m_i, individual for each person) that are present in the Newton equation of classical mechanics [9,10]. Our task now is to see only the general picture of the social movement, and the selected linear relation between $\frac{d\overline{V}}{dt}$ and the function of interaction $\overline{F}\left(x_{i,j}\right)$ is one of the simplest options for building social dynamics.

• Mass (“m”) – is an additive quantity used in physics to describe systems with many strongly linked particles, for example, atoms. Thus, if people own things and are in close family or friendly relationships, then the sum of all their things, relatives and acquaintances will constitute the mass of a social object.

When two objects with social masses m₁ and m₂ interact, the object with the largest social mass will maintain its direction of social movement with a higher probability. A group of people (family) with a larger material resource (things) and a larger number of members will most likely win in a social conflict between m₁ and m₂.

2.3 Static society and equilibrium equations

Over medium and short periods of time, we can neglect the change in beliefs of all members of society and assume that $\overline{V}=0\text{\hspace{0.17em}and\hspace{0.17em}}\raisebox{1ex}{$d\overline{V}$}\!\left/ \!\raisebox{-1ex}{$dt$}\right.=0$. In this case, the system is in static equilibrium and all members of society perform their daily duties. The equilibrium Equation 4 in this case looks like compensation of all interaction forces acting on each member of a static society:

${\displaystyle \sum _{j=1}^M}\overline{F}\left(i,j\right)=0,(4)$

where $\overline{F}$ (i, j) – is a social force, acting on the ith member of society from the jth member of society.

Let’s divide the whole society into an inner circle (family, friends, colleagues, R people or things in total, R << M) and an outer circle, interaction with which is expressed in a system of social rules, laws and requirements. Then, the first part will depend only on a series of interpersonal distances with close people d_ij, and the second one depends only on the social position of a person in society, say on d = | $\overline{X}$-$\overline{X}$ _C|:

${\displaystyle \sum _{j=1}^R}\overline{f}\left(d_{i,j}\right)+\overline{F}\left(d\right)=0.(5)$

Interpreting the last equation, we can say that workplace problems find their compensation in a family circle, and vice versa, personal life is reflected in professional career and social status, and this allows us to maintain a balance of power.

F (d_i,j) = f(d) is a function of the pairwise person (i) ‒ person (j) distance. This is a complex function, the general form of which is unknown and must be determined from the experiment. Here we are forced once again to simplify the consideration of social interactions. A great simplification is the assumption that it depends only on the scalar Euclidean distance d = | $\overline{X}$-$\overline{Y}$ |. In this case, f(d) is a conservative force [9–11], and can be represented as the gradient of some scalar field u(d)

$f_i\left(d\right)=-\frac{\partial u\left(d\right)}{\partial x_i},(6)$

where index i ‒ is the number of the question in the social questionnaire or, which is the same, the projection onto the i-axis in the constructed N-dimensional social space.

We will further call u(d) ‒ the local social potential of a person in the circle of relatives and friends. The proposed definition of interaction as a gradient of a certain field is widely used in physics to describe electromagnetic and gravitational interactions [12]. In physics, they have developed good mathematics for potential forces and scalar fields, so we know where we are going if we continue the model in that direction.

Some basic properties of u(d) are easy to establish.

1. d → $\infty$: strangers are repelled. Example: people in subway cars, on buses, etc. They prefer to occupy empty seats at a certain distance from other people, and only after they are exhausted, they begin to occupy seats close to other people.

2. d → 0: repulsion dominates. People cannot collapse into one point in the social space as a result of interpersonal relationships. As a rule, people need some independence, some emphasized differences from each other in order to feel individual. In fact, even in the friendliest families, frankness between spouses has limits.

An example of a possible form of u(d) is given in Figure 2a. In general, the form of the function u(d) is close to the function of the potential energy of interaction of atoms in a diatomic molecule. Considering in the same way the function of the strength of paired social interaction F(d), we can introduce the full universal social potential U(d) in the system of any social relations. Rewriting now Equation 5, we get

$\frac{\partial U\left(d_i\right)}{\partial x_k}+{\displaystyle \sum _{j=1}^R}\frac{\partial U\left(d_{i,j}\right)}{\partial x_k}=0(\mathrm{7a})$

Figure 2

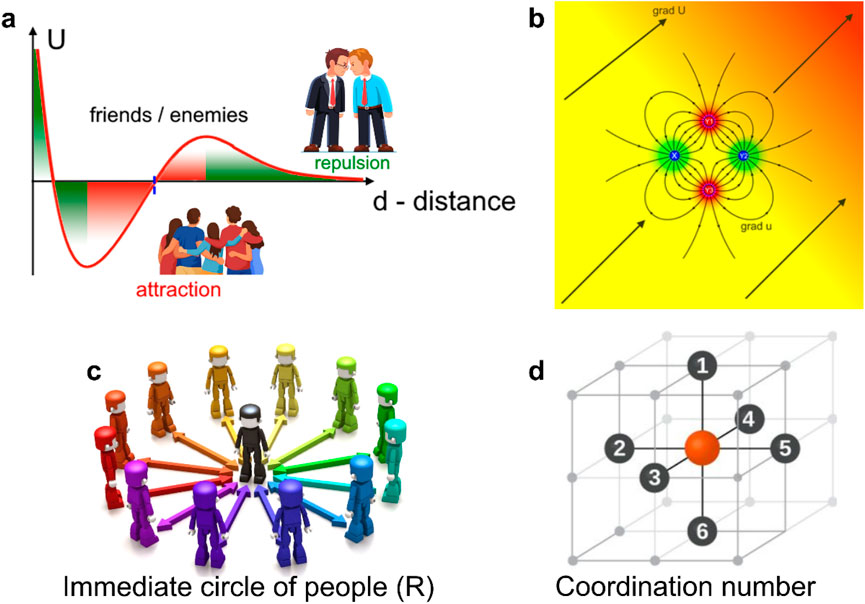
Figure 2. Social interactions as a function of social coordinates and distances. (a) Possible form of the function of universal social potential U(d). One can see the area of social attraction (highlighted in red), where the action of the force F(d) leads, in most cases, to a decrease in the social distance between people over time: d(0) > d(t), as well as the area of social repulsion (highlighted in green), where the force F(d) leads in most cases to an increase in the social distance between people: d(0) < d(t). (b) Illustration of the action of the social field of interactions with the “near” and “distant” circle of people (and things). A physical analogy with the quadrupole electric field distribution is used. Person X interacts strongly with three closest relatives and friends Y₁-Y₃ (field u(d_i,_j)) and at the same time is in a system of social relations U(X) with a relatively slowly changing social potential (c, d) Drawings illustrating the concepts of the inner circle of people and the physical analogy with the coordination number of an atom in a chemical compound.

In Equation 7a, index i ‒ is the index of a particular person, d_i = |X_i - X_C| is his relative social coordinate, and index k ‒ is the index of projection onto the axis (question in the questionnaire) of social space. As we will show below, the social potential function is equivalent to the notion of social status, a concept widely used in the humanitarian sciences.

Form of potential function of social interaction U(d) may be suggested based on a known work of George Zipf [13] that the number of people moving between two cities with a population P₁ and P₂, located at a physical distance D, is proportional to P₁×P₂/D. If we consider any pair of people as such “cities” for things, then the number of things/ideas/information involved in the exchange will be $\propto m_X{m}_Y/$ |$\overline{X}$-$\overline{Y}$ |, where individual masses (see above) m_i–characterize the number of things a person owns. Since number of things that people have are directly related to their social positions, their transfer from $\overline{X}$ to $\overline{Y}$ creates some additional social status proportional to $m_X/$ |$\overline{X}$-$\overline{Y}$ | in the social point of $\overline{Y}$. And, on the contrary, the transfer of things/ideas/information from $\overline{Y}$ to $\overline{X}$ creates some additional social status proportional to $m_Y/$ |$\overline{X}$-$\overline{Y}$ | in the social point of $\overline{X}$. Thus, we can write (Equation 7b)

$U\left(d\right)=-\frac{m}{d}+U^{\prime }\left(d\right),(\mathrm{7b})$

where the first term is responsible for the attraction of the field of things of mass m, and the second term U′(d) is responsible for interpersonal repulsion at short and long social distances (Figure 2a). Under these conditions, the strength of social interaction between ith and jth persons is expressed as

$\overline{F}\left(i,j\right)=\frac{m_i{m}_j}{{\left|\overline{X_i}-\overline{X_j}\right|}^2}\frac{\overline{d}}{\left|\overline{d}\right|}-\frac{\partial U^{\prime }}{\partial d}.(\mathrm{7c})$

If people have nothing to exchange, they have no common ideas, no common things and their social positions are distant, then the attraction between them will be minimal (Equation 7c). All proportionality coefficients throughout this paper are omitted for simplicity.

Here we first encounter derivatives with respect to social coordinates. How to calculate them? For example, the derivative $\frac{\partial u\left(d\right)}{\partial x_i}$ ≈ Δu/Δx_i answers the question how the interaction of two people (#1 and #2) will change if the opinion of person #1 on the ith question changes by Δx_i. We are talking about answering a question like “What will change in our relationships if I (#1) agree or disagree with you (#2)?”. Indeed, changing one’s opinion in favor of agreeing with someone usually leads to better interpersonal relationships.

In a real situation, it is not always possible to simulate a change of opinion. Then we can try to do a statistical analysis: take a large number of different pairs of people and combine them into groups according to the answers to the question i on a grid with a step Δx_i. Then, by determining the average values $\overline{u\left(x_i\right)}$ and $\overline{u\left(x_i+\Delta x_i\right)}$ for all other social coordinates for quantities u(x_i) and u(x_i+Δx_i), we can also calculate the desired derivative: $\frac{\partial u}{\partial x_i}$ ≈ ($\overline{u\left(x_i+\Delta x_i\right)}-\overline{u\left(x_i\right)}$)/Δx_i. Thus, to calculate these spatial derivatives, we need to have quite a lot of information about society, or observe a pair of people for quite a long time in order to obtain information about their interaction at different values of social coordinates.

The interpretation of the introduced “large” and “small” social potentials U(d) and u(d) (Figures 2b–d) is that their gradient serves as a motivating factor for people’s desire to improve their social status (in the case of U(d), Figure 2b), and to seek affection and increase authority among friends, acquaintances and relatives (in the case of u(d)). The described situation of a static society is closest to the theory of solid bodies and statics, known from classical mechanics [9].

As can be seen from Figure 2a, among all states of society there is the most stable (let’s say, “thermodynamically”) state in the absence of movement, when all people are connected by the strongest possible family ties: U_total = N × U_min. As is well known, all early human societies are large family clans. Not surprisingly, such a state was also the longest in human history. Any other state turns out to be less stable and must contain a certain amount of social movement (thus, $\overline{V}\ne 0\text{\hspace{0.17em}and\hspace{0.17em}}\raisebox{1ex}{$d\overline{V}$}\!\left/ \!\raisebox{-1ex}{$dt$}\right.\ne$ 0). It is also easy to notice that there is also a “dynamically” stable state of society: U_total = N × 0 = 0 at the limit d → $\infty$. This is a society of non-interacting people.

2.4 Attraction to the field of things and social repulsion

In addition to people, in our world there is another important substance - these are things (shoes, clothes, decorations, utensils, furniture, dishes, cars, apartments, laptops, smartphones, information, knowledge, organization, etc.) that are the product of our cultural activities. It is something that persists after the death of human’s generations; what we can see in museums. These objects do not have their own opinions, cannot participate in discussions, but, almost always, have owners - people or groups of people, governments of countries. Therefore, we can initially match them with the same social coordinate ($\overline{X}$), what their owner has. Indeed, the owner can use his things to prove his point of view and convince other people that he is right. Thus, things raise the “authority” or “weight” of a person in society. Things attract people even though in the struggle for them people repel and oppose each other.

Things are created by human labor. Especially valuable things are the product of enormous cooperation of hundreds and thousands of people, existing over a long time. Simplifying the situation, we can assume that the number of things created in the social volume ΔV for the time Δt proportional to the concentration (ρ = ΔN/ΔV) of people in this volume and concentration of things (n_t) they have: $\raisebox{1ex}{$\partial n_t$}\!\left/ \!\raisebox{-1ex}{$\partial t$}\right.$ $\propto {\rho n}_t.$ When we come to a museum and look at the huge amount of pottery, copper and bronze utensils that archaeologists have found, we see a reflection of the enormous social concentration of people and social interaction that existed in the past.

The field of things surrounds every person and can be characterized by some social potential U₊($\overline{X}$). How to calculate it? For example, you can consider a group of all people who are in the vicinity of a point in social space $\overline{X}$ with the volume of ΔV and determine the property value ΔU, which they have at their hands–then ΔU/ΔV will be a measure of U₊($\overline{X}$). Simply speaking, the potential of the field of things is the total amount of property that you have in monetary terms.

Indeed, as we will see below, social potential is directly related to a person’s social status in society. The higher the potential, the higher the rank of a person, the more power, money, fame and authority he has. Potential difference between two close social positions U₊($\overline{X}$)-U₊(${\overline{X}}^{\prime }$) sets the force of attraction to a person from a social point $\overline{X}$ to another point ${\overline{X}}^{\prime }$ and the gradient of the field of things (say, the gradient of salary) serves as motivation for changing opinions on certain questions. The peculiarity of people is that they are attracted to more expensive, beautiful and complex things than what they already have, and they do this almost always. The force of attraction (like envy) is stronger the closer people or two social positions are to each other

${\overline{F}}_{+}\propto \frac{U_{+}\left(\overline{X}\right)-U_{+}\left({\overline{X}}^{\prime }\right)}{\overline{X}-{\overline{X}}^{\prime }}=grad{U}_{+}\left(\overline{X}\right).$

This form of the force of attraction, common in scalar field physics, also contains a relationship to questions of fairness in the distribution of wealth. If two people of similar views, intellectual, educational and cultural levels have very different social status with corresponding material frame, then this causes great envy and the desire for an equivalent distribution of benefits. On the other hand, social currents carry along with them the field of things, the equations of evolution of which form the subject of economics. A detailed consideration of the field of things is beyond the scope of this work.

Let us again consider the static state, taking into account the forces of attraction to the field of things. Then we have a zero resultant of the forces of social attraction and repulsion: paired interaction with a huge number of people in a social system leads to repulsion–grad U, which is compensated by the force of attraction to the field of things grad U₊. In total, they practically balance each other, and the system is in equilibrium for short periods of time is

$\frac{\partial U\left(d_i\right)}{\partial x_k}+{\displaystyle \sum _{j=1}^R}\frac{\partial u\left(d_{i,j}\right)}{\partial x_k}=\frac{\partial U_{+}\left(d_i\right)}{\partial x_k}(\mathrm{7d})$

The physical meaning of this Equation 7d is that the imbalance of a person’s free will and issues of fair distribution of material resources finds its way out in relations with a close circle of people. Repulsion is balanced by attraction.

Another way to achieve equal distribution of wealth is to set U₊= const. Then the force of attraction in society will always be zero. This corresponds to an equal distribution of wealth among the members of the community and is in fact equivalent to the absence of a social structure as such. Indeed, then –grad U will act as a repulsive factor and, in the absence of family relations, the elements of such a structure will move away from each other. In other words, increasing inequality in the distribution of wealth compensates for the breakdown of family ties.

Let us now consider a family. In this case, the acting forces will be determined only by the person’s inner circle, his family and friends. If we strive for complete justice and equal distribution of goods here, then we must also set u = const. Then we will come to the state of society known from the physical model of an (ideal) gas [14] of non-interacting socially independent and non-attracting particles (U = U₊ = u), that is, to the complete collapse of all social relations. Thus, any society is necessarily unjust, containing unfair distribution of wealth and inequality in relationships, conflicts, social tension, hatred, repulsion, love and attraction. The breakdown of family ties in human society over the last few hundred years has been offset by ever-increasing wealth inequality.

A person is attracted to the field of things that make his life more convenient and better. This is a fundamental property of people. That is why people left villages and moved to cities. The greater the density of people, the more things they can produce and the greater the density of things. But people do not like each other and are generally repulsed, so they build houses separated by partitions (private flats) in which there is minimal interaction with other people. Inside these apartments, a person is as if in a node of a crystal lattice: only some small fluctuations around the position of social equilibrium are possible, and only rare “jumps” from one position to another are allowed.

2.5 Social dynamics

Over long periods of time, it is necessary to take into account changes in social movements. Let’s rewrite Equation 3 for a person with index i using simplifying assumptions regarding the forces of interaction between people (here grad is the gradient of the scalar field):

$\frac{d\overline{V_i}}{dt}=-gradU\left(d_i\right)-{\displaystyle \sum _{j=1}^R}gradu\left(d_{i,j}\right)+grad{U}_{+}(8)$

Here we again avoid introducing various coefficients of proportionality (in physics this is the mass of particles [11]) and use a different sign for the force originating from the field of things (U₊) to show that there is basically only attraction to the field of things (this is of course a simplification). With further development of the theory, additional coefficients can be introduced into Equation 8 to get better correspondence with the experiment.

Let us imagine that a person’s beliefs {x_i} do not depend on anything and change freely as a person explore the real world and gain experience. This is an ideal situation of free movement in a social space $\frac{d\overline{V_i}}{dt}=0$. No collisions, no shocks or any other events. But that never happens. In the real world, every country, every social group, every family and every relative/friends requires its members, residents or subordinates to be loyal to currently accepted or popular views, laws, ideas and traditions. Children feel inferior if they do not have something that their peers have. Mass pop culture forces teenagers to study the history of popular musical groups and imitate their leaders. Mass media propaganda only supports those points of view that are beneficial to current governments. A few percent of the population have enough willpower to be different from others, to think differently and to openly defend their views.

Thus, every person is constantly in the field of action of certain forces. A person’s social coordinate is almost always in strong interaction with his close environment: acquaintances, colleagues, family members and friends and cannot change freely, but takes part in a collective social movement. This situation is closest to the behavior of liquids in physics (it is called hydrodynamics or fluid dynamics).

In fluid physics, it is common to divide acceleration $\frac{d\overline{V_i}}{dt}$ into two components [15]

$\frac{d\overline{V_i}}{dt}=\frac{\partial \overline{V_i}}{\partial t}+\left(\overline{V_i}\frac{\partial }{\partial \overline{X}}\right)\overline{V_i},(9)$

where the first term $\left(\frac{\partial \overline{V_i}}{\partial t}\right)$, in the Equation 9 in our social interpretation, is associated with one’s own life experience, and the second one – with participation in collective social movements, since the social movements surrounding a person capture him and give him additional acceleration $\left(\overline{V_i}\frac{\partial }{\partial \overline{X}}\right)\overline{V_i}$, which does not follow from his own life experience and beliefs. The resulting equations of social movement coincide with the equations of flow of an ideal fluid, which, in turn, are the same Newton equations for material particles [9,10], rewritten for a continuous medium

$\frac{\partial \overline{V_i}}{\partial t}+\left(\overline{V_i}\frac{\partial }{\partial \overline{X}}\right)\overline{V_i}=-gradU\left(d_i\right)-{\displaystyle \sum _{j=1}^R}gradu\left(d_{i,j}\right)+grad{U}_{+}.(10)$

A few words regarding the interpretation of the contribution of social movements $\left(\overline{V_i}\frac{\partial }{\partial \overline{X}}\right)\overline{V_i}$ in the Equation 10. If the flow has a constant speed in a social space V = const., then the contribution of this term is equal to zero. But if the social flow meets some resistance, and the evolution of social beliefs ΔX is accompanied by a change in the speed of flow ΔV (say, disappointment in the social flow), then the force of pressure on the factor of resistance from the social flow will be equal to VΔV/ΔX. This is illustrated in Figure 5b.

Looking more closely at the analogy with viscous fluid physics, we will find that we now need to define the concept of a continuous social environment described by the density of people in a multidimensional social space, which, obviously, depends on time. Indeed, the growing popularity of a particular profession (for example, IT or artificial intelligence) causes a strong flow of people into this field of knowledge. People in this profession will hold relatively similar views, ensuring a local increase in the social density.

2.6 Density in social space

Since it is much more convenient to enter the volume of social space using a continuous scale of answers to N questions, let’s use just such a scale of answers to survey questions, where x_i ⸦ [0,1], while x = 0.5 corresponds to the answer “I do not know”. In this case, the total volume of social space is equal to 1. Let us define an elementary social volume as a microcube of N-dimensional space with a center at the point $\overline{X}$ = {x_i},

$∆V={\displaystyle \prod _i^N}∆x_i.(11)$

Within this volume (Equation 11), each answer to the i-th question will be in the range from x_i–Δx_i/2 to x_i + Δx_i/2. Then the social density at the point $\overline{X}$ is

$\rho \left(\overline{X}\right)=\frac{dn}{dV}=\underset{∆V\to 0}{\lim }\frac{∆n}{∆V},(12)$

where Δn - is the number of people from the total number M who answered all N questions of the questionnaire in the interval of {x_i–Δx_i/2, x_i + Δx_i/2}. Let’s consider the total number of people in the society $M=\int \rho \left(\overline{X}\right)dV$ independent of time (birth and death will be approximately taken into account later then there is an equation of continuity at any point, expressing the constancy of the number of people not only in physical but also in social space

$\frac{\partial \rho \left(\overline{X}\right)}{\partial t}+\mathit{div}\left(\overline{J}\right)=\frac{\partial \rho }{\partial t}+\mathit{div}\left(\rho \overline{V}\right)=0,(13)$

where social flux density is $\overline{J}$ = $\rho \left(\overline{X}\right)\overline{V}$, i.e., the density (Equation 12) of public opinion multiplied by the speed of social movement (Figure 3). The continuity equation reflects the simple fact that dominant public opinion is the end point of important social movements of the past. These social movements led large numbers of people to certain beliefs. An example is the environmental movements that existed in Europe for a long time at the end of the 20th century and led the majority of the European population to believe in the need to save energy and resources throughout their lives.

Figure 3

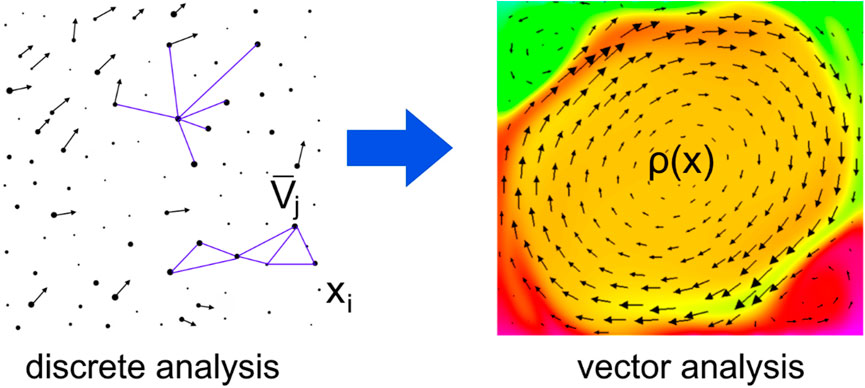
Figure 3. An illustration of the transition from a discrete analysis of the opinions of individuals to a more convenient vector analysis of continuous distributions of the density of public opinion and the vector field of the velocities of social movement in this section.

Social density allows us to define some useful averages, such as the average distance between people in a society $〈d〉\propto {\rho }^{-1/N}$, and the center of society $\overline{X}$ _C = $\frac{1}{M}$ $\int \overline{X}\rho \left(\overline{X}\right)dV$, where $M=\int \rho \left(\overline{X}\right)dV$. The average density of society is $〈\rho 〉=\frac{1}{M}\int {\rho \left(\overline{X}\right)}^{2}dV$, and the real occupied social volume $〈V〉=\frac{M^2}{\int {\rho \left(x\right)}^{2}dV}$. It is important to note that with a constant number of people in society, an increase in the dimension N leads to an increase in the average distance⟨d⟩ between people due to purely geometric considerations, if, of course, we remain within the framework of Euclidean space. The increase in the size of society over time is the subject of a separate study.

Introduced center of society $\overline{X}$ _C = $\frac{1}{M}$ $\int \overline{X}\rho \left(\overline{X}\right)dV$ has a simple social meaning: it is the coordinate of people endowed with the greatest power in society. Indeed, in our language, social coordinate is synonymous with social position and social status. It will be natural not to distinguish between these concepts. To achieve this, we use the social position of each person determined via N questions of the questionnaire as a “hard” social coordinate, and the distance of a person from the center of society is his social status. The social coordinate must be confirmed by real actions. However, the simplicity of the movement $\overline{X}$ → $\overline{X}$ _C to the power, wealth and success, is deceptive since we are not able to change our social coordinate arbitrarily due to the rigidity of our psychological profile. Such a movement requires real action, which we cannot implement without the interaction and help of other people.

As in real physical gases and liquids, there is an intrinsic volume [16] of each person V (d_min) $\propto d_{\mathit{min}}^N$, which is determined by the intimate sphere, entry into which causes repulsion even for the closest people (Figure 1A). Since relationships between people are becoming less and less close on average these days, the volume of the intimate sphere is increasing over time. Then the minimum social volume V_min = MV(d_min) determines the maximum possible social density, which is a decreasing function of dimension N (Equation 14):

$0\le \rho <{\rho }_{\mathit{max}}=\frac{1}{V\left(d_{\mathit{min}}\right)},(14)$

Integral calculus now allows us to describe interactions in society in a more unified way. Let u(d_i,j) be the pair potential of social interaction, then the integral social potential at a point will be equal to the sum of the potentials of interaction with all people in the society

$U\left(\overline{X}\right)=\int \rho \left(\overline{Y}\right)u\left(d_{XY}\right)d{V}_Y,(15)$

where integration in the Equation 15 is carried out over all points $\overline{Y}$ in the social space. Now we do not need to divide a person’s environment into the near and far spheres. The resulting integral potential (Equation 15) contains both components simultaneously. But the expression for force will now change given that the potential U($\overline{X}$) now acts not on an individual person, but on the probability of finding him at a point $\overline{X}$: $\rho \left(\overline{X}\right)dV$, that is, instead of Formula 6 we have

$d\overline{F}\left(\overline{X}\right)=-\rho \left(\overline{X}\right)d{V}_x\frac{\partial U\left(\overline{X}\right)}{\partial \overline{X}},(\mathrm{16a})$

similar to how it is accepted in the theory of electric and gravitational fields.

Finally, if we introduce forces, we need to determine the social pressure on a social surface (site). For simplicity, consider social force Δ$\overline{F_i}$ directed along the i-axis, then social pressure on the surface $∆S_i\left(\overline{X}\right)={\displaystyle {\prod }_{j\ne i}^N}∆x_j$ with the direction of the normal along the axis i is P ($\overline{X}$) = Δ $F_i$/ $∆S_i$. On the other hand, for any closed surface $∆S$, limiting the volume ΔV, the pressure gradient will be equal (Stokes-Cartan theorem) [15,17]

$-{\displaystyle \oint }Pd\overline{S}=-{\displaystyle \int }gradPdV=-{\displaystyle \int }\rho \left(\overline{X}\right)\frac{\partial U\left(\overline{X}\right)}{\partial \overline{X}}dV(\mathrm{16b})$

$gradP=\rho \left(\overline{X}\right)\frac{\partial U\left(\overline{X}\right)}{\partial \overline{X}}(\mathrm{16c})$

A small piece of the social layer $∆S_i$ – this is a group of people whose answers to N-1 questions in the questionnaire are within the range {x_i–Δx_i/2, x_i + Δx_i/2} where i ≠ 1, but the answer to the key question (1) is the same for all. The direction of social force (Equation 16a) shows what kind of belief is socially acceptable, and social pressure (Equations 16b,c) shows the force that anyone seeking to change public opinion in this direction will face. In the general case, when social forces also act on social strata of people who are not directly related to key issues in the life of society, social pressure should be replaced by a tensor of a social stress ${\sigma }_{i,j}=$ Δ $F_i$/ $∆S_j$ as is done in the theory of elasticity [18].

Let’s give a small example. Let us assume that some belief x_i is imposed. Then all members of society answer this question in the same way x_i = const., Δx_i = 0. As a result, local social density $\rho \left(\overline{X}\right)=\frac{∆n}{∆S∆x_i}\to \infty$ goes to infinity or takes on a large value. This leads to strong social repulsion in such thin social strata (unless the distance of forming family relations is reached), which must be compensated by external forces of pressure from the ruling classes or the society.

An interesting property of social pressure is that it increases as one moves up the social ladder. Indeed, the natural characteristic of most people is the desire for a higher salary and power, a larger apartment in a capital city, more delicious food, and better living conditions. In other words, to a greater concentration of more expensive things, to an area with greater potential of the U₊ field of things and the field of people. Thus, the majority of vectors $\overline{V}$ on average are aimed at achieving a higher social position in society. As in many other physical models with gravitational/Coulomb forces in a limited space, such as in planets and stars, their central regions are characterized by exceptionally high pressures, temperatures and densities (Figure 4). Likewise, in human society it is natural to expect that social pressure and social density reach a maximum in the region of the highest social strata that a person can reach. The area of maximum social density and pressure also corresponds to the area of maximum concentration of the field of things (U₊).

Figure 4

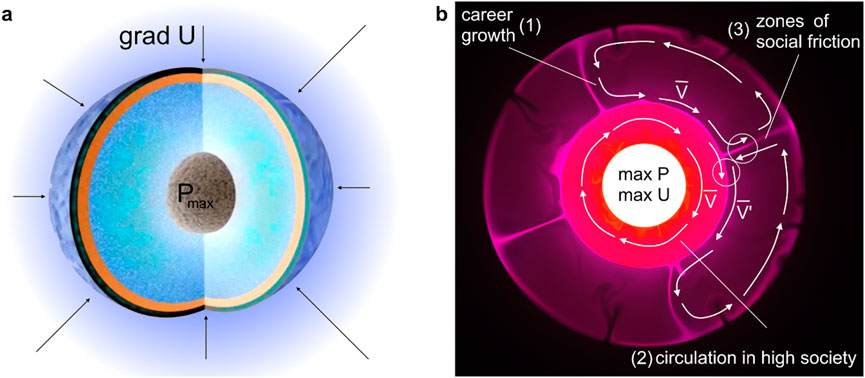
Figure 4. Illustration of the possible structure of society from the point of view of the gradient of social potential, the field of things and pressure (so called “Social sphere”). It does not take into account the influence of a person’s close circle of friends and family, leading to the formation of tight clusters and “molecules”, and implies that the forces of social relations are potential forces. (a) In the center of the multidimensional sphere, pressure and density reach maximum values (e.g., P_max), while the direction of grad U and grad P coincides with the direction to the center of the multidimensional sphere, and the corresponding repulsive force is directly opposite and compensates for the attraction of people to the field of things. (b) Social vortices in society: (1) convective social currents with an increase in social status (study, work, career growth) and a decrease in status (retirement, downshifting, career break, illness). (2) Circulation within one social stratum. White circles also show: (3) the radial zone of social friction, where social flows of different generations meet: young and old; and a zone of tangential friction between different social classes.

2.7 Stationary society and conservation laws

Let us again consider the basic equation of social dynamics (10), rewritten taking into account the definitions of social density and integral social potential (Equation 15) introduced in the previous paragraph

$\frac{\partial \overline{V}}{\partial t}+\left(\overline{V}\frac{\partial }{\partial \overline{X}}\right)\overline{V}=-gradU\left(\overline{X}\right)+grad{U}_{+}=-\frac{gradP}{\rho \left(\overline{X}\right)}+grad{U}_{+}.(17)$

We will call a stationary society a society in which there is no change in beliefs associated with the self-evolution of people’s views, there is no self-development ($\frac{\partial \overline{V}}{\partial t}$ = 0), and also the social density is constant $\frac{\partial \rho }{\partial t}$ = 0. In this case, people’s beliefs in the Equation 17 change only in connection with entering a new social environment while following social trends (rot is the curl operator here):

$\left(\overline{V}\frac{\partial }{\partial \overline{X}}\right)\overline{V}=\frac{1}{2}grad{\overline{V}}^2-\left[\overline{V}rot\overline{V}\right]=-gradU\left(\overline{X}\right)+grad{U}_{+}(18)$

where [] – means the vector product of vectors in 3-dimensional space. But in the N-dimensional space we must write this expression as ${\left[\overline{V}rot\overline{V}\right]=V}_j\left(\frac{\partial V_j}{\partial x_i}-\frac{\partial V_i}{\partial x_j}\right)$ [19]. In projection onto the direction of social movement $\overline{V}$ this Equation 18 gives us value that is conserved when moving along the social trajectory

$\frac{1}{2}{\overline{V}}^2+U\left(\overline{X}\right){-U}_{+}\left(\overline{X}\right)=\frac{1}{2}{\overline{V}}^2{-U}_{+}\left(\overline{X}\right)+\int \rho \left(\overline{Y}\right)u\left(d_{XY}\right)d{V}_Y=\text{const}.$

$\mathit{div}\left(\rho \overline{V}\right)=0.(19)$

This result (Equation 19) corresponds to the Bernoulli equation known from hydrodynamics [15,20], as well as the law of conservation of mechanical energy. Along the social flow, a slowdown in movement is always associated with an increase in the full social potential ($U{-U}_{+}$) and vice versa. The social flow gains greater speed and energy if it leads to an increase in $U_{+}$ and enrichment of movement participants, but loses energy if it leads to the occupation of a high social status and an increase in responsibility and stress without material reward. In a stationary society with constant speeds of social flows ($U{-U}_{+}$) = const. In other words, social status always correlates with material wealth. Indeed, it is precisely this state of affairs that we observe everywhere as the most stable.

Qualitatively connecting the absolute value of the speed of social movement | $\overline{V}$ | with the entrepreneurial or organizational activity of people (social energy), we can express the result obtained with the phrase: activity is shown by those who need to earn a promotion [growth of ($U{-U}_{+}$)] in society; those who have already earned it [high ($U{-U}_{+}$)] has no longer motivation to work. Material reward serves as a driver of social activity. This corresponds well with the surrounding reality.

• Addition to Figure 4. The stellar or planetary model of society can be better understood if we return to the definition of “hard” social coordinates. In these coordinates the answer to any question x_i = 0 corresponds not just to the words “no”, but to active social position, actions and protests corresponding to “no”. The answer “yes” corresponds to active and everyday social activity aimed at supporting x_i = 1. In this coordinate system, most people will take a passive position x_i ≈ 0.5, i.e., will be concentrated near the dense “center” of the social world, and the outer surface will consist of active and radical people who have clear convictions and are ready to act to protect and implement them in life. Here it becomes clear that people belonging to the highest strata of society, occupying the highest social positions and the most wealthy, in fact, do not have any strict beliefs. For them there is nothing fundamentally good or bad, black or white, and there are no strict rules.

In real physical and social systems, the energy conservation law Equation 19 is not satisfied due to the presence of dissipative friction processes. Various social flows interact with each other, intersect, break into smaller ones and fade away. Nevertheless, it is instructive to write down the law of conservation of total energy for an ideal social fluid (V_X is the social volume):

$\frac{1}{2}{\displaystyle \int }\rho \left({\overline{X}\left)\right(\overline{V}}^2-U_{+}\left(\overline{X}\right)\right)d{V}_X+{\displaystyle \int }{\displaystyle \int }\rho \left(\overline{X}\right)\rho \left(\overline{Y}\right)u\left(d_{XY}\right)d{V}_{Y}d{V}_X=\text{social\hspace{0.17em}energy}.(\mathrm{20a})$

Let’s consider several special cases.

1. If repulsion prevails in society, and there is no attraction to the field of things, then u > 0, d_XY →$\infty$, asymptotically society reaches maximum activity with a complete breakdown of social ties, and this activity is due to internal processes of changing beliefs. Total social energy is positive, society always disintegrates.

2. A special case of u = 0: a society of social justice or social gas, where there are no social classes and inequality should have zero interaction energy of members, positive total social energy and disintegrate.

3. And only if attraction prevails in society, u < 0, or there is a large field of things, then increased interaction between people leads to an increase in social activity. If the total social energy is negative, then the society is stable.

Society cannot be stabilized only through interhuman family relations (u(d_XY) in Formula 20a). The presence of an attracting factor is necessary, a kind of “gravity” [21], which would lead to the attraction of people to the center of the community. Movement towards the center of the society should be accompanied by reward and should occur with acceleration. In the absence of this factor, policies aimed at destroying family links and achieving greater freedom for all members of society naturally lead to a breakdown in social relations, an increase in the average social distance between people and difficulties in finding common topics for communication. Then d_XY → $\infty$, u > 0 and repulsion between strangers prevails. Such society then “evaporates” and goes into a state of rarefied gas.

In principle, the theory presented in this work can also be applied to animal communities and can help us understand why some species are collective, while many other animal species live solitary lives.

2.8 Social vortices, convection and dissipation of social energy

In physics, the energy of mechanical systems, the energy of flows of liquids and gases is not conserved due to friction [15,16] - that is, the transformation of macroscopic movement, characterized by speed of flows, into microscopic movement of individual atoms and molecules, characterized by such an average concept as temperature [16]. Translating this into the language of social mechanics or sociophysics, we can recall, for instance, the concept of corruption, when large-scale economic projects lose part of their effectiveness due to the enrichment of certain groups of people and changes in their social coordinates and potential. Another example is simply inefficient work organization, where employees receive a large salary but spend most of their working day playing games, talking, and watching entertainment videos.

Movement losses in social flow must obviously be related to gradients $\frac{\partial \overline{V}}{\partial X_{\perp }}$ of social speed in the direction perpendicular to its vector $\overline{V}$. If there are no such gradients, then it is simply a single social movement. But a constant velocity gradient by itself is not enough to dissipate energy. There is such an important concept in physics as rotational motion [9]. And the rotation of any body as a whole does not lead to energy losses, although the gradient of speed in respect to some coordinate axis $\frac{\partial \overline{V}}{\partial X_{\perp }}=\omega \ne 0$ is not zero. Therefore, to describe friction, the second derivative with respect to coordinates is used, which excludes rotational motion.

It is remarkable that the flow of liquids and gases is accompanied by the formation of vortices, as objects where energy dissipation is minimal due to its close resemblance to rotational motion, minimizing friction. This is similar to the action of Prigogine’s theorem on the minimum production of entropy in the case of irreversible processes in linear systems [22].

To simplify the consideration for society, let’s say that if some social coordinates of a person change periodically, such as views on which political party is better, then we can consider this as a rotation in social space or a social vortex. Since the volume of social space by our definition is finite and equals to 1, then over long periods of time social vortices will be the only possible type of constant social flows with non-zero speed (Figure 4B). Carrying out a planetary analogy, we note that for lonely planets and stars the main motion is their rotational motion relative to the axes passing through them.

Drawing an analogy with the physics of fluids, we write down the equations of social flow taking into account friction forces using all possible gradients of social speed (in projection onto some social axis i, summation is implied over repeating indices) by analogy with the Navier-Stokes equations [15]:

$\begin{array}{ll}\hfill \frac{\partial V_i}{\partial t}+\left(\overline{V}\frac{\partial }{\partial \overline{X}}\right)V_i& ={grad}_i{U}_{+}\left(\overline{X}\right)-\frac{{grad}_{i}P}{\rho \left(\overline{X}\right)}+\frac{1}{\rho \left(\overline{X}\right)}\frac{\partial }{\partial X_k}\left(\eta \frac{\partial V_i}{\partial X_k}\right)\hfill \\ \hfill & +\frac{1}{\rho \left(\overline{X}\right)}\frac{\partial }{\partial X_i}\left(\left(\xi +\frac{1}{3}\eta \right)\mathit{div}\overline{V}\right)\hfill \end{array}$

$\frac{\partial \rho }{\partial t}+\mathit{div}\left(\rho \overline{V}\right)=0(\mathrm{20b})$

In general, social density depends on the social coordinate. In the same way, the parameters ξ and η in the Equation 20b, which are responsible for social friction, also depend on the coordinates. Moreover, this dependence must be established based on the microscopic mechanism of social friction. The resulting system of nonlinear equations in N-dimensional space is already extremely complex. In the case of small social velocities, in particular for asymptotically decaying social flows (see Examples 1, 2), the nonlinear term $\left(\overline{V}\nabla \right)\overline{V}$ can be discarded, which is often used to simplify the analysis of the Navier-Stokes equations. Clarifying the properties of general solutions of the Navier-Stokes (NS) system of equations is one of the unsolved problems of the millennium [23]. But the difficulties do not end there. Energy dissipation will lead to microscopic processes described in thermodynamics and going beyond the dynamics of social flows.

The introduced friction forces consist of two parts, the second of which $\frac{1}{\rho \left(\overline{X}\right)}\frac{\partial }{\partial X_i}\left(\left(\xi +\frac{1}{3}\eta \right)\mathit{div}\overline{V}\right)$ depends on speed divergence (div $\overline{V}$), which is not equal to zero if there are centrifugal or centripetal processes. As we know, the result of friction is the equalization of the speeds of interacting social currents with vanishing of the term $\frac{\partial }{\partial X_k}\left(\eta \frac{\partial V_i}{\partial X_k}\right)$. The social movement in this case can be described as a rotation with periodic changes in social coordinates (people’s opinions on any issues). Human societies have lived in this mode for tens of thousands of years, and nothing prevents remote communities in jungle from continuing to live in the same rotation even now. A good illustration of this is the beginning of Ecclesiastes.

A social vortex has a center, a person or a group of people who attract the attention of other people (the body of the vortex), and there is a field of things in the center - this is what belongs to this group of people and attracts all other participants. The center of the vortex is usually made up of so-called “stars” - famous actors, directors of big companies, billionaires, politicians, celebrities, etc. The vortex and its macroscopic movement are described mainly by the dynamics of the vortex center.

The movement of social particles in a vortex is a rotation in the N-dimensional social space, which has the character of some routine repetitive activity, such as the daily trips of billions of people to/from workplaces by subway or car along a repetitive route, or weekly food shopping at the supermarket for a periodically received salary. From this point of view, almost all of humankind is captured in one or another vortex movement, which is supported by the hope for a change in the situation, for the next government to be better than the previous one, for a promotion, or for retirement. Considering that in general people repel each other, the vortex movement must be stabilized by some attraction to the center of the vortex: the dream and hope of improving living conditions, getting a part of the wealth and glory that people in the center of the vortex have. From the point of view of emotions, making a rotational movement people experience love and hate, hope and disappointment, euphoria and despair, which are repeated in time. From a mathematical point of view, this means that the tensor field ${curl\left(\overline{V}\right)}_{ij}=\raisebox{1ex}{$\partial V_j$}\!\left/ \!\raisebox{-1ex}{$\partial x_i$}\right.-\raisebox{1ex}{$\partial V_i$}\!\left/ \!\raisebox{-1ex}{$\partial x_j$}\right.\ne 0$ takes on non-zero values throughout the real social space.

Vanishing of $\frac{\partial }{\partial X_i}\left(\left(\xi +\frac{1}{3}\eta \right)\mathit{div}\overline{V}\right)$ means the absence of pulsations - compression and expansion of the social sphere with changes in its density (div $\overline{V}$ ≠ 0). This kind of oscillation is characteristic of conflicts and wars with the consolidation and polarization of various parts of the social sphere in some oppositional opinions. If there are no external sources of energy, oscillatory phenomena, as well as strong and fast social currents in society, should fade. Indeed, this is observed in real conditions. Nowadays, it is difficult to expect the same social enthusiasm as during the emergence of great religions. Currently observed huge number of ideas, philosophical movements, religions, and art directions is rather a residual turbulence after the extinction of powerful social movements of the past.

Summing up the preliminary results of the analysis of the constructed model, it must be said that there is no magic wand, no general equation of sociophysics with the help of which we could see the future behavior of society, calculate how this or that war or conflict will end, and what needs to be done to get out from an economic crisis or how to achieve a higher social status. Writing such nonlinear equations of the Navier-Stokes type that describe social dynamics does not give any clues to their specific solution, which is extremely sensitive to all parameters of the equation, initial and boundary conditions of the problem. There are practically no analytical solutions for such equations. After writing the equations, a new huge task arises of collecting data about the initial social coordinates of all people in society, their initial social speeds, interaction potentials, the quantity and quality of things they have, and so on.

Human society is a reflection of the world in which it lives. Our atmosphere, weather, ocean currents, convection of air, water, solar plasma and molten rock inside of our planet follow the same equations as human society. Yes, we can hardly solve the equations of social physics in the general case, but we can solve them approximately within short time intervals if we collect enough information about the current state of the system, measure the social coordinates of as many people as possible, learn more about the potential of interpersonal interaction U(d), measure social density and speed of social movements $\overline{V}$ at the current moment. Then, using modern supercomputers, we will be able to predict what will happen tomorrow and the day after tomorrow with the same accuracy that is achieved for weather forecasting.

2.9 Social thermodynamics

In thermodynamics, such parameters as (social) density (social) volume (social) pressure are usually introduced [16]. We determined all these quantities earlier. Unlike social dynamics, when studying at the micro level we are not interested in collective social flows, therefore the individual speeds of microscopic movement in social space ${\overline{u}}_i$ should be distributed chaotically and the average over them should be zero in most of cases. These are our instant desires. To avoid large changes in the social coordinates of people in our calculations, we must assume that the environment is sufficiently “dense” and the change in direction ${\overline{u}}_i$ occurs quite often, over time Δt, so that $\sqrt{〈{{\overline{u}}_i}^2〉}$ Δt << $\sqrt{〈{\left|\overline{X_i}-{\overline{X}}_C\right|}^2〉}$. That is, the free path is much less than a certain characteristic size of society. And the characteristic time (a time between collisions) for the emergence of new desires is much less than the time of significant changes in a person’s social status. Let’s just say that each person’s behavior depends on his mood. But even with a large variation in mood, a person’s character is still preserved and daily emotional fluctuations do not affect his social behavior on a scale of years.

Let us now consider the scale of short times, say within days and hours. Human behavior at such periods of time depends on emotions and feelings. If a person’s attention is focused on one thing, say, at work, then the time Δt turns out to be long enough to have a significant impact on the person’s social coordinate (it is proportional to $\sqrt{〈{{\overline{u}}_i}^2〉}$ Δt). If there are problems with focusing attention, if it is constantly scattered, jumping from one object to another, then Δt → 0 and we get chaotic movement in social space, similar to Brownian motion [24].

It is impossible to conduct a complete survey every hour and establish the social coordinate $\overline{X}$ of a person. It obviously fluctuates constantly with a small amplitude. But you can ask what a person wants, what he is striving for at the moment and how strongly. The number of short-term desires and goals is much smaller than the dimension of social space. We can say that at the micro level, over short time intervals, the needs of all people are practically the same and constitute a reduced social space of significantly smaller dimensions J ∼ R (and J << N), determined by the need to maintain life and associated with the immediate environment. The value J is the sum of the number of things and people in the immediate environment.

In other words, we need to determine the direction of a person’s movement in social space ${\overline{u}}_i$. At the same time, changes in short-term mood goals, their postponement (scattering), occur as a result of interaction with various interfering factors (Figure 5a). But how to determine the numerical value of $\overline{u}$ _i?

Figure 5

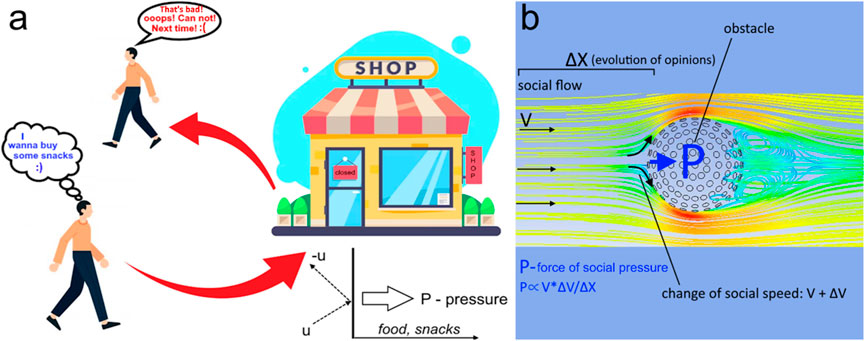
Figure 5. (a) Change in short-term goals as a result of “scattering” by interfering factors. This scattering creates social pressure in the direction of the goal. (b) The dissipation and scattering of a social flow by a resistance factor. For movement participants, such scattering will occur as their social positions evolve with time and they “grow up” in their views. This process of changing social attitudes is accompanied by social pressure or social force (P) applied to the obstacle.

In physics, this is done using an experiment with a rarefied gas, where molecules and atoms can travel long distances. But for a dense modern society, it is very problematic to give complete freedom to people’s instincts and desires. In society, we are always limited by laws, rules and other people.

Another option is to determine the force of influence of such a social particle or the useful work that it can do against some external force. Let’s measure the strength of emotions by some standard, such as how many floors a person can climb to fulfill his desire. This method of measurement gives us the physical coordinate, its increment (number of floors passed, ΔX), execution time (Δt) and, finally, ΔX/Δt = $〈u_i〉$.

As in the usual kinetic theory of gases [16], we can count the number of people who in direction i are trying to achieve the desired by changing the social coordinate in direction i by $∆x_i$ on a small social volume $\overline{S_i}·\overline{∆x_i}$, where density is $\rho \left(\overline{X}\right)$, and the average social chaotic speed $\overline{u_i}$ upon collision, changes to the opposite direction

$\frac{\rho \left(\overline{X}\right)\left(\overline{S_i}·\overline{∆x_i}\right)\overline{∆u_i}}{∆t}=\overline{F_i},or\rho \left(\overline{X}\right){\overline{u_i}}^2=P_i.(\mathrm{21a})$

If we are not talking about the average speed of chaotic movement, but about the division of contributions of different groups of people (j, J) with different “social masses”, then you need to rewrite the Equation 21a as the average for all contributions

$\rho \left(\overline{X}\right)\frac{{\displaystyle \sum _j^J}{u_{ij}}^2}{J}=P_i.(\mathrm{21b})$

This, however, does not fundamentally change anything. We will assume that during chaotic motion there is no chosen direction, and that at the microlevel the space is isotropic, so we do not need the index i in Equations 21a,b. This corresponds to the theorem on the equidistribution of energy across degrees of freedom at the microscopic level. If we assume that the short-term desires and emotions of all people are approximately the same and their number J is much less than the dimension of social space (J = N₀ << N), then such a theorem about the equal distribution of movement across degrees of freedom looks plausible in relation to society (“all people want to eat, drink and sleep”). Then denoting T = ${{\overline{u}}_i}^2$, we obtain the standard equation of state for an ideal gas [16] in the absence of interactions in society

$\rho T=P(\mathrm{21c})$

where all quantities depend on the coordinate in social space, and T is the scalar field of the square of the chaotic component of social speed, or, by analogy with physics, social temperature [16,25]. In general, the equation of state will be some function connecting social density, pressure and temperature, P = P(ρ, T). Thus, large “appetites”, emotions, desires (T) and high density of people create high social pressure.

We above designated the dimension of the space of primitive desires as J = N₀, where N₀ = N (t = 0) is the dimension of human society at the beginning of its evolution, when all the differences between people mainly came down to their needs, to who wants what. In the process of evolution, life goals and desires became more complex, the size and dimension of society increased and continues to increase today.

A frequently used approximation is a simple relationship between social pressure (P) and functional volume P $\propto$ V⁻¹ (see, for instance, Equation 21c). For example, in conditions of confrontation between two communities of similar size, the pressures in both communities will increase equally (P₁ ≈ P₂), forcing societies to contract and reduce their functional and social space volumes. Indeed, during wars and crises, complex fundamental scientific research is usually reduced in favor of producing a large number of standard and cheap weapons. Everything complex disappears, being replaced by the simple and primitive. The growth of pressure in society in such a model is accompanied by its primitivization.

The condition for the absence of macroscopic social flows should be the following equality (Equation 22)

$\frac{gradP}{\rho \left(\overline{X}\right)}=\frac{1}{\rho \left(\overline{X}\right)}\frac{\partial \left(\rho T\right)}{\partial \overline{X}}=\frac{\partial U\left(\overline{X}\right)}{\partial \overline{X}}(22)$

where the external social field U($\overline{X}$), rooted in the structure of society, is balanced by a gradient of social pressure at the microscopic level of elementary passions. The condition for thermodynamic equilibrium for a closed social system will be the equality of social temperatures at all points of the society T = ${{\overline{u}}_i}^2$ = const. This is almost never realized, except in the case of the absence of a social structure U = const. Society is always in a non-stationary state. People in different classes of society can satisfy their desires to different degrees, which means that their social temperature will be different. So, grad T ≠ 0 in a real society.

The next step for studying a nonstationary society is the introduction of a flow of chaotic social movement of passions and drives $\overline{q}$ (flow of internal “social” energy) from one part of society to another, in other words, a social heat transfer [15,16]. This flow in physics is usually introduced as the integral $\oint \overline{q}d\overline{S}$, the value of which corresponds to the change in the social energy of the chaotic social movement inside the volume limited by the surface S.

The heat transfer equation is similar to the continuity equation (the equation for the conservation of the number of people), but only operates with social temperature, the meaning of which includes the momentary desires and needs of people on whom our attention is briefly focused. We must formulate equations for the conservation of human needs. If the number of people is conserved, and all people want, say, to eat and drink, then obviously the quantity of their needs must also be conserved. Let us introduce the flow of internal social energy as is done in the physics of thermal conductivity and diffusion [16].

$\overline{q}=-\kappa grad\mathrm{(T)},(23)$

where $\kappa \left(T,P,\overline{X}\right)$ – is coefficient of thermal conductivity (in physics). The flow of internal social energy (the flow of needs, requests, anger and aggression) is directed from areas with high social temperature to areas with low social temperature. In other words, the hungry takes bread and things from the well-fed and makes him hungrier, and he himself becomes richer. The flow of things is the opposite of the flow of internal social energy.

Now we can turn to the heat conduction equation in the absence of social currents and at constant density. Writing the continuity equation for the internal social energy (Equation 23) as $\raisebox{1ex}{$\partial {\rho c}_{P}T$}\!\left/ \!\raisebox{-1ex}{$\partial t$}\right.+\mathit{div}\left(\overline{q}\right)=0$, we obtain with constant coefficients

$\frac{\partial T}{\partial t}=\gamma ∆T(\mathrm{24a})$

where γ = κ/ρc_p, a certain coefficient, which is called thermal diffusivity in physics [15,16], Δ – is the Laplace operator (div grad). In the absence of sources and sinks of internal energy, we obtain asymptotically T = const., which also means the absence of social trends that arise due to social inequality in the degree of satisfaction of needs and the amount of personal property, i.e., temperature gradient grad T. Returning to the stellar-planetary analogy (Figures 2, 4), we come to the conclusion that the temperature gradient, due to the convection mechanism, generates macroscopic (social) flows.

The sources and sinks of social energy are primarily the processes of birth and death of people. These processes also change both social density and kinetic social energy.

If we now take into account movements in the social fluid, some slow flows, then Equation 24a will be supplemented with a term associated with the transfer of the particle in question over time [15,16].

$\frac{\partial T}{\partial t}+\left(\overline{V}gradT\right)=\gamma ∆T(\mathrm{24b})$

Finally, the movement of social fluid itself leads to friction and a local increase in temperature due to the presence of a gradient of social speeds. In other words, every social idea meets on its path not only supporters, but also people who do not support the idea or even prevent its development. This leads to conflicts and “friction” between people. Some neutral people begin to support the trend, but at the same time slow it down. Resistance based on different opinions leads to aggressive behavior, which can also be expressed in attempts to prove the superiority of one’s point of view by achieving greater personal success than the opponent. Of course, achieving such success distracts people from the direction of the social flow and takes up their time and energy, leading to unsystematic emotional actions. Let us now add to (Equations 24a,b) terms corresponding to an increase in social temperature due to friction [15].

$\left.\frac{\partial T}{\partial t}+\left(\overline{V}gradT\right)=\gamma ∆T+\frac{\eta }{\rho c_p}{\left(\mathit{div}\overline{V}\right)}^2+\frac{\eta }{\rho c_p}{\displaystyle \sum _{i,k}^N}\frac{\partial V_i}{\partial x_k}\frac{\partial V_i}{\partial x_k}\right)(\mathrm{24c})$

where c_p–is a certain “heat capacity” coefficient, which, generally speaking, itself depends on the social density, temperature and other parameters. A non-trivial contribution to the social “heat capacity” will come from interactions between people, just as is observed in physical real gases, liquids and solids. In the Equation 24c, there is also a term $\propto {\left(\mathit{div}\overline{V}\right)}^2$, which is precisely related to oscillations in the volume of society, its growth and contraction, which are often observed during global conflicts. Taking into account the presence of friction processes, we come to the conclusion that over time this kind of oscillations fades out and conflicts cease to be global.

In the most general case, when both the density and heat capacity of the environment depend on social coordinates, and the social flow is not stationary, Equations 24a–c can be written as the law of conservation of total social energy, taking into account both macroscopic movement and internal social energy, which lies in our emotions and feelings, that is

$\begin{array}{ll}\hfill \frac{\partial }{\partial t}\left(\frac{\rho V^2}{2}+\rho \epsilon \right)& =-\mathit{div}\left[\left(\frac{\rho V^2}{2}+\rho \epsilon +P\right)\overline{V}-\kappa gradT\right.\hfill \\ \hfill & \left.-\eta \left(V_i\frac{\partial V_i}{\partial x_k}+V_i\frac{\partial V_k}{\partial x_i}\right)-\left(\xi -\frac{2}{3}\eta \right)\overline{V}\mathit{div}\overline{V}\right]\hfill \end{array}(\mathrm{24d})$

where internal social energy, taking into account interactions for a unit social volume, should be written in the Equation 24d as the sum of all microscopic movements and interactions in a small unit volume of society

$\epsilon ={\displaystyle \sum _{i,j}^N}{u_i}^2+u\left(d_{i,j}\right).(25)$

Social temperature T = < ${\overline{u}}^2$ > is related only to the average kinetic social energy of a person. It does not take into account interactions.

Thus, if we can calculate the “strength” of a person’s emotions in different areas of activity and calculate the average, as well as calculate the energy of local interactions with the immediate environment of things and people $u\left(d_{i,j}\right)$, then we will know the internal energy of a person, which can change due to:

1. Processes of internal friction during social flow and oscillations in society, when participation in certain social movements leads to conflicts at the everyday level (it is $\propto \xi ,\eta$).

2. Due to the processes of internal transfer of “social tension (heat)”, when a “hungry” person takes away or steals something from the “well-fed” person, simply on the basis of his strong desire to have something ($\propto \kappa$).

3. Due to macroscopic transfer, the social flow changes a person’s social coordinates so much that he finds himself in a completely different environment with different interactions between people ($\propto \overline{V}$).

These three mechanisms mainly determine a person’s daily emotional state and his internal social energy. Equations 24c, Equation 25, equation of state P = P (ρ, T) and the continuity Equation 13 together with the definition for pressure (Equation 16b) and the form of the interpersonal interaction potential u (d_i,j) will form a complete system for describing the dynamics and thermodynamics of society without taking into account the contribution of the field of things:

$\left\{\begin{array}{l}\frac{\partial }{\partial t}\left(\frac{\rho V^2}{2}+\rho \epsilon \right)=-\mathit{div}\left[\left(\frac{\rho V^2}{2}+\rho \epsilon +P\left(T,\rho \right)\right)\overline{V}-\kappa gradT\right.\\ \left.-\eta \left(V_i\frac{\partial V_i}{\partial x_k}+V_i\frac{\partial V_k}{\partial x_i}\right)-\left(\xi -\frac{2}{3}\eta \right)\overline{V}\mathit{div}\overline{V}\right],\\ \epsilon ={\displaystyle \sum _{i,j}^N}\left({u_i}^2+u\left(d_{i,j}\right)\right),T={\overline{u}}^2\\ \frac{\partial \rho }{\partial t}+\mathit{div}\left(\rho \overline{V}\right)=0\end{array}\right.(26)$

To study social trends it is necessary to know the local emotional state of people $u_i$, the power of local interactions among the inner circle of people $u\left(d_{i,j}\right)$, which will allow us to determine the internal energy function ε($\overline{X}$) and temperature distribution T($\overline{X}$) in the social space. Knowing the distribution of people in social space, one can calculate the density distribution ρ($\overline{X}$) and using the equation of state of society P(T, ρ), and also, if necessary, introducing attraction potentials to the field of things U₊(X), as well as the potential of hierarchical relations in society U(X), the full social pressure (P) can be obtained. Now doing social research at the next close time point t + Δt, we will obtain the initial distribution of speeds ${\overline{V}}_0$, which will enable us to calculate the distribution of speeds $\overline{V\left(X\right)}$ and density in social space ρ(X) at the next time point, i.e., predict the future of social relations and solve the main problem of social dynamics. Of course, for this, all functions associated with thermal conductivity (for example, κ(T,P,ρ)), social friction: η(T,P,ρ) and ξ(T,P,ρ) must be known from experiment.

2.10 Astrophysical analogy

The parameterization of society proposed in this work is certainly simplified. In physics, to distinguish one object from another, various coefficients are introduced, for example, masses (m_i, for the ith person), charges (e_i, for the ith person), spins, geometric dimensions, parameters of the internal structure, various heat capacities, physical fields and particles that realize the interaction on distance, etc. In the case of describing social movements, this can also be done when necessary to obtain better agreement with the experimentally observed dynamics of society.

Drawing further analogies with physics, constructed model of society corresponds best to various planetary and stellar models. Consider, for example, the Sun. It is located in some boundless space. It does not impose any boundary conditions on the solution of the equations of motion of matter. This is very comfortable. The movement of matter in the Sun is under the influence of a strong central gravitational field of attraction, which prevents the evaporation and dispersion of the star’s matter. The field of things operates in a similar way in the proposed social theory. This field of things attracts people with its conveniences, forces them to live together even though they do not really like each other and are repelled. Otherwise, everyone would live like hermits in the desert.

The field of things and the field of people are closely connected: people create things, and things attract people. In economics, we consider the movement of cash and commodity flows and already know that these flows are of the nature of circulation and convection. Along with the flow of goods, people also move, just like the matter of a star, like water in a heating kettle, they participate in convective movements. An economy stops if the circulation of money and goods stops. In the same way, a society dies if social circulation and social movements between different social strata stop. However, such circulation is accompanied by friction processes, and in order for it to persist, some source of energy is needed. If the source of energy disappears, cores of (social) planets cool and solidify (like the Moon), and stars turn into black dwarfs.

The other side of this analogy is that particles of matter in the Sun create pressure that prevents all the matter from falling into the center of the star. Instead of this fall on the center, intense convection develops from the interior of the star to its surface, there is a strong temperature gradient, and in the center of the star the temperature turns out to be significantly higher than on its surface. Likewise, competition between people for higher social status creates social pressure and higher social density and temperature in the center, in the upper echelons of society. Everyone wants to become rich, famous, and gain power. But there are many such people and they repel each other creating internal pressure in the social structure. The gradient of such social pressure is opposite to the gravitational force of the field of things and pushes people from the upper strata into calmer regions of society. In the center of society, in its upper strata, social pressure is much higher than among “ordinary” people, and in order to move up the social ladder you must have the appropriate internal energy, zeal and will. The center of society is not a zone of calm (the outskirts of the star), it is a zone of continuous and intense struggle. New people replace older people as part of social convection - the flow of matter from the center of a star to its surface.

There are also the outer layers of the Sun, the corona (Figure 6a), where particles of very high energy are concentrated. The temperature in these layers is much higher than in most of the Sun. Likewise, in every society there is a disadvantaged part, the criminal world, the world of the homeless, where physical needs, impulsive actions, hunger and addictions predominate. There are planets in which the surface layer, on the contrary, is completely hard and rigid (Figure 6b), and some kind of convection is observed only in the hot core or in the ocean below the surface. Similarly, the outskirts of social space in human society are often occupied by marginal and radical groups, sects, in which either impulsive actions dominate or a completely hierarchical structure of subordination limits any social trends.

Figure 6

Figure 6. Illustration of a star-planetary model of the structure of society with internal and external layers. (a) A society with a high average temperature, in which significant part of the society is “radicalized” and in social space is located in the same way as the solar corona in relation to the Sun. (b) A society with a low average temperature, in which the lower classes of society provide for the upper classes, but are forced to exist within a rigid hierarchy and discipline in order to survive.

When the star and planets cool, their temperature decreases and the processes of mixing and convection stop. Continuing the analogy, we can say that in such societies the structure is rigid, does not allow career growth, and position in society is passed on from generation to generation. Stars cannot exist without an internal source of heat, nuclear reactions accompanied by the birth of new particles. And in human society, the birth of new people serves as the internal engine that maintains social dynamics.

Finally, almost all planets and stars rotate. Rotation is a movement that is not accompanied by friction and can therefore be maintained indefinitely. The probability of finding such a movement in society is highest. As part of such a movement, social positions on one or more issues and views change periodically. The well-forgotten old becomes new. Within this periodicity, there are many other associated periodic processes to which societies are subject, associated with the change of day and night, seasons, periods of economic growth and decline, electoral cycles, etc.

2.11 Birth and death

If people lived forever, then the mathematical model of such a society would not be dynamic. As stated above, the absence of an energy source would very soon lead to the attenuation of any non-trivial social currents and processes due to the presence of social friction. Some animal communities can probably be described using such models.

In addition to the birth and death of people, one must also take into account the birth and death (destruction) of things. But the study of the processes of production and decommissioning of things is beyond the scope of this work. Just to give an example of how this can be done in principle, I will give some simple ideas. To take into account the birth of new people and the death of old ones, we must make changes to our Equation 26. First of all, this concerns the continuity equation, which should now be re-written, for example, as

$\frac{\partial \rho }{\partial t}+\mathit{div}\left(\rho \overline{V}\right)=-\alpha \rho +\mathrm{\beta }{\rho }^2\left(1-e^{-\frac{U_2}{T}}\right)(27)$

where α is the probability of death per unit of time at the considered point in social space, and β is the probability of birth at the same point per unit of time. Death in the simplest case is related linearly to the density of social space simply as a random event in a group of ρ($\overline{X}$)dV people, whereas birth is proportional to the density of married couples ρ², which depends both on the square of social density (ρ²), and on social temperature, since excess of kinetic energy destroys couples of people. This last dependence can, for example, be written as the Boltzmann term (1-exp (-U₂/T)), where U₂ – is some average social energy of a couple’s breakup [16]. This is often done when studying the behavior of molecules [16,26]. Thus, the density of couples is maximum somewhere in the middle strata of society. Not in the center, where it is too “hot”, but also not on the outskirts of the social space, where there are too few people (ρ → 0) to find a friend with similar interests.

It is very important that in the social model being developed we are already faced at the very beginning with the birth/destruction of social particles and the inapplicability of the continuity equation in its classical form, used in the mechanics of liquids and gases. Without the introduced factor of birth and destruction of social particles (people) and things, it is impossible to imagine a stable developed society with social strata and flows.

What happens when a person is born? He is a thing of his parents at least for some time and has the same initial social coordinate as they do: $\overline{X}$ _kid (t = 0) = $\overline{X}$ _parents. Indeed, a child of rich parents is “worth” (for example, to kidnappers) much more than a child of poor parents. Over time, his social coordinate and answers to questionnaires begin to deviate from the opinion of his parents and the child becomes an independent person.

His initial social speed $\overline{V}$ _kid (t = 0) = $\overline{V}$ _parents is also equal to the social velocity of the parents (family), since the child shares the fate of his parents. At the microscopic level, the child behaves like an animal, he has needs for food, sleep, warmth, care … and he demands their satisfaction, therefore the internal energy ε₀ = ${{\displaystyle {\sum }_i^J}{u}_i}^2$ can take on quite large values, possibly the maximum for a lifetime.

For parents, the child serves as a braking factor, slowing down their social movement. Part of the parents’ movement is transferred to the child and ensures its social acceleration $\raisebox{1ex}{$dV$}\!\left/ \!\raisebox{-1ex}{$dt$}\right.$, just as happens when the inert mass of a physical system increases.

Returning again to the stellar-planetary analogy, we see that the birth of new social particles is a source of internal social movement, just as is observed in stars, where thermonuclear fusion is the main source of stars’ energy.

Since the appearance of new people is accompanied by an increase in internal social energy, we need to introduce energy sources into the simplified equation of the balance of social energy:

$\frac{\partial T}{\partial t}=\gamma ∆T+\frac{\epsilon }{c_p}=\gamma ∆T+\beta \rho \left(1-e^{-\frac{U_2}{T}}\right)\frac{{\epsilon }_0}{c_p},(\mathrm{28a})$

where c_p–is some coefficient of social “heat capacity”. The birth of new people in the Equation 28a will certainly heat up society, increase its social temperature and support its non-trivial social dynamics. An example of this is the theft of food by poor mothers for their children. Here we imply the constancy of social density over time. Generally speaking, this is not so and we must write a more complex Equation 28b for the next approximation (without taking into account the social flows for now)

$\frac{\partial \left(c_p\rho T\right)}{\partial t}=\mathit{div}\left(\kappa gradT\right)+\beta {\rho }^2\left(1-e^{-\frac{U_2}{T}}\right){\epsilon }_0.(\mathrm{28b})$

What happens to social energy when a person dies? Apparently, we also lose some of our internal energy $-\alpha \rho \epsilon$ because this person no longer needs anything. Social density decreases in the process of death, as does social impulse. The deceased’s belongings remain in society and are distributed among his relatives - his field of things also has some social impulse, since things created during life or accumulated for the fulfillment of social duties help other people to fulfill them. A kind of micro-explosion occurs when the things and people surrounding the deceased person lose the connection that attracts them to him and begin to “fly” apart in different directions, moving away from the former center of attraction.

The field of things, a kind of imprint in history, often lasts longer than the lifespan of people. Since we can no longer conduct a survey and find out the social coordinates of a died person, social ties are also broken. People have some memory of the deceased - social currents continue in the direction in which we moved when the person was alive due to social inertia, even if now there are no factors that force us to move. Memory, however, like things, is destroyed over time. Now let’s add mortality to the equation of the balance of social energy (Equation 28c):

$\frac{\partial \left(c_p\rho T\right)}{\partial t}=\mathit{div}\left(\kappa gradT\right)+\beta {\rho }^2\left(1-e^{-\frac{U_2}{T}}\right){\epsilon }_0-\alpha \rho \epsilon .(\mathrm{28c})$

We will take into account the disappearance of part of the impulse as a result of death by decreasing social density, since accidental death does not change the direction of social flows. In the same way, the birth of children does not introduce direct changes into the equations of motion, since the initial social impulse of the child is equal to the social impulse of the parents. The contribution of births appears only through a change in internal social energy and through a change in social “mass” and density.

Rewriting the equations of motion taking into account death and birth, we obtain the same Equations 29a, 30 of motion where density can no longer be considered constant

$\frac{d\rho \overline{V}}{dt}=\frac{\partial \rho \overline{V}}{\partial t}+\left(\overline{V}\frac{\partial }{\partial \overline{X}}\right)\left(\rho \overline{V}\right)=-gradP(\mathrm{29a})$

Social movements will be the weaker the greater the mortality rate in the society in question. The ‒αρ term cause any social movements to die out due to the physical extinction of their participants. Indeed, most social movements exist only for a short time and then disappear, unless they are supported by a gradient of social pressure that captures more and more new participants as the old followers die.

Let us finally rewrite the most complete Equation 26 considering mortality and birth rates:

$\left\{\begin{array}{l}\frac{\partial }{\partial t}\left(\frac{\rho V^2}{2}+\rho \epsilon \right)=\beta {\rho }^2\left(1-e^{-\frac{U_2}{T}}\right){\epsilon }_0-\alpha \rho \epsilon +\mathit{div}\left(\kappa gradT\right)\\ -\mathit{div}\left[\left(\frac{\rho V^2}{2}+\rho \epsilon +P\left(T,\rho \right)\right)\overline{V}\right]+\\ +\mathit{div}\left[\eta \left(V_i\frac{\partial V_i}{\partial x_k}+V_i\frac{\partial V_k}{\partial x_i}\right)+\left(\xi -\frac{2}{3}\eta \right)\overline{V}\mathit{div}\overline{V}\right],\\ \epsilon ={\displaystyle \sum _{i,j}^N}\left({u_i}^2+u\left(d_{i,j}\right)\right),T={{\overline{u}}_i}^2\\ \frac{\partial \rho }{\partial t}+\mathit{div}\left(\rho \overline{V}\right)=-\alpha \rho +\beta {\rho }^2\left(1-e^{-U_2/T}\right),\end{array}\right.(30)$

On this note, we will finish constructing our model of society based on the introduction of a metric social space with interacting social particles moving under the action of potential social forces according to Newton’s equations.

2.12 Example 1: exponential decline in audience interest

In this paper I deliberately avoid any analysis of possible practical applications. In order to apply proposed model quantitatively, it is first necessary to establish the type of dependence of the interaction force on the social distance f(d) and make assumptions regarding the properties, structure and content of the questionnaire for determining the social coordinates of people. This itself constitutes the goal of a separate publication.

However, some simple conclusions can be drawn from the proposed model even without a detailed numerical analysis of the experimental data on human interactions. For example, one of the main conclusions of this work is the indication of the large role of dissipative processes, which lead to the disappearance of any flows both in the physics of liquids and in society in the absence of external sources of energy and matter (Figure 7). The simplest model of dissipative forces is a friction force linear with respect to the flow velocity, leading to the following equation [a special case of Equation 3] and its solution for a velocity (V) of an isolated social flow:

$V^{\prime }+\beta V=0,\text{and\hspace{0.17em}}V=V_0\exp \left(-\beta t\right).(31)$

Figure 7

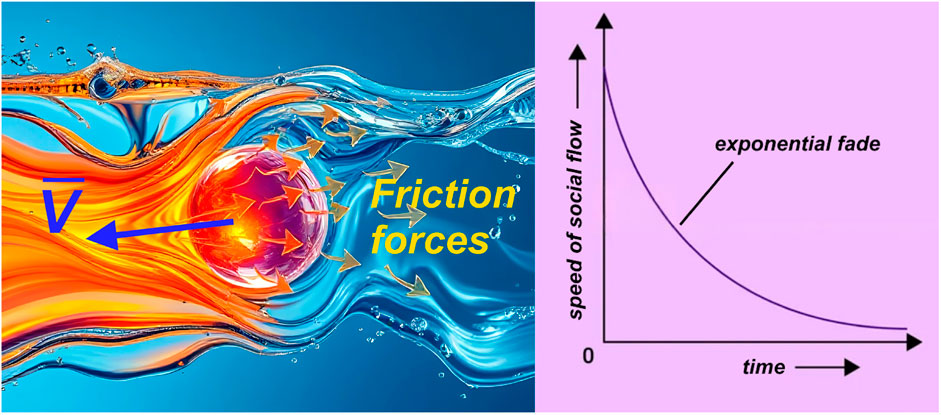
Figure 7. An illustration of the slowing of social flows over time. The movement of bodies (the ball on the left panel) in a viscous fluid slows down exponentially, just as the audience’s interest in any topic/news on the Internet fades over time.

The linear (or even constant) friction force is a first approximation in describing real dissipative forces in nature. We see that the description of the fade of an abstract isolated social flow within the framework of an exponential decay function (Equation 31), for example, interest in a topic or news item on the Internet, is a natural conclusion from the proposed model and, indeed, is widely used in the sociophysics (e.g. [27,28]).

The dissipative terms in the Navier-Stokes equation are a first linear approximation of complex friction phenomena and are applicable in fluid dynamics to the same extent as the exponential law of natural fade of audience interest is applicable in social sciences. In this case, the viscosity coefficients included in the Navier-Stokes equation can be estimated based on this simple experiment on the exponential decrease over time in the number of Internet queries for previously popular topics.

2.13 Example 2: filter bubbles and echo chambers in social media

When studying social media processes, a phenomenon called “echo chambers” is discovered, when a group of like-minded people (co-religionists) finds themselves isolated and stable in their judgments and statements, preserving them in one modification or another over a long period of time [29].

It is not difficult to find an analogy to this phenomenon in fluid dynamics: this is the well-known consideration of isolated current tubes in an ideal fluid, for which the absence of scattering is assumed, and the laws of conservation of energy and momentum are satisfied (Bernoulli’s principle, see Section 7: Stationary society and conservation laws). Indeed, the scattering of social particles would lead to a change in their velocities and an exit from the “echo chamber” space after some time (Figure 8). If a random scattering is absent, then people do not change their interests and continue moving by inertia as a compact, connected object.

Figure 8

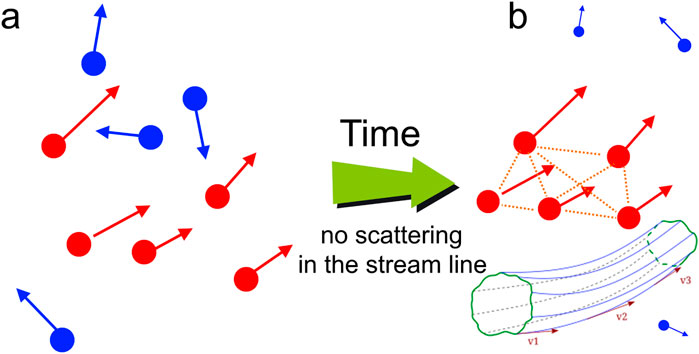
Figure 8. Formation of compact groups of like-minded people (red circles) with strong attraction within the group (i.e., short interpersonal distance, orange dashed lines) in the process of evolution (from panel a to panel b) of a social group with different interests. The red and blue arrows correspond to the directions of people’s interests (social speed), which naturally lead to people losing contact with their old acquaintances (blue circles) and acquiring new acquaintances and friends (red circles) over time.

A group of people forming an echo chamber can be characterized by some average bonding energy E_bond ∼ min U(d) and the number of members M_bond. This binding energy may exceed the bonding energy in families, so that the resulting condensate in this case is closer to a compact rotating solid body than to a liquid. If the interaction energy with the scattering factor exceeds the bonding energy U_scat $\ge$ E_bond, then some of border members of the group may exit the echo chamber. If the scattering factor strong enough U_scat >> M_bondE_bond, then the echo chamber decomposes, starting from its border.

Another interesting phenomenon in the field of social media is the formation of “filter bubbles”, when internet search engines, people’s environment, political parties, or organizations provide information, make promises to voters only within the framework of what a person or group of people wants to see and want to know (based on previous experience of interaction) [30]. Instead of a real picture, a more pleasant virtual world is created that has little in common with reality–this is a filter bubble. The purpose of creating such filter bubbles is to satisfy the audience more, create a force of attraction, and keep high positive level of communication.

Indeed, any social network/search engine/political party/pop star wants to attract more users, members, and fans. And with them, more money, power, and fame. To do this, they need to please people and give them what they want. Then people will use this source of information, they will be attached to it. At the same time, the users are completely different, with completely different views, incompatible with each other in close direct contact.

This situation can be described using the concept of a social vortex motion (Figure 9). In a social vortex there is a center (core), which forms the filter bubble and has the greatest social power, and there is a shell, which contains groups of people of all interests (directions of social speed, arrows in Figure 9), including groups with antagonistic beliefs. Such groups are far from each other and do not interact, but they interact with the core, receiving from it only the information they want to hear.

Figure 9

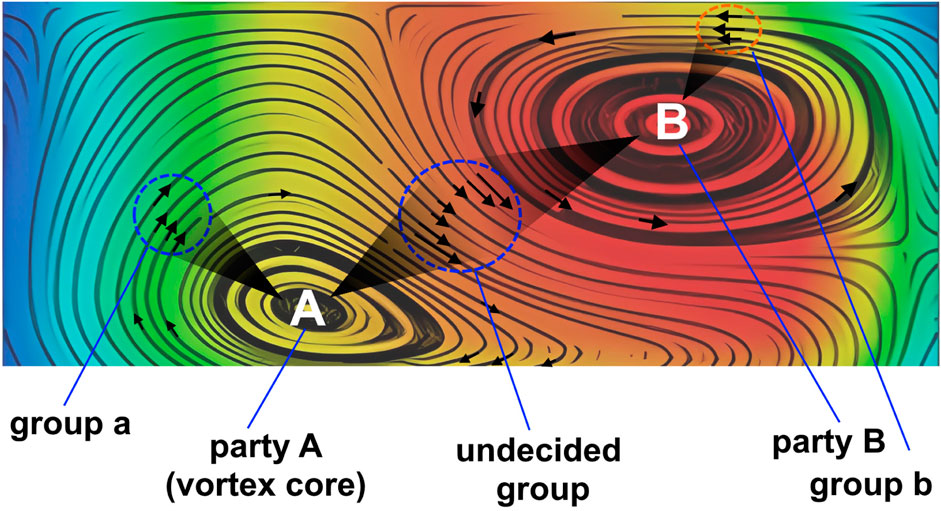
Figure 9. A fragment of the cellular structure of a social vortex flow, in which there are two attracting vortices (A,B) and groups of people (a,b) that are connected to them and are inside the corresponding filter bubbles, and at the same time form a certain echo chamber, belonging to the closest vortex.

The Equation 32 describing the evolution of the non-dissipative vortex motion of an ideal fluid is well known (for 2D case, see also Section 7: Stationary society and conservation laws)

$\frac{\partial curl\overline{V}}{\partial t}=curl\left[\overline{V}\times curl\overline{V}\right],$

$\frac{\partial \overline{\omega }}{\partial t}=curl\left[\overline{V}\times \overline{\omega }\right],(32)$

where $2\overline{\omega }=curl\overline{V}$ – is the field of angular velocities of social rotation (say, “filter bubble density”). In an ideal fluid, the vortex exists indefinitely and, in the case of an external influx of people, (vector product $\left[\overline{V}\times \overline{\omega }\right]$), $\raisebox{1ex}{$\partial \left|\omega \right|$}\!\left/ \!\raisebox{-1ex}{$\partial t$}\right.$ > 0, the rotation accelerates and the filter bubble phenomenon intensifies.

Taking into account dissipative forces leads to the following asymptotic law of (Equation 33) decay of vortices and filter bubbles with time t (at least for the 2D case) [31]:

$\overline{V}\propto \frac{1}{t^{5/2}}.(33)$

This asymptotic law coincides with Millionshchikov’s law of turbulence degeneration in a viscous fluid [32]. Thus, we come to the conclusion that straight social currents fade faster (Equation 27) than vortex structures (Equation 31), which correspond to the filter bubble phenomenon in the proposed model.

3 Discussion

The proposed model describes the behavior of a simplified society, where the behavior of each person is described, in general, by only one universal function U($\overline{X}$) of his social coordinate $\overline{X}$. This potential field, roughly speaking, correlates with a field of social statuses. The central key point of the model (d $\overline{V}$/dt = ‒ grad U) can be roughly interpreted in the following way:

• Statistically, people strive to occupy a higher social position in the society if such an opportunity exists.

For the most of people this is rather true [33,34]. However, not all people behave this way. This is partly due to the presence of repulsion from other people who already occupy the desired social position or its vicinity. In this case, social resistance and repulsion lead people to avoid increasing their social status and the associated risk of responsibility, psychological stress, etc. Repulsion forces are included in the proposed model in the form of a complex dependence U(d_ij), where d_ij is the social interpersonal distance (see Figure 2a), which contains a region of attraction, as well as regions of repulsion.

Manifestations of feelings, emotions, illogical and non-egoistic behavior of people is also present in the proposed model and described in Section 9 “Social thermodynamics”. To consider such behavior, I draw an analogy with random processes of interactions, the physics of which we do not track, using only some “average” parameter to describe them ‒ the average square of the speed of such spontaneous emotional social movements < $\overline{u}$²> = T. If we average the behavior of people over a long period of time, then the emotional component disappears, and the behavior becomes much simpler, more rational, and can be described by analogy with the fluid dynamics.

Various approaches to modeling of social interactions in society are known, but they are either mostly discrete in nature [35], containing complex mathematical constructions that do not allow for demonstrative interpretation [36], or containing only verbal descriptions without clear mathematical formulation [37]. The main advantage of the proposed theory is its mathematical simplicity, clarity, and unambiguity since it is a multidimensional analog of classical mechanics and fluid dynamics, developed over the past 300 years. It is well established; we know every branch of this theory. In the proposed approach, we do not need to create any new models of human interactions and so on. The rules of the game are already defined by a set of known physical effects. What we have to do is make the right analogy between them and the physical world.

Another important advantage of this work is that I try to pay maximum attention to the detailed analysis of basic concepts (social coordinate, velocity, interaction force, etc.) without moving on to more complex physical terms (see, for example, [38]). Without a solid basis, we cannot move forward and build advanced theories and models.

4 Conclusion

Using the analogy of human society with a system of material particles obeying Newton’s laws, and using physical theories of the motion of continuous media, we constructed a mathematical model of the society using the basic assumptions about the metricity of social space and the potentiality of social forces of interpersonal interaction.

The social dynamics of society in the constructed model is similar to the movement of real liquids: in addition to the free will, there are many social flows that capture and carry people away, regardless of their desires. We found out that in the conditions of dominance of repulsive forces between people at large social distances, one of the key roles in stabilizing human society is played by the field of things, the attraction to which compensates for the repulsion between people.

At the same time, the presence of social friction leads to the extinction of social currents in the absence of an internal source of energy in the form of the birth of new people. The similarity and complexity of the obtained equations of the dynamics of society and the equations describing the dynamics of liquids excludes the possibility of both an exact solution of the equations of social dynamics and their numerical solution over any long-time intervals. The impossibility of predicting the future of society is similar to the impossibility of accurately predicting the weather.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

DS: Writing – original draft, Writing – review and editing.

Funding

The author(s) declare that no financial support was received for the research and/or publication of this article.

Conflict of interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2025.1556949/full#supplementary-material

References

1. Marko J, Holme P, Kanazawa K, Takayasu M, Romić I, Wang Z, et al. Social physics. Phys Rep (2022) 948:1–148. doi:10.1016/j.physrep.2021.10.005

CrossRef Full Text | Google Scholar

2. Borgatti SP, Mehra A, Brass DJ, Labianca G. Network analysis in the social sciences. Science (2009) 323(5916):892–5. doi:10.1126/science.1165821

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Helbing D, Molnár P. Social force model for pedestrian dynamics. Phys Rev E (1995) 51(5):4282–6. doi:10.1103/physreve.51.4282

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Castellano C, Fortunato S, Loreto V. Statistical physics of social dynamics. Rev Mod Phys (2009) 81(2):591–646. doi:10.1103/revmodphys.81.591

CrossRef Full Text | Google Scholar

5. Terziyan V. Social Distance metric: from coordinates to neighborhoods. Int J Geographical Inf Sci (2017) 31(12):2401–26. doi:10.1080/13658816.2017.1367796

CrossRef Full Text | Google Scholar

6. Hoff PD, Raftery AE, Handcock MS Latent space approaches to social network analysis. J Am Stat Assoc (2002) 97(460):1090–8. doi:10.1198/016214502388618906

CrossRef Full Text | Google Scholar

7. Burago D, Burago Y, Ivanov S. A course in metric geometry. Providence, RI: American Mathematical Society (2001).

CrossRef Full Text | Google Scholar

8. Solomentsev ED. “Euclidean space”. In: Encyclopedia of mathematics. Helsinki, Finland: European Mathematical Society (EMS)) (2001).

Google Scholar

9. Landau LD, Lifshitz EM Mechanics. 3rd ed., 1. Butterworth-Heinemann (1976).

Google Scholar

10. Newton I The principia, the mathematical principles of natural philosophy. Translated by cohen, I.B. Whitman, A. Los Angeles: University of California Press (1999).

Google Scholar

11. Hand LN, Finch JD Analytical mechanics. Cambridge University Press (1998). p. 41.

CrossRef Full Text | Google Scholar

12. Newton I (1687). Philosophiæ naturalis principia mathematica (Latin for 'mathematical principles of natural philosophy)' (the Principia)).

Google Scholar

13. Zipf GK The P1*P2/D hypothesis: on the intercity movement of persons. Am Sociological Rev (1946) 11(6):677. doi:10.2307/2087063

CrossRef Full Text | Google Scholar

14. Tuckerman ME Statistical mechanics: theory and molecular simulation. 1st ed. (2010). p. 87.

Google Scholar

15. Landau LD, Lifshitz EM Fluid mechanics. 2nd ed., Vol. 6. Oxford, United Kingdom: Butterworth-Heinemann (1987).

Google Scholar

16. Landau LD, Lifshitz EM Statistical physics. 3rd ed., Vol. 5. Oxford, United Kingdom: Butterworth-Heinemann (1980).

Google Scholar

17. Cartan É. Les Systèmes Différentiels Extérieurs et leurs Applications Géométriques. Paris: Hermann (1945).

Google Scholar

18. Landau LD, Lifshitz EM Theory of elasticity. 3rd ed., Vol. 7. Butterworth-Heinemann (1986).

Google Scholar

19. Spiegel MR, Lipschutz S, Spellman D. Vector analysis. 2nd ed. McGraw Hill (US (2009). Schaum's Outlines.

Google Scholar

20. Bernoulli D. Hydrodynamica, sive de viribus et motibus fluidorum commentarii (in Latin, source ETH-Bibliothek Zürich, Rar 5503). Sumptibus Johannis Reinholdi Dulseckeri (1738). Typis Joh. Deckeri, typographi Basiliensis.

Google Scholar

21. Landau LD, Lifshitz EM. The classical theory of fields. 4th ed, Vol. 2, Oxford, United Kingdom: Butterworth-Heinemann (1975).

Google Scholar

22. Glansdorff P, Prigogine I Thermodynamic theory of structure, stability, and fluctuations. London: Wiley-Interscience (1971).

Google Scholar

23. Available online at: https://www.claymath.org/millennium-problems/ (Accessed April 23, 2025).

24. Einstein A Über die von der molekularkinetischen Theorie der Wärme geforderte Bewegung von in ruhenden Flüssigkeiten suspendierten Teilchen [On the Movement of Small Particles Suspended in Stationary Liquids Required by the Molecular-Kinetic Theory of Heat] (PDF). Annalen der Physik (1905) 322(8):549–60.

Google Scholar

25. Thomson W (Lord Kelvin) (1848). On an absolute thermometric scale founded on Carnot's theory of the motive power of heat, and calculated from Regnault's observations, Proc Camb Phil Soc (1843/1863) 1, No. 5: 66–71.

Google Scholar

26. Pauling L. The nature of the chemical bond. Application of results obtained from the quantum mechanics and from a theory of paramagnetic susceptibility to the structure of molecules. J Am Chem Soc (1931) 53(4):1367–400. doi:10.1021/ja01355a027

CrossRef Full Text | Google Scholar

27. Arbesman S. The half-life of facts: why everything we know has an expiration date. The Penguin Publishing Group (2012).

Google Scholar

28. Kim Y, Weon BM. Stretched exponential dynamics in online article views. Front Phys (2021) 8:619729. doi:10.3389/fphy.2020.619729

CrossRef Full Text | Google Scholar

29. Nguyen CT Echo chambers and epistemic bubbles. Episteme (2020) 17(2):141–61. doi:10.1017/epi.2018.32

CrossRef Full Text | Google Scholar

30. Bozdag E. Bias in algorithmic filtering and personalization. Ethics Inf Technology (2013) 15(3):209–27. doi:10.1007/s10676-013-9321-6

CrossRef Full Text | Google Scholar

31. Maslennikova VN. On the decay rate of a vortex in a viscous fluid in the case of two spatial variables. Dokl Acad Nauk USSR (1973) 212(4):834–7. (Proceedings of the Mathematical Institute of the USSR Academy of Sciences, 1973, vol. 126, 46–72.

Google Scholar

32. Millionshchikov MD. Degeneration of homogeneous isotropic turbulence in a viscous incompressible fluid. Dokl Acad Nauk USSR (1939) 22(5):236–40.

Google Scholar

33. Immorlica N, Kranton R, Manea M, Stoddard G. Social status in networks. Am Econ J Microeconomics (2017) 9(1):1–30. doi:10.1257/mic.20160082

CrossRef Full Text | Google Scholar

34. Boyce CJ, Brown GDA, Moore SC Money and happiness. Psychol Sci (2010) 21(4):471–5. doi:10.1177/0956797610362671

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Tsintsaris D, Tsompanoglou M, Ioannidis E. Dynamics of social influence and knowledge in networks: sociophysics models and applications in social trading, behavioral finance and business. Mathematics (2024) 12:1141. doi:10.3390/math12081141

CrossRef Full Text | Google Scholar

36. Kuznetsov DV, Mandel I Statistical physics of media processes: mediaphysics. Physica A: Stat Mech Its Appl (2007) 377(1):253–68. doi:10.1016/j.physa.2006.10.098

CrossRef Full Text | Google Scholar

37. Dinga E, Tănăsescu CR, Ionescu GM. Social entropy and normative network. Entropy (2024) 22(9):1051. doi:10.3390/e22091051

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Tsarev D, Trofimova A, Alodjants A, Khrennikov A. Phase transitions, collective emotions and decision-making problem in heterogeneous social systems. Sci Rep (2019) 9:18039. doi:10.1038/s41598-019-54296-7

PubMed Abstract | CrossRef Full Text | Google Scholar