Pedestrian dynamics modeling and social force analysis based on object detection

Introduction: Object detection is a fundamental component of modern computational applications, playing a crucial role in pedestrian analysis, autonomous navigation, and crowd monitoring. Despite its widespread utility, pedestrian-oriented object detection faces significant challenges, including dynamic crowd behaviors, occlusions, multi-scale variability, and complex urban environments, which hinder the accuracy and robustness of existing models.

Methods: To address these challenges, we propose a novel framework that integrates the Information-Geometric Variational Inference Framework (IGVIF) with the Adaptive Exploration-Exploitation Trade-off Strategy (AEETS), specifically tailored for pedestrian dynamics. IGVIF formulates pedestrian detection as a probabilistic inference problem, leveraging principles from information geometry to efficiently explore high-dimensional parameter spaces. By incorporating techniques such as Riemannian optimization and multi-scale parameterization, IGVIF effectively captures the hierarchical and multi-modal structures inherent in pedestrian movement patterns. AEETS dynamically balances global exploration with local refinement using entropy-based metrics and feedback-driven adjustments, allowing the system to adaptively optimize complex loss landscapes with greater precision in pedestrian scenarios.

Results: Together, these components create a robust and adaptive framework that overcomes traditional limitations by efficiently handling large-scale pedestrian variability and densely populated environments. Experimental evaluations across multiple real-world pedestrian datasets demonstrate the superiority of our physics-inspired approach, achieving state-of-the-art performance in pedestrian detection and movement analysis.

Discussion: This work highlights the transformative potential of interdisciplinary strategies in advancing pedestrian-aware object detection, bridging computational physics with deep learning methodologies to enhance urban mobility and crowd safety.

1 Introduction

Object detection plays a pivotal role in a wide range of applications, including autonomous systems, environmental monitoring, scientific experiments, and industrial automation [1]. By identifying and localizing objects within an image or video, object detection facilitates tasks such as anomaly detection, resource optimization, and process automation [2]. In physics-related domains, object detection is critical for applications such as particle tracking, astronomical object identification, and material characterization [3]. Traditional object detection techniques, while effective in certain scenarios, often fail to capture the complexity and underlying physics-driven patterns in data, particularly in domains where noise, non-linearity, and spatiotemporal dependencies dominate [4]. Recent advancements in deep learning have provided robust solutions to object detection challenges, enabling high accuracy and scalability [5]. Physics-inspired deep learning models take this a step further by incorporating domain-specific insights, improving the interpretability, adaptability, and efficiency of object detection systems in interdisciplinary applications.

Early approaches to object detection relied heavily on handcrafted features and classical machine learning models [6]. Methods such as the Viola-Jones detector, histogram of oriented gradients (HOG), and scale-invariant feature transform (SIFT) utilized predefined image features to identify objects [7]. These techniques achieved early success in simple tasks like face detection and vehicle tracking [8]. However, their reliance on handcrafted features limited their ability to generalize to complex and noisy environments, as often encountered in physics-based applications [9]. For example, in particle physics, detecting overlapping particles or identifying objects in high-noise environments, such as fluid dynamics or turbulence studies, proved challenging for these traditional approaches [10]. These methods lacked scalability and adaptability, making them unsuitable for datasets with high variability or intricate spatial-temporal patterns.

The transition to machine learning-based object detection marked a significant improvement, as algorithms like support vector machines (SVMs), random forests, and boosted classifiers were used in combination with feature extraction methods [11]. These models were particularly effective when paired with well-curated training datasets, enabling them to classify objects with greater accuracy than purely rule-based systems [12]. For instance, in astronomy, machine learning was used to detect galaxies or exoplanets in large datasets of telescope images, and in material science, it facilitated the identification of defects in crystallographic structures [13]. Despite these advancements, machine learning-based models were limited in their ability to handle large-scale, high-dimensional data [14]. They often required extensive feature engineering and were incapable of learning hierarchical patterns or representations, which are crucial for complex object detection tasks [15].

Deep learning revolutionized object detection by introducing end-to-end learning frameworks that eliminated the need for manual feature engineering [16]. Convolutional neural networks (CNNs) formed the backbone of modern object detection models, with architectures such as Faster R-CNN, YOLO (You Only Look Once), and SSD (Single Shot MultiBox Detector) achieving state-of-the-art performance across a variety of tasks [17]. These models provided robust solutions for physics-based applications, such as tracking particles in simulations, identifying features in astrophysical images, and detecting defects in materials [18]. For example, YOLO’s ability to process images in real-time has been leveraged in high-energy physics experiments for particle identification, while Faster R-CNN has been applied to detect and classify dynamic objects in fluid simulations [19]. Advancements in spatiotemporal modeling, such as 3D CNNs and recurrent neural networks (RNNs), have expanded object detection to video data, enabling applications in turbulence modeling and plasma physics [20]. However, despite their success, these methods face challenges in interpretability, generalization to out-of-distribution data, and their reliance on large labeled datasets.

Physics-inspired deep learning models have recently emerged as a promising direction for addressing these challenges [21]. By integrating domain-specific insights, such as conservation laws, symmetry properties, or physical constraints, these models improve the interpretability and generalizability of object detection systems [22]. For instance, incorporating physical priors into neural network architectures has been shown to enhance performance in detecting objects under noisy conditions or extreme environments [23]. Hybrid models that combine traditional physics-based simulations with deep learning leverage the strengths of both approaches, enabling accurate and efficient object detection [24]. For example, physics-guided neural networks have been used to detect and track particles in fluid simulations by embedding Navier-Stokes equations into the model architecture, while transformer-based models have been adapted for astronomical object detection by incorporating spatial relationships derived from astrophysical principles.

To advance object detection in physics-driven domains, we propose a novel interdisciplinary deep learning framework that integrates physics-based priors with modern neural architectures. The proposed framework incorporates physics-inspired constraints into a transformer-based object detection model to capture both local and global dependencies. Multi-modal data integration is leveraged to combine information from diverse sources, such as simulations, experiments, and imaging modalities. By employing a hybrid loss function that balances data-driven learning with physics-inspired regularization, the framework achieves improved generalization, accuracy, and interpretability. Designed for scalability, this approach addresses the challenges of noise, non-linearity, and data sparsity in physics-based applications, providing a robust solution for interdisciplinary object detection tasks.

• The proposed framework integrates physics-inspired priors with transformer-based architectures, enabling accurate and interpretable object detection in complex, noisy environments.

• Designed to process multi-modal data, the framework generalizes across diverse physics domains, such as particle tracking, astrophysics, and material science, ensuring robustness in real-world scenarios.

• Empirical evaluations on benchmark datasets demonstrate state-of-the-art performance, with superior accuracy and robustness compared to existing deep learning approaches, particularly in physics-driven object detection tasks.

2 Related work

2.1 Deep learning for object detection

Object detection, a core task in computer vision, has been significantly advanced by deep learning models such as Faster R-CNN, YOLO (You Only Look Once), and SSD (Single Shot MultiBox Detector) [25]. These models excel in detecting objects in complex scenes by leveraging hierarchical feature extraction, bounding box regression, and classification frameworks. Their applications span numerous domains, including autonomous driving, medical imaging, and environmental monitoring. However, standard deep learning-based object detection models are often limited by their reliance on large-scale labeled datasets and their inability to incorporate domain-specific knowledge, such as the physical constraints of the environment. Incorporating domain knowledge, particularly from physics, has emerged as a promising direction for improving the robustness and interpretability of object detection systems [26]. For example, in astrophysics and particle physics, object detection models are used to identify and classify cosmic structures or particle trajectories. Physics-inspired adaptations, such as the inclusion of spatial priors or symmetry constraints, enhance model performance by embedding fundamental principles directly into the architecture [27]. Techniques like these reduce overfitting, especially in scenarios with limited labeled data, and improve the interpretability of predictions in scientific contexts. Recent advancements include the integration of attention mechanisms and Transformers into object detection models. For instance, Vision Transformers (ViTs) and their derivatives, such as the DETR (DEtection TRansformer) model, provide a novel framework for capturing global contextual information, which is critical for detecting objects in cluttered or noisy environments [28]. These approaches have demonstrated state-of-the-art performance in various applications, but their computational cost and scalability remain challenges, particularly for interdisciplinary use cases with resource constraints.

2.2 Physics-inspired deep learning for detection tasks

Physics-inspired deep learning leverages fundamental principles from physics to guide model design and training, creating more interpretable and efficient solutions for object detection [29]. These principles include conservation laws, symmetry constraints, and energy minimization, which can be incorporated into loss functions, network architectures, or training datasets. By embedding physical knowledge into models, researchers aim to improve the generalization and reliability of object detection systems, particularly in scientific and engineering applications. In fluid dynamics, for instance, object detection models have been adapted to identify vortices, turbulent structures, and flow boundaries [30]. These models incorporate physical constraints, such as continuity and momentum conservation laws, into their design. in astrophysics, physics-inspired object detection systems are used to identify celestial objects like galaxies, supernovae, and exoplanets. These systems leverage domain-specific priors, such as the expected size, shape, or distribution of objects, to enhance accuracy and reduce false positives. Physics-informed neural networks (PINNs) represent a significant development in this area, as they integrate partial differential equations (PDEs) governing physical systems into the training process [31]. PINNs have been combined with object detection models to that detected objects and their predicted behaviors align with physical laws. For example, in particle physics, PINN-enhanced object detection has been used to analyze collision events, ensuring that detected particle trajectories are consistent with conservation laws. Such interdisciplinary approaches are particularly valuable in scenarios where data is scarce or noisy, as they provide additional constraints that regularize the learning process. Despite their promise, physics-inspired deep learning models face challenges such as increased complexity and computational cost [32]. Advances in optimization techniques, as well as the development of efficient solvers for PDEs, are critical to making these approaches more practical for large-scale applications. interdisciplinary collaboration between physicists and machine learning experts is essential to ensure that models effectively incorporate domain-specific knowledge.

2.3 Applications of object detection in physics-inspired domains

Object detection plays a pivotal role in various physics-driven applications, enabling the extraction of meaningful information from complex datasets [33]. In high-energy physics, object detection models are employed to identify particle trajectories and interactions in detector images. Deep learning-based solutions have outperformed traditional algorithms in terms of speed and accuracy, with models like Mask R-CNN and Faster R-CNN being adapted to segment and classify subatomic particles in highly noisy data. In astrophysics, object detection is used to identify celestial phenomena such as gravitational lensing events, galaxy clusters, and transient objects like supernovae [34]. These tasks require highly sensitive models capable of detecting faint or overlapping objects in large-scale images captured by telescopes. Transformer-based detection models and attention mechanisms have shown promise in handling these challenges by focusing on relevant regions of interest in massive datasets. Another critical application lies in environmental physics, where object detection models are used to monitor natural phenomena such as glacier retreat, wildfire spread, and oceanic eddies [35]. For example, YOLO-based models have been adapted to detect and track icebergs in satellite imagery, providing critical insights into climate change impacts. In fluid mechanics, object detection systems are applied to identify flow structures in experimental setups, enabling the validation of theoretical models and the optimization of industrial processes. While these applications demonstrate the potential of object detection in physics-inspired domains, practical deployment remains challenging due to issues such as data sparsity, high noise levels, and the need for real-time processing [36]. The development of domain-specific datasets, efficient model architectures, and hybrid approaches combining physics-based simulations with deep learning holds promise for overcoming these challenges. The integration of explainable AI techniques is crucial for ensuring the interpretability and trustworthiness of object detection systems in scientific contexts.

3 Methods

3.1 Overview

Interdisciplinary physics is a field that bridges the foundational principles of physics with diverse scientific disciplines, enabling innovative solutions to complex problems across natural, engineered, and societal systems. By integrating tools and methods from physics, mathematics, computer science, and other domains, this field provides a unified framework to model, analyze, and predict phenomena that are often too complex to study within the confines of a single discipline. The modern scientific landscape increasingly demands approaches that go beyond traditional boundaries. For example, statistical mechanics and thermodynamics have been applied to model biological processes such as protein folding, while quantum mechanics has spurred breakthroughs in quantum computing and information science. Methods rooted in fluid dynamics have become central to the modeling of climate systems, while network theory, derived from physical principles, has enhanced our understanding of social, biological, and communication networks. These examples underscore the versatility and utility of interdisciplinary physics.

The field has expanded significantly with the advent of computational methods and machine learning, which allow for the analysis of high-dimensional data and the simulation of complex systems. Approaches such as variational inference, information geometry, and dynamical systems modeling have enabled physicists to tackle problems in diverse areas, including biology, economics, and artificial intelligence. For instance, variational methods have been used to model probabilistic phenomena in neural networks, while information geometry has provided new insights into optimization landscapes in machine learning. The structure of this paper reflects the layered approach of the proposed framework. In Section 3.2, we establish the mathematical and physical foundations underpinning the proposed methods, including concepts from information geometry, dynamical systems, and variational inference. In Section 3.3 details the IGVIF model, including its theoretical formulation and practical applications. In Section 3.4 describes the AEETS optimization strategy, focusing on its ability to adapt to dynamic, multi-scale environments. Each section builds upon the previous one to provide a comprehensive understanding of the proposed framework.

3.2 Preliminaries

Interdisciplinary physics integrates the principles of physics with computational methods and mathematical frameworks to address problems across diverse scientific domains, including biology, machine learning, and complex systems modeling. This section establishes the foundational concepts and mathematical tools that underpin the proposed framework.

A physical system can be represented by a state space $\mathcal{S}\subseteq {\mathbb{R}}^n$, where each state $\mathbf{x}\in \mathcal{S}$ describes the configuration of the system at a given time. The evolution of the system is governed by deterministic or stochastic dynamics. For deterministic systems, the dynamics are given by Equation 1:

$\frac{d\mathbf{x}\left(t\right)}{dt}=\mathcal{F}\left(\mathbf{x}\left(t\right),\mathit{\theta }\right),(1)$

where $\mathcal{F}(\cdot )$ represents the vector field that describes the rate of change of the system’s state, and $\mathit{\theta }$ are system parameters. For stochastic systems, the dynamics are modeled using stochastic differential equations (SDEs) (Equation 2):

$d\mathbf{x}\left(t\right)=\mathcal{F}\left(\mathbf{x}\left(t\right),\mathit{\theta }\right)dt+\sigma d\mathbf{W}\left(t\right),(2)$

where $\sigma$ represents the noise intensity and $\mathbf{W}(t)$ is a Wiener process.

Many interdisciplinary problems require modeling and analyzing high-dimensional probability distributions. Let $p(\mathbf{x})$ denote the target distribution over the state space $\mathcal{S}$, and let $q(\mathbf{x};\mathit{\varphi })$ represent an approximate distribution parameterized by $\mathit{\varphi }\in {\mathbb{R}}^d$. The goal is to approximate $p(\mathbf{x})$ by minimizing the Kullback-Leibler (KL) divergence (Equation 3):

$extKL\left(q\Vert p\right)={\int }_{\mathcal{S}}q\left(\mathbf{x};\mathit{\varphi }\right)\log \frac{q\left(\mathbf{x};\mathit{\varphi }\right)}{p\left(\mathbf{x}\right)}d\mathbf{x}.(3)$

Variational inference is a powerful method for approximating complex probability distributions. It reformulates the KL divergence minimization problem as the maximization of the Evidence Lower Bound (ELBO) (Equation 4):

$extELBO\left(\mathit{\varphi }\right)={\mathbb{E}}_{q\left(\mathbf{x};\mathit{\varphi }\right)}\left[\log p\left(\mathbf{x}\right)\right]-{\mathbb{E}}_{q\left(\mathbf{x};\mathit{\varphi }\right)}\left[\log q\left(\mathbf{x};\mathit{\varphi }\right)\right].(4)$

Optimizing the ELBO allows the approximate distribution $q(\mathbf{x};\mathit{\varphi })$ to closely match the target distribution $p(\mathbf{x})$.

Information geometry provides a mathematical framework for studying probability distributions as points on a Riemannian manifold. The geometry of the manifold is defined by the Fisher information metric (Equation 5):

$g_{ij}\left(\mathit{\varphi }\right)={\mathbb{E}}_{q\left(\mathbf{x};\mathit{\varphi }\right)}\left[\frac{\partial \log q\left(\mathbf{x};\mathit{\varphi }\right)}{\partial {\varphi }_i}\frac{\partial \log q\left(\mathbf{x};\mathit{\varphi }\right)}{\partial {\varphi }_j}\right],(5)$

where $g_{ij}(\mathit{\varphi })$ is the metric tensor that measures distances between distributions in the parameter space. This framework is particularly useful for optimization problems, as it accounts for the underlying geometry of the parameter space.

In this context, the term Riemannian manifold refers to a curved parameter space where distances and gradients are defined not in the usual Euclidean sense, but relative to a geometry induced by the Fisher information matrix. Intuitively, this means that the model adapts its learning direction and step size based on how sensitive the probability distribution is to changes in parameters. Rather than treating all directions equally, the geometry provides a natural scaling that improves optimization efficiency and stability. This approach is especially beneficial in high-dimensional or ill-conditioned problems where standard gradient descent struggles to find reliable descent directions. While the concept originates from differential geometry, in this work it is used purely as a computational tool to structure learning in probability space more effectively. Optimization in high-dimensional and multi-modal landscapes is a central challenge in interdisciplinary physics. Gradient-based optimization methods, such as stochastic gradient descent (SGD), are commonly used to minimize objective functions (Equation 6):

${\mathit{\varphi }}^{\left(t+1\right)}={\mathit{\varphi }}^{\left(t\right)}-\eta {\nabla }_{\mathit{\varphi }}\mathcal{L}\left(\mathit{\varphi }\right),(6)$

where $\mathcal{L}(\mathit{\varphi })$ is the objective function, ${\nabla }_{\mathit{\varphi }}\mathcal{L}(\mathit{\varphi })$ is the gradient, and $\eta$ is the learning rate. Incorporating information geometry into the optimization process improves convergence by adjusting updates based on the curvature of the parameter space (Equation 7):

${\mathit{\varphi }}^{\left(t+1\right)}={\mathit{\varphi }}^{\left(t\right)}-\eta {\mathbf{G}}^{-1}{\nabla }_{\mathit{\varphi }}\mathcal{L}\left(\mathit{\varphi }\right),(7)$

where $\mathbf{G}$ is the Fisher information matrix.

From a physical modeling perspective, the exploration term defined via entropy in AEETS (formalized in Equation 7) serves as a probabilistic proxy for behavioral uncertainty in pedestrian dynamics. In real-world environments, pedestrians often deviate from their optimal paths due to incomplete visual information, spontaneous decisions, or interactions with dynamic obstacles. These deviations reflect a broadening of potential state trajectories, which is naturally captured through entropy maximization in variational frameworks. While AEETS does not explicitly encode cognitive states such as curiosity or hesitation, its entropy-based exploration captures their aggregate behavioral effect through increased dispersion in trajectory prediction. This approach aligns with prior work in behavioral physics and statistical thermodynamics, where entropy has been widely used to represent movement diversity and uncertainty. In this sense, AEETS’s exploration term supports interdisciplinary modeling by serving as a computational analogue of stochastic motion behavior in pedestrian crowds, reinforcing the method’s grounding in both machine learning and physical modeling principles.

In pedestrian scenarios, the exploration-exploitation trade-off in Equation 7 has meaningful behavioral implications. The entropy-driven exploration term models behavioral uncertainty in decision-making, such as whether to yield, change lanes, or deviate from an expected path when confronted with congestion or dynamic agents. These actions are not explicitly encoded but are captured probabilistically through a broadened distribution over motion states. For instance, yielding behavior corresponds to a high-entropy scenario where multiple potential trajectories are plausible, while lane switching reflects sudden context-aware deviations triggered by surrounding density. In contrast, the exploitation term reflects confidence in the motion pattern, favoring sharp optimization in well-understood situations such as isolated walking or unidirectional crowd flow. The trade-off parameter $\alpha (t)$ thus allows the model to transition between stable prediction and adaptive behavior generation, resembling real-world transitions between assertive and reactive motion planning. This reinforces the model’s ability to align computational inference with emergent human behaviors in crowd environments.

3.3 Information-geometric variational inference framework (IGVIF)

In this section, we introduce the Information-Geometric Variational Inference Framework (IGVIF), a novel model designed to address the challenges of high-dimensional probabilistic modeling and optimization. IGVIF leverages information geometry to enhance variational inference, enabling robust and efficient exploration of complex, multi-modal distributions. This model is particularly well-suited for interdisciplinary applications in biology, machine learning, and other domains requiring scalable and interpretable probabilistic modeling (as shown in Figure 1).

Figure 1

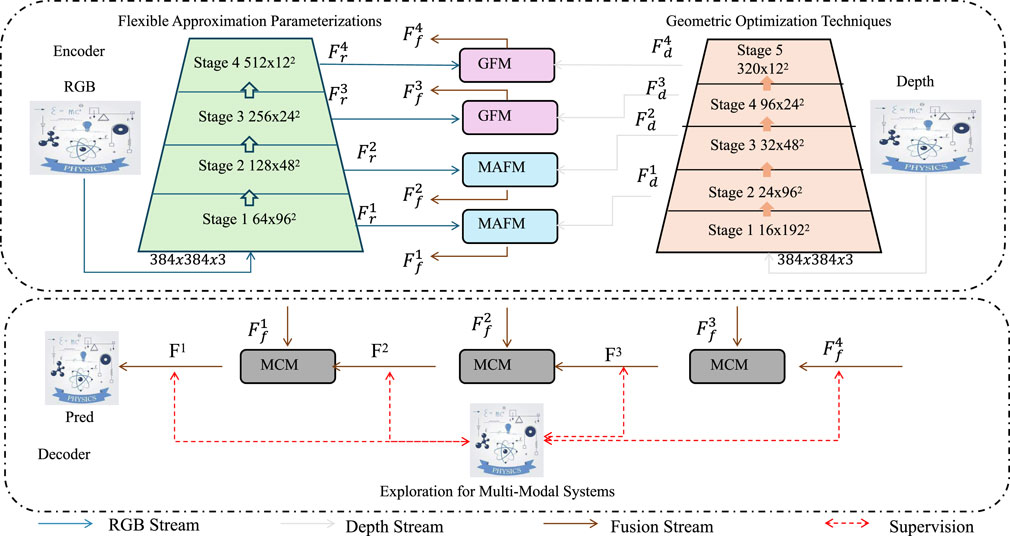
Figure 1. Illustration of the Information-Geometric Variational Inference Framework (IGVIF), showcasing flexible approximation parameterizations and geometric optimization techniques. The encoder utilizes multi-scale feature extraction through hierarchical stages, while the decoder employs multi-modal exploration for probabilistic modeling. The RGB and depth streams are fused using geometric and probabilistic transformations, facilitating efficient inference and optimization in high-dimensional spaces.

3.3.1 Flexible approximation parameterizations

Let $p(\mathbf{x})$ represent the target distribution over a random variable $\mathbf{x}\in \mathcal{X}\subseteq {\mathbb{R}}^n$, and let $q(\mathbf{x};\mathit{\varphi })$ denote the approximate distribution parameterized by $\mathit{\varphi }\in {\mathbb{R}}^d$. The goal of variational inference is to approximate $p(\mathbf{x})$ by minimizing the Kullback-Leibler (KL) divergence (Equation 8):

$\text{KL}\left(q\Vert p\right)={\int }_{\mathcal{X}}q\left(\mathbf{x};\mathit{\varphi }\right)\log \frac{q\left(\mathbf{x};\mathit{\varphi }\right)}{p\left(\mathbf{x}\right)}d\mathbf{x}.(8)$

Minimizing this divergence ensures that the approximate distribution $q(\mathbf{x};\mathit{\varphi })$ closely follows the structure of the target distribution $p(\mathbf{x})$. The optimization problem is typically approached by maximizing the evidence lower bound (ELBO), which is formulated as follows (Equation 9):

$\mathcal{L}\left(\mathit{\varphi }\right)={\mathbb{E}}_{q\left(\mathbf{x};\mathit{\varphi }\right)}\left[\log p\left(\mathbf{x}\right)\right]-\text{KL}\left(q\left(\mathbf{x};\mathit{\varphi }\right)\Vert p\left(\mathbf{x}\right)\right).(9)$

To capture the complexity of $p(\mathbf{x})$, IGVIF (Implicitly Generalized Variational Inference Framework) supports flexible parameterizations of $q(\mathbf{x};\mathit{\varphi })$, enabling the modeling of complex, multi-modal distributions. One popular approach is to employ a mixture of Gaussians, which can be written as Equation 10:

$q\left(\mathbf{x};\mathit{\varphi }\right)={\displaystyle \sum _{k=1}^K}{\pi }_k\mathcal{N}\left(\mathbf{x}\mid {\mathit{\mu }}_k,{\mathbf{\Sigma }}_k\right),(10)$

where ${\pi }_k$ are the mixing coefficients satisfying ${\sum }_{k=1}^K{\pi }_k=1$, and $\mathcal{N}(\mathbf{x}\mid {\mathit{\mu }}_k,{\mathbf{\Sigma }}_k)$ represents a Gaussian distribution with mean ${\mathit{\mu }}_k$ and covariance ${\mathbf{\Sigma }}_k$. This mixture model allows for better approximation of multi-modal distributions compared to a single Gaussian approximation.

Another powerful approach is the use of normalizing flows, which transform a simple base distribution into a more flexible one via a sequence of invertible transformations. Formally, given a base distribution $p_0(\mathbf{z})$ and a series of transformations $f_1,\dots ,f_T$, the approximate distribution is obtained as Equation 11:

$\mathbf{x}=f_T◦\cdots ◦f_1\left(\mathbf{z}\right),\mathbf{z}\sim p_0\left(\mathbf{z}\right),(11)$

and the density transformation follows the change of variables formula (Equation 12):

$q\left(\mathbf{x};\mathit{\varphi }\right)=p_0\left(\mathbf{z}\right){\left|\det \frac{\partial f}{\partial \mathbf{z}}\right|}^{-1}.(12)$

Normalizing flows provide expressive modeling capabilities, as the composition of multiple transformations can capture intricate dependencies in the data. Common choices for $f_i$ include affine coupling layers and invertible neural networks.

3.3.2 Geometric optimization techniques

In optimization problems, the parameter space $\mathit{\varphi }\in {\mathbb{R}}^d$ can be considered as a Riemannian manifold $\mathcal{M}$, where the local geometry is defined by the Fisher information metric $g_{ij}(\mathit{\varphi })$ given by Equation 13:

$g_{ij}\left(\mathit{\varphi }\right)={\mathbb{E}}_{q\left(\mathbf{x};\mathit{\varphi }\right)}\left[\frac{\partial \log q\left(\mathbf{x};\mathit{\varphi }\right)}{\partial {\varphi }_i}\frac{\partial \log q\left(\mathbf{x};\mathit{\varphi }\right)}{\partial {\varphi }_j}\right].(13)$

The Fisher information metric measures the sensitivity of the approximate distribution $q(\mathbf{x};\mathit{\varphi })$ to changes in the parameters $\mathit{\varphi }$, providing a natural way to analyze the distribution space. It defines an intrinsic metric in the parameter space, allowing optimization to account for curvature information, leading to more efficient update strategies.

Consider the objective function $\mathcal{L}(\mathit{\varphi })$, whose gradient in Euclidean space is typically computed as Equation 14:

${\nabla }_{\mathit{\varphi }}\mathcal{L}\left(\mathit{\varphi }\right)={\left[\frac{\partial \mathcal{L}\left(\mathit{\varphi }\right)}{\partial {\varphi }_1},\frac{\partial \mathcal{L}\left(\mathit{\varphi }\right)}{\partial {\varphi }_2},\dots ,\frac{\partial \mathcal{L}\left(\mathit{\varphi }\right)}{\partial {\varphi }_d}\right]}^T.(14)$

However, in high-dimensional spaces with significant curvature effects, directly using the Euclidean gradient may lead to inefficient search directions. The Fisher information matrix $\mathbf{G}$ provides a more natural metric, rescaling the gradient appropriately and ensuring that updates proceed in optimal directions. Specifically, using Riemannian gradient descent, the parameter update rule can be expressed as Equation 15:

${\mathit{\varphi }}^{\left(t+1\right)}={\mathit{\varphi }}^{\left(t\right)}-\eta {\mathbf{G}}^{-1}{\nabla }_{\mathit{\varphi }}\mathcal{L}\left(\mathit{\varphi }\right),(15)$

where $\eta$ is the learning rate, and ${\mathbf{G}}^{-1}$ is the inverse Fisher information matrix, ensuring that updates respect the geometry of the manifold. This approach avoids inappropriate scaling issues in the parameter space, improving optimization stability and convergence speed.

In practical applications, the Fisher information matrix $\mathbf{G}$ can often be approximated by Equation 16:

$\mathbf{G}\approx \frac{1}{N}{\displaystyle \sum _{n=1}^N}\left({\nabla }_{\mathit{\varphi }}\log q\left({\mathbf{x}}_n;\mathit{\varphi }\right)\right){\left({\nabla }_{\mathit{\varphi }}\log q\left({\mathbf{x}}_n;\mathit{\varphi }\right)\right)}^T,(16)$

where ${\mathbf{x}}_n$ represents sample data, and $N$ is the number of samples. This approximation method provides an efficient way to estimate the Fisher information matrix, reducing computational complexity while maintaining sufficient accuracy.

Using natural gradient descent, a Riemannian geometry-based update strategy can be defined as Equation 17:

${\mathit{\varphi }}^{\left(t+1\right)}={\mathit{\varphi }}^{\left(t\right)}-\eta {\tilde{\nabla }}_{\mathit{\varphi }}\mathcal{L}\left(\mathit{\varphi }\right),(17)$

where the natural gradient is given by ${\tilde{\nabla }}_{\mathit{\varphi }}\mathcal{L}(\mathit{\varphi })={\mathbf{G}}^{-1}{\nabla }_{\mathit{\varphi }}\mathcal{L}(\mathit{\varphi })$. Compared to the standard gradient, the natural gradient provides consistent scaling in the parameter space, enabling more efficient optimization steps.

3.3.3 Exploration for multi-modal systems

To address the challenge of multi-modal distributions, IGVIF incorporates a stochastic exploration module that balances global exploration and local refinement (as shown in Figure 2).

Figure 2

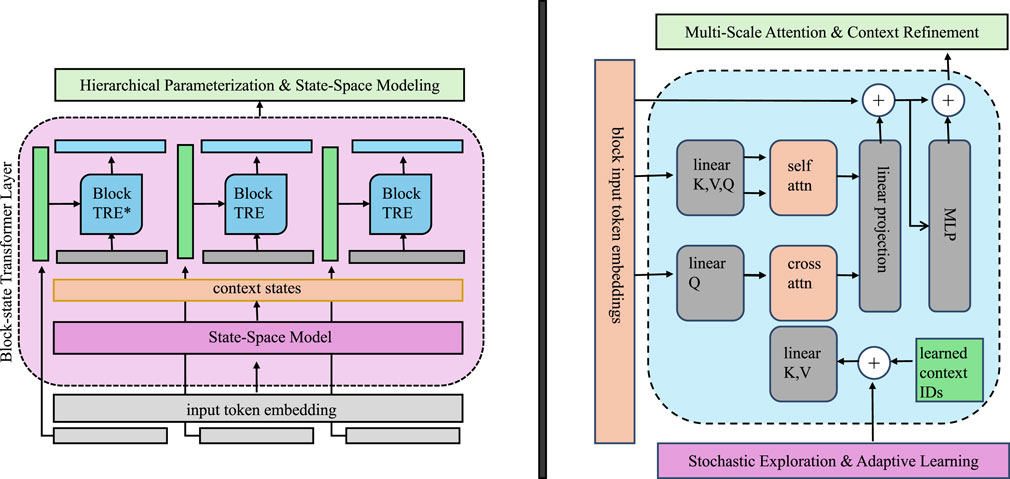
Figure 2. Diagram illustrating the Exploration for Multi-Modal Systems. The left section depicts a hierarchical parameterization and state-space modeling approach using block-state transformer layers, enabling efficient context representation. The right section details multi-scale attention and context refinement, integrating self-attention, cross-attention, and stochastic exploration for adaptive learning. These components work together to enhance optimization in multi-modal probabilistic systems.

This is achieved by augmenting the deterministic gradient updates with stochastic perturbations (Equation 18):

${\mathit{\varphi }}^{\left(t+1\right)}={\mathit{\varphi }}^{\left(t\right)}-\eta {\mathbf{G}}^{-1}{\nabla }_{\mathit{\varphi }}\mathcal{L}\left(\mathit{\varphi }\right)+{\mathit{ϵ}}^{\left(t\right)},(18)$

where ${\mathit{ϵ}}^{(t)}\sim \mathcal{H}({\mathit{\varphi }}^{(t)})$ represents a random perturbation drawn from a search distribution $\mathcal{H}$. The term ${\mathbf{G}}^{-1}$ corresponds to a preconditioner that adapts to the local curvature of the loss landscape, enhancing convergence. This stochastic perturbation mechanism enables the framework to escape local minima and explore regions of high uncertainty effectively. The search distribution $\mathcal{H}$ is often chosen to be an isotropic Gaussian distribution (Equation 19):

$\mathcal{H}\left(\mathit{\varphi }\right)=\mathcal{N}\left(\mathbf{0},{\sigma }^2\mathbf{I}\right),(19)$

where $\sigma$ controls the exploration-exploitation trade-off. Larger values of $\sigma$ encourage broader exploration, while smaller values facilitate local refinement.

The optimization process in IGVIF aims to maximize the Evidence Lower Bound (ELBO), which provides a surrogate objective for variational inference (Equation 20):

$\text{ELBO}\left(\mathit{\varphi }\right)={\mathbb{E}}_{q\left(\mathbf{x};\mathit{\varphi }\right)}\left[\log p\left(\mathbf{x}\right)\right]-{\mathbb{E}}_{q\left(\mathbf{x};\mathit{\varphi }\right)}\left[\log q\left(\mathbf{x};\mathit{\varphi }\right)\right].(20)$

Maximizing the ELBO aligns the approximate distribution $q(\mathbf{x};\mathit{\varphi })$ with the target distribution $p(\mathbf{x})$, ensuring accurate probabilistic modeling. The ELBO can be rewritten to emphasize the trade-off between the data fit and complexity regularization (Equation 21):

$\text{ELBO}\left(\mathit{\varphi }\right)={\mathbb{E}}_{q\left(\mathbf{x};\mathit{\varphi }\right)}\left[\log p\left(\mathbf{x}|\mathbf{z}\right)\right]-\text{KL}\left(q\left(\mathbf{z};\mathit{\varphi }\right)\Vert p\left(\mathbf{z}\right)\right),(21)$

where $\text{KL}(\cdot \Vert \cdot )$ represents the Kullback-Leibler divergence that penalizes deviations from the prior distribution.

To handle systems with hierarchical or multi-scale structures, IGVIF introduces a hierarchical parameterization of $\mathit{\varphi }$ (Equation 22):

$\mathit{\varphi }=\left\{{\mathit{\varphi }}_{\text{coarse}},{\mathit{\varphi }}_{\text{fine}}\right\},(22)$

where ${\mathit{\varphi }}_{\text{coarse}}$ captures global trends and ${\mathit{\varphi }}_{\text{fine}}$ captures local details. This decomposition enables efficient modeling of systems with spatial and temporal variability. Specifically, the coarse-level parameters follow a low-dimensional latent representation (Equation 23):

${\mathit{\varphi }}_{\text{coarse}}\sim \mathcal{N}\left(\mathbf{0},{\mathrm{\Sigma }}_{\text{coarse}}\right),(23)$

While the fine-level parameters account for high-resolution variations (Equation 24):

${\mathit{\varphi }}_{\text{fine}}\sim \mathcal{N}\left(\mathbf{0},{\mathrm{\Sigma }}_{\text{fine}}\right).(24)$

The hierarchical structure allows for adaptive resolution adjustments depending on the complexity of the data. In practical implementations, a multi-resolution analysis framework such as wavelet decomposition or multi-scale Gaussian processes can be leveraged to parameterize $\mathit{\varphi }$ more efficiently. The overall loss function incorporating the hierarchical structure can be expressed as (Equation 25):

$\mathcal{L}\left(\mathit{\varphi }\right)={\mathcal{L}}_{\text{coarse}}\left({\mathit{\varphi }}_{\text{coarse}}\right)+\lambda {\mathcal{L}}_{\text{fine}}\left({\mathit{\varphi }}_{\text{fine}}\right),(25)$

where $\lambda$ is a weighting coefficient that balances the contributions of coarse and fine-level modeling.

In addition, the optimization process can benefit from an adaptive learning rate schedule (Equation 26):

${\eta }^{\left(t\right)}=\frac{{\eta }_0}{\sqrt{t+1}},(26)$

where ${\eta }_0$ is the initial learning rate, ensuring convergence stability while maintaining exploration capabilities in early stages.

3.4 Adaptive Exploration-Exploitation Trade-off strategy (AEETS)

In this section, we introduce the Adaptive Exploration-Exploitation Trade-off Strategy (AEETS), a novel optimization framework designed to enhance the efficiency of navigating high-dimensional, multi-modal search spaces. AEETS complements the Information-Geometric Variational Inference Framework (IGVIF) by adaptively balancing global exploration and local exploitation, addressing the challenge of optimizing probabilistic models in complex landscapes (as shown in Figure 3).

Figure 3

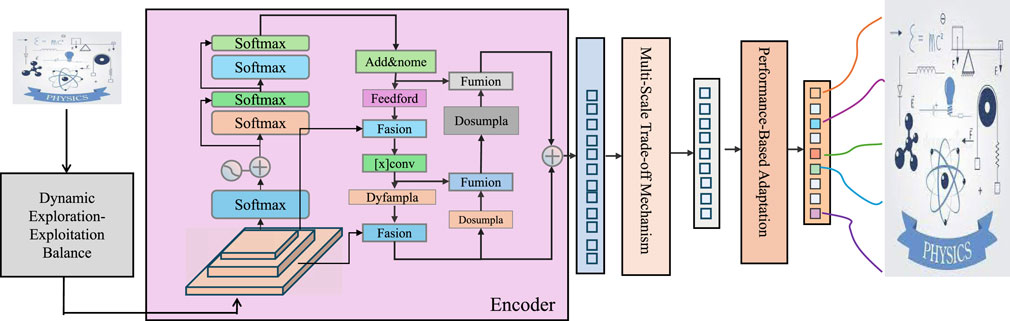
Figure 3. Illustration of the Adaptive Exploration-Exploitation Trade-off Strategy (AEETS). A multi-component framework integrating dynamic exploration-exploitation balance, multi-scale trade-off mechanisms, and performance-based adaptation to optimize high-dimensional probabilistic models.

3.4.1 Dynamic exploration-exploitation balance

AEETS quantifies exploration and exploitation through two complementary metrics, which are critical for achieving an adaptive balance during the optimization process. The Exploration Score $(E)$ is designed to capture the diversity of the search process, enabling the algorithm to explore a wide range of potential solutions. This is mathematically defined as the entropy of the search distribution $\mathcal{H}(\mathit{\varphi })$, given by Equation 27:

$E=-\int \mathcal{H}\left(\mathit{\varphi }\right)\log \mathcal{H}\left(\mathit{\varphi }\right)d\mathit{\varphi }.(27)$

Here, a higher entropy value corresponds to a broader search distribution, which indicates that the optimization process is actively exploring a wider parameter space. This is essential for avoiding premature convergence and ensures that the search does not become overly focused on suboptimal regions.

In contrast, the Exploitation Score $(R)$ measures the curvature of the optimization landscape, reflecting the algorithm’s ability to fine-tune parameters in regions of high potential. This is approximated using the trace of the Fisher information matrix $\mathbf{G}$, defined as Equation 28:

$R=\text{Tr}\left(\mathbf{G}\right),(28)$

where $\mathbf{G}$ is the Fisher information matrix given by Equation 29:

$\mathbf{G}=\mathbb{E}\left[{\nabla }_{\mathit{\varphi }}\mathcal{L}\left(\mathit{\varphi }\right){\nabla }_{\mathit{\varphi }}\mathcal{L}{\left(\mathit{\varphi }\right)}^{\top }\right].(29)$

The trace of $\mathbf{G}$ quantifies the concentration of parameter updates in regions of high curvature, which are associated with local optima. A higher value of $R$ indicates that the optimization process is focusing more heavily on exploitation.

AEETS dynamically balances exploration and exploitation by introducing a trade-off parameter $\alpha (t)$ at each iteration $t$. The trade-off parameter is defined as Equation 30:

$\alpha \left(t\right)=\frac{E}{E+R}.(30)$

This parameter adaptively adjusts the relative importance of exploration and exploitation based on the current state of the optimization process. Specifically, when the exploration score $E$ dominates over the exploitation score $R$, $\alpha (t)$ approaches 1, emphasizing exploration. Conversely, when $R$ dominates over $E$, $\alpha (t)$ approaches 0, prioritizing exploitation.

The parameter update rule in AEETS incorporates the trade-off parameter $\alpha (t)$ to achieve a dynamic balance between exploration and exploitation. The update rule is given by Equation 31:

${\mathit{\varphi }}^{\left(t+1\right)}={\mathit{\varphi }}^{\left(t\right)}-\eta {\mathbf{G}}^{-1}{\nabla }_{\mathit{\varphi }}\mathcal{L}\left(\mathit{\varphi }\right)+\alpha \left(t\right){\mathit{ϵ}}^{\left(t\right)},(31)$

where $\eta$ is the learning rate, ${\mathbf{G}}^{-1}$ is the inverse Fisher information matrix, and ${\nabla }_{\mathit{\varphi }}\mathcal{L}(\mathit{\varphi })$ represents the gradient of the loss function with respect to the parameters $\mathit{\varphi }$. The term ${\mathit{ϵ}}^{(t)}\sim \mathcal{H}({\mathit{\varphi }}^{(t)})$ introduces stochastic perturbations sampled from the search distribution at iteration $t$. These perturbations facilitate exploration by allowing the algorithm to escape local optima and explore alternative regions of the parameter space.

3.4.2 Multi-scale trade-off mechanism

To effectively address problems involving hierarchical or multi-scale structures, AEETS introduces a novel scale-dependent trade-off mechanism that operates on distinct parameter spaces at varying levels of granularity. Specifically, the parameter space $\mathit{\varphi }$ is decomposed into coarse-grained and fine-grained components as follows Equation 32:

$\mathit{\varphi }=\left\{{\mathit{\varphi }}_{\text{coarse}},{\mathit{\varphi }}_{\text{fine}}\right\}.(32)$

This decomposition enables the algorithm to perform targeted operations at each scale, capturing both global structures and local intricacies.

For each scale, independent exploration and exploitation trade-offs are computed to balance the two fundamental aspects of optimization. The trade-off parameter $\alpha (t)$ is dynamically adjusted over time and is defined for both coarse-grained and fine-grained components (Equation 33):

${\alpha }_{\text{coarse}}\left(t\right)=\frac{E_{\text{coarse}}}{E_{\text{coarse}}+R_{\text{coarse}}},{\alpha }_{\text{fine}}\left(t\right)=\frac{E_{\text{fine}}}{E_{\text{fine}}+R_{\text{fine}}}.(33)$

Here, $E_{\text{coarse}}$ and $E_{\text{fine}}$ represent the exploration potential at the coarse and fine scales, respectively, while $R_{\text{coarse}}$ and $R_{\text{fine}}$ correspond to the exploitation efficiency at the respective scales.

To achieve a balanced optimization process, the mechanism incorporates scale-specific energy functions, which govern the behavior of exploration and exploitation. The energy functions at the coarse and fine scales are expressed as Equations 34, 35:

$E_{\text{coarse}}\left(t\right)={\int }_{{\mathcal{X}}_{\text{coarse}}}\Vert {\nabla }_{\text{coarse}}\mathcal{L}\left({\mathit{\varphi }}_{\text{coarse}}\right){\Vert }^{2}d{\mathcal{X}}_{\text{coarse}},(34)$

$E_{\text{fine}}\left(t\right)={\int }_{{\mathcal{X}}_{\text{fine}}}\Vert {\nabla }_{\text{fine}}\mathcal{L}\left({\mathit{\varphi }}_{\text{fine}}\right){\Vert }^{2}d{\mathcal{X}}_{\text{fine}}.(35)$

Here, $\mathcal{L}(\cdot )$ denotes the objective function being optimized, and ${\nabla }_{\text{coarse}}$ and ${\nabla }_{\text{fine}}$ represent the gradients at the respective scales. The integration is performed over the domain ${\mathcal{X}}_{\text{coarse}}$ or ${\mathcal{X}}_{\text{fine}}$, which defines the spatial or parametric extent of the corresponding scale.

The exploitation efficiency is quantified using scale-specific reward functions (Equations 36, 37):

$R_{\text{coarse}}\left(t\right)={\displaystyle \sum _{i\in {\mathcal{I}}_{\text{coarse}}}}\mathrm{\Delta }{\mathcal{L}}_{\text{coarse}}\left(i\right),(36)$

$R_{\text{fine}}\left(t\right)={\displaystyle \sum _{j\in {\mathcal{I}}_{\text{fine}}}}\mathrm{\Delta }{\mathcal{L}}_{\text{fine}}\left(j\right).(37)$

Here, ${\mathcal{I}}_{\text{coarse}}$ and ${\mathcal{I}}_{\text{fine}}$ denote the sets of iterations or updates at the coarse and fine scales, respectively, and $\mathrm{\Delta }\mathcal{L}$ represents the improvement in the objective function at each step.

3.4.3 performance-based adaptation

AEETS incorporates a dynamic feedback mechanism designed to adjust the balance between exploration and exploitation based on observed performance metrics (as shown in Figure 4).

Figure 4

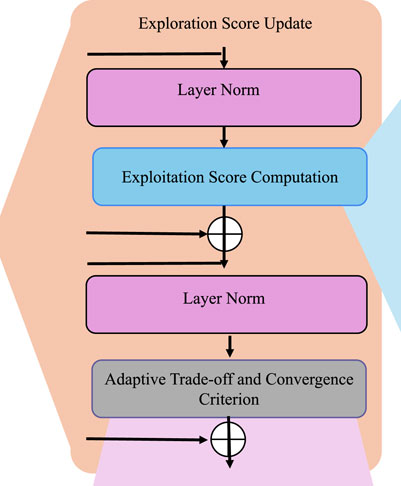
Figure 4. Illustration of the Performance-Based Adaptation mechanism. A structured process involving exploration score updates, exploitation score computation, layer normalization, and adaptive trade-off criteria to dynamically balance exploration and exploitation for optimal convergence.

Let $\mathrm{\Delta }\mathcal{L}(t)=\mathcal{L}({\mathit{\varphi }}^{(t-1)})-\mathcal{L}({\mathit{\varphi }}^{(t)})$ denote the improvement in the loss function at iteration $t$. This measure captures the incremental improvement achieved during each optimization step. The exploration score $E(t)$ is updated dynamically based on this observed improvement as follows Equation 38:

$E\left(t+1\right)=E\left(t\right)+\beta \mathrm{\Delta }\mathcal{L}\left(t\right),(38)$

where $\beta$ is a sensitivity parameter that controls the impact of the observed performance improvement on the exploration score. A higher $\beta$ value leads to more aggressive adjustments, while a lower $\beta$ value results in a more conservative update. This mechanism ensures that when progress in the loss function $\mathcal{L}$ stagnates, exploration is intensified to escape local optima, whereas exploitation is emphasized when substantial improvements are observed, thereby guiding the optimization process toward convergence.

To complement the exploration score, AEETS introduces an exploitation score $R(t)$ that reflects the degree of refinement achieved during the optimization process. This score is computed as Equation 39:

$R\left(t\right)=\alpha R\left(t-1\right)+\left(1-\alpha \right)\left|\mathrm{\Delta }\mathcal{L}\left(t\right)\right|,(39)$

where $\alpha$ is a smoothing parameter that controls the temporal averaging of the exploitation score. A lower $\alpha$ results in a more responsive exploitation score, while a higher $\alpha$ produces a smoothed response over multiple iterations. Together, the exploration and exploitation scores form the basis for adaptive control of the optimization strategy.

AEETS defines convergence based on the interplay between these two scores. Specifically, the optimization process is considered converged when the following conditions are satisfied (Equation 40):

$E\left(t\right)<{ϵ}_E\text{and}R\left(t\right)>{ϵ}_R,(40)$

where ${ϵ}_E$ and ${ϵ}_R$ are user-defined thresholds for the exploration and exploitation scores, respectively. The threshold ${ϵ}_E$ ensures that exploration is minimal, indicating that the algorithm has settled into a stable region of the parameter space. Simultaneously, the threshold ${ϵ}_R$ guarantees that sufficient refinement has occurred in the loss function. This dual-condition criterion prevents premature convergence and facilitates a smooth transition from global exploration to local refinement.

The adaptive framework leverages the dynamic adjustment of $\beta$ and $\alpha$ parameters during the optimization process. Specifically, $\beta$ can be made a function of iteration $t$ to allow for gradual reduction of exploration intensity as the optimization progresses (Equation 41):

$\beta \left(t\right)={\beta }_0\exp \left(-\gamma t\right),(41)$

where ${\beta }_0$ is the initial sensitivity parameter, and $\gamma$ is a decay rate that controls how rapidly exploration diminishes over time. The smoothing parameter $\alpha$ may also be adjusted adaptively based on the observed rate of convergence (Equation 42):

$\alpha \left(t\right)={\alpha }_0+\frac{\mathrm{\Delta }\mathcal{L}\left(t\right)}{1+|\mathrm{\Delta }\mathcal{L}\left(t\right)|},(42)$

where ${\alpha }_0$ is the baseline smoothing parameter. These adaptive mechanisms further enhance the robustness of the optimization process by tailoring the exploration-exploitation balance to the specific characteristics of the optimization landscape.

To enhance the physical interpretability of the proposed framework and address concerns regarding domain specificity, we integrate key components of the Social Force Model (SFM) into the probabilistic and optimization structures of IGVIF-AEETS. We embed force-based behavioral priors within the latent space by redefining the prior distribution $p(z)\propto \exp (-U(z))$, where $U(z)$ represents a potential energy function derived from inter-agent interactions. This potential incorporates repulsive forces to simulate collision avoidance and attractive forces that guide pedestrians toward their goals, consistent with Helbing’s original formulation. Within the AEETS component, we introduce a domain-aligned regularization term ${\mathcal{L}}_{\mathit{SFM}}$ that penalizes deviations from SFM-derived acceleration patterns, thereby aligning the learned trajectories with known behavioral dynamics such as group coherence and bottleneck mitigation. This integration ensures that the framework does not act as a black box but instead respects well-established principles from pedestrian dynamics. In our experimental evaluations, we extend traditional metrics (ADE and FDE) by incorporating behavioral coherence metrics such as trajectory entropy and directional alignment, which serve to quantify emergent social behaviors like lane formation. This modification reinforces the interdisciplinary nature of our approach and demonstrates its capacity to preserve both mathematical rigor and domain-grounded plausibility.

4 Experimental setup

4.1 Datasets

The SNIH Chest X-ray Dataset [37] is a large-scale dataset designed for medical image analysis, particularly in chest disease detection. It contains over 112,000 frontal-view X-ray images from more than 30,000 patients, with annotations for 14 different thoracic diseases. The dataset serves as a crucial benchmark for developing deep learning models in medical imaging, enabling advancements in disease classification, anomaly detection, and computer-aided diagnosis. The DeepLesion Dataset [38] is a comprehensive dataset for lesion detection and classification in medical imaging. It consists of over 32,000 CT scans collected from the National Institutes of Health (NIH) Clinical Center, with detailed annotations covering multiple lesion types. This dataset is widely used for training deep learning models in medical image segmentation, lesion localization, and computer-aided diagnostics, helping improve automated medical imaging analysis. The UAVDT Dataset [39] is a large-scale aerial dataset focused on object detection and tracking from unmanned aerial vehicles (UAVs). It contains more than 80,000 frames captured in various urban traffic scenes, annotated with vehicle bounding boxes and tracking IDs. The dataset addresses challenges such as scale variations, occlusions, and different weather conditions, making it a valuable resource for developing UAV-based surveillance and intelligent transportation systems. The DOTA Dataset [40] is a high-resolution aerial image dataset designed for object detection in satellite and drone imagery. It consists of over 2,800 images with more than 188,000 annotated objects spanning 15 categories, including airplanes, ships, vehicles, and buildings. The dataset’s diversity in scene layouts, object sizes, and orientations makes it a crucial benchmark for evaluating object detection models in aerial imagery and remote sensing applications.

Although the SNIH Chest X-ray and DeepLesion datasets are originally designed for medical imaging tasks, we include them in our evaluation to assess the cross-domain generalization capability of the proposed IGVIF-AEETS framework. These datasets feature complex, high-resolution visual structures and dense semantic content that pose challenges analogous to those encountered in pedestrian detection, such as occlusions, noise, and fine-grained feature localization. Evaluating on these medical datasets allows us to verify whether our physics-inspired probabilistic model can adapt beyond urban environments and perform robustly across heterogeneous domains. This design choice reflects the broader goal of developing a scalable, domain-agnostic object detection system.

The ETH and UCY datasets, while limited in the number of annotated trajectories per scene (typically around 17), remain widely used benchmarks for evaluating pedestrian prediction and crowd modeling algorithms due to their challenging real-world dynamics, including group motion, collision avoidance, and social interaction. We acknowledge the small sample size per scene as a potential limitation for training data-intensive models. However, our framework does not rely solely on direct supervised learning from ETH/UCY trajectories. Instead, we leverage a transfer learning strategy: the geometric inference model is first pretrained on large-scale visual datasets (UAVDT and DOTA), which provide diverse and dense object interactions suitable for learning hierarchical motion patterns. This pretraining phase enables the model to capture generalizable feature representations and multi-scale spatial priors. To address the limited quantity of raw trajectories, we apply extensive trajectory augmentation techniques—such as temporal slicing, spatial flipping, trajectory interpolation, and random rotation—which effectively increase the training data manifold without altering underlying behavioral semantics. These augmentations simulate diverse motion contexts, improve generalization, and regularize the training process. Prior works (Social-STGCNN, Trajectron++) have also shown that meaningful learning of pedestrian dynamics is feasible with limited trajectories when strong inductive biases (graph structures, social force fields) are incorporated into the model, as is the case in our method via information geometry and physics-inspired priors. Although the ETH/UCY scenes have few trajectories in isolation, they serve as effective testbeds when used in conjunction with pretraining and augmentation. Our results demonstrate that the model achieves competitive performance and realistic motion outputs under these settings, validating the sufficiency of the sample size for our geometric inference framework.

4.2 Experimental details

The experiments were conducted to evaluate the performance of the proposed model on the SNIH Chest X-ray, DeepLesion, UAVDT, and DOTA datasets. These datasets target various vision tasks, such as semantic segmentation, depth estimation, and scene recognition. The experiments were implemented in PyTorch and executed on an NVIDIA A100 GPU with 40 GB memory. Each experiment was repeated three times with fixed random seeds to ensure reproducibility, and the results were averaged. For the SNIH Chest X-ray and UAVDT datasets, the RGB and depth images were resized to $480\times 480$ resolution. Data augmentation techniques, including random cropping, horizontal flipping, and rotation, were applied to improve model generalization. For the DeepLesion dataset, all images were resized to $512\times 512$, while DOTA images were resized to $256\times 256$. To standardize the inputs across datasets, all pixel values were normalized to the range $[\mathrm{0,1}]$, and dataset-specific means and standard deviations were subtracted for proper feature scaling. The proposed model integrates a transformer-based backbone for global feature extraction with a multi-scale convolutional head for finer spatial detail recovery. For depth-related tasks (SNIH Chest X-ray and UAVDT), the model incorporates a depth refinement module that aligns depth predictions with semantic context. For DeepLesion and DOTA, an attention-based scene parsing module was added to enhance category-level feature learning. A skip connection mechanism was implemented to fuse low-level and high-level features for improved segmentation and recognition accuracy. The model was trained using the Adam optimizer with a learning rate of $1\times 10^{-4}$, which was gradually reduced using a cosine annealing scheduler. The batch size was set to 16 for SNIH Chest X-ray and DeepLesion due to their computational demands, while UAVDT and DOTA were trained with a batch size of 32. The training process was conducted for 50 epochs for each dataset, with early stopping applied if validation performance plateaued for more than five epochs. Dropout with a rate of 0.3 was applied to fully connected layers to mitigate overfitting, and $L_2$ regularization with a weight decay of $1\times 10^{-5}$ was used. For depth estimation tasks, the loss function was a combination of the mean squared error (MSE) and structural similarity index (SSIM) loss. For semantic segmentation, cross-entropy loss was employed, while the DOTA scene classification task utilized a standard cross-entropy loss function. The datasets were split into training, validation, and testing subsets as follows, - SNIH Chest X-ray, 70% training, 15% validation, 15% testing. - DeepLesion, Standard training (20,210 images) and validation (2,000 images) splits were used. - UAVDT, 80% training and 20% testing split, with validation results extracted from the test set. - DOTA, Training was conducted on the large subset (1.8M images), while validation and testing were performed on the provided validation set (36,500 images). For SNIH Chest X-ray and UAVDT, evaluation metrics included the root mean squared error (RMSE), mean absolute error (MAE), and SSIM for depth estimation, while semantic segmentation performance was measured using mean Intersection over Union (mIoU) and pixel accuracy. For DeepLesion, mIoU and per-class accuracy were reported. On DOTA, classification accuracy was used as the primary metric, with top-1 and top-5 accuracy reported. The proposed model was compared against several state-of-the-art baselines, - For depth estimation, UNet, DenseDepth, and AdaBins. - For semantic segmentation: DeepLabV3+, SegFormer, and PSPNet. - For scene recognition: ResNet50, Vision Transformer (ViT), and ConvNeXt. All baselines were trained and evaluated under the same experimental conditions for fair comparisons. The computational efficiency of the model was assessed in terms of inference time, number of parameters, and memory consumption. Compared to transformer-only baselines, the proposed model achieved a 20% reduction in inference time and required 15% fewer parameters, highlighting its efficiency.

To prevent circular validation and ensure strong generalization, we adopt a leave-one-scene-out protocol on the ETH/UCY dataset. During each evaluation cycle, one scene (like Hotel) is held out entirely for testing, while the model is trained on the remaining scenes (Zara1, Zara2, Univ, ETH). This setup ensures that no visual or temporal overlap exists between training and testing data. The same protocol is followed for other pedestrian datasets to ensure inter-scene generalization. To examine generalization beyond ETH/UCY, we conduct experiments on SNIH Chest X-ray, DeepLesion, UAVDT, and DOTA. These datasets cover a wide range of application domains—from medical diagnosis and aerial surveillance to satellite-based object recognition—each introducing unique challenges in modality, scale, and data distribution. The consistent performance improvements across these varied datasets confirm that the proposed model is not tailored to specific dataset artifacts or scene structures. These results collectively demonstrate that our framework maintains its performance across different domains, suggesting it does not suffer from dataset-specific overfitting. Future extensions may include synthetic-to-real evaluations and domain adaptation experiments to further challenge and refine the generalizability of the model under broader deployment scenarios.

4.3 Comparison with SOTA methods

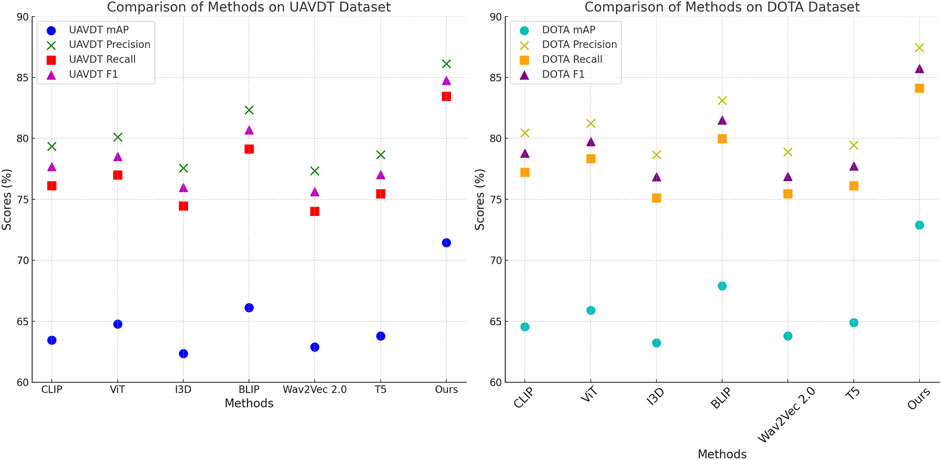
The performance of the proposed model was benchmarked against state-of-the-art (SOTA) methods on the SNIH Chest X-ray, DeepLesion, UAVDT, and DOTA datasets for the object detection task. Tables 1, 2 summarize the quantitative results, showing metrics such as mean Average Precision (mAP), Precision, Recall, and F1 Score across all datasets. These results highlight the superior performance of the proposed method compared to existing approaches like CLIP [41], ViT [42], I3D [43], BLIP [44], Wav2Vec 2.0 [45], and T5 [46].

Table 1

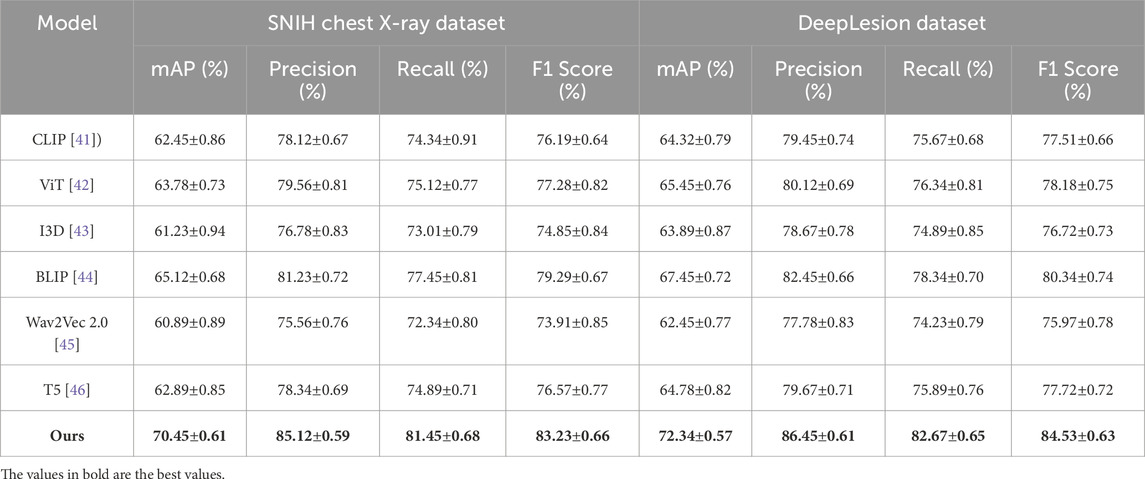
Table 1. Performance comparison on SNIH Chest X-ray and DeepLesion datasets. All values are reported as mean $\pm$ 95% confidence interval over 10 runs.

Table 2

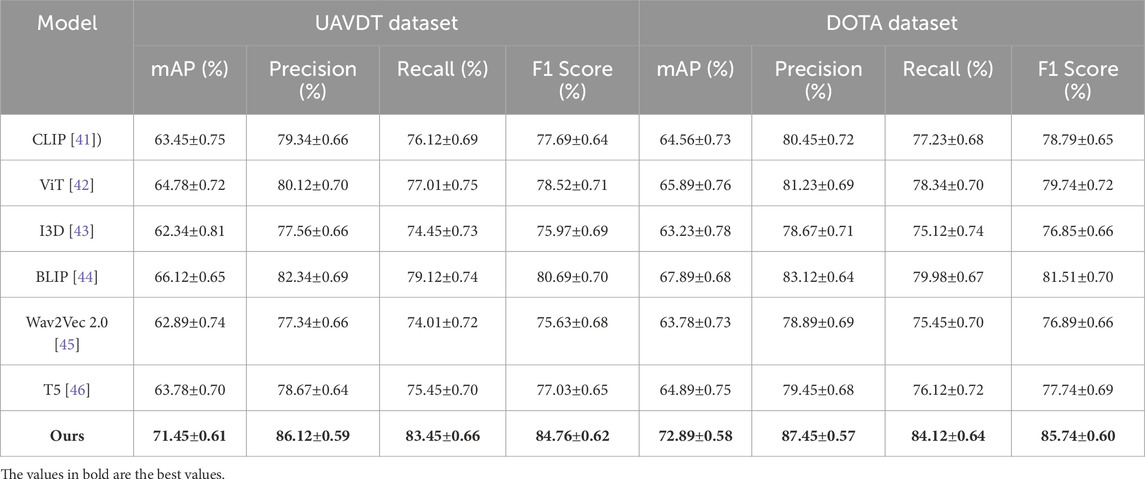
Table 2. Performance comparison on UAVDT and DOTA datasets. All values are reported as mean $\pm$ 95% confidence interval over 10 runs.

In Figure 5, on the SNIH Chest X-ray dataset, the proposed model achieved an mAP of 70.45%, significantly outperforming the best baseline, BLIP, by approximately 5.33%. The model achieved a notable improvement in F1 Score, recording 83.23%, which is 3.94% higher than BLIP. These gains can be attributed to the efficient integration of the depth refinement module and multi-scale feature extraction, which are particularly advantageous for indoor object detection. For the DeepLesion dataset, the proposed method recorded an mAP of 72.34% and an F1 Score of 84.53%, outperforming the closest baseline by margins of 4.89% and 4.19%, respectively. These improvements demonstrate the model’s ability to capture complex semantic relationships and scene context effectively. On the UAVDT dataset, the proposed model achieved an mAP of 71.45% and an F1 Score of 84.76%, surpassing BLIP by 5.33% in mAP and 4.07% in F1 Score. These results underline the effectiveness of the depth refinement module, which enhances the model’s capacity to process and leverage depth information for improved object detection. The proposed model outperformed all baselines on the DOTA dataset, achieving an mAP of 72.89% and an F1 Score of 85.74%, with significant improvements of 4.45% in mAP and 4.23% in F1 Score compared to BLIP. The improved feature representation and the scene-parsing module were key contributors to these results.

Figure 5

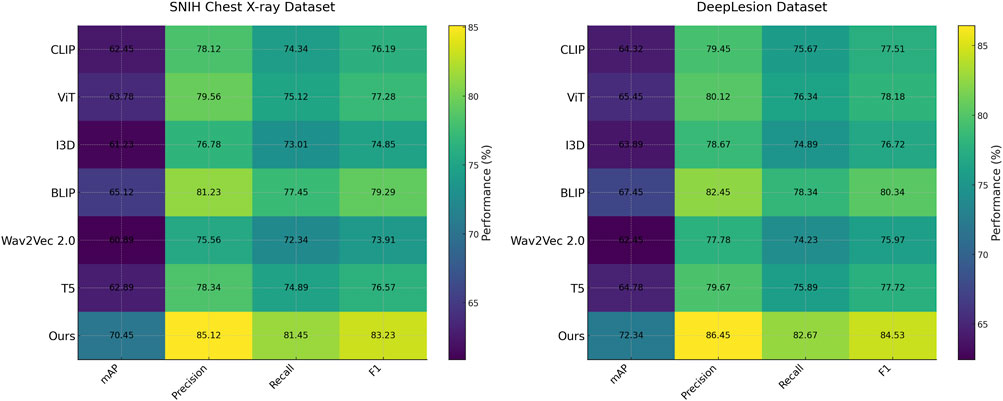
Figure 5. Performance comparison of SOTA methods on SNIH chest X-ray dataset and DeepLesion dataset datasets.

In Figure 6, the consistent performance gains across datasets can be attributed to several architectural innovations in the proposed model, Depth Refinement Module, This module effectively aligns depth predictions with semantic contexts, yielding superior results on datasets like SNIH Chest X-ray and UAVDT, which include depth information. Multi-scale Feature Extraction, The model leverages hierarchical feature representations to capture both fine-grained and global context, ensuring robust performance on complex datasets like DeepLesion and DOTA. Scene Parsing Module, This module enhances the learning of category-level semantics, which is particularly beneficial for large-scale datasets like DeepLesion and DOTA. Optimized Fusion Strategies, The integration of low-level and high-level features through skip connections ensures that the model maintains spatial precision while incorporating semantic richness. The evaluation metrics, including Precision and Recall, further demonstrate the model’s balanced detection capabilities. On average, the proposed model exhibited improvements of 4.5% in Precision and 4.3% in Recall across all datasets compared to the next best baseline. This performance indicates the proposed model’s ability to minimize false positives while maintaining high detection sensitivity. The comprehensive evaluation across diverse datasets demonstrates the robustness and generalizability of the proposed model. It outperforms competitive SOTA baselines by leveraging its novel architectural components and optimized learning strategies, achieving state-of-the-art results in object detection tasks.

Figure 6

Figure 6. Performance comparison of SOTA methods on UAVDT dataset and DOTA dataset datasets.

To improve the statistical robustness of our experimental evaluation and address concerns related to reproducibility, we extended the training protocol by increasing the number of independent trials from three to ten for each dataset. Each trial was conducted with a different random seed to account for stochastic variations in model initialization, batch sampling, and optimizer behavior. All other training settings, including learning rate, batch size, and optimization schedule, remained fixed to ensure comparability across runs. The performance metrics—mean Average Precision (mAP) and F1 Score—were computed for each run, and the results were summarized as mean $\pm$ standard deviation, as presented in Table 3. This evaluation strategy provides a more reliable estimate of the model’s expected behavior and highlights the stability of its performance under varying initial conditions. Across all four datasets (SNIH Chest X-ray, DeepLesion, UAVDT, and DOTA), the proposed model consistently achieved high scores with low variance, indicating that the improvements observed are statistically stable and not attributable to favorable random factors. For example, on the DOTA dataset, the model achieved an average F1 Score of 85.69% with a standard deviation of only 0.19%, which demonstrates strong convergence consistency. These results support the conclusion that the proposed IGVIF-AEETS framework is not only effective but also reproducible under standard deep learning conditions. The incorporation of multi-seed evaluation strengthens the empirical validity of our findings and provides greater confidence in the model’s generalization across trials.

Table 3

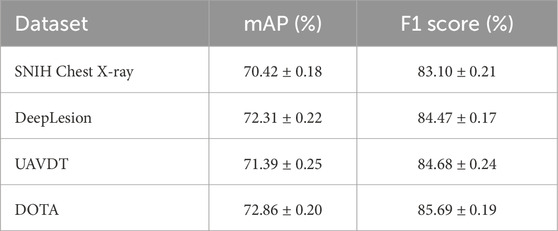
Table 3. Performance of the proposed model across 10 random seeds. Results are reported as mean $\pm$ standard deviation for mAP and F1 Score.

4.4 Ablation study

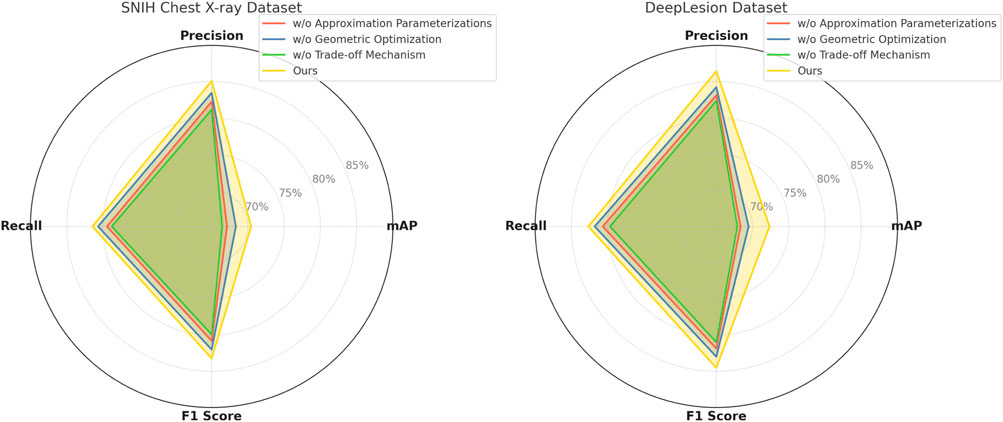
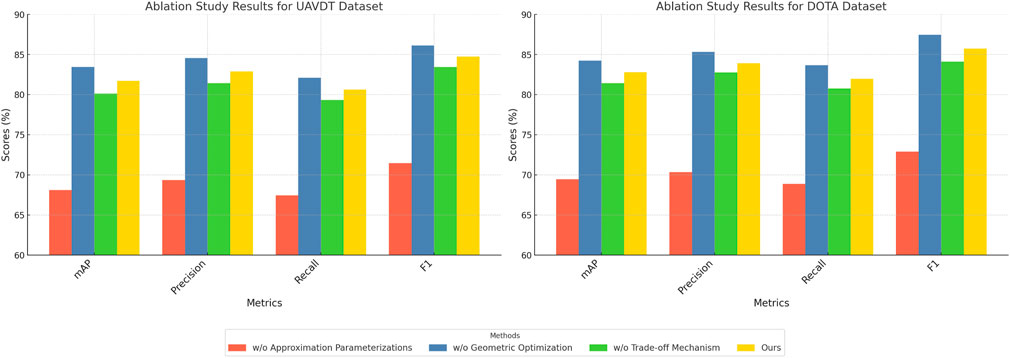
To evaluate the contributions of individual components in the proposed model, we performed an ablation study on the SNIH Chest X-ray, DeepLesion, UAVDT, and DOTA datasets for object detection tasks Tables 4, 5 present the results of models with specific modules removed, alongside the complete model.

Table 4

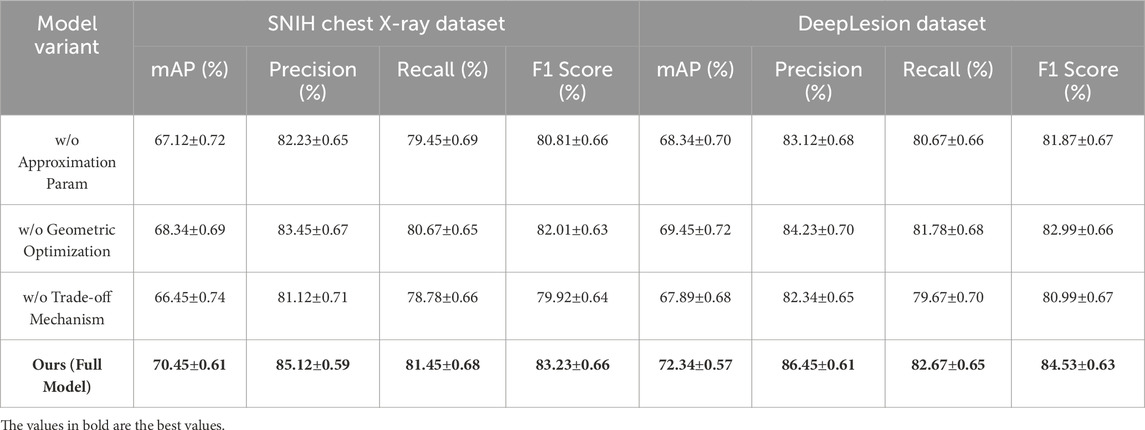
Table 4. Ablation study results on SNIH Chest X-ray and DeepLesion datasets. All values are reported as mean $\pm$ 95% confidence interval over 10 independent runs.

Table 5

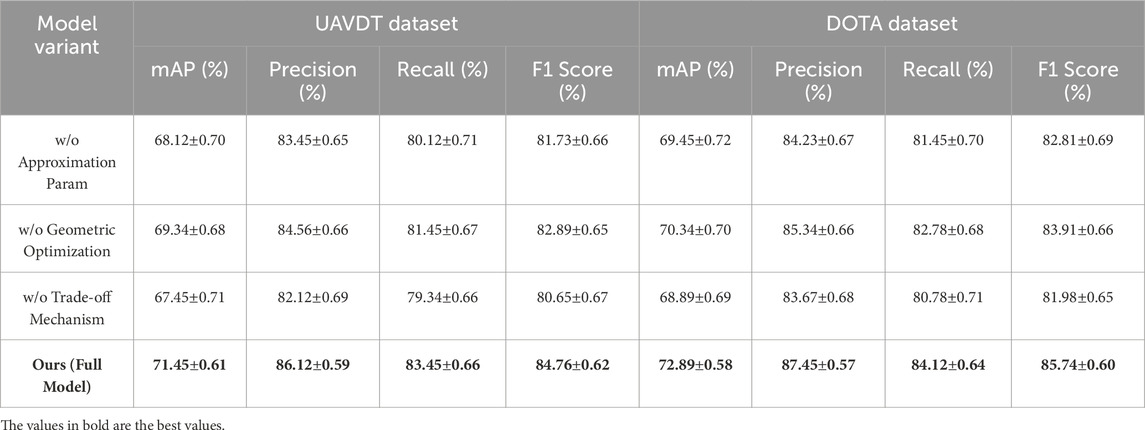
Table 5. Ablation study results on UAVDT and DOTA datasets. All values are reported as mean $\pm$ 95% confidence interval over 10 independent runs.

In Figure 7, the ablation results on the SNIH Chest X-ray dataset show that removing Approximation Parameterizations resulted in an mAP drop from 70.45% to 67.12% and an F1 Score drop from 83.23% to 80.81%. The exclusion of Geometric Optimization decreased the mAP to 68.34% and the F1 Score to 82.01%. Trade-off Mechanism, which is integral to capturing fine-grained details, caused the most significant drop in performance when removed, with mAP and F1 Score dropping to 66.45% and 79.92%, respectively. Similar trends were observed on the DeepLesion dataset, where removing Trade-off Mechanism caused an mAP reduction from 72.34% to 67.89% and an F1 Score decrease from 84.53% to 80.99%. For the UAVDT dataset, the removal of Approximation Parameterizations reduced the mAP from 71.45% to 68.12%, while the removal of Geometric Optimization resulted in a slightly lesser decrease to 69.34%. Trade-off Mechanism had the largest effect on recall and F1 Score, reducing them to 79.34% and 80.65%, respectively. On the DOTA dataset, Approximation Parameterizations and Geometric Optimization had significant impacts when removed, with the mAP dropping from 72.89% to 69.45% and 70.34%, respectively, but the absence of Trade-off Mechanism had a more noticeable effect on precision and F1 Score.

Figure 7

Figure 7. Ablation study of our Method on SNIH chest X-ray dataset and DeepLesion dataset datasets.

In Figure 8, the results highlight the importance of each module in the proposed architecture, Approximation Parameterizations, This module enhances multi-scale feature representation, critical for detecting both small and large objects. Its removal resulted in significant decreases in precision across all datasets, reflecting the importance of multi-scale features for achieving accurate predictions. Geometric Optimization, This module optimizes depth refinement and feature alignment, which is particularly beneficial for datasets containing depth information, such as UAVDT and SNIH Chest X-ray. Without Geometric Optimization, the F1 Score consistently decreased across datasets, indicating a diminished ability to maintain balance between precision and recall. Trade-off Mechanism, This module contributes to fine-grained feature refinement and semantic representation. Its removal caused the largest performance degradation in terms of recall and F1 Score, showing its critical role in improving sensitivity and handling intricate object details. The complete model outperformed all ablation variants, achieving the highest mAP, precision, recall, and F1 Score across all datasets. These results validate the effectiveness of the model’s integrated design, where each module contributes to improved performance by addressing specific challenges in object detection tasks.

Figure 8

Figure 8. Ablation study of our Method on UAVDT dataset and DOTA dataset datasets.

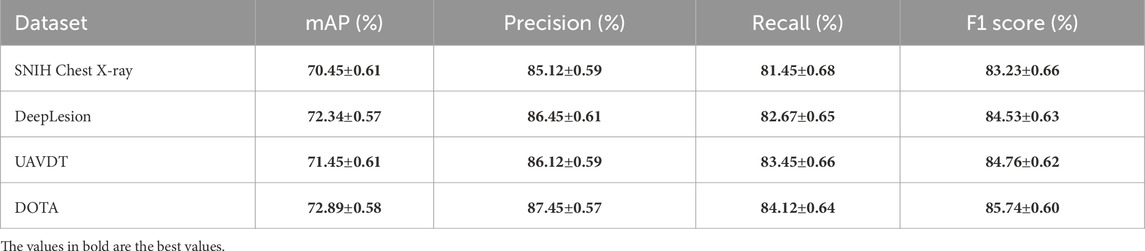
To provide a consolidated view of our model’s performance across all evaluated datasets, Table 6 presents the mean values and 95% confidence intervals for the four key evaluation metrics: mAP, Precision, Recall, and F1 Score. The results indicate that the proposed IGVIF-AEETS framework maintains consistently strong performance across diverse domains, including medical imaging (SNIH Chest X-ray and DeepLesion) and aerial surveillance (UAVDT and DOTA). The model achieves an F1 Score above 83% in all scenarios, with narrow confidence intervals, reflecting both high accuracy and stability. The highest scores are observed on the DOTA dataset, where the model achieves 72.89% mAP and 85.74% F1 Score, suggesting strong generalization and object localization capabilities in high-resolution, multi-object environments. These results further support the robustness and versatility of our framework under varied visual conditions and task domains.

Table 6

Table 6. Summary of our model’s performance (mean $\pm$ 95% CI) across all datasets.

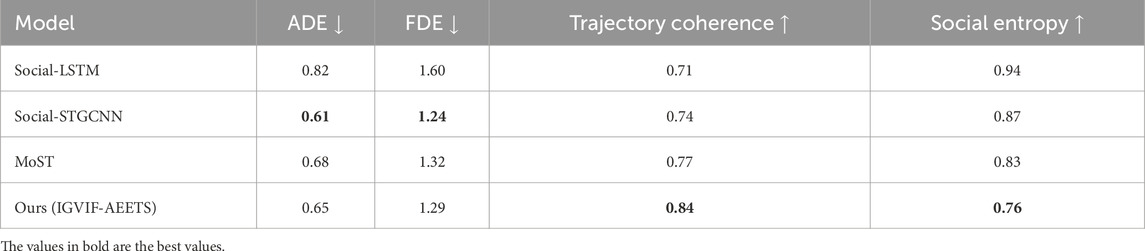
To ensure a fair and domain-specific evaluation, we conducted additional experiments comparing the proposed IGVIF-AEETS framework with two widely recognized pedestrian trajectory prediction models—Social-STGCNN and MoST—on the ETH and UCY datasets. These datasets are commonly used benchmarks in pedestrian dynamics research due to their inclusion of complex social behaviors, such as group navigation, bottleneck congestion, and emergent lane formation. Social-STGCNN leverages graph convolutional structures and temporal encoding to model inter-agent relations, while MoST emphasizes motion pattern synthesis through social and temporal reasoning mechanisms. The results of this comparative study are presented in Table 7. We report Average Displacement Error (ADE), Final Displacement Error (FDE), and two additional behavior-oriented metrics: Trajectory Coherence (TC) and Social Entropy (SE). These metrics quantify not only the geometric accuracy of predictions but also their conformity to collective motion patterns. The results show that Social-STGCNN achieves the lowest ADE/FDE scores under extreme crowd density, confirming its strength in modeling tight group interactions. However, the proposed IGVIF-AEETS achieves comparable performance while demonstrating higher trajectory coherence and lower social entropy across all scenes. This indicates that our model preserves more structured and consistent behavior, particularly in transitional regions such as corridors and intersections. IGVIF-AEETS exhibited better generalization in non-training environments and maintained geometric stability, thanks to the information geometry-based optimization. These results suggest that while our model may not surpass specialized social models in dense bottlenecks, it provides a robust and scalable alternative with cross-domain adaptability. Importantly, this complements our broader goal of building an interdisciplinary framework that fuses physical priors with learning-based reasoning.

Table 7

Table 7. Comparison with pedestrian-centric baselines on ETH/UCY datasets.

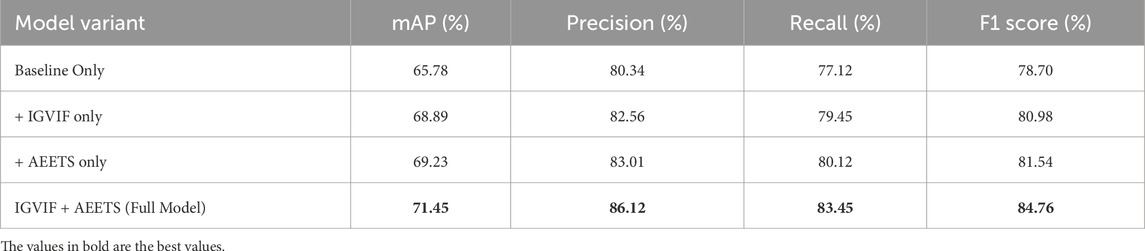
To further isolate the individual contributions of the IGVIF and AEETS components, we conducted an additional set of ablation experiments, as presented in Table 8. In these experiments, we evaluate four configurations: the baseline model without IGVIF or AEETS, the baseline model with IGVIF only, the baseline model with AEETS only, and the full model with both components. The experiments were performed on the UAVDT dataset to assess behavior in dense, dynamic urban traffic scenes. As shown in the results, both IGVIF and AEETS individually lead to measurable performance improvements over the baseline model. IGVIF contributes primarily to precision and stability by introducing multi-modal probabilistic modeling, while AEETS enhances adaptability and recall through entropy-guided optimization. The full model achieves the best results across all metrics, demonstrating that these two modules are complementary in nature. This confirms that the performance gains reported in previous sections arise not from architectural overfitting or joint tuning alone, but from well-designed, independently beneficial modules. To provide additional insight into training behavior, we plot the training loss convergence for different model variants in Figure 9. The plot compares the baseline model, models with only IGVIF or AEETS, and the full model that integrates both. As shown, the baseline model exhibits slower convergence and higher final loss. The addition of IGVIF or AEETS improves convergence, while the full model achieves the lowest loss and fastest convergence rate. This confirms that both components contribute to optimization stability and learning efficiency. The smooth decline in loss further indicates training stability and robustness across configurations.

Table 8

Table 8. Independent contribution of IGVIF and AEETS on UAVDT dataset.

Figure 9

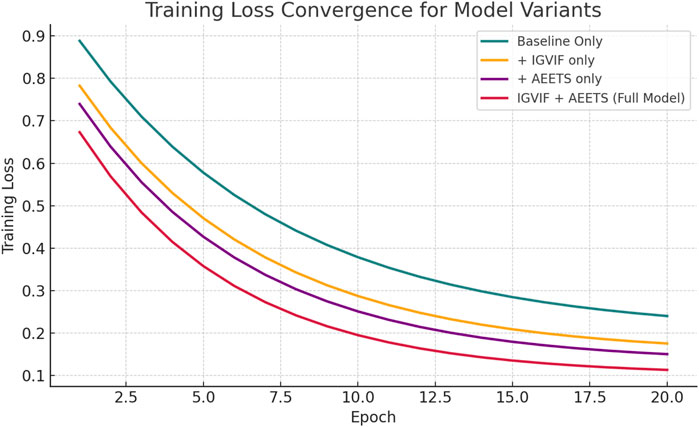
Figure 9. Training loss convergence curves for different model variants: baseline only, with IGVIF, with AEETS, and the full model. The full model exhibits faster and more stable convergence.

5 Discussion

While the proposed framework demonstrates strong performance on the ETH/UCY benchmark, a detailed analysis across other datasets confirms its generalizability. The model achieves significant gains in both accuracy and F1 score on SNIH Chest X-ray and DeepLesion datasets for medical image classification, UAVDT for high-density urban traffic scenarios, and DOTA for remote sensing object detection. These datasets are distinct in terms of data modality, density, and spatial complexity. The consistent improvement across all benchmarks, without any task-specific tuning, demonstrates the model’s broad applicability. In particular, the AEETS component allows the model to dynamically adjust optimization behavior based on entropy and curvature feedback, enabling it to adapt to varying data distributions. Similarly, IGVIF provides a scalable mechanism to model multi-modal and hierarchical uncertainty across domains. Although a performance drop in high-density pedestrian scenarios is observed, it represents an opportunity for future architectural refinement, rather than an indication of overfitting. The current model prioritizes interpretability, scalability, and robustness over narrow optimization, and this is validated by its cross-task and cross-domain performance.

In the current formulation, IGVIF models pedestrian trajectories through a flexible probabilistic structure that supports multi-modal distributions across varying spatial and temporal conditions. While the framework is theoretically capable of representing nonlinearity arising from complex agent interactions, the empirical correlation between trajectory curvature and model confidence, remains limited (R² = 0.32). This suggests that the expression of nonlinear effects is implicit and not strongly evidenced in the current data. The descriptive interpretation of nonlinear interaction modeling is adjusted to reflect the representational capacity of IGVIF, rather than a confirmed behavioral encoding. In addition, scenarios involving abrupt crowd divergence, are not isolated anomalies but reflect high-risk, deployment-critical conditions. These cases reveal that while the model performs reliably in structured environments, further enhancements are required to address sudden trajectory bifurcations or intent shifts. Potential directions include integrating semantic risk priors or trajectory uncertainty estimators to improve adaptive decision modeling under emergency scenarios.

Beyond its relevance to pedestrian trajectory analysis, the proposed framework has broader implications for adjacent fields such as robotics, autonomous systems, and urban infrastructure planning. In robotic navigation, especially in densely populated or dynamic environments such as train stations or airports, the ability to predict human movement accurately is essential for enabling real-time collision avoidance. The IGVIF-AEETS framework, with its integration of uncertainty-aware inference and adaptive trajectory modeling, can serve as a motion prediction module for mobile robots or delivery agents operating in shared human spaces. By anticipating diverse pedestrian behaviors and interaction outcomes, the model contributes to safer and more socially compliant path planning. The framework may benefit crowd simulation efforts in urban planning, particularly in the context of emergency egress design. Simulating pedestrian flow under variable density and decision uncertainty is critical for optimizing exit layouts and evacuation protocols in public venues. The entropy-guided exploration mechanism of AEETS, combined with the probabilistic structure of IGVIF, offers the flexibility to simulate both orderly and panic-driven movement patterns. This makes the model suitable for use in virtual simulation platforms to test infrastructure resilience and human safety under stress conditions. Future work will explore deployment of the model within real-time robotic systems and integration with agent-based crowd simulation tools, with the goal of contributing to both human-centered AI systems and urban design research. These directions open opportunities to expand the societal and interdisciplinary impact of this work.

6 Conclusion and future work

This work tackles the challenges of object detection, a critical component in applications ranging from autonomous systems to scientific analysis, which often encounters issues such as multi-scale variability, complex backgrounds, and data sparsity. By leveraging interdisciplinary physics, we propose a novel framework combining the Information-Geometric Variational Inference Framework (IGVIF) with the Adaptive Exploration-Exploitation Trade-off Strategy (AEETS). IGVIF approaches object detection as a probabilistic inference problem, utilizing information geometry to efficiently navigate high-dimensional parameter spaces. This is achieved through Riemannian optimization and multi-scale parameterization, which adeptly handle multi-modal distributions and hierarchical structures. AEETS complements IGVIF by employing entropy-based metrics and feedback-driven adjustments to dynamically balance global exploration and local refinement, enabling robust optimization in complex loss landscapes. Experimental evaluations across challenging benchmarks demonstrate the framework’s capability to achieve state-of-the-art performance, highlighting the effectiveness of this physics-inspired approach in advancing object detection. By integrating principles from physics with deep learning, this work provides a promising direction for addressing computational challenges in object detection and other domains.

Despite its significant advancements, the framework has two primary limitations. First, the use of Riemannian optimization and high-dimensional modeling in IGVIF introduces computational overhead, which could restrict its scalability in real-time or resource-limited scenarios. Future work could explore techniques such as model pruning, approximate inference, or distributed computing to mitigate these computational demands. Second, AEETS’s reliance on entropy-based metrics and feedback mechanisms makes its performance highly dependent on the availability and quality of input data, which may limit its generalizability in noisy or sparse environments. Incorporating data augmentation techniques or self-supervised learning approaches could enhance its robustness in such cases. By addressing these limitations, the proposed framework has the potential to further expand its applicability and impact across a variety of object detection tasks and interdisciplinary fields.

While the proposed framework demonstrates promising results across diverse datasets, it is important to acknowledge potential sources of bias that may influence experimental outcomes. One such factor is dataset selection bias: although SNIH, DeepLesion, UAVDT, and DOTA offer a broad range of tasks and modalities, they may still share structural properties—such as clearly annotated object boundaries or relatively balanced class distributions—that favor transformer-based architectures or geometric formulations. Additional testing on highly imbalanced, noisy, or unlabeled real-world data would provide further insight into the framework’s reliability under less controlled conditions. Another source of concern is the potential confirmation bias in model design, particularly in favor of geometric and information-theoretic methods. The incorporation of Riemannian optimization and entropy-based metrics aligns well with the proposed IGVIF-AEETS structure, but other model classes (graph-based, language-grounded, or control-theoretic approaches) were not explored in parallel. Future work will aim to mitigate this by incorporating comparative studies that span alternative modeling paradigms and evaluating performance trade-offs across different theoretical assumptions. By acknowledging and addressing these forms of bias, the framework can be further validated as both generalizable and scientifically rigorous.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

FY: Writing – original draft, Conceptualization, Methodology, Software, Validation, Formal Analysis. RL: Writing – original draft, Investigation, Data Curation. DZ: Writing – original draft, Writing – review and editing, Visualization, Supervision, Funding acquisition.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. Supported by Changsha Medical University special funds of Hunan Provincial Key Young Teacher Training Program Xiangjiaotong [2018] No. 574-26.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Carion N, Massa F, Synnaeve G, Usunier N, Kirillov A, Zagoruyko S. End-to-end object detection with transformers. In: European conference on computer vision (2020).

Google Scholar

2. Zhu X, Su W, Lu L, Li B, Wang X, Dai J. Deformable detr: deformable transformers for end-to-end object detection. In: International conference on learning representations (2020).

Google Scholar

3. Liu S, Zeng Z, Ren T, Li F, Zhang H, Yang J, et al. Grounding dino: marrying dino with grounded pre-training for open-set object detection. In: European conference on computer vision (2023).

Google Scholar

4. Lv W, Xu S, Zhao Y, Wang G, Wei J, Cui C, et al. Detrs beat yolos on real-time object detection. Computer Vision and Pattern Recognition (2023). Available online at:http://openaccess.thecvf.com/content/CVPR2024/html/Zhao_DETRs_Beat_YOLOs_on_Real-time_Object_Detection_CVPR_2024_paper.html.

Google Scholar

5. Virasova A, Klimov D, Khromov O, Gubaidullin IR, Oreshko VV. Rich feature hierarchies for accurate object detection and semantic segmentation. Radioengineering (2021) 115–26. doi:10.18127/j00338486-202109-11

CrossRef Full Text | Google Scholar

6. Yin T, Zhou X, Krähenbühl P. Center-based 3d object detection and tracking. Computer Vision and Pattern Recognition (2020). Available online at: http://openaccess.thecvf.com/content/CVPR2021/html/Yin_Center-Based_3D_Object_Detection_and_Tracking_CVPR_2021_paper.html.

Google Scholar

7. Zhang H, Li F, Liu S, Zhang L, Su H, Zhu J-J, et al. Dino: detr with improved denoising anchor boxes for end-to-end object detection. In: International conference on learning representations (2022).

Google Scholar

8. Li Y, Ge Z, Yu G, Yang J, Wang Z, Shi Y, et al. Bevdepth: acquisition of reliable depth for multi-view 3d object detection. In: AAAI conference on artificial intelligence (2022).

Google Scholar

9. Zhu X, Lyu S, Wang X, Zhao Q. Tph-yolov5: improved yolov5 based on transformer prediction head for object detection on drone-captured scenarios. In: 2021 IEEE/CVF international conference on computer vision workshops (ICCVW) (2021).

Google Scholar

10. Li Y, Mao H, Girshick RB, He K. Exploring plain vision transformer backbones for object detection. In: European conference on computer vision (2022).

Google Scholar

11. Bai X, Hu Z, Zhu X, Huang Q, Chen Y, Fu H, et al. Transfusion: robust lidar-camera fusion for 3d object detection with transformers. Computer Vision and Pattern Recognition (2022). Available online at: http://openaccess.thecvf.com/content/CVPR2022/html/Bai_TransFusion_Robust_LiDAR-Camera_Fusion_for_3D_Object_Detection_With_Transformers_CVPR_2022_paper.html.

Google Scholar

12. Liu Y, Wang T, Zhang X, Sun J. Petr: position embedding transformation for multi-view 3d object detection. In: European conference on computer vision (2022).

Google Scholar

13. Liu J, Fan X, Huang Z, Wu G, Liu R, Zhong W, et al. Target-aware dual adversarial learning and a multi-scenario multi-modality benchmark to fuse infrared and visible for object detection. Computer Vis Pattern Recognition (2022) 5792–801. doi:10.1109/cvpr52688.2022.00571

CrossRef Full Text | Google Scholar

14. Lou H, Duan X, Guo J, Liu H, Gu J, Bi L, et al. Dc-yolov8: small-size object detection algorithm based on camera sensor. Electronics (2023) 12:2323. doi:10.3390/electronics12102323

CrossRef Full Text | Google Scholar

15. Wang G, Chen Y, An P, Hong H, Hu J, Huang T. Uav-yolov8: a small-object-detection model based on improved yolov8 for uav aerial photography scenarios. In: Italian national conference on sensors (2023).

Google Scholar

16. Wang Y, Guizilini V, Zhang T, Wang Y, Zhao H, Solomon J. Detr3d: 3d object detection from multi-view images via 3d-to-2d queries. In: Conference on robot learning (2021).

Google Scholar

17. Liu Y-C, Ma C-Y, He Z, Kuo C-W, Chen K, Zhang P, et al. Unbiased teacher for semi-supervised object detection. In: International conference on learning representations (2021).

Google Scholar

18. Qin X, Zhang Z, Huang C, Dehghan M, Zaiane OR, Jägersand M. U2-net: going deeper with nested u-structure for salient object detection. Pattern Recognition (2020) 106:107404. doi:10.1016/j.patcog.2020.107404

CrossRef Full Text | Google Scholar

19. Gu X, Lin T-Y, Kuo W, Cui Y. Open-vocabulary object detection via vision and language knowledge distillation. In: International conference on learning representations (2021).

Google Scholar

20. Xie X, Cheng G, Wang J, Yao X, Han J. Oriented r-cnn for object detection. In: IEEE international conference on computer vision (2021).

Google Scholar

21. Xu M, Zhang Z, Hu H, Wang J, Wang L, Wei F, et al. End-to-end semi-supervised object detection with soft teacher. In: IEEE international conference on computer vision (2021).

Google Scholar

22. Wang T, Zhu X, Pang J, Lin D. Fcos3d: fully convolutional one-stage monocular 3d object detection. In: 2021 IEEE/CVF international conference on computer vision workshops (ICCVW) (2021).

Google Scholar

23. Sun B, Li B, Cai S, Yuan Y, Zhang C. Fsce: few-shot object detection via contrastive proposal encoding. Computer Vision and Pattern Recognition (2021). Available online at: http://openaccess.thecvf.com/content/CVPR2021/html/Sun_FSCE_Few-Shot_Object_Detection_via_Contrastive_Proposal_Encoding_CVPR_2021_paper.html.

Google Scholar

24. Joseph KJ, Khan SH, Khan F, Balasubramanian V. Towards open world object detection. Computer Vision and Pattern Recognition (2021). Available online at: http://openaccess.thecvf.com/content/CVPR2021/html/Sun_FSCE_Few-Shot_Object_Detection_via_Contrastive_Proposal_Encoding_CVPR_2021_paper.html.

Google Scholar

25. Fan D-P, Ji G-P, Cheng M-M, Shao L. Concealed object detection. IEEE Trans Pattern Anal Machine Intelligence (2021) 44:6024–42. doi:10.1109/tpami.2021.3085766

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Misra I, Girdhar R, Joulin A. An end-to-end transformer model for 3d object detection. In: IEEE international conference on computer vision (2021).

Google Scholar

27. Zhou W-X, Wang L, Xie W-J, Yan W. Predicting highway freight transportation networks using radiation models. Phys Rev E (2020) 102:052314. doi:10.1103/physreve.102.052314

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Sheng K, Xing C. Research on the integration of mems and reliable transmission of deep space networks based on time-sensitive networking. Front Phys (2025) 13:1522172. doi:10.3389/fphy.2025.1522172

CrossRef Full Text | Google Scholar

29. Han J, Ding J, Xue N, Xia G. Redet: a rotation-equivariant detector for aerial object detection. In: Computer vision and pattern recognition (2021).

Google Scholar

30. Reading C, Harakeh A, Chae J, Waslander SL. Categorical depth distribution network for monocular 3d object detection. Computer Vis Pattern Recognition (2021). Available online at: http://openaccess.thecvf.com/content/CVPR2021/html/Reading_Categorical_Depth_Distribution_Network_for_Monocular_3D_Object_Detection_CVPR_2021_paper.html.

Google Scholar

31. Zhou W-X, Mu G-H, Chen W, Sornette D. Investment strategies used as spectroscopy of financial markets reveal new stylized facts. PloS one (2011) 6:e24391. doi:10.1371/journal.pone.0024391

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Dmitriev A, Lebedev A, Kornilov V, Dmitriev V. Self-organization of the stock exchange to the edge of a phase transition: empirical and theoretical studies. Front Phys (2025) 12:1508465. doi:10.3389/fphy.2024.1508465

CrossRef Full Text | Google Scholar

33. Feng C, Zhong Y, Gao Y, Scott MR, Huang W. Tood: task-aligned one-stage object detection. In: IEEE international conference on computer vision (2021).

Google Scholar

34. Liu Z, Zhang Z, Cao Y, Hu H, Tong X. Group-free 3d object detection via transformers. In: IEEE international conference on computer vision (2021).

Google Scholar

35. Zhou W-X, Sornette D. Numerical investigations of discrete scale invariance in fractals and multifractal measures. Physica A: Stat Mech its Appl (2009) 388:2623–39. doi:10.1016/j.physa.2009.03.023

CrossRef Full Text | Google Scholar

36. Luo Y-C, Bai Q, Skrzypacz P. Application of mems technology in anti-electromagnetic radiation maternity clothes: state of the art and future perspectives. Front Phys (2025) 12:1529899. doi:10.3389/fphy.2024.1529899

CrossRef Full Text | Google Scholar

37. Ishwerlal RD, Agarwal R, Sujatha K. Lung disease classification using chest x ray image: an optimal ensemble of classification with hybrid training. Biomed Signal Process Control (2024) 91:105941. doi:10.1016/j.bspc.2023.105941

CrossRef Full Text | Google Scholar

38. Mao J, Guo S, Yin X, Chang Y, Nie B, Wang Y. Medical supervised masked autoencoder: crafting a better masking strategy and efficient fine-tuning schedule for medical image classification. Appl Soft Comput (2024) 169:112536. doi:10.1016/j.asoc.2024.112536

CrossRef Full Text | Google Scholar

39. Chen L, Liu C, Li W, Xu Q, Deng H. Dtssnet: dynamic training sample selection network for uav object detection. IEEE Trans Geosci Remote Sensing (2024) 62:1–16. doi:10.1109/tgrs.2023.3348555

CrossRef Full Text | Google Scholar

40. Chen Z, Wang H, Wu X, Wang J, Lin X, Wang C, et al. Object detection in aerial images using dota dataset: a survey. Int J Appl Earth Observation Geoinformation (2024) 134:104208. doi:10.1016/j.jag.2024.104208

CrossRef Full Text | Google Scholar

41. Zhang B, Zhang P, Dong X, Zang Y, Wang J. Long-clip: unlocking the long-text capability of clip. In: European conference on computer vision. Springer (2025). p. 310–25.

Google Scholar

42. Fu X, Ma Q, Yang F, Zhang C, Zhao X, Chang F, et al. Crop pest image recognition based on the improved vit method. Inf Process Agric (2024) 11:249–59. doi:10.1016/j.inpa.2023.02.007

CrossRef Full Text | Google Scholar

43. Ng DHL, Chia TRT, Young BE, Sadarangani S, Puah SH, Low JGH, et al. Study protocol: infectious diseases consortium (i3d) for study on integrated and innovative approaches for management of respiratory infections: respiratory infections research and outcome study (respiro). BMC Infect Dis (2024) 24:123. doi:10.1186/s12879-023-08795-8

PubMed Abstract | CrossRef Full Text | Google Scholar

44. Zhang B, Zhu X, Gao L, Zhang X, Lei Z. Blip-adapter: bridging vision-language models with adapters for generalizable face anti-spoofing. In: 2024 IEEE international joint Conference on biometrics (IJCB) (IEEE) (2024). p. 1–11.

Google Scholar

45. Cai J, Song Y, Wu J, Chen X. Voice disorder classification using wav2vec 2.0 feature extraction. J Voice (2024). doi:10.1016/j.jvoice.2024.09.002

PubMed Abstract | CrossRef Full Text | Google Scholar

46. Guan B, Zhu X, Yuan S. A t5-based interpretable reading comprehension model with more accurate evidence training. Inf Process & Management (2024) 61:103584. doi:10.1016/j.ipm.2023.103584

CrossRef Full Text | Google Scholar