Research on active earth pressure of narrow cohesionless backfill against rigid walls considering the arching effect

Retaining walls are usually located next to existing structures. This runs counter to the traditional theoretical presumption of semi-infinite space, making it unsuitable to continue applying Coulomb’s theory. In order to design retaining walls with narrow backfill, improving the established theory and seeking an economical design theory are necessary. This paper puts forward an analytical approach for estimating the active earth pressure of narrow backfills. The approach, based on the slice-element method, takes into account the arching effect. The results obtained are verified through centrifuge tests, numerical computations, and analytical methods. Additionally, parametric studies are conducted to gain a comprehensive understanding of problems related to earth pressure. These studies consider how sensitive design variables, such as the soil friction angle, the wall–soil interface friction angle, and the aspect ratio, influence the active thrust coefficient and the height of the application point of the active thrust from the base. To enable the practical utilization of this analytical approach, a simplified design table related to the standard Coulomb solutions is provided at the end.

1 Introduction

Retaining walls are mainly used to prevent the fill from slipping or collapsing and ensure the stability and safety of the structure. Earth pressure calculation is an important part of retaining wall design. Traditionally, the active earth pressure acting on rigid retaining walls is computed using Coulomb’s or Rankine’s theory [1, 2]. It is assumed that the active earth pressure along the wall is distributed linearly. However, several studies indicate that the distribution of active earth pressure is non-linear for rough walls [3–5]. This difference between linear and non-linear distributions of earth pressure is mainly due to the wall–soil interface friction angle [6].

The above-mentioned methods are based on the assumptions that the backfill behind the rigid wall extends to a sufficient distance and the sliding plane is fully developed in the backfill. However, retaining walls are constructed adjacent to existing structures or near the rock faces in practical applications, and the backfill behind the wall is of finite width [7]. This conflicts with the assumption of a triangular thrust wedge formed in a soil mass within the semi-infinite space. This may be because the thrust wedge fails to form in the shape and size anticipated by these methods. Therefore, a new analytical approach needs to be presented to more precisely estimate the active earth pressure against rigid walls with narrow backfills.

Previous centrifuge tests have been performed to measure lateral earth pressures behind retaining walls with narrow backfills. The results show that the wall–soil interface friction leads to a rotation of the principal stresses, which causes an arching effect. This leads to a non-linear distribution of earth pressures behind the wall, and the total lateral earth pressure is less than that predicted through conventional methods [8, 9]. The results of field monitoring proved this phenomenon [10]. The arching effect in narrow backfills has a more pronounced effect on the earth pressure distribution. The particle image velocity (PIV) technique has been introduced into model tests to study the distribution of soil stresses at different aspect ratios, which confirms the existence of the soil arch effect [11, 12]. Nevertheless, the progression of experiments has been rather tepid. The root causes lie in the increasing complexity of simulated working conditions and the substantial cost of resources.

Considering the above-mentioned shortcomings, many studies have used cost-effective and powerful numerical tools, such as the finite element method (FEM) [13, 14], the discrete element method (DEM) [15, 16], and finite-element limit analysis (FELA) [17, 18]. Numerical calculations are usually carried out for specific conditions and are more demanding on engineers. Therefore, they are not suitable for widespread use in engineering.

Many analytical methods have been used to estimate the active earth pressures on retaining walls with narrow backfills; the limit equilibrium method and slice-element method are two representative calculation methods. The first method has been used to calculate the total horizontal earth pressure with multiple slip surfaces, but this method was unable to obtain the distribution of earth pressures [19]. Recently, the finite-difference theorem has been used to compensate for the shortcomings [20, 21]. The distribution of earth pressure behind the wall can be easily obtained using the slice-element method [22]. In-depth analytical studies on retaining structures have been conducted, leading to proposed reinforcement strategies and guidelines for soil pressure analysis [23–25]. To estimate the distribution of pressure inside a narrow backfill, an approach for computing the active pressure in a two-dimensional stress solution was presented [26]. This method assumes that the vertical stress σ_z does not vary with the width of the backfill, while it is not completely independent of the width of the backfill in reality. The influence of the width of the backfill on σ_z cannot be ignored. Although existing methods provide theoretical solutions, the complex computational processes limit the practical engineering applications.

This study investigates a rigid retaining wall of height H supporting a cohesionless narrow backfill of width B. Key parameters include the soil internal friction angle $\phi$, the wall–soil interface friction angle δ, and the unit weight r. Based on a sliding plane model, a practical approach for calculating the active earth pressure of the narrow cohesionless backfill is proposed. The validity of proposed solutions is verified by previous studies. The effects of the soil friction angle φ, the wall–soil interface friction angle φ, and the aspect ratio B/H on the earth pressure are investigated. To enhance the practical application of the proposed method, a simplified design table related to the standard Coulomb solutions is provided.

2 Proposed analytical methods

Figure 1A shows an analysis model considering both principal stress transfer mechanisms and failure mechanisms. The model can be used to research the active earth pressure of the narrow cohesionless backfill. The sliding plane intersects with the opposite wall (or rock face), and the depth of intersection from the wall top $z_c$ can be calculated using Equation 1:

$z_c=H-B\tan \mathrm{\alpha },(1)$

where H is the height of the retaining wall, B is the width of the narrow backfill, and α is the rupture angle, which is discussed below.

Figure 1

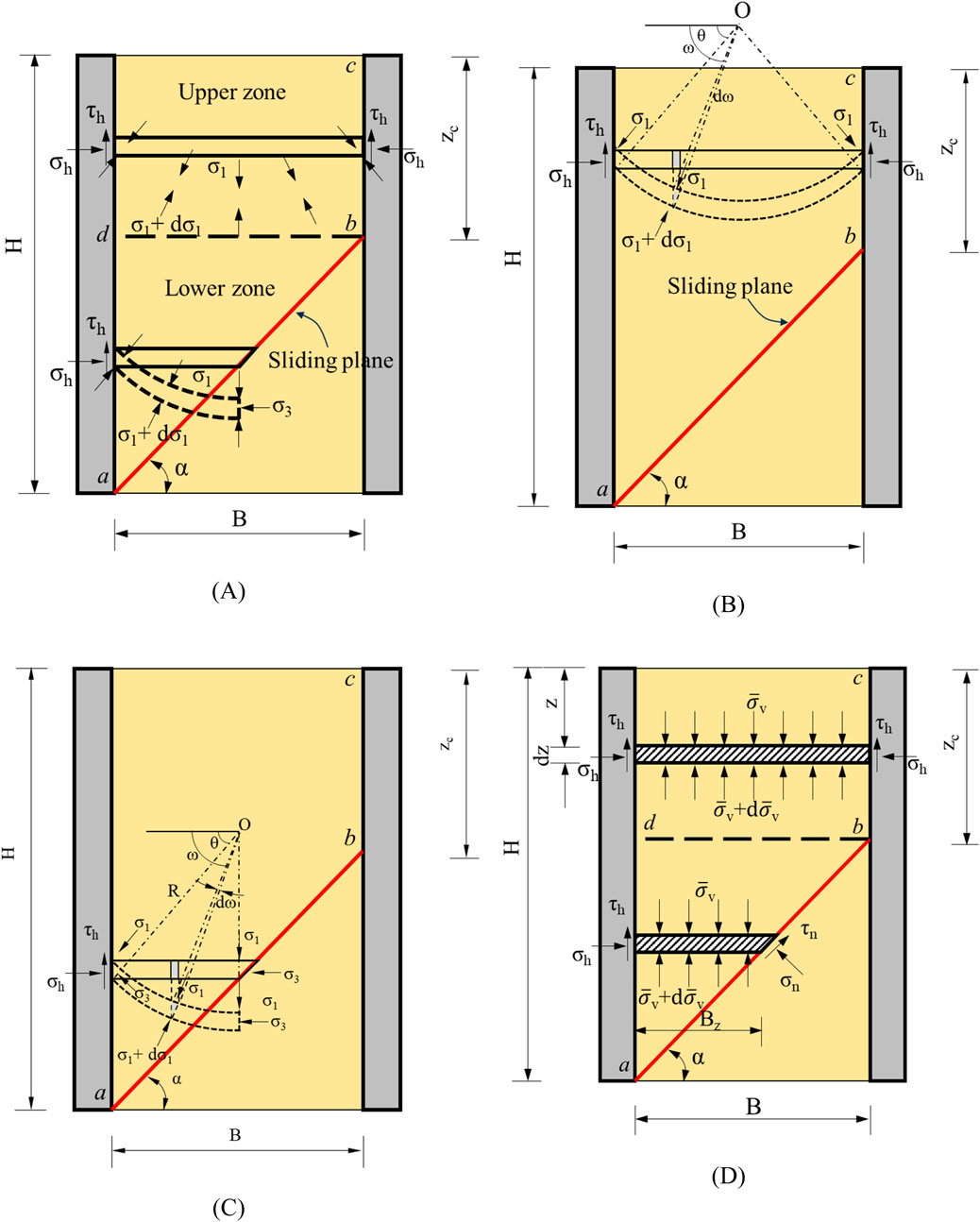
Figure 1. Sliding model for active earth pressure with a narrow fill: (A) trajectory of minor principal stresses, (B) calculation model in the upper zone, (C) calculation model in the lower zone, and (D) free-body diagram of the slice element.

Some basic assumptions are made to simplify the analysis as follows:

(1) The backfill is cohesionless and meets the Mohr–Coulomb failure criterion.

(2) The movement of retaining walls is sufficient to cause the limit state of soil and full mobilization of wall–soil interface strength.

(3) The failure surface consists of two planes: ab and bc. The rupture angle α (angle between the slip surface ab and the horizontal plane) can be determined using Coulomb’s theory, as shown in Equation 2 [27]:

$\alpha =\mathrm{a\; tan}\left(\sqrt{{\tan }^2\phi +\frac{\tan \phi }{\tan \left(\phi +\delta \right)}}+\tan \phi \right),(2)$

where φ is the soil friction angle and δ is the wall–soil interface friction angle.

(4) The trajectories of minor principal stresses in the upper and lower zones (as shown in Figure 1A) are assumed to be circular arcs [28].

2.1 Upper zone

In the upper zone, the slice element is rectangular, as shown in Figures 1B,D, and the lateral earth pressure ${\sigma }_{\mathrm{h}}$ at any depth acting on the wall in the upper zone is governed by Equation 3, which is based on Janssen’s arching theory [29].

${\sigma }_{\mathrm{h}}=\frac{\gamma B}{2\mu }\left(1-e^{-\frac{2K_{\mathrm{a}}\mu }{B}·z}\right),(3)$

where r is the unit weight of the backfill and z is the distance from the top of the wall. $\mu$ can be calculated using Equation 4:

$\mu =\tan \delta .(4)$

$K_{\mathrm{a}}=\frac{3\left(K_{\mathrm{R}}{\cos }^2\theta +{\sin }^2\theta \right)}{3K_{\mathrm{R}}-\left(K_{\mathrm{R}}-1\right){\cos }^2\theta }.(5)$

In Equation 5, $K_{\mathrm{R}}$ is the ratio of major to minor principal stresses, which is provided in Equation 6:

$K_{\mathrm{R}}={\tan }^2\left(45°+\phi /2\right),(6)$

where $\theta$ is the angle between the minor principal stress surface and the horizontal plane at the wall, as shown in Equation 7:

$\theta ={\tan }^{-1}\left[\frac{\left(K_{\mathrm{R}}-1\right)\pm \sqrt{{\left(K_{\mathrm{R}}-1\right)}^2-4K_{\mathrm{R}}{\mu }^2}}{2\mu }\right].(7)$

2.2 Lower zone

In the lower zone, the slice element is trapezoidal, as shown in Figures 1C,D. By summing the vertical forces acting on the slice element, Equation 8 can be obtained:

$\mathrm{d}{\overline{\sigma }}_{\mathrm{v}}{B}_{\mathrm{z}}+{\overline{\sigma }}_{\mathrm{v}}{K}_{\mathrm{a}}\mu \mathrm{d}z=\gamma B_{\mathrm{z}}\mathrm{d}z,(8)$

where ${\overline{\sigma }}_{\mathrm{v}}$ is the average vertical stress across the slice element. Substitution of $B_{\mathrm{z}}=\left(H-z\right)/\tan \alpha$ into Equation 8 yields a differential Equation 9 with a general solution:

${\overline{\sigma }}_{\mathrm{v}}=C·{\left(H-z\right)}^{K_{\mathrm{a}}\mu \tan \alpha }-\frac{\gamma \left(H-z\right)}{1-K_{\mathrm{a}}\mu \tan \alpha },(9)$

where C is an integration constant. It is considered a boundary condition that the average vertical stress ${\overline{\sigma }}_{\mathrm{v}}$ at the interface bd (as shown in Figure 1D) of the upper and lower zones is equal. The average vertical stress ${\overline{\sigma }}_{\mathrm{v}}$ at the interface bd is denoted by ${\overline{\sigma }}_{\text{vc}}$, which can be calculated using Equation 10:

${\overline{\sigma }}_{\text{vc}}=\frac{\gamma B}{2K_{\mathrm{a}}\mu }\left(1-e^{-\frac{2K_{\mathrm{a}}\mu }{B}·z_c}\right).(10)$

Therefore, the particular solution to this differential equation (Equation 8) in the lower zone can be calculated as follows:

${\overline{\sigma }}_{\mathrm{v}}=\left({\overline{\sigma }}_{\text{vc}}+\frac{\gamma \left(H-z_c\right)}{1-K_{\mathrm{a}}\mu \tan \alpha }\right)·{\left(\frac{H-z}{H-z_c}\right)}^{K_{\mathrm{a}}\mu \tan \alpha }-\frac{\gamma \left(H-z\right)}{1-K_{\mathrm{a}}\mu \tan \alpha }.(11)$

The lateral earth stress at any depth acting on the wall in the lower zone can be calculated by multiplying Equation 11 by $K_{\mathrm{a}}$ (which is determined using Equation 5), as shown in Equation 12:

${\sigma }_{\mathrm{h}}=\left({\overline{\sigma }}_{\text{vc}}{K}_{\mathrm{a}}+\frac{\gamma K_{\mathrm{a}}\left(H-z_c\right)}{1-K_{\mathrm{a}}\mu \tan \alpha }\right)·{\left(\frac{H-z}{H-z_c}\right)}^{K_{\mathrm{a}}\mu \tan \alpha }-\frac{\gamma K_{\mathrm{a}}\left(H-z\right)}{1-K_{\mathrm{a}}\mu \tan \alpha }.(12)$

2.3 Magnitude and height of application of the lateral active force

The magnitude of lateral earth pressure exerted on the wall can be calculated using Equation 13:

$\begin{array}{ll}\hfill & \hfill P={\int }_0^H{\sigma }_{\mathrm{h}}dz={\int }_0^{z_c}\frac{\gamma B}{2\mu }\left(1-e^{-\frac{2K_{\mathrm{a}}\mu }{B}·z}\right)dz\\ \hfill & \hfill + {\int }_{z_c}^H\left(\left({\overline{\sigma }}_{\text{vc}}{K}_{\mathrm{a}}+\frac{\gamma K_{\mathrm{a}}\left(H-z_c\right)}{1-K_{\mathrm{a}}\mu \tan \alpha }\right){\left(\frac{H-z}{H-z_c}\right)}^{K_{\mathrm{a}}\mu \tan \alpha }-\frac{\gamma K_{\mathrm{a}}\left(H-z\right)}{1-K_{\mathrm{a}}\mu \tan \alpha }\right)dz.\end{array}(13)$

The moment generated by the lateral earth pressure on the wall can be calculated using the following Equation 14:

$\begin{array}{ll}\hfill & \hfill M={\int }_0^H{\sigma }_{\mathrm{h}}\left(H-z\right)dz={\int }_0^{z_c}\frac{\gamma B}{2\mathit{tan}\delta }\left(1-e^{-\frac{2K_{\text{awn}}\mathit{tan}\delta }{B}·z}\right)\left(H-z\right)dz\\ \hfill & \hfill + {\int }_{z_c}^H\left(\left({\overline{\sigma }}_{\text{vc}}{K}_{\mathrm{a}}+\frac{\gamma K_{\mathrm{a}}\left(H-z_c\right)}{1-K_{\mathrm{a}}\mu \tan \alpha }\right){\left(\frac{H-z}{H-z_c}\right)}^{K_{\mathrm{a}}\mu \tan \alpha }-\frac{\gamma K_{\mathrm{a}}\left(H-z\right)}{1-K_{\mathrm{a}}\mu \tan \alpha }\right)\left(H-z\right)dz,\end{array}(14)$

The modified active earth pressure coefficient K was determined through back-calculation, as shown in Equation 15:

$P=\frac{1}{2}K·\gamma H^2.(15)$

The height of application of the lateral active force h can be calculated using Equation 13 and Equation 14, as shown in Equation 16:

$h=\frac{M}{P}.(16)$

Based on Equation 15, when δ = 0°, the height of application of the lateral active force is one-third of the wall height. This is in agreement with the results obtained from Coulomb’s or Rankine’s theory [1, 2]. When $z_c$ <0, the outer basement wall is outside the influence of the sliding wedge, and the active earth pressure equation for the retaining wall should be reduced to the Paik solution [3].

3 Comparison with previous studies

To verify rationality and accuracy, the proposed method is compared with results from previous geotechnical centrifuge tests, FEM, and analytical solutions in terms of ${\sigma }_{\mathrm{h}}/rH$ on retaining walls with a narrow cohesionless backfill. The active earth pressure on retaining walls near a rock face with narrow, cohesionless backfills at an acceleration of 43.7 g was measured [8]. In this study, the unit weight, internal friction angle, and relative density of the cohesionless backfill were 15.8 kN/m³, 36°, and 70%, respectively. The wall–soil interface friction angle was 25°. The tests were designed under five different aspect ratios (B/H = 0.1, 0.19, 0.22, 0.3, and 1.1). The measured earth pressures at different depths did not explicitly correspond to a specific aspect ratio in the paper. Therefore, representative testing data were compiled for comparison, with the aspect ratio assumed to be 0.235. The value is close to the mean value obtained from the model tests. The geotechnical centrifuge test results are commonly used as a benchmark for comparing the different theories for predicting the lateral earth pressure. Numerical solutions for the active earth pressure against retaining walls with B/H = 0.235 were provided by Fan and Fang using the centrifuge test [14]. Analytical solutions based on the limit equilibrium method without considering the arching effect were presented by Greco, and the arched differential elements were presented by Lai [19, 30].

Figure 2 shows a comparison between the results obtained by the proposed analytical method and those obtained from centrifuge tests, numerical calculations, and existing analytical methods. Considering the diverse aspect ratios comprehensively examined through centrifuge tests, the proposed solutions agree well with the results from centrifuge tests. The proposed analytical method is smaller than the Coulomb solution based on infinite space; this may be because the sliding wedge fails to develop fully in the narrow backfill. The differences among the existing solutions suggest that the assumption of semi-infinite backfill space may not be suitable for the economic design of retaining walls with narrow cohesionless backfills.

Figure 2

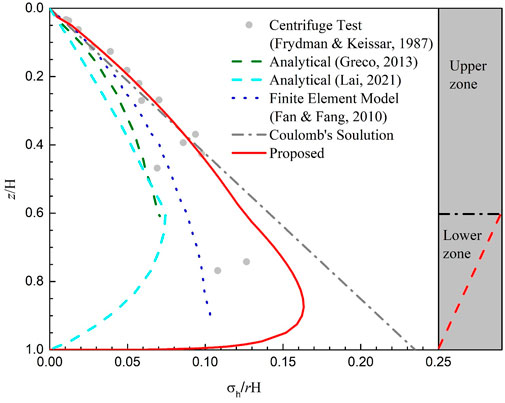
Figure 2. Comparison of the results obtained by the proposed analytical method with those of the centrifuge test, numerical calculation, and existing analytical method.

4 Parametric studies

In this section, a parametric study of the proposed analytical method was conducted. Sensitive influencing parameters were chosen, such as the soil friction angle φ, the wall–soil interface friction angle δ, and the aspect ratio B/H. Calculations were carried out for the height of the application point of active thrust to the base h/H, the active thrust coefficient K, and the normalized horizontal active earth pressure distribution ${\sigma }_{\mathrm{h}}$/rH. These parameters are generally considered routine indicators in retaining wall design. It should be noted that the purpose of a parametric study is to offer more optimal guidance for engineering design. Because the calculated parameters should cover most of the range of practical engineering, the soil friction angle ranges from 20° to 40°, the wall–soil interface friction angle ranges from 0 to 0.8 φ, and the aspect ratios are set from 0.1 to 0.8. Moreover, a wider range of parameters is listed in Table 1 for reference.

Table 1

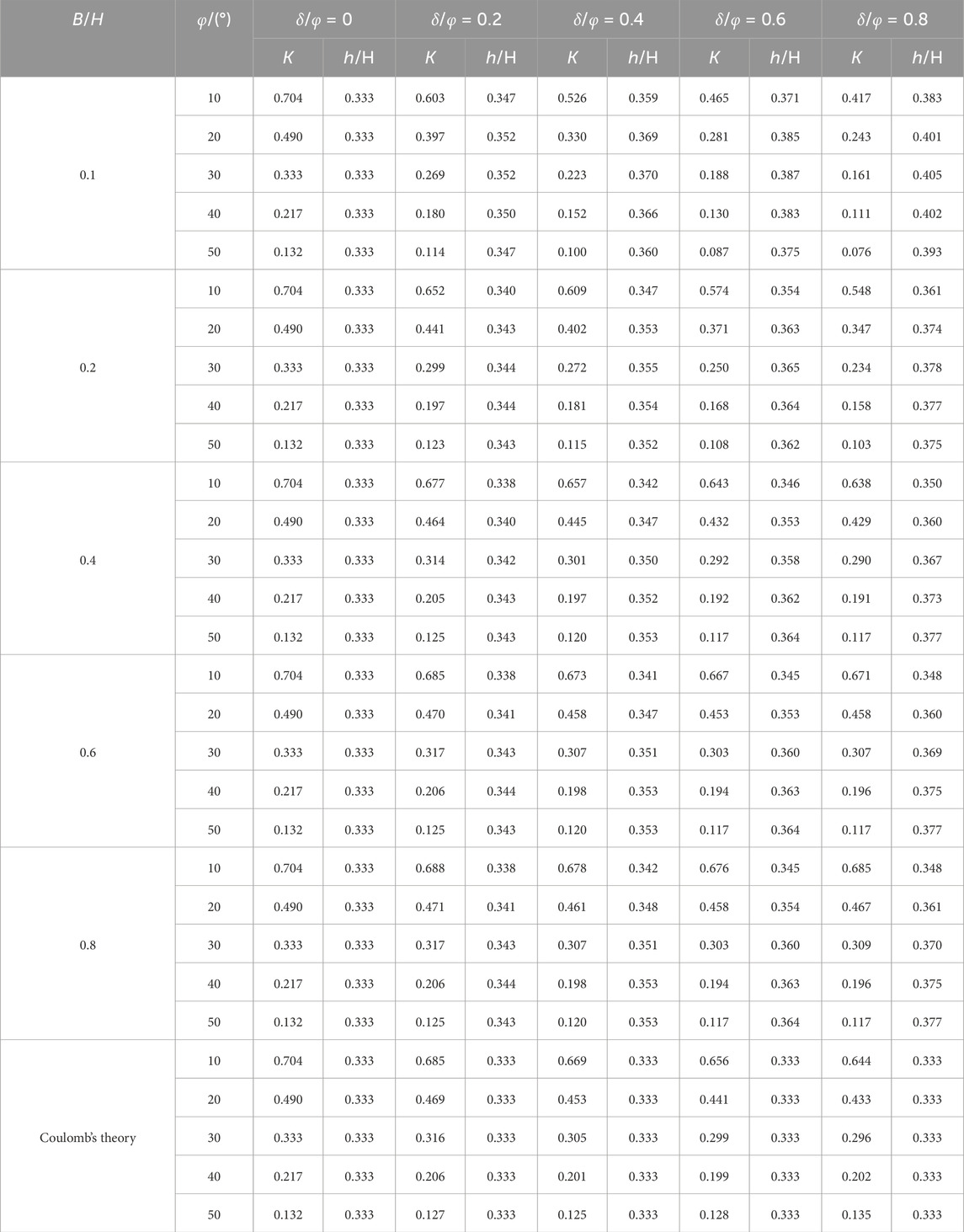
Table 1. Modified active earth pressure coefficient and the height of the application point of active thrust involved in retaining walls with cohesionless backfills.

4.1 Effect of the soil friction angle

The change in the height of the application point of active thrust h/H and the active thrust coefficient K with the soil friction angle φ under different aspect ratios B/H are shown in Figures 3A,B, respectively. It should be noted that the ratio of the wall–soil interface friction angle to the soil friction angle δ/φ is fixed at 0.8 for the investigation of the effect of the soil friction angle. Figure 3A shows that the height of the application point of active thrust h/H obtained by the proposed method is approximately distributed in the range of 0.35H–0.43H, which is slightly higher than that of Coulomb’s theory, and the height of the application point of active thrust h/H is not much affected by the change in the soil friction angle φ for the case of a fixed aspect ratio B/H. The aspect ratio B/H gradually increases with the decrease in the height of the application point of active thrust h/H and is close to the assumption of infinite space. In Figure 3B, due to the arching effect, the active thrust coefficient K decreases in a concave curve with the soil friction angle φ. For a given soil friction angle φ, the larger the aspect ratio B/H, the larger the active thrust coefficient K in a narrow cohesionless backfill. When B > H cotα, ${\sigma }_{\mathrm{h}}$ no longer changes, and K remains constant.

Figure 3

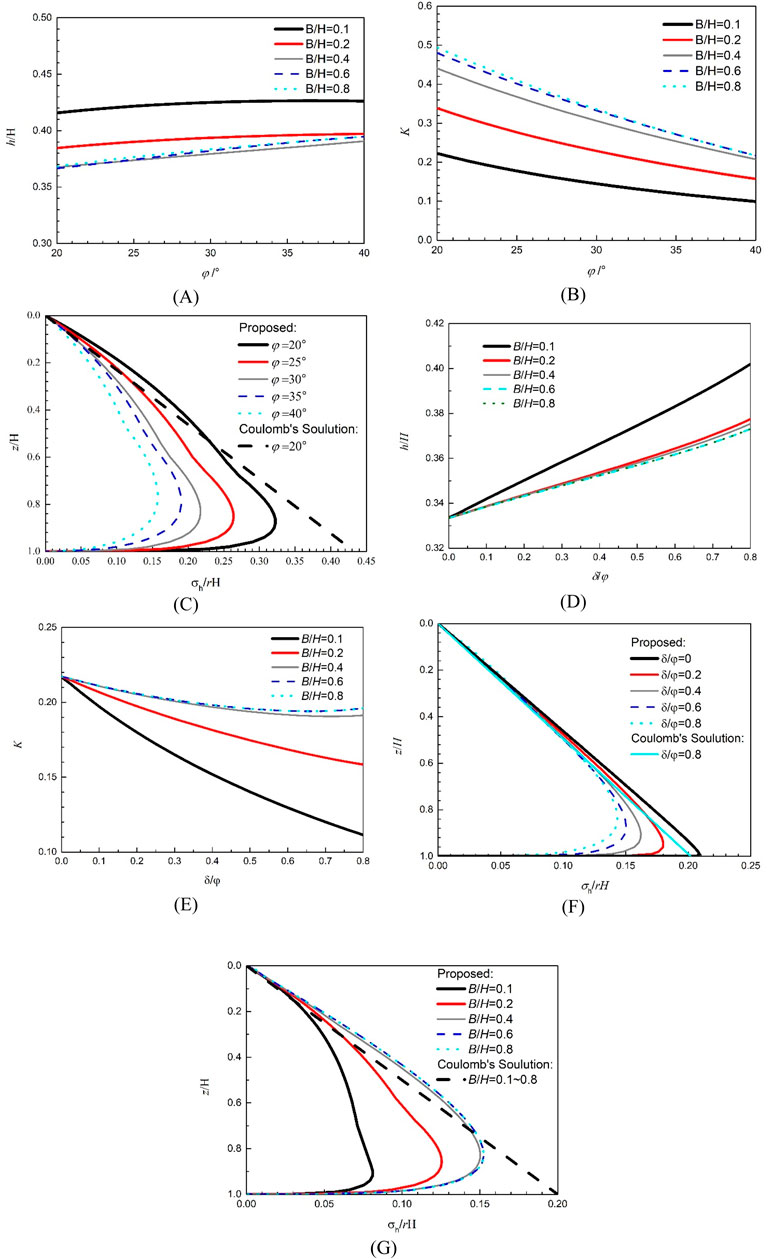
Figure 3. Sensitivity analysis of different parameters: (A) effect of the soil friction angle on the normalized height of the application point of active thrust, (B) effect of the soil friction angle on the active thrust coefficient, (C) effect of the soil friction angle on the active earth pressure distribution, (D) effect of the wall–soil interface friction angle on the normalized height of the application point of active thrust, (E) effect of the wall–soil interface friction angle on the active thrust coefficient, (F) effect of the wall–soil interface friction angle on the active earth pressure distribution, and (G) effect of the aspect ratio on the active earth pressure distribution.

Figure 3C shows the variation in the normalized horizontal active earth pressure ${\sigma }_{\mathrm{h}}$/rH with the depth of the retaining wall z/H under different soil friction angles φ, and the aspect ratio B/H is equal to 0.3. In Equation 1, the height of the sliding zone changes with the change in the rupture angle α. In Equation 2, the soil friction angle φ significantly affects the rupture angle α and has a significant impact on the distribution of ${\sigma }_{\mathrm{h}}$. As the soil friction angle φ increases, the height of the sliding zone gradually increases and ${\sigma }_{\mathrm{h}}$ decreases significantly. This shows that the larger the soil friction angle φ, the stronger the arching effect.

4.2 Effect of the wall–soil interface friction angle

Figures 3D,E show the change in the height of the application point of active thrust h/H and the active thrust coefficient K with the wall–soil interface friction angle δ under different aspect ratios B/H, respectively. It should be noted that the soil friction angle φ is fixed at 40° for the investigation of the effect of the wall–soil interface friction angle. Figure 3D shows the height of the application point of active thrust h/H obtained by the proposed method, and the approximate range is 0.33H–0.41H, which is similar to Figure 3A. When the wall–soil interface friction angle δ is 0, the height of the application point of active thrust h/H coincides with Coulomb’s theory. Figure 3E shows that the active thrust coefficient K decreases with the increase in the wall–soil interface friction angle δ for a narrow backfill. When B/H >0.4, the decreasing trend slows down. When the wall–soil interface friction angle δ is kept constant, the active thrust coefficient K increases with aspect ratios B/H first and then remains constant. When B/H >0.6, the active thrust coefficient K is not affected by aspect ratios B/H because a complete triangular thrust wedge can be formed.

Figure 3F shows the variation in the normalized horizontal active earth pressure ${\sigma }_{\mathrm{h}}$/rH with the depth of the retaining wall z/H under different wall–soil interface friction angles δ, and the aspect ratio B/H is 0.3. For any wall–soil interface friction angle δ, the horizontal soil pressure ${\sigma }_{\mathrm{h}}$ first increases up to a certain point and then decreases rapidly to 0 at the bottom of the wall. It can also be observed that the horizontal earth pressure ${\sigma }_{\mathrm{h}}$ decreases with the increasing wall–soil interface friction angle δ at a given wall depth, which is related to the increase in friction at the wall–soil interface. Friction between walls and soil increases the principal stress rotation angle θ (as shown in Equation 7), which enhances the arching effect. However, the effect of the wall–soil interface friction angle δ on the horizontal soil pressure ${\sigma }_{\mathrm{h}}$ is relatively limited compared to that of the soil friction angle φ.

4.3 Effect of the aspect ratio

Assuming that the soil friction angle φ is 40° and the wall–soil interface friction angle δ is 0.8, the distribution of the horizontal soil pressure ${\sigma }_{\mathrm{h}}$ under different aspect ratios B/H is shown in Figure 3G. It can be observed that the aspect ratio has a significant effect on the magnitude of soil pressure. The horizontal soil pressure ${\sigma }_{\mathrm{h}}$ decreases rapidly with decreasing aspect ratio B/H at a given depth of the retaining wall z/H. When the aspect ratio B/H was reduced from 0.8 to 0.1, the maximum horizontal soil pressure was almost halved. This is because as the aspect ratio B/H decreases, the ratio of contact friction at the wall–soil interface to the self-weight of the narrow backfill increases, leading to a more significant soil arching effect. Once the aspect ratio B/H > cotα, the horizontal soil pressure ${\sigma }_{\mathrm{h}}$ remains constant at a specific depth. This suggests that the use of Coulomb’s theory based on a triangular thrust wedge to calculate narrow retaining walls will greatly overestimate the magnitude of earth pressures and may lead to overly conservative design.

At different aspect ratios B/H, the earth pressure increases with depth to a maximum value first and then decreases rapidly to 0. The depth of this maximum value decreases with the increase in the aspect ratio B/H. One reason may be that as the depth of the retaining wall increases, more vertical load is carried by the wall–soil friction [31]. All the above calculations show that the direct use of Coulomb’s theory without further modifications is not suitable for accurately estimating the active earth pressure on a retaining wall with a narrow backfill.

5 Simplified design methods

It is not very convenient to directly use Equations 12, 13, and 16 to calculate the active earth pressure in practice, which will greatly limit its practical application, and this is the reason why Coulomb’s theory is still widely used in geotechnical engineering design. Based on the above parameter analysis, the modified active earth pressure coefficient K and the height of the application point of active thrust h/H under different working conditions are summarized in Table 1. The Coulomb solution is also listed in Table 1 for comparison.

The ranges of values for the soil friction angle φ, the aspect ratio B/H, and the wall–soil interface friction angle δ were determined to satisfy engineering applications [27, 30]. Table 1 shows the variation in K and h/H with φ and δ/φ for various values of B/H. At δ/φ = 0, K is only relevant to φ, is independent of B/H, and is consistent with Coulomb’s theory. It can also be observed in the table that the value of K decreases with increasing φ at a rate that increases gradually with increasing φ. Table 1 shows that the height of the application point of active thrust h/H increases with δ/φ and decreases with φ. It can be observed that the height of the application point of active thrust h/H for δ/φ is 0·33, regardless of the internal friction angle φ and the aspect ratios B/H. This is consistent with Coulomb’s theory. It should be noted that when B/H > cotα, the triangular thrust wedge behind the rigid wall can develop fully so that K and h/H are no longer related to B/H, as shown in the gray part of Table 1. In Table 1, the earth pressure obtained by Coulomb’s theory does not consider the effect of B/H, and the earth pressure decreases significantly with the decrease in B/H, so Coulomb’s theory is more conservative. The earth pressure obtained by the proposed method is more reasonable. The active earth pressure of the narrow, cohesionless backfill against rigid walls can be obtained using Table 1, while cases involving unsaturated soils and passive earth pressures are not considered.

6 Conclusion

Most of the existing analytical methods for estimating active earth pressures on narrow retaining walls were complex, which hinders their application in practical engineering. In this paper, according to the slice-element method, a practical method is proposed to estimate the active earth pressure of the narrow cohesionless backfill against rigid walls, considering the arching effect. Results of the proposed analytical method are verified using centrifuge tests, numerical calculations, and existing analytical methods. A series of parametric studies revealed the effects of the soil friction angle φ, the wall–soil interface friction angle δ, and the aspect ratio B/H on the height of the application point of active thrust h/H, the modified active thrust coefficient K, and the normalized horizontal active earth pressure distribution ${\sigma }_{\mathrm{h}}$/rH. A table for the calculation of K and h/H is provided for direct use of the proposed analytical method. Based on the above analysis, the following conclusions can be drawn.

(1) The effect of the aspect ratio B/H on the modified active earth pressure coefficient K is significant. When B/H < cotα, K increases with increasing B/H at a rate that decreases gradually with increasing B/H. When B/H > cotα, the triangular thrust wedge behind the rigid wall can develop fully, and K and h/H no longer vary with B/H.

(2) For a given aspect ratio, the modified active thrust coefficient K decreases with the increasing soil friction angle φ and the wall–soil interface friction angle δ. Compared to their effect on K, φ and δ exhibit relatively minor influence on the height h/H, which reaches a maximum value approximately 30% larger than that calculated through Coulomb’s theory. The parameter h/H increases with φ first and then decreases with φ while showing a slight increasing trend with δ.

In this paper, the simplified earth pressure calculation method for retaining walls with a narrow backfill provides insights for the design of excavations close to basement walls, highways through mountainous terrains, and other projects, although several limitations cannot be neglected. This method may not be suitable for the case involving inclined rock or retaining walls since the difference in the interfacial behavior between the two retaining structures is neglected. Nevertheless, the proposed analytical method provides valuable guidance for the practical design of retaining walls with a narrow backfill.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material; further inquiries can be directed to the corresponding author.

Author contributions

YL: Methodology, Writing – original draft. RL: Conceptualization, Funding acquisition, Writing – review and editing. YW: Validation, Writing – review and editing.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. This work was supported by the University Natural Science Foundation of Jiangsu Province (grant no. 24KJB560003) and the Science and Technology Projects of Jiangsu Province Construction System (grant no. 2024ZD038).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Coulomb CA. Essai sur une application des règles de maximis and minimis à quelques problèmes de statique, relatifs à l'architecture. Paris: De l'Imprimerie Royale (1776).

Google Scholar

2. Rankine WJM. On the stability of loose earth. Philos. Philosophical Trans R Soc Lond (1857) 147:9–27.

Google Scholar

3. Paik KH, Salgado R. Estimation of active earth pressure against rigid retaining walls considering arching effects. Géotechnique (2003) 53(7):643–53. doi:10.1680/geot.2003.53.7.643

CrossRef Full Text | Google Scholar

4. Li JP, Wang M. Simplified method for calculating active earth pressureon rigid retaining walls considering the arching effect under translational mode. Int J Geomechanics (2014) 14(2):282–90. doi:10.1061/(ASCE)GM.1943-5622.0000313

CrossRef Full Text | Google Scholar

5. Cao WG, Liu T, Xu Z. Estimation of active earth pressure on inclined retaining wall based on simplified principal stress trajectory method. Int J Geomechanics (2019) 19(7):06019011. doi:10.1061/(ASCE)GM.1943-5622.0001447

CrossRef Full Text | Google Scholar

6. Iskander M, Chen Z, Omidbar M, Guzman I, Elsherif O. Active static and seismic earth pressure for c-φ soils. Soils and Foundations (2013) 53(5):639–52. doi:10.1016/j.sandf.2013.08.003

CrossRef Full Text | Google Scholar

7. Lai FW, Tschuchnigg F, Schweiger HF, Liu SY, Shiau J, Cai GJ. A numerical study of deep excavations adjacent to existing tunnels: integrating CPTU and SDMT to calibrate soil constitutive model. Can Geotechnical J (2025) 62:1–23. doi:10.1139/cgj-2024-0203

CrossRef Full Text | Google Scholar

8. Frydman S, Keissar I. Earth pressure on retaining walls near rock faces. J Geotechnical Eng (1987) 113(6):586–99. doi:10.1061/(asce)0733-9410(1987)113:6(586)

CrossRef Full Text | Google Scholar

9. Take WA, Valsangkar AJ. Earth pressures on unyielding retaining walls of narrow backfill width. Can Geotechnical J (2001) 38(6):1220–30. doi:10.1139/cgj-38-6-1220

CrossRef Full Text | Google Scholar

10. O’Neal TS, Hagerty D. Earth pressures in confined cohesionless backfill against tall rigid walls—a case history. Can Geotechnical J (2011) 48(8):1188–97. doi:10.1139/t11-033

CrossRef Full Text | Google Scholar

11. Khosravi MH, Pipatpongsa T, Takemura J. Experimental analysis of earth pressure against rigid retaining walls under translation mode. Géotechnique (2013) 63(12):1020–8. doi:10.1680/geot.12.P.021

CrossRef Full Text | Google Scholar

12. Rui R, Ye YQ, Han J, Zhang L, Zhai YX. Experimental and theoretical investigations on active earth pressure distributions behind rigid retaining walls with narrow backfill under a translational mode. Int J Geomechanics (2020) 20(10):04020178. doi:10.1061/(ASCE)GM.1943-5622.0001832

CrossRef Full Text | Google Scholar

13. Yang KH, Liu CN. Finite element analysis of earth pressures for narrow retaining walls. J Geoengineering (2007) 2(2):43–52. doi:10.6310/jog.2007.2(2).1

CrossRef Full Text | Google Scholar

14. Fan CC, Fang YS. Numerical solution of active earth pressures on rigid retaining walls built near rock faces. Comput geotechnics (2010) 37(7):1023–9. doi:10.1016/j.compgeo.2010.08.004

CrossRef Full Text | Google Scholar

15. Jiang M, He J, Wang J, Liu F, Zhang W. Distinct simulation of earth pressure against a rigid retaining wall considering inter-particle rolling resistance in sandy backfill. Granular Matter (2014) 16(5):797–814. doi:10.1007/s10035-014-0515-3

CrossRef Full Text | Google Scholar

16. Yang MH, Deng B. Simplified method for calculating the active earth pressure on retaining walls of narrow backfill width based on DEM analysis. Adv Civil Eng (2019) 2019:1507825. doi:10.1155/2019/1507825

CrossRef Full Text | Google Scholar

17. Lin YJ, Chen FQ, Lv YP. Analytical solutions for the earth pressure of narrow cohesive backfill with retaining walls rotating about the top. Acta Geotechnica (2021) 16:2975–95. doi:10.1007/s11440-021-01187-9

CrossRef Full Text | Google Scholar

18. Yang DY, Lai FW, Liu SY. Earth pressure in narrow cohesive-fictional soils behind retaining walls rotated about the top: an analytical approach. Comput geotechnics (2022) 149:104849. doi:10.1016/j.compgeo.2022.104849

CrossRef Full Text | Google Scholar

19. Greco V. Active thrust on retaining walls of narrow backfill width. Comput geotechnics (2013) 50:66–78. doi:10.1016/j.compgeo.2012.12.007

CrossRef Full Text | Google Scholar

20. Chen FQ, Yang JT, Lin YJ. Active earth pressure of narrow granular backfill against rigid retaining wall near rock face under translation mode. Int J Geomechanics (2019) 19(12):04019133. doi:10.1061/(ASCE)GM.1943-5622.0001525

CrossRef Full Text | Google Scholar

21. Lai FW, Zhang NN, Liu SY, Yang DY. A generalised analytical framework for active earth pressure on retaining walls with narrow soil. Géotechnique (2024) 74(11):1127–42. doi:10.1680/jgeot.21.00305

CrossRef Full Text | Google Scholar

22. Yang MH, Tang XC, Wu ZY. Slip surface and active earth pressure of cohesionless narrow backfill behind rigid retaining walls under translation movement mode. Int J Geomechanics (2020) 20(8):04020115. doi:10.1061/(ASCE)GM.1943-5622.0001746

CrossRef Full Text | Google Scholar

23. Liu CQ, Wei XD, Lu Z, Wu HD, Yang YL, Chen LY. Studies on passive flexible protection to resist landslides caused by the May 12, 2008, Wenchuan earthquake. Struct Des Tall Spec Buildings (2017) 26(11):e1372. doi:10.1002/tal.1372

CrossRef Full Text | Google Scholar

24. Liu CQ, Wei XD, Wu HD, Li QF, Ni XY. Research on shear lag effect of T-shaped short-leg shear wall. Periodica Polytechnica-Civil Eng (2017) 61(3):602–10. doi:10.3311/PPci.9491

CrossRef Full Text | Google Scholar

25. Liu CQ, Fang DJ, Zhao LJ. Reflection on earthquake damage of buildings in 2015 Nepal earthquake and seismic measures for post-earthquake reconstruction. Structures (2021) 30:647–58. doi:10.1016/j.istruc.2020.12.089

CrossRef Full Text | Google Scholar

26. Khosravi MH, Sarfaraz H, Pipatpongsa T, Sharifdeljuyi A. Active earth pressure distribution inside narrow backfill considering soil-arching effect. Int J Geomechanics (2022) 22(7):06022013. doi:10.1061/(ASCE)GM.1943-5622.0002434

CrossRef Full Text | Google Scholar

27. Chen JJ, Li MG, Wang JH. Active earth pressure against rigid retaining walls subjected to confined cohesionless soil. Int J Geomechanics (2017) 17(6):06016041. doi:10.1061/(ASCE)GM.1943-5622.0000855

CrossRef Full Text | Google Scholar

28. Handy RL. The arch in soil arching. J Geotechnical Eng (1985) 111(3):302–18. doi:10.1061/(asce)0733-9410(1985)111:3(302)

CrossRef Full Text | Google Scholar

29. Janssen HA. Versuche uber getreidedruck in silozellen. Zeitschr (1895) 39(35):1045–9.

Google Scholar

30. Lai FW, Yang DY, Liu SY, Zhang HB, Cheng YH. Towards an improved analytical framework to estimate active earth pressure in narrow c - φ soils behind rotating walls about the base. Comput Geotechnics (2022) 141:104544. doi:10.1016/j.compgeo.2021.104544

CrossRef Full Text | Google Scholar

31. Chen FQ, Miao GJ, Lai FW. Base instability triggered by hydraulic uplift of pit-in-pit braced excavations in soft clay overlying a confined aquifer. KSCE J Civil Eng (2020) 24(6):1717–30. doi:10.1007/s12205-020-1102-2

CrossRef Full Text | Google Scholar