Effects of electronic excitation on cascade dynamics in tungsten

While tungsten has emerged as a primary candidate for plasma-facing components in future fusion devices, the effects of electronic excitations on the irradiation damage behavior under high-energy irradiation remain unclear. In this work, using a two-temperature (2T-MD) model in molecular dynamics simulations, we investigated the effects of irradiation energy, irradiation temperature, electron density and the electron-phonon (e-ph) coupling activation time on the cascade dynamics in tungsten. The results showed that the electronic effect has significant impacts on the formation of irradiation defects, especially under high-energy irradiation. Compared with the results of classical molecular dynamics calculations, the numbers of peak and surviving defects calculated using 2T-MD model were significantly reduced under high-energy ion irradiation (∼150 keV). The number of peak defects increased with temperature, while the surviving defects showed a similar number. With the increase of electron density, the number of peak defects decreased. However, the number of surviving defects was almost unaffected by the electron density. The later the e-ph coupling activation time, the more the number of peak and surviving defects. The mechanisms were well explained by analyzing the local atomic and electronic temperatures. Our work provides valuable information for understanding the electronic effects on the primary radiation damage in tungsten.

1 Introduction

The development of controlled deuterium-tritium fusion energy is considered to be a promising way to solve the energy problem [1]. In fusion devices, plasma facing materials (PFMs) are exposed to harsh environments such as irradiation from high-energy particles and extremely high temperatures [2–6]. Therefore, the key structural materials in nuclear fusion devices are one of the important factors in realizing the safe application in nuclear fusion reactors [7]. Tungsten (W) has a high melting temperature and thermal conductivity, and is considered as one of the main candidates for plasma facing materials in future fusion devices [8–11].

After high-energy particle irradiation, a large number of defects can be formed in the materials. Since the formation of point defects plays a significant role in the irradiation damage of material, it determines the growth and evolution behaviors of defects in the post-irradiation period. Therefore, it is important to study the formation processes and evolution mechanisms of defects in the early stage of irradiation damage. Classical molecular dynamics (CMD) have been widely used to investigate the formation processes and mechanisms of the defects. Liu et al. [12] studied the effects of primary-knock-on atom (PKA) energy, direction and irradiation temperature on the cascade processes of metal W using CMD methods, established a W displacement cascade database, and clarified the Frenkel pairs, the types and spatial distribution of defects. These results provide a significant reference for the prediction of defect behavior, mechanical and thermal properties of W under the neutron irradiation environment. Zhao et al. [13] studied the effect of temperature on the cascade processes in tungsten using CMD method. It was found that the irradiation resistance of W can be improved with the increase of the temperature.

However, classical molecular dynamics ignores the energy exchange between electronic subsystem and atomic subsystem [14, 15]. For the low-energy ion irradiation, CMD can reasonably describe the irradiation damage processes. But for the high-energy particle irradiation, it is urgent to consider the effect of electronic energy loss on the irradiation damage of materials because most of the energy is lost due to the excitation and ionization of target electrons caused by inelastic scattering. Duffy [16] and Rutherford [17] proposed a two-temperature molecular dynamics (2T-MD) model. This model describes the electron stopping power and electron-phonon (e-ph) interactions, and has been widely used to describe the influence of electronic energy loss on irradiation damage [18–21]. Zarkadoula et al. [18–20] investigated the electronic effects of the displacement cascades in Ni and Ni-based alloys based 2T-MD, and found that the electronic effect has important influence on irradiation damage. The stronger the e-ph coupling, the less the number of surviving defects. They attributed the mechanism to the energy transferred from the electronic subsystem to the atomic system, which facilitates defect recombination, thereby leading to a reduction in the number of defects. In addition, Zarkadoula et al. [21] performed molecular dynamics simulations of high-energy collision cascades in W at 300 K and 800 K based on 2T-MD model. The results showed that the electronic effect has an important influence on the displacement cascades and can result in less damage formation. The number of peak and surviving defects at 800 K are larger than those at 300 K. Although the electronic effects in irradiation damage has been studied to some extent, the damage mechanism is not fully understood, and further research is still needed.

In this work, we investigated the effects of irradiation energy, electron density, irradiation temperature and electron-phonon coupling activation time on the irradiation defects formed in tungsten using 2T-MD method. It was found that the electronic effect has a significant influence on the irradiation defects in tungsten. With the increase of irradiation temperature, the number of peak defects increases, while the surviving defect shows a similar number. The number of peak defects decreases with the increase of electron density. This is attributed to the slower cooling of the electronic subsystem for the higher electron densities. As a result, more energy can be transferred to the atomic subsystem, enhancing the interstitial-vacancy recombination and resulting in the reduction of defects. With the decrease of the e-ph coupling activation time, the numbers of peak and surviving defects decrease.

2 Simulation methods

All calculations in this work were performed using the Large-scale Atomic/Molecular Massively Parallel Simulator (LAMMPS) code [22], which includes the 2T-MD model. The atomic interactions in metal W were described by the F-S type interatomic potential (FS) recently developed by Deng et al. [23]. The Ziegler-Biersack-Littmark (ZBL) universal function [24] was used to describe the short-range interactions of the collision cascade. The ZBL universal function is connected to the interatomic interaction potential through the connection function, which is expressed as Equations 1–3:

$U_{ij}=\left[1-f_F\left(r_{ij}\right)\right]U_{ij}^{\text{ZBL}}+f_F\left(r_{ij}\right)U_{ij}^{\text{FS}}(1)$

$f_F\left(r_{ij}\right)=\frac{1}{1+e^{-A_F\left(r_{ij}-r_C\right)}}(2)$

$U_{ij}^{\text{ZBL}}=\frac{1}{4\pi {ϵ}_0}\frac{Z_i{Z}_j{e}^2}{r_{ij}}\varphi \left(\frac{r_{ij}}{a}\right)(3)$

$A_F$ controls the “steepness” of the transition of potential energy from ZBL to FS, and $r_C$ controls the radius at which the transition occurs.

The cascade collision was initiated by imparting a kinetic energy to a randomly selected PKA. The incident energy of the PKA ranged from 10 keV to 150 keV, which were widely used in cascade simulation of tungsten [25, 26]. To avoid channeling effects, the initial velocity direction of the PKA was chosen to be along the 〈135〉 high-index direction. The cascades started from a point far from the center of the molecular dynamics (MD) box. The simulation systems consisted of 250,000 (50 × 50 × 50 unit cells) and 1,000,000 W atoms (80 × 80 × 80 unit cells), respectively. Periodic boundary conditions were applied in the simulation box. The thickness of the thermostat layer was approximately 8.0 Å, where the atomic velocities were rescaled, preventing energy from re-entering the simulation system.

The evolution of the electronic temperature (T_e) followed the thermal diffusion equation. The two systems were divided into 9 × 9 × 9 and 15 × 15 × 15 finite-difference cells to solve the thermal diffusion equations, respectively [17]. The former contained about 340 atoms/cell, while the latter contained about 300 atoms/cell. In the 2T-MD model, the equations of motion are often formulated as Langevin equation (Equation 4) to describe the particles motion, incorporating both the frictional and random forces [16].

$m\frac{\partial {\mathit{v}}_i}{\partial t}={\mathit{F}}_i\left(t\right)-{\gamma }_i{\mathit{v}}_i+\stackrel{\sim }{\mathit{F}}\left(t\right)(4)$

Here ${\mathit{v}}_i$ and m are the velocity and mass of atom i, respectively, and ${\mathit{F}}_i\left(t\right)$ is the force exerted on atom i by the surrounding atoms, and $\stackrel{\sim }{\mathit{F}}\left(t\right)$ is the random force. At lower speeds, the atoms move in relation to the surrounding atoms, and the rate of energy loss is proportional to the difference between the atomic and electronic temperatures. The friction coefficients γ_s due to electronic stopping and γ_p due to e-ph interactions are given by Equations 5, 6.

${\gamma }_i={\gamma }_{\mathrm{p}}+{\gamma }_{\mathrm{s}}\text{\hspace{1em}for\hspace{1em}}{v}_i>v_0(5)$

${\gamma }_i={\gamma }_{\mathrm{p}}\text{\hspace{1em}for\hspace{1em}}{v}_i\le v_0(6)$

To account for energy transport in the electron subsystem in the model, the thermal diffusion equation (Equation 7) is used to describe the evolution of electronic temperature (T_e), which relates to the specific heat capacity (C_e) of electrons and thermal conductivity (κ_e).

$C_e{\rho }_e\frac{\mathrm{\partial }{T}_e}{\mathrm{\partial }t}=▽\left({\kappa }_e▽T_e\right)-g_p\left(T_e-T_a\right)+g_s{T}_a^{\prime }(7)$

The electron density is given by Equation 8:

${\rho }_e=\frac{N_a\times N_e}{V_c}(8)$

Where $N_a$ represents the number of atoms, $N_e$ represents the number of valence electrons, and $V_c$ represents the volume of a cell.

The electronic stopping parameter γ_s was calculated to be about 203.829 g/mol/ps using the SRIM code [27]. The electron-phonon coupling parameter γ_p was chosen to be 35.203 g/mol/ps, corresponding to the coupling strength of g_p = 5 × 10¹⁷ W∙m⁻³∙K⁻¹ [28]. The activation time for the e-ph coupling is determined through extensive simulations, including cases both with and without the e-ph coupling considered. The heat capacity C_e in the electronic temperature range was given in Ref. [29], and was calculated using first-principle calculations detailed in Ref. [30]. The electronic thermal conductivity κ_e was set to be 174 W∙m⁻¹∙K⁻¹ [31]. Because of the large uncertainty, it was assumed that κ_e and g_p do not depend on the lattice temperature, i.e., were constants. Before the cascade collision, the systems were equilibrated for 20 ps at 300 K and zero pressure using NPT (constant number of atoms, pressure and temperature) ensemble. The microcanonical ensemble (NVE) was applied to simulate the cascade collision processes. The cascade simulation was performed for 720,000 steps, corresponding to a total simulation time of about 100 ps, to ensure the system fully relaxed to equilibrium [32]. An adaptive time step was employed, limiting the maximum displacement to 0.005 Å per step. After the simulation, the Wigner-Seitz cell method in OVITO [33] software was used to visually analyze the Frenkel defects. In all two-temperature model simulations, the e-ph activation time was set to 0 ps by default, while the effect of e-ph coupling activation time was set separately. To ensure data reliability, all numerical results were obtained from a statistical average of at least 10 independent cascade events.

3 Results

The study focuses on the factors and mechanisms that influence the irradiation defects formed in tungsten when the electronic energy loss is considered. We first explored the effects of irradiation energy on the defect production based on CMD and 2T-MD, respectively. In addition, the influences of electron density, irradiation temperature and e-ph coupling activation time on the defect production were investigated under the high-energy ion irradiation based on 2T-MD, respectively.

3.1 Effects of irradiation energy on the irradiation defects

We first calculated the influences of irradiation energy on irradiation defects formed in tungsten based on CMD and 2T-MD, respectively. Figure 1 shows the relationship between Frenkel pairs (FPs) and irradiation energy. As can be seen from the figure, the number of irradiation defects increases with the increase of irradiation energy. The number of peak defects calculated using 2T-MD differs greatly from that calculated by CMD. The number of surviving defects calculated by the two methods are almost the same under low-energy irradiation, and the difference is significant under high-energy irradiation.

Figure 1

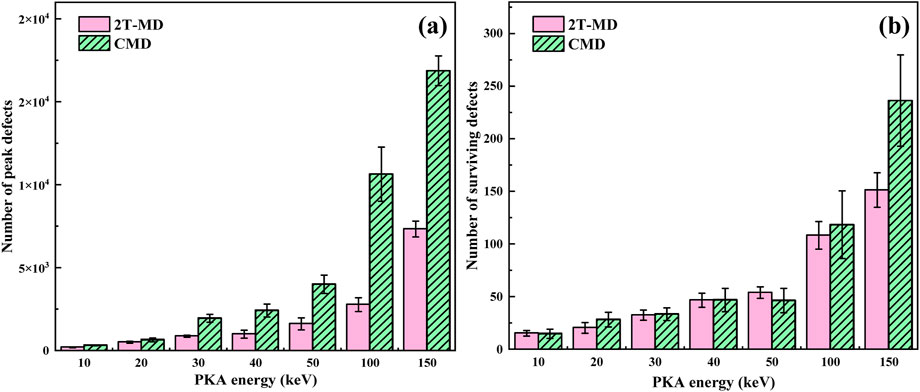
Figure 1. Variations of the numbers of Frenkel pairs calculated by CMD and 2T-MD with the PKA energy, respectively. (a) Peak defect and (b) surviving defect. The error bars represent the standard deviations.

3.2 Effects of electron density on the irradiation defects

Considering that the inner electrons may be excited under high-energy ion irradiation [34–36], we conducted a study of the effects of electron density on the defect production at the irradiation energy of 150 keV. The electron density was expressed as the number of electrons in W. The numbers of 6, 14 and 28 electrons corresponded to the electron densities of 0.378, 0.883 and 1.766 e/ų, respectively. Figure 2 shows the variation of the number of Frenkel defects with electron density. It can be found that the number of peak defects decreases with the increase of electron density, while the number of surviving defects for different electron density does not change much.

Figure 2

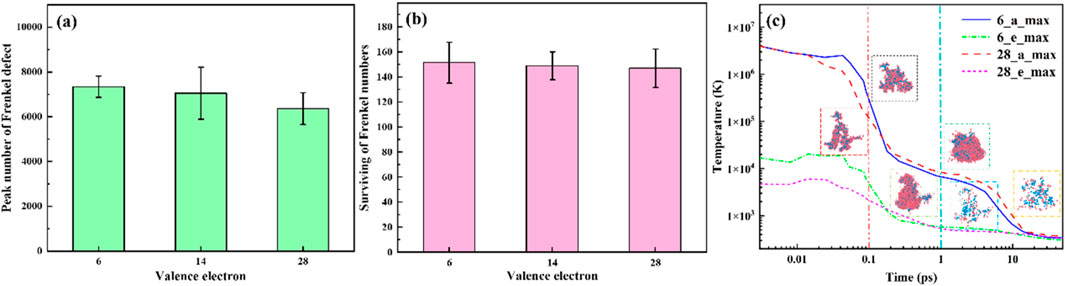
Figure 2. Variations of the numbers of peak (a) and surviving (b) defects calculated by 2T-MD with the electron density at 150 keV. (c) The insets, from left to right, depict the FPs defects at 0.1 ps, 1 ps, and 10 ps, respectively. FPs with electron densities of 6 and 28 are displayed in the upper and lower sections of the panel, respectively. The red and blue spheres represent interstitial atoms and vacancy defects, respectively. The error bars in (a, b) represent the standard deviations.

3.3 Effects of irradiation temperature on the irradiation defects

This subsection aims on the effects of irradiation temperature (from 300 K to 1500 K) on the defects production at the irradiation energy of 150 keV. Figures 3a, b show the effect of irradiation temperature on the peak and surviving defects, respectively. It can be found from the figure that both the numbers of peak defects calculated by the two methods increase with temperature. The number of surviving Frenkel pairs performed by CMD decreases with temperature. However, the surviving defects calculated using 2T-MD show similar numbers with temperature.

Figure 3

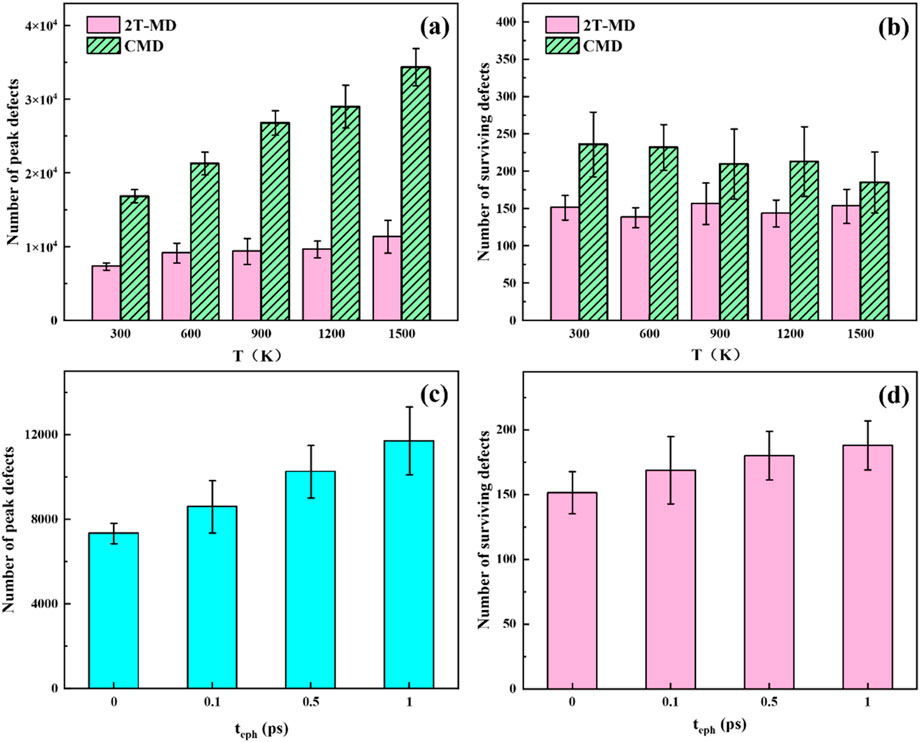
Figure 3. Variation of the number of Frenkel pairs with temperature [(a) peak defects, (b) surviving defects] and e-ph coupling activation time [(c) peak defects, (d) surviving defects] at 150 keV. The error bars represent the standard deviations.

3.4 Effects of e-ph coupling activation time on the irradiation defects

We studied the effects of e-ph coupling activation time on the defect production under the irradiation energy of 150 keV and irradiation temperature of 300 K. The e-ph coupling activation time was chosen to be 0 ps (since the simulation system has an initial temperature of 300 K, the atoms have collective vibration modes at the beginning of irradiation), 0.1 ps, 0.5 ps and 1.0ps, respectively. Figures 3c, d show the peak and surviving defects with different activation time of e-ph coupling (t_e-ph) at 150 keV. As can be seen from the figure, both the numbers of peak and surviving defects decrease with the decrease of the activation time.

4 Discussion

This part mainly presents the discussion of the results in Section 3.

4.1 Effects of irradiation energy on the irradiation defects

Compared with the CMD calculation results (Figure 1), the number of peak defects calculated using 2T-MD model is significantly reduced, meaning that the electronic effect has a significant influence on the irradiation damage, especially under high-energy irradiation. In addition, The results show that the electronic effect has little influence on the surviving defects under low-energy irradiation, and CMD can accurately describe the creation of the surviving defects, which is in good agreement with the results calculated by Fu et al. [37–39]. Table 1 shows the comparison of the number of stable Frenkel defect pairs in pure W at low energy. However, the role of the electronic effect becomes significant under high-energy ion irradiation and thus it is essential to considered the electronic effect.

Table 1

Table 1. Comparison of the number of stable Frenkel defect pairs in pure W.

The typical processes of the irradiation defects calculated using 2T-MD model at 150 keV are exhibited in Supplementary Figure S1. The number of defects reaches the maximum at 1.704 ps, and then gradually decreases, stabilizing at 10.612 ps. To elucidate the formation mechanism of defects, we analyzed the local atomic and electronic temperatures (see Figures 4, 5; Supplementary Videos S1, S2). Meanwhile, the evolution of local temperature was represented in one dimension to describe the local temperature more clearly, as shown in Figure 6. As can be seen from the figure, the local atomic temperature is very high at the beginning of irradiation. We extracted the maximum atomic and electronic temperatures from one-dimensional temperatures (see Figure 7a). It was found that the former is always larger than the latter before equilibrium, indicating that the electronic subsystems act as heat sinks. However, the local electronic temperature can be higher than the local atomic temperature. Figure 7b shows the local atomic and electronic temperatures in a cell (The cell, which is near the center of the MD box, is marked by a triangle in Figure 6). It can be found that the electronic temperature reaches its peak value (∼3,000 K) at close to 0.07 ps, at which time the atomic temperature is relatively low. Thus electronic subsystem can transfer energy to the atomic subsystem via e-ph coupling, resulting in the increase in energy and temperature of the atomic system. As shown in Figure 7b, the atomic temperature reaches its maximum (∼2000 K) at about 0.7 ps. This excess energy of the atomic system can thermally stimulate the recombination of defects, leading to a decline in the number of defects. After 10 ps, the temperatures of the two subsystems reach equilibrium.

Figure 4

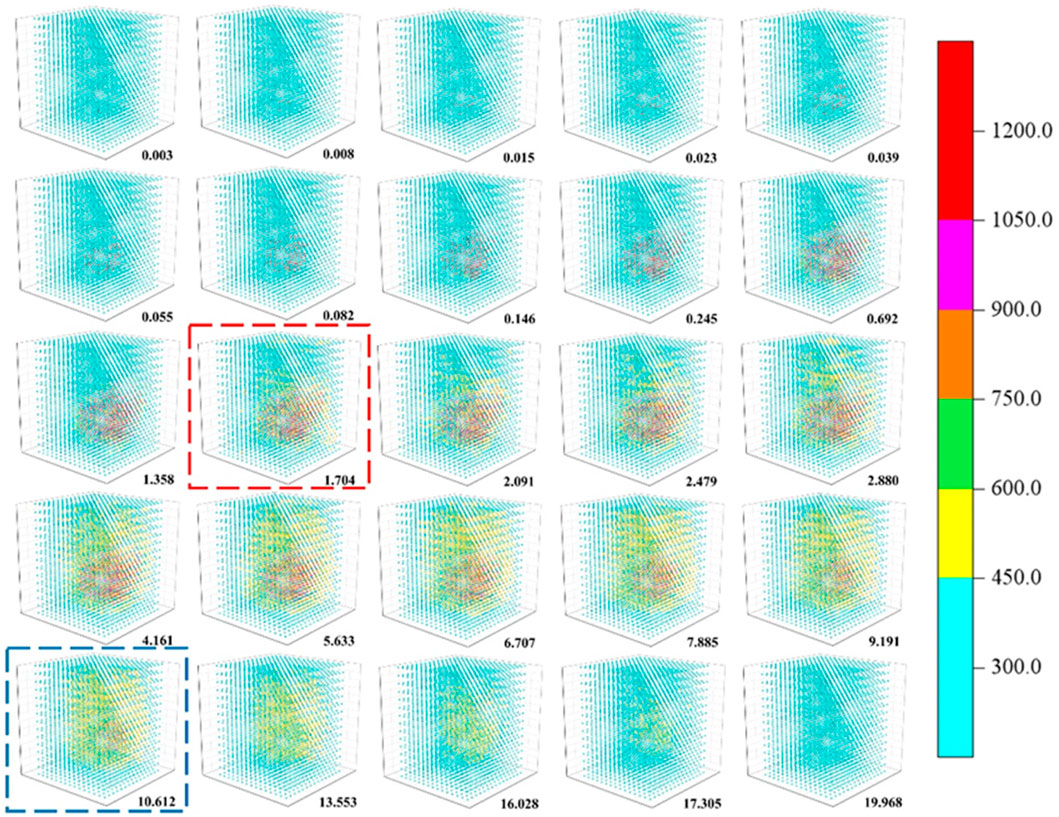
Figure 4. Evolution of local atomic temperature calculated by 2T-MD at 150 keV. The time unit is ps and the temperature unit is K. The red and blue represent the atomic temperatures corresponding to the peak defect and the residual defect, respectively.

Figure 5

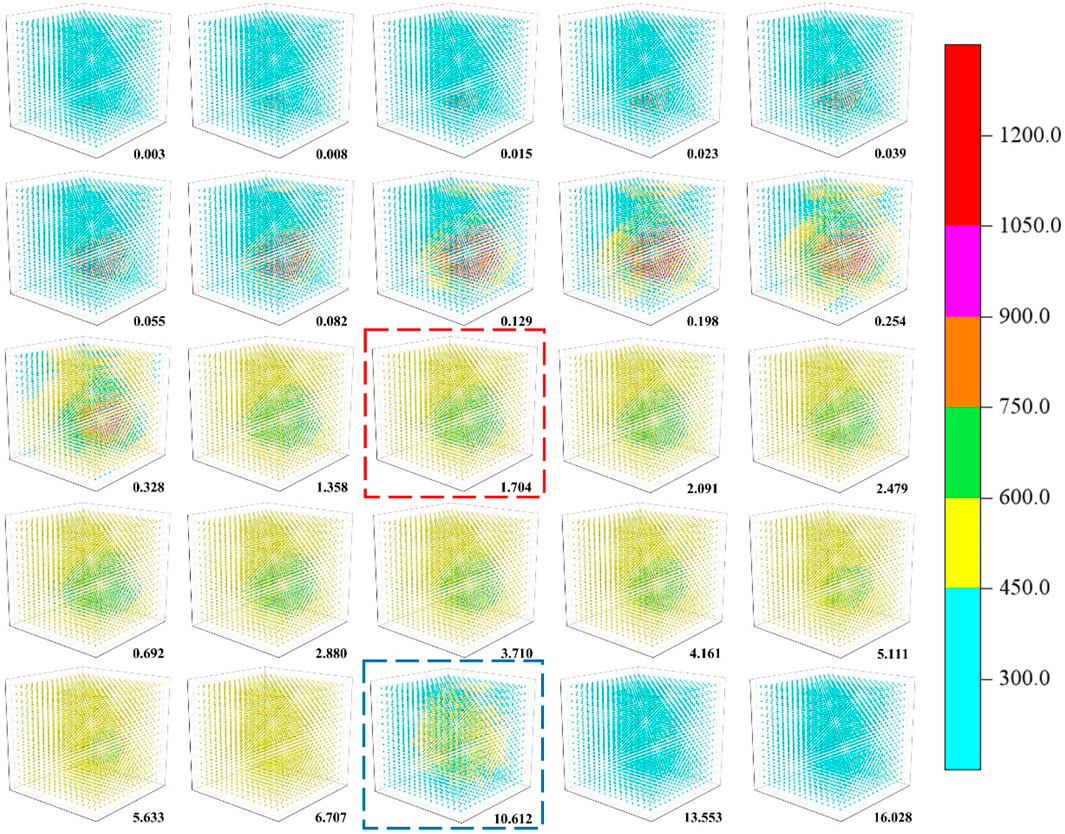
Figure 5. Evolution of local electronic temperature calculated by 2T-MD at 150 keV. The time unit is ps and the temperature unit is K. The red and blue boxes represent the electronic temperatures corresponding to the peak defect and the residual defect, respectively.

Figure 6

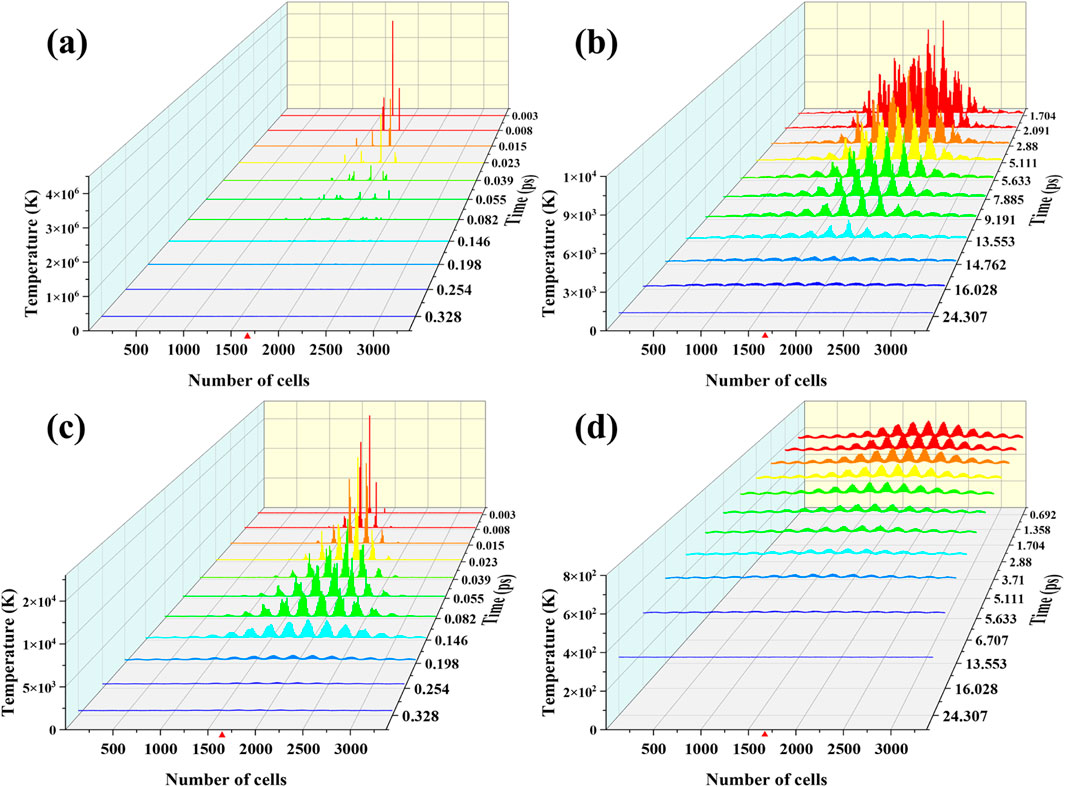
Figure 6. One-dimensional representation of the time evolution of atomic (a, b) and electronic (c, d) temperatures of representative 2T-MD cascades with the PKA energy of 150 keV. MD box contains a total of 3,375 (15 × 15 × 15) coarse-grained cells. The triangle indicates a typical cell near the center of the MD box.

Figure 7

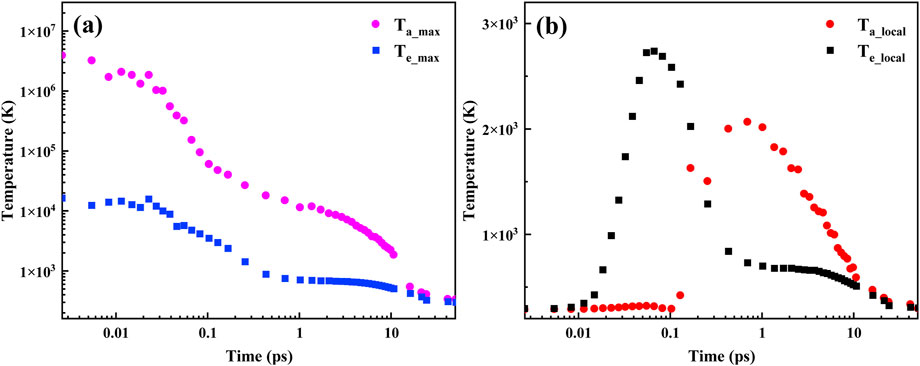
Figure 7. (a) Maximum atomic and electronic temperatures of representative 2T-MD cascades with the PKA energy of 150 keV. (b) Evolution of the atomic and electronic temperatures of a typical cell marked by a triangle in Figure 6.

4.2 Effects of electron density on the irradiation defects

The reason why the number of peak defects decreases with the increase of electron density may be ascribed to the fact that the electronic subsystem cools down slower for higher electronic densities (see Figure 2c). As a result, more energy can be transferred to the atomic subsystem, enhancing interstitial-vacancy recombination and resulting in a decrease in the number of defects. Compared to the maximum atomic temperature with the electron density of 6, the atomic temperature with the electron density of 28 is slightly higher for a longer time (after 0.1 ps), which may enhance the defect recombination and reduce the number of defects. These results indicate that the excitation of inner electrons induced by high-energy ion irradiation may lead to the reduction of defects, especially the number of peak defects. In addition, one should be noted from Figure 2c that both the maximum atomic and electronic temperatures tend to be the same after 10ps, regardless of the electron density. Therefore, the electron density does not seem to have significant effect on the number of surviving defects (see Figure 2b). These results are of great significance to comprehensively understand the influence of electronic effects (including the inner electrons) on the irradiation damage.

4.3 Effects of irradiation temperature on the irradiation defects

As can be seen from Figures 3a, b, both the numbers of peak defects calculated by the CMD and 2T-MD methods increase with temperature, which agrees with the results of Zarkadoula et al. [21]. This suggests that there is on average more defect formation in the thermal spike at higher temperature. The number of surviving Frenkel pairs performed by CMD decreases with temperature, which is consistent with the previous results, such as iron [40, 41] and gold [42]. However, the surviving defects calculated using 2T-MD show similar numbers with temperature. Zarkadoula et al investigated the irradiation defects in W at 300 K and 800 K under 300 keV irradiation based on 2T-MD, and found that the number of surviving defects at 800 K was larger than that at 300 K [21]. In this work, if we only observes the number of irradiation defects at 300 K and 900 K, and can find that the defect number at 900 K is larger than that at 300 K, which is consistent with the above results. However, when the temperature ranges from 300 K to 1,500 K, a similar number of surviving defects are observed using 2T-MD as the temperature increases.

These phenomena may be attributed to several factors. (1) Temperature can cause thermal expansion, weakening atomic bonds and making defects easier to be created. Therefore, the higher the temperature, the more defects can be created. (2) Due to the electronic effect, there may be a lager disordered region for the cascades carried out at high temperatures, that is, the peaks of the cascades are wider [21]. As a result, the defects are able to survive during the annealing process, leading to more defects. (3) As the temperature rises, the thermal spike lifetime increases. This allows more defects to move before cooling, leading to an increase in the interstitial-vacancy recombination [41]. (4) As the temperature increases, the length of the focused collision sequence becomes shorter, and the cascade tends to have a more compact form, thus resulting in less interstitial-vacancy separation. The first two factors may lead to the increase of defect number, and the latter two factors result in the decrease of defect number. Therefore, considering multiple factors (Neither peak defect nor surviving defect may be a single factor), the number of peak defects increases and the number of surviving defects is similar with the increase of temperature.

4.4 Effects of e-ph coupling activation time on the irradiation defects

The number of peak defects decreases with the decrease of the activation time (see Figure 3c), indicating that the number of peak defects increases with the delay of the activation time. This is ascribed to the fact that the e-ph coupling can remove energy from the thermal spike, thus reducing the number of defects produced. Moreover, the surviving defect number also decreases with the decrease of activation time (see Figure 3d). The smaller activation time, the smaller number of surviving defects, which agrees with the findings of Zarkadoula et al. [43]. The mechanism can be explained from two aspects. On the one hand, the number of peak defects decreases with the decrease of the activation time, which can lead to less damage formed in W for the smaller activation time. On the other hand, some energy is fed back to the atomic system locally through the e-ph coupling. This means that local region of the cascade cools more slowly. Therefore, the number of surviving defects is reduced.

5 Conclusion

In summary, a two-temperature molecular dynamics method was used to investigate the influences of irradiation energy, irradiation temperature, electron density and electron-phonon coupling activation time on the irradiation defects formed in tungsten. Compared with CMD calculation results, the numbers of peak and surviving defects calculated using 2T-MD model are significantly reduced under high-energy irradiation, meaning that electronic effect has a significant effect on the irradiation defects. In addition, the electron density has obvious effect on the peak defects, but little effect on the surviving defects. With the increase of temperature, the number of peak defects calculated using 2T-MD increases, while the surviving defects show similar numbers. Furthermore, the number of defects increases with the delay of the e-ph coupling activation time, regardless of peak defect or surviving defect. This is ascribed to the fact that e-ph coupling can remove energy from thermal spikes and allow local energy to feed back into the atomic system, promoting defect recombination and reducing the creation of defects. This study offers a more realistic way for the energy dissipation process of high-energy cascade damage in tungsten, and provides valuable information for understanding the influence of electronic effects on primary radiation damage.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

SS: Data curation, Funding acquisition, Software, Supervision, Writing – original draft. SW: Software, Visualization, Writing – original draft. CeZ: Formal Analysis, Writing – review and editing. CaZ: Conceptualization, Formal Analysis, Writing – review and editing. GP: Formal Analysis, Supervision, Writing – review and editing. B-SL: Supervision, Writing – review and editing.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. This work was supported by the Fund of Beijing Science and Technology Plan under Grant No: Z221100005822005, and the R&D Fund of Wuhu Research Institute, Anhui University of Science and Technology under Grant No: ALW2022YF01.

Conflict of interest

Author CeZ was employed by Beijing Tuobao Additive Manufacturing Technology Co.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2025.1592186/full#supplementary-material

References

1. Ding S, Garofalo AM, Wang HQ, Weisberg DB, Li ZY, Jian X, et al. A high-density and high-confinement tokamak plasma regime for fusion energy. Nature (2024) 629(8012):555–60. doi:10.1038/s41586-024-07313-3

PubMed Abstract | CrossRef Full Text | Google Scholar

2. El-Atwani O, Li N, Li M, Devaraj A, Baldwin JKS, Schneider MM, et al. Outstanding radiation resistance of tungsten-based high-entropy alloys. Sci Adv (2019) 5(3):eaav2002. doi:10.1126/sciadv.aav2002

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Kim SY, Kavak S, Bayrak KG, Sun C, Xu H, Lee MJ, et al. Demonstration of helide formation for fusion structural materials as natural lattice sinks for helium. Acta Materialia (2024) 266:119654. doi:10.1016/j.actamat.2024.119654

CrossRef Full Text | Google Scholar

4. Echols JR, Garrison LM, Reid N, Parish CM, Hasegawa A, Bhattacharya A, et al. Degradation of electrical resistivity of tungsten following shielded neutron irradiation. Acta Materialia (2023) 257:119025. doi:10.1016/j.actamat.2023.119025

CrossRef Full Text | Google Scholar

5. Jian J, Shi L, Zhang B. The behavior of helium bubble evolution under neutron irradiation in different tungsten surfaces. J Nucl Mater (2024) 593:154994. doi:10.1016/j.jnucmat.2024.154994

CrossRef Full Text | Google Scholar

6. Lasa A, Blondel S, Cusentino MA, Dasgupta D, Hatton P, Marian J, et al. Development of multi-scale computational frameworks to solve fusion materials science challenges. J Nucl Mater (2024) 594:155011. doi:10.1016/j.jnucmat.2024.155011

CrossRef Full Text | Google Scholar

7. Luo LM, Zhao ZH, Yao G, Wu YC. Recent progress on preparation routes and performance evaluation of ODS/CDS-W alloys for plasma facing materials in fusion devices. J Nucl Mater (2021) 548:152857. doi:10.1016/j.jnucmat.2021.152857

CrossRef Full Text | Google Scholar

8. Sainju R, Patino M, Baldwin MJ, Atwani OE, Kolasinski R, Zhu Y. In-situ ETEM study of plasma-facing tungsten nanofuzz oxidation at atmospheric pressure: microstructure evolution and substrate-free oxidation kinetics. Acta Materialia (2024) 278:120282. doi:10.1016/j.actamat.2024.120282

CrossRef Full Text | Google Scholar

9. Wang S, Wang H, Yi X, Tan W, Ge L, Sun Y, et al. Damage recovery stages revisited: thermal evolution of non-saturated and saturated displacement damage in heavy-ion irradiated tungsten. Acta Materialia (2024) 273:119942. doi:10.1016/j.actamat.2024.119942

CrossRef Full Text | Google Scholar

10. Chen J, Wang X, Li K, Li M, Fu X, Hu R, et al. A novel performance optimization study in additively manufactured tungsten-5wt.% rhenium alloys reinforced with dilute carbon. Scripta Materialia (2024) 240:115851. doi:10.1016/j.scriptamat.2023.115851

CrossRef Full Text | Google Scholar

11. He G, Yu H, Karamched P, Liu J, Hofmann F. Elastic strain associated with irradiation-induced defects in self-ion irradiated tungsten. Scripta Materialia (2023) 237:115687. doi:10.1016/j.scriptamat.2023.115687

CrossRef Full Text | Google Scholar

12. Liu L, Qiu R, Chen Y, Jiang M, Gao N, Huang B, et al. Displacement cascades database from molecular dynamics simulations in tungsten. J Nucl Mater (2023) 580:154415. doi:10.1016/j.jnucmat.2023.154415

CrossRef Full Text | Google Scholar

13. Zhao H, Zeng X, Yang X, Chen W, Wu J. Investigation of the temperature effect on the primary radiation damage near the grain boundary in tungsten using molecular dynamics simulations. Nucl Instr Methods Phys Res Section B: Beam Interactions Mater Atoms (2020) 476:32–9. doi:10.1016/j.nimb.2020.04.030

CrossRef Full Text | Google Scholar

14. Zhang Y, Weber WJ. Ion irradiation and modification: the role of coupled electronic and nuclear energy dissipation and subsequent nonequilibrium processes in materials. Appl Phys Rev (2020) 7(4):041307. doi:10.1063/5.0027462

CrossRef Full Text | Google Scholar

15. Zhang Y, Silva C, Lach TG, Tunes MA, Zhou Y, Nuckols L, et al. Role of electronic energy loss on defect production and interface stability: comparison between ceramic materials and high-entropy alloys. Curr Opin Solid State Mater Sci (2022) 26(4):101001. doi:10.1016/j.cossms.2022.101001

CrossRef Full Text | Google Scholar

16. Duffy DM, Rutherford AM. Including the effects of electronic stopping and electron–ion interactions in radiation damage simulations. J Phys Condensed Matter (2007) 19(1):016207. doi:10.1088/0953-8984/19/1/016207

CrossRef Full Text | Google Scholar

17. Rutherford AM, Duffy DM. The effect of electron–ion interactions on radiation damage simulations. J Phys Condensed Matter (2007) 19(49):496201. doi:10.1088/0953-8984/19/49/496201

CrossRef Full Text | Google Scholar

18. Zarkadoula E, Samolyuk G, Xue H, Bei H, Weber WJ. Effects of two-temperature model on cascade evolution in Ni and NiFe. Scripta Materialia (2016) 124:6–10. doi:10.1016/j.scriptamat.2016.06.028

CrossRef Full Text | Google Scholar

19. Zarkadoula E, Samolyuk G, Weber WJ. Effects of electronic excitation on cascade dynamics in nickel–iron and nickel–palladium systems. Scripta Materialia (2017) 138:124–9. doi:10.1016/j.scriptamat.2017.05.041

CrossRef Full Text | Google Scholar

20. Zarkadoula E, Samolyuk G, Weber WJ. Effects of electron-phonon coupling and electronic thermal conductivity in high energy molecular dynamics simulations of irradiation cascades in nickel. Comput Mater Sci (2019) 162:156–61. doi:10.1016/j.commatsci.2019.02.039

CrossRef Full Text | Google Scholar

21. Zarkadoula E, Duffy DM, Nordlund K, Seaton MA, Todorov IT, Weber WJ, et al. Electronic effects in high-energy radiation damage in tungsten. J Phys Condensed Matter (2015) 27(13):135401. doi:10.1088/0953-8984/27/13/135401

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Plimpton S. Fast parallel algorithms for short-range molecular dynamics. J Comput Phys (1995) 117(1):1–19. doi:10.1006/jcph.1995.1039

CrossRef Full Text | Google Scholar

23. Chen Y, Fang J, Liu L, Hu W, Jiang C, Gao N, et al. The interactions between rhenium and interstitial-type defects in bulk tungsten: a combined study by molecular dynamics and molecular statics simulations. J Nucl Mater (2019) 522:200–11. doi:10.1016/j.jnucmat.2019.05.003

CrossRef Full Text | Google Scholar

24. Ziegler JF, Biersack JP, Littmark U. The stopping and range of ions in matter. New York: Pergamon Press (1985).

Google Scholar

25. Sand AE, Dudarev SL, Nordlund K. High-energy collision cascades in tungsten: dislocation loops structure and clustering scaling laws. Europhysics Lett (2013) 103(4):46003. doi:10.1209/0295-5075/103/46003

CrossRef Full Text | Google Scholar

26. Chen Y, Liao X, Qiu R, Liu L, Hu W, Deng H. Primary radiation damage in tungsten-based high-entropy alloy: interatomic potential and collision cascade simulations. J Nucl Mater (2023) 585:154646. doi:10.1016/j.jnucmat.2023.154646

CrossRef Full Text | Google Scholar

27. Ziegler JF, Ziegler MD, Biersack JP. SRIM – the stopping and range of ions in matter. Nucl Instr Methods Phys Res Section B: Beam Interactions Mater Atoms (2010) 268(11):1818–23. doi:10.1016/j.nimb.2010.02.091

CrossRef Full Text | Google Scholar

28. Fujimoto JG, Liu JM, Ippen EP, Bloembergen N. Femtosecond laser interaction with metallic tungsten and nonequilibrium electron and lattice temperatures. Phys Rev Lett (1984) 53(19):1837–40. doi:10.1103/physrevlett.53.1837

CrossRef Full Text | Google Scholar

29. Patra P, Srivastava SK. Temperature dependent electron–phonon coupling and heat capacity in thin slabs of topological insulator Bi₂Te₃ as pertinent to the thermal spike model. Nucl Instr Methods Phys Res Section B: Beam Interactions Mater Atoms (2016) 379:9–12. doi:10.1016/j.nimb.2016.01.043

CrossRef Full Text | Google Scholar

30. Lin Z, Zhigilei LV, Celli V. Electron-phonon coupling and electron heat capacity of metals under conditions of strong electron-phonon nonequilibrium. Phys Rev B (2008) 77(7):075133. doi:10.1103/physrevb.77.075133

CrossRef Full Text | Google Scholar

31. Li YG, Zhou WH, Huang LF, Zeng Z, Ju X. Theoretical simulation of thermal behavior in transient heat loads testing of plasma-facing materials. Fusion Eng Des (2011) 86(12):2812–20. doi:10.1016/j.fusengdes.2011.04.011

CrossRef Full Text | Google Scholar

32. Setyawan W, Nandipati G, Roche KJ, Heinisch HL, Wirth BD, Kurtz RJ. Displacement cascades and defects annealing in tungsten, Part I: defect database from molecular dynamics simulations. J Nucl Mater (2015) 462:329–37. doi:10.1016/j.jnucmat.2014.12.056

CrossRef Full Text | Google Scholar

33. Stukowski A. Visualization and analysis of atomistic simulation data with OVITO-the Open Visualization Tool. Model Simulation Mater Sci Eng (2010) 18:015012. doi:10.1088/0965-0393/18/1/015012

CrossRef Full Text | Google Scholar

34. Xiong GG, Jin WQ, Wang F, Mao F. First-principles study of inner-electron excitation of tungsten underproton and helium ion irradiation. Physica Rev B (2024) 109:174314. doi:10.1103/physrevb.109.174314

CrossRef Full Text | Google Scholar

35. Li SM, Mao F, Zhao XD, Li BS, Jin WQ, Zuo WQ, et al. First-principles study of the electronic stoppingpower of indium for protons and He ions. Physica Rev B (2021) 104:214104. doi:10.1103/physrevb.104.214104

CrossRef Full Text | Google Scholar

36. Li SM, Mao F, Zhao XD, Jin WQ, Zuo WQ, Li BS, et al. Contribution offelectron excitation to electronicstopping power of platinum for protons. Phys Rev B (2022) 106:014103. doi:10.1103/physrevb.106.014103

CrossRef Full Text | Google Scholar

37. Fikar J, Schäublin R. Molecular dynamics simulation of radiation damage in bcc tungsten. J Nucl Mater (2009) 386-388:97–101. doi:10.1016/j.jnucmat.2008.12.068

CrossRef Full Text | Google Scholar

38. Park NY, Kim YC, Seok HK, Han SH, Cho S, Cha PR. Molecular dynamics simulation of irradiation damage in tungsten. Nucl Instr Methods Phys Res Section B: Beam Interactions Mater Atoms (2007) 265(2):547–52. doi:10.1016/j.nimb.2007.10.003

CrossRef Full Text | Google Scholar

39. Fu J, Chen Y, Fang J, Gao N, Hu W, Jiang C, et al. Molecular dynamics simulations of high-energy radiation damage in W and W–Re alloys. J Nucl Mater (2019) 524:9–20. doi:10.1016/j.jnucmat.2019.06.027

CrossRef Full Text | Google Scholar

40. Stoller RE, Guiriec SG. Secondary factors influencing cascade damage formation. J Nucl Mater (2004) 329-333:1238–42. doi:10.1016/j.jnucmat.2004.04.288

CrossRef Full Text | Google Scholar

41. Bacon DJ, Gao F, Osetsky YN. The primary damage state in fcc, bcc and hcp metals as seen in molecular dynamics simulations. J Nucl Mater (2000) 276(1):1–12. doi:10.1016/s0022-3115(99)00165-8

CrossRef Full Text | Google Scholar

42. Nordlund K, Averback RS. Point defect movement and annealing in collision cascades. Phys Rev B (1997) 56(5):2421–31. doi:10.1103/physrevb.56.2421

CrossRef Full Text | Google Scholar

43. Zarkadoula E, Samolyuk GD, Weber WJ. Effects of the electron-phonon coupling activation in collision cascades. J Nucl Mater (2017) 490:317–22. doi:10.1016/j.jnucmat.2017.04.020

CrossRef Full Text | Google Scholar