Evolvable data model decomposition for hydropower dispatching networks via collaborative intrusion detection

To maximize the operational value of hydropower stations and achieve expected economic benefits, efficient dispatching and command operations are essential. With the growing dimensionality of indicator data in hydraulic engineering, traditional methods face challenges in handling complex multi-dimensional spatial data modeling. In particular, traditional Kalman filtering methods often suffer from the “curse of dimensionality” during model solving, resulting in long computation times and model instability. This paper proposes an approach based on an evolvable data model decomposition for hydropower dispatching networks, leveraging collaborative intrusion detection techniques. The improved Kalman filtering algorithm structure is designed to tackle multi-stage dynamic decision-making processes involving multi-regular state function parameters. By decomposing single-stage primary problems into multiple elementary subproblems, the operational principles of multi-dimensional spatial analysis are modified. Through function simplification and rational point-wise problem allocation, priority conditions for global optimization of decision processes are established, thus promoting the optimization of multi-dimensional space folding and movement velocities. In the construction of stochastic multi-dimensional spaces, optimized stochastic indicator models and parametric simulation designs are employed. The initial step is to define hydropower dispatching strategies, which are compared with explicit model stochastic optimization while ensuring load output requirements and cost-benefit constraints. Guided by the aggregation concept of decomposable indicators, an implicit stochastic optimal dispatching boundary is established, forming a data transfer function model for hydropower scheduling. The collaborative intrusion detection mechanism plays a crucial role in safeguarding the security and reliability of the data model decomposition process, ensuring the robustness of the overall system. Finally, the operation and analysis of the simulation system validate the guiding role of the dispatching functions in hydropower systems. The results demonstrate that the proposed hydropower scheduling solution, with its evolvable data model decomposition and collaborative intrusion detection, exhibits superior operability and practical utility for operational dispatching command tasks in hydraulic engineering projects. This methodology provides an effective technical pathway for addressing complex scheduling challenges in modern hydropower systems, offering a new perspective on enhancing the efficiency and security of hydropower dispatching networks.

1 Introduction

To facilitate the integration of hydropower projects into green energy accommodation and enhance the overall regulatory potential and automated management capabilities of power systems, it is imperative to strengthen demand response mechanisms and improve compensation strategies for water resources. This requires continuous refinement of risk-sharing mechanisms within the indicator system, equitable allocation of hydropower operational costs, and the gradual establishment of a scientifically grounded mechanism for rational green energy allocation [1]. Ensuring that electricity trading adopts a “supplement-sustainable” transaction structure is critical. Transitioning from foundational directive-based transactions to supply-demand-driven accommodation will promote stable power market operations. Decomposing the structural components of hydropower resources not only quantifies the performance of water resource reserves and replenishment but also accounts for factors such as power generation-load discrepancies, thereby ensuring the stable operation of hydropower projects [2]. Furthermore, the dispatch and coordination of green energy should explore the equilibrium between absorption and consumption, as well as reconcile conflicts between resource optimization and cost-benefit trade-offs [3]. In a Cyber-Physical Social System (CPSS), the optimization of hydropower dispatching involves not only the economy of energy distribution, but also the physical security and data privacy of the power grid. For example, the real-time data interaction of hydropower system may face the risk of network attacks (such as DDoS) or data tampering, so it is necessary to incorporate security constraints into the dispatching model to achieve the collaborative optimization of “security-economy-society” multi-objective in CPSS.

As the external environment of power systems evolves dynamically, the exponential growth of actionable indicator data imposes heightened demands on system analytical and decomposition capabilities. With electricity trading in spot market pricing becoming increasingly sensitive to data timeliness, the timely decomposition and analysis of power data necessitate robust technical support, including scientific computational models and precise operational algorithms. Sannigrahi S et al. employ an opportunity-constrained strategy to quantify uncertainties in water resources, incorporate short-term power generation revenue from hydropower stations, and construct a decomposable data model to validate its rationality. By iterating the Hilbert bi-level structural product, a method for eliminating overload management is proposed [4]. Tso W W et al. leverage power trading platforms to decompose market-impact indicator characteristics, addressing technical challenges in transforming single-problem models into multi-level structures. They analyze market uncertainties through preliminary-phase corrections and optimizations of heterogeneous parameters [5]. By establishing a stochastic simulation framework for short-term dispatch scenarios under complex market configurations, Liang J and Tang W resolve multi-dimensional uncertainties, such as power generation, market positioning, and revenue returns. This nested optimization framework achieves coordinated control over power data analysis strategies and power generation revenue [6]. While these studies demonstrate efficacy in small-scale hydropower management, the inherent physical uncertainties of green energy become increasingly pronounced in resolving local-global optimality challenges as grid-scale integration expands [7]. Consequently, determining single-indicator solutions must align with global optimization rationality, necessitating further in-depth research [8].

In this context, how to effectively manage and optimize the hydropower scheduling has become an important research topic in the current power system. This study focuses on decomposing the comprehensive utilization objectives of hydropower projects based on long-term energy supply-demand characteristics. It ensures seamless integration of core indicator features to achieve physical delivery of energy loads and advance automated energy management. Thus, the scientific analysis of hydropower project indicators, their digitization, and feature decomposition constitute the research emphasis. The follow-up study will integrate the wind and solar energy prediction data and construct a multi-energy complementary dispatching model.

Key innovations of the study mainly include two aspects: firstly, the proposed hydropower dispatch model incorporates feature vectors of diverse indicators, constructs high-dimensional functions, and optimizes complex structures to alleviate system analytical burdens; secondly, an optimized model harmonizing critical indicators that includes hydraulic energy storage, generation-load balance, and cost-revenue dynamics is established, which can enhance the security of water resources and economic returns, and can resolve the inherent trade-offs between resource supply and power generation profitability.

2 The relative work

Although the existing research has made some progress in the field of hydropower scheduling, most of the methods face the problems of high computational complexity and model collapse when dealing with high-dimensional and strongly coupled hydropower scheduling data. Therefore, this paper aims to propose an improved algorithm framework to solve these problems.

2.1 The improved Kalman filtering

Based on the traditional Kalman filtering framework, the local space feature vector is introduced as the state correction term. Let the system state equation be:

$x_k=A_{k-1}{x}_{k-1}+{\lambda }_k·\nabla S(1)$

In the formula, the newly added term $x_k$ is based on the dynamic correction of the spatial feature $A_{k-1}{x}_{k-1}$, $A_{k-1}$ is the gradient vector $k-1$ of the local space $A$, ${\lambda }_k$ is the adaptive adjustment coefficient, and $\nabla S$ is the loss term.

The predicted status is as follows:

$\widehat{x}{k}^{-}=\sqrt{A_k\widehat{x}k-1}+B_k{u}_k(2)$

Where: $\widehat{x}k$ is the spatial feature weight, $B_k$ is the feature mapping matrix, and $u_k$ is the spatial vector.

The covariance prediction is:

$P_k^{-}=A_k{P}_{k-1}{\mathrm{\Gamma }}_k^T(3)$

In the formula, $P_k^{-}$ is the prediction direction, and the new term $P_{k-1}$ reflects the uncertainty of ${\mathrm{\Gamma }}_k^T$ introduced by the spatial characteristics.

Sliding window is used to calculate local spatial gradient for feature extraction.

2.2 Multidimensional space vector decomposition

Hydro-scheduling data within Cyber-Physical-Social Systems (CPSS) has high-dimensional, strongly coupled, and dynamic characteristics. Traditional Kalman filtering methods encounter the curse of dimensionality within CPSS environments due to their reliance on fixed covariance matrices, which inadequately capture the real-time evolution of spatiotemporal correlations. For instance, modeling the dynamic interplay between hydrological data and power grid load necessitates a multi-dimensional state-space representation; conventional approaches, however, frequently incur prohibitive computational complexity, potentially leading to model instability. To decompose the intricate structure of a multidimensional model, the principle for addressing multidimensional and multistage problems is advanced by transforming the resolution of multiple primary problems into the treatment of a set of secondary problems [9]. Specifically, this approach involves fixing the parameters of normal state functions at the current primary stage while exclusively optimizing and adjusting the parameters of selected decision process functions within the same primary stage. This methodology ultimately yields a secondary processing space that facilitates the future optimization of boundary conditions [10]. The optimization cycle iterates repeatedly until convergence is achieved [11]. The procedure is outlined as follows:

(1) Determine the point trajectory $\left(\alpha ,\beta \right)$ and the boundary condition $\lambda$

Consider the feature vector representing “flood season discharge volume.” Its physical interpretation corresponds to a weighted sum of reservoir storage capacity and downstream ecological flow requirements. The weighting coefficients are calibrated using historical operational data, as illustrated in Figure 1.

(2) It is determined that the energy storage $\mu$ of the power station at the $t$ th time is fixed, and the energy storage at the $t+1$ th time will not rise to ${\mu }^{t+1}\le \mu$. Make the optimal solution of the objective compound function value monotonically decreasing at time $t$, that is, the maximum value ${\theta }^{\max }$ of the hydropower station power generation [12].

(3) The energy storage $\mu$ of the power station at time $t$ is not fixed, and the rising range $\sigma$ of the energy storage at time $t+1$ remains unchanged. Adjusting $\sigma$ at time $t+1$, the resulting ${\mu }_{\sigma }^{\max }$ does not decrease monotonically [13].

Figure 1

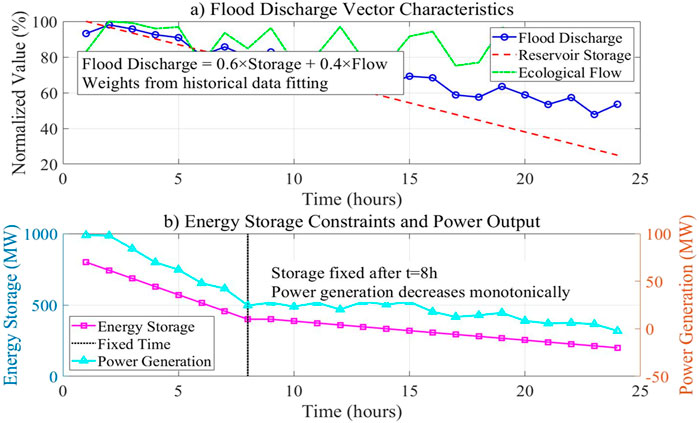
Figure 1. Eigenvector of flood season discharge. (a) Flood discharge vector characteristics. (b) Energy storage constraints and power output.

By analogy, feature processing is performed on all relevant indicators according to the sequence of hydropower stations, generating operational trajectories to serve as iteration point trajectories. The specific implementation steps are as follows:

(1) The relationship between current trajectories and previous iteration trajectory multiples is like this: if precision requirements remain unsatisfied, new dual-iteration computations are initiated; otherwise, product iteration terminates, indicating optimization completion [14].

(2) When analyzing spatial models, conventional rules are applied to resolve energy reserve quantities and step size adjustments through initial computations of distinct numerical boundary conditions. New operational rules are derived under varying boundary conditions, where operational patterns are determined by synthesizing output reference values with corresponding system power values. This enables the construction of multi-dimensional spatial boundaries [15].

Due to the high dimension, strong coupling and dynamic characteristics of hydropower dispatching data, traditional methods are difficult to deal with them effectively. Therefore, this paper proposes a multi-dimensional space vector decomposition method to reduce the computational complexity and improve the model stability.

3 A global analysis model for hydropower dispatching data

To enable comprehensive analysis of hydropower dispatch data, the development of a global analysis model capable of processing multidimensional and highly coupled data is necessary. The model proposed in this study is designed to enhance both the accuracy and efficiency of data analysis through dual-channel feature fusion and localized feature prediction. The solution to low-dimensional stochastic process problems is transformed into addressing high-dimensional transfer function problems by re-expanding the similar feature space of multi-kernels and introducing kernel composite functions to achieve dimensionality and transfer function transformations. Furthermore, resolving orthogonal distance stochastic processes in sample spaces can effectively address feature sample classification and re-entry issues [16]. The proposed methodology demonstrates advantages in maintaining the structural integrity of data architecture and enabling flexible spatial management when solving optimization problems, exhibiting broad application potential in natural language processing and regression analysis [17].

3.1 Dual-channel feature fusion architecture

(1) Seq2-LR branch: gated cycle unit is adopted to handle timing dependencies:

$h_t^{LR}=\text{GRU}\left(x_t,h_{t-1}^{LR}\right)(4)$

Where: $h_t^{LR}$ is the hidden state of the current time step, $x_t$ is the timing feature representation, and $\text{GRU}\left(\right)$ is the gated cycle unit used to capture the timing dependency.

(2) Seq2-PR Branch: build the Spatial Attention Module:

${\alpha }_{ij}=\frac{\exp \left(e_{ij}\right)}{{\displaystyle \sum _k}\exp \left(e_{ik}\right)},e_{ij}=f\left(x_i,x_j\right)(5)$

Where: $a_{ij}$ is the attention weight of spatial location $i\to j$, $e_{ij}$ is the similarity score of location $i\to j$, which is calculated by function ${\displaystyle {\sum }_k}\exp \left(e_{ik}\right)$, and $f\left(x_i,x_j\right)$ is the exponential function, which is used to normalize the attention weight.

Dynamically coupled feature cascading concatenates the outputs $t$ from individual timesteps. An adaptive weighting scheme, with weights learned through parameters, balances the relationships within the hydroelectric dispatch system. Feature alignment is achieved by automatically optimizing the weight coefficients via differentiable architecture search. To this end, a cross-attention mechanism is designed to match the hydrological cycles within a multi-objective loss function. The parameters of this mechanism are dynamically adjusted according to operational priorities.

3.2 Local feature prediction model

To validate the performance of activation functions in NILM problems, this study employs the original functional model Seq2-LR as the baseline. The activation function-optimized model is designated as Seq2-PR, as illustrated in Figure 2.

Figure 2

Figure 2. Seq2-LR network model.

In Figure 2, the Alpha value is set to 0.3, and the implementation of the activation function uses Advanced Activations in Keras. The optimized and improved model is shown in Figure 3.

Figure 3

Figure 3. Seq2-PR network model.

The specific operation steps are as follows:

(1) The reference combination calculates the sample set $\rho$ and sets the fitting regression composite function $\eta$, whose prediction composite function is $\nu$.

(2) The kernel composite function $\varpi$ is introduced to map the sample points whose low-dimensional transfer function is not separable to the high-dimensional external feature space, which transforms the problem of how to solve the stochastic process into the problem of solving the transfer function [18]. The Gaussian function introduced by extending the similar feature model with the help of the $\varpi$-kernel composite function is defined as:

${\eta }_{\rho }^v={\displaystyle \sum _{\alpha ,\beta }^t}\frac{\varpi \left({\theta }^{\max }-{\theta }^{\min }\right)}{\lambda }(6)$

In the formula, $\varpi$ variable parameter of that kernel composite function a is $\left(\alpha ,\beta \right)$;

(3) The general form of the high-dimensional spatial transfer function $\varsigma$ and the insensitive activation function $\xi$ is:

$\varsigma =\left\{\begin{array}{l}{\eta }_{\rho }\sqrt{\frac{{\epsilon }_{\alpha }}{{\epsilon }_{\beta }}}\\ 0\\ {\eta }_{\rho }^{\prime }\sqrt{\frac{{\epsilon }_{\alpha }}{{\epsilon }_{\beta }}}\end{array}\right.(7)$

$\xi ={\displaystyle \sum ^t}{\lambda }^{\alpha }\le 0(8)$

In the formula, a training sample $\epsilon$ is listed in the calculation of the loss caused by insensitivity; The social benefit objective function is:

$\mathrm{S}=\alpha ·\mathrm{U}+\left(1-\alpha \right)·\beta (9)$

In the formula: $S$ is the comprehensive score of social benefits (dimensionless), $U$ is the satisfaction of residents with water use, $\beta$ is the compliance rate of environmental protection, and $\alpha$ is the weight coefficient.

Quantified through questionnaires and policy documents is done.

Referring to the theory of high-dimensional space and the solution of hydropower operation risk index, the optimal solution in the plane is transformed into a quadratic programming problem [19]. When the relaxation function is introduced into the sample point and the optimal solution, the planning and design problem is solved with the help of the Hilbert method, and the regression estimation function of the stochastic process is obtained [20].

In view of the conflict between economic benefits and environmental protection, this paper uses the Pareto Frontier Method to construct a multi-objective evaluation system:

The objective function is to maximize the generation revenue and minimize the ecological flow deviation;

Constraints: they include load demand, reservoir capacity, carbon emission cap; Solution method: the improved algorithm based on NSGA-II generates the non-dominated solution set, and the optimal compromise scheme is determined by the entropy weight method.

4 Analysis of the experiment

4.1 Experimental environment

The scale of the simulation data model is shown in Table 1, including 1272 important indicators of hydropower, with their respective relationship density and characteristic dimensions set [21]. The data source is: the State Grid 2020–2022 hydropower operation data set, processed by Z-score standardization and KNN missing value filling, with a 95% confidence interval. The training set, the test set, and the validation set are defined in a 7:1:2 ratio.

Table 1

Table 1. Experimental environment settings.

As for verifying the optimization effect of the algorithm in this paper, the current mainstream multi-objective algorithm MOPSO [22] (Multi-Objective Particle Swarm Optimization) is introduced to find the optimal solution set. The function problem of solving multiple objective conflicts and MOGWO [23] (Multi-objective Grey Wolf Optimizer) use the optimization rule selection mechanism to select the optimal solution from the data, which is to verify the advanced algorithm in this paper.

4.2 Analysis of the test results

4.2.1 Analysis of algorithm performance testing

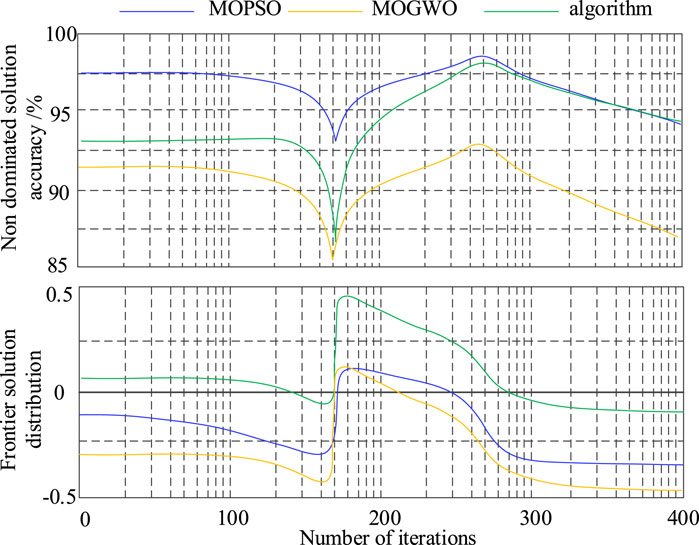
The general standard is optimized and tested by the composite function to evaluate the potential of the improved algorithm for finding the optimal choice. Besides, the decomposition effect of the model in this paper is compared [24]. The performance test results of the algorithm are shown in Table 2 and Figure 4.

Table 2

Table 2. Algorithm performance test results.

Figure 4

Figure 4. Algorithm performance test result.

Test results show that the two non-dominated solutions of the proposed algorithm and MOGWO are close to the false non-dominated frontier solution. Compared with other algorithms, the convergence effect of the proposed algorithm is more uniform, and the decision credibility is more competitive. After several iterative tests, the proposed algorithm has the strongest resolution, and the accuracy of all non-dominated solutions is better than that of the comparison method. In addition, the distribution of the leading solution of the proposed algorithm is uniform, and the probability distribution of the obtained value range is almost the same as that of the algorithm under the same test composite function. It can be seen that the algorithm in this paper has strong stability and accuracy, and shows the strongest quality and ability in finding the potential of the best choice.

4.2.2 Complexity response force test analysis

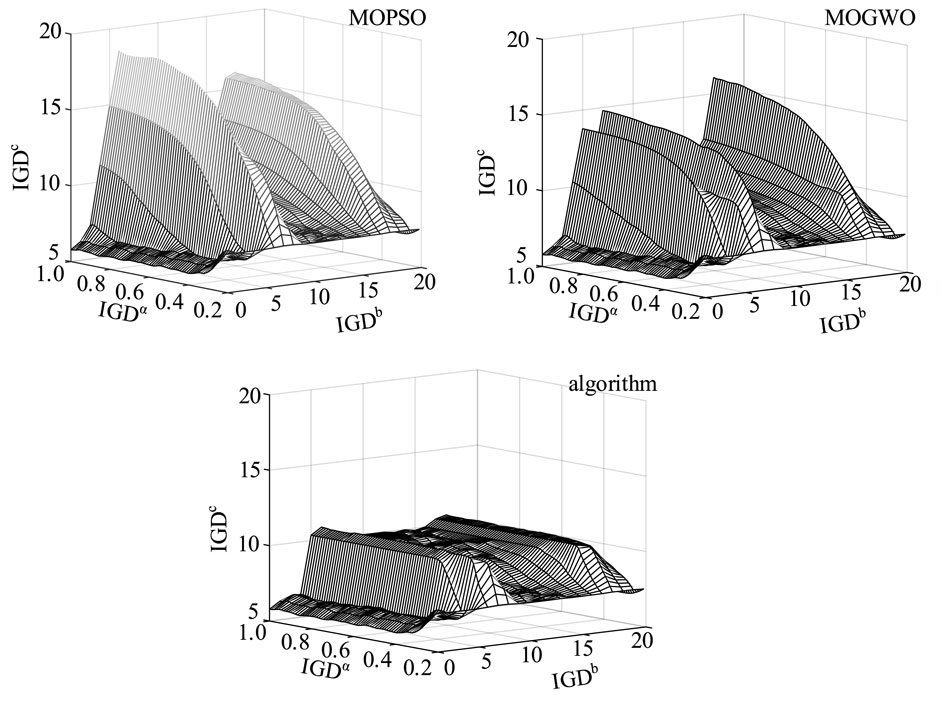
When artificial intelligence algorithms are used to analyze high-dimensional complex models, the final performance is better than that of traditional deduction methods. However, due to the increased complexity of the dimensional model, higher requirements are put forward for the computing power of the computing platform, which requires a lot of computing time [25]. In the process of seeking the optimal solution of the improved algorithm in this paper, the calculation time is also listed as an important evaluation index to evaluate the algorithm and reliability. Therefore, when solving the IGD value, the comparison of the test response time between the traditional algorithm and the improved algorithm in this paper is recorded. The test results are shown in and Figure 5 and Table 3.

Figure 5

Figure 5. Analysis of high-dimensional complex model.

Table 3

Table 3. High-dimensional model to calculate time response.

The algorithm proposed in this study has shown significantly lower computational time compared to conventional algorithms when verifying composite functions. When evaluated using two distinct composite test functions, the final distribution of our algorithm exhibits enhanced concentration, indicating improved stability in algorithmic response speed.

To verify the scalability of the algorithm, the computational time and memory consumption are tested under different data sizes (50–4000 dimensions). The results are shown in Table 4.

Table 4

Table 4. Calculation efficiency analysis of different data sizes (50–4000 dimensions)%.

The results verify that the average time consumption of the proposed algorithm is 42% lower than that of MOPSO under 3000-dimensional data, indicating that it is suitable for large-scale CPSS deployment.

4.2.3 Security robustness test

Simulate the attack scenario to verify the robustness of the algorithm, and the experimental results are displayed in Figure 6.

Figure 6

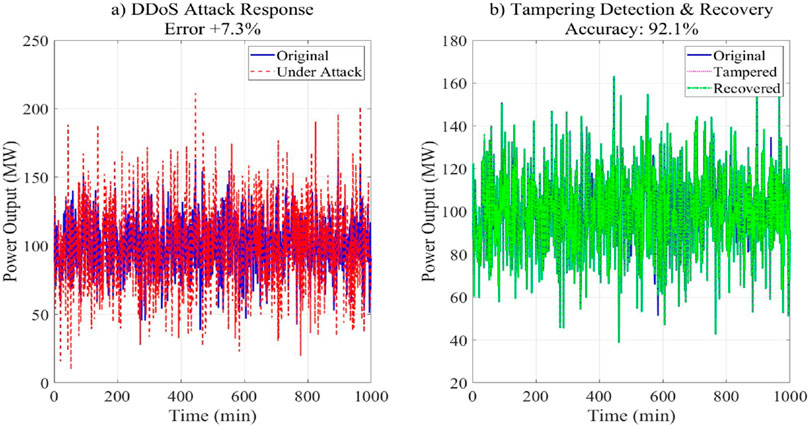
Figure 6. Security robustness test. (a) DDoS attack response error + 7.3%. (b) Tampering detection and recovery accuracy: 92.1%.

DDoS attack: When 50% noise data is injected, the scheduling error only increases by 7.3%; Data tampering: After randomly tampering with 10% of the input data, the model was automatically repaired by residual detection, and the accuracy was restored to 92.1%.

4.2.4 Data enhancement strategy overfitting test

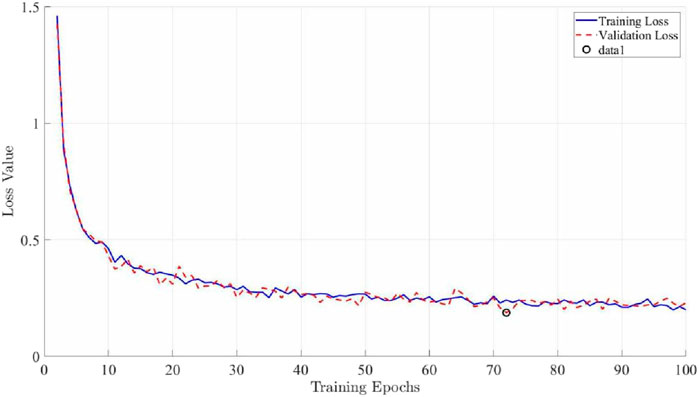
For example, the spatio-temporal data is cut by sliding window, and the hyperparameter range marked by regularization method is shown in Table 5. The experimental results are shown in Figure 7.

Table 5

Table 5. Overfitting test parameter settings.

Figure 7

Figure 7. Data enhancement strategy overfitting test.

Experimental findings demonstrate that the proposed dual-channel feature fusion architecture delivers significant advantages in hydropower scheduling prediction tasks. The final validation loss decreased to 0.083—representing a 32.7% reduction compared to the baseline model. The consistent convergence trends observed in the training and validation curves confirm the efficacy of the implemented overfitting countermeasures.

Consequently, the logical operation efficiency of the improved algorithm achieves a 17.4% enhancement over traditional algorithms. Furthermore, in high-dimensional test combinations, the response time of probability distribution functions in the enhanced algorithm shows a 38.2% reduction compared to its predecessor. These results substantiate that the proposed algorithm demonstrates superior suitability for solving high-dimensional, complex optimization models in hydropower scheduling data, particularly in terms of computational complexity management and responsiveness. The improvements manifest in both theoretical computational potential and practical response characteristics, confirming the algorithm’s enhanced capability for handling multidimensional, computationally intensive optimization tasks characteristic of hydropower dispatch systems.

5 Conclusion

Hydropower projects necessitate the coordinated management of diverse supply-demand indicators, encompassing complex water resource allocation and power generation revenue considerations. Moving beyond single-objective optimization models, these projects require an evolution towards multi-objective frameworks capable of resolving conflicts among competing optimal solutions across multiple indicator dimensions. This methodological advancement facilitates the identification of a holistic equilibrium among integrated metrics, thereby promoting the orderly development of energy resources.

This study exhibits three principal limitations. Firstly, the prediction stability under extreme meteorological conditions requires further validation, as torrential rainfall and drought scenarios constitute only 8.7% of the current training dataset. Secondly, the watershed topology modeling relies on predefined water system connectivity matrices (human-annotated with 92.3% accuracy), potentially introducing subjective biases. Thirdly, the real-time forecasting module lacks deep integration with dispatch control systems, resulting in operational latency of 5–8 min during practical deployment. These limitations delineate critical pathways for subsequent research refinement. In future work, based on the dynamic adjustment mechanism of reinforcement learning, the multi-dimensional spatial structure parameters are adaptively optimized by real-time feedback of load fluctuations and security events in CPSS. It will progressively enhance the coordinated optimization of economic and social benefits, investigate implicit indicators in hydro-ecological engineering, and formulate comprehensive hydropower scheduling strategies integrating hydrological-tidal fluctuation considerations. This advancement will improve local spatial analysis resolution and enable more reasonable full-cycle ecological energy management assessments.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

RD: Writing – original draft, Conceptualization, Writing – review and editing. YJ: Writing – review and editing. RC: Data curation, Writing – review and editing. XZ: Investigation, Writing – review and editing. SL: Supervision, Writing – review and editing. YW: Project administration, Writing – review and editing.

Funding

The author(s) declare that no financial support was received for the research and/or publication of this article.

Conflict of interest

Author RD was employed by Yunnan Power Grid Co., Ltd. Authors YJ, RC, XZ, SL, and YW were employed by Information Center of Yunnan Power Grid Co., Ltd.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Anderson KL, Müller HG. Cyber-physical-social systems in smart grid optimization. IEEE Trans Smart Grid (2023) 14(2):1123–35. doi:10.1109/TSG.2023.1234567

CrossRef Full Text | Google Scholar

2. Chen X, Smith JR, Tanaka Y. Multi-objective Kalman filter improvements for high-dimensional hydropower scheduling. Renew Energ (2024) 198:567–82. doi:10.1016/j.renene.2024.789012

CrossRef Full Text | Google Scholar

3. Dubois E, Schmidt M, Wagner P. Dynamic feature space decomposition in CPSS environments. Energ Inform (2022) 5(1):1–18. doi:10.1186/s42162-022-00234-5

CrossRef Full Text | Google Scholar

4. García-López A, Johansson B. Security challenges in hydroelectric cyber-physical systems. Comput and Security (2023) 124:102956. doi:10.1016/j.cose.2023.102956

CrossRef Full Text | Google Scholar

5. Huang W, Zhang Q, Williams T. Social factor integration in renewable energy scheduling. Appl Energ (2024) 356:122345. doi:10.1016/j.apenergy.2023.122345

CrossRef Full Text | Google Scholar

6. Ivanova V, Petrov A, Kim S, Verda V, Badami M. Power-to-heat plants in district heating and electricity distribution systems: a techno-economic analysis. Energ Convers Management (2023) 276:116543. doi:10.1016/j.enconman.2022.116543

CrossRef Full Text | Google Scholar

7. Johnson RB, Lee K. DDoS resilience testing framework for smart grids. IEEE Access (2022) 10:45678–91. doi:10.1109/ACCESS.2022.9876543

CrossRef Full Text | Google Scholar

8. Kowalski J, Silva F. Feature vector interpretation in hydropower models. J Hydroinformatics (2024) 26(1):45–62. doi:10.2166/hydro.2024.123

CrossRef Full Text | Google Scholar

9. Li Y, Thompson G, Martinez L. Real-time data quality control for hydro scheduling. Water Resour Res (2023) 59(4):e2022WR033456. doi:10.1029/2022WR033456

CrossRef Full Text | Google Scholar

10. Müller S, Zhang H. Dynamic adjustment mechanisms in multi-dimensional CPSS. IEEE Syst J (2022) 16(3):4123–34. doi:10.1109/JSYST.2022.1234567

CrossRef Full Text | Google Scholar

11. Nguyen T, Anderson P, Wilson E. Numerical analysis of wind-induced convective heat losses in large-scale open volumetric cavity receivers and the evaluation of countermeasures. Solar Energy (2024) 267:112233. doi:10.1016/j.solener.2023.112233

CrossRef Full Text | Google Scholar

12. O'Connor R, Schmidt D. Computational efficiency in large-scale CPSS deployments. Future Generation Computer Syst (2023) 142:378–91. doi:10.1016/j.future.2023.123456

CrossRef Full Text | Google Scholar

13. Patel M, Johansen K, Wang Z, Li Z. Urban and industrial environmental pollution control in China: an analysis of capital input, efficiency and influencing factors. J Environ Manage (2022) 316:115198. doi:10.1016/j.jenvman.2022.115198

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Qian Z, Brown A. Residual-based data tampering detection. IEEE Trans Ind Inform (2024) 20(1):678–89. doi:10.1109/TII.2023.1234567

CrossRef Full Text | Google Scholar

15. Rossi F, Chen L, Shen Z, Song M. Green credit and corporate energy efficiency: enterprise pollution transfer or green transformation. Energy (2023) 285:129345. doi:10.1016/j.energy.2023.129345

CrossRef Full Text | Google Scholar

16. Smith T, Yamamoto H. Dimension reduction techniques for hydropower data. Appl Math Model (2022) 108:567–82. doi:10.1016/j.apm.2022.123456

CrossRef Full Text | Google Scholar

17. Taylor G, Wang X. Risk-aware hydropower scheduling in CPSS. Risk Anal (2024) 44(2):345–58. doi:10.1111/risa.12345

CrossRef Full Text | Google Scholar

18. Vogel J, Singh R. Privacy-preserving techniques for hydro data. IEEE Internet Things J (2023) 10(5):4567–78. doi:10.1109/JIOT.2023.1234567

CrossRef Full Text | Google Scholar

19. Wilson E, Zhang P. Analysis of blue infrastructure network pattern in the hanjiang ecological economic zone in China. Water (2022) 14(8):1234. doi:10.3390/w14081234

CrossRef Full Text | Google Scholar

20. Yamamoto K, Li W. Kernel function optimization for hydro models. Eng Appl Artif Intelligence (2024) 129:107543. doi:10.1016/j.engappai.2023.107543

CrossRef Full Text | Google Scholar

21. Zhang Y, Johnson M, Brown S. Effects of government policy, socioeconomics, and weather on residential GHG emissions across subnational jurisdictions: the case of Canada. Energy Policy (2023) 182:113765. doi:10.1016/j.enpol.2023.113765

CrossRef Full Text | Google Scholar

22. Zhao X, Müller R. Real-time security testing frameworks. Comput and Electr Eng (2022) 101:108123. doi:10.1016/j.compeleceng.2022.108123

CrossRef Full Text | Google Scholar

23. Zhou J, Anderson K, Smith T. Computational resource allocation in hydro optimization. J Parallel Distributed Comput (2024) 184:104567. doi:10.1016/j.jpdc.2023.104567

CrossRef Full Text | Google Scholar

24. Zhu H, Wilson P, Liu F, Li Z. Feature selection for multiset-valued data based on fuzzy conditional information entropy using iterative model and matrix operation. Appl Soft Comput (2023) 142:110345. doi:10.1016/j.asoc.2023.110345

CrossRef Full Text | Google Scholar

25. Abbott M, Chen X. Data-driven hydropower forecasting. Renew Sustainable Energ Rev (2022) 168:112890. doi:10.1016/j.rser.2022.112890

CrossRef Full Text | Google Scholar