Reflection and transmission of P-wave incident obliquely at the interface between an elastic solid and a fluid-saturated porous medium: a comprehensive study via the model of soil mechanics

Introduction: A model of soil mechanics is used to study the problem of reflection and transmission of an obliquely incident plane P-waveon a discontinuous interface. Based on the propagation theory of elastic waves in an elastic solid and a fluid-saturated porous medium, the propagation analysis model of P-wave incident obliquely at the interface of such media is established.

Methods: The theoretical formulas of reflection coefficients of P- and SV-waves and the transmission coefficients of P₁-, P₂-, and SV-waves are obtained in terms of the boundary conditions of the interface between an elastic solid and a saturated two-phase medium. Furthermore, the derived formulas in this paper are reduced to the reflection and transmission problems of P-wave incident on two different single-phase media to verify their correctness. Finally, numerical investigations are carried out on the variations of the reflection and transmission coefficients with the incident angle for various boundary conditions, wave frequency, and material characteristics (i.e., dynamic permeability coefficient, porosity, and Poisson’s ratio).

Results: It is shown that the effects of incident angles, boundary conditions, wave frequency, and material characteristics on the reflection and transmission coefficients cannot be ignored.

Discussion: These conclusions are of guiding significancefor theoretical research of soil dynamics and engineering seismic exploration.

1 Introduction

The reflection and transmission of elastic waves at discontinuous interfaces have always been an important subject of soil dynamics, which is of considerable interest in various fields such as soil dynamics, geotechnical engineering, earthquake engineering, geophysics, and so on. The interface between an ordinary elastic solid and a fluid-saturated porous medium is one of the important research branches. For the two-phase medium, due to the existence of pore water in the soil frame, its mechanical properties become very complex, which leads to the problem of wave propagation being much more complicated than that of a single-phase medium [1, 2]. The lower crust can be approximately treated as a single-phase medium, and the upper crust can be regarded as a saturated two-phase medium when the earthquake wave propagates outward from the seismic hypocenter to the surface [3]. Hence, when the seismic wave travels towards the surface, it will encounter the interface between elastic and two-phase medium and show complicated reflection and transmission characteristics.

It is well known that Biot first revealed the existence of three body waves in a two-phase medium, i.e., the fast P₁-wave, the slow P₂-wave, and the S-wave. The three body waves are dispersed and attenuated, the speed and attenuation of which are affected by the frequency and the properties of saturated soil materials [4, 5]. All of the above laid the foundation for the theoretical study of wave propagation in a fluid-saturated porous medium. Since then, more and more researchers studied various aspects of wave propagation in such medium. The P₂-wave with strong dispersion and high attenuation characteristics was successively confirmed through experiments by Plona [6] and Berryman [7]. Following the Biot model, many scholars established different two-phase medium models, including the Zienkiewicz model [8, 9], the Men Fu-lu model [10, 11], the model of soil mechanics [12], and the theory of mixture [13]. Chen and Liao [14] compared the first four models and theoretically explained that the model of soil mechanics is a special case of the Biot model, which has the advantage of the clear physical meaning of modeling parameters.

Gutenberg [15] was the first to study the reflection and transmission of elastic waves incident at the interface between different semi-infinite solid media. After that, numerous researchers made use of the Biot model to investigate the reflection and transmission of elastic waves on the interface between an elastic solid and a fluid-saturated porous medium. The problem of reflection and transmission of elastic waves from one elastic solid to another porous medium was simply examined by Geertsma and Smit [16]. Then, Deresiewicz and Rice [17] derived the expressions for amplitude ratios and phase shifts of the displacements for the P-wave traveling from an elastic solid into a porous medium. However, both publications were confined to a special case of normal incidence. Hajra and Mukhopadhyay [18] considered the obliquely incident seismic waves (P- and SV-waves) across the interface between an elastic solid and a fluid-saturated porous medium and calculated the amplitude and energy ratios for all reflected and refracted waves theoretically and numerically in the absence of dissipation. Sharma and Gogna [19] and Vashisth et al. [20] also studied the reflection and refraction of P- and SV-waves at the interface between an elastic solid and a fluid-saturated porous solid. Unlike Ref. [18], Sharma and Gogna [19] considered the dissipation caused by liquid viscosity. Among them, Hajra and Mukhopadhyay [18] and Sharma and Gogna [19] assumed the interface in welded contact, but Vashisth et al. [20] provided that the boundary is a loosely bonded interface, introduced a bonding constant ψ and stated that the smooth (ψ = 0) and welded interfaces (ψ = 1) are the special cases. Zhao et al. [3, 21] deduced the reflected and transmitted coefficients in the cases of seismic waves (P- and SV-waves) propagating from the elastic solid to the liquid-saturated porous solid (considering the energy dissipation) and P₁-wave traveling through the liquid-saturated porous solid to the elastic solid (free of the energy dissipation). Ye et al. [22] presented the expressions of reflection and refraction coefficients when the S-wave propagates from fluid-saturated soil to elastic soil and analyzed the dependence on the incident angle, wave frequency, and interface drainage condition. The concept of homogeneous pore fluid was applied to the Biot model to simulate the partially saturated soil. Based on this, the reflection and transmission of P- and SV-waves propagating from an elastic solid to partially saturated soil were investigated by Yang [23, 24] and Yang and Sato [25, 26]. Similarly, Li [27] analyzed the reflection and transmission when the P₁-wave in the partially saturated soil was incident on the elastic solid. And they all explained the effect of water saturation on the reflection and transmission. Xu and Xia [28] also studied the reflection and transmission of the incident plane P₁-wave from the nearly saturated soil to the elastic soil, but the model used was the governing equation of nearly saturated soil. Following Fillunger’s model, Kumar et al. [29] discussed the reflection and transmission of waves on the interface between a fluid-saturating incompressible porous medium and an elastic medium. Moreover, the reflection and refraction problem of elastic waves from an elastic solid to other different soil was also widely studied, such as a transversely isotropic liquid-saturated porous medium [30, 31], a double porosity medium [32], an unsaturated medium [33, 34], a swelling porous half-space [35], porous solid saturated with-two immiscible viscous fluids [36, 37], a saturated frozen soil medium [38, 39], and water [40–42], etc. Recently, this wave propagation can be extended to other distinct media [43, 44].

Since Chinese scholar Men proposed the model of soil mechanics, quite a few researchers have also used it to study the wave propagation characteristic in a two-phase medium from theoretical [45–52] and practical views [53–56]. Among them, it is worth mentioning that Chen and Men [54] and Cui [53] presented a new method to understand the mechanism of soil liquefaction. Chen [45] and Chen et al. [46] analyzed the near-field wave motions combining the transmitting boundary. Recently, Xiao et al. [50] investigated the propagation and attenuation characteristics of Rayleigh waves in ocean sites. A preliminary analysis of the characteristics of wave propagation in the infinite and finite saturated medium based on the model of soil mechanics has been conducted by Zhang et al. [51] and Zhang and Qiu [52]. The results showed that the frequency and soil properties significantly shaped the velocity and attenuation coefficient of the three body waves. For this reason, these parameters are bound to affect the reflection and transmission of each wave incident upon the interface between an elastic solid and a fluid-saturated porous medium.

2 Theory of wave propagation

2.1 Elastic solid medium

For the homogeneous isotropic elastic solid, the equation of motion in vector form can be written as [57, 58].

$\left({\lambda }^{\prime }+{\mu }^{\prime }\right)\nabla \left(\nabla ·{\mathit{u}}^{\prime }\right)+\mu \Delta {\mathit{u}}^{\prime }=\rho \ddot{{\mathit{u}}^{\prime }}(1)$

Where, ${\lambda }^{\prime }$ and ${\mu }^{\prime }$ are the Lame’s constants. ${\mathit{u}}^{\prime }$ and $\ddot{{\mathit{u}}^{\prime }}$ are the displacement and acceleration vectors in the elastic solid, respectively. $\rho$ is the mass density of an elastic solid. $\Delta$ denotes the Laplace operator, and $\Delta$ = ${\nabla }^2$. $\nabla$ is the Hamilton operator.

To gain a deeper understanding of plane wave solutions of Equation 1, we assume the direction of wave propagation lies in the x-z plane. Then, we consider a Helmholtz resolution of the displacement ${\mathit{u}}^{\prime }$, which may be the sum of the gradient of scalar potential ${\varphi }^{\prime }$ (for P-wave) and the curl of vector potential ${\mathit{\psi }}^{\prime }$ (for SV-wave), namely, ${\mathit{u}}^{\prime }$ = $\nabla {\varphi }^{\prime }$ + $\nabla \times {\mathit{\psi }}^{\prime }$. For the two-dimensional motion (i.e., P-SV system), the potential functions of P- and SV-waves only contribute to the displacement components in the x and z directions, not to the displacement component in the y direction, so they are independent of y and depend only on x, z, and time t, i.e., ${\varphi }^{\prime }$ = ${\varphi }^{\prime }\left(x,z,t\right)$, and ${\mathit{\psi }}^{\prime }$ = $\left(0,{\psi }^{\prime }\left(x,z,t\right),0\right)$. Hence, the displacement components $u_x^{\prime }$ and $u_z^{\prime }$, the normal stress ${\sigma }_{zz}^{\prime }$, and shear stress ${\sigma }_{xz}^{\prime }$ are described by

$\left\{\begin{array}{l}{u}_x^{\prime }=\frac{\mathrm{\partial }{\varphi }^{\prime }}{\mathrm{\partial }x}-\frac{\mathrm{\partial }{\psi }^{\prime }}{\mathrm{\partial }z}\\ u_z^{\prime }=\frac{\mathrm{\partial }{\varphi }^{\prime }}{\mathrm{\partial }z}+\frac{\mathrm{\partial }{\psi }^{\prime }}{\mathrm{\partial }x}\end{array}\right.(\mathrm{2a})$

$\left\{\begin{array}{l}{\sigma }_{zz}^{\prime }={\lambda }^{\prime }{\nabla }^2{\varphi }^{\prime }+2{\mu }^{\prime }\left(\frac{{\mathrm{\partial }}^2{\varphi }^{\prime }}{\mathrm{\partial }{z}^2}+\frac{{\mathrm{\partial }}^2{\psi }^{\prime }}{\mathrm{\partial }x\mathrm{\partial }z}\right)\\ {\sigma }_{xz}^{\prime }=2{\mu }^{\prime }\frac{{\mathrm{\partial }}^2{\varphi }^{\prime }}{\mathrm{\partial }x\mathrm{\partial }z}+{\mu }^{\prime }\left(\frac{{\mathrm{\partial }}^2{\psi }^{\prime }}{\mathrm{\partial }{x}^2}-\frac{{\mathrm{\partial }}^2{\psi }^{\prime }}{\mathrm{\partial }{z}^2}\right)\end{array}\right.(\mathrm{2b})$

2.2 Fluid-saturated porous medium

Provided that the liquid phase is an ideal fluid, the solid phase is isotropic and elastic, and the solid particles with infinite compression modulus are in point contact. In the model of soil mechanics proceeding as in Men [12], Xiao [50], Zhang [51], and Zhang and Qiu [52], the field equations for a liquid-saturated porous medium are written as follows.

$\left\{\begin{array}{l}\mu \Delta \mathit{u}+\left(\lambda +\mu \right)\nabla \left(\nabla ·\mathit{u}\right)+\left(1-n\right)\nabla p_f+\left[B\right]\left(\dot{\mathit{U}}-\dot{\mathit{u}}\right)={\rho }_1\ddot{\mathit{u}}\\ n\nabla p_f-\left[B\right]\left(\dot{\mathit{U}}-\dot{\mathit{u}}\right)={\rho }_2\ddot{\mathit{U}}\\ \left(1-n\right)\nabla ·\mathit{u}+n\nabla ·\mathit{U}-\frac{n}{E_{\mathrm{w}}}{p}_f=0\end{array}\right.(3)$

where $\mathit{u}$, $\dot{\mathit{u}}$, and $\ddot{\mathit{u}}$ correspond to the displacement, velocity, and acceleration of the solid, respectively, and $\mathit{U}$, $\dot{\mathit{U}}$, and $\ddot{\mathit{U}}$ those of the fluid. ${\rho }_1$ and ${\rho }_2$ are the mass of solid and liquid per unit volume, separately, with ${\rho }_1$ = $\left(1-n\right){\rho }_{\mathrm{s}}$ and ${\rho }_2$ = $n{\rho }_{\mathrm{w}}$. ${\rho }_{\mathrm{s}}$ denotes the mass density of the solid and ${\rho }_{\mathrm{w}}$ that of the liquid. $n$ is the porosity. $p_f$ represents the true pore pressure. $\lambda$ and $\mu$ (i.e., shear modulus) are the Lame’s constants, in which $\lambda$ = $E\nu /\left(\left(1+\nu \right)\left(1-2\nu \right)\right)$ and $\mu$ = $E/2\left(1+\nu \right)$. $\nu$ is the Poisson’s ratio. $E$ is the Young’s modulus of the solid phase. $\left[B\right]$ is a third-order diagonal matrix concerning the dissipation coefficients, of which the diagonal elements $b$ = $b_x$ = $b_y$ = $b_z$ = $n^2/k$. $k$ (Unit: m³ s/kg) refers to the dynamic permeability coefficient, and k = $K/{\rho }_{\mathrm{w}}g$, in which K (Unit: m/s) is the permeability coefficient corresponding to Darcy’s law and g is the gravitation acceleration. $E_{\mathrm{w}}$ is the pore fluid bulk modulus.

Similar to the single-phase medium, to gain the plane wave solutions of a saturated two-phase medium, the Helmholtz decomposition is considered, and the displacement vectors of the solid phase $\mathit{u}$ (liquid phase $\mathit{U}$) can be the sum of the gradient of a scalar potential ${\varphi }_{\mathrm{s}}$ (${\varphi }_{\mathrm{w}}$) and the curl of a vector potential ${\mathit{\psi }}_{\mathbf{s}}$ (${\mathit{\psi }}_{\mathbf{w}}$).

$\left\{\begin{array}{l}\mathit{u}=\nabla {\varphi }_{\mathrm{s}}+\nabla \times {\mathit{\psi }}_{\mathbf{s}}\\ \mathit{U}=\nabla {\varphi }_{\mathrm{w}}+\nabla \times {\mathit{\psi }}_{\mathbf{w}}\end{array}\right.(4)$

Plugging Equation 4 into Equation 3, we can get the wave equations of potentials in the following form [48].

$\left\{\begin{array}{l}{\rho }_1{\ddot{\varphi }}_s-\left(\lambda +2\mu \right)\Delta {\varphi }_s=p_f-{\rho }_2{\ddot{\varphi }}_w\\ {\rho }_1{\ddot{\mathit{\psi }}}_{\mathit{s}}-\mu \Delta {\mathit{\psi }}_{\mathit{s}}=-{\rho }_2{\ddot{\mathit{\psi }}}_{\mathit{w}}\\ n{p}_f-\left[B\right]\left({\dot{\varphi }}_w-{\dot{\varphi }}_s\right)-{\rho }_2{\ddot{\varphi }}_w=0\\ {\rho }_2{\ddot{\mathit{\psi }}}_{\mathit{w}}+\left[B\right]\left({\dot{\mathit{\psi }}}_{\mathit{w}}-{\dot{\mathit{\psi }}}_{\mathit{s}}\right)=0\\ \left(1-n\right)\Delta {\varphi }_s+n\Delta {\varphi }_w-\frac{n}{E_w}{p}_f=0\end{array}\right.(5)$

Similarly, the potentials in the solid phase ${\varphi }_{\mathrm{s}}$ = ${\varphi }_{\mathrm{s}}\left(x,z,t\right)$, and ${\mathit{\psi }}_{\mathbf{s}}$ = $\left(0,{\psi }_{\mathrm{s}}\left(x,z,t\right),0\right)$. The potentials in the liquid phase ${\varphi }_{\mathrm{w}}$ = ${\varphi }_{\mathrm{w}}\left(x,z,t\right)$, and ${\mathit{\psi }}_{\mathbf{w}}$ = $\left(0,{\psi }_{\mathrm{w}}\left(x,z,t\right),0\right)$, in the xz plane. The relations of the displacement components in the solid and liquid phases ($u_x$, $u_z$, $U_x$, and $U_z$) and the stresses (${\sigma }_{zz}$, ${\sigma }_{xz}$, and $p_f$) with potentials are given by

$\left\{\begin{array}{l}{u}_x=\frac{\mathrm{\partial }{\varphi }_{\mathrm{s}}}{\mathrm{\partial }x}-\frac{\mathrm{\partial }{\psi }_{\mathrm{s}}}{\mathrm{\partial }z}\\ u_z=\frac{\mathrm{\partial }{\varphi }_{\mathrm{s}}}{\mathrm{\partial }z}+\frac{\mathrm{\partial }{\psi }_{\mathrm{s}}}{\mathrm{\partial }x}\end{array}\right.(\mathrm{6a})$

$\left\{\begin{array}{l}{U}_x=\frac{\mathrm{\partial }{\varphi }_{\mathrm{w}}}{\mathrm{\partial }x}-\frac{\mathrm{\partial }{\psi }_{\mathrm{w}}}{\mathrm{\partial }z}\\ U_z=\frac{\mathrm{\partial }{\varphi }_{\mathrm{w}}}{\mathrm{\partial }z}+\frac{\mathrm{\partial }{\psi }_{\mathrm{w}}}{\mathrm{\partial }x}\end{array}\right.(\mathrm{6b})$

$\left\{\begin{array}{l}{\sigma }_{zz}=\left(\lambda +\frac{1-n}{n}{E}_{\mathrm{w}}\right){\nabla }^2{\varphi }_{\mathrm{s}}+2\mu \left(\frac{{\mathrm{\partial }}^2{\varphi }_{\mathrm{s}}}{\mathrm{\partial }{z}^2}+\frac{{\mathrm{\partial }}^2{\psi }_{\mathrm{s}}}{\mathrm{\partial }x\mathrm{\partial }z}\right)+E_{\mathrm{w}}{\nabla }^2{\varphi }_{\mathrm{w}}\\ {\sigma }_{xz}=2\mu \frac{{\mathrm{\partial }}^2{\varphi }_{\mathrm{s}}}{\mathrm{\partial }x\mathrm{\partial }z}+\mu \left(\frac{{\mathrm{\partial }}^2{\psi }_{\mathrm{s}}}{\mathrm{\partial }{x}^2}-\frac{{\mathrm{\partial }}^2{\psi }_{\mathrm{s}}}{\mathrm{\partial }{z}^2}\right)\\ p_f=\frac{1-n}{n}{E}_{\mathrm{w}}{\nabla }^2{\varphi }_{\mathrm{s}}+E_{\mathrm{w}}{\nabla }^2{\varphi }_{\mathrm{w}}\end{array}\right.(\mathrm{6c})$

Then, assume that the plane harmonic wave solutions of the potentials are as follows.

$\left\{\begin{array}{l}{\varphi }_{\mathrm{s}}=A_{\mathrm{s}}{e}^{i\left(\omega t-{\mathit{k}}_{\mathbf{P}}·\mathit{r}\right)}\\ {\varphi }_{\mathrm{w}}=A_{\mathrm{w}}{e}^{i\left(\omega t-{\mathit{k}}_{\mathbf{P}}·\mathit{r}\right)}\\ {\psi }_{\mathrm{s}}=B_{\mathrm{s}}{e}^{i\left(\omega t-{\mathit{k}}_{\mathbf{S}}·\mathit{r}\right)}\\ {\psi }_{\mathrm{w}}=B_{\mathrm{w}}{e}^{i\left(\omega t-{\mathit{k}}_{\mathbf{S}}·\mathit{r}\right)}\end{array}\right.(7)$

where $A_{\mathrm{s}}$ and $A_{\mathrm{w}}$ are the amplitudes of P-wave in the solid and liquid phases, $B_{\mathrm{s}}$ and $B_{\mathrm{w}}$ those of S-wave. $i$ = $\sqrt{-1}$. $\mathit{r}$ is the location vector. $\omega$ denotes the circular frequency of a wave. ${\mathit{k}}_{\mathbf{P}}$ and ${\mathit{k}}_{\mathbf{S}}$ are the wave vectors of P- and SV-waves, which indicate the propagation directions of waves. $k_{\mathrm{P}}$ and $k_{\mathrm{S}}$ are the magnitudes (wave numbers). $t$ represents the travel time.

Substituting Equation 7 into Equation 5 provides the characteristic equations of elastic waves [51, 52]. By introducing four variables (A, B, C, and D), the characteristic equations can be reduced to

$\mathrm{A}{\left(\frac{k_{\mathrm{P}}}{\omega }\right)}^4-\mathrm{B}{\left(\frac{k_{\mathrm{P}}}{\omega }\right)}^2+\mathrm{C}=0(\mathrm{8a})$

$\mathrm{D}{\left(\frac{k_{\mathrm{S}}}{\omega }\right)}^2+\mathrm{C}=0(\mathrm{8b})$

where A = $\frac{\left(\lambda +2\mu \right)n{E}_{\mathrm{w}}}{{\rho }_1{\rho }_2}$, B = $\left[\frac{\lambda +2\mu }{{\rho }_1}+\frac{n{E}_{\mathrm{w}}}{{\rho }_2}+\frac{{\left(1-n\right)}^2{E}_{\mathrm{w}}}{n{\rho }_1}\right]-\frac{ib}{\omega {\rho }_1{\rho }_2}\left(\lambda +2\mu +\frac{E_{\mathrm{w}}}{n}\right)$, C = $1-\frac{ib}{\omega }\left(\frac{1}{{\rho }_1}+\frac{1}{{\rho }_2}\right)$, and D = $\frac{ib\mu }{\omega {\rho }_1{\rho }_2}-\frac{\mu }{{\rho }_1}$.

Equations 8a and 8b constitute a general solution of Equation 3. In an unbounded two-phase medium, the phase velocities and attenuation coefficients can be easily extracted from Equations 8a, 8b [51, 52].

3 The reflection and transmission of interface induced by P-wave

As shown in Figure 1, to illustrate in detail the two-dimensional reflection-refraction problem, we set up a Cartesian coordinate system (x, z), with the x-axis as the horizontal direction, and the z-axis as the vertical direction. For convenience, the interface is chosen horizontally, i.e., the plane z = 0, and the direction of z is positive into the fluid-saturated porous medium. As a result, the upper half-space (z < 0) is an elastic solid, and the lower half-space (z > 0) is a two-phase medium. Let a plane harmonic P-wave with an angular frequency ω originate in the elastic solid and be incident obliquely at the interface at an angle θ_IP. For this situation, there will be two refracted compressive (P₁- and P₂-waves) waves and one refracted SV-wave in the semi-infinite porous medium, together with reflected P- and SV-waves in the semi-infinite elastic medium. All the waves generated at the interface travel with the frequency of the incident P-wave. And the angles of refraction for P₁-, P₂-, and SV-waves are θ_T1, θ_T2, and θ_TS, the reflection angles are θ_RP and θ_RS for reflected P- and SV-waves.

Figure 1

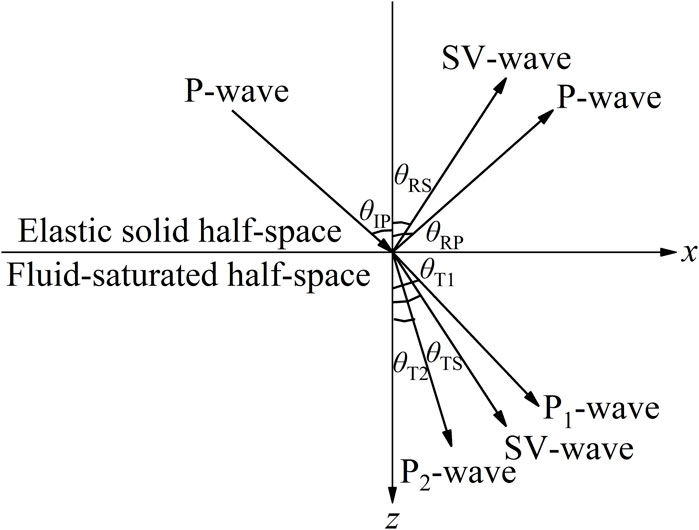
Figure 1. Reflection and transmission of an incident P-wave at the interface between the monophasic and two-phase media.

According to Snell’s law, the relations between the angles of incidence, reflection, and refraction can be expressed by

$\frac{C_{\mathrm{P}}}{\sin {\theta }_{\text{IP}}}=\frac{C_{\mathrm{P}}}{\sin {\theta }_{\text{RP}}}=\frac{C_{\mathrm{S}}}{\sin {\theta }_{\text{RS}}}=\frac{V_{\mathrm{P}1}}{\sin {\theta }_{\mathrm{T}1}}=\frac{V_{\mathrm{P}2}}{\sin {\theta }_{\mathrm{T}2}}=\frac{V_{\mathrm{S}}}{\sin {\theta }_{\text{TS}}}(9)$

where $C_{\mathrm{P}}$ and $C_{\mathrm{S}}$ are the velocities of P- and SV-waves in the elastic solid. $V_{\mathrm{P}1}$, $V_{\mathrm{P}2}$, and $V_{\mathrm{S}}$ are the velocities of P₁-, P₂-, and SV-waves in the two-phase medium. From Equation 9, the angle of reflection (θ_RP) equals the angle of incidence (θ_IP) for the P-wave. In addition, if the wave velocities and the angle of incidence (θ_IP) are given, the angles of reflection and refraction (i.e., θ_RS, θ_T1, θ_T2, and θ_TS) can be calculated.

3.1 Wave potentials in the elastic solid

For the elastic solid in the region z < 0, the reflected P- and SV-waves are generated when the P-wave propagates from an elastic solid to a saturated porous medium. The wave potentials of P- and SV-waves in the elastic solid, ${\varphi }^{\prime }$ and ${\psi }^{\prime }$, are given by Equation 10. The plane wave solutions of wave potentials (${\varphi }^{\prime }$ and ${\psi }^{\prime }$) can be expressed by Equations 11a–11c.

$\left\{\begin{array}{l}{\varphi }^{\prime }={\varphi }^{\mathrm{I}}+{\varphi }^{\mathrm{R}}\\ {\psi }^{\prime }={\psi }^{\mathrm{R}}\end{array}\right.(10)$

${\varphi }^{\mathrm{I}}=A^{\mathrm{I}}\exp \left[i\left(\omega t-k_x^{\mathrm{I}}x-k_z^{\mathrm{I}}z\right)\right](\mathrm{11a})$

${\varphi }^{\mathrm{R}}=A^{\mathrm{R}}\exp \left[i\left(\omega t-k_x^{\mathrm{I}}x+k_z^{\mathrm{I}}z\right)\right](\mathrm{11b})$

${\psi }^{\mathrm{R}}=B^{\mathrm{R}}\exp \left[i\left(\omega t-k_x^{\mathrm{R}}x+k_z^{\mathrm{R}}z\right)\right](\mathrm{11c})$

where ${\varphi }^{\mathrm{I}}$ is the potential of the incident P-wave, which travels in the +x and +z directions, and $A^{\mathrm{I}}$ corresponds to the amplitude. ${\varphi }^{\mathrm{R}}$ and ${\psi }^{\mathrm{R}}$ are the potentials of the reflected P- and SV-waves, which travel in the +x and -z directions, and $A^{\mathrm{R}}$ and $B^{\mathrm{R}}$ are the amplitudes. $k_x^{\mathrm{I}}$ and $k_z^{\mathrm{I}}$ represent the components of the wave number along the x-direction and z-direction, respectively, for the incident P-wave. $k_x^{\mathrm{R}}$ and $k_z^{\mathrm{R}}$ are the components of the wave number in the x and z directions for the reflected SV-wave.

3.2 Wave potentials in the fluid-saturated porous medium

For the fluid-saturated porous medium in the domain z > 0, part of the incident P-wave is converted into three transmitted P₁-, P₂-, and SV-waves. The potentials in the solid phase (${\varphi }_{\mathrm{s}}$ and ${\psi }_{\mathrm{s}}$), and the potentials in the liquid phase (${\varphi }_{\mathrm{w}}$ and ${\psi }_{\mathrm{w}}$) are given by the expression (Equation 12). The plane wave solutions of potentials for each transmitted wave in the solid and liquid phases are written by

$\left\{\begin{array}{l}{\varphi }_{\mathrm{s}}={\varphi }_{\mathrm{s}1}^{\mathrm{T}}+{\varphi }_{\mathrm{s}2}^{\mathrm{T}}\\ {\varphi }_{\mathrm{w}}={\varphi }_{\mathrm{w}1}^{\mathrm{T}}+{\varphi }_{\mathrm{w}2}^{\mathrm{T}}\\ {\psi }_{\mathrm{s}}={\psi }_{\mathrm{s}}^{\mathrm{T}}\\ {\psi }_{\mathrm{w}}={\psi }_{\mathrm{w}}^{\mathrm{T}}\end{array}\right.(12)$

$\left\{\begin{array}{l}{\varphi }_{\mathrm{s}1}^{\mathrm{T}}=A_{\mathrm{s}1}^{\mathrm{T}}\exp \left[i\left(\omega t-k_{1x}^{\mathrm{T}}x-k_{1z}^{\mathrm{T}}z\right)\right]\\ {\varphi }_{\mathrm{w}1}^{\mathrm{T}}=A_{\mathrm{w}1}^{\mathrm{T}}\exp \left[i\left(\omega t-k_{1x}^{\mathrm{T}}x-k_{1z}^{\mathrm{T}}z\right)\right]\end{array}\right.(\mathrm{13a})$

$\left\{\begin{array}{l}{\varphi }_{\mathrm{s}2}^{\mathrm{T}}=A_{\mathrm{s}2}^{\mathrm{T}}\exp \left[i\left(\omega t-k_{2x}^{\mathrm{T}}x-k_{2z}^{\mathrm{T}}z\right)\right]\\ {\varphi }_{\mathrm{w}2}^{\mathrm{T}}=A_{\mathrm{w}2}^{\mathrm{T}}\exp \left[i\left(\omega t-k_{2x}^{\mathrm{T}}x-k_{2z}^{\mathrm{T}}z\right)\right]\end{array}\right.(\mathrm{13b})$

$\left\{\begin{array}{l}{\psi }_{\mathrm{s}}^{\mathrm{T}}=B_{\mathrm{s}}^{\mathrm{T}}\exp \left[i\left(\omega t-k_{\mathrm{s}x}^{\mathrm{T}}x-k_{\mathrm{s}z}^{\mathrm{T}}z\right)\right]\\ {\psi }_{\mathrm{w}}^{\mathrm{T}}=B_{\mathrm{w}}^{\mathrm{T}}\exp \left[i\left(\omega t-k_{\mathrm{s}x}^{\mathrm{T}}x-k_{\mathrm{s}z}^{\mathrm{T}}z\right)\right]\end{array}\right.(\mathrm{13c})$

where ${\varphi }_{\mathrm{s}1}^{\mathrm{T}}$, ${\varphi }_{\mathrm{s}2}^{\mathrm{T}}$, and ${\psi }_{\mathrm{s}}^{\mathrm{T}}$ are the refracted P₁-, P₂-, and SV-waves potentials in the solid phase, and ${\varphi }_{\mathrm{w}1}^{\mathrm{T}}$, ${\varphi }_{\mathrm{w}2}^{\mathrm{T}}$, and ${\psi }_{\mathrm{w}}^{\mathrm{T}}$ are those in the liquid phase. $A_{\mathrm{s}1}^{\mathrm{T}}$, $A_{\mathrm{s}2}^{\mathrm{T}}$, and $B_{\mathrm{s}}^{\mathrm{T}}$ are the amplitudes corresponding to the transmitted P₁-, P₂-, and SV-waves in the solid phase, and $A_{\mathrm{w}1}^{\mathrm{T}}$, $A_{\mathrm{w}2}^{\mathrm{T}}$, and $B_{\mathrm{w}}^{\mathrm{T}}$ those in the liquid phase. $k_{1x}^{\mathrm{T}}$, $k_{1z}^{\mathrm{T}}$, $k_{2x}^{\mathrm{T}}$, $k_{2z}^{\mathrm{T}}$, $k_{\mathrm{s}x}^{\mathrm{T}}$, and $k_{\mathrm{s}z}^{\mathrm{T}}$ are the components of wave numbers in the x and z directions, in which the indices 1, 2, and s denote P₁, P₂, and SV waves, and the superscript T represents refraction. In terms of the negative sign before each wave number, all transmitted waves propagate along the +x and +z directions.

Given the geometric relationship of wave vectors, the wave vectors and their components for various waves fulfill Equation 14. In addition, the apparent velocity along the interface (i.e., z = 0) is the same. Hence, the horizontal components of the wave vector for all mode waves are the same as shown in Equation 15.

$\left\{\begin{array}{l}{\left(k_x^{\mathrm{I}}\right)}^2+{\left(k_z^{\mathrm{I}}\right)}^2={\left(k^{\mathrm{I}}\right)}^2\\ {\left(k_x^{\mathrm{R}}\right)}^2+{\left(k_z^{\mathrm{R}}\right)}^2={\left(k^{\mathrm{R}}\right)}^2\\ {\left(k_{1x}^{\mathrm{T}}\right)}^2+{\left(k_{1z}^{\mathrm{T}}\right)}^2={\left(k_1^{\mathrm{T}}\right)}^2\\ {\left(k_{2x}^{\mathrm{T}}\right)}^2+{\left(k_{2z}^{\mathrm{T}}\right)}^2={\left(k_2^{\mathrm{T}}\right)}^2\\ {\left(k_{\mathrm{s}x}^{\mathrm{T}}\right)}^2+{\left(k_{\mathrm{s}z}^{\mathrm{T}}\right)}^2={\left(k_{\mathrm{s}}^{\mathrm{T}}\right)}^2\end{array}\right.(14)$

$k_x^{\mathrm{I}}=k_x^{\mathrm{R}}=k_{1x}^{\mathrm{T}}=k_{2x}^{\mathrm{T}}=k_{\mathrm{s}x}^{\mathrm{T}}(15)$

For the liquid-saturated medium, it can be seen from Equations 8a, 8b that the amplitude ratios of potentials in Equations 13a–c can be determined as

${\delta }_1=\frac{A_{\mathrm{w}1}^{\mathrm{T}}}{A_{\mathrm{s}1}^{\mathrm{T}}}=\frac{\left(\lambda +2\mu +\frac{1-n}{n}{E}_{\mathrm{w}}\right){\left(k_1^{\mathrm{T}}\right)}^2-{\rho }_1{\omega }^2}{{\rho }_2{\omega }^2-E_{\mathrm{w}}{\left(k_1^{\mathrm{T}}\right)}^2}(\mathrm{16a})$

${\delta }_2=\frac{A_{\mathrm{w}2}^{\mathrm{T}}}{A_{\mathrm{s}2}^{\mathrm{T}}}=\frac{\left(\lambda +2\mu +\frac{1-n}{n}{E}_{\mathrm{w}}\right){\left(k_2^{\mathrm{T}}\right)}^2-{\rho }_1{\omega }^2}{{\rho }_2{\omega }^2-E_{\mathrm{w}}{\left(k_2^{\mathrm{T}}\right)}^2}(\mathrm{16b})$

${\delta }_{\mathrm{s}}=\frac{B_{\mathrm{w}}^{\mathrm{T}}}{B_{\mathrm{s}}^{\mathrm{T}}}=\frac{\mu {\left(k_{\mathrm{s}}^{\mathrm{T}}\right)}^2-{\rho }_1{\omega }^2}{{\rho }_2{\omega }^2}(\mathrm{16c})$

3.3 Boundary conditions and solutions

3.3.1 Boundary conditions

When the P-wave travels from the single-phase medium to the two-phase medium, the reflection and transmission will occur at the interface (say, z = 0). For this situation, the boundary conditions will make a difference to the propagation characteristics of waves, namely the unknown amplitudes $A^{\mathrm{R}}$, $B^{\mathrm{R}}$, $A_{\mathrm{s}1}^{\mathrm{T}}$, $A_{\mathrm{s}2}^{\mathrm{T}}$, and $B_{\mathrm{s}}^{\mathrm{T}}$. On the assumption of the existence of welded contact between two semi-infinite media, we consider two boundary conditions: (a) Open-pore boundary (see expressions (28) to (32) in Philippacopoulos [59]) and (b) Sealed-pore boundary (expressions (19) in Hajra and Mukhopadhyay [18] and Deresiewicz and Skalak [60]). More specifically, the boundary conditions are the continuity of stress and displacement components along the interface. Besides, in case (a), the pore fluid can flow freely into the permeable elastic solid, but in case (b), the flow of fluid (i.e., the relative fluid displacement) is restricted. Consequently, the two different boundary conditions are shown as

$\left\{\begin{array}{l}{\sigma }_{ij\left|z=0^{+}\right.}={\sigma }_{ij\left|z=0^{-}\right.}^{\prime }\\ u_{i\left|z=0^{+}\right.}=u_{i\left|z=0^{-}\right.}^{\prime }\\ p_{f\left|z=0^{+}\right.}=0\end{array}\right.(\mathrm{17a})$

$\left\{\begin{array}{l}{\sigma }_{ij\left|z=0^{+}\right.}={\sigma }_{ij\left|z=0^{-}\right.}^{\prime }\\ u_{i\left|z=0^{+}\right.}=u_{i\left|z=0^{-}\right.}^{\prime }\\ u_{z\left|z=0^{+}\right.}-U_{z\left|z=0^{+}\right.}=0\end{array}\right.(\mathrm{17b})$

where the subscripts i and j (=x and z) denote the components in the x and z directions. ${\sigma }_{ij\left|z=0^{+}\right.}$ and ${\sigma }_{ij\left|z=0^{-}\right.}^{\prime }$ are the total stresses (e.g., normal and shearing stresses) of the fluid-saturated porous medium and elastic solid, respectively. $u_{i\left|z=0^{+}\right.}$ is the displacement component of the soil skeleton in a two-phase medium at the interface, and $u_{i\left|z=0^{-}\right.}^{\prime }$ that of a single-phase medium at the interface. $p_{f\left|z=0^{+}\right.}$ represents the pore pressure at the interface.

3.3.2 Reflection and transmission coefficients

Without loss of generality, set the amplitude of the incident P-wave ($A^{\mathrm{I}}$) equal to unity. After the introduction of Equations 2a, 2b, 6a–6c, together with Equations 14, 15, 16a–16c, through Equations 17a, 17b, we can get the set of equations for the determination of the amplitude ratios (i.e., $A^{\mathrm{R}}/A^{\mathrm{I}}$, $B^{\mathrm{R}}/A^{\mathrm{I}}$, $A_{\mathrm{s}1}^{\mathrm{T}}/A^{\mathrm{I}}$, $A_{\mathrm{s}2}^{\mathrm{T}}/A^{\mathrm{I}}$, and $B_{\mathrm{s}}^{\mathrm{T}}/A^{\mathrm{I}}$) under permeable and impermeable boundaries in the matrix form as

$\left[S_{\mathrm{P}-\text{SV}}\right]{\left\{A^{\mathrm{R}},B^{\mathrm{R}},A_{\mathrm{s}1}^{\mathrm{T}},A_{\mathrm{s}2}^{\mathrm{T}},B_{\mathrm{s}}^{\mathrm{T}}\right\}}^{\mathrm{T}}={\left\{{\lambda }^{\prime }{\left(k^{\mathrm{I}}\right)}^2+2{\mu }^{\prime }{\left(k_z^{\mathrm{I}}\right)}^2,2{\mu }^{\prime }{k}_x^{\mathrm{I}}{k}_z^{\mathrm{I}},k_x^{\mathrm{I}},k_z^{\mathrm{I}},0\right\}}^{\mathrm{T}}(\mathrm{18a})$

$\left[{\overline{S}}_{\mathrm{P}-\text{SV}}\right]{\left\{A^{\mathrm{R}},B^{\mathrm{R}},A_{\mathrm{s}1}^{\mathrm{T}},A_{\mathrm{s}2}^{\mathrm{T}},B_{\mathrm{s}}^{\mathrm{T}}\right\}}^{\mathrm{T}}={\left\{{\lambda }^{\prime }{\left(k^{\mathrm{I}}\right)}^2+2{\mu }^{\prime }{\left(k_z^{\mathrm{I}}\right)}^2,2{\mu }^{\prime }{k}_x^{\mathrm{I}}{k}_z^{\mathrm{I}},k_x^{\mathrm{I}},k_z^{\mathrm{I}},0\right\}}^{\mathrm{T}}(\mathrm{18b})$

where $\left[S_{\mathrm{P}-\text{SV}}\right]$ and $\left[{\overline{S}}_{\mathrm{P}-\text{SV}}\right]$ are the 5 × 5 matrices, which represent permeable and impermeable boundaries respectively, and the elements of the matrices are given in the Appendix. The unknown quantities $A^{\mathrm{R}}$, $B^{\mathrm{R}}$, $A_{\mathrm{s}1}^{\mathrm{T}}$, $A_{\mathrm{s}2}^{\mathrm{T}}$, and $B_{\mathrm{s}}^{\mathrm{T}}$ can be solved as the amplitude reflection and transmission coefficients at the plane interface.

4 Degenerate validation of solutions

4.1 Validation of degenerate formulas

Set the mass density of liquid ${\rho }_w$ = 0 and the bulk modulus of liquid $E_w$ = 0. The analytical formulas in this paper can revert to the classical problem of P-wave incident at the interface between two diverse elastic solids. For this situation, the amplitude ratios of liquid- and solid-phase ${\delta }_1$ = 0, ${\delta }_2$ = 0, and ${\delta }_{\mathrm{s}}$ = 0. The wave vectors of the refracted P₁- and P₂-waves are equal, namely, $k_1^{\mathrm{T}}$ = $k_2^{\mathrm{T}}$ and $k_{1z}^{\mathrm{T}}$ = $k_{2z}^{\mathrm{T}}$. The velocities of refracted P- and SV-waves $V_{\mathrm{P}}$ = $\sqrt{\left(\lambda +2\mu \right)/{\rho }_{\mathrm{s}}}$, $V_{\mathrm{S}}$ = $\sqrt{\mu /{\rho }_{\mathrm{s}}}$, when the two-phase medium degenerates to a single-phase medium. The potential amplitude of the refracted P-wave is equivalent to the sum of the amplitudes of P₁- and P₂-waves, namely, $A_{\mathrm{s}}^{\mathrm{T}}$ = $A_{\mathrm{s}1}^{\mathrm{T}}$ + $A_{\mathrm{s}2}^{\mathrm{T}}$. The formula (Equation 18a) or (Equation 18b) may reduce to

$\left\{\begin{array}{l}\mu \left(\frac{V_{\mathrm{P}}^2}{V_{\mathrm{S}}^2}{\left(k_1^{\mathrm{T}}\right)}^2-2{\left(k_{1x}^{\mathrm{T}}\right)}^2\right)A_{\mathrm{s}}^{\mathrm{T}}+2\mu k_{\mathrm{s}x}^{\mathrm{T}}{k}_{\mathrm{s}z}^{\mathrm{T}}{B}_{\mathrm{s}}^{\mathrm{T}}={\mu }^{\prime }\left(\frac{C_{\mathrm{P}}^2}{C_{\mathrm{S}}^2}{\left(k^{\mathrm{I}}\right)}^2-2{\left(k_x^{\mathrm{I}}\right)}^2\right)\\ \times \left(A^{\mathrm{I}}+A^{\mathrm{R}}\right)-2{\mu }^{\prime }{k}_x^{\mathrm{R}}{k}_z^{\mathrm{R}}{B}^{\mathrm{R}}\\ 2\mu k_{1x}^{\mathrm{T}}{k}_{1z}^{\mathrm{T}}{A}_{\mathrm{s}}^{\mathrm{T}}+\mu \left({\left(k_{\mathrm{s}x}^{\mathrm{T}}\right)}^2-{\left(k_{\mathrm{s}z}^{\mathrm{T}}\right)}^2\right)B_{\mathrm{s}}^{\mathrm{T}}=2{\mu }^{\prime }{k}_x^{\mathrm{I}}{k}_z^{\mathrm{I}}\left(A^{\mathrm{I}}-A^{\mathrm{R}}\right)\\ +{\mu }^{\prime }\left({\left(k_x^{\mathrm{R}}\right)}^2-{\left(k_z^{\mathrm{R}}\right)}^2\right)B^{\mathrm{R}}\\ k_{1x}^{\mathrm{T}}{A}_{\mathrm{s}}^{\mathrm{T}}-k_{\mathrm{s}z}^{\mathrm{T}}{B}_{\mathrm{s}}^{\mathrm{T}}=k_x^{\mathrm{I}}\left(A^{\mathrm{I}}+A^{\mathrm{R}}\right)+k_z^{\mathrm{R}}{B}^{\mathrm{R}}\\ k_{1z}^{\mathrm{T}}{A}_{\mathrm{s}}^{\mathrm{T}}+k_{\mathrm{s}x}^{\mathrm{T}}{B}_{\mathrm{s}}^{\mathrm{T}}=k_z^{\mathrm{I}}\left(A^{\mathrm{I}}-A^{\mathrm{R}}\right)+k_x^{\mathrm{R}}{B}^{\mathrm{R}}\end{array}\right.(19)$

After some simplification, Equation 19 can degenerate into a classical problem in that the P-wave travels from an elastic solid to another one (see expressions (3-45) and (3-46) in [1]). It is interesting to unravel that the reflection and transmission between different elastic solids is a special case in this paper.

4.2 Validation of numerical analysis

To explain the correctness of the formulas graphically, the computed results of Equation 19 are compared with those of Pujol [57]. The parameters of the incident and transmitted media are as follows: ${\lambda }^{\prime }$ = 44.006, ${\mu }^{\prime }$ = 43.729, ${\rho }^{\prime }$ = 3.16, $\lambda$ = 13.32, $\mu$ = 13.34 and ${\rho }_{\mathrm{s}}$ = 2.5 (see in ref. [57]). Figure 2 depicts the variation of reflection and refraction coefficients with the incident angle when the P-wave propagates from one elastic solid to another.

Figure 2

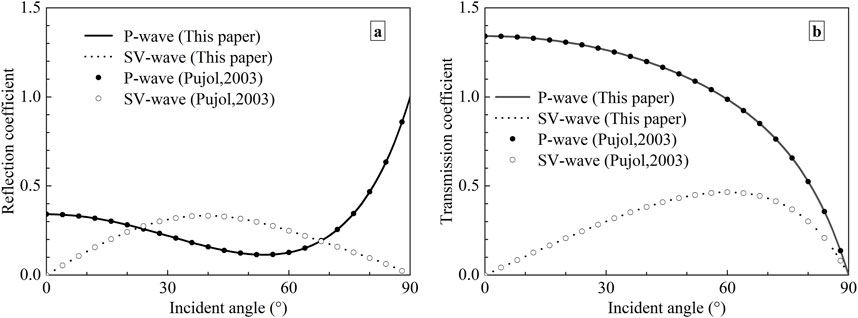
Figure 2. Variation of the amplitude reflection and transmission coefficients with the incident angle for two diverse elastic solids. (a) Reflection coefficients; (b) Transmission coefficients.

From Figure 2, the calculated results of Equation 19 coincide with those shown by Pujol [57]. In a word, the case of P-wave traveling from an elastic solid to another one is a special case of ours, and it is sufficient to demonstrate the rationality and correctness of the formulas derived in this article.

5 Numerical results and discussion

In this section, we consider a model consisting of a fluid-saturated medium in welded contact with the elastic solid. The plane harmonic P-wave propagates through the elastic solid and becomes incident at the interface. The Gauss elimination method is used to calculate Equations 18a, 18b, then we obtain the amplitude ratios. Numerical examples are carried out to investigate the effects of boundary conditions, incident wave frequency, and properties of the saturated two-phase medium (i.e., the dynamic permeability coefficient k, the porosity n, and the Poisson’s ratio υ) on the reflection and transmission coefficients. The physical parameters of the two-phase medium are taken from Refs. [1, 22] and listed in Table 1, together with the single-phase medium.

Table 1

Table 1. Material properties of single- and two-phase media.

Figures 3–7 depict the variation of reflection and transmission coefficients in the form of amplitude computed as described in Equations 18a, 18b with incident angle under diverse conditions, i.e., boundary drainage, wave frequency, permeability coefficient, porosity, and Poisson’s ratio. It is found that the amplitudes of the reflected and refracted waves depend significantly on the angle of incidence, and the nature of dependence is quite different. When the incident P-wave strikes the interface perpendicularly, no reflected or transmitted SV-wave is generated, i.e., the reflection and transmission coefficients of the SV-wave are zero. At the same time, the amplitudes of transmitted P₁- and P₂-waves arrive at the largest values in this case. When the incident P-wave is at grazing incidence (i.e., the incident angle approaches 90°), there is only a reflected compressional P-wave whose reflection coefficient is 1.0. In addition, for transmitted P₁- and P₂-waves, the amplitudes decrease gradually when the angle of incidence (θ_IP) increases from 0° to 90°. The amplitudes of reflected and transmitted SV-waves increase with an increase in the incident angle before reaching their maximum values and thereafter, decrease and approach their minimum values. However, the effect of the incident angle on the amplitude of the reflected P-wave is quite complex, which will be explained in specified sections.

Figure 3

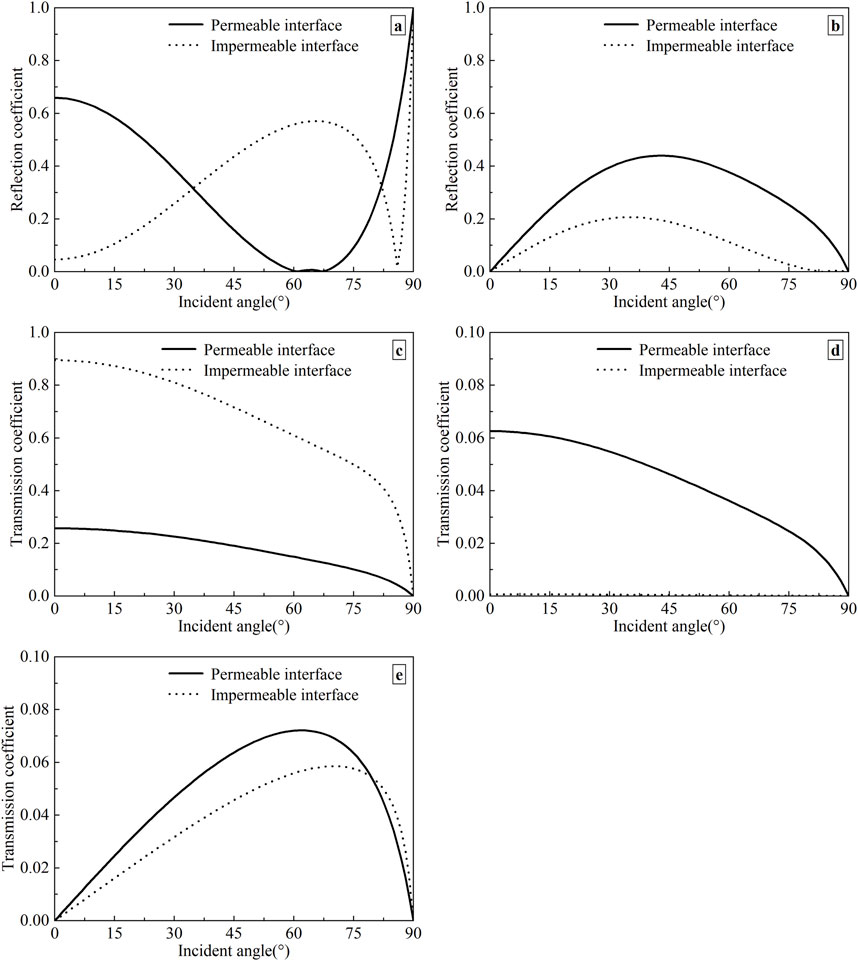
Figure 3. Variation of reflection and transmission coefficients with the incident angle under different drainage conditions. (a) Reflected P-wave; (b) Reflected SV-wave; (c) Transmitted P₁-wave; (d) Transmitted P₂-wave; (e) Transmitted SV-wave.

Figure 4

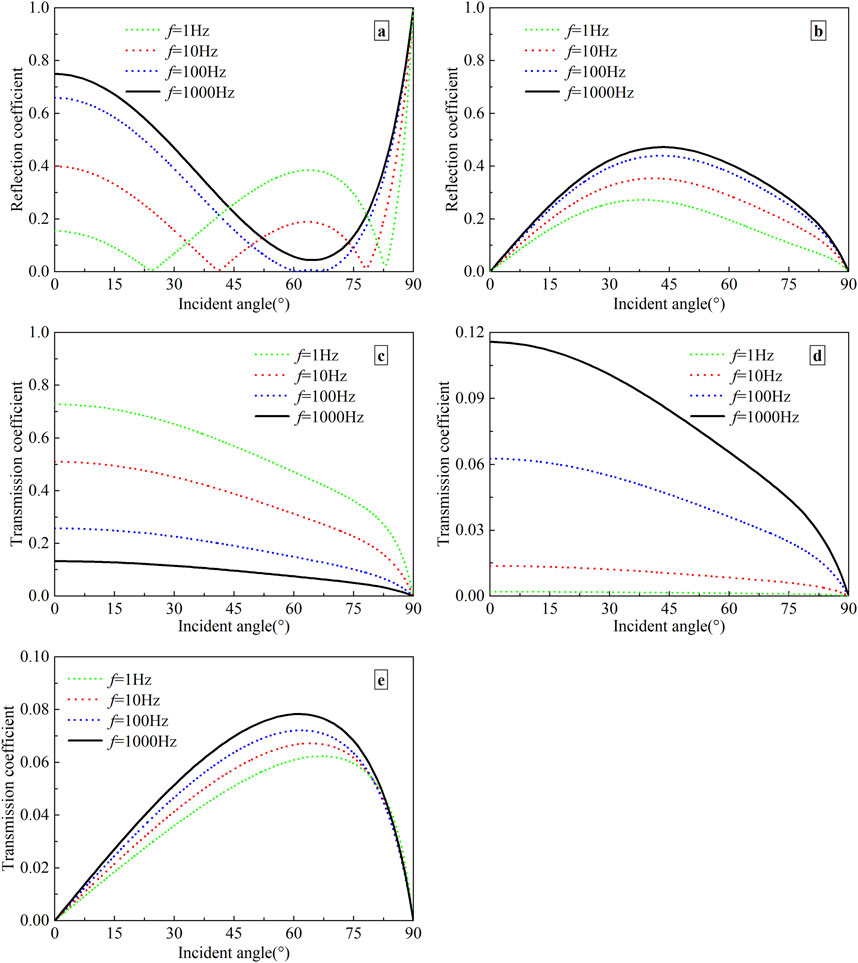
Figure 4. Variation of reflection and transmission coefficients with the incident angle at different frequencies. (a) Reflected P-wave; (b) Reflected SV-wave; (c) Transmitted P₁-wave; (d) Transmitted P₂-wave; (e) Transmitted SV-wave.

Figure 5

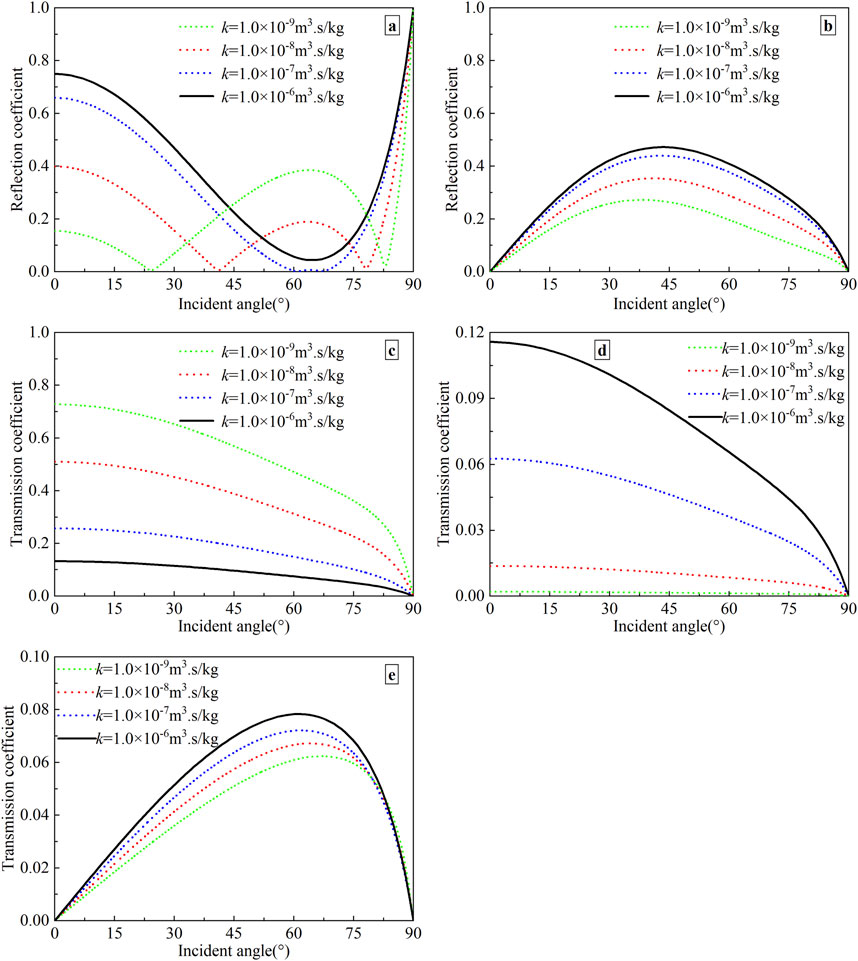
Figure 5. Variation of reflection and transmission coefficients with the incident angle for different values of dynamic permeability coefficient. (a) Reflected P-wave; (b) Reflected SV-wave; (c) Transmitted P₁-wave; (d) Transmitted P₂-wave; (e) Transmitted SV-wave.

Figure 6

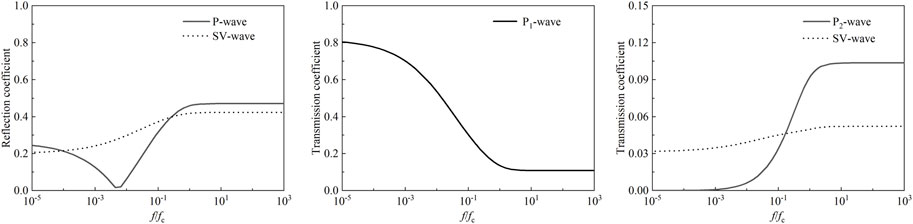
Figure 6. Variation of reflection and transmission coefficients with the non-dimensional frequency ratio.

Figure 7

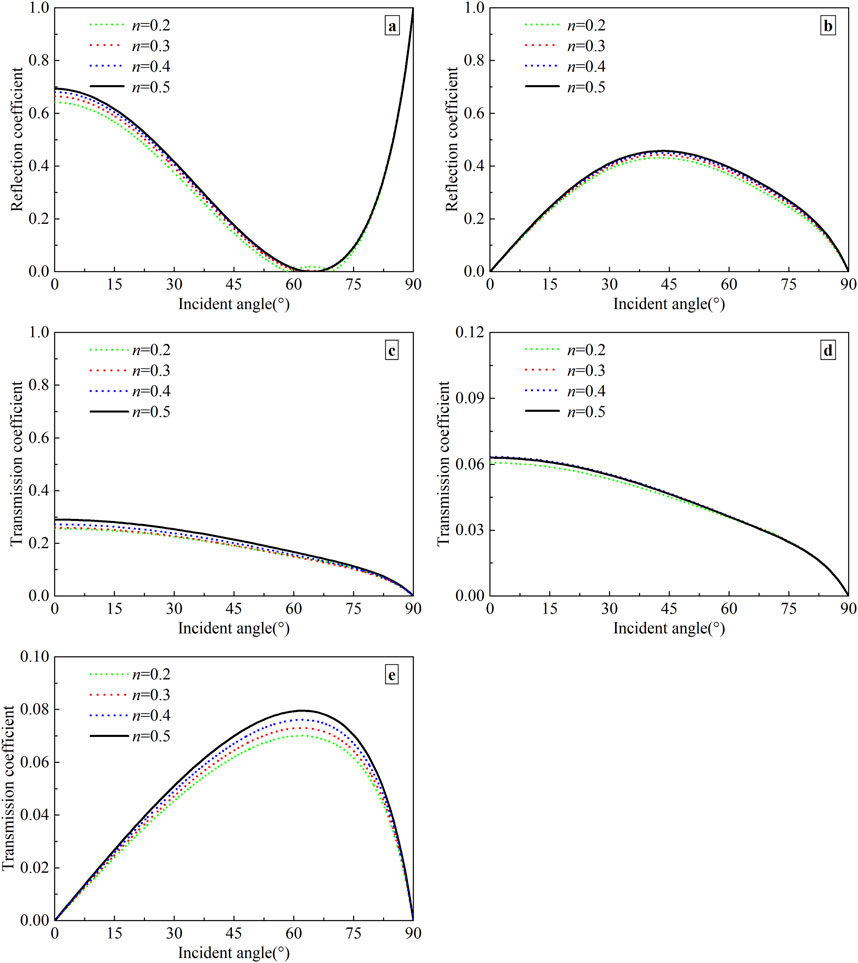
Figure 7. Variation of reflection and transmission coefficients with the incident angle under different porosities. (a) Reflected P-wave; (b) Reflected SV-wave; (c) Transmitted P₁-wave; (d) Transmitted P₂-wave; (e) Transmitted SV-wave.

5.1 The influence of boundary drainage

When the P-wave propagates from the elastic solid to the two-phase medium, the boundary conditions for the interface will play a key role in the reflection and transmission of seismic waves. To study in greater detail the dependence of the reflection and transmission coefficients on the boundary drainage, we select two different boundary conditions (i.e., permeable or impermeable interface). In our calculations, the soil parameters are taken from Table 1, and the wave frequency of the incident wave f = 100 Hz. Figure 3 describes the reflection and transmission coefficients as a function of incident angle at permeable and impermeable interfaces.

It is shown in Figure 3 that whether the interface is drained or not, the reflection and transmission coefficients are affected significantly by the incident angle. The variation of reflection and transmission coefficients of other waves exhibits the same trend with the incident angle under diverse interfaces, except for the reflected P-wave. However, the actual values of reflection and transmission coefficients differ appreciably for the two types of interfaces considered. For the reflected SV-wave, the reflection coefficient in the permeable interface is much larger than that in the impermeable interface. For the transmitted SV-wave, the amplitude in the permeable interface is larger than that in the impermeable interface before reaching 79°; thereafter, the amplitude in the permeable interface is less than that in the impermeable interface. What’s more, the transmission coefficient of P₂-wave under undrained conditions is much smaller than the corresponding one under drained conditions, while the P₁-wave has the reverse regularity. The relative fluid displacement with respect to the soil skeleton is taken to be zero, which causes the difficulty of generating of P₂-wave. It is enough to show that when the interface is permeable, we must pay attention to the P₂-wave, which cannot be ignored because of its slow velocity and fast attenuation, otherwise it may lead to the problem of instability in numerical calculations.

5.2 The influence of wave frequency

The results in Section 5.1 are obtained at a special frequency of 100 Hz. To investigate the effect of frequency on the reflection and transmission coefficients, three typical frequencies (i.e., f = 1, 10, and 1,000 Hz) are added to the numerical calculations, and the properties of the medium are taken from Table 1. The characteristic frequency of the saturated medium f_c = $n/2\pi k{\rho }_f$ = 430 Hz, which is defined by Biot [4, 5]. According to the results of Yang [23], the reflection and transmission coefficients for the permeable interface exhibit a large dispersion in the low-frequency range (i.e., $f/f_{\mathrm{c}}$ ≤0.1). All wave frequencies in this study are below 1,000 Hz, which covers the common frequencies used in seismic and acoustic fields [33]. Given that mentioned above, the boundary is assumed to be permeable. The variation of the computed reflection and transmission coefficients with the incident angle of the P-wave is shown in Figure 4.

For all the cases of wave frequency under consideration, the reflection and transmission coefficients of all waves are affected significantly by it. The transmission coefficient of P₁-wave (P₂-wave) decreases (increases) with the increasing frequency. For the reflected SV wave, the amplitude increases with an increase in frequency. For the transmitted SV-wave, the amplitude increases with a rise in frequency if the incident angle θ_IP < 76°, while the impact of frequency becomes less significant if the incident angle θ_IP > 76°. However, for the reflected P-wave, when the frequency f = 1, 10, and 100 Hz, the reflected P-wave extinguishes at a specific angle of incidence. Under the case that f = 1 Hz (10 Hz), the two special angles are 23° and 83° (43° and 77°). If the frequency f = 100 Hz, the corresponding angles are 61° and 67°.

5.3 The influence of dynamic permeability coefficient

Since the fluid flows in the two-phase medium, it is instructive to investigate the effect of the dynamic permeability coefficient on the reflection and transmission coefficients. In calculations, the properties of the media are taken from Table 1, except for the dynamic permeability coefficient. The frequency of the incident P-wave is 100 Hz, and the interface is assumed to be permeable. The reflection and transmission coefficients as a function of incident angle for four cases of dynamic permeability coefficient (i.e., k = 1.0 × 10⁻⁹, 1.0 × 10⁻⁸, 1.0 × 10⁻⁷, and 1.0 × 10⁻⁶ m³ s/kg) are shown in Figure 5.

As shown in Figure 5, the reflection and transmission coefficients of all waves vary with the dynamic permeability coefficient. For the reflected SV-wave and transmitted P₂-wave, the higher the dynamic permeability coefficient is, the larger the amplitude is. Whereas for the transmitted P₁-wave, the higher the dynamic permeability coefficient is, the smaller the amplitude is. In addition, the transmission coefficient of the SV-wave increases with a rise in the dynamic permeability coefficient before the incident angle reaches 76°. Thereafter, the dynamic permeability coefficient has little effect on the transmission coefficient of SV-wave. For the reflected P-wave, when the dynamic permeability coefficient k = 1.0 × 10⁻⁹, 1.0 × 10⁻⁸, and 1.0 × 10⁻⁷ m³ s/kg, there are special angles that make the reflected SV-wave exist, and the reflected P-wave disappear. Also, different permeability coefficients correspond to different angles of incidence. If k = 1.0 × 10⁻⁹ m³ s/kg (1.0 × 10⁻⁸ m³ s/kg), the two special angles are 23° and 83° (43° and 77°). If k = 1.0 × 10⁻⁷ m³ s/kg, the corresponding angles are 61° and 67°.

By comparing Figure 5 with Figure 4, it is obvious that the reflection and transmission coefficient curves are the same when the product of the permeability coefficient k and frequency ω is equal. The reason is that when kω takes the same value, the velocities of the two-phase medium do not change [51]. If the wave velocities of the two-phase medium remain constant, the reflection and transmission coefficients are also fixed values.

To explain the influence of the dynamic permeability coefficient and frequency on the reflection and transmission coefficients, we introduce a non-dimensional frequency ratio f/f_c (=ρ_wkω/n). In calculations, the incident angle of the P-wave is taken to be 30°, and the boundary is assumed to be permeable. The physical parameters of media are taken from Table 1. Figure 6 shows the variation of reflection and transmission coefficients with the non-dimensional frequency ratio.

From Figure 6, it can be observed that the reflection and transmission coefficients are dispersive, namely, frequency-dependent. And all coefficients are affected by frequency, even in a very low frequency range. Moreover, the reflection and transmission coefficients depend on the function of frequency-permeability product.

5.4 The influence of porosity

The porosity is an important property in the fluid-saturated porous medium, which concerns the soil structure. To analyze the effect of porosity, the porosity n is taken to be 0.2, 0.3, 0.4, and 0.5, respectively. The other physical parameters of media remain constant as listed in Table 1. The wave frequency f = 100 Hz, and the interface is permeable. Figure 7 depicts the angle-dependent reflection and transmission coefficients for the above four values of porosity.

As observed in Figure 7, it is worth noting that the porosity has a slight influence on the reflection and transmission coefficients. The variation of transmission coefficients for P₁- and P₂-waves with porosity is gentle. The reflection and transmission coefficients of the SV-wave increase with a rise in porosity. For the reflected P-wave, there are two zero values, i.e., the incident angles θ_IP = 58° and 72°, when the porosity n = 0.2.

5.5 The influence of Poisson’s ratio

The Poisson’s ratio, one of the characteristic parameters in the two-phase medium, reflects the deformation characteristics of the soil. To investigate the effects of Poission’s ratio on the reflection and transmission coefficients, the parameters of the soil remain invariable as listed in Table 1, except for Poission’s ratio. The wave frequency f = 100 Hz, and the interface is permeable. The variation of reflection and transmission coefficients with the incident angle of the P-wave is depicted in Figure 8.

Figure 8

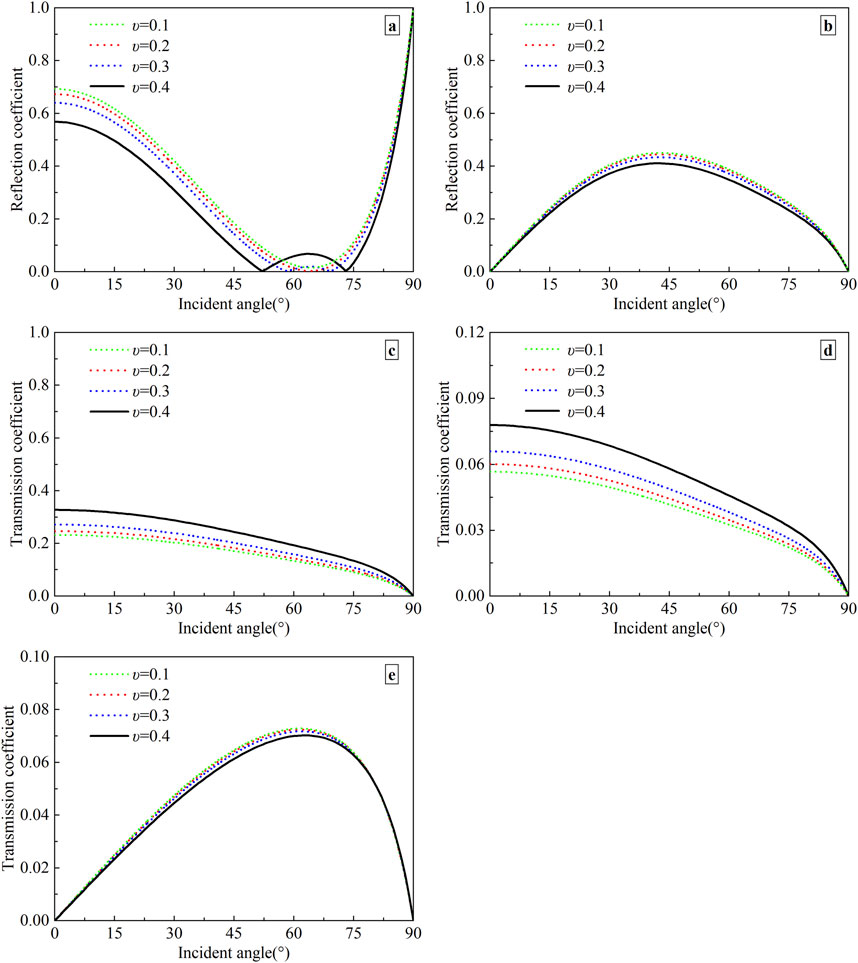
Figure 8. Variation of reflection and transmission coefficients with the incident angle under different Poisson’s ratios. (a) Reflected P-wave; (b) Reflected SV-wave; (c) Transmitted P₁-wave; (d) Transmitted P₂-wave; (e) Transmitted SV-wave.

As described in Figure 8, the effects of the Poisson’s ratio on the reflection and transmission coefficients of each wave are more obvious than those of the porosity in the previous Section 5.4. The transmission coefficients of P₁- and P₂-waves increase as the Poisson’s ratio increases at the same angle of incidence. While the transmission coefficients of SV-wave decrease with the increase in Poisson’s ratio if θ_IP < 68°, thereafter the Poisson’s ratio has little impact on it. The reflection coefficient of the SV-wave decreases with increasing Poisson’s ratio. For the reflected P-wave, when the Poisson’s ratio υ = 0.3 and 0.4, there are special angles that make the reflected SV-wave exist, and the reflected P-wave disappears. Also, different Poisson’s ratios correspond to different angles of incidence. When the Poisson’s ratio υ = 0.3 (0.4), the two special angles are 58° and 68° (52° and 73°).

6 Conclusion

Based on the model of soil mechanics proposed by Men [12], the reflection and transmission of a plane harmonic P-wave traveling from an elastic solid to the fluid-saturated porous media are investigated. The analytical expressions for the reflection and transmission coefficients have been derived for permeable and impermeable boundaries. Numerical calculations are performed to analyze the dependence of reflection and transmission coefficients on the incident angle, boundary drainage, wave frequency, and material properties (dynamic permeability coefficient, porosity, and Poisson’s ratio). Some useful results are obtained as follows: (1) The incident angle has a great influence on the reflection and transmission coefficient of each wave. When the angle of incidence θ_IP = 0°, the reflected and transmitted SV-waves disappear, and the transmission coefficients of P₁- and P₂-waves reach the largest values. Moreover, when the angle of incidence θ_IP = 90°, there is only a reflected P-wave, with which the reflection coefficient is 1.0. (2) The interface flow condition has a great impact on the reflection and transmission coefficients. (3) The reflection and transmission coefficients are dispersive and depend on the product of frequency and permeability. (4) The physical parameters of the two-phase medium (dynamic permeability coefficient, porosity, and Poisson’s ratio) have different influences on the reflection and transmission coefficients of waves.

Hence, it is interesting to study the propagation characteristics of elastic waves at the interface between the elastic solid and the two-phase medium. It is hoped that this paper may be useful in the theoretical and observational studies of wave propagation in the liquid-saturated porous medium. At last, it can be extended to study the reflection and transmission of elastic waves at other various boundaries, e.g., the porous medium/the porous medium [61, 62], the water/porous medium [63, 64], and ocean sediment [65, 66], etc.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

LQ: Writing – original draft, Writing – review and editing, Software, Data curation, Validation. BZ: Supervision, Conceptualization, Writing – review and editing, Funding acquisition, Writing – original draft, Methodology.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. This research work was supported by the Science Research Project of Hebei Education Department, QN2025419, BZ.

Acknowledgments

The authors would like to thank the Science Research Project of Hebei Education Department (Grant No. QN2025419) for funding the work presented in this paper.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Wu S. Wave propagation in soils. Beijing: Science Press (1997). p. 62–84. [in Chinese].

Google Scholar

2. Yang J, Wu S, Cai Y. Characteristics of propagation of elastic waves in saturated soils. J Vib Eng (1996) 9(02):128–37. doi:10.16385/j.cnki.issn.1004-4523.1996.02.011

CrossRef Full Text | Google Scholar

3. Zhao C, Gao F, Zeng Q. The reflection and transmission of plane waves on an interface between solid and liquid-filled porous solid with dissipation of energy. Chin J Rock Mech Eng (1996) 15(s1):470–5. (in Chinese).

Google Scholar

4. Biot MA. Theory of propagation of elastic waves in a fluid-saturated porous solid. I. Low-frequency range. J Acoust Soc Am (1956) 28(2):168–78. doi:10.1121/1.1908239

CrossRef Full Text | Google Scholar

5. Biot MA. Theory of propagation of elastic waves in a fluid-saturated porous solid. II. Higher frequency range. J Acoust Soc Am (1956) 28(2):179–91. doi:10.1121/1.1908241

CrossRef Full Text | Google Scholar

6. Plona TJ. Observation of a second bulk compressional wave in a porous medium at ultrasonic frequencies. Appl Phys Lett (1980) 36:259–61. doi:10.1063/1.91445

CrossRef Full Text | Google Scholar

7. Berryman JG. Confirmation of Biot’s theory. Appl Phys Lett (1980) 37:382–4. doi:10.1063/1.91951

CrossRef Full Text | Google Scholar

8. Zienkiewicz OC, Chang CT, Bettess P. Drained, undrained, consolidating and dynamic behavior assumptions in soils. Geotechnique (1980) 30(4):385–95. doi:10.1680/geot.1980.30.4.385

CrossRef Full Text | Google Scholar

9. Zienkiewicz OC, Shiomi T. Dynamic behaviour of saturated porous media; the generalized Biot formulation and its numerical solution. Int J Numer Anal Meth (1984) 8(1):71–96. doi:10.1002/nag.1610080106

CrossRef Full Text | Google Scholar

10. Men F. Wave propagation in a porous, saturated elastic medium. Acta Geophys Sinica (1965) 14(02):37–44. (in Chinese).

Google Scholar

11. Men F. Problems of wave propagation in porous fluid-saturated media. Acta Geophys Sinica (1981) 24(01):65–76. (in Chinese).

Google Scholar

12. Men F. On wave propagation in fluid-saturated porous media. Conf Soil Dyn Earthq Eng (1982) (1) 225–38.

Google Scholar

13. Bowen RM, Reinicke KM. Plane progressive waves in a binary mixture of linear elastic materials. J Appl Mech (1978) 45(3):493–9. doi:10.1115/1.3424351

CrossRef Full Text | Google Scholar

14. Chen S, Liao Z. Study on mechanic models of two-phase media. Earthq Eng Eng Vib (2002) 22(04):1–8. doi:10.13197/j.eeev.2002.04.001

CrossRef Full Text | Google Scholar

15. Gutenberg B. Energy ratio of reflected and refracted seismic waves. Bull Seismol Soc Am (1944) 34:85–102. doi:10.1785/BSSA0340020085

CrossRef Full Text | Google Scholar

16. Geertsma J, Smit DC. Some aspects of elastic wave propagation in fluid-saturated porous solids. Geophysics (1961) 26(2):169–81. doi:10.1190/1.1438855

CrossRef Full Text | Google Scholar

17. Deresiewicz H, Rice JT. The effect of boundaries on wave propagation in a liquid-filled porous solid: V. Transmission across a plane interface. Bull Seismol Soc Am (1964) 54(1):409–16. doi:10.1785/BSSA0540010409

CrossRef Full Text | Google Scholar

18. Hajra S, Mukhopadhyay A. Reflection and refraction of seismic waves incident obliquely at the boundary of a liquid-saturated porous solid. Bull Seismol Soc Am (1982) 72(5):1509–33. doi:10.1785/BSSA0720051509

CrossRef Full Text | Google Scholar

19. Sharma MD, Gogna ML. Reflection and refraction of plane harmonic waves at an interface between elastic solid and porous solid saturated by viscous liquid. Pure Appl Geophys (1992) 138:249–66. doi:10.1007/bf00878898

CrossRef Full Text | Google Scholar

20. Vashisth AK, Sharma MD, Gogna ML. Reflection and transmission of elastic waves at a loosely bonded interface between an elastic solid and liquid-saturated porous solid. Geophys J R Astron Soc (1991) 105(3):601–17. doi:10.1111/j.1365-246X.1991.tb00799.x

CrossRef Full Text | Google Scholar

21. Zhao C, Gao F, Cui J. Boundary effect of wave propagating from liquid-filled porous medium to solid medium. Earthq Eng Eng Vib (1999) 19(01):1–6. doi:10.13197/j.eeev.1999.01.001

CrossRef Full Text | Google Scholar

22. Ye C, Shi Y, Cai Y. Reflection and refraction at the interface when S waves propagate from saturated soil to elastic soil. J Vib Shock (2005) 24(2):41–5+147. doi:10.13465/j.cnki.jvs.2005.02.012

CrossRef Full Text | Google Scholar

23. Yang J. Importance of flow condition on seismic waves at a saturated porous solid boundary. J Sound Vib (1999) 221(03):391–413. doi:10.1006/jsvi.1998.2036

CrossRef Full Text | Google Scholar

24. Yang J. Influence of water saturation on horizontal and vertical motion at a porous soil interface induced by incident P wave. Soil Dyn Earthq Eng (2000) 19(8):575–81. doi:10.1016/S0267-7261(00)00067-1

CrossRef Full Text | Google Scholar

25. Yang J, Sato T. Influence of viscous coupling on seismic reflection and transmission in saturated porous media. Bull Seismol Soc Am (1998) 88(5):1289–99. doi:10.1785/BSSA0880051289

CrossRef Full Text | Google Scholar

26. Yang J, Sato T. Influence of water saturation on horizontal and vertical motion at a porous soil interface induced by incident SV wave. Soil Dyn Earthq Eng (2000) 19(5):339–46. doi:10.1016/S0267-7261(00)00023-3

CrossRef Full Text | Google Scholar

27. Li W. Influence of water saturation on seismic reflection and transmission coefficients at a mainly water-saturated porous soil interface. Northwest Seismol J (2002) 24(02):303–9. doi:10.3969/j.issn.1000-0844.2002.04.003

CrossRef Full Text | Google Scholar

28. Xu P, Xia T. Reflection and transmission of elastic wave at the interface of nearly saturated soil and elastic soil. Mech Eng (2006) 28(6):58–63. doi:10.3969/j.issn.1000-0879.2006.06.013

CrossRef Full Text | Google Scholar

29. Kumar R, Kumar S, Miglani A. Reflection and transmission of plane waves between two different fluid-saturated porous half-spaces. J Appl Mech Tech Phys (2011) 59(02):773–82. doi:10.2478/v10175-011-0028-8

CrossRef Full Text | Google Scholar

30. Wei Z, Wang Y, Zhang Z. Propagating from a single-phase elastic medium to a transversely isotropic liquid-saturated porous medium. Acta Mech Solida Sin (2002) 23(02):183–9. doi:10.19636/j.cnki.cjsm42-1250/o3.2002.02.009

CrossRef Full Text | Google Scholar

31. Singh P, Chattopadhyay A, Srivastava A, Singh AK. Reflection and transmission of P-waves in an intermediate layer lying between two semi-infinite media. Pure Appl Geophys (2018) 175:4305–19. doi:10.1007/s00024-018-1896-8

CrossRef Full Text | Google Scholar

32. Dai Z, Kuang Z, Zhao S. Reflection and transmission of elastic waves at the interface between an elastic solid and a double porosity medium. Int J Rock Mech Min (2006) 43(6):961–71. doi:10.1016/j.ijrmms.2005.11.010

CrossRef Full Text | Google Scholar

33. Chen W, Xia T, Chen W, Zhai C. Propagation of plane P-waves at interface between elastic solid and unsaturated poroelastic medium. Appl Math Mech (2012) 33(07):829–44. doi:10.1007/s10483-012-1589-6

CrossRef Full Text | Google Scholar

34. Kumar M, Singh A, Kumari M, Barak MS. Reflection and refraction of elastic waves at the interface of an elastic solid and partially saturated soils. Acta Mechanica (2021) 232:33–55. doi:10.1007/s00707-020-02819-z

CrossRef Full Text | Google Scholar

35. Goyal S, Tomar SK. Reflection/Refraction of a dilatational wave at a plane interface between uniform elastic and swelling porous half-spaces. Transp Porous Media (2015) 109:609–32. doi:10.1007/s11242-015-0539-0

CrossRef Full Text | Google Scholar

36. Tomar SK, Arora A. Reflection and transmission of elastic waves at an elastic/porous solid saturated by two immiscible fluids. Int J Sol Struct (2006) 44(17):1991–2013. doi:10.1016/j.ijsolstr.2007.05.021

CrossRef Full Text | Google Scholar

37. Kumar M, Saini R. Reflection and refraction of attenuated waves at boundary of elastic solid and porous solid saturated with two immiscible viscous fluids. Appl Math Mech (2012) 33(6):797–816. doi:10.1007/s10483-012-1587-6

CrossRef Full Text | Google Scholar

38. Jiang H, Ma Q, Shao S, Shao S. Characteristic of energy transmission of plane-S-wave at interface between elastic medium and saturated frozen soil medium. Chin J Rock Mech Eng (2023) 42(04):976–92. doi:10.13722/j.cnki.jrme.2022.0473

CrossRef Full Text | Google Scholar

39. Jiang H, Ma Q, Cao Y. Study on the reflection and transmission of P wave on the interface between elastic medium and saturated frozen soil medium. Rock Soil Mech (2023) 44(03):916–29. doi:10.16285/j.rsm.2022.0329

CrossRef Full Text | Google Scholar

40. Ergin K. Energy ratio of the seismic waves reflected and refracted at a rock-water boundary. Bull Seismol Soc Am (1952) 42(4):349–72. doi:10.1785/BSSA0420040349

CrossRef Full Text | Google Scholar

41. Wang J, Jin F, Zhang C. Dynamic response of ideal fluid layer overlying elastic half-space due to SV-wave incidence. Eng Mech (2004) 21(1):15–20. (in Chinese).

Google Scholar

42. Wang J, Jin F, Zhang C. Dynamic response of ideal fluid layer overlying elastic half-space due to P-wave incidence. Eng Mech (2003) 20(6):12–7. doi:10.3969/j.issn.1000-4750.2003.06.003

CrossRef Full Text | Google Scholar

43. Awad E, Dai W, Sobolev S. Thermal oscillations and resonance in electron-phonon interaction process. Z Angew Math Phys (2024) 75(4):143. doi:10.1007/s00033-024-02277-w

CrossRef Full Text | Google Scholar

44. Awad E, Samir N. A closed-form solution for thermally induced affine deformation in unbounded domains with a temporally accelerated anomalous thermal conductivity. J Phys A-math Theor (2024) 57(45):455202. doi:10.1088/1751-8121/ad878f

CrossRef Full Text | Google Scholar

45. Chen S. Numerical simulation for near-field wave motion in two-phase media. [Dissertation thesis]. Harbin: China Earthquake Administration, Institute of Engineering Mechanics (2002).

Google Scholar

46. Chen S, Liao Z, Chen J. A decoupling FEM for simulating near-field wave motions in two-phase media. Chin J Geophys (2005) 48(4):909–17. doi:10.3321/j.issn:0001-5733.2005.04.025

CrossRef Full Text | Google Scholar

47. Jing L, Zhuo X, Wang X. Effect of complex site on seismic wave propagation. Earthq Eng Eng Vib (2005) 25(6):16–23. doi:10.13197/j.eeev.2005.06.004

CrossRef Full Text | Google Scholar

48. Jing L, Zhuo X, Wang X. The effect of complex media on seismic wave propagation. Chin J Geotech Eng (2005) 27(04):393–7. doi:10.3321/j.issn:1000-4548.2005.04.006

CrossRef Full Text | Google Scholar

49. Wang X. Analysis on wave propagation in two-dimensional saturated media. [Dissertation thesis]. Harbin: China Earthquake Administration, Institute of Engineering Mechanics (2003).

Google Scholar

50. Xiao M, Cui J, Li Y, Jiang J, Shan Y, Duhee P. Propagation characteristics of Rayleigh waves and their influence on seabed dynamics in ocean sites. J Hunan Univ (Natural Sciences) (2023) 50(05):191–203. doi:10.16339/j.cnki.hdxbzkb.2023069

CrossRef Full Text | Google Scholar

51. Zhang B, Chen X, Qiu L, Dong J, Zhou Z, Ji Z, et al. Propagation characteristic of elastic waves in fluid-saturated porous media based on model of soil mechanics. Pure Appl Geophys (2023) 180(6):2309–26. doi:10.1007/s00024-023-03269-z

CrossRef Full Text | Google Scholar

52. Zhang B, Qiu L. Reflection of P₁-wave incident obliquely at the free surface of a fluid-saturated half-space: a comprehensive study via the model of soil mechanics. Front Phys (2025) 13:1540732. doi:10.3389/fphy.2025.1540732

CrossRef Full Text | Google Scholar

53. Cui J. The wave propagation in saturated soil layer and sand liquefaction. [Dissertation thesis]. Harbin: China Earthquake Administration, Institute of Engineering Mechanics (2002).

Google Scholar

54. Chen W, Men F. Study on FEM to simulate slip and seismic liquefaction of slope-field by theory of two-phased dynamics. Earthq Eng Eng Vib (2002) 22(01):132–40. doi:10.13197/j.eeev.2002.01.023

CrossRef Full Text | Google Scholar

55. Chen W. A direct differential method for nonlinear dynamic response of sand layer under water. Rock Soil Mech (2007) 28(s1):698–702. (in Chinese).

Google Scholar

56. Li Y. Analysis on nonlinear ground response in one dimension based on the theory of wave propagation in two-phase media. [Dissertation thesis]. Harbin: China Earthquake Administration, Institute of Engineering Mechanics (2008).

Google Scholar

57. Pujol J. Elastic wave propagation and generation in seismology. Cambridge, UK: Cambridge University Press (2003). p. 53–72.

Google Scholar

58. Seth S, Michael W. An introduction to seismology, earthquakes, and earth structure. Oxford, UK: Blackwell Publishing Ltd (2003). p. 114–64.

Google Scholar

59. Philippacopoulos AJ. Waves in a partially saturated layered half-space: analytic formulation. Bull Seismol Soc Am (1987) 77(5):1838–53. doi:10.1785/BSSA0770051838

CrossRef Full Text | Google Scholar

60. Deresiewicz H, Skalak R. On uniqueness in dynamic poroelasticity. Bull Seismol Soc Am (1963) 53(4):783–8. doi:10.1785/BSSA0530040783

CrossRef Full Text | Google Scholar

61. Singh J, Tomar SK. Reflection and transmission of transverse waves at a plane interface between two different porous elastic solid half-spaces. Appl Math Comput (2006) 176(1):364–78. doi:10.1016/j.amc.2005.09.027

CrossRef Full Text | Google Scholar

62. Wu K, Qiang X. Reflection and transmission of elastic waves at the interface of two fluid-saturated, porous media. J China Univ Sci Technol (1992) 22(1):44–50. (in Chinese).

Google Scholar

63. Gurevich B, Radim C, Denneman AIM. Simple expressions for normal-incidence reflection coefficients from an interface between fluid-saturated porous materials. Geophysics (2004) 69:1372–7. doi:10.1190/1.1836811

CrossRef Full Text | Google Scholar

64. Wang J, Feng J, Zhang C. Reflection and transmission of plane waves at an interface of water/porous sediment with underlying solid substrate. Ocean Eng (2013) 63:8–16. doi:10.1016/j.oceaneng.2013.01.028

CrossRef Full Text | Google Scholar

65. Barak MS, Kumari M, Kumar M. Effect of local fluid flow on the propagation of plane waves at an interface of water/double-porosity solid with underlying uniform elastic solid. Ocean Eng (2018) 147:195–205. doi:10.1016/j.oceaneng.2017.10.030

CrossRef Full Text | Google Scholar

66. Chen W, Jeng D, Zhao H, Chen G, Li X. Motion at surface of a gassy ocean sediment layer induced by obliquely incident P waves. Ocean Eng (2018) 149:95–105. doi:10.1016/j.oceaneng.2017.12.005

CrossRef Full Text | Google Scholar

Appendix

In the 5 × 5 matrices, the elements $m_{ij}$ (i = 1 to 5, j = 1 to 5) and ${\overline{m}}_{ij}$ (i = 5, j = 1 to 5) are given below:

$\left[{\mathit{S}}_{\mathrm{P}-\text{SV}}\right]=\left[\begin{array}{ccccc}{\mathit{m}}_{11}& {\mathit{m}}_{12}& {\mathit{m}}_{13}& {\mathit{m}}_{14}& {\mathit{m}}_{15}\\ {\mathit{m}}_{21}& {\mathit{m}}_{22}& {\mathit{m}}_{23}& {\mathit{m}}_{24}& {\mathit{m}}_{25}\\ {\mathit{m}}_{31}& {\mathit{m}}_{32}& {\mathit{m}}_{33}& {\mathit{m}}_{34}& {\mathit{m}}_{35}\\ {\mathit{m}}_{41}& {\mathit{m}}_{42}& {\mathit{m}}_{43}& {\mathit{m}}_{44}& {\mathit{m}}_{45}\\ {\mathit{m}}_{51}& {\mathit{m}}_{52}& {\mathit{m}}_{53}& {\mathit{m}}_{54}& {\mathit{m}}_{55}\end{array}\right];\left[{\overline{\mathit{S}}}_{\mathrm{P}-\text{SV}}\right]=\left[\begin{array}{ccccc}{\mathit{m}}_{11}& {\mathit{m}}_{12}& {\mathit{m}}_{13}& {\mathit{m}}_{14}& {\mathit{m}}_{15}\\ {\mathit{m}}_{21}& {\mathit{m}}_{22}& {\mathit{m}}_{23}& {\mathit{m}}_{24}& {\mathit{m}}_{25}\\ {\mathit{m}}_{31}& {\mathit{m}}_{32}& {\mathit{m}}_{33}& {\mathit{m}}_{34}& {\mathit{m}}_{35}\\ {\mathit{m}}_{41}& {\mathit{m}}_{42}& {\mathit{m}}_{43}& {\mathit{m}}_{44}& {\mathit{m}}_{45}\\ {\overline{\mathit{m}}}_{51}& {\overline{\mathit{m}}}_{52}& {\overline{\mathit{m}}}_{53}& {\overline{\mathit{m}}}_{54}& {\overline{\mathit{m}}}_{55}\end{array}\right]$

where, $m_{11}$ = $-\left({\lambda }^{\prime }{\left(k^{\mathrm{I}}\right)}^2+2{\mu }^{\prime }{\left(k_z^{\mathrm{I}}\right)}^2\right)$, $m_{12}$ = $2{\mu }^{\prime }{k}_x^{\mathrm{R}}{k}_z^{\mathrm{R}}$,

${\mathit{m}}_{13}=\left(\mathit{\lambda }+\frac{1-\mathit{n}}{\mathit{n}}{\mathit{E}}_{\mathrm{w}}+{\mathit{\delta }}_1{\mathit{E}}_{\mathit{w}}\right){\left({\mathit{k}}_1^{\mathrm{T}}\right)}^2+2\mathit{\mu }{\left({\mathit{k}}_{1\mathit{z}}^{\mathrm{T}}\right)}^2,{\mathit{m}}_{14}=\left(\mathit{\lambda }+\frac{1-\mathit{n}}{\mathit{n}}{\mathit{E}}_{\mathrm{w}}+{\mathit{\delta }}_2{\mathit{E}}_{\mathit{w}}\right){\left({\mathit{k}}_2^{\mathrm{T}}\right)}^2+2\mathit{\mu }{\left({\mathit{k}}_{2\mathit{z}}^{\mathrm{T}}\right)}^2,$

${\mathit{m}}_{15}=2\mathit{\mu }{\mathit{k}}_{\mathrm{s}\mathit{x}}^{\mathrm{T}}{\mathit{k}}_{\mathrm{s}\mathit{z}}^{\mathrm{T}},{\mathit{m}}_{21}=2{\mathit{\mu }}^{\prime }{\mathit{k}}_{\mathit{x}}^{\mathrm{I}}{\mathit{k}}_{\mathit{z}}^{\mathrm{I}},{\mathit{m}}_{22}=-{\mathit{\mu }}^{\prime }\left({\left({\mathit{k}}_{\mathit{x}}^{\mathrm{R}}\right)}^2-{\left({\mathit{k}}_{\mathit{z}}^{\mathrm{R}}\right)}^2\right),{\mathit{m}}_{23}=2\mathit{\mu }{\mathit{k}}_{1\mathit{x}}^{\mathrm{T}}{\mathit{k}}_{1\mathit{z}}^{\mathrm{T}},{\mathit{m}}_{24}=2\mathit{\mu }{\mathit{k}}_{2\mathit{x}}^{\mathrm{T}}{\mathit{k}}_{2\mathit{z}}^{\mathrm{T}},{\mathit{m}}_{25}=\mathit{\mu }\left({\left({\mathit{k}}_{\mathrm{s}\mathit{x}}^{\mathrm{T}}\right)}^2-{\left({\mathit{k}}_{\mathrm{s}\mathit{z}}^{\mathrm{T}}\right)}^2\right),{\mathit{m}}_{31}=-{\mathit{k}}_{\mathit{x}}^{\mathrm{I}},{\mathit{m}}_{32}=-{\mathit{k}}_{\mathit{z}}^{\mathrm{R}},{\mathit{m}}_{33}={\mathit{k}}_{1\mathit{x}}^{\mathrm{T}},{\mathit{m}}_{34}={\mathit{k}}_{2\mathit{x}}^{\mathrm{T}},{\mathit{m}}_{35}=-{\mathit{k}}_{\mathrm{s}\mathit{z}}^{\mathrm{T}},{\mathit{m}}_{41}={\mathit{k}}_{\mathit{z}}^{\mathrm{I}},{\mathit{m}}_{42}=-{\mathit{k}}_{\mathit{x}}^{\mathrm{R}},{\mathit{m}}_{43}={\mathit{k}}_{1\mathit{z}}^{\mathrm{T}},{\mathit{m}}_{44}={\mathit{k}}_{2\mathit{z}}^{\mathrm{T}},{\mathit{m}}_{45}={\mathit{k}}_{\mathrm{s}\mathit{x}}^{\mathrm{T}},{\mathit{m}}_{51}=0,{\mathit{m}}_{52}=0,{\mathit{m}}_{53}=\left(\frac{1-\mathit{n}}{\mathit{n}}+{\mathit{\delta }}_1\right){\mathit{E}}_{\mathrm{w}}{\left({\mathit{k}}_1^{\mathrm{T}}\right)}^2,$

${\mathit{m}}_{54}=\left(\frac{1-\mathit{n}}{\mathit{n}}+{\mathit{\delta }}_2\right){\mathit{E}}_{\mathrm{w}}{\left({\mathit{k}}_2^{\mathrm{T}}\right)}^2,{\mathit{m}}_{55}=0,{\overline{\mathit{m}}}_{51}=0,{\overline{\mathit{m}}}_{52}=0,{\overline{\mathit{m}}}_{53}=\left(1-{\mathit{\delta }}_1\right){\mathit{k}}_{1\mathit{z}}^{\mathrm{T}},{\overline{\mathit{m}}}_{54}=\left(1-{\mathit{\delta }}_2\right){\mathit{k}}_{2\mathit{z}}^{\mathrm{T}},$

${\overline{\mathit{m}}}_{55}=\left(1-{\mathit{\delta }}_{\mathrm{s}}\right){\mathit{k}}_{\mathrm{s}\mathit{x}}^{\mathrm{T}}.$