Fostering collective intelligence in CPSS: an LLM-driven multi-agent cooperative tuning framework

Cyber-Physical-Social Systems (CPSS) have emerged as a transformative paradigm in recent years, embracing computational processes, physical systems, and human social interactions within an integrated architectural framework. Advances in artificial intelligence technologies are targeted at addressing the complexity of CPSS design, especially in modeling human reactions in cyber-physical environment. Notably, LLM-based agents have shown significant potential, and numerous studies have leveraged multi-agent collaboration frameworks to solve reasoning tasks. Some approaches achieve multi-agent collaboration through a debate or communication setting. However, these approaches only use the existing capabilities of LLMs, fail to enhance their problem-solving performance. Other works incorporate the responses of other LLMs into their training trajectories to train individual LLMs in a reinforcement learning setting. We argue that effective collaboration should align not only in input information but also in consistent optimization objectives. Furthermore, in current cooperative frameworks, some LLMs tend to redundantly repeat others’ viewpoints, contributing minimally to solve problems. In this paper, inspired by multi-agent reinforcement learning research, we propose MACT, a Multi-Agent Cooperative Tuning framework to joint train multiple LLMs, ensuring that the optimization of each agent aligns directly with the objective of the global task. We equip each agent with a critic network to facilitate individual optimization. Furthermore, to encourage different agents to complement each other and contribute to the overall task, we employ a mixing network that ensures the value of each agent is monotonically consistent with the total value. Experimental results reveal that our method significantly enhances cooperative problem-solving capabilities in the LLM multi-agent framework, which set strong evidence for the modeling of human reaction within CPSS.

1 Introduction

Cyber-Physical-Social Systems (CPSS) represent the integration of computational elements, physical systems, and human social dynamics into a cohesive framework [1]. So far, CPSS design complexity has evolved due to dynamic uncertainties in both physical environments and human-in-the-loop interactions. As such, a key challenge in CPSS design lies in modeling human reactions and system behaviors under uncertainty while ensuring compliance with strict functional, timing, and performance constraints [2]. In recent years, artificial intelligence (AI) has brought paradigm shifts in multiple domains and the CPSS is no different. The ongoing evolution of embodied intelligence highlights the importance of benefiting human-AI mutual comprehension and collaboration [3]. The cyber system, which emerges from the physical system, possesses increasingly powerful perceptual, cognitive and decision-making abilities [4]. Among all the AI products, an LLM is one such architecture, deemed best able to handle information that is distinctly human. In the cyber scenario, an LLM exhibits not just semantic comprehending and contextual generation, but also zero-shot generalization and adaptive reasoning [5, 6]. On the task of CPSS design, LLMs are promising in yielding profound effects and giving rise to new opportunities.

More recently, LLM-based agents have shown great potential, and a great deal of work has explored how to use the LLM-based multi-agent cooperative framework to improve the factual accuracy and reasoning ability of LLM to solve a range of complex reasoning problems [7–10].

Supervised fine-tuning (SFT) is a widely adopted and effective technique to improve LLM’s capabilities. This technique enhances the ability of LLM to complete complex tasks [11, 12]. Compared to SFT methods, reinforcement learning techniques such as Proximal Policy Optimization (PPO) [13] and Direct Preference Optimization (DPO) [14] offer new tuning strategies for LLM. Recent studies [15–17] have demonstrated the effectiveness of LLM agent autonomously to explore environment and train LLM through reinforcement learning, as shown in Figure 1a. Although the aforementioned techniques significantly improve the performance of individual LLM, these tuning methods cannot improve the cooperative ability of LLM. In essence, this form of collaboration fails to enhance the cooperative performance of LLMs.

Figure 1

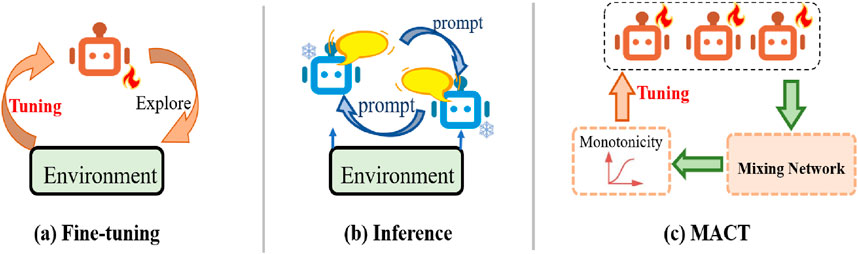
Figure 1. Comparison of existing methods and our proposed method. (a) LLM agents interact with the environment and explore trajectories to fine-tune LLM agents; (b) Multi-agent collaboration through only inference methods to improve the reasoning ability; (c) Our approach enforces consistency constraints to coordinate optimization objectives for multi-agent, enhancing their cooperative abilities.

In most existing LLM-based multi-agent collaboration frameworks, each LLM agent uses the natural language text as prompt to facilitate cooperation, as shown in Figure 1b. These approaches boast strong generality and can leverage powerful models such as GPT [18]. However, in these inference-only collaboration methods, some agents tend to repeat their own or other agents’ viewpoints [19], leading to a lack of substantive incremental contributions to problem solving efforts. Recently, some studies focus on training LLM multi-agent framework [20–22]. To enable collaboration, these methods integrate the generated responses into the training trajectories and use RL training methods to fine-tune LLMs. However, these methods only achieve input-level collaboration among agents, cannot establish optimization-level collaboration.

Research in the field of multi-agent reinforcement learning (MARL) provides viable approaches for improving existing LLM-based multi-agent collaboration frameworks. In cooperative settings, MARL primarily addresses the issue of credit assignment among individual agents and the agent team [23–27]. However, there is a scarcity of research on utilizing these algorithms for LLM-based multi-agent cooperative frameworks. The main distinction and challenge lies in LLM agents operating with natural language text as actions or states, and rewards defined by task-specific rules or human-aligned reward models, whereas traditional MARL algorithms typically function in environments supporting sequential multi-step interactions (e.g., games) with intrinsic reward definitions. Thus, the reward and value signal instability in NLP tasks inherently amplifies training difficulty for LLM-based multi-agent framework.

In the scope of CPSS design and deployment, we propose a LLM-based multi-agent cooperative Tuning framework that establishes a unified optimization objective for all agents, enables coordinated tuning across the framework, and enhances individual contributions to collective problem-solving, as shown in Figure 1c. Specifically, we construct an agent network consisting of a LLM policy and a shared LLM critic network. LLM policy is responsible for the execution of actions, and the critic network calculates the value at the current step. The single agent network optimizes its LLM policy by maximizing the reward to achieve individual optimum. Simultaneously, the values of all agents are aggregated by a mixing network, and get the total value. We ensures each agent’s behavior contributes optimally, and design the optimization process to cooperative train each agent, which can achieve optimization-level coordination and global optimum. This approach enhances the cooperative capability of LLMs. In summary, our contributions are as follows:

$•$ We propose a novel LLM-based Multi-agent cooperative tuning method, which can achieve optimization-level coordination and optimize multiple agents to achieve global optimum.

$•$ Our proposed method is designed to promote positive contributions from individual LLM agents to the entire problem-solving process, and effectively avoid each LLM being a poor apology for the whole team.

$•$ Our method outperformed the benchmark baselines, and the experimental results demonstrate that our method significantly enhances the cooperative abilities of the LLM agents.

2 Related work

2.1 Cyber-physical-social systems

The concept of Cyber-Physical-Social Systems (CPSS) has garnered significant attention across various research domains, emphasizing the integration of physical, cyber, and social components to enhance system functionality and intelligence. Liu et al. [28] provide a foundational perspective by illustrating the operational process of CPSS in command and control contexts, highlighting a self-synchronization mechanism that connects physical networks, cyberspace, mental space, and social networks, thereby facilitating coordinated control operations. This early work underscores the importance of multi-layered integration within CPSS to support complex operational mechanisms.

The importance of data fusion within CPSS is extensively reviewed by Wang et al. [29], who discuss the integration of diverse data sources across cyber, physical, and social spaces. Their comprehensive overview underscores the critical role of data fusion techniques in enabling coherent and reliable system operations, which is essential for the effective functioning of CPSS.

Recent advances in data analysis and collective intelligence further exemplify the evolving capabilities of CPSS. Amiri et al. [30] systematically review deep learning techniques for pattern recognition within CPSS, showcasing how advanced data analytics can enhance system understanding and predictive capabilities. Similarly, Makanda et al. [31] explore the emergence of collective intelligence in industrial CPSS, focusing on collaborative task allocation and defect detection, which underscores the potential for CPSS to facilitate autonomous, intelligent industrial operations.

2.2 LLM cooperation framework

To fully leverage the capabilities of LLM, researchers have explored various LLM-based multi-agent cooperative methods. MAD [7] proposes a method for problem-solving using multi-agent through multi-round debates. The main idea is that multiple LLMs can propose and debate their individual responses and reasoning processes over multiple rounds to arrive at a common final answer. Reconcile [9] designed a round-table discussion framework which multiple LLMs engage in multi-round discussions, learning and persuading each other to improve their answers, using a confidence-weighted voting mechanism to enhance the reasoning capabilities of LLMs. Mixture-of-Agents [10] method leverages the collective strengths of multiple LLMs to enhance natural language understanding and generation capabilities. These approaches possess strong generality and scalability, but there is no tuning process to improve their abilities.

2.3 LLM policy learning

Reinforcement learning from human feedback (RLHF) [32] and its variants such as PPO, DPO [13,14] rapidly become one of the key techniques for tuning LLM agents. ACT [15] method uses an online preference optimization algorithm based on DPO. ETO [16] method utilizes DPO and other contrastive learning methods to update LLM strategies based on collected trajectories. LTC [17] proposed a training method, which enables agents to continuously improve their strategies through interactions with their environment and other agents. However, these approaches only focus on tuning individual LLM agent. Recent studies have focused on training multiple LLM agents, where collaboration is achieved by incorporating all LLMs’ responses into the retraining trajectories, and each LLM using RL framework to train [20–22]. However, in such collaborative training frameworks, LLM agents can only achieve coordination at the input data level, failing to realize coordination at the optimization level. We aim to explore a novel tuning method to optimize multiple LLM agents in a cooperative setting.

2.4 Multi-agent reinforcement learning

In the cooperative environment, multi-agent reinforcement learning (MARL) mainly faces the challenge of how to use the joint and unified reward signals to learn the individual strategies of decentralized agents. Value-based methods such as VDN [24], QMIX [25] and policy-based methods such as MADDPG [26], MAPPO [27] and so on. They all use a centralized critic network to decompose the joint value into the combination of each agent’s value, to promote the learning of better agent individual strategies through constraints. However, research on applying these algorithms in LLM-based multi-agent collaboration frameworks remains scarce. In MARL settings, typical application scenarios involve environments supporting continuous multi-step interactions (e.g., games), and reward signals are intrinsically defined by the environment. The main distinction and challenge lies in LLM agents operating with natural language text as actions or states, and reward is defined by rules or reward models. We propose a feasible solution to address this challenge and utilize the analogous solution to the LLM-based multi-agent cooperative framework.

3 Materials and methods

In the context of CPSS, LLMs are leveraged to widen the cognitive and bridge the gap between cyber model and the reality. In this work, the task is that multi-agent interact with each other to cooperatively find the correct solution to the given problem. In this section, we introduce our Multi-Agent Cooperative Tuning (MACT) Framework. We give the overview of MACT as shown in Figure 2. First, we outline the problem-solving method of the multi-agent framework. Next, we introduce the training methodology, which is divided into the optimization objectives for individual agent and the cooperative optimization objectives for the multi-agent. Finally, we present the training method for the entire framework.

Figure 2

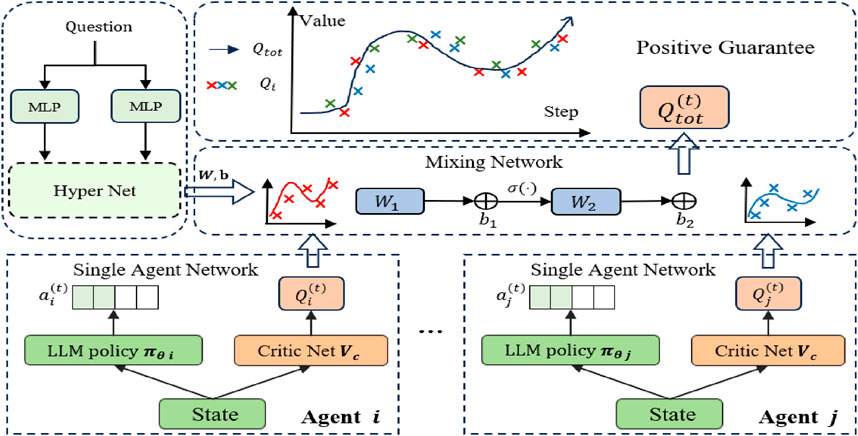
Figure 2. Framework overview. Our Multi-Agent Cooperative Tuning (MACT) framework comprises multiple agent networks, each agent containing a policy and a shared critic network for value estimation. The values from each agent are aggregated through a mixing network to get the a total value. We introduce this mixing network to guarantee monotonic consistency between each agent’s value and the total value. We design the optimization process to cooperative train each agent, which can achieve optimization-level coordination and global optimum.

3.1 Framework

Multi-agent cooperative framework operates as follows: $N$ agents iteratively generate responses to task $x$ over $T$ communication rounds. Each agent interacts with others with prompts that dynamically constructed based on all agents’ outputs from the previous round. All agents equip with a shared critic network, and joint optimize through the loss function designed by the mixing network.

3.2 Single agent network

In this subsection, we will introduce the LLM policy and the LLM critic network in a single agent network. The LLM policy observes the current conversation state and executing actions, and the LLM critic network estimates the current value.

3.2.1 LLM policy

In reinforcement learning settings, we use a Markov Decision Process (MDP) describe LLM’s behavior: for each LLM $i$, its policy is denoted as ${\pi }_{\theta i}$, the MDP for policy ${\pi }_{\theta i}$ can be defined $M=(s,a,t,r,p_o)$. The initial state $p_0$ is the prompt constructed based on the task. In the round $t$ of interaction, the state $s_i^{(t)}$ of ${\pi }_{\theta i}$ is the prompt that constructed from the response in the previous round. The action $a_i^{(t)}$ is a natural language text sequence in the form $a_i^{(t)}=\{w_1,w_2,\dots ,w_n\}$, where $w$ represents each token in the sequence. The reward function $r(x,y)$ evaluates how well the text $x$ matches the standard answer $y$, defined as:

$r\left(x,y\right)=\left\{\begin{array}{cc}\hfill 1& ,\text{if}x=y,\hfill \\ \hfill 0& ,else.\hfill \end{array}\right.(1)$

The referenced prompt specification is detailed in Appendix.

3.2.2 LLM critic

The purpose of the critic network is to evaluate the value of the current state of the policy ${\pi }_{\theta i}$. To better assess the value, we construct the critic network using the LLM architecture. A linear layer is added after the final layer of the LLM architecture to map the hidden state to a scalar value between 0 and 1.

At each round $t$, a shared critic network $V_c$ takes the state from the policy ${\pi }_{\theta i}$ as input and outputs a scalar $Q_i^{(t)}$ representing the value of the current state, denoted as: $Q_i^{(t)}=V_c(s_i^{(t)})$.

To receive an exact value, we need to train a critic network in a supervised manner firstly. We collect trajectories generated by the policy ${\pi }_{\theta i}$. Each trajectory $\tau$ is represented as $\tau =\{s_i^{(1)},a_i^{(1)},r_i^{(1)},s_i^{(2)},a_i^{(2)},r_i^{(2)},\dots ,s_i^{(T)},a_i^{(T)},r_i^{(T)}\}$, where $s_i^{(t)}$ denotes the state, $a_i^{(t)}$ represents the action and $r_i^{(t)}$ indicates the reward at the round $t$, respectively. Let the total reward from round $t$ onward for each trajectory $\tau$ be denoted as Equation 2:

$R_{\tau }^{\left(t\right)}=r_i^{\left(t\right)}+\gamma r_i^{\left(t+1\right)}+\cdots +{\gamma }^{T-t}{r}_i^{\left(T\right)}={\displaystyle \sum _{k=0}^{T-k}}{\gamma }^k{r}_i^{\left(t+k\right)},(2)$

where $\gamma$ is the discount factor. Sampling $M$ times, we compute the average of the total rewards from the $M$ trajectories to obtain the value according to Equation 3:

$Q_i^{\left(t\right)}=E\left[R_{\tau }^{\left(t\right)}\right]=\frac{1}{M}{\displaystyle \sum _{j=1}^M}{R}_{{\tau }_j}^{\left(t\right)}.(3)$

We constructs the loss function of the critic network using temporal difference based on the data in the trajectory $\tau$, according to Equation 4:

$L\left(c\right)={\displaystyle \sum _{t=1}^{T-1}}{\left(r_i^{\left(t\right)}+\gamma Q_i^{\left(t+1\right)}-Q_i^{\left(t\right)}\right)}^2,(4)$

where $c$ represents the parameters of the critic network, and $\gamma$ denotes the discount factor. We update the critic network before training the policy. The critic network is updated only once [33], and then its parameters are frozen to assist the update of the policy. The update of the LLM policy will be introduced in the following sections.

3.3 Mixing network

In this section, we will discuss the construction of the mixing network and its function.

At round $t$, we obtain the value $Q_i^{(t)}$ from the critic network of each agent network $i$. Then the mixing network aggregates the values of all agent networks to obtain the total value $Q_{\mathit{tot}}^{(t)}$. Our goal is to use $Q_{\mathit{tot}}^{(t)}$ to facilitate the coordinated optimization of the entire framework. The mixing network consists of two simple linear layers, and its parameters determined by a hyperparameter network [34]. The input of the hyperparameter network is the embedding vector of the natural language text describing the question. Then, we use this vector and a linear layer to calculate the parameters of the mixing network.

3.4 Positive contribution guarantee

In a multi-agent cooperative framework, coordinating the behaviors of multiple agents to enhance the contribution of individual agents to the entire effort is a primary challenge. In this section, we will introduce the relationship between the value of a single agent $Q_i^{(t)}$ and the output of the mixing network $Q_{\mathit{tot}}^{(t)}$, and use this relationship to establish optimization-level coordination.

To encourage different LLMs to complement each other’s strengths and contribute to the overall task, we ensure the value $Q_i^{(t)}$ maintains monotonic consistency with the whole team’s value $Q_{\mathit{tot}}^{(t)}$. This guarantees equivalence between global argmax on $Q_{\mathit{tot}}^{(t)}$ and concurrent individual argmax operations across all $Q_i^{(t)}$ [35]:

$\text{argmax}{Q}_{\mathit{tot}}^{\left(t\right)}=\left(\begin{array}{c}\hfill \text{argmax}{Q}_1^{\left(t\right)}\hfill \\ \hfill ⋮\hfill \\ \hfill \text{argmax}{Q}_N^{\left(t\right)}\hfill \end{array}\right).(5)$

We take advantage of the mixing network to ensure that the aggregated $Q_{\mathit{tot}}^{(t)}$, derived from all agent networks, aligns with the $Q_i^{(t)}$ of each agent network according to Equation 5. This means that when each agent achieves its maximum individual value, $Q_{\mathit{tot}}^{(t)}$ also reaches its maximum value, it can be shown in Equation 6:

$\frac{\partial Q_{\mathit{tot}}^{\left(t\right)}}{\partial Q_i^{\left(t\right)}}\ge 0,\forall i\in N,\forall t\in T.(6)$

3.5 Multi-agent cooperative tuning

3.5.1 Single agent optimization

For each LLM policy ${\pi }_{\theta i}$, the optimization of the policy has two objectives. First, we use Supervised Fine-Tuning (SFT) as warm-up operation, improving its ability to the downstream task, specifically expressed as Equation 7:

$L_{\mathit{SFT}}\left(\theta i\right)=-E_{\left(x,y\right)\sim D}\left[{\displaystyle \sum _{k=1}^H}log{\pi }_{{\theta }_i}\left(y_k|x,y<k\right)\right],(7)$

where $D$ donates the dataset, $x$ is the task, and $y$ represents the generated text. The second objective is to perform reinforcement learning training on the SFT model, specifically expressed as Equation 8:

$L_{RL}\left(\theta i\right)=-E_{x\sim D}{E}_{y\sim {\pi }_{\theta i}^{RL}\left(x\right)}\left[r\left(x,y\right)-\beta log\frac{{\pi }_{\theta i}^{RL}\left(y|x\right)}{{\pi }_{\theta i}^{\mathit{SFT}}\left(y|x\right)}\right],(8)$

where $r(x,y)$ represents the reward calculation according to Equation 1 provided in Section 3.2.1, and $\beta$ is a hyperparameter that controls the KL divergence.

3.5.2 Multi-agent optimization

Optimizing the single-agent network with the goal of individual optimality may lead to a local optimum. Therefore, during the collaborative optimization phase, we introduce a loss computed by the mixing network to promote coordination among the multiple agent networks within the framework, ultimately achieving a global optimum. The loss of the mixing network consists of a target network and an evaluation network. The evaluation critic network takes each agent’s value $Q_i^{(t)}$ ($i$ from 1 to $N$) as input, and outputs $Q_{\mathit{eval}}^{(t)}$. The target critic network receives the maximum value among $Q_i^{(t)}$ ($i$ from 1 to $N$) and outputs $Q_{\mathit{target}}^{(t)}$. The loss for the mixing network is expressed as Equation 9:

$L_{\mathit{mix}}={\left[Q_{\mathit{target}}^{\left(t\right)}-\left(r_i^{\left(t\right)}+\gamma Q_{\mathit{eval}}^{\left(t\right)}\right)\right]}^2,(9)$

where $r_i^{(t)}$ is the reward for the policy ${\pi }_{\theta i}$ at round $t$, and $\gamma$ is the discount factor. Each agent within the framework updates the its policy by using the following loss function:

$L_{{\pi }_{\theta i}}=L_{RL}\left(\theta i\right)+\alpha L_{\mathit{mix}},(10)$

where $\alpha$ is the hyperparameter that control the trade-off between individual optimality and global optimality. Each agent undergoes multi-round training, and each round continuing from the parameters obtained in the previous round of training.

3.5.3 Training phase

Our training process will be conducted in two stages. First, we perform a single round of SFT by using Equation 7 on all agents to obtain the SFT models. This serves as an effective warm-up mechanism prior to reinforcement learning and the cooperative tuning process [36]. Subsequently, we will train each SFT model ${\pi }_{\theta i}^{\mathit{SFT}}$ multiple times by using the equation defined in Equation 10.

4 Results

Experiments on evaluating the multi-step reasoning ability of LLMs are carried out aligning with the objective of the CPSS design.

4.1 Benchmark

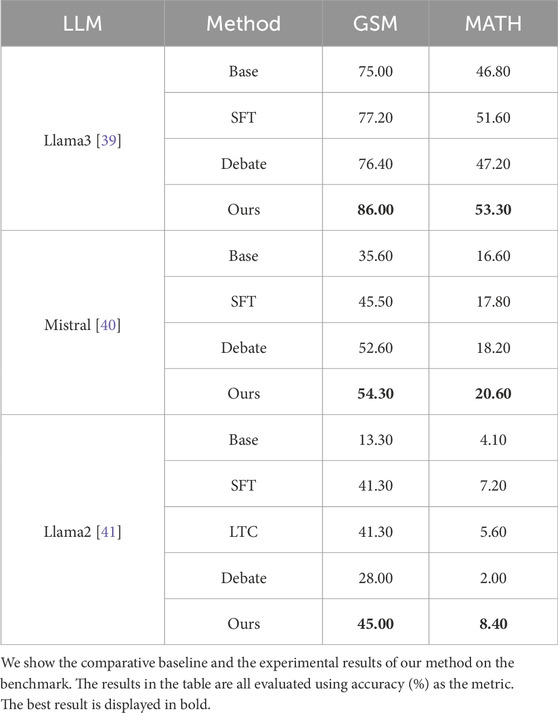
We evaluate our method and baseline on the GSM8K [37] and MATH [38] dataset. These mathematical datasets are crucial for evaluating the logical reasoning capabilities of LLMs. GSM8K. This dataset is specifically designed to assess LLMs’ abilities to solve grade school math problems that necessitate multi-step reasoning. These problems typically involve arithmetic operations and basic algebra, requiring between 2 and 8 steps to solve accurately. The dataset highlights the importance of logical thinking and sequential reasoning. MATH. This dataset serves as a more advanced and challenging benchmark for evaluating the capabilities of LLMs in solving mathematical problems. It includes over 12,500 problems of mathematical competition level, covering a broad spectrum of difficulties from basic to highly advanced. The problems address a variety of mathematical concepts and techniques, including algebra, geometry, number theory, combinatorics, calculus and etc.

4.2 Baseline

We use pre-trained language models [39–41] as base agents. The Base method directly evaluates the capabilities of the foundational LLM by prompting it to generate answers without modifications, while the SFT method will fine-tune the LLM in the data set and then evaluates its performance. LTC method proposes novel approaches that leverage RL to train LLM [17]. In addition, to validate the effectiveness of our approach, we compared it with the multi-agent debate method [7], named Debate. This method does not involve fine-tuning changes to the model but employs multiple LLMs to engage in multi-round conversational discussions and debates, stimulating each LLM to learn from the historical sessions with the aim of enhancing its performance on reasoning tasks.

4.3 Overall performance

Table 1 shows the performance of all methods. We using Llama2-7B, Llama3-8B, and Mistral-7B as the base models for our experiments on both datasets. The performance of each single LLM was relatively modest. The performance of multi-agent methods generally surpasses single base model. This improvement is due to the ability of multi-agent to learn from each other and complement each other’s strengths, with particularly noticeable gains on the GSM dataset. In contrast, the improvement on the MATH dataset is less significant. Our method comprehensively outperforms the aforementioned approaches, with improvements of 9.60%, 1.70%, and 17.00% on the GSM dataset compared to the multi-agent debate methods. On the MATH dataset, our method achieved an average improvement of 6.10%, 2.40%, and 6.20% over the multi-agent debate methods. While multi-agent debate methods facilitate collaboration, the LLM agents in these approaches rely exclusively on language-based interactions and do not optimize the large models for deeper levels of cooperation. Furthermore, in such settings, LLM agents are susceptible to context-driven influences, often leading to repetitive viewpoints. Our method effectively mitigates these issues, resulting in superior performance.

Table 1

Table 1. Main results.

4.4 Ablation study

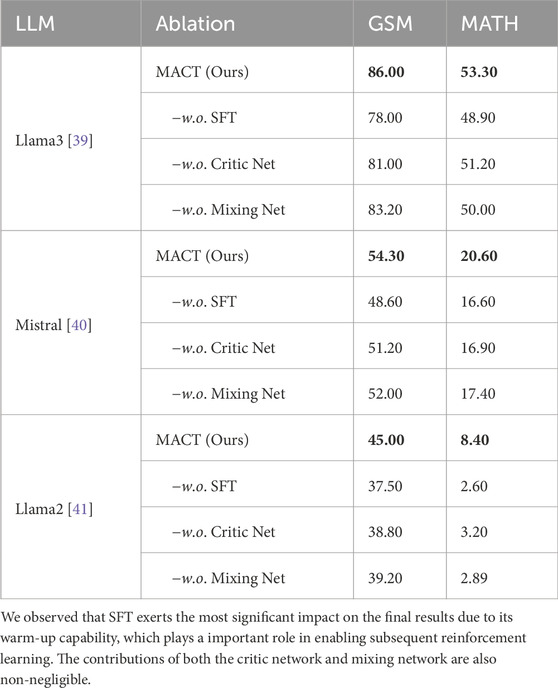
We conducte experiments to analyze the impact of various configurations of our MACT method, as shown in Table 2. Specifically, we explored the effects of supervised fine-tuning ($-w.o$. SFT) and the critic network ($-w.o$. Critic Net) in individual optimization, as well as the mixing network ($-w.o$. Mixing Net) in coordinating global optimization. The experimental results indicate that, from the perspective of individual optimization, removing the SFT results in a decrease in the performance. We believe that supervised fine-tuning as the warm-up operation ensures the performance of LLMs on downstream tasks and serves as a crucial method for optimizing individual agents. Critic network in a single agent network tends to effectively guide the LLM policy updates, resulting in suboptimal outcomes. This further demonstrates that applying reinforcement learning to optimize LLM policy remains a challenging problem. On the other hand, the critic network also serves as a bridge for establishing global optimization. Without the critic network, there would be no involvement of the mixing network. From a global optimization standpoint, the absence of the mixing network leads to a decline of performance, despite each agent achieving individual optimization, the collective performance of all LLMs together does not reach the global optimum. Therefore, our experimental results show that our MACT method not only ensures individual optimization but also enhances the cooperative abilities of LLM agents.

Table 2

Table 2. Ablation study.

4.5 Case study

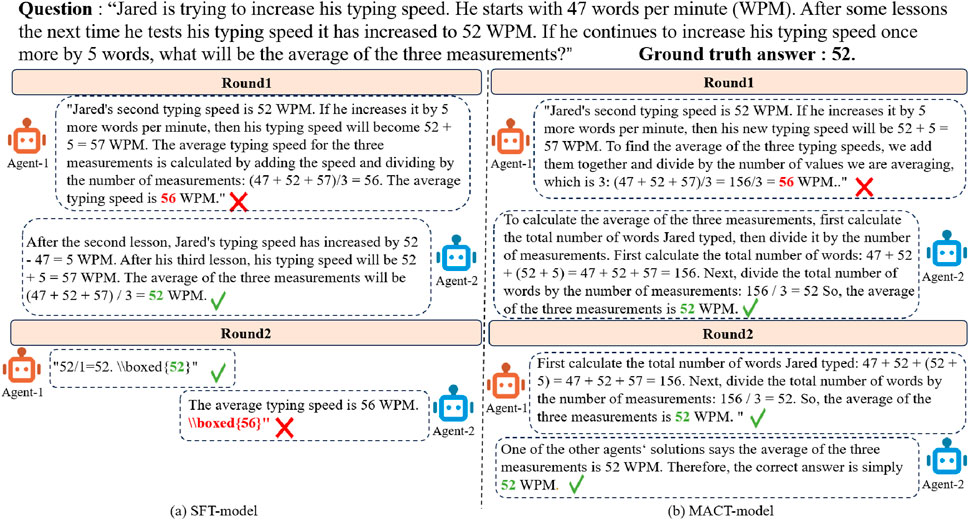
We collected and analyzed different cases from the experimental results, as illustrated in Figure 3. The figure compare the performance of collaborations between SFT-Llama3 models and MACT-Llama3 models. When we used the SFT-Llama3 model in collaboration, we observed that these SFT models still primarily rely on their contextual information, which can lead to the propagation of incorrect information derived from the context. However, the MACT-Llama3 model alleviates this issue to some extent. The MACT model can fully account for the collaborative dynamics and the logic of the task, reducing the tendency for repeated responses or excessive reliance on other agents’ responses.

Figure 3

Figure 3. A case study comparing SFT-Llama3 model and MACT-Llama3 model.

4.6 Different cooperation rounds

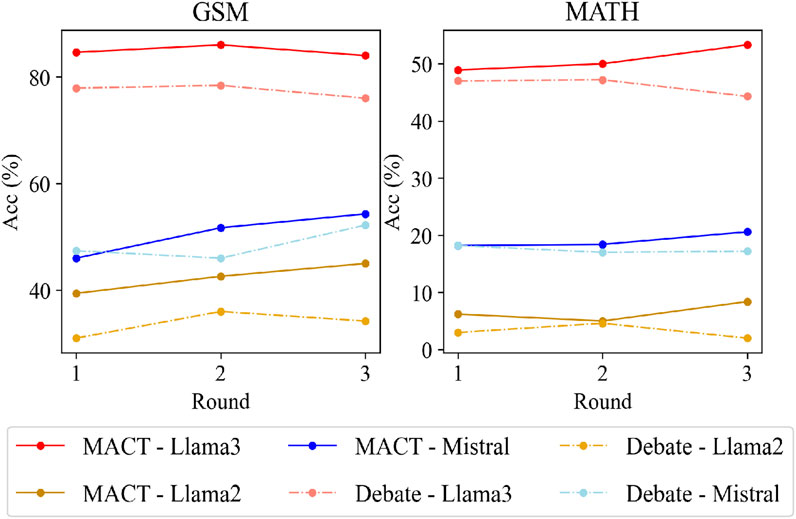
We investigated the impact of varying collaboration rounds by setting the number of rounds to 1, 2, and 3, comparing the MACT method with the Debate method as shown in Figure 4. On the GSM dataset, using Llama3 as the base model, both MACT and Debate methods achieve optimal performance with two collaboration rounds, while accuracy declined with additional rounds. We hypothesize the performance degradation stems from natural language interactions causing the LLM’s input and output length to exceed model constraints. However, when using Mistral and Llama2, MACT-models exhibited consistent accuracy improvements as collaboration rounds increased. On the MATH dataset, MACT-models achieve best results with three collaboration rounds. We attribute this to the dataset’s higher complexity, which challenges LLMs’ inherent problem-solving capabilities, making additional rounds beneficial for providing contextual information to enhance analysis and resolution.

Figure 4

Figure 4. The results when using different numbers of rounds to cooperate.

4.7 Different agents

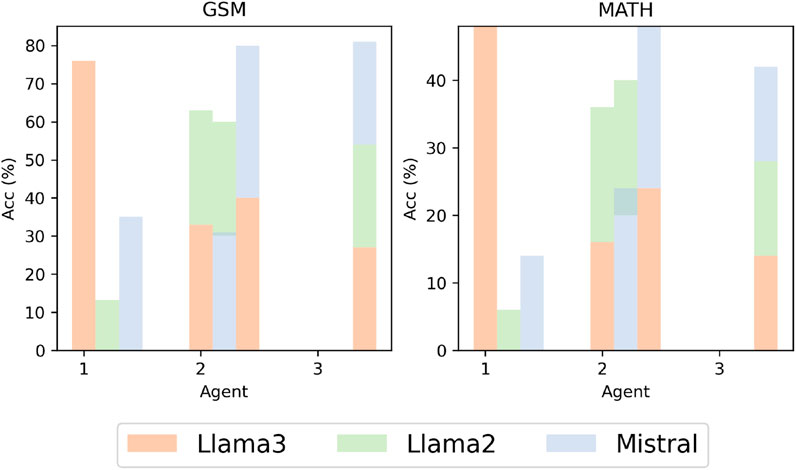
We investigated scenarios with different LLM-based agents, as shown in Figure 5. Using Llama3, Llama2, and Mistral as agents, we explored the effects of collaboration by combining different agents in various arrangements. In experiments with two agents, the results aligned with intuition: weaker models showed significant performance improvements when collaborating with stronger models. When three different agents were used for collaboration, their combined performance achieved further enhancement, validating the effectiveness of our collaborative framework.

Figure 5

Figure 5. The results when using different agents to cooperate. We set the cooperative rounds to 2.

4.8 Complexity analysis

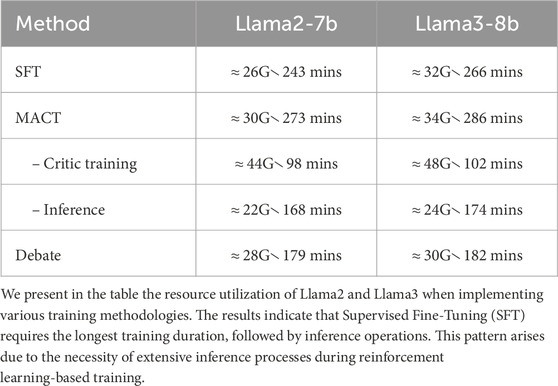
We leverage the vLLM library to accelerate inference. As a result, processing 1,000 data samples, even with multiple LLMs participating in multi-round debates, does not take excessive time and is significantly faster compared to directly invoking the ‘generate ()’ method from the transformers library. One or more LLMs can independently create multiple vLLM processes on the same GPU without conflicts. Additionally, the vLLM library allows the memory usage to be configured using the parameter ‘gpu_memory_utilization.’ Even with limited GPU memory, quantization techniques can be employed to further reduce the memory footprint during inference.

We present the computational consumption during training and inference using different base models, as shown in Table 3. Initially, supervised fine-tuning (SFT) is applied to the base model, requiring less than 35 GB GPU memory and approximately 5 h. This is followed by reinforcement learning (RL) and joint training on the SFT model, where training the critic model consumes around 50 GB of memory and 2 h. Although the critic model shares the same base architecture, its scalar output reduces training duration; however, processing extensive natural language text inputs still demands higher memory allocation. Finally, inference time remains acceptable due to the optimized implementation via the vllm library.

Table 3

Table 3. GPU memory and training time consumption across different base models.

5 Conclusion

With the growing demands for CPSS, an LLM is a promising resolution in promoting the establishment of CPSS. In this paper, we propose a novel LLM-based Multi-Agent Cooperative Tuning (MACT) method, which can significantly enhance the ability of LLM agents to solve problems cooperatively. Our method draws on the research of multi-agent reinforcement learning, and fully discusses the cooperation mechanism between the individual agent and the entire agent team, so that the individual agent can improve the contribution to the entire agent team in the training process through consistency constraints. We conducted experiments on two datasets, our method showes better results than the previous LLM-based single-agent methods and multi-agent methods. This work gives rise to a new opportunity to the human reaction modeling in CPSS establishment, which generates more precise outcomes via the cooperation of LLM-based multi-agents.

6 Limitations

Compared to existing research, our work still employs natural language text as the communication medium between LLM agents. However, the use of natural language text serves merely as an interpretable description and may not be the most efficient means of representation for LLM agents. Furthermore, natural language output can lead to significant consumption of computational resources and time. Therefore, exploring a more suitable communication method for multi-agent systems is a topic worthy of investigation and study. Since this paper focuses on investigating the training methods of LLMs, we retain the communication mechanisms established in prior work.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

RC: Conceptualization, Formal Analysis, Methodology, Resources, Writing – original draft, Writing – review and editing. CH: Resources, Supervision, Writing – review and editing.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. This work was supported in part by the Guangdong Basic and Applied Basic Research Foundation under Grant 2023A1515011370, the National Natural Science Foundation of China (32371114), and Guangdong Provincial Key Lab-oratory (Grant 2023B1212060076).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Selim A, Mo H, Pota H, Dong D. Day ahead scheduling of battery energy storage system operation using growth optimizer within cyber-physical-social systems. Energy (2025) 331:136675. doi:10.1016/j.energy.2025.136675

CrossRef Full Text | Google Scholar

2. An D, Pan Z, Gao X, Li S, Yin L, Li T. Stohmcharts: a modeling framework for quantitative performance evaluation of cyber-physical-social systems. IEEE Access (2023) 11:44660–71. doi:10.1109/access.2023.3272672

CrossRef Full Text | Google Scholar

3. Qu M, Li Q, Fang Z. Cyber-physical-social system: integration, mapping, and interoperability of meta-models, architectures and methodlogies. IFAC-PapersOnLine (2024) 58:139–44. doi:10.1016/j.ifacol.2025.01.170

CrossRef Full Text | Google Scholar

4. Li Q, Fang Z, Qu M. Cyber-physical-social system (cpss) architecture framework and methodology. In: Proceedings of the 3rd international conference on innovative intelligent industrial production and logistics - ei2N. INSTICC SciTePress (2022). p. 206–17. doi:10.5220/0011559600003329

CrossRef Full Text | Google Scholar

5. Brown T, Mann B, Ryder N, Subbiah M, Kaplan JD, Dhariwal P, et al. Language models are few-shot learners. Adv Neural Inf Process Syst (2020) 33:1877–901. doi:10.48550/arXiv.2005.14165

CrossRef Full Text | Google Scholar

6. Wei J, Wang X, Schuurmans D, Bosma M, Xia F, Chi E, et al. Chain-of-thought prompting elicits reasoning in large language models. Adv Neural Inf Process Syst (2022) 35:24824–37. doi:10.48550/arXiv.2201.11903

CrossRef Full Text | Google Scholar

7. Du Y, Li S, Torralba A, Tenenbaum JB, Mordatch I. Improving factuality and reasoning in language models through multiagent debate. (2023). arXiv preprint arXiv:2305.14325.

Google Scholar

8. Liang T, He Z, Jiao W, Wang X, Wang Y, Wang R, et al. Encouraging divergent thinking in large language models through multi-agent debate. arXiv preprint arXiv:2305.19118 (2023). doi:10.18653/v1/2024.emnlp-main.992

CrossRef Full Text | Google Scholar

9. Chen JC-Y, Saha S, Bansal M. Reconcile: round-table conference improves reasoning via consensus among diverse llms. arXiv preprint arXiv:2309.13007 (2023). doi:10.18653/v1/2024.acl-long.381

CrossRef Full Text | Google Scholar

10. Wang J, Wang J, Athiwaratkun B, Zhang C, Zou J. Mixture-of-agents enhances large language model capabilities. (2024). arXiv preprint arXiv:2406.04692.

Google Scholar

11. Wang K, Ren H, Zhou A, Lu Z, Luo S, Shi W, et al. Mathcoder: seamless code integration in llms for enhanced mathematical reasoning. (2023). arXiv preprint arXiv:2310.03731.

Google Scholar

12. Gou Z, Shao Z, Gong Y, Yang Y, Huang M, Duan N, et al. Tora: a tool-integrated reasoning agent for mathematical problem solving. arXiv preprint arXiv:2309.17452 (2023). doi:10.48550/arXiv.2309.17452

CrossRef Full Text | Google Scholar

13. Schulman J, Wolski F, Dhariwal P, Radford A, Klimov O. Proximal policy optimization algorithms. (2017). arXiv preprint arXiv:1707.06347.

Google Scholar

14. Rafailov R, Sharma A, Mitchell E, Manning CD, Ermon S, Finn C. Direct preference optimization: your language model is secretly a reward model. Adv Neural Inf Process Syst (2024) 36. doi:10.48550/arXiv.2305.18290

CrossRef Full Text | Google Scholar

15. Chen M, Sun R, Arık SÖ, Pfister T. Learning to clarify: multi-turn conversations with action-based contrastive self-training. (2024). arXiv preprint arXiv:2406.00222.

Google Scholar

16. Song Y, Yin D, Yue X, Huang J, Li S, Lin BY. Trial and error: exploration-based trajectory optimization for llm agents. (2024). arXiv preprint arXiv:2403.02502.

Google Scholar

17. Wang K, Lu Y, Santacroce M, Gong Y, Zhang C, Shen Y Adapting llm agents through communication. (2023). arXiv preprint arXiv:2310.01444.

Google Scholar

18. Achiam J, Adler S, Agarwal S, Ahmad L, Akkaya I, Aleman FL, et al. Gpt-4 technical report. (2023). arXiv preprint arXiv:2303.08774.

Google Scholar

19. Luo Y, Tang Y, Shen C, Zhou Z, Dong B. Prompt engineering through the lens of optimal control. arXiv preprint arXiv:2310.14201 (2023) 2:241–58. doi:10.4208/jml.231023

CrossRef Full Text | Google Scholar

20. Liang X, Tao M, Xia Y, Shi T, Wang J, Yang J. Cmat: a multi-agent collaboration tuning framework for enhancing small language models. arXiv preprint arXiv:2404.01663 (2024). doi:10.48550/arXiv.2404.01663

CrossRef Full Text | Google Scholar

21. Motwani SR, Smith C, Das RJ, Rybchuk M, Torr PH, Laptev I, et al. Malt: improving reasoning with multi-agent llm training. arXiv preprint arXiv:2412.01928 (2024). doi:10.48550/arXiv.2412.01928

CrossRef Full Text | Google Scholar

22. Estornell A, Ton J-F, Yao Y, Liu Y. Acc-debate: an actor-critic approach to multi-agent debate. arXiv preprint arXiv:2411.00053 (2024). doi:10.48550/arXiv.2411.00053

CrossRef Full Text | Google Scholar

23. Foerster J, Farquhar G, Afouras T, Nardelli N, Whiteson S. Counterfactual multi-agent policy gradients 32. (2018).

Google Scholar

24. Sunehag P, Lever G, Gruslys A, Czarnecki WM, Zambaldi V, Jaderberg M, et al. Value-decomposition networks for cooperative multi-agent learning. (2017). arXiv preprint arXiv:1706.05296.

Google Scholar

25. Rashid T, Samvelyan M, De Witt CS, Farquhar G, Foerster J, Whiteson S. Monotonic value function factorisation for deep multi-agent reinforcement learning. J Machine Learn Res (2020) 21:1–51. doi:10.48550/arXiv.1803.11485

CrossRef Full Text | Google Scholar

26. Lowe R, Wu YI, Tamar A, Harb J, Pieter Abbeel O, Mordatch I. Multi-agent actor-critic for mixed cooperative-competitive environments. Adv Neural Inf Process Syst (2017) 30. doi:10.48550/arXiv.1706.02275

CrossRef Full Text | Google Scholar

27. Yu C, Velu A, Vinitsky E, Gao J, Wang Y, Bayen A, et al. The surprising effectiveness of ppo in cooperative multi-agent games. Adv Neural Inf Process Syst (2022) 35:24611–24. doi:10.48550/arXiv.2103.01955

CrossRef Full Text | Google Scholar

28. Liu Z, Yang D-s, Wen D, Zhang W-m, Mao W. Cyber-physical-social systems for command and control. IEEE Intell Syst (2011) 26:92–6. doi:10.1109/mis.2011.69

CrossRef Full Text | Google Scholar

29. Wang P, Yang LT, Li J, Chen J, Hu S. Data fusion in cyber-physical-social systems: state-of-the-art and perspectives. Inf Fusion (2019) 51:42–57. doi:10.1016/j.inffus.2018.11.002

CrossRef Full Text | Google Scholar

30. Amiri Z, Heidari A, Navimipour NJ, Unal M, Mousavi A. Adventures in data analysis: a systematic review of deep learning techniques for pattern recognition in cyber-physical-social systems. Multimedia Tools Appl (2024) 83:22909–73. doi:10.1007/s11042-023-16382-x

CrossRef Full Text | Google Scholar

31. Makanda ILD, Jiang P, Yang M, Shi H. Emergence of collective intelligence in industrial cyber-physical-social systems for collaborative task allocation and defect detection. Comput Industry (2023) 152:104006. doi:10.1016/j.compind.2023.104006

CrossRef Full Text | Google Scholar

32. Bai Y, Jones A, Ndousse K, Askell A, Chen A, DasSarma N, et al. Training a helpful and harmless assistant with reinforcement learning from human feedback. arXiv preprint arXiv:2204.05862 (2022). doi:10.48550/arXiv.2204.05862

CrossRef Full Text | Google Scholar

33. Ziegler DM, Stiennon N, Wu J, Brown TB, Radford A, Amodei D, et al. Fine-tuning language models from human preferences. (2019). arXiv preprint arXiv:1909.08593.

Google Scholar

34. Ha D, Dai A, Le QV. Hypernetworks. (2016). arXiv preprint arXiv:1609.09106.

Google Scholar

35. Dugas C, Bengio Y, Bélisle F, Nadeau C, Garcia R. Incorporating functional knowledge in neural networks. J Machine Learn Res (2009) 10. doi:10.1007/s10846-008-9291-9

CrossRef Full Text | Google Scholar

36. Chu T, Zhai Y, Yang J, Tong S, Xie S, Schuurmans D, et al. Sft memorizes, rl generalizes: a comparative study of foundation model post-training. (2025). arXiv preprint arXiv:2501.17161.

Google Scholar

37. Cobbe K, Kosaraju V, Bavarian M, Chen M, Jun H, Kaiser L, et al. Training verifiers to solve math word problems. arXiv preprint arXiv:2110.14168 (2021). doi:10.48550/arXiv.2110.14168

CrossRef Full Text | Google Scholar

38. Hendrycks D, Burns C, Kadavath S, Arora A, Basart S, Tang E, et al. Measuring mathematical problem solving with the math dataset. arXiv preprint arXiv:2103.03874 (2021). doi:10.48550/arXiv.2103.03874

CrossRef Full Text | Google Scholar

39. Dubey A, Jauhri A, Pandey A, Kadian A, Al-Dahle A, Letman A, et al. The llama 3 herd of models. (2024). arXiv preprint arXiv:2407.21783.

Google Scholar

40. Jiang AQ, Sablayrolles A, Mensch A, Bamford C, Chaplot DS, Casas D, et al. Mistral 7b. (2023). arXiv preprint arXiv:2310.06825.

Google Scholar

41. Touvron H, Martin L, Stone K, Albert P, Almahairi A, Babaei Y, et al. Llama 2: open foundation and fine-tuned chat models. (2023). arXiv preprint arXiv:2307.09288.

Google Scholar

Appendix: Prompts

We provide a list of prompt terms utilized during our implementation for reference. As outlined in the paper, to better facilitate answer extraction from LLM’s responses, we enforce a specific output format for LLM-generated answers, including the directives provided in theprompt below.

Single-agent prompts

We use the following prompt as input to a single LLM and directly obtain its response:

“‘Can you solve the following math problem? {QUESTION} Provide a bullet point summary of your reasoning. Your final answer should be a single answer, in the form ∖∖boxed{{answer}}, at the end of your response.”’

Multi-agent prompts

In the first round, we provide the same prompt to multiple agents as follows:

“‘Can you solve the following math problem? {QUESTION} Provide a bullet point summary of your reasoning. Your final answer should be a single answer, in the form ∖∖boxed{{answer}}, at the end of your response.”’

In the $t$ rounds of dialogue, we construct the prompt for each agent by using the responses from the previous round of all other agents except itself:

“‘These are the solutions to the problem from other agents: one agent solution: {RESPONSE}. Using each response as additional advice, can you give an updated bullet by bullet answer to {QUESTION}? Your final answer should be in the form ∖∖boxed{{answer}} given at the end of your response.”’

Then we input this prompt to the each agents to generate their next round’s responses.