The influence of defects on the interfacial thermal conductance of β12/χ3 borophene lateral heterostructures

Interfacial thermal transport properties are critical for heat dissipation in micro/nanoelectronic devices. Borophene has structural polymorphism and the lateral heterostructures were often observed. The influence of defect on the interfacial thermal conductance (ITC) of β12/χ3 borophene heterostructures (BHs) was investigated through modified Lennard-Jones potential-based molecular dynamics simulations. The pristine interface exhibits high ITC of 6.57 GW K⁻¹ m⁻². The single-vacancy (SV) and doublevacancy (DV) defects at the interface reduced ITC to 3.14 GW K⁻¹ m⁻² and 1.57 GW K⁻¹ m⁻², respectively. The vibrational density of states (VDOS) overlap analysis shows the opposite trend with the change of ITC. Fortunately, spectral thermal flux and stress distribution can explain the reduction of the ITC for SV-BHs and DV-BHs. The von Mises stress of certain atoms at the interface for DV-BHs reaches up to 40 GPa. SV and DV defects lead to larger stress concentration and stronger phonon scattering near the interface. Defect engineering offers crucial insights into the potential of borophene heterostructures for thermal management.

Introduction

The escalating demand for nanoscale thermal management in advanced electronic devices exhibits the importance of interfacial heat transfer, which critically governs device performance and reliability [1, 2]. Interfacial thermal conductance (ITC), a key parameter characterizing heat transport across interfaces, can be tuned by structural configurations, chemical composition, and defect [3, 4]. For instance, electron-phonon coupling dominates heat transfer at metal-insulator interfaces [5, 6], while wettability and interfacial morphology dictate solid-liquid thermal transport [7].

In recent years, two-dimensional lateral heterostructures have demonstrated unique properties and potential applications to tunnel field-effect transistors, memory devices, and optoelectronic devices [8–10]. Due to the polymorphism of borophene, different phases of the structure can coexist in experimental preparations. As a result, both theoretical and experimental investigations of borophene-based two-dimensional lateral heterostructures have garnered increasing attention [11, 12]. Studies have shown that distinct borophene phases exhibit different phonon dispersion relations, leading to variations in their thermal transport properties [11, 13]. The impact of planar interfaces in borophene on thermal transport is multifaceted: interfaces between different borophene phases can induce a phenomenon of thermal rectification, i.e., a directional asymmetry in thermal transport, thereby providing opportunities for the development of novel thermal management devices [14]. Additionally, the discontinuity of atomic structures at the interfaces generates thermal resistance, impeding heat transfer [15]. The extent of this thermal resistance is closely related to the specific interface structure. Taking graphene-borophene heterostructures as an example, phase boundaries significantly influence phonon transport at interface, thus modulating the system’s ITC [16].

Concurrently, the synthesis of borophene has remained a challenging issue in laboratory settings. The difficulty in synthesizing borophene arises partly from the ability of boron atoms to form two- or three-center B-B bonds, which are more prone to interaction and the formation of polyhedral structures, making the bonding patterns more complex than those between carbon atoms. This often results in various defects during the synthesis process [17–19]. The random vacancy defects in borophene sheet enhance phonon inelastic scattering, thereby reducing thermal conductivity [20]. Researches indicate that interface engineering is an effective means of regulating ITC [21]. For example, the introduction of interface coupling agents in composite materials can enhance thermal conductivity [22], while optimizing the interface structure represents another effective method to improve thermal conductivity [23]. Commonly, the incorporation of defects has been considered to significantly reduce in-plane thermal conductivity [24–26]. However, recent works have indicated that defects can also promote phonon transmission at the asphalt/graphene interface, leading to a substantial increase in ITC [27]. In MOF/TiO₂ heterostructures, hydrogen bond channels is regarded as an important factor for facilitating interfacial heat transfer [28]. Furthermore, certain defects can also guide phonons along specific paths to suppress disordered scattering at the graphene/h-BN interface [29]. Therefore, the influence of the interface on the thermal transport of the low-dimension materials is complexed.

Despite extensive research on various lateral heterostructures, the literature on borophene-based heterostructures (BHs) remains relatively sparse. The polymorphism of borophene in these heterostructures is often overlooked. Therefore, a comprehensive understanding of the role of borophene polymorphism in lateral heterostructures is crucial. Based on prior studies, this work employs molecular dynamics (MD) simulations utilizing a machine-learning-based moment tensor potential (MTP) to investigate the thermal transport properties of the β₁₂/χ₃ mixed-phase borophene interface and the influence of defects on the ITC. Through the analysis of interfacial thermal conductance, spectral heat flux, and stress distribution characteristics, this study aims to enhance the understanding of the mechanisms governing interfacial thermal transport and provide theoretical guidance for the design of high-performance thermal management materials.

Simulation method

The structural optimization was performed using density functional theory (DFT) calculations with the Vienna Ab-initio Simulation Package (VASP). The Generalized Gradient Approximation (GGA) was employed, utilizing the Perdew-Burke-Ernzerhof (PBE) functional to describe electron-electron interactions. The cutoff energy for the plane-wave basis set was set to 500 eV. The convergence criteria for energy and forces were set to 10^–6 eV/Å and 10^–3 eV/Å, respectively. A vacuum layer with a thickness of 20 Å was applied in the direction perpendicular to the borophene sheet. The lattice constants of β₁₂ (χ₃) borophene along the zigzag and armchair directions are 8.41 (5.06) Å and 2.90 (2.93) Å, respectively, which are in excellent agreement with previous studies [30,31]. The atomic configuration of the two-dimensional β₁₂/χ₃ borophene heterostructures are shown in Figure 1A. Given that the lattice constants of the two borophenes along the armchair direction are nearly identical, we selected the zigzag direction perpendicular to it as the interface normal. The residual stress due to lattice mismatch in this case is less than 0.35 GPa. Figures 1B,C display the single-vacancy (SV) and double-vacancy (DV) defects introduced into the original BHs, hereafter referred to as SV-BHs and DV-BHs, respectively. These defects were introduced by removing one boron atom and two adjacent boron atoms, respectively, from the interface of the system, with the missing boron atoms highlighted in purple. The length of the BHs considered in the x-direction is 20.2 nm, and in the y-direction, it is 5.8 nm.

Figure 1

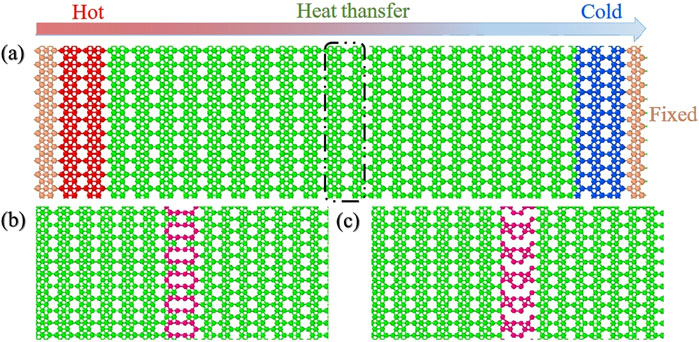
Figure 1. Three types of borophene heterostructures: (a) BHs, (b) SV-BHs and (c) DV-BHs. All these heterostructures are flat at the atomic scale. In the MD simulations, the heat flux flows from β₁₂ borophene (on the left) to χ₃ borophene (on the right).

All MD simulations in this work were performed using the LAMMPS molecular dynamics simulator [32], which has been widely utilized for classical MD simulations. A machine learning-based interatomic potential model, the moment tensor potentials (MTPs) [33], based on the generalized linear framework, was employed to describe the atomic interactions within the B/B system. We have constructed an Ab-initio molecular dynamics (AIMD) dataset consisting of approximately 3,000 configurations for the development of the MTP. Supplementary Figure S1 presents a comparison of the phonon dispersion calculated via DFT and MTP for the χ₃ and β₁₂ structures. The results demonstrate that the phonon dispersion obtained from MTP calculations is in excellent agreement with the DFT results, thereby validating the accuracy of our machine learning model. In the non-equilibrium MD (NEMD) simulations, a schematic of the simulation domain is shown in Figure 1A. To prevent the system from undergoing translational motion during the MD simulation, atoms within the gray regions at both ends, approximately 5 Å in length, were fixed. The time step for the entire simulation process was set to 0.5 fs, and periodic boundary conditions were applied in all three directions. To establish a linear temperature distribution within the system, atoms in the red and blue regions were respectively subjected to heat baths at temperatures of T₀ + ΔT and T₀ - ΔT, where T₀ and ΔT were set to 300 K and 25 K, respectively.

Prior to conducting the thermal transport simulations, the initial borophene heterostructure was optimized through energy minimization using the conjugate gradient method. The atomic velocity distribution was initialized to a Gaussian distribution corresponding to 50 K. Subsequently, the temperature was gradually increased from 50 K to 300 K under zero pressure via an NPT relaxation process. The system was then relaxed under NPT ensemble conditions at 300 K and zero pressure to minimize structural energy. Finally, an NVE ensemble was applied to all atoms (except those that were fixed), and the steady-state heat flux was obtained over a 5 ns period. The temperature of atoms at any given moment within the system is calculated using the following Equation 1:

$T=m{\sum }_{i=1}^N\frac{V_i^2}{3N_i{k}_{\mathrm{B}}}(1)$

In the equation, T represents the atomic temperature; m denotes the atomic mass; V_i is the velocity of the i-th atom; N_i is the total number of atoms; and k_B is the Boltzmann constant. Figure 2A presents the temperature distribution and energy over the final 5 ns, where the linear energy curve confirms the steady-state heat transfer. The slopes of these curves were used to compute the steady-state heat flux (J). The model was divided into 50 segments along the length direction, and the average temperature of atoms within each segment was calculated. The resulting temperature distribution along the length direction of the model at 300 K is shown in Figure 2B. Fourier’s law of heat conduction was employed to calculate the interfacial thermal conductance of the monolayer borophene heterostructures with different configurations by Equation 2:

$\kappa =\frac{J}{A·∆\mathrm{T}}(2)$

Figure 2

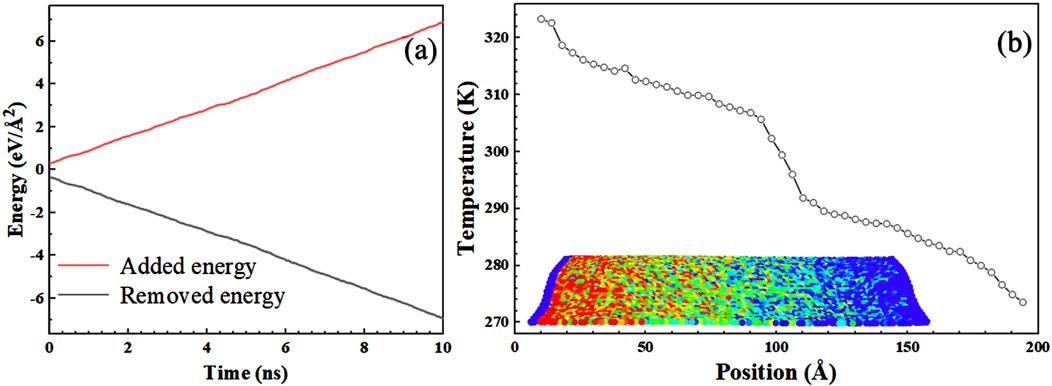
Figure 2. (a) Energy values added to the hot plate and removed from the cold plate during the simulation time steps under the NVT ensemble. (b) Temperature distribution of BHs along the direction of heat flow at 300 K. The illustration depicts the atomic temperature distribution within the model of BHs.

Here, J denotes the heat flux along the free cross-section, and A represents the cross-sectional area through which the heat flux passes. In the present study, the interlayer distance of the monolayer borophene sheets is fixed at 4.26 Å ΔT indicates the temperature gradient across the heterostructure.

Results and discussion

The finite size of the simulation cell inherently constrains the maximum attainable phonon mean free path (MFP), necessitating the consideration of finite size effects. Figure 3A illustrates the dependence of the interfacial thermal conductance of the pristine BHs on their length at 300 K. With the width fixed at 5.8 nm, the ITC of BHs with lengths of 20, 30, 40, 50, and 60 nm was calculated. As the length increases, the ITC of the BHs rises from 6.56 GWK⁻¹m^-2 to 18.31 GWK⁻¹m^-2, exhibiting a relatively high interfacial thermal transport [34,35], which is consistent with the trend observed in the literature for the thermal conductivity of borophene nanoribbons [15]. When the sample size is small, especially when it is smaller than the phonon MFP, the ITC increases sharply with length. The relationship between them is described as follows [36]: $1/\mathrm{\kappa }\left(\mathrm{L}\right)=\left(1+\wedge /\mathrm{L}\right)/\mathrm{\kappa }\left(\infty \right)$, where $\mathrm{\kappa }\left(\mathrm{L}\right)$ denotes the lattice thermal conductivity at a finite length L, while $\mathrm{\kappa }\left(\infty \right)$ represents the lattice thermal conductivity at infinite length. $\wedge$ refers to the effective phonon MFP. This behavior is attributed to the enhanced contribution of low-frequency, long-wavelength phonons to thermal transport. These phonons are more easily transmitted through the interface and exhibit lower inelastic scattering, resulting in a higher ITC [37].

Figure 3

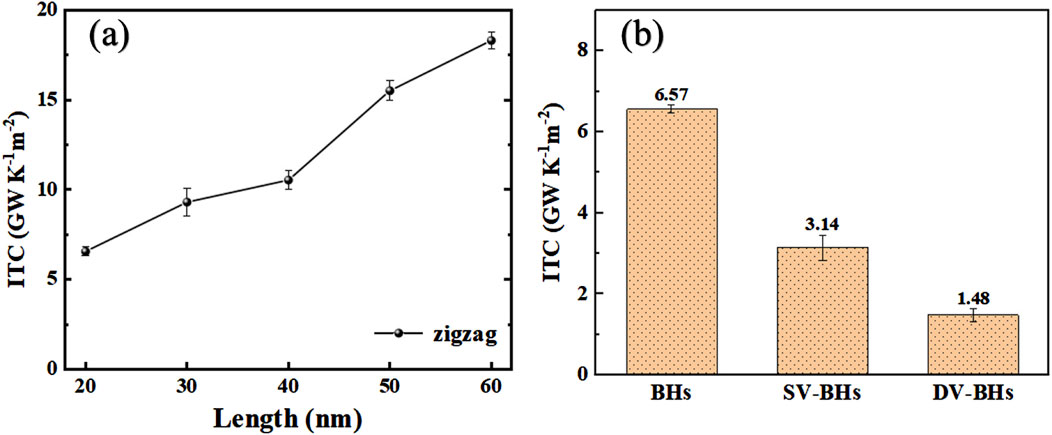
Figure 3. (a) The effect of length on the intrinsic β₁₂/χ₃ heterostructure interfacial thermal conductance at 300 K. (b) ITC of the three types of BHs.

To quantitatively assess the impact of defects on the interface, the ITC of pristine and defective BHs were calculated and presented in Figure 3B. The results indicate that both SV and DV defects in borophene significantly reduce the ITC values. As defects involve atomic vacancies, phonon transport at defect sites leads to local phonon scattering, which introduces local thermal resistance. Moreover, BHs with SV defects exhibit a relatively higher ITC value of 3.14 GW K⁻¹m⁻² approximately double that of BHs with DV defects. The observed variations in ITC are attributed to the geometric discrepancies at the interface and the atomic interactions between the different materials of the heterostructure [38]. The following discussion will delve into the mechanisms by which defects influence the interface behavior.

It is important to note that the atomic interactions at the interface predominantly govern the phonon transport across the interface [39]. To further investigate the vibrational differences at the three interfaces, atomic vibration analysis was performed on atoms located within 2 nm of the interface in the frequency domain. The overlap of the vibrational density of states (VDOS) plays a crucial role in the thermal transport between the two contacting materials. The VDOS of boron atoms on either side of the interface in the borophene heterostructure was calculated using the Fourier transform of the velocity autocorrelation function (VACF) by Equation 3 [40,41]:

$\text{DOS}\left(\omega \right)=\frac{1}{\sqrt{2\pi }}{\int }_0^{\tau }{〈{\mathit{v}}_{\mathit{j}}\left(0\right){\mathit{v}}_{\mathit{j}}\left(t\right)〉e}^{i\omega t}dt(3)$

Here, ω represents the frequency, v denotes the velocity of carbon atoms, and ⟨…⟩ indicates the time and atomic number averaged velocity autocorrelation function, with τ being the computation time duration. The ensemble average in Equation 3 is achieved by performing a time average of the system’s atomic velocities over a 250 ps time span, extracting the velocity every 10 fs from the simulation. Figure 4A presents the VDOS of β₁₂ and χ₃ borophene at the pristine BHs interface, with the selected frequency range (0–40 THz) encompassing the phonon vibrational range of the borophene-based material, primarily originating from the vibrations of covalent B-B bonds. The similar density of states in both regions and the broad frequency range facilitate significant phonon excitation at the interface during thermal transport, thereby enhancing the thermal conductivity. Figures 4B,C illustrate the VDOS curves of the BHs with SV and DV defects. At certain peaks within the VDOS, splitting into multiple peaks occurs, indicating strong phonon scattering at the defects. To quantify the VDOS overlap, we calculated the overlap parameter (S) by Equation 4 as follows [34,42]:

$S={\int }_0^{{\omega }_{\mathit{max}}}\omega A\left(\omega \right)\mathrm{d}\omega (4)$

Figure 4

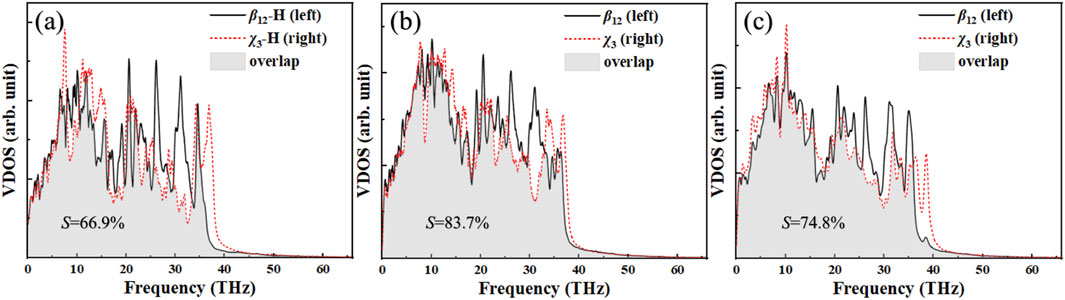
Figure 4. Comparison of the VDOS of β₁₂ and χ₃ borophene at the heterostructure: (a) BHs, (b) SV-BHs, (c) DV-BHs. The S value refers to the overlap factor.

In this context, A(ω) represents the coherent part at frequency ω, which is displayed in the form of the S value in Figure 4. A higher overlap factor indicates a greater degree of phonon matching at the β₁₂/χ₃ interface. The results demonstrate that, compared to pristine borophene, the VDOS curve of borophene at the interface of SV-BHs shows a greater overlap in the low-frequency modes, within the vibrational frequency range of β₁₂ and χ₃ borophene being comparable, yielding an S value of 83.7%. In contrast, the variation for DV-BHs is smaller, with an S value of 74.8%, suggesting that the phonon transport channels at the interface of SV-BHs are more abundant than those in DV-BHs.

Since the phonon transport in borophene exhibits anisotropy across different directions, in-plane transport is significantly faster than out-of-plane transport [43]. The enhanced thermal conductivity between the β₁₂/χ₃ borophene heterostructures can be attributed to the higher overlap between the in-plane and out-of-plane VDOS curves of borophene. To better understand the effects of defects, the total VDOS curve of BHs, as shown in Figure 5, is separated into in-plane and out-of-plane modes. The atomic in-plane vibrational frequency range and intensity of BHs are notably larger than those of the out-of-plane vibrational modes, with the 18–40 THz frequency range predominantly corresponding to in-plane vibrations. Moreover, more characteristic peaks of in-plane vibrations are excited, which are primarily dominated by out-of-plane vibrations. Upon further discussion, the VDOS behavior of defective borophene differs. For defective borophene, as seen in Figures 5B,C, the overlap region of SV-BHs and DV-BHs VDOS does not exhibit significant changes. Simultaneously, the phonon matching degree at the interface under the SV defect is also higher, with an S value of 31.4%, exceeding the 29.5% observed under the DV defect. This agrees well with the general trend where better phonon matching typically results in higher ITC. Unfortunately, the S value for the pristine heterostructures is smaller than that for the defective structures, which can not explain the fact that it has higher ITC.

Figure 5

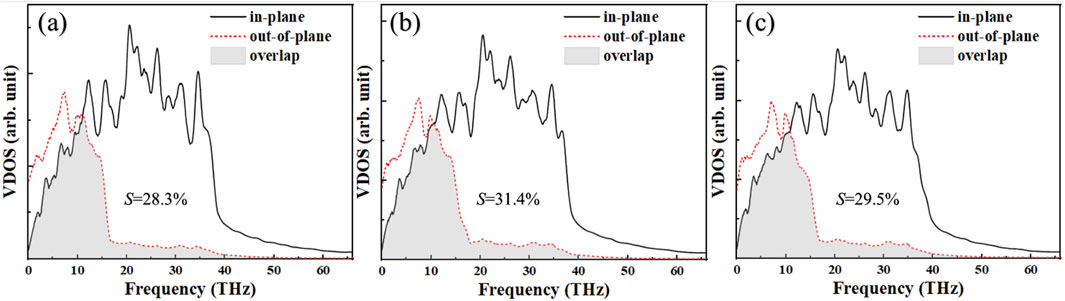
Figure 5. Comparison of the in-plane and out-of-plane VDOS at the borophene interface for (a) BHs, (b) SV-BHs, and (c) DV-BHs. The shaded regions represent the overlap of the VDOS.

Further investigation was conducted using the spectral thermal flux (SHC) decomposition method to calculate the phonon transmission function, aiming to explore phonon heat transport. By analyzing the force-velocity correlation between atoms near the interface, the transmission function from material A to material B can be calculated by Equation 5 as follows [44,45]:

$\mathrm{\Gamma }\left(\omega \right)=\frac{2}{k_{\mathrm{B}}∆TM∆t_s}\text{Re}{\displaystyle \sum _{i\in A}}〈{\widehat{\overrightarrow{\mathit{F}}}}_{\mathit{i}}\left(\omega \right)·{{\widehat{\overrightarrow{\mathit{v}}}}_{\mathit{i}}\left(\omega \right)}^{*}〉(5)$

Here, k_B denotes the Boltzmann constant, M represents the number of samples, Δt_s is the sampling interval, and F_ij refers to the Fourier-transformed interatomic forces between atom-i in the material A region and atom-j in the material B region. The interatomic force and velocity data are recorded within a 2 nm region centered around the interface. In the calculations, we set Δt_s = 10 fs and M = 500000, with the results shown in Figure 6. The transmission curves exhibit similar shapes, reflecting the β₁₂ and χ₃ borophene in the heterogeneous structure. The transmission curves corresponding to BHs exhibit the highest peak, followed by SV-BHs, and then DV-BHs, consistent with the order observed in the ITC. Since phonons are the primary heat carriers, a higher transmission coefficient indicates that more phonons are able to traverse the interface at that frequency, meaning a greater amount of heat can be transferred through the interface. Meanwhile, a redshift is observed in DV-BHs. The defects lead to an increase in the atomic vibration frequency in the interface region (phonon hardening), which subsequently reduces the number of low-frequency phonons. The decreased contribution of low-frequency phonons diminishes thermal conductance [25]. According to Hooke’s law, the relationship between bond strength and phonon frequency can be expressed as $\omega =\frac{1}{2\pi }\sqrt{\frac{k}{\mu }}$, where ω is the phonon frequency, k is the force constant of the chemical bond, and μ is the reduced mass of the bonded atoms. Thus, the red shift of the peak position indicates a weakening of the bond strength at the interface, and weaker atomic bonds are detrimental to thermal conduction. This observation is consistent with the results shown in Supplementary Figure S2. We computed the stress-strain relationship near the heterogeneous structure interface under uniaxial tensile strain along the thermal transport direction. The strain is defined as ε = ΔL/L₀, where ΔL represents the change of the length and L₀ is the initial length. The stress monotonically increases with strain until it rapidly decreases upon reaching the tolerance limit. In the initial linear increasing segment of the stress-strain curve, the slope represents the Young’s modulus (E), which can be utilized to characterize the bond strength. In this context, within the heterogeneous structure, ITC exhibits a positive correlation with the bonding strength near the interface.

Figure 6

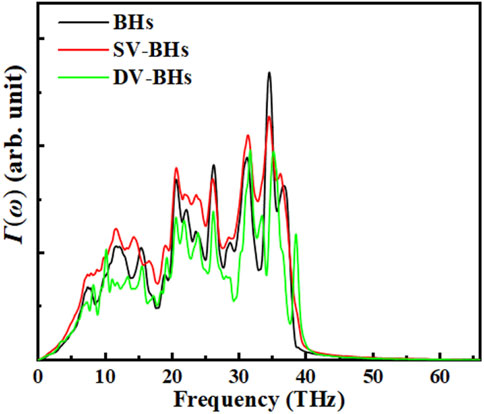
Figure 6. Frequency-resolved phonon transmission coefficients of borophene heterostructures and those with introduced defects.

The improvement in density of states overlap facilitates thermal transfer, whereas excessive lattice distortion (quantified by von Mises stress) induces strong phonon localization effects. Therefore, to address the apparent contradiction between phonon compatibility and the degradation of thermal transport properties, we also calculated the von Mises stress distribution near the interface of three BHs (within 6 nm range). The atomic von Mises stress is defined by Equation 6 as follows [35]:

$\sigma =\sqrt{\frac{1}{2}\left[{\left({\sigma }_{xx}-{\sigma }_{yy}\right)}^2+{\left({\sigma }_{yy}-{\sigma }_{zz}\right)}^2+{\left({\sigma }_{xx}-{\sigma }_{zz}\right)}^2+6\left({{\sigma }_{xy}}^2+{{\sigma }_{yz}}^2+{{\sigma }_{xz}}^2\right)\right]}(6)$

In this context, ${\sigma }_{xx}$, ${\sigma }_{yy}$ and ${\sigma }_{zz}$ represent the normal stresses along the x, y, and z directions, respectively; ${\sigma }_{xy}$, ${\sigma }_{yz}$ and ${\sigma }_{xz}$ denote the shear stresses. The atomic von Mises stress is employed to characterize the plastic behavior of an individual atom or a localized region. As shown in Figure 7, the stress distribution near the interface of the original BHs is relatively uniform, with excellent matching between the two materials in the heterogeneous structure. However, the existence of SV and DV defects result in a significant stress concentration near the interface. The degree of stress concentration in the DV-BHs near the interface is significantly higher than that in the SV-BHs. In the case of DV-BHs, after structural relaxation, the heterostructure adopts a chain-like connectivity, with a pronounced stress concentration. The von Mises stress of certain atoms at the interface reaches up to 40 GPa. Typically, higher stress concentrations inhibit atomic vibrations and increase phonon scattering at the interface, further deteriorating the thermal properties of the borophene-based heterogeneous structure. Consequently, the defects result in the reduction of ITC of β₁₂/χ₃ borophene heterostructures, and the DV-BHs has the lowest ITC.

Figure 7

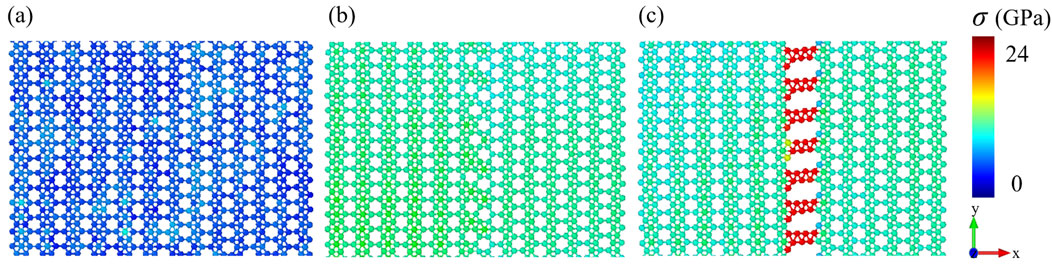
Figure 7. Von Mises stress distribution after full structural relaxation for (a) BHs, (b) SV-BHs and (c) DV-BH.s.

Conclusion

In this study, we investigated the influence of defect on the interfacial thermal conductance of β₁₂/χ₃ borophene lateral heterostructures, employing first-principles calculations and Molecular Dynamics simulations based on MTP potential. The results demonstrate that the ITC of the pristine borophene heterostructures exhibits a pronounced size effect, significantly increasing with length (from 6.56 GW K⁻¹m^-2 to 18.31 GW K⁻¹m^-2). The introduction of single vacancies and double vacancies causes a reduction in ITC. The ITC of DV-BHs decreases to 1.57 GW K⁻¹m^-2. The phenomenon can not be explained by the overlap between the in-plane and out-of-plane VDOS at the interface. Subsequently, by analyzing spectral thermal flux and stress distribution, we revealed that the ITC is regulated by a competition between atomic bond strength and stress, which exacerbates phonon scattering. Our study provides theoretical guidance for the design of thermal management materials in nano-device applications.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

ZL: Investigation, Software, Writing – original draft, Validation, Formal Analysis, Methodology, Data curation, Visualization. LC: Data curation, Software, Writing – original draft, Investigation. DL: Funding acquisition, Project administration, Visualization, Validation, Conceptualization, Writing – review and editing, Supervision, Formal Analysis, Investigation.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. We gratefully acknowledge funding supporting from Scientific and Technological Research of Chongqing Municipal Education Commission (KJZD-K202100602).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2025.1614764/full#supplementary-material

References

1. Zhang P, Yuan P, Jiang X, Zhai S, Zeng J, Xian Y, et al. A theoretical review on interfacial thermal transport at the nanoscale. Small (2018) 14:1702769. doi:10.1002/smll.201702769

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Zha JW, Wang F, Wan B. Polymer composites with high thermal conductivity: theory, simulation, structure and interfacial regulation. Prog Mater Sci (2025) 148:101362. doi:10.1016/j.pmatsci.2024.101362

CrossRef Full Text | Google Scholar

3. Giri A, Hopkins PE. A review of experimental and computational advances in thermal boundary conductance and nanoscale thermal transport across solid interfaces. Adv Funct Mater (2020) 30:1903857. doi:10.1002/adfm.201903857

CrossRef Full Text | Google Scholar

4. Li J, Zhang J. Thermal transport properties of defective graphene/graphyne van der Waals heterostructures elucidated via molecular dynamics and machine learning. Nanoscale (2024) 16:17992–8004. doi:10.1039/D4NR02120G

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Lu Z, Wang Y, Ruan X. Metal/dielectric thermal interfacial transport considering cross-interface electron-phonon coupling: theory, two-temperature molecular dynamics, and thermal circuit. Phys Rev B (2016) 93:064302. doi:10.1103/PhysRevB.93.064302

CrossRef Full Text | Google Scholar

6. Wan K, He J, Shi X. Construction of high accuracy machine learning interatomic potential for surface/interface of nanomaterials—a review. Adv Mater (2024) 36:2305758. doi:10.1002/adma.202305758

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Ma M, Zhang X, Qing S, Wang H. Wettability-dependent thermal transport at the Fe nanoparticle-water interface: molecular dynamics simulations. J Mol Liq (2024) 402:124717. doi:10.1016/j.molliq.2024.124717

CrossRef Full Text | Google Scholar

8. Iannaccone G, Bonaccorso F, Colombo L, Fiori G. Quantum engineering of transistors based on 2D materials heterostructures. Nat Nanotechnol (2018) 13:183–91. doi:10.1038/s41565-018-0082-6

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Xu H, Han X, Dai X, Liu W, Wu J, Zhu J, et al. High Detectivity and Transparent Few-Layer MoS₂/Glassy-Graphene Heterostructure Photodetectors. Adv Mater (2018) 30:1706561. doi:10.1002/adma.201706561

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Wang D, Zhang Z, Huang B, Zhang H, Huang Z, Liu M, et al. Few-Layer WS₂–WSe₂ Lateral Heterostructures: Influence of the Gas Precursor Selenium/Tungsten Ratio on the Number of Layers. ACS Nano (2022) 16:1198–207. doi:10.1021/acsnano.1c08979

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Li D, Gao J, Cheng P, He J, Yin Y, Hu Y, et al. 2D Boron Sheets: Structure, Growth, and Electronic and Thermal Transport Properties. Adv Funct Mater (2020) 30:1904349. doi:10.1002/adfm.201904349

CrossRef Full Text | Google Scholar

12. Liu X, Zhang Z, Wang L, Yakobson BI, Hersam MC. Intermixing and periodic self-assembly of borophene line defects. Nat Mater (2018) 17:783–8. doi:10.1038/s41563-018-0134-1

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Fan Z, Xiao Y, Wang Y, Ying P, Chen S, Dong H. Combining linear-scaling quantum transport and machine-learning molecular dynamics to study thermal and electronic transports in complex materials. J Phys Condens Matter (2024) 36:245901. doi:10.1088/1361-648X/ad31c2

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Yang Z, Yuan K, Meng J, Hu M. Electric field tuned anisotropic to isotropic thermal transport transition in monolayer borophene without altering its atomic structure. Nanoscale (2020) 12:19178–90. doi:10.1039/D0NR03273E

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Pham VT, Fang TH. Understanding porosity and temperature induced variabilities in interface, mechanical characteristics and thermal conductivity of borophene membranes. Sci Rep (2021) 11:12123. doi:10.1038/s41598-021-91705-2

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Chen J, Wang Z, Ma J, Cao Z, Li K, Zhang J. Thermal and electronic properties of borophene in two-dimensional lateral graphene-borophene heterostructures empowered by machine-learning approach. Carbon (2024) 229:119533. doi:10.1016/j.carbon.2024.119533

CrossRef Full Text | Google Scholar

17. Tai G, Hu T, Zhou Y, Wang X, Kong J, Zeng T, et al. Synthesis of Atomically Thin Boron Films on Copper Foils. Angew Chem Int Ed Engl (2015) 54:15473–7. doi:10.1002/anie.201509285

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Kaneti YV, Benu DP, Xu X, Yuliarto B, Yamauchi Y, Golberg D. Borophene: Two-dimensional Boron Monolayer: Synthesis, Properties, and Potential Applications. Chem Rev (2022) 122:1000–51. doi:10.1021/acs.chemrev.1c00233

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Mannix AJ, Zhou X, Kiraly B, Wood JD, Alducin D, Myers BD, et al. Synthesis of borophenes: Anisotropic, two-dimensional boron polymorphs. Science (2015) 350:1513–6. doi:10.1126/science.aad1080

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Xu D, Zhou M, Wu B, Liu J, Zhang P. Molecular dynamics study of phonon thermal transport in borophene with random vacancy defects. Modell Simul Mater Sci Eng (2022) 30:065008. doi:10.1088/1361-651X/ac8173

CrossRef Full Text | Google Scholar

21. Umeno Y, Kubo A, Kurata Y, Sakaniwa D, Ishikawa FN, Yamaguchi K. Molecular dynamics study of thermal transport at interface between alumina and epoxy resin. AIP Adv (2024) 14:025316. doi:10.1063/5.0189335

CrossRef Full Text | Google Scholar

22. Li Z, Wang J, Dong H, Zhou Y, Liu L, Yang JY. Mechanistic insights into water filling effects on thermal transport of carbon nanotubes from machine learning molecular dynamics. Int J Heat Mass Transfer (2024) 235:126152. doi:10.1016/j.ijheatmasstransfer.2024.126152

CrossRef Full Text | Google Scholar

23. Karaaslan Y. Empirical interatomic potential development and classical molecular dynamics simulation of monolayer group-III monochalcogenides: insights into thermal transport properties. J Phys D Appl Phys (2024) 58:015306. doi:10.1088/1361-6463/ad7c58

CrossRef Full Text | Google Scholar

24. Sharma A, Rangra VS. Hydrogenation driven ultra-low lattice thermal conductivity in β₁₂ borophene. J Phys Condens Matter (2024) 36:205704. doi:10.1088/1361-648X/ad2800

PubMed Abstract | CrossRef Full Text | Google Scholar

25. He J, Hu Y, Li D, Chen J. Ultra-low lattice thermal conductivity and promising thermoelectric figure of merit in borophene via chlorination. Nano Res (2022) 15:3804–11. doi:10.1007/s12274-021-3908-8

CrossRef Full Text | Google Scholar

26. Novotný M, Domínguez-Gutiérrez FJ, Krstić P. A computational study of hydrogen detection by borophene. J Mater Chem C (2017) 5:5426–5433. doi:10.1039/C7TC00976C

CrossRef Full Text | Google Scholar

27. Nie F, Chow CL, Lau D. Effect of functionalization and defects on thermal conductivity of graphene sheets modified asphalt nanocomposites. Appl Surf Sci (2023) 621:156804. doi:10.1016/j.apsusc.2023.156804

CrossRef Full Text | Google Scholar

28. Dong P, Gao K, Zhang L, Huan H, Xie MH, Yang XL, et al. Hydrogen bond-assisted construction of MOF/semiconductor heterojunction photocatalysts for highly efficient electron transfer. Appl Catal B Environ (2024) 357:124297. doi:10.1016/j.apcatb.2024.124297

CrossRef Full Text | Google Scholar

29. Zhang N, Zhou B, Li D, Qi D, Wu Y, Zheng H, et al. Near-Interface Defects in Graphene/H-BN In-Plane Heterostructures: Insights into the Interfacial Thermal Transport. Nanomaterials (2022) 12:1044. doi:10.3390/nano12071044

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Feng B, Zhang J, Zhong Q, Li W, Li S, Li H, et al. Experimental realization of two-dimensional boron sheets. Nat Chem (2016) 8:563–8. doi:10.1038/nchem.2491

PubMed Abstract | CrossRef Full Text | Google Scholar

31. He J, Ouyang Y, Yu C, Jiang P, Ren W, Chen J. Lattice thermal conductivity of β₁₂ and χ₃ borophene. Chin Phys B (2020) 29:126503. doi:10.1088/1674-1056/abbbe6

CrossRef Full Text | Google Scholar

32. Plimpton S. Fast Parallel Algorithms for Short-Range Molecular Dynamics. J Comput Phys (1995) 117:1–19. doi:10.1006/jcph.1995.1039

CrossRef Full Text | Google Scholar

33. Shapeev AV. Moment Tensor Potentials: A Class of Systematically Improvable Interatomic Potentials. Multiscale Model Sim (2016) 14:1153–73. doi:10.1137/15M1054183

CrossRef Full Text | Google Scholar

34. Hong Y, Zhang J, Zeng XC. Thermal contact resistance across a linear heterojunction within a hybrid graphene/hexagonal boron nitride sheet. Phys Chem Chem Phys (2016) 18:24164–70. doi:10.1039/C6CP03933B

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Song J, Xu Z, He X, Cai C, Bai Y, Miao L, et al. Effect of strain and defects on the thermal conductance of the graphene/hexagonal boron nitride interface. Phys Chem Chem Phys (2020) 22:11537–45. doi:10.1039/D0CP01727B

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Schelling PK, Phillpot SR, Keblinski P. Comparison of atomic-level simulation methods for computing thermal conductivity. Phys Rev B (2002) 65:144306. doi:10.1103/PhysRevB.65.144306

CrossRef Full Text | Google Scholar

37. Chen J, Chen G, Wang Z, Tang D. Modulation of localized phonon thermal transport at GaN/Al_xGa_1-xN heterointerface: Polar surface, doping, and compressive Strain. Int J Heat Mass Transfer (2024) 220:124945. doi:10.1016/j.ijheatmasstransfer.2023.124945

CrossRef Full Text | Google Scholar

38. Wu Y, Lin S, Yang P. Interfacial thermal conductance of multilayer graphene/MoS₂ heterostructure. Therm Sci Eng Prog (2024) 47:102345. doi:10.1016/j.tsep.2023.102345

CrossRef Full Text | Google Scholar

39. Chen J, Xu X, Zhou J, Li B. Interfacial thermal resistance: Past, present, and future. Rev Mod Phys (2022) 94:025002. doi:10.1103/RevModPhys.94.025002

CrossRef Full Text | Google Scholar

40. Li Y, Wei A, Ye H, Yao H. Mechanical and thermal properties of grain boundary in a planar heterostructure of graphene and hexagonal boron nitride. Nanoscale (2018) 10:3497–508. doi:10.1039/C7NR07306B

PubMed Abstract | CrossRef Full Text | Google Scholar

41. Liang T, Zhang P, Yuan P, Zhai S, Yang D. A molecular dynamics study on the thermal conductivities of single- and multi-layer two-dimensional borophene. Nano Futures (2019) 3:015001. doi:10.1088/2399-1984/aafc8c

CrossRef Full Text | Google Scholar

42. Zhang J, Hong Y, Yue Y. Thermal transport across graphene and single layer hexagonal boron nitride. J Appl Phys (2015) 117:134307. doi:10.1063/1.4916985

CrossRef Full Text | Google Scholar

43. Yin Y, Hu Y, Feng C, Li S, Li BL, Li D. Strongly anisotropic thermal conductivity in planar hexagonal borophene oxide sheet. Phys Lett A (2020) 384:126457. doi:10.1016/j.physleta.2020.126457

CrossRef Full Text | Google Scholar

44. Chen W, Zhou Q, Han Q, Liu C, Jiang X, Gu Y, et al. Elastic and inelastic phonon scattering effects on thermal conductance across Au/graphene/Au interface. J Appl Phys (2024) 135:165107. doi:10.1063/5.0184024

CrossRef Full Text | Google Scholar

45. Sääskilahti K, Oksanen J, Tulkki J, Volz S. Role of anharmonic phonon scattering in the spectrally decomposed thermal conductance at planar interfaces. Phys Rev B (2014) 90:134312. doi:10.1103/PhysRevB.90.134312

CrossRef Full Text | Google Scholar