HiImp-SMI: an implicit transformer framework with high-frequency adapter for medical image segmentation

Accurate and generalizable segmentation of medical images remains a challenging task due to boundary ambiguity and variations across domains. In this paper, an implicit transformer framework with a high-frequency adapter for medical image segmentation (HiImp-SMI) is proposed. A new dual-branch architecture is designed to simultaneously process spatial and frequency information, enhancing both boundary refinement and domain adaptability. Specifically, a Channel Attention Block selectively amplifies high-frequency boundary cues, improving contour delineation. A Multi-Branch Cross-Attention Block facilitates efficient hierarchical feature fusion, addressing challenges in multi-scale representation.Additionally, a ViT-Conv Fusion Block adaptively integrates global contextual awareness from Transformer features with local structural details, thereby significantly boosting cross-domain generalization. The entire network is trained in a supervised end-to-end manner, with frequency-adaptive modules integrated into the encoding stages of the Transformer backbone. Experimental evaluations show that HiImp-SMI consistently outperforms mainstream models on the Kvasir-Sessile and BCV datasets, including state-of-the-art implicit methods. For example, on the Kvasir-Sessile dataset, HiImp-SMI achieves a Dice score of 92.39%, outperforming I-MedSAM by 1%. On BCV, it demonstrates robust multi-class segmentation with consistent superiority across organs. These quantitative results demonstrate the framework’s effectiveness in refining boundary precision, optimizing multi-scale feature representation, and improving cross-dataset generalization. This improvement is largely attributed to the dual-branch design and the integration of frequency-aware attention mechanisms, which enable the model to capture both anatomical details and domain-robust features. The proposed framework may serve as a flexible baseline for future work involving implicit modeling and multi-modal representation learning in medical image analysis.

1 Introduction

Medical image segmentation plays a crucial role in assisting disease diagnosis and guiding clinical treatment. Traditional discrete methods based on convolutional neural networks (CNNs), such as U-Net [1], nnU-Net [2], and PraNet [3], effectively integrate multi-scale features but remain highly sensitive to variations in data distribution, thus limiting cross-domain generalization. Although boundary-aware methods, such as Boundary-aware U-Net [4], WM-DOVA [5], Hausdorff distance-based approaches [6], dropout-based calibration [7], and neural network calibration [8], have improved localization precision and feature representation, these methods still face challenges when dealing with complex medical structures and achieving consistent segmentation performance across different domains. Additionally, multi-scale residual architectures like Res2Net [9] further enhance feature representation but are still limited in boundary preservation.

Recent developments have introduced Transformer-based architectures, such as TransUNet [10] and UNETR [11], leveraging global contextual awareness through self-attention mechanisms [12]. Despite superior global feature capture capabilities, these approaches often underperform in local boundary refinement and require extensive training data for effective generalization. Further advancements, such as LoRA [13], aim to improve Transformer efficiency and generalization but do not explicitly optimize for boundary segmentation accuracy. Furthermore, adaptations based on the Segment Anything Model (SAM) [14], including MedSAM [15], SAM-based 3D extensions [16], and customized SAM models [17], generally improve generalization capabilities but typically neglect fine-grained feature integration, resulting in limited boundary segmentation accuracy. Additional SAM-related studies, such as NTo3D [18], Customized SAM [19], SAM-Med2D [20], DiffDP [21], spatial prior-based approaches [22], and mask-enhanced SAM models [23], have explored further improvements but continue to face challenges with boundary precision.

Beyond conventional deep learning approaches, emerging research spans several interdisciplinary directions that address these challenges. For instance, memristor- and memcapacitor-based neural network models have been proposed to enable neuromorphic hardware implementations [24, 25]; such analog in-memory circuits have demonstrated improved image segmentation speed and accuracy via parallel high-efficiency computations [26, 27]. Recent studies have further explored Hamiltonian conservative chaotic systems integrated with memristors for modeling and FPGA implementation, enhancing the physical interpretability and stability of neuromorphic designs [28]. Similarly, chaotic and hyperchaotic dynamical systems have been exploited in image encryption, leveraging their high-dimensional unpredictability to enhance security. In particular, memristor-coupled cellular neural networks based on resonant tunneling diodes have been applied in forensic digital image protection, offering a secure hardware foundation for sensitive applications [29]. Some studies even integrate memristive chaotic circuits to strengthen resistance against differential attacks [30], and in general hyper-chaos offers greater randomness and key space than lower-dimensional maps [31], yielding encryption schemes with robust immunity to cryptanalytic attacks [32]. Other researchers have implemented novel hyperchaotic systems in FPGA to support audio encryption, demonstrating the practical deployment of such dynamics on low-power reconfigurable hardware [33, 34]. In IoT contexts, researchers have developed lightweight image encryption and steganography techniques to secure multimedia data with minimal computational overhead [35, 36], addressing the limitations of earlier cryptosystems on resource-constrained devices [37]. Moreover, discrete n-dimensional hyperchaotic maps with customizable Lyapunov exponents have been proposed to expand the design space for secure communications and embedded cryptography [38]. Additionally, integrating multi-modal information has become crucial for improving diagnostic accuracy, prompting new architectures that effectively fuse heterogeneous medical data streams [39, 40]. Equally important, domain-generalization strategies are being pursued to ensure models remain robust across disparate imaging domains, tackling the severe performance degradation caused by cross-modality shifts without requiring retraining on target data [41]. Finally, a concerted effort is underway to translate these advances into practical deployments: specialized DSP-based accelerators and other hardware implementations are achieving real-time image processing with low power consumption [42, 43], and even complex neuromorphic networks are being prototyped on DSP platforms [25, 26]. These developments across hardware design, secure encryption, lightweight algorithms, and multi-modal learning collectively strengthen the foundation for next-generation medical image segmentation systems.

Implicit neural representation methods represent another advancement, employing continuous mappings from coordinate spaces to representation spaces, exemplified by OSSNet [44], IOSNet [45], and SWIPE [46]. These models exhibit improved segmentation robustness across resolutions but remain constrained by their reliance on traditional convolutional encoders, limiting their capacity to simultaneously capture detailed boundary information and global contextual features. Further implicit methods, including NeRF [47], NUDF [48], NISF [49], ImplicitAtlas [50], implicit neural representations survey [51], shape reconstruction from sparse measurements [52], implicit functions for 3D reconstruction [53], MRI super-resolution [16], and volumetric SAM adaptations [54], have significant potential but share similar limitations. Frequency-domain adapters, like those in I-MedSAM [55], have enhanced boundary delineation, but single-adapter designs remain insufficient for comprehensive multi-scale feature integration.

To address these challenges, this study introduces HiImp-SMI, an implicit Transformer-based medical image segmentation framework incorporating three key innovations: (1) a Channel Attention Block to explicitly enhance high-frequency boundary information, (2) a Multi-Branch Cross-Attention Block to facilitate efficient hierarchical feature fusion across different scales, and (3) a ViT-Conv Fusion Block designed to integrate global context from Transformer-based architectures with local fine-grained features extracted by convolutional networks. Experimental validations conducted on the Kvasir-Sessile and BCV datasets demonstrate that HiImp-SMI outperforms existing segmentation methods, highlighting its effectiveness in boundary precision, multi-scale feature representation, and cross-dataset generalization capabilities.

The remainder of this paper is organized as follows: Section 2 details the proposed HiImp-SMI framework; Section 3 presents the experimental setup and results; and Section 4 concludes the study, providing directions for future research.

2 Materials and methods

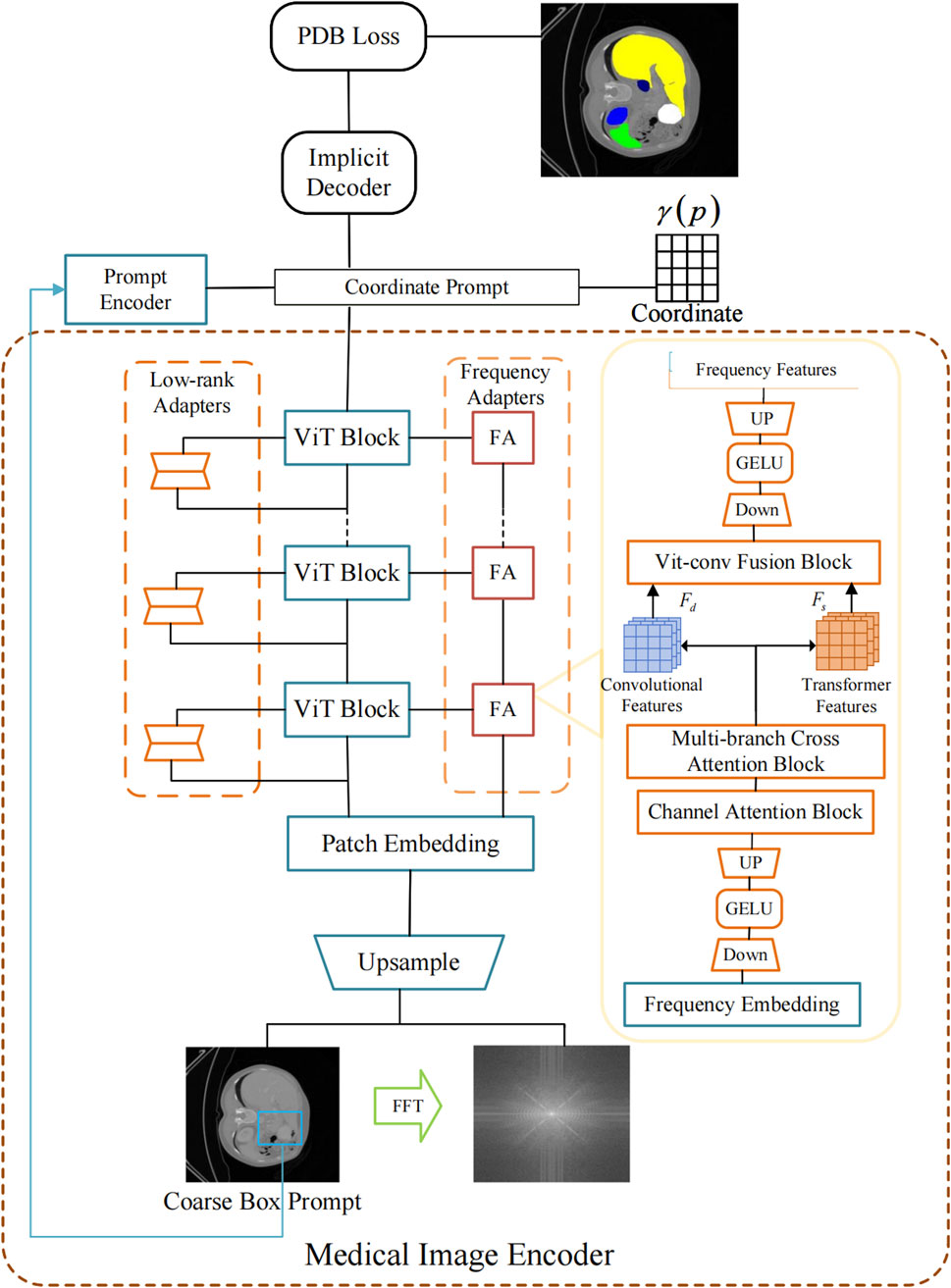
The overall architecture of the proposed HiImp-SMI framework is depicted in Figure 1. It comprises a dual-branch encoder structure that jointly exploits spatial-domain and frequency-domain information. Given an input image $I$, a Fast Fourier Transform (FFT) is applied to derive its frequency representation $I_{\text{FFT}}$, which highlights high-frequency components corresponding to anatomical boundaries and texture transitions. By integrating $I_{\text{FFT}}$ into the encoder, our Channel Attention Block can selectively amplify boundary-sensitive features, enhancing fine-grained localization and generalization to unseen domains. These embeddings are then processed by three key modules: a Channel Attention Block, which selectively enhances high-frequency boundary details; a Multi-Branch Cross Attention Block, designed to enable effective feature exchange across hierarchical levels; and a ViT-Conv Fusion Block, which adaptively integrates global contextual information from the Transformer branch and local structural features from the convolutional branch. Through this architecture, HiImp-SMI aims to achieve more precise boundary segmentation, stronger multi-scale representation, and enhanced cross-domain generalization.

Figure 1

Figure 1. Overall architecture of our proposed model.

2.1 Channel attention block

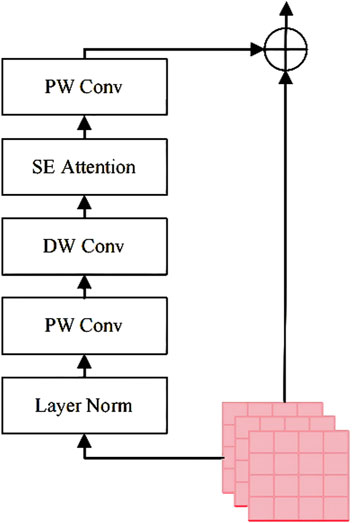
In this study, SAM employs a Vision Transformer (ViT) as the image encoder, pretrained on a large-scale natural image dataset. To preserve the strong feature representation capability of the pretrained ViT, its weights are kept frozen during training. Instead, a local adapter module is introduced to incorporate localized inductive biases into the model, as illustrated in Figure 2.

Figure 2

Figure 2. The Channel Attention Block for domain-specific feature enhancement in the ViT encoder.

The Channel Attention Block enhances the domain-specific feature extraction capability of the pretrained Vision Transformer (ViT) without fine-tuning its weights. The procedure involves the following steps:

Step 1: Obtain the input embedding $F_{\text{vit}}$ from the ViT attention block. This embedding carries high-level semantic features. It serves as the input to the channel attention block.

Step 2: Apply layer normalization (LN) to stabilize feature distributions. LN normalizes each channel to reduce internal covariate shift. This improves training stability and convergence.

Step 3: Perform a pointwise convolution $({\text{Conv}}_{1\times 1})$ to adjust channel dimensions. This operation projects features into a latent space. It preserves spatial structure while enabling channel-wise transformation.

Step 4: Execute a depthwise convolution $({\text{DWConv}}_{3\times 3})$ to capture spatial information. Each channel is convolved independently to extract local patterns. This enhances spatial modeling without increasing parameter count significantly.

Step 5: Apply a Squeeze-and-Excitation (SE) block to model channel-wise dependencies. Specifically, the SE block performs global average pooling followed by two fully connected layers and non-linear activations to generate a channel attention vector $s$, which is then applied to recalibrate the feature map, as shown in Equation 1:

$\left\{\begin{array}{c}z=\frac{1}{H\times W}{\displaystyle \sum _{i=1}^H}{\displaystyle \sum _{j=1}^W}{F}_{ij}\hfill \\ s=\sigma \left(W_2\cdot \delta \left(W_1\cdot z\right)\right)\hfill \\ \text{SE}\left(F\right)=F\otimes s\hfill \end{array}\right.(1)$

Here, $F\in {\mathbb{R}}^{C\times H\times W}$ denotes the input feature map, and $z\in {\mathbb{R}}^C$ is the channel-wise descriptor obtained by global average pooling. $W_1$ and $W_2$ are learnable weight matrices of two fully connected layers. $\delta (\cdot )$ and $\sigma (\cdot )$ denote the ReLU and sigmoid activation functions, respectively. The resulting attention vector $s$ is used to rescale each channel of $F$ via element-wise multiplication, enabling adaptive channel emphasis.

Step 6: Integrate the processed features using another pointwise convolution $(\text{Conv}1\times 1)$ to obtain refined embedding $\widehat{F}\text{vit}$, as defined in Equation 2:

$\widehat{F}\text{vit}=\text{Conv}1\times 1\left(\text{SE}\left(\text{DWConv}3\times 3\left(\text{Conv}1\times 1\left(\text{LN}\left(F_{\text{vit}}\right)\right)\right)\right)\right)(2)$

Step 7: Merge the refined features with the original features through a residual connection, as formulated in Equation 3:

$F_{\text{out}}=F_{\text{vit}}+{\widehat{F}}_{\text{vit}}(3)$

2.2 Multi-branch Cross Attention Block

Figure 3 illustrates the structure of the Multi-branch Cross Attention Block, which integrates deep features from the ViT branch with shallow features from a convolutional branch. The procedure involves the following steps:

Step 1: Extract shallow features $(F_s)$ from the resized input image using a lightweight convolutional block. This step captures low-level visual patterns such as edges and textures. The convolutional block is designed to be efficient for early-stage feature extraction.

Step 2: Generate queries, keys, and values for the ViT branch and convolutional branch separately, as described in Equation 4:

$\left\{\begin{array}{cc}\hfill Q_d& =W_q^d{F}_d,K_d=W_k^d\left[F_b;F_s\right],V_d=W_v^d{F}_s\hfill \\ \hfill Q_s& =W_q^s{F}_s,K_s=W_k^s\left[F_b;F_d\right],V_s=W_v^s{F}_d\hfill \end{array}\right.(4)$

Here, $F_d$ and $F_s$ denote deep features from the ViT branch and shallow features from the convolutional branch, respectively. $F_b$ represents bottleneck features shared across branches. $W_q$, $W_k$, and $W_v$ are learnable linear projection matrices used to obtain queries $(Q)$, keys $(K)$, and values $(V)$ for attention computation.

Step 3: Fuse features across branches using deformable attention, detailed in Equation 5:

$\left\{\begin{array}{cc}\hfill F_d^c& =\text{DeformAttn}\left(Q_d,K_d,V_d\right)\hfill \\ \hfill F_s^c& =\text{DeformAttn}\left(Q_s,K_s,V_s\right)\hfill \end{array}\right.(5)$

Here, $F_d^c$ and $F_s^c$ represent the cross-attended features refined via deformable attention in the ViT and convolutional branches, respectively. Deformable attention adaptively samples spatial locations, enabling the model to focus on semantically relevant regions. This mechanism facilitates more effective feature alignment across the two branches.

Figure 3

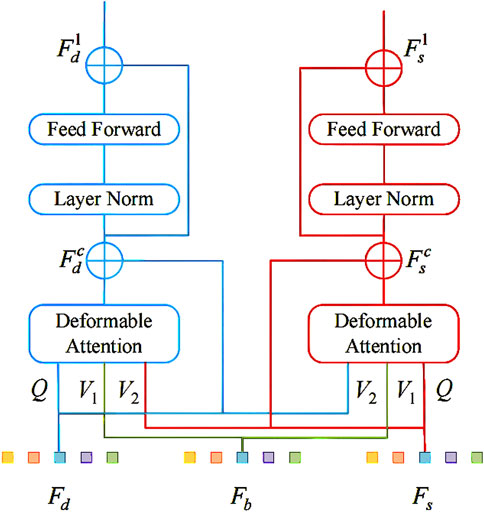
Figure 3. The Multi-branch Cross Attention Block for fusing ViT and convolutional features via cross-attention.

Step 4: Refine the fused features with residual feedforward networks (FFN) and layer normalization (LN)—this refinement is formalized in Equation 6:

$\left\{\begin{array}{cc}\hfill F_d^1& =\text{FFN}\left(\text{LN}\left(F_d+F_d^c\right)\right)+\left(F_d+F_d^c\right)\hfill \\ \hfill F_s^1& =\text{FFN}\left(\text{LN}\left(F_s+F_s^c\right)\right)+\left(F_s+F_s^c\right)\hfill \end{array}\right.(6)$

Here, $F_d^1$ and $F_s^1$ denote the updated deep and shallow features after refinement. The FFN enhances non-linear representation capacity, while LN improves training stability. The residual connection facilitates efficient information preservation and gradient flow.

2.3 ViT-Conv fusion block

A fusion block equipped with an automatic selection mechanism is constructed to integrate the diverse information provided by convolutional features and Transformer features. The architectural details of this module are illustrated in Figure 4.

Figure 4

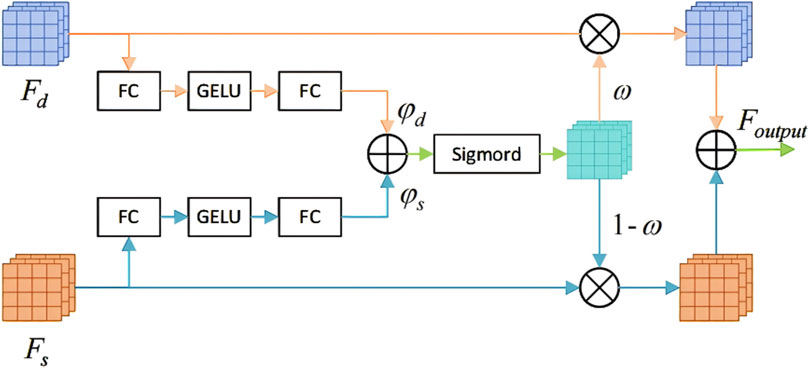
Figure 4. The ViT-Conv Fusion Block for adaptive integration of Transformer and convolutional features.

The ViT-Conv Fusion Block adaptively integrates convolutional and Transformer features through these steps:

Step 1: Process deep $(F_d)$ and shallow $(F_s)$ features individually with a channel attention layer to obtain logits $({\phi }_d,{\phi }_s)$. Channel attention highlights informative channels in each branch. This yields two attention logits representing the feature importance.

Step 2: Aggregate logits from both branches to compute an element- wise selection mask using a sigmoid function. Equation 7 defines this aggregation process.

$\omega =\text{Sigmoid}\left({\phi }_d+{\phi }_s\right)(7)$

Here, $\omega$ denotes the attention-based selection mask used to balance feature contributions from the two branches. The summed logits ${\phi }_d+{\phi }_s$ capture joint channel importance. The sigmoid function constrains the mask values between 0 and 1, enabling soft feature weighting.

Step 3: Compute the final fused output via element-wise multiplication, as specified in Equation 8:

$F_{\text{output}}=F_d^o\otimes \omega +F_s^o\otimes \left(1-\omega \right)(8)$

Here, $F_d^o$ and $F_s^o$ represent the output features from the Transformer and convolutional branches, respectively. $F_{\text{output}}$ denotes the final fused representation. The selection mask $\omega$ adaptively controls the contribution of each branch, enabling dynamic integration of global and local information.

2.4 Loss function

To supervise both the coarse and fine segmentation branches during training, a Progressive Dual-Branch Loss (PDB Loss) is proposed. This loss function dynamically adjusts the supervision weights between the coarse and fine predictions over training epochs. The total training loss is precisely defined by Equation 9:

${\mathcal{L}}_{\text{PDB}}=\frac{1}{B}{\displaystyle \sum _{i=1}^B}\left[\left(1-\alpha \right)\cdot {\mathcal{L}}_{\text{DiceCE}}\left({\widehat{y}}_{\text{coarse}}^{\left(i\right)},y^{\left(i\right)}\right)+\alpha \cdot {\mathcal{L}}_{\text{DiceCE}}\left({\widehat{y}}_{\text{fine}}^{\left(i\right)},y^{\left(i\right)}\right)\right](9)$

Here, ${\widehat{y}}_{\text{coarse}}^{(i)}$ and ${\widehat{y}}_{\text{fine}}^{(i)}$ are the predicted masks from the coarse and fine branches for the $i$-th sample, and $y^{(i)}$ is the corresponding ground truth. $B$ denotes the batch size. $\alpha \in [\mathrm{0,1}]$ is a progressive weight that determines the relative contribution of the fine branch.

For each prediction, a hybrid loss combining Dice and binary cross‑entropy (BCE) is used, aspresented in Equation 10:

${\mathcal{L}}_{\text{DiceCE}}\left(\widehat{y},y\right)={\lambda }_{\text{dice}}\cdot {\mathcal{L}}_{\text{Dice}}\left(\widehat{y},y\right)+{\lambda }_{\text{ce}}\cdot {\mathcal{L}}_{\text{CE}}\left(\widehat{y},y\right)(10)$

The loss weights were set as ${\lambda }_{\mathit{dice}}=0.8$ and ${\lambda }_{ce}=0.2$. To shift the learning focus from coarse to fine predictions over time, the coefficient $\alpha$ was scheduled according to the current epoch $t$ as given in Equation 11:

$\alpha =\min \left(\frac{t+1}{5},1.0\right)(11)$

This progressive weighting strategy encourages the model to learn global structural features in early epochs via the coarse branch and gradually refine local boundaries and details through the fine branch.

3 Experiments

In this section, a series of comprehensive experiments is performed to evaluate the effectiveness of the proposed HiImp-SMI on medical image segmentation tasks. Initially, the experimental setup is detailed, including dataset selection and training configurations. Subsequently, the performance of HiImp-SMI is quantitatively and qualitatively compared with state-of-the-art implicit and discrete segmentation approaches, specifically addressing binary polyp segmentation on the Kvasir-Sessile dataset [13] and multi-class organ segmentation on the BCV dataset [56]. Additionally, robustness analyses under various data distributions are presented. Finally, a systematic ablation study is conducted to elucidate the contributions of individual modules within HiImp-SMI.

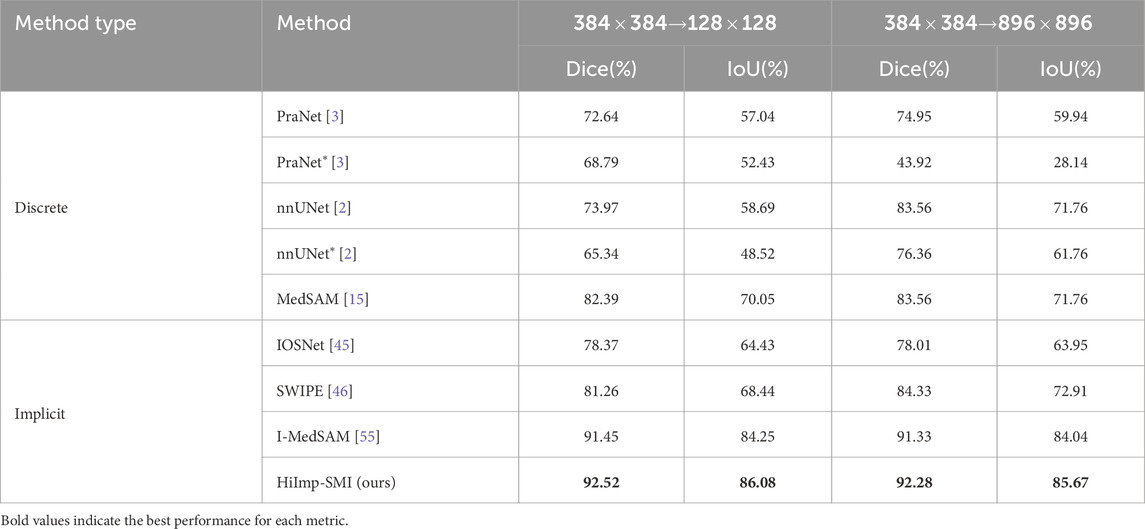
The quantitative comparison results are summarized in Table 1, highlighting mean Dice and IoU scores alongside corresponding standard deviations. The best-performing methods are emphasized in bold, illustrating that HiImp-SMI consistently achieves superior segmentation performance compared to existing state-of-the-art methods.

Table 1

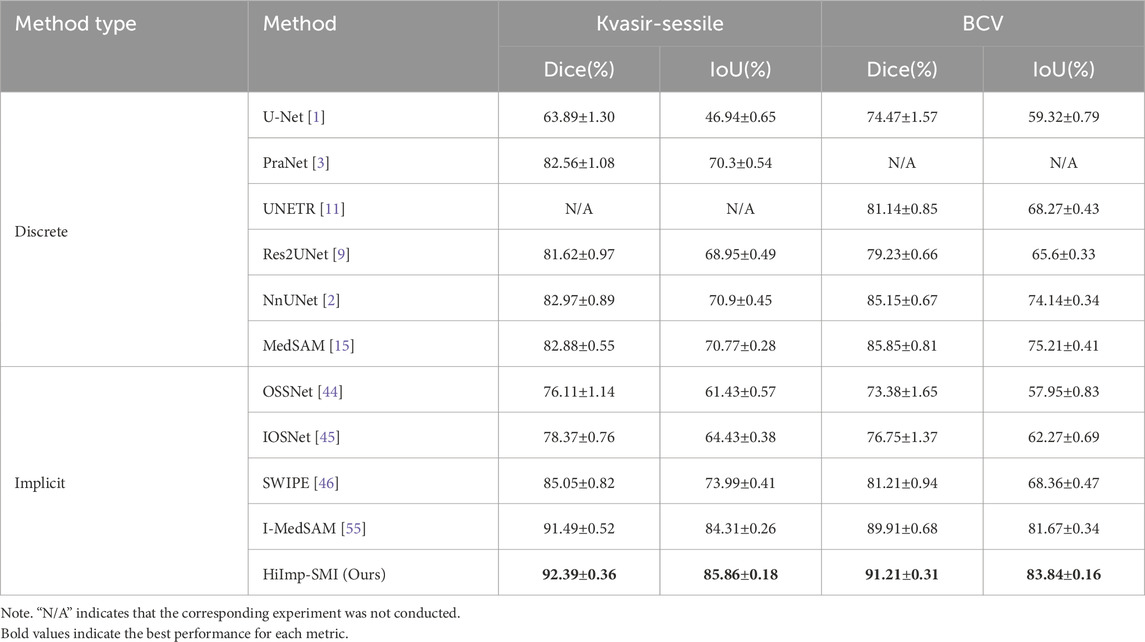
Table 1. Overall segmentation results compared to state-of-the-art discrete and implicit methods. The last two columns present the mean Dice and IoU scores with standard deviation. The best results are highlighted in bold.

3.1 Experimental setup

The model’s performance is evaluated on two distinct medical image segmentation tasks: binary polyp segmentation and multi-class abdominal organ segmentation.

For polyp segmentation, experiments are conducted on the challenging Kvasir-Sessile dataset [13], which contains 196 RGB images of small sessile polyps. To assess the generalization capability of HiImp-SMI, the pretrained model is further evaluated on the CVC-ClinicDB dataset [13], which consists of 612 images extracted from 31 colonoscopy sequences.

For multi-organ segmentation, the model is trained on the BCV dataset [56], which includes 30 CT scans with annotations for 13 organs, and is further evaluated on the AMOS dataset [57], which contains 200 CT training samples, following the same experimental setup as [22]. Since this study focuses on 2D medical image segmentation, slice-wise segmentation is performed on CT images. Following the data preprocessing strategy of SWIPE [46], all datasets are split into training, validation, and test sets in a 6:2:2 ratio, and the reported Dice scores are based on test set results.

The training process involves fine-tuning the SAM encoder [7] with ViT-B as the backbone network. The LoRA rank is set to 4, with amplitude information incorporated in the frequency adapter. The MLP dimensions for the implicit segmentation decoder are [1,024, 512] for Decc and [512, 256, 256, 128] for Decf. During training, 12.5% of the most uncertain points are sampled for refinement, and the dropout probability is set to 0.5. For the multi-organ segmentation task, the final layer of Decc and Decf is adjusted to match the number of target segmentation classes. HiImp-SMI is optimized using AdamW [58] with $\alpha =0.5,\beta =0.1$, a learning rate of ${\lambda }_{\mathit{ada}}=5\times 10^{-5}$ for the encoder adapter, and ${\lambda }_{\mathit{dec}}=1\times 10^{-3}$ for the decoder.

To ensure fair comparison, all methods are trained for 1,000 epochs under the same experimental setup. During testing, Dice scores and Hausdorff distances [6] are reported based on the best validation epoch. The input image resolutions are set to $384\times 384$ (Sessile dataset) and $512\times 512$ (BCV dataset slices).

The baseline approaches are categorized into discrete methods and implicit (continuous) methods. The discrete methods include U-Net [1], PraNet [3], Res2UNet [9], nnUNet [2], UNETR [11], and MedSAM [15]. Among these, MedSAM [15] is also a SAM-based approach, where the original decoder is directly fine-tuned. The implicit methods include OSSNet [44], IOSNet [45], and SWIPE [46] and I-MedSAM [55].

3.2 Quantitative comparison

A Dice score comparison is first presented against baseline methods. Subsequently, experiments are conducted across different resolutions and domains to evaluate the model’s cross-domain generalization ability under data distribution shifts. Finally, Hausdorff Distance (HD) [6] is computed to compare the segmentation boundary quality across different experimental settings.

Discrete methods and implicit methods are compared in terms of trainable parameters and Dice scores (including standard deviation). Specifically, binary segmentation is performed on the Kvasir-Sessile dataset, while multi-class segmentation is conducted on the CT BCV dataset, with results detailed in Table 2. Leveraging the proposed frequency adapter, SAM generates richer feature representations, leading to improved segmentation boundary quality. In contrast, SwIPE, which employs Res2Net-50 [9] as its backbone, exhibits weaker feature extraction capability, resulting in lower segmentation quality.

Table 2

Table 2. Cross-resolution evaluation from $384\times 384$ to $128\times 128$ and from $384\times 384$ to $896\times 896.$

The adaptability of binary polyp segmentation across different resolutions and domains is assessed by comparing it with the best-performing discrete and implicit methods. To adapt to different target resolutions (e.g., low resolution $128\times 128$ and high resolution $896\times 896$), the pretrained HiImp-SMI model, initially trained at $384\times 384$ standard resolution, is modified by scaling the input coordinates to match the target resolution, and the corresponding Dice scores are computed. For discrete methods, the output resolution remains consistent with the input resolution. Input images at the original resolution of $384\times 384$ are provided, and the generated segmentation results are rescaled to the target resolution for evaluation. Additionally, the suffix (*) is used to mark discrete baselines, where the original medical images are resized to the target resolution before being fed into the models, allowing these methods to directly generate segmentation results at the target resolution.

As shown in Table 2, implicit methods exhibit stronger adaptability to spatial resolution changes and consistently outperform discrete methods. Among implicit methods, HiImp-SMI achieves the highest performance across different output resolutions, which can be attributed to the proposed frequency adapter, enhancing HiImp-SMI’s predictive capability across resolutions.

Model performance across different datasets is examined. In binary polyp segmentation, all methods are pretrained on the Kvasir-Sessile dataset and directly evaluated on the CVC dataset. Similarly, in multi-class abdominal organ segmentation, all methods are pretrained on the BCV dataset and evaluated on the AMOS dataset, focusing exclusively on the liver class.

As shown in Table 3, leveraging SAM’s generalization ability, HiImp-SMI outperforms the best discrete method, achieving Dice scores of 91.58% on the CVC dataset and 88.17% on the AMOS dataset.

Table 3

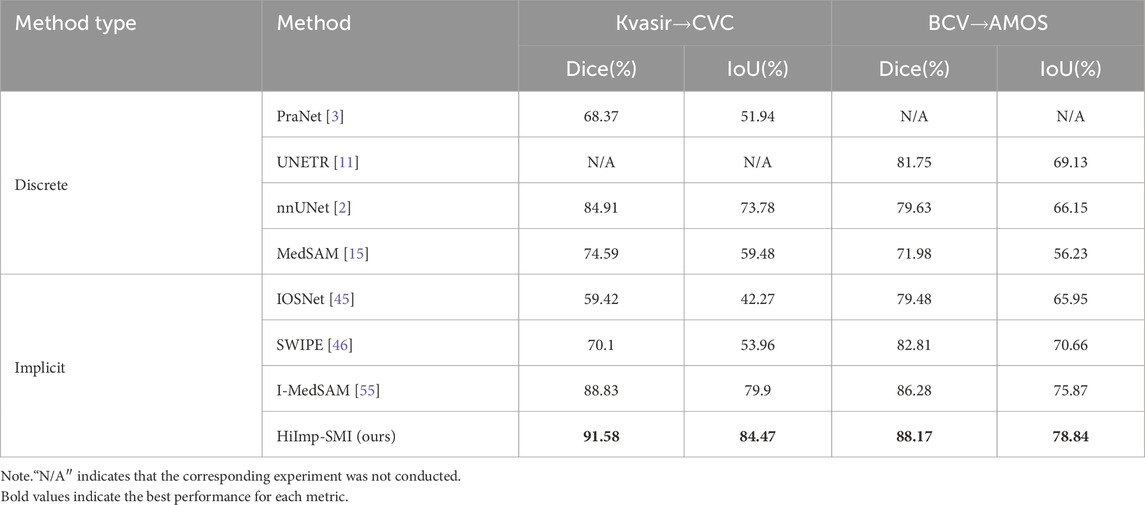
Table 3. Cross-domain results for binary polyp segmentation and multi-class abdominal organ segmentation.

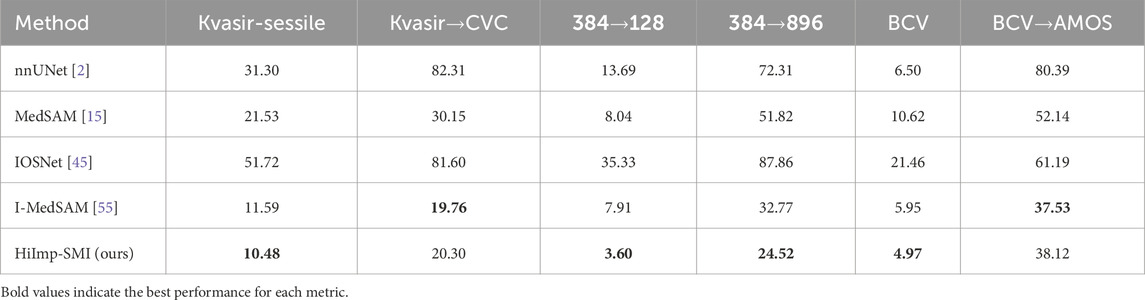
Segmentation boundary quality is further assessed using Hausdorff Distance (HD) [19]. As shown in Table 4, HiImp-SMI achieves lower HD scores, indicating superior boundary precision compared to existing methods.

Table 4

Table 4. HD distance $(\downarrow )$ for different methods and datasets.

3.3 Qualitative comparison

As shown in Figure 5, a qualitative comparison is conducted on the Kvasir-Sessile dataset. Additionally, the input medical images and their corresponding ground truth segmentation masks are provided, where segmentation boundaries are highlighted in green in Figure 5. The sharpness of boundaries in the visual results may be attributed in part to the frequency-domain information introduced via FFT.

Figure 5

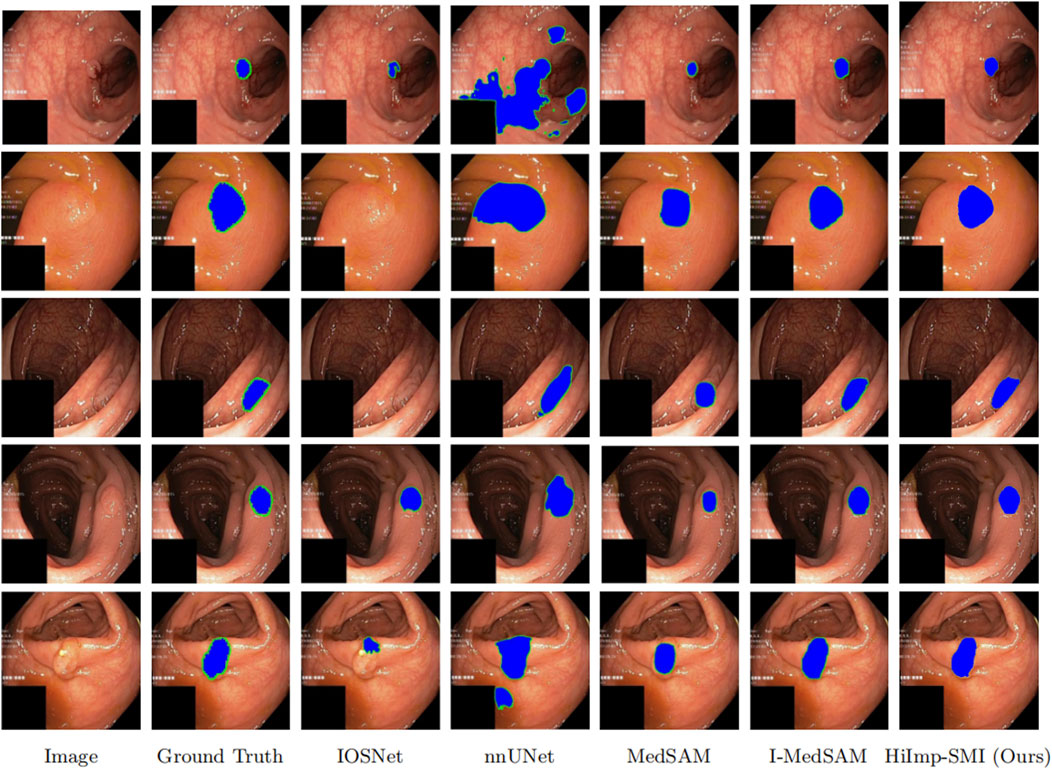
Figure 5. Qualitative comparisons on five representative samples. The last row indicates the method names corresponding to each column.

From the results, it is evident that HiImp-SMI produces more precise segmentation boundaries. By leveraging the proposed modules, HiImp-SMI effectively aggregates high-frequency information from the input, leading to improved segmentation accuracy in the final output.

3.4 Ablation study

An ablation study is conducted to evaluate the effectiveness of each module within the high-frequency adapter. The results are summarized in Table 5.

Table 5

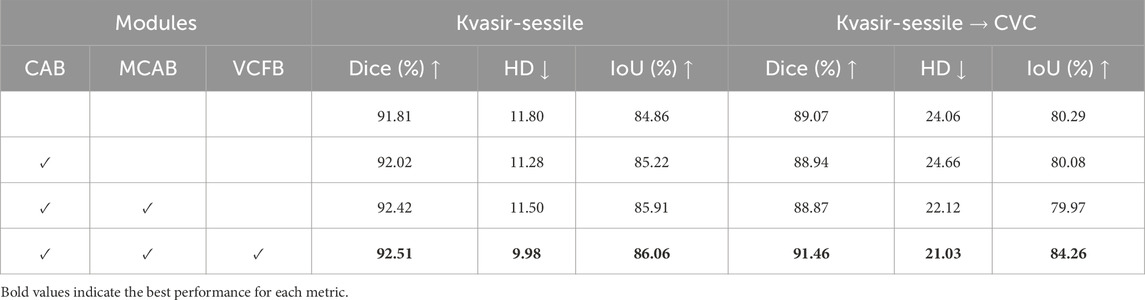
Table 5. Ablation study on the integration of different modules: Channel Attention Block (CAB), Multi-branch Cross Attention Block (MCAB), and ViT-Conv Fusion Block (VCFB). Evaluation is conducted on the Kvasir-Sessile dataset and its cross-domain transfer to the CVC dataset.

In the baseline model, the single frequency adapter module consists of a linear down-projection layer, a GELU activation function, and a linear up-projection layer. On the Kvasir-Sessile dataset [8], the baseline model achieves a Dice score of 91.81% and an HD of 11.80. When transferred to the CVC dataset, the Dice score drops to 89.07%, with an HD of 24.06.

As the channel attention block, bi-directional cross-attention block, and ViT-Conv fusion block are incrementally added, model performance exhibits a significant improvement. When all three modules are incorporated, the Dice score on the Kvasir-Sessile dataset improves to 92.51%, while HD decreases to 9.98. Similarly, on the CVC dataset, the Dice score improves to 91.46%, and HD decreases to 21.03, highlighting the necessity and effectiveness of the proposed modules.

4 Conclusion

In this study, a novel implicit Transformer-based framework, HiImp-SMI, was proposed to overcome key limitations in medical image segmentation, such as poor boundary refinement, weak feature fusion, and limited cross-domain generalization. High-frequency information and multi-scale features were incorporated through three main components: a Channel Attention Block for frequency-domain feature adaptation, a Multi-Branch Cross Attention Block for hierarchical feature exchange, and a ViT-Conv Fusion Block for adaptive context integration. Additionally, a Progressive Dual-Branch Loss was introduced to guide the training process from coarse to fine segmentation. Extensive experiments conducted on the Kvasir-Sessile and BCV datasets demonstrated that HiImp-SMI consistently outperformed state-of-the-art methods, particularly in cross-domain and cross-resolution tasks. Ablation studies further confirmed the effectiveness of each proposed module.

However, the current framework has not yet been validated in clinical or multi-center settings. Future research will aim to evaluate its applicability in real-world clinical workflows.

Overall, HiImp-SMI provided a unified and adaptive solution for precise and generalizable medical image segmentation.

Data availability statement

Publicly available datasets were analyzed in this study. This data can be found here: Kvasir-Sessile Dataset: https://datasets.simula.no/kvasir/ Repository: Simula Research Laboratory Accession Number: Not applicable (open access dataset) CVC-ClinicDB: https://github.com/CVC-ClinicDB Repository: GitHub Accession Number: Not applicableBCV (Beyond Cranial Vault) Dataset: https://www.synapse.org/#!Synapse:syn3193805 Repository: Synapse Accession Number: syn3193805AMOS Dataset: https://amos22.grand-challenge.org/ Repository: Grand Challenge Accession Number: Not applicable.

Author contributions

LH: Conceptualization, Methodology, Validation, Writing – original draft, Supervision, Writing – review and editing, Data curation. FP: Supervision, Writing – review and editing. BH: Data curation, Writing – review and editing, Investigation. YC: Supervision, Writing – review and editing, Methodology, Project administration.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. This work was supported by the Liaoning Provincial Science and Technology Plan Joint Project (Grant No. 2024-MSLH-033).

Acknowledgments

Many thanks to Yinghong Cao and Feng Peng for their help in achieving this work.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Ronneberger O, Fischer P, Brox T. U-net: convolutional networks for biomedical image segmentation. In: N Navab, J Hornegger, WM Wells, and AF Frangi, editors. Proceedings of the 18th International Conference on Medical Image Computing and Computer-Assisted Intervention (MICCAI 2015), 9351. Cham, Switzerland: Springer (2015). p. 234–41. doi:10.1007/978-3-319-24574-4_28

CrossRef Full Text | Google Scholar

2. Isensee F, Jäger PF, Kohl SAA, Petersen J, Maier-Hein KH. Automated design of deep learning methods for biomedical image segmentation. arXiv preprint arXiv:1904 (2019):08128. doi:10.48550/arXiv.1904.08128

CrossRef Full Text | Google Scholar

3. Fan DP, Ji GP, Zhou T, Chen G, Fu H, Shen J, et al. Pranet: parallel reverse attention network for polyp segmentation. In: Proceedings of the 23rd International Conference on Medical Image Computing and Computer-Assisted Intervention (MICCAI 2020), 12266. Cham, Switzerland: Springer (2020). p. 263–73. doi:10.1007/978-3-030-59725-2_26Lecture Notes in Computer Sci

CrossRef Full Text | Google Scholar

4. Alahmadi MD. Boundary aware u-net for medical image segmentation. Arabian J Sci Eng (2023) 48:9929–40. doi:10.1007/s13369-022-07431-y

CrossRef Full Text | Google Scholar

5. Bernal J, Sánchez FJ, Fernández-Esparrach G, Gil D, Rodríguez C, Vilariño F. Wm-dova maps for accurate polyp highlighting in colonoscopy: validation vs. saliency maps from physicians. Comput Med Imaging Graphics (2015) 43:99–111. doi:10.1016/j.compmedimag.2015.02.007

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Huttenlocher DP, Klanderman GA, Rucklidge WJ. Comparing images using the hausdorff distance. IEEE Trans Pattern Anal Machine Intelligence (1993) 15:850–63. doi:10.1109/34.232073

CrossRef Full Text | Google Scholar

7. Gal Y, Ghahramani Z. Dropout as a bayesian approximation: representing model uncertainty in deep learning. In: MF Balcan, and KQ Weinberger, editors. Proceedings of the 33rd international conference on machine learning, New York, NY, USA: PMLR (2016). p. 48. 1050–9.Proc Machine Learn Res

Google Scholar

8. Guo C, Pleiss G, Sun Y, Weinberger KQ. On calibration of modern neural networks. In: D Precup, and YW Teh, editors. Proceedings of the 34th international conference on machine learning, Sydney, Australia: PMLR (2017). p. 1321–30.Proc Machine Learn Res

Google Scholar

9. Gao SH, Cheng MM, Zhao K, Zhang XY, Yang MH, Torr P. Res2net: a new multi-scale backbone architecture. IEEE Trans Pattern Anal Machine Intelligence (2021) 43:652–62. doi:10.1109/TPAMI.2019.2938758

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Chen J, Mei J, Li X, Lu Y, Yu Q, Wei Q, et al. Transunet: rethinking the u-net architecture design for medical image segmentation through the lens of transformers. Med Image Anal (2024) 84:103280. doi:10.1016/j.media.2024.103280

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Hatamizadeh A, Tang Y, Nath V, Yang D, Myronenko A, Landman B, et al. UNETR: transformers for 3D medical image segmentation. In: Proceedings of the IEEE/CVF winter Conference on Applications of computer vision (WACV) (waikoloa, HI, USA: ieee) (2022). p. 574–84. doi:10.1109/WACV51458.2022.00181

CrossRef Full Text | Google Scholar

12. Vaswani A, Shazeer N, Parmar N, Uszkoreit J, Jones L, Gomez AN, et al. Attention is all you need. Adv in Neural Inf Process Syst (2017). p. 5998–6008.

Google Scholar

13. Hu EJ, Shen Y, Wallis P, Allen-Zhu Z, Li Y, Wang S, et al. LoRA: low-rank adaptation of large language models. In: Proceedings of the international conference on learning representations (ICLR). Virtual Event: OpenReview.netAvailable online at: https://openreview.net/forum?id=nZeVKeeFYf9 (2022).

Google Scholar

14. Kirillov A, Mintun E, Ravi N, Mao H, Rolland C, Gustafson L, et al. Segment anything. In: Proceedings of the IEEE/CVF international Conference on computer vision (ICCV) (paris, France: ieee) (2023). p. 4015–26. doi:10.1109/ICCV51070.2023.00371

CrossRef Full Text | Google Scholar

15. Ma J, He Y, Li F, Han L, You C, Wang B. Segment anything in medical images. Nat Commun (2024) 15:654. doi:10.1038/s41467-024-44824-z

PubMed Abstract | CrossRef Full Text | Google Scholar

16. McGinnis J, Shit S, Li HB, Sideri-Lampretsa V, Graf R, Dannecker M, et al. Single-subject multi-contrast MRI super-resolution via implicit neural representations, Med Image Comput Computer Assisted Intervention – MICCAI 2023. (2023). 14230. 173–83. doi:10.1007/978-3-031-43993-3_17

CrossRef Full Text | Google Scholar

17. Wu J, Wang Z, Hong M, Ji W, Fu H, Liu Y, et al. Segment anything model for medical image analysis: an experimental study. Med Image Anal (2023) 89:102918. doi:10.1016/j.media.2023.102918

CrossRef Full Text | Google Scholar

18. Wei X, Zhang R, Wu J, Liu J, Lu M, Guo Y, et al. NTO3D: neural target object 3d reconstruction with segment anything. In: Proceedings of the IEEE/CVF conference on computer vision and pattern recognition (CVPR). Seattle, WA, USA: IEEE (2024). p. 20352–62. doi:10.1109/CVPR52733.2024.01924

CrossRef Full Text | Google Scholar

19. Zhang K, Liu D. Customized segment anything model for medical image segmentation. arXiv preprint arXiv:2304.13785 (2023).

Google Scholar

20. Cheng J, Ye J, Deng Z, Chen J, Li T, Wang H, et al. SAM-Med2D. arXiv preprint arXiv:2308.16184 (2023). doi:10.48550/arXiv.2308.16184

CrossRef Full Text | Google Scholar

21. Bui NT, Hoang DH, Tran MT, Doretto G, Adjeroh D, Patel B, et al. SAM3D: segment anything model in volumetric medical images. arXiv preprint arXiv:2309.03493 (2023). doi:10.48550/arXiv.2309.03493

CrossRef Full Text | Google Scholar

22. Zhang Y, Sapkota N, Gu P, Peng Y, Zheng H, Chen DZ. Keep your friends close and enemies farther: debiasing contrastive learning with spatial priors in 3d radiology images. In: Proceedings of the 2022 IEEE international Conference on Bioinformatics and biomedicine (BIBM) Las Vegas, NV, USA: (IEEE) (2022). p. 1824–9. doi:10.1109/BIBM55620.2022.9995481

CrossRef Full Text | Google Scholar

23. Shi H, Han S, Huang S, Liao Y, Li G, Kong X, et al. Mask-enhanced segment anything model for tumor lesion semantic segmentation. In: Proceedings of the international conference on medical image computing and computer-assisted intervention (MICCAI 2024) (2024). p. 403–13. doi:10.1007/978-3-031-72111-3_38

CrossRef Full Text | Google Scholar

24. Wang X, Mou J, Cao Y, Jahanshahi H. Modeling and analysis of cellular neural networks based on memcapacitor. Int J Bifurcation Chaos (2025) 35. doi:10.1142/S0218127425300101

CrossRef Full Text | Google Scholar

25. Cao H, Cao Y, Lei Q, Mou J. Dynamical analysis, multi-cavity control and dsp implementation of a novel memristive autapse neuron model emulating brain behaviors. Chaos, Solitons and Fractals (2025) 191:115857. doi:10.1016/j.chaos.2024.115857

CrossRef Full Text | Google Scholar

26. Ma Y, Mou J, Jahanshahi H, Alkhateeb AF, Bi X. Design and dsp implementation of a hyperchaotic map with infinite coexisting attractors and intermittent chaos based on a novel locally active memcapacitor. Chaos, Solitons and Fractals (2023) 173:113708. doi:10.1016/j.chaos.2023.113708

CrossRef Full Text | Google Scholar

27. Chen Y, Cao Y, Mou J, Sun B, Banerjee S. A simple photosensitive circuit based on a mutator for emulating memristor, memcapacitor, and meminductor: light illumination effects on dynamical behaviors. Int J Bifurcation Chaos (2024) 34:2450069. doi:10.1142/S021812742450069X

CrossRef Full Text | Google Scholar

28. Yuan Y, Yu F, Tan B, Huang Y, Yao W, Cai S, et al. A class of n-d Hamiltonian conservative chaotic systems with three-terminal memristor: modeling, dynamical analysis, and fpga implementation. Chaos (2025) 35:013121. doi:10.1063/5.0238893

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Yu F, Su D, He S, Wu Y, Zhang S, Yin H. Resonant tunneling diode cellular neural network with memristor coupling and its application in police forensic digital image protection. Chin Phys B (2025) 34:050502. doi:10.1088/1674-1056/adb8bb

CrossRef Full Text | Google Scholar

30. Yu F, He S, Yao W, Cai S, Xu Q. Quantitative characterization system for macroecosystem attributes and states. IEEE Trans Computer-Aided Des Integrated Circuits Syst (2025) 36:1–12. doi:10.13287/j.1001-9332.202501.031

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Han Z, Cao Y, Banerjee S, Mou J. Hybrid image encryption scheme based on hyperchaotic map with spherical attractors. Chin Phys B (2025) 34:030503. doi:10.1088/1674-1056/ada7db

CrossRef Full Text | Google Scholar

32. Liu Z, Li P, Cao Y, Mou J. A novel multimodal joint information encryption scheme based on multi-level confusion and hyperchaotic map. Int J Mod Phys C (2025). doi:10.1142/S012918312550038X

CrossRef Full Text | Google Scholar

33. Zhou S, Yin Y, Erkan U, Toktaş A, Zhang Y. Novel hyperchaotic system: implementation to audio encryption. Chaos, Solitons and Fractals (2025) 193:116088. doi:10.1016/j.chaos.2025.116088

CrossRef Full Text | Google Scholar

34. Yu F, Zhang S, Su D, Wu Y, Gracia YM, Yin H. Dynamic analysis and implementation of fpga for a new 4d fractional-order memristive hopfield neural network. Fractal and Fractional (2025) 9:115. doi:10.3390/fractalfract9020115

CrossRef Full Text | Google Scholar

35. Mou J, Zhang Z, Zhou N, Zhang Y, Cao Y. Mosaic tracking: lightweight batch video frame awareness multi-target encryption scheme based on a novel discrete tabu learning neuron and yolov5. IEEE Internet Things J (2024) 12:4038–49. doi:10.1109/JIOT.2024.3482289

CrossRef Full Text | Google Scholar

36. Mou J, Tan L, Cao Y, Zhou N, Zhou Y. Multi-face image compression encryption scheme combining extraction with stp-cs for face database. IEEE Internet Things J (2025) 12:19522–31. doi:10.1109/JIOT.2025.3541228

CrossRef Full Text | Google Scholar

37. Mou J, Zhang Z, Banerjee S, Zhang Y. Combining semi-tensor product compressed sensing and session keys for low-cost encryption of batch information in wbans. IEEE Internet Things J (2024) 11:33565–76. doi:10.1109/jiot.2024.3429349

CrossRef Full Text | Google Scholar

38. Zhou S, Liu H, Iu HHC, Erkan U, Toktas A. Novel n-dimensional nondegenerate discrete hyperchaotic map with any desired lyapunov exponents. IEEE Internet Things J (2025) 12:9082–90. doi:10.1109/JIOT.2025.3541229

CrossRef Full Text | Google Scholar

39. Shi F, Cao Y, Xu X, Mou J. A novel memristor-coupled discrete neural network with multi-stability and multiple state transitions. Eur Phys J Spec Top (2025). doi:10.1140/epjs/s11734-024-01440-8

CrossRef Full Text | Google Scholar

40. Zhang Z, Cao Y, Zhou N, Xu X, Mou J. Novel discrete initial-boosted tabu learning neuron: dynamical analysis, dsp implementation, and batch medical image encryption. Appl Intelligence (2025) 55:61. doi:10.1007/s10489-024-05918-9

CrossRef Full Text | Google Scholar

41. Ma T, Mou J, Banerjee S, Cao Y. Analysis of the functional behavior of fractional-order discrete neuron under electromagnetic radiation. Chaos, Solitons and Fractals (2023) 176:114113. doi:10.1016/j.chaos.2023.114113

CrossRef Full Text | Google Scholar

42. Mou J, Cao H, Zhou N, Cao Y. A fhn-hr neuron network coupled with a novel locally active memristor and its dsp implementation. IEEE Trans Cybernetics (2024) 54:7333–42. doi:10.1109/TCYB.2024.3471644

PubMed Abstract | CrossRef Full Text | Google Scholar

43. Zhang Z, Mou J, Zhou N, Banerjee S, Cao Y. Multi-cube encryption scheme for multi-type images based on modified klotski game and hyperchaotic map. Nonlinear Dyn (2024) 112:5727–47. doi:10.1007/s11071-024-09292-6

CrossRef Full Text | Google Scholar

44. Reich C, Prangemeier T, Cetin Ö, Koeppl H. Oss-net: memory efficient high resolution semantic segmentation of 3d medical data. In: Proceedings of the British machine vision conference (BMVC) (2021). p. 429.

Google Scholar

45. Khan MO, Fang Y. Implicit neural representations for medical imaging segmentation. Medical image computing and computer assisted intervention – MICCAI 2022 springer. Lecture Notes in Computer Sci (2022) 13431:433–43. doi:10.1007/978-3-031-16443-9_42

CrossRef Full Text | Google Scholar

46. Zhang Y, Gu P, Sapkota N, Chen DZ. SwIPE: efficient and robust medical image segmentation with implicit patch embeddings. In: Medical image computing and computer-assisted intervention – MICCAI 2023. Springer Nature Switzerland (2023). p. 315–26. doi:10.1007/978-3-031-43904-9_31

CrossRef Full Text | Google Scholar

47. Mildenhall B, Srinivasan PP, Tancik M, Barron JT, Ramamoorthi R, Ng R. Nerf: representing scenes as neural radiance fields for view synthesis. Commun ACM (2022) 65:99–106. doi:10.1145/3503250

CrossRef Full Text | Google Scholar

48. Sørensen K, Camara O, Backer OD, Kofoed KF, Paulsen RR. NUDF: neural unsigned distance fields for high resolution 3d medical image segmentation. In: Proceedings of the 19th IEEE international symposium on biomedical imaging (ISBI) (2022). p. 1–5. doi:10.1109/ISBI52829.2022.9761610

CrossRef Full Text | Google Scholar

49. Stolt-Ansó N, McGinnis J, Pan J, Hammernik K, Rueckert D. Nisf: neural implicit segmentation functions. In: Medical Image Computing and Computer-Assisted Intervention – MICCAI 2023, 14231. Vancouver, BC, Canada: Springer (2023). p. 734–44. doi:10.1007/978-3-031-43901-8_70

CrossRef Full Text | Google Scholar

50. Yang J, Wickramasinghe U, Ni B, Fua P. Implicitatlas: learning deformable shape templates in medical imaging. In: Proceedings of the IEEE/CVF Conference on computer Vision and pattern recognition (CVPR) (new Orleans, LA, USA: IEEE) (2022). p. 15861–71.

Google Scholar

51. Molaei A, Aminimehr A, Tavakoli A, Kazerouni A, Azad B, Azad R, et al. Implicit neural representation in medical imaging: a comparative survey. In: Proceedings of the IEEE/CVF international Conference on computer vision workshops (ICCVW) (paris, France: IEEE) (2023). p. 2381–91. doi:10.1109/ICCVW60793.2023.00252

CrossRef Full Text | Google Scholar

52. Amiranashvili T, Lüdke D, Li HB, Menze B, Zachow S. Learning shape reconstruction from sparse measurements with neural implicit functions. In: Proceedings of the 5th international Conference on medical Imaging with deep learning (MIDL) (Zürich, Switzerland: PMLR), 172 (2022). p. 22–34.

Google Scholar

53. Chibane J, Alldieck T, Pons-Moll G. Implicit functions in feature space for 3d shape reconstruction and completion. In: Proceedings of the IEEE/CVF conference on computer vision and pattern recognition (CVPR). Seattle, WA, USA: IEEE (2020). p. 6968–79. doi:10.1109/CVPR42600.2020.00698

CrossRef Full Text | Google Scholar

54. Bui NT, Hoang DH, Tran MT, Doretto G, Adjeroh D, Patel B, et al. Sam3d: segment anything model in volumetric medical images. In: Proceedings of the 2024 IEEE International Symposium on Biomedical Imaging (ISBI). Athens, Greece: IEEE (2024). p. 1–4.

CrossRef Full Text | Google Scholar

55. Wei X, Cao J, Jin Y, Lu M, Wang G, Zhang S. I-medsam: implicit medical image segmentation with segment anything. In: Proceedings of the European Conference on computer vision (ECCV) (Milan, Italy: Springer, 15068 (2024). p. 90–107. doi:10.1007/978-3-031-72684-2_6

CrossRef Full Text | Google Scholar

56. Landman B, Xu Z, Iglesias J, Styner M, Langerak T, Klein A. Miccai multi-atlas labeling beyond the cranial vault—workshop and challenge. Proc MICCAI Multi-Atlas Labeling Beyond Cranial Vault—Workshop Challenge (Munich, Germany) (2015) 5:12.

Google Scholar

57. Ji Y, Bai H, Yang J, Ge C, Zhu Y, Zhang R, et al. Amos: a large-scale abdominal multi-organ benchmark for versatile medical image segmentation. Adv in Neural Inf Process Syst (2022) 35:36722–32.

Google Scholar

58. Loshchilov I, Hutter F. Decoupled weight decay regularization. In: Proceedings of the 7th international Conference on learning representations (ICLR) (New Orleans, LA, USA) (2019).

Google Scholar