Megapixel X-ray ghost imaging with a prior-recorded reference

Introduction: Efficient implementation of X-ray ghost imaging (XGI) with megapixel-level field-of-view and spatial resolution of few microns is key towards practical applications of XGI, but such implementation remains constrained by the time-consuming data acquisition and low-quality reconstruction for megapixel images under insufficient overall sampling rates.

Methods: We propose an efficient implementation scheme based on synthetic aperture X-ray ghost imaging (SAXGI), in which only one set of prior-recorded reference images is needed for ghost imaging of multiple objects.

Results: Experimental results demonstrated that images of three different objects, including tungsten fiber, resolution chart and small fish, can be successfully reconstructed with the same set of prior-recorded references, which implicates that the efficiency of data acquisition can be improved significantly. Taking advantage of SAXGI, image size of 2040 × 1440 pixels and system resolution of 10 μm was achieved. Results of a small fish show that comparable image quality is achieved with a sampling rate of 27.6%, which means that the radiation dose is reduced to about 1/4 of a conventional radiography. Furthermore, an extreme sampling rate down to 0.5% is enough to make out the skeleton of the fish, which further demonstrates high robustness and the low-dose potential of the proposed method for X-ray imaging.

Conclusions: In conclusion, the proposed method with a prior-recorded reference is applicable for XGI of multiple samples and the data acquisition efficiency is greatly improved. Through further hardware improvement of the imaging system, SAXGI with a prior-recorded reference is anticipated to provide an efficient solution for megapixel X-ray ghost imaging.

1 Introduction

X-ray ghost imaging (XGI), known as a non-local imaging method, is promising in simultaneously attaining high resolution and large field-of-view (FOV) with radiation dose lower than that of conventional radiology, which is a pivotal aim among research fields including biomedicine [1], material science [2], brain connectomics [3], etc. In a typical setup of the optical path for ghost imaging [4], a randomly intensity-modulated light beam is split into two identical beams, serving as illumination beams for the object and reference arms respectively. The light beam traversing the object arm is directed through the object into a bucket detector devoid of spatial resolution, while the beam in the reference arm propagates an equivalent distance, directly illuminating a planar detector capable of spatial resolution. The reconstructed image, through the correlation between the object and reference signals, resolves the resolution-FOV dichotomy inherent in local imaging, thereby facilitating the possibility of imaging that compromises neither resolution nor FOV with no substantial demand for full sampling dose as that of conventional radiology.

With the ongoing advancements in high-performance X-ray source capabilities, new methodology in X-ray imaging [5–12] and diversified methods for X-ray ghost imaging have been developed in past few decades [13–22]. With respect to experimental setup for ghost imaging, three strategies prevail in X-ray regime: actual beam-splitting strategy, “virtual” or equivalent beam-splitting strategy, and computational strategy [23]. XGI via the actual beam-splitting strategy, as it is, has two distinctive beams at any given time during the experiments to acquire object and reference signals [24–30]. Such strategy is intuitive in consistence with the typical setup and has the potential of dynamic X-ray ghost imaging. However, its validity is established when the two distinctive beams have truly identical intensity distributions, which is often not the case as expected [31]. Virtual beam-splitting strategy bypasses this problem by assuming that a single beam at distinctive moments can be considered as identical “beams” [32–37]. XGI via virtual beam-splitting strategy records object and reference signals at different moments, with the object being moved into and out of the optical path repeatedly, and such strategy suffers from time-inefficiency and low precision in mechanical alignment. Computational XGI abolishes the experimental recording of the reference signals to achieve efficient data acquisition by applying known masks as the light field modulator [38–43]. However, accurate calibration of X-ray masks is constrained by technical limitations, which makes it arduous to implement megapixel XGI via computational strategy.

We aim to achieve timely efficient while readily available X-ray ghost imaging with megapixel FOV and micron-level resolution at relatively low radiation cost, which is yet impractical through computational strategy due to the limitation of accurate mask calibration, and inefficient via virtual beam-splitting strategy in its repeated acquisition of reference signals for different objects. Here we propose an efficient XGI implementation scheme as a compromise between computational strategy and virtual beam-splitting strategy, which only requires recording high-resolution images in the reference arm once to achieve megapixel imaging of multiple objects. In this way, efficient data acquisition for megapixel XGI is achieved with readily available masks. Firstly, we introduces principles of the implementation scheme, which is based on synthetic aperture X-ray ghost imaging (SAXGI) [44] to achieve megapixel imaging with less measurement. Three types of objects are employed to evaluate the effectiveness of the proposed method for ghost imaging of multiple objects with the same set of prior-recorded references. Finally, conclusion and related discussion are brought out.

2 Principle and method

2.1 SAXGI with prior-recorded reference

Basic experimental setup for ghost imaging consists of two light paths: the object arm and the reference arm, incorporating a bucket detector $S$ in the object arm and an array detector $R$ in the reference arm. In the scenario of synthetic aperture ghost imaging, an array of bucket detectors is utilized in the object arm, while a high-resolution array detector is employed in the reference arm. The pixel size of bucket detector arrays is significantly larger than that of the high-resolution detector in the reference arm. This allows FOV to be unrestricted by the high-resolution detector and, since image reconstruction for SAXGI is based on the pixel units of the bucket detectors, total number of pixels in the imaging FOV is, in principle, unlimited. The area of the pixel units in the bucket detector array is much smaller than the total FOV, enabling high-quality ghost imaging reconstruction with far fewer number of measurements than required by conventional ghost imaging methods. This facilitates the achievement of high-resolution, large FOV, and low-dose X-ray imaging simultaneously.

Let the bucket detector array used on the object arm be denoted as $S={\left\{S^{\left(p,q\right)}\right\}}_{P,Q}$, where each bucket detector $S^{\left(p,q\right)}$ corresponds to the same spatial position as one specific sub-array detector on the reference arm. Accordingly, the sub-array detector on the reference arm can be represented as $R^{\left(p,q\right)}={\left\{R^{\left(p,q\right)}\left(m,n\right)\right\}}_{M,N}$, where the spatial range of signals received by the bucket detector array on the object arm constitutes the FOV of SAXGI imaging system. Denote the signals obtained from the object arm detector and the reference arm detector at the $i$ th measurement as $S_i$ and $R_i$ respectively, then at the $i$ th measurement, both the object and reference arms collect their signals respectively, as shown in Equation 1 for S_i and Equation 2 for R_i:

$S_i={\left[\begin{array}{ccc}{S}_i^{\left(1,1\right)}& \cdots & S_i^{\left(1,Q\right)}\\ ⋮& \ddots & ⋮\\ S_i^{\left(P,1\right)}& \cdots & S_i^{\left(P,Q\right)}\end{array}\right]}_{P\times Q}(1)$

$\begin{array}{c}{R}_i={\left[\begin{array}{ccc}{R}_i^{\left(1,1\right)}& \cdots & R_i^{\left(1,Q\right)}\\ ⋮& \ddots & ⋮\\ R_i^{\left(P,1\right)}& \cdots & R_i^{\left(P,Q\right)}\end{array}\right]}_{P\times Q}\\ \\ ={\left[\begin{array}{ccc}\begin{array}{ccc}{R}_i^{\left(1,1\right)}\left(1,1\right)& \cdots & R_i^{\left(1,1\right)}\left(1,N\right)\\ ⋮& \ddots & ⋮\\ R_i^{\left(1,1\right)}\left(M,1\right)& \cdots & R_i^{\left(1,1\right)}\left(M,N\right)\end{array}& \cdots & \begin{array}{ccc}{R}_i^{\left(1,Q\right)}\left(1,1\right)& \cdots & R_i^{\left(1,Q\right)}\left(1,N\right)\\ ⋮& \ddots & ⋮\\ R_i^{\left(1,Q\right)}\left(M,1\right)& \cdots & R_i^{\left(1,Q\right)}\left(M,N\right)\end{array}\\ ⋮& \ddots & ⋮\\ \begin{array}{ccc}{R}_i^{\left(P,1\right)}\left(1,1\right)& \cdots & R_i^{\left(P,1\right)}\left(1,N\right)\\ ⋮& \ddots & ⋮\\ R_i^{\left(P,1\right)}\left(M,1\right)& \cdots & R_i^{\left(P,1\right)}\left(M,N\right)\end{array}& \cdots & \begin{array}{ccc}{R}_i^{\left(P,Q\right)}\left(1,1\right)& \cdots & R_i^{\left(P,Q\right)}\left(1,N\right)\\ ⋮& \ddots & ⋮\\ R_i^{\left(P,Q\right)}\left(M,1\right)& \cdots & R_i^{\left(P,Q\right)}\left(M,N\right)\end{array}\end{array}\right]}_{\left(MP\right)\times \left(NQ\right)}\end{array}(2)$

Here, the two-dimensional array of bucket detectors on the object arm, denoted as $S_i^{\left(p,q\right)}$, has $P$ and $Q$ pixels in the vertical and horizontal directions respectively. At each vertical position $p$ and horizontal position $q$, the corresponding position on the reference arm $R_i$ is equipped with a sub-array detector $R_i^{\left(p,q\right)}$, which has $M$ and $N$ pixels in its vertical and horizontal directions respectively. Thus, the total pixels of the reference arm in the vertical and horizontal directions are $MP$ and $NQ$ respectively. Synthetic Aperture Ghost Imaging method reconstructs the image using the ghost imaging algorithm $f$ for each pair of signals at vertical and horizontal positions $\left(p\in \left[1,P\right],q\in \left[1,Q\right]\right)$, which corresponds to $S^{\left(p,q\right)}$ and $R^{\left(p,q\right)}$ respectively, thus, the full reconstructed image T is calculated by Equation 3:

$T={\left[\begin{array}{ccc}{T}^{\left(1,1\right)}& \cdots & T^{\left(1,Q\right)}\\ ⋮& \ddots & ⋮\\ T^{\left(P,1\right)}& \cdots & T^{\left(P,Q\right)}\end{array}\right]}_{P\times Q},T^{\left(p,q\right)}=f\left(S^{\left(p,q\right)},R^{\left(p,q\right)}\right)(3)$

where $T$ represents the full reconstructed image of the object, while $T^{\left(p,q\right)}$ denotes the reconstructed sub-image of the object corresponding to the bucket detector at position $\left(p,q\right)$ on the object arm.

To reduce the number of measurements, i.e., lower the sampling rate of the bucket detector array units, the TVAL3 algorithm [45, 46] for reconstruction can be employed. Unlike conventional correlation-based ghost imaging reconstruction methods that typically require sufficient sampling densities, TVAL3 enables significant reduction in sampling requirements while faithfully recovering image details. The TVAL3 reconstruction algorithm for synthetic aperture ghost imaging is formulated as Equations 4–6:

$T_{\text{SAXGI}-\mathrm{T}\text{VAL}3}={\left[\begin{array}{ccc}{T}_{\text{TVAL}3}^{\left(1,1\right)}& \cdots & T_{\text{TVAL}3}^{\left(1,Q\right)}\\ ⋮& \ddots & ⋮\\ T_{\text{TVAL}3}^{\left(P,1\right)}& \cdots & T_{\text{TVAL}3}^{\left(P,Q\right)}\end{array}\right]}_{P\times Q}(4)$

$T_{\text{TVAL}3}^{\left(p,q\right)}=\underset{T^{\left(p,q\right)}}{\arg \min }\left[\text{TV}\left(T^{\left(p,q\right)}\right)+\lambda {‖R^{\left(p,q\right)}·T^{\left(p,q\right)}-S^{\left(p,q\right)}‖}_2^2\right](5)$

$\text{TV}\left(T^{\left(p,q\right)}\right)={\displaystyle \sum _{m=1,n=1}^{M,N}}\left|T^{\left(p,q\right)}\left(m+1,n\right)-T^{\left(p,q\right)}\left(m,n\right)\right|+\left|T^{\left(p,q\right)}\left(m,n+1\right)-T^{\left(p,q\right)}\left(m,n\right)\right|(6)$

Here, the optimization objective $T^{\left(p,q\right)}$ represents the sub-image of the object reconstructed at the position corresponding to $\left(p,q\right)$. $\text{TV}\left(T^{\left(p,q\right)}\right)$ is the total variation regularization term based on L1 norm, which is obtained by summing the absolute values of the differences between all adjacent pixel values of the sub-image $T^{\left(p,q\right)}$ in the vertical direction $m=1,\dots ,M$ and the horizontal direction $n=1,\dots ,N$. ${‖R^{\left(p,q\right)}·T^{\left(p,q\right)}-S^{\left(p,q\right)}‖}_2^2$ is the fidelity term based on L2 norm, introduced as an optimization penalty to ensure that the ideal imaging process $R^{\left(p,q\right)}·T^{\left(p,q\right)}=S^{\left(p,q\right)}$ holds, with $\lambda$ being the corresponding penalty parameter.

Building on the fundamental principles of synthetic aperture ghost imaging, we developed a novel experimental setup with a prior-recorded reference, depicted in Figure 1. According to virtual beam-splitting strategies, the object in question $Y^j$ must be first removed from the optical path to capture the reference signal $R_i^j$ using a high-resolution detector. Subsequently, the object is reintroduced into the optical path to capture the object signal $S_i^j$ corresponding to $Y^j$ with a low-resolution detector. This in-and-out movement is repeated for all number of measurements $i$ to collect complete data for ghost imaging. Acquiring such data typically requires several hours with reasonable number of measurements and exposure time, and the whole process must be repeated every time a new test object $Y^{j^{\prime }}$ is introduced. Low data acquisition efficiency via virtual beam-splitting strategies hampers its broader application.

Figure 1

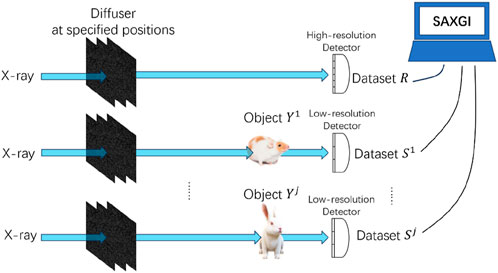
Figure 1. Schematic diagram of the proposed experimental setup with a prior-recorded reference based on Synthetic Aperture X-ray Ghost Imaging (SAXGI). With the random scattering medium positioned at different specified locations ${\left\{\left(x_i,z_i\right)\right\}}_C$, the following images are sequentially captured: (1) high-resolution light field images modulated by the diffuser without object, i.e., the reference signal $R$; (2) low-resolution images in the object arm $S^1,\dots ,S^j,\dots$ when objects $Y^1,\dots ,Y^j,\dots$ are introduced respectively into the optical path. Subsequently, SAXGI reconstruction is performed using all the collected $R$ and $S^1,\dots ,S^j,\dots$ data.

In the process of collecting data for multiple objects, provided that the positions of the random scattering medium precisely match between the two arms, it is possible to utilize a single set of reference arm data for different object reconstructions. Initially, the zeroth dataset is recorded prior to other detection--this is when no object is present in the optical path, and the modulated light field are recorded by a high-resolution detector with the diffuser at specified positions ${\left\{\left(x_i,z_i\right)\right\}}_{i=1,\dots ,C}$. This prior-recorded dataset serves as the reference arm data $R$ for ghost imaging. Subsequent datasets for $j=1,\dots ,J$, where $J$ is the total number of objects to be tested, involve positioning the test object $Y^j$ within the optical path and capturing images at the specified positions ${\left\{\left(x_i,z_i\right)\right\}}_{i=1,\dots ,C}$ with a low-resolution bucket detector array, corresponding to the object arm data $S^j$ for the test object $Y^j$ in ghost imaging. By leveraging the same set of prior-recorded reference data $R$, this approach not only circumvents the time and positioning inaccuracies brought about by repeatedly moving test objects in and out but also facilitates the collection of data from multiple objects in a single experimental operation, markedly improving data acquisition efficiency. Aside from the time-intensive collection of high-resolution data for the reference arm, the data acquisition approach of the proposed method aligns with conventional imaging, promoting the practical application of XGI. Given the significantly larger pixel size of the bucket detector array compared to the high-resolution detector and its enhanced sensitivity, this technique also aims to achieve low-dose imaging of test objects. However, due to the necessity for the random scattering medium to be moved back and forth and accurately repositioned at the specified ${\left\{\left(x_i,z_i\right)\right\}}_{i=1,\dots ,C}$ positions, failure to precisely reposition at the same spot could lead to discrepancies between object and reference arm data, jeopardizing the experiment’s reliability. Therefore, motorized positioning stage that carries random scattering medium must exhibit high repeatability precision and minimal cumulative error. Ideally, the repeatability precision $∆\delta$ of motorized positioning stage and the cumulative error $g\left(p^{\prime }\right)$ corresponding to the traversed distance $p^{\prime }$ between two positioning attempts, $∆\delta +g\left(p^{\prime }\right)$, should be less than a quarter of the pixel size of the high-resolution detector $D_R$, or at the very least, less than half of $D_R$, to ensure images reconstructed with a high signal-to-noise ratio (SNR).

In the optical path of SAXGI with prior-recorded reference, both the high-resolution detector and the low-resolution detector, i.e., the bucket detector array, are required not only to be precisely located at corresponding spatial positions but also to have certain matching in terms of pixel size. Specifically, the pixel size $D_S$ of the low-resolution detector and the pixel size $D_R$ of the high-resolution detector need to satisfy a relationship of integer multiples, as shown in Equation 7:

$D_S=M\times N\times D_R(7)$

so that a pixel $S^{\left(p,q\right)}$ at position $\left(p,q\right)$ on the bucket detector array corresponds to a sub-array $R^{\left(p,q\right)}={\left\{R^{\left(p,q\right)}\left(m,n\right)\right\}}_{M,N}$ on the high-resolution detector. However, detectors with such relationship of multiple integers are not always readily available in general experimental setups. Unlike existing approaches, ensuring precise spatial alignment between the pixel units of the bucket detector array and the corresponding sub-arrays in the reference arm during the signal acquisition for different objects is the greatest challenge for the success of this scheme. Typically, the difference in pixel unit size between the bucket detectors and the high-resolution detector in the reference arm can reach up to 40 times [47], making digital image registration solutions hard to be implemented. Addressing this issue through hardware setup is the most efficient solution.

2.2 Experimental setup

In this experiment, we utilized a customized detector capable of achieving arbitrary pixel number binning to collect signals. Signal of the reference arm was recorded using the high-resolution mode without binning, while for recording signal of the object arm, the detector was binned according to specific requirements. Since the detector’s position remained unchanged while recording signals from both the object and reference arm signals, high-precision registration between the two arms’ signals was ensured. The detector model used was the Hamamatsu C15440-20UP01, with a pixel array of 2304 × 2304 and a pixel size of 6.5 μm × 6.5 μm, corresponding to a FOV of 14.976 mm × 14.976 mm. With a frame rate of 89.1 fps, the detector ensures rapid acquisition of signals from the object arm. During the acquisition of the object signal, pixel binning was performed by merging pixels from left to right, top to bottom, in square regions of $K\times K$ to form a single pixel in the output image (discarding pixels that do not divide evenly), where $K$ is the binning number of pixels on each side of the sub-array in the reference arm corresponding to a bucket detector pixel unit. After merging, each pixel in the object signal corresponds to a $K\times K$ square region in the reference signal, thereby directly acquiring object signals with highly registered positions during data acquisition. Thus, by switching the detector’s binning modes, we achieved the collection of high-resolution and low-resolution signals required for SAXGI using a single optical path and a single detector.

Based on existing numerical simulation results [44], selecting a pixel binning value of $K=M=N=40$ allows for a good balance between the sampling rate and image quality. However, for commercially available detectors, choosing $K=40$ binning directly during acquisition is impractical, as accumulated background noise for each pixel often exceeds the dynamic range of the detector, leading to the signal-to-noise ratio dropping to zero. Figure 2 presents the statistical distribution of the dark field image for the customized Hamamatsu detector used in the experiments. This 16bit detector has a dynamic range of 0–65,535, and in the absence of light signals, it exhibits a background noise with an average value of $\mu =100.97$, a standard deviation of $\sigma =6.74$, and a range of 321. After performing a 40 × 40 pixel binning operation, the average value of the detector’s background noise becomes $40\times 40\times 100.97\approx 160000$, with the detector’s dynamic range fully occupied by dark current, rendering it unusable for object arm signal detection. To reduce the impact of background noise, collecting the object arm signal with fewer pixel binning and then further binning to an appropriate block size in the computer is a practical choice. For example, applying a $4\times 4$ binning operation in the object arm gives a background noise in each binned pixel at an average value of ${\mu }^{\prime }=4\times 4\times \mu =1615.52$ and a standard deviation of ${\sigma }^{\prime }=4\times 4\times \sigma =107.84$. This corresponds to a maximum fluctuation of $\left({\mu }^{\prime }+3{\sigma }^{\prime }\right)/65535=2.96\%$ with respect to the detector’s dynamic range (assuming Gaussian distribution of the noise), which is acceptable for successful SAXGI reconstruction, as demonstrated later in our result images. Considering that software binning in the computer does not introduce additional overflow errors, the proposed workaround addresses the problem of detector’s dynamic range saturation. Since the detection of the object arm signal uses a low-resolution detector with a binned pixel array, the feasibility of the proposed approach can be demonstrated. It should be noted that while we applied a customized detector in our study for the sake of convenience, the workaround of using a $4\times 4$ binning in acquiring object arm signals and then applying software-binning in the computer is practical for most commercially available detectors in that $1\times 1$, $2\times 2$, $4\times 4$ binning option is usually incorporated into the detector system.

Figure 2

Figure 2. Statistical distribution of the dark field image of the customized detector.

We conducted the experiments at the BL13HB beamline of the Shanghai Synchrotron Radiation Facility [48], with a photograph of the experimental setup shown in Figure 3. The experimental apparatus primarily consists of three components: motorized positioning systems for the diffuser (sandpaper), for the objects, and for the customized Hamamatsu detector respectively. Before the experiment, it is crucial to adjust the optical path to ensure the collimation of sandpaper, objects, and the detector along the X-ray beam. The motorized positioning stage for sandpaper scanning in X direction is a Kohzu XA16F-L2101, with a movement range of ±50 mm, a micro-step resolution of 0.5 μm, repeatability accuracy of ≤±0.5 μm, horizontal straightness of ≤4 μm/100 mm, and vertical straightness of ≤2 μm/100 mm. The motorized positioning stage for sandpaper scanning in Z direction is a Kohzu ZA16sA-32F01, with a movement range of $\pm$ 25 mm, micro-step resolution of 0.01 μm, repeatability accuracy of ≤± 0.3 μm, and perpendicularity of ≤8 μm/50 mm. The motorized translation stage for objects in X direction is a Kohzu XA16F-L21, and the lifting stage for objects in Z direction is a Kohzu ZA16A-32F. During the experiments, the pseudothermal light source is generated by a 15 keV beam modulated by the random scattering medium of sandpaper, with the SiC particle size of the sandpaper being approximately 75 μm. The test objects are placed about 3.5 cm in front of the customized Hamamatsu detector with a pixel size of 6.5 μm, approximately 41 cm behind the sandpaper, thus the distance between the detector and the diffuser is 44.5 cm. The detector’s 100 μm LuAG:Ce scintillator converts X-rays into visible light, which is then magnified 2 times by a lens group, resulting in an effective detector pixel size of $D_R=3.25\mu \mathrm{m}$.

Figure 3

Figure 3. Photograph of the experimental setup, primarily composed of three main parts: a motorized positioning stage for random scattering medium (sandpaper), a motorized positioning stage for objects, and the customized Hamamatsu detector. The detector can achieve binning directly through electronic control without the need to change its position.

During the experimental process, we followed the aforementioned experimental scheme. Firstly, a set of high-resolution randomly modulated reference patterns, of the region of interest (ROI) $2040\times 1440$ and an effective pixel size of $D_R=3.25\mu \mathrm{m}$, was recorded. The reference patterns were recorded by using raster-scanning strategy, where the movement of the sandpaper’s center forms a 21 × 21 grid in the X-Z plane perpendicular to the optical axis, and exposure time for a single projection was 400 ms. The displacement for each adjacent step in X or Z direction was the same 455 $\mu \mathrm{m}$, equivalent to 130 effective pixels, which significantly exceeds the 75 μm characteristic size of SiC particles. The moving range in X or Z direction in total is thus $455\mu \mathrm{m}\times \left(21-1\right)=0.91\text{mm}$. By this way, the non-correlation between any pair of reference patterns is ensured. Figure 4 shows the distribution of the center value for normalized 2-dimensional cross correlation of adjacent reference patterns. The histogram exhibits a correlation with mean value 0.050 and standard deviation 0.006 between adjacent reference patterns, which is a rather low correlation degree for the pairs of reference patterns with highest possible correlation. Thus, the incoherence of reference signals was demonstrated.

Figure 4

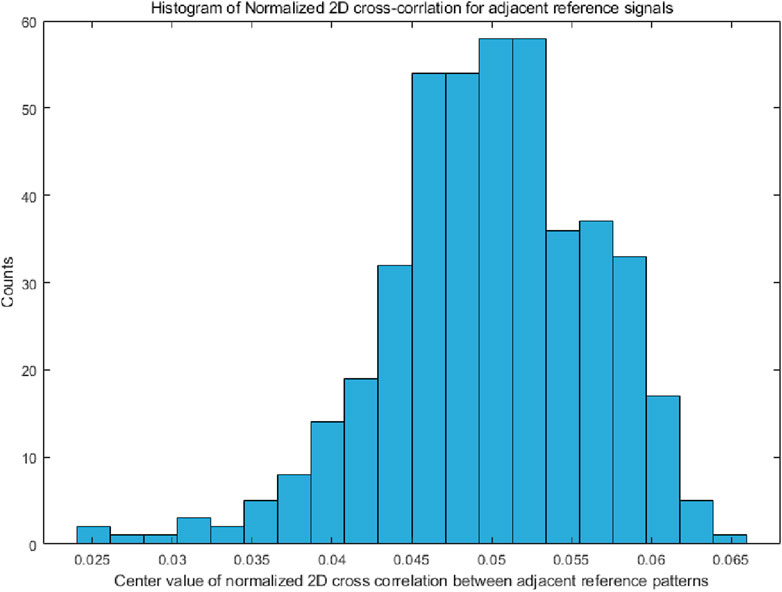
Figure 4. Histogram of the center value for the normalized 2-dimensional cross-correlation between adjacent reference patterns.

The prior-recorded references were then followed by the sequential capture of low-resolution images of the object arm, namely, a small fish (Poecilia reticulata), tungsten wire, and a resolution chart. Considering the impact of the detector’s dynamic range and background noise, a pixel binning of $K_1=4$ is used for the data acquisition in the object arm, resulting in a ROI size of 510 × 360, with a corresponding effective pixel size of 13 μm. Subsequently, a pixel binning of $K_2=10$ was performed in the computer to achieve the pixel combination of $K=K_1{K}_2=40$ required for SAXGI image reconstruction. In other words, the size of the bucket detector array in the object arm used for SAXGI reconstruction corresponds to 51 × 36, with an effective pixel size of $D_S=130\mu \mathrm{m}$. The number of measurements collected by scanning different positions of the sandpaper in the experiment was $C=441$. Typical reference signals as well as object signals acquired directly and processed later are shown in Figure 5, where Figure 5a is a reference signal, with a pixel count of 2040 × 1440 and an effective pixel size of 3.25 μm; Figure 5b is the object signal directly acquired, with a pixel count of 510 × 360 and an effective pixel size of 13 μm; and Figure 5c is the object signal used for SAXGI reconstruction, with a pixel count of 51 × 36 and an effective pixel size of 130 μm. All images were reconstructed using the TVAL3 algorithm.

Figure 5

Figure 5. Typical images obtained from SAXGI data acquisition and subsequent processing, scaled to the same size for ease of comparison. (a) Reference signal with randomly modulated light field, with 2040 × 1440 pixels and an effective pixel size of 3.25 μm; (b) Object signal directly acquired with 4 × 4 binned detector, with 510 × 360 pixels and an effective pixel size of 13 μm; (c) Object signal used for SAXGI reconstruction, with 51 × 36 pixels and an effective pixel size of 130 μm.

3 Results and analysis

To validate SAXGI with prior recorded reference, we selected three test objects: tungsten wire, a resolution target, and a small fish, representing strong absorption objects, regular objects, and complex biological objects respectively. This was done to evaluate the performance of our scheme for different types of objects. We first collected a set of high-resolution images from the reference arm by scanning the sandpaper, then adjusted the detector to a 4 × 4 binning mode and sequentially acquired the object signals of the three objects at positions with their correspondent modulated light field. Subsequently, the same set of reference signals was used in reconstruction with the object signals for different objects. Recording the reference arm signal once to achieve SAXGI reconstruction for three different objects, in principle, verifies the feasibility of the efficient implementation of the proposed scheme for imaging multiple objects with a single reference scanning.

3.1 Sample with strong absorption

A tungsten wire object, approximately 20 μm in diameter, almost entirely absorbs 15 keV X-rays and can be considered a simple binary object. This setup allows us to assess the feasibility of imaging strongly absorbing objects with the proposed approach. Reconstruction results are displayed in Figure 6, with Figure 6a providing the target image of the tungsten wire. Figure 6b depicts the 40-binned image from the bucket detector array of the object arm, revealing that the object’s fine details are indiscernible. Figure 6c showcases the SAXGI reconstruction result, clearly revealing the tungsten wire’s details, including bends and closely spaced wire configurations. Furthermore, the weak absorption tape used to fasten the object is also revealed in the reconstructed image. Compared to the target image shown in Figure 6a, here Figure 6c recaptures all the structural details of the tungsten wire object, albeit with slightly reduced contrast. According to the definition of sampling rate ${\alpha }^{\prime }$ for ghost imaging without synthetic aperture, 441 measurements correspond to a sampling rate of ${\alpha }^{\prime }=$441/(2040*1440) = 0.015%, insufficient for effective ghost imaging reconstruction. However, within the context of synthetic aperture ghost imaging, the sampling rate associated with pixel units in the bucket detector array is $\alpha =$441/(40*40) = 27.6%, ample for the TVAL3 reconstruction algorithm, thereby facilitating the acquisition of a high-quality and large FOV reconstruction of the tungsten wire object. Note that among the three test objects, the reconstruction for tungsten wire exhibits superior contrast relative to that for the resolution chart and the fish. This enhancement stems from the inherent high SNR of tungsten signals, which enables the algorithm to more efficiently mitigate intensity fluctuation during processing. Consequently, the improved noise suppression capability translates into higher-contrast reconstruction outcomes.

Figure 6

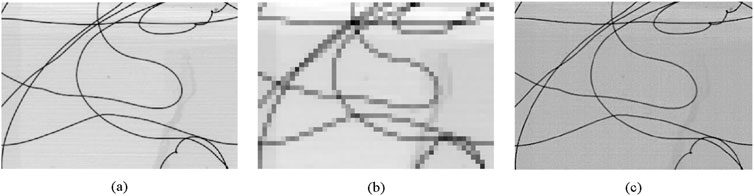
Figure 6. SAXGI with prior-recorded reference of a strong absorption tungsten wire object, where (a) the target image with $2040\times 1440$ pixels; (b) the 40-binned low-resolution image from the object arm, with $51\times 36$ pixels; (c) the SAXGI reconstruction with 441 measurements and a sampling rate of 27.6%, with $2040\times 1440$ pixels.

3.2 Resolution chart

Compared to the tungsten wire, the resolution chart represents a periodic structure object with relatively low absorption, thereby allowing the testing of the signal-to-noise ratio impact on imaging results within the proposed imaging system. Moreover, the spatial structure information of the resolution chart is more abundant, containing grating structures with periods ranging from 15.0 μm to 0.4 μm, which effectively tests the ability of the proposed method in resolving different spatial frequencies.

Figure 7 presents the SAXGI reconstruction for a resolution chart, where Figure 7a is the high-resolution target image of the resolution chart. Figure 7b shows the 40-binned image from the bucket detector array in the object arm, in which all the periodic structures are indiscernible. From the SAXGI reconstruction shown in Figure 7c, the unit with a period of 15 μm is clearly resolved, and the unit with a period of 10 μm is discernible, indicating that the spatial resolution is 10 μm. Due to noise, units with smaller periods are completely indistinguishable. Since individual pixels cannot resolve discrete objects, we conclude that 10 μm, corresponding to approximately 3 effective pixels of 3.25 μm in the reference arm, represents the best achievable spatial resolution of this system. Given the object’s inherently low contrast, the influence of noise is fully manifested in the reconstructed image of Figure 7c, where the primary source of noise could be the registration error between the low-resolution signal of the object arm and the high-resolution image of the reference arm. Scattering of X-rays by the resolution chart itself and its substrate material may also contribute to the significant noises.

Figure 7

Figure 7. SAXGI with prior-recorded reference of a resolution chart, where (a) the target image with $480\times 440$ pixels; (b) the 40-binned low-resolution image from the object arm, with $12\times 11$ pixels; (c) the SAXGI reconstruction with 441 measurements and a sampling rate of 27.6%, with $480\times 440$ pixels.

3.3 Biological specimen

Tungsten wire object with strong absorption and resolution chart object with relatively weakly absorption and periodic structure are both artificial, and the capability to image actual complex objects is a key test of the utility of the method proposed in the paper. A small Poecilia reticulata fish was chosen as the test object to focus on the quality of SAXGI reconstruction to distinguish its skeletal distribution compared to traditional projection imaging. Figure 8 presents the reconstruction results for the small fish object, with Figure 8a showing the high-resolution projection image of the object, with an image size of 2040 × 1440. Figure 8b displays the 40-binned image from the bucket detector array of the object arm, illustrating that the details of the fish’s skeleton are difficult to be discerned. Figure 8c is SAXGI reconstruction result, which clearly resolves the complex skeletal distribution of the small fish. To further compare with the projection image, Figure 8d provides the grayscale distribution profiles at positions marked by the blue and red lines in Figures 8a,c respectively. It can be observed that in areas where the object signal is strong, corresponding to low relative grayscale areas in the absorption image, the SAXGI reconstruction matches well with the projection image. This demonstrates superior reconstruction capabilities of our method for regions with higher SNR. In other areas where the absorption signal is weak, corresponding to high relative grayscale areas, the intensity distribution trends of the two images are consistent, but the ghost imaging reconstruction shows significant random fluctuations in intensity. This indicates that the SAXGI reconstructed images exhibit noticeable noise, leading to reduced imaging contrast in areas where the object signal is weak.

Figure 8

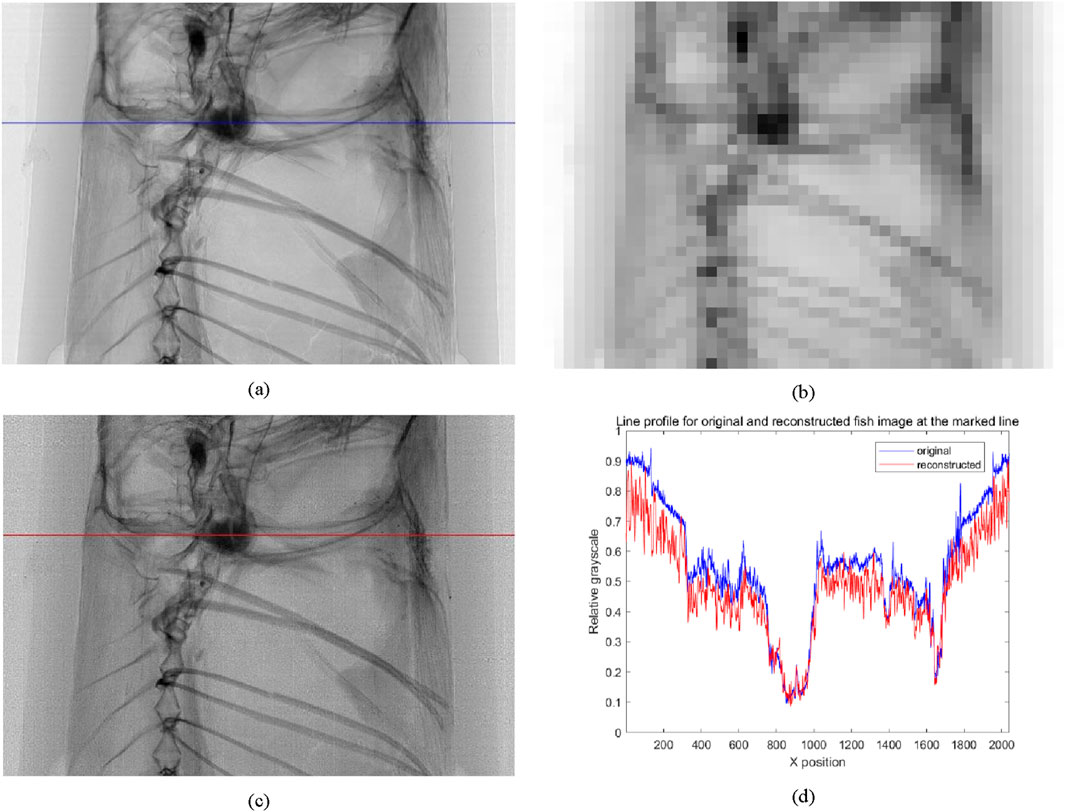
Figure 8. SAXGI with prior-recorded reference of a Poecilia reticulata fish, where (a) the high-resolution projection image with $2040\times 1440$ pixels; (b) the 40-binned low-resolution image from the object arm, with $51\times 36$ pixels; (c) the SAXGI reconstruction with 441 measurements and a sampling rate of 27.6%, with $2040\times 1440$ pixels; (d) Grayscale line profiles at marked lines in (a,c).

Images reconstructed via SAXGI method exhibit irregular fluctuations compared to the original images, which could, on the one hand, originate from the residuals of the modulated speckle patterns and, on the other hand, be related to the spatial misalignment between blocks during segmented reconstruction. These factors, combined with other noise influences, result in the deteriorated signal-to-noise ratio of the SAXGI reconstructed images compared to traditional methods. Imperfect matching between the sandpaper scanning in the object and reference arms during multiple measurements could be a significant cause.

Recording the reference signal priorly and then sequentially collecting the object signals for three different objects, the proposed method is capable of reconstructing with high fidelity the structure details of the objects. These results indicate that the implementation scheme with a prior-recorded reference proposed in the paper can achieve ghost imaging of different objects. Data collection process in the proposed scheme is similar to traditional imaging methods and may favor the widespread application of X-ray ghost imaging.

3.4 Potential of low dose radiology

One potential advantage of SAXGI is the capability to achieve imaging at a low sampling rate, which implicates low radiation dose. The experimental results mentioned above were reconstructed using all 441 measurements. With a sampling rate of 27.6%, combined with compressed sensing algorithms such as TVAL3, satisfactory reconstruction results are achieved. Then, reconstructions will be conducted with fewer measurements to validate the performance of the proposed implementation scheme at even lower sampling rates. The reconstruction of the small fish skeletal structure with reduced sampling rates is shown in Figure 9, where Figure 9a is a full FOV projection image of $2040\times 1440$, and Figures 9b–g represent SAXGI reconstruction results at sampling rates of 27.6%, 12.5%, 6.3%, 3.1%, 1.25%, and 0.5% respectively. For ease of comparison of structure details, only a part of the entire imaging FOV with dimensions of $480\times 720$ is concentrated, as denoted in Figure 9a with a red rectangle.

Figure 9

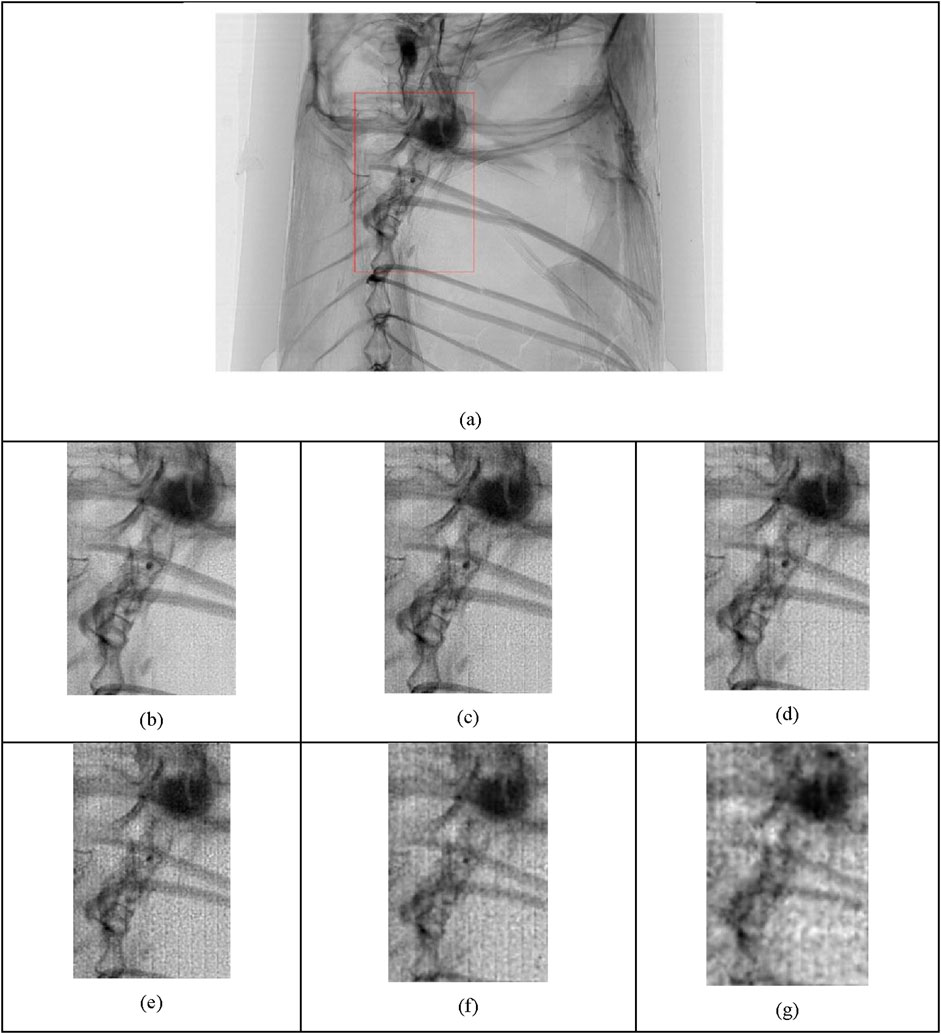
Figure 9. Reconstruction results of a Poecilia reticulata fish at low sampling rates, with an area of 480 × 720 concentrated. (a) High-resolution projection image, image size 2040 × 1440, with the concentrated 480 × 720 area highlighted in a red box; (b) Sampling rate of 27.6%, corresponding to 441 measurements; (c) Sampling rate of 12.5%, corresponding to 200 measurements; (d) Sampling rate of 6.3%, corresponding to 100 measurements; (e) Sampling rate of 3.1%, corresponding to 50 measurements; (f) Sampling rate of 1.25%, corresponding to 20 measurements; (g) Sampling rate of 0.5%, corresponding to 8 measurements.

From Figure 9, it is evident that as the sampling rate decreases, the block effect (see Section 4.1) in the reconstructed images becomes more pronounced, and the impact of noise is more significant. However, even at a sampling rate of 1.3% with 20 measurements used for reconstruction, the main structure of the small fish remains clearly discernible. Even when the number of measurements is reduced to 8, corresponding to a sampling rate of 0.5%, the skeletal outline can still be made out. This indicates that the proposed implementation scheme for SAXGI with a prior-recorded is quite robust, and able to reconstruct object information even at very low sampling rates. In practical applications, an appropriate sampling rate can be selected by compromising the image SNR and radiation dose. By optimizing experimental conditions, especially the scanning precision of the scattering medium, SNR of the reconstructed images at low sampling rates is expected to be improved significantly.

4 Discussion

4.1 Block effect

In the images reconstructed by SAXGI with prior-recorded reference proposed in this article, grid-like boundaries with discontinuous light and dark areas can be observed. This phenomenon, known as the block effect, mainly originates from two sources: (1) Errors caused by the accuracy of the motorized positioning stage during data acquisition. In our experimental scheme, it is necessary to first record the reference at a series of specified positions of the sandpaper, and then collect the object signals at the corresponding positions. Since the motorized positioning stage for sandpaper is not equipped with a closed-loop control system incorporating a grating ruler, its inherent displacement accuracy can lead to certain positioning errors. Moreover, the back-and-forth movement of the sandpaper during scanning contributes to significant positioning errors due to the backlash of the positioning stage. These scanning errors can lead to mismatches between the object and reference arm, resulting in the residual of the sandpaper speckle patterns in the reconstructed images, which affects the imaging contrast. (2) Errors caused by SAXGI reconstruction algorithm. In the reconstruction process of SAXGI, the image is reconstructed based on the signals from the pixel units of the bucket detector array, with the overall imaging FOV composed of blocks formed by the two-dimensional spatial distribution of reconstructed units. Mismatches in spatial positions of object and reference arm signals during data collection, as well as differences in detection sensitivity and quantum efficiency among bucket detector units, can lead to reduced SNR within blocks. Particularly, reconstruction differences between adjacent blocks can cause an abnormal increase in contrast at block edges, resulting in grid-like boundaries.

In the experimental scheme via virtual beam-splitting strategies, the sandpaper did not move during the collection of corresponding object and reference signals, resulting in no spatial registration issues between the object and reference arm signals, and thus no apparent block effect was observed in the reconstruction results of (44), namely, Figure 5d in (44). Numerical simulations also did not reveal the impact of the block effect, as evidenced in Figure 3d in (44), indicating that the SAXGI method itself may not be the main cause of the block effect. Therefore, it can be concluded that in SAXGI with prior-recorded reference proposed in the paper, the block effect mainly arises from the mismatch between the positions of the sandpaper in the object and reference arms during data acquisition.

To further demonstrate that the registration error is the main cause of block effect, we intentionally introduced pixel-level mismatch into our reconstruction process for the tungsten wire to obtain Figure 10. In Figure 10a, one constant leftward pixel mismatch of the diffuser with respect to the detector is introduced, and subsequently evident vertical stripes darker on the left edge and brighter on the right appears, compared to Figure 6c. As a comparison, the reconstruction result Figure 7c also shows block effect mainly as vertical stripes with bright-dark edges, indicating a systematic rightward mismatch in the data acquisition. Similarly in Figure 10b, one upward pixel mismatch of the diffuser with respect to the detector caused horizontal stripes darker on the upper edge and brighter on the lower. These results indicate that registration errors result in block effect as directional boundary artifacts. Note that for this demonstration specifically, since we adopted the experiment data with unknown and non-uniform registration error, stripes in Figure 10 are not as uniform as expected.

Figure 10

Figure 10. Reconstruction results of tungsten wire when displacement is introduced, with other reconstruction conditions the same as in Figure 6c, where here (a) one constant leftward pixel mismatch of the diffuser with respect to the detector is incorporated; (b) one constant upward pixel mismatch of the diffuser with respect to the detector is incorporated; (c) one constant leftward as well as one constant upward pixel mismatch of the diffuser with respect to the detector is incorporated.

With one leftward as well as one upward pixel mismatch of the diffuser with respect to the detector in Figure 10c, stripes in vertical and horizontal directions combine into evident block effect. Experimentally, the intensity variations at image boundaries observed are predominantly non-deterministic, implying that registration errors are not uniform but exhibit random fluctuations. Such omnidirectional perturbations at boundaries prevent the formation of deterministic textures.

By further improving the scanning accuracy of the motorized positioning stage, adding a closed-loop control system with a grating ruler, and refining the existing TVAL3 algorithm during the reconstruction process by considering the relationships between bucket detector units, it is hoped that the impact of the block effect can be effectively eliminated, thereby improving the SNR of the reconstructed images by the proposed method.

4.2 Quantitative evaluation

Peak Signal-to-Noise Ratio (PSNR) and Structural Similarity Index Measure (SSIM) [49] are commonly utilized indicators for assessing image quality. However, as shown in Tables 1, 2, for the reconstruction outcomes of this experiment, these two indicators do not seem to yield consistent results. Accordingly, we introduced the perceptual loss function from the VGG19 deep learning network [50] as an evaluation metric of the image quality. This criterion utilizes a pretrained deep learning network to extract the features of the image at various depth layers, assessing the similarity between two images by comparing the differences in these feature layers, and the perceptual loss function is formulated in Equation 8:

$L\left(T_1,T_2\right)={\displaystyle \sum _{i=1}^K}{\displaystyle \sum _{u=1,v=1}^{U,V}}{c}_i\left|{\phi }_i\left(T_1^{\left(u,v\right)}\right)-{\phi }_i\left(T_2^{\left(u,v\right)}\right)\right|(8)$

within this context, $L$ represents the perceptual loss in the L1 norm between two images $T_1$ and $T_2$ in the VGG19 network, where $T^{\left(u,v\right)}$ denotes the pixel value of image $T$ at the vertical coordinate $u$ and horizontal coordinate $v$, with $U$ and $V$ being the sizes of the image in the vertical and horizontal directions respectively. $K$ denotes the number of network layers, ${\phi }_i\left(T\right)$ represents the parameters output by the $i$ th layer of the network, and $c_i$ are the corresponding layer weights.

Table 1

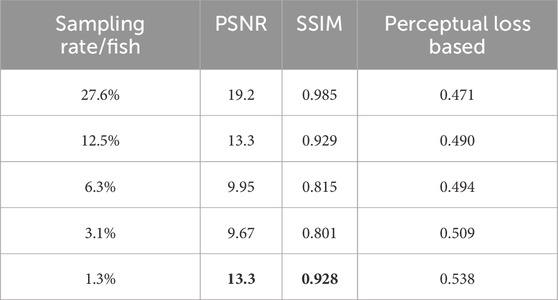
Table 1. Quantitative evaluation of the reconstructed images of fish at different sampling rates, with the bold values being anomalies contrary to expected performance.

Table 2

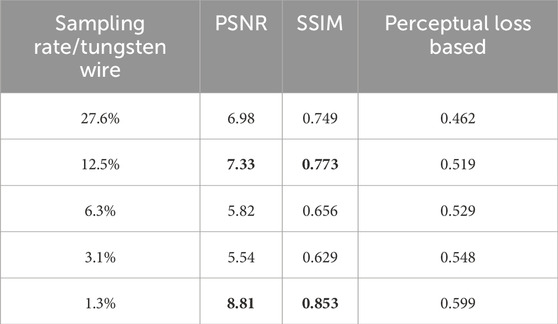
Table 2. Quantitative evaluation of the reconstructed images of tungsten wire at different sampling rates, with the bold values being anomalies contrary to expected performance.

In this study, when performing calculations, the overall network layers $K=5$ was selected, with layer weights $c=\left[1/32,1/16,1/8,1/4,1\right]$. Subsequently, the perceptual loss was added to the mean squared error (MSE) with weighting, resulting in the perceptual-loss-based evaluation metric $L^{\prime }$, as formulated in Equation 9:

$L^{\prime }\left(T_1^{\prime },T_2^{\prime }\right)=10\times L\left(T_1^{\prime },T_2^{\prime }\right)+MSE\left(T_1^{\prime },T_2^{\prime }\right)(9)$

where $T^{\prime }$ is the image $T$ after normalization operations, with pixel values distributed between $\left[-1,1\right]$, and $MSE\left(T_1^{\prime },T_2^{\prime }\right)$ is the mean squared error between $T_1^{\prime }$ and $T_2^{\prime }$.

Tables 1, 2 present various quantitative metrics between SAXGI reconstructed images and target images of traditional projection at different sampling rates for a fish and tungsten wire respectively.

As the sampling rate decreases, the image quality deteriorates. Therefore, the corresponding PSNR and SSIM values should decrease, and the perceptual loss should increase. The bold values highlighted in Tables 1, 2 denote the anomalies in PSNR and SSIM values with decreasing sampling rates, contrary to the expected performance, indicating that these two commonly used metrics may not provide a consistent assessment of image reconstruction. In contrast, the evaluation metric based on perceptual loss from deep learning offers a consistent assessment.

The discrepancy that PSNR/SSIM occasionally fail to reliably assess reconstruction quality may originate from speckle noise artifacts and dynamic range constraints. On the one hand, speckle intensity fluctuations undetectable by PSNR/SSIM, which lack multi-scale sensitivity, induce metric instability, whereas convolutional neural networks effectively decouple diagnostically irrelevant speckle patterns from structural features. On the other hand, SSIM’s luminance term tends to become unreliable due to dynamic range constraints imposed by mandatory contrast adjustment in TVAL3-reconstructed images for visualization when outlier intensities occur.

While perceptual-loss-based metrics demonstrate enhanced correlation with human visual perception, its utility for science imaging is constrained by subjective parameter selection and case-specific optimization tendencies. Perceptual loss function itself is not an objective evaluation metric, and its effectiveness depends on the selection of network type, weights for different feature layers, norms, and other variables, which detracts from its universality as an image evaluation metric. Establishing a concept of normalization for perception loss is challenging, so it only has relative significance and cannot compare the degradation levels of different images. However, test results indicate that this metric can provide a consistent evaluation of the relative quality differences when assessing the reconstruction quality of SAXGI at different sampling rates.

5 Conclusion

Aiming at efficient implementation of megapixel X-ray ghost imaging, we developed an experimental scheme that achieves X-ray ghost imaging of multiple objects, requiring only once acquisition of the signals in the reference arm. By prior-recording and reusing the same set of high-resolution reference images, the data acquisition efficiency has been significantly improved compared to that of the strategies available, reducing the data acquisition time from 6 h to 40 min. Experimental results demonstrate that the proposed scheme can achieve high-quality image reconstruction with a size of 2040 × 1440 pixels. According to the successful reconstruction of the fish skeleton with only 8 measurements, corresponding to a sampling rate of 0.5%, the potential of low dose radiology for the developed method is verified experimentally. Imaging results with a resolution chart demonstrate that a spatial resolution of 10 μm is achieved, comparable to the resolution defined by the effective pixel size of 3.25 μm in the reference arm. By optimizing the scanning speed and positioning control of the random light field modulator, the image acquisition efficiency and the signal-to-noise ratio of the reconstructed images are anticipated to be further improved. With appropriate modifications, the developed experimental scheme is expected to extend the field of view in nano-resolution imaging. In addition, with the development of a dedicated X-ray detector which can switch automatically between high efficiency mode for object arm and high-resolution mode for reference arm, the proposed experimental scheme can be implemented more efficiently.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

JT: Writing – review and editing, Conceptualization, Validation, Supervision, Investigation, Methodology, Software, Formal Analysis, Writing – original draft, Resources, Data curation, Visualization. HZ: Investigation, Conceptualization, Funding acquisition, Formal Analysis, Validation, Writing – review and editing, Methodology, Supervision, Project administration. CZ: Validation, Methodology, Formal Analysis, Conceptualization, Writing – review and editing, Investigation. NZ: Validation, Writing – review and editing, Methodology, Conceptualization, Formal Analysis, Investigation. JW: Writing – review and editing, Software, Formal Analysis. HG: Project administration, Writing – review and editing, Resources, Funding acquisition, Software. TX: Supervision, Investigation, Funding acquisition, Conceptualization, Formal Analysis, Writing – review and editing, Project administration, Resources, Validation, Data curation, Methodology, Writing – original draft.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. This work was supported by National Key Research and Development Program of China under Grant 2022YFA1603601, 2021YFF0601203, 2021YFA1600703 and National Natural Science Foundation of China under Grant 12205361.

Acknowledgments

The authors are grateful to staff members at BL13HB and BL09B of SSRF for their kind help in experiments, including Yan-Ling Xue, Guo-Hao Du, Zhong-Liang Li, along with other members.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Pan A, Zuo C, Yao B. High-resolution and large field-of-view Fourier ptychographic microscopy and its applications in biomedicine. Rep Prog Phys (2020) 83(9):096101. doi:10.1088/1361-6633/aba6f0

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Das S, Pashminehazar R, Sharma S, Weber S, Sheppard TL. New dimensions in catalysis research with hard X-ray tomography. Chem Ingenieur Technik (2022) 94(11):1591–610. doi:10.1002/cite.202200082

CrossRef Full Text | Google Scholar

3. Vogt N. Human brain mapping. Nat Methods (2023) 20(12):1869. doi:10.1038/s41592-023-02106-4

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Pittman TB, Shih YH, Strekalov DV, Sergienko AV. Optical imaging by means of two-photon quantum entanglement. Phys Rev A (1995) 52(5):R3429–32. doi:10.1103/physreva.52.r3429

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Yu F, Du K, Ju X, Wang F, Li K, Chen C, et al. Dynamic X-ray speckle-tracking imaging with high-accuracy phase retrieval based on deep learning. IUCrJ (2024) 11(1):73–81. doi:10.1107/s2052252523010114

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Wang F, Li K, Xu M, Ju X, Xiao T. Move contrast X-ray imaging and its applications. Nucl Instr Methods Phys Res Section A: Acc Spectrometers, Detectors Associated Equipment (2023) 1055:168560. doi:10.1016/j.nima.2023.168560

CrossRef Full Text | Google Scholar

7. Xu M, Li K, Xue Y, Wang F, Liu Z, Song Z, et al. Water refilling along vessels at initial stage of willow cuttage revealed by move contrast CT. Front Phys (2023) 11. doi:10.3389/fphy.2023.1174387

CrossRef Full Text | Google Scholar

8. Ju X-L, Deng B, Li K, Yu F-C, Zhang H-P, Xu M-W, et al. Calibrating the linearity between grayscale and element content for X-ray KES imaging of alloys. Nucl Sci Tech (2022) 33(1):1. doi:10.1007/s41365-022-00986-3

CrossRef Full Text | Google Scholar

9. Choi S, Park E-Y, Park S, Kim JH, Kim C. Synchrotron X-ray induced acoustic imaging. Scientific Rep (2021) 11(1):4047. doi:10.1038/s41598-021-83604-3

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Luo H, Lou Y, He K, Jiang Z. Coupling in-situ synchrotron X-ray radiography and FT-IR spectroscopy reveal thermally-induced subsurface microstructure evolution of solid propellants. Combustion Flame (2023) 249:112609. doi:10.1016/j.combustflame.2022.112609

CrossRef Full Text | Google Scholar

11. Brombal L, Arfelli F, Brun F, Di Trapani V, Endrizzi M, Menk R, et al. Edge-illumination spectral phase-contrast tomography. Phys Med and Biol (2024) 69:075027. doi:10.1088/1361-6560/ad3328

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Xu M, Li K, Xue Y, Wang F, Liu Z, Xiao T. Measurement of mass force field driving water refilling of cuttage. Scientific Rep (2024) 14(1):8947. doi:10.1038/s41598-024-59716-x

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Kingston AM, Myers GR, Pelliccia D, Svalbe ID, Paganin DM. X-ray ghost-tomography: artefacts, dose distribution, and mask considerations. IEEE Trans Comput Imaging (2019) 5(1):136–49. doi:10.1109/tci.2018.2880337

CrossRef Full Text | Google Scholar

14. Schori A, Borodin D, Tamasaku K, Shwartz S. Ghost imaging with paired x-ray photons. Phys Rev A (2018) 97(6):JTh2A.7. doi:10.1364/cleo_at.2018.jth2a.7

CrossRef Full Text | Google Scholar

15. Yu H, Lu R, Han S, Xie H, Du G, Xiao T, et al. Fourier-Transform ghost imaging with hard X rays. Phys Rev Lett (2016) 117(11):113901. doi:10.1103/physrevlett.117.113901

PubMed Abstract | CrossRef Full Text | Google Scholar

16. He Y-H, Zhang A-X, Li M-F, Huang Y-Y, Quan B-G, Li D-Z, et al. High-resolution sub-sampling incoherent x-ray imaging with a single-pixel detector. APL Phontonics (2020) 5(5):056102. doi:10.1063/1.5140322

CrossRef Full Text | Google Scholar

17. Zhang H, Li K, Zhao C, Tang J, Xiao T. Efficient implementation of x-ray ghost imaging based on a modified compressive sensing algorithm. Chin Phys B (2022) 31(6):064202. doi:10.1088/1674-1056/ac48f7

CrossRef Full Text | Google Scholar

18. Zhang H, Du K, Zhao C, Tang J, Si S, Jia W, et al. Optimizing the ordering of the Hadamard masks of ghost imaging suitable for the efficient face reconstruction using the max-projection method. Scientific Rep (2023) 13(1):22702. doi:10.1038/s41598-023-48453-2

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Tan Z, Yu H, Zhu R, Lu R, Han S, Xue C, et al. Single-exposure Fourier-transform ghost imaging based on spatial correlation. Phys Rev A (2022) 106(5):053521. doi:10.1103/physreva.106.053521

CrossRef Full Text | Google Scholar

20. Ratner D, Cryan JP, Lane TJ, Li S, Stupakov G. Pump-probe ghost imaging with SASE FELs. Phys Rev X (2019) 9(1):011045. doi:10.1103/physrevx.9.011045

CrossRef Full Text | Google Scholar

21. Driver T, Li S, Champenois EG, Duris J, Ratner D, Lane TJ, et al. Attosecond transient absorption spooktroscopy: a ghost imaging approach to ultrafast absorption spectroscopy. Phys Chem Chem Phys (2020) 22(5):2704–12. doi:10.1039/c9cp03951a

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Li K, Laksman J, Mazza T, Doumy G, Koulentianos D, Picchiotti A, et al. Ghost-imaging-enhanced noninvasive spectral characterization of stochastic x-ray free-electron-laser pulses. Commun Phys (2022) 5(1):191. doi:10.1038/s42005-022-00962-8

CrossRef Full Text | Google Scholar

23. Shapiro JH. Computational ghost imaging. Phys Rev A (2008) 78(6):061802. doi:10.1103/physreva.78.061802

CrossRef Full Text | Google Scholar

24. Zhang H-P, Zhao C-Z, Ju X-L, Tang J, Xiao T-Q. Improving quality of crystal diffraction based X-ray ghost imaging through iterative reconstruction algorithm. Acta Phys Sin (2022) 71(7):074201. doi:10.7498/aps.71.20211978

CrossRef Full Text | Google Scholar

25. Zhao C-Z, Si S-Y, Zhang H-P, Xue L, Li Z-L, Xiao T-Q. Beam splitting characteristics of crystal X-ray Laue diffraction. Acta Phys Sin (2022) 71(4):046101. doi:10.7498/aps.71.20211674

CrossRef Full Text | Google Scholar

26. CZ Zhao, SY Si, QS Diao, Z Hong, ZL Li, and TQ Xiao. Development of stress-free Laue diffraction crystal for x-ray beam splitting. Proc. SPIE 13069, International Conference on Optical and Photonic Engineering (icOPEN 2023), February 15, 2024 (2024). doi:10.1117/12.3021665

CrossRef Full Text | Google Scholar

27. Pelliccia D, Rack A, Scheel M, Cantelli V, Paganin DM. Experimental X-ray ghost imaging. Phys Rev Lett (2016) 117(11):113902. doi:10.1103/physrevlett.117.113902

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Schori A, Shwartz S. X-ray ghost imaging with a laboratory source. Opt Express (2017) 25(13):14822. doi:10.1364/oe.25.014822

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Pelliccia D, Olbinado MP, Rack A, Kingston AM, Myers GR, Paganin DM. Towards a practical implementation of X-ray ghost imaging with synchrotron light. IUCrJ (2018) 5(4):428–38. doi:10.1107/s205225251800711x

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Zhao C-Z, Zhang H-P, Tang J, Zhao N-X, Li Z-L, Xiao T-Q. X-ray ghost imaging with a specially developed beam splitter. J Synchrotron Radiat (2024) 31(6):1525–33. doi:10.1107/s1600577524008038

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Zhao C-Z, Si S-Y, Zhang H-P, Xue L, Li Z-L, Xiao T-Q. Intensity correlation properties of x-ray beams split with Laue diffraction. Chin Phys B (2024) 33(1):014102. doi:10.1088/1674-1056/acf206

CrossRef Full Text | Google Scholar

32. Zhang A-X, He Y-H, Wu L-A, Chen L-M, Wang B-B. Tabletop x-ray ghost imaging with ultra-low radiation. Optica (2018) 5(4):374–7. doi:10.1364/optica.5.000374

CrossRef Full Text | Google Scholar

33. Sefi O, Klein Y, Strizhevsky E, Dolbnya IP, Shwartz S. X-ray imaging of fast dynamics with single-pixel detector. Opt Express (2020) 28(17):24568. doi:10.1364/oe.396497

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Li H, Hou W, Ye Z, Yuan T, Shao S, Xiong J, et al. Resolution-enhanced x-ray ghost imaging with polycapillary optics. Appl Phys Lett (2023) 123(14):141101. doi:10.1063/5.0168704

CrossRef Full Text | Google Scholar

35. Li H, Ye Z, Yuan T, Hua L, Zhong Y, Hu J, et al. Magnified x ray ghost imaging with tapered polycapillary optics free of the penumbra effect. Opt Lett (2024) 49(2):274–7. doi:10.1364/ol.506276

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Zhao N, Tang J, Zhao C, Wu J, Zhang H, Guo H, et al. Synthetic aperture X-ray ghost imaging with sub-micron pixel resolution. Opt Express (2025) 33(1):972–82. doi:10.1364/oe.547730

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Zhao N, Tang J, Zhao C, Wu J, Zhang H, Guo H, et al. Global ghost imaging. J. Opt. Soc. Am. B(2025). doi:10.1364/JOSAB.546265

CrossRef Full Text | Google Scholar

38. Ceddia D, Paganin DM. Random-matrix bases, ghost imaging, and x-ray phase contrast computational ghost imaging. Phys Rev A (2018) 97(6):062119. doi:10.1103/physreva.97.062119

CrossRef Full Text | Google Scholar

39. Olbinado MP, Paganin DM, Cheng Y, Rack A. X-ray phase-contrast ghost imaging using a single-pixel camera. Optica (2021) 8(12):1538–44. doi:10.1364/optica.437481

CrossRef Full Text | Google Scholar

40. He Y-H, Zhang A-X, Yu W-K, Chen L-M, Wu L-A. Energy-selective X-ray ghost imaging. Chin Phys Lett (2020) 37(4):044208. doi:10.1088/0256-307x/37/4/044208

CrossRef Full Text | Google Scholar

41. Y-H He, A-X Zhang, Y-Y Huang, W-K Yu, L-M Chen, and L-A Wu, editors. Spectroscopic X-ray ghost imaging. 14th pacific rim conference on lasers and electro-optics (CLEO PR 2020). Sydney: Optica Publishing Group (2020).

Google Scholar

42. Klein Y, Sefi O, Schwartz H, Shwartz S. Chemical element mapping by x-ray computational ghost fluorescence. Optica (2022) 9(1):63–70. doi:10.1364/optica.441682

CrossRef Full Text | Google Scholar

43. Klein Y, Schori A, Dolbnya IP, Sawhney K, Shwartz S. X-ray computational ghost imaging with single-pixel detector. Opt Express (2019) 27(3):3284. doi:10.1364/oe.27.003284

PubMed Abstract | CrossRef Full Text | Google Scholar

44. Zhang H, Li K, Wang F, Yu H, Zhao C, Du G, et al. Megapixel X-ray ghost imaging with a binned detector in the object arm. Chin Opt Lett (2022) 20(3):033401. doi:10.3788/col202220.033401

CrossRef Full Text | Google Scholar

45. Li C, Yin W, Jiang H, Zhang Y. An efficient augmented Lagrangian method with applications to total variation minimization. Comput Optimization Appl (2013) 56(3):507–30. doi:10.1007/s10589-013-9576-1

CrossRef Full Text | Google Scholar

46. Li C. An efficient algorithm for total variation regularization with applications to the single pixel camera and compressive sensing [Master]. Houston, Texas, USA: Rice University (2010).

Google Scholar

47. Zhang H. Investigation on megapixel X-ray ghost imaging with low radiation dose [Doctor]. Shanghai, China: The University of Chinese Academy of Sciences Shanghai Institute of Applied Physics (2023).

Google Scholar

48. Xie H-L, Deng B, Du G-H, Fu Y-N, Guo H, Xue Y-L, et al. Methodology development and application of X-ray imaging beamline at SSRF. Nucl Sci Tech (2020) 31(10):102. doi:10.1007/s41365-020-00805-7

CrossRef Full Text | Google Scholar

49. Wang Z, Bovik AC, Sheikh HR, Simoncelli EP. Image quality assessment: from error visibility to structural similarity. IEEE Trans Image Process (2004) 13(4):600–12. doi:10.1109/tip.2003.819861

PubMed Abstract | CrossRef Full Text | Google Scholar

50. Simonyan K, Zisserman A. Very deep convolutional networks for large-scale image recognitions. San Diego, CA, USA: International Conference on Learning Representation (2015).

Google Scholar