First-principles investigations on the thermal transport and thermoelectric properties of anti-perovskite M3OI and M4OI2 (M = K, Rb)

The thermal transport and thermoelectric properties of anti-perovskite M₃IO and M₄I₂O (M = K, Rb) were investigated using first-principles calculations combined with solution of the Boltzmann transport equation. The two-phonon scattering channel was also considered. These structures formed M₆O octahedra, accompanied by a rattling motion of the O atoms. They exhibit ultra-low lattice thermal conductivity, ranging from 0.30 to 0.89 W m^-1 K⁻¹ at room temperature. M₄I₂O demonstrates strong anisotropic thermal transport due to weaker bonding interactions along the zz direction, while M₃IO shows isotropic thermal conductivity. Specifically, Rb₄OI₂ has the lowest lattice thermal conductivity of 0.47 W m^-1 K⁻¹ along the xx direction and 0.30 W m^-1 K⁻¹ along the zz direction. Additionally, M₃IO possesses low lattice thermal conductivity of 0.52 W m^-1K⁻¹, attributed to the softening behavior of the TA branch at the M and R points. The electronic structure of M₃IO and M₄OI₂ reveals a multi-valley phenomenon in the valence band, resulting in a large Seebeck coefficient under p-type doping. Our results indicate maximum thermoelectric figure of merit (ZT) values of 1.91 for p-type Rb₃OI, and 1.41 for p-type Rb₄OI₂ along the zz direction at 900 K. Rb₃OI and Rb₄OI₂ were proposed as potential p-type thermoelectric materials.

1 Introduction

The energy shortage crisis is intensifying, making the search for sustainable and clean energy sources an urgent priority. Thermoelectric (TE) materials, which can convert thermal energy into electrical energy without generating additional pollution [1–3], show great promise in alleviating energy shortages and environmental pollution. Thermoelectric devices have the advantage of compact, lightweight, durable, and noiseless [4, 5]. The thermoelectric efficiency of materials is typically measured by the dimensionless figure of merit (ZT) [6]. High-performance thermoelectric materials must simultaneously exhibit a high thermoelectric power factor and low thermal conductivity [7]. However, the electronic conductivity and thermal conductivity are inherently coupled, which makes it challenging to achieve high electrical conductivity while maintaining a low electronic thermal conductivity. To overcome this challenge, researchers employ strategies such as introducing defects, alloys, nanostructures, and suppressing the lattice thermal conductivity (κ_L) [8–14]. Therefore, searching low lattice thermal conductivity materials are important for improving the thermoelectric performance.

The perovskite structure has been classified as a “phonon glass, electron crystal” structure [15]. The octahedral framework vibrations and rattling behavior in anti-perovskite compounds induce strong anharmonic phonon scattering [16, 17], leading to intrinsically low lattice thermal conductivity. Some anti-perovskite derivatives, such as Rb₃AuO [18], Rb₃ITe [19], Ca₆NFSn₂ and Sr₆NFSn₂ [20] demonstrate exceptional thermoelectric performance due to their ultra-low κ_L. For instance, the room temperature κ_L of Rb₃AuO is 0.73 W m^-1 K⁻¹, and the cubic phase of Rb₃ITe achieves an ultra-low κ_L of 0.16 W m^-1 K⁻¹ at room temperature. At 800 K, both materials attain ZT > 3, outperforming traditional inorganic thermoelectric materials such as Bi₂Te₃ [21], SnSe [22], and lead chalcogenide compounds (with typical ZT values greater than 1) [23]. Moreover, Ca₆NFSn₂ and Sr₆NFSn₂ exhibit higher electrical conductivity than the halide perovskite CsSnI₃ [24]. When coupled with their low lattice thermal conductivity, the calculated ZT values achieve 1.9 and 2.3, respectively.

In this work, we employed first-principles calculations and the Boltzmann transport equation to study the thermal transport and thermoelectric properties of anti-perovskite M₃OI and M₄OI₂(M = K, Rb). Due to their ultra-low lattice thermal conductivity, the dual-phonon channel model was discussed, which includes the contribution of diffuson-like phonon to the lattice thermal conductivity. The calculated κ_L values are about of 0.30–0.89 W m^-1 K⁻¹ at room temperature due to low phonon group velocity and short phonon lifetime. Furthermore, the multi-valley band structure increases the degeneracy of the energy bands, resulting in higher Seebeck coefficients (S) in p-type doping. The p-type anti-perovskite Rb₃OI achieves a maximum ZT of 1.91 at 900 K, demonstrating its potential for thermoelectric applications.

2 Computational methods

First-principles calculations were executed within the framework of the Vienna Ab Initio Simulation Package (VASP). It was performed using the Projector Augmented Wave (PAW) method, incorporating the Perdew–Burke–Ernzerhof (PBE) parametrization of the generalized gradient approximation (GGA) for the exchange correlation functional. The electronic properties were investigated based on the hybrid density functional theory (HSE06). The structures of the primitive cells were optimized until the atomic force converged to less than 10^–4 eV/Å. The energy cutoff and convergence criterion were set to 520 eV and 10^–7 eV, respectively. A 9 × 9 × 9 Γ-centered Monkhorst-Pack k-point mesh was employed to calculate the second- and third-order interatomic force constants (IFCs), which were subsequently utilized to study both harmonic and anharmonic phonon properties. Furthermore, the ShengBTE code was used to compute the lattice thermal conductivity of the materials via the phonon Boltzmann transport equation (BTE), as shown in the following Equation 1:

${\mathit{\kappa }}_{\mathit{\iota }}=\frac{\mathbf{1}}{\mathbf{3}}{\complement }_{\mathit{\nu }}{\mathit{\nu }}_{\mathit{g}}\mathit{\lambda }(1)$

where C_v is the specific heat, V_g is the group velocity, and λ is the mean free path. To ensure the convergence of the thermal conductivity calculations, a cutoff radius of 0.8 nm was implemented to limit the range of the third-order force constants. For the electrical transport properties, the ab initio scattering and transport (AMSET) software package was used to calculate carrier lifetimes, considering scattering processes due to acoustic deformation potential (ADP), ionized impurities (IMP), and polar-optical phonons (POP). The interpolation parameter ‘interpolation_factor’ is added to 110 to ensure the calculation accuracy and convergence. The final electron scattering time was derived using the following Equation 2, based on Matthiessen’s rule:

$\frac{\mathbf{1}}{\mathit{\tau }}=\frac{\mathbf{1}}{{\mathit{\tau }}^{\mathit{A}\mathit{D}\mathit{P}}}+\frac{\mathbf{1}}{{\mathit{\tau }}^{\mathit{P}\mathit{O}\mathit{P}}}+\frac{\mathbf{1}}{{\mathit{\tau }}^{\mathit{I}\mathit{M}\mathit{P}}}(2)$

3 Results and discussion

3.1 Structure and charge density

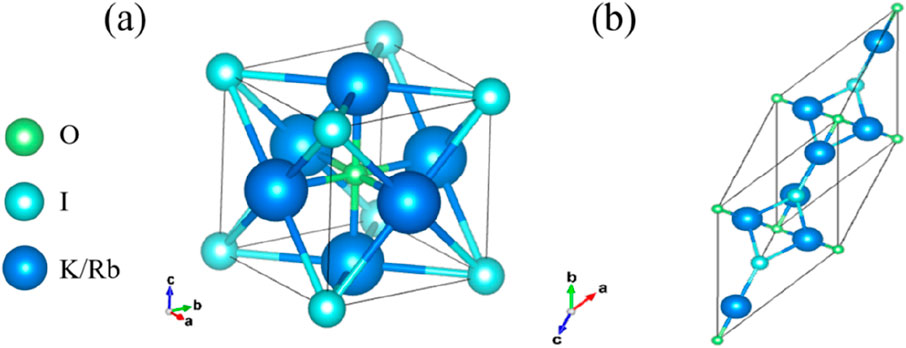
M₃OI (M = K, Rb) compounds exhibit simple anti-perovskite structures, following the general formula ABX₃. As illustrated in Figure 1a, the crystal structures of K₃OI and Rb₃OI crystallize within the Pm3m space group. In these structures, the alkali metals (M = K, Rb) occupy the X-sites within the unit cell, while the oxygen (O) ions occupy the B-sites. This arrangement results in M₆O octahedra formed by the oxygen anions and the alkali metal cations [25, 26]. The iodine (I) atoms are situated at the A-sites, which are located at the corners of the unit cell. Figure 1b depicts the crystal structure of anti-perovskite derivatives K₄OI₂ and Rb₄OI₂, which bear resemblance to the (La, Ba)CuO₄ structure. These compounds belong to the tetragonal crystal system and crystallize in the space group I4/mmm. In this structure, two distinct alkali metal sites are presented, as noted in previous studies [27]. Supplementary Figure S1 highlights the layered nature of this arrangement, where alternating M₃OI and MI layers are stacked along the z-axis(c), mirroring the structural arrangement seen in Na₄OI₂ [28].

Figure 1

Figure 1. (a) The unit cell of K₃OI and Rb₃OI, (b) the unit cell of K₄OI₂ and Rb₄OI₂.

The optimized lattice constants for these four structures are summarized in Table 1. K₃OI has been successfully synthesized in experiments [29]. Additionally, Table 1 provides bond lengths for each structure, along with key mechanical properties such as elastic constants, bulk modulus (B), Young’s modulus (E), shear modulus (G), and the Debye temperature (Θ) [30]. The force constant for M₃OI (M = K, Rb) adheres to the mechanical stability criterion in Equation 3, while M₄OI₂ (M = K, Rb) meets the mechanical stability criterion in Equation 4. Therefore, all four structures are mechanically stable [31].

${\mathit{C}}_{\mathbf{11}}-{\mathit{C}}_{\mathbf{12}}>\mathbf{0};{\mathit{C}}_{\mathbf{11}}+\mathbf{2}{\mathit{C}}_{\mathbf{12}}>\mathbf{0};{\mathit{C}}_{\mathbf{44}}>\mathbf{0}(3)$

${\mathit{C}}_{\mathbf{11}}\left.>\right|{\mathit{C}}_{\mathbf{12}}|;\mathbf{2}{\mathit{C}}_{\mathbf{13}}^{\mathbf{2}}<{\mathit{C}}_{\mathbf{33}}\left({\mathit{C}}_{\mathbf{11}}{+\mathit{C}}_{\mathbf{12}}\right);{\mathit{C}}_{\mathbf{44}}>\mathbf{0};{\mathit{C}}_{\mathbf{66}}>\mathbf{0}(4)$

Table 1

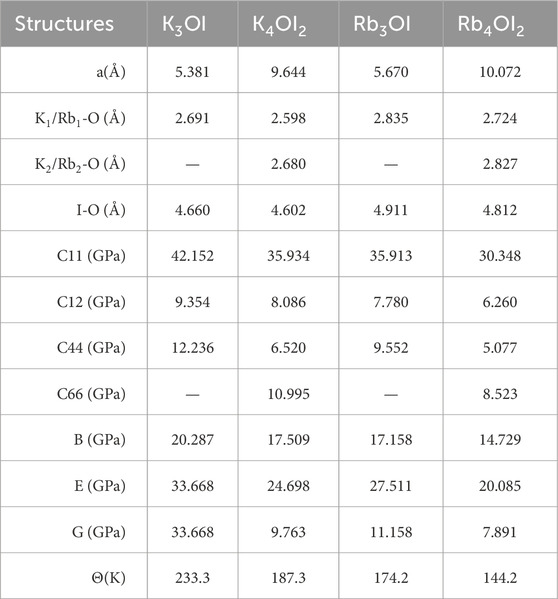
Table 1. Lattice constant (a), bond lengths, elastic constants (C), bulk modulus(B), Young’s modulus(E), shear modulus(G), and Debye temperature(Θ) of the M₃OI and M₄OI₂ (M = K, Rb).

Debye temperature serves as an indicator of the bond strength of materials, with a positive correlation between these two parameters. Among the studied materials, K₃OI exhibits the highest Debye temperature of 233.3 K, followed by K₄OI₂ of 187.3 K and Rb₃OI of 174.2 K. The lowest Debye temperature of 144.2 K is observed in Rb₄OI₂. This trend is consistent with the bond length of them. We find that all the Debye temperatures are significantly below the room temperature of 300 K, suggesting that the M₃OI and M₄OI₂ compounds exhibit pronounced anharmonic behavior.

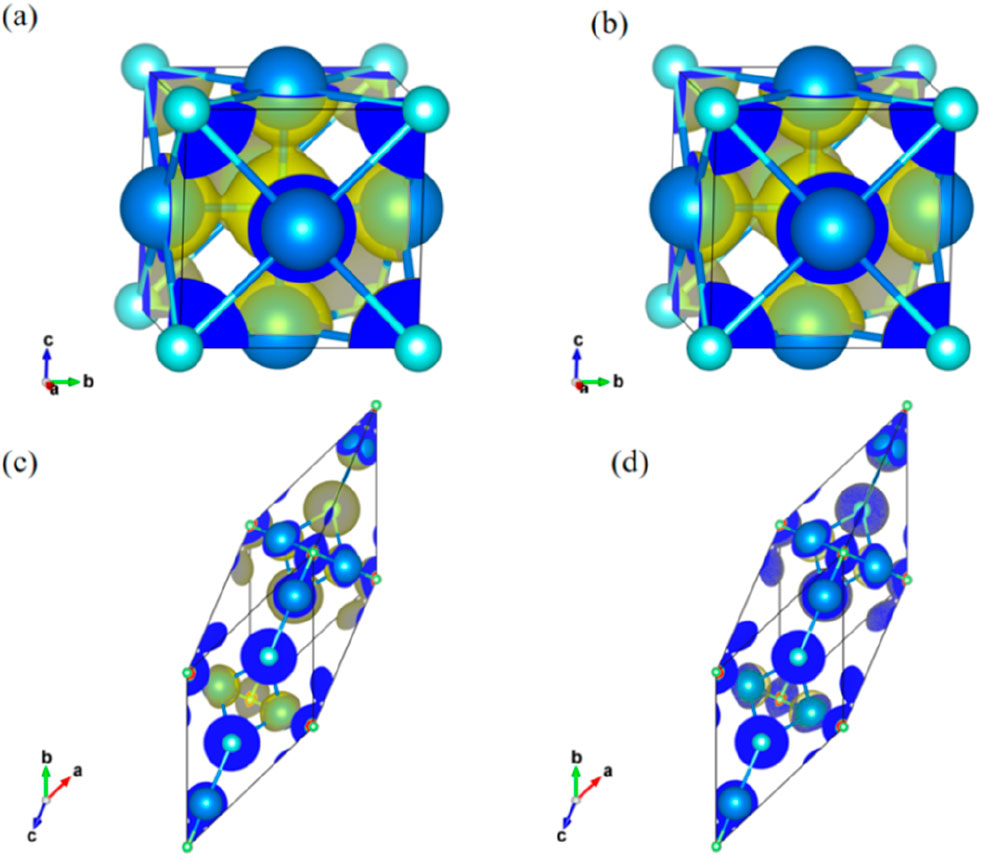
The charge density in Figure 2 shows a typical covalent bond charge distribution between the alkali metal M and the oxygen (O) element. Specifically, the strong covalent bond between the alkali metal M and O forms a stable M₆O octahedral framework structure. In contrast, the iodine (I) element exhibits a strong electronic localization phenomenon, with weaker bonding to other atoms. By comparing the charge densities in Figures 2a,b for K₃OI and Rb₃OI, and in Figures 2c,d for K₄OI₂ and Rb₄OI₂, it can be observed that the Rb-O bond is weaker than the K-O bond, which is consistent with the results of bond length in Table 1.

Figure 2

Figure 2. The charge density plot of (a) K₃OI, (b) Rb₃OI, (c) K₄OI₂ and (d)Rb₄OI₂.

3.2 Thermal transport property

The phonon dispersion spectra show that K₃OI, K₄OI₂, Rb₃OI, and Rb₄OI₂ exhibit no imaginary frequencies under the harmonic approximation in Figure 3, indicating that these materials are thermodynamically stable. The high-frequency optical branches are primarily contributed by the vibration modes of the oxygen (O) atoms, while the low-frequency optical and acoustic branches are dominated by the heavier iodine (I) and alkali metal (K, Rb) elements. The phonon dispersions for all four structures exhibit strong phonon-optical coupling within the low-frequency optical and acoustic branch regions, which is typically accompanied by peaks in the phonon density of states (PDOS). A comparison between Figures 3a,c reveals that the highest optical branch frequency for K₃OI is 9 THz, which is higher than the 8 THz for Rb₃OI. K₃OI exhibits stronger phonon dispersion, particularly in the acoustic branch, with the phonon group velocity for K₃OI (0–1.44 THz) being significantly higher than for K₄OI₂ (0–1.19 THz). Similarly, Figures 3b,d show that the highest optical branch frequencies for K₄OI₂ and Rb₄OI₂ are 9 THz (K₄OI₂) and 8 THz (Rb₄OI₂), respectively, while the highest frequencies for the acoustic branches are 1.11 THz (K₄OI₂) and 1.00 THz (Rb₄OI₂). These materials have lower maximum acoustic branch frequencies compared to strong anharmonic materials such as Na2TlSb [32] (∼1.4 THz) and SnSe [33] (∼1.45 THz). Generally, when atoms of a similar structure are replaced with heavier elements, the phonon modes tend to shift to lower frequencies, which reduces the phonon group velocity and consequently suppresses the thermal conductivity. In the M₄OI₂, the enhanced phonon-optical coupling relative to M₃OI provides more phonon scattering channels for the material. Notably, the phonon dispersion for Rb₃OI shows a pronounced softening of the TA branch at the M and R points, a phenomenon commonly observed in cubic perovskite structures. This ferroelectric-like vibration behavior is typically attributed to vibrations in the octahedral framework [34, 35]. Figure 4 illustrates the TA branch vibration modes at the high-symmetry M and R points for K₃OI and Rb₃OI. At the M point, the I atoms in K₃OI exhibit in-plane motion along the positive and negative z-axis (c) directions, while in Rb₃OI, the I atoms undergo in-plane motion within the xy (ab) plane with some rotational motion, and the O atoms exhibit a rattling behavior similar to that in octahedral structures. Figures 4b,d show that at the R point, the K atoms in K₃OI undergo opposing movements around the axis within the xy plane, leading to octahedral distortion, while in Rb₃OI, the I atoms exhibit in-plane motion along the positive and negative y-axis directions. In addition to the octahedral distortion [36], the rattling behavior within the octahedral cage is often considered a source of strong anharmonicity in anti-perovskite materials [37].

Figure 3

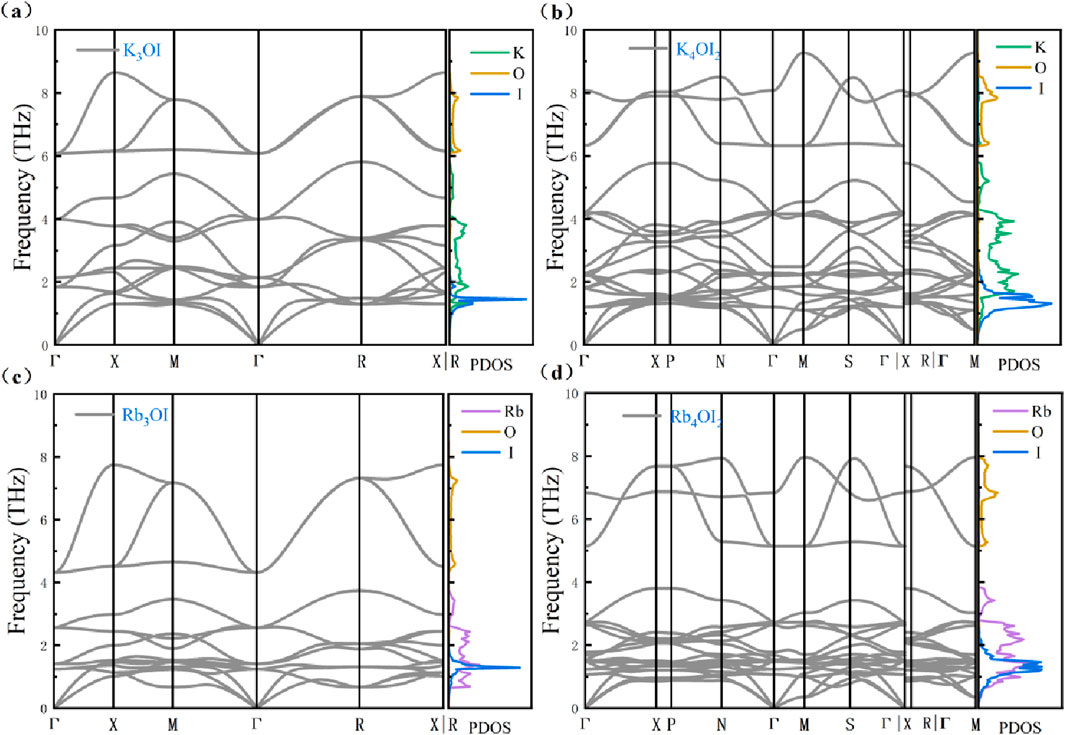
Figure 3. Phonon band and phonon density of states of (a) K₃OI, (b) K₄OI₂, (c) Rb₃OI and (d) Rb₄OI₂.

Figure 4

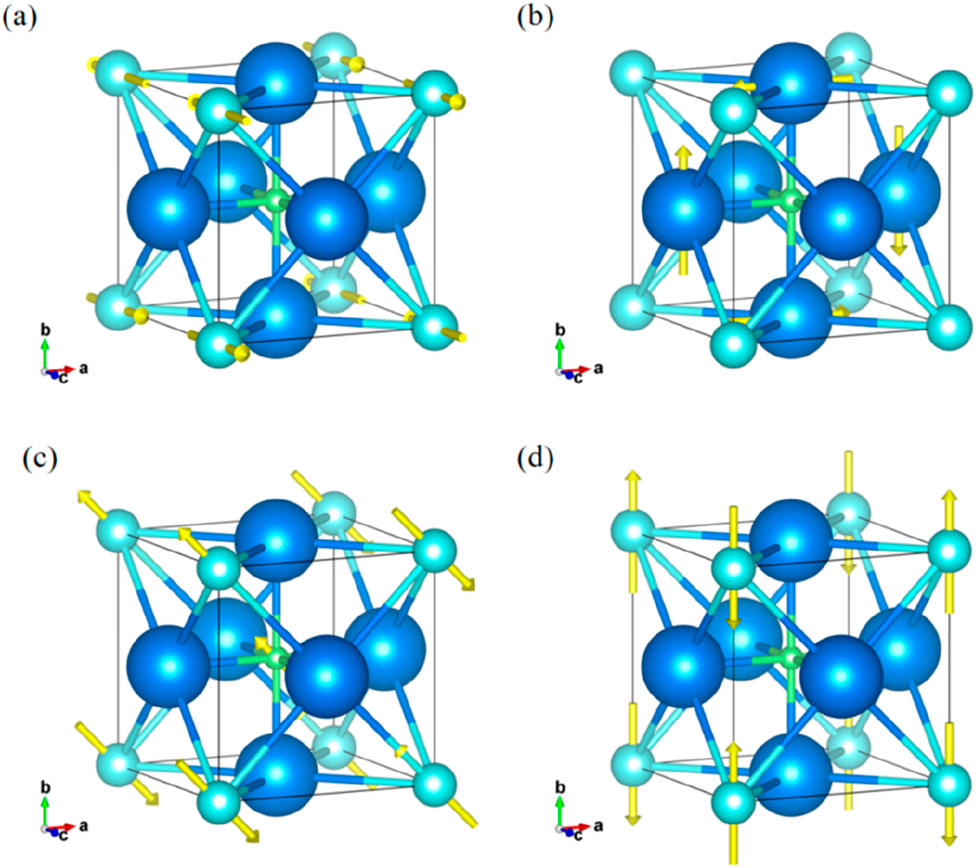
Figure 4. The vibrational modes of the Transverse Acoustic Branch (TA) at high-symmetry points M and R, and yellow arrows indicate the vibration directions, and their lengths represent the vibration amplitudes. (a) The vibrational mode of K₃OI at point M; (b) The vibrational mode of K₃OI at point R; (c) The vibrational mode of Rb₃OI at point M; (d) The vibrational mode of Rb₃OI at point R.

We employed the diffusion-like model of dual-phonon [38] with shengBTE to calculate the κ_L of these materials in the temperature range of 100–900 K. as shown in Figure 5a and Supplementary Figure S2. The lattice thermal conductivity decreases with increasing temperature. We find that Rb₄OI₂ along the zz (c)direction has the lowest thermal conductivity with and without considering the contribution of the diffuson-like phonon. At 300 K, when the two-phonon channel is neglected, it is 0.18 W m^-1 K⁻¹, lower than the 0.20 W m^-1 K⁻¹ reported for SnSe [22]. On the other hand, the K₃OI and Rb₃OI exhibit isotropic thermal conductivity while that for K₄OI₂ and Rb₄OI₂ show significant anisotropy. After considering the dual-phonon channel, the lattice thermal conductivity of K₃OI and Rb₃OI are 0.89 W m^-1 K⁻¹ and 0.52 W m^-1 K⁻¹, respectively. The lattice thermal conductivity of K₄OI₂ and Rb₄OI₂ is 0.71 W m^-1 K⁻¹ and 0.47 W m^-1 K⁻¹ along the xx direction, and 0.42 W m^-1 K⁻¹ and 0.30 W m^-1 K⁻¹ along the zz direction, respectively. At room temperature, the κ_L of these materials is comparable to the industry standard PbTe [39] and significantly lower than most oxide thermoelectric materials [40–43]. At higher temperatures, κ_L remains below 1 W m^-1 K⁻¹, which is a characteristic feature of high-performance thermoelectric materials.

Figure 5

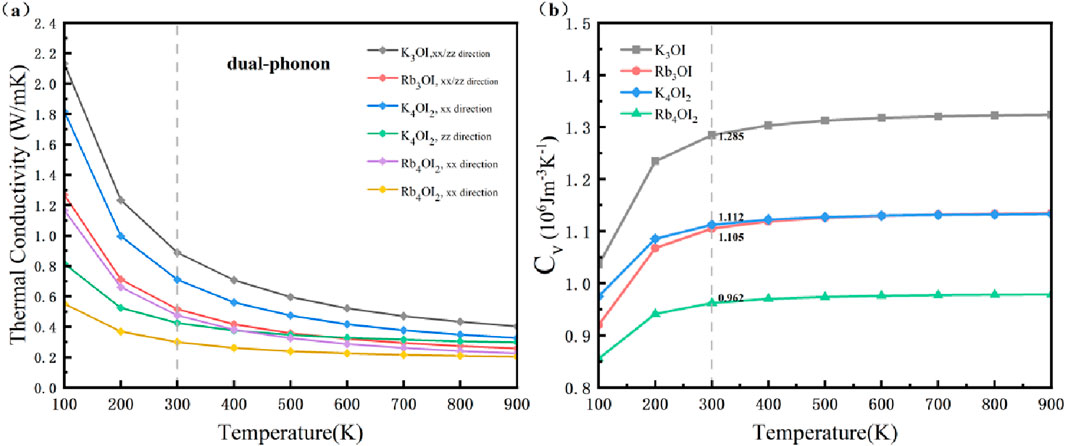
Figure 5. (a) The variation of lattice thermal conductivity (κ_L) with temperature after considering dual-phonon transport. (b) The variation of specific heat capacity (C_v) with temperature.

Heat capacity curve in Figure 5b shows that the specific heat capacity increases gradually with temperature in the range of 100–400 K. After 400 K, the heat capacities of the materials tend to converge. Over the entire temperature range, K₃OI and Rb₄OI₂ exhibit the highest and the lowest specific heat capacity, respetively. At 300 K, the specific heat capacities of K₄OI₂ and Rb₃OI are 1.112 × 10⁶ Jm^-3K⁻¹ and 1.105 × 10⁶ Jm^-3K⁻¹, respectively, while the heat capacity curves of the two materials nearly overlap beyond 400 K. Cumulative lattice thermal conductivity, as shown in Supplementary Figure S3, indicates that at 300 K, the lattice thermal conductivity is primarily contributed by phonon modes with an average free path (MFP) below 10 nm. ShengBTE results reveal that the high-frequency optical branches of these materials significantly contribute to the lattice thermal conductivity due to the strong phonon-optical coupling.

To further investigate the physical mechanisms for the thermal transport of these materials, Figure 6 plots the phonon relaxation time, phonon group velocity, scattering phase space, and Grüneisen parameter. As seen in Figure 6b, at 300 K, the phonon group velocity of K₃OI and K₄OI₂ along the xx direction is higher than that for Rb₃OI and Rb₄OI₂ in the acoustic branches and low-frequency optical branches (0-1.64 THz). In addition, the phonon group velocity of the M₃OI structure is higher than that of the M₄OI₂. The difference in the phonon group velocities between K₃OI and R₃IO or K₄OI₂, is mainly attributed to the increased effective atomic mass. This result aligns well with the phonon dispersion spectrum in Figure 3. The ultra-low lattice thermal conductivity of K₄OI₂ and Rb₄OI₂ in the zz direction, and their remarkable anisotropic structural properties, can be further explained by the softer bonds [44] and the lower phonon group velocity in the zz direction, as seen in Supplementary Figure S4.

Figure 6

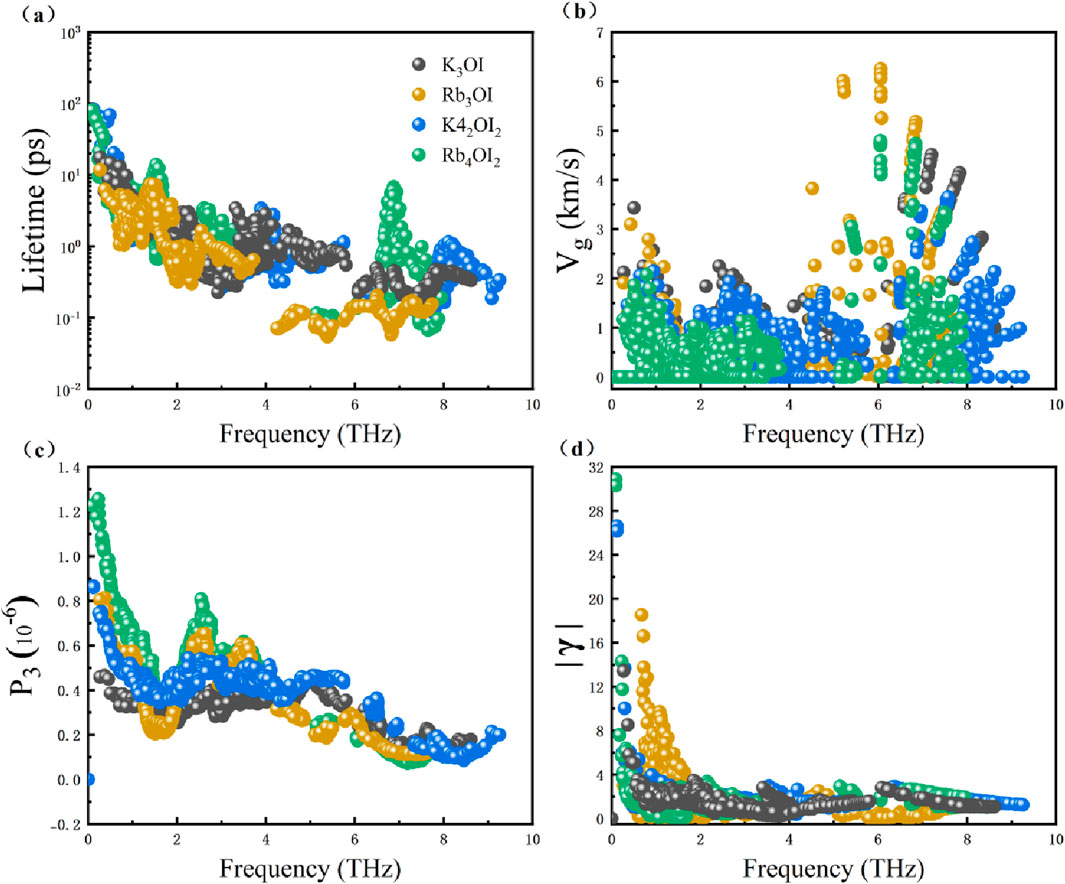
Figure 6. The variation curves of specific phonon thermal transport parameters with phonon frequency at 300 K. (a) Phonon relaxation time, (b) phonon group velocity in the xx direction, (c) P3 scattering phase space, (d) absolute value of the Grüneisen parameter.

Figure 6a presents the phonon relaxation times of these materials. Within the frequency range of the acoustic phonon, K₃OI (0-1.64 THz) and K₄OI₂ (0-1.42 THz) has overall higher phonon relaxation times compared to Rb₃OI (0-1.22 THz) and Rb₄OI₂ (0-1.11 THz), respectively. Moreover, the phonon relaxation times of K₄OI₂ and Rb₄OI₂ structures in the acoustic branch frequency range are larger than those of K₃OI and Rb₃OI structures. Next, we explored the P3 scattering phase space and Grüneisen parameter, as shown in Figures 6c,d. It indicates that K₃OI has the smallest scattering phase space, followed by K₄OI₂, and Rb₄OI₂ exhibits the largest phase space in the low-frequency acoustic branch frequency range (0-1 THz). This phenomenon is attributed to the phonon dispersion becoming more confined in this frequency range (0-1 THz) as the average relative atomic mass increases, which makes it easier for phonon scattering to satisfy the energy conservation law. In the strong phonon-optical coupling frequency range, K₃OI exhibits smaller P3 compared to K₄OI₂, and Rb₃OI is smaller than Rb₄OI₂ due to the increased number of low-frequency optical branches, which strengthens the phonon-optical coupling and increases the scattering channels. Figure 6d displays the Grüneisen parameter at 300 K. The distribution is concentrated in the acoustic and low-frequency optical branch regions, with Rb₃OI showing a distinctly different parameter distribution. Its peak value occurs at ∼1THz, while the other three structures have their peaks near zero frequency. Rb₄OI₂ has a higher Grüneisen parameter than K₄OI₂, and K₄OI₂ is higher than K₃OI. Although Rb₃OI has the lowest Grüneisen parameter in the acoustic branch (0-0.6 THz), its Grüneisen values in the 0.8–1.8 THz range are significantly largest, leading to the highest overall Grüneisen parameter and strongest phonon anharmonicity, and then the lowest phonon relaxation times. Additionally, the Grüneisen parameter distribution in Rb₃OI is influenced by the softening behavior of the transverse acoustic (TA) branch in the corresponding frequency range, which weakens the coupling with the low-frequency optical branch and leads to weaker phonon-optical coupling and a shift of the Grüneisen peak.

3.3 Electrical transport and thermoelectric properties

The electronic band structures were calculated using the hybrid functional HSE06. As shown in Figure 7. The electronic band gaps are 2.18 eV (K₃OI), 2.40 eV (K₄OI₂), 1.61 eV (Rb₃OI), and 1.92 eV (Rb₄OI₂), all of which are direct band gaps. The valence bands are primarily composed of the oxygen (O) orbitals, while the conduction bands are derived from the combined contributions of the alkali metals (K and Rb) and halogen (I) elements. The flat electronic band structure of the valence band indicates that it possesses a larger effective carrier mass, resulting in a lower carrier mobility. On the other hand, the significant band dispersion in the conduction band at the high-symmetry Γ point suggests that carriers near the conduction band exhibit a smaller effective mass and higher mobility. Notably, the valence band demonstrates a distinct multi-valley structure [45], which is often associated with high Seebeck coefficients of thermoelectrics [46].

Figure 7

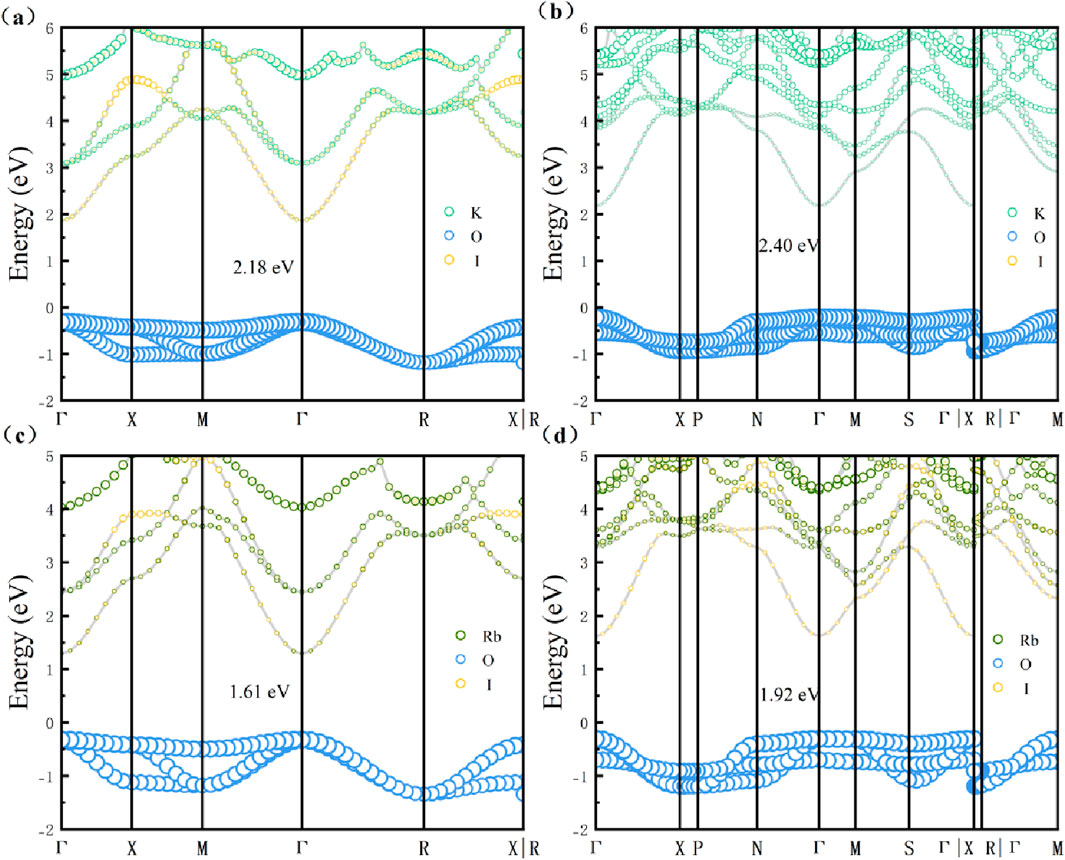
Figure 7. Projected electronic band diagram of (a) K₃OI, (b) K₄OI₂, (c) Rb₃OI, (d) Rb₄OI₂. The diameter of the circle is proportional to their orbital weight.

The electronic transport properties of materials were studied using the AMSET software based on the electronic band structure. Figure 8 presents the computed electrical conductivity (σ), Seebeck coefficient (S), electronic thermal conductivity (κ_e), and power factor (PF) at different temperatures (300 K, 600 K, and 900 K). From Figures 8a,b, the electrical conductivity of n-type semiconductors is one order of magnitude higher than that of the corresponding p-type semiconductors. It is noteworthy that the electrical conductivity of the anisotropic material along the zz direction is the lowest, with a value ∼1 S/m at a carrier concentration of 10¹⁹ cm^-3.

Figure 8

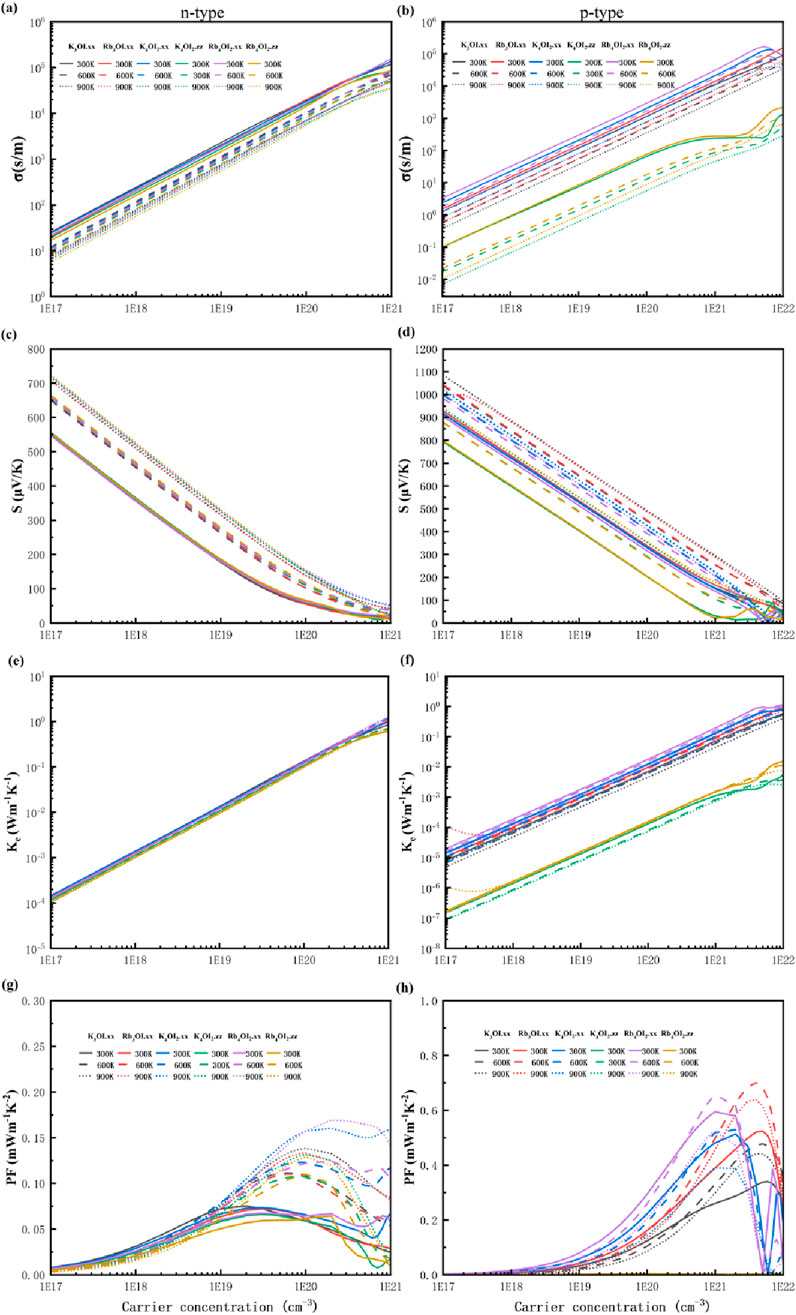
Figure 8. (a) The electronic conductivity (σ), (c) Seebeck coefficient (S), (e) electronic thermal conductivity (κ_e) and (g) power factor (PF) of n-type materials. (b) The electronic conductivity (σ), (d) Seebeck coefficient (S), (f) electronic thermal conductivity (κ_e) and (h) power factor (PF) of p-type materials.

The Seebeck coefficient (S) of the p-type semiconductors is significantly higher than that of n-type ones, which can be attributed to the multi-valley phenomenon in the valence band of the electronic structure. For instance, at a carrier concentration of 10¹⁹ cm^-3, the Seebeck coefficient (S) of Rb₃OI ranges from 527 to 684 µVK^-1 between 300 K and 900K, which is higher than the 600 µVK^-1 of Rb₃AuO [7]. And it is notably higher than the typical range (200–300 µVK^-1) found in thermoelectric power materials [47]. Additionally, S decreases with increasing temperature as the carrier concentration decreases, which is consistent with the trend for the most semiconductor thermoelectric materials due to carrier excitation by heat.

According to the Wiedemann-Franz law, electrical conductivity is proportional to the electronic thermal conductivity. When doping concentration is low, the electronic thermal conductivity can be neglected. However, at higher doping concentrations, the electronic thermal conductivity becomes comparable to or even greater than the lattice thermal conductivity. The PF of the material is calculated based on the S²σ relationship. Due to the larger Seebeck coefficient (S) of the p-type semiconductors, the power factor of p-type materials is higher than that of n-type semiconductors, with the maximum value reaching 0.7 mWm^-1K⁻² for Rb₃OI at 600 K, with a doping concentration of 4 × 10²¹ cm^-3.

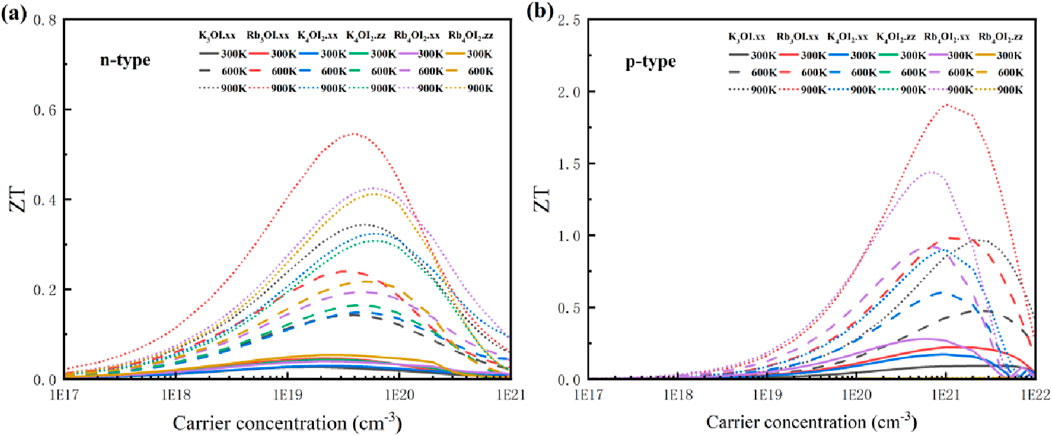
Subsequently, we computed the ZT values for these materials in Figure 9. At 900 K, Rb₃OI exhibits the highest ZT value of 1.91 for p-type doping at the carrier concentration of 1 × 10²¹ cm^-3. The carrier scattering rate of R₃OI with a hole doping concentration of 1 × 10²¹ cm^-3 were shown in Supplementary Figure S5. We found that the carrier scattering rate increased with the rise in temperature due to the thermal excitation of carriers and the scattering rate of carriers was mainly contributed by POP scattering.

Figure 9

Figure 9. Thermoelectric figure of merit (ZT) of M₃OI and M₄OI₂: (a) n-type, (b) p-type.

Next, Rb₄OI₂ shows the maximum ZT value of 1.44 in the zz direction, with a p-type doping concentration of 7 × 10²⁰ cm^-3. In this system, the thermoelectric performance of the p-type semiconductor is superior to that of the n-type, which is attributed to the higher PF resulting from the larger Seebeck coefficient (S). Comparing with the ZT values of some inorganic halide perovskites of CsPbI₃ (0.45), CsSnI₃ (0.95), and CsGeI₃ (1.05) [48], Rb₃OI and Rb₄OI₂ have better thermoelectric performance. The results indicate that Rb₃OI and Rb₄OI₂ have promising potential for advanced thermoelectric device applications.

4 Conclusion

We investigated the thermal transport and thermoelectric properties of M₃IO and M₄I₂O (M = K, Rb). These structures formed M₆O octahedra and rattling behavior of the O atoms existed. The calculated Debye temperatures of these materials are obviously below the room temperature of 300 K. After considering the two-phonon channel, the lattice thermal conductivity ranges from 0.30 to 0.89 W m^-1 K⁻¹ at room temperature. Rb₄OI₂ has the lowest lattice thermal conductivity of 0.47 W m^-1 K⁻¹ and 0.30 W m^-1 K⁻¹ along the xx direction and the zz direction, respectively. Rb₃OI has the lattice thermal conductivity of 0.52 W m^-1K⁻¹. M₃IO exhibits isotropic lattice thermal conductivity while that for M₄I₂O shows significant anisotropy. The phonon group velocity and specific heat capacity of the M₃OI structure are higher than that of the M₄OI₂. However, M₃OI has lower phonon relaxation times due to the softening behavior of the TA branch at the M and R points. And then, their lattice thermal conductivity is comparable. Due to the multi-valley phenomenon in the valence band of the electronic structure, p-type M₃IO and M₄OI₂ have larger Seebeck coefficient (S). The calculated S of Rb₃OI ranges from 527 to 684 µVK^-1 at a carrier concentration of 10¹⁹ cm^-3. We obtained the maximum ZT value of p-type Rb₃OI is 1.91 with the carrier concentration of 1 × 10²¹ cm^-3 at 900 K, and that for p-Rb₄OI₂ is 1.41 in the zz direction at the doping concentration of 7 × 10²⁰ cm^-3. We propose that Rb₃OI and Rb₄OI₂ are promising candidates as p-type thermoelectric materials.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

HX: Visualization, Methodology, Writing – original draft, Formal Analysis, Conceptualization, Data curation, Software, Investigation. TH: Software, Writing – original draft, Investigation, Data curation. PZ: Writing – review and editing, Validation, Supervision. DL: Writing – review and editing, Funding acquisition, Formal Analysis, Validation, Supervision, Project administration.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. We gratefully acknowledge funding supporting from Scientific and Technological Research of Chongqing Municipal Education Commission (KJZD-K202100602).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2025.1619661/full#supplementary-material

References

1. Sootsman J, Chung D, Kanatzidis M. New and old concepts in thermoelectric materials. Angew Chem Int Edition (2009) 48:8616–39. doi:10.1002/anie.200900598

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Yue T, Baolong X, Yinchang Z, Sheng M, Zhenhong D. Ultra-low lattice thermal conductivity and anisotropic thermoelectric transport properties in Zintl compound β-K₂Te₂. Phys Chem Chem Phys (2022) 24(7):4666–73. doi:10.1039/D1CP05248A

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Yinchang Z, Zhenhong D, Chao Z, Chao L, Shuming Z, Geng L, et al. High thermopower and potential thermoelectric properties of crystalline LiH and NaH. Phys Rev B (2017) 95(1):014307. doi:10.1103/PhysRevB.95.014307

CrossRef Full Text | Google Scholar

4. He J, Kanatzidis MG, Dravid VP. High performance bulk thermoelectrics via a panoscopic approach. Mater Today (2013) 16(5):166–76. doi:10.1016/j.mattod.2013.05.004

CrossRef Full Text | Google Scholar

5. Fitriani F, Ovik R, Long BD, Barma MC, Riaz M, Sabri MFM A review on nanostructures of high-temperature thermoelectric materials for waste heat recovery. Renew Sustainable Energy Rev (2016) 64:635–59. doi:10.1016/j.rser.2016.06.035

CrossRef Full Text | Google Scholar

6. Snyder GJ, Toberer ES. Complex thermoelectric materials. Nat Mater (2008) 7(2):105–14. doi:10.1038/nmat2090

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Zhao Y, Lian C, Zeng S, Dai Z, Meng S, Ni J. Anomalous electronic and thermoelectric transport properties in cubic Rb₃AuO antiperovskite. Phys Rev B (2020) 102(9):094314. doi:10.1103/PhysRevB.102.094314

CrossRef Full Text | Google Scholar

8. Zhou LC, Xi H, ZhuYi X, Xie Y. Defect chemistry for thermoelectric materials. J Am Chem Soc (2016) 138(45):14810–9. doi:10.1021/jacs.6b08748

CrossRef Full Text | Google Scholar

9. Hu L, Zhu T, Liu X, Zhao X. Point defect engineering of high-performance bismuth-telluride-based thermoelectric materials. Adv Funct Mater (2014) 24:5211–8. doi:10.1002/adfm.201400474

CrossRef Full Text | Google Scholar

10. Xia Y, Chan MKY. Anharmonic stabilization and lattice heat transport in rocksalt β-GeTe. Appl Phys Lett (2018) 113(19):193902. doi:10.1063/1.5048814

CrossRef Full Text | Google Scholar

11. Chen Z, Gao B, Tang J, Guo X, Li W, Ang R. Low lattice thermal conductivity by alloying SnTe with AgSbTe₂ and CaTe/MnTe. Appl Phys Lett (2019) 115(7):073903. doi:10.1063/1.5109465

CrossRef Full Text | Google Scholar

12. He J, Girard SN, Kanatzidis MG, Dravid VP. Microstructure-lattice thermal conductivity correlation in nanostructured PbTe_0.7S_0.3 thermoelectric materials. Adv Funct Mater (2010) 20:764–72. doi:10.1002/adfm.200901905

CrossRef Full Text | Google Scholar

13. Tadano T, Gohda Y, Tsuneyuki S. Impact of rattlers on thermal conductivity of a thermoelectric clathrate: a first-principles study. Phys Rev Lett (2015) 114(9):095501. doi:10.1103/PhysRevLett.114.095501

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Nolas GS, Poon J, Kanatzidis M. Recent developments in bulk thermoelectric materials. MRS Bull (2006) 31(3):199–205. doi:10.1557/mrs2006.45

CrossRef Full Text | Google Scholar

15. Rowe DM. CRC handbook of thermoelectrics. (1995) 1st ed. Boca Raton: CRC Press doi:10.1201/9781420049718

CrossRef Full Text | Google Scholar

16. Pchelkina ZV, Komleva EV, Irkhina VY, Long Y, Streltsov SV. Rattling phonon modes in quadruple perovskites. JETP Lett (2023) 118(10):738–41. doi:10.1134/S0021364023603202

CrossRef Full Text | Google Scholar

17. Gu T, Scarbrough T, Yang Y, Íñiguez J, Bellaiche L, Xiang HJ. Cooperative couplings between octahedral rotations and ferroelectricity in perovskites and related materials. Phys Rev Lett (2018) 120(19):197602. doi:10.1103/PhysRevLett.120.197602

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Zhao Y, Lian C, Zeng S, Dai Z, Meng S, Ni J. Quartic anharmonicity and anomalous thermal conductivity in cubic antiperovskites A₃BO (A = K, Rb; B = Br, Au). Phys Rev B (2020) 101(18):184303. doi:10.1103/PhysRevB.101.184303

CrossRef Full Text | Google Scholar

19. Shuming Z, Qian S, Lina G, Yinchang Z, Hao H, Geng L, et al. Remarkable thermoelectric efficiency of cubic antiperovskites Rb₃X (Se and Te) I with strong anharmonicity. J Mater Chem A (2023) 11(44):24047–56. doi:10.1039/D3TA04338J

CrossRef Full Text | Google Scholar

20. Dan H, Bonan Z, Zenghua C, Kieran BS, Stefan SR, Wolfgang S, et al. Discovery of multi-anion antiperovskites X₆NFSn₂ (X = Ca, Sr) as promising thermoelectric materials by computational screening. Matter (2024) 7(1):158–74. doi:10.1016/j.matt.2023.10.022

CrossRef Full Text | Google Scholar

21. Ning W, Chen S, Zhehao S, Haiyan X, Hongbin Z, Zongyou Y, et al. High-temperature thermoelectric monolayer Bi₂TeSe₂ with high power factor and ultralow thermal conductivity. ACS Appl Energy Mater (2022) 5(2):2564–72. doi:10.1021/acsaem.1c04109

CrossRef Full Text | Google Scholar

22. Li-Dong Z, Shih-Han L, Yongsheng Z, Hui S, Gangjian T, Ctirad U, et al. Ultralow thermal conductivity and high thermoelectric figure of merit in SnSe crystals. Nature (2014) 508(7496):373–7. doi:10.1038/nature13184

CrossRef Full Text | Google Scholar

23. Witting IT, Chasapis TC, Ricci F, Peters M, Heinz NA, Hautier G, et al. The thermoelectric properties of bismuth telluride. Adv Electron Mater (2019) 5:1800904. doi:10.1002/aelm.201800904

CrossRef Full Text | Google Scholar

24. Wudil YS, Peng Q, Alsayoud AQ, Gondal MA. Hydrostatic pressure-tuning of thermoelectric properties of CsSnI₃ perovskite by first-principles calculations. Comput Mater Sci (2022) 201:110917. doi:10.1016/j.commatsci.2021.110917

CrossRef Full Text | Google Scholar

25. Sales BC, Mandrus D, Williams RK. Filled skutterudite antimonides: a new class of thermoelectric materials. Science (1996) 272(5266):1325–8. doi:10.1126/science.272.5266.1325

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Cohn JL, Nolas GS, Fessatidis V, Metcalf TH, Slack GA. Glasslike heat conduction in high-mobility crystalline semiconductors. Phys Rev Lett (1999) 82(4):779–82. doi:10.1103/PhysRevLett.82.779

CrossRef Full Text | Google Scholar

27. Rahim W, Skelton JM, Scanlon DO. Ca₄Sb₂O and Ca₄Bi₂O: two promising mixed-anion thermoelectrics. J Mater Chem A (2021) 9(36):20417–35. doi:10.1039/D1TA03649A

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Yonggang W, Ting W, Changyong P, Kenney-Benson C, Pravica M, Wenge Y, et al. Robust high pressure stability and negative thermal expansion in sodium-rich antiperovskites Na₃OBr and Na₄OI₂. J Appl Phys (2016) 119(2):025901. doi:10.1063/1.4940020

CrossRef Full Text | Google Scholar

29. Sahrowsky H, Vogt P, Hippler K, Sitla S. Crystal structure of K₃OI. Z für Kristallographie - Crystalline Mater (1991) 196(1–4), pp. 193–6. doi:10.1524/zkri.1991.196.14.193

CrossRef Full Text | Google Scholar

30. Yin Y, Yi M, Guo W. High and anomalous thermal conductivity in monolayer MSi₂Z₄ semiconductors. ACS Appl Mater Inter (2021) 13(38):45907–15. doi:10.1021/acsami.1c14205

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Mouhat F, François-Xavier C. Necessary and sufficient elastic stability conditions in various crystal systems. Phys Rev B (2014) 90(22):224104. doi:10.1103/PhysRevB.90.224104

CrossRef Full Text | Google Scholar

32. Yue T, Zhao Y, Ni J, Meng S, Dai Z. Strong quartic anharmonicity, ultralow thermal conductivity, high band degeneracy and good thermoelectric performance in Na₂TlSb. npj Comput Mater (2023) 9(1):17. doi:10.1038/s41524-023-00970-4

CrossRef Full Text | Google Scholar

33. Carrete J, Mingo N, Curtarolo S. Low thermal conductivity and triaxial phononic anisotropy of SnSe. Appl Phys Lett (2014) 105(10):101907. doi:10.1063/1.4895770

CrossRef Full Text | Google Scholar

34. Wonshik K, Choong HK, Yeong KK, Beomyoung K, Chul K, Woobin J, et al. Electric-field-driven octahedral rotation in perovskite. npj Quan Mater (2021) 6(1):5. doi:10.1038/s41535-020-00306-1

CrossRef Full Text | Google Scholar

35. Animesh B, Tanmoy G, Koushik P, Kewal SR, Kaushik K, Ajay S, et al. Intrinsically low thermal conductivity in the n-type vacancy-ordered double perovskite Cs₂SnI₆: octahedral rotation and anharmonic rattling. Chem Mater (2022) 34(7):3301–10. doi:10.1021/acs.chemmater.2c00084

CrossRef Full Text | Google Scholar

36. Yoonseong J, Wonsik L, Seungbin H, Beom-Soo K, Seung-Jun Y, Hyejin J. Thermal transport properties of phonons in halide perovskites. Adv Mater (2023) 35(43):2204872. doi:10.1002/adma.202204872

CrossRef Full Text | Google Scholar

37. Akizuki Y, Yamada I, Fujita K, Taga K, Kawakami T, Mizumaki M, et al. Rattling in the quadruple perovskite CuCu₃V₄O₁₂. Angew Chem Int Ed (2015) 54:10870–4. doi:10.1002/anie.201504784

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Luo Y, Yang X, Feng T, Wang J, Ruan X. Vibrational hierarchy leads to dual-phonon transport in low thermal conductivity crystals. Nat Commun (2020) 11:2554. doi:10.1038/s41467-020-16371-w

PubMed Abstract | CrossRef Full Text | Google Scholar

39. El-Sharkawy AA, Abou El-Azm AM, Kenawy MI, Hillal AS. Thermophysical properties of polycrystalline PbS, PbSe, and PbTe in the temperature range 300–700 K. Int J Thermophys (1983) 4(3):261–9. doi:10.1007/BF00502357

CrossRef Full Text | Google Scholar

40. Fujita K, Mochida T, Nakamura K. High-temperature thermoelectric properties of NaxCoO₂-δ single crystals. Jpn J Appl Phys (2001) 40(7R):4644. doi:10.1143/JJAP.40.4644

CrossRef Full Text | Google Scholar

41. Ohtaki M, Araki K, Yamamoto K. High thermoelectric performance of dually doped ZnO ceramics. J Electron Mater (2009) 38(7):1234–8. doi:10.1007/s11664-009-0816-1

CrossRef Full Text | Google Scholar

42. Ohta S, Nomura T, Ohta H, Hirano M, Hosono H, Koumoto K. Large thermoelectric performance of heavily Nb-doped SrTiO₃ epitaxial film at high temperature. Appl Phys Lett (2005) 87(9):092108. doi:10.1063/1.2035889

CrossRef Full Text | Google Scholar

43. Kaur T, Sinha MM. Probing thermoelectric properties of high potential Ca₃PbO: an ab initio Study. IOP Conf Ser Mater Sci Eng (2021) 1033(1):012080. doi:10.1088/1757-899X/1033/1/012080

CrossRef Full Text | Google Scholar

44. Chen XK, Zhu J, Qi M, Jia PZ, Xie ZX. Anomalous strain-dependent thermoelectric properties of cubic stuffed-diamond LiCu₃TiQ₄ (Q= S, Se). Phys Rev Appl (2025) 23(3):034085. doi:10.1103/PhysRevApplied.23.034085

CrossRef Full Text | Google Scholar

45. Hongwei M, Zhong-Zhen L, Zhigang Z, Mercouri GK. Strategies and prospects for high-performance Te-free thermoelectric materials. Chem Rev (2025) 125(7):3932–75. doi:10.1021/acs.chemrev.4c00786

CrossRef Full Text | Google Scholar

46. Kumar A, Bano S, Govind B, Bhardwaj A, Bhatt K, Misra DK. A review on fundamentals, design and optimization to high ZT of thermoelectric materials for application to thermoelectric Technology. J Electron Mater (2021) 50(11):6037–59. doi:10.1007/s11664-021-09153-7

CrossRef Full Text | Google Scholar

47. Wen S, Jianming C, Jinyang X, Dong W, Zhigang S. Search for organic thermoelectric materials with high mobility: the case of 2,7-Dialkyl[1]benzothieno[3,2-b][1]benzothiophene derivatives. Chem Mater (2014) 26(8):2669–77. doi:10.1021/cm500429w

CrossRef Full Text | Google Scholar

48. Un-Gi J, Yun-Sim K, Chol-Hyok R, Yun-Hyok K, Chol-Jun Y. High thermoelectric performance in the cubic inorganic cesium iodide perovskites CsBI₃ (B = Pb, Sn, and Ge) from first-principles. The J Phys Chem C (2021) 125(11):6013–9. doi:10.1021/acs.jpcc.0c09929

CrossRef Full Text | Google Scholar