Klein-Gordon oscillator interacting with screened Kratzer potential in a cosmic string space-time with space-like dislocation and AB field

In this paper, we examine the relativistic quantum behaviour of spinless particles interacting through the Klein-Gordon (KG) oscillator and screened Kratzer potentials and influenced by external magnetic field, using the extended Nikiforov-Uvarov method. A detailed analysis of how quantum numbers and cosmic string parameters affect the energy spectra of the KG oscillator are provided. The results obtained reveal that energy spectra are influenced by the quantum numbers and the cosmic string parameters thereby causing a shift, depending on the quantum magnetic flux, dislocation parameter, and other potential parameters considered. Our results agree with results in literature and the study proves to be very useful in the understanding of the behavior of particles in a cosmic space-time with space-like dislocation.

1 Introduction

The recent applications of the Klein-Gordon oscillator (KGO) [1–3] stem from Moshinsky and Szczepanik’s [4] conceptualization of the relativistic quantum Dirac oscillator. Unlike the Dirac oscillator that describes spin half particles, Bruce and Minning [5] conceived their idea for the spinless relativistic model which they referred to as KGO. Many researchers and authors in recent times have devoted their interest in finding the analytical solutions to KGO [6, 7]. Bakke and Furtado [8] considered the influence of a Coulomb-type potential on the KGO by introducing the scalar potential as modification in the mass term of the KGO. In their studies, relativistic bound state solutions to both attractive and repulsive Coulomb-type potentials were obtained. Also, the dependence of angular frequency of the KGO on the quantum states of the system, due to the quantum effect were investigated. Vitoria et al. [9] investigated the quantum dynamics of an electrically charged particle with KGO and Coulomb potential. Here, only specific values of the angular frequency of the KGO were permitted to obtain bound state solutions of the system. Also, the angular frequency and the energy level associated with the ground state of the relativistic system were obtained, in addition to the behaviour of the position-dependent mass particle subject to the KGO and Coulomb potential. The influence of topological defect on the interaction of a scalar field with combined Coulomb-type potential and gauge potential in a space-time uniform magnetic field, with a screw dislocation has been investigated [10]. Here, analytical solutions to the KGO in the space-time with a screw dislocation were studied and analogues effects of the AB effect for bound states of the combined systems obtained.

Interestingly, the limiting cases of the KGO were reduced to the well-known non-relativistic limit of the Schrodinger oscillator. Much research work on KGO with confining harmonic oscillator has been reported. Rao and Kagali [11] described a method of inputting the harmonic oscillator potential into the Klein–Gordon equation, leading to genuine bound states. In their work, the eigenfunctions and eigen energies of the system were obtained explicitly, though corrected Boumali et al. [12], using the annihilation and creation operators. Studies on relativistic and position-dependent spin-zero particles subjected to the KGO and confining potentials have been presented [13, 14].

The KGO finds many applications in physics such as quark-antiquark interaction [15], the Casimir effect [16], scalar bosons [17] and others [18–24]. The concept of including the vector potential in the KG equation is via coupling of the momentum operator in the form: ${\overrightarrow{p}}_{\mu }\to {\overrightarrow{p}}_{\mu }-q{\overrightarrow{A}}_{\mu }\left(r\right)$ [8], with the charge represented by $e$ and the electromagnetic four-vector field indicated as $A_{\mu }=\left(-A_0,\overrightarrow{A}\right)$. Consequently, the component of the scalar potential is added to the mass in the KG equation leading to the replacement $m\to m+S\left(r\right)$. Various metric systems have been employed in studying KGO such as Minskowski space-time [11], Godel-type space-time [25], Gurses-type space-time [26] and others. In addition, Topological space-time defects of the KGO and a linear potential were examined in the Kaluza-Klein theory by Carvalho et al. [27]. Here, a series of topological defects with the KGO were investigated and their energy levels and corresponding eigenfunctions obtained with this background. Their energy levels were seen to depend on the global parameters characterized by these space-times. Quantum particles described by the KGO, interacting with a cosmic dislocation in Som–Raychaudhuri space-time were studied in the presence of homogeneous magnetic field using the Kaluza–Klein theory. It was deduced that the obtained energy levels represent the sum of the terms associated with AB flux and rotation parameters of the considered space-time. KGO with and without magnetic have been examined by Boumali and Messai [28]. The authors employed the generalized parametric Nikiforov-Uvarov (NU) method to obtain their eigensolutions. Also, the influence of the cosmic string space-time on obtained eigensolutions were investigated, to show the level of dependence of the energy levels with the angular deficit, which characterizes the global structure of the metric in the cosmic string space-time. Also, the investigation of the KGO with Cornell potential has been reported [29].

In other developments, the linear central potential with the Lorentz symmetry, governed by a tensor field background on a scalar field with KGO was investigated [30]. The behaviour of the relativistic quantum oscillator under the influence of a Coulomb-type scalar potential in this background was also analyzed. The influence of the tensor field background which violates Lorentz symmetry in the relativistic energy levels was discussed extensively. The rotating effects on a charged scalar field immersed in space-time with a magnetic screw dislocation was investigated [31], by considering the Coulomb-type potential and the KGO. The author obtained the bound state solutions of the systems. These solutions were affected by both the space-time topology and Sagnac-type effect, which were modified by magnetic screw dislocation. da Silva et al. [32] investigated the non-relativistic quantum effects of the topology of the spacetime with the distortion of a vertical line into a vertical spiral on the harmonic oscillator, using the topological defect background of Schrödinger equation (SE). The authors established that the topology of space-time modifies the energy spectrum of the harmonic oscillator, in addition to the existence of the AB-type effect for the energy bound states. Braganca et al. [33] considered the influence of the global monopole Space-time on the Dirac and Klein–Gordon relativistic quantum Oscillator. The analytical energy profile results obtained were seen to be characterized by the curvature of space-time. Also, a hard-wall potential was employed to determine the energy spectrum for relativistic quantum oscillators in this background. Ahmed [34] investigated the interactions of a scalar particle with electromagnetic potential in the background space-time generated by a cosmic string with a space-like dislocation. The KGO was solved in the presence of external fields with an internal magnetic flux field and AB effect. The author also considered Cornell-type scalar potential within this context and analyzed its effects on the relativistic energy eigenvalue and eigenfunction obtained. Recently, Vitoria [34] analyzed a scalar particle in space-time with torsion. Here, the confinement of a scalar particle in a cylindrical shell and that of the KGO were investigated. The relativistic energy profile in the presence of torsion in a spiral-like dislocation space-time were analyzed for the systems considered. In addition, the relativistic quantum dynamics of the oscillator field with generalized KGO, confined in an Ellis-Bronnikov-type wormhole space-time with a topological defect was investigated [35]. By employing the Coulomb and Cornell-type potential functions, the analytical solutions of the systems and the influence of the topological defect of the geometry and the wormhole throat radius were studied. The eigenvalue solution of the oscillator field was seen to exert significant modifications to the entire results, underscoring the impact of the topological defect.

The primary objective of this paper is to determine the energy spectra of relativistic spinless particles interacting with a screened Kratzer potential under the influence of a KGO. Additionally, we seek to explore the impact of quantum numbers (QNs) and the angular parameter of cosmic string space-time on the KGO’s energy spectra. This work unifies the analytical treatment of a relativistic quantum system influenced by both topological space-time defects and a composite potential field as its major strength. It also combines the KGO with a screened Kratzer potential under the effects of cosmic string space-time, Aharonov-Bohm (AB) field, and spatial dislocation. This approach is viewed as a significant addition to theoretical Physics, where relativistic quantum mechanics and topological field theory are bridged.

The structure of this work is organized as follows: Section 2 presents the solutions to the Klein-Gordon equation in both cosmic and space-time dislocation contexts. Section 3 contains the results and discussion, and Section 4 offers a brief conclusion.

2 The KGO in AB field and space-time dislocation

The KG equation describing the dynamics of spin-zero relativistic particles of mass $m$ in a non-linear space-time is defined as [1–3].

$\left\{\left(\frac{1}{\sqrt{-g}}{D}_i\left(\sqrt{-g}{g}^{ij}{D}_j\right)+{\left(m+S\left(r\right)\right)}^2\right)\right\}\psi \left(\overrightarrow{r},t\right)=0(1)$

where $D_i=\left({\mathrm{\partial }}_i-ie{A}_i\right)$, $A_i=\left(\begin{array}{cccc}{A}_0& 0& A_{\phi }& 0\end{array}\right)$, $e{A}_0=V\left(r\right)$ is the vector potential with $e$ as the electric charge on the particle, $S\left(r\right)$ the scalar potential, and $\psi \left(\overrightarrow{r},t\right)$ the wave function. Here, $g^{ij}$ is the metric tensor given by

$g^{ij}=\left(\begin{array}{cccc}-1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& {\alpha }^2{r}^2+{\chi }^2& \chi \\ 0& 0& \chi & 1\end{array}\right),g_{ij}=\left(\begin{array}{cccc}-1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& \frac{1}{{\alpha }^2{r}^2}& -\frac{\chi }{{\alpha }^2{r}^2}\\ 0& 0& -\frac{\chi }{{\alpha }^2{r}^2}& 1+\frac{{\chi }^2}{{\alpha }^2{r}^2}\end{array}\right)(2)$

where $\alpha =1-4\mu$ is the angular parameter and $\mu$ the linear mass density, $\chi$ is the spatial dislocation parameter and $g$ the determinant of the metric tensor with $\sqrt{-g}=\alpha r$ [1–3]. The line element for the spatial dislocation for space-time in cylindrical coordinates is given by [2, 3],

$d{s}^2=g_{ij}d{x}^{i}d{x}^j=-d{t}^2+d{r}^2+{\alpha }^2{r}^{2}d{\phi }^2+{\left(dz+\chi d\phi \right)}^2(3)$

By using Equations 2, 3 with the definition of $D_i$ and $A_i$, Equation 1 becomes [3]$\left(c=\mathrm{\hslash }=1\right)$,

$\begin{array}{ll}\hfill & \hfill \left[-{\left({\mathrm{\partial }}_t-iV\left(r\right)\right)}^2+\frac{1}{r}{\mathrm{\partial }}_r\left(r{\mathrm{\partial }}_r\right)+\frac{1}{{\alpha }^2{r}^2}{\left({\mathrm{\partial }}_{\phi }-ie{A}_{\phi }-\chi {\mathrm{\partial }}_z\right)}^2+{\mathrm{\partial }}_z^2-{\left(m+S\left(r\right)\right)}^2\right]\\ \hfill & \psi \left(\overrightarrow{r},t\right)=0\hfill \end{array}(4)$

Here, we write the KG momentum operator coupling the oscillator as ${\widehat{p}}_i={\widehat{p}}_i+im\mathrm{\Omega }{\widehat{X}}_i$, where $\mathrm{\Omega }$ is the oscillator frequency with the oscillator coordinate ${\widehat{X}}_i$ defined as ${\widehat{X}}_i=\left(\begin{array}{cccc}0,& f\left(r\right),& 0,& 0\end{array}\right)$. Hence, the KGO becomes [2, 3],

$\left[\begin{array}{l}-{\left({\mathrm{\partial }}_t-iV\left(r\right)\right)}^2+\frac{1}{r}\left({\mathrm{\partial }}_r+m\mathrm{\Omega }f\left(r\right)\right)r\left({\mathrm{\partial }}_r-m\mathrm{\Omega }f\left(r\right)\right)\\ +\frac{1}{{\alpha }^2{r}^2}{\left({\mathrm{\partial }}_{\phi }-ie{A}_{\phi }-\chi {\mathrm{\partial }}_z\right)}^2+{\mathrm{\partial }}_z^2-{\left(m+S\left(r\right)\right)}^2\end{array}\right]\psi \left(\overrightarrow{r},t\right)=0(5)$

One of the non-zero components of the four-vector field $A_{\phi }$ is taken as [2, 3],

$A_{\phi }=-\frac{\alpha B_0}{2}{r}^2+\frac{{\mathrm{\Phi }}_{AB}}{2\pi }(6)$

where $B_0$ represents the external magnetic field’s strength, ${\mathrm{\Phi }}_{AB}$ is the AB magnetic flux. The quantity ${\mathrm{\Phi }}_0=\frac{2\pi }{e}$ in the AB field is referred to as the quantum of magnetic flux (${\mathrm{\Phi }}_{AB}$). It is noteworthy that the ${\mathrm{\Phi }}_{AB}$ and the ɸ₀ are related as $\mathrm{\Phi }=\frac{{\mathrm{\Phi }}_{AB}}{{\mathrm{\Phi }}_0}$, where $\mathrm{\Phi }$ represents the magnetic flux in the field. The wave function for the system is now constructed as

$\psi \left(\overrightarrow{r},t\right)=\frac{1}{\sqrt{r}}{e}^{i\left(-E_{nl}t+l\phi +kz\right)}U\left(r\right)(7)$

where $E_{nl}$ is the energy spectrum of the particles, $l=0,\pm ,\pm 2...$ the quantum number for the magnetization, $k$ represents the wave number, and $U\left(r\right)$ the radial wave function. Putting Equations 6, 7 in Equation 5 yields,

$\begin{array}{ll}\hfill & \hfill \frac{d^{2}U\left(r\right)}{d{r}^2}+\left\{\begin{array}{l}{\left(E_{nl}-V\left(r\right)\right)}^2-\frac{m\mathrm{\Omega }f\left(r\right)}{r}-m\mathrm{\Omega }f\left(r\right)-m^2{\mathrm{\Omega }}^2{f}^2\left(r\right)-k^2\\ -{\left(m+S\left(r\right)\right)}^2-\frac{1}{{\alpha }^2{r}^2}{\left(l-\mathrm{\Phi }-k\chi \right)}^2-\frac{2m{\omega }_c}{\alpha }\left(l-\mathrm{\Phi }-k\chi \right)-m^2{\omega }_c^2{r}^2\end{array}\right\}\\ \hfill & \times U\left(r\right)=0\hfill \end{array}(8)$

where, ${\omega }_c=\frac{e{B}_0}{2m}$ is the cyclotron frequency. To solve Equation 8, we consider equal vector and scalar potential of the screened Kratzer type, represented as [36],

$V\left(r\right)=\left(\frac{V_0}{r}+\frac{V_1}{r^2}\right)e^{-\delta r}(9)$

where $V_0,V_1$ and $\delta$ are respectively the parameters for potential and screening. The function $f\left(r\right)$ is taken in the form of Yukawa-like potential type as,

$f\left(r\right)=\frac{a{e}^{-\delta r}}{r}(10)$

Here $a$ is the potential depth. Substituting Equations 9, 10 into Equation 8, we get

$\begin{array}{ll}\hfill & \hfill \frac{d^{2}U\left(r\right)}{d{r}^2}+\left\{\begin{array}{l}{\epsilon }_{nl}^2-2\left(E_{nl}+m\right)V_0\frac{e^{-\delta r}}{r}-2\left(E_{nl}+m\right)V_1\frac{e^{-\delta r}}{r^2}+m\mathrm{\Omega }a\delta \frac{e^{-\delta r}}{r}\\ -m^2{\mathrm{\Omega }}^2{a}^2\frac{e^{-2\delta r}}{r^2}-\frac{1}{{\alpha }^2{r}^2}{\left(l-\mathrm{\Phi }-k\chi \right)}^2-m^2{\omega }_c^2{r}^2\end{array}\right\}\\ \hfill & \times U\left(r\right)=0\hfill \end{array}(11)$

where

${\epsilon }_{nl}^2=E_{nl}^2-k^2-m^2-\frac{2m{\omega }_c}{\alpha }\left(l-\mathrm{\Phi }-k\chi \right)(12)$

The presence of the term $\frac{1}{{\alpha }^2{r}^2}{\left(l-\mathrm{\Phi }-k\chi \right)}^2$ makes Equation 11 very complicated to solve; hence we use the Greene-Aldrich approximation of the form [37]

$\frac{1}{r^2}\approx \frac{{\delta }^2}{{\left(1-e^{-\delta r}\right)}^2},\frac{1}{r}\approx \frac{\delta }{\left(1-e^{-\delta r}\right)},r^2\approx \frac{{\left(1-e^{-\delta r}\right)}^2}{{\delta }^2}(13)$

It is well-known that Equation 13 is applicable when the parameter $\delta$ is small, leading to a short-range potential. By substituting Equation 13 into Equation 11 and using the coordinate transformation, $x=e^{-\delta r}$, Equation 11 takes the form

$\begin{array}{l}\frac{d^{2}U\left(x\right)}{d{x}^2}+\frac{\left(1-x\right)}{x\left(1-x\right)}\frac{dU\left(x\right)}{dx}+\frac{1}{x^2{\left(1-x\right)}^2}\\ \left\{-\lambda x^4+4\lambda x^3+\left(\frac{{\epsilon }_{nl}^2}{{\delta }^2}+{\gamma }_1\right)x^2+\left({\gamma }_2-\frac{2{\epsilon }_{nl}^2}{{\delta }^2}\right)x+\left(\frac{{\epsilon }_{nl}^2}{{\delta }^2}-{\gamma }_3\right)\right\}U\left(x\right)=0\end{array}(14)$

where,

$\begin{array}{l}\lambda ={\left(\frac{m{\omega }_c}{{\delta }^2}\right)}^2,{\gamma }_1=\left(\frac{2\left(E_{nl}+m\right)V_0}{\delta }-ma\mathrm{\Omega }-m^2{a}^2{\mathrm{\Omega }}^2-6\lambda \right),\\ {\gamma }_2=4\lambda -2\left(E_{nl}+m\right)\left(\frac{V_0}{\delta }+V_1\right),{\gamma }_3=\frac{1}{{\alpha }^2}{\left(l-\mathrm{\Phi }-k\chi \right)}^2+\lambda \end{array}(15)$

We can see that Equation 14 is the hypergeometric-type equation that can be solved analytically using the extended Nikiforov-Uvarov (ENU) method [38–40]. Equation 14 has a structure like that of the ENU method [38–40] from which the following polynomials are obtained:

$\begin{array}{l}{\stackrel{\sim }{\tau }}_e\left(x\right)=\left(1-x\right),{\sigma }_e\left(x\right)=x\left(1-x\right)\\ {\stackrel{\sim }{\sigma }}_e\left(x\right)=-\lambda x^4+4\lambda x^3+\left(\frac{{\epsilon }_{nl}^2}{{\delta }^2}+{\gamma }_1\right)x^2+\left({\gamma }_2-\frac{2{\epsilon }_{nl}^2}{{\delta }^2}\right)x+\left(\frac{{\epsilon }_{nl}^2}{{\delta }^2}-{\gamma }_3\right)\end{array}(16)$

The polynomial ${\pi }_e\left(s\right)$ is obtained as follows,

${\pi }_e\left(x\right)=-\frac{x}{2}\pm \sqrt{\begin{array}{l}\lambda x^4-\left(P+4\lambda \right)x^3+\left(P-Q-\frac{{\epsilon }_{nl}^2}{{\delta }^2}-{\gamma }_1+\frac{1}{4}\right)x^2\\ +\left(Q-{\gamma }_2+\frac{2{\epsilon }_{nl}^2}{{\delta }^2}\right)x+\left({\gamma }_3-\frac{{\epsilon }_{nl}^2}{{\delta }^2}\right)\end{array}}(17)$

The polynomial ${\pi }_e\left(x\right)$ is chosen such that it will become a second-degree polynomial of the form

${\pi }_e\left(x\right)=-\frac{x}{2}\pm \left(A+Bx+C{x}^2\right)(18)$

After a little algebra from Equations 17, 18, we obtain the following coefficients

$\begin{array}{l}A=\pm \sqrt{{\gamma }_3-\frac{{\epsilon }_{nl}^2}{{\delta }^2}},B=-\left(A+C\right)\pm \sqrt{{\gamma }_3-{\gamma }_2-{\gamma }_1-3\lambda +\frac{1}{4}},C=\pm \sqrt{\lambda },\\ P=2BC+B^2+2AC+\frac{{\epsilon }_{nl}^2}{{\delta }^2}+\left({\gamma }_1+{\gamma }_2\right)-\frac{1}{4},\\ Q=-C^2-2BC-2AC-4\lambda -{\gamma }_1-\frac{{\epsilon }_{nl}^2}{{\delta }^2}+\frac{1}{4}\end{array}(19)$

By using Equation 19 in Equation 18, the associated polynomial for ${\pi }_e\left(x\right)$ with different values of

$\begin{array}{l}G\left(x\right)=\left(2BC+B^2+2AC+\frac{{\epsilon }_{nl}^2}{{\delta }^2}+\left({\gamma }_1+{\gamma }_2\right)-\frac{1}{4}\right)x\\ \pm \left(-C^2-2BC-2AC-4\lambda -{\gamma }_1-\frac{{\epsilon }_{nl}^2}{{\delta }^2}+\frac{1}{4}\right)\end{array}(20)$

is obtained as follows:

$\begin{array}{ll}\hfill & \hfill \pi \left(x\right)=-\frac{x}{2}\pm \left\{\left(\pm \sqrt{{\gamma }_3-\frac{{\epsilon }_n^2}{{\delta }^2}}\right)+\left(-\left(A+C\right)\pm \sqrt{{\gamma }_3-{\gamma }_2-{\gamma }_1-3\lambda +\frac{1}{4}}\right)x\right.\\ \hfill & \left.+\left(\pm \sqrt{\lambda }\right)x^2\right\}\hfill \end{array}(21)$

The other polynomials associated with ENU are defined as follows.

$h\left(x\right)=Px+Q-\frac{1}{2}\pm \left(B+2Cx\right)(22)$

$\tau \left(x\right)=1-2x\pm 2\left(A+Bx+C{x}^2\right)(23)$

$h_n\left(x\right)=n\mp n\left(B+2Cx\right)-\frac{n\left(n-1\right)}{3}+T_n(24)$

with $T_n$ being the integration constant. By using Equation 22, 24 ($h\left(x\right)=h_n\left(x\right)$) yields the following equation,

$Px+Q-\frac{1}{2}\pm \left(B+2Cx\right)=n\mp n\left(B+2Cx\right)-\frac{n\left(n-1\right)}{3}+C_n(25)$

By setting the coefficients of the linear and constant terms equal in Equation 25, we get

$P\pm 2C=\mp 2nC(26)$

$Q-\frac{1}{2}\pm B=n\mp nB+\frac{n\left(n-1\right)}{3}+C_n(27)$

By setting $T_n=0$ in Equation 26, we get the explicit energy spectrum for the combined system in Aharonov-Bohm flux field and space-time dislocation as,

$\left.\begin{array}{l}{E}_{nl}^2-m^2=-{\delta }^2{\left[\frac{\begin{array}{l}\frac{1}{3}{\left(n+1\right)}^2-\frac{1}{12}+\left(n-3+2\sqrt{\lambda }\right)\sqrt{\mathrm{\Xi }}-\left(n-3+\sqrt{\lambda }+2\sqrt{\mathrm{\Xi }}\right)\sqrt{\lambda }+\frac{2\left(E_{nl}+m\right)V_0}{\delta }\\ -ma\mathrm{\Omega }\left(1+ma\mathrm{\Omega }\right)+\frac{1}{{\alpha }^2}{\left(l-\mathrm{\Phi }-k\chi \right)}^2\end{array}}{\left(n+1+2\sqrt{\lambda }+2\sqrt{\mathrm{\Xi }}\right)}\right]}^2\\ + {\delta }^2{\gamma }_3+k^2+\frac{2m{\omega }_c}{\alpha }\left(l-\mathrm{\Phi }-k\chi \right)\end{array}\right\}(28)$

where

$\mathrm{\Xi }=\left(\frac{1}{4}+\frac{1}{{\alpha }^2}{\left(l-\mathrm{\Phi }-k\chi \right)}^2+ma\mathrm{\Omega }\left(1+ma\mathrm{\Omega }\right)+2\left(E+m\right)V_1\right),(29)$

3 Results and discussion

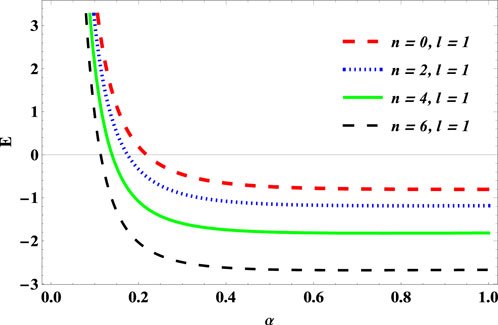
Here we show how the QNs and angular parameter affect the energy spectra of the KGO interacting with the screened Kratzer potential subjected to Yukawa-like potential terms for different potential parameters, AB field, angular frequency, mass of the particle, screening parameter, dislocation parameter, and wave number as shown in Figures 1–10. In Figure 1, we plotted the energy spectrum of KGO as a function of the cosmic string parameter $\alpha$ for different quantum state $\left|n,l\right.〉$. It can be seen in the figure that the energy decreases as the quantum states and cosmic string parameter are enhanced. As the cosmic string parameter is increased the more, we observe a steady energy level corresponding to each quantum state considered. Hence, the shift in energy is only possible for lower values of cosmic string parameters. Our result agrees with a previous study in literature [41].

Figure 1

Figure 1. Energy vs. cosmic string parameter $\alpha$ for various quantum states.

Figure 2

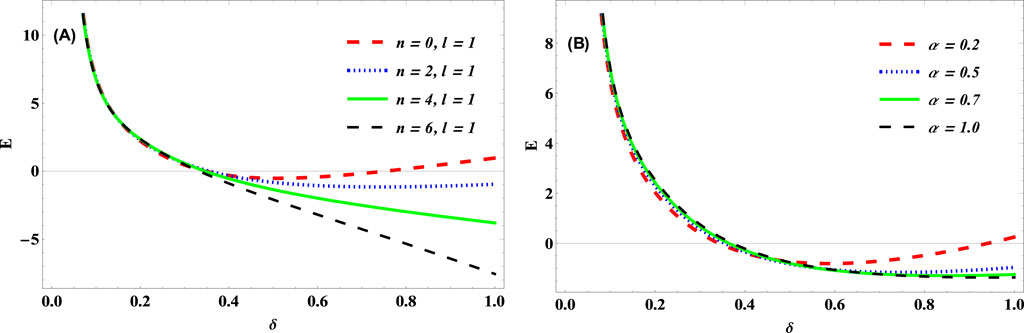
Figure 2. Energy vs. screening parameter, $\delta$ for various (A) quantum states and (B) cosmic string parameter, $\alpha$.

Figure 3

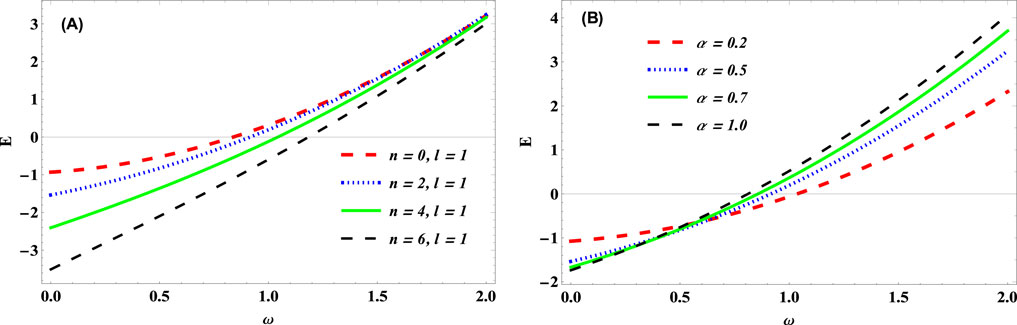
Figure 3. Energy vs. cyclotron frequency, $\omega$ for various (A) quantum states and (B) cosmic string parameter, $\alpha$.

Figure 4

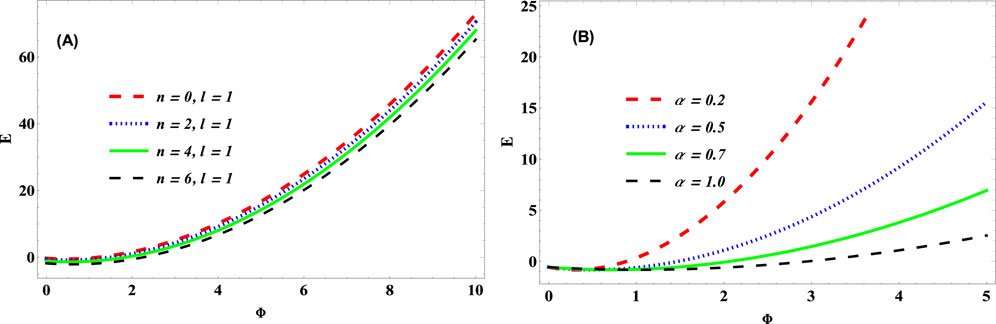
Figure 4. Energy vs. magnetic flux, $\mathrm{\Phi }$ for various (A) quantum states and (B) cosmic string parameter, $\alpha$.

Figure 5

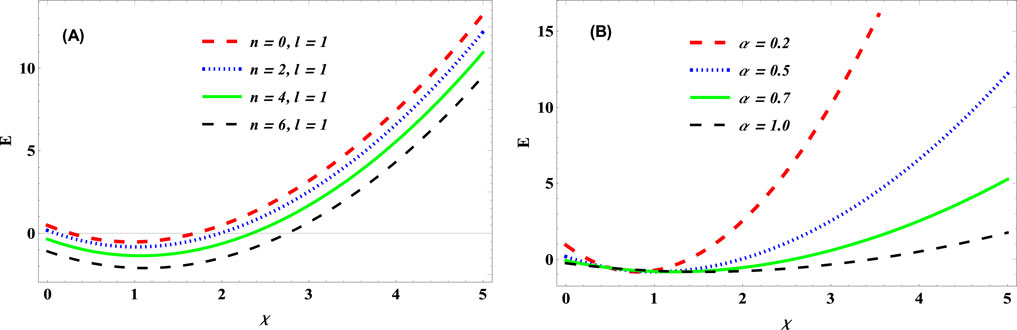
Figure 5. Energy vs. spatial dislocation parameter, $\chi$ for various (A) quantum states and (B) cosmic string parameter, $\alpha$.

Figure 6

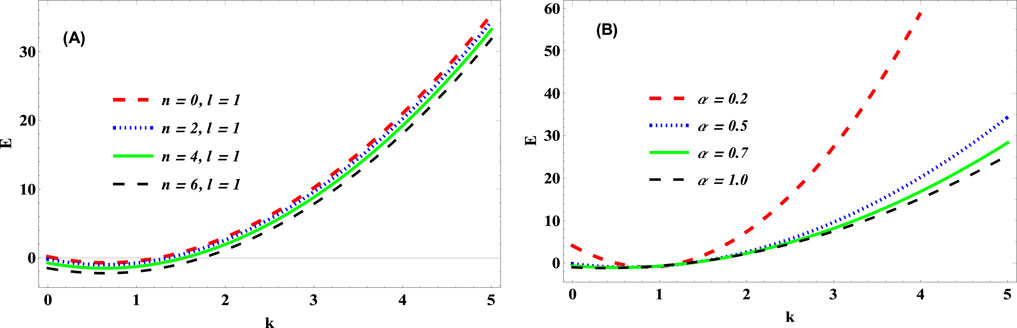
Figure 6. Energy vs. wave number, k for various (A) quantum states and (B) cosmic string parameter, $\alpha$.

Figure 7

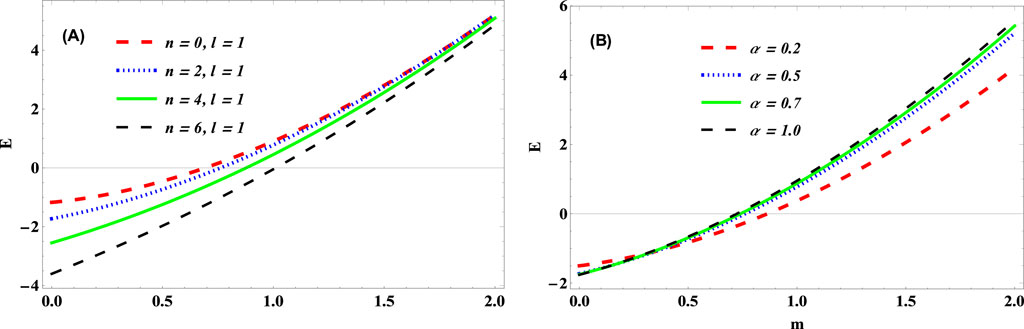
Figure 7. Energy vs. mass of the particle, m for various (A) quantum states and (B) cosmic string parameter, $\alpha$.

Figure 8

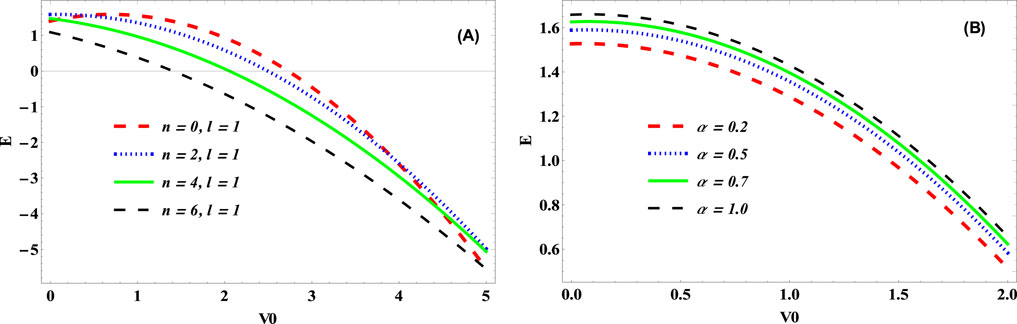
Figure 8. Energy vs. potential parameter, V0 for various (A) quantum states and (B) cosmic string parameter, $\alpha$.

Figure 9

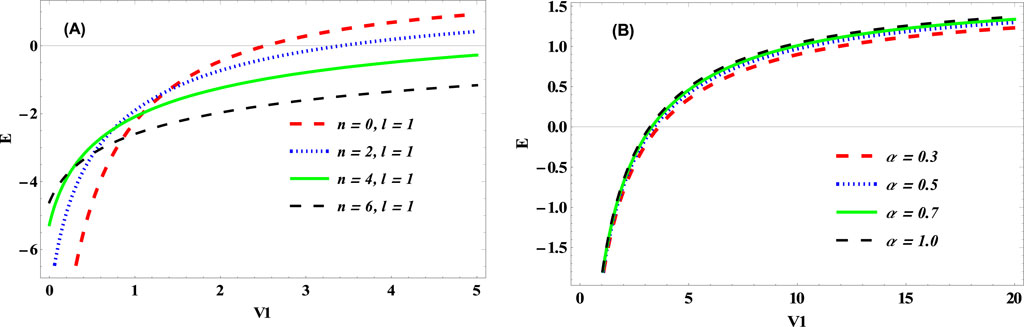
Figure 9. Energy vs. potential parameter, V1 for various (A) quantum states and (B) cosmic string parameter, $\alpha$.

Figure 10

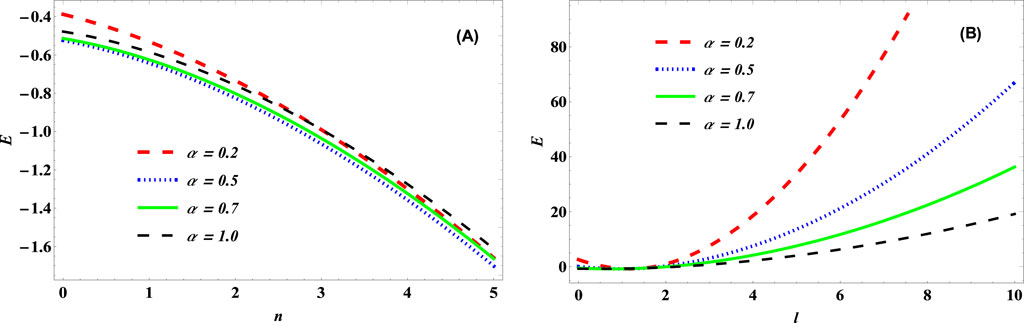
Figure 10. Energy vs. (A) principal quantum number, n and (B) angular momentum quantum number, l, for various cosmic string parameter, $\alpha$.

Figure 2 shows a plot of how the screening parameter $\delta$ affects the energy spectra of KGO, for varying quantum states $\left|n,l\right.〉$ and cosmic string parameter $\alpha$. It is observed in the figure that, as the screening parameter is increased, the energy spectra of the KGO decreases together for different QNs and the cosmic string parameter. In addition, there is a divergence in the energy spectra for each value of quantum states and cosmic string parameter considered, as the screening parameter is enhanced more. Hence, much shift in energy is observed at higher values of screening parameter, corresponding to the quantum states and cosmic string parameters considered.

The effect of the cyclotron frequency on the energy spectra of the KGO for various values of the quantum states and the cosmic string parameter are given in Figure 3. The energy of the KGO increases with increase in cyclotron frequency and becomes more bounded as the cyclotron frequency is enhanced more, for different quantum states (left panel of Figure 3). At specific cyclotron frequency, the energy of the KGO increases with a decrease in quantum states. On the other hand, the energy of KGO also increases as the cyclotron frequency is increased for various value of the cosmic string parameter (Right panel of Figure 3). It is observed here that the energy spectrum diverges at higher cyclotron frequency, for various cosmic string parameters considered. This indicates that more energies can be resonantly absorbed by the particles of the KGO and SKP at lower quantum states and higher cosmic string space-time.

The influence of the QNs and cosmic string parameters on the energy spectra of KGO as a function of quantum magnetic flux are shown in Figure 4. Here, the energy spectra of KGO increases as the quantum magnetic flux is enhanced for different states of QNs and cosmic string parameters. Also, the increase in energy spectra corresponds to increase in the strength of the magnetic field and quantum states. In addition, the energy spectra increase monotonously, as the cosmic string parameters decrease, hence causing a tangible gap corresponding to each cosmic string space-time.

The behaviour of the QNs and cosmic string parameters on the energy spectra of KGO as a function of the dislocation parameter are displayed in Figure 5. The energy of the KGO first decreases to a minimum dislocation parameter value and increases as the dislocation parameter is enhanced. This phenomenon corresponds to the decrease in the values of the QN and cosmic string parameter considered. It can be deduced here that the particle electrons in the KGO are trapped within a lower dislocation value $\left(0<\chi \le 1\right)$, whereby reducing the energy spectra. As the dislocation parameter is enhanced $\left(\chi >1\right)$, the trapped electrons are released, and the energy spectra is increased for the quantum states and cosmic string parameters considered. This phenomenon is mostly applicable in the electrical and optical properties of semiconductors and quantum dots [42, 43].

The variation of the energy of the KGO with changes in the wave number is displayed in Figure 6. The energy of the KGO decreases at the first instance and later increases as the wave number is further enhanced for different quantum states and cosmic string parameters. This indicates that the energy spectra of KGO exhibits shorter wavelengths at higher wave numbers and vice versa, for the quantum states and cosmic string parameters considered.

Figure 7 shows the plot of the energy of the KGO with the mass of the particles. Here, the energy of KGO is bounded (negative energy) at the lower values of the mass of the particles. In addition, the energy of the KGO increases to positive energy as the mass of the particles is increased for different values of QNs and cosmic string parameter. Hence, much energy is needed to distribute heavier particles within the KGO, at different quantum states and cosmic string space-times.

In Figure 8, we plotted the energy of the KGO as a function of the potential parameter $V_0$. The energy of the KGO decreases (negative energy) with an increase in the potential parameter for different quantum states and the energy of the KGO decreases (positive energy) with increase in the potential parameter different values of the cosmic string parameter. The variation of the energy of the KGO against the potential parameter $V_1$ is shown in Figure 9. We found that the energy of the KGO is bounded (negative energies) at lower potential parameter $V_1$ and increases with increase in quantum states and cosmic string parameter. Hence, it can be deduced that the variation of the potential parameters causes changes in the energy spectra of the KGO.

Figure 10 illustrates how the energy spectra of the KGO changes with the quantum states, for various values of cosmic string parameter. The variation of energy of the KGO versus the principal QN (n) shows that the energy of KGO decreases (negative energy) as $n$ is increased (left panel of Figure 10) for different decreasing values of the cosmic string parameter. Also, we plotted the variation of the energy of the KGO as the orbital momentum quantum number ($l$) is changed. It is observed that the energy of the KGO increases (positive energy) as the $l$ is increased for different decreasing values of the cosmic string parameter.

4 Conclusion

In this paper, we constructed compact expressions for the energy spectra and wave functions of the KG equation with a screened Kratzer potential in cosmic space-time and space-time dislocation using the extended Nikiforov-Uvarov method. We thoroughly examined the impact of different quantum states and cosmic string parameters on the energy spectra of the KGO. The variation of the energy spectrum of the KGO versus quantum magnetic flux, dislocation parameter, and potential parameters were also illustrated. A shift in energy levels was observed for lower values of cosmic string parameters. These energy shifts were also seen at higher values of screening parameter, corresponding to the quantum states and cosmic string parameters considered. It was also observed that more energies can be resonantly absorbed by the particles of the KGO and SKP at lower quantum states and higher cosmic string space-time.

Another unique result obtained was the trapping of the particle electrons in the KGO within lower dislocation values, whereby reducing the energy spectra. The trapped electrons were released at higher values of the dislocation parameter, thereby increasing the energy spectra for the quantum states and cosmic string parameters considered.

It can be concluded that these physical parameters affect the relativistic dynamic of the particles and will invariably affect the behaviour and quantum state of the particles. Therefore, the ENU method proves to be an effective and robust approach for solving Schrödinger-like equations involving polynomials up to fourth order. This research holds promise for applications in diverse fields of physics.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

HA: Validation, Writing – original draft, Project administration, Funding acquisition. AI: Writing – review and editing, Formal Analysis, Supervision. UO: Writing – original draft, Investigation, Validation, Conceptualization. GR: Supervision, Software, Writing – review and editing. RH: Writing – review and editing, Methodology, Formal Analysis, Investigation.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. The work was funded by Princess Nourah bint Abdulrahman University Researchers Supporting Project number (PNURSP2025R106), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia.

Acknowledgments

Dr. U. S. Okorie acknowledges the support of the University of South Africa for the Postdoctoral Research Fellowship at the Department of Physics.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Ikot AN, Amadi PO, Okorie US, Horchani R, Okpara N, Obagboye L. Effects of Yukawa confining potential on Klein-Gordon oscillator. EPL (2023) 142:50003. doi:10.1209/0295-5075/acd57d

CrossRef Full Text | Google Scholar

2. Lütfüoğlu BC, Kříž J, Sedaghatnia P, Hassanabadi H. The generalized Klein–Gordon oscillator in a cosmic space-time with a space-like dislocation and the Aharonov–Bohm effect. Eur Phys J Plus (2020) 135:691. doi:10.1140/epjp/s13360-020-00721-0

CrossRef Full Text | Google Scholar

3. Ahmed F. Klein-gordon oscillator in the presence of external fields in a cosmic space-time with a space-like dislocation and aharonov-bohm effect. Adv High Energy Phys. (2020) 2020:1–10. doi:10.1155/2020/5691025

CrossRef Full Text | Google Scholar

4. Moshinsky M, Szczepaniak A. The Dirac oscillator. J Phys A (1989) 22:L817–9. doi:10.1088/0305-4470/22/17/002

CrossRef Full Text | Google Scholar

5. Bruce S, Minning P. The Klein-Gordon oscillator. Nuovo Cimento A (1993) 106:711–3. doi:10.1007/BF02787240

CrossRef Full Text | Google Scholar

6. Vitoria RLL, Bakke K. Aharonov–Bohm effect for bound states in relativistic scalar particle systems in a spacetime with a spacelike dislocation. Int J Mod Phys D (2018) 27:1850005. doi:10.1142/S0218271818500050

CrossRef Full Text | Google Scholar

7. Vitoria RLL, Bakke K. Torsion effects on a relativistic position-dependent mass system. Gen Relativ Gravit (2016) 48:161. doi:10.1007/S10714-016-2156-9

CrossRef Full Text | Google Scholar

8. Bakke K, Furtado C. On the Klein–Gordon oscillator subject to a Coulomb-type potential. Ann Phys (N Y.) (2015) 355:48–54. doi:10.1016/j.aop.2015.01.028

CrossRef Full Text | Google Scholar

9. Vitoria RLL, Furtado C, Bakke K. On a relativistic particle and a relativistic position-dependent mass particle subject to the Klein–Gordon oscillator and the Coulomb potential. Ann Phys (N Y.) (2016) 370:128–36. doi:10.1016/j.aop.2016.03.016

CrossRef Full Text | Google Scholar

10. Vitoria RLL, Bakke K. On the interaction of the scalar field with a Coulomb-type potential in a spacetime with a screw dislocation and the Aharonov-Bohm effect for bound states. Eur Phys J Plus (2018) 133:490. doi:10.1140/epjp/i2018-12310-9

CrossRef Full Text | Google Scholar

11. Rao NA, Kagali BA. Energy profile of the one-dimensional Klein–Gordon oscillator. Phys Scr (2008) 77:015003. doi:10.1088/0031-8949/77/01/015003

CrossRef Full Text | Google Scholar

12. Boumali A, Hafdallah A, Toumi A. Comment on ‘energy profile of the one-dimensional klein–gordon oscillator. Phys Scr (2011) 84:037001. doi:10.1088/0031-8949/84/03/037001

CrossRef Full Text | Google Scholar

13. Kumar R, Chand F. Series solutions to the N-dimensional radial Schrödinger equation for the quark–antiquark interaction potential. Phys Scr (2012) 85:055008. doi:10.1088/0031-8949/85/05/055008

CrossRef Full Text | Google Scholar

14. Vitoria RLL, Bakke K. Relativistic quantum effects of confining potentials on the Klein-Gordon oscillator. Eur Phys J Plus (2016) 131:36. doi:10.1140/epjp/i2016-16036-4

CrossRef Full Text | Google Scholar

15. Bahar MK, Yasuk F. Exact solutions of the mass-dependent klein-gordon equation with the vector quark-antiquark interaction and harmonic oscillator potential. Adv High Energy Phys. (2013) 2013:1–6. doi:10.1155/2013/814985

CrossRef Full Text | Google Scholar

16. Mota HF, Bakke K. Noninertial effects on the ground state energy of a massive scalar field in the cosmic string spacetime. Phys Rev D (2014) 89:027702. doi:10.1103/PhysRevD.89.027702

CrossRef Full Text | Google Scholar

17. Castro LB. Quantum dynamics of scalar bosons in a cosmic string background. Eur Phys J (2015) 75:287. doi:10.1140/epjc/s10052-015-3507-5

CrossRef Full Text | Google Scholar

18. Katanaev MO, Volovich IV. Theory of defects in solids and three-dimensional gravity. Ann Phys (N.Y.) (1992) 216:1–28. doi:10.1016/0003-4916(52)90040-7

CrossRef Full Text | Google Scholar

19. Aharonov Y, Bohm D. Significance of electromagnetic potentials in the quantum theory. Phys Rev (1959) 115:485–91. doi:10.1103/PhysRev.115.485

CrossRef Full Text | Google Scholar

20. Tan WC, Inkson JC. Magnetization, persistent currents, and their relation in quantum rings and dots. Phys Rev B (1999) 60:5626–35. doi:10.1103/PhysRevB.60.5626

CrossRef Full Text | Google Scholar

21. Furtado C, de Lima Ribeiro CA, Azevedo S. Aharonov–Bohm effect in the presence of a density of defects. Phys Lett A (2002) 296:171–5. doi:10.1016/S0375-9601(02)00256-6

CrossRef Full Text | Google Scholar

22. Marques GA, Bezerra VB. Non-relativistic quantum systems on topological defects spacetimes. Quan Gravity (2002) 19:985–95. doi:10.1088/0264-9381/19/5/310

CrossRef Full Text | Google Scholar

23. Cavalcanti de Oliveira AL, Bezerra de Mello ER. Nonrelativistic charged particle-magnetic monopole scattering in the global monopole background. Int J Mod Phys A (2003) 18:3175–87. doi:10.1142/S0217751X03015829

CrossRef Full Text | Google Scholar

24. Cavalcanti de Oliveira AL, Bezerra de Mello ER. Exact solutions of the Klein–Gordon equation in the presence of a dyon, magnetic flux and scalar potential in the spacetime of gravitational defects. Class Quant Grav (2006) 23:5249–63. doi:10.1088/0264-9381/23/17/009

CrossRef Full Text | Google Scholar

25. Figueiredo BD, Soares ID, Tiomno J. Gravitational coupling of Klein-Gordon and Dirac particles to matter vorticity and spacetime torsion. Clas Quant Grav (1992) 9:1593–617. doi:10.1088/0264-9381/9/6/015

CrossRef Full Text | Google Scholar

26. Ahmed F. The klein–gordon oscillator in (1+2)-dimensions Gurses space–time backgrounds. Ann Phys NY (2019) 404:1–9. doi:10.1016/j.aop.2019.02.012

CrossRef Full Text | Google Scholar

27. Carvalho J, Carvalho AMde M, Cavalcante E, Furtado C. Klein–gordon oscillator in kaluza–klein theory. Eur Phys J C (2016) 76:365. doi:10.1140/epjc/s10052-016-4189-3

CrossRef Full Text | Google Scholar

28. Boumali A, Messai N. Klein–Gordon oscillator under a uniform magnetic field in cosmic string space–time. Can J Phys (2014) 92:1460–3. doi:10.1139/cjp-2013-0431

CrossRef Full Text | Google Scholar

29. Hosseini M, Hassanabadi H, Hassanabadi S, Sedaghatnia P. Klein–Gordon oscillator in the presence of a Cornell potential in the cosmic string space-time. Int J Geom Meth Mod Phys (2019) 16:1950054. doi:10.1142/S0219887819500543

CrossRef Full Text | Google Scholar

30. Vitoria RLL, Belich H. Effects of a linear central potential induced by the Lorentz symmetry violation on the Klein–Gordon oscillator. Eur Phys J C (2018) 78:999. doi:10.1140/epjc/s10052-018-6479-4

CrossRef Full Text | Google Scholar

31. Vitoria RLL. Noninertial effects on a scalar field in a spacetime with a magnetic screw dislocation. Eur Phys J C (2019) 79:844. doi:10.1140/epjc/s10052-019-7359-2

CrossRef Full Text | Google Scholar

32. da Silva WCF, Bakke K, Vitoria RLL. Non-relativistic quantum effects on the harmonic oscillator in a spacetime with a distortion of a vertical line into a vertical spiral. Eur Phys J C (2019) 79:657. doi:10.1140/epjc/s10052-019-7166-9

CrossRef Full Text | Google Scholar

33. Baraganca EAF, Vitoria RLL, Belich H, Bezerra de Mello ER. Relativistic quantum oscillators in the global monopole spacetime. Eur Phys J C (2020) 80:206. doi:10.1140/epjc/s10052-020-7774-4

CrossRef Full Text | Google Scholar

34. Vitoria RLL. Relativistic scalar particle systems in a spacetime with a spiral-like dislocation. Axioms (2025) 14:227. doi:10.3390/axioms14030227

CrossRef Full Text | Google Scholar

35. Ahmed F, Aounallah H, Rudra P. Quantum flux effects on generalized Klein-Gordon oscillator field in a topologically charged Ellis-Bronnikov-type wormhole. Ind J Phys (2025) 99:1225–31. doi:10.1007/s12648-024-03340-y

CrossRef Full Text | Google Scholar

36. Ikot AN, Okorie US, Sever R, Rampho GJ. Eigensolution, expectation values and thermodynamic properties of the screened Kratzer potential. Eur Phys J Plus (2019) 134:386. doi:10.1140/epjp/i2019-12783-x

CrossRef Full Text | Google Scholar

37. Greene RL, Aldrich C. Variational wave functions for a screened Coulomb potential. Phys Rev A (1976) 14:2363–6. doi:10.1103/PhysRevA.14.2363

CrossRef Full Text | Google Scholar

38. Karayer H, Demirhan D, Buyukkukihc F. Extension of Nikiforov-Uvarov method for the solution of Heun equation. J Math Phys (2015) 56:06350. doi:10.1063/1.4922601

CrossRef Full Text | Google Scholar

39. Ikot AN, Obagboye LF, Okorie US, Inyang EP, Amadi PO, Okon IB, et al. Solutions of Schrodinger equation with generalized Cornell potential (GCP) and its applications to diatomic molecular systems in D-dimensions using extended Nikiforov–Uvarov (ENU) formalism. Eur Phys J Plus (2022) 137:1370. doi:10.1140/epjp/s13360-022-03590-x

CrossRef Full Text | Google Scholar

40. Alrebdi HI, Ikot AN, Horchani R, Okorie US. A non-relativistic 2D quantum system and its thermo-magnetic properties with a generalized pseudo-harmonic oscillator. Mathematics (2024) 12:2623. doi:10.3390/math12172623

CrossRef Full Text | Google Scholar

41. Alrebdi HI, Ikot AN, Okorie US, Horchani R, Rampho GJ. Klein-Gordon oscillator in the presence of harmonic-like potentials in the rotating cosmic string space-time. Int J Mod Phys (2025) A(23 pages):2550028. doi:10.1142/S0217751X25500289

CrossRef Full Text | Google Scholar

42. You JH, Johnson HT. Chapter 3 effect of dislocations on electrical and optical properties in GaAs and GaN. Solid State Phys (2009) 61:143–261. doi:10.1016/S0081-1947(09)00003-4

CrossRef Full Text | Google Scholar

43. Ashraf F, Castelluccio GM. A robust approach to parameterize dislocation glide energy barriers in FCC metals and alloys. J Mat Sci (2021) 56(29):16491–509. doi:10.1007/s10853-021-06376-1

CrossRef Full Text | Google Scholar