Mul-material decomposition method for sandstone spectral CT images based on I-MultiEncFusion-Net

Material analysis in sandstone is essential for oil and gas extraction. Energy spectrum Computed Tomography (CT) can acquire various spectrally distinct datasets and reconstruct energy-selective images. Additionally, deep learning significantly improves the accuracy of material decomposition by establishing a nonlinear mapping relationship between multi-energy channel reconstructed images and their corresponding multi-material reconstructed images. However, traditional convolutional neural networks (CNNs) demonstrate limited effectiveness in capturing non-local features. In this paper, we present a multi-encoder single-decoder network architecture named I-MultiEncFusion-Net, designed for material decomposition. In this framework, multiple encoders concentrate on the distinctive features of reconstructed images from different energy spectrum channels, while a single decoder enables feature fusion. The encoder incorporates Inception_B modules that utilize three parallel branches to comprehensively capture image features, while integrating a Local-Nonlocal Feature Aggregation (LNFA) module to fuse both local and global characteristics. The non-local feature extraction module constructs non-local neighborhood relationships and employs Euclidean distance metrics to extract global contextual features from images, thereby enhancing the material decomposition process. To further enhance model accuracy, the decoder computes Huber loss between each output and its corresponding label, while simultaneously incorporating correlations of base material images extracted by a High-Resolution Network (HRNet) as an auxiliary loss constraint for material decomposition. Validation experiments using spectral CT data of sandstone demonstrate the method’s efficacy. Both simulated and practical results indicate that I-MultiEncFusion-Net exhibits superior generalization capability, preserves internal image details, and produces decomposed images with sharper edges.

1 Introduction

Computed tomography (CT) has been extensively employed for cross-sectional analysis and three-dimensional structural characterization [1, 2]. In reserve forecasting research, the applications of CT have shown sustained growth over the past decade, evolving into an indispensable tool for critical geological investigations, including reservoir rock analysis and mineral analysis [3–5]. Materials analysis is crucial for determining oil content; however, conventional CT reveals tissue morphology but does not provide information about the elemental composition of the tissues. Spectral CT can acquire X-ray data at different energy levels, allowing for the precise analysis of characteristic attenuation curves to effectively identify and separate material components.

Rocks consist of heterogeneous mixtures of mineral constituents, matrix materials, pore networks, and fracture systems, each exhibiting distinct X-ray attenuation coefficients [6, 7]. The attenuation of photons is influenced by both the material properties and the energy of the X-rays, resulting from a combination of photoelectric absorption and Compton scattering. Spectral CT captures two projection datasets using different energetic spectra, enabling the determination of the electron density and effective atomic number of various materials [8, 9]. This critical physical information is vital for characterizing material mixtures and differentiating between tissue types.

There are several mainstream material decomposition technologies. Alvarez and Macovski [10] firstly presents the theory of a technique for obtaining essentially complete energy dependent information in a computerized tomography system by making simple, low-resolution, energy spectrum measurements. This technique enables material differentiation and constituent identification by leveraging the energy-dependent attenuation properties of substances across distinct photon energy spectra. Building upon these foundations, two main algorithms subsequently developed are the one-step method and the two-step method. The one-step method refers to a direct iterative material decomposition approach. Michael [11] presents a method which makes use of both pre- and post-reconstruction data in an iterative manner to achieve accurate beam hardening correction and decomposition into basis materials. Such methods integrate material decomposition and image reconstruction into a single process, simplifying the workflow but potentially reducing computational speed. The Two-step method includes material decomposition approaches based on both the projection domain and the image domain [12–14]. Projection domain material decomposition methods can effectively reduce the impact of beam hardening artifacts on reconstructed images [15, 16]. However, they require precise estimation of the X-ray emission spectrum and have high spatial consistency requirements for energy spectrum CT projection data. In contrast, image domain material decomposition algorithms are more flexible, with relatively simple material decomposition models that are easier to implement [17–19]. This paper focuses on image-domain decomposition due to its implementational robustness in handling real-world spectral CT datasets making them the focus of this study.

Emerging deep learning (DL) can extract non-linear relationships in a data driven way, enabling the discovery of complex features and representations [20]. These methods have been widely and successfully utilized in applications such as image classification, super-resolution imaging, and image denoising [21, 22]. Convolutional Neural Networks (CNNs) can learn the characteristics of complex nonlinear relationships, thereby further improving the accuracy of material decomposition and advancing deep learning-based material decomposition algorithms. Current algorithms, including convolutional networks such as Incept-Net, Fully Convolutional Dense Network (FCDense-Net), and Squeeze-and-Excitation Neural Architecture Search Network (SeNAS-Net), have been widely applied to material decomposition [23]. By analyzing images across different energy spectra, material decomposition enhances performance by improving robustness, boosting sensitivity to dose variations, and minimizing noise and artifacts. The developed feedforward neural network projection decomposition techniques have successfully achieved multi-material projection decomposition on simulated data [17, 24–26]. GECCU-Net employs edge-conditioned convolutional layers to aggregate non-local features, effectively mitigating the impact of non-local noise on decomposition results [27]. MPU-Net proposes an encoder-multi-decoder architecture that utilizes High-Resolution Network (HRNet) to extract correlations between material images, thereby constraining the material decomposition model through these learned correlations [28]. Transformer-based architecture has demonstrated remarkable capabilities in capturing long-range dependencies and contextual features, particularly in medical image analysis tasks. Wang et al. [29] proposed framework integrates both convolutional neural networks and a Transformer module to effectively combine local and global information for direct material decomposition from single-energy CT images. The Butterfly Convolutional Neural Network (Butterfly Net) exhibits significant advantages over traditional Fully Convolutional Networks (FCN) in material decomposition [30]. Previous studies have confirmed that combining traditional model-driven decomposition methods with data-driven CNN to construct hybrid model-driven deep learning approaches results in improved projection decomposition performance of the neural network methods. Using a joint model-driven CNN for DE-CT image processing not only avoids the limitations of traditional reconstruction methods but also reduces image noise and artifacts, thereby improving the accuracy and efficiency of the decomposition. However, existing methods using traditional convolutional neural network (CNN) operators exhibit limited ability to capture non-local and global contextual features, restricting their effectiveness in optimizing material decomposition accuracy. Additionally, deep learning frameworks inadequately exploit cross-spectral correlations and energy-specific differences in multi-channel spectral CT data, leading to suboptimal utilization of spectral information for robust decomposition. Furthermore, existing algorithms have been rarely applied in the decomposition of rock materials.

To address these limitations, this paper proposes I-MultiEncFusion-Net, a multi-encoder single-decoder network designed to exploit spectral differences across energy channels while integrating local and non-local feature representations. The encoder employs Inception_B modules with parallel branches to capture multi-scale features and an LNFA module that aggregates both local textures and global contextual patterns through non-local neighborhood relationships measured by Euclidean distance. To optimize decomposition accuracy, the decoder incorporates Huber loss for each output channel and leverages HR Net-derived material correlations as a constraint within the loss function. Validated on spectral CT data of sandstone samples, I-MultiEncFusion-Net demonstrates superior generalization, enhanced detail preservation, and sharper edge delineation in both simulated and real-world experiments.

2 I-MultiEncFusion-net for multi-material decomposition

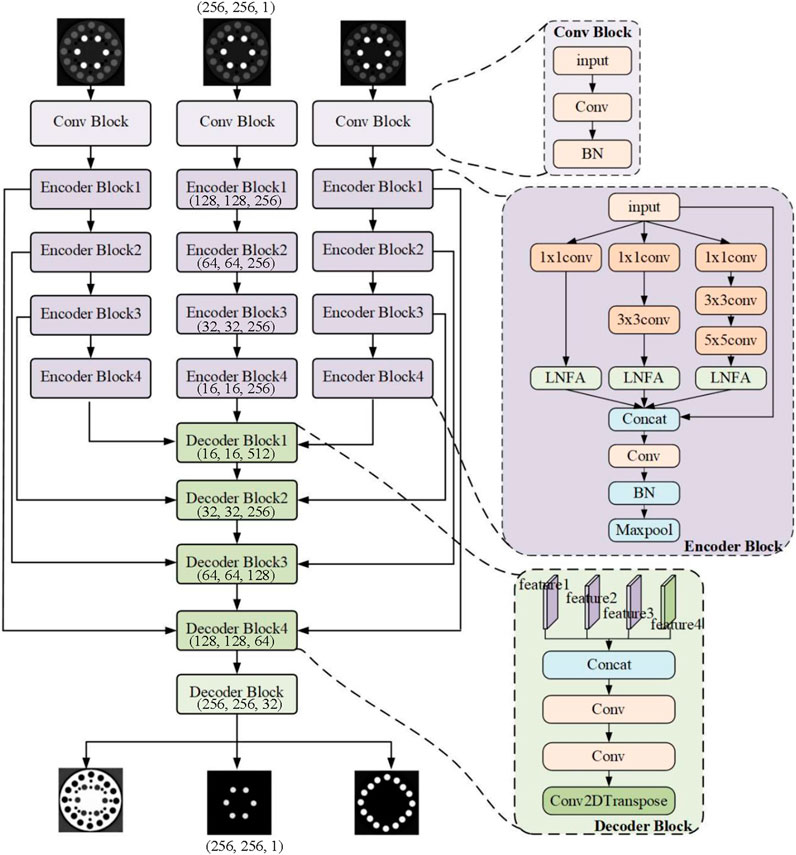
To comprehensively capture feature representations from reconstructed images across all energy channels in spectral CT imaging, this paper introduces an enhanced encoder-decoder architecture named I-MultiEncFusion-Net, building upon the foundation of Incept-Net (I-Net). The proposed framework employs a multi-encoder-single-decoder configuration to achieve cross-channel feature integration, where encoder and decoder components are interconnected through skip connections. The quantity of encoders precisely corresponds to the spectral dimension of CT energy channels (as shown in Figure 1). Each encoder performs hierarchical downsampling while the unified decoder executes progressive upsampling. Experimental validation utilizes tri-channel spectral CT data, corresponding to the design of three specialized encoder branches aimed at extracting energy-specific characteristics. The encoder section utilizes the Inception_B module structure, employing three parallel branches to comprehensively extract multi-scale and multi-directional features from the images. Finally, the LNFA module is introduced to achieve cross-modal feature fusion and material decomposition tasks through a unified decoder.

Figure 1

Figure 1. I-MultiEncFusion-Net architecture.

2.1 I-MultiEncFusion-net architecture

For spectral CT image, there exists a nonlinear relationship between the decomposed materials and the reconstructed images across three energy spectra. This study proposes an enhanced feature aggregation network to improve material decomposition accuracy through optimization of an encoder-decoder architecture. Initially, the multiscale feature extraction is implemented through an Inception_B module, a composite convolutional architecture comprising three parallel processing branches. Each branch initiates with a 1 × 1 convolution for dimensionality reduction, followed by 3 × 3 convolutional kernels of varying depths (0, 1, and 2 layers) to extract multiscale local features, with the convolutional layers configured to have 32, 64, and 128 channels, respectively. Additionally, to address local-nonlocal feature aggregation challenges, the U-Net architecture is enhanced through novel integration of a LNFA as the encoder, constructing fine-grained feature representations to strengthen feature extraction capabilities. The network processes three independent input images, with each input branch employing same structure for feature extraction. Each branch begins with a convolutional layer followed by a batch normalization (BN) layer for preliminary feature extraction, utilizing L₂ regularization to mitigate overfitting. Subsequently, four Inception_B modules are used for deep feature extraction. The outputs from the three branches are concatenated with the original input feature maps, followed by a 3 × 3 convolutional layer with 256 channels, a BN layer, and a ReLU activation function. Finally, downsampling is achieved through a MaxPooling layer, while the architecture enhances feature representational capacity through multi-scale convolutional operations and non-local context aggregation. The HRNet multi-resolution supervision mechanism is utilized, incorporating the Huber loss function to enhance noise robustness. This approach effectively regulates the material decomposition process, thereby improving the model’s robustness and accuracy.

Since the decomposed materials are correlated with the reconstructed images across three energy levels, a decoder is implemented to enable feature fusion within this framework. The decoder utilizes a deconvolution operation with a kernel size of 2 and a stride of 2 for upsampling, progressively reconstructing the feature maps from the encoder to match the original input resolution. After each upsampling operation, the resulting feature maps are fused with the corresponding feature maps from the encoder layers to obtain multi-scale feature information. Following two convolutional layers with a 3 × 3 kernel and a stride of 1, the number of channels in each decoder block is 256, 128, 64, and 32, corresponding to the channel counts of the encoder. After the final decoder block, a convolutional layer with a kernel size of 1 × 1 and 3 output channels are employed to perform a linear transformation on the feature maps, effectively aggregating the information within the feature maps, with the output channels aligned to the dimensions of the material decomposition targets.

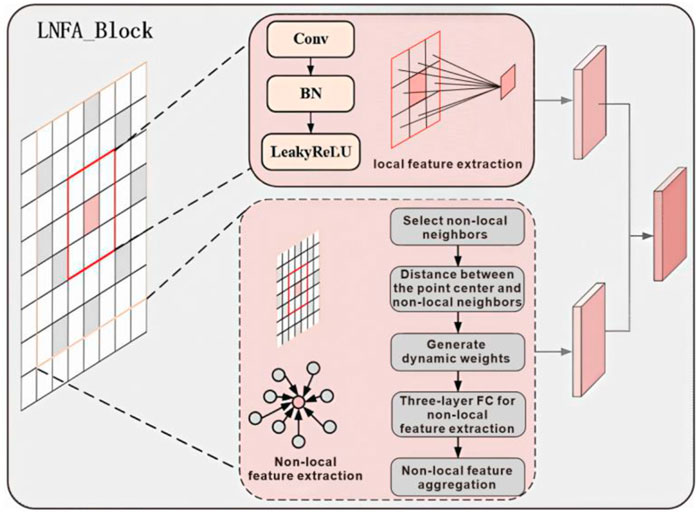
2.2 LNFA model

With effective capabilities in the extraction and aggregation of both local and non-local features, the LNFA module is specifically designed to enhance model performance in deep learning. However, in the LNFA module, non-local features are extracted by Edge Convolution (ECC), which emphasizes the representation of local spatial structures. It should be noted that the integration of global information in the decomposition of materials within spectral computed tomography (CT) images enhances the model’s representational capacity and decomposition accuracy, thereby improving the precision of material identification and separation. This study proposes a method for extracting local structural features by modeling spatial differences between adjacent points, emphasizing the integration of global information. This approach enables the dynamic synthesis of multi-regional feature representations, thereby enhancing the learning capacity of the network. The local feature extraction branch employs convolutional, normalization, and activation operations to capture detailed information within the local receptive field, facilitating the identification of low-level features such as textures and edges. And the non-local feature extraction branch constructs a non-local neighborhood to capture relationships between distant pixels across a broader spatial extent. It computes dynamic weights based on the similarity in Euclidean space, thereby enabling the weighted integration of non-local features (as shown in Figure 2).

Figure 2

Figure 2. Dual-branch feature extraction architecture of LNFA block.

Firstly, local features are extracted using a 3 × 3 convolutional layer, followed by BN and a Leaky ReLU activation function (Equation 1):

$z_i^L=Leaky\text{Re}LU\left(BN\left(Conv\left(x\right)\right)\right)(1)$

where, x is input feature map, Conv represents the convolution operation, BN signifies batch normalization, LeakyReLU refers to the Leaky ReLU activation function. The extracted local features are denoted as $z_i^L$, with i serving as an index corresponding to a specific position within the feature map.

Then, non-local features are extracted by selecting eight non-local neighborhoods randomly within a range of [-3, 3] centered around $z_i$. The Euclidean distance between the center point and the randomly selected non-local neighborhoods is computed and utilized as the weight for the edges:

$E_{i-j}={‖z_i-n_j‖}^2(2)$

where $n_j$ is the feature vector of the jth non-local neighborhood point. $E_{i-j}$ represents the edge weight between the center point $z_i$ and the non-local neighborhood $n_j$.

A three-layer fully connected neural network is employed to generate dynamic aggregation weights based on these edge weights (Equation 3):

${\theta }_{i-j}=F^l\left(E_{i-j},{\overline{\omega }}_j\right)(3)$

where $F^l$ represents the three-layer fully connected neural network, ${\overline{\omega }}_j$ denotes the trainable parameters that generate the dynamic edge weight (Equation 4). ${\theta }_{i-j}$ corresponding to the jth node:

$\begin{array}{l}{v}_1=\text{ReLU}\left(W_1·E_{i-j}+b_1\right)\\ v_2=\text{ReLU}\left(W_2·v_1+b_2\right)\\ {\theta }_{i-j}=W_3·v_2+b_3\end{array}(4)$

where $W_i$ denotes the weights of the fully connected layer, $b_i$ represents the biases of the fully connected layer. Subsequently, the dynamic weights are aggregated with the non-local features, followed by batch normalization and activation (Equation 5):

$z_i^{NL}=\frac{1}{\left|P_i\right|}{\displaystyle \sum _{j=1}^k}{\theta }_{i-j}·n_j+b(5)$

where $P_i$ represents the neighborhood set of the central point $v_i$ (non-local neighborhood). $\left|P_i\right|$ indicates the number of neighboring points, and k denotes the total count of non-local neighborhoods.

Finally, the extracted local features are concatenated with the aggregated non-local features, followed by fusion through a 1 × 1 convolutional layer, BN, and Leaky ReLU activation, resulting in the final feature representation (Equation 6):

$z_i^{concat}=\text{concat}\left(z_i^L,z_i^{NL}\right)(6)$

The LNFA module enhances feature expressiveness by integrating both local and non-local information, enabling the model to learn more robust and informative features when processing data characterized by local and non-local attributes.

2.3 Loss function

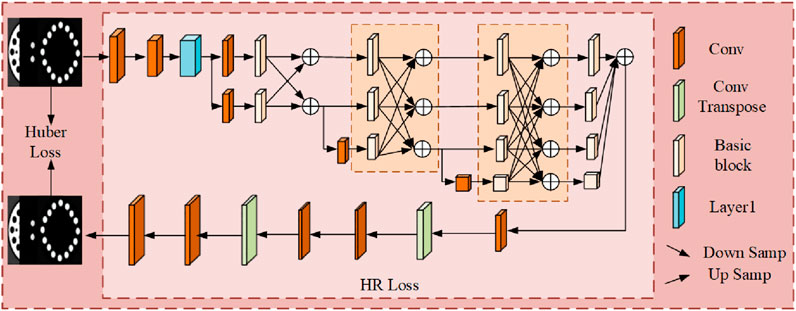
The HRNet architecture is distinguished by its ability to simultaneously capture fine-grained high-resolution features and rich contextual information. This characteristic is particularly relevant for material decomposition, where features of different materials may exhibit substantial variations across scales. In this study, HRNet is employed to extract relevant features from spectral CT images, utilizing the feature extraction module of HRNet to generate high-resolution loss that constrains the training process of the material decomposition model. Specifically, we compare real data with the outputs of the material decomposition model, using this comparative analysis as a basis for constraining the model’s loss function, thereby enhancing the accuracy of material decomposition. HRNet effectively maintains the integration of high-resolution and low-resolution features through repeated multi-scale feature fusion across the entire network architecture. To further improve decomposition accuracy, we have enhanced HRNet by two upsampling layers and additional convolutional layers (as shown in Figure 3).

Figure 3

Figure 3. Loss function.

The Huber loss function and the HR loss function (Equation 7) are employed for training the network. In the presence of outliers within the dataset, traditional loss functions can negatively impact model performance. The Huber loss function effectively combines the benefits of mean squared error (MSE) and mean absolute error (MAE): it behaves as MSE for small errors while transitioning to MAE for larger errors, thus enhancing robustness against outliers:

$L_{\delta }\left(a\right)=\left\{\begin{array}{l}\frac{1}{2}{a}^2\\ \delta \left(\left|a\right|-\frac{1}{2}\delta \right)\end{array}\right.\begin{array}{l}for\left|a\right|\le \delta \\ for\left|a\right|>\delta \end{array}(7)$

where, $a=y-\widehat{y}$ represents the discrepancy between the true value y and the predicted value $\widehat{y}$. $\delta$ is a hyperparameter that governs the threshold of the loss function. The Huber loss function exhibits a linear growth characteristic similar to that of MAE when the error is significant, thereby reducing the influence of outliers on the model. And the Huber loss function is smooth at the threshold, contributing to greater stability during optimization and facilitating faster convergence. Furthermore, by adjusting the hyperparameter $\delta$, a flexible balance can be achieved between MSE and MAE, making it suitable for various application scenarios.

During the training process, the Huber loss utilizes the correlations among materials to impose constraints on the model. Additionally, the output from each decoder is computed in conjunction with its corresponding labels to generate the Huber loss. The overall loss of the I-MultiEncFusion-Net (Equation 8) can be expressed as follows:

$L_{loss}=L_{Huber1}+L_{Huber2}+L_{Huber3}+\alpha L_{HR}(8)$

where $L_{Huber1}$, $L_{Huber2}$, and $L_{Huber3}$ denote the Huber losses corresponding to the three materials. $L_{HR}$ represents the HR loss, $\alpha$ indicates the magnitude of the HR loss. For the HRNet, we employ a self-supervised approach for training and apply the Huber loss function to constrain the model. Dynamic weighting optimizes PSNR/SSIM, effectively addressing the limitations of single-loss functions, as shown in Table 1.

Table 1

Table 1. Ablation of loss.

3 Experiments and result

The proposed I-MultiEncFusion-Net is implemented within the Keras and TensorFlow frameworks on an NVIDIA RTX 4090D GPU. Learning rate is set to 1 × 10⁻⁵, and the Adam optimization algorithm is employed to minimize the loss function. The Structural Similarity Index (SSIM) and Peak Signal-to-Noise Ratio (PSNR) are utilized as assessment metrics to quantify the similarity between predicted outcomes and ground truth labels. Notably, both simulated sandstone models and real data are utilized as test datasets, and I-MultiEncFusion-Net exhibits substantial performance advantages in all test datasets.

3.1 Simulation experiment

The spectral computed tomography (CT) system is simulated using the Spekpy v2.0 spectral simulation software. The X-ray source is positioned 100 mm from the rotation center, and the detector, which has a length of 20 mm, consists of 256 individual detection elements. For each scan, data is acquired at intervals of 1.4 degrees, resulting in a total of 256 projections over 360 degrees. Figure 4 illustrates the structure of the simulated phantom used in this experiment, which consists of air, quartz and sodium feldspar (SiO₂), calcite (CaCO₃), and pyrite (FeS₂), with a reconstruction image resolution of 256 × 256 pixels. The simulation experiment selects three energy channels: [20,30) keV, [30,40) keV, and [40,50) keV, resulting in the generation of 800 datasets, of which 700 are designated for the training dataset and 100 for the testing dataset.

Figure 4

Figure 4. The result of materials decomposition with different Net.

3.1.1 Comparison of I-MultiEncFusion-net and other net

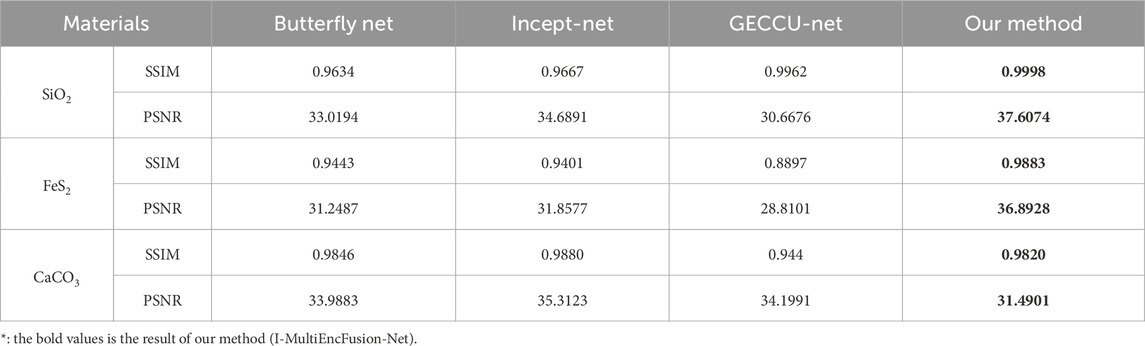
Four famous net, Butterfly Net, Inecpt-Net, GECC and GECC, are selected to compared with I-MultiEncFusion-Net. These networks are representative of the current state-of-the-art in their respective domains and provide a robust framework for evaluating the performance of our approach. To ensure an objective assessment of each network’s performance, we maintained consistency in the datasets utilized and the number of training iterations. Figure 4 illustrates the decomposition results for the three networks. And Table 1 presents the quantitative analysis outcomes.

As illustrated in Figure 4, the first column displays the input images, while the second column presents the corresponding label images for SiO₂, FeS₂, and CaCO₃. Columns three through six sequentially showcase the decomposition results for SiO₂, FeS₂, and CaCO₃ using various Nets. It can be shown that DishNet, Inept-Net, and GECCU-Net achieve the material identification and decomposition. However, the performance of these networks in decomposing FeS₂ is notably inadequate, characterized by blurred edges and insufficient detail in the internal structure. Additionally, GECCU-Net’s results for CaCO₃ decomposition are similarly unsatisfactory, whereas DishNet and Inept-Net demonstrate comparatively superior performance in this task. Notably, our method I-MultiEncFusion-Net significantly enhances both the clarity of internal structures and the accuracy of edge recovery in the decomposition results, thereby demonstrating its exceptional capability in material decomposition.

The cross-channel semantic fusion in I-MultiEncFusion-Net operates through three-stage process: first, encoder outputs from three energy-specific pathways undergo spatial interaction through concatenation followed by 3 × 3 convolution and batch normalization to establish local feature correlations; second, these integrated features enter the LNFA block where self-attention mechanisms model global dependencies across energy channels, capturing contextual relationships between materials like CaCO₃ or SiO₂ spatial distributions; finally, learnable dynamic weights based on the similarity in Euclidean space, thereby enabling the weighted integration of non-local features, enabling adaptive fusion optimized for mineral decomposition tasks. As shown in Table 2, the results show that our method exhibits exceptional performance in decomposition tasks, particularly demonstrating superior efficacy in the decomposition of SiO₂ and FeS₂. For SiO₂, the ILNF-Net achieved a SSIM of 0.9998, effectively reconstructing the original image structure, with a PSNR of 37.6074, significantly outperforming other models. In the decomposition of FeS₂, our method attained SSIM and PSNR values of 0.9883 and 36.8928, respectively, again surpassing all comparative models. The decomposition performance for CaCO₃ was slightly lower than that of other Net, with a comparatively reduced SSIM and modest PSNR. This difference may arise from the complexity of CaCO₃’s characteristics during component extraction, which resulted in minor overfitting during training. In future work, we will further investigate the introduction of adaptive attention mechanisms and multi-scale feature fusion strategies to optimize the network’s ability to extract features from such materials, in order to improve decomposition accuracy. Despite the relatively lower performance of our method in the decomposition of CaCO₃, as indicated by the SSIM in comparison to DishNet and Incept-Net, and a modest PSNR, it demonstrated significant efficacy in the decomposition of complex materials overall.

Table 2

Table 2. The SSIM and PSNR of different nets.

3.1.2 Shape generalization

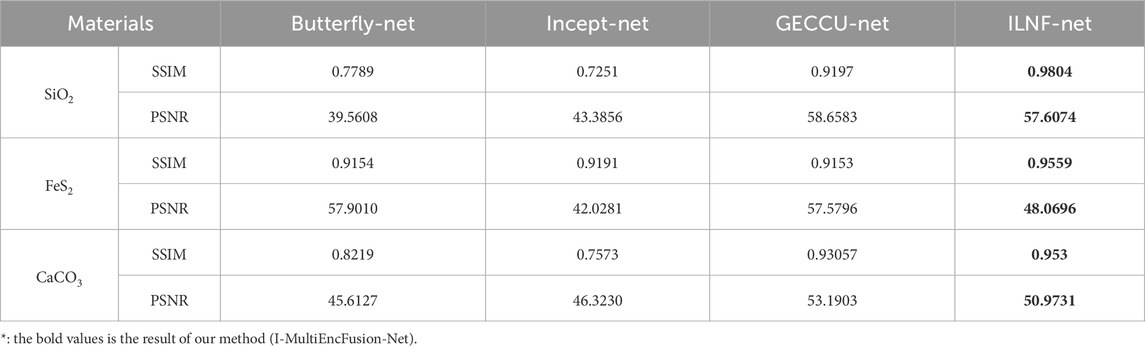
The heterogeneity of rock material structures necessitates a higher generalization capability in models. To evaluate the generalization performance of the proposed network, a newly constructed modeling dataset was utilized as the test set. The previously uniform circular structures were replaced with synthetic geometric structures of varied shapes, including triangles, rectangles, and squares, as illustrated in Figure 5. Experimental results reveal that DishNet, Incept-Net, and GECCU-Net encounter significant challenges in achieving satisfactory outcomes for complex decomposition tasks. Specifically, DishNet was unable to decompose FeS₂, partially decomposed CaCO₃, and showed substantial residual CaCO₃ during the decomposition of SiO₂. Incept-Net could not effectively decompose either CaCO₃ or SiO₂ but managed to partially decompose FeS₂. GECCU-Net failed to decompose FeS₂ while successfully decomposing both CaCO₃ and SiO₂. Notable, the proposed I-MultiEncFusion-Net, although exhibiting lower brightness in the decomposition of FeS₂ compared to CaCO₃ and SiO₂, effectively decomposed all three materials.

Figure 5

Figure 5. New test dataset with different geometrical shapes, where squares represent SiO₂, rectangles denote CaCO₃, and triangles signify FeS₂.

Table 3 shows the analysis results of SSIM and PSNR for various networks applied to different materials. The results show that the proposed I-MultiEncFusion-Net demonstrates robust adaptability and stability in both SSIM and PSNR metrics. In the SiO₂ decomposition task, I-MultiEncFusion-Net achieved an SSIM of 0.9804, significantly outperforming other models. The PSNR value of 57.6074 is comparable to that of GECCU-Net at 58.6583, while still surpassing other models, thereby highlighting I-MultiEncFusion-Net’s robust capabilities in detail preservation and noise management. For the FeS₂ decomposition, I-MultiEncFusion-Net recorded an SSIM of 0.9559, surpassing all competing models, particularly excelling in structural reconstruction. Although the PSNR of 48.0696 is slightly lower than that of the butterfly network and GECCU-Net, it still reflects commendable robustness. In the CaCO₃ decomposition, I-MultiEncFusion-Net achieved an SSIM of 0.953, surpassing GECCU-Net and significantly outperforming both the butterfly network and Incept-Net, with a PSNR of 50.9731 that is comparable to GECCU-Net, thereby demonstrating consistent performance. Overall, I-MultiEncFusion-Net exhibits outstanding generalization capabilities in complex tasks, particularly showing a significant advantage in structural similarity (SSIM) and stable adaptability across various material decomposition challenges. In real scanning experiments, the presence of noise in rock images is influenced by factors such as voltage fluctuations. This study also analyzes the sensitivity to noise by introducing Gaussian noise $N\left(0,{\delta }^2\right)$. The resulting images and experimental outcomes are shown in Appendix A. The results indicate that the proposed I-MultiEncFusion-Net model demonstrates robust performance under noise interference, effectively facilitating material decomposition. Notably, it demonstrates superior efficacy in the decomposition of CaCO₃, the primary component of rocks.

Table 3

Table 3. The results of materials decomposition for a new test dataset.

3.2 Ablation of architecture

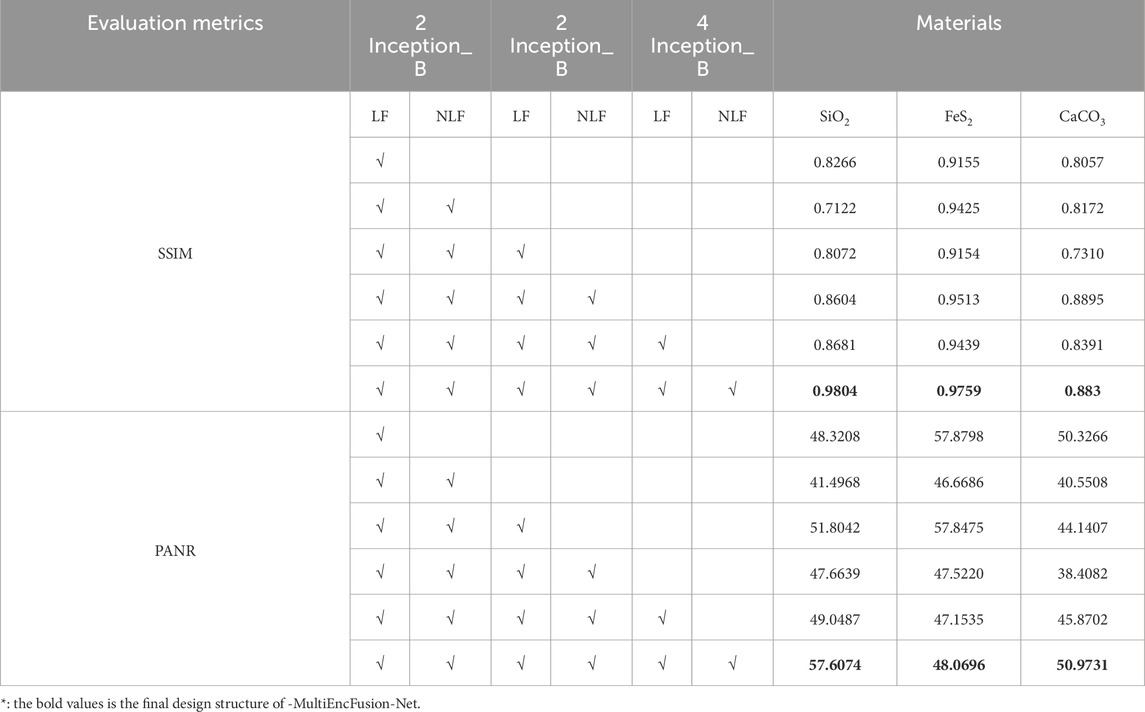
In the I-MultiEncFusion-Net, the effectiveness of material decomposition is affected by the quantity of Inception_B modules and the sampling structures utilized for local (LF) and non-local (NLF) feature extraction. The increase in the number of Inception_B modules does not lead to an improvement in performance. And a simple combination of LF and NLF structures does not effectively enhance performance. Therefore, this study conducted an ablation analysis regarding the number of Inception_B modules and the LF and NLF structures, with results showed in Table 4. As the number of Inception_B modules increases from 2 to 4, the model does not demonstrate a linear improvement in performance. However, a comparative analysis of the SSIM values presented in the table (e.g., 0.9155 vs. 0.8266) reveals that the configuration with 4 modules effectively enhances the network’s performance. Further analysis of structural factors reveals that a simple combination of LF and NLF (as indicated in the “2 Inception_B” column of Table 3) does not result in significant performance improvements. The ablation study results regarding the number of Inception_B modules and the implementation of the LF and NLF structures indicate that the configuration comprising 4 Inception_B modules in conjunction with LF and NLF achieves the highest SSIM value. These results indicate that a increase in model depth, combined with the use of local and non-local sampling structures, is effective for materials decomposition, particularly exhibiting notable advantages in the decomposition of SiO₂ materials. The implementation of 4 Inception_B modules, combined with both local and non-local sampling techniques, demonstrates a superior overall balance in performance. However, the results also indicate that the decomposition performance of CaCO₃ does not exhibit significant enhancement under the optimal configuration, suggesting the necessity for further investigation into optimization methodologies in future research.

Table 4

Table 4. Results of ablation study on architecture experiment.

3.3 Real scan experiment

To evaluate the decomposition performance of the proposed I-MultiEncFusion-Net in practical applications, experiments were conducted using sandstone samples. These samples were made by the Calcite In-situ Precipitation System (CIPS). To simulate the natural cementation of reservoir rocks, the samples were primarily composed of calcium carbonate and quartz cement. Medium-grained quartz sand (150–300 μm), pre-washed and dried, was uniformly packed into a 20 × 20 × 10 cm³ mold, followed by the injection of a water-based chemical solution to finish the final samples within the CIPS system. Medium-grained quartz sand (150–300 μm), which was pre-washed and dried, was uniformly packed into a 20 × 20 × 10 cm³ mold, after which a water-based chemical solution was injected to complete the final samples within the CIPS system.

The scanning was conducted using the NanoVoxel-3000HX X-ray three-dimensional high-resolution imaging system from Tianjin Sanying Precision Instrument, operating at a tube voltage of 70 kV. Two energy channels were utilized, specifically [25, 35) keV and [45, 55) keV. The distance from the X-ray source to the specimen was 14.6 mm, while the distance from the X-ray source to the detector was 648.9 mm. This model assumes the presence of three components—pores, CaCO₃, and SiO₂—in the artificial sandstone samples, each exhibiting different volumetric attenuation coefficient in the CT images. Furthermore, the X-ray attenuation of each voxel in the artificial sandstone is equivalent to the sum of the X-ray absorption contributions from the pores, CaCO₃, and SiO₂ within that voxel. A total of 150 CT slices from layers 200 to 349 were designated as the training set, while 20 CT slices from layers 400 to 419 were allocated as the testing set. Figure 6a presents representative images from the training set across various energy ranges, highlighting the challenges of mineral decomposition in rocks, which require simultaneous consideration of diverse mineral compositions. Based on the composition of the rock, the network primarily decomposes CaCO₃ and silicon dioxide SiO₂, with the remaining voids represented as pores. The results indicate that the Butterfly Network is unable to effectively decompose CaCO₃, whereas the other networks successfully achieve decomposition of both substances. However, in the enlarged view of the region of interest, it is evident that the edges of the CaCO₃ decomposition produced by GECCU exhibit significant blurriness, while Incept-Net demonstrates suboptimal recovery of the internal structure during the decomposition of SiO₂ (as shown in Figure 6b). These limitations arise primarily because 7 mineral decomposition demands joint modeling of local textures7and non-local contextual features 7, a capability uniquely addressed by our I-MultiEncFusion-Net. Notably, I-MultiEncFusion-Net demonstrates superior performance in preserving the integrity of both the composition and structure of the materials.

Figure 6

Figure 6. (a) The training data under different energy. (b) The materials decomposition results by different Net.

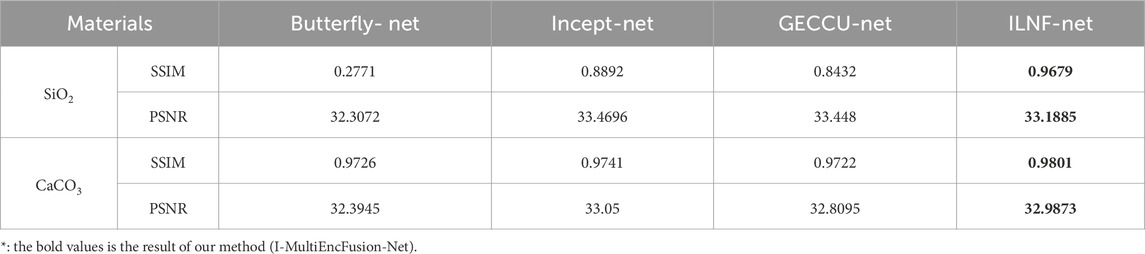
The performance of different networks in material segmentation was evaluated using SSIM and PSNR, as shown in Table 5. The I-MultiEncFusion-Net demonstrates superior performance in the task of material decomposition in the real CT image.

Table 5

Table 5. The results of material decomposition of sandstone based on real CT scanning images.

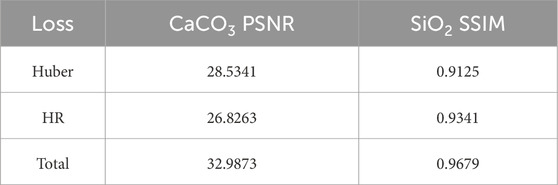
For the decomposition of SiO₂, I-MultiEncFusion-Net achieved a SSIM of 0.9679, significantly surpassing that of other models. In terms of PSNR, I-MultiEncFusion-Net also exhibited outstanding results, with a value of 33.1885, comparable to those of Incept-Net and GECCU-Net. For the decomposition of CaCO₃, I-MultiEncFusion-Net achieved an SSIM of 0.9801, slightly surpassing that of other networks, while its PSNR performance remained among the best in the field at 32.9873. Overall, I-MultiEncFusion-Net exhibits enhanced decomposition quality and visual accuracy in image decomposition, particularly demonstrating a notable advantage in structural similarity (SSIM).

4 Conclusion

To address the limitations of traditional CNNs in extracting non-local features from CT images, this study proposes a multi-encoder-single-decoder architecture, named as I-MultiEncFusion-Net, which demonstrates superior material decomposition performance across both simulated and real datasets. Specifically, this architecture integrates parallel encoders designed to capture common features of base material images (through shared parameters for multimodal input) and distinctive features (via differential feature extraction). These features are fused across modalities using a single decoder, enabling the multi-encoder structure to effectively integrate information from multiple input images while emphasizing their differences, with the single decoder promoting feature sharing. Through ablation studies, this research identifies the optimal configuration of the Inception_B structure and the LNFA module, where the Inception_B module serves as an efficient feature extraction unit specifically designed for image-domain material decomposition tasks, capable of effectively capturing multi-scale features, while the LNFA module enhances the aggregation of local and non-local features, thereby optimizing the material decomposition process. Furthermore, this study innovatively employs the correlation between material images as a loss function to impose constraints on the model, resulting in improved stability and accelerated convergence during the optimization process. The superiority of the proposed model’s performance is validated by results from both simulation experiments and artificial sandstone tests.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

YW: Writing – review and editing, Supervision, Funding acquisition, Writing – original draft, Software, Resources, Investigation, Validation, Project administration, Conceptualization, Methodology, Formal Analysis, Data curation, Visualization. RZ: Methodology, Project administration, Investigation, Writing – original draft. HK: Software, Writing – original draft. PC: Writing – original draft, Funding acquisition. YZ: Data curation, Funding acquisition, Writing – review and editing.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. This research was funded by National Key Research and Development Program of China under grant 2023YFE0205800; National Nature Science Foundation of China under grants (U23A20285, 42207205); Provincial Natural Science Foundation of Shanxi, China under grants (202403021223006, 202403021211025), Shanxi Key Research and Development Program under grant (202302150401011), Technology Development Fund Project of Shanxi Province under grant (202304021301028), Shanxi Province Overseas Study Program under grants (2023-129).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Cong W, Xi Y, Fitzgerald P, De Man B, Wang G. Virtual monoenergetic CT imaging via deep learning. Patterns (2020) 1(100128):100128. doi:10.1016/j.patter.2020.100128

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Wu Y, Xiao Z, Li J, Li S, Zhang L, Zhou J, et al. ShaleSeg: deep-learning dataset and models for practical fracture segmentation of large-scale shale CT images. Int. J Rock Mech Mining Sci (2024) 180:105820. doi:10.1016/j.ijrmms.2024.105820

CrossRef Full Text | Google Scholar

3. Cnudde V, Boone MN. High-resolution X-ray computed tomography in geosciences: a review of the current technology and applications. Earth-Science Rev (2013) 123:1–17. doi:10.1016/j.earscirev.2013.04.003

CrossRef Full Text | Google Scholar

4. Sun XK, Li X, Zheng B, He J, Mao T. Study on the progressive fracturing in soil and rock mixture under uniaxial compression conditions by CT scanning. Eng Geology (2020) 279:105884–9. doi:10.1016/j.enggeo.2020.105884

CrossRef Full Text | Google Scholar

5. Yan G, Xu Y-H, Xu W-L, Bai B, Bai Y, Fan YP, et al. Shale oil resource evaluation with an improved understanding of free hydrocarbons: insights from three-step hydrocarbon thermal desorption. Geosci Front (2023) 14(6):101677. doi:10.1016/j.gsf.2023.101677

CrossRef Full Text | Google Scholar

6. Duan Y, Li X, Zheng B, He J, Hao J. Cracking evolution and failure characteristics of longmaxi shale under uniaxial compression using real-time computed tomography scanning. Rock Mech Rock Eng (2019) 52(9):3003–15. doi:10.1007/s00603-019-01765-0

CrossRef Full Text | Google Scholar

7. Guo P, Li X, Li S, Yang W, Wu Y, Li G. Quantitative analysis of anisotropy effect on hydrofracturing efficiency and process in shale using X-ray computed tomography and acoustic emission. Rock Mech Rock Eng (2021) 54:5715–30. doi:10.1007/s00603-021-02589-7

CrossRef Full Text | Google Scholar

8. Patino M, Prochowski A, Agrawal MD, Simeone FJ, Gupta R, Hahn PF, et al. Material separation using dual-energy CT: current and emerging applications. Radiographics (2016) 36(4):1087–105. doi:10.1148/rg.2016150220

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Wei J, Chen P, Liu B, Han Y. A multienergy computed tomography method without image segmentation or prior knowledge of X-ray spectra or materials. Heliyon (2022) 8(11):e11584. doi:10.1016/j.heliyon.2022.e11584

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Alvarez RE, Macovski A. Energy-selective reconstructions in x-ray computerised tomography. Phys Med and Biol (1976) 21(5):733–44. doi:10.1088/0031-9155/21/5/002

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Michael G. Tissue analysis using dual energy CT. Australas Phys and Eng Sci Med (1992) 15(1):75–87. Available online at: http://europepmc.org/abstract/MED/1575646

PubMed Abstract | Google Scholar

12. Brody WR, Butt G, Hall A, Macovski A. A method for selective tissue and bone visualization using dual energy scanned projection radiography. Med Phys (1981) 8(3):353–7. doi:10.1118/1.594957

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Fang W, Wu D, Kim K, Kalra MK, Singh R, Li L, et al. Iterative material decomposition for spectral CT using self-supervised Noise2Noise prior. Phys Med and Biol (2021) 66(15):155013. doi:10.1088/1361-6560/ac0afd

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Ying Z, Naidu R, Crawford CR. Dual energy computed tomography for explosive detection. J X-ray Sci Technology (2006) 14(4):235–56. doi:10.3233/xst-2006-00163

CrossRef Full Text | Google Scholar

15. Ducros N, Abascal JFPJ, Sixou B, Rit S, Peyrin F. Regularization of nonlinear decomposition of spectral x-ray projection images. Med Phys (2017) 44(9):e174–87. doi:10.1002/mp.12283

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Xue Y, Jiang Y, Yang C, Lyu Q, Wang J, Luo C, et al. Accurate multi-material decomposition in dual-energy CT: a phantom study. IEEE Trans Comput Imaging (2019) 5(4):515–529. doi:10.1109/TCI.2019.2909192

CrossRef Full Text | Google Scholar

17. Niu T, Dong X, Petrongolo M, Zhu L. Iterative image-domain decomposition for dual-energy CT. Med Phys (2014) 41(4):041901. doi:10.1118/1.4866386

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Tao S, Rajendran K, McCollough CH, Leng S. Material decomposition with prior knowledge aware iterative denoising (MD-PKAID). Phys Med and Biol (2018) 63(19):195003. doi:10.1088/1361-6560/aadc90

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Zhao W, Niu T, Xing L, Xie Y, Xiong G, Elmore K, et al. Using edge-preserving algorithm with non-local mean for significantly improved image-domain material decomposition in dual-energy CT. Phys Med and Biol (2016) 61(3):1332–51. doi:10.1088/0031-9155/61/3/1332

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Kalmet PH, Sanduleanu S, Primakov S, Wu G, Jochems A, Refaee T, et al. Deep learning in fracture detection: a narrative review. Acta orthopaedica (2020) 91(2):215–20. doi:10.1080/17453674.2019.1711323

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Li J, Tian Y, Chen J, Wang H. Rock crack recognition technology based on deep learning. Sensors (2023) 23(12):5421. doi:10.3390/s23125421

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Yu J, Wu C, Li Y, Zhang Y. Intelligent identification of coal crack in CT images based on deep learning. Comput Intelligence Neurosci (2022) 2022:1–10. doi:10.1155/2022/7092436

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Wu X, He P, Long Z, Guo X, Chen M, Ren X, et al. Multi-material decomposition of spectral CT images via fully convolutional DenseNets. J X-Ray Sci Technology (2019) 27(3):461–71. doi:10.3233/xst-190500

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Gong H, Tao S, Rajendran K, Zhou W, McCollough CH, Leng S. Deep-learning-based direct inversion for material decomposition. Med Phys (2020) 47(12):6294–309. doi:10.1002/mp.14523

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Ji X, Lu Y, Zhang Y, Zhuo X, Kan S, Mao W, et al. SeNAS-net: self-supervised noise and artifact suppression network for material decomposition in spectral CT. Ieee Trans On Comput Imaging (2024) 10:677–89. doi:10.1109/tci.2024.3394772

CrossRef Full Text | Google Scholar

26. Peng J, Chang C-W, Fan M, et al. Image-domain material decomposition for dual-energy CT using a conditional diffusion model, 12930. SPIE (2024). 517–22.Proc Med Imaging 2024: Clin Biomed Imaging2024. doi:10.1117/12.3006941

CrossRef Full Text | Google Scholar

27. Shi Z, Kong F, Cheng M, Cao H, Ouyang S, Cao Q. Multi-energy CT material decomposition using graph model improved CNN. Med and Biol Eng and Comput (2024) 62(4):1213–28. doi:10.1007/s11517-023-02986-w

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Zhang L, Kong F, Zhang C, et al. MPU-net: multi-decoder U-net based on prior information for multi-material decomposition in spectral CT. In Proceedings 2023 16th international congress on image and signal processing, BioMedical engineering and informatics (CISP-BMEI)2023. IEEE (2023). p. 1–5.

CrossRef Full Text | Google Scholar

29. Wang G, Liu Z, Huang Z, Zhang N, Luo H, Liu L, et al. Improved GAN: using a transformer module generator approach for material decomposition. Comput Biol Med (2022) 149(2022):105952. doi:10.1016/j.compbiomed.2022.105952

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Zhang W, Zhang H, Wang L, Wang X, Hu X, Cai A, et al. Image domain dual material decomposition for dual-energy CT using butterfly network. Med Phys (2019) 46(5):2037–51. doi:10.1002/mp.13489

PubMed Abstract | CrossRef Full Text | Google Scholar

Appendix

FIGURE A1

FIGURE A1. A nosie generalization. (a) Images under three energy bands with added noise. (b) Decomposed materials of the image under three energy bands with added noise.