- 1Department of Civil Engineering, The University of Hong Kong, Pokfulam, Hong Kong SAR, China
- 2WA School of Mines: Minerals, Energy and Chemical Engineering, Curtin University, Perth, WA, Australia
In far-from-equilibrium chemical systems, self-organizing diffusion-reaction processes can give rise to complex patterns. Such self-organizing patterns are commonly found in diverse rocks, emerging as periodic stripes, rings, and various polygons. While these patterns are well documented, the drivers of their diversity and the mechanisms behind pattern selection remain unclear. This study investigates how geometric heterogeneity influences the formation of Liesegang patterns in natural geological materials such as Zebra rocks, pyrite ores, and orbicular granites. Using numerical simulations based on phase-field modeling, we replicate various Liesegang pattern morphologies observed in nature, such as circular, triangular, and interacting bands, and analyze their dependence on initial geometry and boundary conditions. We demonstrate that the spatial distribution of reactive fluids and the shape of nucleation zones play critical roles in determining the final pattern morphology. Our results provide insight into the self-organization processes in geochemical systems and offer a predictive framework for understanding rhythmic mineral banding in rocks.
1 Introduction
Liesegang patterns—periodic precipitation structures formed via reaction–diffusion mechanisms—are widely observed in geological settings [1–5]. These patterns arise from spontaneous chemical self-organization under non-equilibrium conditions and are commonly found in sedimentary and igneous rocks. Understanding the factors that govern their formation is crucial for deciphering paleofluid flow dynamics and geochemical evolution.
This work explores the influence of geometric constraints on Liesegang pattern [6] development through numerical simulations. We focus on three representative geological examples: hematite banding in Zebra rocks, pyrite zoning in ore deposits, and orbicular granites with concentric mineral rings. By varying the initial configuration of fluid sources and domain boundaries, we reproduce key features of these natural patterns and identify deviations from classical Liesegang behavior.
Rhythmic patterns in rocks are prevalent, originating from self-organized processes within a non-equilibrium, nonlinear geochemical system [1–5]. These periodic patterns appear across various scales, ranging from microscopic to millimeter, and even up to kilometer scales. Such periodic patterns are frequently associated with the Liesegang phenomenon, which involves rhythmic precipitation in gels. The Liesegang pattern formation is understood through the interaction between the diffusion of dissolved reactants and the kinetics of precipitate formation, including nucleation, growth, and ripening [6]. Analogous patterns in rocks include parallel mineral bands, concentric rings, oscillatory zoning, concretions, orbicules, among other forms. Numerous rock types exhibit patterned textures with periodic banding, potentially involving a Liesegang-type scenario. Examples include banded iron oxide minerals [7, 8], Zebra rocks [9–11], orbicular granites [12–14], and periodic oscillatory zoning [15, 16]. A thorough review of studies elucidating the analogy between Liesegang bands and geochemical banding is presented in [1, 2, 17].
Two primary models have been proposed to explain the mechanism behind Liesegang band formation. The “pre-nucleation” model [18] hypothesizes that nucleation and growth of precipitates occur when the reactant activity product exceeds a certain threshold, such as the critical supersaturation for nucleation or the solubility product for growth. Conversely, the “post-nucleation” model suggests that pattern formation arises from the instability and subsequent break-up of a uniform precipitate sol, driven by Ostwald ripening [19] and the Lifshitz-Slyozov instability [20]. Among post-nucleation models, one introduced two decades ago [21, 22] is based on phase separation theory. This model assumes that pattern formation results from spontaneous phase separation (unmixing) of the mixture. The phase separation model, underlying by the Cahn-Hilliard dynamics, has since gained prominence in multiple disciplines due to its conceptual simplicity and capacity to simulate irregular patterns and transitions between stripes and spots [23–26]. Our recent research has extended the phase separation model to replicate hematite patterns observed in Zebra rock from northern Western Australia [10, 11].
However, these studies have predominantly focused on regular geometries, overlooking the impact of geometric heterogeneity—defined here as the diversity in the spatial distribution, number, and shape of nucleation (initialization) regions—on Liesegang patterning in geological materials. In our context, geometric heterogeneity encompasses both the arrangement (e.g., regular or random) and the geometric shapes (e.g., circular, triangular) of nucleation centers, which collectively influence the resulting pattern complexity and interaction. This approach better reflects the intricate geochemical patterns observed in nature. Recent studies have also highlighted the importance of domain geometry and boundary conditions in shaping Liesegang-type structures. For example, [27] employed a vertex-based finite volume method to explore post-nucleation Liesegang patterns in confined geometries, demonstrating how symmetry and reversibility are affected by initial spatial constraints. Similarly, [28] combined reaction-diffusion equations with a Cahn-Hilliard-type precipitation model to simulate geochemical banding in limestones, including fractal analysis of pattern interfaces—an approach closely aligned with our interest in linking numerical simulations to natural textures. While our work builds upon spinodal decomposition principles similar to those used in [28], we emphasize the role of heterogeneous initialization regions in controlling pattern emergence, extending previous findings to more complex geological morphologies.
In this study, we integrate the phase separation model with explicit forms of geometric heterogeneity to replicate several complex geological patterns in rocks. First, we design a circular initialization region to reproduce the formation of single rhythmic pyrite rings observed in the Xingqiao sediment-hosted massive sulfide deposits [16]. Next, we model triangular-like Liesegang banding found in Zebra rocks from the Western Australian East Kimberley region. We then simulate more intricate Liesegang rings in rocks with multiple and heterogeneous initialization cores, using orbicular granites as a case study to replicate Liesegang ring interactions with various regular distributions. Finally, we reexamine the formation of heterogeneous pyrite rings observed in Xiaoqiao deposits with randomly distributed nucleation regions. A schematic figure is provided to categorize and illustrate these types of geometric heterogeneity.
The paper is structured as follows. In Section 2, we first present the phase separation theory for Liesegang pattern formation, followed by a discussion of three types of Liesegang patterns in rocks, casting their formation mechanisms within the phase separation model framework. Then, we state the problem and detail the numerical setup. Section 3 explores the influence of geometric heterogeneity on the formation of single and complex Liesegang patterns in three selected rock types, containing both regular and randomly distributed initialization shapes. Finally, we conclude our study in Section 4, highlighting potential directions for future research.
2 Methods
2.1 Phase separation model
Consider a closed system comprising two distinct components, denoted as
in which the constant
where, the notation
The reaction product
where
where,
The bulk free energy functional
in which
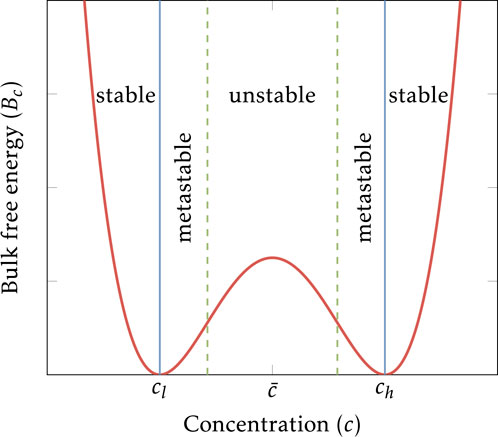
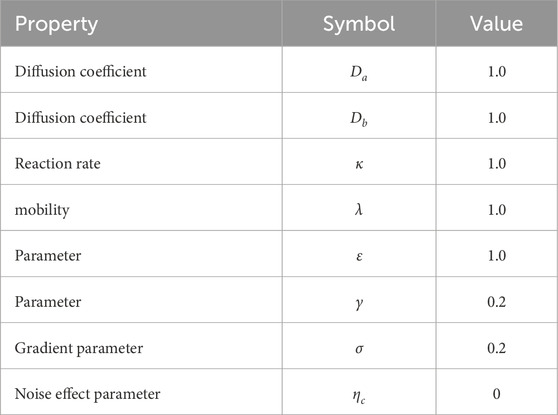
Figure 1. Sketch of double-well bulk free energy profile against concentration, with two minima at
Taking the derivative of the free energy of
We rewrite Equation 2, 3 in a dimensionless form by defining the normalized concentration, time, and length scales as
and shifting the normalized concentration as
Coupling Equations 2–8, we obtain the dimensionless final set of equations governing the pattern-forming process:
where
2.2 Three Liesegang patterns in rocks
This section provides three periodic patterns in rocks that potentially arise from cyclic precipitation as mineral-rich water infiltrates a porous rock and reacts to form an insoluble product, namely pyrite bands, Zebra rocks, and orbicular granites, see Figure 2. This occurs through the coupling of the precipitation reaction with diffusion and shows similar features to the Liesegang patterns. Here, we cast their formation mechanisms into the phase separation model framework.
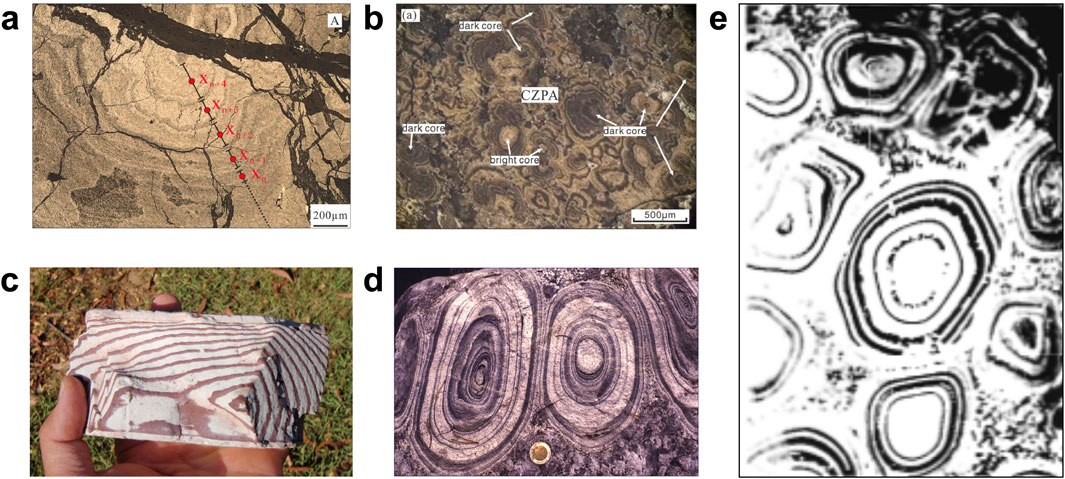
Figure 2. Diverse Liesegang patterns appear in rocks: (a,b) single and complex oscillatory zoning observed in the pyritic ores in the Xingqiao deposit, respectively, from [16]; (c) Hematitic patterns with a triangular Liesegang pattern in Zebra rocks from the northern region of Western Australia; (d,e) two and multiple orbicules from [12] formation and interaction in igneous rocks.
2.2.1 Pyrite bands
One notable class of rhythmic geochemical patterns is observed in pyrite, the most prevalent sulfide mineral near the Earth’s surface, which appears in various forms, from microscopic framboids to macroscopic structures (see Figures 2a,b). This paper examines the formation of pyrite rings within the Xingqiao sediment-hosted massive sulfide deposits. These pyrite patterns exhibit periodic fluctuations in concentration within a single crystal, from core to rim, characterized by two main zones: dark zones rich in siderite and bright zones dominated by pyrite. Despite extensive research on the formation mechanism of pyrite rings, the process remains debated. Self-organization processes, linked to the Liesegang ring phenomenon, offer a promising explanation for these patterns. Recently, Qiu et al. proposed a Liesegang model based on pre-nucleation to explain pyrite ring formation and replicate textures in the Xingqiao deposits [16]. We reexamine this possibility using our post-nucleation model to reproduce similar pyrite patterns in the same geological context.
Our phase separation model hypothesizes that periodic pyrite rings form through the reaction of two soluble reactants
We note that while
2.2.2 Hematite patterns
Ferric oxide (hematite and goethite) concentrations can develop in various sedimentary rocks, forming distinct spatial patterns such as concentric bands, planar bands, or columns. Hematite concentric bands are commonly found in chert concretions and nodules within limestones, indicating true self-organization during diagenesis, as these concretions are of diagenetic origin. Although these hematitic patterns are geologically minor, understanding their formation could highlight the complex kinetic interactions between reaction and transport in rocks, providing significant geochemical insights.
We examine the Zebra rock pattern from the northern region of Western Australia, known for its distinctive and prominent rhythmic hematite concentrations. Among all hematite banding patterns, Zebra Rock stands out due to its clarity and richness, making it an excellent model for studying pattern-forming processes related to subsurface environmental evolution. Zebra rock features reddish-brown bands, rods, and elliptical spots on a white or light background, as depicted in Figure 2c. Our previous research connected Zebra Rock formation to the Liesegang phenomenon, where supersaturation, nucleation, and depletion interact to create banded patterns. This connection was drawn because certain Zebra rock patterns resemble Liesegang bands. However, our earlier study did not account for the impact of complex geometries on pattern formation. Therefore, we now investigate how heterogeneous geometries influence morphological patterns in Zebra rocks.
Hematite in Zebra rock is a late-stage transformation product of Fe-Oxyhydroxide, precipitated from ferrous ions in an acidic geothermal environment, as described by the following chemical reaction in Equation 11:
2.2.3 Orbicular granites
Igneous rocks such as granites and diorites, including more basic plutonic rocks, sometimes feature ovoid structures known as orbicules [12]. These orbicules, ranging from several centimeters to about 1 m in diameter, consist of concentric, alternating light and dark mineral layers. They are believed to form through rhythmic selective crystallization of minerals around a foreign rock nucleus. The light-colored layers primarily contain plagioclase crystals with some dark minerals like hornblende or biotite, while the dark-colored layers are mainly composed of biotite or hornblende with minor plagioclase, see Figures 2d,e. The mineral distribution within each shell is irregularly circular or semi-circular, not symmetrically centered. It is suggested that orbicules form through counter-diffusion of heat and silicate components under conditions of rapid growth, potentially relating to self-organization and the Liesegang phenomenon.
Similarities between Liesegang patterns and multi-shelled orbicular granites, such as the geometric progression of band positions, imply that a Liesegang-like mechanism may partly explain their formation. In [13], Wang and Merino proposed an isothermal transport-reaction model based on a pre-nucleation framework to study orbicular granites. Although this model has been applied to the orbicular granite system, they concluded that a post-nucleation mechanism is essential for shell formation. Additionally, [33] noted that post-nucleation or hybrid pre- and post-nucleation models can more accurately reproduce realistic patterns in igneous layering or orbicular granite. In this study, we adapt the reaction-diffusion model by Wang and Merino to a post-nucleation phase separation model. The generic pathway for mineral precipitation follows this form:
in which
As for the oscillatory plagioclase in the orbicular granite, the specific chemical reaction in Equation 12 becomes:
Taking the above chemical reaction into the framework of
2.3 Numerical analysis
This section presents the numerical setup and finite element discrete formulations to apply the proposed phase separation model to simulate periodic patterns in stones and rocks.
2.3.1 Problem statement
We examine a two-dimensional initial-boundary value problem defined within a square domain
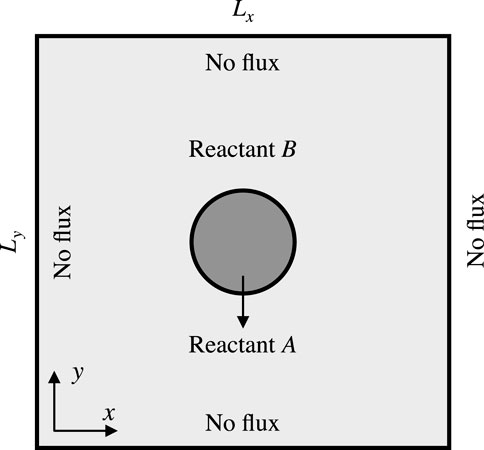
Figure 3. Sketch of initial and boundary conditions for Liesegang patterns formation and interaction.
Initially, the inner electrolyte
The scaled initializations used are
2.3.2 Finite element discretization
The coupled nonlinear partial differential equation (Equation 9) is solved using the open-source, high-performance phase-field software PRISMS-PF [34], based on the finite element method (FEM) through the deal.II library [35]. This framework supports adaptive mesh refinement, massively parallel computations, and matrix-free finite element simulations—features particularly advantageous for resolving fine-scale pattern evolution under complex geometric constraints. In contrast, [27] employed a vertex-based finite volume method (vb-FVM) to simulate Liesegang-type patterns in arbitrary domains, emphasizing flexibility in handling unstructured meshes and geometric confinement. While both FEM and vb-FVM are suitable for simulating reaction–diffusion systems on non-uniform grids, FEM offers superior accuracy in capturing sharp interfaces and gradient-driven dynamics due to its variational formulation and higher-order basis functions. Additionally, the matrix-free implementation in PRISMS-PF enhances computational efficiency, enabling scalable simulations of complex, heterogeneous nucleation scenarios that are central to our study.
The weak formulation of the coupled Equation 9, incorporating the Neumann boundary Equation 14 and initial conditions Equation 15, is derived using the following trial and test functions in Equation 16:
and integration by parts. By adopting the forward Euler method for time discretization, the corresponding weak forms become
The subsequent numerical analysis is conducted using an implementation of Equation 17 within the PRISMS-PF framework. The computational code is parallelized utilizing the Message Passing Interface (MPI) from the PETSc library (available at https://www.mcs.anl.gov/petsc). To enhance computational efficiency, a matrix-free finite element framework and an adaptive meshing technique are utilized, offering superior performance compared to conventional finite element methodologies.
3 Results and discussion
The numerical algorithm is developed and validated across various domains where the reactants (
3.1 Single pattern formation
3.1.1 Circular geometry
Figure 4a gives one sample of concentrically zoned pyrite aggregates (CZPA) of the pyritic ores in the Xingqiao deposit. This zoning pattern can be explained by Liesegang diffusion-reaction through the interaction between the diffusion of soluble reactants and the precipitation of solids in a permeable medium. Specifically,
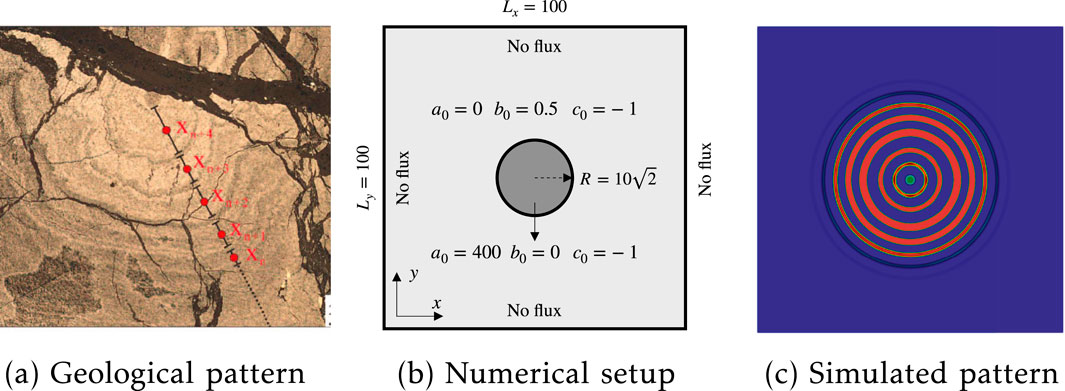
Figure 4. Liesegang ring formation: (a) pyrite patterns in Xingqiao sediment-hosted massive sulfide deposits from [16]; (b) numerical setup with the position and size of an initialized circular region; (c) simulated patterns.
Figure 4c illustrates the generated patterns from our post-nucleation phase-separation model. One can observe that our simulation can reproduce the oscillatory zoning observed in the CZPA of the pyritic ores in the Xingqiao deposit. Figure 4a depicts the location and band widths of the selected CZPA. We assume that the diffusion direction of
3.1.2 Triangle geometry
We subsequently compare the primary features captured by our simulations with those observed in a specific Zebra rock sample, as depicted in Figure 5a. One can observe a triangular-shaped Liesegang band pattern diffuses from the lower-left region throughout the entire sample. We postulate the presence of a fluid channel in the core region, which supplies Fe-bearing fluid flow, thereby generating the rhythmic hematite. Upon examination, two primary deviations from classical Liesegang patterns are noticeable. Firstly, the band thickness decreases from the core to the rim, and secondly, the distance between adjacent bands diminishes as the diffusion process progresses. To replicate these counterintuitive phenomena, we devised a numerical setup featuring a triangular-shaped initialization region for the Fe-bearing fluid, as illustrated in Figure 5b. In this configuration, the constant outer reactants diffuse from the center to the periphery, interact with the dolomite, and eventually form periodic hematite.
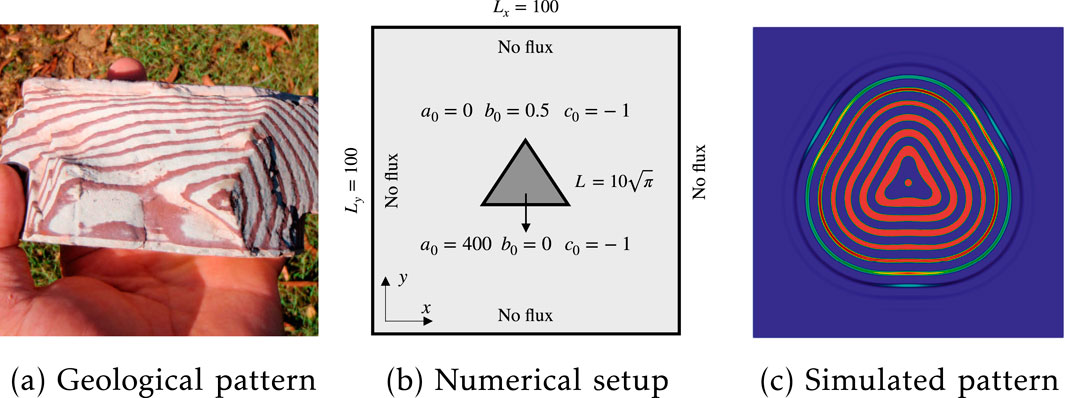
Figure 5. Triangular-like Liesegang ring formation: (a) hematite patterns in Zebro rocks in the northern region of Western Australia; (b) numerical setup with the position and size of an initialized triangular region; (c) simulated patterns.
In Figure 5c, we present the spatial concentration distribution of the precipitate
3.2 Multiple pattern formation and interaction
Apart from the single Liesegang ring formation, we examine our phase separation model for multiple Liesegang ring formation. Specifically, we first present the two and multiple orbicular granite formations in igneous systems. We then model the irregular distribution of the pyrite rings formation in the Xiaoqing deposit.
3.2.1 Multiple circular geometries
Many previous hypotheses regarding the pattern formation in orbicular granite have assumed that crystallization initiates at the core, with subsequent band formation propagating outward [2, 37]. The presence of orbicular granites also indicates an interaction between different connected orbicular rings. Figures 6b, 7b illustrate the interactions of two and nine orbicular granites within igneous systems, respectively. One difference is the appearance of morphological patterns; Figure 6b shows two oval Liesegang rings, whereas Figure 7 shows more circular Liesegang patterns. To distinguish the oval and circular morphological occurrence in orbicular granite, we conduct two numerical simulations. One simulation includes two oval cores with initialized metal melt, while another contains nine circular cores. The metal melt is capable of diffusing and reacting with the silicate melt, thereby forming rhythmic orbicular rings, as described by Equation 13. Detailed numerical geometries and boundary conditions are provided in Figures 6b, 7b, respectively.

Figure 6. Two Liesegang rings formation and interaction: (a) orbicular granite in igneous rocks; (b) numerical setup with the position and size of two initialized oval regions; (c) simulated patterns.
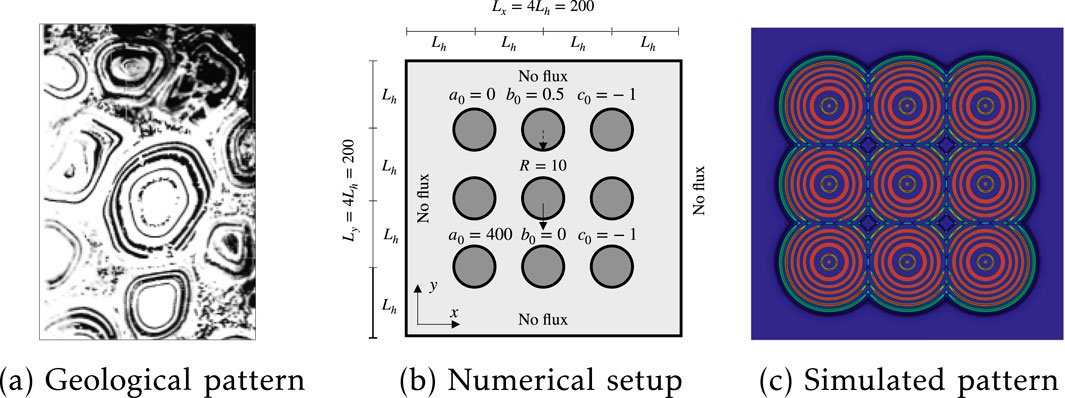
Figure 7. Nine Liesegang rings formation and interaction: (a) orbicular granite in igneous rocks from [12]; (b) numerical setup with the position and size of nine initialized circular regions; (c) simulated patterns.
The resultant pattern morphologies for the interaction of two orbicular granites are depicted in Figure 6c. It is observed that the thickness of the bands is greater near the core, which is consistent with observations of natural orbicular granites. Additionally, the distance between neighboring orbicular rings increases from the core to the rim. Notably, when the orbicular rings approach one another, the formation of one ring is impeded by the presence of another. This simulated interaction behavior qualitatively mirrors field observations of orbicular granites.
To further validate our phase separation model, we increase the number of initial cores from two to nine and change the initialized shape from ovals to circles, as shown in Figure 7b. A significant difference from the interaction of two orbicular rings is the occurrence of the Ostwald ripening phenomenon. Several spots between the connected orbicular rings can be observed in the field, as illustrated in Figure 7a. This phenomenon is also captured in our simulation, where only the outer rings interact with rings from other orbicular structures. Overall, while further quantitative analysis is warranted, the primary features observed in the field can be replicated in our numerical simulations of orbicular pattern formation.
3.2.2 Randomly distributed circular geometries
In Section 3.1.1, we simulate the formation of zoning rings using a single circular pattern. However, the CZPA typically exhibits more complex distributions within the depositional environment, which suggests a heterogeneous distribution of
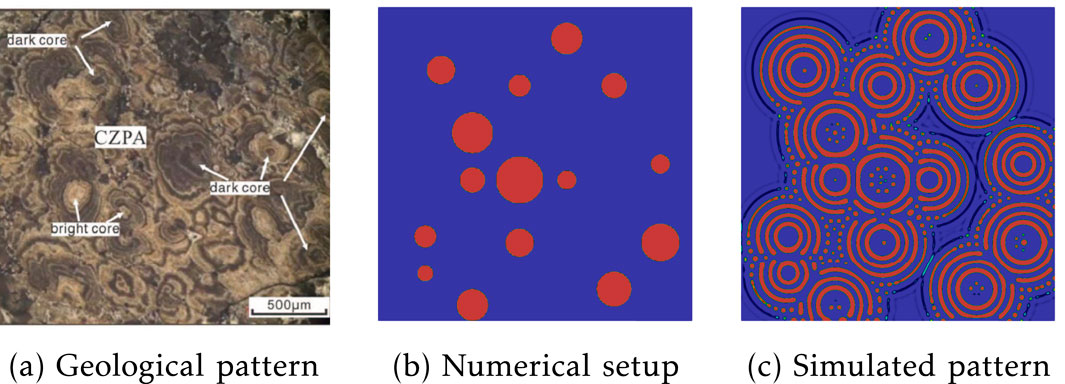
Figure 8. Randomly distributed Liesegang ring formation: (a) heterogeneous distributed pyrite patterns in Xingqiao sediment-hosted massive sulfide deposits from [16]; (b) numerical setup with the position and size of 15 initialized circular regions; (c) simulated patterns.

Table 2. The coordinates and sizes of the circular initialization regions of the Fe-bearing fluid. The circular region is ordered by increasing
Figure 8c displays the simulated irregular distribution of pyrite rings. These irregular pyrite patterns closely resemble the field observations of pyrite distribution depicted in Figure 8a. A key question concerning the CZPA at Xinqiao is whether it formed from a core outward or from a shell inward. The presence of bright cores suggests the former, while dark cores imply the latter. Qiu and colleagues have proposed two different setups to replicate both the dark and bright cores observed in CZPA. One hypothesis involves the diffusion of
4 Conclusion
This study employs a phase separation model to examine the rhythmic patterns in rocks, with a particular focus on oscillatory zoning in pyrite, hematite patterns in Zebra rocks, and orbicular granites. The simulation results elucidate the influence of geometric heterogeneity on the development of both simple and complex periodic patterns in these three rock types, considering both regular and randomly distributed initial conditions. The simulated patterns qualitatively replicate the Liesegang patterns observed in natural settings, thereby demonstrating the capacity of the phase separation model to reproduce periodic rock patterns. Nonetheless, further research is necessary, particularly through detailed geochemical analyses of these patterns and quantitative comparisons between the simulated patterns and those observed in the field. This study establishes a foundational framework for utilizing the phase separation model to analyze self-organized patterns in heterogeneous geological contexts.
Data availability statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Author contributions
CL: Validation, Conceptualization, Visualization, Methodology, Formal Analysis, Investigation, Writing – review and editing, Writing – original draft, Software. KR-L: Supervision, Funding acquisition, Writing – review and editing. MH: Funding acquisition, Writing – review and editing, Supervision.
Funding
The author(s) declare that financial support was received for the research and/or publication of this article. We acknowledge the funding support from the Research Grant Council of Hong Kong (MH: ECS 27203720 and GRF 17206521) and the Australian Research Council (KR.L.: ARC DP200102517, DP170104550, LP170100233).
Acknowledgments
The computations were performed using the research facilities offered by Information Technology Services, the University of Hong Kong.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Generative AI statement
The author(s) declare that no Generative AI was used in the creation of this manuscript.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Ortoleva PJ, Merino E, Moore C, Chadam J. Geochemical self-organization I; reaction-transport feedbacks and modeling approach. Am J Sci (1987) 287:979–1007. doi:10.2475/ajs.287.10.979
2. L’Heureux I. Self-organized rhythmic patterns in geochemical systems. Philosophical Trans R Soc A: Math Phys Eng Sci (2013) 371:20120356. doi:10.1098/rsta.2012.0356
3. Yatsuda Y, Tsushima K, Fang Q, Nabika H. Chemical model for pattern formation in rocks via periodic precipitation of iron oxide minerals. ACS Earth Space Chem (2023) 7:2042–9. doi:10.1021/acsearthspacechem.3c00165
4. Walimbe P, Itatani M, Kulkarni P, Lagzi I, Kulkarni S. A quasi universal matalon–packter law for a periodically precipitating system of iron (II) hydroxide involving volumes and concentrations of the invading electrolyte. Langmuir (2023) 39:13420–9. doi:10.1021/acs.langmuir.3c00778
5. Coward AJ, Brugger J, Wilson S, Slim AC, Williams T, Pillans B, et al. Mineralogy and geochemistry of pattern formation in print stone from the Pilbara, Australia. Mineralogical Mag (2025) 1–33. doi:10.1180/mgm.2025.11
6. Liesegang RE. Eine scheinbar chemische Fernwirkung. Annalen der Physik (1906) 324:395–406. doi:10.1002/andp.19063240210
7. Wang Y, Chan MA, Merino E. Self-organized iron-oxide cementation geometry as an indicator of paleo-flows. Scientific Rep (2015) 5:10792–15. doi:10.1038/srep10792
8. Yoshida H, Katsuta N, Sirono S, Nishimoto S, Kawahara H, Metcalfe R. Concentric fe-oxyhydroxide bands in dacite cobbles: rates of buffering chemical reactions. Chem Geology (2020) 552:119786. doi:10.1016/j.chemgeo.2020.119786
9. Kawahara H, Yoshida H, Yamamoto K, Katsuta N, Nishimoto S, Umemura A, et al. Hydrothermal formation of Fe-oxide bands in zebra rocks from northern Western Australia. Chem Geology (2022) 590:120699. doi:10.1016/j.chemgeo.2021.120699
10. Liu C, Calo V, Regenauer-Lieb K, Hu M. Coefficients of reaction-diffusion processes derived from patterns in rocks. J Geophys Res Solid Earth (2023) 128:e2022JB026253. doi:10.1029/2022jb026253
11. Liu C, Calo VM, Regenauer-Lieb K, Hu M. Deriving flow velocity and initial concentration from Liesegang-like patterns. J Geophys Res Solid Earth (2024) 129:e2024JB029379. doi:10.1029/2024jb029379
12. Leveson DJ. Orbicular rocks: a review. Geol Soc America Bull (1966) 77:409–26. doi:10.1130/0016-7606(1966)77[409:orar]2.0.co;2
13. Wang Y, Merino E. Oscillatory magma crystallization by feedback between the concentrations of the reactant species and mineral growth rates. J Petrology (1993) 34:369–82. doi:10.1093/petrology/34.2.369
14. Ghaoui J, L’Heureux I. Model of layered pattern formation in binary igneous systems. Solid Earth Sci (2021) 6:80–94. doi:10.1016/j.sesci.2021.04.001
15. Ortoleva PJ. Self-organization and nonlinear dynamics in sedimentary basins. Philosophical Trans R Soc Lond Ser A: Phys Eng Sci (1993) 344:171–9. doi:10.1098/rsta.1993.0085
16. Qiu WJ, Zhou MF, Williams-Jones AE. Numerical simulation of the self-organizational origin of concentrically zoned aggregates of siderite and pyrite in sediment-hosted massive sulfide deposits. J Geophys Res Solid Earth (2024) 129:e2023JB028101. doi:10.1029/2023jb028101
17. Ortoleva P, Chadam J, Merino E, Sen A. Geochemical self-organization II; the reactive-infiltration instability. Am J Sci (1987) 287:1008–40. doi:10.2475/001c.60405
20. Lifshitz IM, Slyozov VV. The kinetics of precipitation from supersaturated solid solutions. J Phys Chem Sol (1961) 19:35–50. doi:10.1016/0022-3697(61)90054-3
21. Antal T, Droz M, Magnin J, Rácz Z. Formation of liesegang patterns: a spinodal decomposition scenario. Phys Rev Lett (1999) 83:2880–3. doi:10.1103/physrevlett.83.2880
22. Antal T, Droz M, Magnin J, Pekalski A, Rácz Z. Formation of liesegang patterns: simulations using a kinetic ising model. The J Chem Phys (2001) 114:3770–5. doi:10.1063/1.1342858
23. Hantz P, Biró I. Phase separation in the wake of moving fronts. Phys Rev Lett (2006) 96:088305. doi:10.1103/physrevlett.96.088305
24. Thomas S, Lagzi I, Molnár JF, Rácz Z. Probability of the emergence of helical precipitation patterns in the wake of reaction-diffusion fronts. Phys Rev Lett (2013) 110:078303. doi:10.1103/physrevlett.110.078303
25. Dayeh M, Ammar M, Al-Ghoul M. Transition from rings to spots in a precipitation reaction–diffusion system. RSC Adv (2014) 4:60034–8. doi:10.1039/c4ra11223g
26. Liu C, Hu M, Regenauer-Lieb K. Liesegang patterns interpreted as a chemo-hydromechanical instability. In: Proceedings of 12th international workshop on bifurcation and degradation in geomechanics. Springer (2022). p. 59–66. doi:10.1007/978-3-031-22213-9_7
27. Abi Mansour A, Al-Ghoul M. Vertex-based finite volume simulation of liesegang patterns on structureless meshes. Phys Rev E (2014) 89:033303. doi:10.1103/physreve.89.033303
28. Al-Ghoul M, Sultan R. Simulation of geochemical banding: theoretical modeling and fractal structure in acidization-diffusion-precipitation dynamics. Phys Rev E (2019) 100:052214. doi:10.1103/physreve.100.052214
29. Cahn JW, Hilliard JE. Free energy of a nonuniform system. I. Interfacial free energy. The J Chem Phys (1958) 28:258–67. doi:10.1063/1.1744102
30. Cahn JW. On spinodal decomposition. Acta Metallurgica (1961) 9:795–801. doi:10.1016/0001-6160(61)90182-1
31. Rickard D, Luther GW. Chemistry of iron sulfides. Chem Rev (2007) 107:514–62. doi:10.1021/cr0503658
32. Schoonen M, Barnes H. Reactions forming pyrite and marcasite from solution: I. Nucleation of FeS2 below 100°C. Geochimica et Cosmochimica Acta (1991) 55:1495–504. doi:10.1016/0016-7037(91)90122-l
33. Feeney R, Schmidt S, Strickholm P, Chadam J, Ortoleva P. Periodic precipitation and coarsening waves: applications of the competitive particle growth modela. The J Chem Phys (1983) 78:1293–311. doi:10.1063/1.444867
34. DeWitt S, Rudraraju S, Montiel D, Andrews WB, Thornton K. PRISMS-PF: a general framework for phase-field modeling with a matrix-free finite element method. npj Comput Mater (2020) 6:29. doi:10.1038/s41524-020-0298-5
35. Arndt D, Bangerth W, Blais B, Clevenger TC, Fehling M, Grayver AV, et al. The deal.II library, version 9.2. J Numer Mathematics (2020) 28:131–46. doi:10.1515/jnma-2020-0043
36. Liu C, Calo VM, Regenauer-Lieb K, Hu M. Dendritic growth patterns in rocks: inverting the driving and triggering mechanisms. J Geophys Res Solid Earth (2023) 128:e2023JB027105. doi:10.1029/2023jb027105
Keywords: liesegang pattern, self-organization, geometry heterogeneity, zebra rock, orbicular granite, pyrite rock
Citation: Liu C, Regenauer-Lieb K and Hu M (2025) Influence of geometry heterogeneity on Liesegang patterns in rocks. Front. Phys. 13:1628328. doi: 10.3389/fphy.2025.1628328
Received: 14 May 2025; Accepted: 16 July 2025;
Published: 11 August 2025.
Edited by:
Rabih Sultan, American University of Beirut, LebanonReviewed by:
Mazen Al-Ghoul, American University of Beirut, LebanonMasaki Itatani, Hokkaido University, Japan
Mohd Hariri Arifin, National University of Malaysia, Malaysia
Copyright © 2025 Liu, Regenauer-Lieb and Hu. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Chong Liu, Y2hvbmdsaXVAY29ubmVjdC5oa3UuaGs=
 Chong Liu
Chong Liu Klaus Regenauer-Lieb
Klaus Regenauer-Lieb Manman Hu
Manman Hu