Electric dipole polarizability constraints on neutron skin and symmetry energy

We review the experimental knowledge on the dipole polarizability (DP) of nuclei and its relation to the neutron skin thickness and properties of the neutron-rich matter equation of state (EOS). The discussion focuses on recent experiments using relativistic Coulomb excitation in inelastic proton scattering at extreme forward angles covering a mass range from ⁴⁰Ca to ²⁰⁸Pb. Constraints on the neutron skins and the density dependence of the symmetry energy are derived from a systematic comparison to calculations based on density functional theory (DFT) and ab initio methods utilizing interactions derived from chiral effective field theory ($\chi$EFT). The results consistently favor a soft EOS around or slightly below the saturation point. An outlook is provided on possible improvements in the precision achievable in stable nuclei and studies of exotic neutron-rich unstable nuclei with upcoming experimental facilities.

1 Introduction

The nuclear equation of state (EOS) describes the energy per nucleon of nuclear matter as a function of proton $({\rho }_p)$ and neutron $({\rho }_n)$ densities [1]. It governs the properties of nuclei and neutron stars [2, 3] as well as the dynamics of core-collapse supernovae [4] and neutron star mergers [5]. As an example, Figure 1A illustrates the bounds of the mass–radius dependence of neutron stars predicted by different EOS models. A systematic description of the EOS from nuclear densities to those in neutron stars is a central goal of current physics [6]. Despite a wealth of new data at high densities from observations on the properties of neutron stars and neutron star mergers [7] and information on the intermediate density regime from central heavy ion collisions [8, 9], experimental constraints on the EOS around the saturation density of nuclear matter $n_0\sim 0.16$ ${\text{fm}}^{-1}$ are still insufficient.

Figure 1

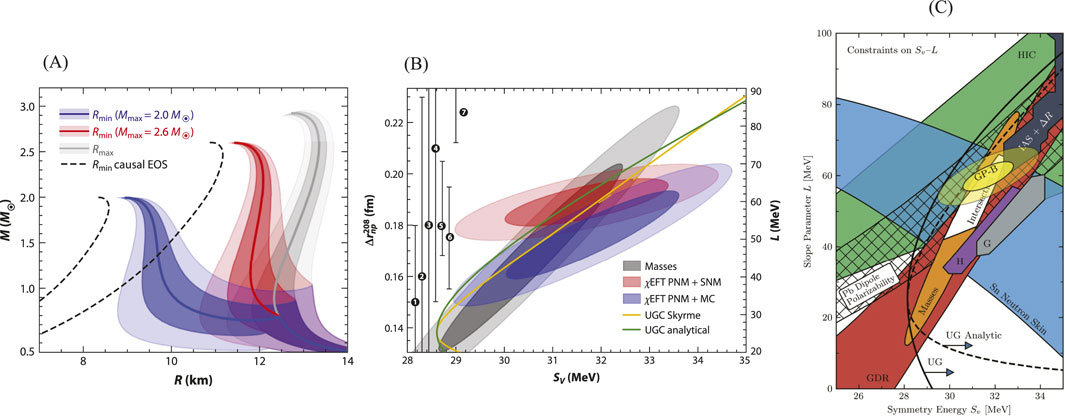
Figure 1. (A) Predictions of the mass–radius relation of neutron stars from different EOS. Figure taken from [3]. (B) Theoretical constraints on the relation of $J$ (or $S_V$) and $L$. The points with vertical error bars on the left side represent measurements of the neutron skin thickness in ²⁰⁸Pb. Figure taken from [3], where the original references can be found. (C) Experimental and theoretical constraints on the relation of $J$ (or $S_V$) and $L$. Figure taken from [10], where the original references can be found.

The nuclear matter EOS can be approximately written as a sum of the energy per nucleon of symmetric matter and an asymmetry term

$E\left(\rho ,\delta \right)=E\left(\rho ,\delta =0\right)+S\left(\rho \right){\delta }^2+O\left({\delta }^4\right),(1)$

where the nucleon density $(\rho )$ and the asymmetry parameter $(\delta )$ are defined by the neutron $({\rho }_n)$ and proton $({\rho }_p)$ density as

$\rho \equiv {\rho }_n+{\rho }_p,\delta \equiv \frac{{\rho }_n-{\rho }_p}{{\rho }_n+{\rho }_p}.(2)$

The symmetry energy factor $S(\rho )$ in Equation 1 can be expanded around the saturation density ${\rho }_0\sim 0.16$ ${\text{fm}}^{-3}$ as

$S\left(\rho \right)=J+\frac{L}{3{\rho }_0}\left(\rho -{\rho }_0\right)+\frac{K_{\text{sym}}}{18{\rho }_0^2}{\left(\rho -{\rho }_0\right)}^2+\cdots .(3)$

Here, $L$ is the slope parameter at density ${\rho }_0$.

The first term in Equation 1 representing symmetric nuclear matter is fairly well constrained by the compressibility derived from systematic measurements of the isoscalar giant monopole resonance (ISGMR) in nuclei [1]. Figures 1B,C [3, 10] illustrate the variety of experimental and theoretical constraints on $J$ (also called $S_V$ in the literature) and $L$ defined in Equation 3. While these confine possible values of $J$ to a range of approximately 30–35 MeV, the uncertainties of $L$ are much larger.

As detailed below, all relevant theoretical models predict a strong correlation between $L$ and two experimentally accessible quantities, viz., the neutron skin thickness and the dipole polarizability. The connection is illustrated in Figure 2. The density distributions of neutrons ${\rho }_n(r)$ and protons ${\rho }_p(r)$ in the ground state can be determined from the condition of minimum energy. They approximately have the shape of Fermi distributions, as illustrated in Figure 2, for a nucleus with $N\gg Z$. The mean square radius of neutrons, $R_n={⟨r^2⟩}_n^{1/2}$, is slightly larger than that of protons $R_p={⟨r^2⟩}_p^{1/2}$. The difference between the two, $r_{\mathit{skin}}=R_n-R_p$, is defined as the neutron skin thickness.

Figure 2

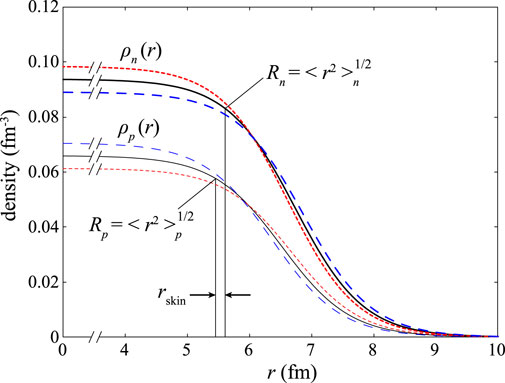
Figure 2. Neutron and proton density distributions are schematically shown by the thick and thin solid lines, respectively. For a larger (smaller) $L$ value, the inner density difference between neutrons and protons becomes smaller (larger), as illustrated by the dashed blue (dotted red) lines with a larger (smaller) difference at the surface, resulting in a larger (smaller) neutron skin thickness.

The neutron skin thickness is sensitive to the $L$ value due to the following reason. As discussed above, the symmetry energy of nuclear matter at a given nucleon density depends on the square of the asymmetry parameter $\delta$, defined in Equation 2. The first-order density dependence of the symmetry energy is represented by the slope parameter $L$. Suppose that the density distributions in Figure 2 were determined for an $L$ value to have the minimum energy. There are density differences between the neutrons and protons in the inner part (higher nucleon density) and at the surface part (lower nucleon density). For a larger $L$ value, the density distributions change to have less density difference in the inner part, thereby reducing the symmetry energy in the higher density part. Consequently, the neutron skin thickness and the symmetry energy at the surface become larger for a conserved number of neutrons and protons.

The neutron skin thicknesses of medium-mass and heavy nuclei have been extracted from experiments studying elastic proton scattering [11], coherent ${\pi }^0$ production [12], antiprotonic atoms [13, 14], and the isovector (IV) spin–dipole resonance [15]. Of particular importance are experiments using parity-violating polarized elastic electron scattering [16]. The parity-violating part of the reaction is mediated by the weak interaction and, due to the dominance of the neutron form factor, allows for extracting the neutron density distribution in an almost model-independentway [48]. Such experiments have been performed for ²⁰⁸Pb (lead radius experiment, or PREX) [1] and ⁴⁸Ca (calcium radius experiment, or CREX) [2]. Neutron skins were determined by comparison with the well-known charge radii.

The dipole polarizability (DP) of nuclei can be obtained from measurements of the photoabsorption cross-sections. A connection between DP, neutron skin thickness, and parameters of the symmetry energy can only be made through models. Such calculations are presently based either on density functional theory (DFT) [20] or ab initio coupled-cluster calculations [21] using interactions derived from $\chi$EFT [22]. Both types of models predict a strong correlation between the magnitudes of dipole polarizability, $r_{skin}$, and $L$. The considerable experimental challenges of direct measurements of the neutron skin and the model dependencies of methods that extract the neutron skin from the difference of mass and charge radius [23] call for an alternative experimental observable. Because properties of the symmetry energy cannot be extracted directly from experiments but require theory input, measurement of the dipole polarizability provides independent constraints.

While several experimental techniques to measure the DP are discussed, the present review mainly focuses on recent progress using relativistic Coulomb excitation in forward-angle proton scattering at energies of several hundred MeV [24]. One advantage of this method is consistent results across the neutron separation energy, while many of the other experimental techniques are limited to either the energy region below or above. Even more important, measurements of the $E1$ strength with relativistic Coulomb excitation can be extended to exotic nuclei at rare isotope beam facilities like RIKEN, FRIB, and the GSI Facility for Antiproton and Ion Research (FAIR). Such experiments are performed in inverse kinematics, where the virtual photon flux can be boosted by using a high-$Z$ target and efficient setups with almost $4\pi$ solid angle coverage for detection of neutron emission above [25] and $\gamma$ emission below the neutron threshold [26, 27]. In combination with the large cross sections, this will permit access to nuclei with extremely large neutron excess, much closer to the properties of neutron-rich matter relevant to the physics of neutron stars. In addition to the antiProton Unstable Matter Annihilation (PUMA) project [28] aiming at the neutron skin thickness in unstable nuclei using antiproton annihilation, dipole polarizability measurements with relativistic Coulomb excitation are probably the only experimental probe promising insight into properties of the symmetry energy over a wide range of neutron-to-proton ratios.

The paper is organized as follows. Section 2 discusses how information on the neutron skin thickness and symmetry energy can be inferred from model calculations based on DFT (Section 2.1) and ab initio methods (Section 2.2). Section 3 is devoted to experimental issues. A short discussion of the available techniques in Section 3.1 is followed by a description of methods to disentangle electric and magnetic contributions to the DP in Section 3.2. The relevance of experimental information in the energy region of the isovector giant dipole resonance (IVGDR), as well as below the neutron threshold and above the IVGDR, is compared in Section 3.3, Section 3.4, and Section 3.5. The comparison of experimental and theoretical results (Section 4) for a range of nuclei from ⁴⁰Ca to ²⁰⁸Pb and constraints on neutron skin thickness and the parameters of the symmetry energy extracted thereof are presented in Section 4.1 for DFT and Section 4.2 for ab initio approaches. Section 4.3 focuses on the difficulties of simultaneously describing the results of parity-violating elastic electron scattering and DP experiments with present-day models. Finally, Section 4.4 discusses the systematics of the DP and the role of volume and surface contributions to the symmetry energy. A summary and an outlook are given in Section 5.

2 Relation between dipole polarizability, neutron skin thickness, and symmetry energy

In this section, we discuss how information on the neutron skin thickness and parameters of the symmetry energy can be inferred from the comparison of the experimental dipole polarizability to theoretical predictions. At the moment, there are two classes of models, based on either DFT or an ab initio coupled-cluster approach. Because isovector observables are not well constrained in DFT, quantitative predictions of the DP can vary considerably. However, one can establish a robust correlation between the parameters $J$ and $L$ of the symmetry energy through ${\alpha }_D$. With ab initio-based models, one aims at an absolute prediction of ${\alpha }_D$, and the underlying symmetry energy parameters of the interaction can be used to calculate the EOS.

The dipole polarizability ${\alpha }_D$ is related to the reduced $B(E1)$ transition strengths and the photoabsorption cross sections ${\sigma }_{abs}$ by

${\alpha }_D=\frac{\hslash c}{2{\pi }^2}{\int }_0^{\infty }\frac{{\sigma }_{\mathit{abs}}}{E_x^2}\mathrm{d}{E}_x=\frac{8\pi }{9}{\int }_0^{\infty }\frac{B\left(E1\right)}{E_x}\mathrm{d}{E}_x.(4)$

While the integral runs to infinity in principle, because of the inverse energy weighting a measurement of the $E1$ strength up to excitation energies of about 60 MeV in light [29] or 30 MeV in heavy nuclei [30] is sufficient to achieve saturation. Thus, ${\alpha }_D$ is dominated by the isovector giant dipole resonance (IVGDR), but contributions from the energy regions below and above are non-negligible, as discussed in Section 3.

2.1 Connections in density functional theory

An approximately linear correlation between $r_{\mathit{skin}}$ and $L$ was demonstrated in Hartee–Fock calculations of ²⁰⁸Pb with relativistic [31] and Skyrme [32] density functionals, as illustrated in Figure 3A. A comprehensive investigation of correlations between IV experimental observables and the bulk parameters of DFT models [33] demonstrates that these two quantities are also correlated with ${\alpha }_D$ in heavy nuclei. Figure 3B shows, as an example, the correlations with the neutron form factor of ²⁰⁸Pb, which can be derived from a parity-violating elastic electron scattering experiment.

Figure 3

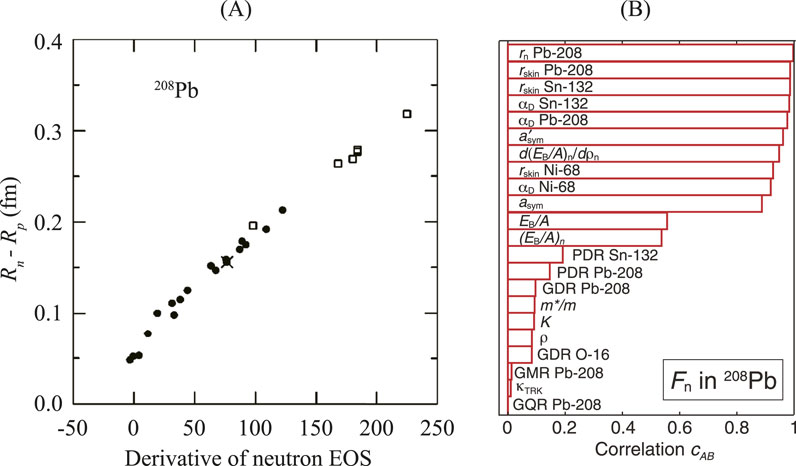
Figure 3. (A) Correlation between the neutron skin thickness in ²⁰⁸Pb and $L$ for a large set of DFT interactions. Figure taken from [31]. (B) Correlation of various observables in ²⁰⁸Pb with the neutron form factor at momentum transfer $q=0.45$ ${\text{fm}}^{-1}$. Figure taken from [33].

While this type of correlation is observed for all interactions, absolute values show large differences. In general, the magnitude of IV quantities like ${\alpha }_D$ is not well constrained in DFT models because the model parameters are typically fitted to binding energies and charge radii of selected nuclei, which show little sensitivity to the IV parts of the nuclear interaction. A study of the relation between ${\alpha }_D$ and the neutron skin in ²⁰⁸Pb for a large number of interactions illustrates the problem [34]. Figure 4A shows that the predictions for the neutron skin vary from 0.12 fm to 0.32 fm, and for a given value of $r_{skin}$, predictions for ${\alpha }_D$ scatter wildly. However, the product of ${\alpha }_D\times J$ plotted versus $r_{skin}$ (or $L$) shows a linear dependence with a high correlation coefficient [34], cf. Figure 4B. This relation can be understood within the droplet model [35] and provides a correlated range of $J,L$ values, as indicated for the case of ²⁰⁸Pb [36] in Figure 1C.

Figure 4

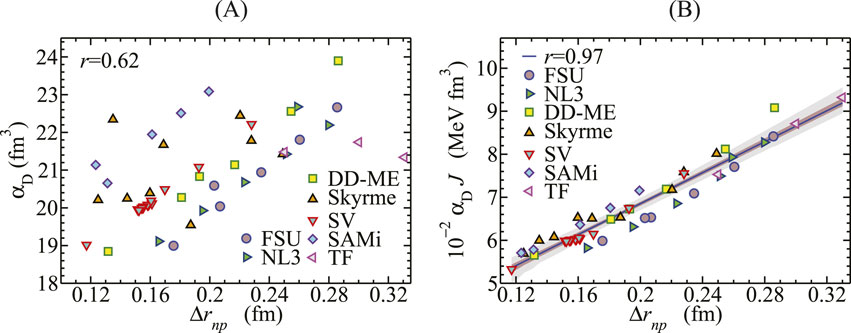
Figure 4. (A) Dipole polarizability against neutron skin thickness in ²⁰⁸Pb Pb predicted by modern DFT interactions. (B) The same for dipole polarizability times symmetry energy at saturation density. The results are well described by a linear fit. Figures taken from [34], where the original references for the various interactions can be found.

2.2 Connections in ab initio models

Ab initio calculations based on interactions derived from $\chi$EFT play an important role in the attempt to systematically describe the EOS of neutron-rich matter at all densities [2]. Figure 5A displays examples of next-to-next-to-next-to-leading order predictions of the density behavior in the nuclear regime [37]. The upper and lower parts present the neutron and symmetric matter results, respectively, for two different families of interactions with somewhat different symmetry energy parameters shown in the left and right columns. The gray boxes indicate the value of the saturation density. The colored curves correspond to different cutoff parameters of the model space; for details, see [37].

Figure 5

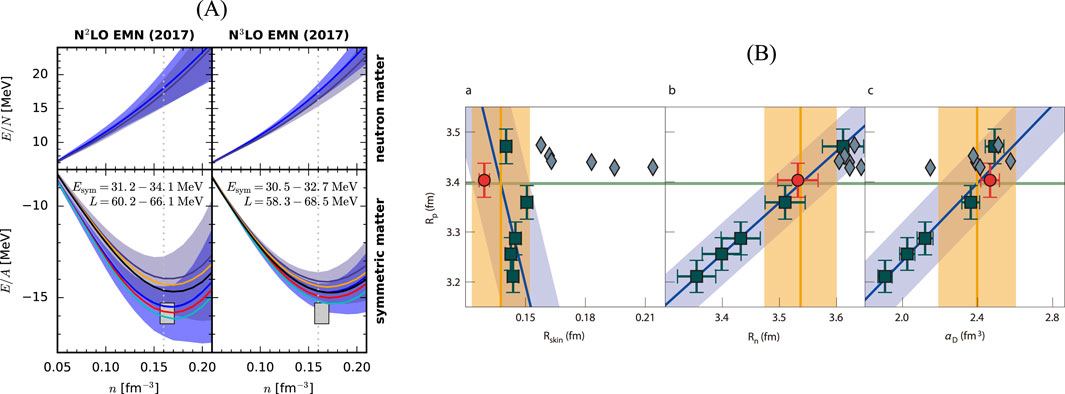
Figure 5. (A) Energy per particle in neutron matter (top row) and symmetric nuclear matter (bottom row) based on chiral interactions at ${\mathrm{N}}^2$LO (first column) and ${\text{N}}^3$LO (second column) fit to the empirical saturation region (gray box). The blue and gray bands estimate the theoretical uncertainty assuming different parameter constraints. Figure taken from [37]. (B) Predictions of the neutron skin (a), point-neutron radius (b), and electric dipole polarizability (c) versus the point-proton radius for ⁴⁸Ca. Ab initio results with the ${\text{NNLO}}_{\text{sat}}$ interaction [38] and chiral interactions [39] are shown as red circles and squares, respectively. The diamonds represent selected DFT results. The blue line represents linear fits to the ab initio predictions with uncertainties indicated by the blue bands. The horizontal green line marks the experimental value of the ⁴⁸Ca charge radius. Its intersection with the blue lines and the blue bands yields the vertical orange lines and orange bands, respectively, giving the predicted range for the ordinates. Figure taken from [40], where the original references of the shown DFT interactions can be found.

Predictions of ${\alpha }_D$ and correlations with proton and neutron radii based on $\chi$EFT interactions have been obtained from calculations based on a coupled-cluster expansion of the wave functions [21] combined with the Lorentz-integral-transform approach to extract the $E1$ strength [41]. An example of such calculations for ⁴⁸Ca [40] is presented in Figure 5B, where the correlation of $r_p$ with $r_n$, $r_{\mathit{skin}}$ and ${\alpha }_D$ is displayed together with representative examples of DFT predictions. While the DFT results predict neutron skin values ranging from 0.16 fm to 0.22 fm, the ab initio results based on a set of interactions from [38, 39] consistently favor rather small values varying from 0.12 fm to 0.15 fm.

A major difference between the two theoretical approaches lies in the predicted relation between the proton and neutron radii. The DFT predictions of $r_p$ are approximately constant, most likely because the charge radius of ⁴⁸Ca is in all cases part of the data set used to fix the model parameters. The ab initio calculations, on the other hand, predict a linear correlation, leading to the approximate constancy of the neutron skin. The absolute value of ${\alpha }_D$ in the ab initio models shows a larger variation than the DFT calculations but can be well described by a linear correlation similar to $r_n$. As discussed in the following, these correlations allow extracting constraints on the range of symmetry energy parameters based on the successful description of experimentally measured polarizabilities and charge radii. This type of calculation has been limited so far to closed-(sub)shell nuclei. For recent attempts of an extension to open-shell nuclei, see [42, 43].

3 Dipole polarizability from experiment

In this section, we discuss the experimental methods to extract the $B(E1)$ distribution in nuclei and the DP. It is technically difficult to directly measure the DP of nuclei as the response to a static electric field, although there exist exceptional cases of very light nuclei; see, for example, the works studying the deviation of elastic scattering cross section from Rutherford scattering [44, 45]. Instead, $B(E1)$ or ${\sigma }_{\mathit{abs}}$ distributions are measured and integrated to determine the DP by Equation 4. Some of the experimental methods discussed below are restricted in the accessible excitation energy range; that is, the techniques are applicable below or above the neutron emission threshold $(S_n)$ only. Thus, the role of contributions to the DP below $S_n$ from the IVGDR and from the energy region above the IVGDR is discussed in more detail. Both $E1$ and $M1$ transitions are excited, and possible ways of their distinction are briefly presented.

3.1 Experimental methods

3.1.1 Photoneutron measurement

The photoexcitation of nuclei above the neutron separation energy was intensively studied by using photoneutron measurements. The photoneutron reaction is conventionally written as $(\gamma ,xn)$, where $x$ stands for the number of emitted neutrons after photoexcitation. The $(\gamma ,xn)$ cross-section is the sum of the $(\gamma ,1n)$, $(\gamma ,2n)$, …+ $(\gamma ,np)$ above the respective thresholds. From the 1960s to the 1980s, positron annihilation in flight was used for producing a quasi-monoenergetic $\gamma$-ray beam at Lawrence Livermore National Laboratory (LLNL) and at Saclay. Neutrons emitted after interaction with a target were thermalized and detected. For details, see [46, 47].

Neutron emission is the dominant decay process after photoexcitation for a nucleus as heavy as ²⁰⁸$\mathrm{P}\mathrm{b}$ because charged-particle decays are strongly suppressed by the Coulomb barrier and the $\gamma$ decay branch is as low as 1%–2% [48]. Thus, the $(\gamma ,xn)$ cross-sections in heavy nuclei can be compared with total photoabsorption cross-sections. The ²⁰⁸$\mathrm{P}\mathrm{b}(\gamma ,xn)$ cross-sections are plotted in Figure 6. The data were taken at LLNL (open light blue circles [49] and solid blue circles [50]) and at Saclay (half-filled red circles [51]). The results from the two laboratories show clear discrepancies, which is also true for some other nuclei. Kawano et al. [52] reported that “in general, the Saclay $(\gamma ,n)$ cross sections are larger than the Livermore data, whereas the Saclay $(\gamma ,2n)$ cross-sections are smaller than the corresponding Livermore data.”

Figure 6

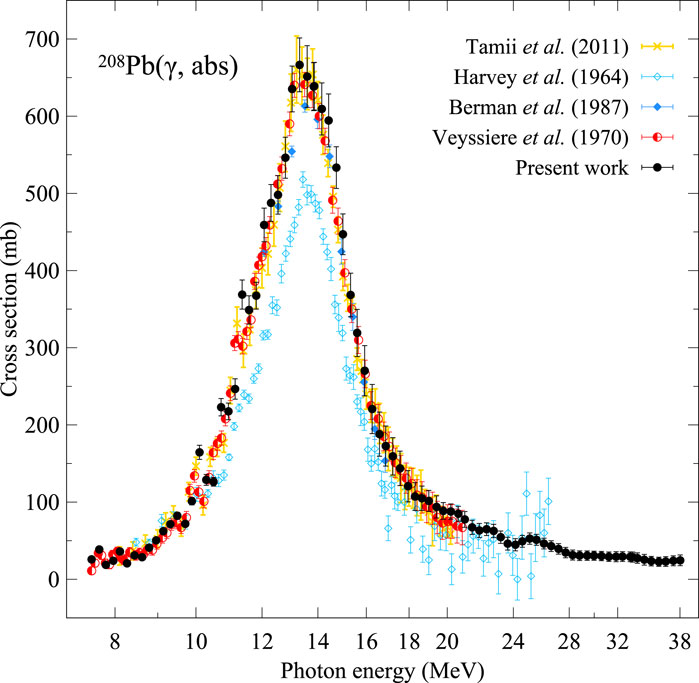
Figure 6. Comparison of the photoabsorption cross-sections of ²⁰⁸Pb from different experiments. Figure taken from [53], where the original references can be found.

Later, quasi-monoenergetic photon beams produced by laser Compton backscattering (LCBS) became available at the National Institute of Advanced Industrial Science and Technology (AIST) [54], the High Intensity $\gamma$-ray Source (HI$\gamma$S) facility at the Triangle University National Laboratory [55] and the NewSUBARU facility [56, 57]. An electron beam in a storage ring is irradiated by laser photons to produce high-energy photons by head-on collisions [52]. The scattered photons are collimated to have a narrow energy distribution. The photon energy is variable either by changing the electron beam energy or the laser frequency. The ²⁰⁸$\mathrm{P}\mathrm{b}(\gamma ,xn)$ cross-section data measured at NewSUBARU [53] are plotted as solid black circles in Figure 6.

3.1.2 Total photoabsorption

Total photon absorption was studied by applying transmission measurements. In this method, the attenuation of photons in a thick target was measured as a function of the photon energy for extraction of the photoabsorption cross sections. At the Mainz electron accelerator, a narrow photon beam was produced by the bremsstrahlung of an electron beam. The average photon flux was $10^9$ photons/MeV at 20 MeV. Two identical Compton spectrometers monitored the photon flux before and after a natural abundance target with a thickness of 40–200 cm [58]. The dominant atomic photoabsorption cross sections needed to be subtracted. A high-resolution transmission measurement at AIST was reported for ²⁸$\mathrm{S}\mathrm{i}$ using a HPGe detector [59]. Recently, an experimental setup for photon transmission measurements has been in operation at the photon tagger NEPTUN [60] at the S-DALINAC accelerator in Darmstadt.

3.1.3 Compton scattering

Compton scattering from ²⁰⁸$\mathrm{P}\mathrm{b}$ was measured at Mainz using quasi-monoenergetic photons produced by positron annihilation in flight [61] up to a photon energy of 143 MeV. The flux of the photon beam was monitored with a Compton spectrometer. Elastically scattered photons were detected by large-volume NaI scintillation counters. The multipolarity-dependent cross sections were analyzed using the angular distributions. The imaginary part of the scattering cross sections at zero degrees is related to the total photon cross section.

3.1.4 Bremsstrahlung excitation functions

Photonuclear cross sections have been extracted from the radioactive decay of residual nuclei populated in particle emission after irradiation with thick-target bremsstrahlung. The excitation energy dependence can be determined by variation of the bremsstrahlung endpoint energy with an unfolding procedure [62]. However, this requires precise knowledge of the bremsstrahlung spectra, which is experimentally not available. While such spectra can be reliably calculated [63] with present-day Monte Carlo codes such as GEANT4 [64], older versions contained poor approximations [65]. Results deduced from phenomenological approximations or using the analytical description of thin-target bremsstrahlung have potentially very large systematic uncertainties, typically not included in the quoted errors.

3.1.5 Relativistic Coulomb excitation

Relativistic Coulomb excitation is an important experimental tool to study the electric dipole response at radioactive ion beam (RIB) facilities. At beam energies of several hundred MeV/nucleon, cross sections are large and cover an excitation energy range including the IVGDR. The small number of beam particles can be compensated for neutron-rich nuclei by placing a neutron detector under $0°$ because, at highly relativistic velocities, a small angular opening is sufficient to cover the full 4$\pi$ solid angle range in the center-of-mass system. The method has been applied to study, for example, halo nuclei [66] and neutron-rich oxygen isotopes [67]. DP measurements in heavier nuclei have been performed for ⁶⁸Ni [26, 27] and ^130,132Sn [23].

The method has also been developed to study stable nuclei using inelastic proton scattering under extreme forward angles, including $0°$. Such experiments require advanced methods to remove the background from the beam halo and atomic small-angle scattering in the target. Zero-degree setups have been realized at the Research Center for Nuclear Physics (RCNP), Osaka, Japan, for proton energies up to 400 MeV [68] and at the iThemba Laboratory for Accelerator-Based Science, Faure, South Africa, for 200 MeV [69]. An overview of experiments, data analysis, and physics problems addressed is provided in [24].

3.1.6 Nuclear resonance fluorescence

Nuclear resonance fluorescence (NRF) or $(\gamma ,{\gamma }^{\prime })$ experiments study the $\gamma$ emission after resonant absorption of a photon. The reaction selectively excites states with large ground-state branching ratios. The cross-section contributions due to the decay to excited states can be estimated in spherical and vibrational nuclei from the population of the lowest excited states. The experiments can be performed with Ge detectors and thus offer a unique energy resolution. The measured quantities depend on the product of photoabsorption cross sections and ground-state branching ratios; thus, the method is limited to excitation energies below the neutron threshold because of the dominance of particle decay widths in the continuum. Experimental methods, physics, and applications are discussed in a recent review [70].

3.2 Decomposition of $E1$ and $M1$ contributions

A general problem of all experimental methods discussed above is the removal of magnetic contributions to the photoabsorption cross sections and the derived DP. Overall, contributions of $M1$ strength to the DP are small except for very light nuclei [71]. However, they become relevant in the excitation energy region of the spinflip $M1$ resonance [72]. Therefore, techniques to decompose $E1$ and $M1$ contributions are important.

No $E1/M1$ decomposition can be performed for the photoneutron and total photoabsorption experiments. In the excitation energy regime relevant to determining the DP, they can be distinguished in Compton scattering by combining measurements at forward and backward angles. The multipolarity can also be determined in NRF experiments using transversely polarized photons [73]. Measurements of the response relative to the polarization plane permit a unique assignment of the electric or magnetic character of the emitted radiation. A polarized beam can be extracted from off-axis bremsstrahlung or LCBS. The latter method is particularly efficient because the polarization of the laser light is fully transferred to the photon beam [70].

In relativistic Coulomb excitation, the virtual photon spectrum in the forward direction is dominated by $E1$. However, in the proton scattering experiments close to $0°$, one must consider contributions to the cross sections due to the nuclear excitation of the spinflip $M1$ strength. Two independent methods have been applied to separate $E1$ and $M1$ cross section parts based either on the total spin transfer derived from the combined information of polarization-transfer observables or from a multipole decomposition analysis (MDA) of the cross section angular distributions [24]. Figure 7 presents some illustrative examples. The lower panel of Figure 7A displays the total spin transfer at $0°$ for the nucleus ¹²⁰Sn [30] derived from measurements of the polarization-transfer observables $D_{LL}$ and $D_{SS}$ [74]. The upper panel presents the differential cross sections at $0°$ and their decomposition in non-spinflip ($E1$ from Coulomb excitation) and spinflip ($M1$ from nuclear excitation) parts.

Figure 7

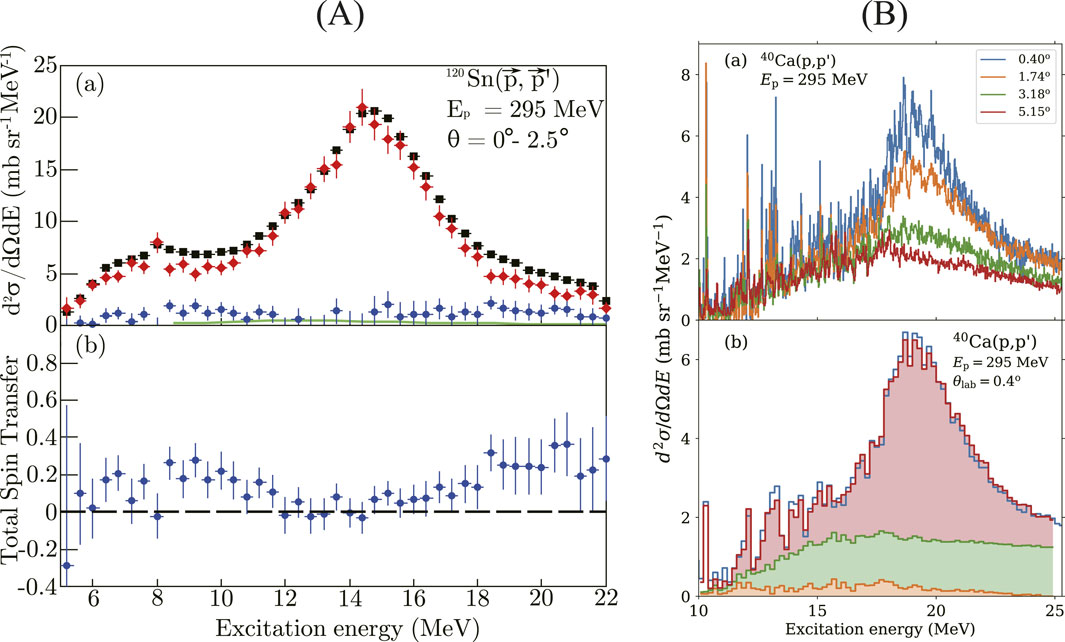
Figure 7. (A) Top: Double differential cross sections of the ¹²⁰Sn$(\vec{p},{\vec{p}}^{\prime })$ reaction (black squares) and decomposition into non-spinflip (red diamonds) and spinflip (blue circles) parts. The solid green line shows the cross sections due to excitation of the isoscalar giant quadrupole resonance (ISGQR). Bottom: Total spin transfer as defined in [74]. Figure taken from [30]. (B) Top: Spectra of the ⁴⁰Ca$(p,p^{\prime })$ reaction at $E_p=295$ MeV and different scattering angles. Bottom: Example of the decomposition of the spectrum at ${\mathrm{\Theta }}_{\mathit{lab}}=0.4°$ into contributions of $L>1$ multipoles (orange), continuum background (green), and $E1$ (red). Figure taken from [29].

An example of the MDA analysis is presented in Figure 7B for ⁴⁰Ca [29]. Spectra at different scattering angles are displayed in the upper panel, demonstrating strongly forward-peaked cross sections in the energy region of the IVGDR expected for Coulomb excitation. The lower panel shows the partial contributions to the cross sections at the most forward angle measured resulting from the MDA: $E1$ (red), multipoles $L>1$ (orange), and nuclear background from quasifree scattering (green). Note that $M1$ strength was neglected for ⁴⁰Ca because it is concentrated in a single state [75]. A comparison of the two independent methods was made in studies of ⁹⁶Mo [76], ¹²⁰Sn [30], and ²⁰⁸Pb [36], and good correspondence of the resulting $E1$ and $M1$ cross sections was found. The results shown in Figure 7A have also been confirmed in an MDA analysis [77]. Because the polarization-transfer measurements require secondary scattering, statistics are limited. Thus, in most $(p,p^{\prime })$ experiments, the $E1/M1$ decomposition was restricted to MDA.

3.3 Contributions from the IVGDR

The largest contribution to the DP stems from the IVGDR, whose energy centroids lie well above $S_n$. It is experimentally accessible with different techniques, and the comparison of results for the same nucleus provides an estimate of the typical accuracy of the DP. One can also average over results obtained with independent methods, thereby reducing the error bars. Some illustrative examples are presented in Figures 8A,B for ⁴⁸Ca and ¹¹⁶Sn, respectively.

Figure 8

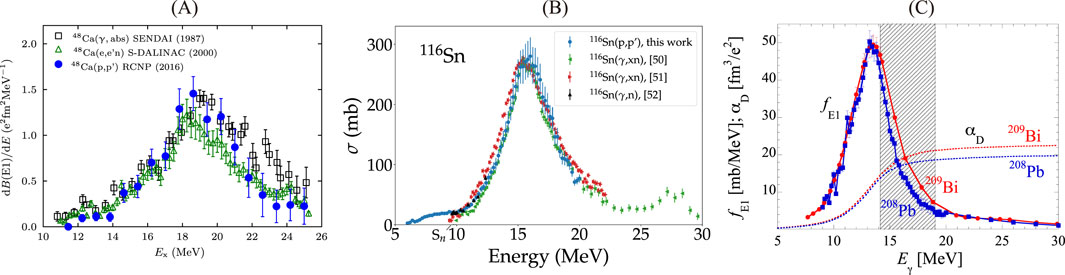
Figure 8. Comparison of photoabsorption cross sections from different experiments. (A) $B(E1)$ strength distributions in ⁴⁸Ca. (B) Photoabsorption cross sections in ¹¹⁶Sn. (C) Photon strength functions (solid lines) of ²⁰⁸Pb (blue squares) and ²⁰⁹Bi (red circles) and the corresponding estimate of the contribution to the DP (dashed lines). Figures taken from (A) [78], (B) [79], and (C) [80], where the original references can be found.

The $B(E1)$ strength distributions in ⁴⁸Ca obtained from $(p,p^{\prime })$ [78] (blue circles) and $(e,e^{\prime }n)$ [81] (green triangles) agree well. Results derived from the bremsstrahlung-induced activity of ⁴⁷Ca [82] agree on the low-energy wing of the resonance but are significantly larger than the other data on the high-energy side. This can probably be traced back to the problems discussed in Sec. 3.1.4. The second example (B) compares photoabsorption cross sections for ¹¹⁶Sn from relativistic Coulomb excitation [79] (blue squares) with $(\gamma ,xn)$ data [83, 84] (green left arrows and red right arrows). Reasonable agreement is observed in the maximum region of the IVGDR, but one finds significant differences on the low-energy flank. Such deviations are systematically observed in the stable Sn isotope chain, and for some isotopes also at the high-energy flank [77].

In general, studies of the $(\gamma ,n)$ and $(\gamma ,xn)$ reactions with LCB beams at NewSUBARU agree well with the $(p,p^{\prime })$ results from the RCNP; see, for example, [85] for a study of Sn isotopes (black upward arrows in Figure 8B) or for ²⁰⁸Pb [53] in Figure 6. However, a puzzling result reported for ²⁰⁹Bi is shown in Figure 8C. Although it differs from ²⁰⁸Pb by only one extra neutron, additional strength is seen on the high-energy side of the IVGDR, leading to a difference in ${\alpha }_D$ not predicted by any model. This particular case certainly needs further investigation.

3.4 Contributions from the PDR

All particle-emission coincidence experiments accessing the $E1$ strength are limited to the excitation region above the lowest particle separation threshold. Experimental evidence has accumulated that in nuclei with significant neutron excess $E1$ strength—often concentrated in a resonance-like structure commonly termed pygmy dipole resonance (PDR)—can be found below [86, 87]. Low-energy $E1$ strength is also found in lighter nuclei with $N\approx Z$. Its contribution to the DP can be significant because of the inverse energy weighting, cf. Equation 4. As examples, they amount to approximately 10% in ⁵⁸Ni [43] and 8%–13% in the stable Sn isotopes [79].

Most data on low-energy $E1$ strength stem from $(\gamma ,{\gamma }^{\prime })$ experiments [70]. They suffer from the problem that branching ratios to excited states are typically unknown, and the extracted strength based on the g.s. transitions represents a lower limit only. Taking ¹²⁰Sn as an example, the resulting $B(E1)$ strength distribution [88] reasonably agrees with a $(p,p^{\prime })$ experiment [89] measuring the total excitation strength up to approximately 6.5 MeV but totally underestimates the strength at higher excitation energies, cf. Figure 9A. Attempts have been made to model the inelastic contributions assuming statistical decay (see, e.g., [90]) but tend to overestimate contributions at low excitation energies. However, progress has been made recently by analyzing the cumulative population of the first $2^{+}$ state in even-even nuclei [70]. For the quoted example ¹²⁰Sn, good agreement between the two experimental methods is achieved [88].

Figure 9

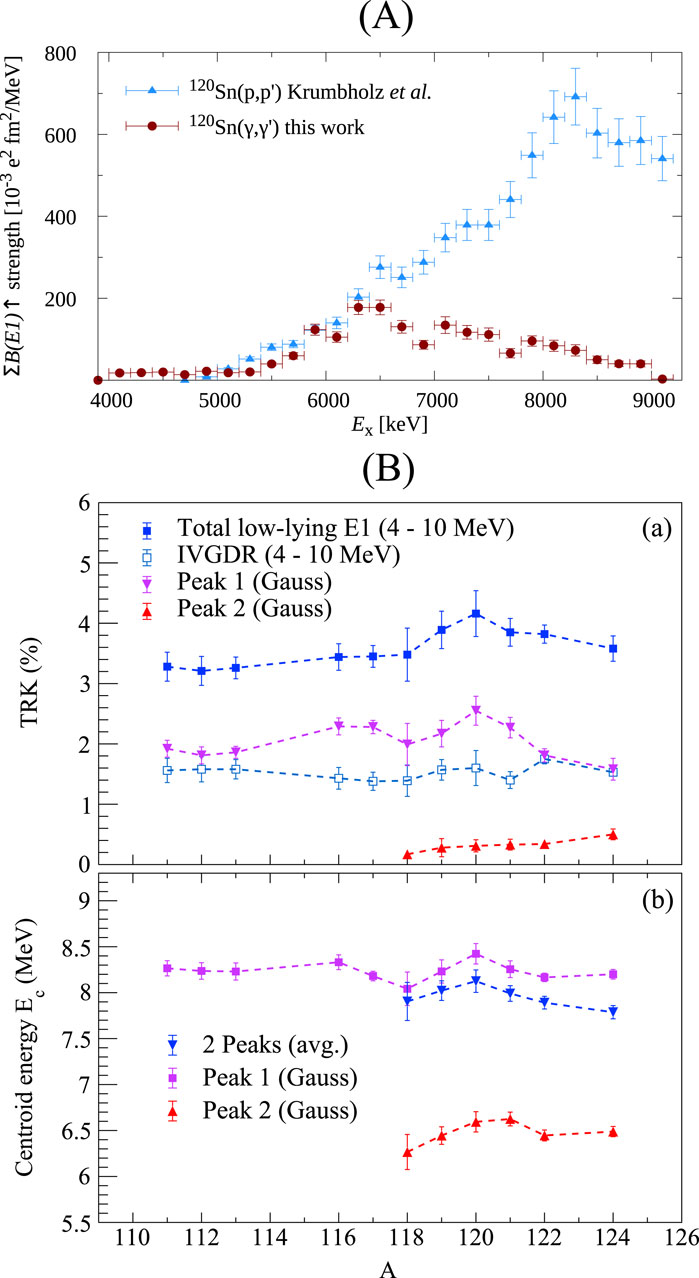
Figure 9. (A) Comparison of $B(E1)$ strength distributions in ¹²⁰Sn from resolved states in an NRF experiment (red circles) [88] from the $(p,p^{\prime })$ reaction (blue triangles) [89]. Figure taken from [88]. (B) Systematics of the total electric dipole strength in ^111–124Sn integrated over the energy region 4 - 10 MeV and its decomposition into contributions from the tail of the IVGDR and one or two (for masses $\ge 118$) resonances. Top: Strengths in % of the Thomas–Reiche–Kuhn (TRK) sum rule. Bottom: Centroid energies. Figure taken from [91].

The origin of the low-energy $E1$ strength in nuclei with neutron excess is a topic of current debate. It has been suggested to arise from an oscillation of the excess neutrons forming a skin against the (approximately) isospin-saturated core [92, 93]. If true, its strength should be related to the neutron skin thickness and, in turn, to the parameters of the symmetry energy [94–96]. However, a recent study of the Sn isotope chain for mass numbers 111–124 casts doubts on such a picture [91]. The correlation between neutron excess and neutron skin thickness in Sn isotopes has been experimentally demonstrated with different methods [97], but based on combined data from Oslo [98–100] and $(p,p^{\prime })$ experiments [77], only a minor fraction of the photoabsorption cross section (expressed as fraction of the Thomas-Reiche-Kuhn (TRK) sum rule) can be related to the PDR [101]. A decomposition into the tail of the IVGDR and two resonance-like structures is shown in Figure 9B [91]. The contribution interpreted as PDR is much smaller than those of the IVGDR and the prominent structure approximately 8 MeV. These findings rather point to an interpretation of the PDR as a low-energy part of a toroidal $E1$ mode [102, 103]. At present, understanding the nature of the PDR remains an open problem. It is clear, however, that DFT predictions restricted to 1p-1h excitations cannot reliably estimate the low-energy $E1$ strength distribution for cases where data are unavailable [91].

3.5 Contributions from high excitation energies

At excitation energies beyond the giant resonance region, photonuclear cross sections typically contribute a few percent only to the DP. However, for precision results, they must be considered. Data up to the pion threshold have been measured for a few cases, viz., ^natCa [58], ^natSn [104], and ²⁰⁸Pb [61, 51]. They show approximately constant cross sections as a function of excitation energy and were considered for the extraction of the DP from $(p,p^{\prime })$ experiments [30, 36], neglecting an isotopic dependence. The dominant excitation mechanism in this energy regime is the quasi-deuteron effect [105]. It has been pointed out by Roca-Maza et al. [106] that these contributions are not included in model calculations based on DFT and should thus be removed compared to theoretical predictions. For heavy nuclei, they can be estimated using [107], while in light nuclei, they are negligible in the energy range covered by the models [29, 43, 78].

The ratio of Coulomb excitation to quasifree cross sections in the $(p,p^{\prime })$ experiments [24] drops with decreasing mass number limiting, in some cases, the excitation energy range accessible with an MDA for the extraction of $E1$ cross sections. In such cases, model-dependent corrections must be applied. In the study of the Sn isotopic chain [79], these were based on quasiparticle random phase approximation (QRPA) calculations folded with a Lorentzian to reproduce the experimentally measured width of the IVGDR. A particularly promising approach is discussed in [43] for the example of ⁵⁸Ni. An extension of the QRPA calculations to include quasiparticle vibration coupling has been successful in describing the width of the ISGMR and curing a longstanding discrepancy between the compressibility values extracted from ²⁰⁸Pb and lighter nuclei [108, 109]. The application to ⁵⁸Ni demonstrates that the predicted high-energy tail of the IVGDR is largely independent of the chosen interaction [43]. This can be understood to result from the dominance of stochastic coupling [110]; that is, the strength distribution is mainly determined by the density of states and an average coupling matrix element between the 1p-1h and more complex states.

4 Extracting neutron skin thickness and symmetry energy properties from dipole polarizability data

In this section, we discuss constraints on the neutron skin thickness and symmetry energy properties derived from the comparison between model predictions and experimental studies of the DP. These refer to specific nuclei like ⁴⁰Ca, ⁴⁸Ca, and ²⁰⁸Pb but also systematic isotopic trends or a global mass dependence. The difficulties that presently available models have in simultaneously accounting for measured polarizabilities and asymmetries in parity-violating elastic electron scattering are illuminated.

4.1 Constraints based on density functional theory

The DPs of ⁴⁰Ca and ⁴⁸Ca have been studied in [29, 78], respectively. Figure 10A depicts their correlation and a comparison to selected DFT results. The four functionals are representative of widely used forms: non-relativistic Skyrme functionals SV [111] and RD [112] with different forms of density dependence, and relativistic functionals DD [113] with finite-range meson-exchange coupling and PC [114] with point coupling. All four have been calibrated to the same set of ground-state data to determine the model parameters.

Figure 10

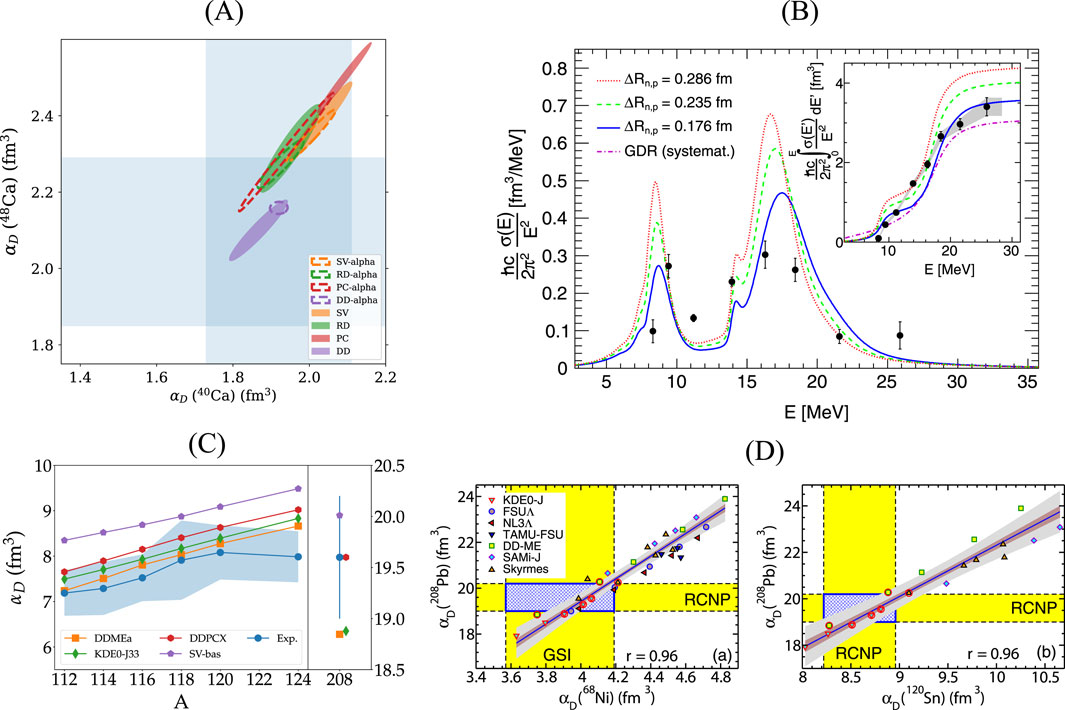
Figure 10. (A) Correlation of the experimental DP of ⁴⁰Ca and ⁴⁸Ca (blue bands) in comparison with DFT calculations without (full ellipses) and with (dashed ellipses) inclusion of the experimental DP of ²⁰⁸Pb [36] in the parameter fit. (B) $E1$ strength distribution in ⁶⁸Ni (black circles) compared to DFT calculations systematically varying the neutron skin thickness [115]. The inset shows the running sum of the DP. (C) Systematics of the DP in the stable Sn isotopes (left panel) and in ²⁰⁸Pb (right panel). The experimental values (blue dots) and their errors (blue band) are compared with DFT results from several modern interactions. (D) Correlation (cross-hatched blue histograms) of the DP in ²⁰⁸Pb with ⁶⁸Ni (left panel) and ¹²⁰Sn (right panel) with uncertainties (yellow bands) compared to DFT calculations for a large set of interactions and a linear fit with uncertainty bands. Figures taken from (A) [29], (B) [26], [79], and (D) [106], where the original references can be found.

The predictions are displayed as filled ellipses that represent the $1\sigma$ error as defined in [116]. The DD functional performs rather well. The other models tend to slightly overestimate the experimental mean values of both ⁴⁰Ca and ⁴⁸Ca, but their $1\sigma$ error ellipses do overlap with the experimental bands, except for PC. In all cases, the ${\alpha }_D$ values for both nuclei are highly correlated. The dashed ellipses show the effect of additionally including the experimental ${\alpha }_D$ value of ²⁰⁸Pb [36] in the fit, yielding functionals denoted “-alpha.” This improves the agreement with the experiment and shrinks the error ellipsoids. The models incorporate a span of symmetry energy parameters $J=30-35(30-32)$ MeV and $L=32-82(35-52)$ MeV for the calculations excluding (including) the ²⁰⁸Pb data point.

The $B(E1)$ strength distribution of the unstable neutron-rich nucleus ⁶⁸Ni determined in an experiment measuring Coulomb excitation in inverse kinematics [26] is displayed in Figure 10B. The DP was extracted from a comparison to the model of [115]. The model results show a sensitivity to the assumed neutron skin thickness, as illustrated by the colored curves. A value of 0.17 (2) fm was extracted for the neutron skin thickness from the correlation between the two quantities.

A study of the DP in a long isotopic chain is particularly suited to investigate the connection with the neutron skin thickness. This can be best done in the Sn isotopes with neutron numbers between 50 and 82, where the proton shell closure stabilizes the g.s. deformation. There are many stable isotopes, and a study of the systematics of the DP was presented in [79]. The results are summarized in Figure 10C, which shows the evolution of ${\alpha }_D$ between mass numbers 112 and 124. All DFT calculations predict an approximately linear increase as a function of neutron excess with roughly the same slope. The experimental results indicate a saturation between mass numbers 120 and 124, but the uncertainties (blue band) do not exclude a mass dependence similar to the theoretical results. The rightmost part of Figure 10C shows the predictions of the different models for the ²⁰⁸Pb DP after subtraction of the quasi-deuteron part (see the next paragraph). The models closest in absolute magnitude to the data tend to underpredict ${\alpha }_D$ (²⁰⁸Pb), while those reproducing it overshoot the absolute values in the Sn chain, indicating that the functionals cannot yet fully describe the mass dependence of the DP. We note that $E1$ strength distributions have also been measured for the unstable neutron-rich isotopes ^130,132Sn [25] but the extracted values of ${\alpha }_D$ cannot be compared directly to the results of [79] because the experiment only provided data above neutron threshold.

Roca-Maza et al. [106] combined the experimental DP data for ⁶⁸Ni [26], ¹²⁰Sn [30], and ²⁰⁸Pb [36] to test a large variety of density functionals. Because the DFT calculations do not include contributions from the quasi-deuteron process dominating the photoabsorption cross sections above the energy region of the IVGDR, these had to be removed for a comparison [106]. Figure 10D presents correlation plots between the experimental results and theoretical predictions from a wide range of DFT interactions. Only a handful (marked in red) are capable of simultaneously describing all three data points. Based on this reduced set, systematic predictions of ${\alpha }_D$ for other masses, $r_{\mathit{skin}}$, and the symmetry energy parameters could be derived. The experimental results for ^40,48Ca discussed above are fairly well described by these predictions.

4.2 Constraints based on ab initio models

An experimental study of the DP in ⁴⁸Ca [78] is of particular interest because it is accessible for both DFT and ab initio calculations, and a measurement of the neutron skin with parity-violating electron scattering is available [19]. The comparison is summarized in Figure 11A, where the blue band describes the experimental uncertainty. Ab initio results for the set of interactions from [38, 39] are displayed as green triangles, and a prediction from [40] based on a normalization to the ⁴⁸Ca charge radius is displayed as a green bar. Results from the set of density functionals described in [40] are shown as red squares with some representative error bars, and the prediction from the analysis of [106] discussed above is shown as a black bar.

Figure 11

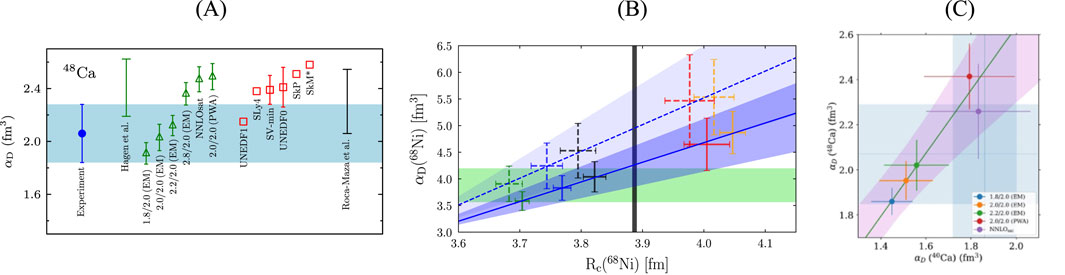
Figure 11. (A) Experimental DP in ⁴⁸Ca (blue band) and predictions from ab initio results based on $\chi$EFT interactions (green triangles) and DFT calculations (red squares). The green and black bars indicate the ab initio prediction selected to reproduce the ⁴⁸Ca charge radius and the range of DP predictions from [106] simultaneously consistent with the DP in ⁶⁸Ni, ¹²⁰Sn, and ²⁰⁸Pb, cf. Figure 10D. (B) Correlation of the experimental DP (green band) and the charge radius (black band) in ⁶⁸Ni with a comparison to the ab initio coupled-cluster calculations up to 2p-2h (dashed crosses) and 3p-3h excitations (full crosses). The dashed and full lines and corresponding error bands result from linear fits to the theoretical results. (C) Correlation of the experimental DP in ⁴⁰Ca and ⁴⁸Ca in comparison with ab initio coupled-cluster calculations including 3p-3h excitations (crosses and purple uncertainty band). Figures taken from (A) [78] and (B) [117], where the original references can be found. (C) is taken from [29] but modified to include an estimate of the theoretical uncertainties shown as a purple band.

The DFT results tend to be somewhat high compared to the experiment. The ab initio results show a significant dependence on the chosen interaction, but it can be well approximated by a linear dependence. In principle, this allows for the derivation of boundaries on the neutron skin thickness and the symmetry energy. However, while the ab initio results shown were truncated in the coupled-cluster expansion at the 2p-2h level, subsequent work [118] demonstrated that inclusion of 3p-3h correlations lowers the ${\alpha }_D$ values by $10-20$%. The refined results in ⁴⁸Ca are plotted in Figure 11C against corresponding calculations for ⁴⁰Ca [29]. A high correlation similar to the DFT results shown in Figure 10A is observed. The purple uncertainty band from the ab initio results overlaps with the crossing of the experimental $1\sigma$ error bands. In particular, the NNLO_sat interaction [38] accurately describing binding energies and radii of nuclei up to ⁴⁰Ca and the saturation point of symmetric nuclear matter now reproduces both DP values. The importance of including 3p-3h correlations has also been demonstrated in a recent measurement of the ⁶⁸Ni charge radius [117]. Figure 11B illustrates the improvement in reproducing the correlation between the charge radius and ${\alpha }_{\text{D}}$ [26] when going from the 2p-2h level (light blue band) to the inclusion of 3p-3h correlations (dark blue band).

As noted in Section 2.2, independent of the chosen interaction, a neutron skin thickness of approximately 0.14 fm is predicted for ⁴⁸Ca, consistent with the value deduced from the measurement of the weak form factor [19]. The simultaneous description of the data in ^40,48Ca and ⁶⁸Ni implies that the underlying symmetry energy parameters are correct. A conservative estimate is provided by taking the full range of values from the set of ab initio interactions, viz., $J=27-33$ MeV and $L=41-49$ MeV.

Recent work has, for the first time, been able to extend the range of ab initio DP calculations based on $\chi$EFT interactions to ²⁰⁸Pb [119]. A different technique was used to construct the interactions by history matching [120] using selected experimental observables in light nuclei. Moreover, low-energy nucleon–nucleon scattering phase shifts were additionally considered. The latter are responsible for tight constraints to rather small values of the resulting neutron skin thickness ($0.14-0.20$ fm for ²⁰⁸Pb). The variation of the density dependence of the symmetry energy in these calculations is $L=38-69$ MeV.

4.3 Tension between polarizability and parity-violating elastic electron scattering in ²⁰⁸Pb

While in ⁴⁸Ca there is fair agreement between the neutron skin thickness and symmetry energy properties derived from the different experiments, the parity-violating elastic electron scattering experiment on ²⁰⁸Pb [18] finds a much larger neutron skin $r_{\mathit{skin}}=0.28(7)$ fm than most other work. Accordingly, an extraction of symmetry energy parameters based on the correlations established in DFT (see Section 2.1) leads to large symmetry energy values of $J=38(5)$ MeV and $L=106(37)$ MeV in contradiction to limits derived from astrophysical observations of neutron star radii and masses as well as the tidal deformability of neutron star mergers [7]. All astrophysical constraints point toward a softer EOS. This has led to speculations about a phase transition at intermediate densities [121].

Because of the strong correlation between $r_{skin}$ and ${\alpha }_D$ for a given nucleus and $r_{skin}$ values of different nuclei in DFT models, Reinhard et al. [116, 122] investigated whether it is possible to construct a DFT interaction capable of simultaneously describing the data for ⁴⁸Ca and ²⁰⁸Pb. The analysis was based on representative families of non-relativistic and relativistic functionals. The isovector properties of EDFs are typically not well constrained by the input data used to fit the model parameters. As illustrated in Figure 12A for the case of ²⁰⁸Pb, it is possible to vary the symmetry energy parameters—and thereby the predicted $r_{\mathit{skin}}$ and ${\alpha }_D$—over a fairly large range maintaining comparable description of ground-state properties [116]. Figure 12B [122] demonstrates that the polarizabilities and the neutron skin thickness of ⁴⁸Ca could be consistently described, but it was impossible to construct an EDF simultaneously accounting for the neutron skin thickness of ²⁰⁸Pb extracted from the PREX experiment [19]. Similar conclusions were drawn in [123, 124]. In another recent attempt [125], a DFT interaction reasonably accounting for the measured parity-violating asymmetries in both the PREX and CREX experiments was constructed, but at the expense of unusual properties of the symmetry energy curvature and a very strong isovector coupling leading to density fluctuations in the nuclear interior.

Figure 12

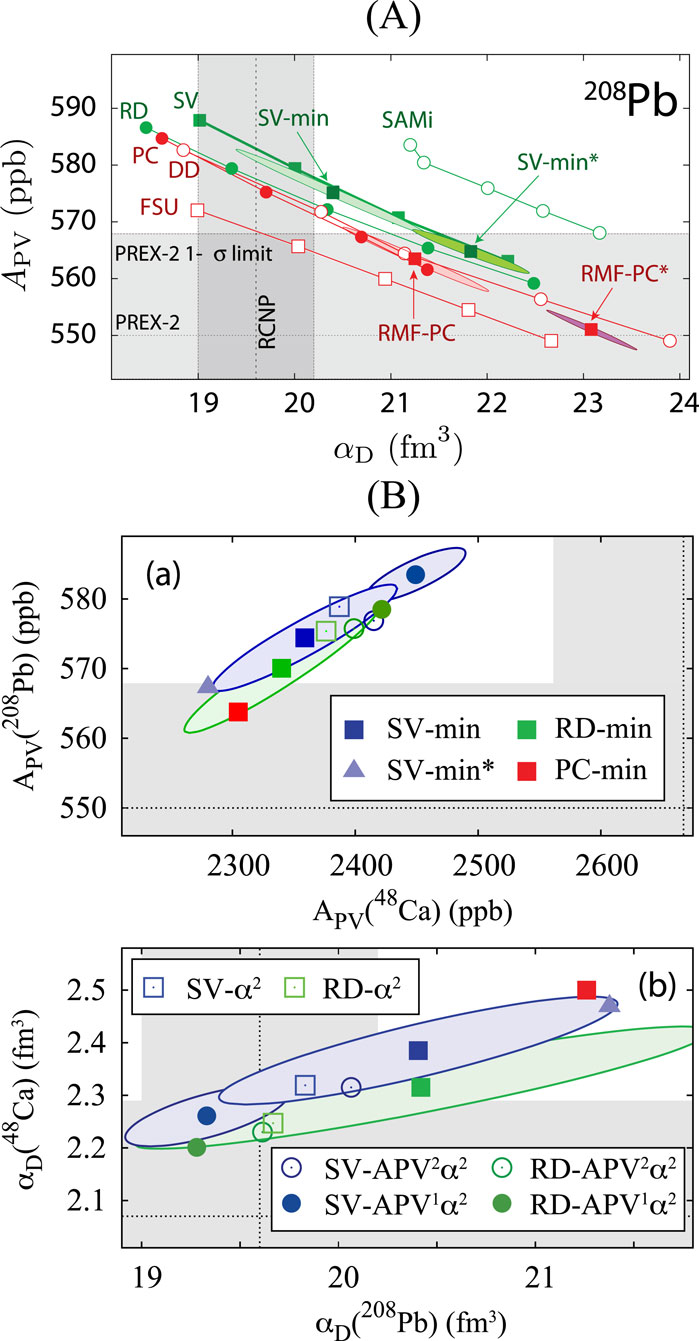
Figure 12. (A) Experimental parity-violating asymmetry versus DP in ²⁰⁸Pb (gray bands) compared to calculations with a set of relativistic (red) and non-relativistic (green) DFT interactions. Sets with systematically varied symmetry energy $J$ are connected by lines. Representative $1\sigma$ error ellipses are shown for the interaction indicated by squares. Figure taken from [116], where the original references can be found. (B) Correlation of experimental parity-violating asymmetries (top) and DP (bottom) in ⁴⁸Ca and ²⁰⁸Pb (gray bands) compared to a set of DFT interactions. Representative $1\sigma$ error ellipses are shown for the interaction indicated by squares. Figure taken from [122], where the original references can be found.

4.4 Volume and surface contributions to the symmetry energy

Another way of extracting properties of the symmetry energy is a study of the mass dependence of the DP. A simple power law ${\sigma }_{-2}\propto A^{5/3}$ based on a model of two interpenetrating fluids has been given by Migdal, where ${\sigma }_{-2}$ denotes the second inverse moment of the photoabsorption cross sections and ${\sigma }_2\simeq {\alpha }_{\text{D}}$ in units of mb/MeV ([126] and Refs. therein). A proportionality constant $2.4\times 10^{-3}$ has been determined by Orce [127] from a fit to $(\gamma ,xn)$ data over a wide mass range. Figure 13 [128] shows a comparison with a combined data set of ${\alpha }_D$ measurements in light nuclei [58] with the then-available (2016) data from relativistic Coulomb excitation for heavier nuclei as a green short-dashed line. Note that results for $A<12$ from [58] are neglected because the hydrodynamical picture is highly questionable and corrections due to the magnetic polarizability are large [71] for these very light nuclei. Results are severely underestimated in lighter nuclei where charged-particle decay dominates. The mass dependence is reasonably described for larger masses, but the proportionality coefficient of [127] is too low because additional contributions from the strength below the neutron threshold, as discussed in Sec. 3.3, must be considered.

Figure 13

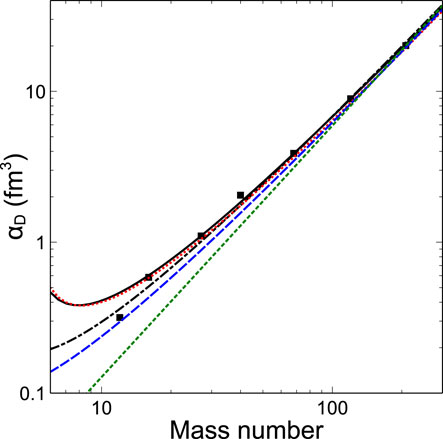
Figure 13. Experimental DP for a set of nuclei as a function of mass number (full squares). The green and blue lines are fits with the original Migdal model (Equations 1, 2) in [127]. The black lines are fits of Equation 5 allowing for a surface term of the symmetry energy, including (dashed-dotted) and excluding (full) the data point for ¹²C. The red line shows a fit with the prediction of [129] using the “${\mu }_n$” approach. Figure taken from [128], where the original references can be found.

For masses $A\le 40$, surface contributions must be considered, modifying the volume term of the symmetry energy dominating for heavy nuclei. These can be parameterized as [128]

${\sigma }_{-2}=\frac{0.0518A^2}{S_v\left(A^{1/3}-\kappa \right)}\mathrm{m}\mathrm{b}/\mathrm{M}\mathrm{e}\mathrm{V}.(5)$

Here $\kappa =S_s/S_v$, and $S_s$ and $S_v$ denote the surface and volume coefficients of the symmetry energy, respectively. The numerical coefficient in Equation 5 is obtained from Migdal’s approach. A fit with $S_s,S_v$ parameters from binding energies of isobaric nuclei [130] shown in Figure 13 as a long-dashed blue line still underestimates the lower-mass data. Parameters of the study of [129] provide a better description (dotted red line). Results of a free fit of Equation 5 crucially depend on the inclusion (dotted-dashed black line) or exclusion (solid black line) of the ¹²C data point. The latter provides a better fit with $S_v=25.6(8)$ MeV, $\kappa =1.66(5)$ [128] close to [129]. $S_v$ can be interpreted as $J$, but measured at about $2/3$ of the saturation density [34, 131].

5 Conclusion and outlook

We present a review of methods to measure the isovector $E1$ response in nuclei and the extraction of the dipole polarizability from these data. The discussion focuses on recent results obtained with inelastic proton scattering under extreme forward angles at RCNP. At energies of a few hundred MeV, relativistic Coulomb excitation dominates the cross sections in these kinematics. The method combines certain advantages compared to other experimental techniques: 1) it measures the absorption and is thus independent of the knowledge of branching ratios; 2) a separation of $E1$ and $M1$ contributions to the cross sections can be achieved with different independent approaches; 3) the relevant excitation energy region from well below the neutron threshold across the IVGDR can be covered in a single experiment.

Constraints on the neutron skin thickness of nuclei and the parameters of the symmetry energy can be extracted from the strong correlations between these three quantities seen in all microscopic models. Results from nuclei covering a mass range between ⁴⁰Ca and ²⁰⁸Pb consistently favor small neutron skins and a soft density dependence of the EOS around saturation density. In ²⁰⁸Pb serving as a benchmark for theory, this finding is at variance with the PREX results, while a similar study of ⁴⁸Ca by the CREX collaboration conforms. The PREX result, hard to interpret in the framework of present theory, has led to an initiative (called Mainz radius experiment, or MREX) for a study with improved statistical and systematic errors at the new high-current Mainz energy-recovering superconducting accelerator (MESA) [132].

While the mass dependence of the DP is reasonably well-covered by the available data, future work should explore other degrees of freedom, such as the variation of neutron excess along isotopic chains and the role of deformation. The experimental uncertainties of the DP for key nuclei can be improved by the availability of independent measurements, as illustrated in Figure 6. New high-brilliance LCBS photon beam facilities are under construction at the Extreme Light Infrastructure–Nuclear Physics (ELI-NP) in Bucharest [133, 134] and the Shanghai Laser Electron Gamma Source (SLEGS) at the Shanghai Synchrotron Radiation Facility [135]. Combined with advanced techniques for neutron detection [136], these facilities promise a new quality of precision for $(\gamma ,xn)$ experiments.

Major steps can be expected in the future at radioactive ion beam facilities, providing access to cases with much larger neutron excess than achievable for stable nuclei. Experimental tools for measuring relativistic Coulomb excitation in reverse kinematics are available, and pioneering studies of the dipole response in unstable nuclei have been performed at GSI [25, 26, 27]. First results for the neutron-rich isotope ⁵²Ca investigated at RIKEN have been reported [137]. Because of the high energy/nucleon availability, future experiments at FAIR are particularly promising for research on the dipole polarizability of exotic neutron-rich nuclei [138].

Author contributions

PN-C: writing – original draft and writing – review and editing. AT: writing – original draft and writing – review and editing.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. This work was supported by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Contract No. SFB 1245 (Project ID No. 79384907), by the Research Council of Norway through its grant to the Norwegian Nuclear Research Centre (Project No. 341985), by the JSPS KAKENHI Grant Number 25H00641, and by the Japan-South Africa Bilateral Funding Grant Number JPJSBP 120246502.

Acknowledgments

PvNC thanks the nuclear physics group at the University of Oslo for their kind hospitality during a stay where major parts of this work were done.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Roca-Maza X, Paar N. Nuclear equation of state from ground and collective excited state properties of nuclei. Prog Part Nucl Phys (2018) 101:96–176. doi:10.1016/j.ppnp.2018.04.001

CrossRef Full Text | Google Scholar

2. Huth S, Pang PTH, Tews I, Dietrich T, Le Fèvre A, Schwenk A, et al. Constraining neutron-star matter with microscopic and macroscopic collisions. Nature (2022) 606:276–80. doi:10.1038/s41586-022-04750-w

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Lattimer J. Neutron stars and the nuclear matter equation of state. Annu Rev Nucl Part Sci (2021) 71:433–64. doi:10.1146/annurev-nucl-102419-124827

CrossRef Full Text | Google Scholar

4. Yasin H, Schäfer S, Arcones A, Schwenk A. Equation of state effects in core-collapse supernovae. Phys Rev Lett (2020) 124:092701. doi:10.1103/PhysRevLett.124.092701

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Raaijmakers G, Greif SK, Hebeler K, Hinderer T, Nissanke S, Schwenk A, et al. Constraints on the dense matter equation of state and neutron star properties from NICER’s mass–radius estimate of PSR J0740+6620 and multimessenger observations. Astrophys J Lett (2021) 918:L29. doi:10.3847/2041-8213/ac089a

CrossRef Full Text | Google Scholar

6. Koehn H, Rose H, Pang PTH, Somasundaram R, Reed BT, Tews I, et al. From existing and new nuclear and astrophysical constraints to stringent limits on the equation of state of neutron-rich dense matter. Phys Rev X (2025) 15:021014. doi:10.1103/PhysRevX.15.021014

CrossRef Full Text | Google Scholar

7. Lattimer J. Constraints on nuclear symmetry energy parameters. Particles (2023) 6:30–56. doi:10.3390/particles6010003

CrossRef Full Text | Google Scholar

8. Estee J, Lynch WG, Tsang CY, Barney J, Jhang G, Tsang MB, et al. Probing the symmetry energy with the spectral pion ratio. Phys Rev Lett (2021) 126:162701. doi:10.1103/PhysRevLett.126.162701

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Tsang MB, Stone JR, Camera F, Danielewicz P, Gandolfi S, Hebeler K, et al. Constraints on the symmetry energy and neutron skins from experiments and theory. Phys Rev C (2012) 86:015803. doi:10.1103/PhysRevC.86.015803

CrossRef Full Text | Google Scholar

10. Drischler C, Furnstahl RJ, Melendez JA, Phillips DR. How well do we know the neutron-matter equation of state at the densities inside neutron stars? A Bayesian approach with correlated uncertainties. Phys Rev Lett (2020) 125:202702. doi:10.1103/PhysRevLett.125.202702

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Zenihiro J, Sakaguchi H, Murakami T, Yosoi M, Yasuda Y, Terashima S, et al. Neutron density distributions of ^204,206,208Pb deduced via proton elastic scattering at E_p = 295 MeV. Phys Rev C (2010) 82:044611. doi:10.1103/physrevc.82.044611

CrossRef Full Text | Google Scholar

12. Tarbert CM, Watts DP, Glazier DI, Aguar P, Ahrens J, Annand JRM, et al. Neutron skin of ²⁰⁸Pb from coherent pion photoproduction. Phys Rev Lett (2014) 112:242502. doi:10.1103/PhysRevLett.112.242502

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Kłos B, Trzcińska A, Jastrzebski J, Czosnyka T, Kisieliński M, Lubiński P, et al. Neutron density distributions from antiprotonic ²⁰⁸Pb and ²⁰⁹Bi atoms. Phys Rev C (2007) 76:014311. doi:10.1103/PhysRevC.76.014311

CrossRef Full Text | Google Scholar

14. Trzcińska A, Jastrzȩbski J, Lubiński P, Hartmann FJ, Schmidt R, von Egidy T, et al. Neutron density distributions deduced from antiprotonic atoms. Phys Rev Lett (2001) 87:082501. doi:10.1103/PhysRevLett.87.082501

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Krasznahorkay A, Fujiwara M, van Aarle P, Akimune H, Daito I, Fujimura H, et al. Excitation of isovector spin-dipole resonances and neutron skin of nuclei. Phys Rev Lett (1999) 82:3216–9. doi:10.1103/PhysRevLett.82.3216

CrossRef Full Text | Google Scholar

16. Mammei JM, Horowitz CJ, Piekarewicz J, Reed BT, Sfienti C. Neutron skins: weak elastic scattering and neutron stars. Annu Rev Nucl Part Sci (2024) 74:321–42. doi:10.1146/annurev-nucl-102122-024207

CrossRef Full Text | Google Scholar

17. Horowitz CJ, Pollock SJ, Souder PA, Michaels R. Parity violating measurements of neutron densities. Phys Rev C (2001) 63:025501. doi:10.1103/PhysRevC.63.025501

CrossRef Full Text | Google Scholar

18. Adhikari D, Albataineh H, Androic D, Aniol K, Armstrong DS, Averett T, et al. Accurate determination of the neutron skin thickness of ²⁰⁸Pb through parity-violation in electron scattering. Phys Rev Lett (2021) 126:172502. doi:10.1103/PhysRevLett.126.172502

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Adhikari D, Albataineh H, Androic D, Aniol KA, Armstrong DS, Averett T, et al. Precision determination of the neutral weak form factor of ⁴⁸Ca. Phys Rev Lett (2022) 129:042501. doi:10.1103/PhysRevLett.129.042501

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Bender M, Heenen P-H, Reinhard P-G. Self-consistent mean-field models for nuclear structure. Rev Mod Phys (2003) 75:121–80. doi:10.1103/RevModPhys.75.121

CrossRef Full Text | Google Scholar

21. Hagen G, Papenbrock T, Hjorth-Jensen M, Dean D. Coupled-cluster computations of atomic nuclei. Rep Prog Phys (2014) 77:096302. doi:10.1088/0034-4885/77/9/096302

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Epelbaum E, Hammer H-W, Meißner U-G. Modern theory of nuclear forces. Rev Mod Phys (2009) 81:1773–825. doi:10.1103/RevModPhys.81.1773

CrossRef Full Text | Google Scholar

23. Thiel M, Sfienti C, Piekarewicz J, Horowitz CJ, Vanderhaeghen M. Neutron skins of atomic nuclei: per aspera ad astra. J Phys G (2019) 46:093003. doi:10.1088/1361-6471/ab2c6d

CrossRef Full Text | Google Scholar

24. von Neumann-Cosel P, Tamii A (2019). Electric and magnetic dipole modes in high-resolution inelastic proton scattering at 0°. Eur Phys J A 55, 110. doi:10.1140/epja/i2019-12781-7

CrossRef Full Text | Google Scholar

25. Adrich P, Klimkiewicz A, Fallot M, Boretzky K, Aumann T, Cortina-Gil D, et al. Evidence for pygmy and giant dipole resonances in ¹³⁰Sn and ¹³²Sn. Phys Rev Lett (2005) 95:132501. doi:10.1103/PhysRevLett.95.132501

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Rossi DM, Adrich P, Aksouh F, Alvarez-Pol H, Aumann T, Benlliure J, et al. Measurement of the dipole polarizability of the unstable neutron-rich nucleus ⁶⁸Ni. Phys Rev Lett (2013) 111:242503. doi:10.1103/PhysRevLett.111.242503

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Wieland O, Bracco A, Camera F, Benzoni G, Blasi N, Brambilla S, et al. Search for the pygmy dipole resonance in ⁶⁸Ni at 600 MeV/nucleon. Phys Rev Lett (2009) 102:092502. doi:10.1103/PhysRevLett.102.092502

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Aumann T, Bartmann W, Boine-Frankenheim O, Bouvard A, Broche A, Butin F, et al. PUMA, antiproton unstable matter annihilation. Eur Phys J A (2022) 58:88. doi:10.1140/epja/s10050-022-00713-x

CrossRef Full Text | Google Scholar

29. Fearick RW, von Neumann-Cosel P, Bacca S, Birkhan J, Bonaiti F, Brandherm I, et al. Electric dipole polarizability of ⁴⁰Ca. Phys Rev Res (2023) 5:L022044. doi:10.1103/PhysRevResearch.5.L022044

CrossRef Full Text | Google Scholar

30. Hashimoto T, Krumbholz AM, Reinhard P-G, Tamii A, von Neumann-Cosel P, Adachi T, et al. Dipole polarizability of ¹²⁰Sn and nuclear energy density functionals. Phys Rev C (2015) 92:031305. doi:10.1103/PhysRevC.92.031305

CrossRef Full Text | Google Scholar

31. Typel S, Brown BA. Neutron radii and the neutron equation of state in relativistic models. Phys Rev C (2001) 64:027302. doi:10.1103/PhysRevC.64.027302

CrossRef Full Text | Google Scholar

32. Brown BA. Neutron radii in nuclei and the neutron equation of state. Phys Rev Lett (2000) 85:5296–9. doi:10.1103/PhysRevLett.85.5296

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Reinhard P-G, Nazarewicz W. Information content of a new observable: the case of the nuclear neutron skin. Phys Rev C (2010) 81:051303. doi:10.1103/PhysRevC.81.051303

CrossRef Full Text | Google Scholar

34. Roca-Maza X, Brenna M, Colò G, Centelles M, Viñas X, Agrawal BK, et al. Electric dipole polarizability in ²⁰⁸Pb: insights from the droplet model. Phys Rev C (2013) 88:024316. doi:10.1103/PhysRevC.88.024316

CrossRef Full Text | Google Scholar

35. Myers W, Swiatecki W. The nuclear droplet model for arbitrary shapes. Ann Phys (N.Y.) (1974) 84:186–210. doi:10.1016/0003-4916(74)90299-1

CrossRef Full Text | Google Scholar

36. Tamii A, Poltoratska I, von Neumann-Cosel P, Fujita Y, Adachi T, Bertulani CA, et al. Complete electric dipole response and the neutron skin in ²⁰⁸Pb. Phys Rev Lett (2011) 107:062502. doi:10.1103/PhysRevLett.107.062502

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Drischler C, Hebeler K, Schwenk A. Chiral interactions up to next-to-next-to-next-to-leading order and nuclear saturation. Phys Rev Lett (2019) 122:042501. doi:10.1103/PhysRevLett.122.042501

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Ekström A, Jansen GR, Wendt KA, Hagen G, Papenbrock T, Carlsson BD, et al. Accurate nuclear radii and binding energies from a chiral interaction. Phys Rev C (2015) 91:051301. doi:10.1103/PhysRevC.91.051301

CrossRef Full Text | Google Scholar

39. Hebeler K, Bogner SK, Furnstahl RJ, Nogga A, Schwenk A. Improved nuclear matter calculations from chiral low-momentum interactions. Phys Rev C (2011) 83(R):031301. doi:10.1103/PhysRevC.83.031301

CrossRef Full Text | Google Scholar

40. Hagen G, Ekström A, Forssén C, Jansen GR, Nazarewicz W, Papenbrock T, et al. Neutron and weak-charge distributions of the ⁴⁸Ca nucleus. Nat Phys (2016) 12:186. doi:10.1038/nphys3529

CrossRef Full Text | Google Scholar

41. Bacca S, Pastore S. Electromagnetic reactions on light nuclei. J Phys G (2014) 41:123002. doi:10.1088/0954-3899/41/12/123002

CrossRef Full Text | Google Scholar

42. Bonaiti F, Bacca S, Hagen G, Jansen GR. Electromagnetic observables of open-shell nuclei from coupled-cluster theory. Phys Rev C (2024) 110:044306. doi:10.1103/PhysRevC.110.044306

CrossRef Full Text | Google Scholar

43. Brandherm I, Bonaiti F, von Neumann-Cosel P, Bacca S, Colò G, Jansen GR, et al. Electric dipole polarizability of ⁵⁸Ni. Phys Rev C (2025) 111:024312. doi:10.1103/PhysRevC.111.024312

CrossRef Full Text | Google Scholar

44. Lynch WG, Tsang MB, Bhang HC, Cramer JG, Puigh RJ. Relativity, nuclear polarizability, and screening in sub-Coulomb elastic scattering. Phys Rev Lett (1982) 48:979–82. doi:10.1103/PhysRevLett.48.979

CrossRef Full Text | Google Scholar

45. Rodning NL, Knutson LD, Lynch WG, Tsang MB. Measurement of the electric polarizability of the deuteron. Phys Rev Lett (1982) 49:909–12. doi:10.1103/PhysRevLett.49.909

CrossRef Full Text | Google Scholar

46. Berman BL, Fultz SC. Measurements of the giant dipole resonance with monoenergetic photons. Rev Mod Phys (1975) 47:713–61. doi:10.1103/RevModPhys.47.713

CrossRef Full Text | Google Scholar

47. Dietrich SS, Berman BL. Atlas of photoneutron cross sections obtained with monoenergetic photons. Data Nucl Data Tables (1988) 38:199–338. doi:10.1016/0092-640X(88)90033-2

CrossRef Full Text | Google Scholar

48. Beene JR, Bertrand FE, Horen DJ, Auble RL, Burks BL, Gomez del Campo J, et al. Heavy-ion Coulomb excitation and photon decay of the giant dipole resonance in ²⁰⁸Pb. Phys Rev C (1990) 41:920–32. doi:10.1103/PhysRevC.41.920

PubMed Abstract | CrossRef Full Text | Google Scholar

49. Harvey RR, Caldwell JT, Bramblett RL, Fultz SC. Photoneutron cross sections of Pb²⁰⁶, Pb²⁰⁷, Pb²⁰⁸, and Bi²⁰⁹. Phys Rev (1964) 136:B126–31. doi:10.1103/PhysRev.136.B126

CrossRef Full Text | Google Scholar

50. Berman BL, Pywell RE, Dietrich SS, Thompson MN, McNeill KG, Jury JW. Absolute photoneutron cross sections for Zr, I, Pr, Au, and Pb. Phys Rev C (1987) 36:1286–92. doi:10.1103/PhysRevC.36.1286

PubMed Abstract | CrossRef Full Text | Google Scholar

51. Veyssiere A, Beil H, Bergère R, Carlos P, Leprêtre A. Photoneutron cross sections of ²⁰⁸Pb and ¹⁹⁷Au. Nucl Phys A (1970) 159:561–76. doi:10.1016/0375-9474(70)90727-X

CrossRef Full Text | Google Scholar

52. Kawano T, Cho Y, Dimitriou P, Filipescu D, Iwamoto N, Plujko V, et al. IAEA photonuclear data library 2019. Nucl Data Sheets (2020) 163:109–62. doi:10.1016/j.nds.2019.12.002

CrossRef Full Text | Google Scholar

53. Gheorghe I, Goriely S, Wagner N, Aumann T, Baumann M, van Beek P, et al. Photoneutron cross section measurements on ²⁰⁸Pb in the giant dipole resonance region. Phys Rev C (2024) 110:014619. doi:10.1103/PhysRevC.110.014619

CrossRef Full Text | Google Scholar

54. Toyokawa H, Goko S, Hohara S, Kaihori T, Kaneko F, Kuroda R, et al. Recent progress in generation and application of AIST laser-Compton gamma-ray beam. Nucl Instrum Methods A (2009) 608:S41–3. doi:10.1016/j.nima.2009.05.062

CrossRef Full Text | Google Scholar

55. Weller HR, Ahmed MW, Gao H, Tornow W, Wu YK, Gai M, et al. Research opportunities at the upgraded HIγS facility. Prog Part Nucl Phys (2009) 62:257–303. doi:10.1016/j.ppnp.2008.07.001

CrossRef Full Text | Google Scholar

56. Amano S, Horikawa K, Ishihara K, Miyamoto S, Hayakawa T, Shizuma T, et al. Several-MeV γ-ray generation at NewSUBARU by laser Compton backscattering. Nucl Instrum Methods A (2009) 602:337–41. doi:10.1016/j.nima.2009.01.010

CrossRef Full Text | Google Scholar

57. Horikawa K, Miyamoto S, Amano S, Mochizuki T. Measurements for the energy and flux of laser compton scattering γ-ray photons generated in an electron storage ring: NewSUBARU. Nucl Instrum Methods A (2010) 618:209–15. doi:10.1016/j.nima.2010.02.259

CrossRef Full Text | Google Scholar

58. Ahrens J, Borchert H, Czock K, Eppler H, Gimm H, Gundrum H, et al. Total nuclear photon absorption cross sections for some light elements. Nucl Phys A (1975) 251:479–92. doi:10.1016/0375-9474(75)90543-6

CrossRef Full Text | Google Scholar

59. Harada H, Furutaka K, Ohgaki H, Toyokawa H. Fine structure of giant resonance in the ²⁸Si(γ, abs) reaction. J Nucl Sci Technol (2001) 38:465–9. doi:10.1080/18811248.2001.9715055

CrossRef Full Text | Google Scholar

60. Savran D, Lindenberg K, Glorius J, Löher B, Müller S, Pietralla N, et al. The low-energy photon tagger NEPTUN. Nucl Instrum Methods A (2010) 613:232–9. doi:10.1016/j.nima.2009.11.038

CrossRef Full Text | Google Scholar

61. Schelhaas K, Henneberg J, Sanzone-Arenhövel M, Wieloch-Laufenberg N, Zurmühl U, Ziegler B, et al. Nuclear photon scattering by ²⁰⁸Pb. Nucl Phys A (1988) 489:189–224. doi:10.1016/0375-9474(88)90149-2

CrossRef Full Text | Google Scholar

62. Penfold AS, Leiss JE. Analysis of photonuclear cross sections. Phys Rev (1959) 114:1332–7. doi:10.1103/PhysRev.114.1332

CrossRef Full Text | Google Scholar

63. Rasulova FA, Aksenov NV, Alekseev SI, Belyshev SS, Chuprakov I, Fursova NY, et al. Photonuclear reactions on stable isotopes of molybdenum at bremsstrahlung endpoint energies of 10–23 MeV. Phys Rev C (2025) 111:024604. doi:10.1103/PhysRevC.111.024604

CrossRef Full Text | Google Scholar

64. Agostinelli S, Allison J, Amako K, Apostolakis J, Araujo H, Arce P, et al. GEANT4—a simulation toolkit. Nucl Instrum Methods A (2003) 506:250–303. doi:10.1016/S0168-9002(03)01368-8

CrossRef Full Text | Google Scholar

65. von Neumann-Cosel P, Huxel N, Richter A, Spieler C, Carroll J, Collins C. Absolute calibration of low energy, thick target bremsstrahlung. Nucl Instrum Methods A (1994) 338:425. doi:10.1016/0168-9002(94)91326-9

CrossRef Full Text | Google Scholar

66. Nakamura T, Vinodkumar AM, Sugimoto T, Aoi N, Baba H, Bazin D, et al. Observation of strong low-lying E1 strength in the two-neutron halo nucleus ¹¹Li. Phys Rev Lett (2006) 96:252502. doi:10.1103/PhysRevLett.96.252502

PubMed Abstract | CrossRef Full Text | Google Scholar

67. Leistenschneider A, Aumann T, Boretzky K, Cortina D, Cub J, Pramanik UD, et al. Photoneutron cross sections for unstable neutron-rich oxygen isotopes. Phys Rev Lett (2001) 86:5442–5. doi:10.1103/PhysRevLett.86.5442

PubMed Abstract | CrossRef Full Text | Google Scholar

68. Tamii A, Fujita Y, Matsubara H, Adachi T, Carter J, Dozono M, et al. Measurement of high energy resolution inelastic proton scattering at and close to zero degrees. Nucl Instrum Methods A (2009) 605:326–38. doi:10.1016/j.nima.2009.03.248

CrossRef Full Text | Google Scholar

69. Neveling R, Fujita H, Smit F, Adachi T, Berg G, Buthelezi E, et al. High energy-resolution zero-degree facility for light-ion scattering and reactions at iThemba LABS. Nucl Instrum Methods A (2011) 654:29–39. doi:10.1016/j.nima.2011.06.077

CrossRef Full Text | Google Scholar

70. Zilges A, Balabanski D, Isaak J, Pietralla N. Photonuclear reactions – from basic research to applications. Prog Part Nucl Phys (2022) 122:103903. doi:10.1016/j.ppnp.2021.103903

CrossRef Full Text | Google Scholar

71. Knüpfer W, Richter A. Effect of the nuclear magnetic susceptibility on the evaluation of the electric dipole polarizability. Phys Lett B (1981) 107:325–6. doi:10.1016/0370-2693(81)90333-6

CrossRef Full Text | Google Scholar

72. Heyde K, von Neumann-Cosel P, Richter A. Magnetic dipole excitations in nuclei: elementary modes of nucleonic motion. Rev Mod Phys (2010) 82:2365–419. doi:10.1103/RevModPhys.82.2365

CrossRef Full Text | Google Scholar

73. Pietralla N. Photons and nuclear structure. Eur Phys J A (2024) 60:108. doi:10.1140/epja/s10050-024-01285-8

CrossRef Full Text | Google Scholar

74. Suzuki T. Polarization transfer invariants at forward angle and spin-dependent excitations in nuclei. Prog Theo Phys (2000) 103:859–64. doi:10.1143/PTP.103.859

CrossRef Full Text | Google Scholar

75. Gross W, Meuer D, Richter A, Spamer E, Titze O, Knüpfer W. A strong magnetic dipole excitation in ⁴⁰Ca observed in high-resolution inelastic electron scattering and coherent spin-flip transitions due to ground-state correlations. Phys Lett B (1979) 84:296–300. doi:10.1016/0370-2693(79)90043-1

CrossRef Full Text | Google Scholar

76. Martin D, von Neumann-Cosel P, Tamii A, Aoi N, Bassauer S, Bertulani CA, et al. Test of the Brink-Axel hypothesis for the pygmy dipole resonance. Phys Rev Lett (2017) 119:182503. doi:10.1103/PhysRevLett.119.182503

PubMed Abstract | CrossRef Full Text | Google Scholar

77. Bassauer S, von Neumann-Cosel P, Reinhard P-G, Tamii A, Adachi S, Bertulani CA, et al. Electric and magnetic dipole strength in ^{112,114,116,118,120,124}Sn. Phys Rev C (2020) 102:034327. doi:10.1103/PhysRevC.102.034327

CrossRef Full Text | Google Scholar

78. Birkhan J, Miorelli M, Bacca S, Bassauer S, Bertulani CA, Hagen G, et al. Electric dipole polarizability of ⁴⁸Ca and implications for the neutron skin. Phys Rev Lett (2017) 118:252501. doi:10.1103/PhysRevLett.118.252501

PubMed Abstract | CrossRef Full Text | Google Scholar

79. Bassauer S, von Neumann-Cosel P, Reinhard PG, Tamii A, Adachi S, Bertulani CA, et al. Evolution of the dipole polarizability in the stable tin isotope chain. Phys Lett B (2020) 810:135804. doi:10.1016/j.physletb.2020.135804

CrossRef Full Text | Google Scholar

80. Goriely S, Péru S, Colò G, Roca-Maza X, Gheorghe I, Filipescu D, et al. E1 moments from a coherent set of measured photoneutron cross sections. Phys Rev C (2020) 102:064309. doi:10.1103/PhysRevC.102.064309

CrossRef Full Text | Google Scholar

81. Strauch S, von Neumann-Cosel P, Rangacharyulu C, Richter A, Schrieder G, Schweda K, et al. Giant resonances in the doubly magic nucleus ⁴⁸Ca from the (e, e′n) reaction. Phys Rev Lett (2000) 85:2913–6. doi:10.1103/PhysRevLett.85.2913

PubMed Abstract | CrossRef Full Text | Google Scholar

82. O’Keefe G, Thompson M, Assafiri Y, Pywell R, Shoda K. The photonuclear cross sections of ⁴⁸Ca. Nucl Phys A (1987) 469:239–52. doi:10.1016/0375-9474(87)90108-4

CrossRef Full Text | Google Scholar

83. Fultz SC, Berman BL, Caldwell JT, Bramblett RL, Kelly MA. Photoneutron cross sections for Sn¹¹⁶, Sn¹¹⁷, Sn¹¹⁸, Sn¹¹⁹, Sn¹²⁰, Sn¹²⁴, and indium. Phys Rev (1969) 186:1255–70. doi:10.1103/PhysRev.186.1255

CrossRef Full Text | Google Scholar

84. Leprêtre A, Beil H, Bergère R, Carlos P, De Miniac A, Veyssière A, et al. A study of the giant dipole resonance of vibrational nuclei in the 103 ≤ A ≤ 133 mass region. Nucl Phys A (1974) 219:39–60. doi:10.1016/0375-9474(74)90081-5

CrossRef Full Text | Google Scholar

85. Utsunomiya H, Goriely S, Kamata M, Kondo T, Itoh O, Akimune H, et al. γ-ray strength function for ^116,117Sn with the pygmy dipole resonance balanced in the photoneutron and neutron capture channels. Phys Rev C (2009) 80:055806. doi:10.1103/PhysRevC.80.055806

CrossRef Full Text | Google Scholar

86. Bracco A, Lanza E, Tamii A. Isoscalar and isovector dipole excitations: nuclear properties from low-lying states and from the isovector giant dipole resonance. Prog Part Nucl Phys (2019) 106:360–433. doi:10.1016/j.ppnp.2019.02.001

CrossRef Full Text | Google Scholar

87. Savran D, Aumann T, Zilges A. Experimental studies of the pygmy dipole resonance. Prog Part Nucl Phys (2013) 70:210–45. doi:10.1016/j.ppnp.2013.02.003

CrossRef Full Text | Google Scholar

88. Müscher M, Wilhelmy J, Massarczyk R, Schwengner R, Grieger M, Isaak J, et al. High-sensitivity investigation of low-lying dipole strengths in ¹²⁰Sn. Phys Rev C (2020) 102:014317. doi:10.1103/PhysRevC.102.014317

CrossRef Full Text | Google Scholar

89. Krumbholz A, von Neumann-Cosel P, Hashimoto T, Tamii A, Adachi T, Bertulani C, et al. Low-energy electric dipole response in ¹²⁰Sn. Phys Lett B (2015) 744:7. doi:10.1016/j.physletb.2015.03.023

CrossRef Full Text | Google Scholar

90. Rusev G, Schwengner R, Beyer R, Erhard M, Grosse E, Junghans AR, et al. Enhanced electric dipole strength below particle-threshold as a consequence of nuclear deformation. Phys Rev C (2009) 79:061302. doi:10.1103/PhysRevC.79.061302

CrossRef Full Text | Google Scholar

91. Markova M, von Neumann-Cosel P, Litvinova E. Systematics of the low-energy electric dipole strength in the Sn isotopic chain. Phys Lett B (2025) 860:139216. doi:10.1016/j.physletb.2024.139216

CrossRef Full Text | Google Scholar

92. Lanza E, Pellegri L, Vitturi A, Andrés M. Theoretical studies of pygmy resonances. Prog Part Nucl Phys (2023) 129:104006. doi:10.1016/j.ppnp.2022.104006

CrossRef Full Text | Google Scholar

93. Paar N, Vretenar D, Khan E, Colò G. Exotic modes of excitation in atomic nuclei far from stability. Rep Prog Phys (2007) 70:R02. doi:10.1088/0034-4885/70/5/R02

PubMed Abstract | CrossRef Full Text | Google Scholar

94. Bertulani CA. Pygmy resonances and symmetry energy. Eur Phys J A (2019) 55:240. doi:10.1140/epja/i2019-12883-2

CrossRef Full Text | Google Scholar

95. Carbone A, Colò G, Bracco A, Cao L-G, Bortignon PF, Camera F, et al. Constraints on the symmetry energy and neutron skins from pygmy resonances in ⁶⁸Ni and ¹³²Sn. Phys Rev C (2010) 81:041301. doi:10.1103/PhysRevC.81.041301

CrossRef Full Text | Google Scholar

96. Klimkiewicz A, Paar N, Adrich P, Fallot M, Boretzky K, Aumann T, et al. Nuclear symmetry energy and neutron skins derived from pygmy dipole resonances. Phys Rev C (2007) 76:051603(R). doi:10.1103/PhysRevC.76.051603

CrossRef Full Text | Google Scholar

97. Krasznahorkay A, Akimune H, van den Berg A, Blasi N, Brandenburg S, Csatlós M, et al. Neutron-skin thickness in neutron-rich isotopes. Nucl Phys A (2004) 731:224–34. doi:10.1016/s0375-94740490024-3

CrossRef Full Text | Google Scholar

98. Markova M, Larsen AC, Tveten GM, von Neumann-Cosel P, Eriksen TK, Bello Garrote FL, et al. Nuclear level densities and γ-ray strength functions of ^111,112,113Sn isotopes studied with the Oslo method. Phys Rev C (2023) 108:014315. doi:10.1103/PhysRevC.108.014315

CrossRef Full Text | Google Scholar

99. Markova M, Larsen AC, von Neumann-Cosel P, Bassauer S, Görgen A, Guttormsen M, et al. Nuclear level densities and γ-ray strength functions in ^120,124Sn isotopes: impact of Porter-Thomas fluctuations. Phys Rev C (2022) 106:034322. doi:10.1103/PhysRevC.106.034322

CrossRef Full Text | Google Scholar

100. Markova M, von Neumann-Cosel P, Larsen AC, Bassauer S, Görgen A, Guttormsen M, et al. Comprehensive test of the Brink-Axel hypothesis in the energy region of the pygmy dipole resonance. Phys Rev Lett (2021) 127:182501. doi:10.1103/PhysRevLett.127.182501

PubMed Abstract | CrossRef Full Text | Google Scholar

101. Markova M, Larsen AC, von Neumann-Cosel P, Litvinova E, Choplin A, Goriely S, et al. Systematic study of the low-lying electric dipole strength in Sn isotopes and its astrophysical implications. Phys Rev C (2024) 109:054311. doi:10.1103/PhysRevC.109.054311

CrossRef Full Text | Google Scholar

102. Repko A, Nesterenko VO, Kvasil J, Reinhard P-G. Systematics of toroidal dipole modes in Ca, Ni, Zr, and Sn isotopes. Eur Phys J A (2019) 55:242. doi:10.1140/epja/i2019-12770-x

CrossRef Full Text | Google Scholar

103. von Neumann-Cosel P, Nesterenko VO, Brandherm I, Vishnevskiy PI, Reinhard P-G, Kvasil J, et al. Candidate toroidal electric dipole mode in the spherical nucleus ⁵⁸Ni. Phys Rev Lett (2024) 133:232502. doi:10.1103/PhysRevLett.133.232502

PubMed Abstract | CrossRef Full Text | Google Scholar

104. Leprêtre A, Beil H, Bergère R, Carlos P, Fagot J, De Miniac A, et al. Measurements of the total photonuclear cross sections from 30 MeV to 140 Mev for Sn, Ce, Ta, Pb and U nuclei. Nucl Phys A (1981) 367:237–68. doi:10.1016/0375-9474(81)90516-9

CrossRef Full Text | Google Scholar

105. Levinger JS. The high energy nuclear photoeffect. Phys Rev (1951) 84:43–51. doi:10.1103/PhysRev.84.43

CrossRef Full Text | Google Scholar

106. Roca-Maza X, Viñas X, Centelles M, Agrawal BK, Colò G, Paar N, et al. Neutron skin thickness from the measured electric dipole polarizability in ⁶⁸Ni, ¹²⁰Sn, and ²⁰⁸Pb. Phys Rev C (2015) 92:064304. doi:10.1103/PhysRevC.92.064304

CrossRef Full Text | Google Scholar

107. Chadwick MB, Obloinský P, Hodgson PE, Reffo G. Pauli-blocking in the quasideuteron model of photoabsorption. Phys Rev C (1991) 44:814–23. doi:10.1103/PhysRevC.44.814

PubMed Abstract | CrossRef Full Text | Google Scholar

108. Li ZZ, Niu YF, Colò G. Toward a unified description of isoscalar giant monopole resonances in a self-consistent quasiparticle-vibration coupling approach. Phys Rev Lett (2023) 131:082501. doi:10.1103/PhysRevLett.131.082501

PubMed Abstract | CrossRef Full Text | Google Scholar

109. Litvinova E. Relativistic approach to the nuclear breathing mode. Phys Rev C (2023) 107:L041302. doi:10.1103/PhysRevC.107.L041302

CrossRef Full Text | Google Scholar

110. von Neumann-Cosel P, Ponomarev VY, Richter A, Wambach J. Gross, intermediate and fine structure of nuclear giant resonances: Evidence for doorway states. Eur Phys J A (2019) 55:224. doi:10.1140/epja/i2019-12795-1

CrossRef Full Text | Google Scholar

111. Klüpfel P, Reinhard P-G, Bürvenich TJ, Maruhn JA. Variations on a theme by Skyrme: a systematic study of adjustments of model parameters. Phys Rev C (2009) 79:034310. doi:10.1103/PhysRevC.79.034310

CrossRef Full Text | Google Scholar

112. Erler J, Klüpfel P, Reinhard P-G. Misfits in Skyrme-Hartree-Fock. J Phys G (2010) 37:064001. doi:10.1088/0954-3899/37/6/064001

CrossRef Full Text | Google Scholar

113. Nikšić T, Vretenar D, Finelli P, Ring P. Relativistic Hartree-Bogoliubov model with density-dependent meson-nucleon couplings. Phys Rev C (2002) 66:024306. doi:10.1103/PhysRevC.66.024306

CrossRef Full Text | Google Scholar

114. Nikšić T, Vretenar D, Ring P. Relativistic nuclear energy density functionals: adjusting parameters to binding energies. Phys Rev C (2008) 78:034318. doi:10.1103/PhysRevC.78.034318

CrossRef Full Text | Google Scholar

115. Piekarewicz J. Pygmy resonances and neutron skins. Phys Rev C (2011) 83:034319. doi:10.1103/PhysRevC.83.034319

CrossRef Full Text | Google Scholar

116. Reinhard P-G, Roca-Maza X, Nazarewicz W. Information content of the parity-violating asymmetry in ²⁰⁸Pb. Phys Rev Lett (2021) 127:232501. doi:10.1103/PhysRevLett.127.232501

PubMed Abstract | CrossRef Full Text | Google Scholar

117. Kaufmann S, Simonis J, Bacca S, Billowes J, Bissell ML, Blaum K, et al. Charge radius of the short-lived ⁶⁸Ni and correlation with the dipole polarizability. Phys Rev Lett (2020) 124:132502. doi:10.1103/PhysRevLett.124.132502

PubMed Abstract | CrossRef Full Text | Google Scholar

118. Miorelli M, Bacca S, Hagen G, Papenbrock T. Computing the dipole polarizability of ⁴⁸Ca with increased precision. Phys Rev C (2018) 98:014324. doi:10.1103/PhysRevC.98.014324

CrossRef Full Text | Google Scholar

119. Hu B, Jiang W, Miyagi T, Sun Z, Ekström A, Forssén C, et al. Ab initio predictions link the neutron skin of ²⁰⁸Pb to nuclear forces. Nat Phys (2022) 18:1196–200. doi:10.1038/s41567-022-01715-8

PubMed Abstract | CrossRef Full Text | Google Scholar

120. Vernon I, Goldstein M, Bower R. Galaxy formation: Bayesian history matching for the observable universe. Statist Sci (2014) 29:81. doi:10.1214/12-STS412

CrossRef Full Text | Google Scholar

121. Han S, Steiner AW. Tidal deformability with sharp phase transitions in binary neutron stars. Phys Rev D (2019) 99:083014. doi:10.1103/PhysRevD.99.083014

CrossRef Full Text | Google Scholar

122. Reinhard P-G, Roca-Maza X, Nazarewicz W. Combined theoretical analysis of the parity-violating asymmetry for ⁴⁸Ca and ²⁰⁸Pb. Phys Rev Lett (2022) 129:232501. doi:10.1103/PhysRevLett.129.232501

PubMed Abstract | CrossRef Full Text | Google Scholar

123. Piekarewicz J. Implications of PREX-2 on the electric dipole polarizability of neutron-rich nuclei. Phys Rev C (2021) 104:024329. doi:10.1103/PhysRevC.104.024329

CrossRef Full Text | Google Scholar

124. Yüksel E, Paar N. Implications of parity-violating electron scattering experiments on ⁴⁸Ca (CREX) and ²⁰⁸Pb (PREX-II) for nuclear energy density functionals. Phys Lett B (2023) 836:137622. doi:10.1016/j.physletb.2022.137622

CrossRef Full Text | Google Scholar

125. Reed BT, Fattoyev FJ, Horowitz CJ, Piekarewicz J. Density dependence of the symmetry energy in the post–PREX-CREX era. Phys Rev C (2024) 109:035803. doi:10.1103/PhysRevC.109.035803

CrossRef Full Text | Google Scholar

126. Orce JN. Polarizability effects in atomic nuclei. Int J Mod Phys E (2020) 29:2030002. doi:10.1142/S0218301320300027

CrossRef Full Text | Google Scholar

127. Orce JN. New formulas for the (−2) moment of the photoabsorption cross section, σ₋₂. Phys Rev C (2015) 91:064602. doi:10.1103/PhysRevC.91.064602

CrossRef Full Text | Google Scholar

128. von Neumann-Cosel P. Comment on New formulas for the (−2) moment of the photoabsorption cross section, σ₋₂. Phys Rev C (2016) 93:049801. doi:10.1103/PhysRevC.93.049801

CrossRef Full Text | Google Scholar

129. Steiner A, Prakash M, Lattimer J, Ellis P. Isospin asymmetry in nuclei and neutron stars. Phys Rep (2005) 411:325–75. doi:10.1016/j.physrep.2005.02.004

CrossRef Full Text | Google Scholar

130. Tian J, Cui H, Zheng K, Wang N. Effect of Coulomb energy on the symmetry energy coefficients of finite nuclei. Phys Rev C (2014) 90:024313. doi:10.1103/PhysRevC.90.024313

CrossRef Full Text | Google Scholar

131. Centelles M, Roca-Maza X, Viñas X, Warda M. Nuclear symmetry energy probed by neutron skin thickness of nuclei. Phys Rev Lett (2009) 102:122502. doi:10.1103/PhysRevLett.102.122502

PubMed Abstract | CrossRef Full Text | Google Scholar

132. Schlimme S, Aulenbacher K, Baunack S, Berger N, Denig A, Doria L, et al. The MESA physics program. EPJ Web Conf (2024) 303:06002. doi:10.1051/epjconf/202430306002

CrossRef Full Text | Google Scholar

133 Gales S, Tanaka K, Balabanski D, Negoita F, Stutman D, Tesileanu O, et al. The extreme light infrastructure-nuclear physics (ELI-NP) facility: new horizons in physics with 10 PW ultra-intense lasers and 20 MeV brilliant gamma beams. Rep Prog Phys (2018) 81:094301. doi:10.1088/1361-6633/aacfe8

PubMed Abstract | CrossRef Full Text | Google Scholar

134. Tanaka KA, Spohr KM, Balabanski DL, Balascuta S, Capponi L, Cernaianu MO, et al. Current status and highlights of the ELI-NP research program. Matter Radiat Extremes (2020) 5:024402. doi:10.1063/1.5093535

CrossRef Full Text | Google Scholar

135. Wang H-W, Fan G-T, Liu L-X, Xu H-H, Shen W-Q, Ma Y-G, et al. Commissioning of laser electron gamma beamline SLEGS at SSRF. Nucl Sci Tech (2022) 33:87. doi:10.1007/s41365-022-01076-0

CrossRef Full Text | Google Scholar

136. Gheorghe I, Utsunomiya H, Stopani K, Filipescu D, Ari-izumi T, Belyshev S, et al. Updated neutron-multiplicity sorting method for producing photoneutron average energies and resolving multiple firing events. Nucl Instrum Methods A (2021) 1019:165867. doi:10.1016/j.nima.2021.165867

CrossRef Full Text | Google Scholar

137. Togano Y, Nakamura T, Kobayashi T, Aumann T, Baba H, Boretzky K, et al. Electric dipole strength of ⁵²Ca. Il Nuovo Cim C (2024) 47:30. doi:10.1393/ncc/i2024-24030-3

CrossRef Full Text | Google Scholar

138. Aumann T, Bertulani CA, Duer M, Galatyuk T, Obertelli A, Panin V, et al. Nuclear structure opportunities with GeV radioactive beams at FAIR. Phil Trans R Soc A (2024) 382:2275. doi:10.1098/rsta.2023.0121

PubMed Abstract | CrossRef Full Text | Google Scholar