Computing offloading in hierarchical aerial computing based on matching games

In unmanned aerial vehicle (UAV) networks, efficient and reliable cooperation among UAVs is crucial for enabling UAV-assisted internet of things (IoT) services. In this paper, we consider a hierarchical aerial computing framework composed of multiple UAVs that assume different network roles based on their capabilities, providing data collection and computation services for diverse IoT applications. We then formulate a task offloading problem subject to delay and resource constraints, taking into account the service revenue requirements and computational demands of different UAVs. The problem aims to meet the service demands of UAVs while satisfying multiple constraints related to task delay and resource availability, resulting in an integer programming problem that is challenging to solve. Considering the complexity of exhaustive search, we propose a matching game-based solution algorithm to obtain the optimal task offloading decision among UAVs and prove that the algorithm is stable. Simulation results show that the algorithm proposed in this paper outperforms the benchmark scheme in terms of service benefits.

1 Introduction

In recent years, Unmanned Aerial Vehicles (UAVs), due to their advantages such as low cost, high altitude, and ease of deployment [1], have been widely applied in various scenarios, such as Internet of vehicle [1] and marine IoT [2]. Depending on the service requirements of different network scenarios, UAVs can play various roles in the network [3]. UAVs can act as end-users and offload tasks to edge computing servers on the ground for computation [4]. A UAV can be equipped with an edge server to function as an airborne MEC server, assisting ground-based end devices with computation tasks [5]. The UAV can serve as an airborne relay node that transmits user tasks to terrestrial edge servers (?). The UAV can be used as a complement to the ground network to provide effective coverage in areas where the ground infrastructure is unavailable or overloaded.

Existing IoT devices usually have very limited computational power and cannot handle complex computational tasks [6]. UAVs can collect data in close proximity to sensors and help process it in a timely manner [7]. Especially in complex, harsh, or remote environments, UAVs serve as ideal tools for data collection. Meanwhile, edge computing brings computational resources closer to devices and helps relieve the computational burden on the network. By equipping UAVs with edge computing servers, IoT devices with limited computational power can offload their computationally intensive tasks to the UAVs, thereby reducing computational pressure and improving the overall performance of the network [8].

Considering that UAVs in a UAV network may have different capabilities, this can lead to a hierarchical structure. For example, UAVs with abundant computational resources can assist other UAVs in completing computational tasks. Additionally, due to individual differences among UAVs, they can play various roles in heterogeneous networks. Depending on the service requirements, UAVs can function as computation servers or data collection nodes. As a result, the service relationships among UAVs can directly impact the overall performance of the network. Therefore, this paper focuses on the computation offloading problem in hierarchical UAV networks.

A hierarchical aerial computing system consists of ground terminals and various types of vehicles, each with a different level of computational resources. In [9], the authors consider a hierarchical airborne computing framework that includes user devices, UAVs, and high-altitude platforms (HAP), and propose a deep reinforcement learning-based trajectory optimization and task offloading algorithm to maximize network resource utilization. In [10], the authors proposed an algorithm based on Multi-agent proximal policy optimization (MAPPO) to maximize the amount of computational tasks while satisfying the quality of service requirements, taking into account the limited resources and coverage of UAVs. In [11], a hierarchical framework based on the Stackelberg game was proposed to address the energy consumption problem of aerial computing networks from a distributed perspective. In [12], UAVs and HAPs are considered as aerial edge computing platforms. The authors consider the fixed coverage area of UAVs and propose a multi-agent deep deterministic policy gradient (MADDPG) algorithm for user association, partial offloading and communication resource allocation to maximize the IoT service satisfaction while minimizing their total energy consumption. In [8], the authors formulate a discrete Stackelberg game with multiple leaders and followers for a hierarchical multi-coalition UAV MEC network to achieve joint computational offloading for multiple UAVs. Although the above work investigates the computational offloading problem for airborne hierarchical computing, it ignores the service requirements of UAVs with different roles in the UAV network.

In this paper, we address the task offloading decision-making problem between UAVs by adopting a matching game approach. First, the task offloading problem is analyzed using matching theory and game theory, and a multi-objective optimization problem is formulated based on the benefits of each party. Second, the problem is modeled as a bilateral one-to-many matching game to analyze the interactions among UAVs. The construction of preference lists for each participant is a key step in solving the UAV-to-task matching problem, as the objective function and multiple constraints must be implicitly reflected in the preference lists. Additionally, since offloading decisions between UAVs may alter these preference lists, this phenomenon is referred to as an externality. Finally, to handle the challenge of dynamic preference lists, we propose stable matching algorithms that aim to achieve stable task-to-UAV assignments while balancing the interests of UAVs. Specifically, the main contributions of this paper are summarized as follows.

$•$ We propose a hierarchical computing offloading framework involving multiple UAVs and multiple tasks. In this computational framework, the benefits of each hierarchical UAV are not only considered, but also the service requirements of the computational tasks.

$•$ The optimization problem is modeled as a one-to-many matching game between a set of tasks and UAVs. Meanwhile, a task offloading algorithm based on bilateral matching is proposed, which can effectively realize the allocation of UAV computing tasks.

$•$ The effectiveness of the proposed algorithm is verified through simulations, and the performance of different algorithms is evaluated based on numerical results. In addition, the impact of system parameters, such as UAV computing power, on overall system performance is also analyzed.

The rest of the paper is organized as follows. The system model and problem formulation are given in Section 2. In Section 3, a matching game based solution method is proposed. Numerical simulations given in Section 4 validate the effectiveness of the proposed scheme. Finally, Section 5 concludes the paper.

2 System model and problem formulation

In this section, we introduce the network model, communication model, energy consumption model, UAV utility function and problem formulation. For a clear understanding of nations in this paper, their detailed descriptions are provided in Table 1.

Table 1

Table 1. Description of key notation.

2.1 Network model

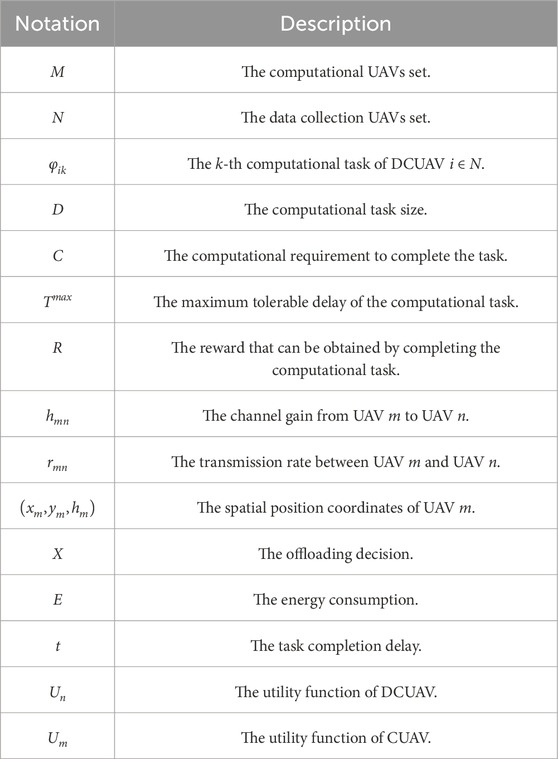
The network architecture of the multi-layer UAV-assisted edge computing system considered in this paper is shown in Figure 1, which consists of a top layer, an middle layer and a lower layer. The top layer consists of $M$ UAVs, which are represented by the set $M=\left\{\mathrm{1,2},\dots .,m\right\}$. The middle layer consists of $N$ UAVs, denoted by the set $N=\left\{\mathrm{1,2},\dots .,n\right\}$. The lower layer mainly consists of some ground terminal devices. In this hierarchical architecture, the terminal devices have no computing capability, and the UAVs in the middle layer are responsible for collecting data from terminals within their service coverage areas and dividing computing tasks based on the collected data. Additionally, the UAV in the top layer acts as a stable aerial base station. To facilitate the differentiation between the different spatial layers of UAVs, we define the UAVs located in the middle layer as data collection UAVs (DCUAVs) and the UAVs located in the top layer as computational UAVs (CUAVs), based on their functional characteristics. It is noted that rotary wing UAVs are considered in the scheme, which are able to perform services in the air in a hovering manner. Therefore, the hierarchical aerial computing model in this paper is considered quasi-static [13–15]. All UAVs are equipped with edge computing servers, and CUAVs have more load capacity than DCUAVs. The middle-layer UAVs can offload tasks to the top-layer UAVs to improve the efficiency of network services.

Figure 1

Figure 1. System model.

Let ${\phi }_{ik}=\left\{D,C,T^{\mathit{max}},R\right\}$ denote the $k$-th computational task of DCUAV $i\in N$, where $D$ denotes the computational task size, $C$ denotes the computational requirement to complete the task, $T^{\mathit{max}}$ denotes the maximum tolerable delay of the computational task, and $R$ denotes the reward that can be obtained by completing the computational task. We assume that the computing tasks of the UAVs are atomic, i.e., the tasks are not splittable. The DCUAV can offload the computing tasks to the CUAV to improve the computational efficiency. The computational power of a CUAV is logically divided into homogeneous virtual resource units (VRU), where each VRU has a computational power called $F$ [16]. For a CUAV, the number of the VRU, also known as its quota, is denoted by $q$. Consider the variability of UAV loads, so the number of VRUs and computational power may differ between UAVs. However, in the same CUAV, we consider that each VRU has the same computational power. Since a VRU can host a task, the maximum number of parallels of the CUAV regarding the task processing depends on $q$.

2.2 Communication model

This paper primarily focuses on the computation task processing of DCUAVs, while the data collection aspect is not the main subject of consideration. Therefore, only the communication between DCUAV and CUAV is considered in this paper. Considering the height and maneuverability of UAVs, it is reasonable to assume that the wireless link between UAVs and CUAVs mainly consists of Line-of-Sight (LoS) communication links [17–20]. Therefore, the channel gain from UAV $m$ to UAV $n$ can be expressed as

$h_{mn}=\frac{h_0}{{\left(H_m-H_n\right)}^2+{\left(x_m-x_n\right)}^2+{\left(y_m-y_n\right)}^2},(1)$

where $h_0$ denotes the channel gain at the reference distance for $1m$, and $\left(x_m,y_m,H_m\right)$ and $\left(x_n,y_n,H_n\right)$ denote the spatial position coordinates of UAV $m$ and UAV $n$, respectively. Similar to [21], the transmission rate between UAV $m$ and UAV $n$ can be expressed as

$r_{mn}=Blo{g}_2\left(1+\frac{p_n{h}_{mn}}{N_0}\right),m\in M,n\in N,(2)$

where $B_{mn}$ denotes the channel bandwidth between UAVs, $p_m$ denotes the transmission power of UAV $m$, and $N_0$ denotes the power noise.

2.3 Energy consumption model

In this paper, we define the energy consumption for completing a task computation from the perspective of a DCUAV and a CUAV, respectively. For each computing task, the DCUAV needs to decide whether to process the task locally or offload the task to a CUAV with idle computing resources for execution. The offloading decision is denoted by the binary variable $X_{\mathit{ikj}}\in \left\{\mathrm{0,1}\right\}$, where $i\in M$, $k\in K$, $j\in N$, where $X_{\mathit{ikj}}=1$ denotes that the DCUAV $i$ decided to offload its $k$-th task to the CUAV $j$, and conversely, $X=0$,denotes that the DCUAV chose to be computing locally. Each task can only be processed by one UAV or on a local device.

When the DCUAV chooses to process task $k$ locally, the energy consumption to accomplish the task computation mainly depends on the local computation energy consumption. The local computation energy consumption usually depends on the hardware performance (e.g., processor speed) of the UAV, the complexity of the task, etc. Here, we consider that different devices have different processing speeds, and the power consumption of the device processor is proportional to the speed. Therefore, the DCUAV local computational energy consumption is expressed as

$E_i^{\mathit{loc}}=\gamma C{f}_i^2,i\in N,(3)$

where $\gamma$ denotes the capacitance parameter of the DCUAV processor and $f_i$ denotes the local computing power of the DCUAV.

Similar to the DCUAV local computation, the computational energy consumption of CUAV can be expressed as

$E_j^c=\gamma C{F}^2,j\in M,(4)$

where $F$ denotes the computational power of the VRU in the CUAV.

When the DCUAV offloads the computing task $k$ to the CUAV, its energy consumption mainly consists of the DCUAV’s transmission energy and the CUAV’s computing energy. The energy consumption of UAV $i$ offloading task $k$ to UAV $j$ can be expressed as

$E_i^{\mathit{off}}=p_i\frac{D}{r_{ij}}+\gamma C{F}^2,i\in N,j\in M,(5)$

Based on the above analysis, the energy consumption of a DCUAV includes the computational energy consumption for locally executing a task, or the transmission energy consumption for offloading a task. Therefore, the energy consumption of the CDUAV with respect to task k can be expressed as

$e_{\mathit{ikj}}^{\mathit{task}}\left(X_{\mathit{ikj}},X_{-ikj}\right)=\left\{\begin{array}{cc}{X}_{\mathit{ik0}}{E}_{\mathit{ik0}}^{\mathit{loc}},\hfill & j=0\hfill \\ X_{\mathit{ikj}}{E}_{\mathit{ikj}}^{\mathit{off}},\hfill & j\in M\hfill \end{array}\right.(6)$

The total delay with respect to task $k$ can be expressed as

$t_{\mathit{ikj}}^{\mathit{task}}\left(X_{\mathit{ikj}},X_{-ikj}\right)=\left\{\begin{array}{cc}{X}_{\mathit{ik0}}\frac{C}{f_i},\hfill & j=0\hfill \\ X_{\mathit{ikj}}\left(\frac{D}{r_{ij}}+\frac{C}{F}\right),\hfill & j\in M\hfill \end{array}\right.(7)$

2.4 The UAV utility function

Based on the delay requirement $T$ of the computational task and the actual task completion delay $t$, consider the delay satisfaction of the computational task as a negative exponential curve [22], which can be expressed as

$\rho =\left\{\begin{array}{cc}1,\hfill & T⩾t\hfill \\ \frac{2}{9}+\frac{7}{9}{e}^{-0.3005\nu },\hfill & T<t\hfill \end{array}\right.(8)$

where $\nu =t_{-}T$. To ensure satisfactory task computation while minimizing the energy consumption of the DCUAV, we define the satisfactory utility function $U_n$ of the DCUAV as

$U_{n,m}=\lambda {\rho }_{n,m}-\xi E_{n,m}^{\mathit{off}},(9)$

where $\lambda$ and $\xi$ denote the delay and energy consumption weight factors, respectively. The values of $\lambda$ and $\xi$ depend on the type of computational tasks and business requirements. For delay-sensitive services, appropriately increasing $\lambda$ can guide the selection of CUAVs with sufficient computational resources, thereby improving delay satisfaction.

The benefit gained by a CUAV from performing task $k$ is defined as the difference between the task processing gain and the computational energy consumption, and can be expressed as

$U_{k,m}=R_k-\delta E_m^c,(10)$

where $\delta$ denotes the weighting factor for computing energy consumption.

2.5 Problem formulation

Based on the above analysis, the objective of DCUAV is to maximize its utility while considering the task delay constraints. Therefore, the optimization problem of DCUAV can be written as,

$\begin{array}{cc}\hfill & {\max }_X{U}_n\hfill \\ \hfill \text{s.t.}& C1:X_{\mathit{ikj}}\frac{C_{ik}}{f_i}+\left(1-X_{\mathit{ikj}}\right)\left(\frac{D_{ik}}{r_{\mathit{ikj}}}+\frac{C_{ik}}{F}\right)\le T_{ik}^{\max },\hfill \\ \hfill & C2:X_{\mathit{ikj}}\in \left\{\mathrm{0,1}\right\}\forall j\in M\cup \left\{0\right\},\hfill \\ \hfill & C3:{\displaystyle \sum _{j=0}^M}{X}_{\mathit{ikj}}\le 1,i\in N,\hfill \end{array}(11)$

where C1 denotes the delay constraint of the computing task, C2 denotes the task offloading policy constraint, and C3 denotes the selection of at most one UAV to be offloaded for each computing task.

The objective of CUAV is to maximize its utility while taking into account the computing service constraints. The optimization problem of CUAV can be written as,

$\begin{array}{cc}\hfill & {\max }_X{U}_m\hfill \\ \hfill \text{s.t.}& C1:{\displaystyle \sum _{i=1}^N}{\displaystyle \sum _{k=1}^K}{X}_{\mathit{ikj}}\le q_j,j\in M,\hfill \\ \hfill & C2:X_{\mathit{ikj}}\in \left\{\mathrm{0,1}\right\}\forall j\in M\cup \left\{0\right\},\hfill \\ \hfill & C3:{\displaystyle \sum _{j=0}^M}{X}_{\mathit{ikj}}=1,i\in N,\hfill \end{array}(12)$

where C1 denotes the constraint on the number of task loads for a CUAV, C2 denotes the constraint on task offloading, and C3 denotes that each computing task is allowed to offload to only one CUAV.

Our overall goal is to maximize the utility of both DCUAV and CUAV. Since the two optimization problems have the same solution under the same variables, they can be expressed as a joint optimization problem, denoted as

$\begin{array}{cc}\hfill & {\max }_X{U}_n\&{\max }_X{U}_m\hfill \\ \hfill \text{s.t.}& C1:X_{\mathit{ikj}}\frac{C_{ik}}{f_i}+\left(1-X_{\mathit{ikj}}\right)\left(\frac{D_{ik}}{r_{\mathit{ikj}}}+\frac{C_{ik}}{F}\right)\le T_{ik}^{\max },\hfill \\ \hfill & C2:{\displaystyle \sum _{i=1}^N}{\displaystyle \sum _{k=1}^K}{X}_{\mathit{ikj}}\le q_j,j\in M,\hfill \\ \hfill & C3:X_{\mathit{ikj}}\in \left\{\mathrm{0,1}\right\}\forall j\in M\cup \left\{0\right\},\hfill \\ \hfill & C4:{\displaystyle \sum _{j=0}^M}{X}_{\mathit{ikj}}=1,i\in N,\hfill \end{array}(13)$

The above optimization problem is an NP-hard problem, and the optimal solution can be found by searching all possible offloading decisions. To solve this problem efficiently with low complexity, a task offloading strategy based on matching game is proposed considering that the computing task of DCUAV is independent from CUAV.

3 The task offloading policy based on bidirectional matching

In this section, we first model the above task offloading problem as a bilateral one-to-many matching game. Then, the preference profiles of the players are considered and a matching algorithm is proposed to realize task offloading. Finally, the stability of the proposed algorithm is analyzed.

Based on matching game theory, UAVs can form several task alliances according to different objectives. In matching games, each participant can select the optimal matching object based on their own resource status (such as remaining computing power and battery capacity) and task attributes (such as computing power and delay sensitivity). At the same time, the matching game can also support distributed solutions in hierarchical air computing.

3.1 Matching game concepts

Let we transform the task offloading problem into a bilateral one-to-many matching game. In the matching game model, it is assumed that both DCUAVs and CUAVs are rational, self-interested participants who make matching decisions based on their personal preferences. To model the optimization problem as a one-to-many matching game with resource and delay constraints, we consider the set of tasks $\mathrm{\Gamma }=\left\{\mathrm{1,2},\dots ,n\right\}\times \left\{\mathrm{1,2},\dots ,K\right\}$, and the set of CUAVs $M=\left\{\mathrm{1,2},\dots m\right\}$ as the two sides of the participants. It is worth noting that bilateral matching denotes that a task is accepted by a given CUAV only if that CUAV recognizes that task. Next, we give the matching game definition as shown in the following definition.

Definition 1. In the scenario considered in this paper, the bilateral matching game is defined by a tuple $G\left(\mathrm{\Gamma },N,\succ \right)$, where $\mathrm{\Gamma }$ denotes the set of computational tasks, $N$ denotes the set of CUAVs and $\succ$ denotes the preference of a task (CUAV) with respect to a CUAV (task).

Definition 2. Given two disjoint sets $\mathrm{\Gamma }$ and $M$, a one-to-many matching function $\Phi$ is defined such that all $i$ and $j$ satisfy the following relationship:

$\begin{array}{cc}\hfill & \left.1\right)\Phi \left(\tau \right)\subseteq \left\{m\right\}and\Phi \left(\tau \right)\in \left\{\mathrm{0,1}\right\};\hfill \\ \hfill & \left.2\right)\Phi \left(m\right)\subseteq \left\{\tau \right\}and\Phi \left(\tau \right)\le q_m,\tau \in \mathrm{\Gamma },m\in M;\hfill \\ \hfill & \left.3\right)\Phi \left(\tau \right)=m\iff \Phi \left(m\right)=\tau ,\tau \in \mathrm{\Gamma },m\in M.\hfill \end{array}(14)$

In Definition 2, Condition 1 denotes that each computational task is offloaded onto at most one CUAV, Condition 2 denotes the maximum number of offloaded tasks that each CUAV can accept, which corresponds to C2 of Problem P3, and Condition 3 denotes that if a task $\tau \in \mathrm{\Gamma }$ matches a CUAV $n$, then the CUAV $n$ also matches to a task $\tau$. The output of the matching game as defined in this paper is the set of matching pairs between a task and a CUAV, i.e., $⟨\tau ,n⟩$.

3.2 Preference profiles of players

For each player, the preference profile is used to rank the other players. In the proposed game, tasks and CUAVs can construct their preference lists with available information [23], respectively.

Definition 3. The preference of each task for different CUAVs can be defined as

$P_{\tau }\left(m\right)=\lambda \rho +\xi \frac{1}{r_{m,\tau }},\tau \in \mathrm{\Gamma },(15)$

The preference function based on Definition 3 is designed to reduce the energy consumption and delay required to complete the tasks. Each task prefers to associate with a CUAV at the maximum transmission rate. Based on the preference function, the task prioritizes the CUAV with larger bandwidth, more computational resources, and closer proximity.

Definition 4. The preferences of each CUAV for different tasks can be defined as

$P_m\left(\tau \right)=R_{\tau }-\delta \frac{1}{C},m\in M,(16)$

For CUAV, computing tasks with low complexity can save its computational energy consumption. Meanwhile, tasks with high rewards can increase service revenue. Therefore, CUAV prefers tasks with high rewards and requiring fewer CPU cycles.

3.3 Algorithm design

The matching game-based task offloading algorithm is shown in Algorithm 1. In the beginning of the algorithm, all tasks are unmatched. First, each computing task constructs a preference list based on network information and sorts the list. Similarly, CUAV constructs their own preference list based on the network information and completes the sorting of the list. Then, the computing task selects the CUAV based on the preference list, and the CUAV selects the computing task based on the preference. Finally, the algorithm stops iterating until all tasks are matched.

Algorithm 1

Algorithm 1. Matching game-based task offloading algorithm.

3.4 Algorithm analysis

In this subsection, we analyze the stability of the proposed algorithm in a theoretical way to evaluate the principle and performance of the algorithm.

The goal of Algorithm 1 is to find a stable offloading decision making both parties satisfied, where stability is a key concept in matching theory [24]. In the stability of the algorithm, we first give the relevant definitions as follows.

Definition 5. In the matching mechanism, a pair $\left(\tau ,m\right),\tau \in \mathrm{\Gamma },m\in M$is defined as a blocking pair if and only if UAV $m$ strictly prefers task $\tau$ to at least one of its currently assigned tasks, and task $\tau$ strictly prefers UAV $m$ to at least one of its currently assigned UAVs.

Definition 6. A match $\phi$ is stable if there are no blocking pairs.

Theorem 1. The matching result obtained by Algorithm 1 is stable.

Proof: Assuming that the matches obtained by Algorithm 1 are unstable, there exists a pair of matching results $(v,e)$that prefer each other over the current match. Then there are two cases: 1) task $v$ never sends a match request to CUAV $e$, which means that task $v$ prefers the current match to CUAV $e$, which contradicts the hypothesis; and 2) task $v$ sends a match request to CUAV $e$, but it is rejected. This means that $e$ prefers its current match to $v$, which is contradictory to the hypothesis. Therefore, there exists no such pair of matching results $\left(v,e\right)$ and hence the matching obtained by the algorithm is stable. According to Definition 5, there is no blocking pair of matching results obtained by Algorithm 1. According to Definition 6, the matching results obtained by Algorithm 1 are stable.

4 Performance evaluation

4.1 Simulation settings

We consider that all UAVs are randomly distributed in an aerial target area of $2000m\times 2000m$, where DCUAVs fly at an altitude of $100m$ and CUAVs fly at an altitude of 200 m. Specifically, DCUAVs fly at a low altitude to collect data from their coverage area and generate the corresponding computational tasks, and CUAVs fly at a high altitude to provide computational services. The channel bandwidth between the UAVs is considered to be $20MHz$, and the transmit power is $0.5W$. The computing power of the DCUAV is uniformly set to $0.5GHz$, and that of the CUAV is sized at $\left[\mathrm{5,10}\right]$ GHz. The input data size D and the required CPU cycles $C$ of each computational task are uniformly distributed over $\left[\mathrm{1,3}\right]Mb$ and $\left[0.1,1\right]$ Gcycles, respectively. The default number of CUAVs is 4 with quota $\left[\mathrm{3,1,2,4}\right]$ and the number of tasks per DCUAV is 2.

In addition, to further evaluate the advantages of the models and algorithms designed in this paper, we use the following baseline task offloading algorithms for comparative analysis: 1) Randomized offloading (RO) strategy: this strategy randomly assigns tasks to CUAVs based on the number of computing tasks, offloading constraints, and the load constraints of CUAVs; 2) Greedy task utility (GTU) strategy: in this strategy, the computing task selects the node that maximizes the utility of the computing task for matching, i.e., the computing task selects the node with the highest utility according to Equation 9; 3) Greedy computational benefit (GCB) strategy: in this strategy, the CUAV selects the task with the largest computing gain for matching, i.e., the CUAV selects the computing task with the largest gain according to Equation 10.

4.2 Performance evaluation

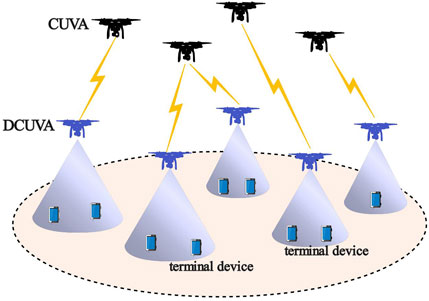
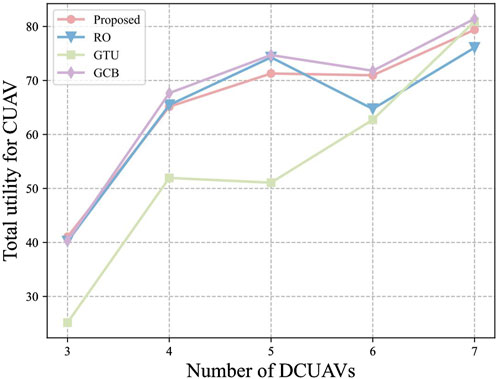
Figure 2 illustrates the trend of computing task utility with different number of DCUAVs. In Figure 2, the computing task utility increases with the increase with the number of DCUAVs. This is because as the number of DCUAVs increases, the number of computing tasks also increases gradually and thereby the total utility of computing tasks also increases. It can be observed that the algorithm proposed in this paper is able to achieve better computing task benefits as compared to other strategies. This is because the task offloading strategy based on the matching game considers the benefits of each computing task during the matching process and makes each computing task achieve better benefits under satisfied constraints. Figure 3 illustrates the trend of CUAV benefits under different numbers of CUAVs. In Figure 3, the overall benefit of CUAV increases with the number of DCUAVs. This is because as the number of DCUAVs increases, the number of computing tasks also increases gradually and the CUAV is able to provide computing services for more computing tasks. It can be observed that the algorithm proposed in this paper is able to achieve better CUAV benefits. This is because the algorithm optimizes the computational benefits of the CUAV. Meanwhile, the loss of total computational benefit is caused to balance the benefits between the objectives.

Figure 2

Figure 2. Total utility of computing tasks under different number of DCUAVs.

Figure 3

Figure 3. Total CUAV utility under different number of DCUAVs.

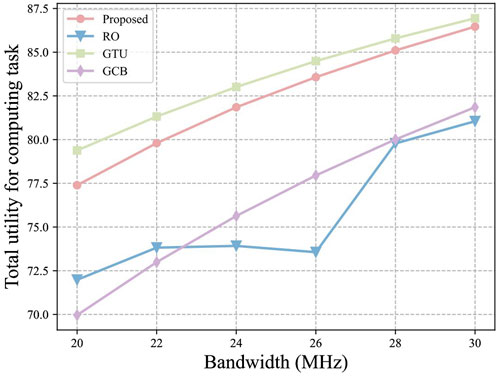
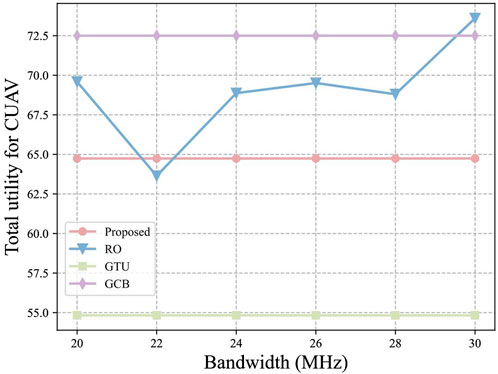
We analyze the effect of bandwidth size on the utility of computing tasks and the benefits of CUAVs, where the number of DCUAVs is considered to be 5. As shown in Figure 4, the total utility of the computing tasks increases as the bandwidth increases. This is because the increase in bandwidth increases the transmission rate between the UAVs, which reduces the transmission delay of the computing task. It can be observed that the algorithm proposed in this paper is able to achieve a higher utility for the computing tasks. The computing task utility of the algorithm proposed in this paper is lower than that of the GTU strategy because the benefit of the CUAV needs to be considered in the matching game process. From Figure 5, it can be seen that the benefit of CUAV is not affected by the size of bandwidth. This is that the increase in bandwidth does not change the task offloading strategy, so the CUAV benefit does not change. The CUAV benefit changes dynamically because the offloading strategy of RO strategy is randomized for each time.

Figure 4

Figure 4. Total utility of computing tasks under different bandwidth sizes.

Figure 5

Figure 5. Total CUAV utility under different bandwidth sizes.

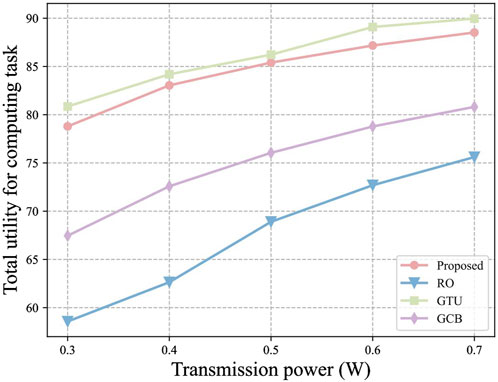
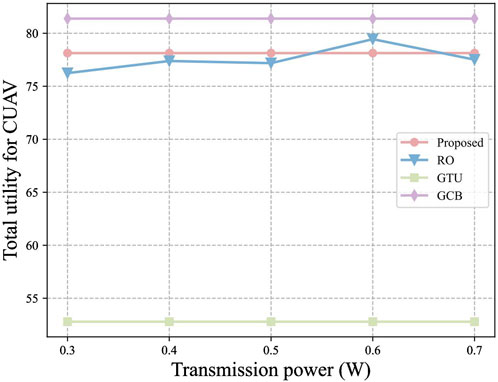
In addition, we analyze the effect of DCUAV transmission power on the computing task utility and CUAV benefits, where the number of DCUAVs is considered to be 5. As shown in Figure 6, the total utility of the computing task increases with the increase of DCUAV transmission power. This is because the increase in the DCUAV transmission power increases the transmission rate between the UAVs, which reduces the transmission delay of the computational task. It can be observed from Figure 7 that the CUAV benefits are not affected by the DCUAV transmission power. The DCUAV transmission power does not affect the task offloading strategy, so there is no change in the CUAV benefits. Meanwhile, the computing task benefit of the algorithm proposed in this paper is lower than that of the GCB strategy because the computing task utility needs to be considered in the matching game process.

Figure 6

Figure 6. Total utility of computing tasks under different transmission power sizes.

Figure 7

Figure 7. Total utility of computing tasks under different transmission power sizes.

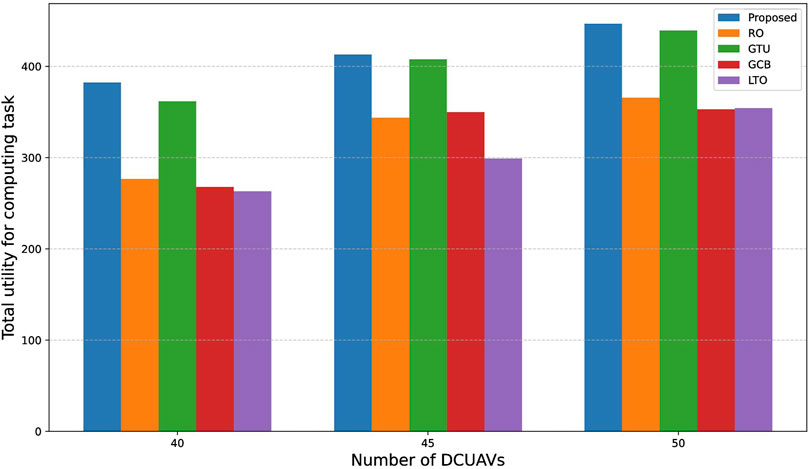
To further evaluate the performance of the proposed algorithm, we consider a large-scale UAV swarm scenario where each DCUAV is assigned a single computing task and the swarm consists of 10 CUAVs. In this scenario, a learning-based task offloading (LTO) algorithm with a $\epsilon$-greedy strategy is employed as the baseline for comparison [25].

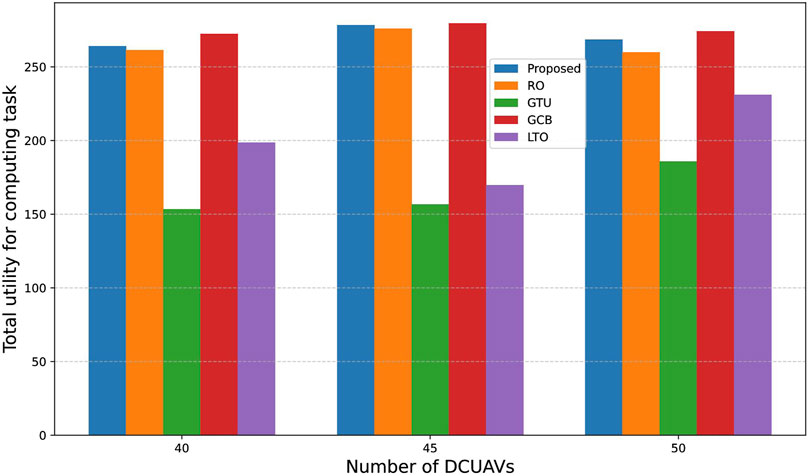
Figure 8 illustrates the utility of computational tasks for UAV clusters of different sizes. It can be seen that for UAV swarms of different sizes, significant differences exist in the total utility of computational tasks among the algorithms. Overall, the proposed algorithm consistently achieves the highest utility, and its advantage becomes more pronounced as the number of UAVs increases, demonstrating good scalability and stability. Figure 9 depicts the CUAV utility under different cluster sizes. The CUAV utility values obtained by all methods remain high and relatively stable as the number of drones increases. Compared to other methods, our proposed algorithm achieves higher CUAV utility, indicating superior task allocation and resource utilization. Based on the above analysis, the proposed algorithm demonstrates significant advantages in enhancing both the utility of drone swarm computing tasks and CUAV service utility, demonstrating its suitability for large-scale UAV swarm computing scenarios.

Figure 8

Figure 8. Total utility of computing tasks in UAV swarms of different sizes.

Figure 9

Figure 9. Total CUAV utility in UAV swarms of different sizes.

5 Conclusion

In this paper, we investigate hierarchical aerial computing systems, in which network services are provided to ground-based IoT devices through collaboration among UAVs. First, we propose a hierarchical computing offloading framework for multiple UAVs. To implement this framework, the task offloading process is modeled as a distributed multi-objective maximization problem. Second, we consider that the complexity of the task offloading problem increases with the problem size, making it difficult to find a feasible solution efficiently. To address this challenge and obtain a solution in polynomial time, the offloading problem is formulated as a one-to-many matching game between computational tasks and CUAVs. Subsequently, we propose a matching game-based task offloading algorithm and provide a rigorous theoretical analysis. Finally, to verify the performance of the proposed solution, we present a comparison with greedy and random strategies. Simulation results demonstrate the correctness and effectiveness of the proposed algorithm, particularly in delivering low-delay computing services for IoT applications in hierarchical aerial computing systems.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

ML: Writing – review and editing. TL: Writing – original draft, Writing – review and editing. JX: Writing – review and editing.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. This study was supported by Guangdong Basic and Applied Basic Research Foundation (NO.2024A1515110126).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Any alternative text (alt text) provided alongside figures in this article has been generated by Frontiers with the support of artificial intelligence and reasonable efforts have been made to ensure accuracy, including review by the authors wherever possible. If you identify any issues, please contact us.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Djigal H, Xu J, Liu L, Zhang Y. Machine and deep learning for resource allocation in multi-access edge computing: a survey. IEEE Commun Surv and Tutorials (2022) 24:2449–94. doi:10.1109/comst.2022.3199544

CrossRef Full Text | Google Scholar

2. Lyu T, Xu H, Liu F, Li M, Li L, Han Z. Computing offloading and resource allocation of noma-based uav emergency communication in marine internet of things. IEEE Internet Things J (2023) 11:15571–86. doi:10.1109/jiot.2023.3348164

CrossRef Full Text | Google Scholar

3. Kuang Z, Pan Y, Yang F, Zhang Y. Joint task offloading scheduling and resource allocation in air–ground cooperation uav-enabled mobile edge computing. IEEE Trans Vehicular Technology (2023) 73:5796–807. doi:10.1109/tvt.2023.3334143

CrossRef Full Text | Google Scholar

4. Shehzad MK, Ahmad A, Hassan SA, Jung H. Backhaul-aware intelligent positioning of uavs and association of terrestrial base stations for fronthaul connectivity. IEEE Trans Netw Sci Eng (2021) 8:2742–55. doi:10.1109/TNSE.2021.3077314

CrossRef Full Text | Google Scholar

5. Yang Z, Bi S, Zhang Y-JA. Dynamic offloading and trajectory control for uav-enabled mobile edge computing system with energy harvesting devices. IEEE Trans Wireless Commun (2022) 21:10515–28. doi:10.1109/twc.2022.3184953

CrossRef Full Text | Google Scholar

6. Zhao Z, Zhao R, Xia J, Lei X, Li D, Yuen C, et al. A novel framework of three-hierarchical offloading optimization for mec in industrial iot networks. IEEE Trans Ind Inform (2019) 16:5424–34. doi:10.1109/tii.2019.2949348

CrossRef Full Text | Google Scholar

7. Wei Z, Zhu M, Zhang N, Wang L, Zou Y, Meng Z, et al. Uav-assisted data collection for internet of things: a survey. IEEE Internet Things J (2022) 9:15460–83. doi:10.1109/jiot.2022.3176903

CrossRef Full Text | Google Scholar

8. Wu Q, Chen J, Xu Y, Qi N, Fang T, Sun Y, et al. Joint computation offloading, role, and location selection in hierarchical multicoalition uav mec networks: a stackelberg game learning approach. IEEE Internet Things J (2022) 9:18293–304. doi:10.1109/jiot.2022.3158489

CrossRef Full Text | Google Scholar

9. Hu Z, Yang Y, Gu W, Chen Y, Huang J. Drl-based trajectory optimization and task offloading in hierarchical aerial mec. IEEE Internet Things J (2024) 12:3410–23. doi:10.1109/jiot.2024.3480248

CrossRef Full Text | Google Scholar

10. Kang H, Chang X, Mišić J, Mišić VB, Fan J, Liu Y. Cooperative uav resource allocation and task offloading in hierarchical aerial computing systems: a mappo-based approach. IEEE Internet Things J (2023) 10:10497–509. doi:10.1109/jiot.2023.3240173

CrossRef Full Text | Google Scholar

11. Fang T, Chen J, Wu D, Yang W, Cai Y. When uav meets computing: stackelberg game-based hierarchical framework in aerial computing. IEEE Wireless Commun (2022) 29:116–22. doi:10.1109/mwc.002.2100253

CrossRef Full Text | Google Scholar

12. Lakew DS, Tran A-T, Dao N-N, Cho S. Intelligent offloading and resource allocation in heterogeneous aerial access iot networks. IEEE Internet Things J (2022) 10:5704–18. doi:10.1109/jiot.2022.3161571

CrossRef Full Text | Google Scholar

13. Jia Z, Wu Q, Dong C, Yuen C, Han Z. Hierarchical aerial computing for internet of things via cooperation of haps and uavs. IEEE Internet Things J (2022) 10:5676–88. doi:10.1109/jiot.2022.3151639

CrossRef Full Text | Google Scholar

14. Liu W, Xu Y, Wu D, Wang H, Chu X, Xu Y. Qoe-aware data aggregation in mec-enabled uav systems: a matching game approach. In: 2022 IEEE 8th international conference on computer and communications (ICCC). IEEE (2022). p. 725–30.

Google Scholar

15. Kim S. Hierarchical aerial offload computing algorithm based on the stackelberg-evolutionary game model. Computer Networks (2024) 245:110348. doi:10.1016/j.comnet.2024.110348

CrossRef Full Text | Google Scholar

16. Gu B, Zhou Z, Mumtaz S, Frascolla V, Bashir AK. Context-aware task offloading for multi-access edge computing: matching with externalities. In: 2018 IEEE global communications conference (GLOBECOM). IEEE (2018). p. 1–6.

CrossRef Full Text | Google Scholar

17. Liu Y, Xiong K, Ni Q, Fan P, Letaief KB. Uav-assisted wireless powered cooperative mobile edge computing: joint offloading, cpu control, and trajectory optimization. IEEE Internet Things J (2019) 7:2777–90. doi:10.1109/jiot.2019.2958975

CrossRef Full Text | Google Scholar

18. Zhou F, Wu Y, Hu RQ, Qian Y. Computation rate maximization in uav-enabled wireless-powered mobile-edge computing systems. IEEE J Selected Areas Commun (2018) 36:1927–41. doi:10.1109/jsac.2018.2864426

CrossRef Full Text | Google Scholar

19. Hu X, Wong K-K, Yang K, Zheng Z. Uav-assisted relaying and edge computing: scheduling and trajectory optimization. IEEE Trans Wireless Commun (2019) 18:4738–52. doi:10.1109/twc.2019.2928539

CrossRef Full Text | Google Scholar

20. Zheng G, Xu C, Wen M, Zhao X. Service caching based aerial cooperative computing and resource allocation in multi-uav enabled mec systems. IEEE Trans Vehicular Technology (2022) 71:10934–47. doi:10.1109/tvt.2022.3183577

CrossRef Full Text | Google Scholar

21. Wei Y, Wu S, Ji Z, Yu Z, Jiang C, Kuang L. Multi-uav collaborative edge computing algorithm for joint task offloading and channel resource allocation. J Commun Inf Networks (2024) 9:137–50. doi:10.23919/jcin.2024.10582826

CrossRef Full Text | Google Scholar

22. Li M, Wang X. Delay and rate satisfaction for data transmission with application in wireless communications. IEEE Netw (2015) 29:70–5. doi:10.1109/mnet.2015.7293308

CrossRef Full Text | Google Scholar

23. Swain C, Sahoo MN, Satpathy A, Muhammad K, Bakshi S, Rodrigues JJ, et al. Meto: matching-theory-based efficient task offloading in iot-fog interconnection networks. IEEE Internet Things J (2020) 8:12705–15. doi:10.1109/jiot.2020.3025631

CrossRef Full Text | Google Scholar

24. Bayat S, Li Y, Song L, Han Z. Matching theory: applications in wireless communications. IEEE Signal Process. Mag (2016) 33:103–22. doi:10.1109/msp.2016.2598848

CrossRef Full Text | Google Scholar

25. Huang J, Huang X, Lu Z, Xu J. Learning-based task-offloading for mobile edge computing with user mobility. In: 2023 9th international conference on computer and communications (ICCC). IEEE (2023). p. 860–4.

Google Scholar