Energy-saving retrofitting of traditional dwellings in the Hehuang region via multiobjective optimization

Introduction: Energy consumption and indoor thermal comfort are critical issues in building design, especially in regions with harsh climates. In rural areas, traditional dwellings face challenges in managing heating demands and maintaining comfort during winter. This study proposes a multi-objective optimization strategy to improve energy efficiency and thermal comfort in these buildings.

Methods: Using the Non-dominated Sorting Genetic Algorithm II (NSGA-II) and EnergyPlus simulations, the study optimizes key design parameters such as roof insulation, wall insulation, and window thermal transmittance.

Results: The findings highlight the importance of selecting appropriate insulation materials and their optimal thicknesses to balance energy savings and comfort. The results provide practical insights for energy-saving retrofits in cold, dry climates, offering a cost-effective and scientifically validated approach for enhancing building performance.

Discussion: As rural communities, including those in the Hehuang region, face increasing natural disasters, this research provides timely guidance for building designs that improve resilience and sustainability.

1 Introduction

In recent years, the high energy consumption of traditional rural residences has increasingly attracted widespread academic attention, especially in rural areas of China. As the stock of rural residential buildings continues to grow, reducing energy consumption and improving the living environment have become key issues in the construction of new rural areas. To address this issue, an increasing number of studies are exploring ways to improve energy efficiency and thermal comfort through building energy-saving retrofits. Lin et al. [1] studied the green retrofit of concrete brick apartments in Chengdu, emphasizing the necessity of energy-saving retrofits for old buildings and proposing the feasibility of improving building performance through green retrofitting. In order to further enhance energy-saving effects, Liu et al. [2] focused on energy-saving and ecological retrofits for buildings in cold regions, exploring specific measures to optimize building energy efficiency in low-temperature environments. Meanwhile, Magnier and Haghighat [3] proposed a multi-objective optimization method combining TRNSYS simulation, genetic algorithms, and artificial neural networks, providing more accurate decision support for energy-saving strategies during the building design phase. With the continuous development of building energy-saving technologies, more and more studies have focused on optimizing design methods and tools to improve energy efficiency in buildings. By developing different optimization methods and tools, researchers help building designers achieve energy-saving goals at the early design stage, such as the model and software-based energy-saving optimization methods proposed by Bayata and Temiz [4], the building façade energy-saving design optimization tool developed by Mostavi et al. [5], the integrated energy-saving optimization model using BIM dynamic simulation and multi-objective decision analysis developed by Liu et al. [6], the review of flexible building energy management methods by Pedram et al. [7], and the surrogate model-based multi-objective optimization method for energy-efficient building design proposed by Chen and Shi [8].

In recent years, many new methods and studies have been proposed to more effectively address the optimization of building energy efficiency and retrofitting, especially with technical solutions that integrate renewable energy sources like solar power. For instance, multi-objective optimization combining solar energy and desalination systems has been widely applied, with the optimized systems significantly improving the thermal comfort and energy utilization of buildings [9–11]. This series of studies has provided new perspectives on building energy-saving design and helped researchers explore more efficient and intelligent building design methods.

With the development of multi-objective optimization technologies, the direction of building energy-saving retrofits is becoming increasingly efficient, intelligent, and sustainable. Research has shown that by integrating solar desalting unit systems, building energy efficiency can be further optimized while improving comfort [12]. Furthermore, by optimizing design solutions, reducing heat loss, and maximizing solar energy utilization, this is crucial for energy-saving in modern buildings [13]. These achievements provide new optimization pathways for building design in terms of energy saving and environmental benefits, particularly when combining solar technology.

In addition, many mathematical models have begun to be used for optimizing design solutions, aiming to optimize building energy efficiency and comfort through precise analysis. For example, optimizing solar distillation systems through precise mathematical analysis can minimize building energy consumption while enhancing comfort and efficiency [14]. This study provides more detailed and scientific theoretical support for building energy-saving and comfort optimization.

To address the optimization issues of building energy-saving and retrofitting, many studies in recent years have proposed multi-objective optimization algorithms as effective solutions. Liang and Jing [15] evaluated the thermal insulation performance of building façades using multi-objective optimization algorithms to optimize building energy efficiency. Liu et al. [16] applied intelligent algorithms to the multi-objective optimization of modern building heritage, balancing the relationship between building preservation and energy efficiency. Luo et al. [17] used a hybrid particle swarm optimization algorithm to optimize multiple objectives in building design, further improving the comprehensive performance of building designs. Laili et al. [18] achieved significant optimization effects in multi-objective workflow scheduling using deep-Q-network-based multi-agent reinforcement learning. In the process of building energy-saving retrofitting, finding the best balance between energy efficiency, economics, and comfort has always been a challenge. Therefore, advanced optimization technologies, such as multi-objective optimization methods, have become key tools for improving energy-saving effects. These include methods such as MOEA/D-GEK [19], hull shape multi-objective optimization [20], preference-based multi-objective evolutionary algorithms [21], continuous Hopfield neural network algorithms [22], and reliability-based multi-objective optimization methods [23]. These research results show that with the development of multi-objective optimization technologies, building energy-saving retrofits are moving towards more efficient, intelligent, and sustainable directions.

In the field of building energy-saving and retrofitting, optimization methods have been widely applied in the design and retrofit phases, especially in improving energy efficiency and comfort. Alanani et al. [24] proposed a multi-objective optimization method that demonstrated its potential in structural design by analyzing the structural layout of high-rise buildings under dynamic wind loads. Alghamdi et al. [25] showed that optimizing the design parameters of higher education buildings not only significantly improves energy efficiency but also enhances comfort. Allmendinger et al. [26] emphasized the broad prospects of multi-objective optimization methods in building energy-saving design. Asadi et al. [27] developed the RETROSIM model optimization tool, which provides decision support for improving energy efficiency in building retrofits, further verifying the importance of optimization decision-making in retrofit projects. Overall, these studies demonstrate that multi-objective optimization methods play an important role in building energy-saving and retrofitting, effectively improving energy efficiency and comfort.

It is worth noting that in the research on building energy-saving and comfort improvement, multi-objective optimization methods are widely applied, especially in the design and retrofitting phases. Chen et al. [28] further explored an evolution-based bi-level optimization method for multi-objective transformations, promoting the application of multi-objective optimization in building design and improving energy-saving performance. In building energy efficiency optimization, Carli et al. [29] proposed a decision optimization method specifically for improving building energy efficiency, providing actionable decision support for building retrofit projects. Bignon et al. [30] proposed the DMulti-MADS method, a grid adaptive direct multi-search method that effectively addresses multi-objective problems in building energy-saving design, offering new technological solutions for achieving optimal design. Borcsok et al. [31] applied multi-objective optimization methods to solve the thermal energy supply problems in Budapest’s residential sector, optimizing energy supply and demand to enhance energy efficiency. Boron [32] explored how to use time criteria and utility functions for comprehensive analysis in multi-objective optimization, providing theoretical support for balancing multiple objectives in building design. The research on building energy-saving and comfort optimization shows that multi-objective optimization methods have broad applications in building design, retrofitting, and energy efficiency enhancement. These methods can not only optimize building energy efficiency but also improve building comfort and sustainability [4, 33, 34].

With the development of building energy-saving technologies, more and more research is focusing on how to achieve maximum building energy efficiency through multi-objective optimization algorithms. Multi-objective optimization involves balancing not only energy consumption reduction but also thermal comfort, building cost, and environmental impact. For example, Liu et al. [35] demonstrated that by combining Building Information Modeling (BIM) and multi-objective optimization algorithms, energy consumption can be optimized in the design stage, while also improving the environmental friendliness and user comfort of buildings. Additionally, Kapoor and Singhal [36] explored the impact of innovative insulation materials on the thermal efficiency of residential building façades, noting that the selection of efficient insulation materials could significantly reduce building energy consumption and carbon emissions, thus promoting the green transformation of buildings. To further enhance the effectiveness of building energy-saving retrofits, Karytsas and Theodoropoulou [37] proposed a home energy retrofitting scheme based on incentive mechanisms, which not only promotes the widespread adoption of energy-saving technologies but also accelerates the green transformation of the construction industry.

With the development of building energy-saving technologies, multi-objective optimization methods have become important tools for improving building energy efficiency, comfort, and environmental impact. Several studies have shown that building designs based on computational intelligence and multi-objective optimization can achieve a good balance between energy consumption, environmental benefits, and costs. For example, Karatas and El-Rayes [38] found that multi-objective optimization for residential building façade design can balance environmental benefits and construction costs, effectively reducing energy consumption. Furthermore, with the development of intelligent building materials, the application of nanotechnology and innovative insulation materials has further improved building energy efficiency and comfort. Kumari and Yadav [39] pointed out that nano-engineered building materials can significantly reduce energy consumption and enhance a building’s environmental adaptability and comfort. Through these optimization methods, building design can not only achieve energy-saving effects but also lay the foundation for long-term sustainable development, providing strong support for achieving green building goals [40–45].

While much of the existing literature on energy-efficient retrofitting has focused on urbanized or well-established regions, the Hehuang region, as a representative of cold-dry, rural plateau areas, presents unique challenges and opportunities for optimizing energy use and thermal comfort in vernacular architecture. This region, characterized by its distinct climatic conditions and traditional building techniques, underscores the necessity for context-specific retrofitting strategies. Although previous studies have provided valuable insights into architectural design and cultural preservation, fewer have addressed the integrated effects of thermal comfort and energy consumption, particularly in regions with limited research, such as Hehuang. Furthermore, quantitative analyses in this domain remain sparse.

This study aims to address these gaps by proposing optimized building envelope design parameters tailored to the traditional dwellings of Hehuang. Utilizing a multi-objective genetic algorithm, it identifies Pareto-optimal solutions and develops customized retrofitting strategies that balance energy efficiency and thermal comfort. The results offer important insights for energy-saving interventions in Hehuang and similar plateau regions, providing a scientific foundation for future retrofitting efforts in climates with comparable environmental challenges.

2 Research methods and models

2.1 Multi-objective optimization method and definition of objective functions

The multi-objective optimization method is renowned for its ability to effectively handle multiple conflicting objective functions, providing a set of optimal solutions for engineering and scientific problems. A key characteristic of multi-objective optimization lies in its use of the Pareto optimality concept. Instead of searching for a single optimal solution, it generates a set of solutions, each balancing the trade-offs across different objectives. This approach is well-suited for complex decision-making problems, such as energy-efficient building design, which involves multiple goals like cost, efficiency, and environmental impact. By employing heuristic and meta-heuristic algorithms such as genetic algorithms and particle swarm optimization, multi-objective optimization efficiently explores the solution space while ensuring solution diversity and comprehensiveness. Furthermore, this method emphasizes solution interpretability and decision-makers’ preferences, making it highly adaptable and practical in real-world applications.

In this study, the objective is to simultaneously minimize the annual discomfort hours of the indoor thermal environment and the energy consumption for heating. To achieve this, the following two objective functions are defined:

The first objective function $f_1\left(x\right)$ represents the total annual hours of thermal discomfort in the indoor environment. Specifically, it calculates the total duration in hours throughout the year during which the indoor temperature falls outside the comfortable range. It can be formally expressed as in Equation 1:

$\mathit{min}{f}_1\left(x\right)=t={\displaystyle \sum _{t=1}^{8760}}Ú\left(T_{in}\left(t,x\right)<T_{\mathit{min}}or{T}_{in}\left(t,x\right)>T_{\mathit{max}}\right)(1)$

• ${T_i}_n\left(t,x\right)$ is the indoor temperature at time t, which depends on the design parameters of the building envelope (e.g., wall insulation thickness, window thermal transmittance, etc.).

• $T_{\mathit{min}}$ and $T_{\mathit{max}}$ are the lower and upper limits of the comfort temperature range, respectively.

• $Ú\left(·\right)$ is an indicator function, which equals 1 when the condition inside the parentheses is true., when the comfort requirements are not met and 0 otherwise.

• 8760 represents the total number of hours in a year.

The second objective function $f_2\left(x\right)$ represents the total annual heating energy consumption. It is calculated based on the heat loss through the building envelope, solar radiation gain, and internal heat gain. The specific formula is as follows in Equation 2:

$\mathit{min}{f}_2\left(x\right)=t={\displaystyle \sum _{t=1}^{8760}}\left(Q_{loss}\left(t,x\right)-Q_{solar}\left(t\right)-Q_{internal}\left(t\right)\right)·{\eta }^{-1}(2)$

• $Q_{loss}\left(t,x\right)$: Represents the heat loss through the building envelope at time t, which depends on design parameters such as insulation thickness, window thermal transmittance, and overall envelope performance.

• $Q_{solar}\left(t\right)$: Denotes the solar radiation heat gain at time t, which can effectively reduce the heating demand by providing natural thermal energy.

• $Q_{internal}\left(t\right)$: Refers to the internal heat gain generated by occupants, appliances, and indoor equipment at time t, contributing to the indoor temperature.

• $\eta$: Represents the efficiency factor of the heating equipment, indicating the energy conversion efficiency of the system.

By integrating these two objective functions, the multi-objective optimization problem in this study can be formulated as in Equation 3:

$\mathit{min}\left\{f_1\left(x\right),f_2\left(x\right)\right\}=\min \left\{{\displaystyle \sum _{t=1}^{8760}}Ú\left(T_{in}\left(t,x\right)<T_{\mathit{min}}or{T}_{in}\left(t,x\right)>T_{\mathit{max}}\right),{\displaystyle \sum _{t=1}^{8760}}\left(Q_{loss}\left(t,x\right)-Q_{solar}\left(t\right)-Q_{internal}\left(t\right)\right)·{\eta }^{-1}\right\}(3)$

In the optimisation we explicitly consider six practical envelope parameters that dominate energy use and comfort in Hehuang’s traditional houses: roof-insulation thickness 5–9 cm, external-wall insulation thickness 7–11 cm, window thermal transmittance 3.5–4.0 Wm⁻² K⁻¹, glazing solar heat-gain coefficient 0.65–0.75, air-change rate 2.5–3.3 h⁻¹, and insulation material (EPS with λ ≈ 0.036 Wm⁻¹ K⁻¹ or XPS with λ ≈ 0.029 Wm⁻¹ K⁻¹). These ranges come from field surveys, the national code GB 50176-2016 and current product catalogues. Every candidate solution fed into the NSGA-II algorithm is simply one unique combination of those six items, after which EnergyPlus returns its annual heating demand and hours outside the comfort band; the genetic search then weighs the trade-off between the two outcomes.

2.2 Model calibration and research analysis

2.2.1 Field investigation and data collection

To thoroughly evaluate the energy-saving retrofitting effects of traditional dwellings in the Hehuang region, this study selected a typical brick-wood structure dwelling built in 2003 as the research subject. The building is oriented north-south, with a total floor area of 201 square meters and a courtyard area of 209 square meters, featuring good natural ventilation and insulation characteristics, providing an ideal setting for evaluating energy-saving retrofitting strategies. The building’s envelope during the testing period included walls insulated with a straw-mud composite material (brick wall thickness: 0.3 m; thermal conductivity: 1.15 W/(m·K)) and a roof insulation layer with a thickness of 300 mm. The building floor plan is shown in Figure 1.

Figure 1

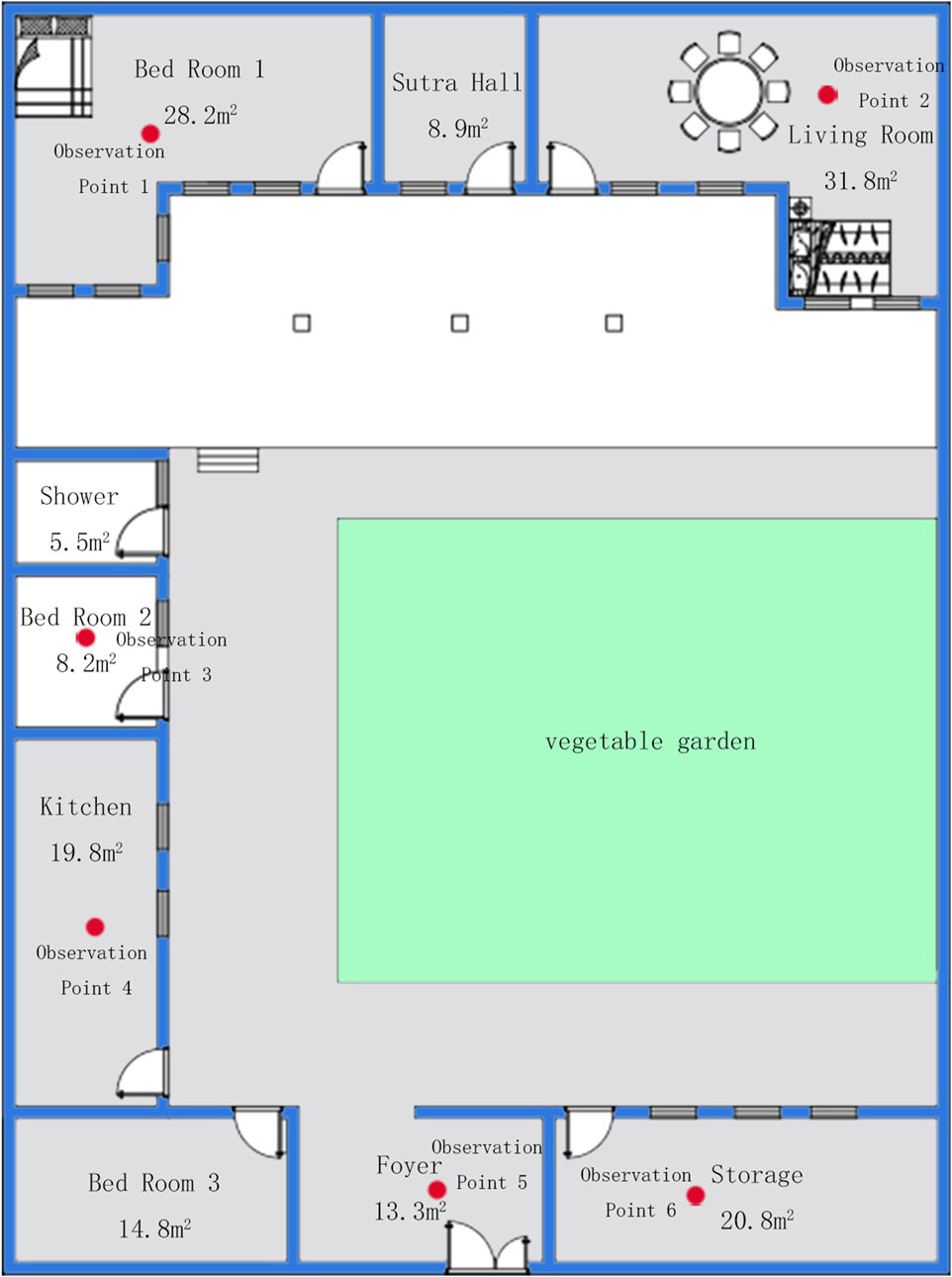
Figure 1. Layout of temperature survey observation points in a typical brick-wood structure residence in the Hehuang region.

To accurately simulate the indoor thermal environment and its response to external climatic conditions, six temperature observation points were set up indoors. These observation points were strategically distributed across different functional areas of the dwelling, including the bedroom, living room, kitchen, and storage room. This distribution was designed to capture temperature variations across different spaces, ensuring that reliable baseline data would be collected for subsequent model calibration and optimization.

During the preliminary testing phase, the experiment was conducted continuously for 48 h, with data recorded at 10-min intervals. These short-term measurements provided a calibration foundation for broader annual energy consumption simulations and multi-objective optimization analyses. Data points such as indoor temperature were carefully tracked to understand the impact of the building’s insulation performance and the external climate on heating demand.

The experiment was designed to calibrate the simulation model, ensuring that the results of the proposed energy-saving retrofitting solutions were scientifically valid and applicable. All collected data were cross-verified with simulation results, and any discrepancies were adjusted for through iterative refinements. This calibration ensured the reliability of the model in representing real-world thermal performance.

2.2.2 Model calibration and validation

To ensure the accuracy of the proposed optimization model and EnergyPlus simulation results, this study used a 24-h temperature dataset from October 8, 2023, 14:00, to October 9, 2023, 14:00, comparing the measured indoor temperatures with the simulation results. This method validated the model’s consistency with actual conditions, increasing the reliability of the study’s results. The results indicated that the measured average temperature in Bedroom 1 was 19.0°C, while the simulated temperature was 18.75°C. For Bedroom 2, the measured temperature was 15.8°C, and the simulated temperature was 15.5°C. In the living room, the measured temperature was 17.88°C, and the simulated temperature was 17.5°C. The trends in the measured and simulated temperatures were generally consistent, confirming the accuracy of the EnergyPlus simulation.

Based on the field test results, it was observed that the insulation performance of the current building during autumn and winter is relatively poor, particularly during nighttime and early morning, when indoor temperatures are significantly lower. To address this issue, the NSGA-II multi-objective optimization algorithm and EnergyPlus simulations were applied to optimize parameters including roof insulation, exterior wall insulation, window thermal transmittance, solar heat gain coefficient, and ventilation rate. The optimization objectives were to reduce annual discomfort hours and winter heating energy consumption. Through the careful selection of insulation materials and the optimization of ventilation strategies, the study aims to significantly lower energy consumption while improving indoor comfort.

To ensure the reliability of the EnergyPlus model, calibration was performed using the field test data. By analyzing indoor and outdoor temperature and humidity data, adjustments were made to parameters such as the thermal transmittance of the roof and exterior walls, window thermal transmittance, and ventilation rate to better align the simulation results with actual conditions. The final calibrated parameters were as follows:

• Roof insulation thickness: 0.08 m

• Exterior wall insulation: a 2 cm layer of expanded polystyrene (EPS) insulation combined with a 20 cm brick wall

• Window thermal transmittance: 3.7 W/m²·K

• Ventilation rate: 3 air changes per hour

After multiple iterations, the calibrated model achieved an error margin of within ±1°C, fully validating its reliability for analyzing the thermal performance of buildings under the climatic conditions of the Hehuang region. This robust calibration provides a solid foundation for subsequent optimization analyses.

2.2.3 Instrument specifications and accuracy

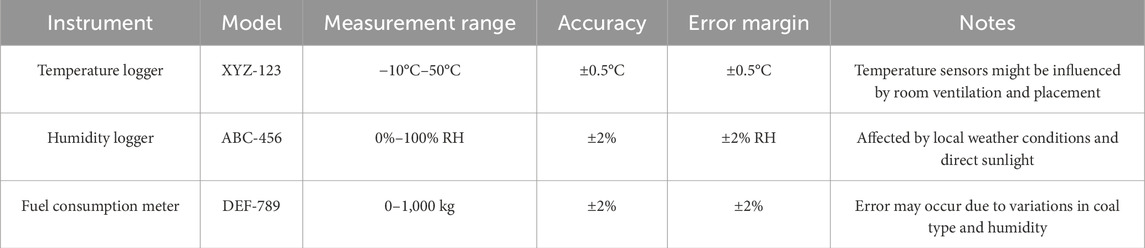
To ensure the reliability of the measured data, high-precision instruments were used in this study for temperature, humidity, and energy consumption measurements. The specifications, limitations, and possible sources of error for each instrument are summarized in Table 1.

Table 1

Table 1. Instrument specifications and measurement accuracy.

The temperature and humidity loggers used in this study have a typical error margin of ±0.5°C for temperature and ±2% RH for humidity. These errors can be influenced by external factors such as ventilation, sunlight exposure, and sensor calibration. Additionally, the fuel consumption meter, which measures coal consumption, has an error margin of ±2%, which could be influenced by the type of coal and environmental conditions. However, these errors are within the acceptable range and are considered negligible in the overall analysis.

2.3 NSGA-II optimization process

In the multi-objective optimization process, the Non-dominated Sorting Genetic Algorithm II (NSGA-II) was employed. This algorithm is capable of handling multiple conflicting objectives and was therefore used to optimize the design of building envelopes. First, design parameters were encoded as genes to generate a population of chromosomes representing different envelope design schemes. The design parameters include roof insulation thickness, wall insulation thickness, window U-value, solar heat gain coefficient, and ventilation rate. These parameters were carefully selected to reflect the most important factors influencing energy consumption and thermal comfort.

Next, the NSGA-II algorithm was implemented using Python, in conjunction with EnergyPlus software, to simulate the energy consumption and thermal environment performance of each design, with a particular focus on winter heating energy consumption. The simulation process incorporated both internal heat gains (e.g., from occupants and appliances) and external factors (e.g., solar radiation and weather data). Each design solution was evaluated based on its ability to balance heating demand and discomfort hours.

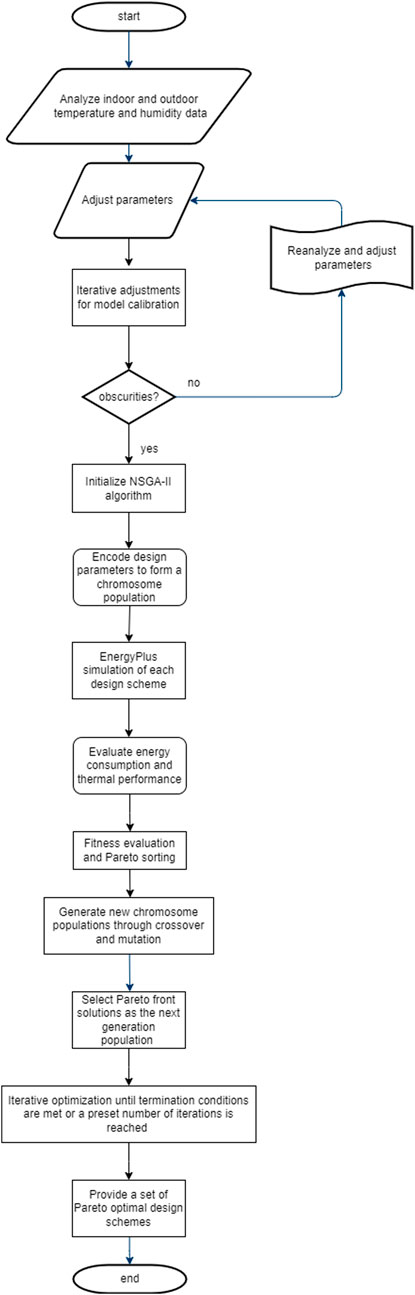
As illustrated in Figure 2, the entire NSGA-II optimization process includes data collection and analysis, model calibration, chromosome generation, crossover and mutation operations, fitness calculation, and the final output of the Pareto-optimal solutions. The optimization process was repeated over multiple generations, with each new population of solutions being evaluated and refined until a set of non-dominated solutions was identified. These Pareto-optimal solutions represent the best trade-offs between conflicting objectives, offering a range of design options for decision-makers.

Figure 2

Figure 2. NSGA-II-based multi-objective optimization flowchart.

In each generation of design schemes, new chromosome populations were generated through crossover and mutation operations. EnergyPlus calculated the fitness of each chromosome based on the simulation results. Subsequently, Pareto sorting was used to identify non-dominated solutions. After multiple iterations, the solutions on the Pareto front were used as the basis for the next-generation until the termination criteria were met or the predefined number of iterations was reached. Ultimately, the optimization results yielded a set of Pareto-optimal design solutions, showcasing balanced performance in improving thermal comfort, reducing energy consumption, and minimizing CO₂ emissions. This provides a scientific basis for decision-making in the design of building envelopes for traditional dwellings in the Hehuang region, demonstrating the effectiveness of considering both energy efficiency and environmental impact during the design process.

In identifying the Pareto front, the algorithm compares the dominance relationships between solutions to identify those that are not dominated by any other solutions. These solutions collectively form the Pareto front, representing the trade-offs between competing objectives.

3 Measurement study design and implementation

3.1 Comparative study of measured and simulated energy consumption

The Hehuang region is characterized by a temperate semi-arid continental climate with distinct plateau features. Summer temperatures are relatively low, with the average temperature in July (the hottest month) ranging from 14.2°C to 19.8°C and maximum temperatures between 21°C and 27°C. Consequently, additional cooling systems are not required during summer, and the focus of energy-saving design is primarily on addressing winter heating demands and improving indoor thermal comfort.

This study collected temperature and humidity data, as well as heating equipment energy consumption, across functional zones of the dwelling during typical winter months. To scientifically validate the effectiveness of the optimized design, high-precision temperature and humidity loggers and fuel consumption recording devices were used to collect data every 10 min, dynamically capturing variations in indoor and outdoor thermal environments and heating energy consumption characteristics. The measured data were then compared with simulation results, and error analysis was conducted to evaluate the accuracy of the simulation results. This process verifies the validity and feasibility of the multi-objective optimization strategy, providing a scientific basis for energy-saving designs in traditional dwellings of the Hehuang region.

To assess the reliability of the simulation model and the measured data, an uncertainty analysis was performed, considering both the inherent uncertainties in the measurement process and the model’s input parameters. For instance, variability in the indoor temperature measurements, caused by sensor inaccuracies or fluctuations in occupant behavior, could contribute to the discrepancies observed between the measured and simulated results. Additionally, uncertainties related to the heating system’s thermal efficiency, coal consumption, and local climatic conditions were taken into account during the comparison. To quantify the impact of these uncertainties, a sensitivity analysis was conducted on key parameters, such as thermal transmittance, ventilation rates, and heating system efficiency. The results showed that while the trends in the measured and simulated data were generally consistent, certain variations in the heating system’s performance and the external weather conditions could explain some of the observed differences.

The winter climate in the Hehuang region is harsh, with minimum temperatures often reaching as low as −10°C. Residents traditionally rely on coal, firewood, or cow dung for heating. During the heating season, this study measured the coal consumption of the selected dwelling and converted it into heating energy consumption data for comparison with EnergyPlus simulation results. The total energy consumption during the heating season, EEE, is calculated using the following formula:

$E=Q\times H\times \eta (4)$

• E: Total heating energy consumption (unit: GJ).

• Q: Coal consumption (unit: kg), obtained from measurements.

• H: Heating value of coal (unit: MJ/kg), typically ranging from 20 to 30 MJ/kg for local coal.

• $\eta$: Thermal efficiency of the heating system, with an average value of approximately 70%

Figure 3 illustrates the comparison between measured and simulated daily energy consumption during the heating season. The measured daily energy consumption (black curve) fluctuates around 1.0 GJ, occasionally exceeding 1.2 GJ on certain days. In contrast, the simulated daily energy consumption (red curve) is more stable, consistently ranging between 0.8 GJ and 1.0 GJ.

Figure 3

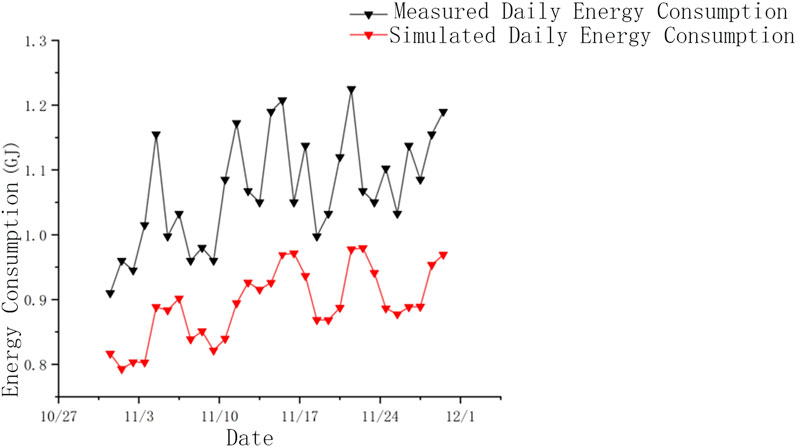
Figure 3. Comparison of measured and simulated daily energy consumption during the heating season. The comparison between measured and simulated daily energy consumption, showing fluctuations in the measured data and stable simulation results.

Overall, the measured data exhibit greater variability, indicating that actual energy consumption is significantly influenced by external factors such as weather changes or user behavior. Meanwhile, the simulation results remain relatively stable, reflecting the model’s ability to control variables effectively. Despite some discrepancies, the trends of the measured and simulated data are generally consistent, demonstrating that the model provides reliable predictions of energy consumption.

3.2 Annual thermal comfort evaluation and model validation

To comprehensively evaluate the thermal comfort performance of the optimized design across all seasons, this study extended indoor temperature data collection beyond the heating season (winter) to include spring, summer, and autumn, thereby covering the annual indoor thermal comfort conditions. For each season, temperature measurements were conducted on typical days across all functional areas and compared with EnergyPlus simulation results.

The annual data indicate that indoor temperatures during winter ranged from 12.1°C to 19.0°C, with the discrepancies between measured and simulated results controlled within ±1°C. This demonstrates that the optimized design significantly improved winter thermal comfort. For spring and autumn, the indoor temperatures on typical days were maintained between 15.3°C and 19.7°C, within the comfort range, validating the effectiveness of the optimized design during transitional seasons.

In summer, when outdoor average temperatures ranged from 14.2°C to 19.8°C, no additional cooling was required to maintain comfortable conditions. Both measured and simulated data indicated indoor temperatures ranging from 17.8°C to 20.5°C, confirming that the optimized design naturally sustained thermal comfort during summer.

Figure 4 presents the typical daily indoor temperature variation curves for different seasons throughout the year. The curves show that the simulation data closely align with the measured temperature variations, further validating the reliability of the optimization strategy across all seasons. This consistency underscores the robustness of the design in enhancing thermal comfort and its adaptability to varying seasonal conditions.

Figure 4

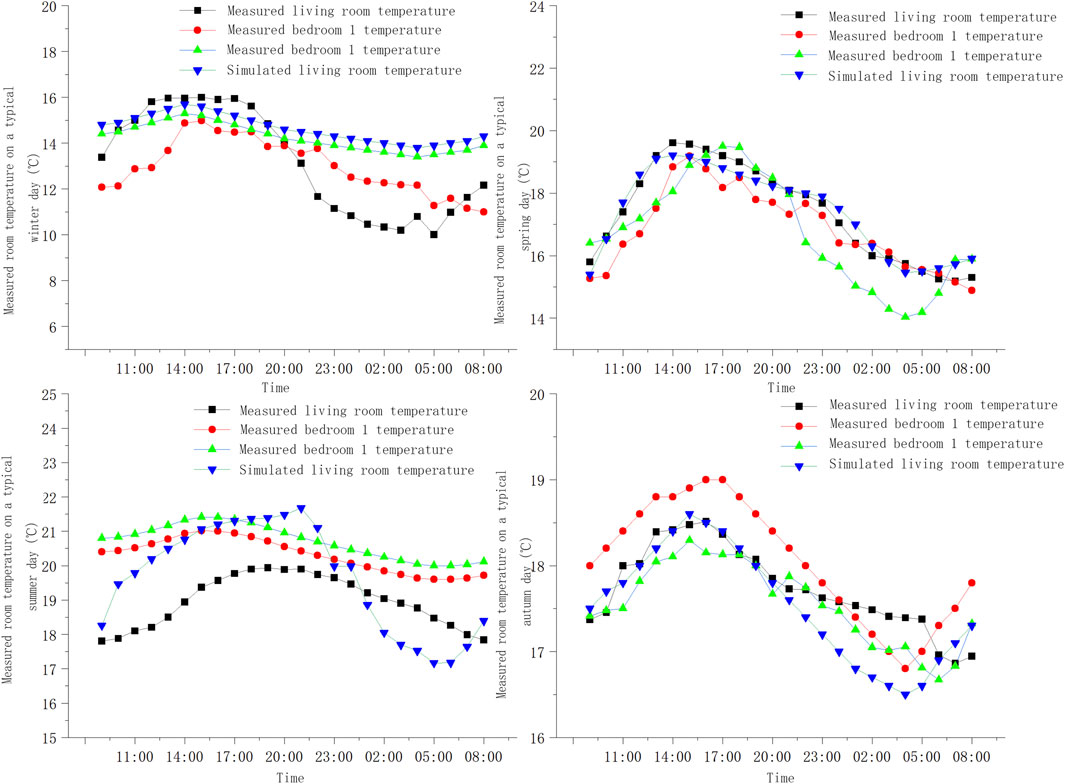
Figure 4. Indoor temperature variation curves on typical days in different seasons. Indoor temperature variations across seasons, demonstrating the effectiveness of the optimized design in maintaining comfort.

4 Optimization results and analysis

4.1 Multi-objective optimization results presentation

4.1.1 Pareto optimization analysis of heating demand and comfort

Figure 5 illustrates the baseline wall structure used for the initial energy consumption simulation and comparative analysis in multi-objective optimization. The exterior wall consists of a 2 cm thick expanded polystyrene (EPS) insulation layer, a 20 cm thick brick wall, and inner and outer plaster layers of 2.5 cm each. This baseline configuration serves as the reference scenario for evaluating the performance improvements of optimized designs.

Figure 5

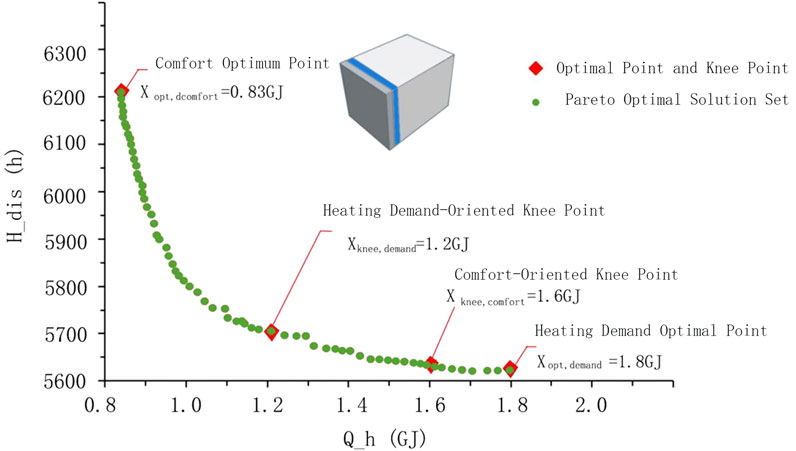
Figure 5. Pareto optimal solution set and key knee points for heating demand and discomfort hours. The Pareto front showing trade-offs between heating demand and discomfort hours, with knee points representing balanced solutions.

Compared to the baseline scenario, the optimized solutions demonstrate significant enhancements in terms of insulation thickness and material selection. The Pareto front, derived from the optimization process, highlights the trade-offs between heating demand and thermal comfort, showcasing a range of solutions that balance these objectives effectively. The results indicate that increasing the EPS insulation thickness and optimizing material combinations can substantially reduce energy consumption while maintaining or improving indoor comfort levels.

These findings provide a scientific foundation for recommending specific design adjustments to enhance energy efficiency and thermal comfort in traditional dwellings in the Hehuang region. Detailed comparative analysis of the optimization results is shown in the following figures and tables, illustrating the impact of varying EPS insulation thickness and alternative material choices on energy performance and comfort.

In the analysis of this chart, the trade-off relationship between heating demand (Q_h) and discomfort hours (H_dis) is illustrated through the design solutions generated by multi-objective optimization. Each green point on the Pareto front represents a non-dominated solution, meaning no other design outperforms it in both objectives simultaneously. Red points highlight specific critical solutions, such as the optimal points prioritizing comfort or heating demand.

The chart reveals a clear inverse relationship between heating demand and discomfort hours. Designs with lower heating demand are typically associated with a higher number of discomfort hours, while reducing discomfort hours often requires increased energy consumption to maintain indoor thermal comfort. The “knee points” represent balanced solutions where a slight increase in one objective (e.g., discomfort hours) significantly improves the other (e.g., reduced energy consumption).

• Comfort-optimal solution (X_opt, comfort = 0.83 GJ): This solution minimizes discomfort hours (Hdis ≈ 6200H), ensuring a high level of indoor thermal comfort but at the cost of higher heating demand.

• Demand-optimal solution (X_opt, demand = 1.8 GJ): This solution minimizes heating demand but results in higher discomfort hours (Hdis ≈ 5600H).

• Knee-point solutions (X_knee, demand = 1.2 GJ, X_knee, comfort = 1.6 GJ) provide trade-offs between the two objectives. These solutions are particularly suitable for scenarios where neither extreme comfort nor minimal energy consumption is the sole priority.

These knee points offer a balanced approach, allowing decision-makers to select solutions tailored to specific needs, balancing comfort and energy efficiency effectively. This flexibility underscores the practical value of the optimization process in real-world applications.

Overall, the chart supports the optimization strategy, demonstrating that there is no single solution that performs best across all objectives simultaneously. Instead, it provides a set of optimal trade-off solutions, allowing for informed decision-making based on the specific goals of a given project. This highlights the flexibility of the multi-objective optimization process, where stakeholders can select the most appropriate design solution depending on whether the priority is energy efficiency, thermal comfort, or a balance between the two.

To illustrate the practical value of the Pareto front, we quantify two knee-point solutions and contrast them with the baseline dwelling (2 cm EPS on walls, 0 cm on the roof). Upgrading to 4 cm EPS cuts the annual heating demand from 175 GJ to 150 GJ (−14.3%) and shortens discomfort hours from 6 500 h to 5 720 h (−12%), while the simple pay-back period is 3.8 years at the current coal price (900 CNY t^-1). A 6 cm XPS retrofit achieves a deeper reduction—142 GJ (−18.9%) and 5 100 h (−21.5%)—but its higher material cost extends the pay-back to 5.1 years. The flattening of energy savings beyond 6 cm confirms the “diminishing-returns” knee identified in Figure 5 and agrees with the 7 cm threshold reported for cold-dry districts by Lin et al. (2023) [1]. These data show that a moderate increase in insulation delivers most of the attainable benefit, providing designers with a clear, cost-effective target thickness for the Hehuang climate.

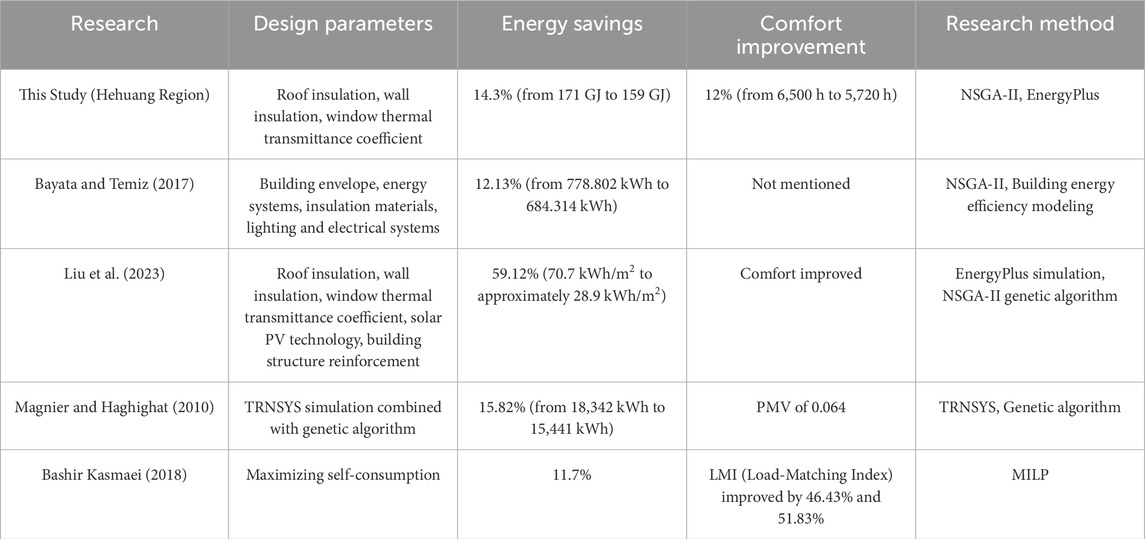
Table 2 presents a comparison of energy savings and comfort improvements between this study (focused on the Hehuang region) and several other retrofit studies. The table outlines the design parameters, energy-saving percentages, comfort improvements, and research methods for each study, providing a clear comparison of the performance outcomes across different approaches. This comparison highlights the relative effectiveness of various retrofit strategies for improving building energy efficiency and indoor thermal comfort.

Table 2

Table 2. Comparison of energy-saving and comfort improvement in building retrofit studies.

4.1.2 Optimization analysis of heating cost and comfort with different insulation thicknesses

This study not only analyzed the overall heating demand and thermal comfort issues of traditional residential buildings in the Hehuang region but also explored the specific impact of different insulation materials and thicknesses. The optimization analysis revealed that insulation material choice and thickness are key factors in determining heating costs and energy efficiency. We focused on the performance of common insulation materials, EPS and XPS, and analyzed the heating costs and energy-saving effects of EPS at different thicknesses. The results showed that as EPS thickness increased, heating demand decreased, but beyond a certain point, the energy-saving benefits diminished. Additionally, thicker insulation improved comfort but increased costs. XPS, while offering better insulation, is more expensive, affecting overall cost-effectiveness. The findings provide valuable insights for selecting insulation materials and thicknesses to balance comfort and cost in the region’s residential buildings.

Figure 6 shows the impact of different insulation thicknesses (ranging from 0 to 50 cm) of EPS (expanded polystyrene foam board) on the total cost and composition of energy-saving renovation for traditional residential buildings in the Hehuang region. From the chart, it is evident that as the thickness of EPS insulation increases, the heating costs gradually decrease, particularly when the insulation thickness increases from 0 cm to 6 cm, where a significant reduction in heating costs is observed. This indicates that EPS material provides good insulation performance at thinner thicknesses, effectively reducing heat loss from the building and thus lowering heating demand.

Figure 6

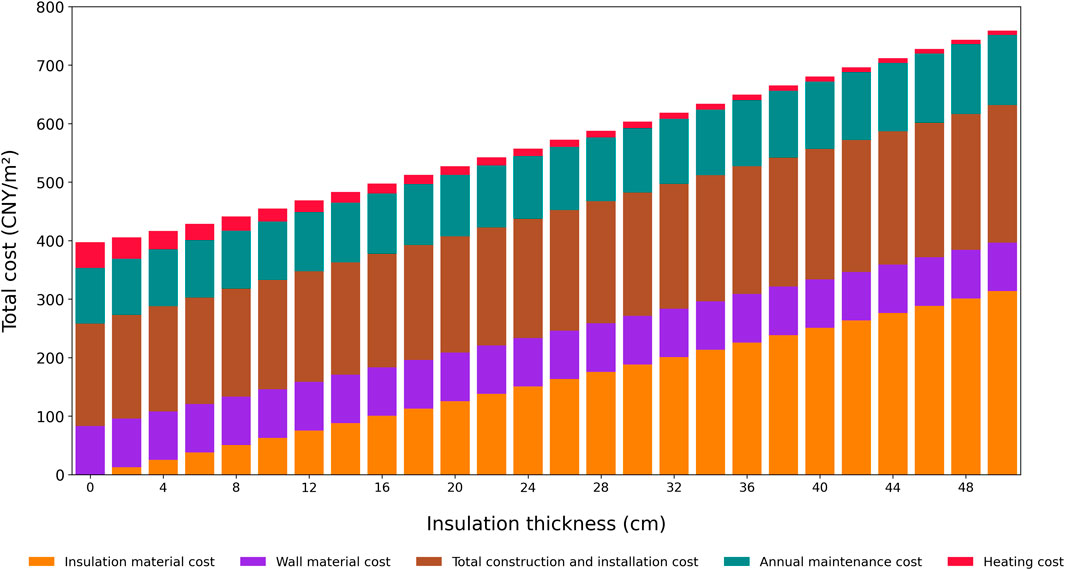
Figure 6. A breakdown of the total cost per square meter for different EPS insulation thicknesses, illustrating the trade-off between rising upfront investment (material and construction) and decreasing long-term heating expenses.

However, when the insulation thickness exceeds 6 cm, the rate of decrease in heating costs slows down, displaying a “knee point” characteristic. This means that after the thickness reaches a certain level, although increasing the insulation thickness continues to reduce heating costs, the incremental energy-saving benefits become limited, with diminishing marginal returns. This phenomenon suggests that within a certain critical thickness range, the investment in insulation material reaches a balance with the energy-saving effect, and further increases in thickness are no longer as cost-effective.

For thinner insulation layers (such as 2 cm–4 cm), EPS insulation boards can significantly improve the building’s insulation performance while maintaining low material and construction costs, offering a good cost-performance ratio. However, when the thickness increases to 6 cm or more, although insulation performance continues to improve, the increased material and construction costs may start to offset the further energy-saving benefits. Therefore, finding the optimal balance between cost and benefit is crucial, and a thickness of around 4 cm may be an ideal choice for many building designs, as it meets insulation requirements while controlling initial costs.

From the perspective of long-term energy savings, increasing the EPS insulation thickness to 8 cm or more helps to further improve the thermal comfort of the building and significantly reduce heating demand in extremely cold climates. However, this increase in thickness also brings higher material and construction costs, so a balance between initial investment and long-term benefits must be carefully considered.

Figure 7 shows the impact of different insulation thicknesses on comfort (annual discomfort hours) and winter heating demand when using XPS (extruded polystyrene foam board) insulation material. XPS insulation has excellent thermal performance, so even at smaller thicknesses, it can significantly improve the thermal comfort of the building. The data shows that as the thickness of XPS increases, the annual discomfort hours gradually decrease, reflecting its effectiveness in improving indoor thermal conditions. However, XPS material is relatively expensive, and as heating demand decreases, the rise in material and construction costs becomes more significant. Especially when the insulation thickness exceeds 8 cm, the reduction in heating demand slows down, but the total cost continues to rise.

Figure 7

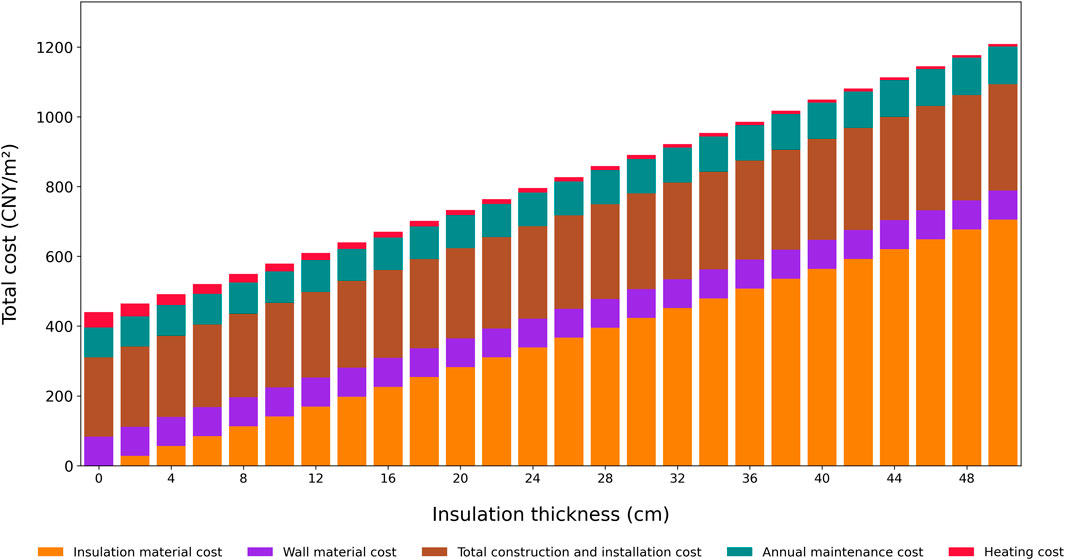
Figure 7. A breakdown of the total cost per square meter for different XPS insulation thicknesses, illustrating the trade-off between rising upfront investment (material and construction) and decreasing long-term heating expenses.

From the chart, it can be observed that the “knee point” for XPS material appears around 6 cm thickness. In this thickness range, XPS insulation strikes a balance between comfort and energy consumption, providing optimal insulation performance while keeping costs relatively controllable. Further increasing the thickness improves thermal performance, but the marginal benefits diminish, and cost-effectiveness starts to decline.

By comparing the optimization results of EPS (Figure 6) and XPS (Figure 7), it is clear that there are significant differences between the two in insulation thickness, total cost, and comfort improvement.

First, in terms of cost, EPS material has a lower total cost, and the cost increase with thickness is relatively gradual. The knee point appears around 4 cm, where EPS can effectively reduce heating demand, and material and construction costs remain within a reasonable range. Therefore, for projects with limited budgets, EPS material offers better cost performance.

In contrast, XPS material provides significantly better insulation performance at smaller thicknesses, particularly in the 4 cm–6 cm range, where its insulation effect is much better than that of EPS. However, due to the higher cost of XPS material, although it provides better comfort improvement at thinner thicknesses, the total cost increases significantly. The chart shows that at a 6 cm thickness, XPS achieves a good balance between comfort and heating demand, but its material and construction costs are still higher than EPS.

In terms of comfort and energy efficiency optimization, XPS material performs more efficiently. Even at smaller insulation thicknesses, XPS can significantly reduce annual discomfort hours, particularly in winter heating demand, where XPS performs exceptionally well in the 4 cm–6 cm thickness range. In comparison, EPS requires a thicker insulation layer to achieve similar energy-saving and comfort improvements.

Ultimately, the choice between the two materials should be based on the project’s needs. If budget is the main constraint, EPS material at around 4 cm thickness is a better option, offering significant comfort improvement at a lower total cost. For projects that prioritize indoor comfort and energy efficiency, XPS material at a 6 cm thickness provides a better balance of energy performance, despite its higher initial investment.

4.2 Comparison and analysis of typical scenarios

Through detailed analysis of frequency distribution and consideration of the specific climatic conditions of the Hehuang region, we determined the direction of parameter optimization, using the NSGA-II algorithm to optimize heating demand (GJ) and discomfort hours (hours). The region’s temperate semi-arid continental climate, with cold winters and relatively mild summers, significantly impacts the heating demand and thermal comfort of traditional dwellings. Table 3 presents the design parameters and optimized objective values for typical optimization scenarios, where each scenario achieves a balance between heating demand and comfort under different design parameter combinations. These scenarios take into account the region’s climate, such as the winter heating requirements and solar heat gain, and provide scientific guidance for building energy-saving renovations in the Hehuang region.

Table 3

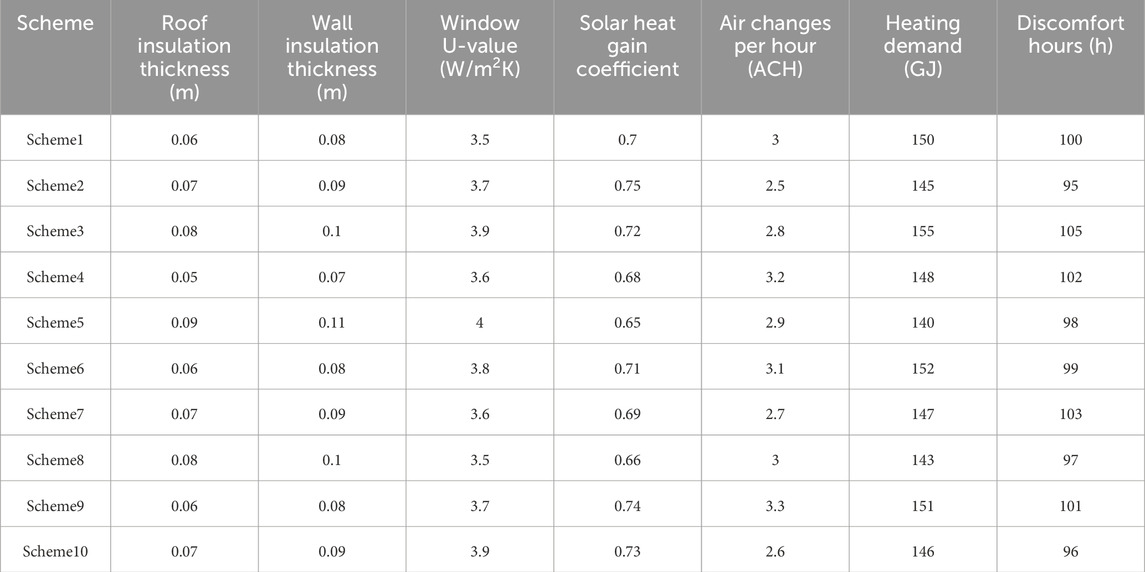
Table 3. Comparison of building parameters and thermal performance for different energy-saving renovation schemes.

The data in the table shows the varying impacts of different design parameter combinations on energy consumption and comfort. Scheme 1 and Scheme 6 both use the same roof thickness (0.06 m) and external wall insulation thickness (0.08 m), but they differ slightly in window heat transfer coefficient and solar heat gain coefficient. Both schemes achieve a fairly economical insulation effect and comfort with medium insulation thickness, making them suitable for users with limited budgets. Additionally, ventilation rates between 3.0 and 3.1 air changes per hour help reduce winter heat loss while maintaining air quality, making them suitable for cold, windy climates.

Scheme 2 and Scheme 5 have the lowest heating demand (145 GJ and 140 GJ), making them ideal for users looking to minimize heating costs. In particular, Scheme 5, with an external wall insulation thickness of 0.11 m, a window heat transfer coefficient of 4.0 W/m²K, and a solar heat gain coefficient of 0.65, provides optimal insulation during cold winters, making it suitable for users willing to invest in insulation materials.

Scheme 3 and Scheme 10 perform excellently in comfort optimization (with discomfort hours of 105 h and 96 h, respectively). Particularly Scheme 10, with a roof and external wall insulation thickness of 0.07 m and 0.09 m, maintains a high level of comfort. Given the cold and prolonged winter temperatures in the Hehuang region, these schemes are suitable for users who place a high priority on winter comfort.

Overall, users with limited budgets can choose Scheme 1 and Scheme 6, which provide good insulation and comfort. For those looking to reduce energy consumption, Scheme 2 and Scheme 5 are ideal. Users with higher comfort requirements can consider Scheme 3 and Scheme 10. For those seeking a balance between energy consumption and comfort, Scheme 7 and Scheme 8 provide a good compromise, performing equally well in energy savings and comfort.

Architectural designers can select suitable energy-saving renovation designs from the above schemes based on client needs and the climate characteristics of the Hehuang region, ensuring the dual goals of energy savings and comfort are met.

4.3 Feasibility and economic analysis of technical measures

This study, combined with the actual situation of the Hehuang region, analyzes and verifies the specific technical measures of the design strategies. Through surveys, it was found that most users recognize the need for energy-saving renovations but are sensitive to initial investment costs. Considering the economic capacity of users and the convenience of construction, it is recommended to prioritize the use of 4 cm thick EPS insulation, which has an investment recovery period of approximately 3.75 years. This solution effectively reduces heating costs and offers a high cost-performance ratio. For users with higher budgets, 6 cm thick XPS insulation offers better indoor comfort, with a recovery period of 5 years.

The study shows that with 4 cm thick EPS material, heating demand decreases from 175 GJ to 150 GJ (a reduction of 14.3%), and discomfort hours decrease from 6,500 h to 5,720 h (a reduction of 12%). This renovation scheme meets both energy-saving needs and significantly improves indoor thermal comfort. Moreover, by comparing measured and simulated data, the model’s prediction results align with actual trends, confirming the reliability and applicability of the optimized design, with temperature differences controlled within ±1°C.

Considering the economic level and climate characteristics of different regions, this design strategy has strong potential for promotion. In practice, insulation thickness and material type can be adjusted based on local material prices and user needs, further enhancing renovation effects and user acceptance.

5 Conclusion and outlook

5.1 Optimization analysis of energy-saving renovation plans and material selection

This study employed multi-objective optimisation to refine six envelope variables—roof and wall insulation thickness, window U-value, glazing SHGC, ventilation rate and insulation type—for traditional dwellings in the Hehuang region. The best Pareto-front solution, consisting of 6 cm XPS on the roof and 8 cm EPS on exterior walls, lowers annual heating demand from the baseline 175 GJ–142 GJ (−18.9%) and cuts annual discomfort hours from 6 500 h to 5 100 h (−21.5%). At the local coal price of 900 CNY t-¹, this package achieves a simple pay-back period of 3.8 years and avoids roughly 8.6 t CO₂ yr⁻¹, providing a quantified target for designers in cold-dry plateau climates.

Figures 6, 7 further clarify the cost–comfort trade-off between EPS and XPS. For walls, 4 cm EPS delivers most of the attainable benefit—heating demand 150 GJ (−14.3%) and discomfort hours 5 720 h (−12%)—while keeping initial cost lowest; its pay-back period is 3.1 years. 6 cm XPS excels in comfort (5 100 h) and energy savings (142 GJ) but raises first-costs by 27%, extending the pay-back to 5.1 years. The “knee point” analysis shows that once wall insulation exceeds 6 cm, each additional centimetre yields <2% extra energy saving, confirming the diminishing-returns plateau highlighted in Figure 5. Consequently, EPS 4–6 cm is recommended for cost-sensitive retrofits, whereas XPS 6–8 cm suits projects that prioritise comfort over initial investment.

5.2 Future research directions and theoretical foundation

Future research can further expand by incorporating more climate data and building materials to enhance the applicability of the model. Additionally, the use of optimization charts provides broad possibilities for developing energy-saving design plans. By continuously improving the models and optimization strategies, more effective guidance can be provided for energy-saving renovations in the Hehuang region and other regions with similar climates. The findings of this study provide scientific references for energy-saving renovations of traditional dwellings and lay the theoretical foundation for broader building energy-saving designs, promoting the sustainable development of the construction industry.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

WZ: Conceptualization, Writing – original draft, Supervision, Writing – review and editing, Data curation. ZW: Visualization, Methodology, Project administration, Writing – review and editing, Writing – original draft. PZ: Investigation, Conceptualization, Writing – review and editing, Project administration. LL: Software, Writing – review and editing, Visualization.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. This research was supported by the Gansu Provincial Basic Research Program–Soft Science Special Project (Grant No. 23JRZA464), Fundamental Research Funds for the Central Universities (Grant No. 31920240124), Gansu Provincial University Teachers Innovation Fund Project (Grant No. 2024B-035), and the National Natural Science Foundation of China (Grant No. 52362014). The authors gratefully acknowledge this support.

Acknowledgments

We thank all team members involved in field investigation and data collection, as well as the organizations that provided assistance. Special thanks to all participants and volunteers for their cooperation.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that Generative AI was used in the creation of this manuscript. Generative AI (ChatGPT by OpenAI) was used to assist in refining the language, grammar, and structure of the manuscript. The authors reviewed, edited, and take full responsibility for all content, including any AI-assisted portions. No AI-generated content was used for data analysis, original research findings, or results interpretation.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Lin Y, Cui C, Liu X, Mao G, Xiong J, Zhang Y. Green renovation and retrofitting of old buildings: a case study of a concrete brick apartment in Chengdu. Sustainability (2023) 15(16):12409. doi:10.3390/su151612409

CrossRef Full Text | Google Scholar

2. Liu Y, Chen D, Wang J, Dai M. Energy-saving and ecological renovation of existing urban buildings in severe cold areas: a case study. Sustainability (2023) 15(17):12985. doi:10.3390/su151712985

CrossRef Full Text | Google Scholar

3. Magnier L, Haghighat F. Multiobjective optimization of building design using TRNSYS simulations, genetic algorithm, and artificial neural network. Building Environ (2010) 45(3):739–46. doi:10.1016/j.buildenv.2009.08.016

CrossRef Full Text | Google Scholar

4. Bayata Ö, Temiz İ. Developing a model and software for energy efficiency optimization in the building design process: a case study in Turkey. Turkish J Electr Eng Computer Sci (2017) 25(5):4172–86. doi:10.3906/elk-1612-13

CrossRef Full Text | Google Scholar

5. Mostavi E, Asadi S, Boussaa D. Framework for energy-efficient building envelope design optimization tool. J Architectural Eng (2018) 24(2):04018008. doi:10.1061/(asce)ae.1943-5568.0000309

CrossRef Full Text | Google Scholar

6. Liu C. Influencing factors for an integrated model of green building energy consumption using bim dynamic simulation and multiobjective decision-making. Mobile Inf Syst (2022):7006765. doi:10.1155/2022/7006765

CrossRef Full Text | Google Scholar

7. Pedram O, Asadi E, Chenari B, Moura P, Gameiro da Silva M. A review of methodologies for managing energy flexibility resources in buildings. Energies (2023) 16(17):6111. doi:10.3390/en16176111

CrossRef Full Text | Google Scholar

8. Chen Y, Shi X. Surrogate based multi-objective optimization for energy-saving building design. In: Proceedings of the 2022 International Conference on Green Building, Civil Engineering and Smart City (2023). p. 311–8.

Google Scholar

9. Singh AK. An inclusive study on new conceptual designs of passive solar desalting systems. Heliyon (2021) 7(2):e05793. doi:10.1016/j.heliyon.2020.e05793

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Singh AK, Samsher S. Techno-environ-economic-energy-exergy-matrices performance analysis of evacuated annulus tube with modified parabolic concentrator assisted single slope solar desalination system. J Clean Prod (2022) 332:129996. doi:10.1016/j.jclepro.2021.129996

CrossRef Full Text | Google Scholar

11. Singh AK, Yadav RK, Mishra D, Prasad R, Gupta L, Kumar P. Active solar distillation technology: a wide overview. Desalination (2020) 493:114652. doi:10.1016/j.desal.2020.114652

CrossRef Full Text | Google Scholar

12. Singh AK, Samsher S. A review study of solar desalting units with evacuated tube collectors. J Clean Prod (2021) 279:123542. doi:10.1016/j.jclepro.2020.123542

CrossRef Full Text | Google Scholar

13. Singh AK. Samsher. Tech-en-econ-energy-exergy-matrix (T4EM) observations of evacuated solar tube collector augmented solar desaltification unit: a modified design loom. Mater Today Proc (2022) 61:258–63. doi:10.1016/j.matpr.2021.09.088

CrossRef Full Text | Google Scholar

14. Singh AK. Mathematical analysis of optimized requisites for novel combination of solar distillers. J Eng Res (2023) 11(4):515–25. doi:10.1016/j.jer.2023.100121

CrossRef Full Text | Google Scholar

15. Liang D, Jing F. Evaluation of thermal insulation performance of building exterior wall based on multiobjective optimization algorithm. Mobile Inf Syst (2022)2022):2672894. doi:10.1155/2022/2672894

CrossRef Full Text | Google Scholar

16. Liu Y, Chen J. A multi-objective optimization study of modern architectural heritage based on intelligent algorithms. In: Proceedings of SPIE (2023).1264543

Google Scholar

17. Luo C, Liu Y, Li X. Hybrid multiobjective particle swarm optimization and estimation of distribution algorithm. J Chongqing Univ (2010) 33(4):31–6. doi:10.11835/j.issn.1000-582X.2010.04.006

CrossRef Full Text | Google Scholar

18. Laili Y, Tao J, Zhang X. Multi-objective workflow scheduling with deep-q-network-based multi-agent reinforcement learning. IEEE Access (2019) 7:31633–45. doi:10.1109/ACCESS.2019.2902846

CrossRef Full Text | Google Scholar

19. Liu F, Zhang Q, Han Z. MOEA/D with gradient-enhanced kriging for expensive multiobjective optimization. Nat Comput (2023) 22(2):329–39. doi:10.1007/s11047-022-09907-0

CrossRef Full Text | Google Scholar

20. Liu J, Zhang B. Multiobjective optimization of hull form based on global optimization algorithm. J Shanghai Jiaotong Univ (Science) (2022) 27(3):346–55. doi:10.1007/s12204-022-2445-2

CrossRef Full Text | Google Scholar

21. Li L, Yevseyeva I, Fernandes VB, Trautmann H, Jing N, Emmerich MTM, et al. Building and using an ontology of preference-based multiobjective evolutionary algorithms. In: H Trautmann, G Rudolph, and K Klamroth, editors. Evolutionary multi-criterion optimization. EMO 2017. Lecture notes in computer science, 10173 (2017). p. 406–21.

Google Scholar

22. Lv Z, Cheng R, Li Y, Yu L. Optimization operation of urban building network based on continuous Hopfield neural network. In: 2023 IEEE 6th International Conference on Automation, Electronics and Electrical Engineering (AUTEEE) (2023). p. 270–4.

Google Scholar

23. Marano GC. Reliability based multiobjective optimization for design of structures subject to random vibrations. J Zhejiang University-Science A (2008) 9(1):15–25. doi:10.1631/jzus.a072128

CrossRef Full Text | Google Scholar

24. Alanani M, Brown T, Elshaer A. Multiobjective structural layout optimization of tall buildings subjected to dynamic wind loads. J Struct Eng (2024) 150(7):04024069. doi:10.1061/jsendh.steng-12366

CrossRef Full Text | Google Scholar

25. Alghamdi S, Tang W, Kanjanabootra S, Alterman D. Optimal configuration of architectural building design parameters for higher educational buildings. Energy Rep (2023) 10:1925–42. doi:10.1016/j.egyr.2023.08.066

CrossRef Full Text | Google Scholar

26. Allmendinger R, Ehrgott M, Gandibleux X, Geiger MJ, Klamroth K, Luque M. Navigation in multiobjective optimization methods. J Multi-Criteria Decis Anal (2017) 24(1–2):57–70. doi:10.1002/mcda.1599

CrossRef Full Text | Google Scholar

27. Asadi E, Chenari B, Gaspar AR, Gameiro da Silva M. Development of an optimization model for decision-making in building retrofit projects using RETROSIM. Adv Building Energy Res (2023) 17(3):324–44. doi:10.1080/17512549.2023.2204872

CrossRef Full Text | Google Scholar

28. Chen L, Cheung Y-M, Liu H-L, Lai Y. Evolutionary bilevel optimization via multiobjective transformation-based lower-level search. IEEE Trans Evol Comput (2024) 28(3):733–47. doi:10.1109/tevc.2023.3236455

CrossRef Full Text | Google Scholar

29. Carli R, Dotoli M, Pellegrino R, Ranieri L. A decision making technique to optimize a buildings' stock energy efficiency. IEEE Trans Syst Man, Cybernetics: Syst (2017) 47(5):794–807. doi:10.1109/tsmc.2016.2521836

CrossRef Full Text | Google Scholar

30. Bigeon J, Le Digabel S, Salomon L. DMulti-MADS: mesh adaptive direct multisearch for bound-constrained blackbox multiobjective optimization. Comput Optimization Appl (2021) 79(2):301–38. doi:10.1007/s10589-021-00272-9

CrossRef Full Text | Google Scholar

31. Borcsok E, Gerse A, Fulop J. Applying multiobjective optimization for the heat supply in the residential sector in Budapest. In: 2018 IEEE 12th international symposium on applied computational intelligence and informatics (SACI) (2018). p. 213–8.

Google Scholar

32. Boron J. Modeling of time criterion and utility function for multiobjective synthesis. In: Proceedings of the ISCA 17th International Conference on Computers and Their Applications (2002). p. 198–200.

Google Scholar

33. Chacon L, Chen Austin M, Castano C. A multiobjective optimization approach for retrofitting decision-making towards achieving net-zero energy districts: a numerical case study in a tropical climate. Smart Cities (2022) 5(2):405–32. doi:10.3390/smartcities5020023

CrossRef Full Text | Google Scholar

34. Barbosa LZ, Coelho LS, Lebensztajn L. Particle swarm optimization and strength Pareto to solve multiobjective optimization problems. Int J Appl Electromagnetics Mech (2013) 43(1–2):137–49. doi:10.3233/IAE-131717

CrossRef Full Text | Google Scholar

35. Li J, Zhang S, Qi H. Multi-objective optimization design of low-carbon modular building. J Phys Conf Ser (2024) 2706(1):012074. doi:10.1088/1742-6596/2706/1/012074

CrossRef Full Text | Google Scholar

36. Kapoor G, Singhal M. Impact of innovative thermal insulation materials in the building envelope on energy efficiency of residential buildings. Mater Today Proc (2024). doi:10.1016/j.matpr.2024.04.041

CrossRef Full Text | Google Scholar

37. Karytsas S, Theodoropoulou E. Awareness and utilization of incentive programs for household energy-saving renovations: empirical findings from Greece. Sustainability (2023) 15(18):13923. doi:10.3390/su151813923

CrossRef Full Text | Google Scholar

38. Karatas A, El-Rayes K. Optimal trade-offs between housing cost and environmental performance. J Architectural Eng (2016) 22(2):04015018. doi:10.1061/(asce)ae.1943-5568.0000199

CrossRef Full Text | Google Scholar

39. Kumari A, Kumar Yadav S. Moving towards sustainable nanoengineered building materials with less energy consumption. Energy and Buildings (2024) 318:114475. doi:10.1016/j.enbuild.2024.114475

CrossRef Full Text | Google Scholar

40. Wu X, Li X, Qin Y, Xu W, Liu Y. Intelligent multiobjective optimization design for NZEBs in China: four climatic regions. Appl Energy (2023) 339:120934. doi:10.1016/j.apenergy.2023.120934

CrossRef Full Text | Google Scholar

41. Wu Z, Xia X, Wang B. Improving building energy efficiency by multiobjective neighborhood field optimization. Energy and Buildings (2015) 87:45–56. doi:10.1016/j.enbuild.2014.10.079

CrossRef Full Text | Google Scholar

42. Li X, Zhang Y, Guo D. Surrogate-assisted multi-objective particle swarm optimization for building energy saving design. In: H Ishibuchi, C Coelho Coello, and P Bouvry, editors. Evolutionary Multi-Criterion Optimization: 11th International Conference, EMO 2021, Shenzhen, China, March 28–31, 2021, Proceedings, 12654 (2021). p. 593–604. doi:10.1007/978-3-030-72062-9_47

CrossRef Full Text | Google Scholar

43. Xie J, Yuan J, Yuan Y. A study on optimization of building life cycle energy consumption. In: 2011 International Conference on Consumer Electronics, Communications and Networks (CECNet) (2011). p. 1942–4.

Google Scholar

44. Yang M-D, Lin M-D, Lin Y-H, Tsai K-T. Multiobjective optimization design of green building envelope material using a non-dominated sorting genetic algorithm. Appl Therm Eng (2017) 111:1255–64. doi:10.1016/j.applthermaleng.2016.01.015

CrossRef Full Text | Google Scholar

45. Zhang Q, Liu W, Tsang E, Virginas B. Expensive multiobjective optimization by MOEA/D with Gaussian process model. IEEE Trans Evol Comput (2010) 14(3):456–74. doi:10.1109/TEVC.2009.2033671

CrossRef Full Text | Google Scholar