Theoretical study of spin-orbit coupling and laser cooling for HBr molecule with first-overtone spectral calculations

Introduction: The electronic structure of the HBr molecule was investigated with particular attention to the spin–orbit coupling effect, aiming to assess its suitability for laser cooling applications.

Methods: Ab initio CASSCF/MRCI+Q calculations were carried out to obtain low-lying adiabatic potential energy curves with and without spin–orbit coupling taken into consideration. Static and transition dipole moments were evaluated, and the DUO and ExoCross programs were employed to simulate rovibronic spectra. Franck–Condon factors were calculated for transitions between the ground and excited electronic states.

Results: The spectroscopic constants of several electronic states were derived and compared with available literature values, showing good agreement. The Franck–Condon factor analysis identified a transition as favorable for Doppler and Sisyphus laser cooling. Radiative lifetimes, branching ratios, Doppler and recoil temperatures, and slowing distances were determined. A four-laser cooling scheme in the deep-UV region was proposed. Simulated absorption spectra for the P(2) and R(7) transitions in the first-overtone (v = 0–2) band reproduced experimental data with reasonable accuracy.

Discussion: These findings confirm HBr as a promising candidate for laser cooling, supported by reasonably accurate ab initio potential and dipole moment curves. The proposed scheme and agreement with experimental spectra strengthen the feasibility of experimental implementation.

1 Introduction

Hydride halide molecules have been studied extensively, experimentally, and theoretically over several decades [1–6]. Because of its simple structure and rich photochemical dynamics, the HBr molecule is helpful in many fields of science; in metrology, it is used as a benchmark for numerous spectroscopic studies, and it is used to calibrate the spectrometers and tunable laser devices [7–9]. The accurate functioning of a high-resolution infrared spectrometer is determined with the HBr molecule; it is used as a leading gas in the poly-Si plasma etch for the fabrication of integrated circuits. Because it plays a vital role in the depletion mechanism, this molecule is essential for studying the atmosphere of the Earth, the Sun, and stellar objects [10, 11]; it interacts with the ozone molecules, which contribute to the thinning of the ozone layer. Care must be taken while using and releasing this gas into the atmosphere.

With the Cold and ultracold molecules, new techniques have been introduced to probe new states of quantum matter with high-precision measurements of both fundamental and applied science. These molecules enable quantum simulations of condensed matter phenomena with new platforms for quantum computing. Bose-Einstein condensate material, precise control of molecular dynamics, and nanolithography are provided with the cold and ultracold molecules [12].

Despite the availability of numerous experimental [13, 14] and theoretical [15–20] studies in the literature, only a limited number provide a thorough and accurate account of the spectroscopic characteristics of the low-lying excited states of the HBr molecule, particularly when considering both the inclusion and exclusion of spin-orbit coupling effects. Furthermore, there is a scarcity of detailed information regarding its vibrational manifolds (including the vibrational energy levels, vibrational transition calculations, Franck-Condon factors, Einstein coefficients, and lifetimes, etc.). These aspects are very useful in assessing the potential of the HBr molecule as a candidate for laser cooling and presenting a laser cooling scheme in the deep ultraviolet region, a concept that, to our knowledge, has not yet been explored for the HBr molecule. All these gaps serve as the primary motivation for the present investigation.

Since the electronic structure of HBr is essential for understanding its chemical behavior, the molecular spectra, and the interactions with external fields, we investigate the potential energy curves of the ground and the low-lying excited electronic states, along with the spectroscopic constants Te, R_e, ω_e, and B_e which are respectively, the transition energy with respect to the minimum of the ground state, the equilibrium bond length, the harmonic frequency, and the rotational constant. These calculations have been done using the ab initio method (CASSCF/MRCI+Q) with Davidson correction in the two representations ^2S+1Λ^+/− and Ω^(±). With the small difference ΔR_e between the ground and some of the excited states, one can find that this molecule is a good candidate for laser cooling. Accordingly, the Franck-Condon Factors (FCFs), the Einstein coefficients, the radiative lifetime, and the branching ratio among specific vibrational levels have been calculated with the experimental parameters, including the slowing distance, the Doppler and the recoil temperatures, and the maximal deceleration of the molecules. A laser cooling scheme is presented with four lasers in the ultraviolet region. Because of the importance of the infrared spectra of hydrogen halides as absolute wavelength standards, its observation in the stratosphere, and its need for in situ sensors for the semiconductor patterning process, the first-overtone (v = 0–2) absorption spectra of the P(2) and R(7) transitions of the HBr molecule have been investigated and compared with high accuracy with those obtained experimentally based on our investigated potential energy curve with the dipole moment curve of the ground state.

2 Computational approach

The present theoretical study is based on the use of the ab initio methods, which are performed by utilizing the state-averaged complete active space self-consistent field (CASSCF) followed by the multi-reference configuration interaction (MRCI) method with Davidson correction (+Q) [21]. This calculation was done using the computational chemistry program MOLPRO [22] and taking advantage of the graphical interface program GABEDIT [23]. For the ground state, we performed the calculation by using the three basis sets ECP28MWB [24], Stuttgart RLC [25], and SBKJC_VDZ [26] with two different ways of the active space in the C_2v symmetry group for the Br atom and aug-cc-PV5Z for the hydrogen atom as given in Table 1. For the excited electronic states, we adopted the quasi-relativistic pseudopotential ECP28MWB [24] for s, p, and d functions, with 28 electrons to be frozen within the core and seven active electrons to be treated, while for the hydrogen atom, the augmented correlation-consistent polarized valence quintuple–zeta (aug-cc-PV5Z) [27] basis set is used. The active space in the C_2v symmetry group then contains 8σ(Br:4s,4p₀,5s,4d₀, 4d₊₂, 5p_0, 6s H: 1s), 3π (Br: 4p_±1,4d_±1, 5p_±1),1δ (Br: 4d_-2).

Table 1

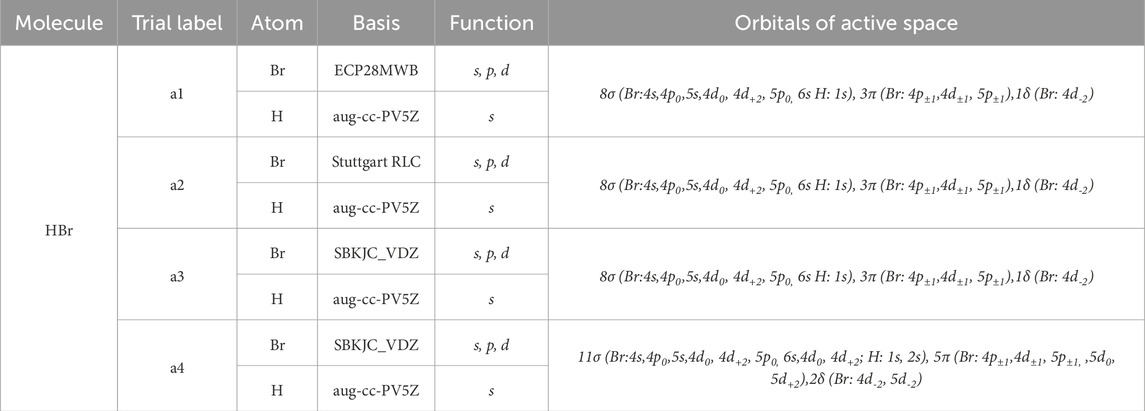
Table 1. Orbitals of active space of the basis sets ECP28MWB, Stuttgart RLC, and SBKJC_VDZ of the Br atom, and aug-cc-PV5Z for the Hydrogen atom.

3 Results and discussion

3.1 Potential energy curves and spectroscopic constants of HBr molecule

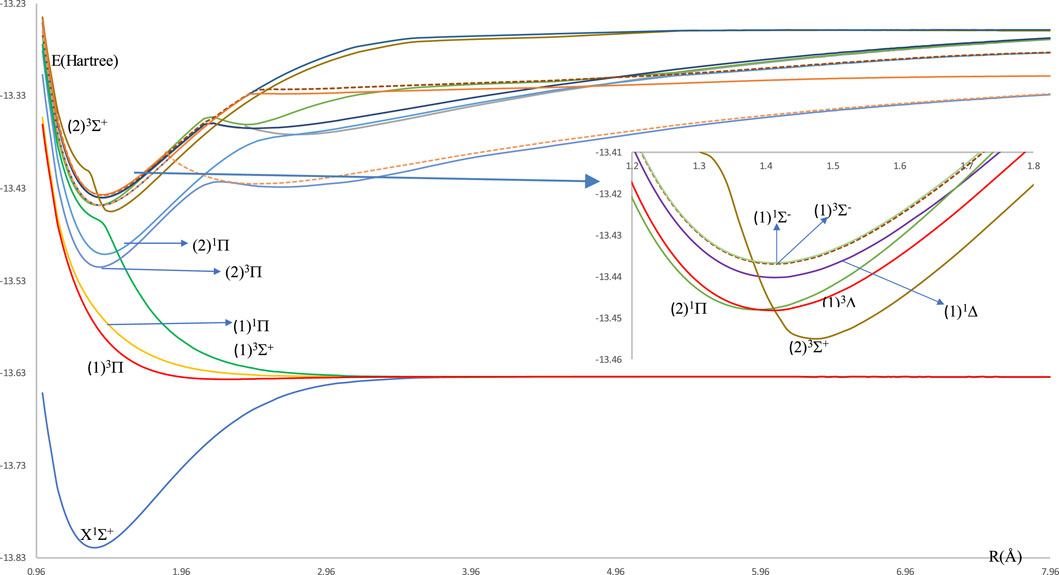
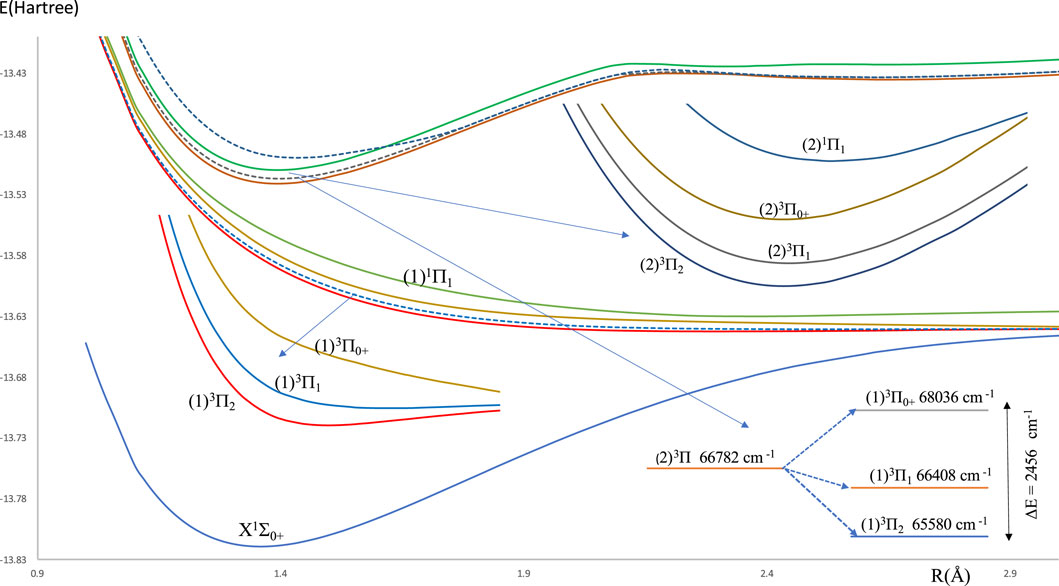
The investigated potential energy curves (PECs) for 14 singlet and triplet low-lying electronic states for the molecule HBr without the spin-orbit coupling effect are given in Figure 1. Most of these curves are bound and deep except the two electronic states (1)¹Π and (1)³Σ⁺ are unbound, and the state (1)³Π is shallow. From these (PECs), we noticed the small difference between the internuclear distance ΔR_e = 0.034 Å of the ground and (2)³Π states. This first step for the laser cooling of a molecule encouraged us to investigate the spin-orbit coupling of the low-lying electronic states of the considered molecule, where their potential energy curves are given in Figure 2. One can notice some unbound electronic states where the repulsive Coulomb forces overcome the attractive forces within the taken range of internuclear distance. These potential energy curves of all the investigated electronic states are plotted as a function of the internuclear distance R in the range of 0.96 Å to 7.96 Å. With the H atom at the origin, the investigated permanent dipole moment curves of the lowest electronic states with and without spin-orbit coupling of the molecule HBr are given in Supplementary Figure S1 in the Supplementary Material. In this Figure, some curves smoothly approach zero at large distances, where the molecule dissociates into neutral fragments. While other states as (2)³Π₀, (2)³Π_1, (2)³Π₂, and (1)³Δ dissociated into ionic fragments in the negative region, and the state (2)¹Σ⁺ dissociates in the positive region.

Figure 1

Figure 1. Potential energy curves for the molecule HBr without spin-orbit coupling effect.

Figure 2

Figure 2. Potential energy curves for the molecule HBr with spin-orbit coupling effect.

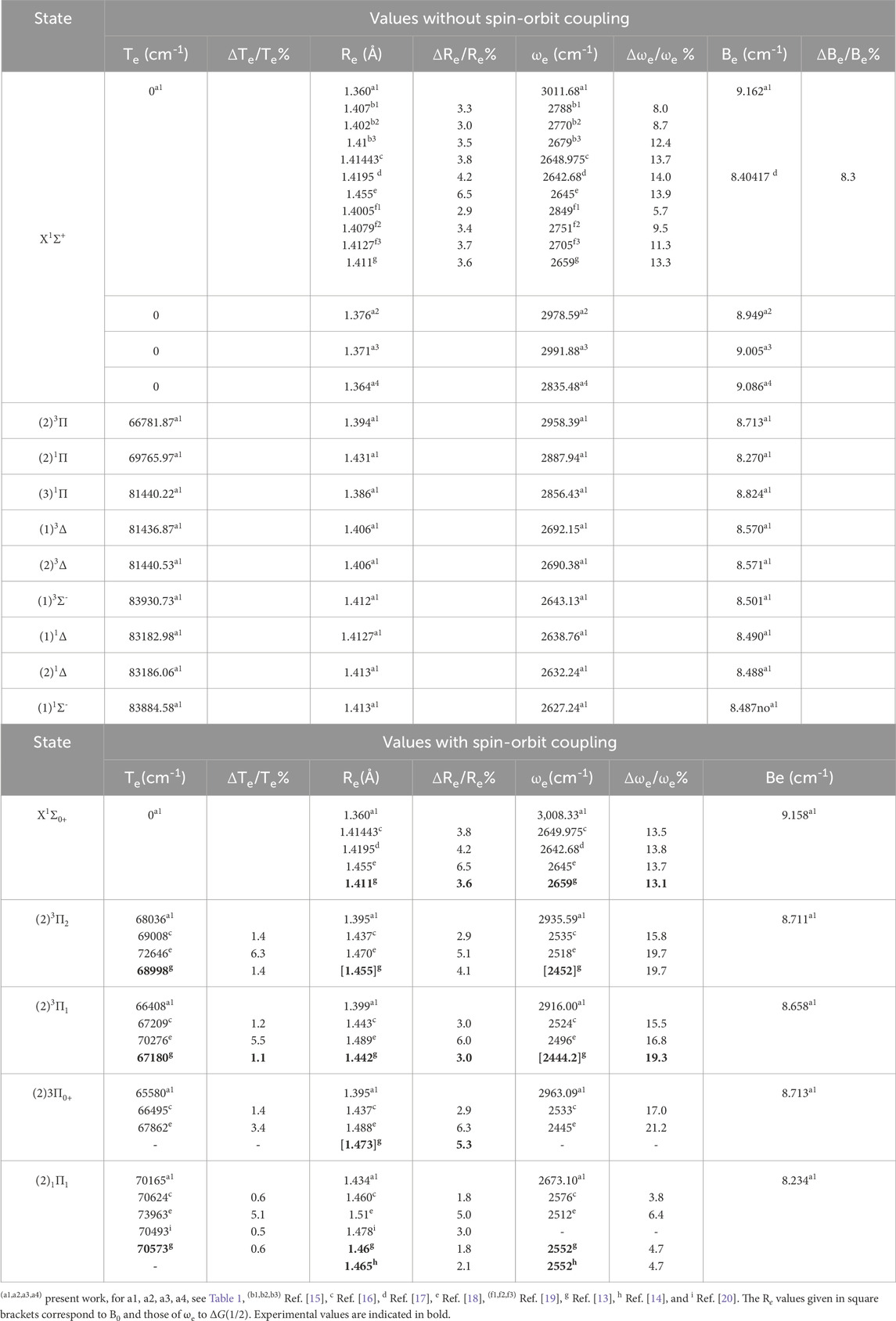
The harmonic frequency ω_e, the electronic energy with respect to the ground state T_e, and the rotational constant B_e have been calculated for the investigated bound electronic states upon fitting the corresponding potential energy curve into a polynomial around the internuclear distance at equilibrium R_e. Table 2 illustrates the spectroscopic constants for the lowest singlet and triplet electronic states of the HBr molecule with and without spin-orbit coupling, along with the available data in the literature. By analyzing the provided information, we confirm that ¹Σ⁺ is the lowest ground electronic state of the molecule HBr. The calculation of these constants for this state was done using three basis sets for the Br-atom with two different active spaces in the C_2v symmetry group, as shown in Table 1. This calculation shows the influence of these calculations on the values of the harmonic frequency ω_e, which varies between 3,011.68 cm⁻¹ and 2835.48 cm⁻¹, while the influences on R_e and B_e are limited, as given in Table 2. By adopting the basis sets ECP28MWB [24] and aug-cc-PV5Z [27] for the Br and H atoms respectively with the 8σ (Br:4s,4p₀,5s,4d₀, 4d₊₂, 5p_0, 6s H: 1s), 3π (Br: 4p_±1,4d_±1, 5p_±1),1δ (Br: 4d_-2 orbitals active space, the spectroscopic constants of the ground and the excited states with and without spin-orbit coupling are given in Table 2. The comparison of our calculated values of R_e with those available in the literature for the ground state without spin-orbit coupling shows a good agreement with the relative difference of 2.9% [19] <ΔR_e/R_e<6.5% [18]. Comparing our value of the rotational constant B_e with the only available value in the literature [17] shows the acceptable relative difference ΔB_e/B_e = 8.3%. Based on the two basis sets ECP28MWB [24] and SBKJC_VDZ [26] (basis set a4), the relative differences between our calculated values and those available in the literature for the harmonic frequency ω_e without spin-orbit coupling are respectively 5.7% [19] <Δω_e/ω_e <14.0% [17] and 0.5% [19]<Δω_e/ω_e< 7.3% [17]. These results on ω_e show excellent agreement with some theoretical data [19] in the literature and are barely acceptable with other theoretical results [17]. There is no comparison of the spectroscopic constants of the free spin excited states with other results since they are given here for the first time. By adopting the basis set ECP28MWB [24] ((a1) of Table 1), the comparison of our calculated values of the spectroscopic constants of the spin-orbit coupling electronic states X¹Σ₀₊, (2)³Π₂, (2)³Π₁, (2)³Π₀₊, and (2)¹Π₁ with those available in the literature (Table 2) shows very good agreement for T_e and R_e with the relative differences 0.5% [20] <ΔT_e/T_e< 6.3% [18] and 1.8% [13, 16] <ΔR_e/R_e< 6.5% [18] respectively. For the electronic state, (2)¹Π₁, our calculated value of ω_e is in good agreement with the experimental values of [13, 14] with the same relative differences of 4.7%. For the two states, X¹Σ₀₊, (2)³Π, our calculated value of ω_e is larger than those given in the literature, with an average relative difference of 12.6%. One can notice that our calculated values of the spectroscopic constants better agree with the recent work of Alekseyev et al. [16]. The spin-orbit coupling splitting energy is calculated and plotted in Figure 2 for the electronic state (2)³Π where the maximum splitting energy is 2456 cm⁻¹.

Table 2

Table 2. Spectroscopic constants of the molecule HBr with and without spin-orbit coupling.

3.2 Laser cooling study of the HBr molecule

From the investigated values of the spectroscopic constants of Table 2, we noticed the small difference in the internuclear distance ΔR_e = 0.035Å between the ground X¹Σ₀₊ and the (2)³Π₀₊ states, which is the first step for the study of the suitability of a molecule for laser cooling. The main criterion for laser cooling this molecule with a closed-cycle loop is a diagonal Franck-Condon factor (FCF) without intervening states influencing the cycling between the two considered states. Between the two electronic states X¹Σ₀₊ and the (2)³Π₀₊ states, one can notice the existence of the four intervening electronic states (1)³Π₀₊, (1)³Π₁, (1)³Π₂, and (1)¹Π_1. Two of these states, (1)³Π₁ and (1)³Π_2, are unbound, so it is impossible to give spontaneous emission life and FCFs of the transitions (2)³Π₀₊-(1)³Π₁ and (2)³Π₀₊-(1)³Π₂ [28]. While the two others are very shallow bound states. Figures 3b,c show the non-diagonality of the FCF of transitions (2)³Π₀₊ - (1)³Π₀₊, and (2)³Π₀₊ - (1)¹Π₁ among the vibrational levels v' = v = 0 (calculated by using the LEVEL 11 program [29]). For the vibrational levels v' = v = 0, the FCF of the transition (2)³Π₀₊ - X¹Σ₀₊ is highly diagonal (Figure 3a), which is the first condition for a direct laser cooling of the molecule HBr. The second condition is the non-influence of the intermediate states (1)³Π₀₊ and (1)¹Π₁ on the cycling loop between X¹Σ₀₊ and (2)³Π₀₊ states. This second condition is verified by the non-diagonality of the FCF of the two transitions (2)³Π₀₊ - (1)³Π₀₊, and (2)³Π₀₊ - (1)¹Π₁ given in Figures 3b,c. The third criterion for a successful laser cooling process which maximizes the cooling rate and produces a strong Doppler force for the electronic transition (2)³Π₀₊ - X¹Σ₀₊ is a short radiative lifetime, which is given by τ_v′ = 1/Σ_vA_v′v, where the Einstein coefficient A_v’v is formulated as in Equation 1 [30]

$A_{v^{\prime }v}=\frac{\left(3.1361891\right)\left({10}^{-7}\right){\left(\Delta E\right)}^3{\left({\psi }_{{\nu }^{\prime }}\left|M\left(r\right)\right|{\psi }_{\nu }\right)}^2}{2}(1)$

Figure 3

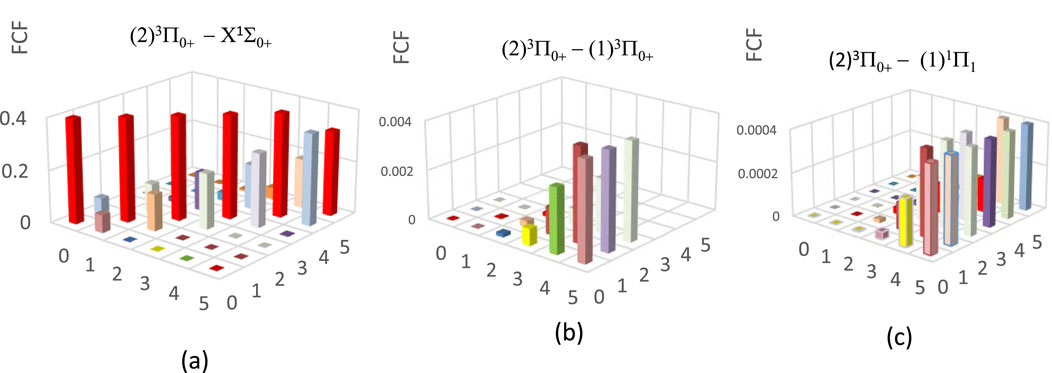
Figure 3. Franck-Condon factor for electronic states of the molecule HBr with spin-orbit coupling effect. (a) For the transition:(2)3p0+- X1S0. (b) For the transition:(2)3p0+ - (1)3P. (c) For the transition:(2)3p0+ - (1)1P.

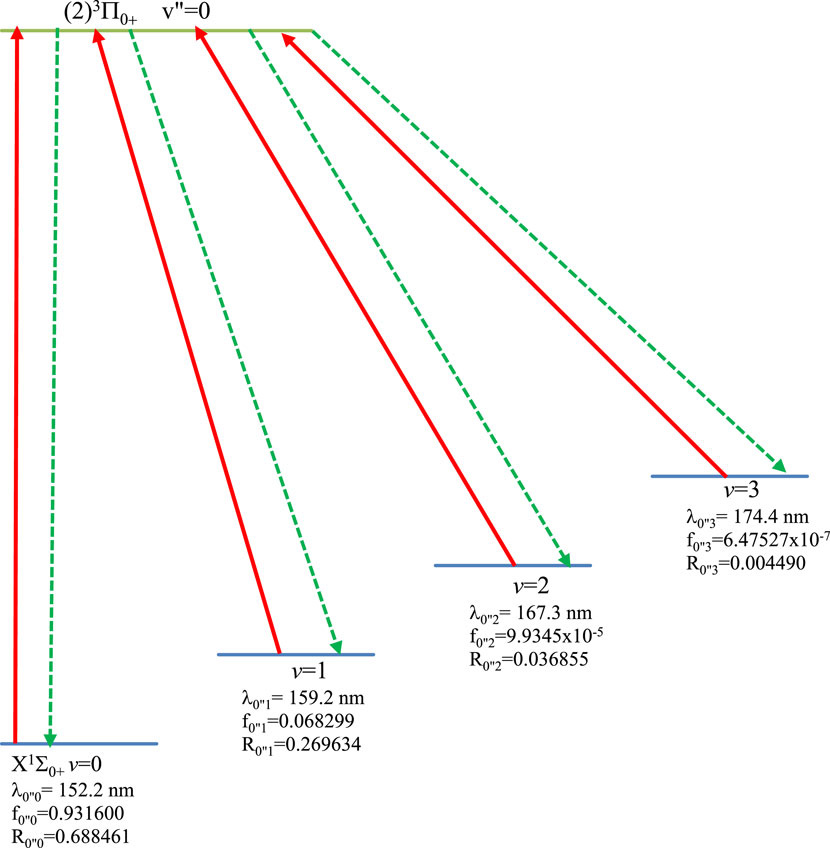
By using LEVEL 11 program [29], the energy difference between the two electronic states X¹Σ₀₊ and (2)³Π₀₊ is ΔE and the computed value of the electronic transition dipole moment M(R) between these two states (in Debye) is plotted in Figure 4. Because of the non-influence of the intermediate states (1)³Π₀₊, (1)³Π₁, (1)³Π₂, and (1)¹Π₁ on the cycling loop of the transition (2)³Π₀₊ - X¹Σ₀₊ the calculated values of the vibrational branching ratio for six vibrational levels of this transition (which is given by given by R_v″v = $\frac{A_{v^{″}v}}{{\sum }_v{A}_{v^{″}v}}$ [31–34], along with the radiative lifetime, are given in Table 3. For this transition and for a short radiative lifetime of 5.51 ns > τ > 8.93 ns, the molecule HBr is a good candidate for direct laser cooling for the transition (2)³Π₀₊ - X¹Σ₀₊. Our proposed laser cooling scheme for a direct laser cooling of the molecule HBr is given in Figure 5, where the red lines represent the cycling pumping lasers. The wavelength of the main pumping laser is λ_{0″ 0} = 152.2 nm, and three other pumping lasers of wavelengths λ_0″1 = 159.2 nm, λ_0″2 = 167.3 nm, and λ_0″3 = 174.4 nm close the leaks from the higher vibrational level, while the dotted green lines represent the spontaneous decay. Since these lasers are in the deep ultraviolet range, recent advances in solid-state laser technology have proven the obtention of laser beams in the ultraviolet regime possible. However, the lowest obtained corresponding wavelength until now is about 170 nm [35–37]. According to our scheme, the laser cooling of the HBr molecule will probably need to wait until new technology leads to lowering this threshold limit to values as low as 150 nm. The calculated values of the vibrational FCF (f_v″v) and the branching ratio R_v″v of the considered transition (2)³Π₀₊ - X¹Σ₀₊ are given in Figure 5. The total number N of cycles for photon absorption/emission which is the reciprocal of the total loss is given by

$\mathrm{N}=1/\left(1-\eta \right)=5525$

with η = R_0″0 + R_0″1 + R_0″2 + R_0″3 [38–40]. The calculated values of the needed experimental parameters are given in Equations 2–6 [41]:

$V_{rms}=\frac{hN}{m{\lambda }_{00}}=180.8\mathrm{m}/\mathrm{s}(2)$

${\mathrm{T}}_{\mathrm{i}\mathrm{n}\mathrm{i}}=\frac{m{V}^2}{2k_B}=159.0\mathrm{K}(3)$

${\mathrm{a}}_{\max }=\frac{h{N}_e}{N_{tot}m{\lambda }_{00}\tau }=1.62\mathrm{x}{10}^6\mathrm{m}/{\mathrm{s}}^2(4)$

$L_{\mathit{min}}=\frac{k_B{T}_{ini}}{m{a}_{\mathit{max}}}=1.02\text{\hspace{0.17em}cm}(5)$

$\begin{array}{ll}\hfill {\mathrm{T}}_{\mathrm{D}}& \hfill \hspace{0.17em}=\mathrm{h}/\left(4\times \mathrm{\pi }\times \mathrm{\tau }\times {\mathrm{k}}_{\mathrm{B}}\right)=944.8\mathrm{\mu }\mathrm{K}\text{\hspace{0.17em}and\hspace{0.17em}}{\mathrm{T}}_{\mathrm{r}}={\mathrm{h}}^2/\left(\mathrm{m}\times {\mathrm{\lambda }}_{00}^2\times {\mathrm{k}}_{\mathrm{B}}\right)\\ \hfill & \hfill =10.4\mathrm{\mu }\mathrm{K}\end{array}(6)$

Figure 4

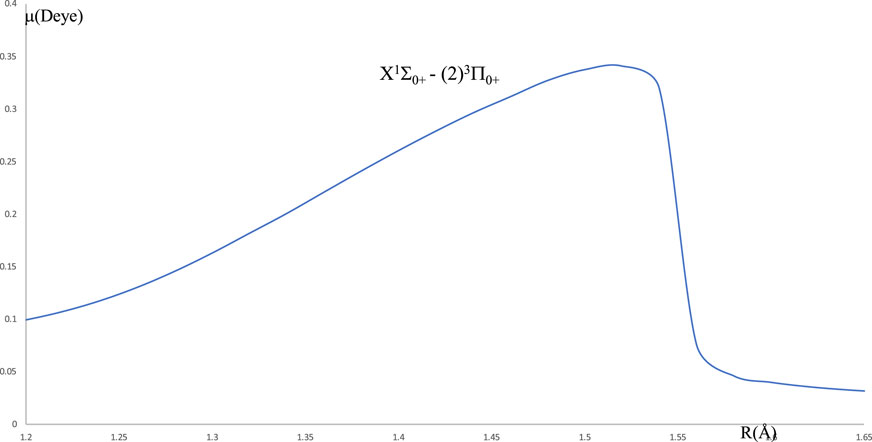
Figure 4. Transition dipole moment between the two electronic states X¹Σ₀₊ - (2)³Π₀₊ of the molecule HBr.

Table 3

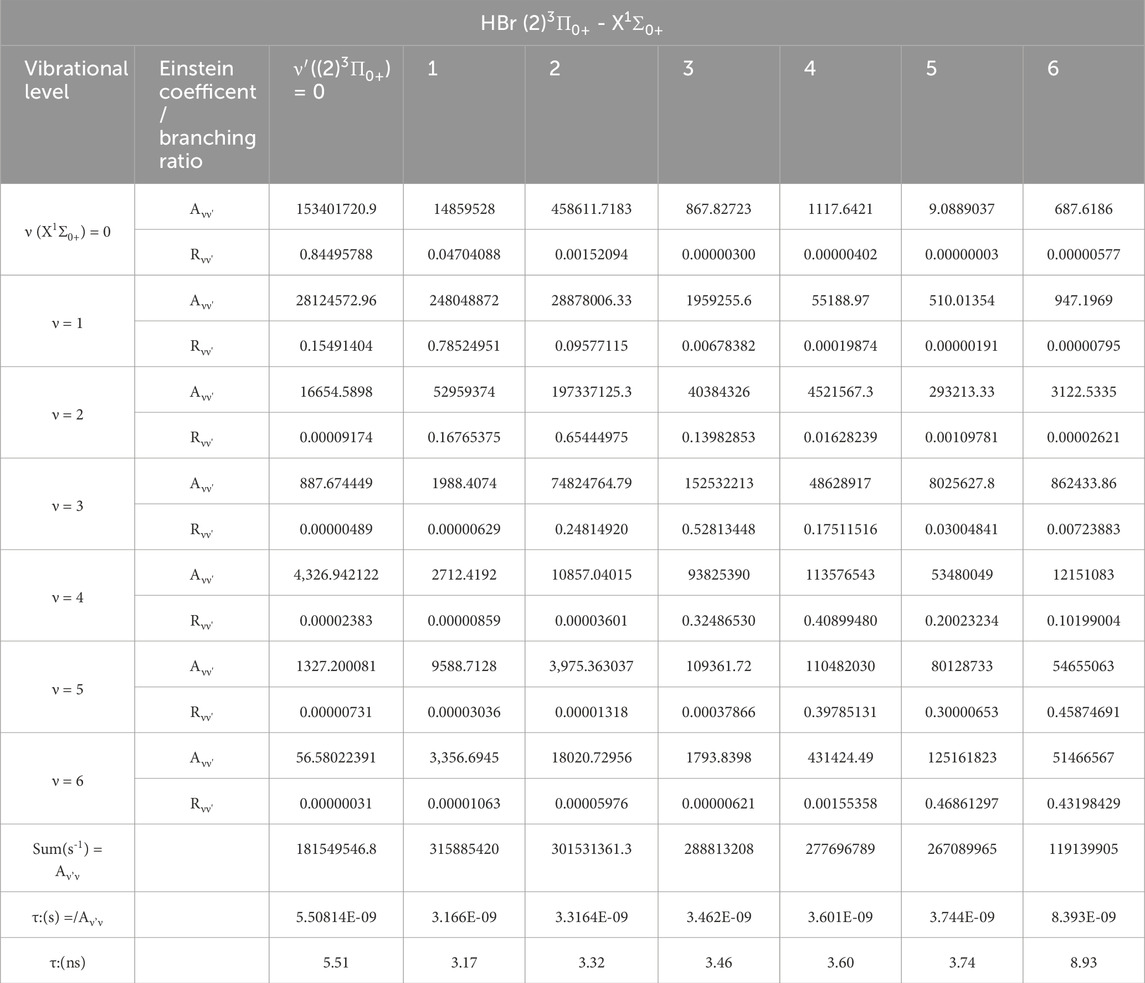
Table 3. The radiative lifetimes τ, and the Einstein coefficients and branching ratios of the vibrational transitions between the electronic states X¹Σ₀₊ - (2)³Π₀₊ of the molecule HBr.

Figure 5

Figure 5. Laser cooling scheme of the transition X¹Σ₀₊ - (2)³Π₀₊ of the molecule HBr.

Where m, T_ini, and a_max are, respectively, the mass, the initial temperature, and the maximum acceleration of the molecule, V_rms is the rms velocity, L_min is the minimum slowing distance, and T_r and T_d are the recoil and the Doppler temperatures respectively.

3.3 Absorption spectra of the P(2) and R(7) transitions in the HBr first-overtone band

To further assess the accuracy of our theoretical spectroscopic model and laser cooling study, we computed the line lists of the HBr molecule based on our ab initio calculations. These line lists were generated using the DUO [42], a general nuclear motion program developed by the ExoMol group at University College London, which can compute rotational, rovibrational, and rovibronic spectra of diatomic molecules. However, the potential energy curve and the permanent dipole moment curve of the X¹Σ⁺ ground state were used as DUO inputs to generate rovibrational energy levels of the X¹Σ⁺ state and the line lists of the X¹Σ⁺ − X¹Σ⁺ transition for the HBr. The primary approach employed by DUO to solve the radial equation is the sinc DVR (discrete variable representation) method. This technique typically ensures rapid convergence (faster than polynomial) of the computed energies and wavefunctions concerning the number of grid points, N_p. In our DUO calculations, a grid-based sinc DVR basis with 501 points, covering a range from 1.0 to 8 Å, is used to establish the vibrational basis functions. This study considers vibrational states up to $v\le 2$ and rotational states up to $J\le 50$, as our primary focus is on the lowest vibrational energy levels to investigate the first-overtone (v = 0–2) band of HBr. The line lists in this work follow the basic ExoMol format [43]. This format consists of an energy file (.states) (Supplementary Table S1) containing all the necessary information to describe each energy level and a transition file (.trans) (Supplementary Table S2), which provides the Einstein A coefficients for each transition. All data are available in the Supplementary Material. Subsequently, the absorption spectra of the P(2) and R(7) in the first-overtone band of the HBr molecule in the form of cross-sections were simulated using the generated line lists of the X¹Σ⁺ − X¹Σ⁺ transition. All spectra simulations were performed using ExoCross [44], a Fortran code for generating absorption/emission spectra at different temperatures and pressures. In our ExoCross calculations, we adopted the temperature at 294 K and the pressure at 100 mTorr (1.33 $\times$ 10⁻⁴ bar) to align with the experimental conditions. To compare our simulated spectra with the available experimental data work [45], the aim is to evaluate the absorption strength “absorbance” and present the absorption spectra of P(2) and R(7) in terms of absorbance values. According to the Beer-Lambert law, absorbance is related to the cross-section by $A=\sigma NL$ where σ denotes the molecular absorption cross-section (in cm²/molecule), N represents the number density of the absorbing molecules (in molecules/cm³), and L is the path length (in cm) through which the absorber is present. In the experiment [45], the path length was given as 73 cm, and the number density N can be determined using the relation: $N=P/k_{B}T$; where P is the pressure (in dyne/cm³), $k_B$ is the Boltzmann constant (1.38 $\times$ 10⁻¹⁶ erg/K), and T is the temperature (in Kelvin). An overview of the absorption spectra of the P(2) and R(7) transitions in the first-overtone band of the HBr molecule is illustrated in Figures 6, 7, respectively, where it is compared with the experimentally determined transitions by Chou et al. [45]. As shown in Figures 6, 7, the line positions for the P(2) and R(7) transitions of the HBr first overtone band are presented in terms of relative frequency (relative frequency = absolute frequency - the central frequency) for better comparison. In this study, the calculated central frequencies for P(2) and R(7) are 5,686.55 cm⁻¹ and 5,838.36 cm⁻¹, respectively, while the experimentally reported values are 4,993.02 cm^-1 and 5,126.9 cm⁻¹. Therefore, the theoretical and experimental frequencies show good agreement, with a relative percentage difference of 12%. Furthermore, our calculated absorbance values for the P(2) and R(7) transitions agree well with the previous measurement recorded by Chou et al. [45], as presented in Figures 6, 7, demonstrating the reliability of our results.

Figure 6

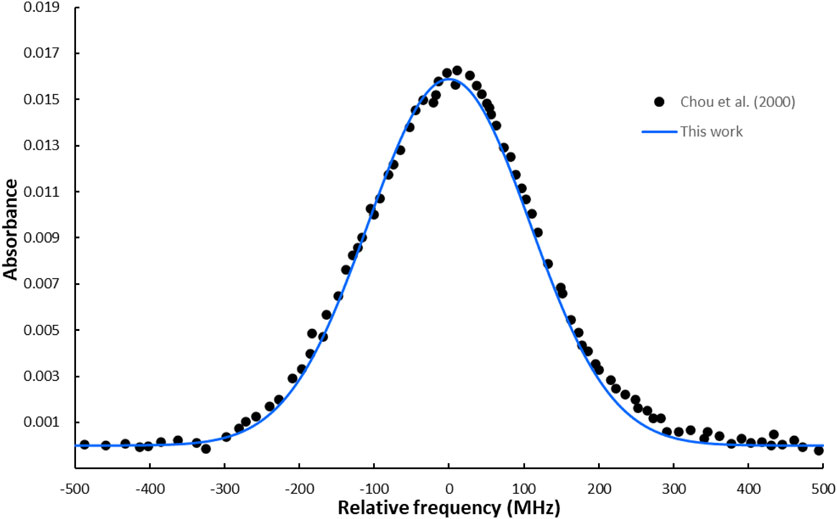
Figure 6. The simulated absorption spectrum of the P(2) transition in the first-overtone band of the HBr molecule using the Gaussian line profile at T = 294 K and a pressure of 100 mTorr.

Figure 7

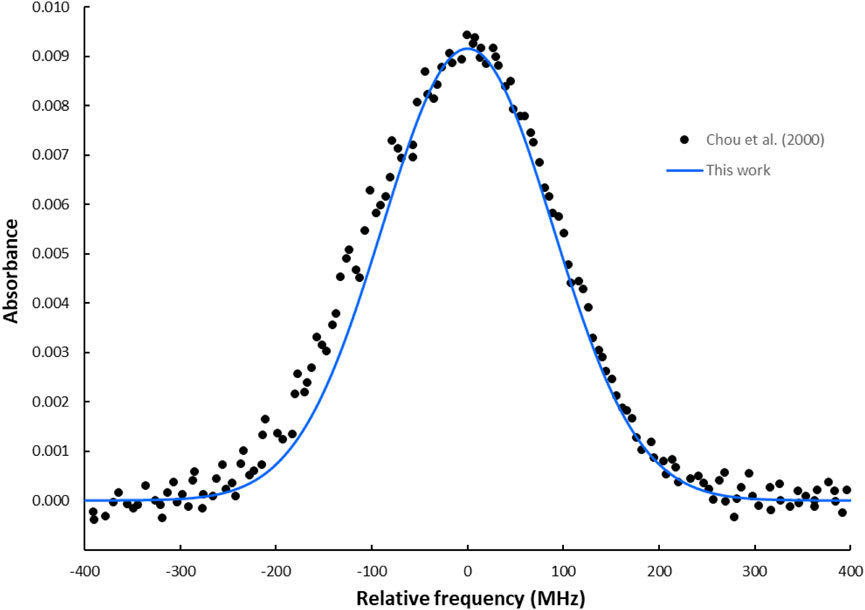
Figure 7. The simulated absorption spectrum of the R(7) transition in the first-overtone band of the HBr molecule using the Gaussian line profile at T = 294 K and a pressure of 100 mTorr.

4 Conclusion

In the present work, an ab initio calculation has been done for 13 free spin electronic states and nine electronic states, including the spin-orbit coupling effect of the molecule HBr. With the CASSCF/MRCI method, the potential energy curves and spectroscopic constants ${\mathrm{T}}_{\mathrm{e}}$, ${\mathrm{\omega }}_{\mathrm{e}}$ , ${\mathrm{B}}_{\mathrm{e}}$, ${\mathrm{R}}_{\mathrm{e}}$ have been calculated for the investigated electronic states, along with the static and transition dipole moments. The calculated values of the Franck-Condon factor, the Einstein coefficients $A_{v{v}^{\prime }}$, and the spontaneous radiative lifetime of the molecule HBr for the transition X¹Σ₀₊ - (2)³Π₀₊ shows its candidacy for direct laser cooling. Accordingly, the vibrational branching ratios, the number of cycles (N) for photon absorption/emission, the experimental parameters of this cooling, and the recoil and Doppler temperatures have been calculated. With four pumping and repumping lasers in the deep ultraviolet region, a laser cooling scheme is presented. By analyzing the potential energy and dipole moment curves and utilizing the DUO and ExoCross programs, we have investigated the absorption spectra of the P(2) and R(7) transitions in the first overtone (v = 0–2) band of the HBr molecule. The results demonstrate high accuracy when compared with experimental data, highlighting the reliability of our theoretical approach.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

KY: Writing – original draft. NE-K: Conceptualization, data curation, and writing – review and editing. NA: Writing – review and editing, Software, Formal Analysis. GY: Conceptualization, Writing – review and editing, Validation. MK: Writing – review and editing.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. This publication is based upon work supported by the Khalifa University of Science and Technology under Award No. RIG-2024-053 and the Abu-Dhabi Department of Education and Knowledge under award AARE20-031.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Any alternative text (alt text) provided alongside figures in this article has been generated by Frontiers with the support of artificial intelligence and reasonable efforts have been made to ensure accuracy, including review by the authors wherever possible. If you identify any issues, please contact us.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2025.1635859/full#supplementary-material

References

1. Barrow RF, Stamper JG. The absorption spectrum of gaseous hydrogen bromide in the schumann region I. Rotational Analysis Proc Roy Sot A (1961) 263:259. doi:10.1098/rspa.1961.0159

CrossRef Full Text | Google Scholar

2. Barrow RF, Stamper JG. The absorption spectrum of gaseous hydrogen bromide in the schumann region-II. Electronic states. Proc Roy Sot A (1961) 263:277. doi:10.1098/rspa.1961.0160

CrossRef Full Text | Google Scholar

3. Tilford SG, Ginter ML, Bass M. Electronic spectra and structure of the hydrogen halides the b³Π_i and C¹Π states of HI and DI. J Mol Spectrosc (1970) 34:327–40. doi:10.1016/0022-2852(70)90098-6

CrossRef Full Text | Google Scholar

4. Ginter ML, Tilford SC. Electronic spectra and structure of the hydrogen halides: states associated with the (σ²π³)cπ and (σ²π³)cσ configurations of HBr and DBr. J Mol Spectrosc (1971) 37:159–78. doi:10.1016/0022-2852(71)90049-X

CrossRef Full Text | Google Scholar

5. Stamper JG, Barrow RF. The v(¹σ⁺)—n(¹σ⁺) transition of hydrogen bromide. J Phys Chem (1961) 65:250–1. doi:10.1021/j100820a014

CrossRef Full Text | Google Scholar

6. Odashima H H. Isotopically invariant analysis of vibration–rotation transitions of HBr and its isotopologues. J Mol Spectrosc (2006) 240:69–74. doi:10.1016/j.jms.2006.08.010

CrossRef Full Text | Google Scholar

7. Regan MP, Langford SR, Orr-Ewing AJ, Ashfold MNR. The ultraviolet photodissociation dynamics of hydrogen bromide. J Chem Phys (1999) 110:281–8. doi:10.1063/1.478063

CrossRef Full Text | Google Scholar

8. Smolin AG, Vasyutinskii OS, Balint-Kurti GG, Brown A. Photodissociation of HBr. 1. Electronic structure, photodissociation dynamics, and vector correlation coefficients. J Phys Chem (2009) A110:5371–8. doi:10.1021/jp0562429

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Valero R, Truhlar DG, Jasper AW. Adiabatic states derived from a spin-coupled diabatic transformation: semiclassical trajectory study of photodissociation of HBr and the construction of potential curves for LiBr⁺. J Phys Chem A (2008) 112:5756–69. doi:10.1021/jp800738b

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Mahieu E, Zander R, Duchatelet P, Hannigan JW, Coffey MT, Mikuteit S, et al. Comparisons between ACE-FTS and ground-based measurements of stratospheric HCl and ClONO2 loadings at northern latitudes. Geophys Res Lett (2005) 32:L15S08. doi:10.1029/2005gl022396

CrossRef Full Text | Google Scholar

11. Jura M. Chlorine-bearing molecules in interstellar clouds. Astrophys J Lett (1974) 190:L33. doi:10.1086/181497

CrossRef Full Text | Google Scholar

12. Lincoln CD, DeMille D, Roman KV, Jun Y. Cold and ultracold molecules: science, technology, and applications. arXiv:0904.3175v1 [quant-ph] (2009) 11:055049. doi:10.1088/1367-2630/11/5/055049

CrossRef Full Text | Google Scholar

13. Huber KP, Herzberg G. Molecular spectra and molecular structure, vol. 4. Constants of diatomic molecules. Princeton: Van Nostrand (1979).

Google Scholar

14. Baig MA, Hormes J, Connerade JP, Garton WRS. Rotational analysis of a new electronic transition of HBr and DBr. J Phys B (1981) 14:L 147–51. doi:10.1088/0022-3700/14/4/006

CrossRef Full Text | Google Scholar

15. Pettersson LGM, Langhoff S. Theoretical electric dipole moments and dissociation energies for the ground states of GaH-BrH. J Chem Phys (1986) 85:3130–1. doi:10.1063/1.451025

CrossRef Full Text | Google Scholar

16. Alekseyev AB, Liebermann HP, Vázquez GJ, Lefebvre-Brion H. Coupled-channel study of the Rydberg-valence interaction in HBr. J Chem Phys (2018) 148:084302. doi:10.1063/1.5018167

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Shi D, Sun J, Chen Z, Liu Y, Zhu Z. Spectroscopic investigations on HBr (X¹Σ⁺) molecule using MRCI method in combination with correlation-consistent quintuple basis set augmented with diffuse functions. J Mol Struct Theochem (2009) 913:85–9. doi:10.1016/J.THEOCHEM.2009.07.022

CrossRef Full Text | Google Scholar

18. Chapman DA, Balasubramanian K, Lin SH. A theoretical study of spectroscopic properties and transition moments of HBr. Chem Phys (1987) 118:333–43. doi:10.1016/0301-0104(87)85068-1

CrossRef Full Text | Google Scholar

19. Botschwina P, Meyer W. A PNO–CEPA calculation of the barrier height for the collinear atom exchange reaction H′ + BrH→H′Br + H. Chem Phys (1977) 67:2390–1. doi:10.1063/1.435083

CrossRef Full Text | Google Scholar

20. Zlotkova SZ. Ph.D.thesis. Montreal: Concordia University (2006).

Google Scholar

21. Hans-Joachim W, Knowles JP. An efficient internally contracted multiconfiguration–reference configuration interaction method. J Chem Phys (1988) 89:5803–14. doi:10.1063/1.455556

CrossRef Full Text | Google Scholar

22. Werner HJ. Version, 2010.1, a package of ab initio programs (2010). Available online at: http://www.molpro.net/info/users.

Google Scholar

23. Allouche AR. Gabedit—A graphical user interface for computational chemistry softwares. J Comput Chem (2011) 32:174–82. doi:10.1002/jcc.21600

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Dolg M, Stoll H, Preuss H. Energy-adjusted ab initio pseudopotentials for the rare Earth elements. J Chem Phys (1989) 90:1730–4. doi:10.1063/1.456066

CrossRef Full Text | Google Scholar

25. Martin ML, Andreas S. Correlation consistent valence basis sets for use with the stuttgart–dresden–bonn relativistic effective core potentials: the atoms Ga–Kr and In–Xe. J Chem Phys (2001) 114:3408–20. doi:10.1063/1.1337864

CrossRef Full Text | Google Scholar

26. Walter SJ, Morris K, Harold B, Paul JG. Relativistic compact effective potentials and efficient, shared-exponent basis sets for the third-fourth-and fifth-row atoms. Can J Chem (1992) 70:612–30. doi:10.1139/v92-085

CrossRef Full Text | Google Scholar

27. Yousaf KE, Peterson AK. Optimized complementary auxiliary basis sets for explicitly correlated methods: Aug-cc-pVnZ orbital basis sets. Chem Phys Lett (2009) 476:303–7. doi:10.1016/j.cplett.2009.06.003

CrossRef Full Text | Google Scholar

28. Yang QS, Gao T. The feasibility of laser cooling: an investigation of ab initio of MgBr, MgI, and MgAt molecular. Spectrochimica Acta A: Mol Biomol Spectros (2020) 231:118107. doi:10.1016/j.saa.2020.118107

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Le Roy RJ. LEVEL: a computer program for solving the radial schrödinger equation for bound and quasibound levels. J Quant Spectrosc Radiat Transf (2017) 186:167–78. doi:10.1016/j.jqsrt.2016.05.028

CrossRef Full Text | Google Scholar

30. Bernath PF. Spectra of atoms and molecules. Oxford University Press (2020).

Google Scholar

31. Kang SY, Kuang FG, Jiang G, Li DB, Luo Y, Feng-Hui P, et al. Ab initio study of laser cooling of AlF⁺ and AlCl⁺ molecular ions. J Phys B At. Mol Opt Phys (2017) 50:105103. doi:10.1088/1361-6455/aa6822

CrossRef Full Text | Google Scholar

32. El Kher NA, Korek M, Alharzali N, El-Kork N. Electronic structure with spin-orbit coupling effect of HfH molecule for laser cooling investigations. Spectrochimica Acta A: Mol Biomol.r Spectros.y (2024) 314:124106. doi:10.1016/j.saa.2024.124106

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Zeid I, El-Kork N, Chmaisani W, Korek M. A theoretical electronic structure with a feasibility study of laser cooling of LaNa molecules with a spin-orbit effect. Phys Chem Chem Phys (2022) 24:7862–73. doi:10.1039/d1cp05210a

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Li R, Yuan X, Liang G, Wu Y, Wang J, Yan B. Laser cooling of the SiO⁺ molecular ion: a theoretical contribution. Chem Phys (2019) 525:110412. doi:10.1016/j.chemphys.2019.110412

CrossRef Full Text | Google Scholar

35. Peng Q, Zong N, Zhang SJ, Wang ZM, Yang F, Zhang FF, et al. DUV/VUV all-solid-state lasers: twenty years of progress and the future. IEEE J selected Top Quan Electron (2018) 24(5):1–12. doi:10.1109/JSTQE.2018.2829665

CrossRef Full Text | Google Scholar

36. Ceflas AC, Dubinskii MA, Sarantapoulou E, Abdulsabirov RY, Korabbeva SL, Naumov AK, et al. On the development of new VUV and UV solid state laser sources for photochemical applications. Laser Chem (1993) 13:143–50. doi:10.1155/1993/75972

CrossRef Full Text | Google Scholar

37. Xuan H, Igarashi H, Ito S, Q. C, Zhao Z, Kobayashi Y. High-power, solid-state, deep ultraviolet laser generation. Appl Sci (2018) 8:233. doi:10.3390/app8020233

CrossRef Full Text | Google Scholar

38. Metcalf HJ, Van der Straten P. Laser cooling and trapping of atoms. J Opt Soc Am B (2003) 20:887. doi:10.1364/JOSAB.20.000887

CrossRef Full Text | Google Scholar

39. Moussa A, El-Kork N, Korek M. Laser cooling and electronic structure studies of CaK and its ions CaK^±. New J Phys (2021) 23:013017. doi:10.1088/1367-2630/abd50d

CrossRef Full Text | Google Scholar

40. El-Kork N, AlMasri AA, Abu El Kher N, Assaf J, Ayari T, Alhseinat E, et al. Laser cooling with intermediate state of spin-orbit coupling of LuF molecule. Scientific Rep (2023) 13:7087. doi:10.1038/s41598-023-32439-1

CrossRef Full Text | Google Scholar

41. Barry JF Laser cooling and slowing of a diatomic molecule, CT. YALE UNIV NEW HAVEN (2013).

Google Scholar

42. Yurchenko SN, Lodi L, Tennyson J, Stolyarov AV. Duo: a general program for calculating spectra of diatomic molecules. Computer Phys Commun (2016) 202:262–75. doi:10.1016/j.cpc.2015.12.021

CrossRef Full Text | Google Scholar

43. Tennyson J, Hill C, Yurchenko SN. Data structures for exomol: molecular line lists for exoplanet and other atmospheres. AIP Conf Proc (2013) 1545:186–95. doi:10.1063/1.4815853

CrossRef Full Text | Google Scholar

44. Yurchenko SN, Al-Refaie AF, Tennyson J. Exocross: a general program for generating spectra from molecular line lists. Astron and Astrophysics (2018) 614:A131. doi:10.1051/0004-6361/201732531

CrossRef Full Text | Google Scholar

45. Chou S-I, Baer DS, Hanson RK. High-resolution measurements of HBr transitions in the first overtone band using tunable diode lasers. J Mol Spectrosc (2000) 200:138–42. doi:10.1006/jmsp.1999.8038

PubMed Abstract | CrossRef Full Text | Google Scholar