Analysis and application for the source-free circuits

Introduction: Memristor systems and their application circuits have attracted growing research interest. When a memristor circuit/network is designed, both memristors and conventional electronic components are inevitably required, particularly energy storage elements (e.g., capacitors and inductors). It has found that most existing studies focus on oscillatory phenomena generated by memristive systems, such as chaotic attractors, period-doubling oscillations, spiking and bursting oscillations. However, there is a notable lack of literature exploring and analyzing the energy exchange between these components, as well as the resulting oscillatory behaviors and outcomes arising from such interactions. It is well known that the unit of a memristor, like that of a resistor, is the ohm (Ω). In general circuits, the energy exchange between resistors and energy storage elements can induce nonlinear behaviors such as step functions, damping phenomena, both of which stem from the energy exchange between resistors and capacitors/inductors. So, when a memristor (though physical implementations are rare, several classic mathematical models exist) exchanges energy with energy storage elements, will similar behaviors emerge?

Methods: In this paper, to advance the theoretical completeness of memristive systems and take the classical HP memristor model as an example, four source-free circuit topologies integrating memristors with energy-storage elements are investigated deeply. They are categorized into two types: R_MC/R_ML circuits and series/parallel R_MLC circuits. Firstly, through mathematical modeling, the four circuits are all found to be governed by transcendental equations. Secondly, two types of four-component source-free circuits are configured and analysis. Finally, the application circuits comprising four fundamental components was configured and explored.

Results and Discussion: Simulation results for the mathematical models of the four circuits demonstrate memristor states (R₀, kR_d) and energy-storage elements collectively regulate response characteristics, damped oscillatory and decay behavior. The active power and apparent power curves reveal distinct energy exchange behaviors between components, differing fundamentally from conventional RL, RC, and RLC circuits. These findings demonstrate that due to the presence of memristors, such circuits cannot be employed for step response generation, but are exclusively applicable for energy memorization and dissipation. Then, the following conclusion on two types of source-free circuits are demonstrated: (1) capacitor and inductor provide energy (i.e., ϕ and q) to the system, while memristors exhibit hysteretic behavior, collectively and fundamentally co-modulating oscillation modes and attractor phenomenon; (2) The dual characteristics of memristors—memory capability and energy dissipation—endow them with the potential to break the von Neumann bottleneck, making them essential candidates for implementing next-generation neural networks and AI systems. Finally, the application circuits reveal that even within the same circuit, varying memristor placements can lead to distinct topological configurations and divergent nonlinear output behaviors. This phenomenon further validates the unique characteristics of memristors as an emerging field. These findings establish a solid theoretical and experimental foundation for future exploration and development of memristive systems, including next-generation neural networks, artificial intelligence applications, and aerospace technologies.

1 Introduction

The memristor has been hypothesized as the fourth fundamental circuit component [1] and named. Its fingerprint is a pinched hysteresis loop [2], which is the recovery of pure resistance (no hysteresis) for high frequencies [1, 2]. Subsequently, the HP-memristor was proposed and fabricated as a canonical model. Due to the special electrical properties of nonvolatile memory and extraordinary nonlinearity, the memristor is usually adopted to design the artificial neural networks, memristive circuits, oscillation circuits and employed for unmanned aerial vehicles and motors. Currently, the discussion is focused not only on the application to computation and memory storage, but also on the fundamental role in nonlinear circuit theory. For instance, real synaptic circuits [3, 4]. biological neurons [5–8], behaviors of some neural network models [9, 10], and even some complex systems [11, 12] with memristors or memristor emulators [11, 13–16, 29]. Also, some meaning and interesting nonlinear behaviors and application have also been discovered and published [17], integration to mention just a few.

Totally, all above involved results contributed to improving the circuit theory and exploring related applications in the fields of circuit engineering, such as mathematics, physics, and aerospace circuits. According to the definition of the memristor, whose value depends on its internal parameter, which in turn has to evolve dynamically according either to current and voltage [2]. In other words, when the memristor was configured into one real circuit, the relationship $(d\mathrm{\Phi }=R_{M}dq)$ between its resistance and the state variable is the essence of characterizing the memristor [15, 18], which have been considered as the basic information to analyze the nonlinear and oscillation behaviors [15, 18], such as chaotic circuits [19], damping circuits [20], Bessel filter [21], diode bridge rectifier [22], and oscillation memristive circuit [23, 30], etc. Some of them addressed and studied the dynamics, and the other showed the complicated chaotic phenomenon [24–26]. Furthermore, there are some literatures focused on the memristive oscillators, chaotic attractors [12, 24, 31], and application in synaptic [3], neuron networks [4–7, 10, 11, 24, 27, 28], and oscillation phenomenon [14, 16, 17], and so on.

Furthermore, it has found that most existing studies focus on oscillatory phenomena generated by memristive systems, such as chaotic attractors, period-doubling oscillations, spiking and bursting oscillations. However, there is a notable lack of literature exploring and analyzing the energy exchange between these components, as well as the resulting oscillatory behaviors and outcomes arising from such interactions. It is well known that the unit of a memristor, like that of a resistor, is the ohm $(\mathrm{\Omega })$. In general circuits, the energy exchange between resistors and energy storage elements can induce nonlinear behaviors such as step functions, damping phenomena, both of which stem from the energy exchange between resistors and capacitors/inductors. So, when a memristor (though physical implementations are rare, several classic mathematical models exist) exchanges energy with energy storage elements, will similar behaviors emerge? In this paper, to advance the theoretical completeness of memristive systems and take the classical HP memristor model as an example, four source-free circuit topologies integrating memristors with energy-storage elements are investigated deeply. They are categorized into two types: $R_{M}C/R_{M}L$ circuits and series/parallel $R_{M}LC$ circuits. Firstly, through mathematical modeling, the four circuits are all found to be governed by transcendental equations. Simulation results demonstrate memristor states $R_0$, $k{R}_d$ and energy-storage elements collectively regulate response characteristics, damped oscillatory and decay behavior. The active power and apparent power curves reveal distinct energy exchange behaviors between components, differing fundamentally from conventional $RL$, $RC$, and $RLC$ circuits. These findings demonstrate that due to the presence of memristors, such circuits cannot be employed for step response generation, but are exclusively applicable for energy memorization and dissipation. Secondly, two types of four-component source-free circuits are configured and the following conclusion are demonstrated: (1) energy-storage elements provide energy (i.e., $\varphi$ and $q$): to the system, while memristors exhibit hysteretic behavior, collectively and fundamentally co-modulating oscillation modes and attractor phenomenon; (2) The dual characteristics of memristors—memory capability and energy dissipation—endow them with the potential to break the von Neumann bottleneck, making them essential candidates for implementing next-generation neural networks and AI systems. Finally, the application circuits comprising four fundamental components was configured and explored. The study reveals that even within the same circuit, varying memristor placements can lead to distinct topological configurations and divergent nonlinear output behaviors. This phenomenon further validates the unique characteristics of memristors as an emerging field. These findings establish a solid theoretical and experimental foundation for future exploration and development of memristive systems, including next-generation neural networks, artificial intelligence applications, and aerospace technologies. Moreover, once the fundamental rules are improved, more and more foundations could be refined and continual applications in the theories and overall design process, such as nonlinear circuits, the avionics for unmanned aerial vehicle systems, as we shall see.

The remainder of this paper is organized as follows: In Sec II, the information on HP memristive system and two types of general source-free circuits are presented. In Section III, both source-free circuits are introduced, that is, $R_{M}C$ and $R_{M}L$ circuits. Then, their mathematical models, novel time constant, the response curves, the trajectories of the power dissipated and energy absorbed are performed, respectively. In Section IV, both series and parallel source-free $R_{M}LC$ circuits are analyzed. In Section V, the application circuits with four components are provided and demonstrate the influence of energy storage elements or memristors on the frequency and oscillatory behaviors. Finally, the paper is summarized in Section VI.

Notably, all the curves in this paper are tested by the software MATLAB R2018a Version, which is a programming and numeric computing platform used by millions of engineers and scientists to analyze data, develop algorithms, and create models.

2 HP memristor and gerenal source-free circuits

As both one fundamental 2-port electric component and the classical model, HP-memristor $(R_M)$ has been proposed and manufactured as the charge-controlled memristor [2–4, 20–22]. Its model could be given as follows

$R_M=\frac{d\phi }{dq}=R_{\mathit{off}}-\frac{{\mu }_v{R}_{\mathit{off}}}{D^2}{R}_{on}\cdot q\left(t\right)(1)$

where, there are two regions: one region with a high dopant concentration with low resistance $R_{on}$, the other region has a low concentration of dopant with a considerably higher resistance $R_{\mathit{off}}$. Also, the Equation 1 was named as the linear drift model due to the velocity of the width being linearly proportional to the current. Then, the variable $q(t)$ has been considered as the charge and means the integral of the current $i(t)$.

In order to study the universality of this class of memristive systems, it can be re-written as

$\left\{\begin{array}{c}{R}_M=R_0+k{R}_d\int idt=R_0+k{R}_d\cdot q\hfill \\ R_M=u_M\left(t\right)/i_M\left(t\right)\hfill \end{array}\right.(2)$

where the variable $u_M(t)$ is the cross voltage, $i_M(t)$ as one function of current and has been defined as the rate of change of the state variable. Defining the parameters $R_0$, $k$ and $R_d$ jointly reflect the relationship between $u_M(t)$ and $i_M(t)$. Then, the parameter $R_0$ stands in the region which has a low concentration of dopant with a considerably higher resistance $R_{\mathit{off}}$. The parameter $R_d$ is one region with a high dopant concentration and low resistance $R_{on}$. The parameter $k=-\mu V{R}_{\mathit{off}}/D^2$ is defined as a coefficient.

The important trajectory curves are depicted in Figure 1.

Figure 1

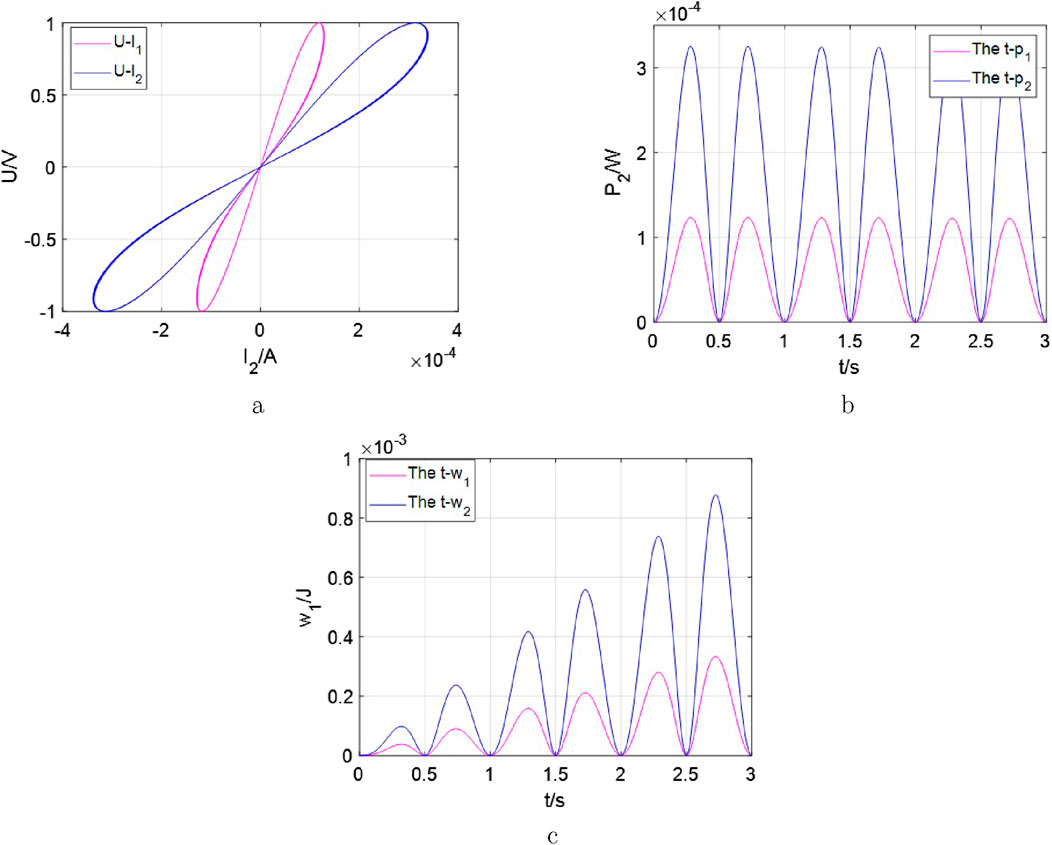
Figure 1. Several important relationships between different variants for the memristors, $k{R}_{d1}=10^6$, $R_{01}=16k$ in $R_{M1}$ and $R_{02}=6k$, $k{R}_{d1}$ = $10^6$ in $R_{M2}$, $dq(t)/dt=i(t)=sin(2t)$. (a) the curves of $v-i$ phase. (b) $p(t)$ by the memristor. (c) $w(t)$ by the memristor.

From Figure 1, it can be seen that these curves are the fingerprints, the dissipated power and energy absorbed in time-domain graphs for the single memristor. They are so complex but cannot be applied directly like the other general discrete elements. Due to the characteristics of the memristive system, its power exhibits a frequency doubling phenomenon. Thus, the related basic fundamentals should be examined as soon as possible via the $n$-order circuit model with the $R_M$ and an energy storage element.

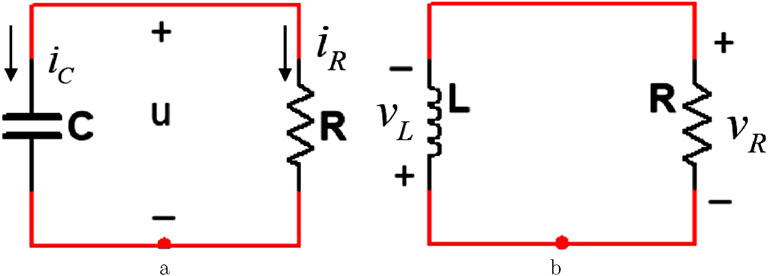
In circuit theory, for an ordinary circuit, there are two excitation methods. One method involves independent sources. The other utilizes the initial conditions of storage elements within the circuit, which are so-called source-free circuits. When energy is initially stored in capacitive or inductive elements, this stored energy drives current flow, which is gradually dissipated in resistors. The rate of dissipation can be calculated by Kirchhoff’s laws. This way has been considered as a sufficient, powerful set of tools to analyze a large variety of electric circuits all the time. Now, this method could be utilized to analyze the following circuits, such as $R_{M}C$ and $R_{M}L$ circuits. The classical first-order source-free circuits are shown as Figure 2.

Figure 2

Figure 2. Two types of the classical source-free circuits. (a) $RC$ circuit. (b) $RL$ circuit.

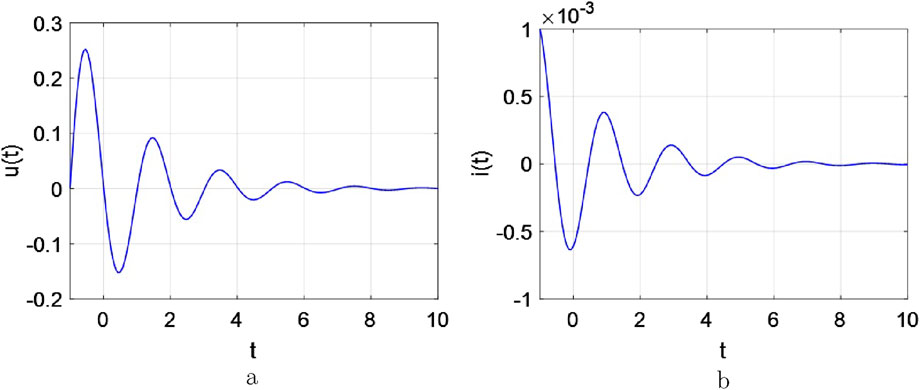
Observing from Figure 2a, when the initial condition is $u(0)=U_0$, the voltage response of the $RC$ circuit could be expressed by an exponential decay of the initial voltage. Also, this result is attributed to the initially stored energy and the circuit’s intrinsic characteristics, rather than its external voltage or current sources. Similar to Figure 2b, it is shown that the natural response of the $RL$ circuit is also an exponential decay of the initial current. Furthermore, the time constant for both $RC$ and $RL$ circuits have been defined as $\tau =RC$ and $\tau =L/R$. Subsequently, the natural response could be illustrated graphically in Figures 3, 4. It has been evidence that an exponential decay of the initial condition, dissipated power and the absorbed energy by the resistor for the $RC$ circuit are also given by Equation 3, as the current responses for the $RL$ circuit are shown by Equation 4.

Figure 3

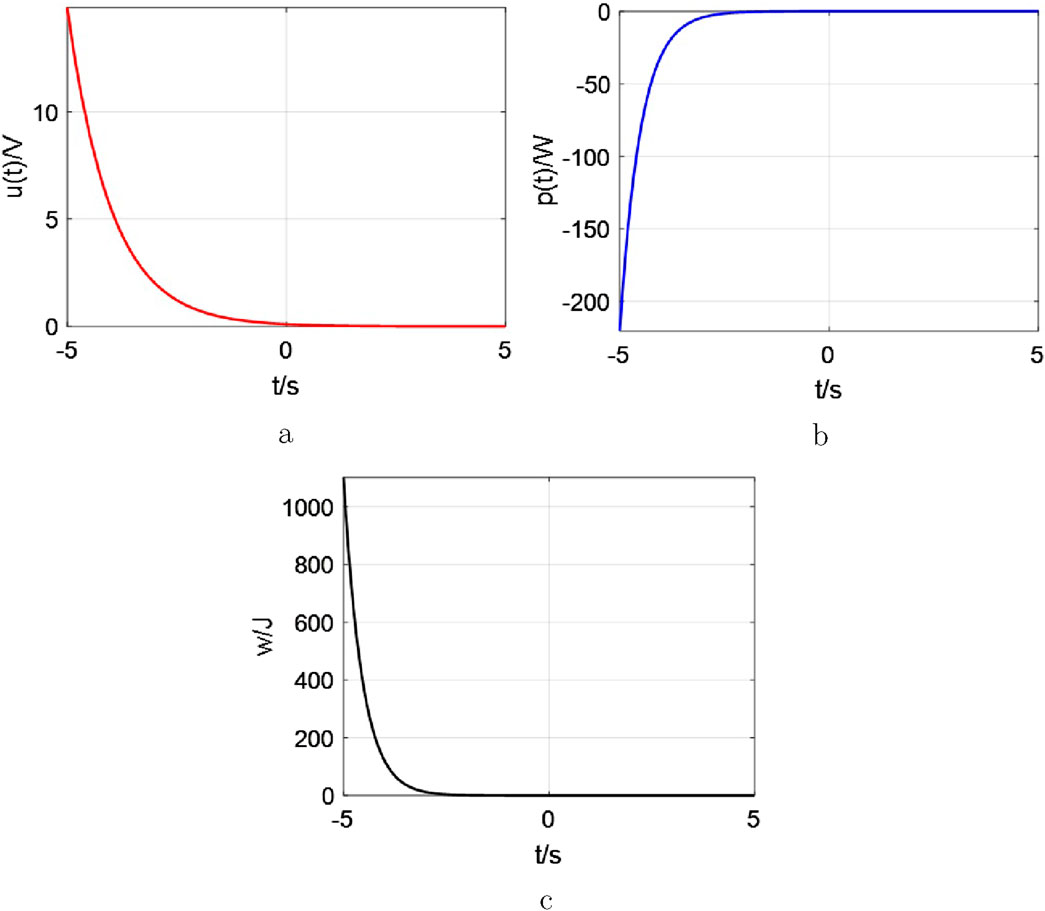
Figure 3. The natural response of the $RC$ circuits, $u(t_0)=U_0=0.1V$, $R=1$, $C=1F$. (a) the curve of the voltage response. (b) $p(t)$ by the resistor. (c) $w(t)$ absorbed by the resistor.

Figure 4

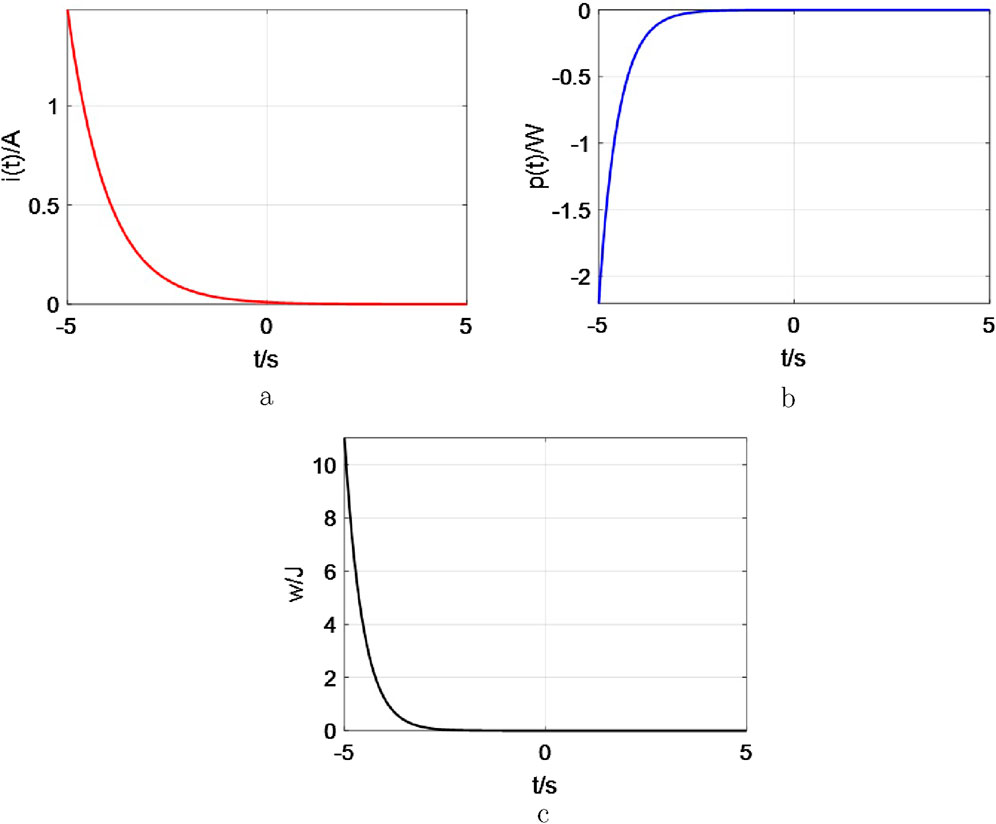
Figure 4. The natural response of the $RL$ circuits, $i(t_0)=I_0=0.01A$, $R=1$, $L=1H$. (a) the curve of current response. (b) $p(t)$ by the resistor. (c) $w(t)$ by the resistor.

For the source-free $RC$ circuit, when the initial condition $u(t_0)=u(0)=U_0$, the results could be given as follows

$\left\{\begin{array}{c}\begin{array}{cc}\hfill u\left(t\right)=U_0{e}^{-t/\tau },\hfill & \hfill \tau =RC\hfill \end{array}\hfill \\ p\left(t\right)=u\left(t\right)i_R\left(t\right)=-\frac{U_0^2}{R}{e}^{-2t/\tau }\hfill \\ w\left(t\right)={\int }_0^{t}p\left(t\right)dt=\frac{1}{2}C{U}_0^2\left(1-e^{-2t/\tau }\right)\hfill \end{array}\right.(3)$

For the source-free $RL$ circuit, when the initial condition $i(t_0)=i(0)=I_0$, the results could be computed as follows

$\left\{\begin{array}{c}\begin{array}{cc}\hfill i\left(t\right)=I_0{e}^{-t/\tau },\hfill & \hfill \tau =L/R\hfill \end{array}\hfill \\ p\left(t\right)=u\left(t\right)i_R\left(t\right)=I_0^{2}R{e}^{-2t/\tau }\hfill \\ w\left(t\right)={\int }_0^{t}p\left(t\right)dt=\frac{1}{2}L{I}_0^2\left(1-e^{-2t/\tau }\right)\hfill \end{array}\right.(4)$

Observed from Figures 3, 4, when $t\to \infty$, $w_R\left(\infty \right)\to \frac{1}{2}C{U}_0^2$ for the $RC$ circuit and $w_R\left(\infty \right)\to \frac{1}{2}L{I}_0^2$ for the $RL$ circuit could be observed. They are the same as the energy initially stored in the capacitor $(w_c(0))$ element in Equation 3 and inductor $(w_L(0))$ element in Equation 4.

The above has already provided a complete description for the properties of classical first-order circuits. Next, we pose a question: when resistors are substituted with memristors (e.g., HP memristors), what kind of conclusions could be obtained? For this purpose, the following$R_{M}C$ and $R_{M}L$ circuits will be configured and analyzed in the next section.

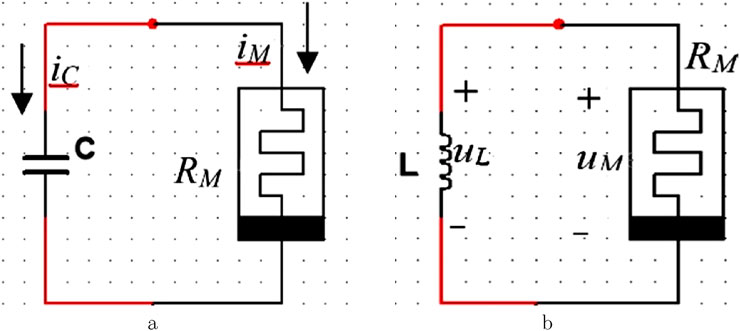
3 The source-free $R_{M}C$ and $R_{M}L$ circuits

3.1 The source-free $R_{M}C$ circuits

The produced source-free $R_{M}C$ circuit could be drawn as Figure 5a. Applying Kirchhoff’s Laws $(i=i_C=i_M)$ yields

$\left(R_0+k{R}_{d}q\right)C\frac{d{u}_c}{dt}+u_c=0(5)$

where, the variable $u(t)=u_c(t)$ stands for the voltage of the capacitor. Notably that $dq(t)/dt=i(t)=i_M(t)=i_C(t)$ is the intrinsic variable for Figure 5a. Let ${\tau }_0=R_{0}C$ and $b=k{R}_{d}C/R_0$, the terms could be depicted as

$\ln u+b\cdot u=-\frac{t}{{\tau }_0}(6)$

Figure 5

Figure 5. The source-free circuits with charge-controlled memristor. (a) $R_{M}C$ circuit. (b) $R_{M}L$ circuit.

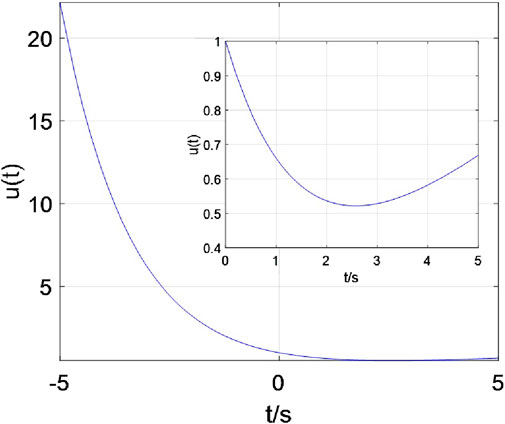
Obviously, Equation 6 a transcendental equation whose solution can only be computed using approximations and cannot be obtained exactly. The natural response curve of the Equation 5 could be illustrated graphically in Figure 6.

Figure 6

Figure 6. The natural response of the $R_{M}C$ circuits, the initial value of $k{R}_d=0.8\ast 10^6$, $R_0=16k$, $C=1mF$

From Figure 6, this response curve is fundamentally distinct from that of an $RC$ circuit (characterized by a single exponential curve), where the energy stored in the capacitor is entirely dissipated by the resistor. It is more complex and constitutes both exponential and non-exponential functional components. Crucially, although the memristor’s unit is also the ohm $(\mathrm{\Omega })$, its model reveals that it consists of both linear and nonlinear resistive components [1,2]. Here, the linear resistive component exhibits the conventional ”energy-dissipation” characteristic of resistors, as manifested by the exponential segment of the curve. However, the energy stored in the capacitor is not fully consumed the remaining portion is ”memorized” by the nonlinear component, which corresponds to the non-exponential segment of the curve. Then, according to the definition of the time constant, setting ${\tau }_0=R_{0}C$ and calculators $b$ for this $R_{M}C$ circuit. When the circuit is excited, $C$ provides the stored energy to the $R_M$, the $R_M$ works for both memorizing the information and energy dissipation profile, immediately. Memory speed depends on this new time constant $({\tau }_0)$.

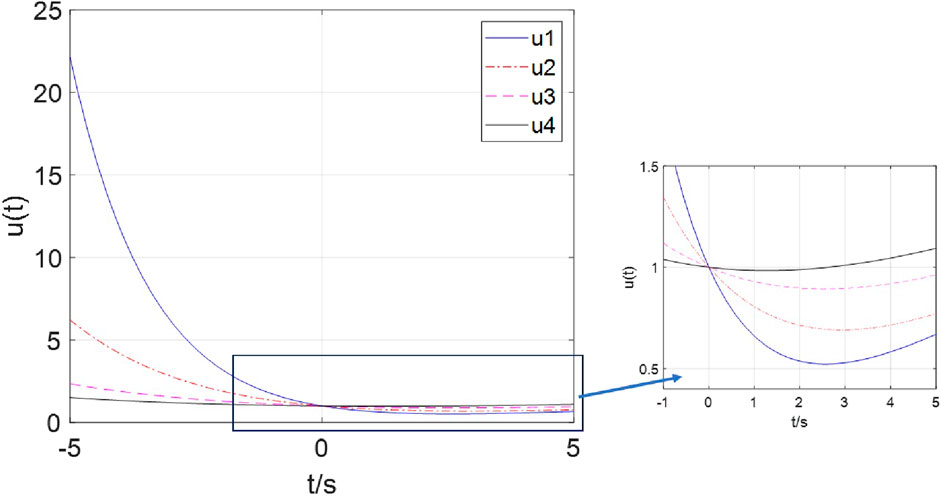
There are three variables related to the decay of the voltage response $u_C(t)$, which are $R_d$, $R_0$ and $C$. Next, the decay behavior would be discussed when only one variable is changed and the other ones are fixed.

(1) when $k{R}_d=0.8\ast 10^4$ and $C=1mF$, changing the variable $R_0$, the response $u_C(t)$ are illustrated in Figure 7.

Figure 7

Figure 7. The curve of the voltage response with $R_{01}=16k$ in blue, $R_{02}=26k$ in red, $R_{03}=46k$ in pink, $R_{04}=66k$ in black.

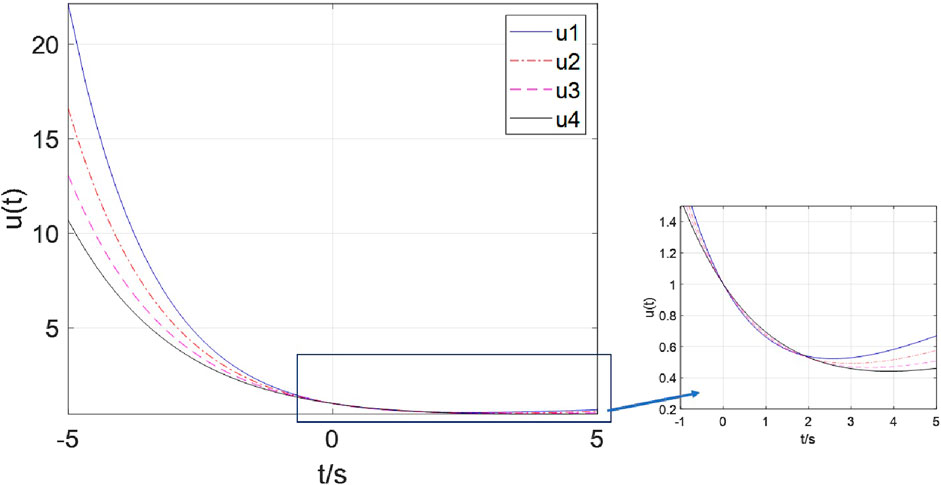
Observe from Figure 7, When $t<0$, the blue curve resides innermost while the black curve lies outermost; when $t>0$, the blue curve shifts to the bottom position and the black curve to the top. This demonstrates that as the value of $R_{01}$ increases, the curves become progressively flatter, indicating slower rates for both energy dissipation (“consumption”) and memory retention (“memorization”). Then, the following conclusion could be drawn:

i. A smaller $R_0$ results in a larger ${\tau }_0$ with faster decay dynamics.

ii. A smaller $R_0$ value leads to a significant increase in the proportion of the exponential segment of the curve. The more pronounced the “energy dissipation” component becomes, the more enhanced the ”memory” effect appears.

iii. A certain energy exists to memorize information for the memristor. Therefore, the voltage $u_C(t)$ cannot decay to 0 at the $t=0$.

(2) when $k{R}_d=0.8\ast 10^4$ and $R_0=16k$, changing the capacitance $C$, the response $u_C(t)$ are illustrated in Figure 8.

Figure 8

Figure 8. The curve of the voltage response with $C=1mF$ in blue, $C=1.1mF$ in red, $C=1.2mF$ in pink, $C=1.3mF$ in black.

From Figure 8, when $t<0$, the blue curve resides innermost while the black curve lies outermost; However, when $t>0$, the blue curve shifts to the top position and the black curve to the bottom. This demonstrates that as the value of $C$ increases, the curves exhibits a significantly steepened profile, indicating faster rates for both energy dissipation (“consumption”) and memory retention (“memorization”). Then, similar results are still observed.

i. A smaller $C$ results in a larger ${\tau }_0$ with faster decay dynamics.

ii. A smaller $C$ value leads to a significant increase in the proportion of the exponential segment of the curve. The more pronounced the “energy dissipation” component becomes, the more enhanced the “memory” effect appears.

iii. A certain voltage is required to memorize information for the memristor. Therefore, the voltage $u_C(t)$ cannot decay to 0 at the $t=0$. However, the different capacitor $C$ could provide the different storage voltage to the memory.

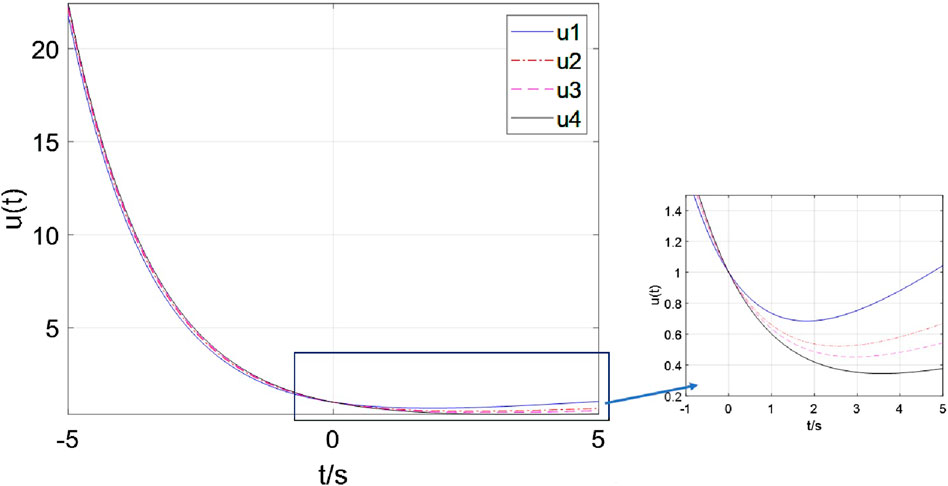
(3) when $C=1mF$ and $R_0=16k$, changing the variable $R_d$, the response $u_C(t)$ are illustrated in Figure 9.

Observed from Figure 9, when $t<0$, the black curve resides innermost while the blue curve lies outermost; when $t>0$, the blue curve shifts to the top position and the black curve to the bottom. This demonstrates that as the value of $k{R}_d$ increases, the curves exhibits a significantly steepened profile, indicating faster rates for both energy dissipation (“consumption”) and memory retention (“memorization”). Due to the minimal variation in $k{R}_d$, the distinction between the curves is not particularly pronounced. Then, different results can be obtained:

i. A larger $k{R}_d$ results in a larger ${\tau }_0$ with faster decay dynamics.

ii. A larger $k{R}_d$ value leads to a significant increase in the proportion of the exponential segment of the curve. The more pronounced the “energy dissipation” component becomes, the more enhanced the “memory” effect appears.

iii. A certain energy exists to memorize information for the memristor. Then, the voltage $u_C(t)$ cannot decay to 0 at the $t=0$.

Figure 9

Figure 9. The curve of the voltage response with $k{R}_{d1}=0.5\ast 10^4$ in blue, $k{R}_{d2}=0.8\ast 10^4$ in red, $k{R}_{d3}=10^4$ in pink, $k{R}_{d4}=1.5\ast 10^4$ in black.

It should be noted that when applying both $RC$ and $RL$ circuits, they could be treated as the step functions to configure plenty of circuit-networks. However, both $R_{M}C$ and $R_{M}L$ circuits are not the step functions. They do not focus on storing and consuming energy, but on memorizing pieces of information. Secondly, the speed of memorizing information is associated with the determined new time constant $({\tau }_0)$. The larger ${\tau }_0$ could lead to the faster the decay as well as speed of memorizing pieces of information. Thirdly, the memristor $(R_M)$ satisfies dual properties: memory $(R_0)$ and energy consumption $(k{R}_d)$.

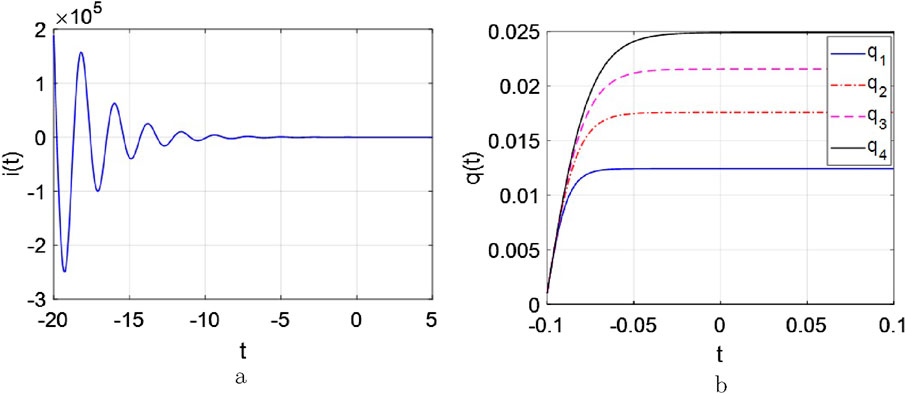
Finally, the dissipated power and the absorbed energy by the memristor for the $R_{M}C$ circuit are depicted in Figure 10.

Figure 10

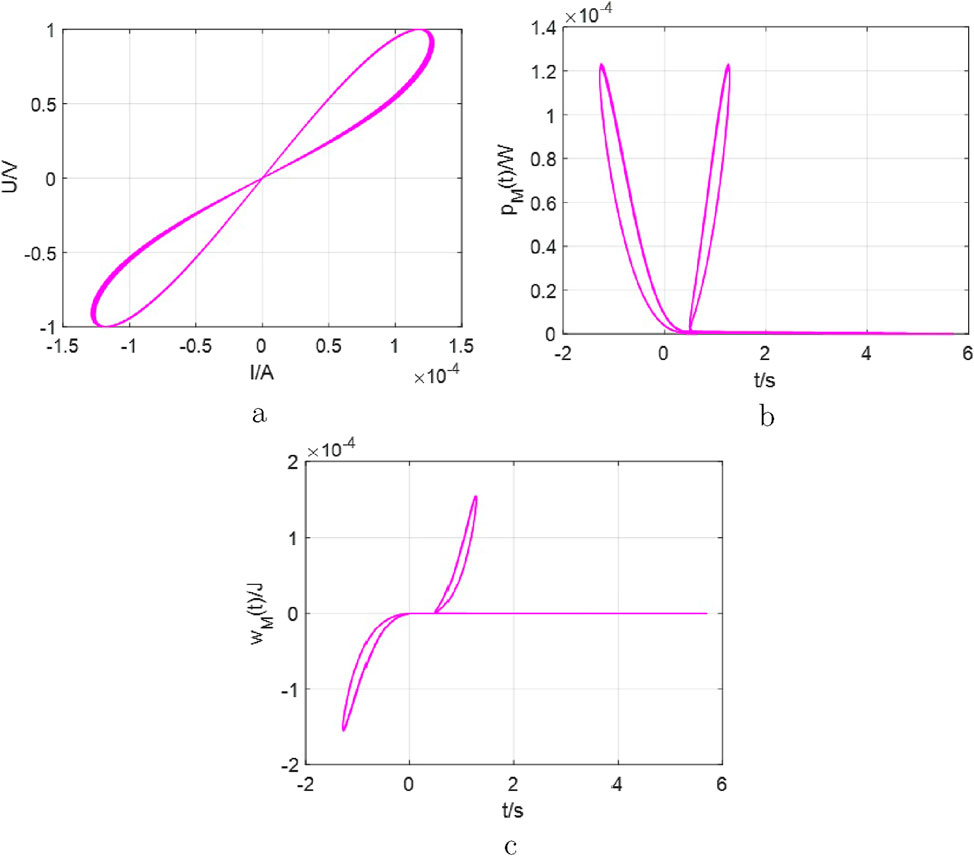
Figure 10. The curves for the $R_{M}C$ circuit with the parameters $k{R}_d=0.8\ast 10^6$, $R_0=16k$, $C=1mF$. (a) the fingerprint characterizes of $v-i$ for $R_M$). (b) the dissipated power by the memristor up to time $t/s$). (c) the energy $(w(t))$ absorbed by the memristor up to time $t/s$).

Between Figure 1 and Figure 10a, the fingerprint characteristics have been presented. Observed from Figure 10b, some information could be memorized by $R_{M}C$ circuit. Furthermore, dissipative power and absorbed energy are utilized for information storage. This reaffirms the memristor’s fundamental divergence from resistors even though they shared dimensional homogeneity and common unit of ohms $(\mathrm{\Omega })$. Moreover, their distinct time constants $({\tau }_0)$ manifests the memory functionality, not the energy dissipation profile.

3.2 The source-free $R_{M}L$ circuits

The inductor $(L)$ is the other type of energy storage element. In this subsection, the $R_{M}L$ circuit would be configured and discussed. Similar to analyzing the $R_{M}C$ circuit, consider one memristor circuit as shown in Figure 5b.

Applying Kirchhoff’s Laws $u_L+u_M=0$, $i=i_L=i_M$ and Figure 4b, yields

$L\frac{di}{dt}+R_{0}i+k{R}_{d}q\cdot i=0(7)$

where the variable $i(t)$ stands for the current through the inductor. Hereby, $dq(t)/dt=i(t)=i_M(t)=i_L(t)$ is the determined relationship. Also, let ${\tau }_0=L/R_0$. Obviously, this is also a higher-order transcendental equation. Its natural response curve of the Equation 7 could be illustrated graphically in Figure 11.

Figure 11

Figure 11. The natural response of the $R_{M}L$ circuits, the initial value of $k{R}_d=0.8\ast 10^6$, $R_0=16k$, $L=0.1H$. (a) $i(t)-t$). (b) $q(t)-t$).

As shown in Figure 11, the depicted response curve bears similarities to the general $RL$ circuit in Figure 2b but also exhibits significant differences. Model (7) reflects more complex and faster nonlinear behavior of higher-order functions. Then, according to the definition of this new time constant $({\tau }_0=L/R_0)$, when this circuit is excited, $R_M$ immediately begins to store information. At the same time, the inductor $(L)$ is busy converting energy to the memristor. Notably, the speed of memorization depends on ${\tau }_0$.

The decay of the current response $i(t)$ is influenced by three variables: $R_d$, $R_0$ and $L$. Next, the decay behavior would be discussed when only one variable is varied and the other remains fixed.

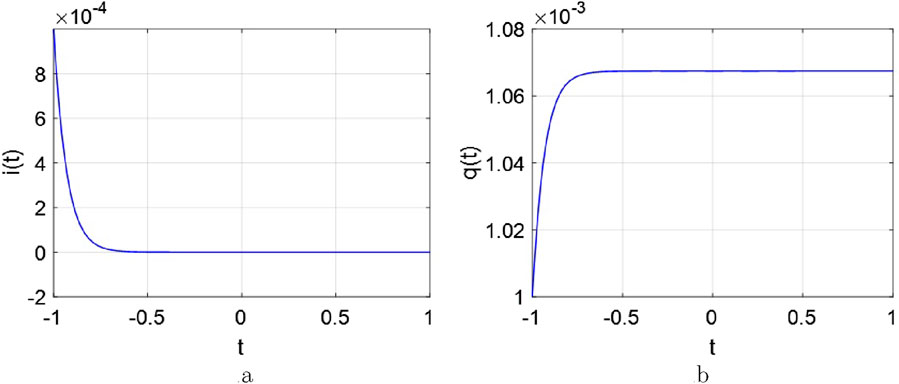
(1) when $k{R}_d=0.8\ast 10^4$ and $L=0.1H$, changing the variable $R_0$, the response $u_C(t)$ are illustrated in Figure 12.

Observe from Figure 12, the following conclusion could be obtained:

i. A large $R_0$ brings a small ${\tau }_0$, and decays the fast.

ii. A certain current is required, when a memristor memorizes information. Therefore, the current $i(t)$ cannot decay to 0 even at $t=0$.

iii. The memory characteristics could be occurred by $R_0$.

Figure 12

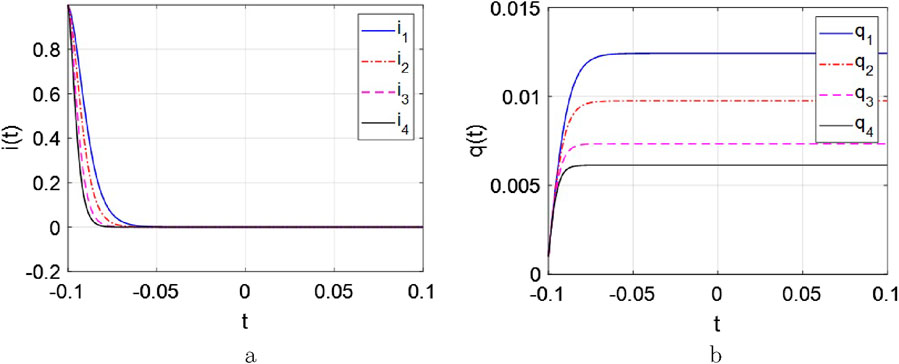
Figure 12. The curves of the current and charge response with $R_{01}=16k$ in blue, $R_{02}=26k$ in red, $R_{03}=46k$ in pink, $R_{04}=66k$ in black. (a) $i(t)-t$. (b) $q(t)-t$.

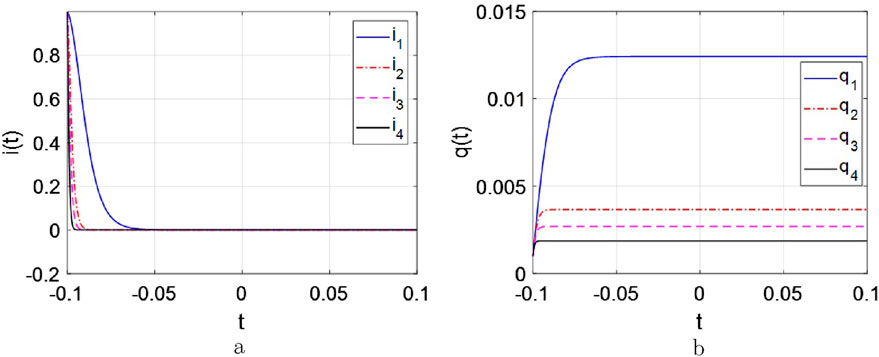
(2) when $k{R}_d=0.8\ast 10^4$ and $R_0=16k$, changing the inductance $L$, the response $i(t)$ are illustrated in Figure 13.

Figure 13

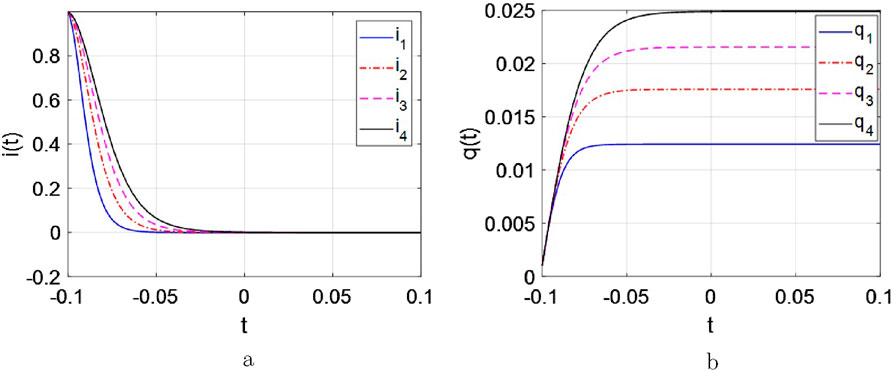
Figure 13. The curve of the current and charge response with $L_1=0.1H$ in blue, $L_2=0.2H$ in red, $L_3=0.3H$ in pink, $L_4=0.4H$ in black. (a) $i(t)-t$). (b) $q(t)-t$.

From Figure 13, the similar results could be got:

i. A large inductive $L$ brings a large ${\tau }_0$, and decays the slow.

ii. When a memristor is utilized for information storage, the current $(i)$ and charge $(q)$ are altered. Furthermore, the role of the energy storage element $L$ can be demonstrated.

(3) when $L=1H$ and $R_0=16k$, changing the variable $R_d$, the response $u_C(t)$ are illustrated in Figure 14.

Observed from Figure 14, the following results could be given as:

i. A large $k{R}_d$ also leads to decay the fast similar to Figure 12.

ii. The energy consumption characteristics exist and are presented by $k{R}_d$.

Figure 14

Figure 14. The curves for the $R_{M}C$ circuit with the parameters $k{R}_d=0.8\ast 10^6$, $R_0=16k$, $C=1mF$. (a) $i(t)-t$). (b) $q(t)-t$).

Finally, Figure 15 presents the dissipated power of the $R_{M}L$ circuit and the energy absorbed by the memristor.

Figure 15

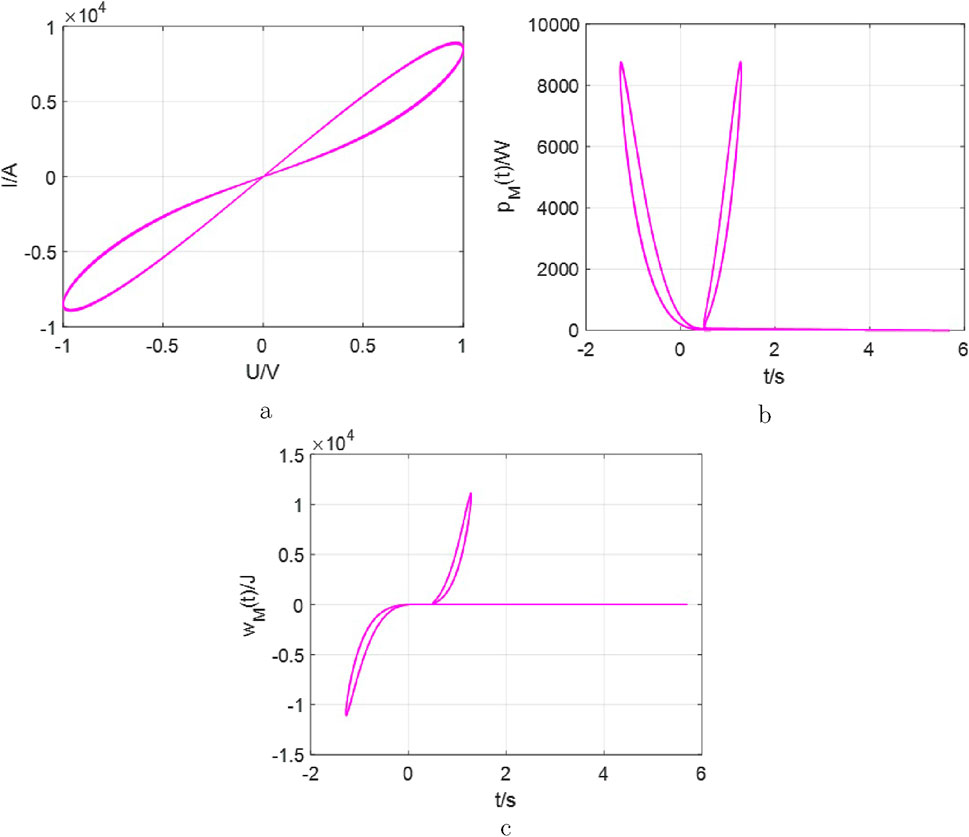
Figure 15. The curves for the $R_{M}L$ circuit. (a) the fingerprint characterizes of $v-i$ for $R_M$). (b) the dissipated power by the memristor up to time $t/s$). (c) the energy $(w(t))$ absorbed by the memristor up to time $t/s$).

Similar to the $R_{M}C$ circuit, when designing a source-free circuit using an inductor and a memristor, its behavior cannot be treated as a step function, too. Because its primary purpose is to store information. The smaller the new time constant leads to the faster the decay. Furthermore, a higher-order transcendental equation has been obtained and more complex nonlinear behaviors have been captured. There are three crucial points in a source-free $R_{M}L$ circuit to determine the calculator $i_L(t)$, that is, the initial current $I_0$, new time constant ${\tau }_0$, and the integral of the charge $q(t)$ in $R_M$. Thirdly, the memristor is presented with dual characteristics: the memory behavior (represented by $R_0$) and the energy consumption characteristics (described by $k{R}_d$).

4 The $R_{M}LC$ circuits

Importantly, building memristive circuits is inseparable from energy storage components, similarly, the study of source-free circuits cannot proceed without them. In the aforementioned analysis and discussion of the natural response of the source-free circuits, two transcendental equations incorporating memristor models have been established. Additionally, the new time constant for the both circuits has been redefined. In this section, similar to the analysis of $RLC$ circuits, $R_{M}LC$ circuits could also be connected in two configurations: series and parallel circuits, see Figure 16.

Figure 16

Figure 16. The source-free $R_{M}LC$ circuits with charge-controlled memristors. (a) the series circuit. (b) the parallel circuit.

4.1 A.Series circuit

Applying Kirchhoff’s Laws $(i=i_R=i_C=i_L=i_M)$ and Figure 16a, according to the description of Equation 2, the following Equation 8 could be built as following

$\left\{\begin{array}{c}Ri+\left(R_0+k{R}_{d}q\right)i+L\frac{di}{dt}+u=0\hfill \\ i=C\frac{du}{dt}\hfill \\ q=\int idt\hfill \\ \begin{array}{cc}\hfill i\left(0\right)=I_0,\hfill & \hfill u\left(0\right)=U_0\hfill \end{array}\hfill \end{array}\right.(8)$

where the variables $i(t)=i_L(t)$, $u(t)=u_c(t)$ stand for the current flowing through the inductor and voltage across the capacitor. From the preceding analysis, when energy storage elements are integrated with memristors in a circuit, their response models can be established as transcendental and higher-order equations. In Figure 16a, let $q=A{e}^{(st)}$ and $i=As{e}^{(st)}$, where $s$ and $t$ critical variables that must be discussed and determined. Additionally, the necessary derivatives can be derived as

$s^3+\left(\frac{RC+R_{0}C+k{R}_{d}q}{L}+\frac{Ak{R}_d}{L}{e}^{st}\right)s^2+\frac{1}{LC}s=0(9)$

There is no doubt that Equation 9 is still a high-order transcendental equation. Thus, the natural response curve could be depicted graphically in Figure 17.

Figure 17

Figure 17. The response curves of the source-free $R_{M}LC$ series circuits, $I_0=0.001A$, $U_0=0.001V$, $k{R}_d=1\ast 106$, $R_0=16k$, $R=1$, $L=0.1H$, $C=1mF$. (a) $u(t)-t$. (b) $i(t)-t$.

Comparison with a conventional $RLC$ (second-order) series circuit, the solution of system (9) also could exhibit damping characteristics and generate the type of resonance phenomenon. By varying the values of $R_M$, $L$ or $C$, it discusses whether the system could observe the three damping conditions (overdamped, critically damped, and underdamped) analogous to traditional $RLC$ circuits. These three cases might be illustrated and analyzed in the following Figures 18–20, respectively.

Figure 18

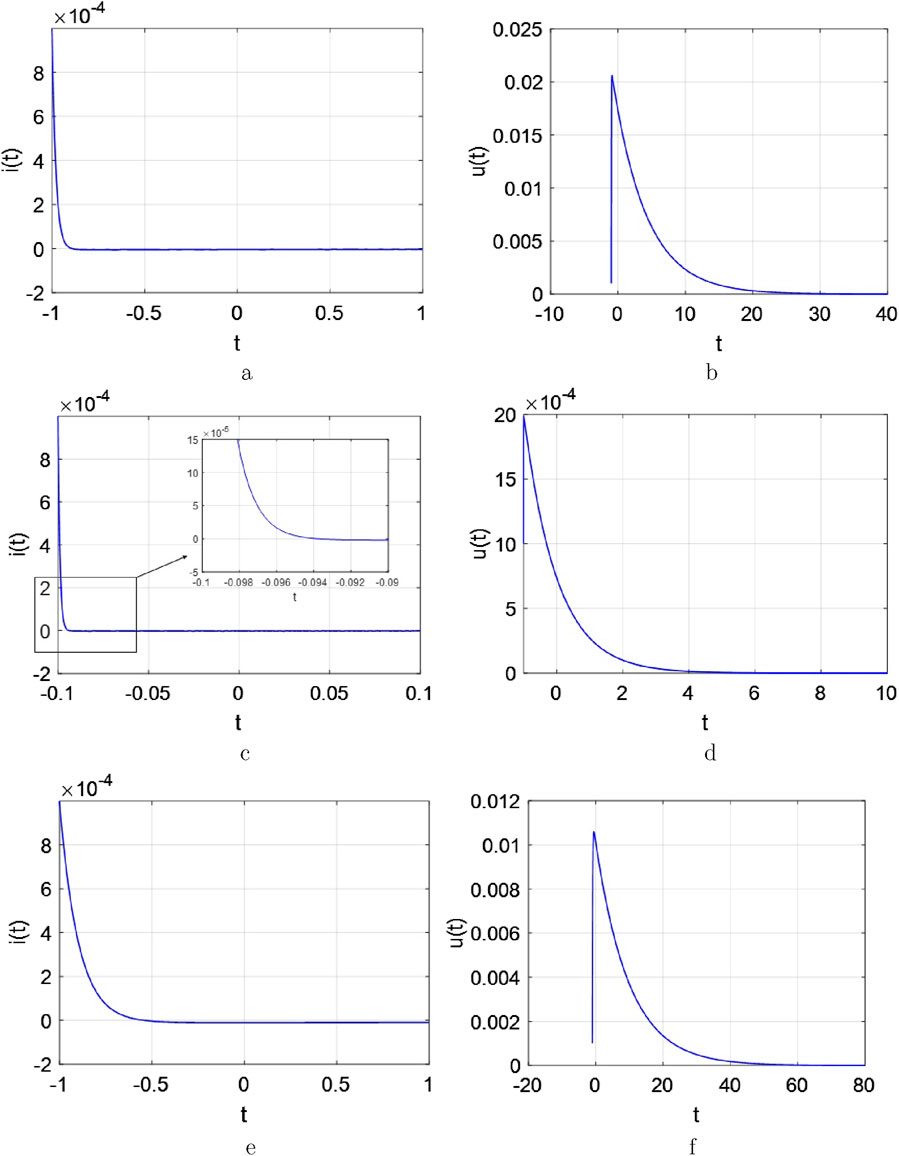
Figure 18. The response of current and voltage curves for the $R_{M}LC$ series circuit. (a) $i(t)-t$ with $R=5k$, $L=0.1H$, and $C=1mF$. (b) $u(t)-t$ with $R=5k$, $L=0.1H$, and $C=1mF$. (c) $i(t)-t$ with $R=1k$, $L=1mH$, and $C=1mF$. (d) $u(t)-t$ with $R=1k$, $L=1mH$, and $C=1mF$. (e) $i(t)-t$ with $R=1k$, $L=0.1H$, and $C=10mF$. (f) $u(t)-t$ with $R=1k$, $L=0.1H$, and $C=10mF$.

Figure 19

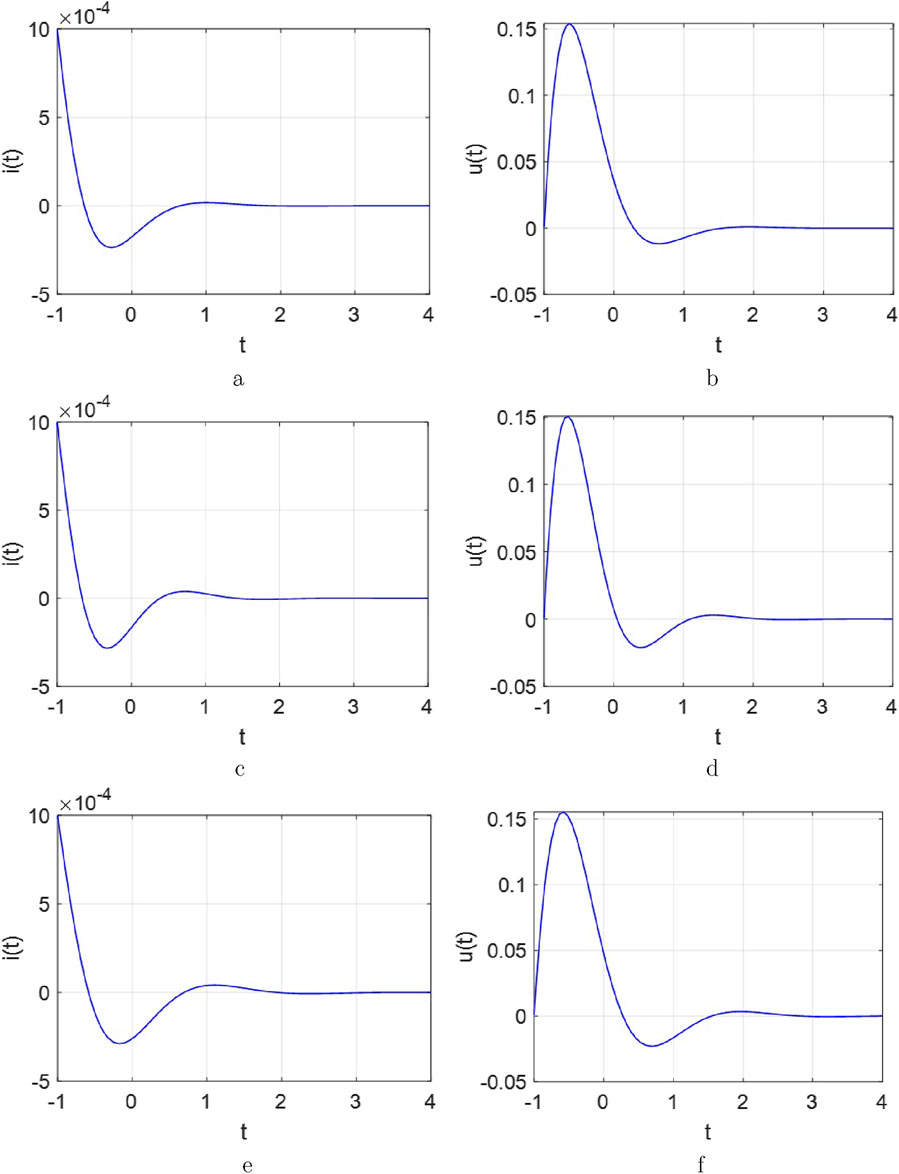
Figure 19. The response of current and voltage curves for the $R_{M}LC$ series circuit. (a) $i(t)-t$ with $R=400$, $L=0.1H$, and $C=1mF$. (b) $u(t)-t$ with $R=400$, $L=0.1H$, and $C=1mF$. (c) $i(t)-t$ with $R=300$, $L=0.08H$, and $C=1mF$. (d) $u(t)-t$ with $R=300$, $L=0.08H$, and $C=1mF$. (e) $i(t)-t$ with $R=300$, $L=0.1H$, and $C=1.2mF$. (f) $u(t)-t$ with $R=300$, $L=0.1H$, and $C=1.2mF$.

Figure 20

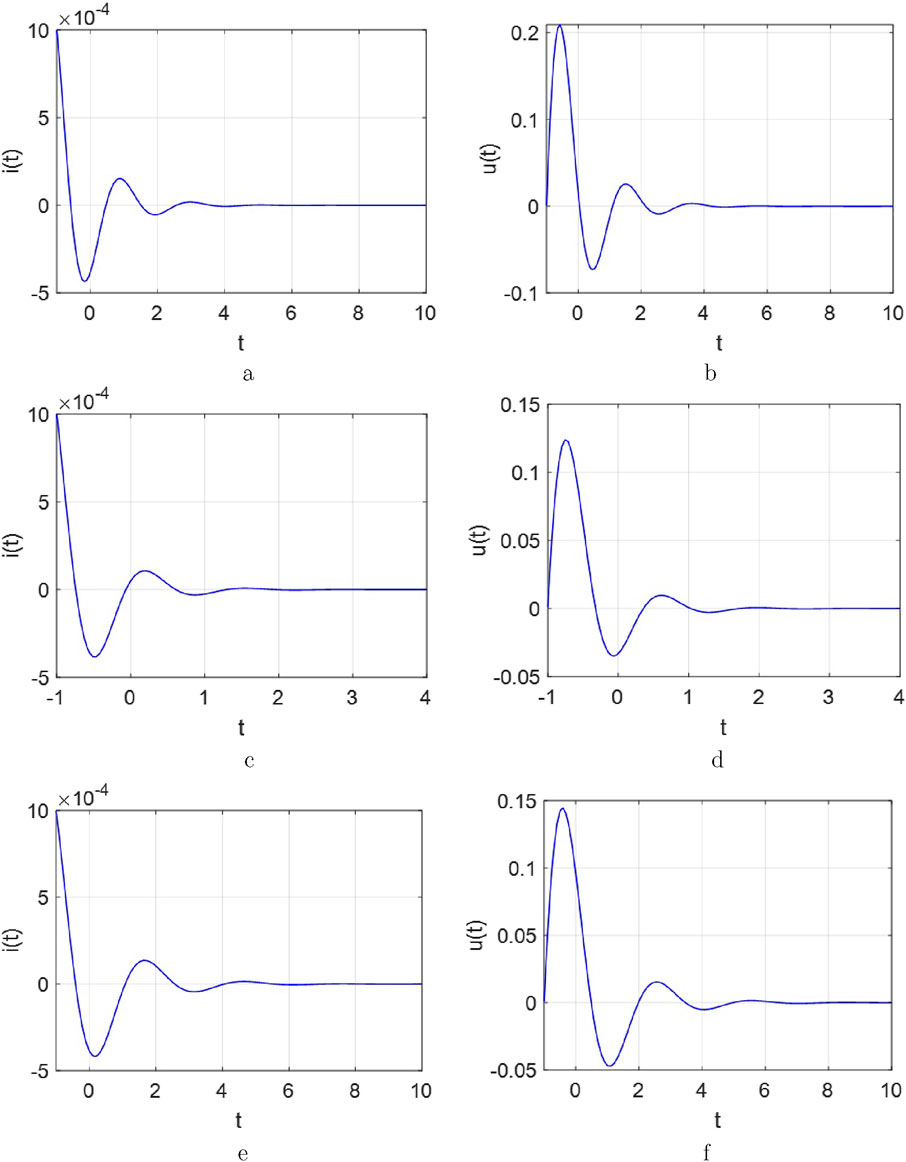
Figure 20. The response of current and voltage curves for the $R_{M}LC$ series circuit. (a) $i(t)-t$ with $R=350$, $L=0.12H$, and $C=1mF$. (b) $u(t)-t$ with $R=35$, $L=0.12H$, and $C=1mF$. (c) $i(t)-t$ with $R=1k$, $L=1H$, and $C=1mF$. (d) $u(t)-t$ with $R=1k$, $L=1H$, and $C=1mF$. (e) $i(t)-t$ with $R=1k$, $L=0.12H$, and $C=120uF$. (f) $u(t)-t$ with $R=1k$, $L=0.12H$, and $C=120uF$.

4.1.1 Overdamped case

When the following conditions are assigned, both response curves of $i(t)$ and $u(t)$ are shown in Figure 18. The decay approaches zero as $t$ increases.

Observed from Figure 17 and Figure 18, the overdamping phenomenon occurs when the memristance increases (i.e., increasing $R_0+R$), the inductance decreases, or the capacitance increases, while other parameters remain fixed.

4.1.2 Critically damped case

When the following conditions are set, both the current and voltage of the system exhibit maximum and minimum values in Figure 19, respectively. Also, the delays all the way to zero.

Between Figure 17 and Figure 19, the critically damped phenomenon presents immediately when the memristance increases (i.e., increasing $R_0+R$) but remains much smaller than that in the overdamped case, the inductance decreases, or the capacitance increases, respectively, while other conditions remain fixed.

4.1.3 Underdamped case.

The oscillation period in both $i(t)$ and $u(t)$ curves are depicted in Figure 20. Moreover, the delays all the way to zero.

Compared with Figure 17 and Figure 20, the underdamped phenomenon has been shown as the same situation.

From Figures 18–20, the special characteristics of the $R_{M}LC$ series circuit could be summarized as follows:

i. In HP-memristor is known as the linear drift model. When current flows through a designed circuit incorporating energy storage elements and a memristor, a higher-order mathematical model can be derived, which surpasses the complexity of conventional $RLC$ series circuit models.

ii. Similar to the $RLC$ series circuit, its behavior could be characterized by damping phenomena, where the gradual loss of initial stored energy results in a continuous reduction of response amplitude. This explains why such nonlinear circuits with memristors exhibit abundant oscillatory behaviors and strange attractors.

iii. The damping phenomenon arises because a memristor integrates two functional aspects: memory $(R_0)$ and energy dissipation $(k{R}_d)$. The oscillation period determines the damping rate of the response. To achieve overdamped, critically damped, or underdamped behavior, three discusses can be employed: increasing memristance $(R+R_0)$ but remains much smaller than that in the both overdamped and critically damped cases, or capacitance $(C)$ or decreasing the inductance $(L)$, while keeping other parameters fixed, respectively.

iv. The damped oscillation is possible due to the presence of the nonlinear elements (i.e., $R_M$, $L$, and $C$). Furthermore, the delays all the way to zero, which stems from the ability of the storage elements and memory element to transfer energy back and forth between them.

v. All subplots uniformly validate that the same initial conditions but different component parameters would manifest a similar yet quite different output waveform. This variance could be thought as a kind of catalyst to get various application areas in the future, simultaneously revealing characteristics of chaotic oscillations. It further demonstrates the influence of $(R+R_0)$, $L$, and $C$ on the decay rate. Therefore, during the design and application of memristive circuits, memristors with appropriate $R_0$ could be chosen according to the needs of the actual oscillation and decay rate.

4.2 Parallel circuit

From Figure 16b, when the conditions $(u=u_R=u_C=u_L=u_M)$ are satisfied for this parallel circuit, and according to the description of Equation 2, the following Equation 10 have been set as

$\left\{\begin{array}{c}\frac{du}{dt}=-\frac{1}{C}\left(\frac{u}{R}+\frac{u}{R_0+k{R}_{d}q}+i\right)\hfill \\ \frac{di}{dt}=\frac{u}{L}\hfill \\ \frac{dq}{dt}=i\hfill \\ \begin{array}{cc}\hfill i\left(0\right)=I_0,\hfill & \hfill u\left(0\right)=U_0\hfill \end{array}\hfill \end{array}\right.(10)$

where the variables $i(t)=i_L(t)$, $u(t)=u_c(t)$ stand for the current flowing through the inductor and voltage across the capacitor. System (10) is also a third-order function. Let $u=A{e}^{(st)}$ where $s$ and $t$ critical variables. Additionally, the necessary derivatives can be derived as

$R_{0}C{s}^2+\left(1+\frac{R_0}{R}\right)s+\frac{R_0}{L}+\left(k{R}_{d}C{s}^2+\frac{k{R}_d}{R}s+\frac{k{R}_d}{L}\right)A{e}^{st}=0(11)$

Equation 11 is still a transcendental equation. Its solution could be obtained through approximately methods. Now, the nature response curve could be drawn in Figure 21.

Figure 21

Figure 21. The response curves of the source-free $R_{M}LC$ parallel circuits, $I_0=1A$, $U_0=10V$, $k{R}_d=1\ast 10^6$, $R_0=16k$, $R=1k$, $L=0.12H$, $C=1mF$. (a) $i(t)-t$. (b) $u(t)-t$.

Next, we investigate the impact of varying parameters ($R_M$, $L$ or $C$) and observe whether analogous responses emerge. The current and voltage response curve are presented in Figures 22–24. There are also three cases:

Figure 22

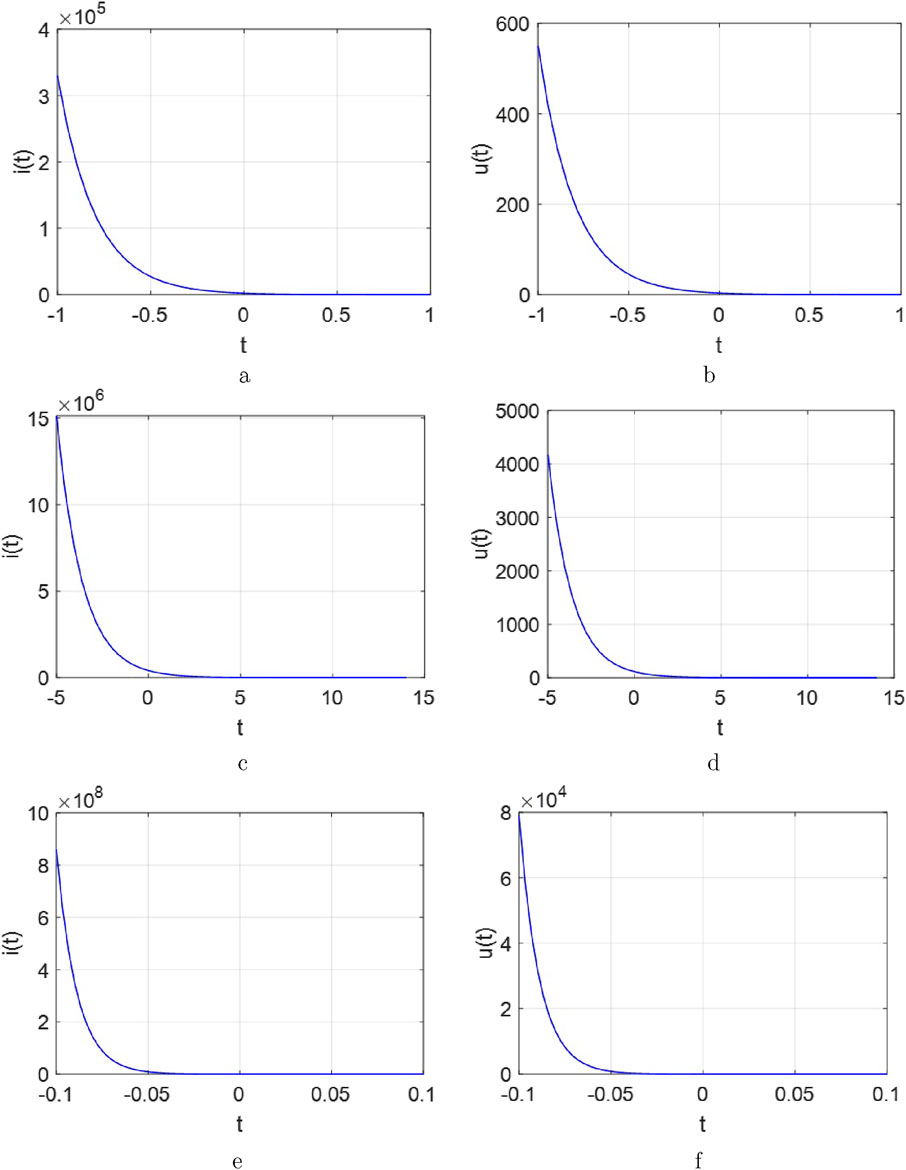
Figure 22. The response curves for the $R_{M}LC$ parallel circuit. (a) $i(t)-t$ with $R=150\mathrm{\Omega }$, $L=0.12H$, and $C=1mF$. (b) $u(t)-t$ with $R=15\mathrm{\Omega }$, $L=0.12H$, and $C=1mF$. (c) $i(t)-t$ with $R=1k$, $L=50H$, and $C=1mF$. (d) $u(t)-t$ with $R=1k$, $L=50H$, and $C=1mF$. (e) $i(t)-t$ with $R=1k$, $L=0.12H$, and $C=10uF$. (f) $u(t)-t$ with $R=1k$, $L=0.12H$, and $C=10uF$.

Figure 23

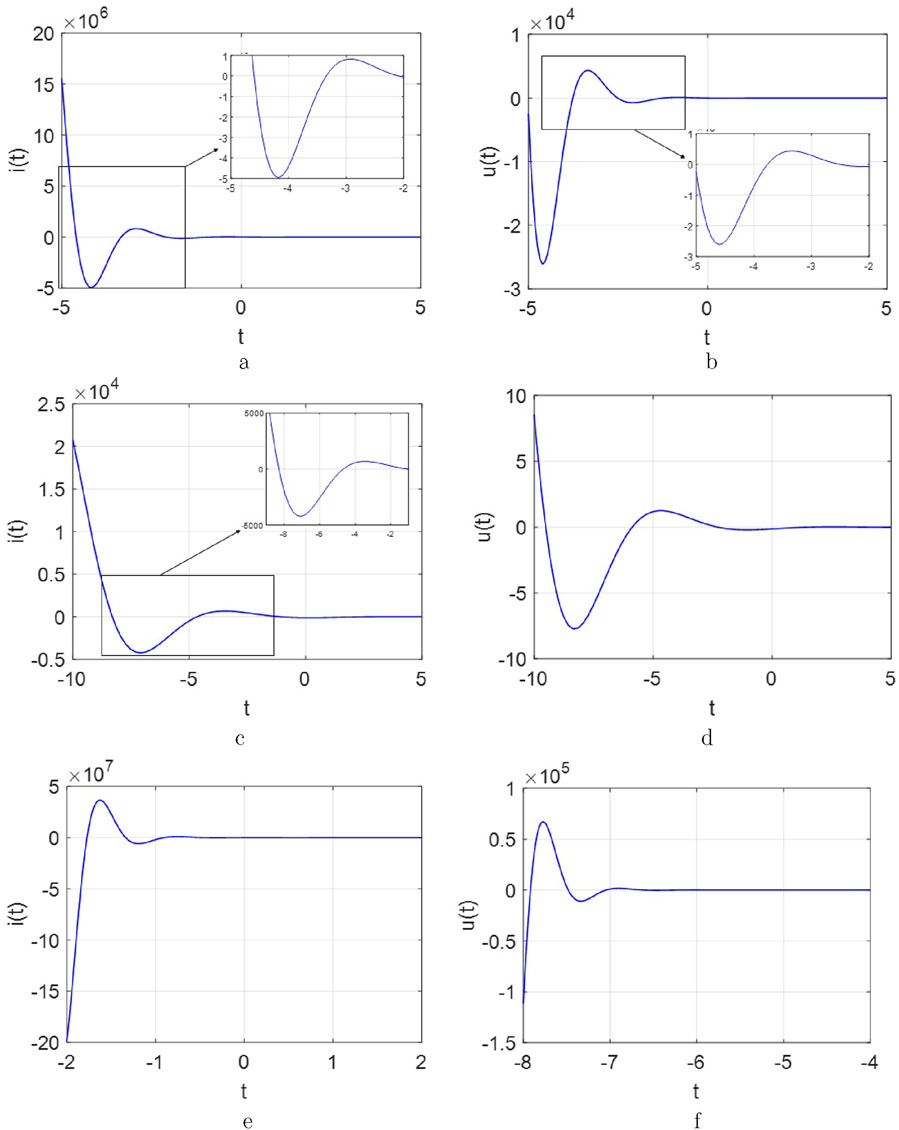
Figure 23. The response curves for the $R_{M}LC$ parallel circuit. (a) $i(t)-t$ with $R=350$, $L=0.12H$, and $C=1mF$. (b) $u(t)-t$ with $R=350$, $L=0.12H$, and $C=1mF$. (c) $i(t)-t$ with $R=1k$, $L=1H$, and $C=1mF$. (d) $u(t)-t$ with $R=1k$, $L=1H$, and $C=1mF$. (e) $i(t)-t$ with $R=1k$, $L=0.12H$, and $C=120uF$. (f) $u(t)-t$ with $R=1k$, $L=0.12H$, and $C=120uF$.

Figure 24

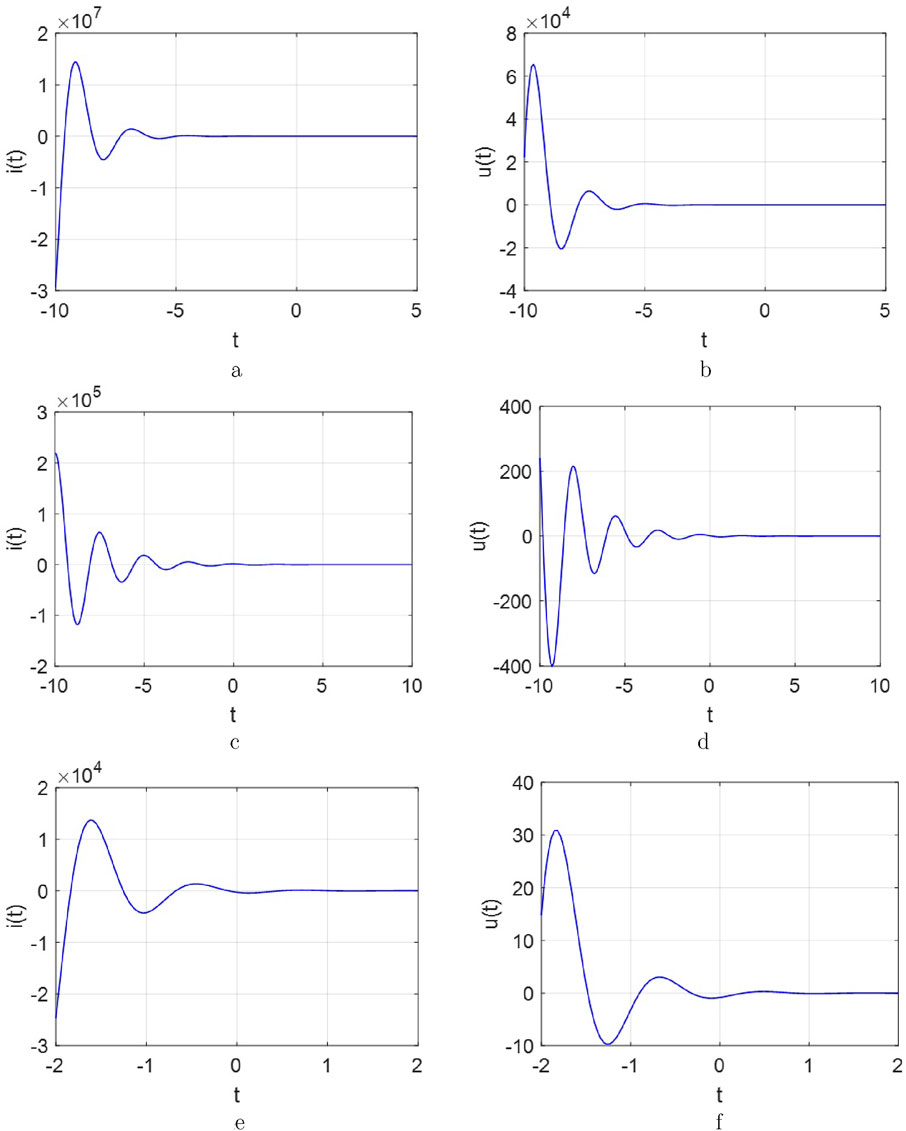
Figure 24. The response curves for the $R_{M}LC$ parallel circuit. (a) $i(t)-t$ with $R=500$, $L=0.12H$, and $C=1mF$. (b) $u(t)-t$ with $R=500$, $L=0.12H$, and $C=1mF$. (c) $i(t)-t$ with $R=1k$, $L=0.55H$, and $C=1mF$. (d) $u(t)-t$ with $R=1k$, $L=0.55H$, and $C=1mF$. (e) $i(t)-t$ with $R=1k$, $L=0.12H$, and $C=250uF$. (f) $u(t)-t$ with $R=1k$, $L=0.12H$, and $C=250uF$.

4.2.1 Overdamped case.

When the following conditions are assigned, both response curves of $i(t)$ and $u(t)$ are shown in Figure 22.

Between Figure 21 and Figure 22, the overdamping phenomenon occurs when the memristance decreases (i.e., decreasing $R_0+R$), the inductance increases, or the capacitance decreases, while other parameters remain fixed.

4.2.2 Critically damped case.

When the following conditions are given, both the current and voltage exhibit maximum and minimum values, respectively (see Figure 23). Also, the delays all the way to zero.

Observed from Figure 21 and Figure 23, the critically damped phenomenon have happened when the memristance decreases (i.e., decreasing $R_0+R$) but remains much larger than that in the overdamped case, the inductance increases, or the capacitance decreases, while other conditions remain fixed.

4.2.3 Underdamped case.

The oscillation period in both $i(t)$ and $u(t)$ curves are depicted in Figure 24. Moreover, the delays all the way to zero. Compared with Figure 21 and Figure 24, the underdamped phenomenon has been shown under the same conditions.

To summarize the conclusions according to the Figures 22–24 for one $R_{M}LC$ parallel circuit as follows:

i. Similar to the $RLC$ parallel circuit, when energy storage elements and a memristor are integrated into the same parallel system, the energy would be back and forth between them, thereby establishing a damping decay curve.

ii. The coexistence of memory storage and energy dissipation characteristics in this circuit arises from the dual-resistance structure of the memristor, characterized by $R_0$ and $k{R}_d$.

iii. The conditions for achieving overdamped, critically damped, or underdamped phenomena differ from those in $R_{M}LC$ series circuits. Specifically, these damping regimes can be realized by adjusting the resistance $(R+R_0)$ but remains much larger than that in the both overdamped and critically damped cases or capacitance $(C)$ should be decreasing or increasing the inductance $(L)$, while keeping all other parameters constant under each configuration.

iv. Under identical initial current and voltage conditions but with varying circuit component values, all subplots in the figure were analyzed. These results validate the influence of $(R+R_0)$, $L$ and $C$ on the decay rate. The single regrettable drawback resides in the waveforms lacking sufficient resolution to reveal detailed distinctions between the $R_{M}LC$ circuit and conventional variable $RLC$ systems. However, in the design and application of one memristive circuit, memristors should be selected according to the needs of the actual oscillation and decay rate based on the analysis and discussion in thoery.

5 Application of classic circuits with four fundamental components

A classical four-component application circuit is presented, as shown in Figure 25.

Figure 25

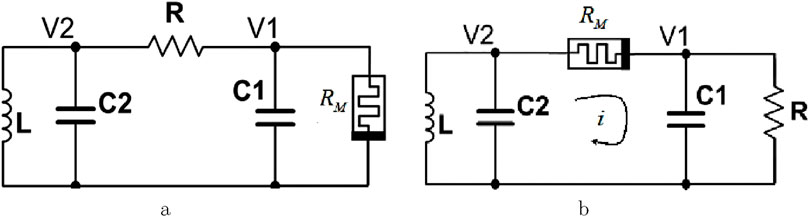
Figure 25. A circuit with HP-memristor. (a) Replacing the Chua diode with an HP memristor. (b) Transposing the positions of HP memristor and resistor.

The following analysis would demonstrate how energy storage elements or memristors influence the memory characteristics and oscillatory behavior. The Figure 25a, this circuit shares the same topological structure as the Chua system, but features a different memristor configuration. Consequently, it also produces different phase trajectory curves, the mathematical model has been built and analyzedin the following form:

$\left\{\begin{array}{c}{C}_1\cdot \frac{d{V}_1}{dt}=-\frac{1}{R}{V}_1+\frac{1}{R}{V}_2-\frac{1}{R_M}\cdot V_1\hfill \\ C_2\cdot \frac{d{V}_2}{dt}=\frac{1}{R}{V}_1-\frac{1}{R}{V}_2+i_L\hfill \\ L\cdot \frac{d{i}_L}{dt}=-V_2\hfill \\ \frac{dq}{dt}=i_L\hfill \end{array}\right.(12)$

Secondly, when transposing the positions of the HP memristor and resistor in this circuits, the mathematical model is given as follows:

$\left\{\begin{array}{c}{C}_1\cdot \frac{d{V}_1}{dt}=-\frac{1}{R_M}{V}_1+\frac{1}{R_M}{V}_2-\frac{1}{R}\cdot V_1\hfill \\ C_2\cdot \frac{d{V}_2}{dt}=\frac{1}{R_M}{V}_1-\frac{1}{R_M}{V}_2+i_L\hfill \\ L\cdot \frac{d{i}_L}{dt}=-V_2\hfill \\ \frac{d\phi }{dt}=\frac{d\phi }{dq}\cdot \frac{dq}{dt}=V_1-V_2\hfill \end{array}\right.(13)$

Setting the variable $x=V_1$, $y=V_2$, $z=i_L$ and $\omega =q$; parameters $p_1=1/(R{C}_1)$, $q_1=1/(R{C}_2)$, $a_2=1/(R{C}_1)$, $b=1/C_2$, $r=1/L$, $a_1=p_2=1/[(R_0+k{R}_{d}q)C_1]$, $q_2=1/[(R_0+k{R}_{d}q)C_2]$, both the built as Equation 12 and Equation 13 can be rewritten in the following dimensionless forms:

$\left\{\begin{array}{c}{\displaystyle \dot{x}}=p_1\left(y-x\right)-a_1.x\hfill \\ {\displaystyle \dot{y}}=q_1\left(x-y\right)+b.z\hfill \\ {\displaystyle \dot{z}}=-r.y\hfill \\ {\displaystyle \dot{\omega }}=z\hfill \end{array}\right.(14)$

and

$\left\{\begin{array}{c}{\displaystyle \dot{x}}=p_2\left(y-x\right)-a_2.x\hfill \\ {\displaystyle \dot{y}}=q_2\left(x-y\right)+b.z\hfill \\ {\displaystyle \dot{z}}=-r.y\hfill \\ {\displaystyle \dot{\omega }}=x-y\hfill \end{array}\right.(15)$

For Figure 25a, setting the parameters $p_1=7.9$, $q_1=1$, $b=1$, $r=14.5$ are fixed in Equation 14. The phase trajectory curves exhibit the chaotic attractor as shown in Figure 26a. When transposing the positions of the HP memristor and resistor, the phase trajectory becomes a single-scroll attractor as demonstrated in Figure 26b.

Figure 26

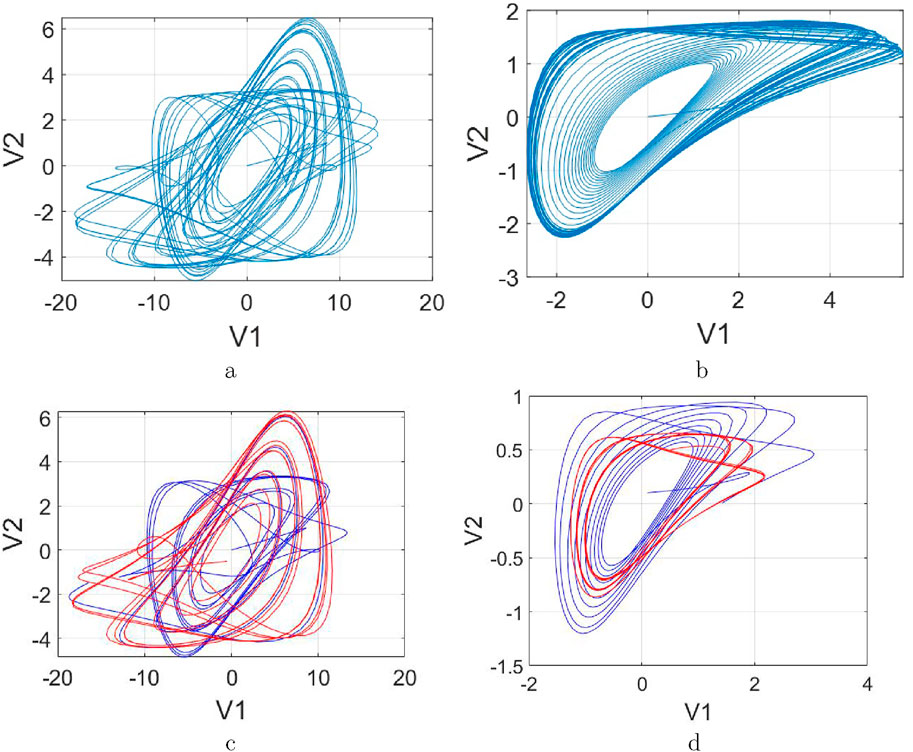
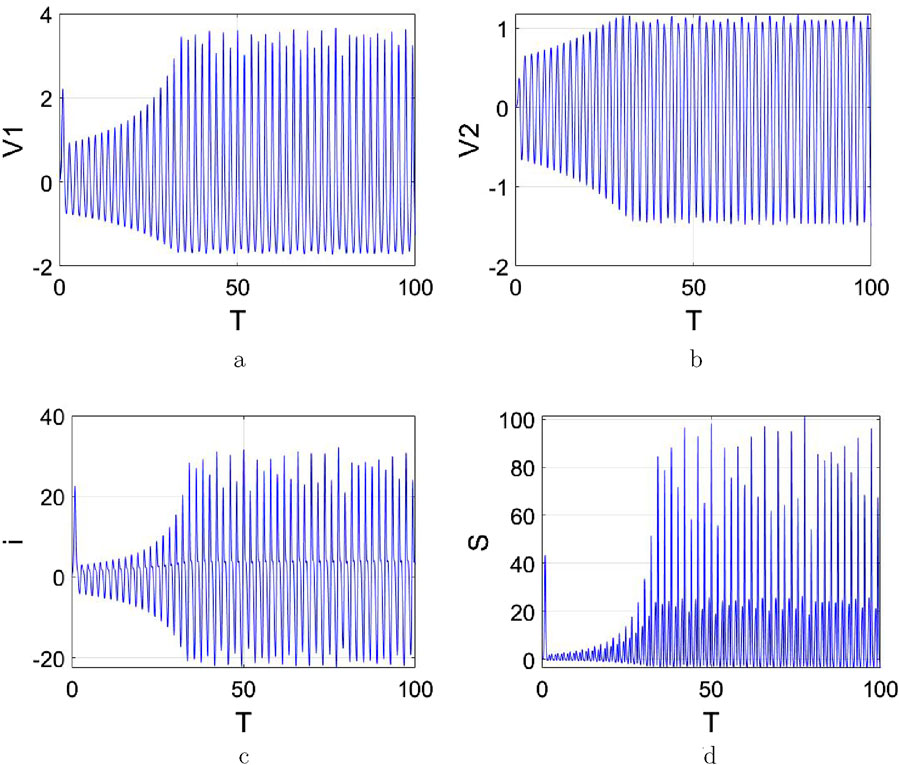
Figure 26. Phase portrait in $v_1-v_2$ and their coexistence attractors. (a) replacing Chua Diodes with HP Memristors. (b) replace the resistance $(R)$ in original Chua’s circuit with an HP memristor. (c) Coexistence attractor. (d) Hidden attractor.

These observations demonstrate that as initial values vary, the system not only exhibits irregular oscillations but also manifests chaotic attractors, coexisting attractors in Figure 26c and hidden attractors in Figure 26d. These characteristics serve as critical evidence for the system’s capability to facilitate the construction of complex neural networks with memory properties.

Let $p_2=1/(6.23-0.9q)$, $q_2=1/(8.49-4.33q)$, $a_2=7.9$, $b=1$, $r=14.5$, and the initial condition $[x,y,z,w]=[0.01,0.01,0.01,0.01]$, the time domain curves of Equation 15 can be obtained as shown, seeing Figure 27.

Figure 27

Figure 27. Time domain curves. (a) $v_1(t)-t$. (b) $v_2(t)-t$. (c) $i(t)-t$. (d) $S(t)-t$.

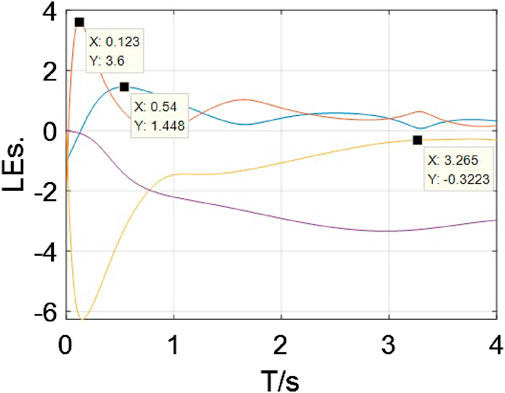
Then, the Lyapunov exponent spectrum corresponding to parametrically configured is illustrated in Figure 28.

Figure 28

Figure 28. The Lyapunov Exponents spectrum.

This provides another perspective to demonstrate that the chaotic oscillation arises from the energy to transfer energy back and forth between the memristor and energy storage elements. From Figure 28, the $LEs$ are calculated and illustrated, $L{E}_1=3.6$, $L{E}_2=1.448$, $L{E}_3=-0.3223$, $L{E}_4=-3.339$. Two positive Lyapunov exponents confirm that the system is a hyperchaotic system. Next, in order to verify the conclusions derived from previous analyses, we systematically modify the values of energy storage elements of Figure 25b to investigate their impact on the memory characteristics and oscillatory behaviors of the HP-memristor from the response of voltage curves.

Observed from Figures 29a–c, they illustrate the effect of varying the inductance $L$ on output voltage $(v_2)$ of the system (15). As inductance $L$ increases, the decay rate diminishes. Conversely, reduction of $L$ induces damped and overdamped dynamical manifestations. When inductance values decrease below critical thresholds, oscillatory phenomena and chaotic attractors undergo complete termination.

Figure 29

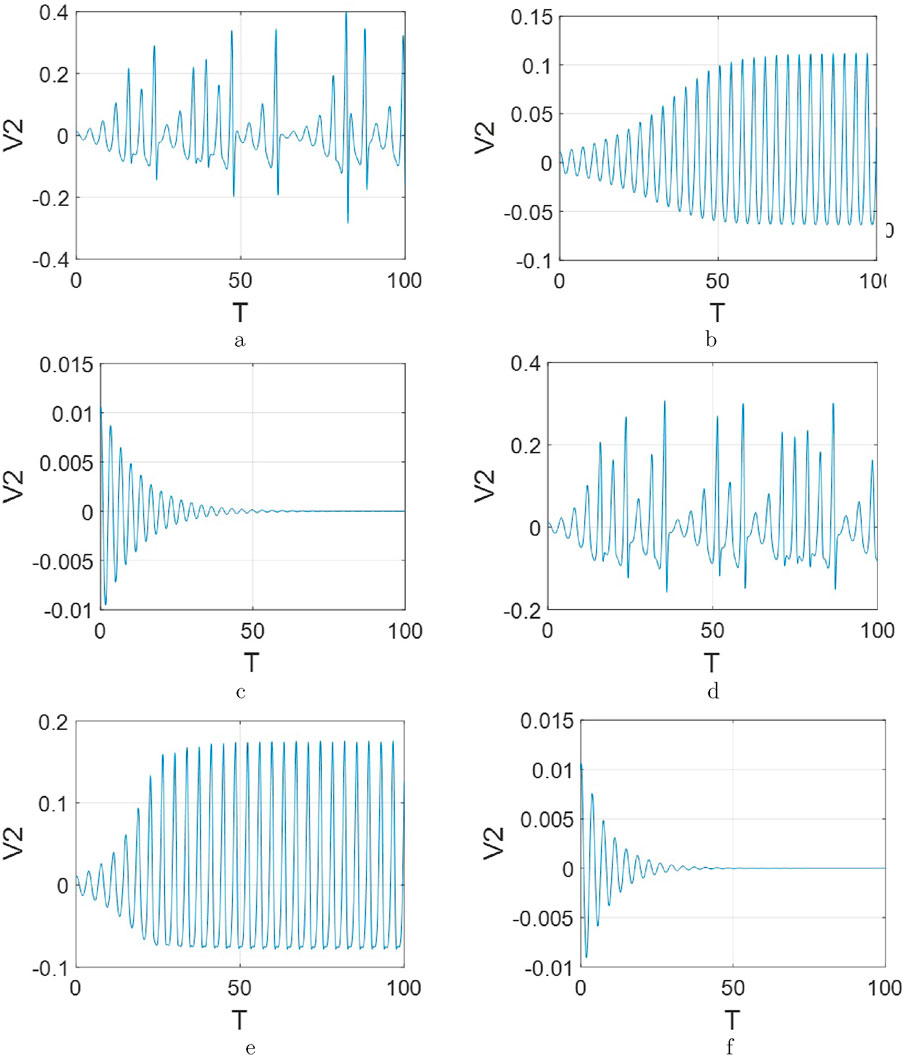
Figure 29. The response of voltage curves $(v_2)$ of system (13). (a) $a_2=7.9$, $b=1$, $p_2=1/(0.9-6.23q)$, $q_2=1/(8.49-4.33q)$, $r=14.1$. (b) $a_2=7.9$, $b=1$, $p_2=1/(6.23-0.9q)$, $q_2=1/(8.49-4.33q)$, $r=16$. (c) $a_2=7.9$, $b=1$, $p_2=1/(6.23-0.9q)$, $q_2=1/(8.49-4.33q)$, $r=18$. (d) $a_2=7.9$, $b=1$, $p_2=1/(6.23-0.9q)$, $q_2=1/(8.0-4.11q)$, $r=14.5$. (e) $a_2=7.9$, $b=1$, $p_2=1/(6.23-0.9q)$, $q_2=1/(8.92-4.33q)$, $r=14.5$. (f) $a_2=7.9$, $b=1$, $p_2=1/(6.23-0.9q)$, $q_2=1/(9.2-4.92q)$, $r=14.5$.

Similarly, Figures 29d–f demonstrates the impact of changing the capacitance $C_2$ on the output voltage $(v_2)$. As capacitance $C_2$ increases, the decay rate also diminishes. Conversely, reduction of $C_2$ induces damped and overdamped dynamical manifestations. When capacitance values decrease below critical thresholds, oscillatory phenomena and chaotic attractors undergo complete termination.

6 Conclusion

To advance the fundamental theory of memristive circuits, this study investigates four types of source-free circuits incorporating memristors and energy storage elements following the research methodology of classical source-free circuit analysis.

These circuits are categorized into two groups: one group consists of a memristor combined with a single energy-storing element (denoted as $R_{M}C$ and $R_{M}L$ circuits), while the other group includes $R_{M}LC$ series and parallel circuits. Firstly, their models are built and analyzed, which reveals that they are transcendental equations. Secondly, new time constants are introduced (It pertains exclusively to a specific resistance region in the memristor, such as its low-resistance state $R_0$, that is, ${\tau }_0=R_{0}C$ and ${\tau }_0=L/R_0$), along with key factors influencing the decay rate. Furthermore, this study further verifies that two distinct regions in the memristor manifest two properties: memory characteristics and energy-dissipative behavior. Finally, through a systematic analysis using a classical application circuit with four fundamental circuit elements, we revalidate the critical role of both energy storage components and memristor in modulating oscillatory dynamics and attractor morphologies. More significantly, the characteristics of circuits combining memristors and energy-storage components have been refined, ensuring continuous advancement in memristive circuit principles. This establishes a robust theoretical foundation for innovative applications of memory elements across nonlinear circuits, avionics for UAV systems, and integrated theoretical-design frameworks.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding authors.

Author contributions

XG: Writing – original draft, Writing – review and editing, Supervision. YQ: Formal Analysis, Investigation, Writing – review and editing. SL: Data curation, Methodology, Writing – review and editing. WL: Conceptualization, Data curation, Formal Analysis, Writing – review and editing. YS: Investigation, Supervision, Writing – review and editing. YL: Writing – review and editing, Writing – original draft.

Funding

The author(s) declare that no financial support was received for the research and/or publication of this article.

Conflict of interest

Authors XG, YQ, SL, and WL were employed by Aerospace Times FeiHong Technology Company Limited.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Any alternative text (alt text) provided alongside figures in this article has been generated by Frontiers with the support of artificial intelligence and reasonable efforts have been made to ensure accuracy, including review by the authors wherever possible. If you identify any issues, please contact us.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Chua LO. If it’s pinched it’s a memristor. Semiconductor Sci Technology (2014) 49(10):104001. doi:10.1088/0268-1242/29/10/104001

CrossRef Full Text | Google Scholar

2. Caravelli F, Carbajal JP. Memristors for the curious outsiders. Technologies (2018) 6(4):118. doi:10.3390/technologies6040118

CrossRef Full Text | Google Scholar

3. Zhang Y, Wang X, Li Y, Friedman EG. Memristive model for synaptic circuits. IEEE Trans Circ Syst.–II: Express Briefs (2017) 64(7):767–71. doi:10.1109/TCSII.2016.2605069

CrossRef Full Text | Google Scholar

4. Bao H, Zhang Y, Liu W, Bao B. Memristor synapse-coupled memristive neuron network: synchronization transition and occurrence of chimera. Nonlinear Dyn (2020) 100:937–50. doi:10.1007/s11071-020-05529-2

CrossRef Full Text | Google Scholar

5. Tan Y, Wang C. A simple locally active memristor and its application in HR neurons. Chaos (2020) 30(5):053118. doi:10.1063/1.5143071

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Huang L, Wang S, Lei T, Li C. Coupled HR–HNN neuron with a locally active memristor. Int J Bifurcation Chaos (2024) 34(2):2450022. doi:10.1142/S0218127424500226

CrossRef Full Text | Google Scholar

7. Shama F, Haghiri S, Imani MA. FPGA realization of Hodgkin-Huxley neuronal model. IEEE Trans Neural Syst Rehabil Eng (2020) 28(5):1059–68. doi:10.1109/TNSRE.2020.2980475

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Yu F, Shen H, Yu Q, Kong X, Sharma PK, Cai S. Privacy protection of medical data based on multi-scroll memristive Hopfield neural network. IEEE Trans Netw Sci Eng (2022) 10:845–58. doi:10.1109/TNSE.2022.3223930

CrossRef Full Text | Google Scholar

9. Eshraghian JK, Cho K, Zheng C, Nan M, Iu HH, Lei W, et al. Neuromorphic vision hybrid rram-cmos architecture. IEEE Trans Very Large-Scale Integration (VLSI) Syst (2018) 26(12):2816–29. doi:10.1109/TVLSI.2018.2829918

CrossRef Full Text | Google Scholar

10. Yu F, Zhang S, Su D, Wu Y, Gracia YM, Yin H. Dynamic analysis and implementation of FPGA for a new 4D fractional-order memristive hopfield neural network. Fractal and Fractional (2025) 9(2):115. doi:10.3390/fractalfract9020115

CrossRef Full Text | Google Scholar

11. Liu Y, Iu HH, Qian Y. Implementation of Hodgkin-Huxley neuron model with the novel memristive oscillator. IEEE Trans Circ Syst.–II: Express Briefs (2021) 68(8):2982–6. doi:10.1109/TCSII.2021.3066471

CrossRef Full Text | Google Scholar

12. Song Z, Liu Y. Generation of neuromorphic oscillators via second-order memristive circuits with modified Chua corsage memristor. IEEE Access (2023) 11:103712–24. doi:10.1109/ACCESS.2023.3318117

CrossRef Full Text | Google Scholar

13. Yu D, Zhao X, Sun T, Iu HHC, Fernando T. A simple floating mutator for emulating memristor, memcapacitor, and meminductor. IEEE Trans Circ Syst.–II: Express Briefs (2020) 67(7):1334–8. doi:10.1109/TCSII.2019.2936453

CrossRef Full Text | Google Scholar

14. Feali MS, Ahmadi A, Hayati M. Implementation of adaptive neuron based on memristor and memcapacitor emulators. Neurocomputing (2018) 309(2):157–67. doi:10.1016/j.neucom.2018.05.006

CrossRef Full Text | Google Scholar

15. Liu Y, Iu HH, Guo Z, Si G. The simple charge-controlled grounded/floating mem-element emulator. IEEE Trans Circ Syst.–II: Express Briefs (2021) 68(6):2177–81. doi:10.1109/TCSII.2020.3041862

CrossRef Full Text | Google Scholar

16. Yu F, Su D, He S. Resonant tunneling diode cellular neural network with memristor coupling and its application in police forensic digital image protection. Chin Phys B (2021) 34(5):050502. doi:10.1088/1674-1056/adb8bb

CrossRef Full Text | Google Scholar

17. Chai Q, Liu Y. MARR-GAN attention recurrent residual generative Adversarial Network with memristor for Raindrop Removal. Micromachiness (2024) 15(2):15020217. doi:10.3390/mi15020217

CrossRef Full Text | Google Scholar

18. Liu Y, Guo Z, Chau TK, Iu HHC, Si G. Nonlinear circuits with parallel-/series-connected HP-type memory elements and their characteristic analysis. Int J Circ Theor Appl (2021) 49(2):513–32. doi:10.1002/cta.2915

CrossRef Full Text | Google Scholar

19. Corinto F, Ascoli A. Memristive diode bridge with LCR filter. Electronics Lett (2012) 48(14):824–5. doi:10.1049/el.2012.1480

CrossRef Full Text | Google Scholar

20. Ntinas V, Vourkas I, Sirakoulis GC. LC filters with enhanced memristive damping. In: 2015 IEEE international symposium on circuits and systems (ISCAS) (2015). p. 2664–7. doi:10.1109/ISCAS.2015.7169234

CrossRef Full Text | Google Scholar

21. Torebayev G, Nandakumar A. Implementation of memristor in Bessel filter with RLC components. Int Conf Comput Netw Commun (Coconet) (2018) 190–4. doi:10.1109/CoCoNet.2018.8476913

CrossRef Full Text | Google Scholar

22. Sadecki J, Marszalek W. Analysis of a memristive diode bridge rectifier. Electronics Lett (2019) 55(3):120–2. doi:10.1049/el.2018.6921

CrossRef Full Text | Google Scholar

23. Li C, Zhou Y, Yang Y, Li H, Feng W, Li Z, et al. Complicated dynamics in a memristor-based RLC circuit. Eur Phys J Spec Top (2019) 228:1925–41. doi:10.1140/epjst/e2019-800195-8

CrossRef Full Text | Google Scholar

24. Liu Y, Wang K, Qian Y, Liu X, Wang S. Neuromorphic oscillators and electronic implementation of one novel MFNN model. IEEE Access (2023) 11:16076–84. doi:10.1109/ACCESS.2022.3233771

CrossRef Full Text | Google Scholar

25. Dautovic S, Samardzic N, Juhas A, Ascoli A, Tetzlaff R. Analytical solutions for charge and flux in HP ideal generic memristor model with Joglekar and Prodromakis window functions. IEEE Access (2024) 12:94870–84. doi:10.1109/ACCESS.2024.3424568

CrossRef Full Text | Google Scholar

26. So-Yeon K, Heyi Z, Rivera-Sierra G, Fenollosa R, Rubio-Magnieto J, Bisquert J. Introduction to neuromorphic functions of memristors: the inductive nature of synapse potentiation. J Appl Phys (2025) 137:111101. doi:10.1063/5.0257462

CrossRef Full Text | Google Scholar

27. Liu Y, Liu F, Luo W, Wu A, Li H. AC power analysis for second-order memory elements. Front Phys (2023) 11:1135739. doi:10.3389/fphy.2023.1135739

CrossRef Full Text | Google Scholar

28. Yu F, He S, Yao W, Cai S, Xu Q. Bursting firings in memristive hopffeld neural network with image encryption and hardware implementation. IEEE Trans Computer-Aided Des Integrated Circuits Syst (2025) 161–73. doi:10.1109/TCAD.2025.3567878

CrossRef Full Text | Google Scholar

29. Liu Y, Li H, Guo S, Iu HH. Generation of multi-lobe chua corsage memristor and its neural oscillation. Micromachines (2022) 13(8):1330–43. doi:10.3390/mi13081330

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Liu Y, Iu HH. Novel floating and grounded memory interface circuits for constructing mem-elements and their applications. IEEE Access (2020) 8:114761–72. doi:10.1109/ACCESS.2020.3004160

CrossRef Full Text | Google Scholar

31. Liu Y, Iu HH, Guo S, Li H. Chaotic dynamics in memristive circuits with different -q characteristics. Jul 2021 Int J Circ Theor Appl (2022) 49(11):3540–58. doi:10.1002/cta.3112

CrossRef Full Text | Google Scholar