A surrogate model for predicting bimorph microscale piezoelectric energy harvester performance under base vibration and thermal effects

Microscale piezoelectric energy harvesters (PEHs) are promising devices for converting ambient thermal and vibrational energy into usable electrical power. However, their performance is strongly influenced by geometric, material, and thermal parameters, leading to nonlinear behavior that complicates accurate prediction. This study investigates a three-layer clamped bimorph beam consisting of PZT-5H piezoelectric outer layers and an aluminum core, modeled using Euler–Bernoulli beam theory under base excitation and thermal gradients. To overcome the high computational cost of solving the governing equations, a surrogate model based on Gaussian Process Regression (GPR) is developed. The training dataset is generated using Latin Hypercube Sampling, enabling efficient exploration of the design space. The surrogate model accurately predicts both output power and natural frequency across diverse design configurations. Validation against numerical simulations demonstrates excellent agreement, with coefficient of determination (R²) values exceeding 0.99. The proposed framework significantly reduces computational effort while maintaining high predictive accuracy. It provides a reliable tool for design optimization of thermal–vibrational energy harvesting systems, enhancing their efficiency and robustness.

1 Introduction

The field of energy harvesting, which integrates micro- and nano-electromechanical systems with smart materials, has significantly transformed the development of innovative systems. Over the past two decades, researchers have shown considerable interest in capturing energy from ambient sources to power low-energy electronic devices. The primary goal of this technology is to supply electrical energy in remote or inaccessible locations and to recharge energy storage devices, such as batteries and capacitors [1]. The three primary conversion mechanisms are electrostatic [2], piezoelectric [3–5], and electromagnetic transduction [6]. Electrostatic harvesters rely on vibration-dependent variable capacitors, where mechanical energy is converted into electricity as plate separation alters capacitance, though this method requires an external voltage source and is well-suited for micro-scale applications [7–9]; Meninger et al. pioneered variable capacitors for electrostatic conversion in 1998 [10], later refined by Roundy et al. [11]. Electromagnetic harvesters operate via a moving coil within a magnetic field, inducing voltage, though bulky magnets and low output voltages hinder their scalability ($0.1-0.2V$) [12, 13]. Piezoelectric transducers, which generate charge under mechanical deformation, offer higher energy density than electrostatic and electromagnetic methods and are increasingly studied for vibration energy harvesting [14, 15]; clamped beams are commonly used to maximize strain [16–18]. In recent years, research and development on piezoelectric transducers have increased significantly. This rise is mainly because piezoelectric devices have a higher energy density than electrostatic and electromagnetic options. Their greater energy density makes piezoelectric converters better at turning mechanical energy into electrical energy. This ability benefits sensors, actuators, and devices that gather energy. As a result, researchers and engineers have focused on improving piezoelectric materials and systems’ performance, efficiency, and flexibility over the past decade. This trend highlights the essential role that piezoelectric technology plays in advancing various fields, including consumer electronics, automotive systems, and renewable energy solutions. [19]. Modifying the configuration of piezoelectric energy harvesting systems significantly enhances the amount of harvested energy. This modification can be achieved through various techniques, such as changing the type of piezoelectric material, altering the electrode pattern, adjusting the polarization direction, layering the material to increase the active volume, and tuning the excitation frequency of the device. The type of piezoelectric material has a significant impact on the efficiency of the energy harvesting system. Various piezoelectric materials have been used in this field, among which PZT is the most commonly used [20–22]. In energy harvesting device modeling, solving the governing equations of the dynamic behavior of microscale energy harvesters is essential for determining harvested power. These nonlinear equations must be solved repeatedly, even within evolutionary optimization algorithms, to achieve optimal performance. Machine learning techniques now enable the development of surrogate models capable of learning the input-output relationships of complex systems using appropriate [23–25]. Such models have broad applicability and are increasingly utilized in various domains, including modeling nonlinear dynamic phenomena and harvested power in energy harvesters [26–28]. Microscale piezoelectric energy harvesters are increasingly integrated into various real-world applications where inherent thermal gradients significantly impact device performance. For instance, industrial sensors deployed in manufacturing environments frequently experience fluctuating temperature conditions due to machinery operation and ambient changes, which can alter the harvester’s piezoelectric material properties and mechanical stresses. Similarly, wearable devices that harvest energy from body movements are exposed to non-uniform temperature distributions caused by body heat and environmental variations. These temperature gradients influence the devices’ dynamic response and electrical output, making it essential to incorporate thermal effects into the design and analysis for reliable and efficient operation under realistic operating conditions [30, 31]. In recent years, machine learning-based surrogate modeling has emerged as a powerful tool for predicting the performance of complex energy harvesting systems, offering a practical alternative to computationally expensive numerical simulations. Among the various approaches, models such as artificial neural networks (ANNs), random forests (RF), and support vector regression (SVR) have demonstrated notable success in handling nonlinearity and multidimensional parameter spaces. However, each technique presents unique trade-offs regarding interpretability, generalization, and sensitivity to hyperparameter tuning. In this study, we adopt an optimizable Gaussian Process Regression (GPR) model, which offers high predictive accuracy, probabilistic confidence intervals, and robust generalization even with moderate-sized datasets. Using Bayesian optimization for hyperparameter tuning further enhances the model’s adaptability, making it particularly well-suited for capturing the coupled nonlinear effects inherent in thermo-mechanical piezoelectric energy harvesting [32, 33].

While previous studies on piezoelectric energy harvesting have predominantly focused on vibrational excitation under isothermal conditions, the explicit consideration of thermal gradients remains relatively unexplored. Many existing models either neglect thermal effects or treat them simplistically, which limits their applicability in practical scenarios where temperature variations are unavoidable. This study addresses this critical gap by integrating steady-state thermal gradients into a bimorph microscale piezoelectric harvester’s coupled electromechanical modeling framework. Furthermore, using an optimized Gaussian Process Regression surrogate model allows efficient exploration of the complex nonlinear interactions between temperature, mechanical deformation, and electrical output, thereby advancing the predictive accuracy and practical relevance of energy harvester design under realistic thermal environments. The analytical solution is applied to bimorph configurations, and temperature effects are modeled for symmetric and asymmetric modes. In piezoelectric energy harvesting systems, the output power exhibits a strong nonlinear dependence on design parameters such as transducer geometry, piezoelectric material properties, boundary conditions, and excitation frequency. This nonlinear relationship indicates that small parameter changes can cause significant and unpredictable variations in harvested power. Modifying the transducer’s length, thickness, or electrode configuration can substantially affect efficiency. Additionally, aligning the harvester’s natural frequency with the excitation frequency is essential for maximizing power output. Accordingly, the design of such systems necessitates a thorough analysis of their dynamic behavior and the application of advanced nonlinear modeling techniques to improve performance under varying conditions. In this context, a novel surrogate model has been developed to accurately predict the maximum power output of energy harvesters subjected to thermal variations. This model eliminates the need for repeated evaluations of complex coupled governing equations, which are traditionally time-consuming and computationally intensive. By streamlining this process, the surrogate model significantly accelerates the optimization workflow, enabling rapid design iterations and performance enhancements. This advancement represents a substantial step forward in the efficient design and development of energy harvesting systems.

2 Dynamic coupled mechanical-electrical-thermal responses

Over the past decade, most energy harvesters have been designed and analyzed as cantilever beams. Before formulating the governing equations, several simplifying assumptions were made to reduce the complexity of the analytical model while preserving its physical fidelity. The Euler-Bernoulli beam theory assumes that the beam is slender and that transverse shear deformation can be neglected. Heat transfer is considered steady-state and one-dimensional, with no internal heat generation present. The piezoelectric layers are modeled as linear, homogeneous, and isotropic materials. Dielectric losses and internal electrical resistance are assumed to be negligible. Furthermore, perfect bonding is assumed between all layers, with no interfacial slip. These assumptions collectively enable a more tractable and analytically manageable model, while still capturing the essential physical behavior of the system. In this context, energy harvesting specifically refers to vibrational energy harvesting, where energy is extracted from base excitation. As the base undergoes transverse vibrations, the beam experiences mechanical strain, leading to electrical polarization in the piezoelectric layers and generating an electric potential along the beam’s polarization axis. This enables the production of electrical power. Thin conductive electrodes are applied along the entire length of the beam to collect the induced electric field and extract electrical energy. Additional assumptions include negligible dielectric losses and internal electrical resistance in the harvesting layers, allowing the electric field to be uniform along the beam’s length. Figure 1 illustrates the configuration of the bimorph piezoelectric energy harvester, while Figures 1a,b show the electrode arrangements for parallel and series electrical connections, respectively. Mechanical strain in the piezoelectric layers arises either from vibrational excitation at the base or from thermal gradients across the composite structure. This strain induces an electric potential, $V$, along the beam’s polarization direction. The corresponding electrical power, $P$, is extracted via conductive electrodes connected to an external resistive element, R, functioning as the load. While both configurations share identical geometrical and material characteristics, their electromechanical coupling mechanisms differ, thereby influencing the harvester’s frequency response behavior. A set of geometric and thermal parameters defines the system. The thickness of each piezoelectric layer is represented by h_p, while h_h denotes the thickness of the homogeneous substrate layer. The temperatures at the upper and lower surfaces of the piezoelectric layers are indicated by T_t and T_b, respectively, with T_h signifying the temperature of the homogeneous layer. In this study, the assumption of one-dimensional, steady-state heat conduction without internal heat generation is adopted based on the energy harvesting system’s physical characteristics and operating conditions. The device consists of thin laminated layers with high surface-area-to-volume ratios, which promote rapid thermal equilibration in the thickness direction while minimizing lateral heat flow. Moreover, the harvester is assumed to operate under stable thermal boundary conditions, such as fixed surface temperatures or constant ambient exposure, where thermal transients decay much faster than the characteristic time scales of the mechanical vibrations. As a result, the temperature field reaches a steady state before the dynamic response becomes significant. Additionally, the absence of internal heat sources further supports this assumption. This modeling approach aligns with the typical environmental conditions under which such piezoelectric harvesters are deployed, particularly in structural and aerospace applications. It allows for a physically accurate yet computationally efficient representation of the thermal behavior. Although transient thermal effects may be relevant in scenarios involving rapidly changing thermal loads, such cases fall outside the scope of the current work. Based on these assumptions, the temperature distribution is established through specific Equations [14]:

${\mathit{T}}_{\mathit{h}}\left(\mathit{z}=\mathbf{0}\right)={\mathit{T}}_{\mathit{b}}={\mathit{T}}_{\mathit{o}},{\mathit{T}}_{\mathit{t}}={\mathit{T}}_{\mathit{P}\mathit{t}}\left(\mathit{z}={\mathit{h}}_{\mathit{C}}\right)={\mathit{T}}_{\mathit{P}\mathit{b}}\left(\mathit{z}=-{\mathit{h}}_{\mathit{C}}\right)(\mathrm{1a})$

${\mathit{T}}_{\mathit{h}}\left(\mathit{z}\right)={\mathit{T}}_{\mathit{b}}+\frac{{\mathit{T}}_{\mathit{t}}-{\mathit{T}}_{\mathit{b}}}{\frac{\mathbf{1}}{\mathbf{2}{\mathit{K}}_{\mathit{h}}}{\mathit{h}}_{\mathit{h}}+\frac{{\mathit{h}}_{\mathit{P}}}{{\mathit{K}}_{\mathit{P}}}}\left[\frac{\mathbf{1}}{{\mathit{K}}_{\mathit{h}}}\right]\left[\mathit{Z}-\mathbf{0}\right],\mathbf{0}\le \mathit{Z}\le {\mathit{h}}_{\mathit{a}}(\mathrm{1b})$

$\begin{array}{ll}\hfill & \hfill \Delta {\mathit{T}}_{\mathit{P}\mathit{t}}\left(\mathit{Z}\right){=\mathit{T}}_{\mathit{P}\mathit{t}}-{\mathit{T}}_{\mathbf{0}}={\mathit{T}}_{\mathit{b}}+\frac{{\mathit{T}}_{\mathit{t}}-{\mathit{T}}_{\mathit{b}}}{\frac{\mathbf{1}}{\mathbf{2}{\mathit{K}}_{\mathit{h}}}{\mathit{h}}_{\mathit{h}}+\frac{{\mathit{h}}_{\mathit{P}}}{{\mathit{K}}_{\mathit{P}}}}\left[\frac{\mathbf{1}}{{\mathit{K}}_{\mathit{h}}}\left(\frac{{\mathit{h}}_{\mathit{h}}}{\mathbf{2}}\right)+\frac{\mathbf{1}}{{\mathit{K}}_{\mathit{P}}}\left(\mathit{Z}-{\mathit{h}}_{\mathit{a}}\right)\right],\\ \hfill & \times {\mathit{h}}_{\mathit{a}}\le \mathit{Z}\le {\mathit{h}}_{\mathit{C}}\hfill \end{array}(\mathrm{1c})$

$\begin{array}{cc}\Delta {\mathit{T}}_{\mathit{P}\mathit{b}}\left(\mathit{Z}\right)=\hfill & \hfill {\mathit{T}}_{\mathit{P}\mathit{b}}-{\mathit{T}}_{\mathbf{0}}={\mathit{T}}_{\mathit{b}}+\frac{{\mathit{T}}_{\mathit{t}}-{\mathit{T}}_{\mathit{b}}}{\frac{\mathbf{1}}{\mathbf{2}{\mathit{K}}_{\mathit{h}}}{\mathit{h}}_{\mathit{h}}+\frac{{\mathit{h}}_{\mathit{P}}}{{\mathit{K}}_{\mathit{P}}}}\\ \hfill & \times \left[\frac{\mathbf{1}}{{\mathit{K}}_{\mathit{h}}}\left(\frac{{\mathit{h}}_{\mathit{h}}}{\mathbf{2}}\right)+\frac{\mathbf{1}}{{\mathit{K}}_{\mathit{P}}}\left(-\mathit{Z}+{\mathit{h}}_{\mathit{a}}\right)\right]-{\mathit{h}}_{\mathit{a}}\le \mathit{Z}\le -{\mathit{h}}_{\mathit{C}}\hfill \end{array}(\mathrm{1d})$

Figure 1

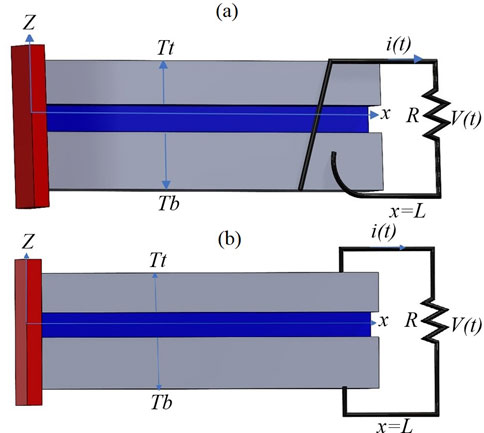
Figure 1. Frequency response of the harvested power with respect to the dimensionless frequency Ω in the first case, for different values of ${\mathrm{T}}_{\mathrm{t}}$; (a) parallel connection (b) series connection of piezoelectric layers.

In these expressions, where $T_{Pt}$, $T_{Pb}$ and $T_h$ represent the temperature distributions within the upper piezoelectric layer, lower piezoelectric layer, and the homogeneous (substrate) layer, respectively. The thermal conductivities of the piezoelectric and homogeneous materials are denoted by $K_P$ and $K_h$, respectively. Equations 2–4 define the axial mechanical stress ${\sigma }_x^h$ in the homogeneous layer and the electric displacement $D_z$, in the piezoelectric layers.

${\mathit{\sigma }}_{\mathit{x}}^{\mathit{h}}={\mathit{C}}_{\mathit{x}\mathit{x}}^{\mathit{h}}-{\mathit{\beta }}_{\mathit{h}}\Delta {\mathit{T}}_{\mathit{h}}\left(\mathit{z}\right)(2)$

${\mathit{\sigma }}_{\mathit{x}}^{\mathit{p}}={\mathit{C}}_{\mathit{x}\mathit{x}}^{\mathit{p}}-{\mathit{e}}_{\mathit{z}\mathit{x}}{\mathit{E}}_{\mathit{z}}-{\mathit{\beta }}_{\mathit{p}}\Delta {\mathit{T}}_{\mathit{p}}\left(\mathit{z}\right)(3)$

${\mathit{D}}_{\mathit{z}}={\mathit{e}}_{\mathit{z}\mathit{x}}{\mathit{ϵ}}_{\mathit{x}}+{\mathit{h}}_{\mathit{z}\mathit{z}}{\mathit{E}}_{\mathit{z}}+{\mathit{P}}_{\mathit{z}}\Delta {\mathit{T}}_{\mathit{p}}\left(\mathit{z}\right)(4)$

The coefficients $C_{xx}^P$, $C_{xx}^h$, represent the elastic stiffness of the piezoelectric and homogeneous layers, respectively. The parameters $e_{zx}$ and $h_{zz}$ denote the piezoelectric and dielectric coefficients, while ${\beta }_P$, ${\beta }_h$, are the thermal stress constants for each material. The axial mechanical strain is indicated ${\epsilon }_x$ and $E_z$ stands for the electric field. The distributed piezoelectric coefficient in the layer’s thickness is denoted by $P_z$. The electric field $E_z$ is related to the applied voltage V(t) and the piezoelectric layer thickness, considering parallel and series configurations (Table 1). The total transverse displacement W(x,t) combines base excitation W_b(t) and relative deflection W_rel(x,t). Different boundary conditions significantly influence energy harvesting systems’ dynamic behavior and overall performance by altering key parameters such as natural frequency, mode shapes, stress distribution, and deflection amplitude. For instance, a fixed-fixed configuration increases structural stiffness, which raises the system’s natural frequencies and reduces vibration amplitude under the same excitation level. This can lower strain levels in piezoelectric layers, decreasing harvested power. Similarly, supported or free-free conditions tend to exhibit symmetrical mode shapes and limited localized deformation, making them less efficient in concentrating strain energy in regions optimal for transducer placement. Moreover, complex boundary conditions may introduce mode coupling or require more sophisticated mounting mechanisms, complicating device fabrication and tuning. Therefore, although alternative boundary conditions may offer particular advantages in specific applications, they typically reduce the energy conversion efficiency and design simplicity compared to the cantilever (fixed-free) configuration, which remains the most efficient and widely adopted choice in vibration-based energy harvesting systems. The fixed-free (cantilever) boundary condition plays a pivotal role in designing and analyzing energy harvesting systems due to its favorable dynamic characteristics. This configuration offers mechanical flexibility, enabling significant tip deflections that enhance strain energy conversion efficiency in piezoelectric and other transduction mechanisms. The cantilever structure exhibits a lower natural frequency than fixed-fixed or supported conditions. It is well-suited for harvesting ambient low-frequency vibrations commonly encountered in real-world environments. Alternative boundary conditions, such as fixed-fixed or free-free, often increase system stiffness or mode shapes that reduce energy conversion efficiency or complicate the design and implementation. Moreover, the simplicity of the cantilever setup facilitates easier fabrication, integration, and tuning of the harvester for targeted frequency ranges. Consequently, the fixed-free condition remains the preferred choice in many practical energy harvesting applications, balancing mechanical performance and manufacturability while maximizing power output. Equation 5 describes the governing differential equation for the forced vibration of the cantilever beam under thermal loading, based on Euler-Bernoulli beam theory:

$\frac{{\mathit{\partial }}^{\mathbf{2}}{\mathit{M}}^{\mathit{T}\mathit{S}}}{\mathit{\partial }{\mathit{x}}^{\mathbf{2}}}+\mathit{E}{\mathit{I}}_{\mathit{e}\mathit{q}}\frac{{\mathit{\partial }}^{\mathbf{4}}{\mathit{w}}_{\mathit{r}\mathit{e}\mathit{l}}^{\mathit{S}}}{\mathit{\partial }{\mathit{x}}^{\mathbf{4}}}+\left({\mathit{N}}^{\mathit{T}\mathit{S}}+\mathbf{2}{\mathit{N}}^{\mathit{T}\mathit{P}}\right)\frac{{\mathit{\partial }}^{\mathbf{2}}{\mathit{w}}_{\mathit{r}\mathit{e}\mathit{l}}^{\mathit{S}}}{\mathit{\partial }{\mathit{x}}^{\mathbf{2}}}+\mathit{\rho }{\mathit{A}}_{\mathit{e}\mathit{q}}\frac{{\mathit{\partial }}^{\mathbf{2}}{\mathit{w}}_{\mathit{r}\mathit{e}\mathit{l}}^{\mathit{S}}}{\mathit{\partial }{\mathit{t}}^{\mathbf{2}}}+$

${\mathit{\vartheta }}^{\mathit{S}}{\mathit{V}}^{\mathit{S}}\left(\mathit{t}\right)\left[\frac{\mathit{d}\mathit{\delta }\left(\mathit{x}\right)}{\mathit{d}\mathit{x}}-\frac{\mathit{d}\mathit{\delta }\left(\mathit{x}-\mathit{L}\right)}{\mathit{d}\mathit{x}}\right]=-\mathit{m}\frac{{\mathit{\partial }}^{\mathbf{2}}{\mathit{w}}_{\mathit{r}\mathit{e}\mathit{l}}^{\mathit{S}}}{\mathit{\partial }{\mathit{t}}^{\mathbf{2}}}(5)$

To determine the electric charge q(t) on the electrodes, Gauss’s law can be applied. The charge is obtained by integrating the electric displacement D_z over the cross-sectional area of the electrodes. When q(t) is considered a time-dependent quantity, the corresponding electric current i(t) at the electrode terminals can be derived by taking the time derivative of the charge.

$\mathit{i}\left(\mathit{t}\right)=\frac{\mathit{d}\mathit{q}\left(\mathit{t}\right)}{\mathit{d}\mathit{t}}=-{\mathit{e}}_{\mathit{z}\mathit{x}}\left({\mathit{h}}_{\mathit{a}}+\mathbf{0.5}{\mathit{h}}_{\mathit{c}}\right)\mathit{b}{\int }_{\mathbf{0}}^{\mathit{L}}\frac{{\mathit{\partial }}^{\mathbf{3}}{\mathit{w}}_{\mathit{r}\mathit{e}\mathit{l}}}{\mathit{\partial }{\mathit{x}}^{\mathbf{2}}\mathit{\partial }\mathit{t}}\mathit{d}\mathit{x}-{\mathit{h}}_{\mathit{z}\mathit{z}}\frac{\mathit{b}\mathit{L}}{{\mathit{h}}_{\mathit{p}}}{\dot{\mathit{V}}}^{\mathit{S}}\left(\mathit{t}\right)+{\mathit{P}}_{\mathit{z}}\mathit{b}\mathit{L}\frac{{\mathit{\partial }\mathit{T}}_{\mathit{P}}\left({\mathit{h}}_{\mathit{a}}+\mathbf{0.5}{\mathit{h}}_{\mathit{c}}\right)}{\mathit{\partial }\mathit{t}}(6)$

Using Equation 6 and Ohm’s Law, which relates the voltage v(t) across a resistor to the current i(t) flowing through it with the equation v(t) = R × i(t), we can derive the corresponding electrical governing equation as follows:

$\frac{\mathit{V}\left(\mathit{t}\right)}{\mathit{R}}+{\mathit{C}}_{\mathit{P}}\frac{\mathit{d}\mathit{V}\left(\mathit{t}\right)}{\mathit{d}\left(\mathit{t}\right)}=-{\mathit{e}}_{\mathit{z}\mathit{x}}\left({\mathit{h}}_{\mathit{a}}+\mathbf{0.5}{\mathit{h}}_{\mathit{c}}\right)\mathit{b}{\int }_{\mathbf{0}}^{\mathit{L}}\frac{{\mathit{\partial }}^{\mathbf{3}}{\mathit{w}}_{\mathit{r}\mathit{e}\mathit{l}}}{\mathit{\partial }{\mathit{x}}^{\mathbf{2}}\mathit{\partial }\mathit{t}}\mathit{d}\mathit{x}+{\mathit{P}}_{\mathit{z}}\mathit{b}\mathit{L}\frac{{\mathit{\partial }\mathit{T}}_{\mathit{P}}\left({\mathit{h}}_{\mathit{a}}+\mathbf{0.5}{\mathit{h}}_{\mathit{c}}\right)}{\mathit{\partial }\mathit{t}}(7)$

Assuming the harvesting system has no internal heat sources, and temperature variations are steady over time, Equation 7 is derived under these conditions. As a result, the term $P_{z}bL\frac{{\partial T}_P\left(h_a+0.5h_c\right)}{\partial t}$, which represents the time rate of change of temperature at a specific location within the piezoelectric layer, is effectively zero. The method of separation of variables is employed to solve the governing differential equations obtained in the previous section. This involves expressing the transverse displacement as a product of spatial and temporal components, represented by the rth transverse mode shape $X_r\left(x\right)$ and the corresponding modal displacement $W_r\left(t\right)$, respectively. This modal analysis approach facilitates the solution of the system’s dynamic response (Equation 8).

${\mathit{w}}_{\mathit{r}\mathit{e}\mathit{l}}\left(\mathit{x}.\mathit{t}\right)={\displaystyle \sum _{\mathit{r}=\mathbf{1}}^{\mathit{\infty }}}{\mathit{X}}_{\mathit{r}}\left(\mathit{x}\right){\mathit{W}}_{\mathit{r}}\left(\mathit{t}\right)(8)$

The rth normal mode shape, denoted as $X_r\left(x\right)$, is essential for characterizing the linear transverse vibrations of a cantilever beam. This function is vital for accurately analyzing and predicting the beam’s dynamic response, making it a crucial component in engineering design and structural analysis. The mathematical expression for the rth mode shape is provided by Equation 9 as follows:

${\mathit{X}}_{\mathit{r}}\left(\mathit{x}\right)=\frac{l}{\sqrt{\mathit{m}\mathit{L}}}\left[\mathit{cosh}{\mathit{ϴ}}_{\mathbf{1}}\mathit{x}-\mathit{cos}{\mathit{ϴ}}_{\mathbf{2}}\mathit{x}+{\mathit{\Lambda }}_{\mathit{r}}\left(-\mathit{sinh}{\mathit{ϴ}}_{\mathbf{1}}\mathit{x}+\frac{{\mathit{ϴ}}_{\mathbf{1}}}{{\mathit{ϴ}}_{\mathbf{2}}}\mathit{sin}{\mathit{ϴ}}_{\mathbf{2}}\mathit{x}\right)\right](9)$

Equation 10 describes the energy harvester’s rth natural frequency w_r, taking thermal loads into account. Temperature gradients within the beam generate stresses that affect its stiffness and dynamic behavior. Consequently, the natural frequencies depend not only on the material properties but also on the prevailing thermal conditions.

${{\mathit{\omega }}_{\mathit{r}}}^{\mathbf{2}}=\frac{{\mathit{E}\mathit{I}}_{\mathit{e}\mathit{q}}}{{\mathit{m}}_{\mathit{e}\mathit{q}}}\left[{\left({\mathit{ϴ}}_{\mathbf{1}}^{\mathbf{2}}-\frac{{\mathit{N}}^{\mathit{T}}}{\mathbf{2}\mathit{E}{\mathit{I}}_{\mathit{e}\mathit{q}}}\right)}^{\mathbf{2}}-{\left(\frac{{\mathit{N}}^{\mathit{T}}}{\mathbf{2}\mathit{E}{\mathit{I}}_{\mathit{e}\mathit{q}}}\right)}^{\mathbf{2}}\right](10)$

The governing equations describe the dynamic behavior of the energy harvester under harmonic base excitation and thermal effects. A transverse displacement amplitude, W_A, characterizes the base excitation​. The imaginary unit is represented by j. Under these conditions, the vibration response of the beam can be expressed using modal coordinates W_r(t), along with the corresponding electric voltage V(t).

$\mathit{V}\left(\mathit{t}\right)=\frac{{\displaystyle {\sum }_{\mathit{r}=\mathbf{1}}^{\mathit{\infty }}}\frac{\mathit{j}\mathit{\omega }{\mathit{\lambda }}_{\mathit{r}}{\mathit{F}}_{\mathit{A}\mathit{r}}}{\left[\left({\mathit{\omega }}_{\mathit{r}}^{\mathbf{2}}-{\mathit{\omega }}^{\mathbf{2}}\right)+\mathit{j}\left(\mathbf{2}{\mathit{\zeta }}_{\mathit{r}}{\mathit{\omega }}_{\mathit{r}}\mathit{\omega }\right)\right]}{\mathit{e}}^{\mathit{j}\mathit{\omega }\mathit{t}}}{\left[\left(\frac{\mathbf{1}}{{\mathit{\psi }}_{\mathit{R}}\mathit{R}}+{\mathit{\psi }}_{\mathit{C}}\mathit{j}\mathit{\omega }{\mathit{C}}_{\mathit{p}}\right)+{\displaystyle {\sum }_{\mathit{r}=\mathbf{1}}^{\mathit{\infty }}}\frac{\mathit{j}\mathit{\omega }{\mathit{\lambda }}_{\mathit{r}}^{\mathbf{2}}}{\left[\left({\mathit{\omega }}_{\mathit{r}}^{\mathbf{2}}-{\mathit{\omega }}^{\mathbf{2}}\right)+\mathit{j}\left(\mathbf{2}{\mathit{\zeta }}_{\mathit{r}}{\mathit{\omega }}_{\mathit{r}}\mathit{\omega }\right)\right]}\right]}(11)$

The term $w_{rel}\left(x.t\right)c$ and Equation 11 denotes the displacement of each point on the structure relative to the base and is mathematically expressed as follows:

${\mathit{w}}_{\mathit{r}\mathit{e}\mathit{l}}\left(\mathit{x}.\mathit{t}\right)=\left[\mathbf{1}-\frac{{\displaystyle {\sum }_{\mathit{r}=\mathbf{1}}^{\mathit{\infty }}}\frac{\mathit{j}\mathit{\omega }{\mathit{\lambda }}_{\mathit{r}}}{\left[\left({\mathit{\omega }}_{\mathit{r}}^{\mathbf{2}}-{\mathit{\omega }}^{\mathbf{2}}\right)+\mathit{j}\left(\mathbf{2}{\mathit{\zeta }}_{\mathit{r}}{\mathit{\omega }}_{\mathit{r}}\mathit{\omega }\right)\right]}}{\left[\left(\frac{\mathbf{1}}{{\mathit{\psi }}_{\mathit{R}}\mathit{R}}+{\mathit{\psi }}_{\mathit{C}}\mathit{j}\mathit{\omega }{\mathit{C}}_{\mathit{p}}\right)+{\displaystyle {\sum }_{\mathit{r}=\mathbf{1}}^{\mathit{\infty }}}\frac{\mathit{j}\mathit{\omega }{\mathit{\lambda }}_{\mathit{r}}^{\mathbf{2}}}{\left[\left({\mathit{\omega }}_{\mathit{r}}^{\mathbf{2}}-{\mathit{\omega }}^{\mathbf{2}}\right)+\mathit{j}\left(\mathbf{2}{\mathit{\zeta }}_{\mathit{r}}{\mathit{\omega }}_{\mathit{r}}\mathit{\omega }\right)\right]}\right]}\right]\times \frac{\mathit{X}\left(\mathit{x}\right){{\mathit{F}}_{\mathit{A}\mathit{r}}\mathit{e}}^{\mathit{j}\mathit{\omega }\mathit{t}}}{\left[\left({\mathit{\omega }}_{\mathit{r}}^{\mathbf{2}}-{\mathit{\omega }}^{\mathbf{2}}\right)+\mathit{j}\left(\mathbf{2}{\mathit{\zeta }}_{\mathit{r}}{\mathit{\omega }}_{\mathit{r}}\mathit{\omega }\right)\right]}(12)$

The electrode current i(t) is derived using Ohm’s law in Equation 12. With both the current and voltage available at the electrode terminals, the harvested power P(t) can then be calculated as follows:

$\mathit{P}\left(\mathit{t}\right)=\frac{\mathbf{1}}{\mathbf{2}\mathit{R}}\frac{{\displaystyle {\sum }_{\mathit{r}=\mathbf{1}}^{\mathit{\infty }}}\frac{{\left(\mathit{j}\mathit{\omega }{\mathit{\lambda }}_{\mathit{r}}{\mathit{F}}_{\mathit{A}\mathit{r}}\right)}^{\mathbf{2}}}{{\left[\left({\mathit{\omega }}_{\mathit{r}}^{\mathbf{2}}-{\mathit{\omega }}^{\mathbf{2}}\right)+\mathit{j}\left(\mathbf{2}{\mathit{\zeta }}_{\mathit{r}}{\mathit{\omega }}_{\mathit{r}}\mathit{\omega }\right)\right]}^{\mathbf{2}}}{\mathit{e}}^{\mathit{j}\mathbf{2}\mathit{\omega }\mathit{t}}}{{\left[\left(\frac{\mathbf{1}}{{\mathit{\psi }}_{\mathit{R}}\mathit{R}}+{\mathit{\psi }}_{\mathit{C}}\mathit{j}\mathit{\omega }{\mathit{C}}_{\mathit{p}}\right)+{\displaystyle {\sum }_{\mathit{r}=\mathbf{1}}^{\mathit{\infty }}}\frac{\mathit{j}\mathit{\omega }{\mathit{\lambda }}_{\mathit{r}}^{\mathbf{2}}}{\left[\left({\mathit{\omega }}_{\mathit{r}}^{\mathbf{2}}-{\mathit{\omega }}^{\mathbf{2}}\right)+\mathit{j}\left(\mathbf{2}{\mathit{\zeta }}_{\mathit{r}}{\mathit{\omega }}_{\mathit{r}}\mathit{\omega }\right)\right]}\right]}^{\mathbf{2}}}(13)$

The constants γ_R and γ_C in the Equation 13 depend on the specific configuration; their corresponding values are provided in Table 2.

Table 1

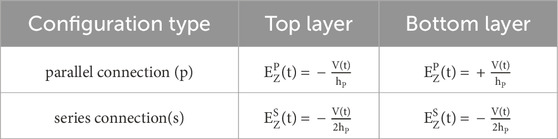
Table 1. Electric field expressions in piezoelectric layers as influenced by parallel and series wiring schemes.

Table 2

Table 2. Constant parameter values corresponding to various system configurations.

2.1 Numerical extraction of the maximum harvested power

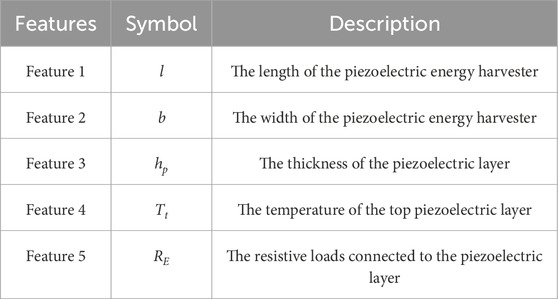
We conducted a frequency sweep analysis to identify the system’s maximum harvest power. We tested the system at different excitation frequencies, creating a power-frequency curve that showed a clear peak. This peak represents the frequency where the system works most efficiently and matches its resonance condition, which helps us find the best point for energy harvesting. The analysis also highlights the system’s sensitivity to excitation frequency, which is essential for design and tuning. Table 3 outlines the properties and dimensions of the piezoelectric harvesting beam, made from PZT-5H and aluminum, with an assumed initial ambient temperature of 20°C applied uniformly to both surfaces. As can be seen from the extracted equations, the parameters affecting the harvester’s design include the beam layers’ length L, width b, the thickness of the layer h_p, h_h, the electrical resistance of the two ends of the electrodes R, and the temperature difference between the harvester layers T_t. This study adopts a representative average damping ratio following the approach commonly used in previous investigations on piezoelectric energy harvesting beams. This simplification is justified given the microscale harvester’s operating conditions and the inherent uncertainties in exact damping characterization. While damping influences the system’s dynamic response and power output, especially near resonance, its effect under thermal gradients is indirect through changes in structural stiffness and natural frequencies—thermal-induced variations in stiffness shift resonance frequencies, modifying the interaction between damping and vibrational response. Higher damping values generally broaden the resonance peak and reduce maximum harvested power, whereas lower damping sharpens the response but may lead to sensitivity under thermal fluctuations. The chosen damping value practically balances model fidelity and computational tractability. Future work may consider a parametric study to comprehensively assess the coupled impact of damping and thermal effects on harvester performance. For example, Figures 2, 3 illustrate the effect of two of these parameters on the frequency response performance in the parallel mode. After plotting the frequency response of the generated power, the maximum power points for each mode are extracted. This process is repeated across the entire design range of the influential parameters to compile comprehensive data capturing the numerical relationship between the input variables and the outputs of interest.

Table 3

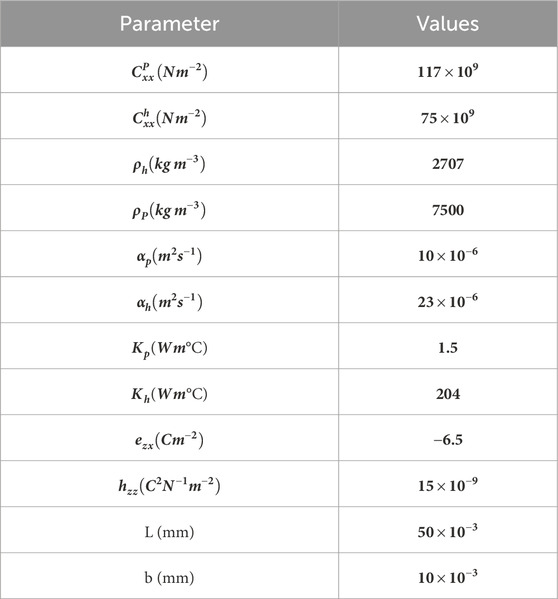
Table 3. Summary of material characteristics and dimensional attributes of the bimorph harvester’s layered structure.

Figure 2

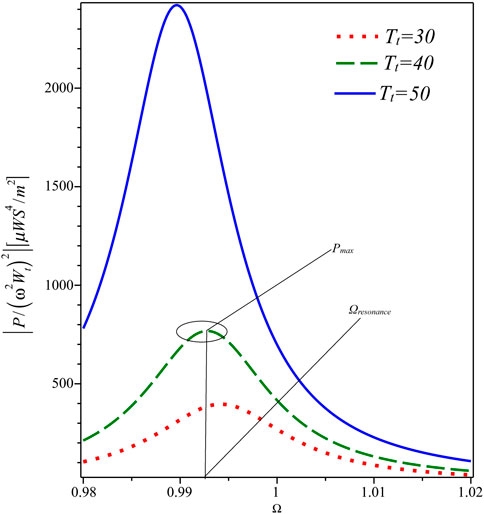
Figure 2. Frequency response of the harvested power with respect to the dimensionless frequency Ω in the parallel case for different values of ${\mathrm{T}}_{\mathrm{t}}$

Figure 3

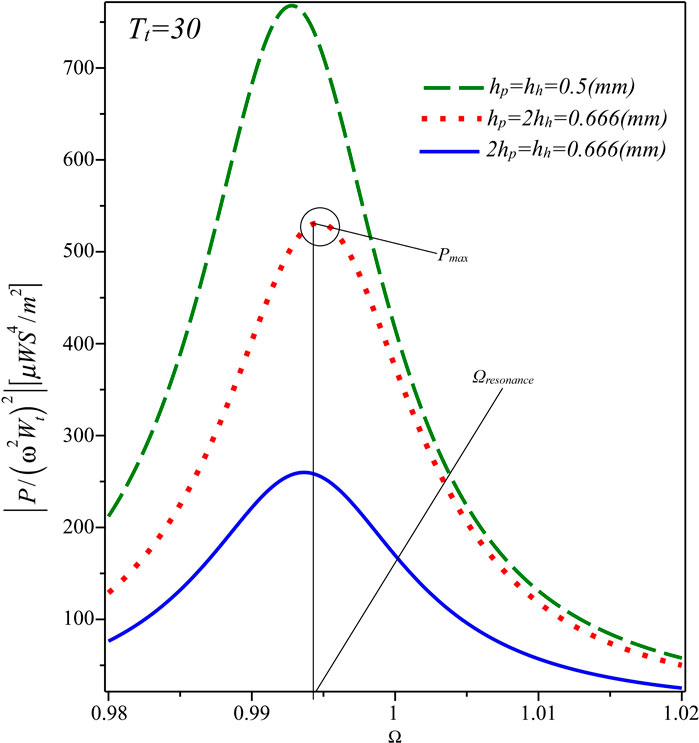
Figure 3. Frequency response of the harvested power with respect to the dimensionless frequency Ω in the parallel case for different values of the thickness ratio.

One key modeling consideration in piezoelectric energy harvesting systems is the electrical configuration of the piezoelectric layers, whether connected in series or parallel. This choice significantly influences the harvester’s output characteristics, such as voltage, current, and overall harvested power. The results demonstrate that the series connection yields significantly higher output power, voltage, and current values than the parallel configuration under the same excitation and boundary conditions. This behavior can be attributed to the cumulative voltage effect in series configurations, where the electrical potential generated by each layer adds up constructively. Additionally, in series mode, the mechanical deformation of the beam results in a more pronounced stress distribution across the layers, leading to stronger electromechanical coupling and enhanced energy conversion efficiency. In contrast, in parallel configurations, while the voltage remains lower due to shared potential, the current may distribute more uniformly, making it suitable for applications requiring stable current flow rather than high voltage.

From a design standpoint, these findings offer practical guidelines for selecting connection schemes tailored to specific application requirements. For instance, series configurations are evidently advantageous in low-power autonomous sensor networks where higher voltage is crucial for charging small-scale storage devices or activating low-current electronic circuits. Conversely, parallel configurations may be preferable for applications with critical current stability, such as power conditioning systems or devices requiring smooth charging cycles. Furthermore, the impact of thermal conditions slightly amplified the benefits of the series configuration, particularly in environments with temperature gradients that affect the mechanical response of the piezoelectric beam. These insights underscore the necessity of considering the electrical connection scheme as a fundamental design variable, rather than a post-processing decision. The empirical modeling conducted in this study, supported by machine learning-driven surrogate models, enables a robust and computationally efficient comparison between the two configurations over a broad design space. As such, the presented framework captures the nuanced performance differences between series and parallel modes and equips engineers and designers with a decision-making tool for optimizing piezoelectric harvesters under coupled thermal and vibrational loading scenarios.

3 Surrogate modeling

In the previous section, it was demonstrated that the harvested power depends on multiple parameters. Therefore, designing an optimal energy harvester requires using an optimization algorithm that involves repeatedly solving the governing differential equation. However, this process is computationally expensive and only provides the generated power for specific input conditions, rather than the maximum extractable power. To overcome this limitation, a suitable surrogate model can be employed to approximate the relationship between the input variables (energy harvester parameters) and the output (generated power). In this study, the most influential variables are first identified (Table 3). Subsequently, a dataset is created by sampling various combinations of these variables, referred to as design points. These key variables are henceforth called features, by machine learning terminology. This section examines three key relationships for the problem defined in the previous sections. A suitable dataset is prepared for each case, and a surrogate model is trained accordingly. The first relationship explores how the features (variables listed in Table 4) affect the power generated by a piezoelectric energy harvester with a parallel connection. The second relationship considers the features of the power generated by a piezoelectric energy harvester with a series connection. Finally, the relationship between the energy harvester’s features and natural frequency is analyzed.

Table 4

Table 4. The definition of the features used in this study.

3.1 Providing an appropriate dataset

Constructing a highly relevant dataset requires meticulous selection of design points. In this study, design points were generated using a multifaceted approach. First, the Latin Hypercube Sampling (LHS) technique was applied to create an initial set of 360 design points. An iterative z-score filtering method was employed three times to improve dataset quality. This process examined the output values in each dataset, removing outliers beyond a robust threshold of |z| < 3. After each iteration, z-scores were recalculated based on the remaining data, ensuring a thorough refinement that removed anomalies while preserving the statistical integrity of the dataset.

Following this outlier removal procedure, the cleaned datasets contained 347 and 341 design points for power prediction in parallel and series configurations, respectively. In contrast, the dataset for natural frequency prediction retained all 360 points. The resulting datasets are thus well-tuned for subsequent analysis and model training. Figure 4 (below) illustrates the data distribution before and after outlier removal, shown on the left side. Outliers were effectively removed from the first and second datasets, with 21 outliers detected and excluded from the third dataset and 29 from the second. The third dataset showed no significant outlier issues and maintained a uniform distribution throughout. As a result, the third model is expected to face fewer challenges during prediction. On the right side of Figure 4, the sensitivity of the response variables—namely, the extracted power in parallel and series configurations, and the ratio of natural frequency under thermal conditions to that without thermal effects is analyzed concerning each of the five input features, both before and after outlier removal. This analysis reveals that outlier removal increases the correlation between each feature and the corresponding response variable, suggesting that models trained on the cleaned datasets will likely exhibit improved predictive performance.

Figure 4

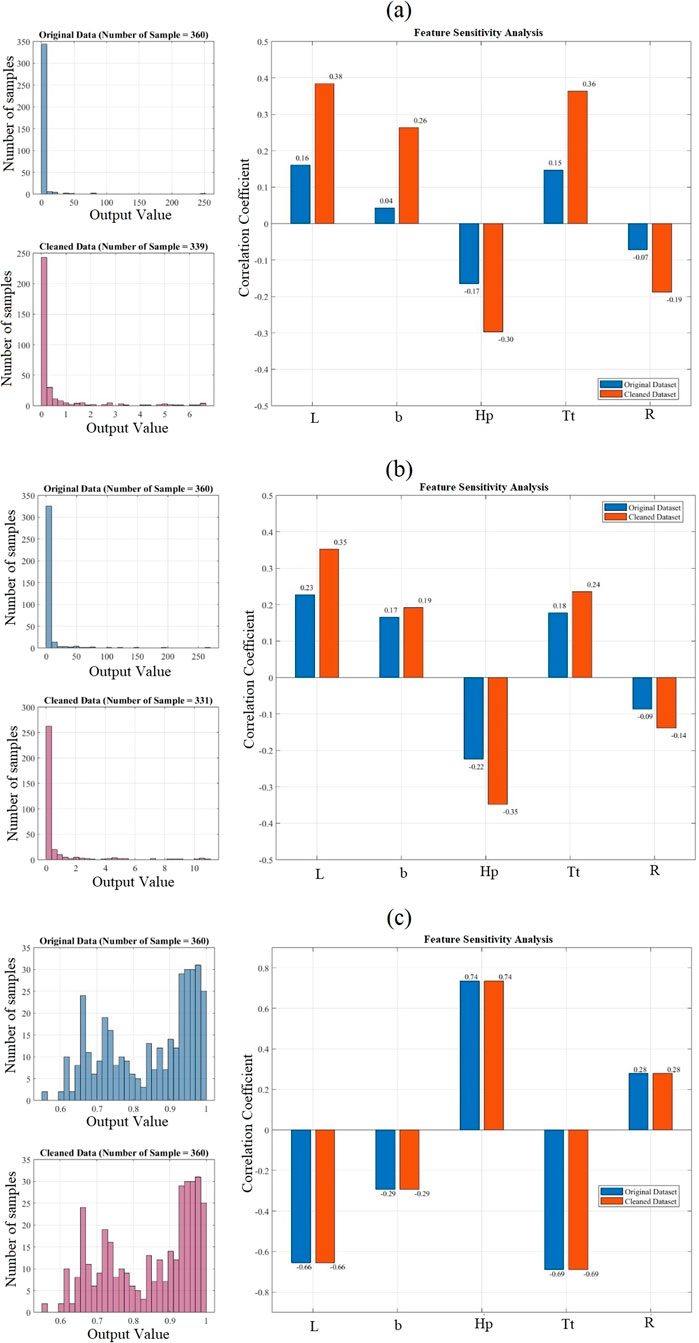
Figure 4. Data distribution in the original dataset and the cleaned dataset after outlier removal for the power outputs in (a) parallel and (b) series connections, and (c) natural frequency of the system.

Figure 5

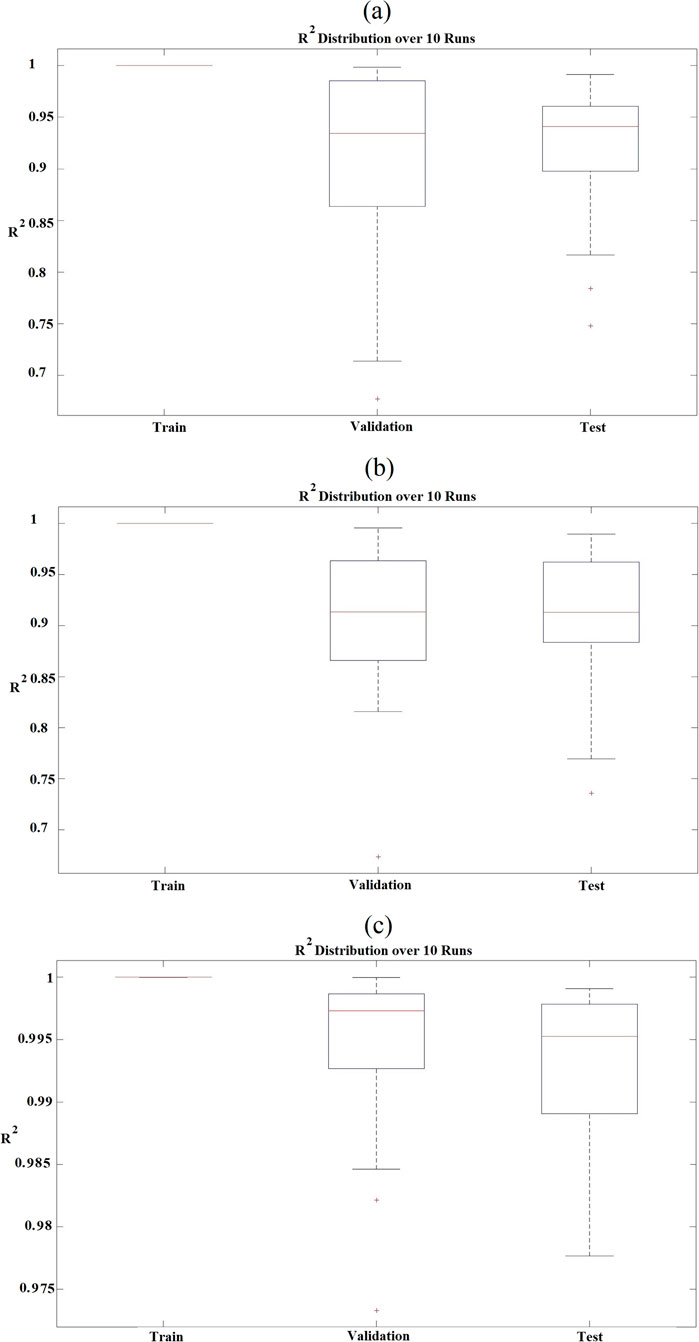
Figure 5. Validation of the average R² value on the prediction of the power outputs in (a) parallel and (b) series connections, and (c) natural frequency of the system.

Compared to the third, the non-uniform data distribution and relatively low feature-response correlations in the first two models indicate nonlinear relationships between inputs and outputs. Thus, the decision to remove outliers is well justified. Outliers pose several challenges: as seen in the earlier figures, a sudden increase in extracted power within a narrow response range reflects nonlinear and highly complex behavior; additionally, Latin Hypercube Sampling results in sparse data around this nonlinear region. Concentrating more samples there would yield a low correlation with the rest of the dataset. Therefore, two options arise: either remove the extreme outliers or focus exclusively on the nonlinear region, disregarding others. This study adopts the former approach by excluding the outliers.

3.2 Surrogate modeling

After preparing a suitable dataset, a surrogate model was trained using an optimizable Gaussian Process Regression (GPR) framework. In recent years, surrogate modeling has become a vital computational strategy in energy harvesting research, allowing researchers to approximate complex multiphysics simulations with efficient, data-driven alternatives. While the current study adopts Gaussian Process Regression (GPR) as its surrogate modeling framework, due to its inherent advantages in probabilistic prediction and interpretability, it is essential to briefly contextualize this choice within the broader landscape of surrogate modeling methods. Several machine learning algorithms have been successfully applied in similar contexts, including Artificial Neural Networks (ANNs), Support Vector Regression (SVR), and Random Forests (RFs), each offering distinct advantages and limitations.

ANNs are widely utilized for their remarkable capacity to capture highly nonlinear relationships between input and output variables, particularly in systems with strong coupling such as piezoelectric energy harvesters. However, they typically require large volumes of training data and are prone to overfitting unless carefully regularized. Moreover, the interpretability of ANNs remains limited due to their black-box nature.SVR is another robust approach capable of handling nonlinearity in high-dimensional datasets with limited samples. Its reliance on kernel functions makes it suitable for smaller datasets; however, its computational efficiency declines as dataset size increases, and it lacks built-in mechanisms for uncertainty quantification. RFs, on the other hand, offer good predictive accuracy and are relatively resilient to noise and overfitting. They provide feature importance insights but are often less effective in extrapolation tasks, especially in problems involving continuous and smooth physical responses. In contrast, GPR combines the strengths of these methods while providing a unique advantage, its probabilistic nature not only yields point predictions but also offers uncertainty estimates, which are especially valuable in engineering applications with sparse or expensive data generation. Using a nonisotropic Matérn 5/2 kernel further enhances its flexibility to model varying degrees of smoothness across different input dimensions. Optimizing GPR hyperparameters through Bayesian inference also ensures a balance between accuracy and generalization. Thus, the selection of GPR in this study is methodologically justified and practically advantageous. It offers a superior trade-off between model complexity, accuracy, and computational cost. It is particularly well-suited for modeling the coupled thermo-mechanical behavior of microscale energy harvesters under diverse operating conditions.

The model’s hyperparameters were tuned via Bayesian optimization, employing a nonisotropic Matérn 5/2 kernel with a kernel scale of 0.0011616 and a noise standard deviation (sigma) of 14.3246. To simplify the mean structure, the basis function was set to zero. Hyperparameter optimization was performed within defined search ranges: kernel scale (0.001–1000), sigma (0.0001–14.3636), and kernel function choices including isotropic and nonisotropic variants such as Exponential, Matérn 3/2, Rational Quadratic, and Squared Exponential kernels. The data was standardized prior to training to ensure consistent scaling. Bayesian optimization used an expected improvement per second plus acquisition function over 30 iterations to efficiently identify the optimal model configuration, balancing predictive accuracy and computational efficiency. A 10-fold cross-validation strategy was employed for training, validation, and testing. To assess robustness, the datasets were randomly split 20 times into training, validation, and testing subsets at 70%, 15%, and 15%, respectively. The mean and standard deviation of performance metrics across these splits were computed for all three surrogate models. These statistics comprehensively understand each model’s behavior throughout training, validation, and testing phases. The results are summarized in Table 5. The mean R² value for the third model, which predicts the effect of thermal conditions on the natural frequency, is observed to exceed 0.99 (as shown in Figures 5a–c). This indicates that the model can simulate this behavior with extremely high accuracy. On the other hand, the second model performs the prediction of the extracted power by the piezoelectric harvester in the second case (series configuration) with a mean R² of 0.9066. This value is acceptable given the nature of the problem and the inherent nonlinearity in the behavior, as the relationship between harvested power and frequency within the resonance region is nonlinear. Therefore, the model’s agreement with this behavior is deemed satisfactory. The residual histograms show the difference between the predicted and actual values for each design point in the training dataset (Figures 6a–c). The figures below display these histograms for all three models. Most design points are clustered around zero, indicating that the models have been trained effectively and that the predicted values closely align with the actual values.

Table 5

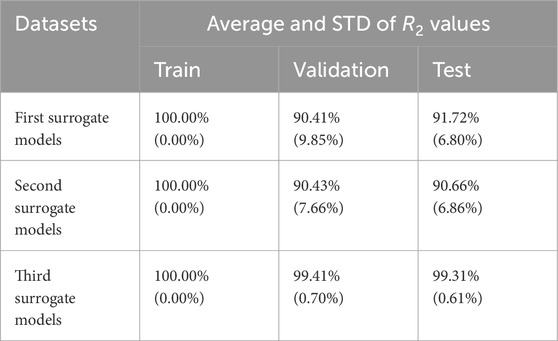
Table 5. Average and STD of ${\mathbf{R}}^{\mathbf{2}}$ values for the training, validation, and testing datasets for three surrogate models.

Furthermore, the box plots presented below (corresponding to models 1, 2, and 3) illustrate the training, validation, and testing performance of the three surrogate models over 20 independent runs. The range of variation observed in the first and second models remains within acceptable limits, indicating consistent model behavior. The surrogate models’ performance was also evaluated using predicted-versus-actual plots, a common visualization technique in regression analysis. These plots compare predicted values against actual observations, providing an intuitive assessment of model accuracy and predictive capability. Figures 7a–c present these plots for the three models, respectively. Each panel displays data points ideally clustered closely along the red diagonal line, which represents perfect predictions. This line is a benchmark, indicating where model predictions match actual outcomes. A tight grouping of points around this diagonal visually confirms the models’ accuracy and reliability, highlighting their effectiveness in making precise forecasts. Based on the comparative analysis of series and parallel configurations in bimorph piezoelectric energy harvesters, it is evident that each connection scheme offers distinct advantages depending on the intended application. The series configuration, which demonstrated superior performance in output voltage, current, and harvested power, is particularly suitable for applications requiring higher electrical energy density, such as wireless sensor nodes, low-power microelectronic devices, or remote structural health monitoring systems. Conversely, the parallel configuration may be advantageous in scenarios where stability of current and reduced voltage levels are desired, such as in energy storage systems or powering low-voltage electronic components. These findings underscore the importance of carefully selecting the connection topology to tailor the energy harvester’s output to specific operational requirements and environmental conditions.

Figure 6

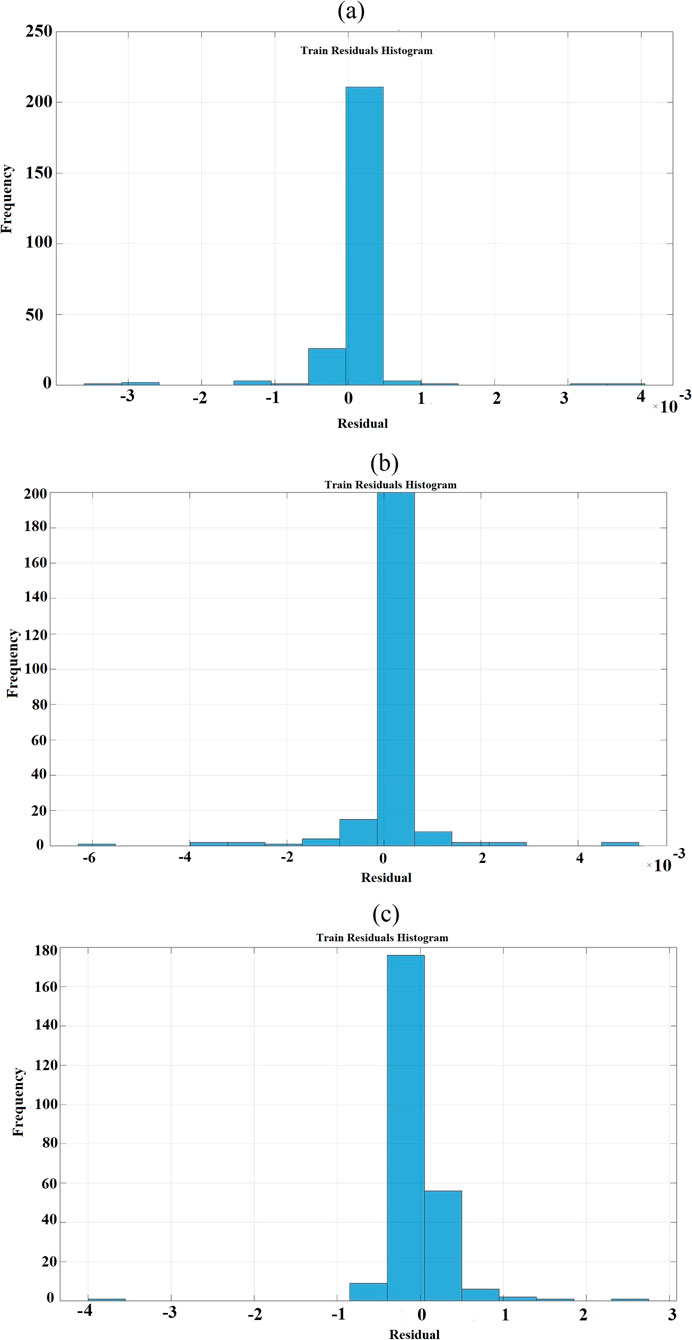
Figure 6. Train residual histogram, the difference between the predicted and actual values of each design point of the power outputs in (a) parallel and (b) series connections and (c) natural frequency of the system.

Figure 7

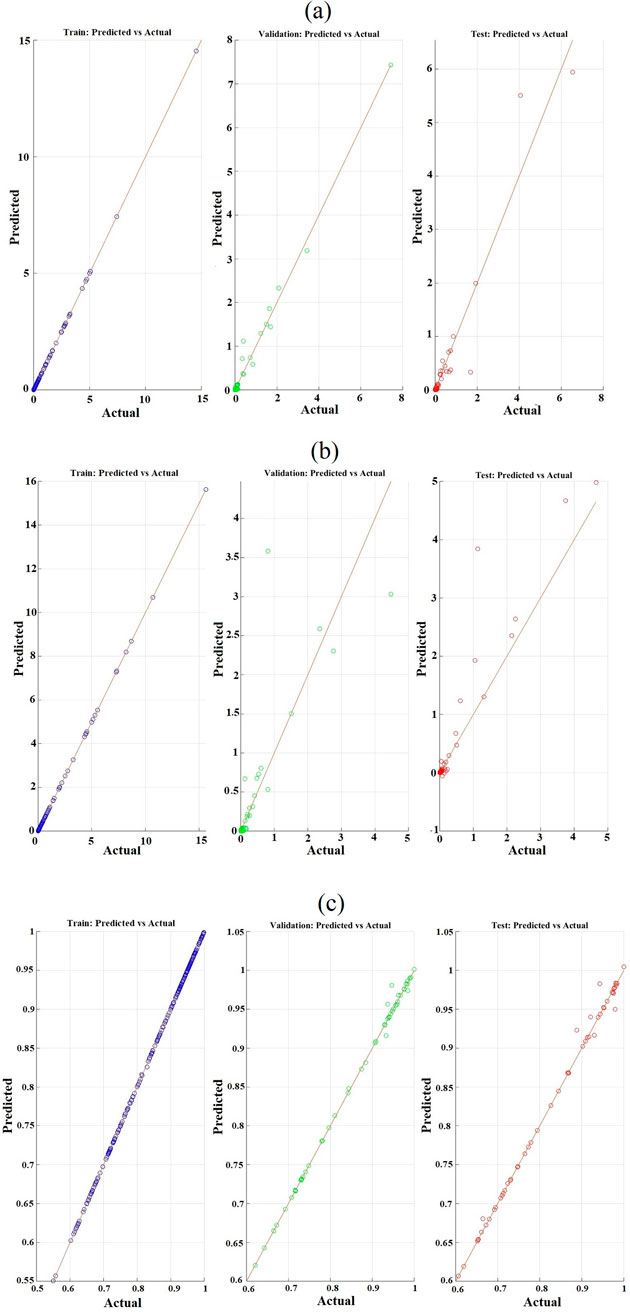
Figure 7. Performance of the three surrogate models for training, validation, and testing datasets of the power outputs in (a) parallel and (b) series connections and (c) natural frequency of the system.

4 Conclusion

This study presents a comprehensive investigation into the performance prediction of bimorph microscale piezoelectric energy harvesters under the combined effects of base excitation and thermal gradients. A simplified analytical model was derived based on Euler–Bernoulli beam theory and thermal conduction assumptions to describe the system’s mechanical, electrical, and thermal coupling. The study comprehensively analyzed the influence of critical geometric dimensions and thermal conditions to assess their effects on the power output generated and the system’s natural frequency. By varying key parameters such as the shape and size of the device and the thermal gradients applied, the research aimed to understand how these factors intricately interact and ultimately contribute to optimizing the efficiency of power harvesting and achieving desirable dynamic responses. This investigation sheds light on the underlying mechanisms that govern performance, providing valuable insights for future advancements in the field. A sophisticated surrogate model grounded in machine learning principles was developed utilizing Gaussian Process Regression (GPR). This model was meticulously trained on a rigorously filtered dataset designed to address the prohibitive computational costs associated with repeatedly solving complex, nonlinear, coupled equations. Three distinct surrogate models were created to enhance predictive capabilities, each tailored to forecast the output power in both parallel and series electrical configurations. Additionally, these models account for the natural frequency shifts induced by thermal effects, allowing for a comprehensive understanding of the system’s behavior under varying conditions. The predictive models demonstrated exceptional capabilities, achieving R² values exceeding 0.99 in multiple instances, reflecting their high accuracy in forecasting outcomes. This research highlights that a series configuration of energy harvesting systems generally yields higher power outputs than a parallel connection. This is primarily due to the significantly improved induced deformation in series setups, which enhances the system’s ability to convert energy. Furthermore, the study emphasizes the critical role of temperature gradients and excitation frequency in influencing the system’s overall efficiency and performance metrics. The innovative surrogate modeling framework developed in this research enables rapid and precise estimations of system performance to address the complexities of these variables. This advancement proves to be a vital tool for optimizing microscale energy harvesting systems, streamlining the design process, and ensuring more effective energy utilization. Such enhancements advance our understanding of microscale energy dynamics and pave the way for more efficient energy solutions in various applications.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

MS: Data curation, Validation, Visualization, Methodology, Formal Analysis, Investigation, Project administration, Writing – review and editing, Conceptualization, Writing – original draft. DM: Resources, Writing – review and editing, Funding acquisition, Validation, Data curation, Supervision, Writing – original draft, Conceptualization, Methodology. SA: Investigation, Resources, Writing – original draft, Validation, Project administration, Writing – review and editing, Visualization, Data curation, Formal Analysis. EK-N: Data curation, Formal Analysis, Resources, Investigation, Writing – review and editing, Project administration, Software, Writing – original draft.

Funding

The author(s) declare that no financial support was received for the research and/or publication of this article.

Acknowledgments

The analytical expressions presented in this study are shown without complete derivations. For detailed step-by-step derivations, refer to preprint [29].

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Any alternative text (alt text) provided alongside figures in this article has been generated by Frontiers with the support of artificial intelligence and reasonable efforts have been made to ensure accuracy, including review by the authors wherever possible. If you identify any issues, please contact us.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Anand A. A review on the performance enhancement techniques of piezoelectric energy harvesters. Nanomater Energy (2025) 14:1–22. doi:10.1680/jnaen.23.00109

CrossRef Full Text | Google Scholar

2. Hassena MAB, Samaali H, Ouakad HM, Najar F. 2D electrostatic energy harvesting device using a single shallow arched microbeam. Int J Non-Linear Mech (2021) 132:103700. doi:10.1016/j.ijnonlinmec.2021.103700

CrossRef Full Text | Google Scholar

3. Man DW, Zhang Y, Tang LP, Xu QH, Chen D, Jiang BD. Nonlinear dynamical characteristics of a hybrid tri-stable piezoelectric energy harvester utilizing rotational motion. Facta Universitatis, Ser Mech Eng (2024) 257–73. doi:10.22190/fume240118033m

CrossRef Full Text | Google Scholar

4. Milić P, Marinković D, Klinge S, Ćojbašić Ž. Reissner-mindlin based isogeometric finite element formulation for piezoelectric active laminated shells. Tehnički vjesnik (2023) 30(2):416–25. doi:10.17559/TV-20230128000280

CrossRef Full Text | Google Scholar

5. Ray AR, Koley S. Performance of piezoelectric beam type energy harvester under flow-induced vibration. Scientific Rep (2025) 15(1):13433. doi:10.1038/s41598-025-98147-0

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Saffari PR, Saffari PR, Senjuntichai T, Askarinejad S, Ghabraie K, Thongchom C. Energy harvesting performance of fluid-immersed bimorph FG-GPLRC sandwich microplates in thermal gradient and magnetic field environments: a modified strain gradient theory approach. Eur J Mechanics-A/Solids (2025) 112:105635. doi:10.1016/j.euromechsol.2025.105635

CrossRef Full Text | Google Scholar

7. Tang X, Wang X, Cattley R, Gu F, Ball AD. Energy harvesting technologies for achieving self-powered wireless sensor networks in machine condition monitoring: a review. Sensors (2018) 18(12):4113. doi:10.3390/s18124113

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Lytle J, Radewych Z, Mai KV, Fung AS. A review and characterization of energy-harvesting resources in buildings with a case study of a commercial building in a cold climate—toronto, Canada. Energies (2025) 18(8):1913. doi:10.3390/en18081913

CrossRef Full Text | Google Scholar

9. Eun Y, Kwon DS, Kim MO, Yoo I, Sim J, Ko HJ. A flexible hybrid strain energy harvester using piezoelectric and electrostatic conversion. Smart Mater Structures (2014) 23(4):045040. doi:10.1088/0964-1726/23/4/045040

CrossRef Full Text | Google Scholar

10. Meninger S, Mur-Miranda JO, Amirtharajah R, Chandrakasan A, Lang J. Vibration-to-electric energy conversion. In: Proceedings of the 1999 international symposium on Low power electronics and design. IEEE (1999)). p. 48–53.

CrossRef Full Text | Google Scholar

11. Roundy SJ. Energy scavenging for wireless sensor nodes with a focus on vibration to electricity conversion. Berkeley: University of California (2003).

Google Scholar

12. Yang B, Lee C, Xiang W, Xie J, He JH, Kotlanka RK. Electromagnetic energy harvesting from vibrations of multiple frequencies. J micromechanics microengineering (2009) 19(3):035001. doi:10.1088/0960-1317/19/3/035001

CrossRef Full Text | Google Scholar

13. Pradeesh EL, Udhayakumar S, Sathishkumar C. Investigation on various beam geometries for piezoelectric energy harvester with two serially mounted piezoelectric materials. SN Appl Sci (2019) 1:1648–11. doi:10.1007/s42452-019-1709-4

CrossRef Full Text | Google Scholar

14. Alavi SE, Shirbani MM, Hassani AM. Analytical investigation of the effect of temperature difference between layers of unimorph piezoelectric harvesters. Iranian J Sci Technol Trans Mech Eng (2024) 48(1):293–306. doi:10.1007/s40997-023-00652-y

CrossRef Full Text | Google Scholar

15. Kachapi SHH, Kachabi SGH. Nonclassical and nonlinear stability analysis of viscous fluidic piezoelectric biomedical nanosensor. Spectr Mech Eng Oper Res (2025) 2(1):59–77. doi:10.31181/smeor21202530

CrossRef Full Text | Google Scholar

16. Shirbani MM, Alavi SE. Multi-objective optimization and performance analysis of bimorph magneto-electro-elastic energy harvesters. Facta Universitatis, Ser Mech Eng (2024). doi:10.22190/FUME231102003S

CrossRef Full Text | Google Scholar

17. Kang X, Wang X, Xia G. Ultra-low frequency vibration energy harvesting of piezoelectric vibration systems with an adjustable device. Alexandria Eng J (2024) 100:92–110. doi:10.1016/j.aej.2024.05.035

CrossRef Full Text | Google Scholar

18. Godfrey D, Nirmal D, Arivazhagan L, Kannan RR, Nelson PI, Rajesh S. A novel ZnPc nanorod derived piezoelectric nanogenerator for energy harvesting. Physica E: Low-dimensional Syst Nanostructures (2020) 118:113931. doi:10.1016/j.physe.2019.113931

CrossRef Full Text | Google Scholar

19. Elvin NG, Elvin AA, Spector M. A self-powered mechanical strain energy sensor. Smart Mater structures (2001) 10(2):293–9. doi:10.1088/0964-1726/10/2/314

CrossRef Full Text | Google Scholar

20. Choi WJ, Jeon Y, Jeong JH, Sood R, Kim SG. Energy harvesting MEMS device based on thin film piezoelectric cantilevers. J Electroceramics (2006) 17:543–8. doi:10.1007/s10832-006-6287-3

CrossRef Full Text | Google Scholar

21. Luo A, Tan Q, Xu W, Huang J, Gu S, Guo X. A comprehensive review of energy harvesting from kinetic energy at low frequency. Adv Mater Tech (2025) 10:2401731. doi:10.1002/admt.202401731

CrossRef Full Text | Google Scholar

22. Erturk A, Hoffmann J, Inman DJ. A piezomagnetoelastic structure for broadband vibration energy harvesting. Appl Phys Lett (2009) 94(25):254102. doi:10.1063/1.3159815

CrossRef Full Text | Google Scholar

23. Huang B, Sun M, Chen H, Wu Z. Stochastic static finite element model updating using the Bayesian method integrating homotopy surrogate model. Comput and Structures (2025) 315:107769. doi:10.1016/j.compstruc.2025.107769

CrossRef Full Text | Google Scholar

24. Cheng Y, Yan J, Zhang F, Li M, Zhou N, Shi C. Surrogate modeling of pantograph-catenary system interactions. Mech Syst Signal Process (2025) 224:112134. doi:10.1016/j.ymssp.2024.112134

CrossRef Full Text | Google Scholar

25. Qin S, Han S, Liao S, Zhou Y. Finite element model updating of a bridge using ambient vibration measurements with an improved adaptive kriging model. Eng Optimization (2024) 57:1778–99. doi:10.1080/0305215x.2024.2371841

CrossRef Full Text | Google Scholar

26. Kachapi SHH. Nonlinear vibration response of piezoelectric nanosensor: influences of surface/interface effects. Facta Universitatis, Ser Mech Eng (2023) 21(2):259–72. doi:10.22190/fume210612064k

CrossRef Full Text | Google Scholar

27. Ren M, Wang C, Moshrefi-Torbati M, Yurchenko D, Shu Y, Yang K. Optimization of a comb-like beam piezoelectric energy harvester using the parallel separated multi-input neural network surrogate model. Mech Syst Signal Process (2025) 224:111939. doi:10.1016/j.ymssp.2024.111939

CrossRef Full Text | Google Scholar

28. Mohammadi A, Nayyeri P, Zakerzadeh MR, AyatollahzadehShirazi F. Power optimization of a piezoelectric-based energy harvesting cantilever beam using surrogate model. Energy Equipment Syst (2020) 8(1):81–90. doi:10.22059/ees.2020.39012

CrossRef Full Text | Google Scholar

29. Moory Shirbani M, ehsan alavi S, Hassani AM. Analysis of thermal performance of bimorph piezoelectric energy harvesters. Res Square (2023). doi:10.21203/rs.3.rs-2864335/v1

CrossRef Full Text | Google Scholar

30. Madhvapathy SR, Arafa HM, Patel M, Winograd J, Kong J, Zhu J. Advanced thermal sensing techniques for characterizing the physical properties of skin. Appl Phys Rev (2022) 9(4):041307. doi:10.1063/5.0095157

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Cheng Y, Wang K, Xu H, Li T, Jin Q, Cui D. Recent developments in sensors for wearable device applications. Anal Bioanal Chem (2021) 413(24):6037–57. doi:10.1007/s00216-021-03602-2

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Williams CK, Rasmussen CE. Gaussian processes for machine learning. MIT Press (2006) 2 Cambridge, MA.

Google Scholar

33. Samadian D, Muhit IB, Dawood N. Application of data-driven surrogate models in structural engineering: a literature review. Arch Comput Methods Eng (2025) 32(2):735–84. doi:10.1007/s11831-024-10152-0

CrossRef Full Text | Google Scholar